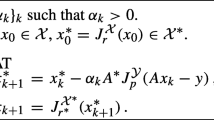A nested primal–dual iterated Tikhonov method for regularized convex optimization

Abstract

Proximal–gradient methods are widely employed tools in imaging that can be accelerated by adopting variable metrics and/or extrapolation steps. One crucial issue is the inexact computation of the proximal operator, often implemented through a nested primal–dual solver, which represents the main computational bottleneck whenever an increasing accuracy in the computation is required. In this paper, we propose a nested primal–dual method for the efficient solution of regularized convex optimization problems. Our proposed method approximates a variable metric proximal–gradient step with extrapolation by performing a prefixed number of primal–dual iterates, while adjusting the steplength parameter through an appropriate backtracking procedure. Choosing a prefixed number of inner iterations allows the algorithm to keep the computational cost per iteration low. We prove the convergence of the iterates sequence towards a solution of the problem, under a relaxed monotonicity assumption on the scaling matrices and a shrinking condition on the extrapolation parameters. Furthermore, we investigate the numerical performance of our proposed method by equipping it with a scaling matrix inspired by the Iterated Tikhonov method. The numerical results show that the combination of such scaling matrices and Nesterov-like extrapolation parameters yields an effective acceleration towards the solution of the problem.

1 Introduction

We consider the following problem

$$\begin{aligned} \underset{u\in \mathbb {R}^d}{{\text {argmin}}} \ f(u) + h(Wu), \end{aligned}$$

(1)

where $f:\mathbb {R}^d\rightarrow \mathbb {R}$ is convex and smooth, $h:\mathbb {R}^{d'}\rightarrow \mathbb {R}\cup \{\infty \}$ is convex and possibly nonsmooth, and $W\in \mathbb {R}^{d'\times d}$ is a linear operator. Problem (1) lies at the core of several inverse problems arising in imaging, such as image deblurring, denoising, inpainting, compressed sensing, super-resolution and others [1,2,3,4]. We may think of the term f as a discrepancy measure between the data and the imaging model, e.g. the least squares cost function, whereas we may interpret $h\circ W$ as a penalty term enforcing some regularization property on the problem, e.g. a vectorial norm composed with either the identity or the gradient operator.

First order methods are particularly useful to solve problem (1) with a mild-to-moderate accuracy while keeping the computational cost per iteration low, especially when the size d is large. Among these is the proximal–gradient method [5,6,7], which alternates a gradient step on f and a proximal evaluation on $h\circ W$ as follows

$$\begin{aligned} u_{n+1}&= {\text {prox}}_{\alpha h \circ W}(u_n-\alpha \nabla f(u_n))\nonumber \\&=\underset{u\in \mathbb {R}^d}{{\text {argmin}}} \ \frac{1}{2}\Vert u-(u_n-\alpha \nabla f(u_n))\Vert ^2+\alpha h(Wu), \quad \forall \ n\ge 0, \end{aligned}$$

(2)

where $\alpha >0$ is the steplength parameter along the descent direction $-\nabla f(u_n)$ and ${\text {prox}}_{\alpha h \circ W}$ is the proximal operator of the nonsmooth term $\alpha h\circ W$. The convergence of method (2) to a solution of (1) is ensured whenever f has a $L-$Lipschitz continuous gradient and $\alpha$ is smaller than 2/L, see for instance [6].

The scheme (2) has two practical drawbacks. On the one hand, it might converge slowly to the desired solution whenever the prefixed steplength $\alpha$ is too small, which typically happens when only a coarse (large) estimate of the Lipschitz constant L is available. A possible remedy to this issue consists in accelerating the scheme by either computing the proximal–gradient step with respect to a variable metric that encapsulates some second order information of the differentiable part [8,9,10,11,12], or inserting an extrapolation step that exploits the information relative to the previous iterates [13, 14]. On the other hand, the scheme (2) is based on the implicit assumption that ${\text {prox}}_{\alpha h \circ W}$ is computable in closed form, which excludes several regularization terms such as Total Variation, overlapping group Lasso or fused Lasso penalties [1, 15]. Alternative splitting approaches that circumvent the explicit evaluation of ${\text {prox}}_{\alpha h \circ W}$ include primal–dual methods based on the reformulation of (1) as a convex–concave saddle point problem [16,17,18], proximal–gradient methods with inexact proximal evaluations computed through a primal–dual inner solver [8, 19, 20], and the alternating direction method of multipliers (ADMM) and its variants based on the alternating minimization of the augmented Lagrangian [21,22,23].

In the following, we focus our attention on proximal–gradient methods where acceleration techniques based on variable metrics and extrapolation are combined and inexact proximal evaluations are allowed, namely

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{u}_n = u_n + \gamma _n(u_n-u_{n-1})\\ u_{n+1} \approx \text {prox}^{P_n}_{\alpha _n h \circ W}(\bar{u}_n - \alpha _n P_{n}^{-1}\nabla f(\bar{u}_n)), \end{array}\right. } \quad \forall \ n\ge 0, \end{aligned}$$

(3)

where $\alpha _n>0$ and $P_n\in \mathbb {R}^{d\times d}$ are, respectively, the steplength parameter and the symmetric positive definite scaling matrix, ${\text {prox}}_{\alpha _n h\circ W}^{P_n}$ is the proximal operator of $\alpha _n h\circ W$ with respect to the norm induced by $P_n$, and $\gamma _n\ge 0$ is the extrapolation parameter. The symbol “$\approx$” denotes an approximation of the proximal–gradient point, which is required whenever the proximal operator is not computable in closed form.

The parameters $\alpha _n$ and $P_n$ define the variable metric with respect to which the proximal–gradient point $u_{n+1}$ in (3) is computed. While $\alpha _n$ represents the inverse of a local Lipschitz constant of the gradient that is dynamically computed through a backtracking procedure [5], the matrix $P_n$ aims at identifying some second order information of the smooth part of the objective function. Practical choices for $P_n$ include the Hessian matrix or its regularized versions [24, 25], Hessian approximations based on Quasi-Newton strategies [11, 12, 26, 27], or diagonal matrices obtained by the split gradient strategy for nonnegatively constrained problems [28,29,30]. The extrapolation parameter $\gamma _n$ is usually computed according to the prefixed sequence formerly proposed for smooth problems by Nesterov [31] and then successfully adapted to nonsmooth problems by Beck and Teboulle [5], which guarantees an optimal $\mathcal {O}(1/n^2)$ convergence rate for the function values.

The approximation of the proximal operator in (3) is typically achieved by means of a nested iterative solver, which is applied, at each iteration, to the minimization problem associated to the computation of the proximal–gradient point. If the convex conjugate $h^*(v)=\sup _{u\in \mathbb {R}^{d'}}\langle v,u\rangle -h(u)$ has an easy-to-compute proximal operator, then the desired proximal approximation can be computed by means of a primal–dual routine that involves only the computation of $\nabla f(u_n)$, ${\text {prox}}_{h^*}$ and the matrix–vector products with $W,W^T,P_n^{-1}$ [20, 29, 32]. In this respect, we can distinguish between two different approaches in the literature. On the one hand, one could approximate the proximal–gradient point with increasing accuracy, which means that the number of inner iterations of the nested solver grows unbounded as the outer iterations proceed [11, 20, 26, 29, 33]. The main drawback of this approach is that the computational cost per iteration may increase in an unsustainable manner, leading to a computational bottleneck in a few iterations. On the other hand, one could compute the approximated proximal–gradient point by means of a prefixed number of inner iterations, while employing an appropriate starting condition for the inner solver; this is advantageous in order to keep the computational cost per iteration low and fixed. Some methods exploiting this latter approach are available in the literature; see e.g. [13], which considers an inexact version of the popular FISTA that corresponds to (3) with $P_n$ equal to the identity matrix, $\gamma _n$ selected according to Nesterov’s sequence, and $u_{n+1}$ computed through a prefixed number of primal–dual inner iterates with null initialization for the inner solver; [32], where the scheme (3) is presented without extrapolation nor variable metrics and is equipped with a prefixed number of primal–dual inner iterates, which are warm-started with the outcome of the previous outer iteration; [34], where the authors generalize the algorithm in [32] by adding an extrapolation step. Nonetheless, to the best of our knowledge, a method of the form (3) equipped with a prefixed number of inner iterations that include simultaneously variable steplengths, metrics, and extrapolation, has yet to be proposed in the literature.

Contribution. In this paper, we devise and analyse a nested primal–dual method based on the scheme (3) for solving problem (1). At every iteration, our proposed method first performs an extrapolation step on the previous iterates and then computes a prefixed number of primal–dual iterates to approximate a variable metric proximal–gradient step taken from the extrapolated iterate. Furthermore, the steplength parameter is adjusted by means of a backtracking procedure based on a local approximation of the Lipschitz constant of the gradient. From the theoretical viewpoint, we prove the convergence of the iterates sequence towards a minimum point of problem (1), under a relaxed monotonicity assumption on the scaling matrices and a shrinking condition on the extrapolation parameters. Numerically, we focus on the solution of Total-Variation regularized least–squares problems of the form

$$\begin{aligned} \underset{u\in \mathbb {R}^d}{{\text {argmin}}} \ \frac{1}{2}\Vert Au-b\Vert ^2 + TV(u), \end{aligned}$$

(4)

where $A\in \mathbb {R}^{d\times d}$, $b\in \mathbb {R}^d$, and TV(u) denotes the Total Variation function [35]. We investigate the performance of our proposed nested primal–dual algorithm for solving (4) by equipping it with the following scaling matrix

$$\begin{aligned} P_n = A^TA+\nu _nI_d, \quad \forall \ n\ge 0, \end{aligned}$$

(5)

where $I_d\in \mathbb {R}^{d\times d}$ is the identity matrix and $\{\nu _n\}_{n\in \mathbb {N}}$ is either a positive constant or a monotone sequence of positive real numbers. Such a matrix is inspired by works on regularizing preconditioning for image deblurring, drawing inspiration from the Iterated Tikhonov method [36,37,38]. We show that the combination of such preconditioning matrices and Nesterov-like extrapolation parameters yields an effective acceleration towards the solution of the problem.

Related work. Note that our proposed method generalizes the nested primal–dual method with extrapolation in [34], by allowing for the presence of variable metrics and steplengths. Other inexact variable metric proximal–gradient algorithms with extrapolation that can be cast in the scheme (3) have been proposed in [11, 29]. Our proposed algorithm differs from these two competitors in at least three aspects. (i) We compute the proximal–gradient point with a prefixed number of primal–dual iterates, whereas in [11, 29] the number of inner iterations increases unbounded as the outer iterations proceed. (ii) The extrapolation parameter in [11, 29] coincides precisely with Nesterov’s sequence, whereas in our approach the extrapolation parameter must satisfy an additional shrinking condition for theoretical purposes. (iii) In the numerical experiments, the scaling matrix $P_n$ in [11, 29] is computed by following either Quasi-Newton or split gradient strategies, whereas our proposed algorithm computes $P_n$ according to an Iterated Tikhonov approach. Regarding the latter aspect, we remark that regularized Hessian matrices (such as the one in (5)) have already been considered in the context of proximal–gradient algorithms, see e.g. [12, 25, 27]. However, to the best of our knowledge, the effect of Hessian regularization combined with extrapolation has yet to be extensively explored in the literature. In our numerical experiments, we investigate the combination of these two techniques within our proposed algorithm for solving the regularized problem (4) in the context of image deblurring.

Paper organization. The paper is organized as follows. In Sect. 2 we recall some basic notions of convex analysis. Section 3 is devoted to presenting our algorithm and analyzing its convergence under suitable hypotheses on the extrapolation parameter and the variable metric. Section 4 concerns the application of our algorithm to Total Variation based image deblurring. Conclusions and future work are discussed in Sect. 5.

2 Preliminaries

Throughout the paper, we denote with $\mathbb {R}^{d\times d}$ the space of $d\times d$ real-valued matrices and $I_d\in \mathbb {R}^{d\times d}$ the $d \times d$ identity matrix. The symbol $\langle \cdot ,\cdot \rangle$ denotes the standard inner product on $\mathbb {R}^d$. If $v\in \mathbb {R}^d$ and $W\in \mathbb {R}^{d'\times d}$, $\Vert v\Vert =\sqrt{\langle v, v\rangle }$ is the Euclidean norm of v, whereas $\Vert W\Vert$ is the spectral norm of W, i.e., the largest singular value of W. We denote with $\mathcal {S}(\mathbb {R}^{d})$ the set of all $d\times d$ symmetric matrices, and $\mathcal {S}_+(\mathbb {R}^d)$ the set of all $d\times d$ symmetric positive definite matrices. We recall the definition of the Loewner partial ordering relation, i.e.,

$$\begin{aligned} \forall P_1,P_2\in \mathcal {S}(\mathbb {R}^d) \quad P_1\preceq P_2 \quad \Leftrightarrow \quad \langle u,P_1u\rangle \le \langle u, P_2u\rangle , \ \forall \ u\in \mathbb {R}^d. \end{aligned}$$

Given $P\in \mathcal {S}_+(\mathbb {R}^d)$, the norm induced by P is defined as $\Vert u\Vert _{P}=\sqrt{\langle u,Pu\rangle }$ for all $u\in \mathbb {R}^d$. We denote with $\mathcal {D}_{\eta }\subseteq \mathcal {S}_+(\mathbb {R}^{d})$ the set of matrices whose eigenvalues belong to the interval $[\eta ,\infty [$ and $\mathcal {D}^{\mu }_{\eta }\subseteq \mathcal {S}_+(\mathbb {R}^{d})$ the set of matrices whose eigenvalues belong to the interval $[\eta ,\mu ]$. If $P\in \mathcal {D}_{\eta }^{\mu }$, then we have

$$\begin{aligned} \eta \Vert u\Vert ^2\le \Vert u\Vert _{P}^2\le \mu \Vert u\Vert ^2, \quad \forall \ u\in \mathbb {R}^d, \end{aligned}$$

(6)

and likewise

$$\begin{aligned} \mu ^{-1}\Vert u\Vert ^2\le \Vert u\Vert _{P^{-1}}^2\le \eta ^{-1}\Vert u\Vert ^2, \quad \forall \ u\in \mathbb {R}^d. \end{aligned}$$

(7)

Finally, we recall that the relative interior of $\Omega \subseteq \mathbb {R}^d$ is the set ${\text {relint}}(\Omega )=\{u\in \Omega : \exists \ \epsilon >0 \ \text {s.t.} \ B(u,\epsilon )\cap {\text {aff}}(\Omega )\subseteq \Omega \}$, where $B(u,\epsilon )$ is the ball of center u and radius $\epsilon$, and ${\text {aff}}(\Omega )$ is the affine hull of $\Omega$.

2.1 Basic definitions and results

Definition 1

A function $f:\mathbb {R}^d\rightarrow \mathbb {R}$ is said to have a $L-$Lipschitz continuous gradient if the following property holds

$$\begin{aligned} \Vert \nabla f(\tilde{u})-\nabla f(\bar{u})\Vert \le L\Vert \tilde{u}-\bar{u}\Vert , \quad \forall \ \tilde{u},\bar{u}\in \mathbb {R}^d. \end{aligned}$$

For our purposes, it is useful to recall the following variant of the well-known Descent Lemma, where the standard Euclidean norm is replaced by the norm induced by a symmetric positive definite matrix.

Lemma 1

[8, Lemma 6] Let $f: \mathbb {R}^d\rightarrow \bar{\mathbb {R}}$ be a continuously differentiable function with $L-$Lipschitz continuous gradient. If $P\in \mathcal {D}_{\eta }$ and $\bar{L}\ge L/\eta$, we have

$$\begin{aligned} f(\tilde{u})\le f(\bar{u})+\langle \nabla f(\bar{u}),\tilde{u}-\bar{u}\rangle +\frac{\bar{L}}{2}\Vert \tilde{u}-\bar{u}\Vert _P^2, \quad \forall \ \tilde{u},\bar{u}\in \mathbb {R}^d. \end{aligned}$$

(8)

Definition 2

[39, p. 104] Given a proper, convex, lower semicontinuous function $\varphi :\mathbb {R}^d\rightarrow \mathbb {R}\cup \{\infty \}$, the convex conjugate of $\varphi$ is the function

$$\begin{aligned} \varphi ^*:\mathbb {R}^d\rightarrow \mathbb {R}\cup \{\infty \}, \quad \varphi ^*(w)=\underset{u\in \mathbb {R}^d}{{\sup }}\ \langle w,u\rangle - \varphi (u), \ \forall \ w\in \mathbb {R}^d. \end{aligned}$$

The following well-known result holds for the biconjugate function $(\varphi ^*)^*$.

Lemma 2

[39, Theorem 12.2] Let $\varphi :\mathbb {R}^d\rightarrow \mathbb {R}\cup \{\infty \}$ be proper, convex, and lower semicontinuous. Then $\varphi ^*$ is convex and lower semicontinuous and $(\varphi ^*)^*=\varphi$, namely,

$$\begin{aligned} \varphi (u)=\underset{w\in \mathbb {R}^d}{{\sup }}\ \langle u,w\rangle - \varphi ^*(w), \ \forall \ u\in \mathbb {R}^d. \end{aligned}$$

Definition 3

[40, p. 278], [10, p. 877] The proximal operator of a proper, convex, lower semicontinuous function $\varphi$ with parameter $\gamma >0$ is the map $\textrm{prox}_{\gamma \varphi }:\mathbb {R}^d\rightarrow \mathbb {R}^d$ defined as

$$\begin{aligned} \textrm{prox}_{\gamma \varphi }(a) = \arg \min _{u\in \mathbb {R}^d}\varphi (u)+\frac{1}{2\gamma }\Vert u-a\Vert ^2, \quad \forall \ a\in \mathbb {R}^d. \end{aligned}$$

Similarly, we define the proximal operator with respect to the norm induced by $P\in \mathcal {D}_{\eta }$ as

$$\begin{aligned} \textrm{prox}^P_{\gamma \varphi }(a) = \arg \min _{u\in \mathbb {R}^d}\varphi (u)+\frac{1}{2\gamma }\Vert u-a\Vert _P^2, \quad \forall \ a\in \mathbb {R}^d. \end{aligned}$$

The following result holds for proximal points evaluated at perturbed points.

Lemma 3

[32, Lemma 3.3] Let $\varphi :\mathbb {R}^d\rightarrow \mathbb {R}\cup \{\infty \}$ be proper, convex, and lower semicontinuous, and $x,e\in \mathbb {R}^d$. Then the equality $y={\text {prox}}_{\varphi }(x+e)$ is equivalent to the following inequality:

$$\begin{aligned} \Vert y-z\Vert ^2\le \Vert x-z\Vert ^2-\Vert x-y\Vert ^2+2\langle y-z,e \rangle + 2\varphi (z)-2\varphi (y), \quad \forall \ z\in \mathbb {R}^d. \end{aligned}$$

Finally, the following three technical lemmas will be required in order to derive the convergence analysis of our proposed algorithm.

Lemma 4

[19, Lemma 1] Let $\{a_n\}_{n\in \mathbb {N}}$, $\{b_n\}_{n\in \mathbb {N}}$, $\{c_n\}_{n\in \mathbb {N}}$ be sequences of real nonnegative numbers, with $\{b_n\}_{n\in \mathbb {N}}$ being a monotone nondecreasing sequence, satisfying the following recursive property

$$\begin{aligned} a_n^2\le b_n+\sum _{k=1}^{n}c_ka_k, \quad \forall \ n\ge 1. \end{aligned}$$

(9)

Then the following inequality holds:

$$\begin{aligned} a_n\le \frac{1}{2}\sum _{k=1}^{n}c_k+\left( b_n+\left( \frac{1}{2}\sum _{k=1}^{n}c_k\right) ^2\right) ^{\frac{1}{2}}, \quad \forall \ n\ge 1. \end{aligned}$$

(10)

Lemma 5

[41] Let $\{a_n\}_{n\in \mathbb {N}}$, $\{b_n\}_{n\in \mathbb {N}}$ and $\{b_n\}_{n\in \mathbb {N}}$ be sequences of real nonnegative numbers such that $a_{n+1} \le (1+b_n)a_n + c_n$ and $\sum _{n=0}^\infty b_n < \infty$, $\sum _{n=0}^\infty c_n < \infty$. Then, the sequence $\{a_n\}_{n\in \mathbb {N}}$ converges.

Lemma 6

[42, Lemma 2.3] Let $\{P_n\}_{n\in \mathbb {N}}\subseteq \mathcal {D}_{\eta }^{\mu }$ be a sequence of scaling matrices satisfying Assumption 2(ii). Then, there exists $P\in \mathcal {D}_{\eta }$ such that $\lim _{n\rightarrow \infty }P_n = P$ pointwise.

2.2 Problem formulation

From now on, we consider the optimization problem (1) under the following assumptions.

Assumption 1

• (i) $f:\mathbb {R}^d\rightarrow \mathbb {R}$ is continuously differentiable with $L-$Lipschitz continuous gradient.

• (ii) $h:\mathbb {R}^{d'}\rightarrow \mathbb {R}\cup \{+\infty \}$ is proper, lower semicontinuous and convex.

• (iii) $W\in \mathbb {R}^{d'\times d}$ and there exists $u_0\in \mathbb {R}^d$ such that $Wu_0\in {\text {relint}}({\text {dom}}(h))$.

• (iv) Problem (1) admits at least one solution $\hat{u}\in \mathbb {R}^d$.

We remark that the assumption on W is needed to guarantee that the subdifferential rule $\partial (h \circ W)(u)=W^T\partial h(Wu)$ holds, so that we can interpret the minimum points of (1) as solutions of appropriate variational equations, as stated below.

Lemma 7

[32, Lemma 3.1] Under Assumption 1, a point $\hat{u}\in \mathbb {R}^d$ is a solution of problem (1) if and only if the following conditions hold

$$\begin{aligned} {\left\{ \begin{array}{ll} \nabla f(\hat{u})+W^T\hat{v}=0\\ \hat{v}={\text {prox}}_{\beta \alpha ^{-1}h^*}(\hat{v}+\beta \alpha ^{-1}W\hat{u}), \end{array}\right. }\quad \forall \ \alpha ,\beta >0. \end{aligned}$$

(11)

Due to Lemma 2, we can equivalently reformulate the convex problem (1) as the following convex-concave saddle-point problem

$$\begin{aligned} \min _{u\in \mathbb {R}^d}\max _{v\in \mathbb {R}^{d'}} \ \mathcal {L}(u,v)\equiv f(u)+\langle Wu,v\rangle -h^*(v), \end{aligned}$$

(12)

where $\mathcal {L}(u,v)$ denotes the primal–dual function. A solution of (12) is any point $(\hat{u},\hat{v})\in \mathbb {R}^d\times \mathbb {R}^{d'}$ such that

$$\begin{aligned} \mathcal {L}(\hat{u},v)\le \mathcal {L}(\hat{u},\hat{v})\le \mathcal {L}(u,\hat{v}), \quad \forall \ u\in \mathbb {R}^d, \ \forall \ v\in \mathbb {R}^{d'}. \end{aligned}$$

(13)

2.3 Inexact proximal evaluations via primal–dual iterates

In this section, we show that the proximal operator with a metric defined by a symmetric positive definite matrix P can be approximated by an appropriate sequence of primal–dual iterates. The following result generalizes the one derived in [34, Theorem 1] by taking into account the presence of the scaling matrix.

Lemma 8

Suppose that $h:\mathbb {R}^{d'}\rightarrow \mathbb {R}\cup \{\infty \}$ and $W\in \mathbb {R}^{d'\times d}$ satisfy Assumption 1(ii–iii). Let $P\in \mathbb {R}^{d\times d}$ be a symmetric positive definite matrix and $a\in \mathbb {R}^d$. Choose $\alpha >0$, $0<\beta <2/\Vert WP^{-1}W^T\Vert$, $v^0\in \mathbb {R}^{d'}$, define the sequence

$$\begin{aligned} v^{k+1} = {\text {prox}}_{\beta \alpha ^{-1}h^*}(v^k+\beta \alpha ^{-1}W(a-\alpha P^{-1}W^Tv^k)), \quad \forall \ k\ge 0, \end{aligned}$$

(14)

and its limit $\hat{v}= \lim _{k\rightarrow \infty }v^k$. Then we have

$$\begin{aligned} {\text {prox}}_{\alpha h\circ W}^P(a) = a - \alpha P^{-1} W^T\hat{v}. \end{aligned}$$

(15)

Proof

Let $\hat{a} = \textrm{prox}^P_{\alpha h \circ W}(a)$, which is equivalent to writing

$$\begin{aligned} \hat{a}=\underset{u\in \mathbb {R}^d}{{\text {argmin}}}\ \frac{1}{2\alpha }\Vert u-a\Vert _P^2+ h(Wu). \end{aligned}$$

By applying Lemma 7 to the above minimization problem, we obtain the following system of variational equations

$$\begin{aligned} \hat{a}={\text {prox}}^P_{\alpha h\circ W}(a)&\iff {\left\{ \begin{array}{ll} P(\hat{a}-a)+\alpha W^T\hat{v} = 0\\ \hat{v}={\text {prox}}_{\beta \alpha ^{-1} h^*}\left( \hat{v} +\beta \alpha ^{-1} W\hat{a}\right) \end{array}\right. }\nonumber \\&\iff {\left\{ \begin{array}{ll} \hat{a}=a-\alpha P^{-1}W^T\hat{v}\\ \hat{v}={\text {prox}}_{\beta \alpha ^{-1} h^*}\left( \hat{v} +\beta \alpha ^{-1} W\hat{a}\right) . \end{array}\right. } \end{aligned}$$

(16)

Consider the sequences $\{a^k\}_{k\in \mathbb {N}}$ and $\{v^k\}_{k\in \mathbb {N}}$ (with arbitrary $v^0$) given by

$$\begin{aligned} {\left\{ \begin{array}{ll} a^k=a-\alpha P^{-1}W^Tv^k\\ v^{k+1}={\text {prox}}_{\beta \alpha ^{-1} h^*}\left( v^k +\beta \alpha ^{-1} Wa^k\right) \end{array}\right. }, \quad k =0,1,\ldots \end{aligned}$$

(17)

or equivalently

$$\begin{aligned} v^{k+1}={\text {prox}}_{\beta \alpha ^{-1} h^*}\left( v^k +\beta \alpha ^{-1} W(a-\alpha P^{-1}W^Tv^k)\right) , \quad k=0,1,\ldots . \end{aligned}$$

In virtue of (16), the sequence $\{v^{k}\}_{k\in \mathbb {N}}$ can be interpreted as a fixed-point iteration applied to the operator

$$\begin{aligned} T(v) = {\text {prox}}_{\beta \alpha ^{-1}h^*}(v+\beta \alpha ^{-1}W(a-\alpha P^{-1}W^Tv)). \end{aligned}$$

(18)

By Banach fixed-point theorem, the sequence $\{v^k\}_{k\in \mathbb {N}}$ converges to a fixed-point of T provided that T is a contraction. Since the operator ${\text {prox}}_{\beta \alpha ^{-1} h^*}$ is non-expansive, we have

$$\begin{aligned} \Vert T(v)-T(u)\Vert&\le \Vert v-u+\beta \alpha ^{-1}(\alpha W P^{-1} W^T u - \alpha WP^{-1} W^T v)\Vert \\&= \Vert (I-\beta W P^{-1} W^T)(v-u)\Vert \\&\le \Vert I-\beta W P^{-1} W^T\Vert \Vert v-u\Vert , \end{aligned}$$

so T is a contraction as long as $\Vert I-\beta W P^{-1} W^T\Vert <1$. Since P is symmetric, it holds $\Vert I-\beta W P^{-1} W^T\Vert = \rho (I-\beta W P^{-1} W^T)$, where $\rho (\cdot )$ denotes the spectral radius of a matrix, and hence T is a contraction if and only if $0<\beta < 2/\Vert W P^{-1} W^T\Vert$. Therefore, $\{v^k\}_{k\in \mathbb {N}}$ converges to a fixed-point $\hat{v}$ of T, and by continuity, the sequence $a^k$ also converges to the point $\hat{a} = a - \alpha P^{-1}W^T\hat{v}$. Thus (16) yields the thesis. $\square$

We remark that, although Lemma 8 will not be employed in the convergence analysis, it will enable us to interpret our proposed method as a particular variable metric proximal–gradient method with extrapolation of the form (3), where the proximal operator is computed through the primal–dual procedure (14). We refer the reader to the upcoming Sect. 3.1 for more details on this issue.

3 A nested primal–dual variable metric method

In this section, we propose and analyse our nested primal–dual variable metric method for solving problem (1). The resulting scheme can be considered as a variable metric proximal–gradient algorithm with extrapolation, where the proximal operator is approximated by means of a prefixed number of primal–dual steps. Note that our proposed method generalizes the one in [34], by including a backtracking procedure for the steplength and the selection of a variable scaling matrix.

Algorithm 1

Nested Primal–Dual Variable Metric method

3.1 The proposed method

We report our proposed method in Algorithm 1. It requires the choice of the prefixed number of primal–dual iterates $k_{\max }\in \mathbb {N}$, the initial guesses $u_0=u_{-1}\in \mathbb {R}^d$, $v_{-1}^{k_{\max }}\in \mathbb {R}^{d'}$, the parameters $\epsilon ,\delta \in (0,1)$, an approximation of the Lipschitz constant $L_{-1}>0$ and the metric parameters $\eta >0$, $\alpha _{-1}=\epsilon /L_{-1}$, $P_{-1}\in \mathcal {D}_{{\eta }}$.

In Step 1, we choose the extrapolation parameter $\gamma _n\ge 0$ and compute the extrapolated iterate $\bar{u}_n$ according to (19), whereas Step 2 is devoted to the choice of the scaling matrix $P_n\in \mathcal {D}_{{\eta }}$.

At Step 3, we initialize the approximation of the Lipschitz constant $L_n$ as the value computed at the previous iteration, the primal steplength as $\alpha _n=\epsilon /L_n$, the dual steplength as $\beta _n=\epsilon /{\Vert P_n^{-1}\Vert }\Vert W\Vert ^2$, and the initial dual iterate as $v_n^0=v_{n-1}^{k_{\max }}$, i.e., the inner primal–dual loop is warm-started with the outcome of the loop at the previous iteration. Such a warm-start strategy is borrowed from the works [32, 34] and is crucial to guarantee the convergence of the algorithm.

Steps 4–7 define the backtracking procedure that is needed for adaptively computing the approximation of the Lipschitz constant $L_n$, the corresponding steplength $\alpha _n$ and the next iterate $u_{n+1}$. First, we compute $k_{\max }$ primal–dual iterates according to the procedure discussed in Sect. 2.3 (Step 4). More precisely, equations (20)-(21) represent $k_{\max }$ iterations of the primal–dual method (14) with $a= \bar{u}_n-\alpha _n P_n^{-1}\nabla f(\bar{u}_n)$, $\alpha =\alpha _n$, $P=P_n$ and $\beta = \beta _n$; then, in virtue of Lemma 8, the sequence $\{u_n^k\}_{k=0}^{k_{\max }-1}$ can be considered as approximating the proximal–gradient point ${\text {prox}}_{\alpha _n h\circ W}^{P_n}(\bar{u}_n-\alpha _n P_{n}^{-1}\nabla f(\bar{u}_n))$. Next, we compute an additional primal iterate $u_n^{k_{\max }}$ (Step 5) and average the primal iterates $\{u_n^{k}\}_{k=1}^{k_{\max }}$ over the number of inner iterations (Step 6). Finally, we check a backtracking condition based on Lemma 1 (Step 7); if the condition is satisfied, then we accept the average of the primal iterates as the next iterate (Step 8), otherwise we increase $L_n$ by a factor $1/\delta$ and repeat the backtracking procedure.

Remark 1

Note that the backtracking procedure at Steps 4–7 terminates in a finite number of steps, as the backtracking condition at Step 7 is accepted whenever $L_n\ge L/\eta$ (see Lemma 1). Furthermore, the sequence $\{\alpha _n\}_{n\in \mathbb {N}}$ is nonincreasing thanks to Step 3 and the backtracking procedure at Steps 4–7. Note that $\{\alpha _n\}_{n\in \mathbb {N}}$ is also bounded away from zero: indeed, either $L_n< L/\eta$ and hence $\alpha _n>\epsilon \eta /L$ for all $n\ge 0$, or otherwise let $n^*\ge 0$ be the first iteration such that $L_{n^*}\ge L/\eta$; in the latter case, if $n^*=0$, then Lemma 1 and Steps 7–8 of Algorithm 1 imply $\alpha _n = \alpha _0$ for all $n\ge 0$, otherwise it must be $\delta L_{n^*} < L/\eta$ and thus $\alpha _n\ge \alpha _{n*}> (\epsilon \delta \eta )/L$ for all $n\ge 0$. In conclusion, the following inequalities hold:

$$\begin{aligned} 0<\min \left\{ \alpha _0,\frac{\epsilon \delta \eta }{L}\right\} \le \alpha _n\le \alpha _{n-1}\le \alpha _{-1}, \quad \forall \ n\ge 0. \end{aligned}$$

(23)

3.2 Convergence analysis

In this section, we carry out the convergence analysis for Algorithm 1. Under appropriate conditions on the extrapolation parameter and the scaling matrix, we show that the iterates sequence $\{u_n\}_{n\in \mathbb {N}}$ converge to a solution of problem (1).

For our purposes, we define the sequence of matrices $\{D_n\}_{n\in \mathbb {N}}\subseteq \mathbb {R}^{d'\times d'}$ as

$$\begin{aligned} D_n = I_{d'}- \beta _n W P_{n}^{-1}W^T, \quad \forall \ n\ge 0. \end{aligned}$$

(24)

Note that, by construction, the matrix $D_n$ are real and symmetric since $P_n\in \mathcal {D}_{\eta }$. Moreover, we can prove the following.

Lemma 9

Let $\{D_n\}_{n\in \mathbb {N}}$ be the sequence of matrices defined as in (24). Then, for all $n\ge 0$, $D_n$ is a real symmetric positive definite matrix and its eigenvalues are bounded away from zero by a constant independent of n.

Proof

We just need to prove that $D_n$ is positive definite and, since it is symmetric, it is sufficient to show that $\lambda _{\textrm{min}}(D_n)>0$. In this respect, we have that

$$\begin{aligned} \lambda _{\textrm{min}}(D_n)&=1-\beta _n\lambda _{\textrm{max}}(WP_{n}^{-1}W^T)\nonumber \\&= 1-\beta _n\Vert WP_{n}^{-1}W^T\Vert \nonumber \\&\ge 1-\beta _n{\Vert P_{n}^{-1}\Vert \Vert W\Vert ^2}\nonumber \\&{=} 1-\epsilon >0, \quad \forall \ n\ge 0, \end{aligned}$$

(25)

where the first inequality follows from the submultiplicative property of the spectral norm and (7), and the last equality is due to the choice of $\beta _n$ in Algorithm 1. The final result holds because $\epsilon \in (0,1)$. $\square$

Based on the previous result, we can consider the norm induced by $D_n$, i.e.,

$$\begin{aligned} \Vert v\Vert _{D_n}^2&= \Vert (I-\beta _nWP_n^{-1}W^T)^{\frac{1}{2}}v\Vert ^2\nonumber \\ &= v^T(I-\beta _nWP_n^{-1}W^T)v \nonumber \\&=\Vert v\Vert ^2 - \beta _n \Vert P_{n}^{-\frac{1}{2}}W^Tv\Vert ^2, \quad \forall \ v\in \mathbb {R}^{d'}. \end{aligned}$$

(26)

The following lemma contains some crucial descent inequalities involving the primal–dual function $\mathcal {L}$ and the iterates generated by Algorithm 1. The proof of this result is similar to the one of [34, Lemma 7], although some modifications are needed in order to address the presence of the variable metric and the backtracking procedure on the steplength $\alpha _n$, which were absent in [34]. Unlike in [34], the inequalities are not given for a generic primal–dual sequence, rather they specifically hold at the iterates obtained by averaging the primal and dual inner iterates of Algorithm 1.

Lemma 10

Suppose that Assumption 1 holds. Let $\{(u_n,v_n^0)\}_{n\in \mathbb {N}}$ be the primal-dual sequence generated by Algorithm 1, and let $(\hat{u},\hat{v})\in \mathbb {R}^d\times \mathbb {R}^{d'}$ be a solution of the primal-dual problem (12).

• (i) Define the sequence of dual iterates $\{\tilde{v}_n\}_{n\in \mathbb {N}}$ as

  $$\begin{aligned} \tilde{v}_{n}=\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}v_n^{k+1}, \quad \forall \ n\ge 0. \end{aligned}$$

  (27)

  Then, for all $n\ge 0$ and for all $u'\in \mathbb {R}^d$, we have

  $$\begin{aligned}&\mathcal {L}(u_{n+1},\tilde{v}_n)+\frac{1}{2\alpha _n}\Vert u_{n+1}-u'\Vert ^2_{P_n}\nonumber \\&\le \mathcal {L}(u',\tilde{v}_n)+\frac{1}{2\alpha _n}\Vert \bar{u}_n-u'\Vert ^2_{P_n}-\frac{1}{2}\left( \frac{1}{\alpha _n}-L_n\right) \Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}. \end{aligned}$$

  (28)

• (ii) For all $n\ge 0$ and for all $v'\in \mathbb {R}^{d'}$, we have

  $$\begin{aligned}&\mathcal {L}(u_{n+1},v')+\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_{n+1}^{0}-v'\Vert ^2_{D_n}\nonumber \\&\le \mathcal {L}(u_{n+1},\tilde{v}_n)+\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_{n}^{0}-v'\Vert ^2_{D_n}-\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2. \end{aligned}$$

  (29)

• (iii) For all $n\ge 0$, for all $u'\in \mathbb {R}^d$ and $v'\in \mathbb {R}^{d'}$, we have

  $$\begin{aligned}&\mathcal {L}(u_{n+1},v')+\frac{1}{2\alpha _n}\Vert u_{n+1}-u'\Vert ^2_{P_n}+\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_{n+1}^{0}-v'\Vert ^2_{D_n}\nonumber \\&\le \mathcal {L}(u',\tilde{v}_n)+ \frac{1}{2\alpha _n}\Vert \bar{u}_n-u'\Vert ^2_{P_n}+\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_{n}^{0}-v'\Vert ^2_{D_n}\nonumber \\&\quad -\frac{1}{2}\left( \frac{1}{\alpha _n}-L_n\right) \Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}-\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2. \end{aligned}$$

  (30)

Proof

See Appendix A. $\square$

We now discuss the assumptions needed on the inertial parameters $\{\gamma _n\}_{n\in \mathbb {N}}$ and the scaling matrices $\{P_n\}_{n\in \mathbb {N}}$ in order to ensure the convergence of Algorithm 1.

Assumption 2

• (i) The sequence of inertial parameters $\{\gamma _n\}_{n\in \mathbb {N}}$ of Algorithm 1 complies with the following condition

  $$\begin{aligned} \sum _{n=0}^{\infty }\gamma _n\Vert u_n-u_{n-1}\Vert <\infty . \end{aligned}$$

  (31)

• (ii) The sequence of scaling matrices $\{P_n\}_{n\in \mathbb {N}}$ of Algorithm 1 is chosen so that

  $$\begin{aligned} P_{n}\preceq (1+\zeta _{n-1})P_{n-1}, \ \forall \ n\ge 0, \quad \text {where }\zeta _{n-1}\ge 0, \ \sum _{n=0}^\infty \zeta _{n-1}<\infty . \end{aligned}$$

  (32)

Remark 2

Condition (31) has been previously employed in [34] for proving the convergence of a special instance of Algorithm 1 devoid of variable metrics and backtracking procedures. It can be easily implemented in practice, as it depends only on the past iterates $u_n,u_{n-1}$. As observed in [34], (31) has the practical effect of “shrinking” the inertial parameter when the iteration number n is large.

In a similar fashion, condition (32) is forcing the matrices $\{P_n\}_{n\in \mathbb {N}}$ to converge to a symmetric positive definite matrix at a sufficiently fast rate controlled by the parameters sequence $\{\zeta _n\}_{n\in \mathbb {N}}$. Such a condition can be easily enforced if one selects the scaling matrix as a diagonal matrix, computed according to a specific update rule such as the Majorization–Minimization strategy or the Split-Gradient decomposition [8, 9, 28], and then constrains its elements to an interval of diminishing size. In section 4.2 we show that the preconditioning matrices (5) naturally comply with this assumption.

Remark 3

If condition (32) is assumed to be satisfied, then [42, Lemma 2.1] and (7) yield the following matrix relations

$$\begin{aligned} ((1+\zeta _{n-1})P_{n-1})^{-1}\preceq P_{n}^{-1}{\preceq \frac{1}{\eta }I_d}. \end{aligned}$$

(33)

Since the spectral norm is monotone [43, Ex. 2.2-10], the above relation implies

$$\begin{aligned} \eta \le \frac{1}{\Vert P_{n}^{-1}\Vert }\le \frac{1+\zeta _{n-1}}{\Vert P_{n-1}^{-1}\Vert }. \end{aligned}$$

Consequently, the parameters $\{\beta _n\}_{n\in \mathbb {N}}$ satisfy the following inequalities

$$\begin{aligned} 0<\frac{\epsilon \eta }{\Vert W\Vert ^2}\le \beta _n\le (1+\zeta _{n-1})\beta _{n-1}, \quad \forall \ n\ge 0. \end{aligned}$$

(34)

Remark 4

Regarding the sequence of matrices $\{D_n\}_{n\in \mathbb {N}}$, we derive the following inequalities

$$\begin{aligned} \Vert v\Vert ^2_{D_n}&=\Vert v\Vert ^2-\beta _n \Vert W^Tv\Vert _{P_n^{-1}}^2\\&\le \Vert v\Vert ^2-\frac{\beta _n}{1+\zeta _{n-1}} \Vert W^Tv\Vert _{P_{n-1}^{-1}}^2\\&= \frac{(1+\zeta _{n-1})\Vert v\Vert ^2-\beta _n\Vert W^Tv\Vert ^2_{P_{n-1}^{-1}}}{1+\zeta _{n-1}}\\&= \frac{\Vert v\Vert ^2_{D_{n-1}}+\zeta _{n-1}\Vert v\Vert ^2+(\beta _{n-1}-\beta _{n})\Vert W^Tv\Vert ^2_{P_{n-1}^{-1}}}{1+\zeta _{n-1}}\\&\le \Vert v\Vert ^2_{D_{n-1}}+\zeta _{n-1}\Vert v\Vert ^2+\frac{(\beta _{n-1}-\beta _n)\Vert W\Vert ^2}{\eta }\Vert v\Vert ^2\\&\le \left( 1+\frac{\zeta _{n-1}}{1-\epsilon }+\frac{(\beta _{n-1}-\beta _n)\Vert W\Vert ^2}{\eta (1-\epsilon )}\right) \Vert v\Vert _{D_{n-1}}^2, \end{aligned}$$

where the first inequality follows from (33) and the last one is due to the combination of (6) and (25). In conclusion, there exists a sequence $\{\tilde{\zeta }_{n-1}\}_{n\in \mathbb {N}}$ such that

$$\begin{aligned} D_n\preceq \left( 1+\tilde{\zeta }_{n-1}\right) D_{n-1}, \ \forall \ n\ge 0, \quad \text {where } \tilde{\zeta }_{n-1}\ge \zeta _{n-1}\ge 0, \ \sum _{n=0}^\infty \tilde{\zeta }_{n-1}<\infty .\nonumber \\ \end{aligned}$$

(35)

The main convergence result for Algorithm 1 is stated below. The line of proof employed is analogous to the one in [34, Theorem 2], even though it must be adapted to the presence of variable metrics and variable steplengths.

Theorem 1

Suppose that Assumption 1 holds and let $(\hat{u},\hat{v})\in \mathbb {R}^d\times \mathbb {R}^{d'}$ be a solution of the primal-dual problem (12). Let $\{(u_n,v_n^0)\}_{n\in \mathbb {N}}$ be the primal-dual sequence generated by Algorithm 1. Suppose that the inertial parameters $\{\gamma _n\}_{n\in \mathbb {N}}$ and scaling matrices $\{P_n\}_{n\in \mathbb {N}}$ of Algorithm 1 comply with Assumption 2. Then the following statements hold true.

• (i) The sequence $\{(u_n,v_n^0)\}_{n\in \mathbb {N}}$ is bounded.

• (ii) Given a saddle point $(\hat{u},\hat{v})$ solution of (12), the sequence $\{\beta _{n-1} k_{\max }\Vert \hat{u}-u_n\Vert _{P_{n-1}}^2+\alpha _{n-1}^2\Vert \hat{v}-v_n^0\Vert ^2_{D_{n-1}}\}_{n\in \mathbb {N}}$ converges.

• (iii) The sequence $\{(u_n,v_n^0)\}_{n\in \mathbb {N}}$ converges to a solution of (12).

Before going into the technical details of the proof, let us briefly summarize how we intend to prove each item of Theorem 1.

• (i) The proof of item (i) relies on an upper bound on the quantity $\Vert u_{n+1}-\hat{u}\Vert _{P_n}$, which is obtained by employing Lemma 4 in combination with Assumption 2.

• (ii) Item (ii) follows by applying Lemma 5 to the sequence $\{\beta _{n-1} k_{\max }\Vert \hat{u}-u_n\Vert _{P_{n-1}}^2+\alpha _{n-1}^2\Vert \hat{v}-v_n^0\Vert ^2_{D_{n-1}}\}_{n\in \mathbb {N}}$, which is possible thanks to item (i).

• (iii) For item (iii), we first show that any limit point $(u^\dagger ,v^\dagger )\in \mathbb {R}^{d}\times \mathbb {R}^{d'}$ of the sequence $\{(u^n,v_n^0)\}_{n\in \mathbb {N}}$ is a solution to problem (12); then, the thesis follows by applying item (ii) with the choice $(\hat{u},\hat{v})=(u^\dagger ,v^\dagger )$.

Proof

(i) Consider inequality (30) with $u'=\hat{u}$, $v'=\hat{v}$ and the term $-\frac{1}{2}\left( \frac{1}{\alpha _n}-L_n\right) \Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}-\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2$ discarded, which amounts to writing

$$\begin{aligned} \mathcal {L}(u_{n+1},\hat{v})&+\frac{1}{2\alpha _n}\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n}+\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_{n+1}^{0}-\hat{v}\Vert ^2_{D_n}\\&\le \mathcal {L}(\hat{u},\tilde{v}_n)+ \frac{1}{2\alpha _n}\Vert \bar{u}_n-\hat{u}\Vert ^2_{P_n}+\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_{n}^{0}-\hat{v}\Vert ^2_{D_n}. \end{aligned}$$

By observing that $\mathcal {L}(u_{n+1},\hat{v})\ge \mathcal {L}(\hat{u},\tilde{v}_n)$, due to the fact that $(\hat{u},\hat{v})$ is a solution of the primal-dual problem (12), and multiplying the above inequality by $\alpha _n\beta _n$, we deduce the inequality

$$\begin{aligned} \frac{\beta _n}{2}\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n}+\frac{\alpha _n^2}{2 k_{\max }}\Vert v_{n+1}^{0}-\hat{v}\Vert ^2_{D_n} \le \frac{\beta _n}{2}\Vert \bar{u}_n-\hat{u}\Vert ^2_{P_n}+\frac{\alpha _n^2}{2 k_{\max }}\Vert v_{n}^{0}-\hat{v}\Vert ^2_{D_n}.\nonumber \\ \end{aligned}$$

(36)

By recalling that the sequences $\{\alpha _n\}_{n\in \mathbb {N}}$ and $\{\beta _n\}_{n\in \mathbb {N}}$ satisfy (23) and (34), respectively, and applying conditions (32) and (35) to inequality (36), we get

$$\begin{aligned}&\frac{\beta _n}{2}\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n}+\frac{\alpha _n^2}{2 k_{\max }}\Vert v_{n+1}^{0}-\hat{v}\Vert ^2_{D_n} \nonumber \\&\le (1+\tilde{\zeta }_{n-1}){(1+\zeta _{n-1})}\left( \frac{\beta _{n-1}}{2}\Vert \bar{u}_n-\hat{u}\Vert ^2_{P_{n-1}}+\frac{\alpha _{n-1}^2}{2 k_{\max }}\Vert v_{n}^{0}-\hat{v}\Vert ^2_{D_{n-1}}\right) \nonumber \\&{= (1+\chi _{n-1})\left( \frac{\beta _{n-1}}{2}\Vert \bar{u}_n-\hat{u}\Vert ^2_{P_{n-1}}+\frac{\alpha _{n-1}^2}{2 k_{\max }}\Vert v_{n}^{0}-\hat{v}\Vert ^2_{D_{n-1}}\right) }, \end{aligned}$$

(37)

where $\chi _{n-1}=\zeta _{n-1}+\tilde{\zeta }_{n-1}+\zeta _{n-1}\tilde{\zeta }_{n-1}$ for all $n\ge 0$ and $\{\chi _n\}_{n\in \mathbb {N}}$ is still a nonnegative summable sequence. Since $\bar{u}_n = u_n+\gamma _n(u_n-u_{n-1})$, an application of the Cauchy-Schwarz yields

$$\begin{aligned}&\frac{\beta _{n}}{2}\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n}+\frac{\alpha _n^2}{2 k_{\max }}\Vert v_{n+1}^{0}-\hat{v}\Vert ^2_{D_n} \nonumber \\&\le (1+{\chi _{n-1}})\left( \frac{\beta _{n-1}}{2}\Vert u_n-\hat{u}\Vert ^2_{P_{n-1}}+\frac{\alpha _{n-1}^2}{2 k_{\max }}\Vert v_{n}^{0}-\hat{v}\Vert ^2_{D_{n-1}}\right) \nonumber \\&+\beta _{n-1}(1+{\chi _{n-1}})\left( \frac{\gamma _n^2}{2}\Vert u_n-u_{n-1}\Vert ^2_{P_{n-1}}+\gamma _n\langle u_n-\hat{u},P_{n-1}(u_n-u_{n-1})\rangle \right) \nonumber \\&\le (1+{\chi _{n-1}})\left( \frac{\beta _{n-1}}{2}\Vert u_n-\hat{u}\Vert ^2_{P_{n-1}}+\frac{\alpha _{n-1}^2}{2 k_{\max }}\Vert v_{n}^{0}-\hat{v}\Vert ^2_{D_{n-1}}\right) \nonumber \\&+\beta _{n-1}(1+{\chi _{n-1}})\left( \frac{\gamma _n^2}{2}\Vert u_n-u_{n-1}\Vert ^2_{P_{n-1}}+\gamma _n\Vert u_n-\hat{u}\Vert _{P_{n-1}}\Vert u_n-u_{n-1}\Vert _{P_{n-1}}\right) . \end{aligned}$$

(38)

By applying recursively inequality (38), we get

$$\begin{aligned}&\frac{\beta _n}{2}\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n}+\frac{\alpha _n^2}{2 k_{\max }}\Vert v_{n+1}^{0}-\hat{v}\Vert ^2_{D_n} \\&\le \left( \prod _{k=0}^{n}(1+{\chi _{k-1}})\right) \left( \frac{\beta _{-1}}{2}\Vert u_{0}-\hat{u}\Vert ^2_{P_{-1}}+\frac{\alpha _{-1}^2}{2 k_{\max }}\Vert v_{0}^0-\hat{v}\Vert ^2_{D_{-1}}\right) \\&+\sum _{k=0}^{n}\beta _{k-1}\left( \prod _{i=k}^{n}(1+{\chi _{i-1}})\right) \left( \frac{\gamma _{k}^2}{2}\Vert u_k-u_{k-1}\Vert ^2_{P_{k-1}}+\gamma _k\Vert u_k-\hat{u}\Vert _{P_{k-1}}\Vert u_k-u_{k-1}\Vert _{P_{k-1}}\right) . \end{aligned}$$

Now, if we consider the sequence

$$\begin{aligned} \Lambda _n = \prod _{k=0}^{n}(1+{\chi _{k-1}}), \quad n \ge 0, \end{aligned}$$

we note that $\Lambda _n=(1+{\chi _{n-1}})\Lambda _{n-1}$, which implies that $\{\Lambda _n\}_{n\in \mathbb {N}}$ is an increasing and convergent sequence, see Lemma 5. By setting $\Lambda =\lim _{n\rightarrow \infty }\Lambda _n$, it follows that $\Lambda _n\le \Lambda$ for all $n\ge 0$, $\prod _{i=k}^{n}(1+{\chi _{i-1}})\le \Lambda$ for $0\le k\le n$, and the previous inequality yields

$$\begin{aligned}&\frac{\beta _n}{2}\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n}+\frac{\alpha _n^2}{2 k_{\max }}\Vert v_{n+1}^{0}-\hat{v}\Vert ^2_{D_n} \le \Lambda \left( \frac{\beta _{-1}}{2}\Vert u_{0}-\hat{u}\Vert ^2_{P_{-1}}+\frac{\alpha _{-1}^2}{2 k_{\max }}\Vert v_{0}^0-\hat{v}\Vert ^2_{D_{-1}}\right) \nonumber \\&+\sum _{k=0}^{n}\beta _{k-1}\Lambda \left( \frac{\gamma _{k}^2}{2}\Vert u_k-u_{k-1}\Vert ^2_{P_{k-1}}+\gamma _k\Vert u_k-\hat{u}\Vert _{P_{k-1}}\Vert u_k-u_{k-1}\Vert _{P_{k-1}}\right) . \end{aligned}$$

(39)

By discarding the term proportional to $\Vert v_{n+1}^{0}-\hat{v}\Vert ^2_{D_n}$ on the left-hand side of the previous inequality, multiplying both sides by a factor $2/\beta _n$, using the inequalities $(\epsilon \eta )/\Vert W\Vert ^2\le \beta _k\le {(1+\zeta _{k-1})\beta _{k-1}\le \Lambda _k\beta _{-1}\le \Lambda \beta _{-1}}$ for $k=0,\ldots ,n$, and adding the term $\frac{2{\Lambda ^2}\Vert W\Vert ^2}{\epsilon \eta }\gamma _{n+1}\Vert u_{n+1}-\hat{u}\Vert _{P_{n}}\Vert u_{n+1}-u_{n}\Vert _{P_{n}}$ to the right-hand side, one gets

$$\begin{aligned} \Vert u_{n+1}- \hat{u}\Vert ^2_{P_n}&\le \frac{\Lambda \Vert W\Vert ^2}{\epsilon \eta }\Bigg (\beta _{-1}\Vert u_{0}-\hat{u}\Vert ^2_{P_{-1}}+\frac{\alpha _{-1}^2}{ k_{\max }}\Vert v_{0}^0-\hat{v}\Vert ^2_{D_{-1}}+\sum _{k=0}^{n}{\Lambda }\beta _{-1}\gamma _{k}^2\Vert u_k-u_{k-1}\Vert ^2_{P_{k-1}}\Bigg )\\&\quad +\sum _{k=0}^{n+1}\frac{2{\Lambda ^2}\Vert W\Vert ^2\beta _{-1}}{\epsilon \eta }\gamma _k\Vert u_k-u_{k-1}\Vert _{P_{k-1}}\Vert u_k-\hat{u}\Vert _{P_{k-1}}. \end{aligned}$$

At this point, we can apply Lemma 4 with $a_n=\Vert u_{n}-\hat{u}\Vert _{P_{n-1}}$, $b_n=\frac{\Lambda \Vert W\Vert ^2}{\epsilon \eta }\beta _{-1}\Vert u_{0}-\hat{u}\Vert ^2_{P_{-1}}+\frac{\Lambda \Vert W\Vert ^2}{\epsilon \eta }\frac{\alpha _{-1}^2}{k_{\max }}\Vert v_{0}^0-\hat{v}\Vert ^2_{D_{-1}}+\frac{\Lambda \Vert W\Vert ^2}{\epsilon \eta }\sum _{k=0}^{n}{\Lambda }\beta _{-1}\gamma _{k}^2\Vert u_k-u_{k-1}\Vert ^2_{P_{k-1}}$ and $c_n = \frac{2{\Lambda ^2}\Vert W\Vert ^2\beta _{-1}}{\epsilon \eta }\gamma _n\Vert u_n-u_{n-1}\Vert _{P_{n-1}}$, thus obtaining

$$\begin{aligned} \Vert u_{n+1}-\hat{u}\Vert _{P_n}&\le \frac{1}{2}\sum _{k=0}^{n+1}\frac{2{\Lambda ^2}\Vert W\Vert ^2\beta _{-1}}{\epsilon \eta } \gamma _k\Vert u_k-u_{k-1}\Vert _{P_{k-1}}\nonumber \\&+\Bigg (\frac{\Lambda \Vert W\Vert ^2}{\epsilon \eta }\Big (\beta _{-1}\Vert u_{0}-\hat{u}\Vert ^2_{P_{-1}} +\frac{\alpha _{-1}^2}{ k_{\max }}\Vert v_{0}^0-\hat{v}\Vert ^2_{D_{-1}}\nonumber \\&+\sum _{k=0}^{n}{\Lambda }\beta _{-1}\gamma _{k}^2\Vert u_k-u_{k-1}\Vert ^2_{P_{k-1}}\Big )\nonumber \\&+\left( \frac{1}{2}\sum _{k=0}^{n+1}\frac{2{\Lambda ^2}\Vert W\Vert ^2\beta _{-1}}{\epsilon \eta } \gamma _k\Vert u_k-u_{k-1}\Vert _{P_{k-1}}\right) ^2\Bigg )^{\frac{1}{2}}. \end{aligned}$$

(40)

By recursively applying condition (32) to (31), we get

$$\begin{aligned} \sum _{k=0}^{\infty }\gamma _k\Vert u_k-u_{k-1}\Vert _{P_{k-1}}&\le \sum _{k=0}^{\infty }\gamma _k\Lambda _k\Vert u_k-u_{k-1}\Vert _{P_{-1}}\nonumber \\&\le \Lambda \Vert P_{-1}\Vert ^\frac{1}{2}\sum _{k=0}^{\infty }\gamma _k\Vert u_k-u_{k-1}\Vert <\infty . \end{aligned}$$

(41)

By applying the previous inequality to (40) and recalling that $P_n\in \mathcal {D}_{\eta }$, it follows that the sequence $\{u_n\}_{n\in \mathbb {N}}$ is bounded. Finally, by discarding the term proportional to $\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n}$ in (39), employing again (41), the boundedness of $\{u_n\}_{n\in \mathbb {N}}$, the lower bound (25) on the eigenvalues of $D_n$ and $\beta _{k-1}\le {\Lambda }\beta _{-1}$, we conclude that also $\{v_n^0\}_{n\in \mathbb {N}}$ is bounded.

(ii) Item (i) guarantees the existence of a constant $M>0$ such that $\Vert u_n-\hat{u}\Vert _{P_n}\le M$ for all $n\ge 0$. Furthermore, we have $\beta _{n-1}\le {\Lambda }\beta _{-1}$ for all $n\ge 0$. Then, from (38), we deduce the following inequality

$$\begin{aligned} \beta _n k_{\max }&\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n}+\alpha _n^2\Vert v_{n+1}^0-\hat{v}\Vert ^2_{D_n}\\&\le (1+{\chi _{n-1}})(\beta _{n-1} k_{\max }\Vert u_n-\hat{u}\Vert ^2_{P_{n-1}}+\alpha _{n-1}^2\Vert v_n^0-\hat{v}\Vert ^2_{D_{n-1}})\\&+{\Lambda }\beta _{-1}k_{\max }(1+{\chi _{n-1}})(\gamma _n^2\Vert u_n-u_{n-1}\Vert ^2_{P_{n-1}}+2M\gamma _n\Vert u_n-u_{n-1}\Vert _{P_{n-1}}). \end{aligned}$$

The previous inequality and (41) allow us to apply Lemma 5 with $a_n =\beta _{n-1} k_{\max }\Vert u_n-\hat{u}\Vert ^2_{P_{n-1}}+\alpha _{n-1}^2\Vert v_n^0-\hat{v}\Vert ^2_{D_{n-1}}$, $b_n = {\chi _{n-1}}$ and $c_n = {\Lambda }\beta _{-1}k_{\max }(1+{\chi _{n-1}})(\gamma _n^2\Vert u_n-u_{n-1}\Vert ^2_{P_{n-1}}+2\,M\gamma _n\Vert u_n-u_{n-1}\Vert _{P_{n-1}})$, thus we get the thesis.

(iii) In virtue of (23)-(34), the sequences $\{\alpha _n\}_{n\in \mathbb {N}}$ and $\{\beta _n\}_{n\in \mathbb {N}}$ both satisfy the hypotheses of Lemma 5 and are bounded away from zero; hence, there exist $\alpha >0$ and $\beta >0$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\alpha _n=\alpha , \quad \lim _{n\rightarrow \infty }\beta _n = \beta . \end{aligned}$$

(42)

From inequality (41), we deduce that $\{P_n\}_{n\in \mathbb {N}}\subseteq \mathcal {D}_{\eta }^{\Lambda ^2 \Vert P_{-1}\Vert }$; likewise, we have $\{D_n\}_{n\in \mathbb {N}}\subseteq \mathcal {D}_{1-\epsilon }^{\Lambda ^2 \Vert D_{-1}\Vert }$. Thus, by Lemma 6, there exists $P\in \mathcal {D}_{\eta }$ and $D\in \mathcal {D}_{1-\epsilon }$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty } P_n = P, \quad \lim _{n\rightarrow \infty } D_n = D. \end{aligned}$$

(43)

Since $\{(u_n,v_n^0)\}_{n\in \mathbb {N}}$ is bounded, there exists $(u^\dagger ,v^\dagger )\in \mathbb {R}^d\times \mathbb {R}^{d'}$ and $I\subseteq \mathbb {N}$ such that

$$\begin{aligned} \lim _{n\in I}u_n = u^{\dagger }, \quad \lim _{n\in I}v_n^0 = v^{\dagger }. \end{aligned}$$

(44)

Let us show that $(u^{\dagger },v^{\dagger })$ is a solution of problem (12). To this aim, we consider inequality (30) with $u'=\hat{u}$, $v'=\hat{v}$, and by observing that $\mathcal {L}(u_{n+1},\hat{v})\ge \mathcal {L}(\hat{u},\tilde{v}_n)$, applying relation $\bar{u}_n=u_n+\gamma (u_n-u_{n-1})$ and the Cauchy-Schwarz inequality, we obtain

$$\begin{aligned}&\frac{1}{2}\left( \frac{1}{\alpha _n}-L_n\right) \Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}+\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n^2}{2}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2\nonumber \\&\le \frac{\beta _n}{2}(\Vert u_n-\hat{u}\Vert ^2_{P_n}-\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n})+\frac{\alpha _n^2}{2 k_{\max }}(\Vert v_n^0-\hat{v}\Vert ^2_{D_n}-\Vert v_{n+1}^0-\hat{v}\Vert ^2_{D_n})\nonumber \\&+\frac{\beta _n\gamma _n^2}{2}\Vert u_n-u_{n-1}\Vert ^2_{P_n}+\beta _n\gamma _n\Vert u_n-\hat{u}\Vert _{P_{n-1}}\Vert u_n-u_{n-1}\Vert _{P_{n-1}}. \end{aligned}$$

(45)

Since $\{(u_n,v_n^0)\}_{n\in \mathbb {N}}$ is bounded, there exist constants $M>0$ and $\tilde{M}>0$ such that

$$\begin{aligned} \Vert u_n-\hat{u}\Vert _{P_n}\le M, \quad \Vert v_n^0-\hat{v}\Vert _{D_n}\le \tilde{M}, \quad \forall \ n\ge 0. \end{aligned}$$

(46)

Additionally, by Step 7 of Algorithm 1, we observe that

$$\begin{aligned} \frac{1}{\alpha _n}-L_n=L_n\left( \frac{1}{\epsilon }-1\right) \ge L_{0}\left( \frac{1}{\epsilon }-1\right) >0, \quad \forall \ n\ge 0. \end{aligned}$$

(47)

By employing bounds (46–47), conditions (32–35), the fact that $\alpha _n\le \alpha _{n-1}$ and $\beta _n\le (1+\zeta _{n-1})\beta _{n-1}\le (1+\chi _{n-1})\beta _{n-1}\le \Lambda \beta _{-1}$ as seen in (23) and (34), respectively, and the lower bounds on the eigenvalues of $\{P_n\}_{n\in \mathbb {N}}$ and $\{D_n\}_{n\in \mathbb {N}}$, we derive from (45) the following inequality

$$\begin{aligned}&\frac{\eta L_0}{2}\left( \frac{1}{\epsilon }-1\right) \Vert u_{n+1}-\bar{u}_n\Vert ^2+\frac{\min \left\{ \alpha _0^2,\frac{\epsilon ^2\delta ^2\eta ^2}{L^2}\right\} (1-\epsilon )}{2k_{\max }}\sum _{k=0}^{k_{\max }-1}\Vert v_n^k-v_n^{k+1}\Vert ^2\\&\le \frac{1}{2}(\beta _{n-1}\Vert u_n-\hat{u}\Vert ^2_{P_{n-1}}-\beta _n\Vert u_{n+1}-\hat{u}\Vert ^2_{P_n})\\&+\frac{1}{2 k_{\max }}(\alpha ^2_{n-1}\Vert v_n^0-\hat{v}\Vert ^2_{D_{n-1}}-\alpha _n^2\Vert v_{n+1}^0-\hat{v}\Vert ^2_{D_n})+\frac{1}{2}\left( {\Lambda }\beta _{-1}M^2+\frac{\alpha _{-1}^2\tilde{M}^2}{ k_{\max }}\right) {\chi _{n-1}}\\&+\frac{{\Lambda }\beta _{-1}\gamma _n^2(1+{\chi _{n-1}})}{2}\Vert u_n-u_{n-1}\Vert ^2_{P_{n-1}}+{\Lambda }\beta _{-1}M\gamma _n\Vert u_n-u_{n-1}\Vert _{P_{n-1}}. \end{aligned}$$

We sum the previous relation over $n=0,\ldots ,N$, thus obtaining

$$\begin{aligned}&\frac{\eta L_0}{2}\left( \frac{1}{\epsilon }-1\right) \sum _{n=0}^N\Vert u_{n+1}-\bar{u}_n\Vert ^2+\frac{\min \left\{ \alpha _0^2,\frac{\epsilon ^2\delta ^2\eta ^2}{L^2}\right\} (1-\epsilon )}{2k_{\max }}\sum _{n=0}^{N}\sum _{k=0}^{k_{\max }-1}\Vert v_n^k-v_n^{k+1}\Vert ^2\\&\le \frac{1}{2}(\beta _{-1}\Vert u_0-\hat{u}\Vert ^2_{P_{-1}}-\beta _N\Vert u_{N+1}-\hat{u}\Vert ^2_{P_N})\\&+\frac{1}{2 k_{\max }}(\alpha _{-1}^2\Vert v_0^0-\hat{v}\Vert ^2_{D_{-1}}-\alpha _{N}^2\Vert v_{N+1}^0-\hat{v}\Vert ^2_{D_N})+\frac{1}{2}\left( {\Lambda }\beta _{-1}M^2+\frac{\alpha _{-1}^2\tilde{M}^2}{ k_{\max }}\right) \sum _{n=0}^{N}{\chi _{n-1}}\\&+\sum _{n=0}^{N}\frac{{\Lambda }\beta _{-1}\gamma _n^2(1+{\chi _{n-1}})}{2}\Vert u_n-u_{n-1}\Vert ^2_{P_{n-1}}+\sum _{n=0}^{N}{\Lambda }\beta _{-1}M\gamma _n\Vert u_n-u_{n-1}\Vert _{P_{n-1}}. \end{aligned}$$

Taking the limit for $N\rightarrow \infty$ and using conditions (35) and (41) yields

$$\begin{aligned} \sum _{n=0}^{\infty }\Vert u_{n+1}-\bar{u}_n\Vert ^2<\infty , \quad \sum _{n=0}^{\infty }\sum _{k=0}^{k_{\max }-1}\Vert v_n^k-v_n^{k+1}\Vert ^2<\infty , \end{aligned}$$

which trivially leads to

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert u_{n+1}-\bar{u}_n\Vert ^2=0, \quad \lim _{n\rightarrow \infty }\Vert v_n^k-v_n^{k+1}\Vert = 0, \quad k =0,\ldots ,k_{\max }-1. \end{aligned}$$

(48)

Since $\lim _{n\in I}v_n^0=v^{\dagger }$, the latter limits in (48) imply that

$$\begin{aligned} \lim _{n\in I}v_n^k = v^{\dagger }, \quad k =1,\ldots ,k_{\max }. \end{aligned}$$

(49)

Note also that, based on condition (31), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert \bar{u}_n-u_n\Vert =\lim _{n\rightarrow \infty }\gamma _n\Vert u_n-u_{n-1}\Vert =0, \end{aligned}$$

which means that

$$\begin{aligned} \lim _{n\in I}\bar{u}_n = u^{\dagger }. \end{aligned}$$

(50)

In turn, the above limit and the former one in (48) imply

$$\begin{aligned} \lim _{n\in I}u_{n+1}=u^{\dagger }. \end{aligned}$$

(51)

By plugging limits (42), (43), (44), (49), (50) and (51) inside relation (A1) in Appendix A, we obtain

$$\begin{aligned} \nabla f(u^{\dagger })+W^Tv^{\dagger } = 0. \end{aligned}$$

(52)

Likewise, by inserting the same limits inside relation (A3), we get

$$\begin{aligned} \lim _{n\in I} u_n^{k+1}=u^{\dagger }, \quad k =0,\ldots ,k_{\max -1}. \end{aligned}$$

In particular, for $k=0$, we have $\lim _{n\in I} u_n^{1}=u^{\dagger }$. By combining this last fact with (42), (49) and the continuity of the operator ${\text {prox}}_{\beta \alpha ^{-1}h^*}$ inside the dual step (21), we conclude that

$$\begin{aligned} v^{\dagger } = {\text {prox}}_{\beta \alpha ^{-1}h^*}(v^{\dagger }+\beta \alpha ^{-1}Wu^{\dagger }). \end{aligned}$$

(53)

Thanks to equations (52) and (53), we can apply Lemma 7 and conclude that $(u^{\dagger },v^{\dagger })$ is a solution of problem (12). Hence, it follows from item (ii) that the sequence $\{\beta _{n-1}k_{\max }\Vert u^{\dagger }-u_n\Vert ^2_{P_{n-1}}+\alpha _{n-1}^2\Vert v^{\dagger }-v_n^0\Vert ^2_{D_{n-1}}\}_{n\in \mathbb {N}}$ converges and, by definition of limit point, it admits a subsequence converging to zero. Then the sequence $\{(u_n,v_n^0)\}_{n\in \mathbb {N}}$ converges to $(u^{\dagger }, v^{\dagger })$. $\square$

4 Application to image deblurring

In this section, we focus our attention on the deblurring problem

$$\begin{aligned} \arg \min _{u\in \mathbb {R}^{{d}}}\frac{1}{2}\Vert Au-b\Vert _2^2+\lambda TV(u), \end{aligned}$$

(54)

where TV stands for the Total Variation operator, $\lambda >0$ is the regularization parameter, $A\in \mathbb {R}^{{d}\times {d}}$ is the blurring operator and $b\in \mathbb {R}^{{d}}$ is the observed image affected by white Gaussian noise. Problem (54) can be reformulated as (1) by setting

$$\begin{aligned} f(u)= \frac{1}{2}\Vert Au-b\Vert _2^2, \quad h(Wu)=TV(u) = \sum _{i=1}^{{d}^2}\Vert \nabla _i u\Vert _2, \end{aligned}$$

where $W=(\nabla _1^T,\ldots ,\nabla _{{d}^2}^T)^T\in \mathbb {R}^{2{d}^2\times {d}}$ represents the discrete gradient operator and $h:\mathbb {R}^{2{d}^2}\rightarrow \mathbb {R}\cup \{\infty \}$ is defined as

$$\begin{aligned} h(t) = \sum _{i=1}^{{d}^2}\left\| \left( \begin{matrix} t_{2i-1}\\ t_{2i} \end{matrix}\right) \right\| . \end{aligned}$$

Furthermore, it is straightforward to conclude that the minimization problem (54) satisfies Assumption 1.

4.1 Parameter choice

In the following, we detail how to appropriately select the parameters in Algorithm 1 applied to problem (54).

We equip Algorithm 1 with scaling matrices $\{P_n\}_{n\in \mathbb {N}}$ of the form

$$\begin{aligned} P_n = A^TA+\nu _nI_d, \quad \forall \ n\ge 0, \end{aligned}$$

(55)

where $I_d\in \mathbb {R}^{d\times d}$ is the identity matrix and $\{\nu _n\}_{n\in \mathbb {N}}$ is either a positive constant sequence $\nu _n\equiv \nu >0$ or a monotone sequence of positive real numbers converging to a positive value $\nu ^*>0$. These scaling matrices draw inspiration from the Iterated Tikhonov method [36,37,38]. Hence, from now on, we will refer to Algorithm 1 as NPDIT - Nested Primal–Dual Iterated Tikhonov method.

Note that the matrices $\{P_n\}_{n\in \mathbb {N}}$ defined in (55) can be diagonalized and inverted by two fast Fourier transforms (FFTs) since A is a convolution operator that can be diagonalized by FFT. Moreover, they comply with Assumption 2 (ii), as stated in the following result.

Lemma 11

Let $\{\nu _n\}_{n\in \mathbb {N}}\subseteq \mathbb {R}_{> 0}$ be a sequence that is either constant or monotone convergent to a positive value $\nu ^*>0$. Then, there exists a summable sequence of positive scalar $\{\zeta _n\}_{n\in \mathbb {N}}$ such that the sequence of matrices $\{P_n\}_{n\in \mathbb {N}}$ satisfies Assumption (2) (ii) that is

$$\begin{aligned} P_{n}\preceq (1+\zeta _{n-1})P_{n-1}, \quad \forall \ n\ge 0. \end{aligned}$$

Proof

If $\{\nu _n\}_{n\in \mathbb {N}}$ is a constant sequence such that $\nu _n\equiv \nu >0$, then Assumption 2 (ii) trivially follows with $\zeta _n\equiv 0$.

If $\{\nu _n\}_{n\in \mathbb {N}}$ is a nonincreasing sequence converging to a positive value $\nu ^*>0$, then $P_n\in \mathcal {D}_{\nu _n}$ for all $n\ge 0$ and $P_{n}\preceq P_{n-1}$ because $\nu _n \le \nu _{n-1}$. Hence, the sequence $\{P_n\}_{n\in \mathbb {N}}$ satisfies Assumption 2 (ii) with $\zeta _{n}\equiv 0$.

Finally, if $\{\nu _n\}_{n\in \mathbb {N}}$ is a nondecreasing sequence converging to a positive value $\nu ^*>0$, then $P_n\in \mathcal {D}_{\nu _0}$ for all $n\ge 0$ and it follows that

$$\begin{aligned} u^TP_{n}u&= u^T(A^TA+\nu _{n} I_d)u\\&= u^T(A^TA+\nu _{n-1}I_d)u+(\nu _{n}-\nu _{n-1})u^Tu\\&\le u^TP_{n-1}u +(\nu _{n}-\nu _{n-1})\nu _{0}^{-1}u^TP_{n-1}u\\&= (1+(\nu _{n}-\nu _{n-1})\nu _{0}^{-1})u^TP_{n-1}u, \quad \forall \ u\in \mathbb {R}^d. \end{aligned}$$

where the inequality follows from the left-hand inequality in (6). By setting $\zeta _{n-1} = (\nu _{n}-\nu _{n-1})\nu _{0}^{-1}\ge 0$, we note that

$$\begin{aligned} \sum _{n=1}^{N}\zeta _{n-1}=\nu _0^{-1}(\nu _N-\nu _{0}) \quad \Rightarrow \quad \sum _{n=1}^{\infty }\zeta _{n-1}<\infty . \end{aligned}$$

Hence, the sequence $\{P_n\}_{n\in \mathbb {N}}$ satisfies Assumption 2 (ii). $\square$

According to the selection of the parameter $\nu _n$ in (55), we consider three different implementations of NPDIT. In the first one, we let

$$\begin{aligned} \nu _n\equiv \nu , \quad \nu >0, \end{aligned}$$

(56)

where $\nu >0$ is a constant that must be prefixed in advance by the user. The selection of $\nu$ significantly influences the performance and stability of the method throughout the iterations. Estimating it accurately can be challenging, which is why we have also explored two non-stationary strategies. More precisely, a non-stationary implementation - denominated $\mathrm {NPDIT_{D}}$ - adopts a decreasing geometric sequence for $\nu _n$ defined as

$$\begin{aligned} \nu _n = a_0q^n + \nu _{\textrm{final}}, \quad \forall \ n\ge 0 \end{aligned}$$

(57)

where we set $a_0 = \frac{1}{2}$, $q = 0.85$, and $\nu _{\textrm{final}} = 10^{-2}$ in the numerical results. In a second non-stationary implementation - denominated $\mathrm {NPDIT_{I}}$ - employs an increasing sequence for $\nu _n$ defined as

$$\begin{aligned} \nu _n = 1-\frac{1}{{n+1}}+\nu _{\textrm{initial}}, \quad \forall \ n\ge 0 \end{aligned}$$

(58)

with $\nu _{\textrm{initial}}= 10^{-2}$ in the numerical examples.

Initially, we also considered the trivial choice $P_n\equiv I_d$ for our tests; however, we noted that such a choice yields inferior performances when compared with the preconditioners (55). For this reason, we did not report the related results in the manuscript.

In the NPDIT algorithm and its two non-stationary variants, a backtracking strategy is employed to compute the steplength $\alpha _n$. Particularly, at each step n, we compute $\alpha _n=\epsilon /L_n$, where $\epsilon =0.99$ and $L_n>0$ is such that

$$\begin{aligned} f(\tilde{u}_{n}) \le f(\bar{u}_n) + \nabla f(\bar{u}_n)^T(\tilde{u}_{n}-\bar{u}_n) + \frac{L_n}{2}\Vert \tilde{u}_{n}-\bar{u}_n\Vert ^2_{P_n}, \end{aligned}$$

(59)

where $\tilde{u}_n$ and $\bar{u}_n$ are defined as in (22) and (19), respectively. We recall that the resulting sequence $\{\alpha _n\}_{n\in \mathbb {N}}$ is monotonically nonincreasing. We start with an initial value of $L_0 = 0.1$ and iteratively increase it by a factor of $\delta =0.8$ until condition (59) is satisfied, or $L_n > 1$, in which case we simply set $L_n=1$ and $\alpha _n = \epsilon$. This choice is justified by the following remark.

Remark 5

If $f(u) = \frac{1}{2}\Vert Au-b\Vert _2^2$ and $P_n = A^TA+\nu _n I$, then condition (59) is satisfied for $L_n = 1$. Indeed, using a second-order Taylor expansion at $u = \bar{u}_n$, we have

$$\begin{aligned} f(\tilde{u}_n) = f(\bar{u}_n) + \nabla f(\bar{u}_n)^T(\tilde{u}_n-\bar{u}_n) +\frac{1}{2}(\tilde{u}_n-\bar{u}_n)A^TA(\tilde{u}_n-\bar{u}_n)^T. \end{aligned}$$

From the fact that the matrix $A^TA$ is positive semidefinite, we obtain

$$\begin{aligned} f(\tilde{u}_n)&\le f(\bar{u}_n) + \nabla f(\bar{u}_n)^T(\tilde{u}_n-\bar{u}_n) +\frac{1}{2}(\tilde{u}_n-\bar{u}_n)(A^TA+\nu _nI)(\tilde{u}_n-\bar{u}_n)^T \\ &= f(\bar{u}_n) + \nabla f(\bar{u}_n)^T(\tilde{u}_n-\bar{u}_n) +\frac{1}{2}\Vert \tilde{u}_n-\bar{u}_n\Vert _{P_n}^2. \end{aligned}$$

The choice of the $\beta _n$ parameter must be coherent with Step 3 of Algorithm 1. Therefore, in both nonstationary versions of the NPDIT method, we select $\beta _n$ at each iteration $n\in \mathbb {N}$ as follows:

$$\begin{aligned} \beta _n= \frac{\epsilon \nu _n}{8} = \frac{\epsilon \nu _n}{\Vert W\Vert ^2}, \end{aligned}$$

where $\epsilon \in (0,1)$.

Finally, the value of $\gamma _n$ for the inertial step was chosen following the strategy proposed in [34] and detailed below:

$$\begin{aligned} \gamma _n = {\left\{ \begin{array}{ll} 0, & n=0 \\ \min \left\{ \gamma _n^{\text {FISTA}}, \frac{C\rho _n}{\Vert u_n - u_{n-1}\Vert }\right\} , & n=1,2,\ldots . \end{array}\right. } \end{aligned}$$

(60)

In all of the three considered examples, we chose $C = 0.1\Vert u_1 - u_0\Vert$ for the stationary version of NPDIT and for $\mathrm {NPDIT_D}$, while we selected $C =\Vert u_1 - u_0\Vert$ for the increasing case. Then, for all NPDIT implementations, we used the same value for $\rho _n$, which is $\rho _n = \frac{1}{n^{1.1}}$. In (60), the parameter $\gamma _n^{\text {FISTA}}$ is defined by the usual FISTA rule:

$$\begin{aligned} t_0 = 1,\quad {\left\{ \begin{array}{ll} t_{n+1} = \frac{1 + \sqrt{1 + 4t_n^2}}{2}, \\ \gamma _n^{\text {FISTA}} = \frac{t_{n-1}}{t_{n+1}}, \end{array}\right. }\quad n=0,1,\ldots . \end{aligned}$$

(61)

The number of primal–dual iterations is set for simplicity to $k_{\max } = 1$. This choice is coherent with the numerical experimentation carried out in [34] for a special instance of Algorithm 1, where it was observed that $k_{\max }=1$ could be seen as a good trade-off between accuracy and complexity.

Finally, we remark that an automated method for computing the regularization parameter $\lambda$ has not been implemented in the tests. Consequently, we will specify the value or values used for each example.

4.2 Numerical results

The following numerical results were obtained using MATLAB R2023a on a MacBook Pro equipped with the M2 Pro chip and a 10-core CPU (6 performance cores and 4 efficiency cores), along with 16GB of RAM.

We provide three image deblurring examples in which we compare the three implementations of our NPDIT method with the following competitors:

• The Nested Primal–Dual (NPD) method proposed in [34], which can be seen as a special instance of Algorithm 1 obtained by setting $P_n\equiv I_d$, $\eta _n\equiv 1$, $\alpha _0= 1$, $\beta _n\equiv \beta < 1/8$ and $\gamma _n$ computed according to (60) with $C = 10\Vert u_1 - u_0\Vert$; unlike Algorithm 1, NPD chooses a fixed steplength $\alpha _n\equiv \alpha _0$ without performing any backtracking procedure; note that the chosen value for $\alpha _0$ is such that the backtracking condition at Step 7 of Algorithm 1 is automatically satisfied for all $n\ge 0$ with $\alpha _n=\alpha _0$;

• The preconditioned version of the Chambolle-Pock method ($\mathrm {CP_{prec}}$), the popular primal–dual algorithm for composite convex optimization proposed in [44];

• A first order primal–dual method with linesearch (PD–LS) proposed by Malitsky and Pock in [17];

• The inexact version of FISTA with approximate proximal evaluations proposed in [29], whose practical implementation resembles Algorithm 1, in the sense that it can be seen as a nested primal–dual algorithm with extrapolation for solving problems of the form (1); however, unlike Algorithm 1, the number of inner iterations varies with the outer iteration according to an appropriate stopping criterion, the extrapolation parameter is computed as proposed by Chambolle and Dossal in [45], and there is no variable metric.

The blurred image is obtained by circular two-dimensional convolution, ensuring that the deblurring model is not affected by boundary ringing effects. Consequently, the numerical results only depend on the applied numerical method. Of course, in real applications, appropriate boundary conditions affecting the structure of the matrix A should be adopted, see [46].

In order to evaluate the performance of the different methods, we use the Relative Reconstruction Error (RRE) functional, defined as

$$\begin{aligned} \textrm{RRE}(u_n) = \frac{\Vert u_{\textrm{true}}-u_n\Vert }{\Vert u_{\textrm{true}}\Vert }, \end{aligned}$$

where $u_{\textrm{true}}$ represents the original image.

The relative decrease of the objective function is computed by the quantity

$$\begin{aligned} \frac{R(u_{n})-R(u^{*})}{R(u^{*})}, \end{aligned}$$

where R is the objective function and $u^*$ is the best reconstruction obtained among all the methods considered, achieving the minimum value of the objective function. This solution was precomputed by running all the methods for $10^3$ iterations.

Example 1: Cameraman with $1\%$ of noise.

In this example, we considered an image of a Cameraman with dimensions of $256 \times 256$. The image was blurred using a $10 \times 10$ Gaussian Point Spread Function (PSF) with a standard deviation of 2. Additionally, white noise with an intensity level of $1\%$ was added to the blurred image. This implies that the norm of the noise is equal to $1\%$ of the norm of the blurred image. For this example, we set $\lambda = 10^{-4}$ as the regularization parameter.

Fig. 1

Example 1—First row: RRE functional over 400 iterations and over 2 s of time. Second row: Relative decrease of the objective function over the number of iterations and time

In the first row of Fig. 1, we depict the behavior of the RRE functional over 400 iterations (left) and over 2 s of time (right) for all the methods considered. For the stationary NPDIT case, we set $\nu = 0.01$. We observe that our proposal, both stationary and non-stationary, outperforms all the other competitors. Indeed, we achieve lower values of the RRE in fewer iterations, which are also faster to compute compared to all the other cases. For $\mathrm {NPDIT_I}$, i.e., the version of our proposal where $\nu _n$ is increasing, we note a significant speed-up in the initial iterations due to the small value of $\nu _n$. However, as iterations progress, the performance worsens because $\nu _n$ approaches 1 and consequently slows down the convergence of the method.

In the second row of Fig. 1, we compare the relative decrease of the objective function. Similarly, the stationary method and the non-stationary method NPDIT-D achieve better results than all the other competitors. However, there are two observations worth mentioning. The inexact version of FISTA proposed in [29] seems to perform comparably to NPDIT-D as the iterations progress, but the time required to achieve these results is significantly greater than that required by our proposal. Secondly, the performance of $\mathrm {NPDIT_I}$ is similar to the standard NPD algorithm. This is mainly due to the choice of the regularization parameter $\lambda$. As we will show in the last part of the numerical examples, $\mathrm {NPDIT_I}$ works better when the regularization parameter $\lambda$ is underestimated.

Fig. 2

Example 1—RRE for different values of $\nu$ for $\lambda = 10^{-4}$

Figure 2 shows the convergence behavior of the RRE functional for NPDIT$_I$, NPDIT$_D$, and the stationary variant of NPDIT equipped with three different values of the parameter $\nu$. The plots for the non-stationary methods and the case with $\nu =0.01$ are identical to those shown in Fig. 1. For $\nu = 10^{-3}$, it is noticeable that the method introduces some instability and the speed of convergence is also reduced. When $\nu = 0.1$, the algorithm is stable again but it is slower than in the other cases. This demonstrates that the convergence speed and the stability of the method are affected by the choice of $\nu$ for stationary values $\nu _n = \nu$. Therefore, the decreasing sequence of $\nu _n$ in equation (57) provides a good trade-off without requiring the estimation of $\nu$.

The reconstructed images shown in Fig. 3 are obtained at various iterations for both the NPD and the NPDIT method with $\nu = 0.01$. For completeness, the upper part of the figure includes the true image, the PSF, and the observed image b. Additionally, the achieved RRE value is reported for each reconstruction. Notably, the NPDIT method achieves satisfactory reconstructions with just 20 iterations, while the NPD method requires at least 100 iterations to achieve a similar level of accuracy.

Fig. 3

Example 1—Reconstruction obtained at different iterations. First row: original data. Second row: images obtained with NPD. Third row: images obtained with NPDIT ($\nu =0.01$)

Example 2: Peppers.

In this second example, we examined the image of Peppers with dimensions $256\times 256$ and applied an out-of-focus PSF with dimensions $10\times 10$ for blurring. Additionally, we introduced white Gaussian noise with an intensity level of $1\%$ to the image. For this case, we chose $\lambda = 10^{-4}$ as the regularization parameter.

The comparison between all the methods follows the same structure as in the previous case. In the first row of Fig. 4, we present the RRE functional, while in the second row we focus on the relative decrease of the objective function. In this example, we observe that both the NPDIT method with $\nu =0.01$ and the non-stationary version $\mathrm {NPDIT_D}$ achieve excellent results. Concerning the $\mathrm {NPDIT_I}$ algorithm, we notice a rapid decrease in the first iterations for the objective function, followed by a deterioration in performance as the iterations increase. Again, we note that the FISTA method outperforms all of our proposals in the relative decrease of the objective function after 400 iterations. However, as in Example 1, the time required is significantly greater than those of the stationary NPDIT and the $\mathrm {NPDIT_D}$ method.

Finally, in Fig. 5, we display the reconstructions obtained by the NPD method and the NPDIT with $\nu =0.01$ fixed. Once again, in the first row, we present the true image, the PSF used for blurring, and the observation corrupted by noise. For this example, it is evident that the stationary version NDPIT requires only 10 iterations to achieve excellent results, while the NPD algorithm needs almost four times more iterations to obtain the same quality in the reconstruction.

Fig. 4

Example 2—First row: RRE functional over 400 iterations and over 2 s of time. Second row: Relative decrease of the objective function over the number of iterations and time

Fig. 5

Example 2—Reconstruction obtained at different iterations. First row: original data. Second row: images obtained with NPD. Third row: images obtained with NPDIT ($\nu =0.01$)

Example 3: Overlapping group TV

In this final numerical example, we replace the TV term with the Overlapping Group sparsity TV (OG-TV) regularizer proposed in [47], which is defined as

$$\begin{aligned} h(Wx) = \sum _{i=1}^{d^2}\Vert B_i\nabla ^hx\Vert + \Vert B_i\nabla ^vx\Vert , \end{aligned}$$

where $\nabla ^h,\nabla ^v\in \mathbb {R}^{d^2\times d^2}$ are the horizontal and vertical discrete gradient operators, while $B_i\in \mathbb {R}^{m^2\times d^2}$ is a unitary diagonal matrix such that $B_ix$ is the vector whose entries are the pixel i of the image x and its $m^2-1$ first neighbors. In this case we have that $\Vert W\Vert ^2 = 8m^2$.

In order to test the performances of our methods on this new problem, we consider the jetplane image, which has been blurred and artificially corrupted with white Gaussian noise as in Example 1. For this case, we choose $\lambda = 5\times 10^{-5}$ as the regularization parameter.

Fig. 6

Example 3—First row: RRE functional over 400 iterations and over 5 s of time. Second row: Relative decrease of the objective function over the same number of iterations and time as before

The analysis of this experiment follows the same structure as in the previous examples. In the first row of Fig. 6, we report the RRE functional as a function of the number of iterations (left side) and time (right side). The second row is devoted to the relative decrease of the objective function, again depending on the number of iterations and time. Even in this case, we can clearly state that all our proposals outperform the other methods in terms of both quality and speed.

Fig. 7

Example 3—Reconstruction obtained at different iterations. First row: original data. Second row: images obtained with NPD. Third row: images obtained with NPDIT ($\nu =0.01$)

Lastly, in Fig. 7, we compare the reconstruction obtained with the NPD method and the stationary NPDIT method equipped with $\nu = 0.01$. The final images were computed after different numbers of iterations, and we can see that, even in this case, NPDIT achieves remarkable reconstructions even after just 10 iterations.

4.3 Stability

As a final illustration, we investigated the robustness of the methods with respect to the regularization parameter $\lambda$ under the condition of a stationary sequence $\nu _n=\nu$. To achieve this, we explored different values of this parameter for each example presented earlier. Furthermore, we conducted a detailed analysis of the behavior of the proposed method with respect to the two non-stationary sequences employed in $\textrm{NPDIT}_D$ and $\textrm{NPDIT}_I$.

The comparison among the methods is carried out by assessing the quality of reconstructions using the RRE functional. Figure 8 presents a summary of the results as follows: each row corresponds to one of the mentioned examples. In particular, the i-th row corresponds to Example i, where $i=1,2,3$. Each column is associated with a specific value of $\lambda \in \{10^{-3}, 10^{-4}, 10^{-5}\}$ for the first two rows and $\lambda \in \{10^{-4}, 10^{-5}, 10^{-6}\}$ for the last one.

In accordance with the analysis conducted in Sect. 4.2, the $\textrm{NPDIT}_D$ method exhibits behavior very similar to that of $\textrm{NPDIT}$, avoiding the selection of the stationary parameter $\nu$. Regarding the $\textrm{NPDIT}_I$ method, it is observed to be more beneficial in cases of underestimation of the regularization parameter $\lambda$, as indicated by the theoretical analysis in [48] for the Iterated Tikhonov method. Specifically, from the rightmost column, we observe greater stability around the minimum point compared to other methods. However, whenever $\lambda$ is underestimated, it is advisable to implement an effective stopping criterion (e.g., the discrepancy principle) to terminate the process before the RRE grows excessively.

Fig. 8

From top to bottom: RRE functional with respect to the number of iterations for example 1 (top row), example 2 (middle row) and example 3 (bottom row). From left to right: comparison for different values of $\lambda$, i.e., $\lambda \in \{10^{-3},10^{-4},10^{-5}\}$ for the first two rows, $\lambda \in \{10^{-4},10^{-5},10^{-6}\}$ for the third one

5 Conclusions and future work

In this paper, we have formulated and analysed a nested primal–dual method tailored for solving regularized convex optimization problems. Our proposed approach approximates a variable metric proximal–gradient step with extrapolation by executing a fixed number of primal-dual iterates, while dynamically adjusting the steplength parameter through a specialized backtracking procedure. The convergence of the iterates sequence towards a solution of the problem has been established by assuming a relaxed monotonicity condition on the scaling matrices, as well as a specific shrinking criterion on the extrapolation parameters. Extensive numerical experiments have shown that our algorithm performs well in comparison to other similar competitors on some Total-Variation regularized least-squares problems arising in image deblurring, especially when it is equipped with scaling matrices inspired by the Iterated Tikhonov method.

Future work may include the application of our algorithm to other imaging problems such as computer tomography, its adaptation to more accurate boundary conditions for image deblurring, and its extension to more general optimization problems. In particular, for applications not addressed in this paper, the matrix–vector product with the proposed scaling matrices might be computationally expensive. Therefore, we plan to investigate its approximation in suitable subspaces from both a theoretical and practical standpoint. Moreover, we will investigate the extension of our proposed algorithm to problems where constraints on the primal variable are imposed, and the definition of novel nested primal–dual algorithms where the backtracking procedure based on the Descent Lemma is replaced by a linesearch along the descent direction.

Proof of Lemma 10

Proof

(i) We start by observing that

$$\begin{aligned} u_{n+1}=\tilde{u}_n&= \frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}u_n^{k+1}\nonumber \\&= \frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}(\bar{u}_n-\alpha _n P_{n}^{-1}\nabla f(\bar{u}_n)-\alpha _n P_n^{-1}W^Tv_n^{k+1})\nonumber \\&= \bar{u}_n - \alpha _n P_n^{-1}\nabla f(\bar{u}_n)-\alpha _n P_n^{-1}W^T\tilde{v}_n. \end{aligned}$$

(A1)

Then, we can proceed from the value $\mathcal {L}(u',\tilde{v}_n)$ as follows:

$$\begin{aligned} \mathcal {L}(u',\tilde{v}_n)&= f(u')+\langle Wu',\tilde{v}_n\rangle - h^*(\tilde{v}_n)\\&\ge f(\bar{u}_n)+\langle u'-\bar{u}_n,\nabla f(\bar{u}_n)\rangle +\langle W u',\tilde{v}_n\rangle - h^*(\tilde{v}_n)\\&=f(\bar{u}_n)+\langle u_{n+1}-\bar{u}_n,\nabla f(\bar{u}_n)\rangle -\langle u_{n+1}-u',\nabla f(\bar{u}_n)\rangle \\&+\langle Wu',\tilde{v}_n\rangle - h^*(\tilde{v}_n)\\&\ge f(u_{n+1})-\frac{L_n}{2}\Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}-\langle u_{n+1}-u',\nabla f(\bar{u}_n)\rangle \\&+\langle Wu',\tilde{v}_n\rangle - h^*(\tilde{v}_n), \end{aligned}$$

where the first inequality follows from the convexity of f, and the second one is based on the backtracking condition at Step 7 of Algorithm 1. By summing and subtracting the term $W^T\tilde{v}_n$ in the second argument of the scalar product $\langle u_{n+1}-u',\nabla f(\bar{u}_n)\rangle$, we can extend the chain of inequalities as below:

$$\begin{aligned} \mathcal {L}(u',\tilde{v}_n)&\ge f(u_{n+1})-\frac{L_n}{2}\Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}-\langle u_{n+1}-u',\nabla f(\bar{u}_n)+W^T\tilde{v}_n\rangle \\&+\langle Wu',\tilde{v}_n\rangle + \langle u_{n+1}-u',W^T\tilde{v}_n\rangle - h^*(\tilde{v}_n)\\&=f(u_{n+1})+\langle u_{n+1},W^T\tilde{v}_n\rangle -h^*(\tilde{v}_n)\\&-\frac{1}{\alpha _n}\langle u_{n+1}-u',P_n(\alpha _nP_n^{-1}\nabla f(\bar{u}_n)+\alpha _nP_n^{-1}W^T\tilde{v}_n)\rangle \\&-\frac{L_n}{2}\Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}\\&= \mathcal {L}(u_{n+1},\tilde{v}_n) +\frac{1}{\alpha _n}\langle u_{n+1}-u',P_n(u_{n+1}-\bar{u}_n) \rangle -\frac{L_n}{2}\Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}\\&= \mathcal {L}(u_{n+1},\tilde{v}_n) +\frac{1}{2\alpha _n}\Vert u_{n+1}-u'\Vert _{P_n}^2+\frac{1}{2\alpha _n}\Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}\\&-\frac{1}{2\alpha _n}\Vert \bar{u}_n-u'\Vert ^2_{P_n}-\frac{L_n}{2}\Vert u_{n+1}-\bar{u}_n\Vert ^2_{P_n}, \end{aligned}$$

where the second equality follows from (A1) together with the definition of $\mathcal {L}$ in (12), and the third one is due to the application of the three-point equality

$$\begin{aligned} \Vert a-c\Vert _{P_n}^2=\Vert a-b\Vert ^2_{P_n}+\Vert b-c\Vert ^2_{P_n}+2\langle a-b, P_n(b-c)\rangle , \end{aligned}$$

with $a = u'$, $b = u_{n+1}$, $c=\bar{u}_n$. By rearranging the various terms, we get (28). (ii)

Starting from the value $\mathcal {L}(u_{n+1},v_n^{k+1})$ and applying Lemma 3 with $\varphi = \beta _n \alpha _{n}^{-1} h^*$, $y=v_{n}^{k+1}$, $x=v_n^k$, $e=\beta \alpha _n^{-1}Wu_n^k$ and $z=v'$, we get

$$\begin{aligned} \mathcal {L}(u_{n+1},v_n^{k+1})&= f(u_{n+1}) +\langle Wu_{n+1},v_n^{k+1}\rangle -h^*(v_n^{k+1})\nonumber \\&\ge f(u_{n+1}) +\langle Wu_{n+1},v_n^{k+1}\rangle -h^*(v')-\langle v_n^{k+1}-v' ,Wu_n^k\rangle \nonumber \\&+\frac{\alpha _n}{2\beta _n}\Vert v_n^{k+1}-v'\Vert ^2-\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v'\Vert ^2+\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert ^2\nonumber \\&=\mathcal {L}(u_{n+1},v')+\langle v_n^{k+1}-v',W(u_{n+1}-u_n^{k+1})\rangle \nonumber \\&-\langle v_n^{k+1}-v',W(u_n^k-u_n^{k+1})\rangle \nonumber \\&+\frac{\alpha _n}{2\beta _n}\Vert v_n^{k+1}-v'\Vert ^2-\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v'\Vert ^2+\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert ^2. \end{aligned}$$

(A2)

From Step 4 of Algorithm 1 and (A1), we also have the following relations

$$\begin{aligned} u_{n+1}-u_n^{k+1}&= \alpha _nP_n^{-1}W^T(v_n^{k+1}-\tilde{v}_n)\nonumber \\ u_n^k-u_n^{k+1}&= \alpha _n P_n^{-1}W^T(v_n^{k+1}-v_n^k). \end{aligned}$$

(A3)

Plugging the above relations inside (A2) yields

$$\begin{aligned} \mathcal {L}(u_{n+1},v_n^{k+1})&\ge \mathcal {L}(u_{n+1},v')+\alpha _n\langle W^T(v_n^{k+1}-v'),P_n^{-1}W^T( v_n^{k+1} -\tilde{v}_n)\rangle \nonumber \\&-\alpha _n\langle W^T(v_n^{k+1}-v'),P_n^{-1}W^T(v_n^{k+1}-v_n^k)\rangle \nonumber \\&+\frac{\alpha _n}{2\beta _n}\Vert v_n^{k+1}-v'\Vert ^2-\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v'\Vert ^2+\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert ^2. \end{aligned}$$

(A4)

Note that the first scalar product in the previous inequality can be lower bounded as follows

$$\begin{aligned} \langle W^T(v_n^{k+1}-v'),P_n^{-1}W^T(v_n^{k+1}-\tilde{v}_n)\rangle&= \frac{1}{2}\Vert P_n^{-\frac{1}{2}}W^T(v_n^{k+1}-v')\Vert ^2\\&+\frac{1}{2}\Vert P_{n}^{-\frac{1}{2}}W^T(v_n^{k+1}-\tilde{v}_n)\Vert ^2\\&-\frac{1}{2}\Vert P_{n}^{-\frac{1}{2}}W^T(\tilde{v}_n-v')\Vert ^2\\&\ge \frac{1}{2}\Vert P_n^{-\frac{1}{2}}W^T(v_n^{k+1}-v')\Vert ^2\\&-\frac{1}{2}\Vert P_{n}^{-\frac{1}{2}}W^T(\tilde{v}_n-v')\Vert ^2, \end{aligned}$$

whereas the second one can be rewritten as

$$\begin{aligned} -\langle W^T(v_n^{k+1}-v'),P_n^{-1}W^T(v_n^{k+1}-v_n^k)\rangle&= -\frac{1}{2}\Vert P_n^{-\frac{1}{2}}W^T(v_n^{k+1}-v')\Vert ^2\\&-\frac{1}{2}\Vert P_n^{-\frac{1}{2}}W^T(v_n^{k+1}-v_n^k)\Vert ^2\\&+\frac{1}{2}\Vert P_n^{-\frac{1}{2}}W^T(v_n^k-v')\Vert ^2. \end{aligned}$$

By inserting the previous relations inside (A4) and recalling the definition of $D_n$ and $\Vert \cdot \Vert _{D_n}$ in (24–26), we come to

$$\begin{aligned} \mathcal {L}(u_{n+1},v_n^{k+1})&\ge \mathcal {L}(u_{n+1},v')-\frac{\alpha _n}{2}\Vert P_n^{-\frac{1}{2}}W^T(\tilde{v}_n- v')\Vert ^2\nonumber \\&+\frac{\alpha _n}{2\beta _n}\Vert v_n^{k+1}-v'\Vert ^2-\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v'\Vert ^2_{D_n}+\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2. \end{aligned}$$

(A5)

We proceed as follows

$$\begin{aligned} \mathcal {L}(u_{n+1},\tilde{v}_n)&=\mathcal {L}\left( u_{n+1},\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}v_n^{k+1}\right) \\&\ge \frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\mathcal {L}(u_{n+1},v_n^{k+1})\\&\ge \mathcal {L}(u_{n+1},v')-\frac{\alpha _n}{2}\Vert P_n^{-\frac{1}{2}}W^T(\tilde{v}_n- v')\Vert ^2\\&+\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2\beta _n}\Vert v_n^{k+1}-v'\Vert ^2-\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v'\Vert ^2_{D_n}+\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2\\&\ge \mathcal {L}(u_{n+1},v')-\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2}\Vert P_n^{-\frac{1}{2}}W^T(v_{n}^{k+1} - v')\Vert ^2\\&+\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2\beta _n}\Vert v_n^{k+1}-v'\Vert ^2-\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v'\Vert ^2_{D_n}+\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2, \end{aligned}$$

where the first inequality is obtained by concavity of $\mathcal {L}(u_{n+1},\cdot )$, the second one from applying (A5), and the third one follows from the definition of $\tilde{v}_n$ and the concavity of $-\Vert P_{n}^{-\frac{1}{2}}W^T(\cdot -v')\Vert ^2$. We further extend the above chain of inequalities as done below

$$\begin{aligned} \mathcal {L}(u_{n+1},\tilde{v}_n)&\ge \mathcal {L}(u_{n+1},v')+\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2\beta _n}\Vert v_n^{k+1}-v'\Vert ^2_{D_n}-\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v'\Vert ^2_{D_n}\\&+\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2\\&=\mathcal {L}(u_{n+1},v')+\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_n^{k_{\max }}-v'\Vert ^2_{D_n}-\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_n^0-v'\Vert ^2_{D_n}\\&+\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2\\&=\mathcal {L}(u_{n+1},v')+\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_{n+1}^{0}-v'\Vert ^2_{D_n}-\frac{\alpha _n}{2\beta _n k_{\max }}\Vert v_n^0-v'\Vert ^2_{D_n}\\&+\frac{1}{k_{\max }}\sum _{k=0}^{k_{\max }-1}\frac{\alpha _n}{2\beta _n}\Vert v_n^k-v_n^{k+1}\Vert _{D_n}^2, \end{aligned}$$

where the first inequality has been obtained by recalling once again the definition of $D_n$ in (24), and the last equality is a consequence of the warm-start strategy at Step 3 of Algorithm 1. By rearranging terms, we finally get inequality (29).

(iii) Inequality (30) follows by summing (28) with (29). $\square$