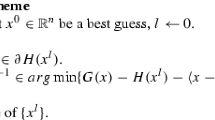Abstract
Sparse optimization is about finding minimizers of functions characterized by a number of nonzero components as small as possible, such paradigm being of great practical relevance in Machine Learning, particularly in classification approaches based on support vector machines. By exploiting some properties of the k-norm of a vector, namely, of the sum of its k largest absolute-value components, we formulate a sparse optimization problem as a mixed-integer nonlinear program, whose continuous relaxation is equivalent to the unconstrained minimization of a difference-of-convex function. The approach is applied to Feature Selection in the support vector machine framework, and tested on a set of benchmark instances. Numerical comparisons against both the standard \(\ell _1\)-based support vector machine and a simple version of the Slope method are presented, that demonstrate the effectiveness of our approach in achieving high sparsity level of the solutions without impairing test-correctness.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The sparse counterpart of a mathematical program is aimed at finding optimal solutions that have as few nonzero components as possible, this feature playing a significant role in several applications, mainly (but not solely) arising in the broad fields of data science and machine learning. Indeed, this is one of the reason why sparse optimization has recently become a topic of great interest in the field of mathematical optimization.
Accounting for sparsity in a mathematical program amounts to embed into its formulation a measure dependent on the number of zero components of a solution-vector. The mathematical tool that is most naturally suited to such task is the \(\ell _0\)-(pseudo-)norm \(\Vert \cdot \Vert _0\), often simply referred to as the \(\ell _0\)-norm, defined as the number of nonzero components of a solution, it rather being a measure of vector density. Thus, a sparse optimization problem should also encompass the \(\ell _0\)-norm minimization in order to achieve the largest possible sparsity. Such feature highlights the intrinsic bi-objective nature of sparse optimization, that makes it fit to two commonplace single-objective formulations, the \(\ell _0\)-regularization problem and the cardinality-constrained problem, depending on whether one aims at pushing for sparsity or at ensuring an assigned sparsity level, respectively.
Given a real-valued function \(f:\mathbb {R}^n \rightarrow \mathbb {R}\), with \(n\ge 2\), the (unconstrained) \(\ell _0\)-regularization problem has the following structure

where the \(\ell _0\)-norm penalty term inside the objective function pushes towards sparse solutions, and a fixed penalty-parameter \(\sigma >0\) ensures the trade-off between the two (possibly) conflicting objectives. Problem (\(\textrm{SOP}\)) has a nonconvex and discontinuous nature (see, e.g., [1] for a study on complexity issues), that makes it unfit to be faced by means of standard nonlinear optimization approaches. In fact, it has been usually tackled by replacing the \(\ell _0\)-norm with the \(\ell _1\)-norm, thus obtaining an optimization problem, the \(\ell _1\)-regularization one (\(\textrm{SOP}_1\)), whose tractability rather depends on the properties of f, the \(\ell _1\) term being a convex function. It has been proved (see [16, 17, 21]) that, under appropriate conditions the solutions of (\(\textrm{SOP}\)) and (\(\textrm{SOP}_1\)) coincide. Nevertheless, in many practical applications the equivalence conditions do not hold true and the solutions obtained from the \(\ell _1\) minimization problem are less sparse that those of the \(\ell _0\) problem.
A different viewpoint in dealing with the bi-objective nature of sparse optimization is given by the cardinality-constrained formulation

where sparsity is ensured by forcing the \(\ell _0\)-norm to be not larger than a given integer \(t \in \{ 1,\ldots ,n-1 \}\), thus obtaining minimizers with at least \(n-t\) zero components. Such a problem has been studied in depth in recent years due to its possible application in areas of relevant interest such as compressed sensing [21] and portfolio selection [10]. We refer the reader to [37] for an up-to-date survey. Here, we only mention [4], on the theoretical side, where necessary optimality conditions have been analyzed, and [15, 24], on the methodological side, where reformulations as mathematical programs with complementarity constraints have been proposed.
In this paper we focus on sparse optimization as an effective way to deal with Feature Selection (FS) in Machine Learning (ML), see [32], where the problem is to detect the sample parameters which are really significant in applications such as unsupervised learning (see [22]) and regression (see [45]). In particular, we restrict our attention to supervised binary classification, an area where intensive research activity has been performed in the last decades, mainly since the advent of Support Vector Machine (SVM) as the election classification methodology, see [19, 47].
Most of the applications of sparse optimization to feature selection fall into two classes of methods, those where the \(\ell _0\)-norm has been approximated by means of appropriate concave functions (see, e.g., [13, 14, 42, 49]) and those where sparsity of the solution has been enforced by resorting to the definition of appropriate sets of binary variables, giving rise to Mixed Integer Linear (MILP) or even Mixed Integer Non Linear (MINLP) problems. In fact, it is natural to associate to any continuous variable an appropriate binary one according to its property of being zero or nonzero. Mixed integer reformulations have been widely adopted in relevant areas of Machine Learning such as classification, logistic regression, medical scoring etc. (see e.g. [7, 8, 20, 43, 46] and the references therein). As for the SVM literature we cite here [6, 29, 39].
The model we propose is inspired by the possibility of connecting the \(\ell _0\)-norm to the vector k-norm, which is defined as the sum of the k largest absolute-value components of any vector, and is a polyhedral norm, thus relatively easy to be treated by standard tools of convex nonsmooth optimization. Properties of the vector k-norm have been investigated in several papers (see, e.g., [30, 41, 50]). We particularly recall the applications to matrix completion, see [40], and to linear system approximation, see [48], as a possible alternative to the use of classic \(\ell _1\), \(\ell _2\) and \(\ell _{\infty }\) norms.
More recently, vector k-norm has been proved to be an effective tool for dealing with sparse optimization, see [31], also with specific applications to feature selection in the SVM framework, see [28]. The use of k-norm is somehow evoked also in the trimmed LASSO model described in [9].
The novelty of this paper is the development of a continuous k-norm-based model which is obtained as the continuous relaxation of a MINLP problem. The objective function comes out to be nonconvex, in particular of the Difference-of-Convex (DC) type, thus our approach is closer to the trimmed LASSO [9] than to the SLOPE method [5, 11]. Other DC-like approaches are presented in [23, 38, 52].
The remainder of the article is organized as follows. In Sect. 2 we summarize the properties of vector k-norms, and we introduce a couple of MINLP reformulations of the \(\ell _0\)-regularization problem (\(\textrm{SOP}\)). In Sect. 3 we consider the continuous relaxations of both such reformulations, and we focus in Sect. 4 to the one based on vector k-norm, which consists of a DC (Difference of Convex) optimization problem. In Sect. 5 we cast the SVM-based Feature Selection problem into our sparse optimization setting. Finally, in Sect. 6 we report on the computational experience, obtained on some benchmark datasets for binary classification, of both relaxed MINLP reformulations, highlighting the role of k-norms in increasing sparsity levels of the solutions.
Notation Vectors are represented in lower-case bold letters, with \(\textbf{e}\) and \(\textbf{0}\) representing vectors with all the elements equal to one and to zero, respectively. The inner product of vectors \(\textbf{x}\) and \(\textbf{y}\) is denoted by \(\textbf{x}^\top \textbf{y}\). Given any vector in \(\mathbb {R}^n\), say \(\textbf{x} = (x_1,\ldots ,x_n)^\top \), we denote the \(\ell _p\)-norm, with \(1\le p < +\infty \), and the \(\ell _\infty \)-norm, respectively, by
Furthermore, we recall the definition of the \(\ell _0\)-norm
and some of its relevant properties:
-
(i)
\(\Vert \textbf{x}\Vert _0=0 \quad \Leftrightarrow \quad \textbf{x}=\textbf{0}\);
-
(ii)
\(\Vert \textbf{x}+\textbf{y}\Vert _0 \le \Vert \textbf{x}\Vert _0+ \Vert \textbf{y}\Vert _0\);
-
(iii)
\(\Vert \alpha \textbf{x} \Vert _0 \ne |\alpha | \Vert \textbf{x}\Vert _0\);
-
(iv)
\( (\Vert \cdot \Vert _p)^p \rightarrow \Vert \cdot \Vert _0 \quad \text{ when }\quad p \rightarrow 0\);
-
(v)
\( \lim \inf _{\textbf{x} \rightarrow \overline{\textbf{x}}} \Vert \textbf{x}\Vert _0 \ge \Vert \overline{\textbf{x}}\Vert _0 \), i.e., \(\Vert \cdot \Vert _0\) is lower semicontinuous.
2 MINLP-based formulations of the \(\ell _0\)-regularization problem
Introducing an n-dimensional binary decision-vector \(\textbf{z}\), associated to \(\textbf{x}\), whose kth component \(z_k\) is set to one if \(x_k>0\) and set to zero otherwise, an obvious and classic reformulation of problem (\(\textrm{SOP}\)) is the following
where the positive “big” M parameter denotes a uniform bound on the absolute value of any single component of \(\textbf{x}\). It is easy to verify that any minimizer \((\textbf{x}^*,\textbf{z}^*)\) of (MISOP) is such that
and, consequently, the term \(\textbf{e}^\top \textbf{z}^*\) actually represents the \(\ell _0\)-norm of \(\textbf{x}^*\). It is worth observing that an ideal threshold for M is \(M^*\triangleq \Vert \textbf{x}^*\Vert _{\infty } \), where \(\textbf{x}^*\) is any global minimum of (SOP), as indeed any \(M \ge M^*\) guarantees equivalence of (SOP) and (MISOP).
In view of introducing an alternative MINLP-based reformulation of (\(\textrm{SOP}\)), we first recall, for \(k\in \{1,\ldots ,n\}\), the polyhedral vector k-norm \(\Vert \textbf{x}\Vert _{[k]}\), defined as the sum of the k largest unsigned components of \(\textbf{x}\). In particular, given \(\textbf{x}=(x_1,\ldots ,x_n)^\top \), and adopting the following notation
such that
the vector k-norm of \(\textbf{x}\) can be expressed as
Moreover, it is easy to see that \(\Vert \cdot \Vert _{[k]}\) fulfills the following properties:
Now, focusing in particular on the equivalence (9), and introducing an n-dimensional binary decision-vector \(\textbf{y}\), whose kth component \(y_k\) is set to one if \(\Vert \textbf{x}\Vert _1-\Vert \textbf{x}\Vert _{[k]}>0\) and set to zero otherwise, it is possible to state yet another mixed binary reformulation of problem (\(\textrm{SOP}\)) as the following
where the sufficiently large parameter \(M'>0\) has been introduced. An equivalence between (MIkSOP) and (SOP) can be obtained in the constrained case where \(\textbf{x}\) is restricted to stay in a compact set \(S \subset \mathbb {R}^n\). In fact, letting \(D\triangleq \max _{\textbf{x} \in S}\Vert \textbf{x}\Vert _1\), and observing that
then any \(M' \ge \left( 1-\frac{1}{n}\right) D\) ensures the equivalence. Unlike (MISOP) formulation (1)–(4), the (MIkSOP) formulation (10)–(12) is characterized by the presence of a set of nonconvex constraints (11), whose left hand sides are, in particular, DC functions. Furthermore, as for the objective function, we remark that the only feasible solutions of (MIkSOP) which are candidates to be optimal are those \((\textbf{x},\textbf{y})\) for which the equivalence
holds for every \(k \in \{1,\ldots ,n\}\). Observing that at any of such solutions it is necessarily \(y_n=0\) and that, provided \(\textbf{x} \ne \textbf{0}\), there holds
it follows that
which implies that if \((\textbf{x}^*,\textbf{y}^*)\) is optimal for problem (MIkSOP), then \(\textbf{x}^*\) is optimal for problem (SOP) as well.
In the sequel, we analyze the continuous relaxation of the MINLP-based formulations (MISOP) and (MIkSOP), assuming in particular that f is a convex function, not necessarily differentiable.
3 Continuous relaxation of MINLP-based SOP formulations
We start by studying the continuous relaxation (RSOP) of (MISOP), obtained by replacing the binary constraints \(\textbf{z} \in \{0,1\}^n\) with \(\textbf{0} \le \textbf{z} \le \textbf{1}\). A simple contradiction argument ensures that any minimizer \((\overline{\textbf{x}},\overline{\textbf{z}})\) of (RSOP) satisfies by equality at least one constraint of the pair \(x_k \le Mz_k\) and \(x_k \ge -Mz_k\), for every \(k \in \{1,\ldots , n\}\). More precisely, if \(\overline{x}_k \ne 0\) then either \(M\overline{z}_k = \overline{x}_k> 0 > -M\overline{z}_k\), or \(-M\overline{z}_k = \overline{x}_k< 0 < M\overline{z}_k\), while if \(\overline{x}_k \ne 0\) then \(\overline{z}_k=0\). Summarizing, \((\overline{\textbf{x}},\overline{\textbf{z}})\) is such that \(\overline{z}_k= \displaystyle \frac{|\overline{x}_k|}{M}\) for every \(k \in \{1,\ldots , n\}\), from which it follows that
and the relaxed problems (RSOP) can be written as
In other words, the continuous relaxation of (MISOP) just provides the \(\ell _1\)-regularization of function f, often referred to as LASSO model, a convex, possibly nonsmooth program due to the assumption made on f (for a discussion on LASSO and possible variants see, e.g., [52]).
Consider now the continuous relaxation (RkSOP) of (MIkSOP), where \(\textbf{0} \le \textbf{y} \le \textbf{1}\) replace \(\textbf{y} \in \{0,1\}^{n}\). Note that any minimizer \((\widetilde{\textbf{x}},\widetilde{\textbf{y}})\) of (RkSOP) satisfies by equality all the constraints (11), since if this were not the case for some k, the corresponding \(\widetilde{y}_k\) would be reduced, leading to a reduction in the objective function without impairing feasibility. Consequently,every continuous variable \(\widetilde{y}_k\), with \(k\in \{1,\ldots ,n\}\), is such that
implying that
As a consequence, (RkSOP) can be stated as

We observe that, recalling (7), the sum of the k-norm of \(\textbf{x}\) can be written as
Hence, taking into account the definition of \(\Vert \textbf{x}\Vert _1\), we obtain that
and, consequently, we come out with the problem
The latter formula highlights that increasing weights are assigned to decreasing absolute values of the components of \(\textbf{x}\), i.e., the smaller is the absolute value the bigger is its weight; this somehow indicates a kind of preference towards reduction of the small components, which is, in turn, in favor of reduction of the \(\ell _0\)-norm of \(\textbf{x}\).
Remark 1
Formula (16) clarifies the differences between our approach and the SLOPE method (see [5, 11]), the trimmed LASSO method (see [9]), the approach proposed in [28] and the \(\ell _{1-2}\) method [51]. In SLOPE, a reverse ordering of the weights with respect to our model is adopted, as components \(|x_{j_s}|\) are associated to non-increasing penalty weights. In fact, the resulting convex program is
with \(\lambda _1 \ge \lambda _2\ge \cdots \ge \lambda _n\). Given any \(\sigma > 0\), a possible choice of parameters is
for some sparsity parameter \(t \in \{1,\ldots ,n-1\}\). Under such a choice problem (17) becomes the following convex penalized k-norm model:
In trimmed LASSO, given a sparsity parameter \(t \in \{1,\ldots ,n-1\}\), the following nonconvex problem is addressed
where, unlike our approach, components of \(\textbf{x}\) with the highest absolute values are not penalized at all, whereas the \((n-t)\) smallest ones are equally penalized. As for the approach presented in [28], it can be proved that, for a given penalty parameter \(\sigma >0\), letting \(J_\sigma (\textbf{x})\triangleq \big \{j \in \{1,\ldots ,n\} : x_j> \frac{1}{\sigma }\big \}\), the proposed DC (hence nonconvex) program can be formulated as
which tends to (\(\textrm{SOP}\)) as \(\sigma \rightarrow \infty \). Finally, we remark the substantial difference between the method we propose and the \(\ell _{1-2}\) approach [51], where the \(\ell _0\) pseudo-norm is approximated by the DC model \(\Vert \textbf{x}\Vert _1-\Vert \textbf{x}\Vert _2 \).
A better insight into the differences between the two formulations (RSOP) and (Rk-SOP) can be gathered by appropriate setting of the constants M and \(M'\). Since the former is referred to single vector components and the latter to norms, it is natural to set
With such choice the objective function \(\widetilde{F}(\cdot )\) of (RkSOP) becomes:
We observe that function \(\widetilde{F}(\cdot )\) is the difference of two convex functions, namely,
with
and
As a consequence, (RkSOP) can be handled by resorting to both the theoretical and the algorithmic tools of DC programming (see, e.g., [2, 33, 44]). Moreover, we observe that \(f_1\) is exactly the objective function of (RSOP), thus it is
Summing up, \(\overline{F}(\textbf{x})\) is convex and majorizes the (nonconvex) \(\widetilde{F}(\textbf{x})\), with \(f_2(\textbf{x}) \) being the nonnegative gap, whose value depends on the sum of the k-norms.
4 Properties of problem (RkSOP) and its solutions
We start by analyzing some properties of function \(f_2(\cdot )\). First, taking into account (14) and (26), we rewrite \(f_2\) as
where \(c_s=1- \frac{(s-1)}{n}\), for every \(s \in \{1,\ldots ,n\}\), with \(c_1> c_2> \cdots > c_n\). Next, in order to study the behavior of \(f_2(\cdot )\) at equal \(\ell _1\)-norm value, we consider any ball \(B(\textbf{0}, \rho ) \triangleq \{\textbf{x} \in \mathbb {R}^n: \, \Vert \textbf{x}\Vert _1=\rho \}\), centered at the origin with radius \(\rho >0\), and we focus on the following two optimization problems \((P^{\textrm{max}})\) and \((P^{\textrm{min}})\), respectively.

and

We observe that, denoting by \(\Pi \) the set of all permutations of \(\{1,\ldots ,n\}\), both problems can be decomposed in several problems of the type

and

respectively, for every \(\pi \in \Pi \). We remark that (\(P^{\textrm{max}}_\pi \)) and (\(P^{\textrm{min}}_\pi \)) are nonconvex programs, due to the nonconvex ordering constraints \(|x_{\pi _s}| \ge |x_{\pi _{s+1}}|\), and we denote their global solutions by \(\textbf{x}_\pi ^{(\textrm{max})}\) and \(\textbf{x}_\pi ^{(\textrm{min})}\), respectively.
Proposition 4.1
For any given \(\pi \in \Pi \), the following properties regarding optimal solutions of (\(P^{\textrm{max}}_\pi \)) and (\(P^{\textrm{min}}_\pi \)) hold:
-
(i)
Problem (\(P^{\textrm{max}}_\pi \)) has two maximizers \(x^{(\textrm{max})}_{\pi _1} = \pm \rho \), \(x^{(\textrm{max})}_{\pi _2}=\cdots =x^{(\textrm{max})}_{\pi _n}=0\). They are both global, with objective function value \(f_2(\textbf{x}^{(\textrm{max})})= \frac{\rho \sigma }{M}\);
-
(ii)
Problem \((P^{min})\) has \(2^n\) global minimizers \(|x^{(\textrm{min})}_{\pi _1}|=\cdots =|x^{(\textrm{min})}_{\pi _n}|= \frac{\rho }{n}\), with objective function value \(f_2(\textbf{x}^{(\textrm{min})})= \frac{\rho \sigma }{M}\big (\frac{n+1}{2n}\big )\).
Proof
-
(i)
The property follows by observing that the solutions \(|x^{(\textrm{max})}_{\pi _1}|=\rho \), \(x^{(\textrm{max})}_{\pi _2}=x^{(\textrm{max})}_{\pi _3}=\cdots =x^{(\textrm{max})}_{\pi _n}=0\), due to (27), are optimal for the relaxation obtained by eliminating the ordering constraints from (\(P^{\textrm{max}}_\pi \)), and that such solutions are also feasible for (\(P^{\textrm{max}}_\pi \)).
-
(ii)
We observe first that the monotonically decreasing structure of the cost coefficients \(c_s\) guarantees that at the optimum \(|x^{(\textrm{min})}_{\pi _s}|>|x^{(\textrm{min})}_{\pi _{s+1}}|\) cannot occur for any index \(s \in \{1,\ldots ,(n-1)\}\). Consequently, it comes out from satisfaction of the ordering constraints in (\(P^{\textrm{min}}_\pi \)), and from \(\textbf{x}^{(\textrm{min})} \in B(\textbf{0}, \rho )\), that the optimal solutions satisfy \(|x^{(\textrm{min})}_{\pi _1}|=\cdots =|x^{(\textrm{min})}_{\pi _n}|= \frac{\rho }{n}\) and the property follows.
\(\square \)
Remark 2
The optimal solutions of (\(P^{\textrm{max}}_\pi \)) depend on \(\pi \), in particular on the choice of the index \(\pi _1\), but they have all the same optimal value. Thus problem (\(P^{\textrm{max}}\)) has a total number of 2n global solutions, with \(f_2^{\textrm{max}} = \frac{\rho \sigma }{M}\). As for problem (\(P^{\textrm{min}}_\pi \)), the \(2^n\) optimal solutions are independent of \(\pi \), hence they are also global solution for (\(P^{\textrm{min}}\)), with \(f_2^{(\textrm{min})}= \frac{\rho \sigma }{M}\big (\frac{n+1}{2n}\big )\). As a consequence, the variation \(\Delta (\rho )\) of \(f_2\) on \(B(\textbf{0},\rho )\) is
Remark 3
The \(\ell _0\)-norm of the optimal solutions of problem (\(P^{\textrm{max}}\)) is equal to 1, while the \(\ell _0\)-norm of those of (\(P^{\textrm{min}}\)) is equal to n. As a consequence, the (subtractive) gap \(f_2\), for a fixed value of the \(\ell _1\) norm, is maximal when \(\Vert \textbf{x}\Vert _0=1\) and it is minimal when all components are nonzero and equal in modulus, that is \(\Vert \textbf{x}\Vert _0=n\); in other words, model (RkSOP) exhibits a stronger bias towards reduction of the \(\ell _0\)-norm than (RSOP). Of course, the price to be paid to obtain such an advantage is the need of solving the DC (global) optimization problem (RkSOP) instead of the convex program (RSOP).
An additional insight into properties of the solutions of (RkSOP) can be obtained by focusing on the related necessary conditions for global optimality. In particular, at any global minimizer \(\widetilde{\textbf{x}}\), taking into account the DC decomposition (24), the inclusion
is satisfied, see [34]. Before introducing a property of minimizers in terms of their \(\ell _0\) norm, we recall some differential properties of the k-norm, see [31]. The subdifferential at any point \(\textbf{x} \in \mathbb {R}^n\) is
In particular, given any \(\overline{\textbf{x}} \in \mathbb {R}^n\), and denoting by \(J_{[k]}(\overline{\textbf{x}}) \triangleq \{j_1,\ldots ,j_k\}\) the index set of k largest absolute-value components of \(\overline{\textbf{x}}\), a subgradient \(\overline{\textbf{g}}^{[k]} \in \partial \Vert \overline{\textbf{x}}\Vert _{[k]}\) can be obtained as
Moreover, we note that the subdifferential \(\partial \Vert \cdot \Vert _{[k]}\) is a singleton (i.e., the vector k-norm is differentiable) any time the set \(J_{[k]}(\cdot )\) is uniquely defined.
As for the subdifferential \(\partial \Vert \cdot \Vert _1\) of the \(\ell _1\) norm, we recall that its element are the subgradients \(\overline{\textbf{g}}^{(1)}\) at \(\overline{\textbf{x}}\) whose jth component, for every \(j \in \{1,\ldots ,n\}\), is obtained as
where \(\alpha _j \in [-1,1]\). Summing up, we get
and
The following proposition provides a quantitative evaluation of the effect of the penalty-parameter \(\sigma \) on the \(\ell _0\)-norm of a global minimizer.
Proposition 4.2
Let \(\widetilde{\textbf{x}}\) denote a global minimizer of the k-norm relaxation (RkSOP), and L denote the Lipschitz constant of f. Then, the following inequality holds at \(\widetilde{\textbf{x}}\):
Proof
Satisfaction of the inclusion (28) at \(\widetilde{\textbf{x}}\) implies that, for each subgradient \(\widetilde{\varvec{\xi }}^{(2)} \in \partial f_2(\widetilde{\textbf{x}})\) there exists a couple of subgradients \(\widetilde{\varvec{\xi }} \in \partial f(\widetilde{\textbf{x}})\) and \(\widetilde{\varvec{\xi }}^{(1)} \in \frac{\sigma }{M}\partial \Vert \textbf{x}\Vert _1\) such that
Now suppose \(\Vert \widetilde{\textbf{x}}\Vert _0=r\), for some \(r \in \{1,\ldots ,n\}\) and, w.l.o.g., assume that
with the remaining components, if any, equal to zero, that is \(J_{[k]}(\widetilde{\textbf{x}})=\{1,2,\ldots ,k\}\), for every \(k \in \{1,\ldots ,n\}\). Now pick, for \(k=1,\ldots ,n\), a subgradient in \(\partial \Vert \widetilde{\textbf{x}}\Vert _{[k]}\) defined as in (30) and calculate \(\widetilde{\varvec{\xi }}^{(2)} \in \partial f_2(\widetilde{\textbf{x}})\) as
By simple calculation we get
where
By a component-wise rewriting of condition (32), and taking into account only the components \(j \in \{1,\ldots ,r\}\) such that \(\widetilde{x}_j \ne 0\), from (31) we obtain that at the minimizer \(\widetilde{\textbf{x}}\), for some \(\widetilde{\varvec{\xi }} \in \partial f(\widetilde{\textbf{x}})\) it is
that is
Then, taking into account \(|\widetilde{\xi }_j| \le L\), the thesis follows by observing that condition (33) implies
\(\square \)
Remark 4
Proposition 4.2 suggests a quantitative way to control sparsity of the solution acting on parameter \(\sigma \). It is worth pointing out, however, that the bound holds only if a global minimizer is available. This is not necessarily the case if a local optimization algorithm is adopted, as we do in Sect. 6.
5 Feature selection in support vector machine (SVM)
In the SVM framework for binary classification two (labeled) point-sets \(\mathcal{A} \triangleq \{ \textbf{a}_1, \ldots , \textbf{a}_{m_1} \}\) and \(\mathcal{B} \triangleq \{\textbf{b}_1, \ldots , \textbf{b}_{m_2} \}\) in \(\mathbb {R}^n\) are given, the objective being to find a hyperplane, associated to a couple \((\textbf{x} , \gamma ) \in \mathbb {R}^n \times \mathbb {R}\), strictly separating them. Thus, it is required that the following inequalities hold true:
The existence of such a hyperplane is ensured if and only if \(\textrm{conv} \mathcal A \cap \textrm{conv} \mathcal B =\emptyset \), a property hard to be checked. A convex, piecewise linear and nonnegative error function of \((\textbf{x}, \gamma )\) is thus defined. It has the form
being equal to zero if and only if \((\textbf{x}, \gamma )\) actually defines a (strictly) separating hyperplane satisfying (34–35).
In the SVM approach the following convex problem
is solved, where the norm of \(\textbf{x}\) is added to the error function aiming to obtain a maximum-margin separation, C being a positive trade-off parameter.
The \(\ell _1\) and \(\ell _2\) norms are in general adopted in model (37), but, in case feature selection is pursued, the \(\ell _0\)-norm looks as the most suitable tool, although the \(\ell _1\)-norm is usually considered as a good approximation. In the following, we will focus on the feature selection \(\ell _0\)-norm problem
by applying a relaxed model of the type (RkSOP) and the relative machinery. Note that, to keep the notation as close as possible to that commonly adopted in the SVM framework, the trade-off parameter C, unlike the classical formulation of (SOP), where parameter \(\sigma \) is present, is now equivalently put in front of the error term \(e(\textbf{x}, \gamma )\).
Our MINLP formulation of problem of (38), along the guidelines of the (MIkSOP) model (10–12), letting \(M=1\) and \(M'=n\) (see (22)), is
By adopting the same relaxation scheme described in §3, we obtain the DC continuous program (SVM-RkSOP)

an SVM model, tailored for feature selection, as it exploits the continuous relaxation of (MISOP), whose computational behavior will be analyzed in the next section.
6 Computational experience
We have evaluated the computational behavior of our SVM-based feature selection model (SVM-RkSOP) by testing it on 8 well known datasets whose relevant details are listed in Table 1. In particular, we remark that such datasets can be partitioned in two groups depending on the relative proportion between the number of points (\(m_1+m_2\)) and the number of features (n). From this viewpoint, datasets 1 to 4 have a large number of points compared to the small number of features, whilst datasets 5 to 8 have a large number of features compared to the small number of points.
We recall that (SVM-RkSOP) is a DC optimization problem, analogous to (24), where
and
that can be tackled by adopting techniques, like those described in [3, 27, 36], which require to calculate at each iterate-point the linearization of function \(f_2(\cdot )\). In fact, such linearization can be easily calculated by applying (30) at any point \(\overline{\textbf{x}} \in \mathbb {R}^n\) to a get a subgradient \(\overline{\textbf{g}}^{[k]} \in \partial \Vert \overline{\textbf{x}}\Vert _{[k]}\). In particular, we have implemented a version of the DCA algorithm, see [2], exploiting the fact that at an iterate point \(\overline{\textbf{x}}\), once obtained a linearization \(h_2(\overline{\textbf{x}},\cdot )\) of \(f_2(\cdot )\) at \(\overline{\textbf{x}}\), the new iterate-point can be calculated by minimizing the function
that can be easily turned into an equivalent linear program. Hence, applying DCA to (SVM-RkSOP) amounts to solving a sequence of linear programs as long as a decrease of the objective function is obtained. In order to evaluate the effectiveness of (SVM-RkSOP) solved by DCA, we will also make some comparison against the behavior of the convex standard \(\ell _1\)-norm-based SVM model (SVM-RSOP)
whose solution can be easily obtained by solving just one equivalent linear program, next referred to as LP-SVM-RSOP. The experimental plan for both approaches is based on a two-level cross-validation protocol to tune parameter C and to train the classifier. In fact, the tenfold cross-validation approach has been adopted at the higher level to train the classifier, every dataset being randomly partitioned into 10 groups of equal size. Then, 10 different blocks (the training sets) are built, each containing 9 out of 10 groups. Every block is used to train the classifier, using the left out group as the testing-set that returns the percentage of correctly classified bags (test correctness). Before executing the training phase, at the lower level it is needed to tune parameter C. A grid of 20 values, ranging between \(10^{-3}\) and \(10^{2}\), has been selected, and a five-fold cross-validation approach has been adopted on each training set (the model-selection phase). For each training set, we choose the C value as the one returning the highest average test-correctness. As for the selection of an appropriate starting point for DCA applied to (SVM-RkSOP), next referred to as DCA-SVM-RkSOP, denoting by \(\textbf{x}_a\) the barycenter of all the \(\textbf{a}_i\) instances, and by \(\textbf{x}_b\) the barycenter of all the \(\textbf{b}_l\) instances, we have selected the starting point \((\textbf{x}_0,\gamma _0)\) by setting
and choosing \(\gamma _0\) such that all the \(\textbf{b}_l\) instances are well classified. We have implemented the DCA-SVM-R k SOP algorithm [26] in Python 3.6, and run the computational experiments on a 2.80 GHz Intel(R) Core(TM) i7 computer. The LP solver of IBM ILOG CPLEX 12.8 [35] has been used to solve linear programs. The numerical results regarding DCA-SVM-RkSOP and LP-SVM-RSOP are reported in Table 2 and Table 3, respectively, where we list the percentage correctness averaged over the 10 folds of both the testing and the training phases. Moreover, we report the values ft0, ft-2, ft-4, and ft-9, representing the percentage average of features for which the corresponding component of the minimizer \(\textbf{x}^*\) is larger than 1, \(10^{-2}\) , \(10^{-4}\) , \(10^{-9}\), respectively. Hence, small values of ft-9 denote high sparsity of \(\textbf{x}^*\). Finally we also report the cpu time (measured in seconds) regarding the execution time of DCA-SVM-R k SOP and LP-SVM-RSOP in the training phase, averaged over the 10 training folds.
The results clearly show the benefits of the regularization model obtained by exploiting vector-k-norms. In fact, for all datasets DCA-SVM-RkSOP returns average test-correctness never significantly worse than LP-SVM-RSOP, managing to improve on sparsity levels. If the latter outcome is apparent although not particularly relevant for small-size problems, it turns out very significant for large-size problems for which sparsity increases of an order of magnitude. Take, for an example, the Leukemia/ALLAML dataset, having 5327 features: while LP-SVM-RSOP manages to get an average test-correctness of 95.42% using around 33 features, DCA-SVM-RkSOP returns an average test-correctness of 93.81% using only 5 features. As expected, such improvement is obtained at the expenses of an increased computational time.
Finally, to evaluate (SVM-RkSOP) not only against the \(\ell _1\)-norm-based SVM model (SVM-RSOP), we have implemented the convex k-norm-based model (19), that, as previously remarked, can be seen as a special case of the SLOPE approach (17), based on the weight setting (18) for some \(t \in \{1,\ldots ,n-1\}\). In fact we have defined the (SVM-kPURE) model as follows:

To handle such problem we have used the solver *|NCVX|, a general-purpose code for nonsmooth optimization described in [25].
We have adopted different experimentation strategies for datasets 1–4 and 5–8. In particular for the first group we have set \(t=0.6 n\) (with possible rounding) and have tested \(\sigma =1\) and \(\sigma =100\). The results are in Tables 4 and 5, respectively. As for datasets 5–8, characterized by large values of n, we have tested two different settings of t. The first one is the same as for datasets 1–4, that is \(t=0.6n\). The second one comes from the results obtained by (SVM-RSOP). In fact, letting \(t_{\text{ svm }}=n(\text{ ft-9})/100\), where \(\text{ ft-9 }\) is available in the bottom half part of Table 3, we have selected \(t=t_{\text{ svm }}\) as the average number of significant components of \(\textbf{w}\) at the solution of (SVM-RSOP). Since we have observed that the results are rather insensitive to the parameter \(\sigma \), we report in Tables 6 and 7 only the ones obtained for \(\sigma =1\).
The results demonstrate that the simplistic use of the k-norm in the convex setting provides poor performance, definitely worse even than the \(\ell _1\)-norm model. Taking in fact \(\text{ ft-9 }\) as a measure of sparsity, we observe that on datasets of the first group (Tables 4 and 5) no significant sparsity is enforced for \(\sigma =1\), while for \(\sigma =100\) the results for the two datasets Diabetes and Heart are sparse, at the expenses of a severe reduction of the classification correctness. As for the datasets of the second group, for both choices of t we observe (Tables 6 and 7) that the solutions are not at all sparse, while the large difference between training and testing correctness indicates the presence of overfitting.
We remark that in our experiments we have not considered the comparison of our model with the plain MILP formulation (MISOP), as the superiority of the k-norm based approaches has been elsewhere demonstrated (see [28, 29]), at least for problems of reasonable size. As for comparison with the k-norm based approach \(\texttt {SVM}_\texttt {0}\) described in [28], it has to be taken into account that the results therein (see Tables 6 and 7) are strongly affected by the penalty parameter choice. Nevertheless, as far as test-correctness is considered, from comparison of Table 2 with [28, Table 5], we observe that each of the two approaches \(\texttt {SVM}_\texttt {0}\) and DCA-SVM-RkSOP prevails on four of the eight datasets considered in both papers. As for sparsity of the solutions, the behavior is comparable on the data sets of the second group, while \(\texttt {SVM}_\texttt {0}\) exhibits stronger sparsity enforcement on the first group of datasets, somehow at expenses of test-correctness.
7 Conclusions
We have introduced a novel continuous nonconvex k-norm-based model for sparse optimization, which is derived as the continuous relaxation of a MINLP problem. We have applied such model to Feature Selection in the SVM setting and the results suggest the superiority of the proposed approach over other attempts to simulate the \(\ell _0\) pseudo-norm (e.g., the \(\ell _1\) norm penalization). On the other hand, we have also observed that the mere replacement of the \(\ell _0\) pseudo-norm with the k-norm, evoked in some methods available in the literature, does not provide satisfactory results, at least in the experimentation area considered in this paper.
Data availability
The datasets analyzed during the current study are available in the following repository: https://github.com/GGiallombardo/DCA-SVM-RkSOP.
References
Amaldi, E., Kann, V.: On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems. Theoret. Comput. Sci. 209(1–2), 237–260 (1998)
An, L.T.H., Tao, P.D.: The DC (difference of convex functions) programming and DCA revisited with DC models of real world nonconvex optimization problems. Ann. Oper. Res. 133, 23–46 (2005)
An, L.T.H., Nguyen, V.V., Tao, P.D.: A DC programming approach for feature selection in support vector machines learning. Adv. Data Anal. Classif. 2, 259–278 (2008)
Beck, A., Eldar, Y.C.: Sparsity constrained nonlinear optimization: Optimality conditions and algorithms. SIAM J. Optim. 23(3), 1480–1509 (2013)
Bellec, P.C., Lecué, G., Tsybakov, A.B.: Slope meets lasso: Improved oracle bounds and optimality. Ann. Stat. 46(6B), 3603–3642 (2018)
Bertolazzi, P., Felici, G., Festa, P., Fiscon, G., Weitschek, E.: Integer programming models for feature selection: New extensions and a randomized solution algorithm. Eur. J. Oper. Res. 250(2), 389–399 (2016)
Bertsimas, D., King, A., Mazumder, R., et al.: Best Subset Selection via a Modern Optimization Lens. Ann. Stat. 44(2), 813–852 (2016)
Bertsimas, D., King, A.: Logistic regression: from art to science. Stat. Sci. 32(3), 367–384 (2017)
Bertsimas, D., Copenhaver, M.S., Mazumder, R.: The trimmed Lasso: sparsity and robustness. arXiv preprint (2017b) https://arxiv.org/pdf/1708.04527.pdf
Bienstock, D.: Computational study of a family of mixed-integer quadratic programming problems. Math. Programm. Ser. B Part A 74(2), 121–140 (1996)
Bogdan, M., van den Berg, E., Sabatti, C., Su, W., Candès, E.J.: Slope-adaptive variable selection via convex optimization. Ann. Appl. Stat. 9(3), 1103–1140 (2015)
Bolón-Canedo, V., Sánchez-Maroño, N., Alonso-Betanzos, A., Benítez, J.M., Herrera, F.: A review of microarray datasets and applied feature selection methods. Inf. Sci. 282, 111–135 (2014)
Bradley, P.S., Mangasarian, O.L.: Feature selection via concave minimization and support vector machines. In: Machine Learning proceedings of the fifteenth international conference (ICML ’98). Shavlik J editor, Morgan Kaufmann, San Francisco, California, 82–90 (1998)
Bradley, P.S., Mangasarian, O.L., Street, W.N.: Feature selection via mathematical programming. INFORMS J. Comput. 10(2), 209–217 (1998)
Burdakov, O.P., Kanzow, C., Schwartz, A.: Mathematical programs with cardinality constraints: Reformulation by complementarity-type conditions and a regularization method. SIAM J. Optim. 26(1), 397–425 (2016)
Candés, E.J., Romberg, J.K., Tao, T.: Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 59, 1207–1223 (2006)
Candés, E.J., Tao, T.: Decoding by linear programming. IEEE Trans. Inf. Theory 51, 4203–4215 (2005)
Chang, C.-C., Lin, C.-J.: LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2(27), 1–27 (2011)
Cristianini, N., Shawe-Taylor, J.: An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge University Press (2000)
Dedieu, A., Hazimeh, H., Mazumder, R.: Learning sparse classifiers: continuous and mixed integer optimization perspectives. (2020) arXiv preprint https://arxiv.org/pdf/2001.06471.pdf
Donoho, D.L.: Compressed sensing. IEEE Trans. Inf. Theory 52, 1289–1306 (2006)
Dy, J.G., Brodley, C.E., Wrobel, S.: Feature selection for unsupervised learning. J. Mach. Learn. Res. 5, 845–889 (2004)
Fan, J.Q., Li, R.Z.: Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96(456), 1348–1360 (2001)
Feng, M., Mitchell, J.E., Pang, J.-S., Shen, X., Wäcther, A.: Complementarity formulations of \(\ell _0\)-norm optimization problems. Pac. J. Optim. 14(2), 273–305 (2018)
Fuduli, A., Gaudioso, M., Giallombardo, G.: Minimizing nonconvex nonsmooth functions via cutting planes and proximity control. SIAM J. Optim. 14(3), 743–756 (2004)
Gaudioso, M., Giallombardo, G., Miglionico, G.: The DCA-SVM-RkSOP approach (2023) https://github.com/GGiallombardo/DCA-SVM-RkSOP
Gaudioso, M., Giallombardo, G., Miglionico, G., Bagirov, A.M.: Minimizing nonsmooth DC functions via successive DC piecewise-affine approximations. J. Global Optim. 71(1), 37–55 (2018)
Gaudioso, M., Gorgone, E., Hiriart-Urruty, J.B.: Feature selection in SVM via polyhedral \(k\)-norm. Optim. Lett. 14, 19–36 (2020)
Gaudioso, M., Gorgone, E., Labbé, M., Rodríguez-Chía, A.M.: Lagrangian relaxation for SVM feature selection. Comput. Oper. Res. 87, 137–145 (2017)
Gaudioso, M., Hiriart-Urruty, J.-B.: Deforming \(\Vert \cdot \Vert _1\) into \(\Vert \cdot \Vert _{\infty }\) via polyhedral norms: a pedestrian approach. SIAM Rev. 64(3), 713–727 (2022)
Gotoh, J., Takeda, A., Tono, K.: DC formulations and algorithms for sparse optimization problems. Math. Programm. Ser. B 169(1), 141–176 (2018)
Guyon, I., Elisseeff, A.: An introduction to variable and feature selection. J. Mach. Learn. Res. 3, 1157–1182 (2003)
Hiriart-Urruty, J.-B.: Generalized differentiability/duality and optimization for problems dealing with differences of convex functions. In Convexity and duality in optimization. Lecture Notes in Economics and Mathematical Systems (1985)
Hiriart-Urruty, J.-B.: From convex optimization to nonconvex optimization: necessary and sufficient conditions for global optimality. In: Nonsmooth Optimization and Related Topics, pp. 219–240. Plenum, New York/London (1989)
IBM ILOG CPLEX 12.8 User Manual (2018) IBM Corp. Accessed 13 May 2023. https://www.ibm.com/docs/SSSA5P_12.8.0/ilog.odms.studio.help/pdf/usrcplex.pdf
Joki, K., Bagirov, A.M., Karmitsa, N., Mäkelä, M.M.: A proximal bundle method for nonsmooth DC optimization utilizing nonconvex cutting planes. J. Global Optim. 68(3), 501–535 (2017)
Levato, T.: Algorithms for \(\ell _0\): norm optimization problems. Doctoral Dissertation, Dipartimento di Ingegneria dell’Informazione, Università di Firenze, Italia (2019)
Liu, Y.L., Bi, S.J., Pan, S.H.: Equivalent Lipschitz surrogates for zero-norm and rank optimization problems. J. Glob. Optim. 72, 679–704 (2018)
Maldonado, S., Pérez, J., Weber, R., Labbé, M.: Feature selection for Support Vector Machines via Mixed Integer Linear Programming. Inf. Sci. 279, 163–175 (2014)
Miao, W., Pan, S., Sun, D.: A Rank-Corrected Procedure for Matrix Completion with Fixed Basis Coefficients. Math. Program. 159, 289–338 (2016)
Overton, M.L., Womersley, R.S.: Optimality conditions and duality theory for minimizing sums of the largest eigenvalues of symmetric matrices. Math. Program. 62(1–3), 321–357 (1993)
Rinaldi, F., Schoen, F., Sciandrone, M.: Concave programming for minimizing the zero-norm over polyhedral sets. Comput. Optim. Appl. 46, 467–486 (2010)
Sato, T., Takano, Y., Miyashiro, R., Yoshise, A.: Feature subset selection for logistic regression via mixed integer optimization. Comput. Optim. Appl. 64(3), 865–880 (2016)
Strekalovsky, A.S.: Global optimality conditions for nonconvex optimization. J. Global Optim. 12, 415–434 (1998)
Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 58(1), 267–288 (1996)
Ustun, B., Rudin, C.: Supersparse linear integer models for optimized medical scoring systems. Mach. Learn. 102, 349–391 (2016)
Vapnik, V.: The Nature of the Statistical Learning Theory. Springer (1995)
Watson, G.A.: Linear best approximation using a class of polyhedral norms. Numer. Algorithms 2, 321–336 (1992)
Weston, J., Elisseeff, A., Schölkopf, B., Tipping, M.: Use of the zero-norm with linear models and kernel methods. J. Mach. Learn. Res. 3, 1439–1461 (2003)
Wu, B., Ding, C., Sun, D., Toh, K.-C.: On the Moreau-Yosida regularization of the vector \(k-\)norm related functions. SIAM J. Optim. 24(2), 766–794 (2014)
Yin, P., Lou, Y., He, Q., Xin, J.: Minimization of \(\ell _{1-2}\) for compressed sensing. SIAM J. Sci. Comput. 37(2), 536–563 (2015)
Zhang, C.H.: Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38, 894–942 (2010)
Funding
Open access funding provided by Universitá della Calabria within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gaudioso, M., Giallombardo, G. & Miglionico, G. Sparse optimization via vector k-norm and DC programming with an application to feature selection for support vector machines. Comput Optim Appl 86, 745–766 (2023). https://doi.org/10.1007/s10589-023-00506-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-023-00506-y