Abstract
We present a branch-and-prune procedure for discrete Nash equilibrium problems with a convex description of each player’s strategy set. The derived pruning criterion does not require player convexity, but only strict convexity of some player’s objective function in a single variable. If satisfied, it prunes choices for this variable by stating activity of certain constraints. This results in a synchronous branching and pruning method. An algorithmic implementation and numerical tests are presented for randomly generated instances with convex polyhedral strategy sets and convex quadratic as well as non-convex quadratic objective functions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The formulation of the Nash equilibrium for an n-person game by Nash in 1950 and 1951 was a landmark in the economic sciences and is still a key model in game theory [11, 12]. In the setting of this game, finitely many players can choose their individual strategies independently, but their payoffs depend on the strategies of all players. In the absence of coalitions, each player aims to maximize her payoff given the other players’ strategies. A situation in the game where no player has an incentive to unilaterally deviate from her strategy defines the famous Nash equilibrium, and finding such a situation is the so-called Nash equilibrium problem (NEP).
Over the last years, research gained interest in the numerical solution of NEPs, and there are a couple of algorithms tackling this issue. However, although integer optimization is applied in many fields and intensely studied, there are only few attempts to solve Nash equilibrium problems with integer variables. Sagratella’s publication [14] identifies this as an "important gap in literature". The latter paper proposes a branch-and-prune method to compute all solutions of NEPs with box-constrained discrete strategy sets. Subsequently, the theory was extended to generalized NEPs with linear coupling constraints and mixed-integer variables [15]. More recently, there were several publications on computing Nash equilibria for a special class of mixed-integer NEPs, the so-called integer programming games (IPG), which were first introduced in [9]. In IPGs, the feasible set of each player consists of linear constraints in her private variables, which are partially integrality constrained, and the payoff functions are only required to be continuous. For these general IPGs, [3] presents an algorithm for the computation of Nash equilibria based on algorithms for strategic games in normal-form. Furthermore, [2] introduced another subclass of mixed-integer NEPs, namely reciprocally-bilinear games (RBG), where the closure of the convex hull of each player’s feasible set is required to be a polyhedron and the payoff function is bilinear in her own and the rivals’ strategies. However, we will extend Sagratella’s framework beyond the box-constrained case and propose a novel branch-and-prune approach for discrete NEPs which takes convexity of the strategy sets explicitly into account.
We introduce the problem and describe preliminary results in Sect. 2. In Sect. 3, we deliver a pruning criterion for NEPs with convex strategy sets. Section 4 provides an algorithmic application of the criterion for convex polyhedral strategy sets with finite upper and lower bounds on each variable. In Sect. 5 we apply these findings numerically to discrete Nash equilibrium problems with convex polyhedral strategy sets and convex quadratic as well as non-convex quadratic objective functions. To the best of our knowledge, this is the first implemented and tested branch-and-prune procedure for this problem class. Finally, we wrap up our insights in Sect. 6.
2 Problem description and preliminary results
We study discrete Nash games with N players. In this setting, each player \(\nu = 1, \ldots , N \) aims to solve the optimization problem
The vector \(x^\nu \) lies in \({\mathbb {R}}^{n_\nu }\) and represents all variables which are controlled by the \(\nu \)-th player. The vector of all decision variables \(x= \left( x^1,\ldots ,x^N \right) \in {\mathbb {R}}^n\) then is of dimension \(n = \sum _{\nu = 1}^{N} n_\nu \), and the vector \(x^{-\nu }=\left( x^1,\ldots , x^{\nu -1},x^{\nu +1},\ldots ,x^N \right) \in {\mathbb {R}}^{n-n_\nu }\) contains all decision variables except player \(\nu \)’s. The notation \(x =\left( x^\nu ,x^{-\nu } \right) \) emphasizes those variables, but does not reorder the entries of x. The objective function \(\theta _\nu : \Omega \rightarrow {\mathbb {R}}\) has the domain
hence the player’s objective function value depends on her own strategy as well as on the other players’ strategies. The discrete feasible set
is called the \(\nu \)-th player’s strategy set. It is defined by the function \(g^\nu : {\mathbb {R}}^{n_\nu } \rightarrow {\mathbb {R}}^{m_\nu }\).
In this context, the Nash equilibrium is the most important and commonly used solution concept. A vector \(x^\star \) is called Nash equilibrium of this game, if for each \(\nu = 1,\ldots , N\), the vector \(x^{\star ,\nu }\) is an optimal point of \(Q^\nu (x^{\star ,-\nu })\), i.e., \(x^\star \in \Omega \) and
hold. The resulting Nash equilibrium problem may hence be formulated as
Our suggestion of a branch-and-prune approach for solving NEP will use its continuous relaxation \(\widehat{\textit{NEP}}\). There each player \(\nu \) solves the continuous problem
where the integrality condition is dropped in the strategy set
The domain \({\widehat{\Omega }}:= {\widehat{X}}_1 \times \ldots \times {\widehat{X}}_N\) of the objective functions is defined analogously, and a vector \({\widehat{x}}^\star \) is a Nash equilibrium of \(\widehat{\textit{NEP}}\) if \({\widehat{x}}^{\star ,\nu }\) solves \({\widehat{Q}}^\nu ({\widehat{x}}^{\star ,-\nu })\) for all \(\nu = 1,\ldots ,N\).
From now on, we use the following assumption.
Assumption 1.1
All entries of the function \(g^\nu \) are convex for each player \(\nu = 1,\ldots ,N\).
Note that we will state a stronger assumption on the strategy sets for the algorithmic implementation in Sect. 4. Clearly, under Assumption 2.1, each player’s relaxed strategy set \({{\widehat{X}}}_\nu \) is convex. If additionally each player’s objective function \(\theta _\nu \) is convex with respect to \(x^\nu \), \(\widehat{\textit{NEP}}\) is called player convex, which is a standard assumption for continuous NEPs. There are several possibilities to characterize and compute solutions of \(\widehat{\textit{NEP}}\) under player convexity. For example, if \({{\widehat{\Omega }}}\) satisfies the Slater condition, a vector \({{\widehat{x}}}^\star \) is a Nash equilibrium of \(\widehat{\textit{NEP}}\) if and only if \({{\widehat{x}}}^{\star ,\nu }\) is a Karush-Kuhn-Tucker (KKT) point of \({\widehat{Q}}^\nu (\widehat{x}^{\star ,-\nu })\) for each player (see [5, Prop. 1]). Other prominent solution techniques for \(\widehat{\textit{NEP}}\) are the variational inequality (VI) and the Nikaido-Isoda (NI) approaches [6]. Unfortunately, none of these approaches carry over to the discrete problem NEP. For the KKT and VI approaches this is due to the missing convexity of the discrete strategy sets \(X_\nu \). The NI-function, on the other hand, may be defined for NEP, but it turns out to be structurally nonsmooth, nonconvex and discontinuous, and thus hard to treat algorithmically [15]. We mention that the minimization of the NI-function of the NEP’s "convexified instance", as introduced in [8], is in some cases algorithmically tractable. However, we will not follow this approach, because we try to impose mild assumptions on the objective functions, which makes the required computation of their convex envelope rather impractical.
Instead, we will formulate an approach motivated by integer optimization techniques, where branch-and-bound algorithms are commonly used. Let us briefly recap the three key aspects of branch-and-bound for integer optimization, namely relaxation, branching and bounding. Firstly, branch-and-bound exploits that it is easier to compute an optimal point of the continuous relaxation and that, if this point is integer, it also solves the integer optimization problem over this set. Secondly, if the obtained solution is not integer, it is removed by branching the feasible set. Thirdly, it is essential that the minimal value over some subset of the continuously relaxed feasible set serves as a lower bound for objective values of the integer feasible points in this subset. Thus one can discard subsets if the minimal value over their relaxation is larger than the objective value of the best known integer solution in the whole feasible set. This feature is called bounding.
The following example will help to illustrate how, if at all, relaxation, branching and bounding carry over to the discrete problem NEP.
Example 2.2
For two players, each one controlling a scalar variable, let us consider the NEP with objective functions
and strategy sets
as well as their continuous relaxations
Since for any fixed \(x^{-\nu }\), the loss function of each player \(\nu \) is convex quadratic, the relaxed problem \(\widehat{\textit{NEP}}\) is player convex.
For any \(x^2\in {{\widehat{X}}}_2\) the unconstrained minimal point of \(\theta _1(\cdot ,x^2)\) is given by \(\nabla _{x^1}\theta _1(x^1,x^2)=0\), lies in \({{\widehat{X}}}_1\) and is, thus, the best response of player 1 to \(x^2\). On the other hand, only for \(x^1\in [0,3/2]\) the unconstrained minimal point of \(\theta _2(x^1,\cdot )\), characterized by \(\nabla _{x^2}\theta _2(x^1,x^2)=0\), lies in \({{\widehat{X}}}_2\), but for any \(x^1\in [3/2,3]\) the boundary point \(x^2=0\) is the best response to \(x^1\). Figure 1 illustrates that, thus, exactly the two points (0, 2) and (8/3, 0) solve \(\widehat{\textit{NEP}}\).
In contrast, the discrete problem NEP possesses exactly the three solutions (0, 2), (1, 1) and (3, 0). In particular, although the point (1, 1) lies close to the solution (0, 2) of NEP as well as of \(\widehat{\textit{NEP}}\), it is an equilibrium. Moreover, as opposed to the point (3, 0), it may not be obtained by rounding the entries of any of the solutions of \(\widehat{\textit{NEP}}\).
Feasible set of Example 2.2. Values \((\theta _1(x), \theta _2(x))\) are listed at each grid point
Regarding relaxation, in Example 2.2 the continuously relaxed problem \(\widehat{\textit{NEP}}\) is easy to solve, and the single discrete solution of \(\widehat{\textit{NEP}}\) also solves NEP. Also in general, the KKT, VI or NI methods can be employed to solve a player convex problem \(\widehat{\textit{NEP}}\) with differentiable defining functions, and the following result from [14, Prop. 2.1] guarantees that discrete solutions of the continuously relaxed problem solve the original discrete problem.
Proposition 1.3
Any solution \(x^\star \in {\mathbb {Z}}^n\) of \(\widehat{\textit{NEP}}\) also solves NEP.
Note that this result also holds without player convexity, but that in this case \({\widehat{NEP}}\) may not be easy to solve, even under Assumption 2.1. In Sect. 4 we will explain how we deal with non-convex objective functions. This means that with regard to relaxation we are in an analogous situation as in integer optimization. Concerning the branching step, we can also branch the strategy sets if the obtained solution is not integer, so that this situation is analogous as well.
In contrast, the bounding step poses some difficulties. Firstly and most obviously, there are multiple objective functions. Equilibrium points are required to be minimal for each player’s objective function with respect to the other players’ decisions. However, we are interested in a single criterion telling us whether there may exist Nash equilibria on a given subset of the strategy space. More specifically, the bounding idea relies on some function p on the joint strategy set \(\Omega \) whose minimal points coincide with the solutions of NEP. For the continuous problem \(\widehat{\textit{NEP}}\) such functions can be obtained by the VI and NI approaches [4, 13] but, as mentioned above, the latter are impossible or hard to apply in the discrete framework.
Under the additional assumption of NEP being a potential game [10] there exists a potential function \(p:{\mathbb {R}}^n \rightarrow {\mathbb {R}}\) with
for all \(\nu = 1,\ldots ,N\) and all \(x^{-\nu }\in X_{-\nu }\). It is straightforward to show that then any optimal point of the integer program
solves NEP. However, in general not all solutions of NEP are optimal for \({\mathcal {P}}\), as required for a bounding procedure relying on p. In fact, Example 2.2 provides a potential game with potential function
but the potential values
of the three solutions of NEP are not identical. In any case, potential games form only a small subclass of NEPs, and their restrictive assumptions cover, e.g., cases where all players unconsciously minimize the same objective function. We, on the other hand, aim to handle non-potential games.
Since, if the solution of \(\widehat{\textit{NEP}}\) does not happen to be integer, we do not seem to be able to draw any conclusions for discarding subsets of \(\Omega \) by a bounding procedure, we will instead follow the branch-and-prune approach from [14, 15]. There, relations between equilibria of NEP and \(\widehat{\textit{NEP}}\) are exploited algorithmically. Regarding such relations, Example 2.2 illustrates that NEP may possess more solutions than \(\widehat{\textit{NEP}}\) and that not every solution of NEP may be obtained by rounding the fractional components of a solution of \(\widehat{\textit{NEP}}\). There are also examples where NEP possesses less solutions than \(\widehat{\textit{NEP}}\). In particular, the solvability of \(\widehat{\textit{NEP}}\) does not entail the solvability of NEP (see [14, Ex. 2]). Additional requirements for the latter are given in [14, Cor. 4.4].
3 Theoretical foundation
The purpose of this section is to define a pruning criterion for discrete NEPs under Assumption 2.1. Moreover, for each player \(\nu = 1,\ldots ,N\) we assume \(g^\nu \) to be continuously differentiable and \(\theta _\nu \) to be twice continuously differentiable. We use the term pruning criterion to refer to criteria under which we can exclude parts of a player’s strategy set because they are shown not to contain any Nash equilibrium. With effective pruning, we can substantially reduce the search region in order to compute Nash equilibria more efficiently.
The theorem we present in this section generalizes Proposition 3.1 from [14] (see “Appendix A”). Instead of boxes as in [14], it treats arbitrary convexly described strategy sets. It provides a set of verifiable conditions under which we are able to prune choices for values of single variables from some player’s strategy set. We shall also motivate the underlying geometrical concept.
Our approach uses local approximations of the continuously relaxed problem \(\widehat{\textit{NEP}}\) to infer properties of the discrete problem NEP. As opposed to [14, 15] we use arbitrary continuous strategies, rather than only solutions of \(\widehat{\textit{NEP}}\), to obtain these approximations. This enables us to deal with non-convexities in the objective functions. For the approximations we employ the concept of the (outer) linearization cone
of player \(\nu \)’s continuously relaxed strategy set \({\widehat{X}}_\nu = \{x^\nu \in {\mathbb {R}}^{n_\nu } \mid g^\nu (x^\nu ) \le 0 \}\) at the strategy \({\bar{x}}^\nu \in {\widehat{X}}_\nu \), where
denotes the active index set. Under the convexity property of the strategy constraints from Assumption 2.1 it is straightforward to prove that any linearization cone for player \(\nu \) provides an outer approximation of her relaxed strategy set in the following sense.
Lemma 1.4
Let \(g^\nu _i\) be convex for \(i=1,\ldots , m_\nu \) and let \({\bar{x}}^\nu \in {\widehat{X}}_\nu \). Then we have
Theorem 1.5
Let Assumption 2.1 hold, let \({\bar{x}}\in {\widehat{\Omega }}\) and, for an arbitrary player \(\nu \), let there exist an index i such that \(\theta _\nu \) is strictly convex with respect to \(x^\nu _i\). Then the following two statements hold:
-
(i)
Let \(F^\nu _i = \nabla _{x^\nu _i}\theta _{\nu }\) be convex, let \(F^\nu _i({\bar{x}})\ge 0\) and for each player \(\mu = 1,\ldots ,N\) let
$$\begin{aligned} \langle \nabla _{x^\mu }F_i^\nu ({\bar{x}}), d^\mu \rangle \ge 0 \quad \forall d^\mu \in L_\le ({\bar{x}}^\mu , {\widehat{X}}_\mu ). \end{aligned}$$(1)Then any strategy \({\widetilde{x}}\in \Omega \) for which
 , defined by
, defined by 
is also feasible cannot be a solution of NEP.
-
(ii)
Let \(F^\nu _i = \nabla _{x^\nu _i}\theta _{\nu }\) be concave, let \(F^\nu _i({\bar{x}})\le 0\) and for each player \(\mu = 1,\ldots ,N\) let
$$\begin{aligned} \langle - \nabla _{x^\mu }F_i^\nu ({\bar{x}}), d^\mu \rangle \ge 0 \quad \forall d^\mu \in L_\le ({\bar{x}}^\mu , {\widehat{X}}_\mu ). \end{aligned}$$(2)Then any strategy \({\widetilde{x}}\in \Omega \) for which \({\widehat{x}}\), defined by
$$\begin{aligned} {\widehat{x}}^\mu _j = {\widetilde{x}}^\mu _j \text { for all } (\mu , j) \ne (\nu , i), \text { and } {\widehat{x}}^\nu _i = {\widetilde{x}}^\nu _i+1, \end{aligned}$$is also feasible cannot be a solution of NEP.
Proof
In order to show that \({\widetilde{x}}\) is not a Nash equilibrium, we will show that player \(\nu \) can choose a strictly better strategy.
On the one hand, if (i) holds and if we can show

the assertion follows by the feasibility of  for the discrete NEP. The strict inequality
for the discrete NEP. The strict inequality

holds because of the strict convexity of \(\theta _{\nu }\) in the component \(x^\nu _i\), being the only value in which  and \({\widetilde{x}}\) differ. Hence, (3) follows, when
and \({\widetilde{x}}\) differ. Hence, (3) follows, when

holds. Firstly, the equation comes from the defined notation and  . Secondly, the left inequality follows from convexity of \(F^\nu _i\). Thirdly, the non-negativity comes from
. Secondly, the left inequality follows from convexity of \(F^\nu _i\). Thirdly, the non-negativity comes from
-
\(F^\nu _i({\bar{x}}) \ge 0\) by precondition,
-
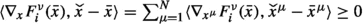 , because from Lemma 3.1 follows
, because from Lemma 3.1 follows 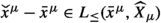 so that every summand is non-negative by (1).
so that every summand is non-negative by (1).
On the other hand, if (ii) holds, the Eqs. (3) and (4) can be stated for \({\widehat{x}}\) instead of  as well with all requirements fulfilled. It remains to show that the chain of inequalities
as well with all requirements fulfilled. It remains to show that the chain of inequalities
also holds. Firstly, the equation comes again from notation and \({\widehat{x}}^\nu _i = {\widetilde{x}}^\nu _i+1\). Secondly, the left inequality is valid due to the concavity of \(F^\nu _i\), and the non-negativity comes from
-
\(-F^\nu _i({\bar{x}}) \ge 0\) by precondition,
-
\(\langle -\nabla _x F^\nu _i({\bar{x}}),{\widehat{x}}-{\bar{x}}\rangle = \sum _{\mu = 1}^{N} \langle -\nabla _{x^\mu }F^\nu _i({\bar{x}}),{\widehat{x}}^\mu -{\bar{x}}^\mu \rangle \ge 0\), because from Lemma 3.1 follows \({\widehat{x}}^\mu -{\bar{x}}^\mu \in L_\le ({\bar{x}}^\mu ,{\widehat{X}}_\mu )\) so that every summand is non-negative by (2).
\(\square \)
To verbalize the statement of Theorem 3.2, we use the point \({\bar{x}}\) to construct outer approximations of all players’ complete strategy sets. This actually results in the outer approximation
of \({{\widehat{\Omega }}}\). If, on this whole set \({{\bar{x}}}+L_\le (\bar{x},{{\widehat{\Omega }}})\), some player’s variable \(x^\nu _i\) has a favorable impact on the objective function \(\theta _{\nu }\) when it is increased or decreased without the new point becoming infeasible, then this player can deviate and realize this positive impact, which is impossible in a Nash equilibrium. In other words, under the given assumptions in a Nash equilibrium \({{\widetilde{x}}}\) the constructed deviation must result in an infeasible point. Figure 2 shows the two dimensional strategy set \(X_\nu \) of a discrete N player game. Assume that for \({\bar{x}}\) and \(i=2\) all requirements of Theorem 3.2.(i) hold. Then there is always a positive impact in the \(\nu \)-th player’s objective function, when she sets \(x^\nu _2\) to a lower value. As a result, e.g. \({\widetilde{x}}\) cannot be a Nash equilibrium, because  is feasible and a better answer for player \(\nu \). In \(X_\nu \), the set of possible best answers and thus the candidates for solutions of NEP shrinks to the pairs of "minimum feasible" \(x^\nu _2\)-values for any given \(x^\nu _1\). Roughly speaking, only integer points for which at least one constraint is "active" in the sense that \(x^\nu _2\) cannot be set to a lower value without changing other components of \(x^\nu \) can be Nash equilibria. This criterion will enable us to reduce the search space significantly in Sects. 4 and 5.
is feasible and a better answer for player \(\nu \). In \(X_\nu \), the set of possible best answers and thus the candidates for solutions of NEP shrinks to the pairs of "minimum feasible" \(x^\nu _2\)-values for any given \(x^\nu _1\). Roughly speaking, only integer points for which at least one constraint is "active" in the sense that \(x^\nu _2\) cannot be set to a lower value without changing other components of \(x^\nu \) can be Nash equilibria. This criterion will enable us to reduce the search space significantly in Sects. 4 and 5.
Pruning of \({\widetilde{x}}\), when Theorem 3.2.(i) is fulfilled for \(i=2\). In particular \(\nabla _{x^\nu }F^\nu _2({\bar{x}})\) needs to lie in the dual cone C of \(L_\le ({\bar{x}}^\nu ,{\widehat{X}}_\nu )\)
For the algorithmic exploitation of Theorem 3.2 we define linear optimization problems to check if (1) and (2) are satisfied. The statement (1) is clearly valid if and only if the optimization problem
has a non-negative optimal value \(v_{F_{(1)}}\ge 0\). In the same way, (2) holds if and only if
has a non-negative optimal value \(v_{F_{(2)}} \ge 0\). By definition of the linearization cone, \(d^\mu = 0\) is always feasible for \(F_{(1)}\) and \(F_{(2)}\), so that the above optimal values are actually zero. If, on the other hand, there exists any direction \(d^\mu \) with a negative objective value, the problems are unbounded, because the feasible set is a cone. Therefore, we only have to check if these linear optimization problems are bounded in order to verify the statements. We remark that (1) and (2) require that the vectors \(\nabla _{x^\mu }F_i^\nu ({\bar{x}})\) and \(-\nabla _{x^\mu }F_i^\nu ({\bar{x}})\), respectively, lie in the dual cone of \(L_\le ({\bar{x}}^\mu , {\widehat{X}}_\mu )\). In view of possibly non-unique cone coefficients in the absence of an appropriate constraint qualification it may, however, be algorithmically challenging to determine these cone coefficients explicitly, so that we rather work with the above optimization formulation.
We emphasize that we need the strict convexity of the objective function \(\theta _\nu \) in the component \((\nu ,i)\) in order to apply Theorem 3.2. The (strict) convexity in single variables does not require convexity in all of player \(\nu \)’s variables \(x^\nu \), as defined in player convexity. However, the additional assumption might be helpful in the sense that it increases the likelihood of finding \((\nu ,i)\)-components in which \(\theta _\nu \) is strictly convex.
4 Algorithmic application
In this section, we define a branch-and-prune procedure for discrete NEPs by employing the pruning criterion from the previous section. The branching method is a generalization of [14, Alg. 1]. It is defined in Sect. 4.1 and calls a pruning procedure, which we define in Sect. 4.2.
4.1 Branching method
Algorithm 1 shows the high-level approach for discrete NEPs with convexly constrained, bounded strategy sets. In most aspects, it coincides with [14, Alg. 1]. For better readability, we repeat each step of the method. In particular, we describe the adjustments that were necessary to integrate the novel pruning procedure. This procedure computes all equilibria of an instance NEP. Within the procedure, we maintain two lists. In one list, we save all equilibria which were already detected (E). The other list \({\mathcal {L}}\) contains all strategy subsets which may contain additional equilibria. It is initialized with the whole joint strategy set \(\Omega \).
In each iteration of the while-loop a joint strategy set \(Y\subseteq \Omega \) is taken from the list \({\mathcal {L}}\). If the continuous relaxation \({{\widehat{Y}}}\) is empty, there are clearly no equilibria in this set and we are done. Otherwise, a point \({\bar{x}} \in {\widehat{Y}}\) is computed. Here, the feasibility of \({\bar{x}}\) for \({\widehat{Y}}\) is a minimum requirement but, given the target of finding solutions of NEP as quickly as possible, in view of Proposition 2.3 computing a solution \({{\bar{x}}}\) of the continuously relaxed problem \(\widehat{\textit{NEP}}\) may be advantageous, depending on the effort for such a computation.
Afterwards, the first pruning and simultaneous branching can be started in line 7. In this step, Algorithm 1 differs from [14, Alg. 1], in which the pruning procedure only returns one set. Here, the pruning procedure returns a list of sets \({\mathcal {B}}= \{B_1,\ldots , B_k \}\). This disjunctive structure arises from the additional treatment of other constraints than bounds. We briefly name the assumptions for such a procedure.
Assumption 1.6
The output of a pruning procedure, called with \(Y\subseteq \Omega \) and \({{\bar{x}}} \in {{\widehat{Y}}}\), is a list \({\mathcal {B}} = \{B_1,\ldots , B_k \}\) with the following properties:
-
(P1)
The set \(Y \setminus \{ \bigcup \limits _{i=1}^k B_i \}\) does not contain any Nash equilibrium
-
(P2)
\(B_i \subseteq Y\) for all \(i = 1, \ldots , k\)
-
(P3)
the sets in \({\mathcal {B}}\) are pairwise disjoint, i.e. \(B_i \cap B_j = \emptyset \) for \(i,j \in \{1,\ldots , k\}, i\ne j\)
-
(P4)
we have \({\bar{x}} \in {{\widehat{B}}}_1\) if \({\bar{x}} \in \bigcup \limits _{i=1}^k {{\widehat{B}}}_i\)
Firstly, property (P1) ensures that we are not pruning any Nash equilibrium. Secondly, property (P2) and (P3) are crucial in branching techniques to not allow additional points and avoid that a point needs to be processed multiple times. Lastly, property (P4) is more technical. On the one hand, a pruning procedure could exclude \({\bar{x}}\). On the other hand we further process the point, so we need to know which of the subsets contains it. Algorithm 2 in the next subsection presents a procedure which satisfies (P1)-(P4) and is able to handle convex polyhedral strategy sets.
Starting in line 9, the second branching process depends on whether \({\bar{x}}\in {\mathbb {Z}}^n\) or not. If so, the vector is potentially an equilibrium of the discrete problem \(\textit{NEP}\) and can, after verification, be appended to E, the list of all Nash equilibria. The equilibrium property can be verified by checking if \({\bar{x}}^\nu \) is a solution of \(Q^\nu ({\bar{x}}^{-\nu })\) for all \(\nu = 1,\ldots ,N \). More specifically, we need to solve these N integer (non-)convex programs and check, if their respective optimal values are attained at the given points \({\bar{x}}^\nu \) (line 10). The appearing integer (non-)convex problems can be solved with techniques from mixed-integer (non-)convex optimization (see e.g. [1]). The efficient implementation of this step of course depends on the state-of-the-art of available solvers. After knowing whether \({\bar{x}}\) is a solution, we can release it and search in the remaining feasible set for Nash equilibrium points. By Algorithm 3 ( [14] and “Appendix B”), we obtain a partition of sets \({\mathcal {B}}^+\) which cover all other possible equilibria. Any integer point \({\widetilde{x}}\in B_1\) other than \({\bar{x}}\) is in one of the sets from \({\mathcal {B}}^+\). Additionally, these sets are pairwise disjoint subsets of \(B_1\).
If otherwise \({\bar{x}}\notin {\mathbb {Z}}^n\), the branching step resembles the one common in integer optimization. One fractional component in \({\bar{x}}\) is selected and two sets are added to the list \({\mathcal {L}}\). In the first one, the value of this component is bounded to be greater or equal the nearest larger integer. In the second one, it is bounded to be less or equal the nearest smaller integer.
When the strategy sets \(X_1,\ldots ,X_N\) are bounded, the termination of Algorithm 1 is ensured because there are finitely many integer strategies. This property can be established by setting finite upper and lower bounds for each variable. Note that the efficiency of Algorithm 1 mainly depends on the effectiveness of the pruning procedure. All points which are not pruned will be enumerated and checked in line 10.
4.2 Pruning procedure for convex polyhedral strategy sets
We now define a pruning procedure for discrete Nash games, where every player’s strategy set \(X_\nu \) can be characterized by linear inequalities, which is a special case of Assumption 2.1:
With each player having \(m_\nu \) inequality constraints, \(B^\nu \) is an integer valued \((m_\nu \times n_\nu )\)-matrix and \(b^\nu \in {\mathbb {Z}}^{m_\nu }\) a vector. We will refer to the k-th row of \(B^\nu \) as \(B^\nu _{k\star }\). The player’s decision vector \(x^\nu \) has explicitly defined lower and upper bounds \({l^\nu \in {\mathbb {Z}}^{n_\nu }}\) and \({u^\nu \in {\mathbb {Z}}^{n_\nu }}\), respectively. We call a discrete strategy set \(X_\nu \) convex polyhedral, if the continuous relaxation of this strategy set \({\widehat{X}}_\nu \) is convex and polyhedral.
Previously, we determined conditions under which in an equilibrium of NEP it is not possible to increase or decrease the value of a variable to the next integer and remain feasible. Accordingly, at least one inequality (or the box restriction) must be active in a way that the next integer value in one direction is not feasible anymore. We formalize this kind of activity for a linear constraint.
Definition 1.7
For a feasible point \({\widetilde{x}}\in \Omega \) the inequality k is called
-
\((\nu ,i)^-\)-active if for
 , defined as
, defined as  for \((\mu ,j)\ne (\nu ,i)\) and
for \((\mu ,j)\ne (\nu ,i)\) and 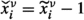 , we have
, we have  ,
, -
\((\nu ,i)^+\)-active if for \({\widehat{x}}\), defined as \({\widehat{x}}^\mu _j = {\widetilde{x}}^\mu _j\) for \((\mu ,j)\ne (\nu ,i)\) and \({\widehat{x}}^\nu _i = {\widetilde{x}}^\nu _i+1\), we have \(B^\nu _{k\star } {\widehat{x}}^\nu > b^\nu _k\).
We now investigate under which conditions inequality k is \((\nu ,i)^-\)- or \((\nu ,i)^+\)-active for a feasible point \({{\widetilde{x}}}\). With these conditions we will be able to perform pruning steps. Firstly, by Definition 4.2 an inequality k is \((\nu ,i)^-\)-active for \({\widetilde{x}}\) if

holds. Because of the integrality assumptions for \(B^\nu \) and \(b^\nu \), this is exactly true, when
holds. Due to feasibility of \({\widetilde{x}}\), this condition can only be satisfied if \(B^\nu _{ki}<0\) holds. Similarly, an inequality k is \((\nu ,i)^+\)-active for \({\widetilde{x}}\) if
and thus
holds. This argumentation results in Corollary 4.3.
Corollary 1.8
Let \({\widetilde{x}}\) be a solution of a problem NEP with strategy sets as defined in (5). Then the following two statements hold:
-
(i)
Suppose all requirements of Theorem 3.2.(i) hold for some \({\bar{x}}\in {\widehat{\Omega }}\) and an index pair \((\nu ,i)\). Then \({\widetilde{x}}^\nu _i=l^\nu _i\) holds or there exists at least one inequality k with (6) and \(B^\nu _{ki}<0\).
-
(ii)
Suppose all requirements of Theorem 3.2.(ii) hold for some \({\bar{x}}\in {\widehat{\Omega }}\) and an index pair \((\nu ,i)\). Then \({\widetilde{x}}^\nu _i=u^\nu _i\) holds or there exists at least one inequality k with (7) and \(B^\nu _{ki}>0\).
Now we can state Algorithm 2. This procedure can be applied in an arbitrary point \({\bar{x}}\in {\widehat{\Omega }}\) in order to reduce the search space. Two outer for-loops, starting in line 2 and 3, iterate through all variables of the game. For each variable, the requirements of Theorem 3.2 are checked. If case (i) or (ii) is applicable, we perform a partition of the set according to Corollary 4.3.
Suppose that for \((\nu ,i)\) the if-statement in line 4 is true. Then the first statement of Corollary 4.3 holds. Consequently in any Nash equilibrium x, \(x^\nu _i\) is at its lower bound \(l^\nu _i\) or at least one inequality from the index set \(J^{\nu ,i}\) must be \((\nu ,i)^-\)-active. Integer points for which none of this holds are pruned in lines 5–12 by introducing new inequalities and splitting the set(s) up. In line 6, there is an inner for-loop which ensures that the subdivision is done for every set in the list \({\mathcal {B}}\). At first, \({\mathcal {B}}\) only contains Y, but as soon as the if-statements hold true for more than one index pair, this step is performed for all sets from the previous subdivisions. Thus for every set from the current list \({\mathcal {B}}\) the partition is added to a new list \({\mathcal {C}}\), which replaces \({\mathcal {B}}\) afterwards. We will now describe in detail how lines 7–11 yield a pairwise disjoint subdivision. In line 7, all points for which \(x^\nu _i\) is at its lower bound are added to \({\mathcal {C}}\) and line 8 ensures that the next sets are disjoint. Then in lines 9–11, for all inequalities with \(B^\nu _{ki}<0\) the points for which firstly (6) holds and secondly are not contained in previous sets are added to \({\mathcal {C}}\). The latter is done in every iteration by stating the negation of (6) for all sets which will be added to \({\mathcal {C}}\) successively in this for-loop. We can state the negation of inequality (6) as

Note that (6) and (\(\lnot 6\)) form a split disjunction.
In lines 13–21 the analogous approach is implemented for the case when the requirements of Theorem 3.2.(ii) hold and Corollary 4.3.(ii) can be applied. We illustrate in Example 4.4 how the procedure works in detail.
Example 4.4
Figure 3 depicts how the two inner for-loops in Algorithm 2 partition one player’s strategy set into three sets \(C_1, C_2\) and \(C_3\). The illustration shows the first player’s strategy (sub-)set for an arbitrary game with two variables. The gray area is the continuously relaxed strategy set \({{\widehat{Y}}}_1\). In this situation, Algorithm 2 was executed with Y and some \({\bar{x}}\in {\widehat{Y}}\), which we do not have to name explicitly. We just suppose that the if-statement in line 4 holds true for \(x^1_2\) and \({\mathcal {B}}=\left\{ Y\right\} \) still holds. Thus there is only one iteration of the for-loop starting in line 6 which we consecutively describe.
At first, in line 7 the algorithm puts the set \(C_1 \times {{\widehat{Y}}}_2\) into \({\mathcal {C}}\). It contains all possible strategies with active lower bound \(x^1_2=l^1_2\). This happens by posing the inequality labeled by "1" in Fig. 3 for this set. For all future sets of this iteration, inequality \(\lnot 1\), with \(x^1_2\ge l^1_2+1\), is stated in line 8 without excluding any feasible points.
At this point, the innermost for-loop starts in line 9. The index set \(J^{1,2}\) contains only two elements as there are only two linear constraints with \({B^1_{j2}<0}\) which can be \((1,2)^-\)-active. We can identify them because they are avoiding that \(x^1_2\) is decreased at some point in \({{\widehat{Y}}}_1\). Thus there are two iterations of this loop. The first one is performed with the left inequality. In line 10, we put \(C_2 \times {{\widehat{Y}}}_2\) into \({\mathcal {C}}\), where inequality 2 coming from (6) holds. Afterwards, we state inequality \(\lnot 2\) to prevent an overlap to all incoming sets. The second iteration is done with the right inequality. For this restriction, in addition to the inequalities \(\lnot 1\) and \(\lnot 2\), 3 must hold in \(C_3 \times {{\widehat{Y}}}_2\) which is put into \({\mathcal {C}}\) in line 10. In line 11, the inequality \(\lnot 3\) is stated for future sets which is not necessary anymore, as we exit the two for-loops and replace \({\mathcal {B}}\) with the three sets in \({\mathcal {C}}\).
As a result, we have 3 strategy subsets and for player one there are overall 7 integer points remaining, which could be choices in a Nash equilibrium.
In Sect. 5 we will see that Example 4.4 is not an isolated case, but that often a considerable part of the feasible set can be pruned by Algorithm 2.
5 Numerical results
In this section, we will solve discrete Nash equilibrium problems with the branch-and-prune procedure presented in Sect. 4. Our aims are, firstly, to demonstrate the effectiveness of our method with initial experiments. In particular, we would like to show in random instances to what extent the pruning criterion facilitates the search for equilibria by shrinking the search area. Secondly, we want to give an impression of the limitations of this approach and which parts of the algorithm are the most challenging and computationally intensive, thus providing starting points for further improvements.
In the following experiments, all players’ feasible sets are polyhedral, as defined in (5). The objective functions are defined as
with a symmetric, but not necessarily positive semidefinite \((n_\nu \times n_\nu )\)-matrix \(Q^\nu \), an \({(n_\nu \times (n-n_\nu ))}\)-matrix \(C^\nu \) and a vector \(d^\nu \in {\mathbb {R}}^{n_\nu }\) for each player \(\nu = 1,\ldots ,N\). We will consider player convex games as well as games which satisfy Assumption 2.1, but in which the objective functions are only required to be strictly convex with respect to individual variables \(x^\nu _i\) for \(i=1,\ldots , n_\nu \).
In the following, we firstly give details on the concrete implementation of the algorithms. Secondly, we describe how test instances were generated. Lastly, we evaluate and discuss the results.
5.1 Implementation
All algorithms are implemented in Matlab R2020a. We solve all occurring optimization problems via the Matlab interface of Gurobi 9.5.0 which enables us to solve non-convex quadratic optimization problems. The script for the numerical test is executed on an Intel Core i7-9700K CPU @ 3.60GHz with Linux Mint 20 and 32 GB RAM.
Some details of the algorithms from Sect. 4 can be implemented in various ways and are specified below. The complete code is available in a Git repository.Footnote 1
Algorithm 1 At first, the feasible strategy in line 4 is computed with a Gauss-Seidel best response scheme (see [7, Algorithm 1]), because we favor \({\bar{x}}\) to be already a continuous Nash equilibrium. Within this Gauss-Seidel procedure, we avoid exhaustive calculations if there is only slow or no convergence by executing the while-loop at most 10 times. Note that in this case our approach works as well, as it does not rely on \({{\bar{x}}}\) being a continuous Nash equilibrium, but only a feasible point. Secondly, the if-statement in line 7 is verified by solving the optimization problem \(Q^\nu ({{\bar{x}}}^{-\nu })\) and compare its optimal value to \(\theta _\nu ({\bar{x}})\) for each player. Thirdly, for the considered games, we can use Algorithm 2 as pruning procedure in line 5.
Algorithm 2 The description in Sect. 4.2 is tailored for convex polyhedral strategy sets. Consecutively, we explain how the if-statements are checked. For each variable, the strict convexity of \(\theta ^\nu _i\) in \(x^\nu _i\) is fulfilled when \(Q^\nu _{ii}>0\). Further, \(F^\nu _i\) is a linear function and therefore both, convex and concave. Naturally, we can calculate \({F^\nu _i({\bar{x}})=Q^\nu _{i\star }{\bar{x}}^\nu + C^\nu _{i\star }{\bar{x}}^{-\nu }+d^\nu _i}\). Equations (1) and (2) are validated by checking the boundedness of \(F_{(1)}\) and \(F_{(2)}\). Lastly, in line 7–11 and 16–20, we ensure that \({\bar{x}}\) is always in the first entry of \({\mathcal {B}}\) (if it is not pruned) by some additional logical queries.
5.2 Generation of test instances
We randomly generate instances of Nash games and name them \(C/N\star X\star Y_k\). The first letter is C, if the instance is player convex and N, if not. The second and third signs denote the number of players X and the number of variables Y which each player controls, and k is an index to distinguish instances with similar attributes. For example, the instance \(C32_k\) consists of three players with two-dimensional strategy sets and player convexity holds. Table 1 lists all instances and their properties. In the next two paragraphs, we explain these properties and sketch how the instances were generated. For further details we refer to our implementation.
Strategy sets The aim is to generate an arbitrary convex polytope as strategy set for each player. Our approach is to start with a box which has equal side lengths and its center in the origin. We initiate \(X_\nu \) from (5) with \(l^\nu _i = -5\), \(u^\nu _i = 5\), \(i=1,\ldots ,n_\nu \). Afterwards we sequentially add m linear inequalities. We perform the following steps to add a constraint \(B^\nu _{k\star }x^\nu \le b^\nu _k\):
-
1.
To determine the number of nonzero values in \(B^\nu _{k\star }\) we draw a number from a uniform discrete distribution between two and the number of variables. The indices are selected as a random permutation.
-
2.
We set each nonzero value in \(B^\nu _{k_\star }\) as follows. We draw a number from \({\mathcal {N}}(5,1.5)\), round it and switch the sign with 0.5 probability.
-
3.
The choice of \(b^\nu _k\in {\mathbb {Z}}\) is based on geometric considerations. To avoid redundancy, we can set it so that the distance of the new inequality from the origin is less than half the initial box diameter. By setting it on a positive value we ensure consistency.
The mean density of all matrices \(B^\nu \) of each instance is listed in Table 1. Note that the complexity of Algorithm 2 significantly increases with the number of inequalities. For the purpose of later comparisons, we also compute the cardinality of \(\Omega \) which is simply the number of integer points in the common feasible set.
Objective functions For each instance, we compute \(C^\nu \), \(d^\nu \) and \(Q^\nu \) filled with random values from the interval \((-1,1)\) for each player. Each entry in \(C^\nu \) and \(d^\nu \) is set to zero with a probability of 0.5 in order to reduce density.
For generating a test bed of player convex problems, we update \(Q^\nu = (Q^\nu )^\intercal Q^\nu \). For those instances, we list the minimum eigenvalue \(\lambda _{\min }\) of all \(Q^\nu \) in Table 1.
In the non-convex test bed, we set \(Q^\nu := 0.5 \cdot (Q^\nu )^\top + 0.5 \cdot Q^\nu \) and replace the diagonal entries by their absolute values. By this, we have a symmetric matrix and \(\theta _\nu \) is convex in single variables \(x^\nu _i\), \(i=1,\ldots ,n_\nu \). In this procedure, the matrices often turn out to be, by chance, positive definite. We discard instances where this happens for all players. In Table 1 we can see in the column \(N_{NC}\), how many players have non-positive-semidefinite matrices \(Q^\nu \) and have thus a non-convex objective function.
Test bed Besides convexity, we subdivide the instances according to their sizes. The small test bed are all instances of type \(\star 22_\star \). The maximum number of integer points is bounded below 12,000. The medium test bed consists of all \(\star 23_\star \) and \(\star 32_\star \) instances. In \(\star 23_{5-8}\), the complexity is increased by adding twice as many constraints. Finally the large test bed are all \(\star 24_\star \), \(\star 33_\star \) and \(\star 25_\star \) problems. The number of integer points drastically increases due to exponential growth of the strategy sets in the number of variables. Here, we can only expect convergence in a reasonable time if the pruning procedure eliminates an enormous part of the feasible sets.
5.3 Evaluation
Subsequently, we investigate if Algorithm 1 is able to compute some or even all equilibria of the test instances. Additionally, we examine how much of the feasible set can be pruned by Algorithm 2 and compare the performance on convex and non-convex instances.
In Table 2 we can see the statistics of the solving process for all player convex instances. We can see in column \(|E |\), how many solutions of the NEP are found within the time limit of \(t_{max}=3600\) seconds. The column \(t_1\) marks the run time in seconds, when the first equilibrium was found, \(t_2\) when the last equilibrium was found and \(t_3\) when the solving process ended. If, \(t_3 = t_{\max }\), the process did not finish and there is no guarantee that all solutions were found. The statistic \(O(t_k)\) displays how often the if-statement in line 6 of Algorithm 1 held true, hence how many integer points were processed at these timestamps. Note that, if the algorithm finished, \(O(t_3)/|\Omega |\) tells us the share of integer points that needed to be processed, the rest was pruned by Algorithm 2.
In the small test bed we report that the algorithm completed and all equilibria were found. The properties of the instances are quite different: While \(C22_1\) and \(C22_3\) have two solutions, \(C22_4\) has none. In the medium test bed we report that for 11 of 12 instances we were able to find provably all solutions within one hour, \(C32_3\) being an exception. For this instance, we found three equilibria but did not finish. Notably, there are five instances certified to have no equilibria. Lastly, in the large test bed there was no instance for which the procedure finished within an hour. Nevertheless, we found a solution for two instances.
If we were able to compute equilibria, the first one was mostly found in the first ten seconds of the run time. We now analyse the 15 instances for which \(t_3<t_{\max }\) holds. In four cases less than 5% of the integer points in \(\Omega \) were processed, in seven others this share is under 8%. We note that often a large proportion of feasible points could be pruned, the arithmetic mean is 92.5% and the standard deviation 3.6%. We point out that, if \(t_3=t_{\max }\), the column \(O(t_3)/|\Omega |\) has no similar interpretation. It only says how many integer points were processed in the given time.
For the non-convex test bed, displayed in Table 3, we see similar results. We report that all small and 10 of 12 medium instances were solved completely. We have six provably inconsistent instances. Again, there was no large instance solved completely in the time limit, but we found a solution for three instances. For the instances with \(t_3<t_{\max }\), the mean share of pruned points is 92.7% with a standard deviation of 3.4%. Hence, in our randomly generated test bed the convexity in individual variables is sufficient to be able to prune a large proportion of feasible points.
In contrast, we detect differences in the run time between the convex and the non-convex case. Table 4 reports how much of the total run time is caused by solving optimization problems and checking consistency with Gurobi (\(GT_{tot}\)). Of this time, we see on the left the fractions caused by different tasks. In the non-convex test bed, aiming to solve the continuously relaxed problems with the Gauss-Seidel method and checking whether \({{\bar{x}}}\) solves the NEP takes on average a larger proportion of \(GT_{tot}\) (47% and 16% instead of 41% and 11%). For these two tasks, non-convex optimization problems need to be solved. The other two columns only report the time fractions needed for consistency checks. Overall, one can also see in the tables which parts of the algorithms require the most run time, to assess where improvements are most beneficial. For example, one could try to determine \({{\bar{x}}}\) with a faster inexact procedure. Furthermore, one may use additional simple logical queries to discard empty sets more efficiently.
All in all, we can say that in the considered low dimensional test instances the presented algorithm is able to prune a considerable share of feasible points. However, because of an exponential growth in the cardinality of the joint feasible set in the number of variables, a computation of all equilibria seems to be prohibitive for higher dimensions.
6 Conclusion
This paper presents novel theoretical results on pruning for discrete Nash equilibrium problems. The required activity of particular constraints leads to synchronous branching and pruning of the strategy sets. Furthermore, we showed in a numerical study that a noteworthy part of the joint feasible set can be pruned by following this rationale. This was demonstrated for polyhedral strategy sets and (not necessarily convex) quadratic objective functions. It remains to be investigated if these results can also be applied to broader problem classes like, for example, generalized Nash equilibrium problems.
Data availibility
The data sets generated and analyzed during the current study are available in the GitHub repository, https://github.com/schwarze-st/nep_pruning.
References
Belotti, P., Kirches, C., Leyffer, S., Linderoth, J., Luedtke, J., Mahajan, A.: Mixed-integer nonlinear optimization. Acta Numer. 22, 1–131 (2013)
Carvalho, M., Dragotto, G., Lodi, A., Sankaranarayanan, S.: The cut and play algorithm: Computing nash equilibria via outer approximations. Preprint arXiv:2111.05726v2 (2022)
Carvalho, M., Lodi, A., Pedroso, J.P.: Computing equilibria for integer programming games. Eur. J. Oper. Res. 303(3), 1057–1070 (2022)
Dreves, A., Kanzow, C., Stein, O.: Nonsmooth optimization reformulations of player convex generalized Nash equilibrium problems. J. Glob. Optim. 53(4), 587–614 (2012)
Facchinei, F., Fischer, A., Piccialli, V.: Generalized Nash equilibrium problems and Newton methods. Math. Program. 117(1–2), 163–194 (2009)
Facchinei, F., Kanzow, C.: Generalized Nash equilibrium problems. Ann. Oper. Res 5(3), 173–210 (2007)
Facchinei, F., Piccialli, V., Sciandrone, M.: Decomposition algorithms for generalized potential games. Comput. Optim. Appl. 50(2), 237–262 (2011)
Harks, T., Schwarz, J.: Generalized nash equilibrium problems with mixed-integer variables. Preprint arXiv:2107.13298v2 (2022)
Köppe, M., Ryan, C.T., Queyranne, M.: Rational generating functions and integer programming games. Oper. Res. 59(6), 1445–1460 (2011)
Monderer, D., Shapley, L.S.: Potential games. Games Econom. Behav. 14(1), 124–143 (1996)
Nash, J.F.: Equilibrium points in n-person games. Proc. Natl. Acad. Sci. 36(1), 48–49 (1950)
Nash, J.F.: Non-cooperative games. Ann. Math. 54(2), 286–295 (1951)
Pappalardo, M., Mastroeni, G., Passacantando, M.: Merit functions: a bridge between optimization and equilibria. 4OR 12(1), 1–33 (2014)
Sagratella, S.: Computing all solutions of Nash equilibrium problems with discrete strategy sets. SIAM J. Optim. 26(4), 2190–2218 (2016)
Sagratella, S.: On generalized Nash equilibrium problems with linear coupling constraints and mixed-integer variables. Optimization 68(1), 197–226 (2019)
Acknowledgements
The authors are grateful to two anonymous reviewers and the associate editor for their precise and constructive remarks which helped to significantly improve this paper.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the contents of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Theorem 3.2 generalizes [14, Prop. 3.1]
Subsequently, it will be shown that Theorem 3.2 is a generalization of Proposition 3.1 from [14]. This article considers box-constrained strategy sets \(X_\nu \) with
Obviously, the gradient \(\nabla _{x^\nu }g^\nu _j(x^\nu )\) of the constraint j equals the unit vector \(e_j\) for \(j\in \{1,\ldots ,n_\nu \}\) and \(-e_j\) for \(j\in \{n_\nu +1,\ldots ,2n_\nu \}\), respectively.
Proposition A.1
[14, Proposition 3.1] Suppose that \(\Omega \) is defined by box constraints. Let \({\bar{x}}\in \Omega \) be an integer solution of the continuously relaxed problem \(\widehat{\textit{NEP}}\). Let us consider a generic player \(\nu \). Suppose that an index \(i\in \{1,\ldots ,n_\nu \}\) exists, such that \(\theta _{\nu }\) is strictly convex with respect to \(x^\nu _i\) and that one of the two possibilities holds:
-
(i)
Given that \({\bar{x}}^\nu _i = l^\nu _i\), \(F^\nu _i\) is convex and for each player \(\mu \in \{1,\ldots ,N\}\) and each index \(j\in \{1,\ldots ,n_\mu \}\), such that \((\mu ,j)\ne (\nu ,i)\), it holds \({\bar{x}}^\mu _j=l^\mu _j\) if \(\nabla _{x^\mu _j}F^\nu _i({\bar{x}})>0\) and \({\bar{x}}^\mu _j=u^\mu _j\) if \(\nabla _{x^\mu _j}F^\nu _i({\bar{x}})<0\).
-
(ii)
Given that \({\bar{x}}^\nu _i = u^\nu _i\), \(F^\nu _i\) is concave and for each player \(\mu \in \{1,\ldots ,N\}\) and each index \(j\in \{1,\ldots ,n_\mu \}\), such that \((\mu ,j)\ne (\nu ,i)\), it holds \({{\bar{x}}^\mu _j=u^\mu _j}\) if \(\nabla _{x^\mu _j}F^\nu _i({\bar{x}})>0\) and \({\bar{x}}^\mu _j=l^\mu _j\) if \(\nabla _{x^\mu _j}F^\nu _i({\bar{x}})<0\).
Then any point \({\widetilde{x}}\in \Omega \) such that \({\widetilde{x}}^\nu _i \ne {\bar{x}}^\nu _i\) cannot be a solution of NEP.
More specifically, it will now be proven that, if all prerequisites of Proposition A.1 are fulfilled, Theorem 3.2 is applicable and yields the same result. Lemma A.2 shows that the requirements on \(F^\nu _i({\bar{x}})\) in Theorem 3.2.(i)/(ii) follow from the assumptions in Proposition A.1.(i)/(ii). Given that, Corollary A.3 proves that (1) and (2) also follow for the respective cases and that Theorem 3.2 yields the same result.
Lemma A.2
Suppose that \(\Omega \) is defined by box constraints and that \(\theta _{\nu }\) is strictly convex with respect to \(x^\nu _i\), as stated in Proposition A.1. From \({\bar{x}}\) being a solution of \(\widehat{\textit{NEP}}\) and \(l^\nu _i \ne u^\nu _i\) follow the two statements:
-
(i)
If \({\bar{x}}^\nu _i = l^\nu _i\), then \(F^\nu _i({\bar{x}})\ge 0\) must hold.
-
(ii)
If \({\bar{x}}^\nu _i = u^\nu _i\), then \(F^\nu _i({\bar{x}})\le 0\) must hold.
Proof
Since \({{\bar{x}}}\) is a solution of \(\widehat{\textit{NEP}}\), for each \(\nu \) the point \({{\bar{x}}}^\nu \) is a minimal point of the problem \({{\widehat{Q}}}^\nu ({{\bar{x}}}^{-\nu })\). Since the gradients of active box restrictions are linearly independent, \({\bar{x}}^\nu \) is a KKT point of \({{\widehat{Q}}}^\nu ({{\bar{x}}}^{-\nu })\) and
holds with \(\lambda _j \in {\mathbb {R}}_{\ge 0}\) for all \(j\in I_0({\bar{x}}^\nu ,{{\widehat{X}}}_\nu )\). For the i-th row of this equation, solely the gradients of the i-th variable’s upper and lower bound constraints are non-zero, \(\nabla _{x^\nu } g^\nu _i = e_i\) and \(\nabla _{x^\nu } g^\nu _{n_\nu +i} = -e_i\). By \(l^\nu _i \ne u^\nu _i\) only one of them can be in the active index set.
-
If \({\bar{x}}^\nu _i = l^\nu _i\), the constraint \(g^\nu _{n_\nu +i}\) is active and statement (i) follows from \(F^\nu _i({\bar{x}}) + \lambda _{n_\nu +i} \cdot (-1)=0\).
-
If \({\bar{x}}^\nu _i = u^\nu _i\), the constraint \(g^\nu _i\) is active and statement (ii) follows from \(F^\nu _i({\bar{x}}) + \lambda _i \cdot 1=0\).
\(\square \)
Corollary A.3
Theorem 3.2 is a generalization of Proposition A.1.
Proof
Since, as stated in Proposition A.1, the set \(\Omega \) is defined by box constraints, the strategy sets are defined by convex (linear) functions. Given Lemma A.2, it remains to show that (1) and (2) follow in the two particular cases and that the consequential statements are equivalent.
Firstly, we start with Proposition A.1.(i). For an arbitrary player \(\mu \) we have:
-
Let \(J_\mu \subseteq \left\{ 1,\ldots ,n_\mu \right\} \) be the set of all indices j such that \((\mu ,j)\ne (\nu ,i)\) and \(\nabla _{x^\mu _j}F_i^\nu ({\bar{x}})<0\). Thus, \({\bar{x}}^\mu _j = u^\mu _j\) for all \(j\in J_\mu \) and the box constraint \(g^\mu _j(x^\mu )=x^\mu _j- u^\mu _j\) is active (\(j \in I_0({\bar{x}}^\mu ,{{\widehat{X}}}_\mu \))). From \(\nabla _{x^\mu }g^\mu _j(x^\mu ) = e_j\) follows
$$\begin{aligned} d^\mu _j \le 0 \text { for all } d^\mu \in L_\le ({\bar{x}}^\mu ,{{\widehat{X}}}_\mu ). \end{aligned}$$ -
Let \(K_\mu \subseteq \left\{ 1,\ldots ,n_\mu \right\} \) be the set of all indices k such that \((\mu ,k)\ne (\nu ,i)\) and \(\nabla _{x^\mu _k}F_i^\nu ({\bar{x}})>0\). Thus, \({\bar{x}}^\mu _k = l^\mu _k\) for all \(k\in K_\mu \) and the box constraint \(g^\mu _{n_\mu +k}(x^\mu )=l^\mu _k - x^\mu _k\) is active (\(n_\mu +k \in I_0({\bar{x}}^\mu ,{{\widehat{X}}}_\mu \))). From \(\nabla _{x^\mu }g^\mu _{n_\mu +k}(x^\mu ) = -e_k\) follows
$$\begin{aligned} d^\mu _k \ge 0 \text { for all } d^\mu \in L_\le ({\bar{x}}^\mu ,{{\widehat{X}}}_\mu ). \end{aligned}$$If \(\mu =\nu \), this also applies to the index i:
-
\(\nabla _{x^\nu _i}F^\nu _i({\bar{x}})>0\) due to strict convexity of \(\theta _\nu \) in this component,
-
\(g^\nu _{n_\nu +i}(x^\mu )\) is also active and \(\nabla _{x^\nu } g^\nu _{n_\nu +i}(x^\mu )=-e_i\).
-
Together, for every player \(\mu \in \left\{ 1,\ldots ,N\right\} \) the scalar product
is non-negative for all \(d^\mu \in L_\le ({\bar{x}}^\mu ,\widehat{X}_\mu )\) and therefore (1) is fulfilled. This is easy to verify with help of the statements above. For each index \({p \in \left\{ 1,\ldots , n_\mu \right\} }\) one of these three possibilities holds:
-
\(p \in J_\mu \): \(\nabla _{x^\mu _p}F_i^\nu ({\bar{x}})<0\) and \(d^\mu _p \le 0\).
-
\(p \in K_\mu \): \(\nabla _{x^\mu _p}F_i^\nu ({\bar{x}})>0\) and \(d^\mu _p \ge 0\).
-
\(\nabla _{x^\mu _p}F_i^\nu ({\bar{x}})=0\).
For any point \({\widetilde{x}} \in \Omega \) with \({\widetilde{x}}^\nu _i \ne {\bar{x}}^\nu _i\) it follows that \({\widetilde{x}}^\nu _i \ge {\bar{x}}^\nu _i +1 = l^\nu _i +1\) and directly the feasibility of  , which is constructed like in Theorem 3.2. Therefore, the conclusion of both rationales is equivalent.
, which is constructed like in Theorem 3.2. Therefore, the conclusion of both rationales is equivalent.
Secondly, in the case of Proposition A.1.(ii) we obtain that (2) holds with similar argumentation and yields the same conclusion, we present it for the sake of completeness. With the sets \(J_\mu \) and \(K_\mu \) defined as above, for an arbitrary player \(\mu \) and index p one of these three possibilities holds:
-
\(p\in J_\mu \): Thus \({\bar{x}}^\mu _p = l^\mu _p\) and the box restriction \(g^\mu _{n_\mu +p}(x^\mu )=l^\mu _p - x^\mu _p\) is active. From \(\nabla _{x^\mu }g^\mu _{n_\mu +p}(x^\mu ) = -e_p\) follows
$$\begin{aligned} d^\mu _p \ge 0 \text { for all } d^\mu \in L_\le ({\bar{x}}^\mu ,{{\widehat{X}}}_\mu ). \end{aligned}$$ -
\(p\in K_\mu \): Thus \({\bar{x}}^\mu _p = u^\mu _p\) and the box restriction \(g^\mu _{p}(x^\mu )=x^\mu _p -u^\mu _p \) is active. From \(\nabla _{x^\mu }g^\mu _{p}(x^\mu ) = e_p\) follows
$$\begin{aligned} d^\mu _p \le 0 \text { for all } d^\mu \in L_\le ({\bar{x}}^\mu ,{{\widehat{X}}}_\mu ). \end{aligned}$$If \((\mu ,p)=(\nu ,i)\), this also applies:
-
\(\nabla _{x^\nu _i}F^\nu _i({\bar{x}})>0\) due to strict convexity of \(\theta _\nu \) in this component,
-
\(g^\nu _{i}(x^\mu )\) is also active and \(\nabla _{x^\nu } g^\nu _{i}(x^\mu )=e_i\).
-
-
\(\nabla _{x^\mu _p}F_i^\nu ({\bar{x}})=0\).
Together, for every player the scalar product
is non-negative for all \(d^\mu \in L_\le ({\bar{x}}^\mu ,\widehat{X}_\mu )\) and therefore (2) is fulfilled.
For any point \({\widetilde{x}} \in \Omega \) with \({\widetilde{x}}^\nu _i \ne {\bar{x}}^\nu _i\) it follows that \({\widetilde{x}}^\nu _i \le {\bar{x}}^\nu _i -1 = u^\nu _i -1\) and directly the feasibility of \({\widehat{x}}\). Again, the conclusion of both rationales is equivalent. \(\square \)
Remark A.4
The assumption in Proposition A.1 that \({\bar{x}}\) is an integer solution of \(\widehat{\textit{NEP}}\) is not necessary to obtain the statement, but it is sufficient to require that \({\bar{x}}\) is any solution of \(\widehat{\textit{NEP}}\). Nevertheless, this does not restrict the applicability of Proposition A.1 very much, because for all variables \(x^\mu _j\) with \(\nabla _{x^\mu _j}F^\nu _i({\bar{x}})\ne 0\) it is required that their value coincides with one of the integer valued bounds anyway.
Algorithm 3: Remove strategy from search space
Algorithm 3 is employed after \({\bar{x}}\) is processed by Algorithm 1. As we have \({\bar{x}}\in B_1\), this set is divided into at most \(2\cdot n\) sets, excluding \({\bar{x}}\) and preserving all other integer points from \(B_1\), i.e.
Note that at least one component of a point x in any new subset of \(B_1\) must be different from \({\bar{x}}\) in order to achieve the exclusion. Moreover, in lines 8–9, Algorithm 3 ensures that all sets from \({\mathcal {B}}^+\) are pairwise disjoint.
[14, Procedure C] Branching out a single point from the strategy set
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schwarze, S., Stein, O. A branch-and-prune algorithm for discrete Nash equilibrium problems. Comput Optim Appl 86, 491–519 (2023). https://doi.org/10.1007/s10589-023-00500-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-023-00500-4






 , defined by
, defined by 
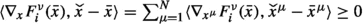 , because from Lemma
, because from Lemma 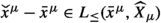 so that every summand is non-negative by (
so that every summand is non-negative by (

 , defined as
, defined as  for
for 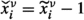 , we have
, we have  ,
,

