Abstract
We present a new variant of the Chambolle–Pock primal–dual algorithm with Bregman distances, analyze its convergence, and apply it to the centering problem in sparse semidefinite programming. The novelty in the method is a line search procedure for selecting suitable step sizes. The line search obviates the need for estimating the norm of the constraint matrix and the strong convexity constant of the Bregman kernel. As an application, we discuss the centering problem in large-scale semidefinite programming with sparse coefficient matrices. The logarithmic barrier function for the cone of positive semidefinite completable sparse matrices is used as the distance-generating kernel. For this distance, the complexity of evaluating the Bregman proximal operator is shown to be roughly proportional to the cost of a sparse Cholesky factorization. This is much cheaper than the standard proximal operator with Euclidean distances, which requires an eigenvalue decomposition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Optimization methods based on Bregman distances offer the possibility of matching the Bregman distance to the structure in the problem, with the goal of reducing the complexity per iteration. In this paper, we apply this idea to the centering problem in sparse semidefinite programming. The paper is motivated by the difficulty of exploiting sparsity in large-scale semidefinite programming in general and, for proximal methods, the need for eigendecompositions to compute Euclidean projections on the positive semidefinite matrix cone. By replacing the Euclidean projection with a generalized Bregman projection, we take advantage of the efficiency and scalability of algorithms for sparse Cholesky factorization and several related computations [3, 54].
We consider semidefinite programs (SDPs) in the standard form
with primal variable \(X\in \mathbf {S}^n\) and dual variables \(S\in \mathbf {S}^n\), \(y\in {\mathbf{R}}^m\), where \(\mathbf {S}^n\) is the set of symmetric \(n\times n\) matrices. The linear operator \({\mathcal {A}} :\mathbf {S}^n \rightarrow {\mathbf{R}}^m\) is defined as
and \({\mathcal {A}}^*(y) = \sum _{i=1}^m y_iA_i\) is its adjoint operator. The coefficients \(C, A_1,\ldots ,A_m\) are symmetric \(n \times n\) matrices. The notation \(\mathbf {S}^{n}_{+}\) is used for the cone of positive semidefinite (PSD) matrices in \(\mathbf {S}^n\).
In many large-scale applications of semidefinite programming, the coefficient matrices are sparse. The sparsity pattern of a symmetric \(n\times n\) matrix can be represented by an undirected graph \(G= (V,E)\) with vertex set \(V=\{1,2,\ldots ,n\}\) and edge set E. The set of matrices with sparsity pattern E is then defined as
In this paper, E will denote the common (or aggregate) sparsity pattern of the coefficient matrices in the SDP, i.e., we assume that \(C, A_1,\ldots , A_m\in \mathbf {S}^{n}_{E}\). Note that the sparsity pattern E is not uniquely defined (unless it is dense, i.e., the sparsity graph G is complete): if the coefficients are in \(\mathbf {S}^{n}_{E}\) then they are also in \(\mathbf {S}^{n}_{E'}\) where \(E \subset E'\). In particular, E can always be extended to make the graph \(G=(V,E)\) chordal or triangulated [14, 54]. Without loss of generality, we will assume that this is the case.
The primal variable X in (1) generally needs to be dense to be feasible. However, the cost function and the linear equality constraints only depend on the diagonal entries \(X_{ii}\) and the off-diagonal entries \(X_{ij}=X_{ji}\) for \(\{i,j\} \in E\). For the other entries the only requirement is to make the matrix positive semidefinite. In the dual problem, \(S\in \mathbf {S}^{n}_{E}\) holds at all dual feasible points. These observations imply that the SDPs (1) can be equivalently rewritten as a pair of primal and dual conic linear programs
with sparse matrix variables \(X,S\in \mathbf {S}^{n}_{E}\), and a vector variable \(y \in {\mathbf{R}}^m\). The primal cone K in this problem is the set of matrices in \(\mathbf {S}^{n}_{E}\) which have a positive semidefinite completion, i.e., \(K = \Pi _{E}(\mathbf {S}_+^{n})\) where \(\Pi _E\) stands for projection on \(\mathbf {S}^{n}_{E}\). The dual cone \(K^*\) of K is the set of positive semidefinite matrices with sparsity pattern E, i.e., \(K^*=\mathbf {S}_+^{n} \cap \mathbf {S}^{n}_{E}\). The formulation (2) is attractive when the aggregate sparsity pattern E is very sparse, in which case \(\mathbf {S}^{n}_{E}\) is a much lower-dimensional space than \(\mathbf {S}^n\).
The centering problem for the sparse SDP (2) is
where \(\phi\) is the logarithmic barrier function for the cone K, defined as
The centering parameter \(\mu >0\) controls the duality gap at the solution. Since the barrier function \(\phi\) is n-logarithmically homogeneous, the optimal solution of the centering problem is a \((\mu n)\)-suboptimal solution for the original SDP (2). The centering problem (3) is useful as an approximation to the original problem, because it yields more easily computed suboptimal solutions, with an accuracy that can be controlled by the choice of barrier parameter. The centering problem is also a key component of barrier methods, in which a sequence of centering problems with decreasing values of the barrier parameter are solved. Traditionally, the centering problem in interior-point methods is solved by Newton’s algorithm, possibly accelerated via the preconditioned conjugate gradient method [10, 55], but recent work has started to examine the use of proximal methods such as the alternating direction method of multipliers (ADMM) or the proximal method of multipliers for this purpose [37, 48].
Contributions The contribution of this paper is two-fold. First, we formulate a non-Euclidean (Bregman) proximal method for the centering problem of the sparse SDP. In the proposed method, the proximal operators are replaced by generalized proximal operators defined in terms of a Bregman generalized distance or divergence. We show that if the Bregman divergence generated by the barrier function \(\phi\) for the cone K is used, the generalized projections can be computed very efficiently, with a complexity dominated by the cost of a sparse Cholesky factorization with sparsity pattern E. This is much cheaper than the eigenvalue decomposition needed to compute a Euclidean projection on the positive semidefinite cone. Hence, while the method only solves an approximation of the SDP (2), it can handle problem sizes that are orders of magnitude larger than the problems solved by standard interior-point and proximal first-order methods.
For the solution of the centering problem, we apply a variant of the primal–dual method proposed by Chambolle and Pock [22]. The version of the algorithm described in [22] requires careful tuning of primal and dual step size parameters. Acceptable values of the step sizes depend on the norm of the linear operator \({\mathcal {A}}\) and the strong convexity constants for the distance function. These parameters are often difficult to estimate in practice. As a second contribution, we propose a new version of the algorithm, in which the step sizes are not fixed parameters, but are selected using an easily implemented line search procedure. We give a detailed convergence analysis of the algorithm with line search and show an O(1/k) ergodic convergence rate, which is consistent with previous results in [22, 39].
Related work Sparse structure in semidefinite programming has been extensively studied by many authors. The scalability of interior-point methods is limited by the need to form and solve a set of m linear equations in m variables, known as the Schur complement system, at each iteration. This system is usually dense. Sparsity in the coefficients \(A_i\) can be exploited to reduce the cost of assembling the Schur complement equations. This process is efficient especially in extremely sparse problems, where the coefficients \(A_i\) may also have low rank. In dual barrier methods, one can also take advantage of sparsity of dual feasible variables S. These properties are leveraged in the dual interior-point methods described in [9,10,11,12,13].
In another line of research, techniques based on properties and algorithms for chordal sparsity patterns have been applied to semidefinite programming since the late 1990s [3, 13, 18, 29, 30, 34, 35, 42, 46, 50, 51, 58]; see [54, 60] for recent surveys. An important tool from this literature is the conversion or clique decomposition method proposed by Fukuda et al. [30, 42]. It is based on a fundamental result from linear algebra, stating that for a chordal pattern E, a matrix \(X\in \mathbf {S}^{n}_{E}\) has a positive semidefinite completion if and only if \(X_{\gamma _k\gamma _k} \succeq 0\) for \(k=1,\ldots ,r\), where \(\gamma _1\), ..., \(\gamma _r\) are the maximal cliques in the graph [31]. In the conversion method, the large sparse variable matrix X in (2) is replaced with smaller dense matrix variables \(X_k = X_{\gamma _k\gamma _k}\). Each of these new variables is constrained to be positive semidefinite. Linear equality constraints need to be added to couple the variables \(X_k\), as they represent overlapping subblocks of a single matrix X. Thus, a large sparse SDP is converted in an equivalent problem with several smaller, dense variables \(X_k\), and additional sparse equality constraints. This equivalent problem may be considerably easier to solve by interior-point methods than the original SDP (1). Recent examples where the clique decomposition is applied to solve large sparse SDPs can be found in [27, 58].
Proximal splitting methods, such as (accelerated) proximal gradient methods [7, 8, 43], ADMM [16], and the primal–dual hybrid gradient (PDHG) or Chambolle–Pock method [20, 28, 47], are perhaps the most popular alternatives to interior-point methods in machine learning, image processing, and other applications involving large-scale convex programming. When applied to the SDPs (1), they require at each iteration a Euclidean projection on the positive semidefinite cone \(\mathbf {S}^n_+\), hence, a symmetric eigenvalue decomposition of order n. This contributes an order \(n^3\) term to the per-iteration complexity. In the nonsymmetric formulation (2) of the sparse SDP, the projections on \(K^*\) or (equivalently) K cannot be computed directly, and must be handled by introducing splitting variables and alternating projection on \(\mathbf {S}^{n}_{E}\), which is trivial, and on \(\mathbf {S}^n_+\), which requires an eigenvalue decomposition. The clique decomposition used in the conversion method described above, which was originally developed for interior-point methods, lends itself naturally to splitting algorithms as well. It allows us to replace the matrix constraint \(X\in K\) with several smaller dense inequalities \(X_k\succeq 0\), one for each maximal clique in the sparsity graph. In a proximal method, this means that projection on the \(n\times n\) positive semidefinite cone can be replaced by less expensive projections on lower-dimensional positive semidefinite cones [38, 52, 59, 61]. This advantage of the conversion method is tempered by the large number of consistency constraints that must be introduced to link the splitting variables \(X_k\). First-order methods typically do not compute very accurate solutions and if the residual error in the consistency constraints is not small, it may be difficult to convert the computed solution of the decomposed problem back to an accurate solution of the original SDP [27].
Outline The rest of the paper is organized as follows. In Sect. 2 we describe the Bregman distance generated by the barrier function and show how generalized projections can be efficiently computed without expensive eigenvalue decomposition. The primal–dual proximal algorithm and its convergence are discussed in Sect. 3. Section 4 contains results of numerical experiments.
2 Barrier proximal operator for sparse PSD matrix cone
2.1 Centering problem
We will assume that the equality constraints in (2) include an equality constraint \(\mathop \mathbf{tr}(NX)=1\), where \(N\in \mathbf {S}_{++}^{n} \cap \mathbf {S}^{n}_{E}\). To make this explicit we write the centering problem (2) as
For \(N=I\), the normalized cone \(\{X\in K \mid \mathop \mathbf{tr}(NX) = 1\}\) is a matrix extension of the probability simplex \(\{x \succeq 0 \mid \varvec{1}^Tx=1\}\), sometimes referred to as the spectraplex. With minor changes, the techniques we discuss extend to a normalization in the inequality form \(\mathop \mathbf{tr}(NX) \le 1\), with \(N\in \mathbf {S}_{++}^{n} \cap \mathbf {S}^{n}_{E}\). However, we will discuss (4) to retain the standard form of the centering problem.
The constraints \(\mathop \mathbf{tr}(NX) = 1\) and \(\mathop \mathbf{tr}(NX)\le 1\) guarantee the boundedness of the primal feasible set, a common assumption in first-order methods. The added constraint does not diminish the generality of our approach. In many applications an equality \(\mathop \mathbf{tr}(NX)=1\) is implied by the contraints \({\mathcal {A}}(X) = b\) and easily derived from the problem data (see Sect. 4 for two typical examples). When an equality constraint of this form is not readily available, one can add a bounding inequality \(\mathop \mathbf{tr}(NX) \le 1\) with N sufficiently small to ensure that the optimal solution is not modified.
To apply first-order proximal methods, we view the problem (4) as a linearly constrained optimization problem
where f is defined as
and \(\delta _H\) is the indicator function of the hyperplane \({\mathcal {H}}\). The algorithm we apply to (5) can be summarized as
where d is the Bregman distance generated by the barrier function \(\phi\):
The choices of \(\theta _k\), \(\sigma _k\), and \(\tau _k\), together with the details and origins of the algorithm, will be discussed in Sect. 3. In the remainder of this section we focus on the most expensive step in the algorithm, the optimization problem in the X-update (7b).
In Sects. 2.2 and 2.3 we first review some facts from the theory of generalized distances and the logarithmic barrier functions for the primal and dual cones K and \(K^*\). Sections 2.4 and 2.5 describe the details of the barrier kernel and the associated generalized proximal operator applied in (7b).
2.2 Bregman distance
Let h be a convex function, defined on a domain that has nonempty interior, and suppose h is continuously differentiable on \(\mathop \mathbf{int}{(\mathop \mathbf{dom}h)}\). The generalized distance generated by h is defined as the function
with domain \(\mathop \mathbf{dom}d = \mathop \mathbf{dom}h \times \mathop \mathbf{int}{(\mathop \mathbf{dom}h)}\). The function h is called the kernel function that generates the generalized distance d. For \(h(x) = \Vert x\Vert _2^2/2\) and the standard inner product \(\langle u,v\rangle = u^Tv\), we obtain \(d(x,y)= \Vert x-y\Vert _2^2/2\). The best known non-quadratic example is the relative entropy
This generalized distance is generated by the kernel \(h(x) = \sum _i x_i \log x_i\), if we use the standard inner product.
Generalized distances are not necessarily symmetric (\(d(x,y) \ne d(y,x)\) in general) but share some other important properties with the squared Euclidean norm. An important example is the triangle identity [23, Lemma 3.1]
which holds for all \(x\in \mathop \mathbf{dom}h\) and \(y, z\in \mathop \mathbf{int}{(\mathop \mathbf{dom}h)}\). This generalizes the identity
Additional conditions may have to be imposed on the kernel function h, depending on the application and the algorithm in which the generalized distance is used [19]. For now we only assume convexity and continuous differentiability on the interior of the domain. Other properties will be mentioned when needed.
The proximal operator of a closed convex function f is defined as
If f is closed and convex, then the minimizer in the definition exists and is unique for all y [40]. We will use the following extension to generalized distances. Suppose f is a convex function with the property that for every a and every \(y\in \mathop \mathbf{int}{(\mathop \mathbf{dom}h)}\), the optimization problem
has a unique solution \({\hat{x}}\) in \(\mathop \mathbf{int}{(\mathop \mathbf{dom}h)}\). Then we denote the minimizer \({\hat{x}}\) by
and call the mapping \(\mathrm {prox}_f^d\) the generalized proximal operator of f. From the second expression we see that \({\hat{x}}=\mathrm {prox}_f^d(y,a)\) satisfies
If \(d = \Vert x-y\Vert _2^2/2\), it is easily verified that \(\mathrm {prox}_f^d(y,a) = \mathrm {prox}_f (y-a)\), where \(\mathrm {prox}_f\) is the standard proximal operator.
In contrast to the Euclidean case, it is difficult to give simple general conditions that guarantee that for every a and every \(y\in \mathop \mathbf{int}{(\mathop \mathbf{dom}h)}\) the problem (9) has a unique solution in \(\mathop \mathbf{int}{(\mathop \mathbf{dom}h)}\). However, we will use the definition only for specific combinations of f and d, for which problem (9) is particularly easy to solve. In those applications, existence and uniqueness of the solution follow directly from the availability of a fast algorithm for computing it. A classical example is the relative entropy distance with f given by the indicator function of the hyperplane \(\{ x\mid \varvec{1}^Tx = 1\}\). Problem (9) can be written as
For any a and any positive y, the solution of (9) is unique and equal to the positive vector
Research on proximal methods for semidefinite programming has been largely based on the standard Euclidean proximal operators and the distance defined by the matrix entropy [6]. For these distances, projections on the positive semidefinite cone require eigenvalue decompositions, which limits the size of the variables that can be handled and precludes applications to large sparse SDPs. In the following sections, we introduce a generalized proximal operator designed for sparse semidefinite programming. The generalized proximal operator can be evaluated via a simple iterative algorithm with a complexity dominated by the cost of a sparse Cholesky factorization.
2.3 Primal and dual barrier
The logarithmic barrier functions for the cones \(K^*=\mathbf {S}_+^{n} \cap \mathbf {S}^{n}_{E}\) and \(K=\Pi _{E}(\mathbf {S}_+^{n})\) are defined as
with domains \(\mathop \mathbf{dom}\phi _*= \mathop \mathbf{int}K^*\) and \(\mathop \mathbf{dom}\phi = \mathop \mathbf{int}K\), respectively. Note that \(\phi (X)\) is the conjugate of \(\phi _*\) evaluated at \(-X\).
In [3, 54] efficient algorithms are presented for evaluating the two barrier functions, their gradients, and their directional second derivatives, when the sparsity pattern E is chordal. The value of the dual barrier \(\phi _*(S)=-\log \det S\) is easily computed from the diagonal entries in a sparse Cholesky factor of S. The gradient and Hessian are given by
Given a Cholesky factorization of S, these expressions can be evaluated via one or two recursions on the elimination tree [3, 54], without explicitly computing the entire inverse \(S^{-1}\) or the matrix product \(S^{-1}VS^{-1}\). The cost of these recursions is roughly the same as the cost of a sparse Cholesky factorization with the sparsity pattern E [3, 54].
The primal barrier function \(\phi\) and its gradient can be evaluated by solving the optimization problem in the definition of \(\phi (X)\). The optimal solution \({\hat{S}}_X\) is the matrix in \(\mathbf {S}_{++}^{n} \cap \mathbf {S}^{n}_{E}\) that satisfies
Its inverse \({\hat{S}}_X^{-1}\) is also the maximum determinant positive definite completion of X, i.e., \(Z={\hat{S}}_X^{-1}\) is the solution of
(where we take \(\mathbf {S}^n_{++}\) as the domain of the cost function). From \({\hat{S}}_X\), one obtains
Comparing the expressions for the gradients of \(\phi\) and \(\phi _*\) in (16) and (13), and using (14), we see that \(\nabla \phi\) and \(\nabla \phi _*\) are inverse mappings, up to a change in sign:
For general sparsity patterns, the determinant maximization problem (15) or the convex optimization problem in the definition of \(\phi\) must be solved by an iterative optimization algorithm. If the pattern is chordal, these optimization problems can be solved by finite recursive algorithms, again at a cost that is comparable with the cost of a sparse Cholesky factorization for the same pattern [3, 54].
2.4 Barrier kernel
The primal barrier function \(\phi\) is convex, continuously differentiable on the interior of the cone, and strongly convex on \(\mathop \mathbf{int}K \cap \{X \mid \mathop \mathbf{tr}(NX) = 1\}\). It generates the Bregman divergence
On line 2 we used the properties (16) to express \(\phi (Y)\) and \(\nabla \phi (Y)\). The generalized proximal operator (10) for the function f defined in (6), which is the key step in the X-update (7b) of algorithm (7), then becomes
where
To compute \({\hat{X}}\) we therefore need to solve an optimization problem
where \(B\in \mathbf {S}^{n}_{E}\) and \(N\in \mathbf {S}_{++}^{n} \cap \mathbf {S}^{n}_{E}\). If we introduce a Lagrange multiplier \(\nu\) for the equality constraint in (17), the optimality condition can be written as
Equivalently, since \(\nabla \phi _*(S)= -(\nabla \phi )^{-1}(-S)\),
Eliminating X we obtain a nonlinear equation in \(\nu\):
(The projection in \(\mathop \mathbf{tr}(N\Pi _E((B+\nu N)^{-1}))\) can be omitted because the matrix N has the sparsity pattern E.) The unique solution \(\nu\) that satisfies \(B+\nu N \succ 0\) defines the solution \(X = \Pi _E ((B+\nu N)^{-1})\) of (17).
The Eq. (18) is also the optimality condition for the Lagrange dual of (17), which is a smooth unconstrained convex optimization problem in the scalar variable \(\nu\):
2.5 Newton method for barrier proximal operator
In this section we discuss in detail Newton’s method applied to the dual problem (19) and the equivalent nonlinear Eq. (18). We write the equation as \(\zeta (\nu ) = 1\) where
The function \(\zeta\) and its derivative can be expressed in terms of the generalized eigenvalues \(\lambda _i\) of (B, N) as
Figure 1 shows an example with \(n=4\), \(N=I\), and eigenvalues \(10, 5, 0, -5\).
We are interested in computing the solution of \(\zeta (\nu ) = 1\) that satisfies \(B+\nu N \succ 0\), i.e., \(\nu > -\lambda _\mathrm {min}\), where \(\lambda _\mathrm {min} = \min _i \lambda _i\) is the smallest generalized eigenvalue of (B, N). We denote this interval by \(J = (-\lambda _\mathrm {min}, \infty )\). The equation \(\zeta (\nu )=1\) is guaranteed to have a unique solution in J because \(\zeta\) is monotonic and continuous on this interval, with
Furthermore, on the interval J, the function \(\zeta\) and its derivative can be expressed as
Therefore \(\zeta (\nu )\) and \(\zeta '(\nu )\) can be evaluated by taking the inner product of N with
Since \(B, N\in \mathbf {S}^{n}_{E}\), these quantities can be computed by the efficient algorithms for computing the gradient and directional second derivative of \(\phi _*\) described in [3, 54].
We note a few other properties of \(\zeta\). First, the expressions in (21) show that \(\zeta\) is convex, decreasing, and positive on J. Second, if \(\nu \in J\), then \({\tilde{\nu }} \in J\) for all \({\tilde{\nu }}\) that satisfy
This follows from
and is also a simple consequence of the Dikin ellipsoid theorem for self-concordant functions [44, Theorem 2.1.1.b].
The Newton iteration for the equation \(\zeta (\nu )-1 = 0\) is
where \(\alpha\) is a step size. The same iteration can be interpreted as a damped Newton method for the unconstrained problem (19). If \(\nu ^+ \in J\) for a unit step \(\alpha =1\), then
from strict convexity of \(\zeta\). Hence after one full Newton step, the Newton iteration with unit steps approaches the solution monotonically from the left. If \(\zeta (\nu ) < 1\) then in general a non-unit step size must be taken to keep the iterates in J. From the Dikin ellipsoid inequality (22), we see that \(\nu ^+ \in J\) for all positive \(\alpha\) that satisfy
The theory of self-concordant functions provides a step size rule that satisfies this condition and guarantees convergence:
where \(\eta\) is a constant in (0, 1). As an alternative to this fixed step size rule, a standard backtracking line search can be used to determine a suitable step size \(\alpha\) in (23). Checking whether \(\nu ^+ \in J\) can be done by attempting a sparse Cholesky factorization of \(B+\nu ^+ N\).
Figure 1 shows that the function \(\zeta\) can be quite nonlinear around the solution of the equation if the solution is near \(-\lambda _\mathrm {min}\). Instead of applying Newton’s method directly to (20), it is useful to rewrite the nonlinear equation as \(\psi (\nu ) = 0\) where
The negative smallest eigenvalue \(-\lambda _\mathrm {min}\) is a pole of \(\zeta (\nu )\), but a zero of \(1/\zeta (\nu )\). Also the derivative of \(\psi\) changes slowly near this zero point; in Fig. 1, the function \(\psi\) is almost linear in the region of interest. This implies that Newton’s method applied to (24), i.e.,
should be extremely efficient in this case. Starting the line search at \(\beta =1\) is equivalent to starting at \(\alpha = \zeta (\nu )\) in (23). This often requires fewer backtracking steps than starting at \(\alpha =1\).
Newton’s method requires a feasible initial point \(\nu _0 \in J\). Suppose we know a positive lower bound \(\gamma\) on the smallest eigenvalue of N. Then \({\hat{\nu }}_0 \in J\) where
A lower bound on \(\lambda _\mathrm {min}(B)\) can be obtained from the Gershgorin circle theorem, which states that the eigenvalues of B are contained in the disks
Thus, \(\lambda _\mathrm {min}(B) \ge \min _i{(B_{ii}-\sum _{j \ne i} |B_{ij}|)}\). Apart from the above initialization, we find another practically useful initial point \({\tilde{\nu }}_0 = n - \mathop \mathbf{tr}B/\mathop \mathbf{tr}N\), which is the solution for \(\mathop \mathbf{tr}(N(B+\nu N)^{-1})=1\) when B happens to be a multiple of N. This choice is efficient in many practical examples but, unfortunately, not guaranteed to be feasible. Thus, in the implementation, we use \({\tilde{\nu }}_0\) if it is feasible and \({\hat{\nu }}_0\) otherwise.
3 Bregman primal–dual method
The proposed algorithm (7) is applicable not only to sparse SDPs, but to more general optimization problems. To emphasize its generality and to simplify notation, we switch in this section to the vector form of the optimization problem
where f is a closed convex function. Most of the discussion in this section extends to the more general standard form
where f and g are closed convex functions. Problem (25) is a special case with \(g = \delta _{\{b\}}\), the indicator function of the singleton \(\{b\}\). While the standard form (26) offers more flexibility, it should be noted that methods for the equality constrained problem (25) also apply to (26) if this problem is reformulated as
We also note that (25) includes conic optimization problems in standard form
if we define \(f(x) = c^Tx + \delta _C(x)\), where \(\delta _C\) is the indicator function of the cone C.
In Sect. 3.1 we review some facts from convex duality theory. Section 3.2 describes the algorithm we propose for solving (25), and in Sect. 3.3 we analyze its convergence.
3.1 Duality theory
The Lagrangian for problem (25) will be denoted by
This function is convex in x and affine in z, and satisfies
where \(f^*(y) = \sup _x{(y^Tx - f(x))}\) is the conjugate of f. The function \(f^*(-A^Tz)\) is the objective in the dual problem
A point \((x^\star , z^\star )\) is a saddle point of the Lagrangian if
Existence of a saddle point is equivalent to the property that the primal and dual optimal values are equal and attained. The left-hand equality in (29) holds if and only if \(Ax^\star = b\). The right-hand equality holds if and only if \(-A^Tz^\star \in \partial f(x^\star )\). Hence \((x^\star , z^\star )\) is a saddle point if and only if it satisfies the optimality conditions
Throughout this section we assume that there exists a saddle point \((x^\star , z^\star )\).
Some of the convergence results in Sect. 3.3 are expressed in terms of the merit function
It is well known that for sufficiently large \(\gamma\), the term \(\gamma \Vert Ax-b\Vert _2\) is an exact penalty. Specifically, if \(\gamma > \Vert z^\star \Vert _2\), where \(z^\star\) is a solution of the dual problem (28), then optimal solutions of (30) are also optimal for (25).
3.2 Algorithm
The algorithm for (25) presented in this section involves a generalized distance d in the primal space, generated by a kernel function \(\phi\). It will be assumed that \(\phi\) is strongly convex on \(\mathop \mathbf{dom}f\). This property can be expressed as
for all \(x \in \mathop \mathbf{dom}\phi \cap \mathop \mathbf{dom}f\) and \(y\in \mathop \mathbf{int}{(\mathop \mathbf{dom}\phi )} \cap \mathop \mathbf{dom}f\), where \(\Vert \cdot \Vert\) is a norm, scaled so that the strong convexity constant in (31) is one. (More generally, if \(\phi\) is \(\rho\)-strongly convex with respect to \(\Vert \cdot \Vert\), then the factor 1/2 is replaced with \(\rho /2\). By scaling the norm, one can assume \(\rho =1\).) We denote by \(\Vert A\Vert\) the matrix norm
The algorithm is summarized as follows. Select starting points \(z_{-1} = z_0\) and \(x_0 \in \mathop \mathbf{int}(\mathop \mathbf{dom}\phi ) \cap \mathop \mathbf{dom}f\). For \(k=0,1,\ldots\), repeat the following steps:
Step (33b) can be written more explicitly as
The parameters \(\tau _k\), \(\sigma _k\), \(\theta _k\) are determined by one of two methods.
-
Constant parameters: \(\theta _k=1\), \(\tau _k= \tau\), \(\sigma _k=\sigma\), where
$$\begin{aligned} \sqrt{\sigma \tau } \Vert A\Vert \le \delta . \end{aligned}$$(35)The parameter \(\delta\) satisfies \(0 < \delta \le 1\). In practice, \(\delta =1\) can be used, but some convergence results will require \(\delta < 1\); see Sect. 3.3.4.
-
Varying parameters. The parameters \(\tau _k\), \(\sigma _k\), \(\theta _k\) are determined by a backtracking search. At the start of the algorithm, we set \(\tau _{-1}\) and \(\sigma _{-1}\) to some positive values. To start the search in iteration k we choose \({\bar{\theta }}_k \ge 1\). For \(i=0,1,2,\ldots\), we set \(\theta _k = 2^{-i}{\bar{\theta }}_k\), \(\tau _k=\theta _k\tau _{k-1}\), \(\sigma _k=\theta _k\sigma _{k-1}\), and compute \({\bar{z}}_{k+1}\), \(x_{k+1}\), \(z_{k+1}\) using (33). If
$$\begin{aligned} (z_{k+1}-{\bar{z}}_{k+1})^T A(x_{k+1}-x_k) \le \frac{\delta ^2}{\tau _k} d(x_{k+1}, x_k) + \frac{1}{2\sigma _k} \Vert {\bar{z}}_{k+1} - z_{k+1}\Vert _2^2, \end{aligned}$$(36)we accept the computed iterates \({\bar{z}}_{k+1}\), \(x_{k+1}\), \(z_{k+1}\) and step sizes \(\tau _k\), \(\sigma _k\), and terminate the backtracking search. If (36) does not hold, we increment i and continue the backtracking search.
The constant parameter choice is simple, but it is often overly pessimistic. Moreover it requires an estimate or tight upper bound for \(\Vert A\Vert\), which is difficult to obtain in large-scale problems. Using a loose bound for \(\Vert A\Vert\) in (35) may result in unnecessarily small values of \(\tau\) and \(\sigma\), and can dramatically slow down the convergence. The definition of \(\Vert A\Vert\) further depends on the strong convexity constant for the kernel \(\phi\); see (31) and (32). This quantity is also difficult to estimate for most kernels.
The varying parameters option does not require estimates or bounds on \(\Vert A\Vert\) or the strong convexity constant of the kernel. It is more expensive because in each backtracking iteration the three updates in (33) are computed. However, the extra cost is well justified in practice. If the line search process takes more than a few backtracking iterations, it indicates that the inequality (36) is much weaker than the conservative step size condition (35), and the algorithm with line search takes much larger steps than would be used by the constant parameter algorithm. In practice, the parameter \({\bar{\theta }}_k\) can be set to one in most iterations. The backtracking search then first checks whether the previous step sizes \(\tau _{k-1}\) and \(\sigma _{k-1}\) are acceptable, and decreases them only when needed to satisfy (36). The option of choosing \({\bar{\theta }}_k > 1\) allows one to occasionally increase the step sizes.
Algorithm (33) is related to several existing algorithms. With constant parameters, it is a special case of the primal–dual algorithm in [22, Algorithm 1], which solves the more general problem (26) and uses generalized distances for the primal and dual variables. Here we take \(g(y) = \delta _{\{b\}}\) and use a generalized distance only in the primal space. The line search condition (36) for selecting step sizes does not appear in [22].
With standard proximal operators (for squared Euclidean distances), the primal–dual algorithm of [22] is also known as the primal–dual hybrid gradient (PDHG) algorithm, and has been extensively studied as a versatile and efficient algorithm for large-scale convex optimization; see [20, 21, 24, 25, 28, 33, 45, 47, 49, 56, 57] for applications, analysis, and extensions. The line search technique for the primal–dual algorithm proposed by Malitsky and Pock [39] is similar to the one described above, but not identical, even when squared Euclidean distances are used.
The algorithm can also be interpreted as a variation on the Bregman proximal point algorithm [19, 26, 32], applied to the optimality conditions
In each iteration of the proximal point algorithm the iterates \(x_{k+1}\), \(z_{k+1}\) are defined by the inclusion
where \(\phi _\mathrm {pd}(x,z)\) is a Bregman kernel. If we choose a kernel of the form
then (37) reduces to
In the generalized proximal operator notation defined of (10) and (11), this condition can be expressed as two equations
These two equations are coupled and difficult to solve because \(x_{k+1}\) and \(z_{k+1}\) each appear on the right-hand side of an equality. The updates (33b) and (33c) are almost identical but replace \(z_{k+1}\) with \({\bar{z}}_{k+1}\) in the primal update. The iterate \({\bar{z}}_{k+1}\) can therefore be interpreted as a prediction of \(z_{k+1}\). This interpretation also provides some intuition for the step size condition (36). If \({\bar{z}}_{k+1}\) happens to be equal to \(z_{k+1}\), then (36) imposes no upper bound on the step sizes \(\tau _k\) and \(\sigma _k\). This makes sense because when \({\bar{z}}_{k+1}=z_{k+1}\) the update is equal to the proximal point update, and the convergence theory for the proximal point method does not impose upper bounds on the step size.
He and Yuan [33] have given an interesting interpretation of the primal–dual algorithm of [20] as a “pre-conditioned” proximal point algorithm. For the algorithm considered here, their interpretation corresponds to choosing
as the generalized distance in (37). It can be shown that under the strong convexity assumptions for \(\phi\) mentioned at the beginning of the section, the function (38) is convex if \(\sqrt{\sigma \tau } \Vert A\Vert \le 1\). With this choice of Bregman kernel, the inclusion (37) reduces to
which can be written as
Except for the indexing of the iterates, this is identical to (33) with constant step sizes (\(\theta _k=1\), \(\tau _k=\tau\), \(\sigma _k=\sigma\)).
3.3 Convergence analysis
In this section we analyze the convergence of the algorithm following the ideas in [22, 39, 49]. The main result is an ergodic convergence rate, given in Eq. (49).
3.3.1 Algorithm parameters
We first prove two facts about the step sizes in the two versions of the algorithm.
Constant parameters If \(\theta _k=1\), \(\tau _k=\tau\), \(\sigma _k=\sigma\), where \(\tau\) and \(\sigma\) satisfy (35), then the iterates \({\bar{z}}_{k+1}\), \(x_{k+1}\), \(z_{k+1}\) satisfy (36).
Proof
We use the definition of the matrix norm \(\Vert A\Vert\), the arithmetic–geometric mean inequality, and strong convexity of the Bregman kernel:
The last inequality follows from (35). \(\square\)
The result implies that we can restrict the analysis to the algorithm with varying parameters. The constant parameter variant is a special case with \({\bar{\theta }}_k=1\), \(\tau _{-1}=\tau\), and \(\sigma _{-1}=\sigma\).
Varying parameters In the varying parameter variant of the algorithm the step sizes are bounded below by
where \(\beta = \sigma _{-1}/\tau _{-1}\).
Proof
We proved in the previous paragraph that the exit condition (36) in the backtracking search certainly holds if
From this observation one can use induction to prove the lower bounds (39). Suppose \(\tau _{k-1} \ge \tau _\mathrm {min}\) and \(\sigma _{k-1} \ge \sigma _\mathrm {min}\). This holds at \(k=0\) by definition of \(\tau _\mathrm {min}\) and \(\sigma _\mathrm {min}\). The first value of \(\theta _k\) tested in the search is \(\theta _k = {\bar{\theta }}_k\ge 1\). If this value is accepted, then
If \(\theta _k= {\bar{\theta }}_k\) is rejected, one or more backtracking steps are taken. Denote by \({\tilde{\theta }}_k\) the last rejected value. Then \({\tilde{\theta }}_k \sqrt{\sigma _{k-1}\tau _{k-1}} \Vert A\Vert > \delta\), and the accepted \(\theta _k\) satisfies
Therefore
\(\square\)
3.3.2 Analysis of one iteration
We now analyze the progress in one iteration of the varying parameter variant of algorithm (33).
Duality gap For \(i\ge 1\), the iterates \(x_i\), \(z_i\), \({\bar{z}}_i\) satisfy
for all \(x \in \mathop \mathbf{dom}f \cap \mathop \mathbf{dom}\phi\) and all z.
Proof
The second step (33b) defines \(x_{k+1}\) as the minimizer of
By assumption the solution is uniquely defined and in the interior of \(\mathop \mathbf{dom}\phi\). Therefore \(x_{k+1}\) satisfies the optimality condition
Equivalently, the following holds for all \(x\in \mathop \mathbf{dom}\phi \cap \mathop \mathbf{dom}f\):
(The triangle identity (8) is used on the second line.) The dual update (33c) implies that
This equality at \(k=i-1\) is
The equality (42) at \(k=i-2\) is
We evaluate this at \(z=z_{i}\) and add it to the equality at \(z=z_{i-2}\) multiplied by \(\theta _{i-1}\):
Now we combine (41) for \(k=i-1\), with (43) and (44). For \(i\ge 1\),
The first inequality follows from (41). In the last step we substitute (43) and (44). Next we note that the line search exit condition (36) implies that
Substituting this in (45) gives the bound (40). \(\square\)
Monotonicity properties Suppose \(x^\star \in \mathop \mathbf{dom}\phi\), and \(x^\star\), \(z^\star\) satisfy the saddle point property (29). Then
where \(\beta = \sigma _{-1}/\tau _{-1}\). Moreover
These inequalities hold for any value \(\delta \in (0,1]\) in the line search condition (36). The second inequality implies that \({\bar{z}}_i-z_{i-1} \rightarrow 0\). If \(\delta < 1\) it also implies that \(d(x_i, x_{i-1}) \rightarrow 0\) and, by the strong convexity assumption on \(\phi\), that \(x_i-x_{i-1} \rightarrow 0\).
Proof
We substitute \(x=x^\star\), \(z=z^\star\) in (40) and note that \(L(x_i, z^\star ) - L(x^\star , {\bar{z}}_i) \ge 0\) (from the saddle-point property (29)):
With \(\beta =\sigma _{i-1}/\tau _{i-1} = \sigma _{-1}/\tau _{-1}\), this gives the inequality
Since the left-hand side is nonnegative, the inequality (46) follows. Summing from \(i=1\) to k gives (47). \(\square\)
3.3.3 Ergodic convergence
We define averaged primal and dual sequences
We first show that the averaged sequences satisfy
for all \(x\in \mathop \mathbf{dom}f\cap \mathop \mathbf{dom}\phi\) and all z. This holds for every choice for \(\delta \in (0,1]\) in (36).
Proof
From (40),
Since L is convex in x and affine in z,
Dividing by \(\sum _{i=1}^k \tau _{i-1}\) gives (48). \(\square\)
If we substitute in (48) an optimal \(x=x^\star\) (which satisfies \(Ax^\star = b\)), we obtain that
for all z. Maximizing both sides over z subject to \(\Vert z\Vert _2\le \gamma\) shows that
The first two terms on the left-hand side form the merit function (30). For \(\gamma > \Vert z^\star \Vert _2\), the penalty function in the merit function is exact, so \(f(x) + \gamma \Vert Ax-b\Vert _2 - f(x^\star ) \ge 0\) with equality only if x is optimal. (The use of an exact penalty function to express a convergence result is inspired by [49, page 287].) Since \(\tau _i \ge \tau _\mathrm {min}\), the inequality shows that the merit function decreases as O(1/k).
3.3.4 Convergence of the iterates
We now make two additional assumptions about the Bregman kernel \(\phi\) [19].
-
1.
For fixed x, the sublevel sets \(\{y \mid d(x,y) \le \alpha \}\) are closed. In other words, the distance d(x, y) is a closed function of y.
-
2.
If \(y_k\in \mathop \mathbf{int}{(\mathop \mathbf{dom}\phi )}\) converges to \(x\in \mathop \mathbf{dom}\phi\), then \(d(x,y_k)\rightarrow 0\).
These two assumptions are not restrictive, and in particular, they are satisfied by the logarithmic barrier \(\phi\) (12). We also make the (minor) assumptions that \(\delta < 1\) in (36) and that \(\theta _k\) is bounded above (which is easily satisfied, since the user chooses \({\bar{\theta }}_k\)). With these additional assumptions it can be shown that the sequences \(x_k\), \(z_k\) converge to optimal solutions.
Proof
The inequality (46) and strong convexity of \(\phi\) show that the sequences \(x_k\), \(z_k\) are bounded. Let \((x_{k_i}, z_{k_i})\) be a convergent subsequence with limit \(({\hat{x}}, {\hat{z}})\). With \(\delta < 1\), (47) shows that \(d(x_{k_i+1}, x_{k_i})\) converges to zero. By strong convexity of the kernel, \(x_{k_i+1} - x_{k_i} \rightarrow 0\) and therefore the subsequence \(x_{k_i+1}\) also converges to \({\hat{x}}\). Since \(z_{k_i+1}- z_{k_i} \rightarrow 0\), the subsequence \(z_{k_i+1}\) converges to \({\hat{z}}\). Since \(\theta _k\) is bounded above, \({\bar{z}}_{k_{i+1}} = z_{k_i} + \theta _k (z_{k_i} - z_{k_i-1})\) also converges to \({\hat{z}}\).
The dual update (33c) can be written as
Since \(z_{k_i+1} -z_{k_i} \rightarrow 0\) and \(\sigma _{k_i} \ge \sigma _\mathrm {min}\), the left-hand side converges to zero, so \(A{\hat{x}}= b\).
From (46), \(d(x^\star , x_{k_i})\) is bounded above. Since the sublevel sets \(\{ y \mid d(x^\star , y)\le \alpha \}\) are closed subsets of \(\mathop \mathbf{int}{(\mathop \mathbf{dom}\phi )}\), the limit \({\hat{x}}\) is in \(\mathop \mathbf{int}{(\mathop \mathbf{dom}\phi )}\). The left-hand side of the optimality condition
converges to \(-A^T{\hat{z}}\), because \(\tau _k\ge \tau _\mathrm {min}\) and \(\nabla \phi\) is continuous on \(\mathop \mathbf{int}{(\mathop \mathbf{dom}\phi )}\). By maximal monotonicity of \(\partial f\), this implies that \(-A^T {\hat{z}} \in \partial f({\hat{x}})\) (see [17, page 27] [53, lemma 3.2]). We conclude that \({\hat{x}}\), \({\hat{z}}\) satisfy the optimality conditions \(A{\hat{x}}=b\) and \(-A^T{\hat{z}} \in \partial f({\hat{x}})\).
To show that the entire sequence converges, we substitute \(x ={\hat{x}}\), \(z={\hat{z}}\) in (40):
The left-hand side is nonnegative by the saddle point property (29). Therefore
for all k. This shows that
for all \(k\ge k_i\). By the second additional kernel property mentioned above, the right-hand side converges to zero. Therefore \(d({\hat{x}}, x_k) \rightarrow 0\) and \(z_k \rightarrow {\hat{z}}\). If \(d({\hat{x}}, x_k) \rightarrow 0\), then the strong convexity property of the kernel implies that \(x_k \rightarrow {\hat{x}}\). \(\square\)
4 Numerical experiments
In this section we evaluate the performance of algorithm (7), the Bregman PDHG algorithm (33) applied to the centering problem (5). The numerical results illustrate that the cost for evaluating the Bregman proximal operator (17) is comparable to the cost of a sparse Cholesky factorization with sparsity pattern E. This prox-evaluation dominates the computational cost in each iteration of (7), since \({\mathcal {A}}\) and \({\mathcal {A}}^*\) are usually easy to evaluate for large-scale problems with sparse or other types of structure. In particular, the proposed method does not need to solve linear equations involving \({\mathcal {A}}\) or \({\mathcal {A}}^*\), an important advantage over ADMM and interior-point methods.
In this section we consider the centering problem for two sets of sparse SDPs, the maximum cut problem and the graph partitioning problem. The experiments are carried out in Python 3.6 on a laptop with an Intel Core i5 2.4GHz CPU and 8GB RAM. The Python library for chordal matrix computations CHOMPACK [4] is used to compute chordal extensions (with the AMD reordering [1]), sparse Cholesky factorizations, the primal barrier \(\phi\), and the gradient and directional second derivative of the dual barrier \(\phi _*\). Other sparse matrix computations are implemented using CVXOPT [2].
In the experiments, we terminate the iteration (33) when the relative primal and dual residuals are less than \(10^{-6}\). These two stopping conditions are sufficient for our algorithm, as suggested by the convergence proof, in particular, Eqs. (50) and (51). The two residuals are defined as
where \(\Vert Y\Vert _\mathrm {max}=\max _{i,j} |Y_{ij}|\).
4.1 Maximum cut problem
Given an undirected graph \(G=(V,E)\), the maximum cut problem is to partition the set of vertices into two sets in order to maximize the total number of edges between the two sets. (If every edge \(\{i,j\} \in E\) is associated with a nonnegative weight \(w_{ij}\), then the maximum cut problem is to maximize the total weight of the edges between the two sets.) One can show that the maximum cut problem can be represented as a binary quadratic optimization problem
where \(L \in \mathbf {S}^n\) is the Laplacian of an undirected graph \(G=(V,E)\) with vertices \(V=\{1,2,\ldots ,n\}\). The SDP relaxation of the maximum cut problem is
with variable \(X \in \mathbf {S}^n\). The operator \(\mathop \mathbf{diag}:\mathbf {S}^n \rightarrow {\mathbf{R}}^n\) returns the diagonal elements of the input matrix as a vector: \(\mathop \mathbf{diag}(X)=(X_{11}, X_{22}, \ldots , X_{nn})\). If moderate accuracy is allowed, we can solve the centering problem of the SDP relaxation
with optimization variable \(X \in \mathbf {S}^{n}_{E^\prime }\) where \(E^\prime\) is a chordal extension of E. Note that \(\mathop \mathbf{tr}(X) = n\) for all feasible X. The centering problem has the form of (5) with
The Lagrangian of (53) is in the form of (27) where f is defined in (6), and z is the Lagrange multiplier associated with the equality constraint \(\mathop \mathbf{diag}(X)=\varvec{1}\). Thus we have
where \(X^\star\) and \(z^\star\) are the primal and dual optimal solutions of the centering problem (53), and \(p^\star _\mathrm {sdp}\) is the optimal value of the SDP (52).
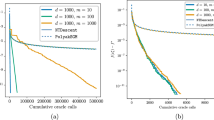
Numerical results We first collect four MAXCUT problems of moderate size from SDPLIB [15]. The SDP relaxation (52) is solved using MOSEK [41] and the optimal value computed by MOSEK is denoted by \(p^\star _\mathrm {sdp}\). (Note that the source file for the graph maxcutG55 was unfortunately incorrectly converted into SDPA sparse format. Thus the objective value for the maxG55 problem obtained from the original data file is \({1.1039 \times 10^4}\) instead of \({9.9992 \times 10^3}\) as reported in SDPLIB.)
In (53), we set \(\mu =0.001/n\), and report in column 4 of Table 1 the difference between \(p^\star _\mathrm {sdp}\) and the cost function \((1/4)\mathop \mathbf{tr}(LX)\) at the suboptimal solution returned by the algorithm.
The last two columns of Table 1 give the relative primal and dual residuals. These results show that the proposed algorithm is able to solve the centering SDP (53) with the desired accuracy. A comparison of the third and fourth columns of Table 1 confirms (54), i.e., the objective value of the SDP at X is within \(\mu n = 10^{-3}\) of the optimal value. Considering the values of \(p^\star _\mathrm {sdp}\), we see that the computed points on the central path are close to the optimal solutions of the SDPs.
To test the scalability of algorithm (33), we add four larger graphs from the SuiteSparse collection [36]. In Table 2 we report the time per Cholesky factorization, the number of Newton steps per iteration, the time per PDHG iteration, and the number of iterations in the primal–dual (PDHG) algorithm for the eight test problems.
As can be seen from the table, the number of Newton iterations per prox-evaluation remains small even when the size of the problem increases. Also, we observe that the time per PDHG iteration is roughly the cost of a sparse Cholesky factorization times the number of Newton steps. This means that the backtracking in Newton’s method does not cause a significant overhead. Since the evaluations of \({\mathcal {A}}\) and \({\mathcal {A}}^*\) in this problem are very cheap, the cost per prox-evaluation is the dominant term in the per-iteration complexity.
4.2 Graph partitioning
The problem of partitioning the vertices of a graph \(G=(V,E)\) in two subsets of equal size (here we assume an even number of vertices), while minimizing the number of edges between the two subsets, can be expressed as
where L is the graph Laplacian. The ith entry of the n-vector x indicates the set that vertex i is assigned to. To obtain an SDP relaxation we introduce a matrix variable \(Y=xx^T\) and write the problem in the equivalent form
and then relax the constraint \(Y=xx^T\) as \(Y\succeq 0\). This gives the SDP
The dual SDP is
with variables \(\xi \in {\mathbf{R}}\) and \(z \in {\mathbf{R}}^n\).
The aggregate sparsity pattern of the SDP (55) is completely dense, because the equality constraint \(\varvec{1}^TY\varvec{1}=0\) has a coefficient matrix of all ones. We therefore eliminate the dense constraint using the technique described in [30, page 668]. Let P be the \(n\times (n-1)\) matrix
The columns of P form a sparse basis for the orthogonal complement of the multiples of the vector \(\varvec{1}\). Suppose Y is feasible in (55) and define
From \(\varvec{1}^TY\varvec{1}= 0\), we see that
and therefore \(v=0\). Since the matrix (56) is positive semidefinite, we also have \(u = 0\). Hence every feasible Y can be expressed as \(Y = P XP^T\), with \(X\succeq 0\). If we make this substitution in (55) we obtain
The \((n-1)\times (n-1)\) matrix \(P^TLP\) has elements
Thus the sparsity pattern \(E^\prime\) of the matrix \(P^TLP\) is denser than E, i.e., \(E \subseteq E^\prime\). The n constraints \(\mathop \mathbf{diag}(PXP^T) = \varvec{1}\) reduce to
To apply algorithm (33), we first rewrite the graph partitioning problem as
where \(E^{\prime \prime }\) is a chordal extension of the aggregate sparsity pattern \(E^\prime\). Note that \(\mathop \mathbf{tr}(P^TPX) = n-1\) for all feasible X. The centering problem for this sparse SDP is of the form (5) with
Numerical results Table 3 shows the numerical results for four problems from SDPLIB [15].
The SDP relaxation (55) is solved by MOSEK and its optimal value is denoted by \(p^\star _\mathrm {sdp}\). In solving (57), we set \(\mu =0.001/n\), and report in Table 3 the value \((1/4)\mathop \mathbf{tr}(P^TLPX)\), where X is the solution returned by the algorithm (33). As in the first experiment, the numerical results show that the algorithm is able to solve the centering SDP (57) with desired accuracy.
In addition, we test the algorithm for four additional graphs from the SuiteSparse collection [36]. Table 4 reports the time per Cholesky factorization, the number of Newton steps per iteration, the time per PDHG iteration, and the number of iterations in the primal–dual algorithm.
The same observations as in Sect. 4.1 apply: the number of Newton steps remains moderate as the size of the problem increases, and the cost per iteration is roughly linear in the cost of a Cholesky factorization.
5 Conclusions
We presented a Bregman proximal algorithm for the centering problem in sparse semidefinite programming. The Bregman distance used in the proximal operator is generated by the logarithmic barrier function for the cone of sparse matrices with a positive semidefinite completion. With this choice of Bregman distance, the per-iteration complexity of the algorithm is dominated by the cost of a Cholesky factorization with the aggregate sparsity pattern of the SDP, plus the cost of evaluating the linear mapping in the constraints and its adjoint.
The proximal algorithm we used is based on the primal–dual method proposed by Chambolle and Pock [22]. An important addition to the algorithm is a new procedure for selecting the primal and dual step sizes, without knowledge of the norm of the linear mapping or the strong convexity of the Bregman kernel. In the current implementation the ratio of the primal and dual step sizes is kept fixed throughout the iteration. An interesting further improvement would be to relax this condition, choosing \(\beta =\sigma _k / \tau _k\) adaptively [5, 39].
The standard primal–dual hybrid gradient algorithm is known to include several important algorithms as special cases. The Bregman extension of the algorithm is equally versatile. We mention one interesting example. Suppose the matrix A in (25) is a product of two matrices \(A= CB\). Then (25) is equivalent to
where \(g(y) = \delta _{\{b\}}(Cy)\). The standard (Euclidean) proximal operator of g is the mapping
The PDHG algorithm applied to the reformulated problem requires in each iteration an evaluation of the Bregman proximal operator of f, matrix–vector products with B and \(B^T\), and the solution of the least norm problem in the definition of \(\mathrm {prox}_g\). For \(C=A\), \(B=I\), this can be interpreted as a Bregman extension of the Douglas–Rachford algorithm, or of Spingarn’s method for convex optimization with equality constraints.
References
Amestoy, P., Davis, T., Duff, I.: An approximate minimum degree ordering. SIAM J. Matrix Anal. Appl. 17(4), 886–905 (1996)
Andersen, M., Dahl, J., Vandenberghe, L.: CVXOPT: A Python Package for Convex Optimization, Version 1.2.4. www.cvxopt.org (2020)
Andersen, M.S., Dahl, J., Vandenberghe, L.: Logarithmic barriers for sparse matrix cones. Optim. Methods Softw. 28(3), 396–423 (2013). https://doi.org/10.1080/10556788.2012.684353
Andersen, M.S., Vandenberghe, L.: CHOMPACK: A Python Package for Chordal Matrix Computations, Version 2.2.1 (2015). cvxopt.github.io/chompack
Applegate, D., Dóaz, M., Hinder, O., Lu, H., Lubin, M., O’Donoghue, B., Schudy, W.: Practical large-scale linear programming using primal-dual hybrid gradient. arXiv (2021)
Auslender, A., Teboulle, M.: Interior gradient and proximal methods for convex and conic optimization. SIAM J. Optim. 16(3), 697–725 (2006)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2(1), 183–202 (2009)
Beck, A., Teboulle, M.: Gradient-based algorithms with applications to signal recovery. In: Y. Eldar, D. Palomar (eds.) Convex Optimization in Signal Processing and Communications. Cambridge University Press (2009)
Bellavia, S., Gondzio, J., Morini, B.: A matrix-free preconditioner for sparse symmetric positive definite systems and least-squares problems. SIAM J. Sci. Comput. 35(1), A192–A211 (2013)
Bellavia, S., Gondzio, J., Porcelli, M.: An inexact dual logarithmic barrier method for solving sparse semidefinite programs. Math. Program. 178(1–2), 109–143 (2019)
Bellavia, S., Gondzio, J., Porcelli, M.: A relaxed interior point method for low-rank semidefinite programming problems with applications to matrix completion. arXiv (2019)
Benson, S.J., Ye, Y.: Algorithm 875: DSDP5-software for semidefinite programming. ACM Trans. Math. Softw. (TOMS) 34(3), 16 (2008)
Benson, S.J., Ye, Y., Zhang, X.: Solving large-scale sparse semidefinite programs for combinatorial optimization. SIAM J. Optim. 10, 443–461 (2000)
Blair, J.R.S., Peyton, B.: An introduction to chordal graphs and clique trees. In: A. George, J.R. Gilbert, J.W.H. Liu (eds.) Graph Theory and Sparse Matrix Computation. Springer-Verlag (1993)
Borchers, B.: SDPLIB 1.2, a library of semidefinite programming test problems. Optim. Methods Softw. 11(1-4), 683–690 (1999)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2011)
Brézis, H.: Opérateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert. North-Holland Mathematical Studies, Vol. 5. North-Holland (1973)
Burer, S.: Semidefinite programming in the space of partial positive semidefinite matrices. SIAM J. Optim. 14(1), 139–172 (2003)
Censor, Y., Zenios, S.A.: Parallel Optimization: Theory, Algorithms, and Applications. Numerical Mathematics and Scientific Computation. Oxford University Press, New York (1997)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40, 120–145 (2011)
Chambolle, A., Pock, T.: An introduction to continuous optimization for imaging. Acta Numerica pp. 161–319 (2016)
Chambolle, A., Pock, T.: On the ergodic convergence rates of a first-order primal-dual algorithm. Math. Prog. Ser. A 159, 253–287 (2016)
Chen, G., Teboulle, M.: Convergence analysis of a proximal-like minimization algorithm using Bregman functions. SIAM J. Optim. 3, 538–543 (1993)
Condat, L.: A primal-dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 158(2), 460–479 (2013)
Davis, D., Yin, W.: A three-operator splitting scheme and its optimization applications (2015). arxiv.org/abs/1504.01032
Eckstein, J.: Nonlinear proximal point algorithms using Bregman functions, with applications to convex programming. Math. Oper. Res. 18(1), 202–226 (1993)
Eltved, A., Dahl, J., Andersen, M.S.: On the robustness and scalability of semidefinite relaxation for optimal power flow problems. Optimization and Engineering pp. 1–18 (2020)
Esser, E., Zhang, X., Chan, T.: A general framework for a class of first order primal-dual algorithms for convex optimization in imaging science. SIAM J. Imag. Sci. 3(4), 1015–1046 (2010)
Fujisawa, K., Kojima, M., Nakata, K.: Exploiting sparsity in primal-dual interior-point methods for semidefinite programming. Math. Program. 79(1–3), 235–253 (1997)
Fukuda, M., Kojima, M., Murota, K., Nakata, K.: Exploiting sparsity in semidefinite programming via matrix completion I: general framework. SIAM J. Optim. 11, 647–674 (2000)
Grone, R., Johnson, C.R., Sá, E.M., Wolkowicz, H.: Positive definite completions of partial Hermitian matrices. Linear Algebra Appl. 58, 109–124 (1984)
Güler, O.: Ergodic convergence in proximal point algorithms with Bregman functions. In: D.Z. Du, J. Sun (eds.) Advances in Optimization and Approximation, pp. 155–165. Springer (1994)
He, B., Yuan, X.: Convergence analysis of primal-dual algorithms for a saddle-point problem: from contraction perspective. SIAM J. Imag. Sci. 5(1), 119–149 (2012)
Kim, S., Kojima, M., Mevissen, M., Yamashita, M.: Exploiting sparsity in linear and nonlinear matrix inequalities via positive semidefinite matrix completion. Math. Program. 129, 33–68 (2011)
Kobayashi, K., Kim, S., Kojima, M.: Correlative sparsity in primal-dual interior-point methods for LP, SDP, and SOCP. Appl. Math. Optim. 58(1), 69–88 (2008)
Kolodziej, S., Aznaveh, M., Bullock, M., David, J., Davis, T., Henderson, M., Hu, Y., Sandstrom, R.: The suitesparse matrix collection website interface. J. Open Source Softw. 4(35), 1244 (2019)
Lin, T., Ma, S., Ye, Y., Zhang, S.: An ADMM-based interior-point method for large-scale linear programming. Optim. Methods Softw. 36(2–3), 389–424 (2021)
Madani, R., Kalbat, A., Lavaei, J.: ADMM for sparse semidefinite programming with applications to optimal power flow problem. In: Proceedings of the 54th IEEE Converence on Decision and Control, pp. 5932–5939 (2015)
Malitsky, Y., Pock, T.: A first-order primal-dual algorithm with linesearch. SIAM J. Optim. 28(1), 411–432 (2018)
Moreau, J.J.: Proximité et dualité dans un espace hilbertien. Bull. Math. Soc. France 93, 273–299 (1965)
MOSEK ApS: The MOSEK Optimization Tools Manual. Version 8.1. (2019). Available from www.mosek.com
Nakata, K., Fujisawa, K., Fukuda, M., Kojima, M., Murota, K.: Exploiting sparsity in semidefinite programming via matrix completion II: implementation and numerical details. Math. Program. Ser. B 95, 303–327 (2003)
Nesterov, Y.: Lectures on Convex Optimization. Springer Publishing Company, Incorporated (2018)
Nesterov, Y., Nemirovskii, A.: Interior-Point Polynomial Methods in Convex Programming, Studies in Applied Mathematics, Vol. 13. SIAM, Philadelphia, PA (1994)
O’Connor, D., Vandenberghe, L.: On the equivalence of the primal-dual hybrid gradient method and Douglas-Rachford splitting. Math. Program. 179(1–2), 85–108 (2020)
Pakazad, S.K., Hansson, A., Andersen, M.S., Rantzer, A.: Distributed semidefinite programming with application to large-scale system analysis. IEEE Trans. Autom. Control 63(4), 1045–1058 (2018)
Pock, T., Cremers, D., Bischof, H., Chambolle, A.: An algorithm for minimizing the Mumford-Shah functional. In: Proceedings of the IEEE 12th International Conference on Computer Vision (ICCV), pp. 1133–1140 (2009)
Pougkakiotis, S., Gondzio, J.: An interior point-proximal method of multipliers for convex quadratic programming. Comput. Optim. Appl. 78 (2021)
Shefi, R., Teboulle, M.: Rate of convergence analysis of decomposition methods based on the proximal method of multipliers for convex minimization. SIAM J. Optim. 24(1), 269–297 (2014)
Srijuntongsiri, G., Vavasis, S.: A fully sparse implementation of a primal-dual interior-point potential reduction method for semidefinite programming (2004). arXiv:cs/0412009
Sun, Y., Andersen, M.S., Vandenberghe, L.: Decomposition in conic optimization with partially separable structure. SIAM J. Optim. 24, 873–897 (2014)
Sun, Y., Vandenberghe, L.: Decomposition methods for sparse matrix nearness problems. SIAM J. Matrix Anal. Appl. 36(4), 1691–1717 (2015)
Tseng, P.: A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control. Optim. 38(2), 431–446 (2000)
Vandenberghe, L., Andersen, M.S.: Chordal graphs and semidefinite optimization. Found. Trends Optim. 1(4), 241–433 (2014)
Vandenberghe, L., Boyd, S.: A primal-dual potential reduction method for problems involving matrix inequalities. Math. Program. 69(1), 205–236 (1995)
Vũ, B.C.: A splitting algorithm for dual monotone inclusions involving cocoercive operators. Adv. Comput. Math. 38, 667–681 (2013)
Yan, M.: A new primal-dual algorithm for minimizing the sum of three functions with a linear operator. J. Sci. Comput. 76(3), 1698–1717 (2018)
Zhang, R.Y., Lavaei, J.: Sparse semidefinite programs with guaranteed near-linear time complexity via dualized clique tree conversion. Math. Program. 188(1), 351–393 (2021)
Zheng, Y., Fantuzzi, G., Papachristodolou, A., Goulart, P., Wynn, A.: Fast ADMM for semidefinite programs with chordal sparsity. In: 2017 American Control Conference (ACC), pp. 3335–3340 (2017)
Zheng, Y., Fantuzzi, G., Papachristodoulou, A.: Chordal and factor-width decompositions for scalable semidefinite and polynomial optimization. Annu. Rev. Control (2021). https://doi.org/10.1016/j.arcontrol.2021.09.001
Zheng, Y., Fantuzzi, G., Papachristodoulou, A., Goulart, P., Wynn, A.: Chordal decomposition in operator-splitting methods for sparse semidefinite programs. Math. Program. 180, 489–532 (2020)
Acknowledgements
We thank Martin S. Andersen for suggestions that greatly improved the implementation used in Sect. 4. We also thank the editor and the reviewers for their insightful feedback and valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research supported in part by NSF Grant ECCS 1509789.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jiang, X., Vandenberghe, L. Bregman primal–dual first-order method and application to sparse semidefinite programming. Comput Optim Appl 81, 127–159 (2022). https://doi.org/10.1007/s10589-021-00339-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-021-00339-7