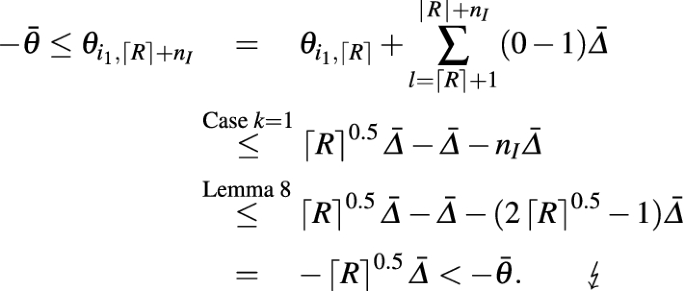On mixed-integer optimal control with constrained total variation of the integer control

Abstract

The combinatorial integral approximation (CIA) decomposition suggests solving mixed-integer optimal control problems by solving one continuous nonlinear control problem and one mixed-integer linear program (MILP). Unrealistic frequent switching can be avoided by adding a constraint on the total variation to the MILP. Within this work, we present a fast heuristic way to solve this CIA problem and investigate in which situations optimality of the constructed feasible solution is guaranteed. In the second part of this article, we show tight bounds on the integrality gap between a relaxed continuous control trajectory and an integer feasible one in the case of two controls. Finally, we present numerical experiments to highlight the proposed algorithm’s advantages in terms of run time and solution quality.

Introduction

Mixed-Integer Optimal Control has been established as a useful tool for modeling real-world problems [6, 10, 22, 33]. In practice, only an optimal control policy is realistic that avoids frequent switching between the system modes. However, it remains an open research question as to how switching costs or a limited number of switches can be efficiently incorporated into the optimization problem.

In this article, we follow a first-discretize-then-optimize approach because in contrast to indirect methods and dynamic programming, a more generic problem class can be solved for which efficient numerical methods, in particular, a decomposition approach used in this article, are available. By this approach, the control problem is discretized via, e.g., Direct Multiple Shooting [5] or Direct Collocation [29], which leads to a mixed-integer nonlinear program (MINLP). This problem class is NP-hard in general, so that it has been proposed to reduce complexity by solving first the relaxed problem with dropped integrality constraint, which is a nonlinear program (NLP), before approximating relaxed controls in a second step with binary controls as part of a mixed-integer linear program (MILP). The second problem is usually referred to as combinatorial integral approximation (CIA) problem [27], whereas the whole algorithm is called CIA decomposition [31]. It is common to use the fast Sum-Up Rounding (SUR) heuristic [24] to find a feasible approximative solution for the CIA problem, so that this second step is also named rounding. However, standard SUR does not consider time-coupled combinatorial constraints, which is why the use of the CIA problem is necessary in this case. The variable time transformation [2, 11, 21] method also avoids solving a MINLP by assuming a given sequence of the system modes so that only their durations as part of an NLP have to be computed. Recently, De Marchi extended this approach by including switching costs with sparse optimization methods [9]. As part of the CIA decomposition, Sager [24], Kirches [16], and Rieck [20] proposed to add penalty terms to the control problem objective in order to account for switching costs or to reduce the number of switches between active controls. Recently, Kirches et al. [17] investigated this approach for the setting with implicit switches and where jumps of the differential state values may occur. One issue of the penalization approach is the appropriate choice of the penalty factor since heavy penalization can in some instances [16] attract solutions involving frequent switching. Bestehorn et al. [3, 4] presented an idea to incorporate switching costs into the problem by fixing a small control deviation tolerance in the rounding problem and minimizing switching costs subject to this deviation tolerance.

This work builds on [27], where it has been proposed to solve the CIA problem with constraints that limit the total variation (TV) of the integer control. By this, the original optimal control objective remains untouched, and we require only the number of switches to be less than a desired threshold. Our idea is to use generally a Branch & Bound (BNB) scheme [7] for solving this CIA problem, but, as we will show in this article, this can be replaced for certain instances by a sequence of rounding scheme evaluations. Furthermore, we evaluate upper bounds on the CIA objective subject to these discrete TV constraints. It has been shown that the integer approximation error, i.e., the difference of relaxed optimal control objective value and CIA rounded objective value, can be driven to zero under mild conditions and if the grid length is driven to zero [19, 27]. This result does not hold anymore if discrete TV constraints are included. Still, we expect our approach to yield feasible solutions of the MIOCP with an a priori integer gap.

Contribution

To accelerate the CIA solving process, we propose the Maximum Dwell Rounding (MDR) scheme, which is a fast rounding heuristic. It is based on the idea to activate a chosen control mode as long as possible without violating a desired integrality gap $\theta$, i.e., the accumulated deviation of relaxed and binary controls, and then perform this with the next promising mode. We apply it iteratively as part of the Adaptive Maximum Dwell Rounding (AMDR) algorithm for finding binary controls that satisfy time-coupled combinatorial constraints such as a TV bound and derive optimality conditions of the obtained binary control function with respect to the CIA problem. Based on this scheme, we prove the tightest possible upper bound on the integrality gap for equidistant discretization and the case of two binary controls, which reads

$$\begin{aligned} \theta \le \frac{N+\sigma _{\text {max}}+1}{3+2\sigma _{\text {max}}}\bar{\Delta }, \end{aligned}$$

where N denotes the number of intervals, $\sigma _{\text {max}}$ the TV bound and $\bar{\Delta }$ the maximum grid length. We are going to establish further bounds for the situation of non-equidistant grids or more than two binary controls.

Outline

We give a problem definition of the MIOCP of interest in Sect. 2 and describe the proposed CIA decomposition algorithm with (CIA) as subproblem in Sect. 3. Next, we introduce auxiliary CIA problems and derive a lower bound for these problems in Sect. 4. We define the MDR scheme in Sect. 5 and show its usefulness with respect to solving the CIA problem subject to discrete TV constraints. We continue by analyzing the worst-case integrality gap for $n_{\omega }=2$ in Sect. 6, respectively for $n_{\omega }>2$ in Sect. 7. Finally, we present numerical experiments in Sect. 8 and conclusions in Sect. 9.

Notations

Let $[n] := \{1, \ldots , n\}, [n]_0 := \{0\}\cup [n],$ for $n \in \mathbb {N}$. We use Gauss’ bracket notation, i.e. $\lfloor x \rfloor := \max \{k\in \mathbb {Z}\, \mid \, k\le x\}, \, x\in \mathbb {R}$, and analogously for $\lceil x \rceil$. We indicate by $\lceil x \rceil ^{0.5}$ the rounding up of $x\in \mathbb {R}$ to the next multiple of 0.5:

$$\begin{aligned} \lceil x \rceil ^{0.5} := \min \{ y \mid y = n\cdot 0.5, \ n\in \mathbb {N}, y\ge x \}. \end{aligned}$$

We write ”for a.e. $t\in \mathcal {T}$” for abbreviating for all $t\in \mathcal {T}\subset \mathbb {R}$ except on a set of measure zero. Moreover, we write control to abbreviate a control realization $\omega _i(\cdot ), i\in [n],$ of a control function $\omega (\cdot )=(\omega _1(\cdot ),\ldots ,\omega _n(\cdot ))^\intercal$.

Mixed-integer optimal control problem

Mixed-integer optimal control problems (MIOCPs) can be equivalently reformulated into problems with affinely entering binary controls in the right-hand side of the ordinary differential equation via the (partial) outer convexification method, see [24] for further details. Therefore, we declare this reformulated MIOCP as the problem of interest and provide the corresponding definitions in this section.

We consider problems on a given time horizon $\mathcal {T}:=[t_0 ,t_f]\subset \mathbb {R}$. Throughout this paper, we assume a problem involving ${n_\omega }\ge 2$ binary control realizations. We introduce the binary control function after defining the TV of a function and its associated space.

Definition 1

(Total Variation of a function and BV space) The TV of a function $\omega :\mathcal {T} \rightarrow \mathbb {R}^{n_\omega }$ is defined to be the quantity

$$\begin{aligned} TV(\omega ) := \sup \limits _{P\in \mathcal {P}}\left\{ \frac{1}{2} \sum \limits _{i\in [{n_\omega }]} \sum \limits _{j\in [n_P]}|\omega _i(t_j)-\omega _i(t_{j-1})|\right\} , \end{aligned}$$

(2.1)

where $P=(t_0,\ldots ,t_{n_{P}})$ is a partition out of the set of all partitions $\mathcal {P}$ of the interval $\mathcal {T}$ and $n_P$ denotes the partition specific number of time points.

We group the functions $\omega$ with finite TV into the space of bounded variation BV:

$$\begin{aligned} BV(\mathcal {T},\mathbb {R}^{n_\omega }):= \{\omega :\mathcal {T} \rightarrow \mathbb {R}^{n_\omega }\ \mid \ TV(\omega ) < \infty \}. \end{aligned}$$

Definition 2

(Binary ${\varvec{\omega }}$ and relaxed control functions ${\varvec{\alpha }}$) Let the vector of binary controls ${\varvec{\omega }}$ on the simplex and its corresponding vector of relaxed controls ${\varvec{\alpha }}$ defined by their function space domains

$$\begin{aligned} \Omega:= & {} \left\{ {\varvec{\omega }} \in BV(\mathcal {T},\{0,1\}^{n_\omega }) \, \mid \, \sum \limits _{i\in [{n_\omega }]} \omega _i(t) = 1, \ {\text { for a.e. }} t\in \mathcal {T} \right\} , \\ \mathcal {A}:= & {} \left\{ {\varvec{\alpha }} \in BV(\mathcal {T},[0,1]^{n_\omega }) \, \mid \, \sum \limits _{i\in [{n_\omega }]} \alpha _i(t) = 1, \ {\text { for a.e. }} t\in \mathcal {T} \right\} . \end{aligned}$$

Definition 3

(Problems (MIOCP) and (OCP)) Let a maximum number of switches $\sigma _{\text {max}}\in \mathbb {N}$ be given. We refer to the following general problem class as (MIOCP)

$$\begin{aligned}& \underset{\varvec{x}, \,\omega\in \Omega}{\min} \ \Phi \left( {\varvec{x}}(t_f)\right) \\&{\mathrm {s.\,t.}} \qquad \dot{{\varvec{x}}} = {\varvec{f}}_0({\varvec{x}}(t))+\sum \limits _{i\in [{n_\omega }]} \omega _i(t) {\varvec{f}}_i({\varvec{x}}(t)), \qquad {\text { for a.e. }} t\in \mathcal {T}, \end{aligned}$$

(2.2)

$$\begin{aligned}\varvec{x}(t_0) ={\varvec{x}}_0, \hspace{8.7cm}\end{aligned}$$

(2.3)

$$\begin{aligned}TV(\omega) \leq \sigma _{\text {max}} \hspace{8.7cm} \end{aligned}$$

(2.4)

We minimize a Mayer term functional $\Phi \in C^1(\mathbb {R}^{n_{\text {x}}},\mathbb {R})$ over the binary controls ${\varvec{\omega }}_i$ and differential states ${\varvec{x}}\in W^{1,\infty }(\mathcal {T},R^{n_{\text {x}}})$ with fixed initial values ${\varvec{x}}_0 \in \mathbb {R}^{n_{\text {x}}}$. Constraint (2.2) expresses the dynamical system as a switched system in partial outer convexified form, i.e., as a sum of a drift term ${\varvec{f}}_0$ and control specific functions ${\varvec{f}}_i$ both out of $C^0(\mathbb {R}^{{n_{\text {x}}}},\mathbb {R}^{n_{\text {x}}})$. We assume that there exists a solution ${\varvec{x}}$ for the above problem; for this we may assume that a uniform Lipschitz estimate on ${\varvec{f}}_0$ and ${\varvec{f}}_i$ exists so that the theorem by Picard–Lindelöf is applicable. We limit the number of switches between active modes to be at most $\sigma _{\text {max}}$ in the TV constraint (2.4). Finally, we define (OCP) as the canonical relaxation of problem (MIOCP) where we optimize over ${\varvec{\alpha }}\in \mathcal {A}$ instead of ${\varvec{\omega }}\in \Omega$.

Remark 1

When we write that control i is active, we indicate that $\omega _i(t)=1$. In fact, we count the switches in (2.4), respectively in (2.1), twice since we sum up the control that has just been deactivated with the one that has just been activated. That explains the factor of one-half in (2.1). We remark that our study assumes no mode-specific switching limits, but we may also impose them by splitting up (2.4) into ${n_\omega }$ inequalities and by dropping the first sum in (2.1).

Without loss of generality, we omit further constraints and continuous control functions ${\varvec{u}}\in L^\infty (\mathcal {T},\mathbb {R}^{n_u})$ in our problem definition. See [28] how to cope with these and further extensions.

Combinatorial integral approximation decomposition

We propose to solve (MIOCP) with the CIA decomposition [27, 31], which relies on the use of direct methods (first discretize, then optimize approach). This section explains and defines the problem’s temporal discretization and the subproblems that constitute the decomposition algorithm.

Definition 4

($\mathcal {G}_N$, $\Delta$) Let the ordered set $\mathcal {G}_N:=\{t_0< \ldots < t_N=t_f \}$ denote a time grid with N intervals and lengths $\Delta _j:=t_{j}-t_{j-1}$ for $j\in [N]$, $\bar{\Delta }:= \max _{j\in [N]} \Delta _j$ as well as $\underline{\Delta }:= \min _{j\in [N]} \Delta _j$.

Next, we define the matrix sets of the discretized binary and relaxed binary control functions $\Omega _N$, $\mathcal {A}_N$.

Definition 5

(Convex combination constraint (Conv) and $\Omega _N$, $\mathcal {A}_N$) Let $N\in \mathbb {N}$. We express the requirement that the columns of a matrix $(m_{i,j})\in [0,1]^{{n_\omega }\times N}$ sum up to one by

$$\begin{aligned} \sum \limits _{i\in [{n_\omega }]} m_{i,j} =1, \qquad {\text { for }} j\in [N], \end{aligned}$$

(Conv)

and call it convex combination constraint (Conv) in the remainder. Based on this constraint, we define

$$\begin{aligned} \Omega _N := \left\{ {\varvec{w}} \in \{0,1\}^{{n_\omega }\times N} \, \mid \, {\varvec{w}} {\text { satisfies }} (Conv)\right\} , \quad \mathcal {A}_N := \left\{ {\varvec{a}} \in [0,1]^{{n_\omega }\times N} \, \mid \, {\varvec{a}} {\text { satisfies }} (Conv) \right\} . \end{aligned}$$

We introduce a discretized version of the TV constraint (2.4) that relies on ${\varvec{w}}$:

Definition 1

(Discretized version of (2.4)) Let $\mathcal {G}_N$ and $\sigma _{\text {max}}\in \mathbb {N}$ be given. We use auxiliary variables $\sigma _{i,j}\in \mathbb {N}$ for introducing a discretized version of the TV constraint that reads

$$\begin{aligned} \sigma _{\text {max}}\ge & {} \frac{1}{2} \sum \limits _{i\in [{n_\omega }]} \sum \limits _{j\in [N]} \sigma _{i,j}, \end{aligned}$$

(3.1)

$$\begin{aligned} \sigma _{i,j}\ge & {} \pm (w_{i,j}-w_{i,j-1}), \qquad i\in [{n_\omega }], \ j \in [N]. \end{aligned}$$

(3.2)

In order to solve the upcoming subproblems efficiently, we have deliberately formulated the above constraints without an absolute value term. This and replacing ${\varvec{w}}$ with ${\varvec{a}}$ in (3.2) results in a differentiable TV constraint. We define the discretizations of (MIOCP) and (OCP) below.

Definition 6

($({\varvec{NLP}}_{\text {rel}}),\ ({\varvec{NLP}}_{\text {bin}})$) Consider (OCP) with the following modifications:

• We discretize (2.2) with $\mathcal {G}_N$ and by using direct collocation or direct multiple shooting together with an appropriate integrator function (e.g. Runge-Kutta methods [18, 23]).

• The controls are piecewise constant functions on $\mathcal {G}_N$ with $(a_{i,j})\in \mathcal {A}_N$:

  $$\begin{aligned} \alpha _i(t):= a_{i,j}, \qquad {\text { for }} i\in [{n_\omega }], \, t\in [t_{j-1},t_j), \, j\in [N],\, t_j\in \mathcal {G}_N. \end{aligned}$$

• The TV constraint (2.4) is replaced by the constraints (3.1) and (3.2). In (3.2), we replace ${\varvec{w}}$ with ${\varvec{a}}$.

We denote the resulting discretized optimization problem with relaxed binary control functions ${\varvec{a}}\in \mathcal {A}_N$ by $({\varvec{NLP}}_{\text {rel}})$ and by $({\varvec{NLP}}_{\text {bin}})$ for fixed binary control functions ${\varvec{w}}\in \Omega _N$.

Definition 7

[(CIA) problem, $\theta ({\varvec{w}})$] Let ${\varvec{a}}\in \mathcal {A}_N$ be given. Then, we define the problem (CIA) to be

$$\begin{aligned}&\underset{\sigma , \theta ,\, {\varvec{w}}\in \Omega _N}{\min}\qquad \theta \hspace{7cm} \end{aligned}$$

(3.3)

$$\begin{aligned}&{\mathrm {s.\,t.}}\quad \theta \ge \pm \sum \limits _{l\in [j]} (a_{i,l}-w_{i,l})\Delta _l, \qquad {\text { for }} i\in [{n_\omega }], \, j\in [N] \end{aligned}$$

(3.4)

•             TV constraints (3.1) and (3.2).

We denote with $\theta ({\varvec{w}})$ the (CIA) objective value for a feasible solution ${\varvec{w}}\in \Omega _N$.

With these subproblem definitions we are able to summarize the CIA decomposition in Algorithm 1. We first solve the relaxed problem (NLP$_{\mathrm {rel}}$) and approximate the resulting relaxed binary controls with binary values in the (CIA) problem. The last step consists of evaluating (NLP$_{\mathrm {bin}}$) with a fixed binary control function ${\varvec{w}}_{\text {CIA}}$ in order to obtain the objective value of (MIOCP).

We remark that the TV constraints (3.1)–(3.2) in $(\text {NLP}_{\text {rel}})$ and $({\text {NLP}}_{\text {bin}})$ may be replaced by other TV reformulations, such as the ones presented in [17] or even dropped because (CIA) guarantees feasibility with

respect to bounded TV in any case. The algorithmic focus of this article lies on the (CIA) step, so that we omit further considerations of TV reformulations.

We stress that this algorithm solves two problems of which each one is less hard to solve than the original MINLP, which denotes the discretized (MIOCP). It yields only an approximation of the optimal solution of (MIOCP), but Sager et al. [26] showed that—without TV constraints and under certain regularity assumptions—the difference between the differential states based on relaxed and binary control values depends linearly on the difference of the integrals of their corresponding control function. In particular, they proved that the so called integrality gap with feasible solutions constructed by (CIA) is linearly bounded by the maximum grid length $\bar{\Delta }$ in the sense of

$$\begin{aligned} \sup \limits _{t\in \mathcal {T}} \left\| \int _{t_0}^t {\varvec{\alpha }}(\tau )-{\varvec{\omega }}(\tau ) \, {\text {d}}\tau \right\| _{\infty } \le C({n_\omega }) \cdot \bar{\Delta }, \end{aligned}$$

(3.5)

where $C({n_\omega })$ is a constant depending on the number of controls. This implies that the differential state trajectories of (MIOCP) and (OCP)—without the TV constraint—are arbitrarily close with vanishing grid length $\bar{\Delta }$ and by assumed Lipschitz continuity of the objective the same holds also for the objective values.¹

In Sects. 6–7, we are going to show that in the presence of discrete TV constraints (3.1)–(3.2) the rounding error does not vanish in general with grid length going to zero. More precisely, Theorem 4 and Corollary 7 will present concrete results on the rounding error.

(CIA$-\bar{\theta }$), (CIA$-\bar{\theta }-$init) and an associated lower bound

In this section, we address a problem that minimizes the used switches subject to a given approximation error $\bar{\theta }$ that shall not be exceeded by the accumulated control deviation. Afterward, we aim for a lower bound on its objective that will be useful in the next section and introduce useful auxiliary variables and definitions for this.

Definition 8

((CIA$-\bar{\theta }$), (CIA$-\bar{\theta }-$init)) For given ${\varvec{a}}\in \mathcal {A}_N$, $\bar{\theta }>0$ and initial active control $i_0\in [{n_\omega }]$ the problem (CIA$-\bar{\theta }-$init) is defined to be

$$\begin{aligned}&\sigma ^{*} := \underset{{\varvec{w}}\in \Omega_{N}}{\mathrm {min}}~~\frac{1}{2}\sum \limits _{l=1}^{N-1}\sum \limits_{i=1}^{n_{\omega}} |w_{i,l+1}-w_{i,l}| \end{aligned}$$

(4.1)

$$\begin{aligned}&{\mathrm {s.\,t.}}\qquad \bar{\theta } \ge \pm \sum \limits _{l=1}^{j}(a_{i,l} - w_{i,l})\Delta _j ~ \qquad i\in [{n_\omega }], \ j\in [N], \end{aligned}$$

(4.2)

$$\begin{aligned}&\qquad \qquad w_{i_0, 1} = 1. \end{aligned}$$

(4.3)

We define the problem (CIA$-\bar{\theta }$) to be (CIA$-\bar{\theta }-$init) without the constraint (4.3).

Taking the fixed initial active control in (4.3) aside, the problems (CIA$-\bar{\theta }$) and (CIA) from Definition 7 are closely connected with each other because the TV constraints (3.1) and (3.2) are reinterpreted as objective function subject to a fixed approximation error $\bar{\theta }$. This justifies the naming. We will introduce the MDR algorithm in Sect.5 to (heuristically) solve (CIA$-\bar{\theta }-$init). By applying this algorithm to all $i\in [{n_\omega }]$ as initial active controls, we exploit this relationship to solve (CIA$-\bar{\theta }$) as well, which will be used then as part of a bisection algorithm to solve (CIA).

We stress that fixing the initial active control $i_0$ may seem odd, though this fixing reduces the problem complexity, which later yields in Theorem 1, Section 5, an optimality result of the solution constructed by the MDR algorithm concerning (CIA$-\bar{\theta }-$init).

We notice that (CIA$-\bar{\theta }-$init) is very similar to (SCARP) from [3, 4]. The latter problem aims at minimizing the switching costs, representing a generalized objective function of (CIA$-\bar{\theta }-$init), whereas in (CIA$-\bar{\theta }-$init) the initial active control is fixed.

Remark 2

(Link to scheduling theory) On an equidistant grid, (CIA$-\bar{\theta }$) can be reformulated into the following, equivalent, scheduling problem: On a single machine, minimize the total setup costs (TSC) until the Nth processed job, $N\le n$, so that n jobs (f, k) are processed within $f\in [{n_\omega }]$ job families subject to release times $r_{f,k}$, deadlines $d_{f,k}$, equal processing times $\bar{\Delta }$ and sequence-independent setup costs, which can be summarized in scheduling notation [13] as

$$\begin{aligned} \left( 1 | r_{f,k}, d_{f,k}, {\text {SC}}_{\text {si},b}=1, p_{f,k}=\bar{\Delta } |\left. {\text {TSC}}\right| _1^N\right) . \end{aligned}$$

In the following we will revert to scheduling-like concepts, but explicitly dispense with its notation to not distract the reader from the usual MIOCP notation.

Next, we need some definitions to derive a lower bound for (CIA$-\bar{\theta }-$init) at the end of this section. We stress that we establish our results on an equidistant grid but will sometimes drop this assumption in definitions used in later sections.

Definition 9

(Activations, release $r_{i,k}$ and deadline intervals $d_{i,k}$) For each control $i\in [{n_\omega }]$ on an equidistant grid $\mathcal {G}_N$, we introduce the number of possible activations $n_i$ as

Each activation $k\in [n_i]$ is associated with a release and deadline interval, which are defined by:

(4.4)

(4.5)

(4.6)

Finally, we call the kth activation of control i necessary, if $d_{i,k}< \infty$.

Definition 10

(Switch, activation block) Consider ${\varvec{w}}\in \Omega _N$. If we have on interval $j\ge 2$ and for any $i\in [{n_\omega }]$

$$\begin{aligned} w_{i,j-1} =0, \quad w_{i,j} =1, \end{aligned}$$

then we say ${\varvec{w}}$ switches on j. We introduce the set of switches

$$\begin{aligned} \mathcal {S}:=\{ j\in \{2,\ldots ,N\} \mid {\varvec{w}} {\text { switches on }} j\}, \end{aligned}$$

and set $n_s:= |\mathcal {S}|$. We denote by $\tau _j \in [N]$ the corresponding interval of the jth switch of ${\varvec{w}}$, where we set $\tau _0 := 0,\, \tau _{n_s+1} := N$. On an equidistant grid and if $i\in [{n_\omega }]$ is active between two consecutive switches or one switch and the first/last interval, we define the set of activations of i between these switches as an activation block $B \subset [n_i]$. On a general grid, we further define the length of the jth activation block between the $(j-1)$st switch on, i.e. $\tau _{j-1}$, and before the jth switch, i.e. $\tau _{j}-1$, via the auxiliary variable $\delta _j=\sum _{l=\tau _{j-1}}^{\tau _j-1} \Delta _l$ for $j\in [n_s+1]$.

We notice that the switches actually occur on the grid points; however, we have indexed the variables $w_{i,j}$ according to the intervals, and therefore, for simplicity, we refer to switches on intervals. In the following, we will sometimes abbreviate activation block with block. In order to keep the number of used switches small and when deciding to set up a new block, it is highly relevant to know how many activations could be at most included in this block beginning with activation k. An activation $j>k$ cannot be included in the block if its release interval begins later than the deadline interval of activation k plus the number of activations between k and j. We give a definition that formalizes these deadlines for initial activation-dependent deadlines of blocks. Based on these block deadlines, it is straightforward to introduce the notion of a block deadline feasible partition of activations into blocks. The constraint (4.3) imposes that the control $i_0$’s first activation has to be executed on the first interval, for which we introduce the definition of fixed initial active control feasibility.

Definition 11

($db_{i,k}$, block deadline and fiac feasible partition) Consider an equidistant grid. The deadline of a block for $i\in [{n_\omega }]$ that begins with the kth activation, $k\in [n_i],$ is defined by

$$\begin{aligned} db_{i,k} := d_{i,l}, \quad {\text {where}} \quad l:= \max \{ j\ge k \mid r_{i,j} \le d_{i,k} + j-k\}. \end{aligned}$$

(4.7)

Let $P_i$ denote a partition of all activations $[n_i]$ for $i\in [{n_\omega }]$. We call $P_i$ block deadline feasible if for all subsets $B\in P_i$, i.e., all blocks, hold:

$$\begin{aligned} r_{i,\max \{k\in B\}} \le d_{i, \min \{k\in B\}} + |B| -1. \end{aligned}$$

Furthermore, we refer to $P_i$ as a fixed initial active control (fiac) feasible partition if for all $k\in B_1$ hold

$$\begin{aligned} r_{i,k} = k, \end{aligned}$$

where $B_1\in P_i$ denotes the first activation block of $P_i$.

In the last definition, we provided the concept of a control specific partition of all activations.

The kth activation of control $i\in [{n_\omega }]$ does generally not coincide with the kth interval. The following example illustrates the introduced concepts and, in particular, that there may be in total more possible but less necessary activations than intervals N.

Example 1

Let the following matrices ${\varvec{a}}\in \mathcal {A}_N$ and ${\varvec{w}}\in \Omega _N$ for equidistant discretization given:

$$\begin{aligned} {\varvec{a}}:= \left( \begin{array}{ccccccccc} 1 &{} 1 &{} 0.8 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.5 \\ 0 &{} 0 &{} 0.2 &{} 0 &{} 0.1 &{} 0.8 &{} 1 &{} 1 &{} 0.5 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0.9 &{} 0.2 &{} 0 &{} 0 &{} 0 \end{array}\right) , \quad {\varvec{w}}:= \left( \begin{array}{ccccccccc} 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right) , \end{aligned}$$

where ${n_\omega }=3, N=9$. Consider $i=1$ to be the fixed initial active control and a rounding threshold of $\bar{\theta }=1\bar{\Delta }$. Then, we deal with in total eleven possible activations with their release and deadline intervals:

$$\begin{aligned}&i=1: \quad [r_{1,k},d_{1,k}]=[1,1], \ [2,3], \ [3,9], \ [9,\infty ],\\&i=2: \quad [r_{2,k},d_{2,k}]=[1,6], \ [6,7], \ [7,8], \ [8,\infty ],\\&i=3: \quad [r_{3,k},d_{3,k}]=[1,5], \ [4,6], \ [6,\infty ]. \end{aligned}$$

There are 4, 3,  and 2 activations in ${\varvec{w}}$ for the controls $i=1,2,$ and 3, respectively. These activations are grouped into in total 4 activation blocks so that ${\varvec{w}}$ uses 3 switches. For instance, the first block of control $i=1$ has a length of $\delta _1= 3\bar{\Delta }$ and its deadline is $db_{1,1}=d_{1,3}=9$. The partition $P_1=\{ \{1,2,3\}, \{4\} \}$ is fiac feasible for $i=1$. For control $i=3$, the partitions $P_3=\{ \{1,2,3\} \}, \{ \{1,2\}, \{3\} \}$ are amongst others block deadline feasible.

As illustrated in Example 1, a feasible solution ${\varvec{w}}$ of (CIA$-\bar{\theta }-$init) may not use all possible activations. To this end, we define an extension of the set of blocks of ${\varvec{w}}$ to become a partition of $[n_i]$ for all $i\in [{n_\omega }]$ in the following lemma. The extension may seem arbitrary, but is necessary to compare any ${\varvec{w}}\in \Omega _N$ with partitions of $[n_i]$. Thereby, we establish a connection between the above feasibility concepts and a feasible solution ${\varvec{w}}$ of (CIA$-\bar{\theta }-$init).

Lemma 1

For an equidistant grid, let ${\varvec{w}}\in \Omega _N$ be feasible for (CIA$-\bar{\theta }-$init) and let $P_i'$ denote the set of blocks of ${\varvec{w}}$ for control $i\in [{n_\omega }]$. We define $\overline{P_i'}:=\{k \in [n_i] \ | \ \not \exists \ B \in P_i': k\in B \}$ and $P_i := P_i' \bigcup \limits _{k \in \overline{P_i'} } \{ k \}$. Then, $P_i$ is a block deadline feasible partition and if $i=i_0$, $P_i$ is also fiac feasible.

Proof

We first argue that $P_i$ is by definition a partition of $[n_i]$. We need to prove that these partitions are block deadline feasible, respectively fiac feasible. If for $i\in [{n_\omega }]$ and an activation block $B\in P_i$ holds

$$\begin{aligned} r_{i,\max \{k\in B\}} > d_{i, \min \{k\in B\}} + |B|-1, \end{aligned}$$

this would imply that the $(\max \{k\in B\})$th activation of i has been processed before its release interval because B can not be interrupted by activations from other controls. Therefore, the above inequality does not hold and block deadline feasibility is established. We apply the same argument for confirming fiac feasibility. By constraint (4.3), the first activation of $i_0$ is scheduled on the first interval. Hence, all activations $k\in B_1$ of the first block $B_1$ must be processed on the kth interval and require therefore a release interval that is no later than k. $\square$

Remark 3

(Necessary condition for feasibility of (CIA$-\bar{\theta }-$init) The formation of activations into block deadline and for $i_0$ fiac feasible partitions is a necessary feasibility criterion of ${\varvec{w}}\in \Omega _N$ for (CIA$-\bar{\theta }-$init) by virtue of Lemma 1. Nevertheless, it is not a sufficient criterion since the order of the processing of blocks is not clarified. In particular, one might order the blocks to contain an activation whose release interval is later than its executed interval.

Next, we formalize specific partitions of the control i’s possible activations $n_i$ whose blocks are constructed to include as many activations as possible without violating their block deadlines. These quantities serve as tools to derive a lower bound of necessary blocks per control independent of the other control’s blocks. This will result in a lower bound for (CIA$-\bar{\theta }-$init) in Proposition 2. We distinguish between the case that i is the fixed initial active control, i.e., $i=i_0$, or not.

Definition 12

Consider an equidistant grid and the controls $i_0,i\in [{n_\omega }]$. Let

$$\begin{aligned}&k_1:= \max \{j\le n_i \mid d_{i,j} \le db_{i,1} \}, \qquad B_{i,1} := \{1,\ldots ,k_1 \}, \end{aligned}$$

(4.8)

$$\begin{aligned}&k_1^{\,{\text {init}}} := \max \{j\le n_i \mid r_{i_0,j} = j \}, \qquad B_{i_0,1}^{\,{\text {init}}} := \left\{ 1,\ldots ,k_1^{\,{\text {init}}} \right\} . \end{aligned}$$

(4.9)

We write $(\cdot )^{\,{\text {(init)}}}_i$ to indicate that equations or inequalities each apply to the parameters $(\cdot )_i$ and $(\cdot )^{\,{\text {init}}}_{i_0}$. We define the blocks $B_{i,l}^{\,{\text {(init)}}}$ recursively for $l\ge 2$ and while $k_l^{\,{\text {(init)}}}<n_i$ by

$$\begin{aligned} k_l^{\,{\text {(init)}}}:= \max \left\{ j\le n_i \mid d_{i,j} \le db_{i,k_{l-1}^{\,\text {(init)}}+1} \right\} , \quad B_{i,l}^{\,\text {(init)}} := \left\{ k_{l-1}^{\,\text {(init)}}+1,\ldots ,k_l^{\,{\text {(init)}}} \right\} . \end{aligned}$$

(4.10)

Let $nb_{i,\min }^{\,{\text {(init)}}}$ denote the number of blocks $B_{i,l}^{\,{\text {(init)}}}$ and $P_{i,\min }^{\,{\text {(init)}}}$ the partitions of $[n_i]$ constructed by the latter:

$$\begin{aligned} P_{i,\min }^{\,{\text {(init)}}} := \left\{ B_{i,l}^{\,{\text {(init)}}} \mid l \in [nb_{i,\min }^{\,{\text {(init)}}}] \right\} . \end{aligned}$$

The MDR scheme from the next section creates switches that resemble the above $k_l^{\,{\text {(init)}}}$ terms. The latter, though, only expresses the grouping of activations, while the switches explicitly specify the corresponding intervals as well. It turns out that the partitions $P_{i,\min }$ and $P_{i_0,\min }^{\,{\text {init}}}$ are minimal in the number of blocks as indicated in the following proposition.

Proposition 1

For $i_0,i\in [{n_\omega }]$, let the partitions $P_{i,\min }, \, P_{i_0,\min }^{\,{\text {init}}}$ be given as in Definition 12. For any partition $P_i$ of $[n_i]$, with $i=i_0$ included, we define its restriction to the first $\tilde{n}_i \le n_i$ activations as

$$\begin{aligned} \left. P_{i}\right| _{\tilde{n}_i}:= \left\{ B \cap [\tilde{n}_i] \ \mid \ B \in P_{i} \right\} . \end{aligned}$$

Then, the partition $P_{i,\min }$, respectively $P_{i_0,\min }^{\,{\text {init}}}$, consists for any $\tilde{n}_i\le n_i$ of a minimal number of blocks on the first $\tilde{n}_i$ activations compared with all other block deadline feasible, respectively both block deadline and fiac feasible, partitions $P_i$:

$$\begin{aligned} \left| \left. P_{i,\min }^{\,{\text {(init)}}}\right| _{\tilde{n}_i} \right| \le \left| \left. P_{i}\right| _{\tilde{n}_i} \right| . \end{aligned}$$

(4.11)

Proof

We consider first $\left. P_{i,\min }\right| _{\tilde{n}_i}$. It is block deadline feasible because the deadline of the last activation for each block is defined in (4.8) and (4.10) to be less or equal than the corresponding block deadline. Assume there is a block deadline feasible partition $P_i$ for the control $i\in [{n_\omega }]$ with $\left| \left. P_{i}\right| _{\tilde{n}_i} \right| < \left| \left. P_{i,\min }\right| _{\tilde{n}_i} \right|$. In other words, there exists a subset of the first j blocks of $\left. P_{i}\right| _{\tilde{n}_i}$ that includes more activations than the ones included into the first j blocks of $\left. P_{i,\min }\right| _{\tilde{n}_i}$. We consider the minimal number of blocks j with this property:

$$\begin{aligned} j:= \min \left\{ l\in [nb_{i,\min }] \ \mid \ B_{i,l}\in \left. P_{i,\min }\right| _{\tilde{n}_i},\, B'_{i,l}\in \left. P_{i}\right| _{\tilde{n}_i}: \ \max \{k\in B_{i,l} \} < \max \{k\in B'_{i,l} \} \right\} . \end{aligned}$$

(4.12)

The block index j is unique since the association of activations to blocks is monotonically increasing, meaning that there are no $k_1$th, $k_2$th activations, $k_1<k_2$, with $k_1\in B_{i,l_1}, k_2\in B_{i,l_2}$ and $l_1 > l_2$. We conclude

$$\begin{aligned} \min \{k\in B'_{i,j} \} \le \min \{k\in B_{i,j} \}, \quad B'_{i,j}\in \left. P_{i}\right| _{\tilde{n}_i}, \ B_{i,j}\in \left. P_{i,\min } \right| _{\tilde{n}_i}, \end{aligned}$$

(4.13)

so that block $B'_{i,j}$’s first activation $k'$ is smaller or equal than k which marks the earliest activation of $B_{i,j}$. The definition of release intervals (4.54.6) implies $r_{i,k'} \le r_{i,k}$ for $k'\le k$. Similarly, the definition of block deadlines (4.7) implies $db_{i,k'} \le db_{i,k}$ for $r_{i,k'} \le r_{i,k}$ and we find with (4.13) in particular

$$\begin{aligned} db_{i,\min \{k\in B'_{i,j} \}} \le db_{i,\min \{k\in B_{i,j} \}}. \end{aligned}$$

(4.14)

On the other hand, the definition of $P_{i,\min }$ in (4.10) implies

$$\begin{aligned} db_{i,k_{j-1}+1} = \max \{k\in B_{i,j} \}. \end{aligned}$$

(4.15)

Then, the definition of j yields

$$\begin{aligned} db_{i,\min \{k\in B_{i,j} \}} {\mathop {=}\limits ^{(4.10)}} db_{i,k_{j-1}+1} {\mathop {=}\limits ^{(4.15)}} \max \{k\in B_{i,j} \} < \max \{k\in B'_{i,j} \} \le db_{i,\min \{k\in B'_{i,j} \}}, \end{aligned}$$

(4.16)

where the last inequality must hold due to the assumption of $P_i$ being block deadline feasible. Inequality (4.14) contradicts inequality (4.16), or equivalently there is no such partition $P_i$ and $P_{i,\min }$ uses indeed a minimal number of blocks on any $[\tilde{n}_i]\subset [n_i]$.

The same argumentation for $j\ge 2$ in equation (4.12) can be applied in order to prove the result for $P_{i_0,\min }^{\,{\text {init}}}$ as $P_{i_0}$ is also assumed to be block deadline feasible in this case and the same holds for $P_{i_0,\min }^{\,{\text {init}}}$ from the second block on. We just need to take care of the case when $j=1$, i.e., if $B_{i_0,j}$, respectively $B'_{i_0,j}$, is the first block of the control $i_0$. Here, $\max \{k\in B_{i_0,1} \} < \max \{k\in B'_{i_0,1}\}$ cannot appear, since $P_{i_0}$ is assumed to be fiac feasible and the construction of the first block of $P_{i_0,\min }^{\,{\text {init}}}$ implies that no further activation can be added to $B_{i_0,1}$ without violating fiac feasibility. Thus, $j=1$ is impossible in (4.12) and $P_{i_0,\min }^{\,{\text {init}}}$ is also minimal in the number of blocks. $\square$

Corollary 1

Consider the setting of Proposition 1and the controls $i_0,i\in [{n_\omega }]$. We define

$$\begin{aligned} \tilde{n}_{i,N} := \max \{k \mid d_{i,k}\le N \}, \quad nb_{i,\min }^N := \left| \left. P_{i,\min }\right| _{\tilde{n}_{i,N}} \right| , \quad nb_{i_0,\min }^{N,{\text {init}}} := \left| \left. P_{i_0,\min }^{\,{\text {init}}} \right| _{\tilde{n}_{i_0,N}} \right| . \end{aligned}$$

There is no block deadline feasible partition, respectively block deadline and fiac feasible partition, that uses less than $nb_{i,\min }^N$ blocks on $[\tilde{n}_{i,N}]$, respectively $nb_{i_0,\min }^{N,{\text {init}}}$ blocks on $[\tilde{n}_{i_0,N}]$ .

Proof

The result follows directly from Proposition 1 with $\tilde{n}_{i} = \tilde{n}_{i,N}$ and $\tilde{n}_{i_0} = \tilde{n}_{i_0,N}$. $\square$

As a final result for this section, we establish a lower bound for (CIA$-\bar{\theta }-$init) that will be useful in Theorem 1.

Proposition 2

(Lower bound for (CIA$-\bar{\theta }-$init)) Let $\sigma ^*$ be the objective of (CIA$-\bar{\theta }-$init) with equidistant discretization and $i_0$ the fixed initial active control as defined in Definition 8. Let $nb_{i,\min }^N$ for all $i\ne i_0$ and $nb_{i_0,\min }^{N,{\text {init}}}$ be given as in Corollary 1. It results

$$\begin{aligned} \sum \limits _{i\in [{n_\omega }], i\ne i_0} nb_{i,\min }^N + nb_{i_0,\min }^{N,{\text {init}}} -1 \le \sigma ^*. \end{aligned}$$

(4.17)

Proof

By virtue of Lemma 1, a feasible solution of (CIA$-\bar{\theta }-$init) satisfies the necessary condition of generating only block deadline feasible partitions $P_i$ and if $i=i_0$, the activation partition $P_i$ is also fiac feasible. Moreover, all activations are executed no later than their deadline interval. That holds particularly for those that are due no later than N. Hence, we can apply Corollary 1 and conclude the minimum number of blocks of a feasible solution until the in total Nth activation is $nb_{i,\min }^N$, respectively $nb_{i_0,\min }^{N,{\text {init}}}$. Finally, we obtain the claim (4.17) by summing up over all controls and using that the setup of the first block does not count as switch. $\square$

Maximum dwell rounding

This section is dedicated to solving (CIA). Generally, we recommend a tailored BNB algorithm that has been proposed by Jung et al. [15, 27] and implemented in the open-source software package pycombina [7]. The BNB algorithm outperforms standard MILP solvers in a case study [14] by three orders of magnitude. However, in some instances, the algorithm struggles to find the optimal solution quickly because the node relaxation can be quite weak [8]. We, therefore, present a polynomial-time algorithm that constructs good initial guesses for BNB and, in some situations, solves (CIA) even to optimality. We proceed by giving the necessary definitions of the algorithm itself and its auxiliary variables in the first subsection and investigate beneficial properties in the second subsection.

Definition of the algorithm

Definition 13

(Accumulated control deviation $\theta _{i,j}, \gamma _{i,j}$) Let ${\varvec{a}}\in \mathcal {A}_N$ and ${\varvec{w}}\in \Omega _N$. For control $i\in [{n_\omega }]$ and interval $j\in [N]$ we define the accumulated control deviation variables as

$$\begin{aligned} \theta _{i,j} := \sum \limits _{l=1}^j (a_{i,l}-w_{i,l}) \Delta _l, \qquad \gamma _{i,j} := \sum \limits _{l=1}^j a_{i,l}\Delta _l - \sum \limits _{l=1}^{j-1}w_{i,l} \Delta _l, \end{aligned}$$

and set $\theta _{i,0} := 0$.

The following lemma is useful for Proposition 3 on page 11 and Lemma 7 on page 17.

Lemma 2

Consider ${\varvec{a}}\in \mathcal {A}_N$ and ${\varvec{w}}\in \Omega _N$ , for each $j\in [N]$ holds

$$\begin{aligned} \sum \limits _{i\in [{n_\omega }]} \theta _{i,j} = 0, \qquad \sum \limits _{i\in [{n_\omega }]} \gamma _{i,j} = \Delta _j. \end{aligned}$$

Proof

These equations follow directly from the definition of $\theta$ and $\gamma$ as well as from the convexity property of ${\varvec{a}}$ and ${\varvec{w}}$. $\square$

Definition 14

(Inadmissible, next forced and forced activation) Consider a rounding threshold $\bar{\theta }>0$ and ${\varvec{a}}\in \mathcal {A}_N$. Let the values of ${\varvec{w}}\in \Omega _N$ be given until interval $j-1$, with $j\ge 2$. The choice $w_{i,j}=1$ for $i\in [n_{\omega }], \ j \in [N]$ is admissible if we have that

$$\begin{aligned} \theta _{i,j} \ge - \bar{\theta } \end{aligned}$$

and we call the control i otherwise inadmissible. Similarly, the choice $w_{i,j}=1$ is forced if we have that

$$\begin{aligned} \gamma _{i,j} > \bar{\theta }. \end{aligned}$$

Let further $\mathcal {N}_j(i)\in \{j,\ldots N\}$ denote the next interval on which control i would become forced without activation after interval $j-1$:

$$\begin{aligned} \mathcal {N}_j(i):= \left\{ \begin{array}{ll} \mathop {{\text {argmin}}}\limits _{k=j,\ldots ,N} \{ \theta _{i,j-1} + \sum _{l=j}^{k} a_{i,l}\Delta _l> \bar{\theta } \}, \qquad &{} {\text {if }} \theta _{i,j-1} + \sum _{l=j}^{N} a_{i,l}\Delta _l > \bar{\theta },\\ \infty , &{} {\text {else.}} \end{array} \right. \end{aligned}$$

Then, we define a control $i^*\in [{n_\omega }]$ on interval j to be next forced if and only if

$$\begin{aligned} \mathcal {N}_j( i^*) = \min \limits _{i\in [{n_\omega }]}\mathcal {N}_j(i) \quad {\text {and}} \quad \mathcal {N}_j( i^*) < \infty . \end{aligned}$$

The above definition allows more than one control to be next forced or forced for an arbitrary interval $j\in [N]$. This is supposedly not the standard case in our discussion but will also be taken into account in our considerations. The guiding idea behind the above control activations is that we include more and more summands of ${\varvec{w}}$ into the computation of $\theta$ and can choose the next row of ${\varvec{w}}$ accordingly. With this definition we have introduced necessary activation properties of feasible solutions for (CIA$-\bar{\theta }-$init), but neglected so far the fixed initial active control constraint (4.3). The following definition fills this gap.

Definition 15

(Initially admissible control) We define a control $i\in [{n_\omega }]$ to be initially admissible if it is admissible on the first interval and if there is no other control $i_1\ne i$ that is forced on the first interval.

Now, we can define the MDR in Algorithm 2.

The MDR algorithm assumes a given initial control $i_0$ and activates it until it becomes inadmissible or until there is another forced control. We require the control $i_0$ to be initially admissible because otherwise ${\varvec{w}}^{{\text {MDR}}}$ would violate the control accumulation constraint (4.2). Otherwise, the control i with the maximum forward control deviation $\gamma _{i,j}$ is set active and remains so until it becomes inadmissible or another control becomes forced. This procedure is performed forward in time until the end of the time horizon N is reached. We named the algorithm “maximum dwell rounding” because it tries to stay in the current mode as long as possible without violating the given rounding threshold.

The AMDR is defined in Algorithm 3 and can be described as a bisection method. We initialize it with a trivial lower bound LB and upper bound UB for (CIA). The algorithm runs MDR iteratively with different threshold $\bar{\theta }$ and initially admissible control as long as the difference of

lower and upper bound is larger than the chosen tolerance TOL (lines 2–5). If the computed control function satisfies the TV constraint and exhibits a (CIA) objective value that is smaller than the current UB, we update UB, reset the rounding threshold $\bar{\theta }$ via interval halving of $UB - LB$ and save the current best solution (lines 6-10). The evaluation $\theta ({\varvec{w}})$ is necessary since MDR may construct a control function with a rounding gap larger than the desired gap $\bar{\theta }$, as will be discussed in the next subsection. If no computed control function ${\varvec{w}}$ with given initial control and $\bar{\theta }$ fulfills the TV constraint, then we increase the LB (lines 11-14).

Solution quality and properties of MDR (Algorithm 2)

Although the MDR algorithm may seem simple, it generates optimal solutions ${\varvec{w}}$ for (CIA$-\bar{\theta }-$init) under certain conditions, for which we need the following definition.

Definition 16

(Canonical switch) We define a switch $j \in \mathcal {S}$ as defined in Definition 10 to be canonical, if on interval $\tau _j$ holds: exactly one control $i_1$ is inadmissible and exactly one control $i_2\ne i_1$ is forced.

We build our theoretical results of this section mainly on the following assumption.

Assumption 1

(MDR uses only canonical switches) Suppose ${\varvec{w}}^{\text {MDR}}\in \Omega _N$ has been generated by MDR. We assume that all switches of ${\varvec{w}}^{\text {MDR}}$ are canonical.

Properties of the MDR algorithm

Assumption 1 may seem restrictive, although it is satisfied anyway under certain conditions.

Proposition 3

(MDR with $n_{\omega }=2$ and $\bar{\theta }\ge \frac{1}{2}\bar{\Delta }$ uses canonical switches) Consider $n_{\omega }=2$, ${\varvec{a}}\in \mathcal {A}_N$ and any grid $\mathcal {G}_N$. If we choose $\bar{\theta }\ge \frac{1}{2}\bar{\Delta }$, then the control function ${\varvec{w}}^{\text {MDR}}$ constructed by the MDR scheme uses only canonical switches.

Proof

We have to prove:

• 1. If control $i_1$ is forced on interval $j\ge 2$, then it is admissible.

• 2. For all intervals $j\ge 2$ hold: control $i_1$ is inadmissible, if and only if $i_2\ne i_1$ is forced.

1. follows from the definition of forced activation and from $\bar{\theta }\ge \frac{1}{2}\bar{\Delta }$:

$$\begin{aligned} \theta _{i_1,j} = \theta _{i_1,j-1}+ a_{i_1,j}\Delta _{j} -\Delta _{j} {>} \bar{\theta } -\Delta _{j}\ge - \frac{1}{2}\bar{\Delta } \ge - \bar{\theta }. \end{aligned}$$

For proving 2. let us assume $i_1$ is forced on $j\in [N]$, i.e., $\gamma _{i_1,j}>\bar{\theta }$. By virtue of Lemma 2 for $\gamma _{i_2,j}$ we derive

$$\begin{aligned} \theta _{i_2,j-1}+a_{i_2,j}\Delta _j=\gamma _{i_2,j} < - \bar{\theta }+ \Delta _j, \end{aligned}$$

which means $i_2$ is inadmissible on j. Conversely, if $i_1$ is inadmissible on j, we conclude from $\theta _{i_1,j-1} + (a_{i_1,j}-1)\Delta _j < -\bar{\theta }$ and from the equation for $\theta$ in Lemma 2$\gamma _{i_2,j}= \theta _{i_2,j-1} + a_{i_2,j}\Delta _j > \bar{\theta }$. Therefore, $i_2$ is forced. $\square$

Remark 4

Assumption 1 is not necessarily true for a control problem that involves more than two binary controls. It may, however, hold for special cases of such a problem. For instance, if the relaxed values are of bang-bang type, i.e., $a_{i,j}\in \{0,1\}$, and $\bar{\theta }$ is chosen smaller than the smallest activation block, then the situation resembles the case $n_{\omega } = 2$ and Assumption 1 may hold (without proof). On the other hand, Example 3 is going to demonstrate that this assumption can indeed be quite restrictive.

Assumption 1 allows us to prove strong properties of control functions obtained by MDR and AMDR. The first result expresses that the MDR scheme produces indeed control functions which exhibit a (CIA) objective value smaller or equal than $\bar{\theta }$.

Lemma 3

(MDR solution satisfies $\bar{\theta }$ bound) Let Assumption 1 hold and let ${\varvec{w}}^{\text {MDR}}\in \Omega _N$ be constructed by MDR with given threshold $\bar{\theta }$. Then, we obtain $\theta ({\varvec{w}}^{\text {MDR}}) \le \bar{\theta }$.

Proof

As soon as the activated control becomes inadmissible or there is a forced control on interval $j\ge 2$, ${\varvec{w}}^{\text {MDR}}$ has a switch by the definition of MDR. By Assumption 1, the newly activated control is both forced and admissible, hence $\theta _{i,j} \ge - \bar{\theta }$, and there is also no other forced control on j, thus $\theta _{i,j} \le \bar{\theta }$. $\square$

The following example demonstrates that $\theta ({\varvec{w}}^{\text {MDR}}) > \bar{\theta }$ may generally appear without Assumption 1.

Example 2

Consider an equidistant discretization and ${\varvec{a}}\in \mathcal {A}_N$ with the first values given as $a_{1,1}=1,\ a_{2,1}=0,\ a_{1,2}=0.5,\ a_{2,2}=0.5$. For this relaxed value, let ${\varvec{w}}^{\text {MDR}}\in \Omega _N$ be the corresponding binary control function computed by MDR with given threshold $\bar{\theta }=0.4\bar{\Delta }$ and initial control $i=1$. Then, $w^{\text {MDR}}_{1,2}=0,\ w^{\text {MDR}}_{2,2}= 1$ holds since the second control becomes forced on the second interval. At the same time, control $i=2$ is inadmissible on the second interval, hence Assumption 1 is violated, and it results $\theta _{2,2}= -0.6\bar{\Delta } < - \bar{\theta }$.

We reuse concepts from the previous chapter, especially activations and their grouping into blocks.

Theorem 1

(Least switches property of MDR) Let Assumption 1hold. For given ${\varvec{a}}\in \mathcal {A}_N$ and an equidistant grid, let ${\varvec{w}}^{\text {MDR}}$ be constructed by MDR with i as initial control and any $\bar{\theta }>0$, where we assume that i is initially admissible. Let $\sigma ({\varvec{w}}^{\text {MDR}})$ denote the number of switches used by ${\varvec{w}}^{\text {MDR}}$. Then, for the optimal objective value $\sigma ^*$ of (CIA$-\bar{\theta }-$init) with $i_0=i$ as initial control holds

$$\begin{aligned} \sigma ^*= \sigma ({\varvec{w}}^{\text {MDR}}). \end{aligned}$$

(5.1)

Proof

We can conclude ${\varvec{w}}^{\text {MDR}}$ is a feasible solution of (CIA$-\bar{\theta }-$init) by Lemma 3. Combining this with Proposition 2 yields

$$\begin{aligned} \sum \limits _{i\in [{n_\omega }], i\ne i_0} nb_{i,\min }^N + nb_{i_0,\min }^{N,{\text {init}}}-1 \le \sigma ^*\le \sigma ({\varvec{w}}^{\text {MDR}}). \end{aligned}$$

(5.2)

For proving optimality we note that ${\varvec{w}}^{\text {MDR}}$ constructs partitions of the activations $[n_i], i\in [{n_\omega }]$ that are due no later than N and let $P^{\text {MDR}}_i$ denote these partitions. With the notation from Corollary 1 we want to show that these partitions coincide with the partitions constructed in Definition 12

$$\begin{aligned} P_{i_0}^{\text {MDR}} = \left. P_{i_0,\min }^{\,{\text {init}}} \right| _{\tilde{n}_{i_0,N}}, \quad P_{i}^{\text {MDR}} = \left. P_{i,\min } \right| _{\tilde{n}_{i,N}}, {\text { for }} i\ne i_0, \end{aligned}$$

(5.3)

because then Corollary 1 would imply ${\varvec{w}}^{\text {MDR}}$ has $\sum _{i \in [{n_\omega }], i\ne i_0} nb_{i,\min }^N + nb_{i_0,\min }^{N,{\text {init}}}$ activation blocks or equivalently

$$\begin{aligned} \sigma ({\varvec{w}}^{\text {MDR}}) =\sum \limits _{i \in [{n_\omega }], i\ne i_0} nb_{i,\min }^N + nb_{i_0,\min }^{N,{\text {init}}}-1, \end{aligned}$$

and the claim follows from inequality (5.2). Consider the first blocks $B_1 \in P_{i_0}^{\text {MDR}}$ and $B_1^{\,{\text {init}}}\in P_{i_0,\min }^{\,{\text {init}}}$. By Assumption 1, the MDR algorithm activates $i_0$ until it becomes inadmissible on the interval $\tau _1$ of the first switch:

$$\begin{aligned} \theta _{i_0,\tau _1} = \sum \limits _{l=1}^{\tau _1} a_{i_0,l}-w_{i_0,l} {<} - \bar{\theta }/ \bar{\Delta }. \end{aligned}$$

We compare this inequality with the Definition 9 of release intervals and notice that either the next activation $\tau _1$ of control $i_0$ has a release interval that is later than $\tau _1$ or there is no further possible activation. So, if the $\tau _1$th activation exists, then its release interval has not yet been reached:

$$\begin{aligned} r_{i_0,\tau _1}=r_{i_0,\max \{k \in B_1 \}+1}>\max \{k \in B_1 \}+1. \end{aligned}$$

By the definition of $P_{i_0,\min }^{\,{\text {init}}}$ we conclude $B_1=B_1^{\,{\text {init}}}$. Let us now consider the jth blocks $B_j \in P^{\text {MDR}}_{i_0}$ and $B_j^{\,{\text {init}}}\in \left. P_{i_0,\min }^{\,{\text {init}}} \right| _{\tilde{n}_{i_0,N}}$, where $j\ge 2$. Again by the definition of MDR and Assumption 1, $i_0$ is forced on interval $\tau _j$, which is equivalent to $d_{i_0,\min \{k\in B_j\}}=\tau _j$. The MDR scheme activates $i_0$ either until N (then trivially $B_j=B_j^{\,{\text {init}}}$) or until it becomes inadmissible on interval $\tau _{j+1}$ (by Assumption 1). With the argumentation for $j=1$, inadmissible means hereby the $(\max \{k\in B_j\}+1)$th activation has a release interval greater than $\tau _{j+1}$. Using that the block’s first activation $\tau _j$ is processed on its deadline interval $d_{i_0,\min \{k\in B_j\}}$, this yields

$$\begin{aligned} r_{i_0,\max \{k\in B_j\}+1}> d_{i_0,\min \{k\in B_j\}} + |B_j|-1. \end{aligned}$$

The above inequality expresses that $B_j$ contains as many activations as possible without violating its block deadline $db_{i_0,\min \{k\in B_j\}}$ and by construction of $P_{i_0,\min }^{\,{\text {init}}}$ this is equivalent to $B_j=B_j^{\,{\text {init}}}$. This settles the case $i=i_0$ in (5.3). We can reuse the above arguments about forced and inadmissible activation for $j\ge 2$ in order to analogously prove the case $i\ne i_0$ in (5.3). $\square$

Remark 5

Theorem 1 is predicated on the assumption of an equidistant grid. We stress that after grid refinement of the optimal control problem, i.e., after several rounds of applying the CIA decomposition, this might be a restriction.

The following corollary establishes a way to find the optimum of (CIA$-\bar{\theta }-$init) in the setting of Theorem 1.

Corollary 2

(Using MDR to find a control function with minimum number of switches) Consider the setting of Theorem 1. A control function ${\varvec{w}}^*$ that uses a minimum number of switches, i.e., $\sigma \left( {\varvec{w}}^*\right) =\sigma ^*$, can be found by running MDR.

Proof

Let i be the initial control of ${\varvec{w}}^*$. Execute MDR with i as initial control so that the result follows directly from Theorem 1. $\square$

It is not clear which control is the optimal initial active one in order to minimize switches. In practice, MDR must be executed one after the other for all controls $i \in [{n_\omega }]$ as initial active control. This expresses the following corollary.

Corollary 3

(Link between MDR and (CIA$-\bar{\theta }$)) Consider the setting of Theorem 1. We assume that the MDR algorithm constructs for all $i\in [{n_\omega }]$ as initial active controls the control functions ${\varvec{w}}^{\text {MDR}}$ that use only canonical switches. Then, there is a minimizing control ${\varvec{w}}^*\in \Omega _N$ for (CIA$-\bar{\theta }$) that only uses canonical switches. Moreover, there exists $i_0\in [{n_\omega }]$ such that running MDR with $i_0$ as initial control produces ${\varvec{w}}^{\text {MDR}}\in \Omega _N$ that minimizes (CIA$-\bar{\theta }$).

Proof

If the MDR algorithm produces ${\varvec{w}}^{\text {MDR}}$ that only uses canonical switches, ${\varvec{w}}^{\text {MDR}}$ is optimal by Theorem 1 for (CIA$-\bar{\theta }-$init) with the corresponding initial control fixed . Then, the result follows from the fact that the optimal solution of (CIA$-\bar{\theta }$) is contained in the set of optimal solutions for the set of problems (CIA$-\bar{\theta }-$init) with each control $i\in [{n_\omega }]$ initially fixed. $\square$

Lemma 4

Consider ${\varvec{a}}\in \mathcal {A}_N$ on an equidistant grid and assume $n_{\omega }=2$. Let ${\varvec{w}}^{\text {MDR}}$ denote the control function constructed by MDR with $\bar{\theta }>0$ and given initial control. If $\theta ({\varvec{w}}^{\text {MDR}})> \bar{\theta }$, then there is no control function ${\varvec{w}}\in \Omega _N$ with the same initial active control and $\theta ({\varvec{w}})\le \bar{\theta }$.

Proof

We consider the first interval j on which the accumulated control deviation of ${\varvec{w}}^{\text {MDR}}$ is greater than $\bar{\theta }$. Let control $i_1$ be active on j. By definition of the MDR scheme, $|\theta _{i_1,j}|> \bar{\theta }$ or $|\theta _{i_2,j}|> \bar{\theta }$ can only appear if there is a switch on interval j and

• 1. $i_1$ is on interval j both forced and inadmissible or

• 2. both $i_1$ and $i_2$ are inadmissible on interval j.

Proposition 3 establishes that ${\varvec{w}}^{\text {MDR}}$ uses only canonical switches for $\bar{\theta } \ge \frac{1}{2}\bar{\Delta }$ and thus the above cases cannot appear for $\bar{\theta } \ge \frac{1}{2}\bar{\Delta }$. Let us focus on $\bar{\theta } < \frac{1}{2}\bar{\Delta }$. In order to create a control function ${\varvec{w}}$ that does fulfill $\theta ({\varvec{w}})\le \bar{\theta }$, we need to change at least one activation of ${\varvec{w}}^{\text {MDR}}$ on an earlier interval $l<j$. However, we recognize that any earlier change of activation is not possible:

• We cannot extend an activation block at its end, since the active control is inadmissible.

• If the active control $i_1$ is admissible on l, then the other control $i_2$ is not forced on l – otherwise it would be active in the MDR scheme. This means $\theta _{i_2,l-1}+a_{i_2,l}\bar{\Delta }\le \bar{\theta }$. Activating $i_2$ on l results in

  $$\begin{aligned} \theta _{i_2,l}=\theta _{i_2,l-1}+(a_{i_2,l}-1)\bar{\Delta } \le \bar{\theta }- \bar{\Delta }< -\frac{1}{2} \bar{\Delta }< - \bar{\theta }, \end{aligned}$$

  where we applied $\bar{\theta } < \frac{1}{2}\bar{\Delta }$. This indicates the (CIA) objective value of ${\varvec{w}}$ is again greater than $\bar{\theta }$.

Hence, no previous activation ${\varvec{w}}^{\text {MDR}}$ can be changed so that there is no ${\varvec{w}}$ with $\theta ({\varvec{w}})\le \bar{\theta }$. $\square$

Properties of the AMDR algorithm

Theorem 2 states that the AMDR Algorithm is able to find the optimal solution of (CIA) for $n_{\omega }=2$ and equidistant discretization. Otherwise, strict assumptions are required for optimality, and in general, the found feasible solution represents only a promising upper bound.

Theorem 2

(Properties of Algorithm 3) Algorithm 3 terminates for given ${\varvec{a}}\in \mathcal {A}_N$, $TOL>0$ and $\sigma _{\text {max}}\in \mathbb {N}$ after a finite number of iterations. Furthermore, consider an equidistant grid $\mathcal {G}_N$. Let ${\varvec{w}}^{\text {AMDR}}$ denote the solution constructed by Algorithm 3. It follows:

• 1. ${\varvec{w}}^{\text {AMDR}}$ is a feasible solution of (CIA).

• 2.

  • (a) If $n_{\omega }=2$, we have for the optimum $\theta ^*$ of (CIA): $\theta ( {\varvec{w}}^{\text {AMDR}})\le \theta ^*+ TOL$.

  • (b) Let $n_{\omega }>2$. We assume the MDR scheme uses in every run only canonical switches. Furthermore, suppose we have : If the MDR scheme constructs a solution with $\theta ({\varvec{w}}^{\text {MDR}})> \bar{\theta }$, then there is no control function ${\varvec{w}}\in \Omega _N$ with the same initial active control and $\theta ({\varvec{w}})\le \bar{\theta }$. With these assumptions we obtain for the optimum $\theta ^*$ of (CIA): $\theta ( {\varvec{w}}^{\text {AMDR}})\le \theta ^*+ TOL$.

• 3. ADMR has time complexity $\mathcal {O}({n_\omega }\cdot C_{\text {MDR}} \cdot \log _2(\lceil (t_f-t_0)/TOL\rceil ))$, where $C_{\text {MDR}}\in \mathcal {O}(N)$ denotes the time complexity of the MDR scheme.

Proof

AMDR is a bisection algorithm that either decreases UB (line 7-8) or increases LB (line 12-13) by at least one half of $(UB-LB)$ in every while loop iteration (line 2). From this and because of $TOL>0$, we conclude that the while loop and AMDR as a whole terminate after finitely many iterations.

• 1. The objective of (CIA) cannot be greater than $t_f - t_0$, even with no switches allowed, i.e., $\sigma _{\text {max}}=0$. Since we initialize the AMDR algorithm with $UB=t_f - t_0$, it finds in any case a feasible solution.

• 2. Every in line 5 by MDR generated ${\varvec{w}}^{\text {MDR}}$ that satisfies the TV constraints together with $\theta ({\varvec{w}}^{\text {MDR}})<UB$ represents an upper bound on $\theta ^*$, i.e., $UB=\theta ({\varvec{w}}^{\text {MDR}})\ge \theta ^*$. For proving that AMDR constructs valid lower bounds LB on $\theta ^*$ we exploit that ${\varvec{w}}^{\text {MDR}}$ only uses canonical switches for $n_{\omega }=2$ and by assumption for $n_{\omega }>2$ so that Corollary 3 is applicable. If there is no initial control $i\in [{n_\omega }]$ for which MDR produces ${\varvec{w}}^{\text {MDR}}$ for given $\bar{\theta }$ that uses less or equal switches then by the TV constraints required, we conclude by Corollary 3 that there exists no such ${\varvec{w}}\in \Omega _N$ for this specific threshold $\bar{\theta }$ and, hence, $LB=\bar{\theta }\le \theta ^*$ is a true lower bound on the optimal (CIA) objective value. Moreover, if MDR constructs for a given $\bar{\theta }$ and all initial controls $i\in [{n_\omega }]$ control functions ${\varvec{w}}^{\text {MDR}}$ with $\theta ({\varvec{w}}^{\text {MDR}})> \bar{\theta }$, Lemma 4 and the assumption in (b) guarantee that this $\bar{\theta }$ is also a true lower bound on the optimal (CIA) objective value. Altogether, AMDR iteratively generates valid lower LB and upper bounds UB for $\theta ^*$ and produces a feasible solution that is optimal up to the chosen tolerance TOL.

• 3. MDR runs forward in time and computes solely the accumulated control deviation $\gamma$ and $\theta$ for all intervals $j\in [N]$, therefore $C_{\text {MDR}}\in \mathcal {O}(N)$. The interval halving in AMDR ensures that we execute the while loop a maximum of $\log _2((t_f-t_0)/TOL)$ times. Inside this loop, we need to run the MDR scheme in the worst case with all ${n_\omega }$ controls as initial controls. Combining these findings yields the asserted complexity.

$\square$

Remark 6

Several meaningful modifications for the AMDR algorithm are available. We may use it also for finding control functions fulfilling other combinatorial constraints such as minimum dwell time constraints by checking them together with the TV constraint in line 5. As part of the MDR scheme, the control with maximum forward control deviation $\gamma$ is activated if the previously active control is inadmissible. Instead, one may choose a less greedy variant. For instance, we could activate the next forced and admissible control. Lastly, the initial upper bound UB can be reduced, as we will point out in the next section.

Remark 7

If we drop the TV constraint on ${\varvec{w}}$, the AMDR scheme finds a control function with the same objective value as the one obtained by the control function of Sum-Up Rounding [24] (without proof).

Most results of this section are based on the assumption of an equidistant discretization, which is common in practice. However, the assumption of dealing only with canonical switches in the produced control function is critical. The following example illustrates that a control function generated by MDR with non-canonical switches may use more switches than needed or may not satisfy the rounding bound $\bar{\theta }$.

Example 3

Consider an equidistant grid. Let the following two relaxed values ${\varvec{a}}^1,{\varvec{a}}^2\in \mathcal {A}_N$ be defined as

$$\begin{aligned} (a_{i,j}^1)_{i\in [3], j\in [3]}:=\left( \begin{array}{ccc} 1 &{} 0.25 &{} 0 \\ 0 &{} 0.375 &{} 0.5 \\ 0 &{} 0.375 &{} 0.5 \\ \end{array} \right) , \qquad (a_{i,j}^2)_{i\in [3], j\in [3]}:=\left( \begin{array}{ccc} 1 &{} 0.2 &{} 0 \\ 0 &{} 0.4+\epsilon &{} 0 \\ 0 &{} 0.4-\epsilon &{} 1 \\ \end{array} \right) , \qquad 0<\epsilon <0.4. \end{aligned}$$

Then, MDR with $i=1$ as initial control and $\bar{\theta }^1=0.75 \bar{\Delta }$, respectively $\bar{\theta }^2=(0.6+\epsilon )\bar{\Delta }$, constructs the following control functions:

$$\begin{aligned} (w_{i,j}^{\text {MDR},1})_{i\in [3], j\in [3]}:=\left( \begin{array}{ccc} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 \\ \end{array} \right) , \qquad (w_{i,j}^{\text {MDR},2})_{i\in [3], j\in [3]}:=\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array} \right) . \end{aligned}$$

In the first example, two controls are simultaneously forced on the third interval; the (CIA) objective value would be smaller if $w_{3,2}=1$ was chosen. The MDR constructs in the second example a control function that uses two switches, although activating the third control on the second interval would result in only one switch with almost the same (CIA) objective value. Both examples have in common that non-canonical switches are used. Hence, the improved control functions would be

$$\begin{aligned} (w_{i,j}^{\text {OPT},1})_{i\in [3], j\in [3]}:=\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array} \right) , \qquad (w_{i,j}^{\text {OPT},2})_{i\in [3], j\in [3]}:=\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 \\ \end{array} \right) . \end{aligned}$$

Upper bounds on (CIA) with $n_{\omega }=2$

In this section, we use the MDR algorithm and previous results to deduce bounds on (CIA). We consider a given (CIA) problem with grid $\mathcal {G}_N$, relaxed value ${\varvec{a}}\in \mathcal {A}_N$ and maximum number of switches $\sigma _{\text {max}}> 0$. The idea in the following is to construct a control function ${\varvec{w}}^{\text {MDR}}$ that bounds the objective of (CIA). For finding an appropriate initial active control for the MDR scheme, we introduce an auxiliary grid $\tilde{\mathcal {G}}_N$ which ends at $\tilde{t}_f$ and has $\tilde{N}$ intervals:

$$\begin{aligned} \tilde{\mathcal {G}}_N := \mathcal {G}_N \cap \left[ t_0,t_0 + \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}} \right] , \quad \tilde{N}:= |\tilde{\mathcal {G}}_N|-1, \quad \tilde{t}_f:=\max \{t_j \mid t_j \in \tilde{\mathcal {G}}_N \}. \end{aligned}$$

In the definition of $\tilde{\mathcal {G}}_N$ we intersect two sets because we consider given $\mathcal {G}_N$ and $\sigma _{\text {max}}$. To specify the rounding of a value $t_0\le t$ down to the next grid point, we utilize the following brackets notation

$$\begin{aligned} \lfloor t \rfloor _{\mathcal {G}_N}:= \max \{ t_j \in \mathcal {G}_N \ \mid \ t_j\le t \}. \end{aligned}$$

Depending on whether we deal with an equidistant grid or not, we can prove a sharp bound for (CIA). We are going to distinguish between these two cases in the upcoming results and introduce the following constant

$$\begin{aligned} C_1 := \left\{ \begin{array}{cl} \frac{1}{3+2\sigma _{\text {max}}},\qquad &{}\qquad {\text {if }} \mathcal {G}_N \text { equidistant,}\\ 0, &{} \qquad {\text {else.}} \end{array} \right. \end{aligned}$$

(6.1)

We propose to apply the rounding threshold

$$\begin{aligned} \bar{\theta } := \frac{t_f-t_0}{3+2\sigma _{\text {max}}}+ \frac{1}{2}\bar{\Delta }-\frac{C_1}{2}\bar{\Delta } \end{aligned}$$

(6.2)

in the MDR scheme and claim that this choice will be later beneficial for proving upper bounds on (CIA). Next, we establish useful properties of the rounding $\lfloor \cdot \rfloor _{\mathcal {G}_N}$ to the next grid point.

Lemma 5

(Distance to next grid points) Consider $\sigma _{\text {max}}>0$ and the rounding threshold $\bar{\theta }$ defined as above. The following holds true:

• 1. $\lfloor t_0+ j \bar{\theta } \rfloor _{\mathcal {G}_N} \ge t_0+ j \bar{\theta }-\bar{\Delta }+C_1\bar{\Delta }, \quad j\in [2],$

• 2. $\left\lfloor t_0 + \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}} \right\rfloor _{\mathcal {G}_N} \ge t_0+ \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}}-\bar{\Delta }+C_1\bar{\Delta }.$

Proof

• 1. Let us first consider the non-equidistant case. If $t_0+j\bar{\theta }\le t_f$, we deduce that the maximum distance of $t_0+j\bar{\theta }$ to the next smaller or equal grid point is $\bar{\Delta }$. If $t_0+j\bar{\theta } > t_f$, we have $\lfloor t_0+ j \bar{\theta } \rfloor _{\mathcal {G}_N}= t_f$ and obtain

  $$\begin{aligned} t_0 + j \bar{\theta } \le t_0 + 2 \bar{\theta } \le t_0 + 2\frac{t_f - t_0}{3+2\cdot 1}+\bar{\Delta } = \frac{3}{5}t_0 + \frac{2}{5}t_f + \bar{\Delta } < t_f + \bar{\Delta }. \end{aligned}$$

  This settles the non-equidistant case: $\lfloor t_0+ j \bar{\theta } \rfloor _{\mathcal {G}_N} \ge t_0+ j \bar{\theta }-\bar{\Delta }$. For the equidistant case, we observe

  $$\begin{aligned} \bar{\theta }= \frac{t_f-t_0}{3+2\sigma _{\text {max}}}+ \frac{1}{2}\bar{\Delta }-\frac{1}{2(3+2\sigma _{\text {max}})}\bar{\Delta }=\frac{N\bar{\Delta }+(\sigma _{\text {max}}+1)\bar{\Delta }}{3+2\sigma _{\text {max}}}=\frac{(N+\sigma _{\text {max}}+1)\bar{\Delta }}{3+2\sigma _{\text {max}}}. \end{aligned}$$

  We look at the right fraction and notice that the numerator consists of a product of an integer and $\bar{\Delta }$, whereas the denominator is the integer $3+2\sigma _{\text {max}}$. Thus, the maximum cut-off by rounding down to the closest grid point is $\frac{3+2\sigma _{\text {max}}-1}{3+2\sigma _{\text {max}}}\bar{\Delta }$, which is equal to $\bar{\Delta }-C_1\bar{\Delta }$ and proves the claim.

• 2. This follows from a similar argumentation as for the claim “1.”. For the non-equidistant case we need only to consider $t_0 + \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}} \le t_f$, for the equidistant case we take again advantage of $t_f-t_0=N\bar{\Delta }$.

$\square$

We continue with a lemma that quantifies the length of activation blocks in ${\varvec{w}}^{\text {MDR}}$.

Lemma 6

(Length of activation blocks $\delta _l$ ) Consider a feasible control solution for (CIA $-\bar{\theta }$ ) that only uses canonical switches. Then, for the length of its activation block $\delta _l$ , $2\le l \le \sigma _{\text {max}}$ , follows:

$$\begin{aligned} \delta _l \ge 2\bar{\theta }- \bar{\Delta } +C_1\bar{\Delta }. \end{aligned}$$

Proof

Let i be the active control on activation block l. We are using the assumption regarding canonical switches twice. First, i is forced for the earlier switch $l-1$:

$$\begin{aligned} \theta _{i,\tau _{l-1}-1} + a_{i,\tau _{l-1}} \Delta _{\tau _{l-1}} {>} \bar{\theta } \end{aligned}$$

(6.3)

and second, it is inadmissible on interval $\tau _l$:

$$\begin{aligned} \theta _{i,\tau _{l-1}-1} + \sum \limits _{j=\tau _{l-1}}^{\tau _l - 1} (a_{i,j}-1) \Delta _{j} + (a_{i,\tau _l}-1) \Delta _{\tau _l}=\theta _{i,\tau _{l}-1} + (a_{i,\tau _l}-1) \Delta _{\tau _l} {<}- \bar{\theta }. \end{aligned}$$

(6.4)

By definition of activation blocks we have $\delta _l=\sum _{j=\tau _{l-1}}^{\tau _l - 1} \Delta _{j}$ so that we obtain by rearranging (6.4):

$$\begin{aligned} \delta _l >\theta _{i,\tau _{l-1}-1} + \bar{\theta } + \sum \limits _{j=\tau _{l-1}}^{\tau _l - 1} a_{i,j} \Delta _{j} + (a_{i,\tau _l}-1) \Delta _{\tau _l}. \end{aligned}$$

Plugging (6.3) into the above inequality yields

$$\begin{aligned} \delta _l > 2\bar{\theta } - a_{i,\tau _{l-1}} \Delta _{\tau _{l-1}} + \sum \limits _{j=\tau _{l-1}}^{\tau _l - 1} a_{i,j} \Delta _{j} + (a_{i,\tau _l}-1) \Delta _{\tau _l} = 2\bar{\theta } + \sum \limits _{j=\tau _{l-1}+1}^{\tau _l} a_{i,j} \Delta _{j} - \Delta _{\tau _l} \ge 2\bar{\theta } -\bar{\Delta } \end{aligned}$$

which settles the non-equidistant case. For an equidistant grid, we compute

$$\begin{aligned} 2 \bar{\theta } - \bar{\Delta }=\frac{2N\bar{\Delta }}{3+2\sigma _{\text {max}}}+\bar{\Delta }-C_1\bar{\Delta }-\bar{\Delta }=\frac{2N-1}{3+2\sigma _{\text {max}}}\bar{\Delta }, \end{aligned}$$

and because $\delta _l$ is a multiple of $\bar{\Delta }$, it follows from $\delta _l>2\bar{\theta } -\bar{\Delta }$

$$\begin{aligned} \delta _l \ge \frac{2N-1}{3+2\sigma _{\text {max}}}\bar{\Delta } + \frac{1}{3+2\sigma _{\text {max}}}\bar{\Delta }=2\bar{\theta }-\bar{\Delta }+C_1\bar{\Delta }. \end{aligned}$$

$\square$

Next, we propose in Algorithm 4 a specification of the initial active control $i_0$. We observe that a small number of switches on $\tilde{\mathcal {G}}_N$ in terms of $\bar{\theta }$ is sufficient, as quantified in the following lemma.

Lemma 7

The MDR algorithm applied to the auxiliary grid $\tilde{\mathcal {G}}_N$ with rounding threshold $\bar{\theta }$, $n_{\omega }=2$ and $i_0$ from Algorithm 4 as initial control constructs a control function ${\varvec{w}}^{\text {MDR}}$ that uses at most one switch on $\tilde{\mathcal {G}}_N$.

Proof

We distinguish between the three possibilities of the initial control in Algorithm 4.

• 1. If MDR is initialized with $i_2$ and for $i_1$ holds $\sum _{j=1}^{\tilde{N}}a_{i_1,j}\Delta _j \le \bar{\theta }$, the latter does not become forced on $\tilde{\mathcal {G}}_N$. For this reason there is no switch.

• 2. If $i_1$ with $\sum _{j=1}^{\tilde{N}}a_{i_1,j}\Delta _j \le 2\bar{\theta }- \bar{\Delta }+C_1\bar{\Delta }$ is the initial active control, a switch has to occur in case $i_2$ is forced on some interval $\tau _1\in [\tilde{N}]$. We need to prove that $i_1$ does not become forced after the first switch, which is equivalent to $i_2$ does not become inadmissible due to $n_{\omega }=2$ and Lemma 2, because then there is no other switch. For this, we derive a lower bound on the length of the first activation block $\delta _1$, where $i_1$ is active. The control $i_1$ becomes at the earliest inadmissible when it has been active on intervals j with $a_{i_1,j}=0$ whose lengths sum up to be more than $\bar{\theta }$, i.e., $\lfloor t_0+ \bar{\theta } \rfloor _{\mathcal {G}_N} -t_0$. With this observation and Lemma 5.1 we derive

  $$\begin{aligned} \delta _1=\sum \limits _{j=1}^{\tau _1-1}\Delta _j \ge \lfloor t_0+ \bar{\theta } \rfloor _{\mathcal {G}_N} -t_0 {\mathop {\ge }\limits ^{\text {Lemma }5.1}} \bar{\theta } - \bar{\Delta } +C_1\bar{\Delta }. \end{aligned}$$

  Note that $\gamma _{i_1,j}$ is monotonically increasing with increasing interval $j>\tau _1$ as long as $i_1$ is inactive, i.e., $w_{i_1,j-1}=0$. Hence, if we are able to prove $\gamma _{i_1,\tilde{N}}\le \bar{\theta }$ in case of $w_{i_1,j}=0$ for $j>\tau _1$, we also have that $\gamma _{i_1,j}\le \bar{\theta }$ for any interval $j> \tau _1$ meaning there is no second switch. Altogether, we get with the above inequality

  $$\begin{aligned} \gamma _{i_1,\tilde{N}} = \sum \limits _{j=1}^{\tilde{N}}a_{i_1,j}\Delta _j - \delta _1 \le 2\bar{\theta }- \bar{\Delta } +C_1\bar{\Delta } - (\bar{\theta } - \bar{\Delta }+C_1\bar{\Delta } )\le \bar{\theta } \end{aligned}$$

  so that ${\varvec{w}}^{\text {MDR}}$ switches no more than once on $\tilde{\mathcal {G}}_N$.

• 3. Otherwise we have

  $$\begin{aligned} \sum _{j=1}^{\tilde{N}}a_{i,j}\Delta _j > 2\bar{\theta }-\bar{\Delta }+C_1\bar{\Delta }, \qquad i=i_1,i_2, \end{aligned}$$

  (6.5)

  in the else case. We can argue similarly as in the previous case, which is why we only have to prove $\gamma _{i_1,\tilde{N}}\le \bar{\theta }$. Since $i_1$ is a next forced control on the first interval, there is an interval $l\le \tau _1$ with $\sum _{j=1}^{l}a_{i_1,j}\Delta _j>\bar{\theta }$. This implies the interval $\tau _1$ of the earliest possible switch is given by

  $$\begin{aligned} \tau _1 = \mathop {{\text {argmin}}}_{l\in [N]}\left\{ \sum _{j=1}^{l}(a_{i_1,j}-1)\Delta _j<-\bar{\theta } \ \mid \ \sum _{j=1}^{l}a_{i_1,j}\Delta _j>\bar{\theta } \right\} \end{aligned}$$

  from which we find $\sum _{j=1}^{\tau _1}\Delta _j> 2\bar{\theta }$. We conclude for the grid point $t_{\tau _1}= \lfloor t_0+ \sum _{j=1}^{\tau _1}\Delta _j \rfloor _{\mathcal {G}_N} > \lfloor t_0+ 2\bar{\theta }\rfloor _{\mathcal {G}_N}$, which implies $t_{\tau _1-1}= \lfloor t_0+ \sum _{j=1}^{\tau _1-1}\Delta _j \rfloor _{\mathcal {G}_N} \ge \lfloor t_0+ 2\bar{\theta }\rfloor _{\mathcal {G}_N}$. This is equivalent to $\sum _{j=1}^{\tau _1-1}\Delta _j \ge \lfloor t_0+ 2\bar{\theta } \rfloor _{\mathcal {G}_N} -t_0$ and so

  $$\begin{aligned} \delta _1=\sum \limits _{j=1}^{\tau _1-1}\Delta _j \ge \lfloor t_0+ 2\bar{\theta } \rfloor _{\mathcal {G}_N} -t_0 {\mathop {\ge }\limits ^{\text {Lemma }5.1}} 2\bar{\theta } - \bar{\Delta } +C_1\bar{\Delta }. \end{aligned}$$

  (6.6)

  Using the (Conv) property yields $\sum _{j=1}^{\tilde{N}}a_{i_1,j}\Delta _j = \sum _{j=1}^{\tilde{N}}\Delta _j - \sum _{j=1}^{\tilde{N}}a_{i_2,j}\Delta _j,$ and therefore

  $$\begin{aligned} \gamma _{i_1,\tilde{N}}&\le \sum \limits _{j=1}^{\tilde{N}}a_{i_1,j}\Delta _j - \delta _1 {\mathop { \le }\limits ^{(6.5)}} \sum _{j=1}^{\tilde{N}}\Delta _j - \sum _{j=1}^{\tilde{N}}a_{i_2,j}\Delta _j -(2\bar{\theta } - \bar{\Delta }+C_1\bar{\Delta })\\&{\mathop {<}\limits ^{6.5}} \tilde{t}_f-t_0 - (2\bar{\theta }-\bar{\Delta }+C_1\bar{\Delta }) - (2\bar{\theta } - \bar{\Delta }+C_1\bar{\Delta })\\&=\left\lfloor t_0 + \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}}\right\rfloor _{\mathcal {G}_N} - t_0 - \frac{4(t_f-t_0)}{3+2\sigma _{\text {max}}}\\&\le t_0 + \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}} - t_0 - \frac{4(t_f-t_0)}{3+2\sigma _{\text {max}}} \\&= \frac{(t_f-t_0)}{3+2\sigma _{\text {max}}} \\&< \bar{\theta }, \end{aligned}$$

  where we used $\tilde{t}_f=\left\lfloor t_0 + \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}} \right\rfloor _{\mathcal {G}_N}$ in the third equation. To conclude, there is also at most one switch. $\square$

The above three lemmata are crucial for the following theorem, which provides an upper bound on (CIA).

Theorem 3

Consider any grid $\mathcal {G}_N$, relaxed values ${\varvec{a}}\in \mathcal {A}_N$ and a maximum number of switches $\sigma _{\text {max}}> 0$. The objective of (CIA) is bounded by

$$\begin{aligned} \theta \le \frac{N}{3+2\sigma _{\text {max}}}\bar{\Delta } +\frac{1}{2}\bar{\Delta }-\frac{C_1}{2}\bar{\Delta }. \end{aligned}$$

Proof

We want to prove that the control function ${\varvec{w}}^{\text {MDR}}$ constructed by MDR with rounding threshold $\bar{\theta }$ from (6.2) and initial control from Algorithm 4 is feasible and satisfies the claimed bound. We observe $\bar{\theta }\ge \frac{1}{2}\bar{\Delta }$ from its definition in (6.2) and the definition of $C_1$ in (6.1). Thus, we can apply Proposition 3 in connection with Lemma 3 so that ${\varvec{w}}^{\text {MDR}}$ fulfills indeed the claimed bound:

$$\begin{aligned} \theta ({\varvec{w}}^{\text {MDR}}) \le \bar{\theta }=\frac{t_f-t_0}{3+2\sigma _{\text {max}}}+\frac{1}{2}\bar{\Delta }-\frac{C_1}{2}\bar{\Delta }. \end{aligned}$$

What remains to be shown is that ${\varvec{w}}^{\text {MDR}}$ is a feasible solution for (CIA$-\bar{\theta }$), i.e., it does not use more than $\sigma _{\text {max}}$ switches. In the sequel, we write $n=\sigma _{\text {max}}$ in variable indices to improve readability of the latter. We assume there are already $\sigma _{\text {max}}$ switches taken in ${\varvec{w}}^{\text {MDR}}$ and calculate the maximum length of the possibly last activation block, i.e., $\delta _{n+1}=t_f - t_{\tau _{n}-1}$. In Lemma 7 we have derived that at most one switch is used on the reduced grid $\tilde{\mathcal {G}}_N$ until $\tilde{t}_f$, but there may follow another switch shortly afterwards, i.e., $\tau _2\ge \tilde{N}+1$. For the remaining $\sigma _{\text {max}}- 2$ activation blocks until $t_{\tau _{n}-1}$ we can apply Lemma 6, since Proposition 3 states that MDR uses canonical switches for $n_{\omega }=2$. Lemma 6 states

$$\begin{aligned} \delta _l \ge 2\theta - \bar{\Delta }+C_1\bar{\Delta }, \qquad {\text { for }} 3\le l \le \sigma _{\text {max}}. \end{aligned}$$

Combining these findings and using Lemma 5.2 results in

$$\begin{aligned} t_f - t_{\tau _{n}-1}= & {} t_f - \sum \limits _{j=1}^{\sigma _{\text {max}}} \delta _j \le t_f - (\tilde{t}_f + (\sigma _{\text {max}}- 2)( 2\bar{\theta }-\bar{\Delta }+C_1\bar{\Delta })) \nonumber \\\le & {} t_f - \left\lfloor t_0 + \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}} \right\rfloor _{\mathcal {G}_N} - (\sigma _{\text {max}}- 2)( 2\bar{\theta }-\bar{\Delta }+C_1\bar{\Delta })\nonumber \\\le & {} t_f - ( t_0 + \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}} - \bar{\Delta }+C_1\bar{\Delta }) - (\sigma _{\text {max}}- 2)( 2\bar{\theta }-\bar{\Delta }+C_1\bar{\Delta }) \nonumber \\= & {} \frac{(3+2\sigma _{\text {max}})(t_f-t_0)}{3+2\sigma _{\text {max}}} - \frac{5(t_f-t_0)}{3+2\sigma _{\text {max}}} + \bar{\Delta }-C_1\bar{\Delta } - (\sigma _{\text {max}}- 2)\left( \frac{2(t_f-t_0)}{3+2\sigma _{\text {max}}}\right) \nonumber \\= & {} \frac{2(t_f-t_0)}{3+2\sigma _{\text {max}}} + \bar{\Delta }-C_1\bar{\Delta }. \end{aligned}$$

(6.7)

Let i denote the control that is active after the $\sigma _{\text {max}}$th switch of ${\varvec{w}}^{\text {MDR}}$. Note that $\theta _{i,j}$ is monotonically decreasing with increasing interval $j\ge \tau _{n}$ since i is chosen to be active on interval j. Hence, if we are able to show that i is admissible on interval N, then it is also admissible on earlier intervals. We want to prove the admissibility of control i on interval N as in this case there will be no further switch until N. For this, let us assume i is inadmissible on interval N. We obtain

In the second inequality we used that control i is forced on the interval $\tau _n$ of the nth, respectively $\sigma _{\text {max}}$th, switch. With this contradiction, there cannot be a further switch after $\tau _n$; in other words, ${\varvec{w}}^{\text {MDR}}$ uses at most $\sigma _{\text {max}}$ switches and is a feasible solution of (CIA). This completes the proof. $\square$

In the sequel, we are going to elaborate how sharp the upper bound from Theorem 3 is, and we will thereby exclude the case $\sigma _{\text {max}}\ge N-1$; otherwise the TV constraint would be no longer restrictive. Before presenting the main result in this context, we need a technical lemma again.

Lemma 8

For $N,\sigma _{\text {max}}\in \mathbb {N}$, where $1\le \sigma _{\text {max}}\le N-2$, let $R\in \mathbb {Q}$ be defined by

$$\begin{aligned} R:= \frac{N}{3+2\sigma _{\text {max}}}. \end{aligned}$$

We have that

$$\begin{aligned} 2\left\lceil R\right\rceil ^{0.5}-1 \le \left\lfloor \frac{N-\left\lceil R\right\rceil }{\sigma _{\text {max}}+1} \right\rfloor , \end{aligned}$$

(6.8)

where we indicate by $\lceil x \rceil ^{0.5}$ the rounding up of $x\in \mathbb {R}$ to the next multiple of 0.5 as defined in Sect. 1.3.

Proof

Since R is a rational number with $3+2\sigma _{\text {max}}$ in the denominator, we have

$$\begin{aligned} \left\lceil R\right\rceil ^{0.5} \le \frac{N}{3+2\sigma _{\text {max}}}+0.5\left( 1-\frac{1}{3+2\sigma _{\text {max}}}\right) . \end{aligned}$$

(6.9)

Moreover, using basic properties of floor and ceiling functions yields

$$\begin{aligned} \left\lceil R\right\rceil\le & {} \left\lceil R\right\rceil ^{0.5} + 0.5, \end{aligned}$$

(6.10)

$$\begin{aligned} \frac{N- \left\lceil R\right\rceil }{\sigma _{\text {max}}+1} - \frac{\sigma _{\text {max}}}{\sigma _{\text {max}}+1}\le & {} \left\lfloor \frac{N-\left\lceil R\right\rceil }{\sigma _{\text {max}}+1} \right\rfloor . \end{aligned}$$

(6.11)

Next, we calculate

$$\begin{aligned} 2\left( \left\lceil R\right\rceil ^{0.5}-1\right)&= && {} \frac{ (2\left\lceil R\right\rceil ^{0.5}-1)(\sigma _{\text {max}}+1)-1}{(\sigma _{\text {max}}+1)} - \frac{\sigma _{\text {max}}}{\sigma _{\text {max}}+1} \\&= && {} \frac{ (2\left\lceil R\right\rceil ^{0.5}-1)(\sigma _{\text {max}}+1)+\left\lceil R\right\rceil ^{0.5}-1}{(\sigma _{\text {max}}+1)} - \frac{ \left\lceil R\right\rceil ^{0.5}}{(\sigma _{\text {max}}+1)}- \frac{\sigma _{\text {max}}}{\sigma _{\text {max}}+1} \\ &= && {} \frac{ \left\lceil R\right\rceil ^{0.5}(3+2\sigma _{\text {max}})-(\sigma _{\text {max}}+1)-1}{(\sigma _{\text {max}}+1)} - \frac{ \left\lceil R\right\rceil ^{0.5}}{(\sigma _{\text {max}}+1)}- \frac{\sigma _{\text {max}}}{\sigma _{\text {max}}+1} \\ &{\mathop {\le }\limits ^{(6.9)}}&&\frac{\left( \frac{N}{3+2\sigma _{\text {max}}}+0.5-\frac{1}{2(3+2\sigma _{\text {max}})} \right) (3+2\sigma _{\text {max}})-(\sigma _{\text {max}}+2)}{(\sigma _{\text {max}}+1)} - \frac{ \left\lceil R\right\rceil ^{0.5}}{(\sigma _{\text {max}}+1)}- \frac{\sigma _{\text {max}}}{\sigma _{\text {max}}+1} \\&= && {} \frac{N-0.5}{(\sigma _{\text {max}}+1)} - \frac{ \left\lceil R\right\rceil ^{0.5}}{(\sigma _{\text {max}}+1)}- \frac{\sigma _{\text {max}}}{\sigma _{\text {max}}+1}- \frac{1}{2(\sigma _{\text {max}}+1)} \\&{\mathop {\le }\limits ^{(6.10)}}&&\frac{N}{(\sigma _{\text {max}}+1)} - \frac{ \left\lceil R\right\rceil }{(\sigma _{\text {max}}+1)}- \frac{\sigma _{\text {max}}}{\sigma _{\text {max}}+1}- \frac{1}{2(\sigma _{\text {max}}+1)} \\&= && {} \frac{N- \left\lceil R\right\rceil }{(\sigma _{\text {max}}+1)} - \frac{\sigma _{\text {max}}}{\sigma _{\text {max}}+1}- \frac{1}{2(\sigma _{\text {max}}+1)} \\&{\mathop {\le }\limits ^{(6.11)}}&& \left\lfloor \frac{N-\left\lceil R\right\rceil }{\sigma _{\text {max}}+1} \right\rfloor - \frac{1}{2(\sigma _{\text {max}}+1)},\\&< && {} \left\lfloor \frac{N-\left\lceil R\right\rceil }{\sigma _{\text {max}}+1} \right\rfloor . \end{aligned}$$

Both $2\left( \left\lceil R\right\rceil ^{0.5}-1\right) \in \mathbb {Z}$ and $\left\lfloor \frac{N-\left\lceil R\right\rceil }{\sigma _{\text {max}}+1} \right\rfloor \in \mathbb {Z}$ are valid so that we can deduce from the above inequality

$$\begin{aligned} 2\left( \left\lceil R\right\rceil ^{0.5}-1\right) \le \left\lfloor \frac{N-\left\lceil R\right\rceil }{\sigma _{\text {max}}+1} \right\rfloor -1 . \end{aligned}$$

$\square$

Theorem 4

For $N,\sigma _{\text {max}}\in \mathbb {N}$ , where $1\le \sigma _{\text {max}}\le N-2$ , there is an equidistant grid $\mathcal {G}_N$ and an ${\varvec{a}}\in \mathcal {A}_N$ so that (CIA) has an objective value of

$$\begin{aligned} \theta \ge \left\lceil \frac{N}{3+2\sigma _{\text {max}}} \right\rceil ^{0.5} \bar{\Delta }. \end{aligned}$$

(6.12)

Proof

If $\sigma _{\text {max}}+2 \le N< 3+2\sigma _{\text {max}}$, then we define ${\varvec{a}}$ by specifying the values of control $i_1$ for the intervals $j\in [N]$ by

$$\begin{aligned} a_{i_1,j}=\left\{ \begin{array}{ll} 1, \quad &{} {\text {if }} j \text { odd,}\\ 0, \quad &{} {\text {if }} j {\text { even.}} \end{array} \right. \end{aligned}$$

Since there are more intervals N than the maximum number of switches $\sigma _{\text {max}}$ plus one, there is an interval j on which the optimal solution ${\varvec{w}}$ of (CIA) has the value $w_{i_1,j}=1$, while $a_{i_1,j}=0$ holds. This results in $\theta \ge 1 \bar{\Delta } = \lceil \frac{N}{3+2\sigma _{\text {max}}} \rceil ^{0.5} \bar{\Delta }$.

Otherwise, if $N\ge 3+2\sigma _{\text {max}}$, we proceed as follows

• 1. We construct a specific matrix ${\varvec{a}}$ that depends on the choice of $\sigma _{\text {max}}$ and N.

• 2.
  

  We prove that the MDR scheme constructs for both initial active controls, for this ${\varvec{a}}$ value and with a rounding threshold of

  $$\begin{aligned} \bar{\theta }:= \left\lceil \frac{N}{3+2\sigma _{\text {max}}} \right\rceil ^{0.5} \bar{\Delta } - \epsilon , \qquad {\text { for any }} \ 0< \epsilon < \left\lceil \frac{N}{3+2\sigma _{\text {max}}} \right\rceil ^{0.5} \bar{\Delta }, \end{aligned}$$

  (6.13)

  control functions ${\varvec{w}}^{\text {MDR}}$ that use more than $\sigma _{\text {max}}$ switches. Then, we can come back to the idea of the AMDR scheme and Theorem 2.1., which states that ${\varvec{w}}^{\text {AMDR}}$ is feasible for (CIA), i.e. uses at most $\sigma _{\text {max}}$ switches, resulting in

  $$\begin{aligned} \left\lceil \frac{N}{3+2\sigma _{\text {max}}} \right\rceil ^{0.5} \bar{\Delta } \le \theta \left( {\varvec{w}}^{\text {AMDR}}\right) . \end{aligned}$$

  Theorem 2 provides in 2. (a) also a statement about the relation to the optimal solution of (CIA):

  $$\begin{aligned} \theta \left( {\varvec{w}}^{\text {AMDR}}\right) \le \theta ^\star + TOL. \end{aligned}$$

  Because the tolerance TOL can be arbitrarily small, we conclude the optimal solution of (CIA) involves an objective value of at least $\left\lceil \frac{N}{3+2\sigma _{\text {max}}} \right\rceil ^{0.5} \bar{\Delta }$.

1. We reuse the notation of R from Lemma 8 and introduce the auxiliary constant $n_I\in \mathbb {N}$:

$$\begin{aligned} R:= \frac{N}{3+2\sigma _{\text {max}}}, \qquad n_I := \left\lfloor \frac{N-\lceil R \rceil }{\sigma _{\text {max}}+1} \right\rfloor . \end{aligned}$$

Next, we are interested in designing a specific ${\varvec{a}}\in \mathcal {A}_N$ with the property to enforce an improper covering by any ${\varvec{w}}\in \Omega _N$ that satisfies a (CIA) objective of at most $\bar{\theta }$. By improper covering we indicate ${\varvec{w}}\in \Omega _N$ has to use more than $\sigma _{\text {max}}$ switches in order to yield the desired (CIA) objective value of at most $\bar{\theta }$. We create sets of consecutive intervals for ${\varvec{a}}$ on which either ${\varvec{a}}_{i_1}$ or ${\varvec{a}}_{i_2}$ is set to one (and the other control is thereby set to zero). We call these sets of consecutive intervals with the same value here index sections. We generate $\sigma _{\text {max}}+ 2$ index sections, where the two controls are alternately set to one in ${\varvec{a}}$, with the idea that a feasible solution ${\varvec{w}}$ of (CIA) with at most $\sigma _{\text {max}}$ switches shall contain at most $\sigma _{\text {max}}+ 1$ activation blocks. The first index section will include $\lfloor R \rfloor$ intervals, followed by index sections with $n_I$ intervals, and the last index section arises from the remaining intervals until N is reached. After conveying some intuition of the specific ${\varvec{a}}\in \mathcal {A}_N$, we continue with a technical definition of the index set $\mathcal {J}$ that specifies the index sections on which ${\varvec{a}}_{i_1}$ is set to one:

$$\begin{aligned} \mathcal {J}_{\text {even}}:= & {} \left[ \lfloor R \rfloor \right] \cup \left\{ j \mid \left\lceil R \right\rceil + (2k-1)n_I+1 \le j \le \left\lceil R \right\rceil +2kn_I, \ k\in [\lfloor \sigma _{\text {max}}/2\rfloor ]\right\} ,\\ \mathcal {J}:= & {} \left\{ \begin{array}{ll} \mathcal {J}_{\text {even}}, &{} \quad {\text { if }} \sigma _{\text {max}}\text { is even,}\\ \mathcal {J}_{\text {even}} \cup \{ j \mid \left\lceil R \right\rceil + (2\lfloor \sigma _{\text {max}}/2\rfloor +1)n_I+1 \le j \le N\}, &{} \quad {\text { if }} \sigma _{\text {max}}{\text { is odd.}} \end{array}\right. \end{aligned}$$

With these definitions we introduce ${\varvec{a}}$ by fixing the values of control $i_1$.

$$\begin{aligned} a_{i_1,j}=\left\{ \begin{array}{ll} 1, \quad &{} {\text {if }} j \in \mathcal {J},\\ 0.5, \quad &{} \text {if } j= \left\lceil R \right\rceil , \ {\text { and }} \ \lfloor R \rfloor < R \le \lfloor R \rfloor +0.5,\\ 1, \quad &{} \text {if } j= \left\lceil R \right\rceil , \ {\text { and }} \ R > \lfloor R \rfloor +0.5,\\ 0, \quad &{} {\text {else.}} \end{array} \right. \end{aligned}$$

(6.14)

The value of ${\varvec{a}}_{i_1}$ on the $(\left\lceil R \right\rceil )$th interval in the second and third case may seem unintuitive. The idea of this construction is that it results $\theta _{i_1,\left\lceil R \right\rceil }= \left\lceil R \right\rceil ^{0.5}$ if control $i_1$ is neither active on the first index section, nor on the $(\left\lceil R \right\rceil )$th interval. In this way, control $i_1$ needs to be already active on the first index section in order to maintain a (CIA) objective value of at most $\bar{\theta }$.

2. We want to prove that the MDR scheme with the rounding threshold from (6.13) and with ${\varvec{a}}$ defined in (6.14) constructs a control function that uses more than $\sigma _{\text {max}}$ switches, independent of the initial active control. For this, we are going to establish the following claim:

• a) If $i_1$ is the initial active control, the kth switch of ${\varvec{w}}^{\text {MDR}}$ happens before the $\left( \left\lceil R \right\rceil + k n_I\right)$th interval, where $k\in [\sigma _{\text {max}}+1 ]$.

• b) If $i_2$ is the initial active control, the kth switch of ${\varvec{w}}^{\text {MDR}}$ happens before the $\left( \left\lceil R \right\rceil + (k-1) n_I\right)$th interval, where $k\in [\sigma _{\text {max}}+1 ]$.

Assuming the claim is true, ${\varvec{w}}^{\text {MDR}}$ uses indeed more than $\sigma _{\text {max}}$ switches because the $\left( \left\lceil R \right\rceil + (\sigma _{\text {max}}+ 1) n_I\right)$th interval exists, i.e., is smaller than or equal to N:

$$\begin{aligned} \left\lceil R \right\rceil + (\sigma _{\text {max}}+ 1) n_I = \left\lceil R \right\rceil + (\sigma _{\text {max}}+ 1) \left\lfloor \frac{N-\lceil R \rceil }{\sigma _{\text {max}}+1} \right\rfloor \le \left\lceil R \right\rceil + (\sigma _{\text {max}}+ 1) \frac{N-\lceil R \rceil }{\sigma _{\text {max}}+1} =N. \end{aligned}$$

The inequality above shows that there are indeed $\sigma _{\text {max}}+2$ index sections for ${\varvec{a}}$ as described above. With this information we deduce that $\bar{\theta }<\frac{1}{2}\bar{\Delta }$ results directly in more than $\sigma _{\text {max}}$ switches or in control solutions that does not satisfy the claimed optimal (CIA) objective value from (6.12) anyway:

• If ${\varvec{a}}$ consists only of zeros and ones and $\bar{\theta }<\frac{1}{2}\bar{\Delta }$, the MDR algorithm creates switches on all intervals j for which ${\varvec{a}}_{\cdot ,j}\ne {\varvec{a}}_{\cdot ,j-1}$ holds true. Thus, the activation blocks of ${\varvec{w}}^{\text {MDR}}$ would match the index sections of ${\varvec{a}}$, i.e. ${\varvec{w}}^{\text {MDR}} = {\varvec{a}}$. As we derived $\sigma _{\text {max}}+2$ index sections for ${\varvec{a}}$, there are $\sigma _{\text {max}}+2$ blocks for ${\varvec{w}}^{\text {MDR}}$ and therefore $\sigma _{\text {max}}+1$ switches.

• If $a_{i_1,\left\lceil R \right\rceil }=0.5$, then there is no ${\varvec{w}}$ with $\theta ({\varvec{w}})<\frac{1}{2}\bar{\Delta }$ regardless of which control is active on interval $\left\lceil R \right\rceil$ since ${\varvec{a}}$ is either zero or one on all other intervals. Hence, we can exclude the case $\bar{\theta }<\frac{1}{2}\bar{\Delta }$ from further consideration.

Thus, we are left with the case $\bar{\theta }\ge \frac{1}{2}\bar{\Delta }$. In this case, we can apply Proposition 3 and conclude that we deal only with canonical switches. We return to prove the claim, and we proceed via induction.

Base case

• (a)
  

  We consider $k=1$ and conclude from $N \ge 3 + 2 \sigma _{\text {max}}$ that $\left\lceil R \right\rceil ^{0.5} \ge 1$ holds. Plugging this into inequality (6.8) from Lemma 8 results in $\left\lceil R \right\rceil ^{0.5} < n_I,$ and thus

  $$\begin{aligned} \bar{\theta } < n_I \bar{\Delta }. \end{aligned}$$

  (6.15)

  By construction of ${\varvec{a}}$, the values $a_{i_1,j}$ are equal to one for $1\le j \le \left\lfloor R \right\rfloor$. The value $a_{i_1,\left\lceil R \right\rceil }$ is either 0.5 or 1. Therefore, $-0.5\le \theta _{i_1, \left\lceil R \right\rceil } \le 0$ holds for the accumulated control deviation of ${\varvec{w}}^{\text {MDR}}$ with $i_1$ as initial active control. After the $(\left\lceil R \right\rceil )$th interval $n_I$ intervals follow on which $a_{i_1,j}$ is zero. We conclude $i_1$ becomes inadmissible by (6.15) before interval $\left\lceil R \right\rceil + n_I$ and hence, the first switch appears before this interval.

• (b)
  

  We show the claim for the first two switches because we take an interest in a switch that occurs after interval $\left\lceil R \right\rceil$ in the induction step. Let $k=1$. Since

  $$\begin{aligned} \sum \limits _{j=1}^{\left\lceil R \right\rceil } (a_{i_2,j}-1) \bar{\Delta }=\left( \left\lceil R \right\rceil -\left\lceil R \right\rceil ^{0.5} - \left\lceil R \right\rceil \right) \bar{\Delta }< -\left\lceil R \right\rceil ^{0.5} \bar{\Delta } + \epsilon = - \bar{\theta }, \end{aligned}$$

  we conclude control $i_2$ becomes inadmissible the latest on interval $\left\lceil R \right\rceil$ when being the initial active control and, equivalently, ${\varvec{w}}^{\text {MDR}}$ has a switch on interval $\left\lceil R \right\rceil$ at the latest. This is equivalent to at least one activation of $i_1$ up to and including interval $\left\lceil R \right\rceil$, which we use for proving the assertion in case of $k=2$. Let us assume the second switch happens on or after interval $\left\lceil R \right\rceil +n_I$. This implies $i_1$ would be admissible on that interval and we derive

  

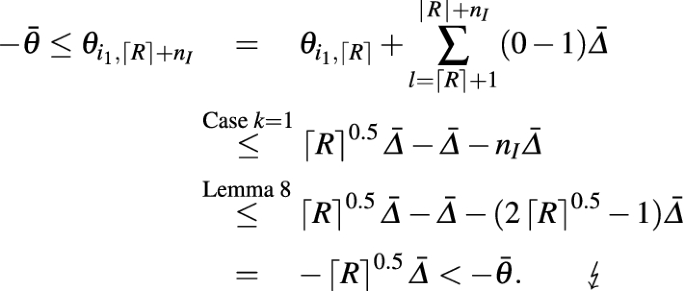
  Consequently, the second switch happens before the $\left( \left\lceil R \right\rceil + n_I\right)$th interval.

Induction step

Assume the assertion holds for $k-1\le \sigma _{\text {max}}$, we show that it is also true for k. At first, we prove an auxiliary result. For $i\in [2]$ and $j\ge \left\lceil R \right\rceil$ we have that

$$\begin{aligned} \theta _{i,j} = \left\lceil R \right\rceil ^{0.5} \bar{\Delta } + z\bar{\Delta }, \qquad \text {for some } \ z\in \mathbb {Z}. \end{aligned}$$

(6.16)

We prove the equation (6.16) by computing the accumulated control deviation:

$$\begin{aligned} \theta _{i_1,j} = \bar{\Delta }\left( \sum \limits _{l=1}^{\left\lceil R \right\rceil }a_{i_1,l}+\sum \limits _{l=1+\left\lceil R \right\rceil }^{j}a_{i_1,l} - \sum \limits _{l=1}^{j}w_{i_1,l}\right) =\left\lceil R \right\rceil ^{0.5}\bar{\Delta }+ \left( \sum \limits _{l=1+\left\lceil R \right\rceil }^{j}a_{i_1,l} - \sum \limits _{l=1}^{j}w_{i_1,l}\right) \bar{\Delta }. \end{aligned}$$

For $j> \left\lceil R \right\rceil$ we have defined $a_{i_1,j}\in \{0,1\}$ so that (6.16) holds with $z= \left( \sum _{l=1+\left\lceil R \right\rceil }^{j}a_{i_1,l} - \sum _{l=1}^{j}w_{i_1,l}\right)$. On the other hand, for the other control $i_2$ holds

$$\begin{aligned} \theta _{i_2,j} = \bar{\Delta }\left( \sum \limits _{l=1}^{\left\lceil R \right\rceil }a_{ i_2,l}+\sum \limits _{l=1+\left\lceil R \right\rceil }^{j}a_{ i_2,l} - \sum \limits _{l=1}^{j}w_{ i_2,l}\right) =(\left\lceil R \right\rceil - \left\lceil R \right\rceil ^{0.5})\bar{\Delta }+ \left( \sum \limits _{l=1+\left\lceil R \right\rceil }^{j}a_{ i_2,l} - \sum \limits _{l=1}^{j}w_{ i_2,l}\right) \bar{\Delta } \end{aligned}$$

and therefore (6.16) is satisfied with $z= \left( \left\lceil R \right\rceil - 2\left\lceil R \right\rceil ^{0.5}+\sum _{l=1+\left\lceil R \right\rceil }^{j}a_{ i_2,l} - \sum _{l=1}^{j}w_{ i_2,l}\right) .$

In order to make use of the established auxiliary result, we need to argue that the $(k-1)$st switch happens after the interval $\left\lceil R \right\rceil$. In case a) the MDR algorithm will not deactivate $i_1$ due to $a_{i_1,j}=1$ before the $\left\lceil R \right\rceil$th interval. So it does on the $\left\lceil R \right\rceil$th interval if $a_{i_1,\left\lceil R \right\rceil }=0.5$ because we have established $\bar{\theta }\ge \frac{1}{2}\bar{\Delta }$. In case b) we use the base case for the second switch. We consider the interval $\tau _1$ of the first switch of case a) and compare the two accumulated control deviations for the two cases a) and b) on $\tau _1$ and obtain $\theta _{i_1,\tau _1}(b)\ge \theta _{i_1,\tau _1}(a)$ because $i_2$ has already been activated in case b) in contrast to case a). Since $\tau _1>\left\lceil R \right\rceil$, we are done.

Now, without loss of generality, let $i_1$ be the active control after the switch on interval $\tau _{k-1}$. We know that $i_2$ is active and thus admissible on interval $\tau _{k-1}-1$:

$$\begin{aligned} - \bar{\theta }\le \theta _{i_2,\tau _{k-1}-1}, \end{aligned}$$

which implies by Lemma 2 for the control $i_1$

$$\begin{aligned} \theta _{i_1,\tau _{k-1}-1} \le \bar{\theta } = \left\lceil R \right\rceil ^{0.5} \bar{\Delta } - \epsilon , \end{aligned}$$

and by equation (6.16) we have for some $z_{i_1}\ge 1$

$$\begin{aligned} \theta _{i_1,\tau _{k-1}-1} = \left\lceil R \right\rceil ^{0.5} \bar{\Delta } - z_{i_1} \bar{\Delta } \le (\left\lceil R \right\rceil ^{0.5}-1) \bar{\Delta }. \end{aligned}$$

(6.17)

The control $i_2$ is inadmissible on interval $\tau _{k-1}$ as there are only canonical switches. If $a_{i_2,\tau _{k-1}}=1$ would be true, then $i_2$ would already have been inadmissible on interval $\tau _{k-1}-1$. Also, $a_{i_2,\tau _{k-1}}=0.5$ is not possible because we derived $\tau _{k-1} > \left\lceil R \right\rceil$. We conclude $a_{i_2,\tau _{k-1}}=0$. From this and the induction hypothesis, which states that the $(k-1)$st switch appears before the $\left( \left\lceil R \right\rceil + (k-1) n_I\right)$th interval, follows $a_{i_1,j}=1$ for the intervals j between $\tau _{k-1}$ and $\left( \left\lceil R \right\rceil + (k-1) n_I\right)$. Hence, $\theta _{i_1,\left\lceil R \right\rceil + (k-1) n_I} \le (\left\lceil R \right\rceil ^{0.5}-1) \bar{\Delta }$ holds due to (6.17). Finally, we assume $i_1$ can stay active up to and including interval $\left\lceil R \right\rceil + k n_I$ without becoming inadmissible. This and $a_{i_1,j}=0$ for $\left\lceil R \right\rceil + (k-1) n_I+1 \le j \le \left\lceil R \right\rceil + k n_I$ imply

Thus, $i_1$ is not active until the $(\left\lceil R \right\rceil + k n_I)$th interval, respectively with an analogous computation for case b) $i_1$ is not active until the $(\left\lceil R \right\rceil + (k-1) n_I)$th interval. Thereby, we showed that indeed the assertion holds for k. Altogether, the constructed control function ${\varvec{w}}^{\text {MDR}}$ uses more than $\sigma _{\text {max}}$ switches for the chosen rounding threshold $\bar{\theta }$ so that the (CIA) objective value is at least $\bar{\theta }$ and we conclude the claimed theorem is true. $\square$

We complete this section by drawing a conclusion from the Theorems 3 and 4.

Corollary 4

Consider an equidistant grid $\mathcal {G}_N$, ${\varvec{a}}\in \mathcal {A}_N$ and $1\le \sigma _{\text {max}}\le N-2$. The objective of (CIA) is bounded by

$$\begin{aligned} \theta \le \frac{N+\sigma _{\text {max}}+1}{3+2\sigma _{\text {max}}}\bar{\Delta }, \end{aligned}$$

(6.18)

which is the tightest possible bound.

Proof

The inequality (6.18) is achieved by Theorem 3 applied to the equidistant case and rearranging terms:

$$\begin{aligned} \theta \le \left( \frac{N}{3+2\sigma _{\text {max}}}+\frac{1}{2}-\frac{1}{2(3+2\sigma _{\text {max}})}\right) \bar{\Delta }=\frac{N+\sigma _{\text {max}}+1}{3+2\sigma _{\text {max}}}\bar{\Delta }. \end{aligned}$$

It is the tightest possible bound by Theorem 4 and the case $N=k(3+2\sigma _{\text {max}})+2+\sigma _{\text {max}}$, $k\in \mathbb {N}_0$:

$$\begin{aligned} \theta \ge \left\lceil \frac{k(3+2\sigma _{\text {max}})+2+\sigma _{\text {max}}}{3+2\sigma _{\text {max}}}\right\rceil ^{0.5}\bar{\Delta } = (k+1)\bar{\Delta }=\frac{N+\sigma _{\text {max}}+1}{3+2\sigma _{\text {max}}}\bar{\Delta }. \end{aligned}$$

$\square$

Upper bounds on (CIA) with $n_{\omega }>2$

Deriving bounds for the (CIA) problem with more than two controls is more difficult compared to the last chapter as the number of possibilities increases significantly. Let $\theta ^{\max }$ denote the maximum possible objective value of (CIA) for any given ${\varvec{a}}\in \mathcal {A}_N$ and $\mathcal {G}_N$ in this section. We will first use known results to derive lower and upper bounds for $\theta ^{\max }$. Then, we dedicate ourselves to the continuous relaxation of (CIA), which allows us to prove a sharper lower bound. Based on this, we state a conjecture about the actual value of $\theta ^{\max }$.

Corollary 5

Let $1\le \sigma _{\text {max}}\le N-2$ and $n_{\omega }>2$. We have that $\theta ^{\max }\ge \frac{N+\sigma _{\text {max}}+1}{3+2\sigma _{\text {max}}}\bar{\Delta }$.

Proof

This bound has been established in Theorem 4 and Corollary 4 for the case $n_{\omega }=2$. The provided example in the proof of Theorem 4 can be also applied to the case $n_{\omega }>2$ by setting the values of the relaxed controls ${\varvec{a}}_i$, for all $i\in [{n_\omega }],\ i>2,$ to zero. $\square$

Corollary 6

Let $1\le \sigma _{\text {max}}\le N-2$ and $n_{\omega }>2$. We have that $\theta ^{\max }\le \frac{2{n_\omega }-3}{2{n_\omega }-2}\left( \frac{t_f-t_0}{\sigma _{\text {max}}+1} +\bar{\Delta } \right)$.

Proof

For the (CIA) problem without TV constraints, but with minimum up time constraints the sharp bound

$$\begin{aligned} \theta \le \frac{2{n_\omega }-3}{2{n_\omega }-2}\left( C_U+\bar{\Delta } \right) \end{aligned}$$

is proven in Theorem 2 in [32], where the constant $C_U\ge 0$ represents the given minimum up time. If we require for (CIA) that an activated control remains active for a time period of at least $\frac{t_f-t_0}{\sigma _{\text {max}}+1}$, at most $\sigma _{\text {max}}$ switches take place. Thus, the TV constraint serves as a relaxation of the minimum up time constraint. $\square$

We tighten the above results by investigating the continuous version of the (CIA) problem.

Definition 17

(CCIA) Let ${\varvec{\alpha }}\in \mathcal {A}$ and $\sigma _{\text {max}}\in \mathbb {N}$ be given. Then, we define the continuou s CIA problem to be

$$\begin{aligned}&\underset{\theta ,\, {\varvec{\omega }}\in \Omega }{\min}\quad \theta \hspace{8cm} \end{aligned}$$

(7.1)

$$\begin{aligned}&\qquad {\mathrm {s.\,t.}}\qquad \theta \ge \pm \int \limits _{t_0}^t (\alpha _{i}(s)-\omega _{i}(s)) \ {\text {d}} s, \quad {\text { for all }} i\in [{n_\omega }], \, t\in \mathcal {T}, \end{aligned}$$

(7.2)

$$\begin{aligned}&\qquad \qquad \sigma _{\text {max}}\ge TV(\omega ) . \hspace{6cm} \end{aligned}$$

(7.3)

Obviously, the problem (CCIA) is a reformulation of

$$\begin{aligned} \min \limits _{\omega \in \Omega }\max \limits _{t\in \mathcal {T}}\left\| \int _{t_0}^t (\alpha (s)-\omega (s)) \ {\text {d}} s \right\| , \quad {\text {s.t. TV constraint}} (7.3). \end{aligned}$$

We stress that the given data ${\varvec{\alpha }}$ lives for (CCIA) in $\mathcal {A}$ not as usually in $\mathcal {A}_N$ and analogously we try to find a binary control function ${\varvec{\omega }}\in \Omega$, not ${\varvec{w}} \in \Omega _N$. We obtain a lower bound for the maximum objective $\theta ^{\max }$ of (CCIA) over all ${\varvec{\alpha }}\in \mathcal {A}$ by constructing a specific instance, as indicated in the following theorem.

Proposition 4

The following lower bound holds true for the maximum objective $\theta ^{\max }$ of (CCIA):

$$\begin{aligned} \theta ^{\max }\ge \left\{ \begin{array}{ll} \frac{t_f-t_0}{\sigma _{\text {max}}+2}, \qquad &{} \qquad {\text {if }} \sigma _{\text {max}}\le {n_\omega }-2, \\ \frac{t_f-t_0}{2\sigma _{\text {max}}+4-{n_\omega }}, \qquad &{} \qquad {\text {else. }} \end{array} \right. \end{aligned}$$

(7.4)

Proof

Let us first prove the bound for $\sigma _{\text {max}}\le {n_\omega }-2$. We abbreviate $\tilde{t}:= \frac{t_f-t_0}{\sigma _{\text {max}}+2}$ and construct the following instance

$$\begin{aligned} \alpha _i(t):= & {} \left\{ \begin{array}{ll} 1, \qquad &{} \qquad {\text {for }}\ t\in [t_0+(i-1)\cdot \tilde{t},\ t_0+ i\cdot \tilde{t}),\\ 0, \qquad &{} \qquad {\text {else, }} \end{array} \right. \qquad {\text {for all }} i\in [\sigma _{\text {max}}+2], \\ \alpha _i(t):= & {} 0 \qquad {\text {for all }} \ i=\sigma _{\text {max}}+3,\ldots , {n_\omega }. \end{aligned}$$

We conclude $\alpha \in \mathcal {A}$ since the convex combination constraint is satisfied on the whole time horizon $\mathcal {T}$. It results $\int _{\mathcal {T}} \alpha _i(s)\ {\text {d}}s = \tilde{t} \ {\text { for all }} \ i\in [\sigma _{\text {max}}+2]$. Thus, we would need to activate each control $\omega _i$ for some time to achieve a lower objective than $\tilde{t}$. But, because the number of switches is restricted to be at most $\sigma _{\text {max}}$, this is not possible. Hence, $\theta \ge \tilde{t}$.

Next, we consider $\sigma _{\text {max}}> {n_\omega }-2$ and we will again construct a specific instance with the claimed objective value of $\theta \ge \frac{t_f-t_0}{2\sigma _{\text {max}}+4-{n_\omega }}$. We abbreviate $\bar{t}:= \frac{t_f-t_0}{2\sigma _{\text {max}}+4-{n_\omega }}$. Similar to the above example, we first let the relaxed controls $\alpha _i$ be active one after the other for a period of $\bar{t}$. After all relaxed controls have been active once and the end of the time horizon has not yet been reached, we activate each control for a period of $2\bar{t}$ according to the ascending index $i\in [{n_\omega }]$ until we reach the end of the time horizon. We express this idea by introducing the domains of activation for all $i\in [{n_\omega }]$:

$$\begin{aligned} \mathcal {I}_i:= & {} [t_0+(i-1)\cdot \bar{t},\ t_0+ i\cdot \bar{t}) \\&\cup \left\{ [t_0+({n_\omega }+2(j-1))\bar{t},\ t_0+({n_\omega }+2j)\bar{t}) \mid j\in [\sigma _{\text {max}}+2 - {n_\omega }], \ j \equiv i \mod {n_\omega }\right\} . \end{aligned}$$

Based on these domains we define the functions $\alpha _i(t)$ via

$$\begin{aligned} \alpha _i(t) := \left\{ \begin{array}{ll} 1, \qquad &{} \qquad {\text {for }}\ t\in \mathcal {I}_i,\\ 0, \qquad &{} \qquad {\text {else, }} \end{array} \right. \qquad {\text {for all }} i\in [{n_\omega }]. \end{aligned}$$

Fig. 1

Exemplary visualization of the relaxed binary control function ${\varvec{\alpha }}$ from the proof to Proposition 4 resulting in a (CCIA) objective value of $\bar{t}$. Since $i=2$ is in this example the last activated control, the maximum number of allowed switches is $\sigma _{\text {max}}= k {n_\omega }+2-2= k {n_\omega },$ for $\ k\ge 2$

Fig.  1 gives a visualization of this specifically defined control function $\alpha$. We have

$$\begin{aligned} {n_\omega }\, \bar{t}+(\sigma _{\text {max}}+2-{n_\omega })2\bar{t}=t_f-t_0 \end{aligned}$$

so that $\cup _{i\in [{n_\omega }]} \mathcal {I}_i = \mathcal {T}$ follows and because the intervals $\mathcal {I}_i$ are all disjoint, we obtain $\alpha _i(t)=1$ for exactly one control i and for all $t\in \mathcal {T}$. Hence, $\alpha \in \mathcal {A}$. The next observation about $\alpha$ is that it consists of ${n_\omega }+(\sigma _{\text {max}}+2-{n_\omega })=\sigma _{\text {max}}+2$ activation blocks (interpreted in this continuous setting), meaning there are $\sigma _{\text {max}}+1$ changes of the active control. Now, let us assume we can approximate $\alpha$ with a binary control function $\omega \in \Omega$ resulting in an (CCIA) objective value of less than $\bar{t}$. We have

$$\begin{aligned} \int \limits _{t_0}^{t_0+i\bar{t}} \alpha _i(s) \ {\text {d}} s = \bar{t}, \qquad {\text {for all }} i\in [{n_\omega }]. \end{aligned}$$

So, each control $\omega _i$, $i \in [{n_\omega }]$ needs to be active for some time until $t_0+i\, \bar{t}$ resulting in at least ${n_\omega }-1$ switches up to and including $t_0+ {n_\omega }\, \bar{t}$. Then, we have that

$$\begin{aligned} \int \limits _{t_0}^{t_0+{n_\omega }\bar{t}} \alpha _i(s)-\omega _i(s) \ {\text {d}} s < \bar{t}, \qquad {\text {for all }} i\in [{n_\omega }]. \end{aligned}$$

This, and using that the next activation blocks of $\alpha$ last for a period of $2\,\bar{t}$, imply each control $\omega _i$ needs to be activated again up to and including $t_0+({n_\omega }+2i)\bar{t}$. If it were possible for some $i\in [{n_\omega }]$ to skip the activation of $\omega _i$ without violating the control deviation bound $\bar{t}$, this would result in

$$\begin{aligned} \left| \int \limits _{t_0}^{t_0+({n_\omega }+2i)\bar{t}} \alpha _i(s)-\omega _i(s) \ {\text {d}} s \right| < \bar{t} \end{aligned}$$

and at the same time, it would hold

$$\begin{aligned} \int \limits _{t_0+({n_\omega }+2(i-1))\bar{t}}^{t_0+({n_\omega }+2i)\bar{t}} \omega _i(s) \ {\text {d}} s =0, \end{aligned}$$

which implies

$$\begin{aligned} \left| \int \limits _{t_0}^{t_0+({n_\omega }+2(i-1))\bar{t}} \alpha _i(s)-\omega _i(s) \ {\text {d}} s \right| > \bar{t} \end{aligned}$$

because of $\int _{t_0+({n_\omega }+2(i-1))\bar{t}}^{t_0+({n_\omega }+2i)\bar{t}} \alpha _i(s) \ {\text {d}} s =2\,\bar{t}$. We apply this argument for all activation blocks of $\alpha$ until $t_f$ and conclude that $\omega$ must use at least one switch for each activation block of $\alpha$ after $t_0+ {n_\omega }\bar{t}$, i.e., it must use at least $(\sigma _{\text {max}}+2-{n_\omega })$ switches. Overall, there are at least ${n_\omega }-1+ (\sigma _{\text {max}}+2-{n_\omega })=\sigma _{\text {max}}+1$ switches. Therefore, any $\omega \in \Omega$ that uses at most $\sigma _{\text {max}}$ switches involves an (CCIA) objective value of at least $\bar{t}$, which settles the lower bound for the case $\sigma _{\text {max}}> {n_\omega }-2$. $\square$

(CIA) can be interpreted as a discretized version of (CCIA). Thereby, we can deduce the following corollary.

Corollary 7

Let $1\le \sigma _{\text {max}}\le N-2$ and $n_{\omega }>2$. We obtain for the maximum optimal objective value $\theta ^{\max }$ of (CIA):

$$\begin{aligned} \theta ^{\max }\ge \left\{ \begin{array}{ll} \frac{t_f-t_0}{\sigma _{\text {max}}+2}, \qquad &{} \qquad {\text {if }} \sigma _{\text {max}}\le {n_\omega }-2,\\ \frac{t_f-t_0}{2\sigma _{\text {max}}+4-{n_\omega }}, \qquad &{} \qquad {\text {else. }} \end{array} \right. \end{aligned}$$

(7.5)

Proof

(CCIA) is a relaxation of (CIA) since every feasible solution of (CIA) corresponds to a feasible solution of (CCIA). Thus, the claim follows from Proposition 4. $\square$

The lower bound in Corollary 7 is generally sharp in the sense that there are combinations of ${n_\omega }$, $\sigma _{\text {max}}$ and $\mathcal {G}_N$ so that $\theta ^{\max }$ equals the claimed lower bound. The following example illustrates this relationship.

Example 4

Let the grid be equidistant with $N=3$ and ${n_\omega }=3$. Consider the following two instances:

$$\begin{aligned} (a_{i,j}^1)_{i\in [3], j\in [3]}:=\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array} \right) , \qquad (a_{i,j}^2)_{i\in [3], j\in [3]}:=\left( \begin{array}{ccc} 1 &{} 0.5 &{} 0 \\ 0 &{} 0.25 &{} 0.5 \\ 0 &{} 0.25 &{} 0.5 \\ \end{array} \right) . \end{aligned}$$

Consider $\sigma _{\text {max}}=1$ in the first example. Then, $\theta =\bar{\Delta }$ and $\theta ^{\max }\ge \bar{\Delta }$ follows from the above corollary. Any asymmetric modification of $(a_{i,j}^1)$ with unequal control accumulation $\sum _{j=1}^3 a_{i_1,j}^1 \ne \sum _{j=1}^3 a_{i_2,j}^1$ would result in a binary control function ${\varvec{w^{\text {OPT}}}}$ that activates the controls with highest control accumulation and hence $\theta < \bar{\Delta }$. We conclude that the claimed bound is sharp, i.e., $\theta ^{\max }= \bar{\Delta }$.

Let us assume $\sigma _{\text {max}}=2$ for the second instance. Then, $w^{\text {OPT}}_{i,j}=1$ for $(i,j)=(1,1),(1,2),2,3)$ and thus $\theta =0.75\bar{\Delta }$. Therefore, the bound in Corollary 7, which amounts to $\theta ^{\max }\ge \frac{3}{5}\bar{\Delta }$, is not tight for this instance.

Finding the exact value of $\theta ^{\max }$ is difficult due to the nonconvex objective $\max _{{\varvec{a}}}\min _{{\varvec{w}}}\max _{i\in [{n_\omega }],j\in [N]}$ and the tremendously increased number of different ${\varvec{\omega }}\in \Omega$ when ${n_\omega }> 2$, but we conjecture that the lower bound in Proposition 4 cannot be improved. We recognize the symmetry of the constructed $\alpha$ in the proof: Any modification of $\alpha$ that alters the length of its activation blocks would result either in less than $\sigma _{\text {max}}+2$ activation blocks or in at least one block with a smaller length compared with the previous length. The latter block length would be smaller than $\frac{t_f-t_0}{2\sigma _{\text {max}}+4-{n_\omega }}$ if the block is the first control’s activation, respectively smaller than $2\cdot \frac{t_f-t_0}{2\sigma _{\text {max}}+4-{n_\omega }}$ else. With the argumentation from the proof of Proposition 4, this would allow us to choose a control function $\omega \in \Omega$ with a (CCIA) objective value smaller than $\frac{t_f-t_0}{2\sigma _{\text {max}}+4-{n_\omega }}$. Furthermore, we argue that the optimal objective value of (CCIA) is at most by $\frac{1}{2} \bar{\Delta }$ smaller than the one of (CIA) because the switching times of the optimal $\omega \in \Omega$ differ at most by one half of the maximum grid length from the optimal ${\varvec{w}}\in \Omega _N$. We close this section by summarizing these thoughts in the following conjecture.

Conjecture 1

Let $1\le \sigma _{\text {max}}\le N-2$ and $n_{\omega }>2$. We obtain for (CIA)

$$\begin{aligned} \theta ^{\max }= \left\{ \begin{array}{ll} \frac{t_f-t_0}{\sigma _{\text {max}}+2}+ \frac{1}{2} \bar{\Delta }, \qquad &{} \qquad {\text {if }} \sigma _{\text {max}}\le {n_\omega }-2, \vspace{0.2cm} \\ \frac{t_f-t_0}{2\sigma _{\text {max}}+4-{n_\omega }}+ \frac{1}{2} \bar{\Delta }, \qquad &{} \qquad {\text {else.}} \end{array} \right. \end{aligned}$$

(7.6)

Numerical experiments

We test the proposed algorithm with a benchmark example from the https://mintOC.de library [25], with a real-world adsorption cooling machine problem [7] and with generic data. We use the CIA decomposition in order to solve these problems, where we applied CasADi v3.4.5 [1] to parse the nonlinear program (NLP) with efficient derivative calculation to the solver Ipopt 3.12.3 [30]. We implemented the AMDR algorithm into an add-on as part of the open-source software package pycombina² [7] and used its BNB solver for benchmarking reasons. The BNB scheme is based on the idea to branch forward in time and exploits that an evaluation of the objective function up to the current grid point yields a valid lower bound that is extremely cheap to compute, see [15, 27] for further details. We set the tolerance parameter of the ADMR algorithm to $TOL=0.0001$. All computational experiments are executed on a workstation with 4 Intel i5-4210U CPUs (1.7 GHz) and 7.7 GB RAM.

Multimode MIOCP

We consider the following MIOCP, which is a modified version of the Egerstedt standard problem from https://mintOC.de:

$$\begin{aligned} \begin{aligned} \min \limits _{{\varvec{x}},\, \omega \in \Omega }\ &x_1(t_f)^2+x_2(t_f)^2 \\ {\text {s.t.}}\ &\ \ {\text {for a.e.}}\ t \in [0,1]: \\&\begin{aligned} \dot{x}_1(t)&= -x_1(t)\omega _1(t)+(x_1(t)+x_2(t))\omega _2(t)+(x_1(t)-x_2(t))\omega _3(t), \quad&\\ \dot{x}_2(t)&= (x_1(t)+2x_2(t))\omega _1(t)+(x_1(t)-2x_2(t))\omega _2(t)+(x_1(t)+x_2(t))\omega _3(t), \quad& \\ {\varvec{x}}(0)&= {\varvec{x_0}}.&\end{aligned} \end{aligned} \end{aligned}$$

(P1)

Obviously, we deal with 3 different modes, i.e., ${n_\omega }=3$. We use as initial values ${\varvec{x_0}}:= (0.5,0.5)^T$. Furthermore, we add the TV constraints (3.1)–(3.2) to (P1), with varying maximum number of switches $\sigma _{\text {max}}$. Fig. 2 illustrates the differential state and control trajectories for $\sigma _{\text {max}}=20$ and with relaxed binary controls as well as binary controls based on SUR, BNB and AMDR. We remark that the control function constructed by SUR uses 70 switches and is therefore infeasible with respect to $\sigma _{\text {max}}=20$. The relaxed control values are greater than zero and less than one around $t\approx 0.45$ and for $t\ge 0.8$ so that the corresponding approximated state trajectories of BNB and AMDR are slightly different from the relaxed one from $t\approx 0.45$ on. We set the BNB iteration limit to $5\cdot 10^6$ so that it stopped after 15.3s with (CIA) objective value $\theta =9.1\cdot 10^{-3}$ and $\Phi =0.991855$ as (P1) objective value. The execution of AMDR took 0.2s and resulted in the improved objective values $\theta =4.6\cdot 10^{-3}$, respectively $\Phi =0.991509$, which can be explained by more uniformly distributed switches compared with the BNB solution.

Fig. 2

Differential state and control trajectories for the test problem (P1). The problem has been discretized with Multiple Shooting and $N=400$ intervals. The state trajectories based on SUR are very similar to the relaxed one (i.e., based on $\alpha$), so that we skip their presentation

Table 1 shows that the BNB algorithm constructs for small instances, e.g. $N=200$, better (CIA) objective values than AMDR if enough time is available. If the BNB scheme finds a good solution, it will usually do so after a few million iterations. While the $\theta$ values of AMDR are close to the ones from BNB for $N=200$, they are clearly outperforming the latter for bigger instances. Its run time is only slightly increasing with a grid’s refinement, from about 0.1 seconds to at most 0.6 seconds. A C++ implementation could still improve the run time as we used so far a prototype implementation in python. It appears that selecting the next-forced control rather than the one with a maximum $\gamma$ value is beneficial as part of the AMDR algorithm and tends to yield the solution with the smallest (CIA) objective value.

Table 1 Comparison of (CIA) objective values and run time of (P1) for different solving methods and varying $\sigma _{\text {max}}$.

Dualmode adsorption cooling machine problem

In [6, 7], a complex renewable energy system in the form of a solar thermal climate system with nonlinear system behavior is introduced as an MIOCP. The system’s core is an adsorption cooling machine, which can be switched on to intensify the cooling down of ambient temperature. The goal is to control the room temperature in a comfort zone and at the same time to minimize the energy costs. We skip a detailed system’s description but refer to [7], and consider the relaxed binary control values as given, as illustrated in Fig. 3 in the left plot. We assume two modes of the adsorption cooling machine, i.e., $n_{\omega }=2$, and a whole day time horizon with control adjustment every four minutes, i.e., $N=360$.

We use the AMDR scheme to calculate a candidate solution of the (CIA) problem depending on $\sigma _{\text {max}}$, which is optimal by virtue of Theorem 2.2. (a). The right plot in Fig. 3 compares these optimal solutions with the (CIA) objective values of BNB solutions with increasing iteration limit. For a small and large number of allowed switches, the deviation of the BNB solutions is small. One explanation for this is the limited degree of freedom for a small $\sigma _{\text {max}}$, so that the width of the BNB tree is very limited. With a large $\sigma _{\text {max}}$, on the other hand, solutions with a small $\theta$ value can be found quickly, with which many nodes can be pruned. The deviation from the optimal solution is particularly striking for medium-sized $\sigma _{\text {max}}$. For some instances, especially for $10\le \sigma _{\text {max}}\le 20$, an increase of the iteration limit hardly leads to an improvement because the BNB algorithm seems to remain in a suboptimal branch. We also compare the optimal solution of (CIA) with the upper bound from Corollary 4 and see that the latter appears between 200 and 600 percent larger.

Fig. 3

Left: Relaxed binary control values $\alpha$ for the adsorption cooling machine problem for the whole time horizon of a day and exemplary approximated binary values $\omega$ obtained by AMDR and with $\sigma _{\text {max}}= 8$. Right: Comparison of the (CIA) objective values based on the upper bound $\theta ^{\max }$ from Corollary 4 and BNB solutions with the optimal solutions constructed by AMDR and varying $\sigma _{\text {max}}$ values. We report the deviation in percent. The number next to BNB indicates the maximum number of iterations, e.g. 2 million

Comparison of optima for (CIA) with upper bounds based on generic data

The two investigated MIOCPs showed a relatively large deviation of the optimal (CIA) objective value compared with the derived upper bounds. Therefore, we generated uniformly distributed random values ${\varvec{a}}\in \mathcal {A}_N$ for $N=40$ equidistant intervals, $n_{\omega }=2,3$ controls, and examined how the ratio of these two values results here. We illustrate this comparison in Fig. 4, where we use the upper bound from Corollary 4 for $n_{\omega }=2$ and the one from Conjecture 1 for ${n_\omega }=3$. The objective values $\theta , \theta ^*$ and bounds $\theta ^{\max }$ decrease logarithmically with the increase of $\sigma _{\text {max}}$, as expected. In contrast to the above MIOCPs, the (CIA) objective values come close to the upper bounds, particularly for small $\sigma _{\text {max}}$, but a relevant gap remains for larger $\sigma _{\text {max}}$. This gap may be further reduced utilizing a larger sample size; we considered here only 1000 (CIA) instances per $\sigma _{\text {max}}$ value. We also note that the values generated by the AMDR algorithm are very close to the optimal ones.

Fig. 4

Optimal objective values $\theta _k^*$ of (CIA) for randomly generated values ${\varvec{a}}\in \mathcal {A}_N$ with $k\in [1000]$ samples, $N=40$ and varying $\sigma _{\text {max}}$ values compared with derived upper bounds $\theta ^{\max }$. We display the maximal, median and minimal objective values of the samples for each given $\sigma _{\text {max}}$. Left: The optima are computed with the AMDR algorithm for the case $n_{\omega }=2$. Right: Comparison of the values constructed by the AMDR algorithm with the optimal values obtained by BNB

Discussion

As expected by the polynomial run time complexity, our prototype implementation of AMDR constructs (CIA) feasible solutions very quickly. Their $\theta$ values are mostly outperforming the ones obtained by the BNB algorithm or are at least close to the latter for a problem with more than two binary controls. Consequently, the AMDR solution is itself a promising (CIA) feasible solution or is a fast option to initialize the BNB with a competitive upper bound. As stated in Remark 6, the AMDR algorithm may also be used to include combinatorial constraints other than the TV constraints.

For comparison with the BNB method, we restrict that we only used the depth-first node selection strategy and could have tuned it a bit more to achieve more competitive feasible solutions of (CIA). Besides, the BNB algorithm can include a variety of combinatorial conditions of the (CIA) problem, so it is generally advantageous.

We also note that our calculations mainly examine the (CIA) objective value because it correlates with the (MIOCP) objective value. With very similar or large (CIA) objective values, however, the smaller value may lead to a worse (MIOCP) objective value—and vice versa. There may be several binary control functions with the same (CIA) objective value but different (MIOCP) objective values. In some instances, we observed that the AMDR algorithm generates a control function with suboptimal (MIOCP) objective value since its switches are structurally delayed compared to the switches on bang-bang-arcs of the relaxed binary values. In this case, we tested, as a heuristic, shifting the AMDR binary values backward in time by $\lfloor \theta / \bar{\Delta } \rfloor$ intervals so that the control function is more similar to the relaxed binary values, which worked well.

Conclusions

In this paper, we have devised a fast rounding method for the MIOCP with constrained TV of the integer control. The proposed algorithm constructs under certain assumptions, e.g., $n_{\omega }=2$, an optimal solution of the (CIA) subproblem. Based on this, we have proven bounds on the integrality gap of (CIA) for the constrained TV case. Our numerical results have shown that the computed control function’s quality outperforms in many cases the BNB solution, for which an iteration limit has been set up. Due to the very short run time, we recommend the proposed method, especially for the mixed-integer model predictive control setting or for instances with a vast number of binary variables. In the future, this algorithmic proposal could be compared with a penalty alternating direction method [12] or extended to switching costs as in [3].