Abstract
Nonsmooth nonconvex optimization problems involving the \(\ell ^p\) quasi-norm, \(p \in (0, 1]\), of a linear map are considered. A monotonically convergent scheme for a regularized version of the original problem is developed and necessary optimality conditions for the original problem in the form of a complementary system amenable for computation are given. Then an algorithm for solving the above mentioned necessary optimality conditions is proposed. It is based on a combination of the monotone scheme and a primal-dual active set strategy. The performance of the two algorithms is studied by means of a series of numerical tests in different cases, including optimal control problems, fracture mechanics and microscopy image reconstruction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the following nonconvex nonsmooth optimization problem
where \(A \in {\mathbb {M}}^{m\times d}\), \({\varLambda } \in {\mathbb {M}}^{r\times d},\)\(b \in {{\mathbb {R}}}^m, p \in (0,1]\) and \(\beta \in {{\mathbb {R}}}^+\). Here
which is a norm for \(p=1\) and a quasi-norm for \(0<p<1\).
Optimization of problems as (1.1) arises frequently in many applications as an efficient way to extract the essential features of generalized solutions. In particular, many problems in sparse learning and compressed sensing can be written as (1.1) with \({\varLambda }=I\), I being the identity (see e.g. [11, 41] and the references therein). In image analysis, \(\ell ^p\)-regularizers as in (1.1) have recently been proposed as nonconvex extensions of the total generalized variation (TGV) regularizer used to reconstruct piecewise smooth functions (e.g. in [24, 42]). Also, the use of \(\ell ^p\)-functionals with \(p\in (0,1)\) is of particular importance in fracture mechanics (see [43]). Recently, sparsity techniques have been investigated also by the optimal control community, see e.g. [9, 22, 27, 32, 48]. The literature on sparsity optimization problems as (1.1) is rapidly increasing, here we mention also [1, 6, 18, 44].
The nonsmoothness and nonconvexity make the study of problems as (1.1) both an analytical and a numerical challenge. Many numerical techniques have been developed when \({\varLambda }=I\) (e.g. in [20, 27, 29, 30]) and attention has recently been given to the case of more general operators, here we mention e.g. [24, 36, 42] and we refer to the end of the introduction for further details. However, the presence of the matrix inside the \(\ell ^p\)-term combined with the nonconvexity and nonsmoothness remains one main issue in the development of numerical schemes for (1.1).
In the present work, we first propose a monotone algorithm to solve a regularized version of (1.1). The scheme is based on an iterative procedure solving a modified problem where the singularity at the origin is regularized. The convergence of this algorithm and the monotone decay of the cost during the iterations are proved. Then its performance is successfully tested in four different situations, a time-dependent control problem, a fracture mechanics example for cohesive fracture models, an M-matrix example, and an elliptic control problem.
We also focus on the investigation of suitable necessary optimality conditions for solving the original problem. Relying on an augmented Lagrangian formulation, optimality conditions of complementary type are derived. For this purpose we consider the case where \({\varLambda }\) is a regular matrix, since in the general case the optimality conditions of complementary type are not readily obtainable. An active set primal-dual strategy which exploits the particular form of these optimality conditions is developed. A new particular feature of our method is that at each iteration level the monotone scheme is used in order to solve the nonlinear equation satisfied by the non zero components. The convergence of the active set primal-dual strategy is proved in the case \({\varLambda }=I\) under a diagonal dominance condition. Finally the algorithm was tested on the same time-dependent control problem as the one analysed for the monotone scheme as well as for a microscopy image reconstruction example. In all the above mentioned examples the matrix inside the \(\ell ^p\)-term appears as a discretized gradient with very different purposes, e.g. as a regularization term in imaging and with modelling purposes in fracture mechanics.
Similar type of algorithms were proposed in [27] and [20] for problems as (1.1) in case of no matrix inside the \(\ell ^p\)-term and in the infinite dimensional sequence spaces \(\ell ^p\), with \(p \in [0,1]\). In particular in [27] a primal-dual active set strategy has been studied for the case \(p=0\), its convergence was proved under a diagonal dominance condition and its performance was tested in three different situations. In the case \(p \in (0,1]\) a monotone convergent scheme was proposed but no numerical tests were made. Then inspired by [27], the two authors of the present paper developed in [20] a primal-dual active set strategy for \(p\in (0,1]\) and tested its performance in diverse test cases. Note that in [20] the convergence of the primal-dual strategy was not investigated. The monotone and primal-dual active set monotone algorithm studied in the present paper are inspired by the schemes proposed respectively in [27] and [20], but with the main novelties that now we treat the case of a regular matrix in the \(\ell ^p\)-term and we provide diverse numerical tests for both the schemes. Moreover, we prove the convergence of the primal-dual active set strategy. Note that the monotone scheme has not been tested in the earlier papers.
Let us recall some further literature concerning \(\ell ^p\), \(p \in (0,1]\) sparse regularizers. Iteratively reweighted least-squares algorithms with suitable smoothing of the singularity at the origin were analysed in [13, 34, 35]. In [37] a unified convergence analysis was given and new variants were also proposed. An iteratively reweighted \(\ell _1\) algorithm ([8]) was developed in [14] for a class of nonconvex \(\ell ^2\)-\(\ell ^p\) problems, with \(p \in (0,1)\). A generalized gradient projection method for a general class of nonsmooth nonconvex functionals and a generalized iterated shrinkage algorithm are analysed respectively in [6] and in [52]. Also, in [44] a surrogate functional approach combined with a gradient technique is proposed. However, all the previous works do not investigate the case of a linear operator inside the \(\ell ^p\)-term.
Then in [42] an iteratively reweighted convex majorization algorithm is proposed for a class of nonconvex problems including the \(\ell ^p\), \(p \in (0,1]\) regularizer acting on a linear map. However, an additional assumption of Lipschitz continuity of the objective functional is required to establish convergence of the whole sequence generated by the algorithm. Nonconvex \(TV^p\)-models with \(p \in (0,1)\) for image restoration are studied in [24] by a Newton-type solution algorithm for a regularized version of the original problem.
We mention also [30], where a primal-dual active set method is studied for problems as in (1.1) with \({\varLambda }=I\) for a large class of penalties including also the \(\ell ^p\), with \(p \in [0,1)\). A continuation strategy with the respect to the regularization parameter \(\beta \) is proposed and the convergence of the primal-dual active set strategy coupled with the continuation strategy is proved. However, in [30], differently from the present work, the nonlinear problem arising at each iteration level of the active set scheme is not investigated. Moreover, in [30] the matrix A has normalized column vectors, whereas in the present work A is a general matrix.
Finally, in [36] an alternating direction method of multipliers (ADMM) is studied in the case of a regular matrix inside the \(\ell ^p\)-term, optimality conditions were derived and convergence was proved. We underline that in [36] the linear map inside the \(\ell ^p\)-term has to be surjective, which can be restrictive per applications. Although the ADMM in [36] is also deduced from an augmented Lagrangian formulation, we remark that the optimality conditions of [36] are of a different nature than ours and hence the two approaches cannot readily be compared. We refer to Remark 4 for a more detailed explanation.
Concerning the general importance of \(\ell ^p\)-functionals with \(p \in (0,1)\), numerical experience has shown that their use can promote sparsity better than the \(\ell ^1\)-norm (see [10, 19, 49]), e.g. allowing possibly a smaller number of measurements in feature selection and compressed sensing (see also [11, 12, 40]). Moreover, many works demonstrated empirically that nonconvex regularization terms in total variation-based image restoration provide better edge preservation than the \(\ell ^1\)-regularization (see [5, 39, 40, 45]). Also, the use of nonconvex optimization can be considered from natural image statistics [26] and it appears to be more robust with respect to heavy-tailed distributed noise (see e.g. [51]).
The paper is organized as follows. In Sect. 2 we present our proposed monotone algorithm and we prove its convergence. In Sect. 3 we report our numerical results for the four test cases mentioned above. In Sect. 4 we derive the necessary optimality conditions for (1.1), we describe our primal-dual active set strategy and prove convergence in the case \({\varLambda }=I\). Finally in Sect. 5 we report the numerical results obtained by testing the active set monotone algorithm in the two situations mentioned above.
2 Existence and monotone algorithm for a regularized problem
For convenience of exposition, we recall the problem under consideration
where \(A \in {\mathbb {M}}^{m\times d}\), \({\varLambda } \in {\mathbb {M}}^{r\times d},\)\(b \in {{\mathbb {R}}}^m, p \in (0,1]\) and \(\beta \in {{\mathbb {R}}}^+\).
Throughout this section we assume
The first result is an existence result for (2.1).
Theorem 1
For any \(\beta >0\), there exists a solution to 2.1.
Proof
Since J is bounded from below, existence will follow from the continuity and coercivity of J. Thus we prove that J is coercive, that is, \(|J(x_k)|_2 \rightarrow + \infty \) whenever \(|x_k|_2\rightarrow + \infty \) for some sequence \(\{x_k\} \subset {{\mathbb {R}}}^d\). By contradiction, suppose that \(|x_k|_2\rightarrow + \infty \) and \(J(x_k)\) is bounded. For each k, let \(x_k=t_kz_k\) be such that \(t_k\ge 0, x_k \in {{\mathbb {R}}}^d\) and \(|z_k|_2=1. \) Since \(t_k \rightarrow + \infty \), \(p<2\), we have for k sufficiently large
and hence
By compactness, the sequence \(\{z_k\}\) has an accumulation point \({{\bar{z}}}\) such that \(|{{\bar{z}}}|=1\) and \({{\bar{z}}} \in \text{ Ker }(A)\cap \text{ Ker }({\varLambda })\), which contradicts 2.2. \(\square \)
Following [27], in order to overcome the singularity of \((|s|^p)'=\frac{ps}{|s|^{2-p}}\) near \(s=0\), we consider for \(\varepsilon >0\) the following regularized version of (2.1)
where for \(t \ge 0\)
and \({\varPsi }_\varepsilon (|{\varLambda } x|^2)\) is short for \(\sum _{i=1}^{r} {\varPsi }_\varepsilon (|({\varLambda } x)_i|^2)\).
Remark 1
Notice that by the coercivity of the functional J in (2.1), the coercivity of \(J_\varepsilon \) and hence existence for (2.3) follow as well.
The necessary optimality condition for (2.3) is given by
where the max-operation is interpreted coordinate-wise. We set \(y={\varLambda } x\). Then
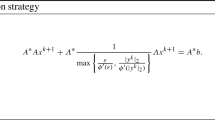
In order to solve (2.5), the following iterative procedure is considered:
where we denote \(y^{k}={\varLambda } x^{k},\) and the second addend is short for the vectors with \(l^{\text{ th }}\)-component \(\sum _{i=1}^d({\varLambda }^*)_{li}\frac{\beta p}{\max (\varepsilon ^{2-p},|y_i^{k}|^{2-p})}y_i^{k+1}\).
We have the following convergence result.
Theorem 2
For \(\varepsilon >0\), let \(\{x_k\}\) be generated by (2.6). Then, \(J_{\varepsilon }(x_k)\) is strictly monotonically decreasing, unless there exists some k such that \(x^k = x^{k+1}\) and \(x^k\) satisfies the necessary optimality condition (2.5). Moreover every cluster point of \(x^k\), of which there exists at least one, is a solution of (2.5).
Proof
The proof follows similar arguments to that of Theorem 4.1, [27]. Multiplying (2.6) by \(x^{k+1}-x^k\), we get
Note that
and
Since \(t \rightarrow {\varPsi }_\varepsilon (t)\) is concave, we have
Then, using (2.7), (2.8), (2.9), we get
From (2.10) and the coercivity of \(J_\varepsilon \) it follows that \(\{x^k\}_{k=1}^\infty \) and thus \(\{y^{k}\}_{k=1}^\infty \) are bounded. Then, from (2.10), there exists a constant \(\kappa >0\) such that
from which we conclude the first part of the theorem. From (2.11), we conclude that
Since \(\{x^k\}_{k=1}^\infty \) is bounded, there exists a subsequence and \({{\bar{x}}} \in {{\mathbb {R}}}^d\) such that \(x^{k_l}\rightarrow {{\bar{x}}}\). By (2.12) and (2.2) we have that \(x^{k_l+1} \rightarrow {{\bar{x}}}\). Then, passing to the limit with respect to k in (2.6), we get that \({\bar{x}}\) is a solution to (2.5). \(\square \)
In the following proposition we establish the convergence of (2.3)–(2.1) as \(\varepsilon \) goes to zero.
Proposition 1
Let \(\{x_\varepsilon \}_{\varepsilon >0}\) be solution to (2.3). Then any cluster point of \(\{x_\varepsilon \}_{\varepsilon >0}\) as \(\varepsilon \rightarrow 0^{+}\), of which there exists at least one, is a solution of (2.1).
Proof
First note that \(J_\varepsilon (x_\varepsilon )\le J_\varepsilon (0)=\frac{1}{2}|b|_2^2+\left( 1-\frac{p}{2}\right) \varepsilon ^p\), and hence \(J_\varepsilon (x_\varepsilon )\) is uniformly bounded for \(\varepsilon \in (0,1]\). Let us argue that \(\{x_\varepsilon \}\) is uniformly bounded for \(\varepsilon \rightarrow 0^+\). Assume to the contrary that this is not the case and that \(\lim _{k \rightarrow \infty } |x_{\varepsilon _k}|_2\rightarrow \infty \), where \(\varepsilon _k \rightarrow 0\) as \(k \rightarrow \infty \). We show that this leads to a contradiction to (2.2). Proceeding similarly as in the proof of Theorem 1 we define \(\{t_k\}\) and \(\{z_k\}\) such that \(x_{\varepsilon _k}=t_kz_k\) with \(t_k \ge 0\), and \(|z_k|=1\) and \(z=\lim _k z_k\). Note that \(\lim _k t_k=\infty \). In the following computation k is sufficiently large, so that \(t_k \ge 1\). Then
where in the last inequality we used that \({\varPsi }_\varepsilon (t)\ge t^{\frac{p}{2}}\).
Since the left-hand side of (2.13) converges to 0 for \(k \rightarrow \infty \) we have
Hence \(z \in \text{ ker }(A) \cap \text{ ker }({\varLambda })=\{0\}\), which contradicts that \(|z|_2=1\).
Then by the uniform boundedness of \(\{x_\varepsilon \}_{\varepsilon }\) there exists a subsequence and \({\bar{x}} \in {{\mathbb {R}}}^d\) such that \(x_{\varepsilon _l} \rightarrow {\bar{x}}\). Since \(\{x_\varepsilon \}_{\varepsilon }\) solves (2.3), by letting \(\varepsilon \rightarrow 0\) and using the definition of \({\varPsi }_\varepsilon \), we easily get that \({\bar{x}}\) is a solution of (2.1). \(\square \)
3 Monotone algorithm: numerical results
The focus of this section is to investigate the performance of the monotone algorithm in practice. For this purpose we choose four problems with matrices A of very different structure: a time-dependent optimal control problem, a fracture mechanics example, the M matrix and a stationary optimal control problem.
3.1 The numerical scheme
For further references it is convenient to recall the algorithm in the following form (see Algorithm 1). Note that a continuation strategy with respect to the parameter \(\varepsilon \) is performed. The initialization and range of \(\varepsilon \)-values is described for each class of problems below.
The system in (3.2) is solved though the MATLAB function mldivive (that is, the backslash command). The algorithm stops when the \(\ell ^\infty \)-norm of the residue of (2.5) is \(O(10^{-3})\) in all the examples, except the fracture problem, where it is \(O(10^{-15})\). At this instance, the \(\ell ^2\)-residue is typically much smaller. Thus, we find an approximate solution of the \(\varepsilon \)-regularized optimality condition (2.5). The initialization \(x^0\) is chosen in the following way
that is, \(x^0\) is chosen as the solution of the problem (2.1) where the \(\ell ^p\)-term is replaced by the \(\ell ^2\)-norm. Our numerical experience shows that for some values of \(\beta \) the previous initialization is not suitable, that is, the residue obtained is too big. In order to get a lower residue, we successfully tested a continuation strategy with respect to increasing \(\beta \)-values.

In the presentation of our numerical results, the total number of iterations shown in the tables takes into account the continuation strategy with respect to \(\varepsilon \). However, it does not take into account the continuation with respect to \(\beta \). We remark that in all the experiments presented in the following sections, the value of the functional for each iterations was checked to be monotonically decreasing accordingly to Theorem 2.
The following notation will hold for the rest of the paper. For \(x \in {{\mathbb {R}}}^d\) we will denote \(|x|_0=\#\{i\, :\, |x_i|> 10^{-10}\},\)\(|x|_0^c=\#\{i\, :\, |x_i|\le 10^{-10}\},\) and by \(|x|_2\) the euclidean norm of x.
3.2 Time-dependent control problem
We consider the linear control system
that is,
where the linear closed operator \({\mathcal {A}}\) generates a \(C_0\)-semigroup \(e^{{\mathcal {A}}t}\), \(t\ge 0\) on the state space X. More specifically, we consider the one-dimensional controlled heat equation for \(y=y(t,x)\):
with homogeneous boundary conditions \(y(t,0)=y(t,1)=0\) and thus \(X=L^2(0,1)\). The differential operator \({\mathcal {A}}y=y_{xx}\) is discretized in space by the second order finite difference approximation with \(n=49\) interior spatial nodes (\({\varDelta } x=\frac{1}{50}\)). We use two time dependent controls \(\overrightarrow{u}=(u_1,u_2)\) with corresponding spatial control distributions \(b_i\) chosen as step functions:
The control problem consists in finding the control function \(\overrightarrow{u}\) that steers the state \(y(0)=0\) to a neighbourhood of the desired state \(y_d\) at the terminal time \(T=1\). We discretize the problem in time by the mid-point rule, i.e.
where \(\overrightarrow{u}=(u_1^1,\ldots , u_1^m,u_2^1,\ldots u_2^m)\) is a discretized control vector whose coordinates represent the values at the mid-point of the intervals \((t_k,t_{k+1})\). Note that in (3.5) we denote by B a suitable rearrangement of the matrix B in (3.3) with some abuse of notation. A uniform step-size \({\varDelta } t=\frac{1}{50}\) (\(m=50\)) is utilized. The solution of the control problem is based on the sparsity formulation (2.1), where \({\varLambda }\) is the backward difference operator acting independently on each component of the control, that is, \({\varLambda }=m(I_2\otimes D)\) where \(I_2\) is the \(2\times 2\) identity matrix and \(D\, :\, {{\mathbb {R}}}^m \rightarrow {{\mathbb {R}}}^m\) is as follows
Also, b in (2.1) is the discretized target function chosen as the Gaussian distribution \(y_d(x)=0.4\,\text{ exp }(-70(x-.7)^2))\) centered at \(x=.7\). That is, we apply our algorithm for the discretized optimal control problem in time and space where x from (2.1) is the discretized control vector \(u \in {{\mathbb {R}}}^{2m}\) which is mapped by A to the discretized output y at time 1 by means of (3.5). Moreover b from (2.1) is the discretized state \(y_d\) with respect to the spatial grid \({\varDelta } x\). The parameter \(\varepsilon \) was initialized with \(10^{-3}\) and decreased down to \(10^{-8}\). Note that, since the second control distribution is well within the support of the desired state \(y_d\), we expect the authority of this control to be stronger than that of the first one, which is away from the target.
In Table 1 we report the results of our tests for \(p=.5\) for \(\beta \) incrementally increasing by factor of 10 from \(10^{-3}\) to 1. We report only the values for the second control \(u_2\) since the first control \(u_1\) is always zero. In the third row we see that \((|Du_2|_0)^c\) increases with \(\beta \), consistent with our expectation. Note also that the quantity \(|Du_2|_p^p\) decreases for \(\beta \) increasing.
For any \(i=1,\ldots , m\), we say that i is a singular component of the vector \(D u_2\) if \(i \in \{i \, :\, |(Du_2)_i|<\varepsilon \}\). In particular, note that the singular components are the ones where the \(\varepsilon \)-regularization is most influential. In the sixth row of Table 1 we show their number at the end of the \(\varepsilon \)-path following scheme (denoted by Sp) and we observe that it coincides with the quantity \(|Du_2|_0^c\), which is reassuring the validity of our \(\varepsilon \)-strategy.
The algorithm was also tested for values of p near to 1, e.g. for \(p=.9\). The results obtained show a less piecewise constant behaviour of the solution with respect to the ones for \(p=.5\). Finally, we remark that if we change the initialization (3.1), the method converges to the same solution with no remarkable modifications in the number of iterations.
3.3 Quasi-static evolution of cohesive fracture models
In this section we focus on a modelling problem for quasi-static evolutions of cohesive fractures. This kind of problems requires the minimization of an energy functional, which has two components: the elastic energy and the cohesive fracture energy. The underlying idea is that the fracture energy is released gradually with the growth of the crack opening. The cohesive energy, denoted by \(\theta \), is assumed to be a monotonic non-decreasing function of the jump amplitude of the displacement, denoted by \(\llbracket u \rrbracket \). Cohesive energies were introduced independently by Dugdale [16] and Barenblatt [3], we refer to [43] for more details on the models. Let us just remark that the two models differ mainly in the evolution of the derivative \(\theta '(\llbracket u\rrbracket )\), that is, the bridging force, across a crack amplitude \(\llbracket u \rrbracket \). In Dugdale’s model this force keeps a constant value up to a critical value of the crack opening and then drops to zero. In Barenblatt’s model, the dependence of the force on \(\llbracket u \rrbracket \) is continuous and decreasing.
In this section we test the \(\ell ^p\)-term \(0<p<1\) as a model for the cohesive energy. In particular, the cohesive energy is not differentiable in zero and the bridging force goes to infinity when the jump amplitude goes to zero. Note also that the bridging force goes to zero when the jump amplitude goes to infinity.
Let us introduce all the elements that we need for the rest of the section. We consider the one-dimensional domain \({\varOmega }=[0,2l]\) with \(l>0\) and we denote by \(u\,:\, {\varOmega } \rightarrow {{\mathbb {R}}}\) the displacement function. The deformation of the domain is given by an external force which we express in terms of an external displacement function \(g\,:\,{\varOmega }\times [0,T] \rightarrow {{\mathbb {R}}}\). We require that the displacement u coincides with the external deformation, that is
We denote by \({\varGamma }\) the point of the (potential) crack, which we chose as the midpoint \({\varGamma }=l\) and by \(\theta (\llbracket u \rrbracket )_{\varGamma }\) the value of the cohesive energy \(\theta \) on the crack amplitude of the displacement \(\llbracket u \rrbracket \) on \({\varGamma }\). Since we are in a quasi-static setting, we introduce the time discretization \(0=t_0<t_1< \cdots <t_T=T\) and look for the equilibrium configurations which are minimizers of the energy of the system. This means that for each \(i \in \{0, \ldots , T\}\) we need to minimize the energy of the system
with respect to a given boundary datum g:
where \(\beta >0\) in J(u) is a material parameter. In particular, we consider the following type of cohesive energy
for \(p \in (0,1)\). We divide \({\varOmega }\) into 2N intervals and approximate the displacement function with a function \(u_h\) that is piecewise linear on \({\varOmega }\backslash {\varGamma }\) and has two degrees of freedom on \({\varGamma }\) to represent correctly the two lips of the fracture, denoting with \(u_{N}^{-}\) the degree on [0, l] and \(u_{N}^{+}\) the one on [l, 1]. We discretize the problem in the following way
where if \(i\le N\) we identify \(u_N=u_N^-\) while for \(i>N, u_N=u_N^+\). We remark that the jump of the displacement is not taken into account in the sum, and the gradient of u is approximated with finite difference of first order. The Dirichlet condition is applied on \(\partial {\varOmega }=\{0,2l\}\) and the external displacement is chosen as
To enforce the boundary condition in the minimization process, we add it to the energy functional as a penalization term. Hence, we solve the following unconstrained minimization problem
where the operator \(A \in {{\mathbb {R}}}^{(2N+1)\times (2N+1)}\) is given by
Here \({\bar{D}} \in {{\mathbb {R}}}^{2N\times (2N+1)}\) denotes the backward finite difference operator \(D \, : \,{{\mathbb {R}}}^{2N+1} \rightarrow {{\mathbb {R}}}^{2N+1}\) without the \(N+1\) row, where D is defined in (3.6). Moreover \(g \in {{\mathbb {R}}}^{2N+1}\) in (3.8) is given by \(g=(0,\ldots , \gamma 2lt_i)'\) and \(\gamma \) is the penalization parameter. To compute the jump between the two lips of the fracture, we introduce the operator \(D_f:{{\mathbb {R}}}^{2N+1} \rightarrow {{\mathbb {R}}}\) defined as \(D_f=(0,\ldots , -1,1,0,\ldots ,0)\) where \(-1\) and 1 are respectively in the N and \(N+1\) positions. Then we write the functional (3.8) as follows
Note that \(\text{ KerA } =0\), hence assumption (2.2) is satisfied and existence of a minimizer for (3.9) is guaranteed.
Our numerical experiments were conducted with a discretization in 2N intervals with \(N=100\) and a prescribed potential crack \({\varGamma }=0.5\). The time step in the time discretization of [0, T] with \(T=3\) is set to \(dt=0.01\). The parameters of the energy functional \(J_h(u_h)\) are set to \(\beta =1, \gamma =50\). The parameter \(\varepsilon \) is decreased from \(10^{-1}\) to \(10^{-12}\).
In Fig. 1 we report three time frames to represent the evolutions of the crack obtained with Algorithm 1 for two different values of p, that is, \(p=.01, .1\) respectively. Each time frame consists of three different time steps \((t_1, t_2, t_3)\), where \(t_2, t_3\) are chosen as the first instant where the prefracture and the fracture appear. The evolution presents the three phases that we expect from a cohesive fracture model:
-
Pure elastic deformation in this case the jump amplitude is zero and the gradient of the displacement is constant in \({\varOmega } \backslash {\varGamma }\);
-
Prefracture the two lips of the fracture do not touch each other, but they are not free to move. The elastic energy is still present.
-
Fracture the two parts are free to move. In this final phase the gradient of the displacement (and then the elastic energy) is zero.
Moreover we remark that the formation of the crack is anticipated for smaller values of p. As we see in Fig. 1, for \(p=.01\) prefracture and fracture are reached at \(t=.3\) and \(t=1.5\) respectively. As p is increased to \(p=.1\), prefracture and fracture occur at \(t=1\) and \(t=3\) respectively. Finally we remark that in our experiments the residue is \(O(10^{-16})\) and the number of iterations is small, e.g. 12, 15 for \(p=.01, .1\) respectively.
3.4 M-matrix
We consider
where A is the backward finite difference gradient
with \(G_1 \in {{\mathbb {R}}}^{d(d+1)\times d^2}, G_2 \in {{\mathbb {R}}}^{d(d+1)\times d^2}\) given by
Here I is the \(d\times d\) identity matrix, \(\otimes \) denotes the tensor product, and \(D\in {{\mathbb {R}}}^{(d+1)\times d}\) is given by
Then \(A^* A\) is an M matrix coinciding with the 5-point star discretization on a uniform mesh on a square of the Laplacian with Dirichlet boundary conditions. Note that (3.10) can be equivalently expressed as
where \(f=A^* b\). If \(\beta =0\) this is the discretized variational form of the elliptic equation
For \(\beta >0\) the variational problem (3.13) gives a solution piecewise constant enhancing behaviour.
Our tests were conducted with f chosen as discretization of \(f=10 x_1\text{ sin }(5x_2)\text{ cos }(7 x_1)\) and
where \(D_1 \in {{\mathbb {R}}}^{d^2\times d^2}, D_2 \in {{\mathbb {R}}}^{d^2\times d^2}\) are defined as follows
and \(D \in {{\mathbb {R}}}^{d\times d}\) is the backward difference operator defined in (3.12) without the \(d+1\)-row. The parameter \(\varepsilon \) was initialized with \(10^{-1}\) and decreased to \(10^{-6}\).
In Tables 2 we show the performance of Algorithm 1 for \(p=.1\), \(h=1/64\) as mesh size and \(\beta \) incrementally increasing by factor of 10 from \(10^{-4}\) to 10. In Fig. 2 we report the graphics of the solutions for different values of \(\beta \) between .01 and .3 where most changes occur in the graphics.
We observe significant differences in the results with respect to different values of \(\beta \). Consistently with our expectations, \(|{\varLambda } x|^c_0\) increases with \(\beta \) (see the third row of Table 2). For example, for \(\beta =1, 10\), we have \(|{\varLambda } x|^c_0=7938\), or equivalently, \(|{\varLambda } x|_0=0\), that is, the solution to (3.13) is constant. Moreover the fourth row shows that \(|{\varLambda } x|^p_p\) decreases when \(\beta \) increases.
The fifth row exhibits the \(\ell ^\infty \) norm of the residue, which is \(O(10^{-4})\) for all the considered \(\beta \). We remark that the number of iterations is sensitive with respect to \(\beta \), in particular it increases when \(\beta \) is increasing from \(10^{-4}\) to \(10^{-1}\) and then it decreases significantly for \(\beta =1,10\).
The algorithm was also tested for different values of p. The results obtained show dependence on p, in particular \(|{\varLambda } x|^c_0\) decreases as p is increasing. For example, for \(p=.5\) and \(\beta =.1\) we have \(|{\varLambda } x|^c_0=188, |{\varLambda } x|^p_p=528\).
In the sixth row of Table 2 we show the number of singular components of the vector \({\varLambda } x\) at the end of the \(\varepsilon \)-path following scheme, that is, \(Sp:=\#\{ i\,\, |\,\, |({\varLambda } x)_i|<\varepsilon \}\). For most values of \(\beta \), we note that Sp is comparable to \(|{\varLambda } x|_0^c\). This again confirms that the \(\varepsilon \)-strategy is effective.
Finally, we remark that if we modify the initialization (3.1), the method converges to the same solution with no remarkable modifications in the number of iterations, which is a sign for the global nature of the algorithm.
Remark 2
The algorithm was also tested in the following two particular cases: \({\varLambda }=I\), where I is the identity matrix of size \(d^2\), and \({\varLambda }=(d+1)D_1\), where \(D_1\) is as in (3.16).
In the case \({\varLambda }=I\) the variational problem (3.13) for \(\beta >0\) gives a sparsity enhancing solution for the elliptic equation (3.14), that is, the displacement y will be 0 when the forcing f is small. Indeed, in this case we have sparsity of the solution increasing with \(\beta \). Also, the residue is \(O(10^{-8})\) and the number of iterations is considerably smaller than in the case \({\varLambda }\) is as in (3.15).
For \( {\varLambda }=(d+1)D_1\) we show the graphics in Fig. 3. Comparing the graphs for \(\beta =.3\) in Figs. 2 and 3, we can find subdomains where the solution is only unidirectionally piecewise constant in Fig. 3 and piecewise constant in Fig. 2. The number of iterations, \(|{\varLambda } x|_0^c, |{\varLambda } x|_p^p\) and the residue are comparable to the ones of Table 2.
3.5 Elliptic control problem
We consider the following two-dimensional control problem
where we minimize over \(u \in L^p({\varOmega })\) such that \(\nabla u \in L^p({\varOmega })\), \({\varOmega }\) is the unit square, \(y_d \in L^2({\varOmega })\) is a given target function, and \(y \in L^2({\varOmega })\) satisfies
We discretize (3.17) by the following \(\frac{1}{d}\)-mesh size discretized minimization problem
where \(E=(A^* A)^{-1}\), A is as in (3.11) (that is, \(A^*A\) is the 5-point star discretization on a uniform mesh on a square of the Laplacian with Dirichlet boundary condition), \( {\varLambda }=(d+1)\left( \begin{array}{c} D_1\\ D_2 \end{array}\right) \) is as in Sect. 3.4 and b is the discretized target function.
For numerical reasons, in order to avoid the inversion of the matrix \(A^*A\), we multiply the necessary optimality condition (2.5) by \((E^{-1})^*\) and we get
where \(y={\varLambda } u\). We introduce
where we denote by N the diagonal matrix with i-entry \((N)_{ii}=\frac{\beta p}{\max (\varepsilon ^{2-p},|y_i|^{2-p})}, \, i=1,\ldots d^2\). Since \(E^{-1}=A^*A\), we can express (3.20) in the form
To solve (3.21) the following iteration procedure is used
where we denote by \(N^{k}\) the diagonal matrix with i-entry \((N^{k})_{ii}=\frac{\beta p}{\max (\varepsilon ^{2-p},|y_i^{k}|^{2-p})}\) for \(i=1,\ldots , d^2\) and \(y^{k}={\varLambda } u^k\). Note that the system matrix (3.22) is symmetric.
In our tests the target b is chosen as the image through E of the linear interpolation inside \([.2,.8]\times [.2,.8]\setminus [.3,.7]\times [.3,.7]\) of the step function \(1000 \chi _{[.3,.7]\times [.3,.7]}\). The parameter \(\varepsilon \) was initialized with \(10^{-1}\) and decreased to \(10^{-6}\). The system in (3.22) is solved though the MATLAB function mldivive (that is, the backslash command). In Table 3 we report the results of our test for \(h=\frac{1}{64}\), \(p=.1\) and \(\beta \) incrementally increasing by factor of 10 from \(10^{-3}\) to 1. As expected, when \(\beta \) increases, \(|{\varLambda } u|_0^c\) increases and \(|{\varLambda } u|^p_p\) decreases. In Fig. 4 we show the graphics of the solution for different values of \(\beta \), thus showing the enhancing piecewise constant behaviour of the solution.
From our tests we conclude that the monotone algorithm is reliable to find a solution of the \(\varepsilon \)-regularized optimality condition (2.5) for a diverse spectrum of problems. It is also stable with respect to the choice of initial conditions. According to the last rows of Tables 1, 2 and 3 we have that \(\#\{i\, |\, |({\varLambda } x)_i|\le 10^{-10}\}\) is typically very close to the number of singular components at the end of the \(\varepsilon \)-path following scheme. Depending on the choice of \(\beta \) the algorithm requires on the order of \(O(10^2)\) to \(O(10^3)\) iterations to reach convergence. In the following sections we aim at analysing an alternative algorithm for which the iteration number is smaller, despite the fact that the convergence can be proved only in special cases.
4 The active set monotone algorithm for the optimality conditions
In the following we discuss an algorithm which aims at finding a solution of the original unregularized problem
where \(A \in {\mathbb {M}}^{m\times d}, b \in {{\mathbb {R}}}^m, p \in (0,1]\) and \( \beta \in {{\mathbb {R}}}^+\) are as in Sect. 2. Differently from the previous sections we now assume throughout that
Existence for the problem (4.1) follows from Theorem 1.
First necessary optimality conditions for problem (4.1) in the form of a complementary systems are derived and a sufficient condition for the uniqueness for solutions to this system are established. Subsequently an active-set strategy is proposed relying on this form of the optimality conditions.
4.1 Necessary optimality conditions
For any matrix \(A \in {\mathbb {M}}^{m\times d}\), we denote by \(A_i\) the i-th column of A. We have the following necessary optimality conditions for a global minimizer of (4.1).
Theorem 3
Assume that (4.2) holds, let \({\bar{x}}\) be a global minimizer of (4.1), and denote \({\bar{y}}={\varLambda } {\bar{x}}\). Then we have
where \({\tilde{A}}=A {\varLambda }^{-1}\), \(\mu _i=\beta ^{\frac{1}{2-p}}(2-p)(2(1-p))^{-\frac{1-p}{2-p}}|{\tilde{A}}_i|_2^{1-\frac{p}{2-p}}\). If \(\left| |{\tilde{A}}_i|_2^2{\bar{y}}_i+\lambda _i\right| =\mu _i\), then \(({\varLambda }{\bar{x}})_i=0\) or \(({\varLambda }{\bar{x}})_i=\left( \frac{2\beta (1-p)}{|{\tilde{A}}_i|_2^2}\right) ^{\frac{1}{2-p}} \text{ sgn } (|{\tilde{A}}_i|_2^2{\bar{y}}_i+\lambda _i)\).
Proof
Note that if \(\bar{x}\) is a global minimizer of (4.1), then \(\bar{y}={\varLambda } {\bar{x}}\) is a global minimizer of
where \({\tilde{A}}=A {\varLambda }^{-1}\). Then, by the same arguments as in [27], Theorem 2.2 applied to the functional (4.4), we get the following property of global minimizers
where \(f_i=b-{\tilde{A}} y+{\tilde{A}}_i{\bar{y}}_i\) and \(\mu _i=\beta ^{\frac{1}{2-p}}(2-p)(2(1-p))^{-\frac{1-p}{2-p}}|{\tilde{A}}_i|_2^{1-\frac{p}{2-p}}\). Moreover, if \(|\langle {\tilde{A}}_i,f_i\rangle |=\mu _i\), then \({\bar{y}}_i=0\) or \({\bar{y}}_i=\left( \frac{2\beta (1-p)}{|{\tilde{A}}_i|_2^2}\right) ^{\frac{1}{2-p}} \text{ sgn } (\langle {\tilde{A}}_i,f_i\rangle )\). We introduce the multiplier \(\lambda \) and we write (4.5) in the following way
Then the optimality conditions (4.3) follows from (4.6) with \({\bar{y}}={\varLambda }{\bar{x}}\). The equality conditions follow similarly by \({\bar{y}}={\varLambda }{\bar{x}}\) and the first equation in (4.6). \(\square \)
Remark 3
We remark that Theorem 3 still hold when considering (4.1) in the infinite dimensional sequence spaces \(\ell ^p\) in the case \({\varLambda }=I\).
From Theorem 3 we can deduce a lower bound for the nonzero components of \({\varLambda } x\) following the arguments in [27], Corollary 2.1. The result of Corollary 1 are of the same order with respect to \(\beta ,p,\) and A, compared to the existing lower bound for \(\ell ^2\)-\(\ell ^p\) problems derived in the literature, see e.g. [15]. However, the proof of [15] is different from the one presented in [27] and relies mainly on second order necessary optimality conditions.
Corollary 1
If \(({\varLambda }{\bar{x}})_i \ne 0\), then \(|({\varLambda }{\bar{x}})_i| \ge \left( \frac{2 \beta (1-p)}{|(A{\varLambda }^{-1})_i|_2^2}\right) ^{\frac{1}{2-p}}.\)
4.2 The augmented Lagrangian formulation and the primal-dual active set strategy
The active set strategy can be motivated by the following augmented Lagrangian formulation for problem (4.1). Let P be a nonnegative self-adjoint matrix P, satisfying
for some \(\eta ,\xi >0\), independent of \(x \in {{\mathbb {R}}}^d\). We set
and let B denote the diagonal invertible operator with entries \(B_i\). Thus, if A is nearly singular, we use \(\eta >0\) and the functional \(\frac{\eta }{2}\langle x,Px\rangle \) to regularize (4.1). Consider the associated augmented Lagrangian functional
Given \(x,\lambda \), we first minimize L coordinate-wise with respect to y. For this purpose we consider
Then, by Theorem 3, the augmented Lagrangian L can be minimized coordinate-wise with respect to y by considering the expressions \(\beta |y_i|^p+\frac{1}{2}\left[ B_i^{\frac{1}{2}}y_i-\left( B_i^{\frac{1}{2}}({\varLambda } x)_i+\frac{\lambda _i}{B_i^{\frac{1}{2}}}\right) \right] ^2\) to obtain
where
Given \(y,\lambda \), we minimize L at x to obtain
where B is the diagonal operator with entries \(B_i\). Thus, the augmented Lagrangian method [28] uses the updates:
If it converges, i.e. \(x^n\rightarrow x, y^n \rightarrow {\varLambda } x^n\), and \(\lambda ^n\rightarrow \lambda \), then
which is the optimality condition for \(J_P(x)=\min _{x \in {{\mathbb {R}}}^d} \frac{1}{2}|Ax-b|_2^2+\beta |{\varLambda } x|_p^p+\frac{\eta }{2}\langle x,Px\rangle \), compare (4.3).
Motivated by the form of the optimality conditions (4.13) obtained by the augmented Lagrangian formulation, we formulate in Algorithm 2 a primal-dual active set strategy for the following system
where \(\varepsilon >0\) in the third equation is a fixed small parameter. Note that according to Corollary 1 system (4.14) coincides with (4.13) if \(\varepsilon < \left( \frac{2 \beta (1-p)}{|(A {\varLambda }^{-1})_i |_2^2} \right) ^{\frac{1}{2-p}}\) for all i with \( \left| B_iy_i +\lambda _i\right| >\mu _i\). The motivation for the parameter \(\varepsilon \) is to avoid the expression \(\frac{\beta p ({\varLambda } x^{n+1})_i}{|({\varLambda } x^{n+1})_i|^{2-p})|}\), where computing the update \( x^{n+1}, \lambda ^{n+1}\) is specified next.

System (4.15)–(4.17) in Algorithm 2 is implicit. It can be solved, for example, by an iterative procedure based on Algorithm 1. The final scheme resulting from the combination of Algorithm 1 and 2 is described in Algorithm 3 in the following section.
Remark 4
The specific choice (4.8) of the penalization constant \(B_i\) in the augmented Lagrangian method (4.9) is crucial to ensure the convergence of the method to the optimality condition (4.3). Indeed, contrary to what would be tempting following the standard penalization technique procedure, here \(B_i\) has to be taken exactly as in (4.8) and in particular it cannot be taken too large. To make this evident, we propose to look at the following one-dimensional example. Suppose we want to minimize
for \(p \in (0,1],\)\( \beta >0\). By Theorem 3, the optimality condition is
where we denote \(\mu :=d_{\beta ,p}\) and \(d_{\beta ,p}=\beta ^{\frac{1}{2-p}}(2-p)(2(1-p))^{-\frac{1-p}{2-p}}\) is given in (4.3). Consider for \(c>0\) the augmented Lagrangian
For y fixed, we minimize with respect to x to obtain
Then, given x fixed, we minimize with respect to y the expression \(\beta |y|^p+\frac{c}{2}|x-y|^2+\lambda y\). First note that
Then by Theorem 3 we obtain
where \(\mu _c=d_{\beta ,p}\sqrt{c}^{\frac{(2-2p)}{2-p}}\). Finally we minimize with respect to \(\lambda \) and we get \(x=y\). Then we obtain the following optimality conditions of complementary type
Note that if we use the formula (4.8) for the penalization term of the augmented Lagrangian formulation (4.9), we get \(c=1\) and then (4.22) coincides with (4.19), as desired. For \(c>1\), on the other hand, the convergence to the solution of the optimality conditions (4.19) is not guaranteed. Indeed, if \(c>1\) and \(b\in (\mu ,\mu _c)\) then \(\mu <\mu _c\), and from the augmented Lagrangian formulation (4.20), we get that \( y=0, x=0, \lambda =-b \) is a solution to (4.22). But \(b>\mu \) implies that \(x=0\) is not a solution of (4.19). This shows that, if the penalization constant c does not satisfy (4.8), then the augumented Lagragian method based on the formulation (4.20) might not converge to the original problem (4.18).
Remark 5
Now consider the following optimality condition for the problem (4.20)
where \(\partial \) denotes the limiting subdifferential. For a definition of the limiting subdifferential we refer to [36], where similar problems to the ones studied in the present paper are solve through optimality conditions as in (4.23), see also the end of this remark for more details.
Since
the optimality condition (4.23) explicitly reads
It is straightforward to notice that (4.25) differs from (4.22), since in (4.25) there is no complementary condition.
For our problem (4.18) from (4.24) and further easy computations, we see that the triple \(x=0, y=0, \lambda =-b\) is a solution of (4.25), whereas, as already remarked, it does not satisfy (4.22). This is strictly connected to the fact that (4.22) is a primal-dual optimality condition of complementary type, which is equivalent to say that (4.22) is a necessary condition for global minimizers. On the contrary (4.25) is a necessary condition for local ones.
Finally we mention that in [36] an alternate direction method of multipliers is proposed to find stationary points of the type (4.25) (see Eq. 4 of [36]). The method is derived from an augmented Lagrangian formulation, where however, differently from the current paper, the penalization term in [36] is chosen ”large enough”.
4.3 Uniqueness and convergence
The goals of this subsection are to provide sufficient conditions for uniqueness of solutions to (4.14) and convergence of Algorithm 2. This algorithm proved to be very efficient in our numerical tests which we shall report on further below. Its analysis, however, is quite challenging and will require additional assumptions. Before specifying them we introduce some additional notation.
For any pair \(x,\lambda \) let
We define the square matrix
and the constants
where \(p \in (0,1]\). We note that \( 1=\gamma + \alpha . \)
We shall employ a diagonal dominance condition expressed as
Additionally we make use of the following strict complementarity conditions for a solution \(x, \lambda \) to (4.14)
for some \(\delta \in [0,1]\) large enough. Here \(\min _{{\mathcal {I}}(x,\lambda )}|B^{-\alpha }(\lambda +B {\varLambda } x)|\) stands for \(\min _{i \in {\mathcal {I}}(x,\lambda )}|B_i^{-\alpha }(\lambda _i+B_i ({\varLambda } x)_i)|\).
We shall choose \(\varepsilon \) such that
Finally we set
where we recall the definition of \(\mu _i\) in (4.11).
Let us make some remarks on these specifications. In the case that Q is a diagonal matrix \(Q-B=0\) and (4.28) is trivially satisfied. We observe that for \(p\rightarrow 0\), we have \(\alpha =\gamma =\frac{1}{2}\). In particular (4.28) coincides when \({\varLambda }=I\) with the diagonal dominance condition considered in [27] to prove the convergence of the primal-dual active set strategy in the case \(p=0\) and \({\varLambda }=I\). Note we note that the admissible range of \(\varepsilon \) in (4.31) decreases with \(\beta \) and \(p< 1\).
We first prove the following lemma, which is a key ingredient for the proof of Theorem 4 and will be used also in the proof of the convergence result Theorem 5.
Lemma 1
Assume that (4.2), (4.28) and (4.31) hold.
-
(i)
Let \(y \in {{\mathbb {R}}}\), \(y\ne 0\), and \(\lambda =\frac{\beta p y}{\max \{\varepsilon ^{2-p}, |y|^{2-p}\}}\). Then for any \(i=1,\ldots , d\) it holds
$$\begin{aligned} |B_i^{-\alpha } \lambda |\le \beta ^{\gamma }C_2. \end{aligned}$$(4.33) -
(ii)
Let \(y^1, y^2 \in {{\mathbb {R}}}^d\) be such that for all \(i=1,\ldots , d\) we have \(y^1_i\ne 0\), \(y^2_i \ne 0\), and
$$\begin{aligned}&B_i^{\gamma }(y_i^1-y_i^2)+B_i^{-\alpha }\left( \frac{\beta p y_i^1}{\max (\varepsilon ^{2-p}, |y_i^1|^{2-p})}-\frac{\beta p y_i^2}{\max (\varepsilon ^{2-p}, |y_i^2|^{2-p})}\right) \nonumber \\&\quad =\left( B^{-\alpha }(B-Q)B^{-\gamma }B^{\gamma }(y^1-y^2)\right) _i. \end{aligned}$$(4.34)Then \(y^1=y^2\).
Proof
We first prove (i). From the definition of \(\lambda \) we have
and by (4.31) we conclude (4.33).
Now we prove (ii). For \(i=1,\ldots , d\), let us define \(h_i : {\mathbb {R}} \rightarrow {\mathbb {R}}\) and \(h_i^\varepsilon : {\mathbb {R}} \rightarrow {\mathbb {R}}\) by
A short computation shows that \(h_i\) has a local minimum at \(y_i^+=\left( \beta (1-p)p B_i^{-1}\right) ^{\frac{1}{2-p}}\), respectively a local maximum at \(y_i^{-}=-\left( \beta (1-p)p B_i^{-1}\right) ^{\frac{1}{2-p}}\). By the choice of \(\varepsilon \) in (4.31), considering the cases \(\varepsilon \ge |z|\) and \(\varepsilon < |z|\), it can be argued that
Together with \(h_i^\varepsilon (0)=0\), it follows that
By (4.34) and recalling that \(\alpha +\gamma =1\), we obtain
Multiplying by \((y^1_i-y^2_i)\), using (4.37) and (4.28) we obtain
Thus \(\tilde{\rho }|B_i^{\gamma }(y_i^1-y_i^2)|_\infty \le \rho |B^{\gamma } (y^1-y^2)|_\infty \) and since \(\tilde{\rho } \in (\rho , 1)\) we get that \(y^1=y^2\). \(\square \)
Theorem 4
(Uniqueness) Assume that (4.2), (4.28), and (4.31) hold. Then there exists at most one solution to (4.14) satisfying (4.29) with \(\delta > \frac{2\rho C_3}{(1-\rho )C_1}.\) An analogous statement holds with (4.29) replaced by (4.30).
Proof
Assume that there exist two pairs \(x,\lambda \) and \({{\hat{x}}}, {\hat{\lambda }}\) satisfying (4.14) and (4.29). Let \(y={\varLambda } x\) and \({{\hat{y}}}={\varLambda } {{\hat{x}}}\). By multiplying (4.14) by \(({\varLambda }^*)^{-1}\) and using the definition of Q, we have
Multiplying (4.38) by \(B^{-\alpha }\) and using that \(\alpha +\gamma =1\), we have
Case 1 First consider the case \(y_i \ne 0\) if and only if \({{\hat{y}}}_i \ne 0\) for each i. From (4.14) we have
By (4.39) we have
that is, y and \({{\hat{y}}}\) satisfy (4.34) with \(y=y^1\) and \({{\hat{y}}}=y^2\). Then by Lemma 1 (i), we conclude that \(y={{\hat{y}}}\).
Case 2 Here we suppose that there exists j such that \(y_j\ne 0\) and \({{\hat{y}}}_j = 0\). The case \({{\hat{y}}}_j\ne 0\) and \( y_j = 0\) can be treated analogously. Before using these settings some considerations are necessary. From (4.14) and since \(\mu _i=\beta ^{\gamma } C_1 B_i^{\alpha }\) we deduce that
and by (4.33)
and combined with (4.41), (4.42) and the definition of \(C_3\)
and thus
For j chosen as above we estimate using (4.28), (4.39), and (4.43)
Now we utilize (4.29) and (4.42) in the last estimate to obtain
or equivalently
which contradicts the choice of \(\delta \).
Case 3 The only remaining case consists in \(y_i={\hat{y}}_i=0\) for all i. But then \(\lambda =\hat{\lambda }\) by (4.14) and \(x={{\hat{x}}}\) by the invertibility of \({\varLambda }\) as desired. This concludes the proof under assumption (4.29).
The case (4.30) can be treated analogously. Note that condition (4.29) (or respectively (4.30)) arises only in Case 2 and therefore the proof of Case 1 and Case 3 can be carried out exactly as above. In Case 2 we proceed as above to get (4.44). Since \(y_j\ne 0\) by the third equation in (4.3) and (4.8), we have
and recalling that \(\mu _j=\beta ^{\gamma } C_1 B_j^{\alpha }\), we get
By (4.30) we get
Putting (4.46) and (4.47) in (4.44), we obtain
and thus \(\delta \le \frac{2\rho C_3}{(1-\rho )C_1}\), which gives the desired contradiction to the choice of \(\delta \). \(\square \)
4.3.1 Convergence
Here we give a sufficient condition for the convergence of the primal-dual active set method. As in [27] we utilize the diagonal dominance condition (4.28) and consider a solution \(x, \lambda \) to (4.14) which satisfies the strict complementary conditions. As such it is unique according to Theorem 4.
At first let us emphasize that the sequence \(\{x^n\}_{n\in {\mathbb {N}}}\) is bounded uniformly in n. Indeed since \(\langle x^{n+1}, \lambda ^{n+1} \rangle \ge 0\) for all n, we have from the first equation in (4.14)
which coupled with (4.7) gives
Setting \(M:=\max (\Vert A\Vert _2|b|_2\xi ^{-1}, |x_0|_2)\), where \(\xi \) is defined in (4.7) we conclude that
Note that the same bound as (4.48) holds also for any solution x of the necessary optimality condition (4.14).
We will use the following notation
where \( \gamma \) and M are defined respectively in (4.27) and (4.48).
Theorem 5
Suppose that (4.2), (4.28), and (4.31) hold. Let \({\bar{x}}, {\bar{\lambda }}\) be a solution to (4.14) satisfying the strict complementary condition (4.29)–(4.30), with \(\delta > \frac{\rho }{(1-\rho )C_1}\left( 2 \rho \beta ^{-\gamma } F +2C_3\right) \), and define the sets
Then \({\mathcal {S}}^n = {\mathcal {I}}({\bar{x}}, {\bar{\lambda }})\) for \(n\ge 2\) and \({\mathcal {T}}^n \subset {\mathcal {T}}^{n+1}\) for \(n\ge 1\). As soon as \({\mathcal {S}}^n={\mathcal {S}}^{n+1}\) and \({\mathcal {T}}^n={\mathcal {T}}^{n+1},\) we have \(x^{n+1}, \lambda ^{n+1}={\bar{x}}, {\bar{\lambda }}\).
Note that \({\mathcal {S}}^n\) is the set of all indices which are inactive both for the \({\bar{x}}, {\bar{\lambda }}\) and for \(x^n, \lambda ^n\), and analogously \({\mathcal {S}}^n\) is the set of active indices for both pairs. Note also that due to the finite dimensionality the case \({\mathcal {T}}^n={\mathcal {T}}^{n+1}\) for some n must occur.
Proof
We divide the proof into three steps. In Step (i) we verify a bound on \(x^n- {\bar{x}}\) which will be used throughout the rest of the proof, in Step (ii) we prove the claimed properties of \({\mathcal {S}}^n\) and \({\mathcal {T}}^n\), and in Step (iii) we conclude the proof of convergence.
Step (i) Let \({\bar{y}}={\varLambda } {\bar{x}}\) and \(y^n={\varLambda } x^n\), for \(n\ge 1\). Multiplying (4.14) by \(({\varLambda }^*)^{-1}\) and using the definition of Q in (4.26), we have
Multiplying (4.50) by \(B^{-\alpha }\) and using that \(\alpha +\gamma =1\) we get
Suppose first that \(y^n_i\ne 0\) and \({\bar{y}}_i\ne 0\) for all i. By (4.51), (4.14), (4.16), and (4.17) we have that \(y^n\) and \({\bar{y}}\) satisfy the assumptions of Lemma 1 (ii) with \(y^1=y^n\) and \(y^2={\bar{y}}\). Then by Lemma 1 (ii) we obtain that \(y^n=\bar{y}\).
Next consider the case \(y^n_i=0, {\bar{y}}_i \ne 0\). For two consecutive iterates we have
and thus, multiplying the equation by \(B^{-\alpha }\) and using that \(\alpha +\gamma =1\) we get
Since \(y^n_i=0\), by (4.16) and (4.17) we have \(|B_i y_i^{n-1}+\lambda _i^{n-1}|\le \mu _i=\beta ^{\gamma }C_1B_i^{\alpha }\), and by (4.53) and (4.28) we get
where F is defined in (4.49). Since \({\bar{y}}_i \ne 0\), by (4.14) and (4.33), we have
By (4.51), (4.54), (4.54) and (4.28) we get
Similarly if \(y^n_i\ne 0\) and \({\bar{y}}_i=0\), we get
Combining (4.55) and (4.56), we have
Summarizing these estimates we have
Step (ii) We first consider the relationship between \({\mathcal {S}}^n\) and \({\mathcal {I}}({\bar{x}}, {\bar{\lambda }})\). Note that if \({\mathcal {I}}({\bar{x}}, {\bar{\lambda }}) = \emptyset \), then \({\mathcal {S}}^n=\emptyset \) for all \(n \ge 0\). Henceforth we consider the case \({\mathcal {I}}({\bar{x}}, {\bar{\lambda }}) \ne \emptyset \). We have
By (4.51), (4.28), and (4.57) we deduce for \(n\ge 1\)
Then by (4.58), (4.59), and (4.29) we obtain for \(i\in {\mathcal {I}}({\bar{x}}, {\bar{\lambda }})\)
Since by assumption
we have
From (4.17) we deduce that \(\lambda _i^{n+1}=\frac{\beta p ({\varLambda } x^{n+1})_i}{\max (\varepsilon ^{2-p}, |({\varLambda } x^{n+1})_i|^{2-p})}\), and thus \(i \in {\mathcal {S}}^{n+1}\). Since \( {\mathcal {S}}^{n+1} \subset {\mathcal {I}}({\bar{x}}, {\bar{\lambda }})\), it follows that \( {\mathcal {S}}^{n+1} = {\mathcal {I}}({\bar{x}}, {\bar{\lambda }})\) for \(n\ge 1\).
For \(i \in {\mathcal {T}}^n\) by (4.51), (4.28) and (4.57) we have
By the definition of \({\mathcal {T}}^n\), (4.61) and the strict complementary condition (4.30), we get
By taking \(\delta \) as in (4.60) we have
and hence \(y_i^{n+1}=0\) and \(i \in {\mathcal {T}}^{n+1}\). Thus \({\mathcal {T}}^n\subseteq {\mathcal {T}}^{n+1}\).
Step (iii) Assume now that \({\mathcal {S}}^n={\mathcal {S}}^{n+1} \) and \({\mathcal {T}}^n={\mathcal {T}}^{n+1}\subset {\mathcal {A}}({\bar{x}}, {\bar{\lambda }})\). Then \({\mathcal {S}}^n={\mathcal {I}}({\bar{x}}, {\bar{\lambda }})\). This is proved in Step 2 for the case \(n\ge 2\) and in case \(n=1\) we have \({\mathcal {S}}^1= {\mathcal {S}}^2= {\mathcal {I}}({\bar{x}}, {\bar{\lambda }})\).
Assume now that \({\mathcal {T}}^n={\mathcal {T}}^{n+1} \subsetneq {\mathcal {A}}({\bar{x}}, {\bar{\lambda }})\) and \(i \in {\mathcal {A}}({\bar{x}}, {\bar{\lambda }}) \backslash {\mathcal {T}}^n\). Then
By (4.17), the first and third equations in (4.63), (4.51), and (4.30) we have
By (4.28) and (4.57) we obtain
from which it follows that
leading to a contradiction to the choice of \(\delta \) in (4.60).
It follows that \({\mathcal {S}}^n={\mathcal {I}}({\bar{x}}, {\bar{\lambda }})\) and \({\mathcal {T}}^n={\mathcal {A}}({\bar{x}}, {\bar{\lambda }})\). Comparing (4.14), which is satisfied by \({\bar{x}}, {\bar{\lambda }}\), and (4.15)–(4.17), which holds with \(y_i^n=y_i^{n+1}, \lambda _i^n=\lambda _i^{n+1}\), we conclude that \(x^{n+1}={\bar{x}}, \lambda ^{n+1}={\bar{\lambda }}\). \(\square \)
Remark 6
If \(\bar{x}_i \ne 0\) for all i we have \({\mathcal {A}}({\bar{x}},{\bar{\lambda }})=\emptyset \). Then by the definition of \({\mathcal {T}}^n\) and Step (ii) of the proof of Theorem 5 we obtain \({\mathcal {T}}^1={\mathcal {T}}^2=\emptyset \) and therefore Algorithm 2 is a 2-step algorithm, in this case.
5 Active set monotone algorithm: numerical results
Here we describe the active set monotone scheme (see Algorithm 3) and discuss the numerical results for two different test cases. The first one is the time-dependent control problem from Sect. 3.2, the second one is an example in microscopy image reconstruction. Typically the active set monotone scheme requires fewer iterations and achieves a lower residue than the monotone scheme of Sect. 2.
5.1 The numerical scheme
The proposed active set monotone algorithm consists of an outer loop based on the primal-dual active set strategy and an inner loop which uses the monotone algorithm to solve the nonlinear part of the optimality condition.
In order to achieve a better numerical performance, we write the optimality condition as explained in the following. At each iteration of the active set strategy (Algorithm 2) we solve the following system in \(x^{n+1}, \lambda ^{n+1}\)
where \({\mathcal {A}}_n=\{i \, : \, |B_i y^n_i+\lambda ^n_i|\le \mu _i\}\) are the active indexes and \({\mathcal {I}}_n={\mathcal {A}}_n^c\) are the inactive ones. We write (5.1) in the following form
where \(N^{n+1}_{{\mathcal {I}}_n}\) is the diagonal operator with i-entries \((N^{n+1}_{{\mathcal {I}}_n})_{ii, i \in {\mathcal {I}}_n}=\frac{\beta p}{\max (\varepsilon ^{2-p},|({\varLambda } x^{n+1})_{i \in {\mathcal {I}}_n}|^{2-p})}\) and \({\varLambda }_{{\mathcal {A}}_n}, {\varLambda }_{{\mathcal {I}}_n}\) are the rows of \({\varLambda }\) corresponding to the active and inactive indexes respectively.
In order to solve (5.2) we apply the following iterative procedure solved for \(x^{k+1,n+1}, \lambda ^{k+1,n+1}\)
where \(N^{k,n+1}_{{\mathcal {I}}_n}\) is the diagonal operator with i-entries \((N^{k,n+1}_{{\mathcal {I}}_n})_{ii, i \in {\mathcal {I}}_n}=\frac{\beta p}{\max (\varepsilon ^{2-p},|({\varLambda } x^{k,n+1})_{i \in {\mathcal {I}}_n}|^{2-p})}\). Note that the iterative procedure of (5.3) is convergent by Theorem (2).
Remark 7
Note that the system matrix associated to (5.3) is symmetric.
The algorithm stops when the residue of (5.2) and (4.3) (for the inner and the outer cycle respectively) is \(O(10^{-12})\) in the control problem and \(O(10^{-8})\) in the microscopy image example.
We remark that in our numerical tests we always took \(\eta =0\). The initialization \(x^0,\lambda ^0\) in the outer cycle is chosen in the following way
In particular \(\lambda ^0\) is the solution of the first equation in (4.3) for \(x=x^0\). As in Sect. 3, for some values of \(\beta \) the previous initialization is not suitable. Following the idea already used for the monotone scheme, we successfully tested an analogous continuation strategy with respect to increasing \(\beta \)-values.
In Algorithm 3 we jump out of at the inner loop in case of presence of singular components. We recall that the singular components are those i such that \(|({\varLambda } x)_i|<\varepsilon \}\), that is, the components where the \(\varepsilon \)-regularization is most influential.

In the case \({\varLambda }\) coincides with the identity the system (5.1) can be written as
Note that in (5.6) we coupled the first and the third equation in (5.1) and we eliminated the dual variable. The advantage is that now we solve the second equation in (5.6) only for the inactive components \(x_{{\mathcal {I}}_n}\), solving a system of \(|{\mathcal {I}}_n|\) equations, whereas in (5.5) we solve \(d +|{\mathcal {A}}_n|\) equations. Finally we remark that in the case \({\varLambda }\) coincides with the identity \(\varepsilon >0\) is fixed. In particular \(\varepsilon =\min _{i}\left( \frac{2 \beta (1-p)}{|A_i|_2^2}\right) ^{\frac{1}{2-p}}\) accordingly to the lower bound on the inactive components given by Corollary 1.
5.2 Sparsity in a time-dependent control problem
We test the active set monotone algorithm on the time-dependent control problem described in Sect. 3.2, with the same discretization in space and time (\({\varDelta } x= {\varDelta } t=\frac{1}{50}\)) and target function b. Also the initialization of x and the \(\varepsilon \)-range are the same. In Tables 4 we report the results of our tests for \(p=.1\) and \(\beta \) incrementally increasing by factor of 10 from \(10^{-3}\) to 1. We report only the values for the second control \(u_2\) since the first control \(u_1\) is always zero. As expected, \(|Du_2|^c_0\) increases and \(|Du_2|^p_p\) decreases when \(\beta \) is increasing. Note that the number of iterations of the inner and outer cycle are both small.
The algorithm was also tested for the same p as in Sect. 3.2, that is \(p=.5\), for the same range of \(\beta \) as in Table 4. Comparing to the results achieved by Algorithm 1, we obtained the same values for the \(\ell ^0\)-term for corresponding values of \(\beta \) and a considerably smaller residue within a significantly fewer number of inner iterations.
Finally we note that if \({\varLambda }=I\) the number of inner iterations is even smaller, that is, 6 on the average.
5.3 Compressed sensing approach for microscopy image reconstruction
In this subsection we present an application of the active set monotone scheme to compressed sensing for microscopy image reconstruction. We focus on the STORM (stochastic optical reconstruction microscopy) method, which is based on stochastically switching and high-precision detection of single molecules to achieve an image resolution beyond the diffraction limit. The literature on the STORM has been intensively increasing, see e.g. [4, 23, 25, 46]. The STORM reconstruction process consists in a series of imaging cycles. In each cycle only a fraction of the fluorophores in the field of view are switched on (stochastically), such that each of the active fluorophores is optically resolvable from the rest, allowing the position of these fluorophores to be determined with high accuracy. Despite the advantage of obtaining sub-diffraction-limit spatial resolution, in these single molecule detection-based techniques such as STORM, the time to acquire a super-resolution image is limited by the maximum density of fluorescent emitters that can be accurately localized per imaging frame, see e.g. [31, 38, 47]. In order to get at the same time better resolution and higher emitter density per imaging frame, compressive sensing methods based on \(l^1\) techniques have been recently applied, see e.g. [2, 21, 50] and the references therein. In the following, we propose a similar approach based on our \(l^p\) with \(p<1\) methods. We mention that \(l^p\) with \(0<p\le 1\) techniques based on a concave-convex regularizing procedure, and hence different from ours, are used in [33].
To be more specific, each single frame reconstruction can be achieved by solving the following constrained-minimization problem:
where \(p \in (0,1]\), x is the up-sampled, reconstructed image, b is the experimentally observed image, and A is the impulse response (of size \(m\times d\), where m and d are the numbers of pixels in b and x, respectively). A is usually called the point spread function (PSF) and describes the response of an imaging system to a point source or point object. The inequality constraint on the \(\ell ^2\)-norm allows some inaccuracy in the image reconstruction to accommodate the statistical corruption of the image by noise [50]. Solving problems as (5.7) is referred to as compressed sensing in the literature of microscopy imaging. Indeed, in the basic compressed sensing problem, an under-determined, sparse signal vector is reconstructed from a noisy measurement in a basis in which the signal is not sparse. In the compressed sensing approach to microscopy image reconstruction, the sparse basis is a high resolution grid, in which fluorophore locations are presented, while the noisy measurement basis is the lower resolution camera pixels, on which fluorescence signal are detected experimentally. In this framework, the optimally reconstructed image is the one that contains the fewest number of fluorophores but reproduces the measured image on the camera to a given accuracy (when convolved with the optical impulse response).
We reformulate problem (5.7) as:
and we solve (5.8) by applying Algorithm 3. Note that we may consider (5.8) arising from (5.7) with \(\beta \) related to the reciprocal of the Lagrange multiplier associated to the inequality constraint \(|A x-b|_2 \le \varepsilon \). We remark also that in the resolution of (5.8) in Algorithm 3 the parameter \(\varepsilon \) is kept constant and equal to the lower bound on the inactive components given by Corollary 1.
First we tested the procedure for same resolution images, in particular the conventional and the true images are both \(128\times 128\) pixel images. Then the algorithm was tested in the case of a \(16\times 16\) pixel conventional image and a \(128 \times 128\) true image. The values for the impulse response A and the measured data b were chosen according to the literature, in particular A was taken as the Gaussian PSF matrix with variance \(\sigma =8\) and size \(3\times \sigma =24\), and b was simulated by convolving the impulse response A with a random 0-1 mask over the image adding a white random noise so that the signal to noise ratio is .01.
We carried out several tests with the same data for different values of \(p,\beta \). We report only our results for \(p=.1\) and \(\beta =10^{-6}, \beta =10^{-9}\) for the same and the different resolution case respectively, since for these values the best reconstructions were achieved. The number of single frame reconstructions carried out to get the full reconstruction was 5, 10 for the same, different resolution case, respectively.
In order to measure the performance of our algorithm, we plot a graphic of the average over six recoveries of the location recovery and the exact recovery (up to a certain tolerance) against the noise. Note that in compressed sensing these quantities are typically used as a measure of the efficacy of the reconstruction method, see for example [17] (where, under certain conditions, a linear decay with respect to the noise is proven) and [7].
The first test is carried out for a sparse 0–1 cross-like image. The STORM reconstructions are presented in Figs. 5 and 6 for the same and different resolution case, respectively. In Fig. 7 the plots of the location and exact recovery are shown. Note that our algorithm can recover quite well the location of the emitters. Also, the location and intensity of the emitters decay linearly with respect to the noise level, in line with the result of [17]. In particular, for small noise both the recoveries are very near to \(d^2=16,384\), that is, the exact recovery is 16, 240, 16, 243 and the location is 16, 384, 16, 360 for the same and the different resolution case, respectively. We observe also that the values of the location recovery are higher than the exact recovery for small values of the noise, as expected.
A second test on a non sparse standard phantom image is carried out. In Fig. 8 we show the reconstruction in the case of same resolution images. Note that a high percentage of emitters is correctly localized and the boundaries of the image are well-recovered. Also in this case the location and exact recoveries show a linear decay with respect to the noise.
In Tables 5 and 6 we report the number of iterations needed for each single frame reconstruction. For the cross image in the different resolution case (Table 5), the number of iterations is averagely 100, 164 for the outer cycle and inner cycle, respectively. Note that for the phantom in the same resolution case (Table 6) the number of iterations is lower, that is averagely 7.2, 9.8 for the outer cycle and inner cycle, respectively. The numbers of iterations for the cross image in case of same resolution are comparable to the ones of Table 5. As shown in the third line of each tables, the residue is always less than or equal to \(10^{-8}\).
We compared our results with the ones obtained by the FISTA in the same situations and same values of the parameters as described above. Figure 9 shows a comparison between the number of surplus and missed emitters recovered (Error+, Error\(-\) respectively) by Algorithm 3 and the FISTA in the case of the cross image and different resolution. We remark that the levels of the location and exact recoveries achieved by the FISTA are lower than the ones obtained by Algorithm 3, at least for values of the noise near .01. In particular, by the FISTA the Error+ is always above 410, whereas by Algorithm 3 is zero for small value of the noise. On the other hand, FISTA is faster than our algorithm (as expected, since our algorithm solves a nonlinear equation for each minimization problem.).
References
Artina, M., Fornasier, M., Solombrino, F.: Linearly constrained nonsmooth and nonconvex minimization. SIAM J. Optim. 23, 1904–1937 (2013)
Babcock, H.P., Moffitt, J.R., Cao, Y., Zhuang, X.: Fast compressed sensing analysis for super-resolution imaging using L1-homotopy. Opt. Express 21, 28583–28596 (2013)
Barenblatt, G.I.: The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Math. Mech. 7, 55–129 (1962)
Betzig, E., Patterson, G.H., Sougrat, R., Lindwasser, O.W., Olenych, S., Bonifacino, J.S., Davidson, M.W., Lippincott-Schwartz, J., Hess, H.F.: Imaging intracellular fluorescent proteins at nanometer resolution. Science 313, 1642–1645 (2006)
Black, M.J., Rangarajan, A.: On the unification of line processes, outlier rejection, and robust statistics with applications in early vision. Int. J. Comput. Vis. 19, 57–91 (1996)
Bredies, K., Lorentz, D.A., Reiterer, S.: Minimization of non-smooth, nonconvex functionals by iterative thresholding. J. Optim. Theory Appl. 165, 78–112 (2015)
Candes, E., Romberg, J., Tao, T.: Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 59, 1207–1223 (2006)
Candes, E.J., Wakin, M.B., Byod, S.: Enhancing sparsity by reweighted \(\ell _1\) minimization. J. Fourier Anal. Appl. 14, 877–905 (2008)
Casas, E., Clason, C., Kunisch, K.: Approximation of elliptic control problems in measure spaces with sparse solutions. SIAM J. Control Optim. 50, 1735–1752 (2012)
Chartrand, R.: Exact reconstruction of sparse signals via noconvex minimization. IEEE Signal Process. Lett. 14, 707–710 (2007)
Chartrand, R.: Fast algorithms for nonconvex compressive sensing: MRI reconstruction from very few data. In: IEEE Interantional Symposium on Biomedical Imaging: From Nano to Macro (2009)
Chartrand, R., Staneva, V.: Restricted isometry properties and nonconvex compressing sensing. Inverse Probl. 24, 035020 (2008)
Chartrand, R., Yin, W.: Iteratively reweighted algorithms for compressing sensing. In: IEEE International Conference on Acoustics, Speech and Signal Processing (2008)
Chen, X., Zhou, W.: Convergence of the reweighted \(\ell _1\) minimization algorithm for \(\ell _2\)-\(\ell _p\) minimization. Comput. Optim. Appl. 59, 47–61 (2014)
Chen, X., Xu, F., Ye, Y.: Lower bound theory of nonzero entries in solutions of \(\ell ^2\)-\(\ell ^p\) minimization. SIAM J. Sci. Comput. 32, 2832–2852 (2010)
Dugdale, D.S.: Yielding of steel sheets containing slits. J. Mech. Phys. Solids 8, 100–104 (1960)
Duval, V., Peyré, G.: Exact support recovery for sparse spikes deconvolution. Found. Comput. Math. 15, 1315–1355 (2015)
Fornasier, M., Ward, R.: Iterative thresholing meets free-discontinuity problems. Found. Comput. Math. 10, 527–567 (2015)
Foucart, S., Lai, M.-J.: Sparsest solutions of underdetermined linear systems via \(\ell _q\)-minimization for \(0<q\le 1\). Appl. Comput. Harmon. Anal. 26, 395–407 (2009)
Ghilli, D., Kunisch, K.: A monotone scheme for sparsity optimization in \(\ell ^p\) with \(p\in (0,1]\). In: IFAC WC Proceedings (2017)
Gu, L., Sheng, Y., Chen, Y., Chang, H., Zhang, Y., Lv, P., Ji, W., Xu, T.: High-density 3D single molecular analysis based on compressed sensing. Biophys. J. 106, 2443–2449 (2014)
Herzog, R., Stadler, G., Wachsmuth, G.: Directional sparsity in optimal control of partial differential equations. SIAM J. Control Optim. 50, 943–963 (2012)
Hess, S.T., Girirajan, T.P., Mason, M.D.: Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys. J. 91, 4258–4272 (2006)
Hintermüller, M.: Wu, Tao: Nonconvex \(TV^q\)-models in image restoration: analysis and a trust-region regularization-based superlinearly convergent solver. SIAM J. Imaging Sci. 6, 1385–1415 (2013)
Huang, B., Babcock, H.P., Zhuang, X.: Breaking the diffraction barrier: super-resolution imaging of cells. Cell 143, 1047–1058 (2010)
Huang, J., Mumford, D.: Statistics of natural images and models. In: International Conference on Computer Vision and Pattern Recognition (CVPR), Fort Collins, pp. 541–547 (1999)
Ito, K., Kunisch, K.: A variational approach to sparsity optimization based on Lagrange multiplier theory. Inverse Probl. 30, 015001 (2014)
Ito, K., Kunisch, K.: Lagrange multiplier approach to variational problems and applications. In: Advances in Design and Control 15. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2008)
Jiao, Y., Jin, B., Lu, X.: A primal dual active set with continuation algorithm for the \(\ell ^0\)-regularized optimization problem. Appl. Comput. Harmon. Anal. 39, 400–426 (2015)
Jiao, Y., Jin, B., Lu, X., Ren, W.: A primal dual active set algorithm for a class of nonconvex sparsity optimization (2013) (preprint)
Jones, S.A., Shim, S.-H., He, J., Zhuang, X.: Fast, three-dimensional super-resolution imaging of live cells. Nat. Methods 8, 499–505 (2011)
Kalise, D., Kunisch, K., Rao, Z.: Infinite horizon sparse optimal control. J. Optim. Theory Appl. 172, 481–517 (2017)
Kim, K., Min, J., Carlini, L., Unser, M., Manley, S., Jeon, D., Ye, J.C.: Fast maximum likelihood high-density low-SNR super-resolution localization microscopy. In: International Conference on Sampling Theory and Applications, Bremen, Federal Republic of Germany, pp. 285–288 (2013)
Lai, M.-J., Wang, J.: An unconstrained \(\ell _q\) minimization with \(0<q\le 1\) for sparse solution of underdetermined linear systems. SIAM J. Optim. 21, 82–101 (2011)
Lai, M.-J., Xu, Y., Yin, W.: Improved iteratively reweighted least squares for unconstrained smoothed \(\ell _q\) minimization. SIAM J. Numer. Anal. 51, 927–957 (2013)
Li, G., Pong, T.K.: Global convergence of splitting methods for nonconvex composite optimization. SIAM J. Optim. 25, 2434–2460 (2014)
Lu, Z.: Iterative reweighted minimization methods for \(\ell _p\) regularized unconstrained nonlinear programming. Math. Program Ser. A 147, 277–307 (2014)
Nieuwenhuizen, R.P.J., Lidke, K.A., Bates, M., Puig, D.L., Grünwald, D., Stallinga, S., Rieger, B.: Measuring image resolution in optical nanoscopy. Nat. Methods 10, 557–562 (2013)
Nikolova, M.: Minimizers of const-functions involving nonsmooth data-fidelity terms: applications to the processing of outliers. SIAM J. Numer. Anal. 40, 965–994 (2002)
Nikolova, M., Ng, M.K., Tam, C.-P.: Fast nonconvex nonsmooth minimization methods for image restoration and reconstruction. IEEE Trans. Image Process. 19, 3073–3088 (2010)
Nikolova, M., Ng, M.K., Zhang, S., Ching, W.-K.: Efficient reconstruction of piecewise constant images using nonsmooth nonconvex minimization. SIAM J. Imaging Sci. 1, 2–25 (2008)
Ochs, P., Dosovitskiy, A., Brox, T., Pock, T.: On iteratively reweighted algorithms for nonsmooth nonconvex optimization in computer vision. SIAM J. Imaging Sci. 8, 331–372 (2015)
Del Piero, G.: A variational approach to fracture and other inelastic phenomena. J. Elast. 112, 3–77 (2013)
Ramlau, R., Zarzer, C.: On the minimization of a Tikhonov functional with non-convex sparsity constraints. Electron. Trans. Numer. Anal. 39, 476–507 (2012)
Roth, S., Black, M.J.: Fields of experts. Int. J. Comput. Vis. 82, 205–229 (2009)
Rust, M., Bates, M., Zhuang, X.: Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methods 3, 793–796 (2006)
Shroff, H., Galbraith, C.G., Galbraith, J.A., Betzig, E.: Live-cell photoactivated localization microscopy of nanoscale adhesion dynamics. Nat. Methods 5, 417–423 (2008)
Stadler, G.: Elliptic optimal control problems with L1-control cost and applications for the placement of control devices. Comput. Optim. Appl. 44, 159–181 (2009)
Sun, Q.-: Recovery of sparsest signals via \(\ell ^q\)-minimization. Appl. Comput. Hamon. Anal. 32, 329–341 (2012)
Zhu, L., Zhang, W., Elnatan, D., Huang, B.: Faster STORM using compressed sensing. Nat. Methods 9, 721–723 (2012)
Zoubir, A., Koivunen, V., Chakhchoukh, Y., Muma, M.: Robust estimation in signal processing: a tutorial-style treatment of fundamental concepts. IEEE Signal Process. Mag. 29, 61–80 (2012)
Zuo, W., Meng, D., Zhang, L., Feng, X., Zhang, D.: A generalized iterated shrinkage algorithm for non-convex sparse conding. In: IEEE International Conference on Computer Vision, pp. 217–224 (2013)
Acknowledgements
Open access funding provided by University of Graz. We thank the referees for very thoughtful suggestions and remarks, which helped to improve our results.
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by the ERC advanced Grant 668998 (OCLOC) under the EU’s H2020 research programme.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ghilli, D., Kunisch, K. On monotone and primal-dual active set schemes for \(\ell ^p\)-type problems, \(p \in (0,1]\). Comput Optim Appl 72, 45–85 (2019). https://doi.org/10.1007/s10589-018-0036-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-018-0036-9
Keywords
- Nonsmooth nonconvex optimization
- Active-set method
- Monotone algorithm
- Optimal control problems
- Image reconstruction
- Fracture mechanics