Impacts of climate change on hurricane flood hazards in Jamaica Bay, New York

Abstract

Sea level rise (SLR) and tropical cyclone (TC) climatology change could impact future flood hazards in Jamaica Bay—an urbanized back-barrier bay in New York—yet their compound impacts are not well understood. This study estimates the compound effects of SLR and TC climatology change on flood hazards in Jamaica Bay from a historical period in the late twentieth century (1980–2000) to future periods in the mid- and late-twenty-first century (2030–2050 and 2080–2100, under RCP8.5 greenhouse gas concentration scenario). Flood return periods are estimated based on probabilistic projections of SLR and peak storm tides simulated by a hydrodynamic model for large numbers of synthetic TCs. We find a substantial increase in the future flood hazards, e.g., the historical 100-year flood level would become a 9- and 1-year flood level in the mid- and late-twenty-first century and the 500-year flood level would become a 143- and 4-year flood level. These increases are mainly induced by SLR. However, TC climatology change would considerably contribute to the future increase in low-probability, high-consequence flood levels (with a return period greater than 100 year), likely due to an increase in the probability of occurrence of slow-moving but intense TCs by the end of twenty-first century. We further conduct high-resolution coastal flood simulations for a series of SLR and TC scenarios. Due to the SLR projected with a 5% exceedance probability, 125- and 1300-year flood events in the late-twentieth century would become 74- and 515-year flood events, respectively, in the late-twenty-first century, and the spatial extent of flooding over coastal floodplains of Jamaica Bay would increase by nearly 10 and 4 times, respectively. In addition, SLR leads to larger surface waves induced by TCs in the bay, suggesting a potential increase in hazards associated with wave runup, erosion, and damage to coastal infrastructure.

Introduction

Coastal areas surrounding Jamaica Bay, which are home to hundreds of thousands of New York residences, are highly susceptible to coastal flooding. Storm surges induced by tropical cyclones (TCs) and extratropical cyclones (ETCs) result in devastating flood events in this region, as best exemplified by historical TCs such as Hurricane Donna in 1960 and Sandy in 2012 and ETCs such as the Great Appalachian Storm of November 1950 and the December 1992 event (Catalano and Broccoli 2018; Catalano et al. 2019). Climate change is expected to impact flood hazards, yet the compound impacts of sea level rise (SLR) and storm climatology change on flood hazards in Jamaica Bay are not fully understood. Recent studies found that ETC climatology change and its impact on future storm surges in the New York region would not be significant (Roberts et al. 2017; Lin et al. 2019). Here, we quantify the compound effects of SLR and TC climatology change on future flood hazards in Jamaica Bay.

Jamaica Bay is a lagoonal (or back-barrier) estuary located in the southern portion of the New York metropolitan area, in the northeastern USA (Fig. 1). The bay is sheltered from swells by the Rockaway Peninsula. Jamaica Bay’s floodplains are predominantly characterized as low-lying dense residential areas and are highly vulnerable to coastal flooding. Coastal flooding due to ETCs is more frequent in the region. Flooding caused by TCs is rare but results in devastating consequences in the New York City (NYC) region including Jamaica Bay. The worst four coastal flood events in the region were caused by TCs, including the 1788 Hurricane, the 1821 Norfolk and Long Island Hurricane, Hurricane Donna in 1960, and Hurricane Sandy in 2012 (Orton et al. 2019). Hurricanes, in specific, result in low-probability, high consequence flood events that cause long-term effects on the coastal environment and socioeconomic impacts. For example, Hurricane Sandy caused at least $50 billion in economic losses and 159 deaths (Blake et al. 2013). The return period of Sandy’s flood level is estimated to be from 260 years (Orton et al. 2016) to 398 years (Lin et al. 2016).

Fig. 1

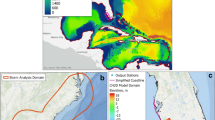
Basin-scale (top left) and high-resolution regional-scale (top right) meshes of ADCIRC model. Bottom panel shows the bathymetry of Jamaica Bay in the high-resolution mesh. The locations of water level measurements are shown by star (USGS gauges) and cross (high water marks) signs. Triangles show locations of NOAA tide gauge stations where SLR data are available. The solid circle in Jamaica Bay shows the bay’s representative location used in the synthetic storm selection

Climate change is expected to make TC-induced coastal flooding more destructive in the coming decades (Lin et al. 2012; Irish et al. 2014). SLR will increase the severity and frequency of coastal flooding worldwide (Hunter et al. 2013; Wu et al. 2017; Rasmussen et al. 2018). Studies of historical water level observations have shown that the global mean sea level and the local mean sea level in many locations worldwide have been raising since the last century and it is projected that SLR will accelerate in the present and following centuries (Kopp et al. 2014; Hay et al. 2015; Chen et al. 2017; Horton et al. 2018). It has been also understood that SLR would increase the frequency of extreme sea levels (e.g., Tebaldi et al. 2012; Karim and Mimura 2008; Rasmussen et al. 2018). For example, under the assumption that the variability of storms will remain constant in the future, Tebaldi et al. (2012) found that the SLR in 2050 would lead to a 100-year storm surge level to become a between 4- and 100-year surge level along the U.S. coasts. Regional scale studies found that SLR has increased the height of historical coastal floods in the NYC region (Kemp and Horton 2013; Talke et al. 2014; Lin et al. 2016). Garner et al. (2017) projected that sea-level rise would cause a substantial increase in flood heights in NYC in coming centuries compared with preindustrial or modern flood heights.

TC climatology change could also worsen flood hazards as previous studies have shown that global warming could result in stronger and possibly more frequent TCs (Webster et al. 2005; Knutson et al. 2010; Emanuel 2013; Bhatia et al. 2018). Knutson et al. (2019) showed that, with a medium-to-high confidence, the global average of TC intensity will increase in the future. Under the 2 °C global greenhouse warming scenario, they found that almost all available projections (from models with a spatial resolution of 60 km or finer) agree on an increase in the proportion of TCs that reach a category 4–5 hurricane intensity.

There is currently little understanding of how future flood hazards in Jamaica Bay would respond to climate change. Recently, Marsooli et al. (2019) studied the compound effects of SLR and TC climatology change on TC flood levels along the U.S. East and Gulf Coasts. According to projections based on six climate models (under RCP8.5), they found that the 100-year flood level in the late twentieth century would become a 1-year flood level by the end of twenty-first century in New York county. However, this county-scale assessment cannot provide information on climate change impacts at the very local scale. A previous local-scale study by Lin et al. (2012) evaluated the effects of climate change on the end-of-twenty-first-century flood return periods for NYC. They found that combined effects of storm climatology change and a 1-m SLR may change the present NYC 100-year surge flood event to between 3- and 20-year event by the end of the century. The study was performed based on flood levels calculated for The Battery NY, i.e., the location of a tide gauge station at the southern tip of Manhattan. Flood hazards for The Battery (or New York County) do not accurately represent the hazards for Jamaica Bay. The Battery is located about 15 km away from the Jamaica Bay’s inlet. A different geometry and bathymetry in Jamaica Bay results in different flood levels in the bay compared to those at The Battery. For example, numerical simulations by Marsooli et al. (2017) showed that the peak storm tide generated by Hurricane Sandy in 2012 in Jamaica Bay was up to 0.7 m smaller than The Battery’s peak storm tide.

Furthermore, previous studies quantified climate change impacts on probabilities of flood levels off the coast of NYC, i.e., coastal floodplains were excluded (e.g., Lin et al. 2012; Lin et al. 2016; Marsooli et al. 2019). For a risk-informed design of coastal infrastructure and flood mitigation strategies, it is also desirable to quantify probabilities of other flood characteristics, e.g., wave heights and the extent of flooding over coastal floodplains. Quantifying such probabilities is a compute-intensive task, owing to the high computational cost of high-resolution hydrodynamic models which are needed for resolving coastal floodplains. In addition, studies that assess the impacts of climate change on future flood hazards should also be performed for multiple time frames, if such studies aim to aid the design and implementation of efficient and effective flood mitigation strategies. A multiple time frame study supports the development of incremental flood mitigation strategies over time. Thus, flood mitigation measures can be designed and built in a way that while mitigating the current and near future flood hazards, they can be updated, instead of replaced, to effectively perform in the further future.

To address the needs mentioned above, we utilize a methodology that combines climatologic-hydrodynamic modeling with high-resolution hydrodynamic-wave modeling to elucidate climate change impacts on TC flood hazards in Jamaica Bay and its coastal floodplains. The goal of the study is to assess the effects of SLR and TC climatology change on TC-induced flood hazards for two future time frames in the twenty-first century. By means of climatology-hydrodynamic modeling and statistical analysis, we quantify changes in return periods of flood levels at a representative site in the bay from the historical period of 1980–2000 (late-twentieth century) to future periods of 2030–2050 (mid-twenty-first century) and 2080–2100 (late-twenty-first century). This analysis, involving a large number of simulations (26,000 synthetic events), is performed based on the basin-scale relatively-low-resolution hydrodynamic modeling mesh developed by Marsooli et al. (2019). The synthetic TC dataset, different from the basin-scale dataset used by Marsooli et al. 2019, is specifically generated for the Jamaica Bay region. In order to further study the coastal flooding characteristics, we generate a regional-scale, high-resolution coupled hydrodynamic and wave model to carry out simulations for extreme scenarios selected based on the climatology-hydrodynamic modeling. This scenario-based high-resolution analysis demonstrates the evolving impacts of climate change on surface waves and the extent of flooding over Jamaica Bay’s floodplains.

Methods

Synthetic TCs and SLR datasets

Synthetic TCs used in this study are generated for the Jamaica Bay area by the statistical/deterministic hurricane model of Emanuel et al. (2008). The hurricane model generates synthetic TCs for a given large-scale atmospheric and oceanic environment estimated from observations or a climate model. We utilize TC datasets generated for the observed climate of the historical period of 1980–2000 (late twentieth century) from the National Centers for Environmental Prediction (NCEP) reanalysis (Kalnay et al. 1996; updated). Records of Atlantic TC counts during the historical period of 1980–2000 indicate an average number of 10.6 TCs per year in the Atlantic basin. TC counts are anomalously low in certain years during this historical period. Sabbatelli and Mann (2007) found that the low TC counts in 1982 and 1997 correspond to prominent El Nino years and the low TC counts in early 1990s correspond to El Nino-like conditions.

We also utilize TC datasets generated for the modeled climates of the historical period of 1980–2000 (late twentieth century) and two future periods including 2030–2050 (mid-twenty-first century) and 2080–2100 (late-twenty-first century). TCs for the future periods are generated under the RCP8.5 greenhouse gas concentration scenario. The modeled climates are based on four global climate models including: GFDL5 (Geophysical Fluid Dynamics Laboratory Climate Model, USA); HadGEM5 (Hadley Centre Global Environment Model, U.K. Meteorological Office); MPI5 (Max–Planck–Institute for Meteorology, Germany); and MRI5 (Meteorological Research Institute, Japan). Each of the 13 utilized TC datasets contains 2000 synthetic TCs that impact the study area. Each synthetic TC passes within a 200 km radius from coordinates (40.61° N and 73.84° W), which is chosen as the representative location for Jamaica Bay (Fig. 1).

SLR data are based on the localized SLR dataset from Kopp et al. (2014). This dataset provides projections of the probability distribution function (PDF) of relative sea levels at global tide gauge stations under various emission scenarios. We select the 2050 and 2100 SLR projections under the RCP 8.5 scenario at the Battery (New York) and Sandy Hook stations (the closest gauge stations to our study area).

Hydrodynamic and wave modeling

We utilize the ADvanced CIRCulation model, ADCIRC (Luettich et al. 1992; Westerink et al. 1994), to simulate storm tides (combination of storm surge and astronomical tide) for all the synthetic TCs. We also utilize the ADCIRC model coupled with the Simulating WAves Nearshore model (Booij et al. 1999; Ris et al. 1999), i.e., ADCIRC+SWAN (Dietrich et al. 2011), to simulate surface waves and the extent of coastal flooding induced by a series of selected TC and SLR scenarios.

We adopt the ADCIRC’s basin-scale computational mesh developed by Marsooli and Lin (2018), shown in Fig. 1, to simulate all synthetic TC storm tides. This mesh provides a balance between the accuracy of simulations and the computational cost, making it an efficient tool for use in probabilistic flood hazard studies where one often needs to simulate thousands of storm scenarios. We generate a high-resolution, regional-scale computational mesh for Jamaica Bay, shown in Fig. 1, to simulate surface waves and coastal flooding using ADCIRC+SWAN. The mesh has a resolution of 20 m over the bay’s floodplains and between 20 m and 50 m in the bay’s deep waters. Additional details and validation of basin-scale and the high-resolution hydrodynamic models can be found in the supplemental material (see Supplementary Fig. S1).

We use the high-resolution ADCIRC+SWAN model of Jamaica Bay to demonstrate the impact of SLR on flood hazards. Due to the high computational cost of the model, we simulate only a limited number of SLR and storm scenarios. Two TCs, associated with 125- and 1300-year storm tide levels in the historical period of 1980–2000, are selected. The TC tracks and intensities are shown in Supplementary Fig. S2. Each TC is simulated under a series of SLR scenarios including 0.19 m, 0.38 m, and 0.59 m in the mid-twenty-first century and 0.44 m, 0.96 m, and 1.54 m in the late-twenty-first century. These selected values of SLR have a specific chance of exceedance at the location of tide gauge stations near Jamaica Bay. For example, in both periods of mid- and late-twenty-first century, the chances of exceedance are, respectively, 95%, 50%, and 5% at the Battery station (see Supplementary Fig. S3). At the Sandy Hook station, the selected SLR scenarios have a slightly larger chance of exceedance.

Statistical analysis

We adopt the extreme value theory to estimate the storm tide return periods based on the TC annual frequency and the cumulative distribution function (CDF) of peak storm tides. Assuming that TCs arrive as a stationary Poisson process under a given climate, the return period of TC-induced storm tide η_TC exceeding a given level h is

$$ {T}_{\eta_{TC}}(h)=\frac{1}{Fr\times \left(1-P\left\{{\eta}_{TC}\le h\right\}\right)} $$

(1)

where P{η_TC ≤ h} is the CDF of peak storm tide and Fr is the TC annual frequency. Extreme events may produce a long tail of the probability distribution. The large number of synthetic storms allows one to estimate the tail directly using an empirical storm tide CDF. However, here we model the tail of the storm tide CDF using the Peaks-Over-Threshold method (POT) with a Generalized Pareto Distribution (GPD) and maximum likelihood estimation (Coles 2001). The rest of the distribution is modeled using a nonparametric density estimation. The analytical CDF reduces the noise at high return periods and can be used to estimate the return periods of extremes that are beyond the empirical points. The threshold value that separates the tail from the rest of the distribution is selected by trial and error so that the root mean square error in the fitted CDF curve (compared to empirical points) is minimal.

To include the effects of SLR, the flood level η is defined as the combination of TC storm tide and relative sea level (RSL). Thus, the return period of flood level η exceeding a given level h is estimated as

$$ {T}_{\eta }(h)=\frac{1}{Fr\times \left(1-P\left\{\eta \le h\right\}\right)} $$

(2)

where P{η ≤ h} is the CDF of flood level which is calculated through a convolution of the CDF of storm tide and the PDF of relative sea level f_s(s) (Lin et al. 2016; Lin and Shullman 2017; Marsooli et al. 2019) as

$$ P\left\{\eta \le h\right\}=P\left\{{\eta}_{TC}+ RSL\le h\right\}={\int}_{-\infty}^{+\infty }P\left\{{\eta}_{TC}\le h- RSL\right\}{f}_s(s) ds $$

(3)

Due to inherent uncertainties of climate models, climate projections and consequently estimates of future flood return levels may be biased. We adopt the bias-correction approach used by Lin et al. (2016) and Marsooli et al. (2019) to calculate and remove biases from projected storm tide flood levels. In this approach, before combining with the PDF of relative sea level, we bias-correct the TC frequency and storm tide CDFs for each climate model by comparing the climate-model-based estimates of the frequencies and storm tide CDFs for the historical period with NCEP-based estimates. The biases calculated for the historical period are assumed to remain the same over time and, thus, are employed to bias-correct the future projections.

We present flood return level projections estimated for each climate model as well as composite projections which represent the weighted-average estimate over all climate models. The weighted-average projections are estimated based on the approach used by Lin et al. (2019) and Marsooli et al. (2019). In this approach, a weighting factor, between zero and one, is calculated for each climate model based on the accuracy of the estimated storm tide return levels for the historical period compared to the NCEP-based return levels for the same period. By comparing the NCEP-based and model-based flood return level estimates for the historical period, not shown here, we find that estimates based on HADGEM5 are the most accurate, followed by MRI5, MPI5, and GFDL5. The weighting factors for these models are calculated to be, respectively, 0.34, 0.25, 0.24, and 0.17.

Results

TC climatology

Figure 2 shows the CDF of synthetic TC properties when TCs are at their closest distance to the reference point of Jamaica Bay. CDFs are estimated based on a generalized extreme value distribution fitted to the data. We perform a t-test to quantify the significance of changes over time in TC properties. We consider changes to be statistically significant when the p value is equal or smaller than 0.05. Averaged over all models, the TC translation speed, V_T, would significantly change from the historical time period to the mid- and late-twenty-first century (p values of 0.010 and 0.019, respectively). We find that the average probability (averaged over all models) of a TC, when at its closest distance to Jamaica Bay, to move with a V_T < 5 m s⁻¹ increases by 0.9% and 5.4% in the mid- and late-twenty-first-century periods, respectively. The average probability that a TC moves with a V_T > 15 m s⁻¹ decreases by 2.2% and 7.2%, respectively. These findings are consistent with the storm characteristics in the basin-scale synthetic TC datasets used by Marsooli et al. (2019), which similarly showed an increase in the number of slow-moving TCs in the future climate in the western North Atlantic basin. While there exists limited discussion on how TC translation speed would change in the future, using global TC “best-track” data, Kossin (2018) found that the global TC translation speed has reduced by 10% over the time period of 1949–2016.

Fig. 2

CDF of TC properties for the late-twentieth-century (black), mid-twenty-first-century (blue), and late-twenty-first-century (red) periods

Projections from all models agree that the radius of maximum wind speed, R_max, would reduce over time. The t-test indicates statistically significant reduction in R_max, with an averaged p value of 0.036 for the mid-twenty-first century and about zero for the late-twenty-first century. Averaged over all models, the probability that a TC has a R_max < 40 km and R_max > 60 km changes by, respectively, 2.2% and − 4.7% by the mid-twenty-first century and 9.8% and − 9.8% by the late-twenty-first century.

Synthetic tracks show an increase in the probability that a TC with a hurricane intensity can reach the region of study by the end of twenty-first century (the region of study covers an area within 200 km from Jamaica Bay) (Supplementary Fig. S4). All models except MRI5 agree that the intensity of TCs (represented here by the maximum wind speed, V_max) would significantly increase by the end of twenty-first century. Averaged over all models, the probability of a TC to have a V_max > 33 m s⁻¹ (hurricane strength) increases by 1.7% (2.3% if MRI5 excluded) by the mid-twenty-first century and 5.9% (7.9%) by the late-twenty-first century. This projected increase in TC intensity in the future climate is consistent with most other projections (Knutson et al. 2019). The projected increase in V_max is also consistent with the projected decrease in R_max, given their physical relationship.

Differences (averaged over all models) between future and historical synthetic TC track densities (see Supplementary Fig. S5) indicate an eastward shift in storm tracks by the end of twenty-first century. This is consistent with Garner et al. (2017) who found an offshore shift of storm tracks at the latitude of NYC.

There are some discrepancies among projections from each individual model. For example, projections from GFDL5, HADGEM5, MPI5, and MRI5 show, respectively, a change of − 15.1%, − 4.5%, − 1.2%, and − 8.0% in the probability that a given TC has a translation speed of greater than 15 m s⁻¹ from the historical period to the late-twenty-first-century period. We performed a bootstrap analysis to assure that our TC track datasets are large enough for making stable conclusions. The analysis showed that the calculated percentage changes in TC parameters agree with the distribution of percentage changes obtained across the bootstrap samples, assuring that our datasets are sufficiently large. For instance, based on the original GFDL5 dataset, the probability of a TC to have a translation speed of smaller than 5 m s⁻¹ would increase by 4.59% from the historical period to the mid-twenty-first century period, which agrees with the distribution of changes calculated based on the bootstrap samples which shows a mean increase of 4.55% and a standard deviation of 0.62%. Therefore, discrepancies among projections from the different climate models can be due to systematic differences in the models such as the resolution, initial conditions, and emphasized physical processes.

Supplementary Table S1 summarizes the annual TC frequency, i.e., the number of TCs (passing within 200 km from Jamaica Bay) in any given year within a specific time period. The annual frequency in 1980–2000 is about 0.39 based on NCEP-based and most model-based datasets. The GFDL5 model shows a smaller frequency for the historical period. However, compared to other models, the GFDL5 model projects a substantial increase (up to 377%) in the future TC frequencies. Projections from HADGEM5 and MPI5 indicate a moderate increase in the TC frequency while projections from MRI5 show only a subtle change.

Flood return levels

Figure 3 shows the estimates of flood return levels at the representative site in the bay (40.60°N and 73.80°W), located near the bay head and the Inwood USGS gauge where the model accurately simulated historical flood levels (see Fig. 1), for the historical and future time periods. The very-likely range (5th–95th percentiles; i.e., 90% statistical confidence interval) is shown by the shaded area. Under the compound effects of SLR and TC climatology change, the flood level for a given return period would substantially increase from the historical period in the late twentieth century to the future periods in the twenty-first century. For example, while the 100-year weighted-average flood level in the historical period is 1.68 m (with a very-likely range of 1.63–1.75 m), it increases to 2.13 m (2.09–2.19 m) and 3.23 m (3.14–3.42 m) in the mid and late twenty-first century, respectively.

Fig. 3

Flood return period curves for the NCEP-based late-twentieth-century period, and model-based mid- and late-twenty-first-century periods. Flood levels are relative to the mean-sea-level vertical datum. Shaded areas cover the very-likely-range estimates (i.e., 90% statistical confidence interval; 5th to 95th percentiles). The future return period curves are bias-corrected. Black circles represent NCEP-based empirical data. Observation-based empirical data are based on water level observation at The Battery gauge station

Flood return periods presented here are bias-corrected based on biases that are estimated by comparing NCEP-based projections for the historical period of 1980–2000 with model-based projections for the same historical period. Thus, it is assumed that NCEP-based projections realistically represent flood hazards for the historical period. One may perform a sanity check by comparing the NCEP-based flood return periods with return periods estimated based on water level observations at tide gauge stations. Because there are no records of water level observations in Jamaica Bay for the historical period of 1980–2000, we use water level observations at a nearby tide gauge station, i.e., The Battery NY station in the Upper Bay, operated by the National Oceanic and Atmospheric Administration (NOAA). The Battery station is located at the southern tip of Manhattan in NYC, about 15 km away from the Jamaica Bay’s inlet.

Figure 3 (circles in magenta) displays flood return periods estimated based on the observed TC-induced water levels at The Battery. No attempt was made to fit a return period curve to the observation-based estimates, given the low number of TC events between 1980 and 2000. The NCEP-based and observation-based return levels compare relatively well but show some discrepancies. We hypothesized that the discrepancies could be due to major geometric and bathymetric differences in Jamaica Bay and Upper Bay, resulting in different flood levels during a single storm. For example, the peak storm tide generated by Hurricane Sandy in 2012 in Jamaica Bay was up to 0.7 m smaller than that at The Battery station. However, based on our model outputs, the NCEP-based return levels at the Battery also show discrepancies with the observations. We investigated the effects of small observed water level sampling size by generating NCEP-based return period curves for small sample chunks from NCEP tracks, but the discrepancies persisted. Thus, the discrepancies exist mainly because, in synthetic modeling approach, the generated NCEP tracks are only statistical representations in the reanalysis climate environment of the historical tracks.

Weighted-average return period curves in Fig. 3 show that, under the effect of only TC climatology change, flood levels with a return period smaller than 100 year barely change. However, the effect of TC climatology change on low-probability flood levels (i.e., return periods greater than 100 year) is non-negligible, especially by the end of twenty-first century. To further illustrate, Fig. 4 displays contributions of SLR and TC climatology change to the flood level increase from the historical period to the future periods. We find that the effects of SLR dominate the effects of TC climatology change. However, TC climatology change becomes a major source of increases in low-probability, high-consequence flood levels, especially in the late-twenty-first-century period. For example, from the historical period of 1980–2000 to the late-twenty-first-century period of 2080–2100, while TC climatology change contributes to only 11% of the increase in 100-year flood level it contributes to 19%, 22%, and 31% of the increases in 500-, 1000-, and 10,000-year flood levels in Jamaica Bay. The large increase in these low-probability flood levels is likely due to the increase in the probability that slower and more intense TCs pass within 200 km from Jamaica Bay by the end of twenty-first century (Figs. 2 and S4).

Fig. 4

Contribution of SLR and TC climatology change to the weighted-average changes in flood return levels from the historical period (NCEP) to the mid- and late-twenty-first-century periods

Similar to the weighted-average projections, projections from each individual model (Fig. 3) suggest that the combined effects of SLR and TC climatology change result in a substantial increase in flood levels. Projections based on GFDL5 show the largest increase in the future flood levels whereas MRI5 projects the smallest change. Projections based on the GFDL5 and HADGEM5 model suggest that TC climatology change by the end of twenty-first century substantially increases flood levels associated with low probability but high consequence events (i.e., flood return periods greater than 100 year). Similar patterns but with a smaller magnitude can be observed from projections based on the MPI5 model. In contrast, projections based on the MRI5 model indicate that while the TC climatology change has negligible effects on flood levels due to high-probability events, it decreases flood levels associated with rare but devastating events in the late-twenty-first-century period. The reason for this projected decrease in flood levels is likely that TC projections based on MRI5 show negligible changes in TC intensity and frequency (Fig. 2 and Table S1) but a profound eastward shift in TC track densities.

Scenario-based coastal flooding

Results presented in the previous section elucidated that the effects of SLR on future flood levels dominate the effects of TC climatology change. Here we use the high-resolution model to quantify effects of SLR on surface waves and the extent of flooding under scenarios described in Section 2.2. The SLR scenarios are simulated for two selected synthetic TCs shown in Supplementary Fig. S2. The return periods of the combined SLR and TC scenarios are estimated based on the climatology-hydrodynamic modeling discussed in the previous section. Under no SLR, the two selected TCs generate flood levels of 1.76 and 2.61 m, which are approximately equal to 125- and 1300-year flood levels in the historical time period of 1980–2000. Hereafter, we refer to these TC scenarios as the historical high- and low-probability TC scenarios. Under a SLR of 0.59 m (5% chance of exceedance in the mid-twenty-first century), for example, these TCs generate flood levels of 2.39 and 3.08 m, which are equal to 214- and 1167-year flood levels in the 2030–2050 time period. Under a SLR scenario with the same chance of exceedance but in the late-twenty-first century (1.54 m), the TCs generate flood levels of 3.13 and 3.97 m, which are equal to 74- and 515-year flood levels in the 2080–2100 time period.

Figures 5 and 6 illustrate the spatial extent of flooding induced by the selected TC and SLR scenarios. The extent of flooding is defined here as the area above the mean-higher-high-water level that is normally dry but becomes wet during a storm event. With a 0.0 m SLR (i.e., control runs), the extent of flooding covers, respectively, 3.55 km² and 13.45 km² of floodplains under the historical high- and low-probability TC scenarios (Table 1). The flooded areas are mainly located on the eastern side of the bay. For the same TCs, the extent of flooding dramatically increases as sea level rises. The extent of flooding induced by the high-probability TC scenario increases, respectively, 38%, 99%, and 210% under SLR scenarios of 0.19 m, 0.38 m, and 0.59 m (which have a chance of exceedance of 95%, 50%, and 5% in the mid-twenty-first century). The extent of flooding induced by the low-probability TC scenario increases, respectively, 28%, 67%, and 106% for the same SLR scenarios. Under SLR scenarios of 0.44 m, 0.96 m, and 1.54 m in the late-twenty-first-century period (which have a chance of exceedance of 95%, 50%, and 5% in the late-twenty-first century), the extent of flooding increases 130%, 477%, and 925% for the high-probability TC and 79%, 160%, and 359% for the low-probability TC scenario.

Fig. 5

Spatial extent of coastal flooding induced by the high-probability TC scenario. SLR scenarios have a 50% and 5% chance of exceedance in the mid-twenty-first century (panels a and b) and the late-twenty-first century (panels c and d). Areas in dark and light blue cover flooded areas (wetted areas above the mean-higher-high-water-level vertical datum)

Fig. 6

Spatial extent of coastal flooding induced by the low-probability TC scenario. SLR scenarios have a 50% and 5% chance of exceedance in the mid-twenty-first century (panels a and b) and the late-twenty-first century (panels c and d). Areas in dark and light blue cover flooded areas (wetted areas above the mean-higher-high-water-level vertical datum)

Table 1 Flooded area and extreme waves area induced by the high- and low-probability TC scenarios under selected SLR scenarios. The chance of SLR exceedance is based on SLR projections at the location of The Battery tide gauge station

In addition to the extent of flooding, rising sea levels amplify wave hazards. As sea level rises, water depth increases which, in turn, allows larger waves to reach currently shallow areas in the bay. Figure 7 compares the peak significant wave height, H_s,max, calculated for the control runs (no SLR) and the 5% exceedance SLR scenarios. For the control runs, wave heights are larger in the deep regions of the bay including the bay’s inlet, shipping channels around the bay, and Grassy Bay (the easternmost region of the bay near the J.F. Kennedy International Airport). Smaller wave heights are calculated in shallow areas in the center of the bay. For the future SLR scenarios, larger wave heights are calculated in the center of the bay as deeper waters allow larger waves to be developed.

Fig. 7

Temporal peak significant wave height H_s,max generated by the historical high-probability (a to c) and low-probability (d to f) TCs under three SLR scenarios

Under no SLR, the calculated H_s,max for the historical high- and low-probability TC scenarios is greater than 1 m in about, respectively, 11.40 km² and 13.16 km² of the study area (Table 1). Under SLR scenarios that have a chance of exceedance of 95% in the mid- and late-twenty-first century, i.e., SLR of 0.19 m and 0.44 m, the area with a H_s,max greater than 1 m is 12.37 km² and 13.96 km² for the high-probability TC scenario and 14.10 km² and 15.54 km² for the low-probability TC scenario, suggesting 8.5%, 22.5%, 7.1%, and 18.1% of increases compared to the no SLR scenarios (see Supplementary Fig. S6). Under SLR scenarios that have a chance of exceedance of 5% in the mid- and late-twenty-first century, i.e., SLR of 0.59 m and 1.54 m, the area of H_s,max greater than 1 m changes to 15.03 km² (31.8% increase) and 23.26 km² (104% increase) for the high-probability TC, and 16.62 km² (26.3% increase) and 28.55 km² (117% increase) for the low-probability TC scenario (Fig. 7).

Discussion

Model projections reveal a substantial increase in TC-induced flood hazards in Jamaica Bay by the end of twenty-first century. For example, we find that the weighted-average best estimate of 100-year flood level changes from 1.68 m in the historical period to 3.23 m in the late-twenty-first century (i.e., an increase of 1.55 m). Our findings agree with those from other studies conducted for nearby regions. For example, Lin et al. (2012) projected an increase of between 0.8 m and 1.75 m in the 100-year flood level at The Battery NY. More recently, based on projections from six climate models, Marsooli et al. (2019) found that the 100-year flood level for the New York county increases between 1.36 m and 1.90 m (with a weighted-average increase of 1.53 m) from the historical period of 1980–2005 to the future period of 2070–2095.

There are some limitations to our estimates of flood return periods. The basin-scale computational mesh used for return period calculations has a spatial resolution of 1 km at the coast and coarser offshore. A higher resolution mesh would better resolve the complex bathymetry and geometry of the study area. We neglected nonlinear interactions between SLR and storm tides. Previous studies have shown that the nonlinear interactions are small in the NYC area (Lin et al. 2012). However, depending on the bathymetry and geometry, the nonlinear interactions could locally influence the tidal range and storm surge heights (e.g. Atkinson et al. 2013; Passeri et al. 2018; Bilskie et al. 2014, 2019; Idier et al. 2019). Accounting for the nonlinear interactions in a probabilistic framework may require simulating large numbers of storms under various SLR scenarios, which is computationally expensive. Future studies may investigate nonlinear interactions between SLR and storm tide in Jamaica Bay and develop cost-effective parametric approximations for use in flood hazard assessment studies.

Flood return period calculations neglected the effects of surface waves on storm tides. Although the short wind fetch in the bay limits the generation of wind waves and the Rockaway Peninsula shelters the bay from swells, neglecting wave effects could introduce additional uncertainties into our projections of the flood return periods. To assess the effects of waves and a higher spatial resolution on model results, one can compare storm tides calculated by the basin-scale and high-resolution models for the same TC. The peak storm tides (at a selected location within the bay) calculated for the high- and low-probability TC scenarios (with no SLR) are, respectively, 1.68 m and 2.51 m from the basin-scale model and 1.76 m and 2.61 m from the high-resolution model. Thus, compared to the high-resolution model, the basin-scale model shows an absolute error of − 4.5% and − 3.8%. Such errors in storm tide simulations can induce uncertainties in the projected flood return periods, which need to be quantified in future studies.

Scenario-based simulations using the high-resolution model showed that the spatial extent of flooding over Jamaica Bay’s floodplains substantially increases by the end of twenty-first century. To protect coastal communities susceptible to flooding, it is essential to plan and implement effective flood mitigation strategies in a timely manner. Such strategies may consider flood hazards due to not only SLR and TC storm tide but also rainfall runoff. Storm climatology change will likely increase TC rainfall rates in the future (Bacmeister et al. 2018; Gutmann et al. 2018). Also, large amounts of rainfall from slow-moving storms (which may become more frequent in the future) can lead to the accumulation of runoff behind flood protection measures and potentially exacerbate flooding (Zhang et al. 2018; Silva-Araya et al. 2018). Flood protection strategies should also take into account the increasing hazards associated with surface waves. Our scenario-based simulations suggested that SLR increases extreme wave heights within the bay which, in turn, can lead to larger wave setup and runup. Larger waves also cause more severe coastal erosion and damage to infrastructure.

Conclusion

Characteristic parameters of the synthetic TCs that pass within a 200-km radius from Jamaica Bay revealed a statistically significant reduction in the TC translation speed from a historical period in the late-twentieth century (1980–2000) to future periods in the mid- and late-twenty-first century (2030–2050 and 2080–2100) under the RCP8.5 scenario. We found that the probability (averaged over four climate models) of a TC to have a translation speed of smaller than 5 m s⁻¹ (when the TC is at its closest distance to the bay) would increase by 0.9% and 5.4% in the mid- and late-twenty-first-century periods, respectively. We also found a reduction in the radius of maximum wind of future TCs. For example, the probability of a TC to have a radius of maximum wind speed smaller than 40 km would increase by, respectively, 2.2% and 9.8% in the mid- and late-twenty-first-century periods. Our analysis showed an increase in the intensity of future TCs (intensity was represented by the maximum wind speed). For instance, we found an increase of 1.7% and 5.9% in the probability of a TC with a maximum wind speed greater than 33 m s⁻¹ in the future periods of mid and late twenty-first century, respectively.

We found a substantial increase in Jamaica Bay’s flood return levels by the end of the twenty-first century. For example, the weighted-average best estimate of 100-year flood level would increase by 27% and 92% from the historical period to the mid- and late-twenty-first-century periods, respectively. Our projections suggested that the effects of SLR on future flood hazards in Jamaica Bay dominate the effects of TC climatology change. However, the effects of TC climatology change become important for low-probability, high-consequence flood levels. For example, from the historical period to the late-twenty-first-century period, while TC climatology change contributes to only 11% of the increase in the 100-year flood level (89% of increase is due to SLR), it contributes to 22% and 31% of the increases in the 1000- and 10,000-year flood levels, respectively. Projections based on two climate models, GFDL5 and HADGEM5, showed that TC climatology change would substantially increase flood levels that have a return period of greater than 100 year. For example, the contribution of TC climatology change to the future increase in 1000-year flood level is 22% based on the weighted-average projections but 38% and 37% based on projections from GFDL5 and HADGEM5, respectively.

We further utilized a high-resolution hydrodynamic-wave model to simulate surface waves and the spatial extent of coastal flooding induced by two selected TCs under different SLR scenarios. The selected TCs generate 125-year and 1300-year flood levels in the historical period. The scenario-based simulations showed that SLR results in a substantial increase in both the surface wave height and the spatial extent of flooding. For instance, model runs for the 125-year TC event showed that the extent of flooding would increase by 2.3, 5.8, 10.3 times under a SLR of 0.44 m, 0.96 m, and 1.54 m, which have, respectively, a chance of exceedance of 95%, 50%, and 5% in the late twenty-first century. Under these SLR scenarios and the same TC, the area with a peak significant wave height greater than 1 m was calculated to be 1.2, 1.6, and 2 times larger than that under no SLR scenario.

The modeling methodology adopted in this study promised future advances in understanding of climate change impacts on coastal flood characteristics. We utilized a computationally cost-effective hydrodynamic-climatologic modeling approach for probabilistic analysis of flood hazards and a high-resolution hydrodynamic-wave modeling approach for scenario-based analysis of coastal flooding characteristics (with probability of scenarios defined based on the probabilistic analysis). The combination can be used for design of flood mitigation measures, which requires the quantification of extremes (hence the large number of simulations and probabilistic analysis) and at the same time local characteristics of coastal flooding. To support specific design, the high-resolution hydrodynamic-wave modeling may be applied to a wider range of SLR and TC scenarios than that considered in this study. The coupled methodology may also be applied to a wider range of SLR, TC, and climate models to better account for the deep uncertainties in flood hazard projections in a changing climate.