Dealing with hurricane surge flooding in a changing environment: part I. Risk assessment considering storm climatology change, sea level rise, and coastal development

Abstract

Coastal flood risk will likely increase in the future due to urban development, sea-level rise, and potential change of storm surge climatology, but the latter has seldom been considered in flood risk analysis. We propose an integrated dynamic risk analysis for flooding task (iDraft) framework to assess coastal flood risk at regional scales, considering integrated dynamic effects of storm climatology change, sea-level rise, and coastal development. The framework is composed of two components: a modeling scheme to collect and combine necessary physical information and a formal, Poisson-based theoretical scheme to derive various risk measures of interest. Time-varying risk metrics such as the return period of various damage levels and the mean and variance of annual damage are derived analytically. The mean of the present value of future losses (PVL) is also obtained analytically in three ways. Monte Carlo (MC) methods are then developed to estimate these risk metrics and also the probability distribution of PVL. The analytical and MC methods are theoretically and numerically consistent. A case study is performed for New York City (NYC). It is found that the impact of population growth and coastal development on future flood risk is relatively small for NYC, sea-level rise will significantly increase the damage risk, and storm climatology change can also increase the risk and uncertainty. The joint effect of all three dynamic factors is possibly a dramatic increase of the risk over the twenty-first century and a significant shift of the probability distribution of the PVL towards high values. In a companion paper (Part II), we extend the iDraft to perform probabilistic benefit-cost analysis for various flood mitigation strategies proposed for NYC to avert the potential impact of climate change.

1 Introduction

Tropical cyclones (TCs; aka hurricanes) have induced devastating storm surge flooding worldwide (e.g., Hurricanes Katrina of 2005 and Sandy of 2012 in the U.S., Cyclone Nargis of 2008 in Myanmar, and Typhoon Haiyan of 2013 in Philippines). The impacts of these storms may worsen in the coming decades because of rapid coastal development (Curtis and Schneider 2011) coupled with sea-level rise (Nicholls and Cazenave 2010) and possibly increasing TC activity due to climate change (Bender et al. 2010; Knutson et al. 2010; Emanuel 2013). Major advances in coastal flood risk management are urgently needed (NRC 2014; Rosenzweig and Solecki 2014). Given the inherent uncertainties in the future climate and social/economic systems, such risk management should be strongly informed by probabilistic risk assessment (Lin 2015).

Various methods of “catastrophe loss modeling” have been developed over the past decades to assess coastal flood risk (Grossi et al. 2005; Wood et al. 2005; Czajkowski et al. 2013, among others). These approaches combine modeling of the hazards (i.e., storm surges induced by tropical and/or extratropical cyclones) and information about the exposure and vulnerability to quantify potential losses and risk. Most of these methods, however, model the hazards primarily based on historical records with “stationary” assumptions and thus are not readily applicable to estimate risk in a changing or “non-stationary” climate. The effect of climate change may be accounted for with pre-assumed factors for sensitivity analyses (Ou-Yang and Kunreuther 2013). To obtain more objective projection of future risk, the catastrophe loss modeling is better coupled with state-of-the-art climate modeling (Hall et al. 2005; Hallegatte et al. 2010). However, only a few studies have translated model-projected climate change to social/economic impacts (Tol 2002a, b; Mendelsohn et al. 2012), and analytical frameworks for projecting future damage risk, especially those related to extreme weather events, are still sparse (Bouwer 2013).

To build a comprehensive framework for projecting future storm surge flood risk, it is necessary to consider climate-model projected change in the relative sea level (RSL; including the effect of land subsidence) and storm surge climatology (i.e., surge frequency and magnitudes) and economic/social-model projected change in the exposure and vulnerability. Various studies have incorporated RSL projections in estimating future flood hazards (Gornitz et al. 2001; Tebaldi et al. 2012; Hunter et al. 2013; Orton et al. 2015; Wu et al. 2016, among others) and flood damage risk (Wu et al. 2002; Kleinosky et al. 2006; Nicholls and Tol 2006; Hallegatte et al. 2011; Hoffman et al. 2011; Hinkel et al. 2014, among others), where projected change in exposure and vulnerability (Jain et al. 2005) have also often been considered. While most of these studies have considered RSL scenarios and/or ranges (Houston 2013), more recently, Kopp et al. (2014) developed probabilistic projections of RSL for various coastal sites globally. Such probabilistic projections of local RSL have been used to estimate future flood hazard probabilities (Buchanan et al. 2015), and they can be further applied to quantify flood damage risk (Lickley et al. 2014).

Potential change in storm surge climatology, on the other hand, has seldom been considered in estimating future flood hazard and damage risk. One reason is that relatively large uncertainties still exist regarding how climate change will affect TCs (Knutson et al. 2010; Emanuel 2013). Another reason is that TCs (unlike extratropical cyclones) cannot be well resolved in typical climate models due to TCs’ relatively small scales (except perhaps in a recently-developed high-resolution climate model, Murakami et al. 2015). Dynamic downscaling methods can be used to better resolve TCs in climate-model projections (Knutson et al. 2013, 2015), but most of these methods are computationally too expensive to be directly applied to risk analysis. Statistical models have been developed to generate synthetic TCs that can vary with influential climate variables such as sea surface temperature (Vickery et al. 2009; Hall and Yonekura 2013; Mudd et al. 2014; Ellingwood and Lee 2016). The statistical-deterministic model developed by Emanuel et al. (2006, 2008), however, is currently the primary method that can generate large numbers of synthetic TCs with physically correlated characteristics (i.e., frequency, track, intensity, size) driven by comprehensive (observed or projected) climate conditions involving the environmental wind and humidity, thermodynamic state of the atmosphere, and thermal stratification of the ocean. This probabilistic TC model has been integrated with hydrodynamic surge models (Westerink et al. 2008; Jelesnianski et al. 1992) into a climatological-hydrodynamic method (Lin et al. 2010, 2012, 2014; Lin and Emanuel 2016) to generate large samples (~10⁴) of synthetic storm surge events and assess the surge hazard probabilities. This method has been applied to investigate storm surge hazards under observed and/or projected climate conditions for various coastal cities, including New York City (NYC; Lin et al. 2010, 2012; Reed et al. 2015); Miami (Klima et al. 2012) and Tampa (Lin and Emanuel 2016) in Florida; Galveston in Texas (Lickley et al. 2014); Cairns in Australia (Lin and Emanuel 2016); and Dubai in the Persian Gulf (Lin and Emanuel 2016).

Such city-scale storm surge hazard estimations can be applied to flood damage risk assessment. First, the generated synthetic surge events under observed/current climate conditions can be conveniently translated to synthetic city- or regional-scale damage/loss events to quantify the current risk (Aerts et al. 2013), overcoming the challenge of using limited historical surge events based on sparse tidal gauge observations. Then, the projected change in storm surge climatology in the future climate can be translated to the projected change in the risk. Aerts et al. (2014) have applied such an approach using Lin et al.’s (2012) surge climatology projection to estimate the future damage risk for NYC and evaluate risk mitigation strategies, considering also RSL scenarios and population growth projection. Lickley et al. (2014) have combined the surge climatology projection with the probabilistic RSL projection of Kopp et al. (2014) to estimate the damage risk for an energy facility in Galveston and develop risk mitigation measures. These studies, however, have focused on assessing and managing the mean risk based on the expected annual damage (EAD). A significant extension is a full probabilistic risk analysis approach that considers not only the mean but also the extreme damages, induced by extreme storm surges, extreme RSL, or both. Such an approach cannot be conveniently developed by incorporating the surge climatology projection into existing risk assessment frameworks that focus on the impact of RSL, considering that the two stochastic quantities are analytically different: RSL has been considered as a continuous process while the occurrence of surge events is viewed as discrete. A new, coherent framework is needed to first combine probabilistic projections of surges and RSL into probabilistic projection of floods (Lin et al. 2016) and then translate it to probabilistic projection of the flood damage risk.

We propose an integrated dynamic risk analysis for flooding task (iDraft) framework to assess coastal flood risk at regional scales with the following merits: (1) integrating climate projections of both storm climatology change and RSL with social/economic projections of future exposure/vulnerability; (2) examining the dynamic evolution of the risk resulted from the dynamic evolution of the climate hazards and exposure/vulnerability; and (3) conducting probabilistic risk analysis within a formal, coherent (stationary and non-stationary) Poisson-process framework. Neglecting dynamic forcing (i.e., stationary case), considering deterministic scenarios (e.g., 90th percentile of the projected RSL), focusing on only the mean risk (e.g., EAD), or considering a specific site (e.g., for a building or facility) are special cases that can also be investigated within the iDraft framework.

Various risk measures can be estimated within the iDraft framework. In the context of coastal flooding, “risk” has been conventionally defined as the EAD (Hall et al. 2005) or the mean of present value of future/lifetime losses (PVL; Hall and Solomatine 2008; Aerts et al. 2014). Here we consider “risk” as the probability distribution, including the mean and the tail, of the event, annual, and lifetime losses. We examine the time-evolution of the return period of various damage levels including extremes as well as the time-evolution of the mean and variance of annual damage, under projected climate change and coastal population growth. Then we study PVL as a temporal integration of discounted losses over a certain time period (e.g., the lifetime of a project or the twenty-first century). We derive the mean of PVL, as well as all other above-mentioned risk metrics, analytically. We also develop a Monte-Carlo method that can be used to estimate all risk measures, including the probability distribution of PVL, which may be difficult or impossible to derive analytically. The MC and analytical methods, grounded in the same Poisson-process framework, verify each other in estimating the risk measures; such verification is particularly useful when considering complex, non-stationary systems as in this flood risk analysis task.

To demonstrate the application of the iDraft framework, we perform a case study to assess the flood risk for NYC. We apply the synthetic surge events in Lin et al. (2012) and FEMA depth-damage models (FEMA 2009) to estimate the current flood hazards and damage risk for all buildings in NYC based on the building stock data from the Applied Research Association (ARA 2007). Then we combine the projection of storm surge climatology in Lin et al. (2012), RSL in Kopp et al. (2014), and building stock growth in Aerts et al. (2014) to estimate how the hazard and damage risk for NYC will evolve over the twenty-first century. In particular, we examine the relative contributions to the change of the risk from the various dynamic factors (i.e., changes in storm climatology, RSL, and building stock). In a companion paper (Part II), we extend the iDraft to carry out probabilistic benefit-cost analysis for various proposed risk mitigation strategies for NYC. In these studies, we focus on hurricanes/tropical cyclones. Extratropical cyclones can also induce coastal flooding for the US Northeast Coast including NYC (Colle et al. 2015), but surge floods induced by extratropical cyclones are less severe and contribute less significantly to the overall and extreme damage risks for the US Northeast Coast. Nevertheless, the iDraft framework will be extended in the future to account for the contribution of extratropical cyclones to the flood hazard and damage risk. Also, here we focus on exposure and vulnerability of the built/physical environment; future extension may consider also social vulnerability (Cutter et al. 2000; Wu et al. 2002; Kleinosky et al. 2006; Ge et al. 2013).

2 Integrated dynamic risk analysis for flooding task (iDraft)

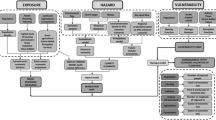
The iDraft framework consists of two main components (Fig. 1). The first is a modeling scheme to collect necessary physical information for risk analysis, specifically data on flood hazards and coastal exposure/vulnerability, and combine them into the estimates of potential consequences and likelihoods. The second is a theoretical scheme to derive various risk measures of interest and quantify them based on the physical information. The theoretical assumption is that the surge events affecting the coastal area of interest are conditionally independent, given the climate environment; i.e., the arrival of surge events is assumed to be Poisson. Analytical derivations are obtained for risk measures that vary over time with the changing climate and built environments, such as the return period of extreme damages and the mean and variance of annual damage. The mean of the present value of future losses (PVL) is also obtained analytically in three ways. An MC simulation method is then developed that can be used to estimate all risk measures including the probability distribution of PVL. The analytical and MC methods are theoretically consistent and shown in the case study to generate similar numerical results.

Fig. 1

Diagram of iDraft framework. Hexagons represent data, and rectangles represent analyses performed on data

2.1 Information based on physical modeling

2.1.1 Hazards

The flood hazards can be characterized by the probabilities of the storm tide and RSL (the storm tide above the mean sea level is composed of the storm surge and astronomical tide). When applied for a region, it is convenient to consider these probabilities/levels and the ways they change with the climate at a reference location. However, to estimate the probabilities of the cumulated damage for the region, it is still necessary to consider the spatial variation of the storm surge based on a set of synthetic events under the observed, current climate. The effects of astronomical tide and changes of storm tide and RSL probabilities due to climate change can then be accounted for by manipulating the estimated surge damage probabilities. Thus, the hazards information in the iDraft framework includes (1) maps of a set of synthetic storm surge events (with estimated frequency) representing the storm surge climatology under the current climate; (2) estimated current and projected future storm tide climatology (frequency and magnitudes) at the reference point; and (3) projected future (preferably probabilistic) RSL at the reference point (Fig. 1). Information on synthetic surge events and storm tide climatology projected over the twenty-first century is available in, e.g., Lin et al. (2012) for NYC and Lin and Emanuel (2016) for Tampa. Probabilistic projection of RSL over the twenty-first century and beyond is available in Kopp et al. (2014) for various coastal sites.

First, we consider the synthetic storms in the current climate, with an estimated annual frequency of λ. Let H ^* be the induced (peak) storm surge at the reference location. Lin et al. (2010, 2012) found that the cumulative probability distribution (CDF) of the storm surge (conditioned on storm arrival), denoted by $F_{{H^{*} }} \left( h \right) = P\left\{ {H^{*}\,\le\,h} \right\},$ is characterized by a long tail; thus they applied a Peaks-Over-Threshold (POT) method to model this tail with a Generalized Pareto Distribution (GPD) and the rest of the distribution with non-parametric density estimation. The storm tide is denoted by H (peak storm tide at the reference point). The CDF of the storm tide (conditioned on storm arrival), $F_{H} \left( h \right) = P\left\{ {H\,\le\,h } \right\},$ can be obtained from the CDF of the storm surge, distribution of astronomical tide (from observation or simulation), and, possibly, estimated nonlinear effects between the surge and tide (Lin et al. 2012).

Second, we consider the effect of climate change on the storm frequency and storm tide distribution (due to the change in storm intensity and other characteristics). Lin et al. (2012) applied various climate models to project future storm frequency and storm tide distribution for NYC. A complexity in applying these climate model projections is that the climate models may be biased, and the projections should first be bias-corrected (Lin et al. 2016). The bias information is available in Lin et al. (2012), where the storm frequency and storm tide CDF are estimated based on both observed and modeled climates for the same “current” climate period. Thus, by comparing the estimates based on the observed and modeled climates for the current period, we can bias-correct the modeled future storm frequency and storm tide CDF, assuming the model bias does not change over the projection period.

In addition to bias-correcting the climate model projections, one may create a single, “mean” climate projection, which is often in demand for decision-making. Due to the high computational demands to generate numerous storm and surge events to capture the tail of the distributions, projections are often limited to a relatively small number of climate models [e.g., Lin et al. (2012) applied four models while Lin and Emanuel (2016) applied six models]. Given also different model accuracies, an arithmetic mean is not very meaningful. Thus, we create a composite projection as a weighted average of the available climate model projections. The weights are determined based on how relatively accurate the climate-model estimates for the current period are compared to the estimates based on observed climate. The obtained composite projection may be considered as the expected or “best” surge climatology projection, while the range of the projections based on the various climate models indicates the uncertainty in the climate modeling.

To project future risk continuously over a time horizon, moreover, one needs time-varying storm frequency and storm tide distribution. However, the future storm frequency and storm tide are usually not projected continuously. Due to high computational demands, such analyses are often performed for certain time periods, e.g., the end of the twentieth century and the end of the twenty-first century (Lin et al. 2012) or the end of the twentieth century and the beginning, middle, and end of the twenty-first century (Lin and Emanuel 2016). Thus, we apply linear interpolation to obtain time-varying yearly storm frequency and storm tide CDF, now denoted as λ(t) and $F_{H\left( t \right)} \left( h \right) = P\left\{ {H\left( t \right)\,\le\,h} \right\},$ respectively, for each of the (bias-corrected) climate-model projections and the composite projection. The linear assumption is made due to the lack of further information from physical modeling; in reality, the storm surge climatology may not be changing linearly. Future physical modeling with higher temporal resolution can improve the accuracy.

Third, we consider the effect of sea-level rise in the future. Let S be the relative sea level (RSL; relative to the current/baseline mean sea level). We define the sum of the storm tide and RSL to be the flood height (denoted by H ^f; for the baseline current climate, the flood height is also the storm tide). Lin et al. (2012) showed that the nonlinearity between the storm tide and RSL is relatively small for coastal areas in the NY region. Then, if this nonlinearity is neglected, the CDF of the flood height in year t, $F_{{H^{f} \left( t \right)}} \left( h \right) = P\left\{ {H^{f} \left( t \right)\,\le\,h } \right\},$ can be calculated by shifting the CDF of the storm tide in year t by the projected RSL in year t. To account for the uncertainty in the RSL projection, the shift can be weighted by the probability density function (PDF) of RSL through a convolution operation (Lin et al. 2012, 2016). Formally,

$$ P\left\{ {H^{f} \left( t \right) } \right.\left. {\,\le\,h} \right\} = P\left\{ {H\left( t \right) + S\left( t \right)\,\le\,} \right.\left. h \right\} = \mathop \int \nolimits_{ - \infty }^{\infty } P\left\{ {H\left( t \right)\,\le\,h - s} \right\}f_{S\left( t \right)} \left( s \right)ds $$

(1)

where the PDF of RSL, f _S(t) (s), can be estimated from probabilistic projections of RSL. Kopp et al. (2014) provide large numbers of probabilistic samples of decadal time series of projected RSL over the twenty-first century (and beyond). Thus, a nonparametric density estimation or a POT model with a GPD tail may be applied to fit the RSL samples for each decade and interpolate to each year to obtain f _S(t) (s). Equation (1) is applied in analytical analysis; in the MC analysis described in Sect. 2.2.4, the probabilistic samples of RSL time series are directly combined with the probabilistic samples of storm tide time series.

We note that Kopp et al.’s (2014) RSL projection is a composite based on a number of climate model projections. Ideally, the flood height distribution should be estimated using the storm tide and RSL distributions projected by the same climate model, as the change in storm climatology and RSL are correlated as they are both affected by the large-scale climate environment (Little et al. 2015). However, as probabilistic RSL projection for individual climate model is currently not available, the composite RSL distribution is used to combine with the storm tide distribution (and associated storm frequency) projected by individual climate models. We also combine the composite RSL distribution with the composite storm tide distribution (and associated storm frequency), which avoids the correlation issue.

2.1.2 Vulnerability

We consider exposure a component of vulnerability. As displayed in Fig. 1, the vulnerability information includes the topography/elevation data describing how susceptible the study area is to surge flooding, the building stock (or generally the exposed assets) within the area, and the fragility of the buildings described by vulnerability models such as FEMA’s depth-damage curves (describing the percentage loss of a specific type of buildings as a function of the water depth). The growth of population and thus building stock in the future is considered to increase the vulnerability of the area, while applying risk mitigation strategies will reduce the vulnerability. For example, applying strengthened building code can reduce the fragility of structures and building a barrier can reduce the overall exposure (Part II). The hazards and vulnerability information can be combined to estimate the consequences and quantify the risk.

2.1.3 Consequences

The consequences may be described by the damage or economic loss and its probability distribution. As Fig. 1 shows, to estimate the economic losses for the current climate, the maps of synthetic surge events are combined with the topography/elevation data to produce maps of flood inundation, through static mapping (Aerts et al. 2013) or dynamic modeling (Ramirez et al. 2016; Yin et al. 2016). The inundation maps can also consider any risk mitigation strategy that reduces the inundation area (e.g., storm surge barriers; discussed in Part II). The building stock data for the region and vulnerability models are used to calculate the damage for each geographic unit of a given inundation map, and damages are summed over all geographic units to obtain the total loss from a given storm. The damages may be reduced if building-level mitigation measures are applied (e.g., elevating houses to reduce the relative water depth; Part II). In this way, we obtain a large set of synthetic damage events for the study area, and statistical analysis can be performed on the modeled synthetic losses to estimate the probability distribution of the loss. This distribution of loss induced by the storm surge (denoted by L ^*; conditioned on storm arrival), $F_{{L^{*} }} \left( l \right) = P\left\{ {L^{*}\,\le\,l\} } \right.,$ is shown to have a long tail (due to the similar property of the surge); thus, we model it with the POT method with a GPD fit to the upper tail.

We consider the effect of astronomical tide by manipulating the loss distribution for the storm surge to obtain the loss distribution for the storm tide. That is, we shift the loss CDF for the storm surge, $F_{{L^{*} }} \left( l \right),$ according to the difference of the storm surge CDF, $F_{{H^{*} }} \left( h \right),$ and storm tide CDF, $F_{H}\,\left( h \right).$ Specifically, let the CDF of the loss induced by the storm tide (denoted by L; conditioned on storm arrival) be $F_{L} \left( l \right) = P\left\{ {L\,\le\,l\} } \right.,$ and it is estimated as

$$ F_{L} \left( l \right) = F_{H } \left( {F_{{H^{*} }}^{ - 1} \left( {F_{{L^{*} }} (l)} \right)} \right). $$

(2)

The loss distribution for the future depends on the future storm tide, RSL, and building stock, as well as mitigation measures. We discuss the effects of mitigation measures in Part II. Here we estimate the loss distribution that varies over time due to the other factors. First, accounting for the building stock change requires new damage calculations and statistical analyses to derive new loss distributions. These calculations and analyses are performed as described above for the current climate, but with projected future building stock data for various points in the future. We can then obtain several loss distributions for various time points and interpolate to each year to obtain the surge damage distribution that varies over time due to building stock change, denoted by $F_{{L^{*} \left( t \right)}} \left( l \right) = P\left\{ {L^{*} \left( t \right)\,\le\,l\} } \right.,$ for a future year t.

Then, let F _L(t) (l) be the flood loss distribution for a future year t (conditioned on storm arrival), accounting for both building growth and the joint effects of astronomical tide and change of storm climatology and RSL. It can be estimated by shifting the surge damage distribution of year t that accounts for building growth, $F_{{L^{*} \left( t \right)}} \left( l \right),$ according to the change of the flood height distribution of year t relative to the current surge distribution. As in the case of Eq. (2), we obtain,

$$ F_{L\left( t \right)} \left( l \right) = F_{{H^{f} \left( t \right) }} \left( {F_{{H^{*} }}^{ - 1} \left( {F_{{L^{*} \left( t \right)}} \left( l \right)} \right)} \right) $$

(3)

where $F_{{H^{f} \left( t \right)}}\,\left( h \right)$ is the flood height CDF obtained in Eq. (1) and $F_{{H^{*} }} \left( h \right)$ is the current storm surge CDF. This time-varying flood loss distribution describes the consequences given the flood hazards and vulnerability for the study region. This distribution and the time-varying storm frequency describing the likelihoods together provide the physical input required for analytical risk assessment discussed in the next section.

As an additional note, we argue that it is reasonable to manipulate the loss distribution as in Eqs. (2) and (3) to account for the effect of astronomical tide, surge climatology change, and RLS. Theoretically, the loss can be considered as a monotonically increasing function of the water level, e.g., $l = g\left( h \right).$ Then, $F_{{L^{*} }} \left( l \right) = F_{{H^{*} }} \left( {g_{1}^{ - 1} \left( l \right)} \right)$ and $F_{L} \left( l \right) = F_{H } \left( {g_{1}^{ - 1} \left( l \right)} \right),$ resulting in Eq. (2); $F_{{L^{*} \left( t \right)}} \left( l \right) = F_{{H^{*} }} \left( {g_{2}^{ - 1} \left( l \right)} \right)$ and $F_{L\left( t \right)} \left( l \right) = F_{{H^{f} ( {\text{t) }}}} \left( {g_{2}^{ - 1} \left( l \right)} \right),$ resulting in Eq. (3). In practice, however, the loss may be considered a constant of zero when the water level is below a threshold, e.g., the lowest water level that can cause any damage or the height of the natural or built flood defense. In such a case, Eqs. (2) and (3) are applied to only the damage values above the lower damage threshold that are considered increasing with the water level; from zero to the damage threshold, the loss CDF is always set to be constant (the loss PDF to be zero except at the zero loss). There is also an upper bound of the loss (i.e., the maximum value the region can loss), beyond which the loss CDF is 1, but in practice this upper bound is far from being reached. It should also be noted that because the manipulation of the loss distribution for the study area is based on the effects of astronomical tide, surge climatology change, and RSL at a reference point, the variation of these effects over the area is neglected. Thus, the study area should be relatively small compared to the spatial variation of these effects. Finally, rather than applying the analytical manipulations discussed above, one may attempt to apply numerical modeling to calculate all possible flood losses under various scenarios and directly estimate the flood loss distributions. Such a numerical approach, however, may be computationally prohibitive, considering the very large number of scenarios involved for different levels of astronomical tide, possible changes in the storm surge and RSL under various climate conditions, and their combinations.

2.2 Risk assessment in a Poisson framework

Considering a time horizon y (e.g., 100 years), we identify each storm happening within y with an index i and denote its arrival time by T _i , the storm tide it induces by H _i , and the loss it induces by L _i . T _i , H _i , and L _i are random variables (whose distributions can vary with time when accounting for the changes in the climate and built environments), as is the total number of arrivals within y, denoted by N (i = 1, 2, …, N, $T_{N}\,\le\,y$). Storm arrivals in a given climate environment may be assumed to be conditionally independent of each other, as physical interactions among storms are relatively small and have yet to be understood scientifically. Given this setting, it is reasonable to model the storm arrival with a Poisson process (Elsner and Bossak 2001; Lin et al. 2012; Onof et al. 2000; Vanem 2011). In the case where environmental changes are neglected, the arrival process is assumed to be a stationary Poisson process. Otherwise, it is assumed to be a non-stationary Poisson process.

2.2.1 Stationary Poisson processes

In a stationary Poisson process with arrival rate λ (storm annual frequency in this case), the number of arrivals in time interval [τ, τ + s] $(\tau ,s\,\ge\,0)$, N _s , has a Poisson distribution:

$$ P\{ N_{s} = n\} = \frac{{(\lambda s)^{n} e^{ - \lambda s} }}{n!},\quad n = 0,1,2, \ldots \infty $$

(4)

and the mean and variance of N _s are both λs. The first arrival time, W ₁, as well as the jth inter-arrival time W _j (j = 1, 2, …, N), has an exponential distribution with parameter λ,

$$ f_{{W_{j} }} (w) = \lambda e^{ - \lambda w} ,\quad w\,\ge\,0 $$

(5)

The ith arrival time T _i is

$$ T_{i} = \sum\limits_{j = 1}^{i} {W_{j} } $$

(6)

and T _i has a Gamma distribution with shape parameter i and scale parameter λ,

$$ f_{{T_{i} }} \left( s \right) = \frac{{\left( {\lambda s} \right)^{i - 1} }}{{\left( {i - 1} \right)!}}\lambda e^{ - \lambda s} , \quad s\,\ge\,0. $$

(7)

Next, we consider a marked Poisson process. Each arrival i is associated with a mark, the storm tide, H _i , induced by the arrival storm with arrival rate of λ. {H _i , i > 0} are independent and identically distributed with the specified probability distribution, $F_{H} \left( h \right) = P\left\{ {H\,\le\,h\} } \right.,$ and they are independent of {T _i , i > 0}. Then, the arrival of storm tide events that exceed a level h is also a Poisson process, with the annual rate of $\lambda \left( {1 - P\left\{ {H\,\le\,h} \right\}} \right),$ and the exceedance probability of the annual maximum storm tide (denoted by H _max ) is (using Eq. 4)

$$ P\left\{ {H_{max} > } \right.\left. h \right\} = 1 - P\left\{ {H_{max}\,\le\,} \right.\left. h \right\} = 1 - e^{{ - \lambda \left( {1 - P\left\{ {H\, \le\, h} \right\}} \right)}} $$

(8)

The reciprocal of this annual exceedance probability is the mean recurrence interval, or (mean) return period, denoted by $\overline{T}_{H} \left( h \right),$

$$ \overline{T}_{H} \left( h \right) = \frac{1}{{1 - e^{{ - \lambda \left( {1 - P\left\{ {H \,\le\, h} \right\}} \right)}} }} $$

(9)

We note that the return period calculated in Eq. (9) is the average waiting time for the arrival of a year with the maximum surge exceeding level h. One may also define the return period as $\frac{1}{{\lambda \left( {1 - P\left\{ {H\,\le\,h} \right\}} \right)}},$ which is the average waiting time for the arrival of an event with the surge exceeding level h (Lin et al. 2016). Numerically, for large values of h (i.e., low probability extremes), the two return periods are very close; for small values of h, the return period estimated in Eq. (9) is longer, as the probability of two or more exceedance events happening in the same year is not negligible. In this study, we use the definition of return period as in Eq. (9).

If we account for the effect of climate change in a specific, stationary future climate, the Poisson storm arrival is associated with the flood height as its mark. Then, the arrival of floods that exceed a level h is also a Poisson process, with the annual rate of $\lambda \left( {1 - P\left\{ {H^{f}\,\le\,h} \right\}} \right),$ where $F_{{H^{f} }} \left( h \right) = P\left\{ {H^{f}\,\le\,h\} } \right.$ is the flood height distribution for the specific climate. The exceedance probability of the annual maximum flood height (denoted by H ^f _max ) is

$$ P\left\{ {H_{max}^{f} > } \right.\left. h \right\} = 1 - e^{{ - \lambda \left( {1 - P\left\{ {H^{f}\,\le\,h} \right\}} \right)}} $$

(10)

The return period of the flood height, denoted by $\overline{T}_{{H^{f} }} \left( h \right)$, is

$$ \overline{T}_{{H^{f} }} \left( h \right) = \frac{1}{{1 - e^{{ - \lambda \left( {1 - P\left\{ {H^{f}\,\le\,h} \right\}} \right)}} }}. $$

(11)

Similarly, we can consider a Poisson process of storm arrivals associated with marks as their induced losses. The loss L _i is induced by the storm i; {L _i , i > 0} are independent and identically distributed with the specified probability distribution, $F_{L} \left( l \right) = P\left\{ {L\,\le\,l\} } \right.,$ and they are independent of {T _i , i > 0}. Then, the arrival of damages that exceed a level l is also a Poisson process, with the annual rate of $\lambda \left( {1 - P\left\{ {L\,\le\,l} \right\}} \right),$ and the exceedance probability of the annual maximum loss (denoted by L _max ) is

$$ P\left\{ {L_{max} > } \right.\left. l \right\} = 1 - e^{{ - \lambda \left( {1 - P\left\{ {L\,\le\,l} \right\}} \right)}}. $$

(12)

The return period of the loss, denoted by $\overline{T}_{L} \left( l \right)$, is

$$ \overline{T}_{L} \left( l \right) = \frac{1}{{1 - e^{{ - \lambda \left( {1 - P\left\{ {L\,\le\,l} \right\}} \right)}} }}. $$

(13)

Another risk metric of particular interest is the expected annual damage/loss (EAD). Note that we account for the possibility of having multiple storms in a year, so the sum of losses induced by all storms that occur within the first year is

$$ A_{1} = \mathop \sum \limits_{i = 1}^{{N_{1} }} L_{i} $$

(14)

where $N_{1}$ is the number of storms that arrive in the first year, and it has a Poisson distribution with mean λ (Eq. 4). Applying the Poisson properties to Eq. (14), it can be shown that the expectation of the first-year loss, and thus of the annual loss in a stationary process, denoted by A, is the product of the storm arrival rate λ and the expectation of the loss,

$$ {\text{E}}\left[ A \right] = \lambda {\text{E}}\left[ L \right] $$

(15)

Moreover, the variance of the annual loss can also be obtained as the product of the storm arrival rate and the second moment of the loss distribution,

$$ {\text{Var}}\left[ A \right] = \lambda {\text{E}}\left[ {L^{2} } \right]. $$

(16)

2.2.2 “Quasi-stationary” assumption

The above (stationary) analysis can be applied to a specific time period when the climate and built environment is considered stationary. To account for the effect of environmental changes, we can apply a “quasi-stationary” approximation. That is, we divide the time horizon into small intervals; within each interval (practically, a year) the process is assumed stationary (i.e., the interval is considered a part of a stationary process that continuous indefinitely). Applying the yearly storm frequency and the CDF of storm tide, flood height, and economic loss, i.e., λ(t), F _H(t)(h), ${F}_{{H^{f} \left( t \right)}} \left( h \right)$, and F _L(t)(l) (t = 1, 2, …, y), we can calculate analytically the return period of the storm tide, flood height, and damage loss, $\overline{T}_{H\left( t \right)} \left( h \right),\,\overline{T}_{{H^{f} \left( t \right)}} \left( h \right)$, and $\overline{T}_{L\left( t \right)} \left( l \right),$ as well as the mean and variance of the annual loss, E[A_t] and Var[A_t], for each year as the stationary case discussed above. Such a discrete approach is taken as it is physically reasonable and practically convenient to assume that the climate is stationary within a small time-interval such as a year. As shown in the case study, the time-varying risk measures estimated analytically based on the “quasi-stationary” assumption with yearly intervals are very close to those estimated numerically based on MC simulations for the continuous non-stationary process.

2.2.3 Present value of future losses (PVL)

In addition to the yearly-varying risk measures as discussed above, temporally integrated quantities such as the PVL are often of great interest, especially for risk management analysis. Let R be the present value of all future losses in the time horizon y (e.g., 100 years), then,

$$ R = \mathop \sum \limits_{i = 1}^{N} \frac{{L_{i} }}{{\left( {1 + r} \right)^{{T_{i} }} }} ,\quad T_{N}\,\le\,y $$

(17)

where r is the discount rate. Here we consider a constant discount rate (e.g., 3%), but a time-varying discount rate, e.g., a decreasing function of time (Lee and Ellingwood 2015), can be similarly applied [by replacing r with r (T _i )] in the analytical and MC methods discussed below. As R (PVL) combines the information of the hazards and vulnerability over the time horizon, we may consider it an overall measure of the risk, especially when we quantify its probability distribution. This probability distribution is difficult or impossible to derive analytically. Thus, we statistically estimate this distribution based on MC simulations as discussed in the next section. In this section we discuss three analytical methods to derive the mean of this distribution.

Calculation with continuous discounting

For analytical convenience, R in Eq (17) can also be written as

$$ R = \mathop \sum \limits_{i = 1}^{\infty } \frac{{L_{i} }}{{\left( {1 + r} \right)^{{T_{i} }} }} 1_{{\left\{ {T_{i}\,\le\,y} \right\}}} $$

(18)

where $1_{{\left\{ {T_{i}\,\le\,y} \right\}}} ,$ the indicator function, equals 1 when $T_{i}\,\le\,y$ or 0 otherwise. First, assume that the storms arrive as a stationary Poisson process with rate λ and L _i  = L. T _i has a Gamma distribution with shape parameter i and scale parameter λ, as in Eq. (7), and L and T _i are independent. Then the expectation of R can be obtained by taking expectations on both sides of Eq. (18),

$$ \begin{aligned} E[R] & = E[L]\sum\limits_{i = 1}^{\infty } {E\left[ {\frac{1}{{(1 + r)^{{T_{i} }} }}1_{{\{ T_{i}\,\le\,y\} }} } \right] = } E[L]\sum\limits_{i = 1}^{\infty } {\int_{0}^{y} {\frac{1}{{(1 + r)^{s} }}\frac{{\lambda e^{ - \lambda s} (\lambda s)}}{(i - 1)!}^{i - 1} ds} } \\ & = \lambda E[L]\int_{0}^{y} {\frac{1}{{(1 + r)^{s} }}ds = \lambda E[L]\frac{{(1 + r)^{y} - 1}}{{(1 + r)^{y} \ln (1 + r)}}} . \\ \end{aligned} $$

(19)

Note that the calculation in Eq. (19) requires that L and $\lambda$ be stationary over the entire time horizon. Now, non-stationary behavior can be approximated with the “quasi-stationary” assumption, by breaking up the time horizon y into discrete stationary time periods (t = 1, 2, …, y), and then

$$ E\left[ R \right] = \mathop \sum \limits_{t = 1}^{y} \frac{{\lambda \left( t \right)E\left[ {L\left( t \right)} \right]}}{{\left( {1 + r} \right)^{t - 1} }}\mathop \int \nolimits_{0}^{1} \frac{1}{{\left( {1 + r} \right)^{s} }}ds = \mathop \sum \limits_{t = 1}^{y} \frac{{\lambda \left( t \right)E\left[ {L\left( t \right)} \right]}}{{\left( {1 + r} \right)^{t} }}\frac{r}{{{ \ln }\left( {1 + r} \right)}}. $$

(20)

Calculation with discrete discounting

The calculation on R can be simplified if we apply discrete discounting; i.e., we ignore the specific arrival time of events within each year and discount the total losses from the discrete annual intervals to the present. We define the sum of all losses in year t to be $A_{t}$ (t = 1, 2, …, y). Then, if $A_{t}$ is assumed to occur at the end of each year, the PVL (R) can be defined in terms of $A_{t}$:

$$ R = \mathop \sum \limits_{t = 1}^{y} \frac{{A_{t} }}{{\left( {1 + r} \right)^{t} }} $$

(21)

The expectation of R can be simply derived as

$$ E\left[ R \right] = \mathop \sum \limits_{t = 1}^{y} \frac{{E\left[ {A_{t} } \right]}}{{\left( {1 + r} \right)^{t} }} $$

(22)

where, similar to the stationary case in Eq. (15), ${\text{E}}\left[ {A_{t} } \right] = \lambda \left( t \right){\text{E}}\left[ {L\left( t \right)} \right].$ If $A_{t}$ is assumed to occur at the beginning of each year,

$$ E\left[ R \right] = \mathop \sum \limits_{t = 1}^{y} \frac{{E\left[ {A_{t} } \right]}}{{\left( {1 + r} \right)^{t - 1} }} $$

(23)

Note that, as we also have ${\text{Var}}\left[ {A_{t} } \right] = \lambda \left( t \right){\text{E}}\left[ {L^{2} \left( t \right)} \right],$ similar to the stationary case in Eq. (16), one may attempt to also calculate the variance of R from the sum of the yearly variances; however, this is not correct in the non-stationary or “quasi-stationary” case as the annual damages are correlated due to the natural correlation of the RSL over time. We account for this correlation in the MC analysis in the next section.

Note that this calculation of the mean of R is necessarily discretized: all losses that occur within the entire year t are lumped together into $A_{t}$ and discounted as if they all occur at the same time. Theoretically such a discretized calculation is less accurate than the calculation with continuous discounting (by accounting for storm arrival time) presented in Eqs. (19, 20). However, we also point out that, as the Poisson rate is a yearly rate (storm annual frequency), we have neglected the seasonal variation of the storm arrival in our specific application problem. As hurricanes often happen in later summer and fall in the Northern Hemisphere, assuming $A_{t}$ happening at the beginning of the year (which overestimates the risk) is less accurate than assuming it happening at the end of the year (which slightly underestimates the risk). Applying the continuous discounting, which neglects the seasonality, slightly overestimates the risk in this case. However, this seasonality effect is relatively small; as we will show in the case study, estimations using these various methods give similar results.

Calculation based on annual exceedance probability

The EAD can be calculated as

$$ {\text{E}}\left[ {A_{t} } \right] = \lambda \left( t \right){\text{E}}\left[ {L\left( t \right)} \right] = \mathop \int \nolimits_{0}^{\infty } \lambda \left( t \right)P\{ L\left( t \right) > l\} dl $$

(24)

as L is a positive random variable. Since $\lambda \left( t \right)P\{ L\left( t \right) > l\}$ is the rate of the Poisson arrivals that induce losses greater than l, $\lambda \left( t \right)P\{ L\left( t \right) > l\}$ can also be calculated from L _max (t), the maximum damage in year t: as in Eq. (12), $P\{ L_{ \hbox{max} } \left( t \right) > l\} = 1- e^{{ - \lambda \left( t \right)P\{ L\left( t \right) > l\} }} .$ Then EAD can be expressed in terms of $L_{ \hbox{max} } \left( t \right)$:

$$ {\text{E}}\left[ {A_{t} } \right] = \mathop \int \nolimits_{0}^{\infty } - { \ln }\left( {1 - {\text{P}}\{ L_{ \hbox{max} } \left( t \right) > l} \right)dl $$

(25)

This means that since ${\text{P}}\{ L_{ \hbox{max} }\,\left( {\text{t}} \right) > l\}$, the annual exceedance probability for the loss, contains information on both L(t) and $\lambda \left( t \right)$, when it is available, Eq. (25) can be directly applied to calculate EAD. The expectation of R can then be calculated in a discretized manner by using Eqs. (22) or (23).

We discuss this method especially considering that EAD has been often calculated as:

$$ {\text{E}}\left[ {A_{t} } \right] \approx \mathop \int \nolimits_{0}^{\infty } {\text{P}}\left\{ {L_{ \hbox{max} } \left( t \right) > l} \right\}dl $$

(26)

or the area under the curve of the annual exceedance probability for the loss (e.g., Wood et al. 2005; Aerts et al. 2013). This method is based on the assumption that $P\{ L_{ \hbox{max} } \left( t \right)\,>\,l\} \approx \lambda \left( t \right)P\{ L\left( t \right) \,>\, l\} ,$ which is a good approximation when $\lambda \left( t \right)P\{ L\left( t \right)\,>\,l\}$ is small, as for the rare and extreme events that risk analysis often focuses on. However, Eq. (26) may underestimate the EAD, since it actually calculates the expectation of L _max(t), the annual maximum damage, to approximate the EAD, the expectation of the annual total damage. In years where more than one storm occurs, although rare, only the largest loss is counted in this method (Eq. 26), as opposed to the sum of all losses. As a result, Eq. (25) is more accurate. We also point out that we do not consider the correlation of damage events given the hazard events; i.e., we assume the damage will be recovered after each hazard event. In reality, if two identical extreme hazard events happen within a short period of time such as a year, the second event may induce less damage, as the losses from the first event may have not been recovered, but that is rare. On the other hand, if two identical relatively small hazard events happen within a year, the second event may induce the same or even larger damage, as the first has weakened the built environment.

2.2.4 MC simulations of stationary and non-stationary Poisson processes

In addition to the analytical methods discussed above, we can apply MC methods to generate random samples of time series of storm arrivals and damages, from which various distributions and risk measures can be estimated statistically. This approach is particularly useful for estimating the distribution for more complex metrics, the analytics of which may be difficult or impossible to derive, such as the present value of future losses discussed above as well as present value of future benefits of mitigation strategies discussed in Part II.

First, it is simple to apply MC simulations for a stationary Poisson process. In the stationary case with arrival rate $\lambda$, arrival times are simulated by first drawing inter-arrival “waiting times,” W _i , from the exponential distribution with parameter $\lambda$ (Eq. 5). Each arrival time T _i (T _i  ≤ y) is then calculated as the sum of the inter-arrival times (Eq. 6). The loss induced by each arrival storm is then sampled from the obtained loss distribution $F_{L} \left( l \right)$.

In the non-stationary case, the simulation of the arrival times with a non-stationary Poisson rate $\lambda \left( t \right)$ can be accomplished by the “thinning” method [$\lambda \left( t \right)$ is now made continuous assuming linearity between yearly time points]. First, storm arrivals are generated with a stationary rate $\lambda_{ \hbox{max} } = { \hbox{max} }\left( {\lambda \left( t \right), 0\,\le\,t\,\le\,y} \right).$ Then, each arrival, at time T _i , is evaluated and accepted with probability

$$ P\left\{ {T_{i} \;{\text{is}}\;{\text{accepted}}} \right\} = \frac{{\lambda \left( {T_{i} } \right)}}{{\lambda_{ \hbox{max} } }} $$

(27)

The accepted arrivals are then reindexed (i = 1, 2, …, N).

The simulation of the losses in a non-stationary process needs further discussion. We cannot simply sample the loss from the (marginal) loss distribution $F_{L\left( t \right)} \left( l \right),$ because the losses are temporally correlated due the temporal correlation of RSL. Thus, we use the original probabilistic RSL time series of Kopp et al. (2014). For each trial of the simulated storm arrivals, one RSL time series is sampled, and each storm arrival i at T _i in the trial is assigned the RSL value of the time series at T _i (linearly interpolated between yearly points), denoted by S _i . The method of adjusting cumulative probabilities is then used to calculate the loss for each storm. Specifically, for storm i, a storm tide H _i is first sampled from the storm tide CDF that accounts for the storm climatology change, $F_{{H\left( {T_{i} } \right)}} \left( h \right)$. The cumulative probability corresponding to the flood height, H _i  + S _i , is then found from the surge CDF curve for the current climate, $F_{{H^{*} }} \left( h \right).$ The loss value corresponding to this cumulative probability on the surge loss CDF that accounts for the building change, $F_{{L^{*} \left( {T_{i} } \right)}} \left( l \right),$ is taken as the loss associated with the storm, denoted by L _i . Formally,

$$ L_{i} = F_{{L^{*} \left( {T_{i} } \right)}}^{ - 1} \left( {F_{{H^{*} }} \left( {H_{i} + S_{i} } \right)} \right) $$

(28)

This formulation is derived, again, based on the assumption that the loss is a monotonically increasing function of the water level.

With a large number of sampled time series of arrival times and losses from either the stationary or non-stationary MC simulations, various risk metrics can be estimated statistically. For example, the mean and variance of annual damage are calculated as the statistical mean and variance of the sum of the damages simulated for each year over all samples. The return level of damages can be found from the samples of the maximum damage for each year; e.g., if 10⁵ MC simulations are applied, the 2000-year damage for a year is the 50th largest of the 10⁵ simulated maximum damages for the year. Obviously, it is necessary to have a large number of simulations for accurately estimating the extremes. The value of R can be calculated directly from Eq. (17) for each sample, and the mean, variance, as well as the full probability distribution of R can be estimated from the samples. As demonstrated in the case study, the MC simulated samples can be used to estimate very closely all of the risk measures obtained by analytical methods for both stationary and non-stationary cases, assuring one that the same samples can be used to estimate the (analytically intractable) probability distribution of R (PVL).

3 Case study: New York City

To demonstrate how the proposed iDraft framework can be applied to a specific region, we analyze the flood risk (without any implemented risk mitigation strategies) to NYC, with specific attention paid to how environmental changes, including building stock growth, sea-level rise, and storm climatology change, are expected to influence this risk over the twenty-first century. Then, we perform a probabilistic benefit-cost analysis on several flood mitigation strategies proposed for NYC in Part II. Both risk assessment and benefit-cost analysis have been performed by Aerts et al. (2014) for NYC by using an EAD framework and considering scenarios of environmental changes at future time points (years 2040 and 2080). This case study builds upon Aerts et al. (2014) to fully consider the dynamics of the integrated environmental changes and better account for the aleatory and epidemic uncertainties within the iDraft framework.

This case study considers the entire NYC (including its five boroughs: Brooklyn, Queens, Manhattan, The Bronx, and Staten Island). The Battery tide gauge near lower Manhattan (where NYC’s economic values are most concentrated) is used as the reference point for manipulating the loss distribution to account for the effects of astronomical tide, storm climatology change, and sea-level rise. Although the storm climatology change and sea-level rise for the city may be represented well at the reference point, the astronomical tide may vary significantly over the city scale (e.g., the high/low tide is about 0.35 m higher/lower at the Kings Point station and 0.25 m lower/higher at the Montauk station compared to that at the Battery). However, this tidal variation has a reduced impact on the overall risk estimation, given that the storm surge has equal probabilities to hit the high and low tides. Also, the impact of this tidal variation is expected to be small compared to the overall impact of the reference astronomical tide, storm climatology change, and sea-level rise. It is theoretically more accurate to apply the methodology to smaller regions, e.g., to each borough of NYC. In that case, however, if the objective is to assess the overall risk for the larger city area, e.g., for developing risk mitigation strategy at the city scale, further analysis will be required to integrate the estimated sub-regional risks, considering their correlation.

3.1 Input data

A set of 549 low-probability synthetic surge events generated by Lin et al. (2012) for NYC for the “current” climate (end of the twentieth century, based on the NCEP reanalysis) is used to estimate the storm surge damage distribution. For each of these storms, the inundation level for every census block in NYC was calculated by static mapping using high-resolution DEM by Aerts et al. (2014). These inundation maps represent the spatial distribution of surge hazards within the city and are used to calculate surge damages in this study. It is noted that although static mapping is in general less accurate than dynamic modeling in estimating the flood extend and inundation depth, they generate similar results for NYC given its relatively incomplex topography near the coast (Yin et al. 2016; Ramirez et al. 2016). The 549 surge events were selected from a larger set of 5000 events generated for NYC; only events with storm surge levels at the Battery greater than 0.9 m above the mean sea level were selected. Thus, the risk analysis assumes that relatively high-probability storms that generate surges lower than 0.9 m at the Battery cause no damage. Neglecting insignificant damages significantly reduces computational burden in the efforts of estimating extremes and overall risk. Setting a low damage threshold is also realistic, considering that coastal cities may be protected to some extent by natural barriers and sea walls of certain heights. For parts of NYC, the height of the sea wall is around 1.5 m (Colle et al. 2010), and thus a surge lower than 0.9 m, even on a high tide of ~0.5 m, may not cause much inundation. However, more formal ways of setting the damage threshold should be explored in future research; possible solutions are to apply dynamic flood modeling that incorporates the flood defense (Yin et al. 2016) or directly model the performance of the flood defense (Wood et al. 2005).

Lin et al. (2012) also developed the storm tide distribution at the Battery by combining the storm surge distribution with the tidal distribution and accounting for surge-tide nonlinearity. To describe the current storm tide climatology, we use the storm tide distribution obtained from the “current” storm surge distribution based on the NCEP reanalysis. To describe the storm tide climatology change, we use the storm tide distributions at the Battery developed by Lin et al. (2012) for both the “current” (end of the twentieth century) and future (end of the twenty-first century) climates using four global climate models (GCMs), under the IPCC SRES A1B emission scenario. The four GCMs are CNRM (CNRM-CM3; Centre National de Recherches Météorologiques, Météo-France), GFDL (GFDL-CM2.0; NOAA/Geophysical Fluid Dynamics Laboratory), ECHAM (ECHAM5; Max Planck Institute), and MIROC (MIROC3.2, Model for Interdisciplinary Research on Climate; CCSR/NIES/FRCGC, Japan). Lin et al. (2012) also reported estimated storm frequencies for each case, which are used in this study.

To consider the effect of sea-level rise for NYC, we employ the probabilistic projections of RSL at the Battery over the twenty-first century generated by Kopp et al. (2014). The dataset consists of 10,000 MC samples of projected RSL time-series for years 2000–2100, discretized by decade, for each of three representative concentration pathways (RCPs): RCP 2.6, RCP 4.5, and RCP 8.5. RCP 8.5 corresponds to high-end business-as-usual emissions, RCP 4.5 corresponds to a moderate mitigation policy scenario, and RCP 2.6 requires a combination of intensive greenhouse gas mitigation and at least modest active carbon dioxide removal (Meinshausen et al. 2011; Kopp et al. 2014). Among these three scenarios, RCP 4.5 is relatively close to the A1B scenario, and thus it is used as the main RSL scenario to be combined with the storm tide projections. The other two RCP scenarios are also used for sensitivity analysis.

For the damage calculations, we consider only the NYC building stock (including the structure and contents of each building), while in Part II, infrastructure (e.g., bridges and tunnels) and indirect losses (e.g., economic losses due to interruption of business) are also accounted for in evaluating overall risk and risk mitigation strategies. NYC building stock data prepared for the New York City Office of Emergency Management by Applied Research Associates (ARA 2007) are used. The data include a current count of buildings in each census block of NYC, organized by building type (e.g., single-family dwelling, multi-family dwelling, retail, schools, government). Using geographic population projections from NYC Department of City Planning (NYC-DCP), Aerts et al. (2014) created a projected count of buildings by census block and building type for year 2040, which is used. Aerts et al. (2014) argued that the population in NYC will become relatively stable after 2040, so here we also assume the building stock will remain the same after 2040.

3.2 Analyses and results

We consider a time horizon of 100 years, over the twenty-first century. We set year 2000 to be the “current” time, or the baseline (with zero RSL). To apply Lin et al.’s (2012) storm tide climatology estimation, we assume that their NCEP-estimated storm tide climatology for the end of the twentieth century represents that for year 2000 and their GCM-projected storm tide climatology for the end of the twenty-first century represents that for year 2100. The GCM-projected storm frequency for 2100 has already been bias-corrected by Lin et al. (2012) by multiplying it with a corrective factor, which is the ratio of the NCEP-estimated frequency and the GCM-estimated frequency for 2000. We bias-correct the GCM-projected storm tide CDF for 2100. Specifically, for each storm tide level, we found the difference in the cumulative probability estimated based on the NCEP reanalysis and the GCM model for 2000, and we add this difference to the cumulative probability estimated by the GCM model for 2100 (bounded above by one). We note that these bias-correction methods are not unique; for example, Lin et al. (2016) applied the quantile–quantile mapping method (Boé et al. 2007) to correct the storm surge CDF. Future research is needed to compare these and other GCM bias-correction methods and evaluate their application to storm tide projection.

We also create a composite storm tide climatology for year 2100 as a weighted average of the four bias-corrected GCM projections for year 2100. To obtain the composite storm frequency, we assign each GCM-projected 2100 frequency a weight that is proportional to the inverse of the absolute difference in the storm frequency estimated based on the NCEP reanalysis and the GCM for 2000. To obtain the composite storm tide CDF, for each storm tide level, we calculate the weighted average of the cumulative probabilities from the four GCM-projected storm tide CDFs for 2100, with the weight proportional to the inverse of the absolute difference in the cumulative probability estimated based on the NCEP reanalysis and the GCM for 2000 (consistent with the bias-correction method). Then, we estimate the return periods for storm tide levels ranging from 0 to 6 m for the bias-corrected and composite GCM projections, assuming the storms arrive as a stationary Poisson process in each climate scenario (Eq. 9).

Figure 2 shows the obtained storm tide climatology estimates at the reference location for NYC, the Battery, for years 2000 and 2100. As it is the storm surge events that are used for damage calculations, the storm surge CDF for year 2000 is also shown for comparison. The difference between the storm surge CDF and storm tide CDF for 2000 is relatively large, which indicates that the effects of astronomical tide should not be neglected in risk analysis. The changes of storm tide CDF between 2000 and 2100 are relatively small for the four GCM-projections and thus for the composite projection. However, storm tide return levels of two out of four GCM projections for 2100 are significantly higher than those of the NCEP 2000 reanalysis because these two GCMs projected significant increase in storm frequency. The other two GCMs projected slightly lower storm frequency and also lower storm tide return levels for 2100 compared to the NCEP 2000 reanalysis. This comparison indicates that relatively large uncertainty exists in climate modeling and should be accounted for in risk assessment. While the uncertainty in storm tide estimation under each climate projection is considered aleatory as described by its probability distribution, we consider the uncertainty in the climate projections epistemic and apply all four available GCM projections to estimate the uncertainty range around the “mean” composite projection.

Fig. 2

Storm tide distribution at the Battery, NYC, for years 2000 (estimated based on NCEP reanalysis data) and 2100 (projected using various climate models). a Bias-corrected and composite storm tide CDF, conditioned on storm arrival. The dashed curve shows storm surge CDF for year 2000, b bias-corrected and composite storm tide return level curves. Storm surge and storm tide data before correction and composition are obtained from Lin et al. (2012)

Figure 3 shows the RSL projection at the Battery based on Kopp et al. (2014). Over the twenty-first century, the RSL is projected to significantly increase, by 0.63–0.97 m for the mean, depending on the RCP scenarios (Fig. 3a). The uncertainty of the projection, however, is large, with a 90% confidence interval of about 0.8–1.12 m around the mean. Such a large uncertainty in RSL projection should be accounted for in risk analysis. This uncertainty may be considered both aleatory and epistemic as it includes uncertainties in both the complex natural processes involved and various GCM models applied. To account for this uncertainty in the analytical risk analysis, we develop the PDF of RSL using kernel density estimation for each decade from 2000 to 2100 (see Fig. 3b for examples).

Fig. 3

Data obtained from Kopp et al. (2014)

RSL distribution at the Battery, NYC, over the twenty-first century, for three RCP scenarios. a Mean (solid) and the 5th–95th percentiles (dash) of RSL distribution over the twenty-first century, b estimated PDF of RSL for years 2020, 2070, and 2100 (for each RCP scenario, PDF shifts towards higher RSL with peak decreasing over time).

We combine the storm tide CDF and RSL PDF to calculate the flood height CDF (Eq. 1), which is then combined with storm frequency to estimate the flood return periods (Eq. 11). This analysis is performed for the storm tide CDF for each climate scenario (now linearly interpolated to each decade between 2000 and 2100) and the RCP 4.5 scenario of the RSL projection. Figure 4 shows the flood height CDF and return periods estimated based on the composite storm tide climatology. The flood hazard is projected to increase continuously and significantly over the twenty-first century, due to the combined effects of sea-level rise and storm climatology change. These decadal projections are further interpolated to yearly projections (t = 1, 2, …, y; y = 100).

Fig. 4

Flood height distribution at the Battery, NYC, years 2000–2100, based on projected RCP 4.5 RSL scenario and composite storm tide climatology. a Flood height CDF, conditioned on storm arrival, b flood height return level curves. Results obtained from analytical analysis

Then, we combine the hazards and vulnerability information to estimate the damage risk for NYC. We first apply damage analysis to both the 2000 building stock and 2040 building stock to obtain the surge damage CDF curves, which are linearly interpolated to each year to obtain the yearly surge damage CDF. This yearly surge damage CDF is manipulated, according to the yearly flood height CDF and the current surge CDF, to obtain the yearly flood damage CDF (Eqs. 2, 3), which is combined with the storm frequency to obtain yearly flood damage return periods (Eq. 13). The obtained yearly flood damage CDF and return periods, under the effects of building growth, RCP 4.5 RSL, and composite storm climatology, are shown in Fig. 5 for each decade over the twenty-first century. The damage return levels are projected to increase dramatically from 2000 to 2100, due to the combined effects of all three dynamic factors.

Fig. 5

Damage distribution for NYC, years 2000–2100, based on projected building stock growth, RCP 4.5 RSL scenario, and composite storm tide climatology. a Damage CDF, conditioned on storm arrival, b damage return level curves. Results obtained from analytical analysis

To better illustrate how the extreme damage levels will increase, Fig. 6 displays the time series over the twenty-first century of the 100-, 500-, 1000-, and 4000-year damage levels under various combinations of the dynamic effects, in comparison with those under the stationary environment of year 2000 (black) (the results under certain and various combinations of the dynamic effects are obtained by neglecting other dynamic effects). Due to only the building stock growth, the 100-year damage increases slightly; however, more extreme damage levels increase substantially, as most of the future building development is projected by NYC-DCP to happen beyond the 100-year flood plain. The increase of the RSL (RCP 4.5), on top of the building growth effect, will dramatically increase the damage at all extreme levels. The change of storm climatology (composite model in this case) further increases the extreme damage levels.

Fig. 6

Time series of various extreme damage levels for NYC, years 2000–2100, under stationary environment of year 2000 (black), non-stationary built environment (green), non-stationary build environment and RCP 4.5 RSL (blue), and non-stationary built environment, RCP 4.5 RSL, and composite storm tide climatology (red). a 100-year damage, b 500-year damage, c 1000-year damage, d 4000-year damage. Results obtained from both analytical analysis (solid curves) and MC simulations (dots)

With the obtained flood damage distribution, we calculate the expectation and variance of the annual damage (Eqs. 15, 16) for each year. Under the stationary environment of year 2000, the estimated EAD is $78 million for NYC and the estimated standard deviation of the annual damage is much larger, at $745.3 million. Our estimation of the EAD is higher than that obtained in Aerts et al. (2014) of about $66.6 million (for buildings), due to three improvements in our methodology. First, we apply statistical analysis on the calculated damages to estimate the surge damage distribution, while Aerts et al. (2014) derived this surge damage distribution directly from the storm surge distribution at the reference location (Battery), which partially neglected the effect of spatial variation of the surge. Second, we consider the effect of astronomical tide on the damage at every surge level (Eq. 2), while Aerts et al. (2014) approximated this effect by shifting the entire surge distribution according to the tidal effect at a single surge level. Third, we calculate the expected total annual damage (Eqs. 24 or 25), while Aerts et al. (2014) calculated the expected maximum annual damage (Eq. 26).

The time-varying EAD over the twenty-first century under each and combined dynamic effects, compared to the stationary case (black), is shown in Fig. 7. The effect of NYC-DCP projected building stock growth is relatively small (Fig. 7a), as expected given previous results related to the extremes (Fig. 6). To investigate the sensitivity of the damage risk to different RCP scenarios of the RSL, we applied all three available RCP scenarios. As Fig. 7b shows, although RSL is the dominant dynamic factor, the effects of the various RCP scenarios are significantly different only in the later decades of the twenty-first century. The EAD is very sensitive to the variation in the storm climatology projection, as shown in Fig. 7c, with the GFDL projection being a case of dramatic increase of the risk (comparable to RCP4.5 RSL) and two out of four climate-model projections (ECHAM and MIROC) being cases of slight decrease of the risk, relative to the stationary case. The composite storm climatology projection induces a moderate increase in the risk, significantly lower than that of RSL but higher than that of the building growth. Finally, under the compound effects of all these dynamic factors (with RCP 4.5 RSL, Fig. 7d), EAD will increase nonlinearly and dramatically, with a large variation range due to the epistemic uncertainty in the climate modeling of the storm climatology. The standard deviation of the annual damage, displayed in Fig. 8, is also projected to increase dramatically over the twenty-first century. The evolution pattern of the standard deviation of the annual damage is similar to that of the EAD, except that although ECHAM and MIROC model projections are similar in the mean, they differ in the standard deviation of the annual damage. Also, the impact of building growth is more substantial on the standard deviation than on the mean of the annual damage.

Fig. 7

Time series of expected annual damage (EAD) for NYC, years 2000–2100, under stationary environment of 2000 (black) and various environmental changes. a Built environment change, b RSL change (for three RCP scenarios), c storm climatology change (for four GCMs and composite), d combined changes in a–c (with RCP 4.5 scenario). Results obtained from both analytical analysis (solid curves) and MC simulations (dots; nearly indistinguishable from analytical curves in all cases)

Fig. 8

Same as for Fig. 7 but for standard deviation of annual damage

With the obtained flood damage distribution, we also calculate the mean of the present value of future losses (PVL) for NYC over the twenty-first century, using the three analytical methods discussed in Sect. 2.2.3, as shown in Table 1. In this case study we use a discount rate of 3% (using a higher or lower discount rate will result in a lower or higher estimate of discounted impact of future climate change and coastal development). Using the continuous discounting method (Eqs. 19, 20), the mean of PVL is about $2503 million under the stationary environment of year 2000, and it is as high as $5002 million under the dynamic environment over the twenty-first century (composite storm climatology and RCP 4.5 RSL). The result based on the discrete discounting method is slightly higher or lower, depending on discounting at the beginning (Eq. 23) or at the end of the year (Eq. 22), as expected. Using the method based on the annual exceedance probability (with Eq. 25; not shown) gives the same results as using the discrete discounting method (with Eq. 24). However, using the approximate method based on the annual exceedance probability that neglects the possibility of having multiple storms in a year (with Eq. 26) slightly underestimates the mean of PVL, as expected. The uncertainty in the estimated mean of PVL due to the epistemic uncertainty in the storm climatology projection is relatively large, as shown in the parentheses in Table 1.

Table 1 Comparison of analytical and MC simulation results for mean of present (2000) value of future losses (PVL) over twenty-first century for NYC, in millions of dollars

Finally, we carry out MC analyses. For each of the cases considered above analytically, we carry out 10⁶ MC simulations. For the stationary environment of year 2000, the storm arrivals are simulated as a stationary Poisson process (Eqs. 5, 6) and the damage values are sampled from the storm tide damage distribution for year 2000; the MC-estimated EAD and standard deviation of the annual damage are $78.8 and $748 million, respectively, very close to those obtained analytically. For the dynamic environment, the storms arrive as a non-stationary Poisson process (Eq. 27), and the damage values are sampled from the surge loss distribution based on the sampled arrival time, storm tide level, and RSL (Eq. 28). As for the analytical analysis, the cases of certain and combinations of the dynamic effects are obtained by neglecting other dynamic effects. The obtained MC estimation of the time-varying mean and standard deviation of the annual damage are very close to the analytical results for all cases (Figs. 7, 8), except that the MC-estimated standard deviation of the annual damage is slightly higher than the analytical values for the very extremes (Fig. 8d), perhaps due to slight different numerical approximations applied towards the limit of the available data. The MC-estimated extreme damage levels compare also very closely with the analytical results (Fig. 6); the fluctuations of MC estimations around the analytical estimations indicate that an extremely large number of simulations would be needed to achieve convergence in the estimation for the very end of the tail of the damage risk. In addition, the MC-estimated mean values of PVL (calculated using Eq. 17) come very close to the analytical results (Table 1), especially those calculated with the continuous discounting method as the MC method considers the storm arrival time within the year.

Analytical methods are simpler and more efficient and thus should be used whenever possible, as explored in this study. MC simulations, after being validated with the analytical results, can be applied to estimate more complex risk measures. We use the MC samples that are validated for both the mean and extreme damage measures (Figs. 6, 7, 8; Table 1) to estimate the probability distribution of PVL. The obtained PDF of PVL (using the nonparametric density method) is displayed in Fig. 9, with representative statistics shown in Table 2.

Fig. 9

PDF of present (2000) value of future losses (PVL) over the twenty-first century for NYC, under stationary environment of 2000 (black) and various environmental changes. a Built environment change, b RSL change (for three RCP scenarios), c storm climatology change (for four GCMs and composite), d combined changes in a–c (with RCP 4.5 scenario). Discount rate is assumed to be 3%. Results obtained from MC simulations

Table 2 Mean; standard deviation; median; and 75th, 95th, and 99th percentiles of present (2000) value of future losses (PVL) over twenty-first century for NYC, in millions of dollars, based on MC simulations (as in Fig. 9)

For the stationary case, the standard deviation of PVL is about 1.2 times the mean, the median is about 0.6 times the mean, and the 95th percentile is about 3.3 times the mean. The effects of the dynamic factors on the overall, temporally integrated damage risk is indicated by the widening and shifting of the PDF of PVL to larger damage values. As expected, the effect of building stock growth is relatively small. The effect of RSL is dominant but is not very sensitive to the RCP emission scenarios, because the difference of the RCPs is largely shown in the later decades (Figs. 7, 8), when the discounting is larger. The effect of storm climatology change shows a small to moderate effect when measured by the composite climate, while large variations exist among the GCM projections even for the same emission scenario (A1B). In the extreme case (GFDL), the effect of storm climatology is larger than the effect of RSL on all PVL levels (see Table 2). Finally, the compound effects of the three dynamic factors would greatly shift the PDF of the PVL. Compared to the stationary case, if all three non-stationary effects are considered with the composite storm climate and RCP 4.5 RSL (the four GCM storm climates and RCP 4.5 RSL), the mean of PVL is estimated to increase by 2.0 (1.5–3.5) times, the standard deviation increase by 1.3 (1.2–1.7) times, the median increase by 2.7 (1.8–5.3) times, and the 95th percentile increase by 1.6 (1.3–2.2) times. Thus, the change in the dynamic risk is apparent not only in the mean but also in the entire distribution of the PVL. Considering the PDF of PVL rather than only the mean is a more comprehensive approach to evaluate the overall flood damage risk as well as the benefit of risk mitigation strategies (Part II).

4 Summary

We have proposed an integrated dynamic risk analysis for flooding task (iDraft) framework for estimating the storm surge flood damage risk at regional scales, considering integrated dynamic effects of storm climatology change, sea-level rise, and coastal development, in a formal, coherent Poisson-process framework. It is shown that various time-varying risk metrics of interest, such as the return period of various damage levels and the mean and variance of annual damage, can be derived analytically, as well as the mean of the present value of future losses (PVL). However, risk measures that involve temporal integration of the stochastic process, such as the probability distribution of PVL, may be difficult or impossible to derive analytically. MC methods are thus developed to estimate such risk measures. The analytical and MC methods are theoretically consistent and validate each other in the complex flood risk analysis task. The iDraft framework should be extended to consider extratropical cyclone surge hazards in addition to tropical cyclone surge hazards and social vulnerability in addition to physical vulnerability of coastal cities.

Although the discrete storm surge events can be reasonably considered as conditionally independent, the continuous RSL is temporally correlated. Future analysis on the correlation of RSL is useful, e.g., for analytically estimating the variance of PVL and perhaps the probability distribution of PVL. When applying climate-model projected storm surge/tide climatology to flood hazard and damage risk analysis, the climate-model bias may be relatively large and should be first corrected. Also, multiple model projections may be combined to obtain a weighted average or “best” climate projection. However, the specific methods of climate-model bias correction and model combination needs to be further developed. Given the estimated flood as a combination of RSL and storm tide, inundation over land can be better modeled with dynamic modeling than static mapping, especially for areas with complex topography. The effect of natural and built flood defense is grossly approximated here; it warrants better consideration in future studies. Vulnerability models that account for effects of not only still water inundation but also dynamic wave impact can more realistically represent damage mechanisms and thus should be developed and applied in the future. These modeling improvements may significantly reduce the epistemic uncertainties in flood risk assessment. In addition, PVL can be very sensitive to the discount rate applied, which should be considered carefully in risk management applications.

The case study for NYC shows that the impact of population growth and coastal development on future damage risk is likely to be small compared to climate change factors, because the city is already heavily built especially at the coastal front. Sea-level rise will significantly increase the damage risk even under the most stringent emission scenario. Storm surges will likely intensify and/or become more frequent, further increasing the flood risk and especially associated uncertainty. The joint effect of coastal development, sea-level rise, and storm climatology change is possibly a dramatic increase of the risk over the twenty-first century and a significant shift of the temporally integrated losses towards high values. Part II of this study will evaluate the cost-effectiveness of various flood mitigation strategies proposed for NYC to avert the potential impact of climate change.