Advertisement

Climatic Change

, Volume 137, Issue 1–2, pp 157–170 | Cite as

Offshore CCS and ocean acidification: a global long-term probabilistic cost-benefit analysis of climate change mitigation

  • Bob van der ZwaanEmail author
  • Reyer Gerlagh
Open Access
Article
First Online:

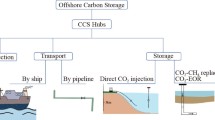
Abstract

Public fear over environmental and health impacts of CO2 storage, or over potential leakage of CO2 from geological reservoirs, is among the reasons why over the past decade CCS has not yet been deployed on a scale large enough so as to meaningfully contribute to mitigate climate change. Storage of CO2 under the seabed moves this climate mitigation option away from inhabited areas and could thereby take away some of the opposition towards this technology. Given that in the event of CO2 leakage through the overburden in the case of sub-seabed CCS, the ocean could function as buffer for receiving this greenhouse gas, instead of it directly being emitted into the atmosphere, offshore CCS could also address concerns over the climatic impacts of CO2 seepage. We point out that recent geological studies provide evidence that to date CO2 has been safely stored under the seabed. Leakage for individual offshore CCS operations could thus be unlikely from a technical point of view, if storage sites are well chosen, well managed and well monitored. But we argue that on a global longterm scale, for an ensemble of thousands or millions of storage sites, leakage of CO2 could take place in certain cases and/or countries for e.g. economic, institutional, legal or safety-cultural reasons. In this paper we investigate what the impact could be in terms of temperature increase and ocean acidification if leakage occurs at a global level, and address the question what the relative roles could be of on- and offshore CCS if mankind desires to divert the damages resulting from climate change. For this purpose, we constructed a top-down energy-environment-economy model, with which we performed a probabilistic Monte-Carlo cost-benefit analysis of climate change mitigation with on- and offshore CCS as specific CO2 abatement options. One of our main conclusions is that, even under conditions with non-zero (permille/year) leakage for CCS activity globally, both onshore and offshore CCS should probably – on economic grounds at least - still account for anywhere between 20 % and 80 % of all future CO2 abatement efforts under a broad range of CCS cost assumptions.

Keywords

Onshore versus offshore CCS Climate change Ocean acidification Cost-benefit analysis Monte Carlo analysis 

1 Introduction

Although aspects of the technical and economic, as well as the legal, political and public acceptance dimensions of CO2 capture and storage (CCS) still require deeper understanding, CCS technology could, and perhaps needs to, play a major role in curbing global CO2 emissions. According to the Special Report on CCS (SRCCS) of the Intergovernmental Panel on Climate Change (IPCC), it is expected that CO2 artificially injected underground can remain securely stored during at least centuries (IPCC 2005). In many cases the probability of long-term CO2 storage integrity is high, and it is likely that storage sites can be found, if well managed and monitored, for which containment is practically guaranteed (Lackner et al. 2012). The Sleipner storage project is a good and iconic example, as at this site since 1996 CO2 has been safely stored in a geological formation deep under the North Sea with quantities of about a million ton of CO2 per year. Likewise, in the Barents Sea at the Snøhvit storage site CO2 has been successfully and securely stored under the seabed since 2008. The findings of the ECO2 project (“Sub-seabed CO2 Storage: Impact on Marine Ecosystems”, funded by the European Commission) confirm that to date CO2 has been safely stored at these two locations. One can thus conclude that contained storage of CO2 in the underground appears possible (ECO2 2015), but that claims on this subject matter need to be made carefully: much more knowledge still needs to be developed about the potential short- and long-term impacts of CO2 storage on marine ecosystems.

While the monitoring techniques applied in the ECO2 project did not detect any CO2 anomalies in the sediments and bottom waters above the Sleipner and Snøhvit storage complexes, high-resolution seismic data revealed a large number of vertical pipes and chimney structures cutting through the sedimentary overburden in the vicinity of both sites (ECO2 2015). The project found out that the seabed above the Snøhvit storage formation was characterized by a high density of circular seafloor pockmarks, probably formed by gas and/or fluid ascent in the geological past. While there is for the moment no evidence that these pockmarks emit any water or gas into the marine environment, some of them possess deep-reaching roots. Seepage of methane from the overburden into the overlying water column was detected at numerous locations around the Sleipner site, which so far seem to result from shallow seabed origins only. Releases of water from a geological formation were detected through a 3 km long fracture-like structure 25 km north of the Sleipner platform, which to date also prove to come from shallow sources. All these newly discovered geological features, however, pose a number of questions, such as whether high permeability pathways exist for gas flows cutting through the overburden and linking storage formations to existing seep sites and pockmarks, and whether CO2 stored below the seabed may eventually leak through the overburden via seismic pipe and chimney structures, fractures or abandoned wells.

In this article we take a global long-term economic approach towards CCS deployment and the integrity of CO2 stored underground (we are thereby complementary to the local “investment under uncertainty” approach taken by Narita and Klepper 2015). In our analysis we allow, probabilistically, for relatively small CO2 leakage rates, based on a number of different types of arguments (see also the online appendix). First, scenarios can be envisaged in which under continued storage activity at sites like Sleipner and Snøhvit CO2 slowly migrates horizontally in the storage formation under the cap-rock to eventually reach a vertical pipe or chimney structure. Depending on their permeability and porosity, such structures could function as transit medium allowing CO2 to dissipate upwards towards the seabed. Thus, despite a variety of geochemical trapping mechanisms the CO2 would be subjected to during its migration path, it is possible that it could ultimately reach the bottom levels of the sea water, at these two storage sites and similarly at other locations with comparable geological features.

Second, in recent CO2 storage projects it proved that sometimes mid-term action is required in order to maintain safe containment conditions. During the initial operation of the Snøhvit CCS project, for instance, it appeared that the storage capacity of the formation initially chosen was insufficient, so that soon after the project’s start another geological formation was chosen, in which the storage of CO2 continued. On the basis of reservoir, seismic and geo-mechanical data obtained at the In Salah CO2 storage project in Algeria, concerns arose about possible vertical leakage of CO2 into the cap-rock, as a result of which the storage activities at this plant were suspended in 2011 (de Coninck and Benson 2014). These two examples demonstrate that not always all features of planned storage formations are fully comprehended before a storage project is actually initiated. Indeed, sometimes more complete understanding of a storage site’s containment integrity is only obtained after a project has been taken into operation. It is imaginable that not in all possible future storage projects in the world a similar adaptive approach is adopted as in these two cases. A lack of such approach could potentially lead to the eventual leakage of CO2 into the ocean, sea or atmosphere above the storage formation’s geological overburden layers.

Third, in the future not in all countries necessarily the same monitoring efforts will be deployed, for a number of different reasons. For example, there may be a lack of technical expertise required for such monitoring in a given country. It is possible that not everywhere the same safety requirements are followed by lack of political will or absence of necessary safety culture. It is conceivable that for institutional reasons no action is taken upon observed breach of storage containment, for example as a result of unclear agreements over responsibilities and liabilities. Whereas economic reasons may exist for initiating a CCS project, such as stimulated by a carbon tax or other policy instrument, economic arguments may also exist for insufficiently managing and monitoring a storage site or unsatisfactorily remediating a leakage in case CO2 dissipation is observed from the storage formation, e.g. if the costs of these activities are high or there is inadequate clarity over who should pay for them. Such economic, institutional, legal or social reasons for possible CO2 leakage phenomena may diverge substantially from one country to the other, but should be taken into account when performing a global long-term analysis of CCS deployment and CO2 storage integrity, as we do in this article.

For the present study we constructed a global top-down energy-environment-economy model, called OCEAN (acronym for On- and offshore CCS and Energy-climate system ANalysis), with which we performed a probabilistic cost-benefit analysis of climate change mitigation with generic abatement activity as well as both on- and offshore CCS as two complementary CO2 abatement options. With this model we try to answer several questions. First, to what extent can CCS still contribute to CO2 emissions abatement if on a global long-term scale leakage occurs at relatively low seepage rates? Second, what can under such conditions be the relative roles of onshore versus offshore CCS, given that CO2 seepage damages incurred to the ocean are likely much less than those to the atmosphere? Third, can moving storage activity from onshore to offshore projects constitute a stimulus for the large-scale deployment of CCS on purely economic grounds, in addition to the possible improvements hereof in terms of public acceptance, in the event that 100 % storage integrity cannot be entirely ascertained for the ensemble of all storage sites internationally into the indefinite future? In Section 2 we describe the main features of the model we use for our analysis and the way in which we apply it for this paper’s purposes (while reserving the online appendix for the details and equations of our model). In Section 3 we report the major findings of our research, in terms of a series of model run outcomes. In Section 4 we summarize our main conclusions.

2 OCEAN model and methodology

For the purpose of answering these questions we constructed an optimal growth model in which prices in the global economy yield general equilibrium between supply and demand of a growing but stabilizing world population (UN 2009). A representative planner optimizes welfare, which is expressed by the discounted sum of utility per time period. Welfare optimization leads to the Ramsey rule for the intertemporal rate of exchange. The OCEAN model thus fits in the tradition of top-down integrated assessment models, as initiated by Nordhaus (1994) with the DICE model. Like DICE, our model accounts for damages incurred as a result of climate change and proffers abatement options with which, at a certain cost, emissions of greenhouse gases can be avoided (see the appendix in the online Support Information for the full details of our model). As in Gerlagh and van der Zwaan (2002); Hoel and Sterner (2007), and Sterner and Persson (2008), OCEAN also includes ‘intangible’ damages (i.e. costs that are hard to quantify or express in monetary terms) associated with climate change (see also Gerlagh 2014).

Our new model has certain similarities with the DEMETER model, which we previously used for related analysis and has been instrumental for studying several climate-related policy questions (see e.g. van der Zwaan et al. 2002, and Gerlagh and van der Zwaan 2006). Our new model, like DEMETER, simulates the global use of fossil fuels, the CO2 emissions resulting from their combustion, as well as the means that allow for avoiding these emissions. It includes generic production and consumption behavior and a basic climate module, and is in several ways an extension of DEMETER, since we have refined the simulation of atmospheric and oceanic CO2 stock build-up as well as the corresponding climate change dynamics, and now explicitly include impacts such as ocean acidification. Over the past years DEMETER has been used specifically for the purpose of studying economic opportunities and conditions for CCS deployment, including issues such as potential CO2 leakage (van der Zwaan and Gerlagh 2009; Gerlagh and van der Zwaan 2012). We here build on that work, as well as the broader and still growing literature on this topic (see, for example, Ha-Duong and Keith 2003; Keller et al. 2008; Keppo and van der Zwaan 2012; Teng and Tondeur 2007).

Unlike with DEMETER, we have now substantially simplified the simulation of energy-transition dynamics, as we do not explicitly represent in our new model the replacement of fossil fuels by mitigation options such as renewables, nor do we assume that the costs of mitigation reduce according to learning-by-doing phenomena. Rather, we keep the energy economy relatively simple, by allowing for a shift away from fossil fuels in a more stylistic way. The social optimizer can choose between either continuing with the use of fossil fuels but experiencing the damages emanating from climate change, or shifting away from them to avoid these impacts but at a given abatement cost. An additional degree of freedom for the social planner is that (like in DEMETER) CCS can be introduced as a means to decarbonize fossil fuels, which would permit their continued usage but under extra abatement costs.

New in our current approach is that we represent two types of CCS options, one for which storage of CO2 takes place onshore, the other one offshore. We make several key assumptions for these options, in an attempt to let our model reflect stylistically some of the main features of mitigation through CCS. First, both these types of CCS are characterized by an energy penalty of 30 % (defined as the share of the electricity output of a power plant that needs to be employed to operate the CCS facility), which yields lower levels of CO2 avoided versus the levels of CO2 stored (Gerlagh and van der Zwaan 2006). Second and critically important in a model such as OCEAN, based on publications such as by the IPCC (2005; 2014); Keppo and van der Zwaan (2012) and Finkenrath (2012), we assume that the costs of onshore CCS amount to 50 €/tCO2 (median) with a lognormal uncertainty range of 17–150 €/tCO2 (2.5 % and 97.5 % probability levels). This uncertainty range is especially broad since large-scale deployment for CCS is still practically untested. Similarly, we assume for offshore CCS costs of 75 €/tCO2 (median) with a lognormal uncertainty range of 25–225 €/tCO2 (2.5 % and 97.5 % probability levels).1 , 2 The difference between the costs of these two types of CCS reflects the fact that offshore activity is more expensive than onshore activity, and that for offshore CCS additional and more advanced technology is required to perform geological injection of CO2 through a layer of sea or ocean water, in comparison to the equipment needed for onshore CCS (even while for the former existing infrastructure such as oil or gas rigs can sometimes be used – see e.g. the Sleipner project (Statoil 2013)). Third, we differentiate between safe and unsafe storage sites, but assume that the type (i.e. safety level) of any particular storage site is unknown in advance. We suppose that the majority of CO2 stored geologically will stay underground forever, which is a necessary assumption if one wants CCS to become deployable on a large scale: we stipulate that the share of storage sites with a perfectly immobilized total quantity of CO2 amounts to 70 % (median) with an uncertainty range of 40–85 % for all injected CO2.

Fourth, we stipulate that for unsafe storage sites, CO2 stored onshore leaks with a rate of 0.33 %/yr. (median) with a lognormal uncertainty range of 0.1–1.0 %/yr.3 The reason for this is not because we think that CO2 cannot be stored safely underground: quite on the contrary, we think that sites can be found for which storage will be permanent or close thereto, if they are well managed and monitored (Kharaka et al. 2006; Klusman 2003; Shaffer 2010). But, as explained above, we leave open the possibility that as a result of economic, institutional or political reasons, and/or given the prevailing safety culture, storage activities in some regions or countries may not necessarily be subjected to the measures required for long-term secure containment. Likewise, we suppose that from unsafe offshore storage sites CO2 leaks with a rate of 0.5 %/yr. (median) with a lognormal uncertainty range of 0.1–2.4 %/yr. As described in the introduction, such leakage levels are speculative and little evidence exists to draw upon, but they are deemed plausible by the CCS research community and match the possible figures 100–1000 tCO2/day estimated in several publications (ECO2 2015; IEAGHG 2009; Statoil 2013). On the basis of the fact that injecting is technologically more challenging, and remediating less trivial, for offshore than onshore CO2 storage activity,4 we justify our choice for higher leakage rates for the former than for the latter.5

Fifth, we assume that CO2 (emitted or leaked) incurs two types of damages to the environment (atmosphere or ocean) into which it is released: tangible and intangible (see e.g. the seminal work by Nordhaus (1994) for a more detailed description of this distinction). We assume that a 3 °C temperature increase leads to a tangible damage cost (emanating from GDP or consumption losses as a result of e.g. sea level rise, extreme weather events or drops in fisheries and tourism) of 2 % (median) of gross domestic product (GDP) with a lognormal uncertainty range of 0.5–8 %. The intangible damages from this temperature rise (such as in terms of reduced human well-being or satisfaction resulting from environmental degradation or biodiversity loss) add another 1 % cost of GDP (median), with a higher lognormal uncertainty range of 0.125–8.0 % to reflect the higher uncertainty for these intangibles.6 The tangible costs resulting from an increase in ocean acidification corresponding to a decrease in the pH parameter equivalent to 550 ppmv atmospheric CO2 concentration increase (including for instance the negative effects of ocean acidification on fisheries) amount to 0.1 % of GDP. Given the large uncertainties in this respect, we assume a wide probability distribution of 0.01–1.0 % for these costs. Similarly, intangible costs resulting from a corresponding drop in the pH-value (reflecting e.g. the loss of marine biodiversity) amount to 1.0 % of GDP, with a lognormal uncertainty range of 0.2–5.0 %. Intangible damages are scaled for the base year (2020) and their value increases with income. The pure rate of time preference is set to 1 %/yr. (range 0.5–2 %/yr). This means that the OCEAN model is calibrated so as to be consistent with a robust decline in returns on capital when economic growth slows down, as argued in Piketty and Zucman (2014). The assumed declining returns imply a robust carbon price, robust optimal emission abatement levels, and moderate climate change as the median outcome.

Of course, a model like ours requires many more assumptions, regarding for example business-as-usual GDP and income growth, baseline fossil fuel use and associated CO2 emissions (energy and non-energy related), the radiative forcing contributions from other greenhouse gases, return on capital investments and the intertemporal elasticity of marginal utility, as well as the costs of generic abatement activity. For the details behind the parameter values we assumed for these variables we refer to the appendix in the online Support Information for this article. We ran 100 scenarios with parameter values that span the indicated uncertainty ranges, and thereby perform a Monte Carlo type of analysis. We consider this in our context a particularly appropriate approach, given the uncertainties involved in many parameter values, but we are appreciative of the other possible frameworks that could be used to explore this topic, among which for example Expected Utility or Decision under Uncertainty analysis (see e.g. Held et al. 2009). We next report our results when running our model in a cost-benefit mode for all these scenarios, for a set of generic emissions-, climate- and ocean-related parameters, and for the listed variable values for the use of CCS and potential leakage of CO2.

3 Simulations and interpretations

3.1 CO2 emissions and climate impacts

Figure 1 shows the results of our Monte Carlo analysis for CO2 emissions until the year 2100. In almost all cases emissions peak before the middle of the century (only a handful of scenario runs involve emissions that still rise after 2050), while more than half of the 100 scenarios yield emission reduction profiles from already in or before 2020 (cf. the 50 % probability line), and only about 10 % of them reach their highest emission level after 2040 (cf. the 90 % probability line). Around 90 % of the scenarios yield zero-level emissions before 2100: our cost-benefit analysis thus implies that the assumed level of climate change damages does no longer allow increases in the atmospheric concentration of CO2 after 2100 in the majority of cases. In Fig. 2 we see that the concentration of CO2 in the atmosphere has reached its peak in more than half of the scenarios before 2050. For only few of the cases this concentration keeps on rising after this century, while emissions start declining during this century for all scenarios except one (see Fig. 1). For all cases depicted in Figs. 1 and 2 we see a stark deviation from the business-as-usual projection, for which both emissions and concentrations of CO2 rise rapidly during the entire 21st century.
Fig. 1

Monte Carlo runs for annual emissions as calculated with the OCEAN model

Fig. 2

Monte Carlo runs for atmospheric CO2 concentration as calculated with the OCEAN model

Figure 3 (with a time scale until 2300) shows that the global stabilized temperature increase stays below the internationally agreed 2 °C limit in about 50 % of the cases, whereas a subset thereof yields a temporary overshoot (during only several decades) slightly above 2 °C around the end of the 21st century. In slightly under 90 % of the scenarios the global average temperature discontinues to rise after 2100. The share of scenarios for which the temperature increase stays always below this target is around 40 %. All scenarios reach their temperature peak before 2300 (but in one case this peak is as high as about 5 °C). Some 10 % of the scenarios stabilize with a temperature increase of around 1 °C or lower, with a peak occurring well before the end of the 21st century of at most 1.5 °C, the enhanced climate change control target adopted at COP-21 in Paris in December 2015 (UNFCCC 2015). For around 10 % of the scenarios we find temperature increase peaks that are above 3.5 °C, which typically take place around the end of the century. In Fig. 4 (with again a time scale until 2300), we see for these scenarios the corresponding oceanic acidification increase, as expressed by measure of pH decrease, since much of the CO2 released into the atmosphere is absorbed by the surface layer of our planet’s oceans. As one can observe from this Figure, the pH decrease amounts to at most 0.1 for around 90 % of the scenarios. In about 10 % of the cases we see that the pH parameter dips deeper than a change of 0.1, and in one case even by as much as 0.3. For all scenarios we see that after a minimum of the pH value around or before 2100, it increases again during the subsequent two centuries: at the background of large-scale emission abatement activity, the pH decrease patterns revert into positive changes from 2100 onwards.
Fig. 3

Monte Carlo runs for global temperature increase from the OCEAN model

Fig. 4

Monte Carlo runs for ocean acidification from the OCEAN model

3.2 Onshore versus offshore CCS

We find that CCS is broadly deployed as CO2 abatement option to manage global climate change, and that CO2 is stored both onshore and offshore. In Figs. 5 and 6 we see that in some 50 % of our scenarios we obtain a level of around 20 GtCO2 of storage per year at some point during the second half of the century, both for onshore and offshore CCS. In the majority of cases we see that already 10 GtCO2 is geologically stored every year by the middle of the century, and for about 10 % of the cases even as much as 40 GtCO2 annually by 2100, with again no large differences between onshore and offshore CCS. Hence, under our set of assumptions, we observe substantial storage activity for both types of CCS, with onshore CCS benefiting from its lesser deployment costs and lower leakage rate, while offshore CCS profiting from the smaller damage it incurs.
Fig. 5

Monte Carlo runs for annual storage of CO2 onshore as calculated with the OCEAN model

Fig. 6

Monte Carlo runs for annual storage of CO2 offshore as calculated with the OCEAN model

Figures 7 shows that if the minimum value of the costs of the two CCS options is 20€/tCO2 or lower, some 80 % of overall CO2 abatement takes place through CCS, rather than other options such as renewables. Even at a minimum cost for CCS at 50€/tCO2, its contribution to total mitigation efforts can still be large, with a share amounting to anywhere between 0 % and 60 %. At CCS costs between 100€/tCO2 and 150€/tCO2, the use of CCS is significantly curtailed, but can still amount to a level contributing by approximately 20 % to overall climate mitigation. In Fig. 8 we indicate under what cost conditions which of the two CCS types dominates. If the injection of CO2 at offshore locations is at most 10 % more expensive than onshore injection, then there is a high probability that offshore CCS is the preferable option, accounting for at least 60 % of all CCS deployment. For a cost difference of 30 %, onshore CO2 storage becomes more attractive, with a high probability that it accounts for more than 60 % of all CCS. The explanation for the fact that relatively higher offshore CCS costs can be permitted is the lower level of damages incurred to the environment in the case of leakage of CO2 into the ocean, in comparison to the case in which leakage occurs into the atmosphere.
Fig. 7

Share of CCS in overall emissions abatement versus costs from the OCEAN model

Fig. 8

Share of offshore CCS in total CCS versus cost differential from the OCEAN model

4 Conclusions

The findings reported in this article are different from the conclusions we drew in our earlier work, in which we asked ourselves similar questions on the economics and feasibility of CCS under leakage of CO2 (van der Zwaan and Gerlagh 2009; Gerlagh and van der Zwaan 2012). We have here attempted to shed light on the possible attractiveness of offshore geological CO2 storage, and have inspected what the economic benefits could be of complementing onshore CCS with offshore CCS. For certain countries, like the UK, this is particularly pertinent, as the majority of potential CO2 storage sites it possesses are located in offshore waters. As was shown in Section 3, we find that by allowing for offshore CO2 storage one could possibly significantly stimulate the usefulness of CCS from a cost-benefit perspective, and thus expand its implementation on such grounds. Offshore CO2 injection may also substantially reduce public opposition to CCS, which currently plays a sizeable role in impeding its deployment onshore. On the basis of both these perspectives, one may conclude that partly moving CCS from onshore to offshore locations may be a beneficial path to take to render CCS practically more feasible as well as more realistic as climate mitigation option.

In short, our argument goes as follows. First, it may well be that CO2 abatement through offshore CCS is more expensive than via onshore CCS – up to 75 €/tCO2, i.e. up to 100 % in relative terms – given that it is harder to undertake geological CO2 injection activity under the seabed than directly in open air at the surface of the underground. Second, while not all uncertainty is yet resolved in this domain (as described in the introduction, including in relation to the so far promising and successful Sleipner and Snøhvit storage projects), it seems likely that near zero-leakage storage sites can be found, operated, maintained and secured (onshore as well as offshore) from a natural scientific point of view. But based on economic, political, institutional and safety cultural arguments one may reason that on a large global scale in which many thousands of CO2 storage sited are operated, leakage may ultimately not be zero. Third, in such a context, one may claim that offshore leakage is potentially higher than onshore leakage, since the injection process is technologically more requiring and remediation, if needed, is less trivial. We hypothesize that leakage rates could be 50 % higher for offshore than for onshore CCS.

One may have different opinions on these three assumptions, and over time they may prove not to hold out. But our main point can be drawn despite these hypotheses: also under these conditions, as we demonstrate, offshore CCS may be as interesting from an economic perspective as onshore CCS. The reason for this finding is that there is high likelihood that the damages from CO2 leakage into the atmosphere are more costly than those from seepage into the ocean. Hence, if the circumstances are one day such that a possibility exists for CO2 leakage, then it becomes less costly to let the leakage occur into a medium in which the damage costs are more modest (whether tangible or intangible) than into one for which these costs are almost certainly high. On the basis of our findings in this economic perspective, we argue that the prospects for CCS could be substantially improved if one were to shift a good share of global CCS activities from onshore to offshore territory. Our outcome is aligned with similar conclusions based on public acceptance arguments, which also point towards a shift from onshore to offshore CCS, since the latter can avoid Not In My Back Yard (NIMBY) sentiments.

In the probabilistic cost-benefit framework that we use for our study, and under the range of stylistic assumptions that we have had to make in order to perform this type of global economic analysis, we find that if offshore storage is at most as costly as onshore storage, then at least 60 % of all CO2 capture and storage should probably take place through offshore CCS. At a 50€/tCO2 cost of CCS we think that CCS’s contribution to total mitigation efforts should typically be about 30 %, whereas with CCS costs between 100€/tCO2 and 150€/tCO2, the use of CCS ought to be significantly diminished but could still amount to a contribution of around 20 % to overall climate mitigation. If the injection of CO2 offshore is at most 10 % more expensive than onshore injection, then offshore CCS is the preferable option, accounting typically for at least 60 % of all CCS deployment. Of course, improvements in other technologies such as renewables have the potential to substantially reduce the deployment of CCS and hence de-emphasize the importance of potential CO2 leakage as expressed in this paper. This is a subject that deserves further research. Likewise, in future work the introduction of learning curves in a model like OCEAN deserves reconsideration, as this form of expressing learning-by-doing phenomena can play a large role in the outcome of scenario runs, as we previously demonstrated with our DEMETER model (see van der Zwaan et al. 2002, and Gerlagh and van der Zwaan 2012).

The ECO2 project, in the context of which much of the above research has been performed, has advanced the field of CCS research substantially, particularly the offshore CO2 storage integrity and marine impacts dimension thereof (ECO2 2015). As was pointed out, the data and knowledge generated in this project have led to further questions related to both the likelihood and mechanisms of leakage. These new questions need to be assessed in what hopefully will be more research projects in this area. They also will have to be considered by storage site operators. When answers are found to (some of) these new questions, and while the field further develops its understanding of the integrity of climate change control induced CO2 storage, we recommend that the local and global economics of onshore and offshore CCS activities are also revisited.

Footnotes

  1. 1.

    From here on we specify all uncertainty ranges as 2.5–97.5 % probability intervals.

  2. 2.

    For the standard abatement option with which CCS competes, marginal costs increase linearly with emission reductions. Full emission reduction is achieved at marginal costs that, for the first period, are lognormally distributed over the range 80–320 €/tCO2, with median 160 €/tCO2. See the online appendix for more details.

  3. 3.

    The average expected leakage is thus 30 % unsafe storage times 0.33 %/yr., which equals 0.1 %/yr. This leakage rate is consistent with the worst case scenarios investigated in the ECO2 project (2015), in which plausible maximum rates of approximately 150 tCO2/day were found (assuming a 1 MtCO2/yr. storage project operated for 50 years).

  4. 4.

    Note that for monitoring the equivalent claim does not hold: offshore leakage detection, using standard hydroacoustic echosounder systems (available at any ship), is much easier than onshore, since these systems are many times more sensitive (and cheaper) than any onshore technique.

  5. 5.

    Indeed, from a purely geological point of view there should essentially be no difference between the two, that is, leakage structures are likely to be approximately the same for offshore and onshore CO2 storage (but in the former case they have perhaps been studied more extensively to date; see ECO2 2015).

  6. 6.

    All modeled climate-change-induced atmospheric damage costs are incurred with a delay of at least decades (given the intrinsic interval between emissions and ensuing temperature change). We thus abstract from possible immediate (tangible and intangible) seepage costs associated with onshore CCS, resulting from e.g. asphyxiation, drinking water pollution, fear and/or social unrest.

Supplementary material

10584_2016_1674_MOESM1_ESM.docx (266 kb)
ESM 1 (DOCX 266 kb)

References

  1. Blackford JC, Jones N, Proctor R, Holt J (2008) Regional scale impacts of distinct CO2 additions in the North Sea. Mar Pollut Bull 56(8):1461–1468CrossRefGoogle Scholar
  2. de Coninck H, Benson S (2014) Carbon dioxide capture and storage: issues and prospects. Annu Rev Environ Resour 39:243–270CrossRefGoogle Scholar
  3. ECO2 (2015) ECO2 Briefing Paper No.4: offshore CO2 storage and marine ecosystems, a scientific summary of the ECO2 project, downloadable from www.eco2-project.eu.
  4. Finkenrath M (2012) Carbon dioxide capture from power generation - status of cost and performance. Chem Eng Technol 35(3):482–488CrossRefGoogle Scholar
  5. Gerlagh, R. (2014). Calculating the social costs of carbon without knowing preferences. Comment on A rapid assessment model for understanding the social costs of carbon, Clim Chang Econ 5.Google Scholar
  6. Gerlagh R, van der Zwaan BCC (2002) Long-term substitutability between environmental and man-made goods. J Environ Econ Manag 44:329–345CrossRefGoogle Scholar
  7. Gerlagh R, van der Zwaan BCC (2006) Options and instruments for a deep cut in CO2 emissions: carbon capture or renewables, taxes or subsidies? Energy J 27(3):25–48CrossRefGoogle Scholar
  8. Gerlagh R, van der Zwaan BCC (2012) Evaluating uncertain CO2 abatement over the very long term. Environ Model Assess 17(1/2):137–148CrossRefGoogle Scholar
  9. Ha-Duong M, Keith DW (2003) Carbon storage: the economic efficiency of storing CO2 in leaky reservoirs. Clean Techn Environ Policy 5:181–189CrossRefGoogle Scholar
  10. Held, H., E. Kriegler, K. Lessmann, O. Edenhofer (2009) Efficient Climate Policies under Technology and Climate Uncertainty, Energy Econ, 31, S50–S61 (contribution in C Böhringer, TP Mennel, TF. Rutherford (Guest Eds.): Technological Change and Uncertainty in Environmental Economics), doi: 10.1016/j.eneco.2008.12.012
  11. Hoel M, Sterner T (2007) Discounting and relative prices. Clim Chang 84:1573–1480CrossRefGoogle Scholar
  12. IEAGHG (2009) Assessment of sub-sea ecosystem impacts. IEA Green-house Gas R&D Report, Cheltenham, UKGoogle Scholar
  13. IPCC (2005) Special report on carbon dioxide capture and storage, intergovernmental panel on climate change. Cambridge University Press, Cambridge UK, Working Group IIIGoogle Scholar
  14. IPCC (2013) Climate change mitigation, fifth assessment report (AR5), working group I. Cambridge University Press, Intergovernmental Panel on Climate ChangeGoogle Scholar
  15. IPCC (2014) Climate change mitigation, fifth assessment report (AR5), working group III. Cambridge University Press, Intergovernmental Panel on Climate ChangeGoogle Scholar
  16. Keller K, McInerney D, Bradford DF (2008) Carbon dioxide sequestration: how much and when? Clim Chang 88(3–4):267–291CrossRefGoogle Scholar
  17. Keppo I, van der Zwaan BCC (2012) The impact of uncertainty in climate targets and CO2 storage availability on long-term emissions abatement. Environ Model Assess 17(1/2):177–191CrossRefGoogle Scholar
  18. Kharaka YK, Cole DR, Hovorka SD, Gunter WD, Knauss KG, Freifeld BM (2006) Gas-water-rock interactions in Frio formation following CO2 injection: implications for the storage of greenhouse gases in sedimentary basins. Geology 34:7CrossRefGoogle Scholar
  19. Klusman RW (2003) Evaluation of leakage potential from a carbon dioxide EOR/sequestration project. Energy Convers Manag 44(12):1921–1940CrossRefGoogle Scholar
  20. Lackner KS, Brennan SA, Matter J, Park A-HA, Wright A, van der Zwaan, BCC (2012), The urgency of the development of CO2 capture from ambient air, Proc Natl Acad Sci, August 14, 109, 33, 13156–13162Google Scholar
  21. Narita, D. and G. Klepper (2015) Economic project risk assessment for sub-seabed CO2 storage, working paperGoogle Scholar
  22. Nordhaus W (1994) Managing the global commons: the economics of climate change. MIT Press, Cambridge MassachusettsGoogle Scholar
  23. Phelps, J.J.C., Blackford, J.C., Holt, J.T., Polton, J.A. (2014), Modelling large-scale CO2 leakages in the North Sea, Int J Greenhouse Gas Control, published onlineGoogle Scholar
  24. Piketty T, Zucman G (2014) Capital is back: wealth-income ratios in rich countries. Q J Econ 1700-2010:1255–1310CrossRefGoogle Scholar
  25. SEI (2012) In: Noone K, Sumaila R, Diaz RJ (eds) Valuing the Ocean. Stockholm Environment Institute, StockholmGoogle Scholar
  26. Shaffer G (2010) Long-term effectiveness and consequences of carbon dioxide sequestration. Nat Geosci 3(7):464–467CrossRefGoogle Scholar
  27. Statoil (2013), Carbon capture and storage, sleipner West, Stavanger/Norway, available from: statoil.com/en/TechnologyInnovation/NewEnergy/Co2CaptureStorage/Pages/SleipnerVest.aspxGoogle Scholar
  28. Sterner T, Persson UM (2008) An even sterner review: introducing relative prices into the discounting debate. Rev Environ Econ Policy 2(1):61–76CrossRefGoogle Scholar
  29. Teng F, Tondeur D (2007) Efficiency of carbon storage with leakage: physical and economical approaches. Energy 32(4):540–548CrossRefGoogle Scholar
  30. UN (2009) Population division of the Department of Economic and Social Affairs of the United Nations secretariat, world population prospects: the 2008 revision. United Nations, New YorkGoogle Scholar
  31. UNFCCC (2015) Paris agreement, conference of the Paries, 21st session, United Nations framework convention on climate change, 12. December 2015Google Scholar
  32. van der Zwaan BCC, Gerlagh R (2009) Economics of geological CO2 storage and leakage. Climate Change 93(3/4):285–309CrossRefGoogle Scholar
  33. van der Zwaan BCC, Smekens K (2009) CO2 capture and storage with leakage in an energy-climate model. Environ Model Assess 14:135–148CrossRefGoogle Scholar
  34. van der Zwaan BCC, Gerlagh R, Klaassen G, Schrattenholzer L (2002) Endogenous technological change in climate change modelling. Energy Econ 24:1–19CrossRefGoogle Scholar
  35. Wilson EJ, Johnson TL, Keith DW (2003) Regulating the ultimate sink: managing the risks of geologic CO2 storage. Environ Sci Technol 37:16CrossRefGoogle Scholar

Copyright information

© The Author(s) 2016

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.Energy research Centre of the Netherlands (ECN), Policy StudiesAmsterdamNetherlands
  2. 2.School of Advanced International StudiesJohns Hopkins UniversityBolognaItaly
  3. 3.Faculty of ScienceUniversity of AmsterdamAmsterdamNetherlands
  4. 4.Economics Department, Tilburg Sustainability Centre, and CentERTilburg UniversityTilburgNetherlands

Personalised recommendations