Abstract
The amount of soil moisture affects water availability, the occurrence of droughts and floods, and the frequency and intensity of heat waves in many regions across the globe. Here, we evaluate historical trends in soil moisture estimated by land-surface models (LSMs) with observed atmospheric forcing and trends simulated by global climate models participating in the Coupled Models Inter-comparison Project Phase 5 (CMIP5). We classify northern hemispheric land into wet and dry regions and analyze soil moisture changes in these regions. We find a significant decrease in soil moisture from 1951 to 2005 in the northern hemispheric land areas, in particular in dry regions, both in LSM and CMIP5 model simulations. Soil moisture trends in wet regions are less consistent among simulations. The increase in the area affected by drought (defined as the area where soil moisture is below its 10th percentile) from 1951 to 2005 is estimated to be 20 % (LSMs) and 30 % (CMIP5 models). A comparison between soil moisture simulated by LSMs and CMIP5 model output under different external forcings suggests that anthropogenic forcing contributed significantly to the observed drying and could explain the increase in the area affected by drought. As increases in atmospheric greenhouse gas concentrations will continue in the near future, dry areas are projected to become drier and larger in extent, which could negatively impact future water supply and food security.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Changes in soil moisture can have significant impacts on water availability and food security and are thus important aspects of climate change that society needs to adapt to. Future changes in the global hydrological cycle can be better estimated if we understand how it has responded to historical warming that is extremely likely due to human influence. An intensification of the water cycle is expected in a warming atmosphere (Held and Soden 2006, Huntington 2006). The warming atmosphere leads to an increase in global near-surface specific humidity (Allen and Ingram 2002, Willett et al. 2007, Back et al. 2013) and an enhancement of existing ocean salinity patterns (Durack et al. 2012). Global total precipitation does not exhibit a clear trend possibly because of opposing trends in different regions (Allen and Ingram 2002, Balan Sarojini et al. 2012) and opposing effects from greenhouse gas concentrations and aerosols (Kaufman et al., 2002). Zonal mean precipitation, however, has been shown to increase in equatorial and mid- to high-latitude regions and decrease in the subtropics (Zhang et al. 2007, Zahn and Allan 2012, Laine et al. 2014, Allan et al. 2014, Marvel and Bonfils 2013). This can be explained by an enhanced moisture flux from regions with climatological moisture divergence (dry, subtropical areas) to regions with moisture convergence and to polar regions (Chou et al. 2009, Bengtsson et al. 2011) that results in dry regions becoming drier and wet regions wetter. Human influences have contributed to observed global scale changes in precipitation patterns (Zhang et al. 2007, Marvel and Bonfils 2013, Bindoff et al. 2013, Polson et al. 2013a).
Over the oceans, dry regions have become drier and wet regions wetter (Durack et al. 2012, Chou et al. 2009). However, this paradigm cannot be easily generalized for land regions. Greve et al. 2014 found that drying occurs more often over wet than dry land areas. However, the analyses were not based on direct measurements of soil wetness, and the results may be implicated by the definition of dry and wet areas. By analyzing precipitation in wet and dry land areas over six latitudinal bands, wetting in wet areas and drying in dry areas is the most robust pattern of precipitation changes in model simulations and observations (Polson et al. 2013b).
The intensification of the hydrological cycle may result in an expansion of global dry areas (Shin et al. 2012, Feng and Fu 2013, Feng et al. 2014). However, there is a large uncertainty in estimating global trends in areas affected by drought (Seneviratne et al. 2012) due to various reasons. Many studies rely on drought indicators because direct, long-term soil moisture observations are lacking. Different formulations of drought indicators may produce different long-term trends. For example, the Palmer Drought Severity Index (PDSI) may be computed using a simple water balance model with observed precipitation and evaporation estimated based on temperature records. PDSI can also be computed based on a more complete understanding of physics which considers changes in available energy, humidity and wind speed. Recent studies have shown large discrepancies in the magnitude of PDSI trends when it is computed using the two different formulations (Sheffield et al. 2012, Seneviratne 2012), or when different time periods or input datasets are used (Trenberth et al. 2014).
Global observations of soil moisture allow a more direct assessment of changes in droughts. Satellite remotely sensed soil moisture data are a promising alternative to in-situ measurements. They show significant drying trends over the period 1988–2010 in most areas of the globe (Dorigo et al. 2012). However, as the sensors can only penetrate to a few centimeters of the top soil layer and the temporal coverage is still quite short, the satellite-based soil moisture data product is not very suitable for the assessment of long-term changes in soil moisture and for the attribution to causes. Instead, we here use soil moisture simulated by land-surface models (LSMs). A diagnostic variable calculated in LSMs driven by observed atmospheric variables, such as temperature, precipitation and wind-speed shall be consistent with those driving variables governed by physical relationships represented in LSMs. Therefore, output from LSMs can be used as proxy for in-situ observations for the investigation of past changes. In a previous study, evaporation simulated by two LSMs has been used for detecting and attributing changes in land evaporation (Douville et al. 2013).
The aim of this study is to analyze past and future changes in soil moisture and in the extent of areas affected by drought. A detection and attribution analysis further provides insight to the question whether past changes can be explained by natural variability of the climate system or natural forcing alone, or whether the human impact on the climate system has substantially contributed to observed changes.
2 Data and Methods
2.1 Observational estimates
Here, we use soil moisture data from LSMs as pseudo-observations to investigate past changes in soil moisture. We include output from four widely used and analyzed LSMs including VIC (Sheffield and Wood 2007), Orchidee (ORCH, Krinner et al. 2005), LPJ (Sitch et al. 2003) and OCN (Zaehle and Friend 2010). All LSMs are driven with data from the University of East Anglia Climatic Research Unit (CRU TS3.1) and National Center for Environmental Prediction (NCEP) historical forcing (reanalysis). For precipitation, cloudiness, relative humidity and temperature, NCEP data is only used to generate the diurnal and daily variability. The model VIC does not account for CO2 effects on evapotranspiration and soil moisture. However, the effect of CO2 on soil moisture is unlikely to be a significant source of uncertainty in the context of this study as Leipprand and Gerten (2006) showed, using simulations from LPJ, that a doubling of CO2 leads to only 1 % increase in soil moisture. Orchidee, LPJ and OCN are obtained from the TRENDY consortium (Sitch et al. 2013, Murray-Tortarolo et al. 2013). Simulations from their S3 set-up were considered, which are driven with carbon dioxide from ice core and NOAA, historical climate forcing from CRU and NCEP, and land use change from the HYDE database (Hurtt et al. 2011). A global evaluation of LSMs is difficult because large scale long-term observations of soil moisture do not exist and its spatial variability is large. Global total runoff in the model Orchidee is 34.9 × 1012 m3 yr.−1 (Krinner et al. 2005) and 35.4 × 1012 m3 yr.−1 in LPJ (Sitch et al. 2003) which is around the range in the literature (36.5x1012 m3 yr.−1 (Chahine, 1992) and 45.5 x 1012 m3 yr.−1 (Cogley, 1998)). A possible global validation dataset for soil moisture are satellite retrievals from 1979 to 2008 (Dorigo et al. 2012). Soil moisture data from our four LSMs compare relatively well with satellite-derived soil moisture over dry and combined regions, but not over wet areas (see Supplementary information S1, and Section 2.4 for definition of dry, wet and combined regions)..
2.2 CMIP5 simulations
Climate model simulations were obtained from the Coupled Model Intercomparison Project Phase 5 (CMIP5) multi model ensemble (Taylor et al. 2011 and 2012) for the years 1951–2005. We use CMIP5 simulations forced with historical natural forcing (solar irradiance and volcanic activity, NAT) and with the combined effect of natural and anthropogenic forcing (ALL) to derive the patterns of climate responses to external forcings. The ensemble used to estimate the signals includes 37 simulations with ALL and 37 with NAT forcing (see Supplementary information Table S1). In addition, we use 380 55 year chunks of model output from unforced pre-industrial control simulations for the estimation of natural variability (Table S2). Future projections of soil moisture are obtained from the simulations for the emission scenario RCP4.5 (Table S1).
2.3 Data processing
We re-grid all data to a common 5 × 5 degree grid and mask CMIP5 output to mimic availability of the LSMs data. We then select the 5 months around the hottest month of the seasonal cycle, as soil moisture changes are most relevant to agriculture during the warm season. In order to estimate the hottest month at every pixel, the seasonal cycle of 2 m-air temperature from the ERA-Interim re-analysis (Dee et al. 2011) is used. We calculate the averages over the 5 months around the hottest for every year to obtain 55 ‘yearly’ values (either 1951–2005 in case of CMIP5 ALL and NAT simulations and LSMs, or 55 year-chunks of control simulations). In order to compare changes in soil moisture among CMIP5 models and LSMs, we standardize soil moisture data because of differences in soil depths (see Table S1) and data units used by different models. This is done by first subtracting the long-term mean from the annual soil moisture values and then dividing by the inter-annual standard deviation of the respective simulation, similar to the standardization done in Orlowsky and Seneviratne (2013). The four LSMs are then averaged to obtain a ‘best estimate’ of soil moisture.
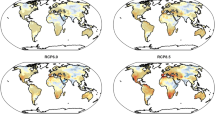
We focus on three northern hemispheric land regions (Fig. 1) which are important for agricultural production and which are often affected by droughts. The data are averaged (with latitude weighting) over these regions. Trends are computed from the regional averages. The detection and attribution analyses are conducted on the three dimensional space (spatio-temporal analysis). Because wet and dry regions have different land-surface feedbacks and to address the question whether dry land regions are becoming drier and wet land regions wetter, we further classify our areas into wet and dry regions (see Section 2.4).
Fraction of model simulations under ALL and NAT forcing and LSMs (a, b, c) which is defined as dry and wet, and dry-wet definition in satellite observations (d, see Supplementary information S1). Boxes indicate the three areas considered
We also analyze changes in the area affected by drought. This area is defined as a region with soil moisture below its 10th percentile over a long period of time, which is 1951–2005 in our analyses. The calculation of drought area, is a second method to make the models comparable despite different soil depths and units. When computing the area affected by drought, the model data are re-gridded to a common 1 × 1 degree grid and are then masked with the coverage of the LSMs. As for the procedure to obtain standardized soil moisture, we then select the 5 months around the hottest and perform the yearly averages over these summer months to obtain timeseries with 55 values. We determine the 10th percentile of these soil moisture values at every grid cell and use it as threshold for drought. We then count the number of grid cells with soil moisture values below this threshold in a) each of the three northern hemispheric areas, and b) the three areas combined.
The annual series of percentage of grid cells below this threshold is considered to be the percent-area affected by drought. The detection and attribution analyses for area affected by drought are also conducted in a three-dimensional space (a). The timeseries from (b) are used for the trend calculation. To make future projections consistent with simulations of the past, we use the past thresholds for calculating the percent area affected by drought in the RCP4.5 projections. The thresholds for RCP4.5 projections from 2010 to 2049 are thus computed from the respective historical ALL simulations for 1951–2005.
2.4 Classification of wet and dry
In the three northern hemispheric regions combined (Fig. 1), we classify 65.4 % as dry and 34.6 % as wet. This ratio of dry to wet is obtained from a map of Feng and Fu (2013). We calculate the soil moisture threshold in the long-term mean (climatology) of each model run that results in 65.4 % dry and 34.6 % wet. Grid boxes with soil moisture values above (below) this threshold are considered to be wet (dry). We chose to distinguish only two levels of dryness (wet and dry) in order to make the land areas as large as possible to increase the signal-to-noise ratio for our detection and attribution analyses. We chose fixed dry and wet areas over the entire time period. This ensures homogeneity of the time-series. Furthermore, Polson et al. (2013b) showed that the location and size of dry and wet regions (derived from precipitation) does not change much over the years. Figure 1 also shows that there is a large consistency between the simulations regarding the definition of dry and wet.
2.5 Trend estimates
We perform the trend analyses for 1951–2005 and, for RCPs, 2010–2049 on the standardized soil moisture anomalies or the fraction of drought affected area averaged over the 5 warmest months. The trends are calculated for the regional averages of 3 northern hemispheric land areas using the Sen’s slope estimator (Sen 1968). The statistical significance of trends is tested using the Mann-Kendall test (Kendall 1975).
2.6 Detection and attribution
We compare simulations from CMIP5 with those from the LSMs, i.e. the pseudo-observations, in a detection and attribution framework. The analysis is conducted on the 5-years mean series of the three spatial dimensions corresponding to the three continental regions. We use the optimal fingerprint method (Allen and Stott 2003) with a regularized covariance matrix which provides more robust estimates (Ribes et al. 2013). The pseudo-observations (average of four LSMs) are regressed onto the signals estimated from CMIP5 simulations. We conduct a single-signal analysis where there is one predictor only, being the model simulated response to the combined effect of anthropogenic and natural forcings (ALL) or to the natural forcing (NAT). We also conduct a two-signal analysis using model simulated responses to anthropogenic forcing (represented by the difference between ALL and NAT) and NAT as predictors. The covariance matrix is estimated using control simulations. A total of 380 55 year samples from control simulations are constructed from the available CMIP5 multi-model ensemble to estimate the internal variability. We split the 380 samples into two halves with a) one half for optimization and b) the second half for testing. The regression is repeated with 2000 bootstraps of this splitting into a) and b) in order to assess the robustness of the detection results to the estimates of internal variability..
We test the consistency between model simulated variability and the regression residual using the residual consistency test (Allen and Tett 1999). Residual consistency tests are reported at the 90 %-confidence level, obtained from 1000 simulations of the test statistics (Ribes et al. 2013).
The confidence intervals are also calculated from 1000 simulations. The scaling factor and its 5–95 % uncertainty range obtained from one splitting into a) and b) are reported. Detection is claimed if the 90 % confidence interval of a scaling factor is above zero and when the residual consistency test does not reject the null-hypothesis. We also report the number of times detection occurred in the 2000 repetitions with covariance estimated from alternative control samples..
3 Results and discussion
3.1 Changes in soil moisture and area of drought
Figure 2 displays warm season standardized soil moisture from 1951 to 2005 averaged over the northern hemispheric areas. Data from individual CMIP5 simulations and from observations-based LSMs are shown. CMIP5 simulations forced with the combined effect of anthropogenic plus natural forcing (left, ALL) show a drying tendency in a large number of runs while simulations forced with natural forcing alone (middle, NAT) do not show a drying tendency. Note that this generalization is true for dry, wet and combined regions, but is more prevalent in dry and combined regions. Three of the four LSMs (right) show drying in dry areas. In wet and combined regions, soil moisture output from LSMs does not show a strong pattern of change.
Time evolution of non-overlapping 5-yr. averages of standardized soil moisture anomalies from 1951 to 2005 in 37 CMIP5 simulations and in 4 LSM simulations. ALL, NAT, and LSMs are shown in the left, middle, and right panels, respectively. Results are shown for wet region (top), dry region (middle) and wet and dry combined (bottom). Blue (red) indicates above (below) average standardized soil moisture values. The number of colors is reduced for CMIP for better visibility.’AVG’ (last row in each graph) indicates the average of the CMIP5 simulations and LSMs, respectively
Figure 3 shows trends (1951–2005) in regional averages of standardized soil moisture and in the fraction of area affected by drought in the ensemble mean of the ALL and NAT simulations and in the average of the four LSM outputs. In dry and combined regions, CMIP5 simulations under ALL forcing show a significant drying trend, similar to that in the observations-driven LSMs, while NAT forcing results in wetting trends. Agreement in trends among individual simulations is high in dry (and combined) areas: 43 % (35 %) of ALL simulations display a significant drying trend, and only 24 % (14 %) a wetting trend (see Tab. S3 and Fig. S2). In wet areas, observational data show a wetting trend, while CMIP5 simulations under ALL forcing show a drying trend. However, compared to dry and combined regions, agreement in soil moisture trends among individual CMIP5 simulations under ALL forcing is relatively poor in wet areas: Only 24 % of the simulations show a significant drying trend and 5 % a wetting trend. The discrepancy in wet regions could also be related to the fact that LSM-based soil moisture does not agree well with satellite observations in wet regions (see Figure S1). We further investigate the sensitivity of the trends to the relative size of dry and wet areas. We find significant drying trends in dry and combined regions but not significant wetting trends in wet regions in the four LSMs with a classification into dry and wet areas with equal sizes of the two regions (Table S4).
Trends in standardized soil moisture (SM) anomalies in wet, dry and combined regions and in fraction of drought affected area as simulated by CMIP5 models under ALL and NAT forcings and LSMs (1951–2005). The left axis indicates trends in soil moisture (no units) and the right axis the area affected by drought (in %). The trends are computed on the ensemble averages of the simulations. The numbers under CMIP ALL and CMIP NAT indicate the percentage of simulations whose trends are significant at the 5 % level and of the same sign as the trend in the ensemble mean (see Table S3). The significance of trends in the LSM-average is indicated with stars above the green bar (* for 10 %- and ** for 5 %-level)
A total of 43 % of the individual CMIP5 simulations under ALL forcing shows a significant expansion of and only 5 % a significant decrease in the areas under drought. This is matched by a positive trend in the observations-based LSMs. During 1951–2005, the fraction of area affected by drought has increased by 30 and 20 % in CMIP5 ALL simulations and in the LSMs, respectively. This increase is consistent with the findings regarding long-term changes in drought affected areas that were computed from precipitation and temperature data (Shin et al. 2012, Feng et al. 2014). The NAT simulations show a very small negative trend in the area affected by drought, but this trend is not statistically significant.
These qualitative comparisons indicate that in dry and combined regions, observed soil moisture trends are not consistent with model simulated soil moisture change under NAT forcing alone. However, they are consistent with simulations under the combined effect of anthropogenic and natural forcing.
3.2 Detection and attribution of soil moisture changes
Figure S3 and Fig. 4 display detection results for the single- and two-signal analyses, respectively (see Methods Section 2.6). In the single-signal analysis, model simulated response to ALL forcing is detected at the 10 %-level in dry and combined regions in the observations-based soil moisture changes (three regional averages combined). Further, the scaling factors are not significantly different from unity. This indicates that observations-based soil moisture changes are consistent with model simulated response to ALL forcing for the region as a whole and for the dry region. The NAT signal cannot be detected in the LSMs data, suggesting that the observations-based changes cannot be explained by natural forcing alone.
Scaling factors for natural (NAT) and anthropogenic (ANT) forcings from two-signal detection analysis for standardized soil moisture anomalies in wet, dry and combined regions as well as for area affected by drought. The best estimates (dots) and the 5–95 %-confidence intervals (whiskers) are shown. Confidence intervals excluding zero and including one indicate that the respective forcing is detected in the observations-based data, i.e. in the average of four LSMs
The two-signal analysis (anthropogenic (ANT) and NAT forcing) shows that the anthropogenic influence is detected at the 10 %-level in dry and combined regions (Fig. 4). The scaling factors for NAT are not significantly different from zero. These results suggest that the changes in soil moisture are mainly responding to ANT forcing rather than NAT forcing. Model simulated responses to ALL, ANT, and NAT are not detected in wet regions in the single-signal nor the two-signal analysis, consistent with the disagreement of model simulated and observations-based trends in wet regions shown in Fig. 3.
The ANT scaling factor for the fraction of drought affected areas in the two-signal analysis is above zero and not inconsistent with unity (Fig. 4). This suggests that external forcings may also have contributed to the observed increase in the fraction of area affected by drought, although there are larger uncertainties in these results (see below).
The uncertainty in the estimate of internal variability has a strong influence on the detection analysis (Ribes et al. 2013, Zhang et al. 2007). Therefore, we investigate the sensitivity of our detection and attribution results to the estimate of internal variability (see Section 2.6). Table 1 displays the percentage of times a signal was detected in the average soil moisture from the four LSMs in 2000 repetitions with internal variability estimates from different noise data samples. The detection of soil moisture response to ALL and ANT forcing in dry and combined regions is robust to the uncertainty in internal variability estimates. On the other hand, the detection of external influence to the fraction of areas affected by drought is not as robust; the response was detected 29 % of the times in the 1-signal analysis for ALL, and 56 % and 44 % of the times in the 2-signal analysis for ANT and NAT, respectively. The higher detection rate in 2-signal ANT and NAT than in 1-signal ALL might be explained by the fact that the 2-signal regression allows the individual scaling factors of ANT and NAT to be different from each other. This can provide a better fit than the regression with only one signal.
We employed two different ways of standardizing values, i.e. calculating standardized soil moisture and the area affected by drought. Therefore, detection of soil moisture changes in dry and combined areas and of changes in the area affected by drought shows that the detection of an anthropogenic influence on a general drying of the land surface is relatively insensitive to the way the data have been standardized.
We further summarize the results when soil moisture data from individual LSMs are used in Table S5. All LSMs are driven with the same input forcing data. The differences in the detection results thus reflect the influence of the uncertainty in the parameterization of the land surface processes. A detection of changes in soil moisture is not consistent between the different LSMs. This is not unexpected given that while the ensemble-average of the LSMs agrees well with the satellite retrievals in dry and combined areas (Figure S1), some of the LSMs do not exhibit the same temporal evolution as the ensemble-average (see Fig. 2).
Table 1 only reports cases where the residual consistency test is passed. The residual consistency test does not reject the null-hypothesis in nearly all cases where detection occurred, indicating that soil moisture variability simulated by CMIP5 models is not inconsistent with internal variability in the LSMs data at time scales relevant to the detection analysis.
3.3 Implications for future changes in droughts
Previous studies have shown a decrease in soil moisture globally as projected by CMIP5 models under the RCP4.5 emission scenario (Orlowsky and Seneviratne 2013, Dai 2013, Cook et al. 2015) and an expansion of global arid and semiarid areas (Feng et al. 2014). Over the northern hemispheric regions used in our detection and attribution analysis, soil moisture is projected to decrease over 2010–2049 in the RCP4.5 simulations in all regions (see Fig. 5). The fraction of drought affected area is projected to increase by nearly 80 % from the historical period to 2049. Our analyses show consistency of changes in soil moisture and fractions of drought affected areas among observations-based LSMs simulations and CMIP5 simulations. This gives confidence in model projected future changes.
4 Conclusions
Our analysis of warm season soil moisture simulated by land-surface models (LSMs) and CMIP5 models shows that northern hemispheric land areas have experienced drying in the last 55 years (1951–2005). The drying trend appears to be most robust (agreement of CMIP5 models) in dry region. During the same period of time, the fraction of drought affected area has increased by 20 % and 30 % in LSMs and CMIP5 model outputs, respectively. In wet areas, LSMs show different trends than satellite observations and climate model simulations, and agreement among simulations by different climate models is also poor.
Trends in soil moisture simulated by CMIP5 models under the combined effect of anthropogenic and natural forcing and under natural forcing alone are of different signs, with small increasing trends corresponding to natural forcing only simulations. The fact that inclusion of anthropogenic forcing in the simulation changes the soil moisture trend from positive to negative suggests that human activities may have contributed to the observed decrease in soil moisture. We test this hypothesis in a formal detection and attribution analysis. We find that the changes in soil moisture simulated by observations-based LSMs in dry and combined regions are consistent with the climate model simulated responses to anthropogenic forcing, or to the combined effect of anthropogenic and natural forcing, but are not consistent with the model simulated response to natural forcing alone. Additionally, there is evidence that anthropogenic forcing may also have contributed to the increase in the fraction of areas affected by drought, though these results are less robust.
The decrease in northern hemispheric soil moisture reported here is consistent with a global drying trend in PDSI (Dai 2013, Burke et al. 2006) even though the magnitude of these trends can be substantially different when different formulations are used to compute the PDSI (Sheffield et al. 2012). PDSI trends are strongly influenced by the precipitation dataset used (Trenberth et al. 2014), which is likely true for soil moisture computed by LSMs as well. Since the CRU TS3.1 dataset, which is used as a forcing dataset for the LSMs, shows a relative wet bias compared to other precipitation datasets since around 1996 (Trenberth et al. 2014), the drying trends found here in dry and combined areas may have also been underestimated. Furthermore, drying trends during the hottest months of the years are consistent with a decrease in precipitation in the dry season found in Chou et al. (2013).
In summary, our results show that dry areas have become drier and areas affected by drought larger over the last 55 years, and that these changes are not consistent with internal variability of the climate system. They are consistent with expected changes due to human induced increases in greenhouse gas concentrations and aerosols. Climate models project further decreases in soil moisture in northern hemispheric land areas due to warming already committed and additional increases in atmospheric greenhouse gas concentrations. This increasing dryness of the land surface would affect areas which are currently important for crop production such as large parts of the US and Europe, as well as already dry areas in Northern Africa.
References
Allan R et al. (2014) Physically consistent responses of the global atmospheric hydrological cycle in models and observations. Surv Geophys 35:533–552
Allen MR, Ingram WJ (2002) Constraints on future changes in climate and the hydrologic cycle. Nature 419:224–232
Allen MR, Stott PA (2003) Estimating signal amplitudes in optimal fingerprinting, part I: theory. Clim Dyn 21:477–491
Allen MR, Tett SFB (1999) Checking for model consistency in optimal fingerprinting. Clim Dyn 15:419–434
Back L et al. (2013) Global hydrological cycle response to rapid and slow global warming. J Clim 26:8781–8786
Balan Sarojini B, Stott PA, Black E, Polson D (2012) Fingerprints of changes in annual and seasonal precipitation from CMIP5 models over land and ocean. Geophys Res Lett 39:L21706.
Bengtsson L, Hodges KI, Koumoutsaris S, Zahn M, Keenlyside N (2011) The changing atmospheric water cycle in polar regions in a warmer climate. Tellus A 63:5
Bindoff NL, et al. (2013) Detection and Attribution of Climate Change: from Global to Regional. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker TF, et al. (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, USA.
Burke EJ, Brown SJ, Christidis N (2006) Modeling the recent evolution of global drought and projections for the twenty-first century with the Hadley Centre climate model. J Hydrometeorol 7:1113–1125
Chahine MT (1992) The hydrologicacl yclea nd its influenceo n climate. Nature 359:373–380
Chou C, Neelin JD, Chen CA, Tu JY (2009) Evaluating the’rich-get-richer’ mechanism in tropical precipitation change under global warming. J Clim 22:1982–2005
Chou C, Chiang JCH, Lan C-W, Chung C-H, Liao Y-C, Lee C-J (2013) Increase in the range between wet and dry season precipitation. Nat Geosci 6:263–267. doi:10.1038/ngeo1744
Cogley, J. G., GGHYDRO (1998) Global Hydrographic Data, release 2.2Trent Clim. Note 98-1Dept. of Geog., Trent Univ., Peterborough, Ont., Canada.
Cook BI, Adult TR, Smerdon JE (2015) Unprecedented 21st century drought risk in the American southwest and central plains. Sci Adv 1:1e1400082
Dai A (2013) Increasing drought under global warming in observations and models. Nat Clim Chang 3:52–58
Dee DP et al. (2011) The ERA-interim reanalysis: configuration and performance of the data assimilation system. Quat J Roy Meteorol Soc 137:553–597
Dorigo W, et al. (2012) Evaluating global trends (1988–2010) in harmonized multi-satellite surface soil moisture. Geophys Res Lett 39:L18405.
Douville H, Ribes A, Decharme B, Alkama R, Sheffield J (2013) Anthropogenic influence on multidecadal changes in reconstructed global evapotranspiration. Nat Clim Chang 3:59–62
Durack PJ, Wijffels SE, Matear RJ (2012) Ocean salinities reveal strong global water cycle intensification during 1950 to 2000. Science 336:455–458
Feng S, Fu Q (2013) Expansion of global drylands under a warming climate. Atmos Chem Phys 13:10081–10094
Feng S et al. (2014) Projected climate regime shift under future global warming from multi-model, multi-scenario CMIP5 simulations. Glob Planet Chang 112:41–52
Greve P, Orlowsky B, Mueller B, Sheffield J, Reichstein M, Seneviratne SI (2014) Global assessment of trends in wetting and drying over land. Nat Geosci. doi:10.1038/ngeo2247
Held IM, Soden BJ (2006) Robust responses of the hydrological cycle to global warming. J Clim 19:5686–5699
Huntington TG (2006) Evidence for intensification of the global water cycle: review and synthesis. J Hydrol 319:83–95
Hurtt GC et al. (2011) Harmonization of land-use scenarios for the period 1500–2100: 600 years of global gridded annual land-use transitions, wood harvest, and resulting secondary lands. Clim Chang 109:117–161
Kaufman YJ, Tanre D, Boucher O (2002) A satellite view of aerosols in the climate system. Nat 419:215–223. doi:10.1038/nature01091
Kendall MG (1975) Rank correlation methods, 4th edn. Charles Griffin, London
Krinner G, et al. (2005) A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob Biogeochem Cycles 19:GB1015.
Laine A, Nakamura H, Nishii K, Miyasaka T (2014) A diagnostic study of future evaporation changes projected in CMIP5 climate models. Clim Dyn 42(9):2745–2761
Leipprand A, Gerten C (2006) Global effects of doubled atmospheric CO2 content on evapotranspiration, soil moisture and runoff under potential natural vegetation. Hydrol Sci J 51:1,171–1,185. doi:10.1623/hysj.51.1.171
Marvel K, Bonfils C (2013) Identifying external influences on global precipitation. Proc Natl Acad Sci U S A 110:19301–19306
Murray-Tortarolo G et al. (2013) Evaluation of land surface models in reproducing satellite-derived LAI over the high-latitude northern hemisphere. Part I: uncoupled DGVMs. Remote Sens 5:4819–4838
Orlowsky B, Seneviratne SI (2013) Elusive drought: uncertainty in observed trends and short- and long-term CMIP5 projections. Hydrol Earth Syst Sci 17:1765–1781
Polson D, Hegerl GC, Allan RP, Balan Sarojini B (2013a) Have greenhouse gases intensified the contrast between wet and dry Regions? Geophys Res Lett 40:4783–4787. doi:10.1002/grl.50923
Polson D, Hegerl GC, Zhang XB, Osborn TJ (2013b) Causes of robust seasonal land precipitation changes. J Clim 26:6679–6697
Ribes A, Planton S, Terray L (2013) Application of regularised optimal fingerprinting to attribution. Part I: method, properties and idealised analysis. Clim Dyn 41(11–12):2817–2836
Sen PK (1968) Estimates of the regression coefficient based on Kendall’s tau. J Am Stat Assoc. 63:1379–1389
Seneviratne SI (2012) Climate science: historical drought trends revisited. Nature 491:338–339
Seneviratne S, et al. (2012) Managing the risks of extreme events and disasters to advance climate change adaptation. A special report of working groups I and II of the Intergovernmental Panel on Climate Change. [Field, CB et al. (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, USA.
Sheffield J, Wood EF (2007) Characteristics of global and regional drought, 1950–2000: Analysis of soil moisture data from off-line simulation of the terrestrial hydrologic cycle. J Geophys Res-Atmos 112:D17115–1–21.
Sheffield J, Wood EF, Roderick ML (2012) Little change in global drought over the past 60 years. Nature 491:435–438
Shin SH, Chung IU, Kim HJ (2012) Relationship between the expansion of drylands and the intensification of Hadley circulation during the late twentieth century. Meteorol Atmos Phys 118:117–128
Sitch S et al. (2003) Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob Chang Biol 9:161–185
Sitch S et al. (2013) Trends and drivers of regional sources and sinks of carbon dioxide over the past two decades. Biogeosci Discuss 10:20113–20177
Taylor CM et al. (2011) Frequency of sahelian storm initiation enhanced over mesoscale soil-moisture patterns. Nat Geosci 4:430–433
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of cmip5 and the experiment design. Bull Am Meteorol Soc 93:485–498
Trenberth KE et al. (2014) Global warming and changes in drought. Nat Clim Chang 4. doi:10.1038/NCLIMATE2067
Willett KM, Gillett NP, Jones PD, Thorne PW (2007) Attribution of observed surface humidity changes to human influence. Nature 449:710–712
Zaehle S, Friend AD (2010) Carbon and nitrogen cycle dynamics in the O-CN land surface model: 1. Model description, site-scale evaluation, and sensitivity to parameter estimates. Glob Biogeochem Cy 24:GB1005.
Zahn M, Allan RP (2012) Climate warming-related strengthening of the tropical hydrological cycle. J Clim 26:562–574
Zhang XB et al. (2007) Detection of human influence on twentieth-century precipitation trends. Nature 448:461–4U4
Acknowledgments
We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and thank the climate modelling groups listed in Tables S1 and S2 for producing and making available their model outputs. For CMIP the US Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. We also thank Jan Sedlacek and Urs Beyerle from IAC ETH for support with downloading, storage and regridding of CMIP5 data. We thank Qiuzi Han Wen for helpful discussions. We further acknowledge Guillermo Murray-Tortarolo from University of Exeter for help with the TRENDY data, Nicolas Viovy from LSCE for Orchidee data, Soenke Zaehle from MPI-BGC for OCN data, Benjamin Poulter from Montana State University for LPJ data, and Justin Sheffield from Princeton University for VIC data. VIC data were obtained from http://hydrology.princeton.edu/. We thank three anonymous reviewers for constructive comments.
Author information
Authors and Affiliations
Corresponding authors
Electronic supplementary material
ESM 1
(PDF 743 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mueller, B., Zhang, X. Causes of drying trends in northern hemispheric land areas in reconstructed soil moisture data. Climatic Change 134, 255–267 (2016). https://doi.org/10.1007/s10584-015-1499-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-015-1499-7