Application of regularised optimal fingerprinting to attribution. Part I: method, properties and idealised analysis

Abstract

Optimal fingerprinting has been the most widely used method for climate change detection and attribution over the last decade. The implementation of optimal fingerprinting often involves projecting onto k leading empirical orthogonal functions in order to decrease the dimension of the data and improve the estimate of internal climate variability. However, results may be sensitive to k, and the choice of k remains at least partly arbitrary. One alternative, known as regularised optimal fingerprinting (ROF), has been recently proposed for detection. This is an extension of the optimal fingerprinting detection method, which avoids the projection step. Here, we first extend ROF to the attribution problem. This is done using both ordinary and total least square approaches. Internal variability is estimated from long control simulations. The residual consistency test is also adapted to this new method. We then show, via Monte Carlo simulations, that ROF is more accurate than the standard method, in a mean squared error sense. This result holds for both ordinary and total least square statistical models, whatever the chosen truncation k. Finally, ROF is applied to global near-surface temperatures in a perfect model framework. Improvements provided by this new method are illustrated by a detailed comparison with the results from the standard method. Our results support the conclusion that ROF provides a much more objective and somewhat more accurate implementation of optimal fingerprinting in detection and attribution studies.

Appendices

Appendix 1: Simulations used for evaluating internal variability

We list here the simulations used to estimate the internal climate variability. The control simulations with pre-industrial conditions are presented in Table 1 (CMIP3 models), and in Table 2 (CMIP5 models). The name of the global coupled model is given together with the length of the simulation, and the number of non-overlapping 110-year segments obtained. The CMIP5 ensembles of simulations used are listed in Table 3, with the name of the model, a subjective name of the ensemble (basically which external forcings were imposed), and the number of simulations, which is also the number of independent realisations provided by the ensemble.

Table 1 List of CMIP3 control simulations used for evaluating the internal climate variability

Table 2 List of CMIP5 control simulations used for evaluating the internal climate variability

Table 3 List of CMIP5 ensembles of simulations used to estimate the internal climate variability

Appendix 2: On-line scripts

The main scripts used in this paper are available on-line via the CNRM-GAME website at the following URL: http://www.cnrm-game.fr/spip.php?article23&lang=en. The routines are written for Scilab, which is a free open-source software package for numerical computation, similar to MatLab. The package allows ROF to be applied in both OLS and TLS statistical models.

The purpose of this package is similar to that of the Optimal Detection Package (ODP), maintained by Dáithí Stone, available at (http://web.csag.uct.ac.za/daithi/idl_lib/detect/idl_lib.html) and written for IDL software. We should point out that the ODP probably includes more options and permits the use of a wider range of statistical analyses introduced over the last 15 years. The interest of our package lies in the implementation of ROF and also in its availability in free, open-source software. Note that our routines were developed independently of the ODP.

At present, two differences have been noted between ODP and our package, both with the TLS statistical model. The first involves the possibility of computing 1-dimensional confidence intervals that have some bounds but that include an infinite slope. The second concerns the uncertainty analysis in TLS. This treatment is described in AS03 and involves the computation of revised singular values $\hat{\lambda}_{i}$ of the matrix Z (following the notation of AS03). We used the formula mentioned in AS03 (formula (34)), i.e.

$$ \hat{\lambda}_i^2 = \frac{u_i^T Z Z^T u_i}{\frac{1}{\mu} u_i^T P \hat{\Upupsilon}_2 \hat{\Upupsilon}_2^T P^T u_i}. $$

(3)

The formula implemented within the current version of ODP can be written as

$$ \hat{\lambda}_{i}^{2} = \frac{u_{i}^{T} Z Z^{T} u_{i}}{\frac{1}{\mu} (u_{i}^{\#2})^{T} (P \hat{\Upupsilon}_{2})^{\#2} {\bf 1}_{n_{2}}}, $$

(4)

where A ^#2 denotes the matrix with entries (a ² _ij ) _i,j if A = (a _ij ) _i,j , and where ${\bf 1}_{n_{2}}$ is a vector of dimension n ₂, with ${\bf 1}_{n_{2}}=(1, \dots, 1)^{T}$.

Appendix 3: Consistency check within the OLS approach

Here we discuss Equation (20) of AT99, used to construct a residual consistency test. Both the statistical model and the consistency check are first recalled briefly in order to introduce the notation.

The OLS statistical model may be seen as the classical regression model:

$$ Y = X \beta + \varepsilon, $$

(5)

where $\hbox{Cov}(\varepsilon) = C$ is assumed to be known. The optimal estimate of β can then be written as the generalised least-square estimate:

$$\widehat{\beta} = (X' C^{-1} X)^{-1} X' C^{-1} Y. $$

(6)

After having estimated β, the residual term $\varepsilon$ can be estimated by

$$ \widehat{\varepsilon} = Y - X \widehat{\beta}, $$

(7)

and then we have

$$ \widehat{\varepsilon}' C^{-1} \widehat{\varepsilon} \sim \chi^2(n-l), $$

(8)

where l = rank(X).

The last equation can be used to assess whether the estimated residuals $\widehat{\varepsilon}$ are consistent with the covariance matrix C. In particular, if the estimated residuals are greater than expected, the quantity $\widehat{\varepsilon}' C^{-1} \widehat{\varepsilon}$ may be outside the range of values expected in (8) (e.g. higher than the 95 % quantile of the χ²(n − l) distribution). This allows a residual consistency test based on Eq. (8) (Allen and Tett 1999) to be introduced.

As noted by AT99 themselves, the covariance matrix C is usually not known, and is estimated from control integration. This estimation procedure means that C is only approximately known. Let us now consider that climate models simulate the real climate perfectly, and that the covariance matrix that would be provided by an infinitely-long control integration is the true one. With these assumptions, the covariance matrices $\widehat{C}_{1}$ and $\widehat{C}_{2}$ used respectively for computing the generalised least-square estimate and for uncertainty analysis, satisfy

$$ \widehat{C}_1 \sim \frac{1}{n_1} W(n_1,C), $$

(9)

$$ \widehat{C}_2 \sim \frac{1}{n_2} W(n_2,C), $$

(10)

where W denotes the Wishart distribution and n ₁ and n ₂ are the number of independent realisations used as a basis for estimating $\widehat{C}_{1}$ and $\widehat{C}_{2}$.

Due to the uncertainty in (9, 10), $\widehat{C}_{1} \neq C$, and (8) no longer holds. The discussion in Sect. 4 of AT99 deals with the case where:

• the exact generalised least-square estimate is used, i.e. $\widehat{C}_{1} = C$ (or equivalently, no error arises from the use of an imperfect prewhitening),

• the consistency test is based on imperfectly estimated covariance matrix $\widehat{C}_{2}$, i.e. $\widehat{C}_{2} \sim \frac{1}{n_{2}} W(n_{2},C)$.

With these assumptions, it can be shown that

$$ \widehat{\varepsilon}' \widehat{C}_{2}^{-1} \widehat{\varepsilon} = \frac{\widehat{\varepsilon}' \widehat{C}_{2}^{-1} \widehat{\varepsilon}}{\widehat{\varepsilon}' C^{-1} \widehat{\varepsilon}} \,\,\, \widehat{\varepsilon}' C^{-1} \widehat{\varepsilon}, $$

(11)

$$ \sim n_{2} \,\, \frac{1}{\chi^{2}(n_{2}-n+1)} \,\, \chi^{2}(n-l), $$

(12)

$$ \sim \frac{n_2 (n-l)}{n_2-n+1} \,\, F(n-l,n_2-n+1) $$

(13)

The formula provided in AT99 using the same assumptions was somewhat different:

$$ \widehat{\varepsilon}' \widehat{C}_2^{-1} \widehat{\varepsilon}\,\sim\,(n-l) F(n-l,n_2). $$

(14)

Both formulas are consistent, however, in the case where n ₂ ≫ n. AT99 focused on the EOF projection approach, so the size n of Y was actually the EOF truncation k (i.e. n = k), which was rather small. Therefore, this assumption was more reasonable.

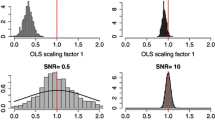
The discrepancies between the three parametric distributions mentioned above [respectively Eqs. (8), (13) and (14)], and the $\mathcal{D}$-distribution as evaluated from Monte Carlo simulations (see Sect. 3.4), are illustrated in Fig. 6. The Monte Carlo simulations are performed with input parameters C and X corresponding to real-case estimated values, at T0 and T2 resolutions: C is the covariance matrix as estimated by the LW estimate from the full sample of control segments Z, and X is the expected responses as simulated by the CNRM-CM5 model (in a 2-forcing analysis, so that l = 2).

Fig. 6

H ₀ distribution of the residual consistency test in OLS analysis, as evaluated from different formulas and under different assumptions: the χ² distribution (blue), the Fisher distribution used in AT99 (red), the corrected Fisher distribution given in Eq. (13) (green), and the distribution derived from Monte Carlo simulations (black histogram)

As expected, the discrepancies between $\mathcal{D}$ and the parametric formulas used by AT99 tend to be reduced when n is much smaller than n ₂ (left-hand side). They become much larger when n is close to n ₂ (right-hand side). In such a case, the distributions have virtually disjoint supports, so the use of one instead of the other would result in very different conclusions. Conversely, the distribution defined by Eq. (13) appears to be relatively suitable in these cases with ROF. This close agreement between the results from the MC simulations and formula (13), where the value of C doesn’t appear, suggests that the null-distribution is not very sensitive to the initial value of C in the MC algorithm.

Finally, it may be noted that the distribution $\mathcal{D}$ is still well defined in the case where n > n ₁, because the regularised estimate $\widehat{C}_{1}$ is always invertible. The case where n > n ₂ is more problematic, because $\widehat{C}_{2}$ is then not invertible. A $\mathcal{D}$-distribution may, however, be computed via Monte Carlo simulations by using the pseudo-inverse of $\widehat{C}_{2}$. In such a case, however, the revisited parametric formula provided by Eq. (13) cannot be used, because n ₂ − n − 1 is negative. This is the reason why results at T4 resolution are not shown in Fig. 6.

Appendix 4: Consistency check within the TLS approach

The discrepancies between the two parametric distributions proposed by AS03 and the null-distribution as evaluated from Monte Carlo simulations when ROF is used, are illustrated in Fig. 7. The Monte Carlo simulations are performed with input parameters C and X corresponding to real-case estimated values, at T0, T2 and T4 resolutions: C is the covariance matrix as estimated by the LW estimate from the full sample of control segments Z, X is the expected responses as simulated by the CNRM-CM5 model (in a 2-forcing analysis, so that l = 2).

Fig. 7

H ₀ distribution of the residual consistency test in TLS analysis for ROF, as evaluated from different formulas and under different assumptions: the χ² distribution used by AS03 (blue), the Fisher distribution used by AS03 (red), and the distribution derived from Monte Carlo simulations (black histogram)

The corresponding results for EOF projection are shown in Fig. 8. The Monte Carlo simulations are then performed with the same input parameters C and X as in Fig. 7 at T4 resolution. Then, the pre-whitening applied in the Monte Carlo algorithm is based on EOF projection instead of involving the LW estimate. Results are shown for several values of the EOF truncation k, corresponding to those used in Part II.

Fig. 8

H ₀ distribution of the residual consistency test in TLS analysis for EOF projection, as evaluated from different formulas and under different assumptions: the χ² distribution used by AS03 (blue), the Fisher distribution used by AS03 (red), and the distribution derived from Monte Carlo simulations (black histogram)