Introduction

The interactions of cellulose with liquids are of fundamental importance both in the plant cell wall and for other cellulose-producing organisms, as well as in all phases of the life cycle of a synthetic cellulose-based material: processing, use, and recycling. Interactions with water are of specific importance. (Solhi et al. 2023) Cellulose is inherently hygroscopic and is always found in the presence of (at least some) moisture. In nature, cellulose fibrils are immersed in a matrix of fully hydrated biopolymers, and from the perspective of materials processing, the drying of nanocellulose from aqueous suspension is both a time-consuming and expensive task. It can also lead to unwanted effects on the fibrils themselves, such as “hornification” (strong aggregation) which is caused by the large capillary forces that arise during the drying process.

Interactions with organic liquids are also of practical importance. One way to reduce agglomeration upon drying is to do successive steps of solvent exchange (Ishii et al. 2003) and finally dry from a liquid with low surface tension to reduce capillary effects. Another example is the prepreg approach to nanocomposite processing, in which dissolved monomers are impregnated into a pre-formed CNF network (Ansari et al. 2014).

Topochemical surface modification is one route to tune cellulose-liquid interactions. By exchanging surface hydroxyls to other chemical functionalities the nanocellulose interface can be tailored to improve both interactions and the stress transfer with, e.g., a polymer matrix, to improve nanocellulose dispersion, and to reduce moisture uptake in the final material (Eichhorn et al. 2010; Eyley and Thielemans 2014). Specifically, surface acetylation has been used to improve mechanical, optical, and hygro-mechanical properties of cellulose nanocomposites (Kim et al. 2002; Ifuku et al. 2007; Abe et al. 2018; Lo Re et al. 2018; Spinella et al. 2015), and wood-based materials (Li et al. 2016; He et al. 2022).

The range of cellulose-liquid interactions and their impact on liquid spreading, liquid imbibition, moisture uptake, solvent exchange, etc., is reflected in the wettability (Hubbe et al. 2015). One of the most well-known experimental methods to analyze wettability is through measurement of contact angles with the standard (yet somewhat arbitrary) classification that an angle of (or around) 0° means complete wetting, angles between 0° to 90°indicate partial wetting, and angles above 90° are classified as non-wetting. Wetting by water is the most studied one among all liquids, and water contact angle measurements are routinely used to characterize cellulose surfaces (Rol et al. 2019). In this case, surfaces that exhibit contact angles below 90° are classified as hydrophilic, whereas contact angles above 90° mean the surface is hydrophobic. Values for untreated nanocellulose range between 15° to 47°, (Lu et al. 2008; Mashkour et al. 2015; Xhanari et al. 2011; Lozhechnikova et al. 2014; Peresin et al. 2017; Kontturi et al. 2011) showing that cellulose substrates exhibit clear hydrophilic characteristics. The large range in experimental data reflects the fact that measurements are complicated by the substrates, which typically consists of nanocellulose films, exhibiting varying degrees of surface roughness and porosity as a result of their preparation. Also the methodology employed will affect the results, most notably the time between the application of the drop until the conatct angle is recorded.

Experimental data for contact angles on cellulose formed by other liquids than water is rare. Khoshkava and Kamal (2013) reported a conatct angle of 10° for glycerol on nanocellulose films, which was lower than their reported contact angle for water (24°). Kontturi et al. (2011) measured a contact angle for formamide that was significantly lower than for water: 9° and 28° depending on preparation method, compared to 27° and 47° for water. Mantanis and Young (1997) reported contact angles of a large set of organic liquids on wood samples. Although that substrate is very different from a nanocellulose film it is notable that all liquids tested were either completely wetting or formed a contact angle significantly lower than that of water. This points to an interesting feature that despite the fact that cellulose rightfully can be considered a hydrophilic molecule, water has low wetting capability compared to other, less polar, liquids.

The contact angle of nanocellulose substrates can be tuned by surface modification. Specifically, surface acetylation increases the contact angle formed by water to varying extent depending on the degree of substitution (DS); at moderate DS the contact angle of acetylated nanocellulose films increased to 67° at a DS of 0.3 (Mashkour et al. 2015) and to 80° at a DS of 0.7 (Rodionova et al. 2010), and at a DS of 1.07, Jonoobi et al. (2010) measured a water contact angle of 115° on films produced from acetylated Kenaf nanofibers, thus exhibiting clear hydrophobic character.

Molecular simulation is an attractive complement to experimental contact angle measurements. In particular, the use of atomistically smooth substrates gives the possibility to isolate the ideal, thermodynamic component to wetting. Moreover, since it was shown that common macroscopic wetting models (e.g. the Young-Dupré equation, see Methods) are valid in molecular dynamics (MD) simulations of nano-sized liquid droplets, (Karna et al. 2021) simulations at this scale has a clear connection even to the wetting behavior at the macroscale. There are several studies that have calculated contact angles of water on cellulose from MD simulations (Karna et al. 2021; Mazeau and Rivet 2008; Trentin et al. 2021). The results show that all possible surfaces, irrespective of crystal plane, are hydrophilic in character, giving contact angles below 90°, or even complete wetting, although the exact value seem to be sensitive to which interaction parameters are employed, especially for the water. However, there is only so far one other study where wetting of a liquid different from water was reported. Malaspina and Faraudo (2019) used tetradecane as a model apolar liquid and observed complete wetting of both hydrophilic [010] and hydrophobic [100] surfaces. Thus, to study the extent of wetting by liquids of varying degrees of polarity would be of interest. Moreover, the effect of topochemical surface modification has been largely neglected. The exception is a recent study which showed that the hydrophobicity (and thus the water contact angle) of cellulose was increased from around 10° to 50° by surface acetylation and even more by grafting longer alkyl chains. (Wang et al. 2022)

To this end, the present study uses MD simulation to characterize the wetting behavior of eight different organic liquids and water on both native and surface-acetylated cellulose substrates. This is done by calculating contact angles of nanodroplets that are allowed to spread on the surface. The results are analyzed in terms of thermodynamic surface energies, local liquid structural ordering, and specific cellulose-liquid hydrogen bonding interactions. Results are also compared to both previous modeling studies and existing experimental data.

Fig. 1
figure 1

Illustration of the solid–liquid contact angle \(\theta\) (A); Molecular structures of all liquids used in the present study (B); Initial configuration for contact angle simulations on native cellulose and the simulation box dimensions (C); Illustration of the setup used for simulating the solid–liquid interface with simulation box dimensions noted (D)

Full size image

Theory and methods

Wetting and Young’s equation

The wetting of solids can be characterized by the equilibrium contact angle formed by a droplet of a liquid which is allowed to spread on the substrate. The solid is assumed to be ideal, i.e., rigid and perfectly flat, and both liquid and solid are in equilibrium with its respective gas-phase. In steady-state, the incremental gain in free energy by covering a larger area is exactly canceled by the incremental loss by exposing a larger liquid surface area to the vapor phase, due to its surface tension. This leads to Young’s equation:

$$\begin{aligned} \gamma _{lv}\cos \theta = \gamma _{sv}-\gamma _{sl} \end{aligned}$$
(1)

where \(\theta\) is the angle formed between the droplet and the surface (Fig. 1A), \(\gamma _{lv}\) is the liquid surface tension, and \(\gamma _{sv}\) and \(\gamma _{sl}\) are the solid and solid–liquid surface energies, respectively. The surface energies are defined as the increase (per unit area) in free energy for creating new solid surface. The reference state is the homogeneous (bulk) solid, and thus the solid surface energy is measured relative the solid’s cohesive energy (Israelachvili 2011). The surface energies are also related to the work of adhesion by the Dupré equation:

$$\begin{aligned} W_{A}=\gamma _{sv} + \gamma _{lv} -\gamma _{sl}, \end{aligned}$$
(2)

which, combined with Eq. 1, becomes the Young–Dupré equation,

$$\begin{aligned} W_{A}=\gamma _{lv}\left( 1 + \cos \theta \right) . \end{aligned}$$
(3)

Here, \(W_A\) is the reversible work needed (per unit area) to separate the solid and the liquid phases in vacuum. Although it has been pointed out that Young’s equation is valid only in the macroscopic regime (Bonn et al. 2009), MD simulations have shown that wetting on the nanoscale to a large extent obeys the macroscopic theory. Specifically, the consistency of the Young–Dupré equation (Eq. 3) for the case of a cellulose-water interface was demonstrated by calculating all variables separately from independent simulations (Karna et al. 2021).

General simulation details

All simulations were performed using GROMACS (Páll et al. 2020) version 2021 or later using a leapfrog algorithm with a basic time step of 1 or 2 fs. Non-bonded interactions used a cutoff of 1.0 nm and long-range electrostatics were included using PME (Darden et al. 1993; E1ssmann et al. 1995) with a grid spacing of 0.1 nm and interpolation order 4. Both electrostatic and weak interactions were excluded for atom pairs separated by less than 3 bonds. All bonds involving hydrogen atoms were kept rigid using LINCS. (Hess 2008). For temperature control, velocity re-scaling algorithm with a stochastic term was used (Bussi et al. 2007) and for pressure control, Parrinello-Rahman barostat (Parrinello and Rahman 1981) was used. Cellulose models were generated using the CHARMM-GUI (Jo et al. 2008; Lee et al. 2016), including acetylations (Jo et al. 2011; Park et al. 2017), and simulated using the CHARMM carbohydrate force field. (Guvench et al. 2008, 2009) Three different models were used for water; SPC/E (Berendsen et al. 1987), TIP3P (Jorgensen et al. 1983) and TIP4P/2005 (Abascal and Vega 2005). All other liquids used parameters from the CHARMM general force field (CGENFF). (Vanommeslaeghe et al. 2010; Yu et al. 2012). Dispersion corrections for pressure and energy were included.

Contact angle simulations and interface simulations

In the contact angle simulations the substrate was modeled as a slab of cellulose chains. The slab was prepared by replicating a supercell containing four cellulose chains, each consisting of 12 glucose units, in the I\(\beta\) structure (Nishiyama et al. 2002). The coordinates of the supercell was obtained from Cellulose Builder (Gomes and Skaf 2012). The chains were 6.7 nm long, directed parallel to the y axis, and fully periodic. The supercell was replicated 50 times in the x direction and 2 times in the z direction, yielding a slab 100 chains wide and four layers thick (Fig. 1C) exposing the \([1{\bar{1}}0]\) crystal plane. The heavy atoms of the bottom two layers were subject to harmonic position restraints with a force constant of 1000 kJ mol\(^{-1}\) nm\(^{-2}\). In addition, a slab where all chains in the top layer were O-acetylated at every C6 exposed to the interface was created (Fig. 1D). Next, a cylindrical droplet of liquid was first created by placing a certain number of liquid molecules in a cylindrical container using PACKMOL. (Martínez et al. 2009). For all liquids, two different liquid droplet sizes were used. For hexane, toluene, acetone, ethanol, DMF, nitrobenzene and DMSO 1500 and 3000 molecules were used. For formamide 3000 and 6000 molecules were used and for water (TIP3P, SPC/E, TIP4P2005) 2250 and 4500 molecules were used. The cylindrical droplet was then placed in the rectangular simulation box containing the cellulose slab, and the height of the box was set to 20 nm (Fig. 1C, D). An NVT simulation was then carried out for, at least, 36 ns during which the droplet was allowed to spread freely on the surface. The temperature was maintained at 300 K. The contact angles were calculated based on the algorithm described in the next section. To reduce the statistical uncertainty in the contact angles, three independent simulations for each liquid were carried out.

In addition to the contact angles simulations, cellulose slabs 8 chains wide (both native and acetylated) solvated by a large liquid volume (2000 liquid molecules) were used to compute liquid density profiles and interfacial hydrogen bonding from 12 ns long simulations (Fig. 1D). In these simulations, pressure was maintained at 1 atm with semi-isotropic coupling such that X and Y dimensions of the slabs were kept constant. The temperature was maintained at 300 K. Uncertainties in H-bonds were calculated using block-averaging over three blocks.

Fig. 2
figure 2

The method used to calculate the contact angle. Illustration of the coordinate system and the grid used to determine liquid molecule positions (A); Example of a liquid density profile at constant z coordinate (B); Fitted polynomials to the calculated Gibb’s dividing surface of the liquid-air interface and the resulting left and right contact angles (C)

Full size image

Contact angle calculations

A similar procedure as described previously (Kanduč 2017; Werder et al. 2003; de Ruijter et al. 1999; Giovambattista et al. 2007) was followed to calculate the contact angle. The calculations used coordinates saved every 200 ps. For each frame, a local coordinate system was defined using the geometric center of the liquid molecules as the origin of the x-axis and a distance \(z_c\) above the cellulose slab as the origin for the z-axis (Fig. 2A). The droplet was then split in two portions (left and right) and contact angle calculations were carried out independently for each portion. For a given portion of the droplet (left or right), the atoms in the droplet were sorted into bins of size \(\Delta x\times \Delta z\times L_y\), based on their atomic positions. The \(\Delta x\), \(\Delta z\) and \(z_{c}\) values are taken to be 4 Å, 1 Å and 2 Å respectively. The number density, \(\rho _{N}\) in each bin was calculated and the density profile in the x direction was thus obtained and fitted by the analytical function (Fig. 2B):

$$\begin{aligned} \rho _{\textrm{fit}}(x)=\frac{\rho _{0}}{2}\left[ 1-\tanh \left( \frac{x-x_{0}}{d}\right) \right] \end{aligned}$$
(4)

The above equation is used for the right portion of the droplet. For the left portion, the same equation was used but after performing a reflective transformation. In Eq. 4, \(x_{0}\) is the location of the equimolar Gibbs dividing surface and d is the thickness of the interface. Here \(\rho _{0}\), \(x_{0}\) and d are all fitting parameters. After obtaining \(x_{0}\) as a function of z, a second degree polynomial of the form \(p(z)=Az^{2}+Bz+C\) was fitted to these points (Fig. 2C). The contact angle was then obtained using the expression

$$\begin{aligned} \theta = \pi /2+\tan ^{-1}\left( \left. \frac{dp(z)}{dz}\right| _{z=0}\right) . \end{aligned}$$
(5)

At each time instant, the contact angles evaluated for the right and the left portions of the droplet were averaged. The contact angle algorithm was implemented in MATLAB.

Figure 3 shows examples of the time evolution of the contact angles of a liquid (SPC/E water), on the native and acetylated cellulose surface. Large fluctuations in the instantaneous contact angle values proved difficult to estimate the equilibrium contact angle. Thus, a running average was calculated to smoothen the data, showing that contact angles for the liquid level off and an equilibrium value is reached within the allocated simulation time. The window of averaging for the running averages was taken to be 10 ns. The final value of this average was taken to be the contact angle of the liquid.

Fig. 3
figure 3

The evolution of contact angles for water (SPC/E force field) with time on native and acetylated cellulose surfaces. Blue lines show the instantaneous values and black lines are ten-nanosecond running averages. The reported contact angle is the average of left and right contact angle

Full size image

Calculation of liquid surface tension

To calculate liquid surface tensions, 3000 liquid molecules were randomly packed in the middle of a parallelepiped cell of dimensions \(L_x = L_y\) and \(L_z = 5L\) (at a density close to liquid bulk densities using PACKMOL. (Martínez et al. 2009) The value of L was at least 4.47 nm, which gives a surface area large enough to avoid finite size effects on surface tension. Liquid surface tensions were calculated from 12 ns long NVT simulations as the time average of the instantaneous surface tension given by the difference between the normal and lateral pressure components

$$\begin{aligned} \gamma _{lv}(t) = \frac{L_z}{2}\left( P_{zz}(t) - \frac{1}{2}\left( P_{xx}(t) + P_{yy}(t). \right) \right) \end{aligned}$$
(6)

Uncertainties were calculated using block-averaging over three blocks.

Force field validation

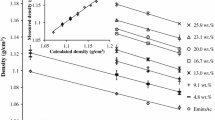
Wetting is governed by the properties of both the solid substrate and the liquid. While the CHARMM carbohydrate forcefield employed in this work has been shown previously to satisfactorily predict properties of both isolated glucan chains (Guvench et al. 2009) and cellulose crystal structures (Oehme et al. 2018; Matthews et al. 2012; Beckham et al. 2011; Payne et al. 2011; Mudedla et al. 2021), the liquid models were subject to validation by comparing their liquid densities \(\rho\) and liquid–vapor surface tension \(\gamma _{lv}\) to experimental data. For most liquids used in this study, experimental data on the aforementioned properties were not available at the desired temperature of 300 K but were found to be available at 293.15 K. Thus for validation purposes, \(\gamma _{lv}\) and \(\rho\) of the liquids were evaluated at 293.15 K. For analysis and interpretations of the results from contact angle simulations and interface simulations, \(\gamma _{lv}\) and \(\rho\) evaluated at 300 K are used. Figure 4 compares simulated values of these properties of the liquids to the corresponding experimental data. An excellent agreement between simulation and experimental values of \(\rho\) and good to moderate agreement between simulation and experimental values of \(\gamma _{lv}\) can be observed. These results provide adequate confidence in the parameters used for the liquids. Values for densities and surface tensions at both 293.15 K and 300 K can be found in the Supporting Information (see Table S1 and Table S2). The simulated values of the surface tension at 300 K of the SPC/E and TIP4P2005 used in this work are slighter lower than the corresponding value reported in literature while the TIP3P value agrees well with previous results. (Vega and de Miguel 2007)

Fig. 4
figure 4

Comparison of calculated values of surface tension \(\gamma _{lv}\) and density \(\rho\) at 293.15 K from MD simulations with the corresponding experimental data. Note that three data points for for water are included representing three different models: TIP3P, SPE/E, and TIP4P/2005

Full size image

Results and discussion

Contact angles from MD simulation and finite size effects

As expected, simulated contact angles differ between both probe liquids and the different cellulose substrates (Table 1 and Fig. 5). All liquids partially wet the native cellulose and form a contact angle larger than zero but below 90°. However, the contact angle of acetone and TIP3P water is too low to be detected by the algorithm and will be reported as being zero. For the acetylated cellulose all liquids wet the surface partially and form a well defined contact angle below 90°.

Simulated contact angles are known to be influenced by liquid droplet size. To check for possible finite size effects, all liquids were simulated using two different droplet sizes (see Methods); one smaller, and one in which the number of solvent molecules was doubled. Water is special as it does not show any appreciable effect of liquid droplet size, while the rest of the liquids did.

For one group of liquids (hexane, acetone, toluene and ethanol) significant evaporation and re-condensation was observed when allowed to spread freely on the surface. These liquids all have relatively low surface tension, below \(\approx 40\) mN m\(^{-1}\). The equilibrium contact angle will, in these cases, be formed by a liquid droplet on top of its own thin film. Thin film formation is favored in cases where there is strong interaction between the liquid molecules and the substrate in relation to the cohesive energy of the liquid phase. The excess liquid molecules will however be constrained by the liquid surface tension and form a droplet on top of the film (see, e.g., Safran (2003)). This phenomenon, denoted precursor film formation, is often detected experimentally on smooth extended flat substrates, and the thicknesses of such films has been seen to vary between a few atomic diameters up to mesoscopic thicknesses on the order of 100 nm. (Popescu et al. 2012) The formation of molecular-scale precursor films has been observed in MD simulations before. (Heine et al. 2005) Obviously, there needs to be a sufficient amount of liquid for a droplet to form under these conditions. Indeed, when using only half the number of liquid molecules (1,500) the simulations showed complete spreading of these liquids on native cellulose surface (see Fig. S1). This situation could easily be mistaken for an indication of complete wetting also in the thermodynamic (macroscopic) sense. In the following, we are considering the cellulose plus the liquid thin film as the substrate, and proceed to calculate contact angles and derive thermodynamic quantities based on this.

For another group of liquids (DMF, DMSO, nitrobenzene and formamide) the calculated contact angles from all simulations are reported in the SI (Table S3) along with plots of their respective convergence (see Fig. S2-S4). It can be observed that the size of the liquid droplets indeed has an influence on the contact angle. Notably the data shows that for the native cellulose surface which is hydrophilic, the contact angle values decrease with increasing droplet size. This effect has been previously observed for hydrophilic surfaces and can be ascribed to the Tolman correction Kanduč (2017). In this group of liquids another interesting effect was observed: the spreading of the droplet is anisotropic, likely as a consequence of the anisotropy of the substrate. Signs of a precursor film is showing but only in one direction (to the right in Fig. 5) and the equilibrium contact angle is different between the two sides. Obviously it would be useful to check even larger systems to study these effects in more detail. Here we use contact angles calculated from the larger systems, averaged over both sides, in the subsequent analysis (Table 1).

Table 1 Simulated contact angles (in degrees) on both native and acetylated cellulose surfaces
Full size table
Fig. 5
figure 5

Snapshots of the final structures for all liquids on native cellulose. TIP4P/2005 is not shown as its appearance almost identical to SPC/E

Full size image
Fig. 6
figure 6

Bar plot of simulated contact angles (in degrees) on native and acetylated cellulose, ordered by increasing liquid surface tension

Full size image

Wetting of native cellulose by water

The contact angle formed by water on native cellulose is of particular interest. Previous MD studies (Mazeau and Rivet 2008; Karna et al. 2021; Malaspina and Faraudo 2019; Trentin et al. 2021; Wang et al. 2022) have noted great variability of water contact angles depending on which water model was used. It appears that the TIP3P water model gives consistently lower contact angles on cellulose than the SPC, TIP4P, and the SPC/E water models. The present study is no exception from this trend. For instance, Trentin et al. (2021) noted complete wetting by TIP3P water of the [110] surface, in agreement with the results presented herein. On the other hand, the SPC/E model gives a contact angle of 11.6°, which is significantly lower than what is reported by both Mazeau and Rivet (2008) and Karna et al. (2021). This discrepancy may be explained by the use of different force field to model the cellulose, PCFF and GLYCAM06, respectively. In systematic investigations (Chen and Smith 2007; Vega and de Miguel 2007) TIP3P water was found to have the lowest surface tension at 300 K of all commonly used water models (\(\sim\) 50 mN m\(^{-1}\)) whereas the value for SPC/E water was significantly higher (\(\sim\)62-64 mN m\(^{-1}\)). The surface tension of TIP4P/2005 water has been calculated to 69.3 mN m\(^{-1}\), thus being closest to the experimental value of 71 mN m\(^{-1}\) of all investigated models. The surface tensions calculated in the present study reproduces this trend, but as mentioned previously the values for SPC/E and TIP4P/2005 are a little bit too low. Apparently the differences in surface tension between the models can have dramatic effects on their respective wetting behaviour. This was also the conclusion arrived at by Malaspina and Faraudo (2023) who, based on these considerations, strongly advised against using TIP3P water at all for studies of wetting. In contrast to the complete wetting noted by Trentin et al. (2021), Wang et al. (2022) noted a contact angle of approx. 13° using the same force field (TIP3P water and CHARMM36 cellulose). They blame this discrepancy on the methodology used for computing the contact angle, although one can note that their result was based on fairly short (2 ns) simulations and that the contact angle curves do not look completely converged. Indeed, in the present work, TIP3P water formed a measurable contact angle on native cellulose still after 2 ns of simulation, which was calculated to 11° (Fig. S5), but the droplet continued spreading and was wetting the surface completely after 40 ns. Thus, the liquid surface tension is critical for the wetting behavior, but other factors such as using different crystallographic planes (Trentin et al. 2021) will also affect simulated water contact angles.

Wetting of native cellulose by organic liquids

Figure 6 shows the contact angle of all probe liquids on native and acetylated cellulose ordered by increasing \(\gamma _{lv}\). Notably, the contact angle is not a simple function of \(\gamma _{lv}\), as predicted by the Young’s equation (Eq. 1), meaning that \(\gamma _{sl}\) is not a simple combination of \(\gamma _{lv}\) and \(\gamma _{sv}\). However, following Adam and Jessop (1925), since \(\gamma _{sv}\) is constant for a given substrate and \(\gamma _{lv}\) is known, we instead consider the parameter \(\Delta \gamma \equiv \gamma _{sv} - \gamma _{sl} = \gamma _{lv}\cos \theta\) to assess the wetting behaviour of liquids. It represents the energy imbalance between the wet and the dry surface: if \(\Delta \gamma\) increases when going from liquid A to liquid B, this means that \(\gamma _{sl}\) decreases, i.e. the solid–liquid interactions become more beneficial. If, however, \(\Delta \gamma\) decreases, \(\gamma _{sl}\) increases meaning that dewetting becomes relatively more favored.

Figure 7 shows a strong correlation between \(\Delta \gamma\) and \(\gamma _{lv}\) with high surface tension indicating strong interaction with the substrate. Water has the highest \(\Delta \gamma\) and thus the most favored interactions with native cellulose. This result highlights the trivial fact that wetting of a given substrate is not only governed by liquid–solid interactions, it is the balance between those interactions and the liquid surface tensions that matters the most. For instance, water interacts more strongly with cellulose than does any other liquid investigated here, but at the same time water has the highest surface tension and, consequently, it forms a contact angle comparable to those of hexane and toluene, which has the lowest \(\Delta \gamma\) of all investigated liquids. These results are in part contradicted by Malaspina and Faraudo (2019), who observed complete wetting of cellulose in simulations by tetradecane. However, in light of precursor film formation discussed above, the number of molecules used in their simulations might have been too low for a stable droplet to form. Experimental numbers for wetting of pure cellulose substrates by organic liquids are hard to find. We note that we achieve qualitative agreement with (Kontturi et al. 2011) who noted larger contact angles for water than formamide on ultrathin cellulose films.

Fig. 7
figure 7

Difference between solid–vacuum (\(\gamma _{sv}\)) and solid–liquid (\(\gamma _{sl}\)) surface energies calculated from simulations. Data is ordered by increasing liquid surface tension (\(\gamma _{lv}\))

Full size image

Critical surface tension and cellulose surface energy from MD data combined with semi-empirical approaches

The critical surface tension, \(\gamma ^c\), is defined as the surface tension below which, for a given substrate, complete wetting is achieved. Thus, \(\gamma ^c\) is a property of the solid alone. The \(\gamma ^c\) is sometimes equated with \(\gamma _{sv}\), although this is only true under the assumption that \(\gamma _{sl}=0\) when \(\theta =0\) (Fox and Zisman 1952). As pointed out, such an assumption is not always true and may not conform to the laws of thermodynamics (Siboni et al. 2004). Nevertheless, the concept of critical surface tension has historically been of great practical importance as a means for determining the surface energy of solids. It is commonly derived using regression to zero contact angle in a plot of \(\cos \theta -1\) versus \(\gamma _l\), a.k.a. a Zisman plot (Fox and Zisman 1950, 1952). Here, the large scatter in simulated data (see Fig. 8) makes determining \(\gamma ^c\) by regression not possible. Even without such analysis, the concept of a critical surface tension for cellulose becomes ambiguous considering the example of TIP3P water. Although it has higher surface surface tension than, e.g., DMF, it exhibits complete wetting while DMF wets the substrate partially. Thus it is clear that a critical surface tension cannot be defined. Indeed, it has been pointed out that one of the most serious pitfalls of the Zisman approach is that it is highly dependent on the particular set of probe liquids used (Lipatov and Feinerman 1979).

Attempts to improve the models for determining the surface energy of the substrate exists. These models make assumptions regarding the work of adhesion, \(W_{A}\) in the Dupré equation (Eq. 2). For instance, Fowkes (1964) hypothesized that surface energies of substrate and liquid can be decomposed into their hydrogen bonding and dispersion components and assumed that only dispersion components of the surface energies contribute to the work of adhesion. The \(W_{A}\) based on this model is given by \(2\sqrt{\gamma _{sv}^{d}\gamma _{lv}^{d}}\). However, for systems where the hydrogen bonding component is important, such as in the present case, Fowke’s model for \(W_{A}\) is no longer appropriate.

The Owens-Wendt model (Owens and Wendt 1969) builds on Fowkes’ ideas by including the hydrogen bonding component to the work of adhesion. Here \(W_{A}\) is given by \(2\sqrt{\gamma _{sv}^d\gamma _{lv}^d}+2\sqrt{\gamma _{sv}^p\gamma _{lv}^p}\) where d and p refers to dispersion and polar, respectively. Combined with Young’s equation and the Dupré equation, this leads to

$$\begin{aligned} \frac{\gamma _{lv}(1+\cos \theta )}{2\sqrt{\gamma _{lv}^d}} = \sqrt{\gamma _{sv}^p}\sqrt{\frac{\gamma _{lv}^p}{\gamma _{lv}^d}} + \sqrt{\gamma _{sv}^d} \end{aligned}$$
(7)

Thus, if a series of liquids with known dispersion and polar contributions are used for measuring \(\theta\), \(\gamma _{sv}\) can be determined by regression. Here, simulated surface tensions were split into \(\gamma _{lv}^d\) and \(\gamma _{lv}^p\) based on the ratio determined from experiments (Shen et al. 2015; Mesić et al. 2022) (see Table S5) in the Supporting Information). Together with the simulated contact angles, the cellulose surface energy was determined from Eq. 7 to 63 mN m\(^{-1}\) with \(\gamma _{sv}^p = 53.3\) mN m\(^{-1}\) and \(\gamma _{sv}^d = 9.6\) mNm\(^{-1}\). This is close to experimental results employing the Owens-Wendt model on nanocellulose films: Lin et al. (2011) obtain \(\gamma _{sv}=61\) mN m\(^{-1}\) and Khoshkava and Kamal (2013) report a value of \(\gamma _{sv}=69\) mN m\(^{-1}\).

The Neumann model (Li and Neumann 1992) differs from the Fowkes and Owens-Wendt models in that it does not assume that the polar and dispersion contributions are additive. Instead the work of adhesion is approximated as \(W=2\sqrt{\gamma _{lv}\gamma _{sv}}e^{-\beta (\gamma _{sv}-\gamma _{lv})^{2}}\) Li and Neumann (1992) leading to

$$\begin{aligned} \cos \theta =-1+2\sqrt{\frac{\gamma _{sv}}{\gamma _{lv}}}e^{-\beta (\gamma _{sv}-\gamma _{lv})^{2}} \end{aligned}$$
(8)

where \(\beta\) is an empirical constant related to the solid surface. After some re-arrangement, the equation becomes

$$\begin{aligned} \ln \left[ \gamma _{lv}\left( \frac{1+\cos \theta }{2}\right) ^2\right] = -2\beta (\gamma _{lv}-\gamma _{sv})^2 + \ln (\gamma _{lv}) \end{aligned}$$
(9)

The left hand side of the equation is computed and plotted against \(\gamma _{lv}\) (Fig. 8). A second order polynomial fit to the data yields \(\beta = 2.2\times 10^{-4}\) and \(\gamma _{sv} = 64.4\) mN/m, respectively. The value for \(\beta\) obtained here is close to the "universal" value of \(1.247\times\)10\(^{-4}\) (Li and Neumann 1992), and \(\gamma _{sv}\) is similar to that obtained from the Owens-Wendt model above.

Fig. 8
figure 8

Fitting different empirical surface free energy models (see text) to simulated wetting data for native cellulose. For the Zisman approach (left) however, fitting was not possible

Full size image

Wetting of acetylated cellulose

For most cases acetylation of the cellulose surface leads to a systematic effect on the wetting behavior: the contact angle of all partially wetting liquids increases (Fig. 6) except for hexane and ethanol where the difference is within the statistical error. Specifically, it can be noted that the contact angle of water increases from 11.6° (SPC/E) and 15.6° (TIP4P/2005) to 34°, which is in agreement with the result of Wang et al. (2022). It is tempting to analyze the effect in terms of a change in solid surface energy, i.e., assuming the chemical modification changes \(\gamma _{sv}\). Tentatively, this could be done through measuring contact angles and using a surface free energy model, e.g. the Neumann or Owen-Wendt model as described above. By doing so, one encounters a problem that is far more fundamental in nature. The solid surface energy (\(\gamma _{sv}\)) is defined relative to the cohesive energy, (Israelachvili 2011) and such state does not exist for the surface-functionalized materials. The same consideration applies to \(\gamma _{sl}\), which is defined relative both the liquid and the solid cohesive energies. Therefore, \(\gamma _{sv}\) and \(\gamma _{sl}\) are not strictly defined for materials that are not isotropic. (Lipatov and Feinerman 1979) On the other hand, \(\Delta \gamma = \gamma _{sv} - \gamma _{sl}\) is independent of any reference state and becomes well defined. Thus, it is possible to compare \(\Delta \gamma\) between liquids.

Figure 7 shows that for Hexane, Toluene, Acetone, and Ethanol, \(\Delta \gamma\) changes only marginally upon acetylation. This can be due to the fact that these liquids are spreading on its own thin film, making the contact angle relatively insensitive to the cellulose substrate below. For all other liquids, \(\Delta \gamma\) is decreased by acetylation meaning that their affinity for the substrate becomes lower. Notably, even after acetylation which is considered a hydrophobization, water has higher affinity than any other liquid, including the relatively more hydrophobic ones.

The work of adhesion was determined from Eq. 3. Figure 9 shows that work of adhesion generally decreases upon surface acetylation, with the exception of hexane, toluene, acetone and ethanol, for which it remains unchanged. For water, specifically, the decrease is \(\sim 8\) mN m\(^{-1}\) for SPC/E and \(\sim 9\) mN m\(^{-1}\) for TIP4P/2005, which is in good agreement with the value \(-9.3\) mN m\(^{-1}\) calculated using a free-energy approach (Chen et al. 2020). In the case of Formamide, the change is similar as for water, but for DMF, Nitrobenzene and DMSO, the decrease in adhesion is smaller in magnitude than for water. This is an important observation meaning that even if the surface in this case is hydrophobized, adhesion is not automatically improved for more hydrophobic liquids other than in relative terms, i.e., with water as the reference.

Fig. 9
figure 9

Work of adhesion calculated from simulations using the Young–Dupré equation

Full size image

Liquid surface structure and hydrogen bonding

One of the strengths of MD simulations is that they offer an atomistic view of thermodynamic phenomena. The wetting of surfaces can potentially be correlated to the liquid structure in the vicinity of the solid–liquid interface. Specifically, water close to purely hydrophobic and weakly interacting surfaces gives rise to fundamentally different density profiles (Chandler 2005) compared to hydrophilic or charged cellulose surfaces. (Kishani et al. 2021) In addition, an atomistic model permits specific interactions, such as hydrogen bonding, to be analyzed.

Liquid density profiles along the surface normal are shown in Fig. 10. For native cellulose, they are all similar with a strong first solvation peak followed by one or two additional solvation layers. Although the height of the first solvation peak may in some cases correlate with the strength of the liquid-substrate interactions, this can not be taken as fundamental truth. For instance, it was shown that a non-interacting hard-sphere liquid can exhibit similar multi-layer formation and liquid ordering as an interacting liquid model. (Krekelberg et al. 2017) Herein, no obvious trend among the different liquid profiles is observed. On the other hand, when comparing profiles between native and acetylated cellulose there is a systematic difference. The first peak is heavily suppressed on acetylated cellulose, for all liquids. This was observed previously for the case of water (Chen et al. 2020) and could be correlated to decreased adhesion of the liquid phase upon acetylation of the surface. This agrees with the observation that \(W_A\) decreases upon acetylation for most liquids.

Due to the abundance of hydroxyl groups on the cellulose surface, hydrogen bonding has been the obvious first mechanism invoked to explain different cellulose-related phenomena (Wohlert et al. 2022), wetting being no exception (Trentin et al. 2021). One possible hypothesis is that if surface interactions are dominated by hydrogen bonding, then \(\Delta \gamma\) will be correlated with the number of hydrogen bonds formed. In Fig. 11 the number of hydrogen bonds bonds per unit area between the liquid and the cellulose surface are reported (see Table S4 for the raw data), and the cases are ordered by their values for \(\Delta \gamma\). As can be seen there is no systematic co-variation. This shows that the cellulose-liquid interaction is not controlled by hydrogen bonding, but rather a balance between dispersion and electrostatics, where of course hydrogen bonding is one contribution. This conclusion is enforced by the observation that the number of hydrogen bonds between water and cellulose remains the same even after acetylation.

Fig. 10
figure 10

Liquid density profiles computed along the normal to the liquid-cellulose interface, \(\rho (z)\). Curves are scaled by their respective liquid bulk density, \(\rho _0\)

Full size image
Fig. 11
figure 11

Number of hydrogen bonds formed between liquid and cellulose substrate per unit interfacial area. Data is ordered by increasing \(\Delta \gamma\) (see Fig. 7)

Full size image

Conclusion

In the present work MD simulations of nanometer-sized droplets of water and several organic liquids were simulated as they were allowed to spread on model surfaces of native and acetylated cellulose. After sufficient time to reach steady state the resulting contact angles were calculated, which were used to derive several thermodynamic properties related to the wetting.

Liquid surface tension is one of the most dominant parameters governing wetting of cellulose. Low-surface tension liquids (below 40 mN m\(^{-1}\)) will form a precursor film of molecular thickness on top of which the excess liquid form a stable droplet with a finite contact angle. Simulations with smaller amount of liquid will thus result in complete wetting. This behavior would be relevant for liquid resins with low viscosity and typical surface energies below this value (e.g., epoxies). The presence of moisture at cellulose surfaces complicates the problem and more work is needed.

Due to the high surface tension of water it forms a stable droplet on top of the substrates despite the fact that it was shown to have the greatest affinity for cellulose. However, by using the TIP3P water model where the surface tension is too low, but still higher than the organic liquids investigated, complete wetting was obtained. Both SPC/E and TIP4P/2005 are thus better options for studying wetting-related problems.

The surface energy of native cellulose was estimated using simulation data in combination with three different empirical models. The Zisman approach was found to be inconclusive, whereas the Owens-Wendt and Neumann models gave solid surface energies of 63 and 64.4 mN m\(^{-1}\), respectively. For acetylated (or any surface-modified) cellulose the surface energy cannot be rigorously defined. It is thus not possible to tell in what way acetylation affects the cellulose surface energy. However, the parameter \(\Delta \gamma\) was seen to decrease systematically after acetylation, with the exception of those forming a precursor film. This lead to the contact angle formed by these liquids was increased, and the cellulose-liquid work of adhesion was reduced. This means that although acetylation is considered a hydrophobization of the cellulose, it does not lead to higher affinity for less polar liquids other than in a relative sense: the affinity decreases less for non-polar liquids than it does for water. Acetylation therefor play a role for reducing the amount of residual water in cellulose processes using other liquids.

The present study shows that MD simulation is a powerful tool to study wetting-related phenomena at an atomistic level of detail. The results presented here have direct implications on our understanding of processes related to the production of cellulose-based nanomaterials, such as the use of adhesives, liquid infiltration of nanocellulose networks and the effects of surface modification.