Introduction

Cellulose nanomaterials (CNMs) have gained increasing attention for their numerous potential applications arising from their nanoscale size, large surface area, ability to be functionalised, and fibril morphology (Foster et al. 2018). However, there is a global need for rapid and robust CNM size characterisation (Balea et al. 2020). The lack of systematic, streamlined, and reliable methods to characterise CNM sizes at industrial-scale has hindered our ability to control their large-scale production and ensure consistent quality (Kaushik et al. 2015). Of particular interest is the CNM aspect ratio (fibre length divided by fibre width), which strongly influences sheet formation and resulting properties of fibrous materials (Varanasi et al. 2013). For example, Ang et al. (2019) showed that as cellulose and NC fibre aspect ratios increased, so did the Young’s moduli, tensile indices, and densities of the produced sheets. Shanmugam et al. (2020) also demonstrated that higher NC aspect ratios produced sheets with lower water vapour permeabilities, a crucial parameter for NC applications in the food packaging industry (Nadeem et al. 2022).

Cellulose nanomaterials can be grouped into different categories based on their size, shapes, surface chemistry and properties, and original source (Foster et al. 2018). Of particular interest are plant-extracted CNMs, which are the most commercially produced nanocellulose (Nechyporchuk et al. 2016). This includes cellulose nanocrystals (CNCs) and cellulose nanofibrils. The “CNF” abbreviation is generally used to describe cellulose nanofibrils, which have typical lengths greater than 1 μm, widths of 20–100 nm, and aspect ratios of 10–100 (Foster et al. 2018). However, commercial cellulose nanofibrils tend to be a combination of nano and microfibrillated cellulose. Consequently, commercial cellulose nanofibrils will be referred to as cellulose nanofibres (CNFs) in this study.

Cellulose nanocrystals have diameters ranging from 5 to 20 nm with aspect ratios of 5 to 30 Cellulose nanofibres have fibre diameters ranging from 20 to a few hundred nm (Larsson et al. 2018), with aspect ratios ranging from 10 to 250 (Raj et al. 2016). In the pulp and paper industry, the terms “fibres” and “fines” are used to describe cellulose particles, depending on the size of the cellulose polymers, where fines refer to fibres that pass through a 76 μm screen (TAPPI 1994). In this study, “fibres” is used to denote all cellulose particles regardless of their size.

There are two main methods for measuring the aspect ratio of CNMs, depending on their size. For small cellulose fibres (fibre diameters below 20 nm) with low aspect ratio (below 40) such as CNCs, the aspect ratio can be determined by individually measuring and comparing fibre lengths and widths from high-resolution images (Chen et al. 2021). These images can be captured using (e.g.) atomic force microscopy (AFM) and transmission electron microscopy (TEM) (Browne et al. 2022). However, sample preparation, image generation, and one-at-a-time fibre measurements are time-consuming, and require sophisticated instrumentation. In addition, the calculated aspect ratio is prone to operator bias, and may be misrepresented due to skewed fibre selection towards larger fibres (Ang et al. 2020b). Furthermore, both fibre lengths and widths need to be discernible within the same image, signifying that long and thin cellulose fibres, such as CNF cannot be characterised using this method (Rol et al. 2019).

For larger cellulose fibres (fibre diameter and aspect ratio above 20 nm and 10, respectively) such as CNFs, the sedimentation method can be used to calculate their aspect ratio (Martinez et al. 2001; Zhang et al. 2012). This is achieved by determining the gel point (GP) concentration to calculate the aspect ratio using the Effective Medium Theory (EMT) (Celzard et al. 2009). The GP corresponds to the lowest concentration at which the fibres form a continuous network (i.e. point of network formation) (Onyianta et al. 2020). However, this method is dependent on the ability of the fibres to form sediments, which requires the fibres to be large enough to settle (Tanaka et al. 2014). As an example, sulfuric acid hydrolysed CNCs with highly charged rods, will not form sediments in water due to their high electrostatic stability (Ma et al. 2021). In addition, settling times are heavily influenced by the solvent used (Kang and Eremin 2021). Based on previous research, CNF disintegrated in distilled water require a minimum of 48 h to fully settle (Raj et al. 2016). This method is also used to characterise wood fibres, which are traditionally used to make paper. Wood fibres produced from the kraft generally have diameters of 2–30 μm (McIntosh et al. 2019), with aspect ratios of 80–120 (Ang et al. 2019).

Many studies have used rheology to characterise CNM suspensions. For CNCs, rheology has been used to investigate their fundamental behaviour and differing properties by manipulating the synthesis conditions, and feed and salts concentrations, among other parameters. Xu et al. (2020) demonstrated that the full complexities of phase behaviours and transitions of CNC suspensions are predominantly dependent on feed concentration, fibre size, and interparticle forces, and are not affected by the CNC source. Buffa et al. (2019) investigated the effect of chemical modifications of CNCs on the flow behaviours and phases of their suspensions. They saw an increase in suspension viscosities and gel behaviour at the same concentrations for TEMPO-oxidised CNCs due to the increase in electrostatic layer.

For CNF and cellulose nanofibrils, rheology has mainly been used as a tool to evaluate the effects of different mechanical and chemical processes, and solvents used on the properties of the products. Aaen et al. (2019) investigated the effect of xanthan gum on the rheological properties of TEMPO-oxidised cellulose nanofibrils with varying electrolyte concentrations. They showed that low electrolyte concentrations produced stronger cellulose nanofibril networks, while higher doses resulted in weaker connections. Schenker et al. (2018) used viscosity and viscoelastic measurements to qualitatively describe the increase in network strength as the degree of fibrillation (DoF) increased in eucalyptus pulp cellulose nanofibres. Yuan et al. (2021) also noted the increase in viscosity flow curves as the DoF increased in CNF samples. They qualitatively linked this to increasing aspect ratios, although their reported fibre aspect ratios were determined by AFM and SEM, not the viscosity profiles.

Despite advances in rheology-based NC characterisation, the application of specific viscosity measurements to directly determine CNM aspect ratio has not yet been achieved nor fundamentally analysed. Here, we present a rapid method to determine cellulose aspect ratios using specific viscosity measurements based on the fundamental principles of polymer entanglement (Mezger 2020, Elias 1986). While the model was developed to describe the behaviours of polymer coils and needle-shapes in solutions, we show that the gel point concentration for cellulose suspensions can be determined using the same model. Consequently, we investigated cellulose nanocrystals, cellulose nanofibres, and wood fibres in the form of Bleached Eucalyptus Kraft (BEK) to validate rheology as a technique to characterise the whole range of cellulose fibre sizes, ranging from the nanoscale up to the macroscale. The aspect ratios for CNCs, CNFs, and BEK were determined with rheology by evaluating the specific viscosity profiles for different concentrations of their suspensions from high (2000 s−1) to low (0.01 s−1) shear rates, and compared to those obtained using sedimentation and AFM methods.

Entanglement hypothesis and application to fibre suspensions

Elias (1986) described the dependence of polymer concentration on the location and behaviour of polymer coils in solvents using polyethylene as an example. Polymer chains were shown to be bound with each other and form coils resembling bean and kidney shapes. A sufficiently dilute polymer solution is made up of individual polymer coils in a vast medium. As the polymer concentration is increased, polymer coils become close enough to freely join and entangle with one another. Under these conditions, more energy is required to move and shift these entangled macromolecules, as demonstrated by an increase in viscosity with increasing polymer concentration. Using these principles, Mezger (2020) developed the entanglement hypothesis, which predicts the theoretical viscosity curves for dilute and concentrated polymer solutions using rotational tests.

In this study, a similar approach is used to generate the profiles for cellulose suspensions. However, the viscosities were converted to specific viscosities. The resulting theoretical specific viscosity profiles are shown in Fig. 1. The specific viscosity describes the increase in viscosity due to the addition of polymeric or cellulosic materials, accounting for the effect of the solvent on the total viscosity and addressing one of the key limitations of the sedimentation method (Mardles 1940). The objective of the specific viscosity tests is to determine the gel point concentration (i.e. point of network formation) by evaluating the specific viscosity profiles of cellulose suspensions at different concentrations.

Fig. 1
figure 1

Theoretical specific viscosity profiles of entangled and disentangled cellulosic suspensions illustrating three critical shear regions: zero-shear, shear-thinning, and infinite-shear (modified from (Mezger 2020))

Full size image

Given a sufficiently high polymer concentration, macromolecular coils will freely entangle with one another at rest. Rest behaviour is best simulated at very low shear rates due to the minimal supply of energy to the system, corresponding to the zero-shear region. Within this window, the specific viscosity is expected to be constant, as there would be no change in coil behaviour that would cause an increase in suspension flow. The shear rates within this region change depending on the material, but for many polymers, this occurs at approximately 1 s−1 and below (Mezger 2020). Beyond the zero-shear region, entangled polymer coils start to orient themselves in the shear direction, resulting in partial disentanglement. This behaviour is also known as shear-thinning. The shear-thinning region begins once the specific viscosity starts to decrease (estimated to start at 1 s−1). Beyond this, given a sufficiently high shear rate, the macromolecules are almost completely disentangled and fully oriented in the direction of shear. As a result, the viscosity will plateau again due to entanglements no longer contributing to the overall resistance to flow, corresponding to the infinite-shear viscosity and region. The start of this region depends on the feedstock, but is generally considered to begin at 1000 s−1 (Mezger 2020). The three shear regions should only be observable for semi-dilute and concentrated polymer suspensions and solutions, signifying that these concentrations are above the gel point. This specific viscosity profile corresponds to the entangled (pink) curve in Fig. 1.

For dilute suspensions, where each coil is unable to form entanglements with neighbouring polymer coils due to the large space in between them, the specific viscosity is expected to follow ideal viscous behaviour. Because there is no expected disentanglement, the specific viscosity is expected to be constant throughout all three shear-regions. This specific viscosity profile corresponds to the disentangled (blue) curve in Fig. 1. Ultimately, the lowest concentration at which cellulose suspensions exhibit entangled behaviour corresponds to the gel point concentration.

Mezger (2020) also used these principles to describe the behaviour of dilute and concentrated needle and platelet-shaped solutes in solutions. It is worth noting that for these particles, the shear-thinning behaviour is dominated by particle orientation rather than chain, coil, and particle disentanglement. As such, the entanglement hypothesis can be applied to characterise the aspect ratio of cellulose nanocrystals (highly charged rigid rods), and cellulose nanofibres and Bleached Eucalyptus Kraft (semi-flexible polymers).

Materials and methods

Materials and sample preparation

Cellulose nanocrystals (grade CelluForce NCV100) were sourced from CelluForce. Commerical cellulose nanofibres was acquired from DAICEL Chemical Industries Limited (grade Celish KY-100S). Wood fibres were supplied in the form of never-dried unrefined Bleached Eucalyptus Kraft (BEK) pulp from Australian Paper Maryvale. Suspensions of 4, 1, and 1 wt% solids content in deionised (DI) water were prepared for CNCs, CNFs, and BEK, respectively. The mixtures were then separately disintegrated at 15,000 revolutions using a 0.5 kW Messmer Disintegrator Mode MK III C. Following disintegration, suspensions were subsampled and further diluted as required. The prepared suspensions were then stored in a fridge at 4 °C.

Atomic force microscopy (AFM) imaging and diameter distribution

Browne et al. (2022) characterised the same grade of CNCs (grade CelluForce NCV100) from CelluForce in their paper using AFM. As such, their aspect ratio and polydispersity results were used in this study to corroborate our rheology results. Briefly, CNCs were imaged using a JPK Nanowizard III atomic force microscope (AFM) using tapping mode with an AC160TS-R3 cantilever with a nominal resonance frequency of 300 kHz. The images were 1st order flattened using Gwyddion (version 2.53). The aspect ratio was determined by dividing the manually determined length and width of each individual CNC particle. Bushell et al. (2021) showed that measuring 100 CNCs produces comparable aspect ratios to those produced by measuring the recommended 250–300 individual particles. Therefore, the results calculated from 139 particles were considered to be representative of the CNC specifications139 individual, separate particles were measured in 20 images, with all distinguishable fibres measured. Full experimental details available in (Browne et al. 2022).

Scanning electron microscope (SEM) imaging and diameter distribution

For scanning electron microscope (SEM) images, CNF and BEK samples were prepared by casting a drop onto a silicon wafer. The drops were air dried and then coated with iridium. The images were captured using a FEI Magellan 400 XHR FEGSEM fitted with a monochromator at 5.0 kV and 13 pA current using secondary emission. CNF and BEK diameter distributions were determined using a modified method from (Ang et al. 2020a). Low magnification images (100 µm scale bar) were taken to analyse the large fibres, and high magnification images (5 μm scale bar) were taken to analyse the smaller fibres. Fibre diameters were measured using ImageJ processing software. A total of 421 CNFs were analysed in 15 SEM images. 362 BEK fibres were analysed in 24 SEM images. All distinguishable fibres were measured.

Optical fibre analysis

BEK diameter distributions were also determined using an optical fibre analysis device (Morfi Neo—Techpap, France) based on a modified method from (Pennells et al. 2022). Three one litre samples at 0.004 wt% were investigated, and over 11,000 fibres per sample were analysed. The fibre length range was set to 2 to 10,000 µm, while the fibre width range was set to 2–100 µm. 2 µm was the limit of detection of the instrument.

Zeta potential

The zeta potential for CNC, CNF, and BEK suspensions were measured in triplicate using a Nanobrook Omni (Brookhaven Instruments) at 25 °C.

Gel point determination via sedimentation

Sedimentation tests were conducted using a similar method to (Zhang et al. 2012). 250 mL CNF and BEK suspensions were prepared at concentrations ranging from 0.1 to 0.01 wt%. Each suspension was mixed using a Waring Commercial immersion blender (model WSB33XNNA), and transferred into 250 mL measuring cylinders. The initial suspension height was measured and recorded (h0). A minimum of 48 h was allowed for the fibres to settle before recording the sediment height (hs). The initial solids concentration was plotted versus the hs/h0 ratio and fitted using a polynomial fit. The linear slope of the line was taken as the gel point concentration in wt%.

Gel point determination via rheology

Shear-viscosities were measured via rotational tests using an air bearing rheometer (MCR 302, Anton Paar) at 25 °C. A cup and bob measuring system (bob effective length and diameter: 40.002 and 26.657 mm, respectively) was used to ensure low viscosity samples were accurately characterised, and the larger particles would not skew the results. Prior to measurements, the samples were shaken at 200 rpm in an Infors HT Ecotron Shaker Incubator at 25 °C for at least thirty minutes to ensure good mixing. Approximately 19.35 mL aliquots were taken for each test. A 5-minute waiting time was set before starting the viscosity measurements to allow for thermal equilibration at 25 °C. The shear rate was logarithmically adjusted from 2000 to 0.001 s−1. With a point density of 4, the time intervals for data collection were logarithmically increased 1–2000 s to limit transient effects. Measurements were conducted in triplicate (three runs per concentration on different samples) and the average value reported. The resulting shear-viscosity measurements were converted to specific viscosities to account for the contributing viscosity of the solvent (DI water) using Eq. 1.

$$\eta_{{{\text{sp}}}} = { }\frac{{\eta - \eta_{s} }}{{\eta_{s} }}$$
(1)

where \({\eta }_{sp}\) corresponds to the specific viscosity (dimensionless), \(\eta\) to the measured shear-viscosity of the whole suspension (mPa.s), and \({\eta }_{s}\) to the measured shear-viscosity of the solvent (mPa.s). Based on the viscosity profile of each suspension, they were assigned to dilute (below gel point) and semi-dilute (above gel point) regions by comparison with the shapes indicated in Fig. 1. Apparent specific viscosities were plotted versus their original concentrations. Power law curves were fitted to the data points in the dilute and semi-dilute region, with the intersection of the trendlines for both regions corresponding to the gel point concentration.

Gel point aspect ratio determination

The gel point aspect ratio was determined using (2), based on the Effective Medium Theory (Varanasi et al. 2013).

$$A = 3.19 \times C_{c}^{ - 0.58}$$
(2)

where A corresponds to the aspect ratio and Cc to the gel point. This equation assumes a cellulose skeletal density of 1500 kg/m3 (Varanasi et al. 2013).

Results and discussion

Specific viscosity profiles

To determine the specific viscosity functions of CNC, CNF, and BEK suspensions, rotational tests were conducted for a series of dilutions ranging from 0.01–4 wt% at 25 °C. These fibrous materials were selected to demonstrate that the aspect ratio of the whole cellulose fibre size range can be determined using rheology. This is relevant for numerous industries producing and processing different types of cellulosic materials. CNCs, CNFs, and BEK can be used for different applications, such as versatile scaffolds for drug delivery, plastic substitution for renewable food packaging, and papermaking, respectively. The shear rate was logarithmically ramped down from 2000 to 0.001 s−1. The resulting profiles are shown in Fig. 2a, c, and e.

Fig. 2
figure 2

Viscosity functions for suspensions of a Cellulose nanocrystals (CNCs); c Cellulose nanofibres (CNFs); e Bleached Eucalyptus Kraft (BEK); and example of gel point (GP) determination using apparent specific viscosities at 1.79 s−1 for b CNCs; d CNFs; f BEK

Full size image

The CNC specific viscosity curves (Fig. 2a) are similar to those predicted by Mezger (2020)’s entanglement hypothesis (Fig. 1). At 2.5 wt% and above, plateaus can be observed below 0.31 s−1 shear rate, marking the zero-shear region for these concentrations. A decrease in specific viscosity is then observed from 0.31 to 750 s−1, denoting the shear-thinning region. Above 750 s−1, plateaus are also observed, corresponding to the infinite-shear region. Conversely, at concentrations below 2.5 wt%, steady-state flow is observed within the shear-thinning region. A decrease in specific viscosity (shear-thinning) is expected for entangled coils or randomly-oriented connected rods, as the increase in shear rate causes the coils to unravel and rods to orient themselves, resulting in increased flow. Therefore, the consistent specific viscosities independent of shear rate in the shear-thinning region for suspensions below 2.5 wt% suggests a discontinuous network. CNC suspensions below 2.5 wt% therefore exhibit ideal viscous behaviour, and the CNC gel point concentration is expected to be between 1.5 and 2.5 wt%.

No plateau is observed at low shear rates for either CNF (Fig. 2c) or BEK (Fig. 2e) suspensions. Instead, their specific viscosities continuously decrease at shear rates from 0.016 to 500 s−1 (CNF) and 750 s−1 (BEK), after which an infinite-shear specific viscosity plateau is observed. Notwithstanding, dilute (below 0.1 wt%) CNF suspensions exhibit ideal viscous behaviour. Dilute BEK suspensions (below 0.5 wt%) also show quasi-ideal viscous behaviour, with minor fluctuations. Consequently, the CNF and BEK gel point concentrations are expected to be between 0.1 and 0.3 wt%, and 0.2 and 0.5 wt% respectively.

The raw shear-viscosity curves for CNC, CNF, and BEK suspensions are shown in Supplementary Information (Fig. S1), demonstrating the challenge in measuring the viscosity of dilute suspensions at low and high shear rates. The viscosity of deionised water could only be accurately measured from 1 to 107 s−1 shear rate. The proximity of the shear-viscosities of dilute concentrations to that of pure water, and the similarity in their curves further supports their assignment to below gel point concentration.

Gel point concentration

To determine the gel point concentrations, the apparent specific viscosities from 1.79 to 107 s−1 were plotted versus the original concentration of their respective suspensions. An example for the specific viscosities recorded at 1.79 s−1 (indicated by the discontinuous vertical black lines in Fig. 2 a, c, and e) are shown in Fig. 2 b, d, and f. For all three cellulose suspensions, significantly steeper trendlines can be observed in the semi-dilute regions compared to those in the dilute region. The crossover point of the trendlines marks the lowest concentration at which a suspension is expected to exhibit entangled behaviour, corresponding to the gel point concentration (i.e. point of network formation). 1.79–107 s−1 was the only window within which the dilute nanocellulose suspensions could be accurately measured.

To determine the gel point concentration of CNF and BEK using the sedimentation method, 250 mL suspensions were prepared at concentrations ranging from 0.01 to 0.1 wt% and allowed to settle in in straight-walled cylinders. The original suspension concentrations were plotted versus the sediment and suspension height ratios to determine the gel point concentration (Varanasi et al. 2013). The CNC gel point concentration could not be determined using the sedimentation method, as the fibres were too electrostatically stable to form sediments. The gel point concentrations as determined by rheology and sedimentation are shown in Table 1.

Table 1 Cellulose gel point concentrations measured from rheology and sedimentation with ± showing the standard deviations
Full size table

Fibre sizing and colloidal stability

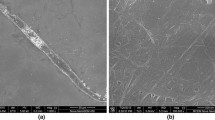
To explain the specific viscosity behaviour and gel point concentrations of CNCs, CNFs, and BEK, their fibre diameters and zeta potentials were measured. An AFM image of CNCs is shown in Fig. 3a and SEM images of CNF and BEK are shown in Fig. 4. CNC diameter distributions are shown in Fig. 3b as reported by (Browne et al. 2022). CNF and BEK diameter distributions based on low (100 μm scale bar) and high (5 μm scale bar) magnifications are shown in Fig. 5.

Fig. 3
figure 3

CNC sizing results for a AFM image of CNCs; and b CNC diameter distribution as determined from AFM images by (Browne et al. 2022)

Full size image
Fig. 4
figure 4

SEM images for dried cellulose fibre suspensions at a low magnification (28 µm × 20 µm) 1 wt% CNF; b high magnification (416 µm × 299 µm) 1 wt% CNF; c low magnification (52 µm × 37 µm) 0.1 wt% BEK; d high magnification (640 µm × 460 µm) 0.1 wt% BEK

Full size image
Fig. 5
figure 5

Fibre diameter distributions as determined from SEM images for a CNF at 1 μm scale bar; b CNF at 100 μm scale bar; c BEK at 1 μm scale bar; and d BEK at 100 μm scale bar and also using MorFi

Full size image

CNCs are significantly less polydisperse compared to CNFs and BEK, as seen in their diameter distributions in Fig. 3b. This is also evident in Fig. 3a, where fibre diameters and lengths are close to each other, ranging from 2.8 to 5.8 nm, and 70 to 165 nm respectively.

As seen in Fig. 5a, CNF has a wide diameter distribution. This is visually evident in the SEM images (Fig. 4a, b), with the low magnification (Fig. 4a) image showing larger fibres of up to a few µm in diameter, and a network of nanofibres with sizes ranging from 20 to 200 nm. BEK also contains a wide distribution of fibre sizes (Fig. 5b), ranging from less than 500 nm to above 34 µm. While Fig. 5b and d show the difficulty in characterising bulk fibre diameters, SEM and MorFi diameter distributions are in reasonable agreement for larger fibres ranging from 7 to 34 μm. SEM analysis shows a bias towards smaller fibre sizes, while the MorFi results are biased towards larger fibres. This is attributed to the limit of detection for both methods, especially the MorFi, as it cannot detect fibres below 2 µm. The wide distribution of BEK fibre sizes is exemplified in Fig. 4c and d. Figure 4c shows an example of a large fibre measuring approximately 9.6 μm in diameter, with some smaller fibre diameters ranging from 100 to 500 nm. Figure 4d shows noticeably longer and larger fibres.

A clear and continuous fibrous network is observed in Fig. 4b. This is expected as a 1 wt% CNF suspension was cast for SEM imaging, a concentration significantly higher than the determined gel point (0.14 wt%). On the other hand, BEK shows a discontinuous network (Fig. 4c and d), as a 0.1 wt% BEK suspension was cast, a lower concentration than the calculated gel point (0.47 wt%).

Because of the high CNC electrostatic stability (Table 2) and increased fibre size uniformity compared to CNFs and BEK (Figs. 3 and 4), the majority of the rods respond (disentangle from each other and orient themselves) similarly with increasing shear rates. Therefore, at low shear rates (simulating rest behaviour), the CNCs do not shift or disentangle, producing zero-shear viscosities. Conversely, due to the heterogeneity (Fig. 5) and lower electrostatic stability of CNF and BEK suspensions (zeta potential less than – 30 mV, Table 2), minute shear forces cause the smaller fibres to disentangle and move around. This is because less energy is required to disrupt smaller and less stable fibres. This produces an immediate decrease in specific viscosity, resulting in no zero-shear viscosities for these samples. The impact of heterogeneity is more distinct for BEK, with small specific viscosity profile fluctuations at concentrations below the gel point (Fig. 2e). The CNC specific viscosity profiles follow the entanglement model for stable polymer solutions (Mezger, 2020).

Table 2 Measurement of Zeta potential to evaluate colloidal stability with ± showing the standard deviations
Full size table

The significantly higher specific viscosity values produced by BEK at the same concentrations compared to CNCs and CNFs (Fig. 2a, c, and e) are attributed to their much larger fibres, as seen in Fig. 5. This is also why CNFs, with larger fibres, have higher specific viscosity values compared to CNCs. Despite the difference in BEK fibre diameters determined via SEM and MorFI, the significant contrast in fibre sizes between CNFs and BEK provides a qualitative explanation for the difference in their viscosity profiles.

Aspect ratio

To determine the CNC aspect ratio using AFM, fibre lengths and widths were measured and compared from AFM images following the method described by (Browne et al. 2022). Because the same CNC batch was analysed, previous aspect ratio results from this study using AFM and rheology could be directly compared. Aspect ratios determined using the rheological and sedimentation gel point concentrations were calculated based on Eq. 2 (All aspect ratio results are shown in Table 3.

Table 3 Cellulose aspect ratios determined from rheology, sedimentation, and AFM with ± showing the standard deviations
Full size table

The rheological aspect ratio results are similar to those produced by sedimentation for both CNF and BEK, as verified with independent t tests at a 95% confidence interval (p—values > 0.05). Independent t-tests could not be performed to compare the AFM and rheology methods, because AFM measures individual fibres to produce an aspect ratio, while rheology measures suspension flow behaviour. Furthermore, due to the considerable difference in sample size between AFM and rheology, neither t-tests nor z-tests can be performed (AFM n = 139 > 30; rheology n = 8 < 30). CNC aspect ratio determined by rheology had a 95% confidence interval of 0.2, while AFM produced a 95% confidence interval of 2.3 Indeed, the aspect ratios are quite close, but not identical within the 95% confidence intervals. The higher aspect ratio fibres influence the suspension behaviour more significantly than the smaller fibres, which is why rheology estimates a larger aspect ratio. This is corroborated with dynamic light scattering analyses (ensemble analysis) producing larger CNC diameters compared to AFM (individual fibre analysis) (Browne et al. 2022). Nevertheless, because the rheological aspect ratio is within the spread of the AFM aspect ratio results, rheology is deemed to be a valid method to measure the aspect ratio for CNCs, with comparable results to those produced by AFM. Furthermore, the aspect ratios based on rheological measurements are similar to those determined by (Reid et al. 2017).

The time required to obtain the results using rheology was significantly shorter compared to AFM and sedimentation. Each viscosity test took only 30 min to complete, including cleaning and sample loading. With AFM, at least 1–2 days was required for sample preparation and image acquisition. With sedimentation experiments, BEK took 48 h to fully settle, while CNFs required approximately 50 days due to the lack of salts, resulting in the fibres repelling each other (Raj et al. 2016). CNF sedimentation heights (hs) were measured twice a week, and the fibres were considered settled once identical heights were recorded over 2 weeks. Despite the known charge screening effect with BEK, their micro-sized fibres were heavy enough to sediment rapidly. Similar BEK behaviours were reported by (Raj et al. 2016). On the other hand, because CNFs are smaller colloidal fibres with significantly larger surface areas, the charge stabilization effect was amplified, requiring a drastic increase in time for the fibres to fully settle.

Figure 4 shows that accurately determining the aspect ratio for CNF and BEK suspensions using microscopic techniques is impossible, as the fibre lengths cannot be measured within a single image. In addition, optical fibre analysers also cannot be used to calculate BEK aspect ratios due to their limit of detection (2 µm). MorFi results estimated BEK aspect ratio at 51, while rheology and sedimentation estimated it to be 72 and 74, respectively. This is expected, as several BEK fibre lengths were below 500 nm, and a decrease in average fibre diameter would result in an increase in aspect ratio, which would not be captured or included in the MorFi analysis. These results also highlight that a small amount of mechanical treatment, such as 15,000 disintegrator revolutions, produces enough nanofibres to skew MorFi aspect ratio determinations. In addition, the smaller aspect ratio of BEK versus CNFs is attributed to the long BEK particles and lower number of small BEK diameters. CNF have a large number of small fibre diameters, skewing towards 30 nm (Fig. 5a), resulting in a higher calculated aspect ratio.

For industrial purposes, the gel point concentration and aspect ratio of a cellulosic single sample can be determined by measuring the specific viscosities of three dilute and three semi-dilute mixtures, which requires three to four hours. Furthermore, this process can be automated, reducing the time required and risk of measurement errors (e.g. during sample loading and mixing) to determine the aspect ratio of cellulose. These results support rheology as a rapid and robust tool to characterise the aspect ratio for the whole range of cellulose fibres, unlike the AFM and sedimentation approaches.

Conclusion

Large-scale production of cellulose nanomaterials has been hindered by a lack of rapid and reliable aspect ratio characterisation methods. The current methods developed for research, including AFM, TEM and sedimentation, are too expensive or time consuming to be industrially relevant. In this study, CNCs, CNFs, and BEK were evaluated by AFM, sedimentation, and rheological methods. Based on the polymer chain entanglement principles, the specific viscosities for the suspensions of the three materials were measured to determine their aspect ratios. The aspect ratios produced with rheology were in good agreement with those generated with AFM and sedimentation. Indeed, rheology was the only method capable of measuring the aspect ratio for the full cellulose fibre size range. Furthermore, viscosity measurements taken on standard laboratory instruments can be used to determine the aspect ratio of a CNM sample in three hours, compared to several days required for AFM or sedimentation analysis. Rheology is therefore an attractive method for industrial CNM characterisation, where rapid and robust techniques are necessary to support full-scale production. Rheology is also an attractive method for wider cellulose fibre applications, where accurate fibre size analysis is critical.