Introduction

Wood and other cellulosic materials are highly sensitive to water. Moisture content governs the physical properties of wood as well as its susceptibility to fungal degradation or chemical treatments (Brischke and Alfredsen 2020; Dinwoodie 2000; Jakes et al. 2019). Many of the macroscopic effects of moisture are traceable down to the interactions between water and the nanoscale constituents of the wood cell walls, and these interactions are not yet fully described. Water-accessibility, diffusion kinetics, and structural effects of moisture changes are also extremely important for more developed applications utilizing wood, including pulp and paper as well as various types of cellulose nanomaterials (Ajdary et al. 2020; Heise et al. 2020; Salmén and Stevanic 2018). Especially, being able to address the irreversible effects of drying on cellulose structure would greatly benefit its utilization.

Based on results from nuclear magnetic resonance (NMR) cryoporometry (Cai et al. 2020; Gao et al. 2015; Kekkonen et al. 2014) and earlier observations by solute exclusion (Hill and Papadopoulos 2001), the main portion of water in water-saturated wood cell walls exists as bound water in pores of the same lengthscale as the diameter of a cellulose microfibril (2–3 nm). The term “micropore” is used in the literature to describe pores that have a diameter below 2 nm. The existence of tightly-bound and loosely-bound fractions of bound water in softwoods has been observed by NMR relaxometry (Cox et al. 2010) and quasi-elastic neutron scattering (Plaza Rodriguez 2017). According to results obtained with small-angle neutron and X-ray scattering (SANS, SAXS), a large portion of water is located in spaces between cellulose microfibrils, where it controls the swelling of microfibril bundles (Fernandes et al. 2011; Jakob et al. 1996; Plaza et al. 2016; Penttilä et al. 2021). Nevertheless, it remains to be shown if the water between loosely aggregated cellulose microfibrils is the only type of bound water present in native wood cell walls. On the other hand, it is not clear if specific locations in the fibrillar architecture are more easily accesible to water than others. This could mean for instance that the accessibility differs between the inner parts of microfibril bundles and their outer surface, as has been proposed for pulps (Lindh and Salmén 2017; Lindh et al. 2017).

Deuterium (\(^2\)H or D) and deuterated water (\(\hbox {D}_2\hbox {O}\)) have been widely utilized to study the accessibility of wood polymers to water (Altgen and Rautkari 2020; Lindh et al. 2017; Reishofer and Spirk 2015; Thybring et al. 2017). This approach is based on the H-to-D exchange (deuteration) of OH groups in direct contact with water, which can be observed as changes in mass or infrared spectrum. The methodology has been applied especially to observe drying-related effects on the water-accessibility of OH groups or to detect signs of irreversible structural changes in dried wood cell walls (Altgen and Rautkari 2020; Salmén and Stevanic 2018; Suchy et al. 2010; Thybring et al. 2017). As a downside of these methods, they are highly averaging and insensitive to the exact location of the molecular groups within the hierarchical cell wall architecture.

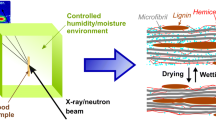
SANS is a non-invasive structural characterization method that allows detecting the presence of water at a specific level of the hierarchical structure of wood. This is due to the scattering length density contrast created by water within the fibrillar structures, which can be further modified by changing the ratio of \(\hbox {H}_2\hbox {O}\) and \(\hbox {D}_2\hbox {O}\) (Martínez-Sanz et al. 2015). Due to advances in the technology of neutron sources and detectors, SANS can nowadays be used for kinetic studies in the time-scale of seconds or even below (Hayward et al. 2018; Lindner and Schweins 2010). At the same time, the analysis of small-angle scattering data from wood samples is facilitated by the recently developed WoodSAS model (Penttilä et al. 2019). This model can be used to determine the diameter of cellulose microfibrils and their packing distance under various moisture conditions (Penttilä et al. 2020b), and in the case of SANS, the diameter of microfibril bundles can also be obtained (Penttilä et al. 2020a).

In this work, we studied how and in what timescale water exchanges at different levels of the wood cell wall nanostructure. We conducted time-resolved SANS measurements to follow how water exchanges by diffusion in the interfibrillar spaces. We also used infrared spectroscopy to observe the time-dependent re-exchange (re-protonation) of deuterated hydroxyl groups of the polysaccharides from OD to OH. This methodology offered us two independent and complementary ways to examine the kinetics of water exchange at the level of cellulose microfibrils. In addition, we assessed the effects of the first drying of wood samples on the water-accessibility by comparing the results of never-dried and dried/rewetted samples.

Experimental

Materials

Stem discs of never-dried Norway spruce (Picea abies (L.) Karst.) were collected from the lowest part of a freshly-felled mature tree near Fiskars village, Southern Finland. The discs were sealed into plastic bags and stored refrigerated at 7\(^\circ\)C. Wood blocks consisting of sapwood and having a tangential width of about 10 mm were separated using a hand saw from the outer part of a stem disc (see Figure S1 in Supplementary Information (SI)) and stored in plastic bags with excess \(\hbox {H}_2\hbox {O}\) at 7\(^\circ\)C. Tangential-longitudinal sections with approximate dimensions of 0.8 mm (radial) \(\times\) 10 mm (tangential) \(\times\) 55 mm (longitudinal) from annual rings 39–47 were prepared using a sliding microtome (Lab-Microtome, Swiss Federal Research Institute WSL, Switzerland). After removing 5 mm from both ends and 0.5–1.0 mm from the radial faces of these sections, they were cut into three pieces with an approximate length of 13–15 mm using a razor blade. The samples were encoded by a combination of a number and letter, so that all three pieces cut from the same section share the same number and letter (see Figure S1 for details). The resulting \(\sim\)0.8 mm (radial) \(\times\) 8–9 mm (tangential) \(\times\) 13–15 mm (longitudinal) sections were immersed either in liquid \(\hbox {H}_2\hbox {O}\) (deionized or MilliQ), \(\hbox {D}_2\hbox {O}\) (Sigma-Aldrich 151882, 99.9 atom %) or a mixture with 65% \(\hbox {H}_2\hbox {O}\)/35% \(\hbox {D}_2\hbox {O}\) (v/v), and stored until further use according to Fig. 1. Complete drying of wood sections from \(\hbox {H}_2\hbox {O}\) or \(\hbox {D}_2\hbox {O}\) solution (soaked for 3–20 days) was done in an automated sorption apparatus (DVS intrinsic, Surface Measurement Systems, UK) under \(\hbox {N}_2\) gas flow (200 SCCM) at 25\(^\circ\)C and 0% target relative humidity for at least 23 h, until a constant weight was reached. The dried samples were stored together with silica gel to keep them dry.

Fig. 1
figure 1

Diagram showing the preparation of samples and the experiments in which they were utilized

Full size image

Small-angle neutron scattering

Wood sections equilibrated for 11–14 weeks in the final conditions shown in Fig. 1 were placed in quartz glass cuvettes with an optical path of 1 mm, having the fiber axis in a roughly vertical orientation. The cuvette was filled with the corresponding \(\hbox {H}_2\hbox {O}\)/\(\hbox {D}_2\hbox {O}\) solvent or left dry, and sealed with Parafilm. For the time-resolved SANS measurements, a sample was taken out from a solution with 65% \(\hbox {H}_2\hbox {O}\)/35% \(\hbox {D}_2\hbox {O}\) and placed into a cuvette with 100% \(\hbox {D}_2\hbox {O}\). The \(\hbox {D}_2\hbox {O}\) in the cuvette was rapidly exchanged two more times, after which the cuvette was placed in the SANS instrument. The resulting \(\hbox {D}_2\hbox {O}\) solution was estimated to contain 80%–90% \(\hbox {D}_2\hbox {O}\).

The SANS experiments (Penttilä et al. 2020c) were conducted at the instrument D11 of Institut Laue–Langevin (ILL) in Grenoble, France. Data were collected using a neutron wavelength of \(\lambda =6\) Å (\(\varDelta \lambda /\lambda =0.09\)), beam size of \(7\times 10\) mm\(^2\) (width \(\times\) height), and sample-to-detector distances of 1.5 m, 8 m, and 34 m. This allowed covering a total q-range from 0.002 to 0.3 Å\(^{-1}\) in the horizontal plane of the detector, with the magnitude of the scattering vector defined as \(q=4\pi \sin {\theta } / \lambda\) with scattering angle \(2\theta\). In the time-resolved experiments, SANS was measured only using the 1.5-m distance and with exposure times down to 30 s per time point. This setting covered a q-range from 0.05 to 0.3 Å\(^{-1}\) in the horizontal plane of the detector, corresponding roughly to the length scale of 2–12 nm. Transmission of all samples was measured at the 8-m distance and at earliest 1–2 h after starting the time-resolved experiments. The two-dimensional SANS images were corrected for dark current and scattering by an empty cuvette, and normalized to absolute scale using the Large Array Manipulation Program (LAMP) of the ILL.

The two-dimensional SANS patterns were processed using custom-written Python scripts and the pyFAI library (Kieffer et al. 2020). The intensities were azimuthally integrated over 25\(^\circ\)-wide equatorial sectors, and the isotropic scattering contribution (including incoherent scattering) was subtracted at each value of q as described elsewhere (Penttilä et al. 2019). One-dimensional intensities from different sample-to-detector distances were merged and the number of points was decreased by rebinning. The resulting equatorial, anisotropic SANS intensities were fitted using SasView 4.2 software (Doucet et al. 2018) and the freely-available WoodSAS plugin (http://marketplace.sasview.org/).

The WoodSAS model has been tailored for small-angle scattering data from wood samples, and it consists of three terms representing different contributions to the scattering (Penttilä et al. 2019):

$$\begin{aligned} I(q) = A I_{cyl}(q,{\bar{R}},\varDelta R,a,\varDelta a) + B e^{-q^2/(2\sigma ^2)} + Cq^{-\alpha } \end{aligned}$$
(1)

The first term (with scaling factor A) corresponds to the cellulose microfibrils, which are approximated as infinite cylinders in a hexagonal array with paracrystalline distortion (Hashimoto et al. 1994). The cylinder radius has a Gaussian distribution with mean \({\bar{R}}\) and standard deviation \(\varDelta R\). The cylinder centre points are separated by distance a and the paracrystalline distortion is described by \(\varDelta a\). The contribution represented by the second term (with scaling factor B) in SANS data from wood has been linked to the aggregation of microfibrils, and it allows determining the diameter of microfibril bundles as \(2\sqrt{2}/\sigma\) (Penttilä et al. 2020a). The third term (with scaling factor C) corresponds to power-law scattering by large pores and cell lumina (Jakob et al. 1996; Nishiyama et al. 2014). The central nanostructural parameters of the model and the effect of contrast variation are illustrated in Fig. 2.

Fig. 2
figure 2

a Illustration of the parameters of the WoodSAS model (Eq. 1), with the microfibril cross-sections depicted as filled black circles. Water is assumed to penetrate the matrix (white) between the cellulose microfibrils but not the microfibrils themselves (black). b Coherent neutron scattering length density (SLD) for crystalline cellulose (density 1.6 g/cm\(^3\)) and a mixture of \(\hbox {D}_2\hbox {O}\) and \(\hbox {H}_2\hbox {O}\), with the point of contrast match (35% \(\hbox {D}_2\hbox {O}\)/65% \(\hbox {H}_2\hbox {O}\)) indicated by an arrow. Illustrations of the contrast conditions at both extremes and the matching point are shown as insets

Full size image

For an alternative, model-free analysis of the data from the time-resolved experiments, azimuthal intensity profiles were computed from the two-dimensional SANS images and averaged between the two halves of the symmetric image. The azimuthal intensity profiles averaged over radial ranges \(q=0.065\)–0.105 Å\(^{-1}\) (microfibril bundles) and 0.126–0.3 Å\(^{-1}\) (individual microfibrils) were fitted using a Gaussian function and a constant background. Here the peak height, full width at half maximum (FWHM) and the level of the isotropic background were used as fitting parameters.

OD/OH re-exchange with ATR FTIR

Wood sections similar to those used for the SANS experiments were stored in liquid \(\hbox {D}_2\hbox {O}\) for at least 11 weeks, after which they were cut into 8 approximately equal pieces using a razor blade. Each of the 8 pieces (\(4\pm 1\) mg dry mass) was immersed in liquid \(\hbox {H}_2\hbox {O}\) at 23\(^\circ\)C for a duration of 0 min, 20 min, 1 h, 8 h, 24 h, 3 days, 7 days, or 28 days, respectively, after which the samples were dried for 1 h in a vacuum oven (minimum pressure 0.01 mbar) at 60\(^\circ\)C. This drying method was chosen to remove water from the samples rapidly but with minimal effects on their structure. Reference samples corresponding to 0 min in \(\hbox {H}_2\hbox {O}\) were taken directly from \(\hbox {D}_2\hbox {O}\) and dried in the same way. Following the drying, the samples were immediately brought to an Fourier-transform infra-red (FTIR) spectrometer (Spectrum Two, PerkinElmer) equipped with an attenuated total reflection (ATR) crystal, and spectra were collected in the wavenumber range 600–4000 cm\(^{-1}\) with resolution 4 cm\(^{-1}\) and 8 accumulations. FTIR data were measured from both sides of each sample (tangential-longitudinal surface), using constant load to press the sample on the ATR crystal. At all other times, the samples were kept sealed inside of plastic bags to avoid contact with ambient air. The same type of FTIR measurement was done to confirm the deuteration of OH groups in the SANS samples dried from \(\hbox {D}_2\hbox {O}\) (Fig. S2).

The relative amount of OD groups \(X_{OD/(OD+OH)}\) was estimated as the ratio of the spectral contribution of the OD groups to the total contribution of OD and OH groups. The contributions of the OD and OH groups were determined by numerical integration in the wavenumber ranges 2350–2670 cm\(^{-1}\) and 3000–3650 cm\(^{-1}\) (Reishofer and Spirk 2015), respectively, prior to which a linear background was subtracted from each of the two spectral regions (see Fig. 5a in the “Results” section). For visual inspection of the spectra on the complete wavenumber range, a constant value corresponding to the spectral contribution around 1800 cm\(^{-1}\) was subtracted and the absorbance was normalized with the value at 1110 cm\(^{-1}\).

Kinetic models

To analyze kinetics from the SANS data, the time-dependent data was fitted by using one of two exponential models:

$$\begin{aligned} f(t)= & {} c_1(1-e^{-k_1 t}) \end{aligned}$$
(2)
$$\begin{aligned} g(t)= & {} c_2 + c_3 e^{-k_2 t} \end{aligned}$$
(3)

Equation 2 was used to model an exponential increase from 0 to \(c_1\) and Eq. 3 to model an exponential decrease from \(c_2+c_3\) to \(c_2\) (constants \(k_1,k_2,c_1, c_2,c_3>0\)) as a function of time t and with time-constants \(k_1^{-1}\) and \(k_2^{-1}\), respectively. Exponential functions are widely used to model sorption kinetic data and other dynamic processes (Glass et al. 2021), and the physical meaning of the variables depends on the parameter they are used to model. Here, Eq. 3 was applied only in analysing the time-dependent decrease of the isotropic background of the azimuthal intensity profiles, whereas Eq. 2 was used for all other parameters determined by SANS.

For analysing the kinetics of OD/OH re-exchange from ATR FTIR data, the following power law model was used:

$$\begin{aligned} h(t) = c_4 t^{\kappa } \,. \end{aligned}$$
(4)

The function gets the value 0 at \(t=0\) and increases continuously at large t, reaching the value 1 at \(t=c_4^{-1/\kappa }\) (constants \(\kappa ,c_4>0\)).

Fitting of the kinetic models was done using the curve_fit function of the SciPy Python library (Virtanen et al. 2020), taking into account the errors of individual data points when available.

Results

SANS at equilibrium

SANS data from wood samples at different equilibrium conditions were collected in order to detect any indications of irreversibility related to drying. Representative SANS data from selected samples are shown in Fig. 3. No differences were observed between the data from never-dried and dried/rewetted samples in \(\hbox {D}_2\hbox {O}\). This was further confirmed by fitting the data with the WoodSAS model of Eq. 1 (Fig. S3), which yielded almost identical results for the two types of samples (Table 1). In fact, the variation between samples from the same annual ring was even smaller, as can be seen from the fitting results of individual samples in Table S1. Based on this data, SANS could not detect any irreversible effect of drying on the wood cell wall nanostructure.

Fig. 3
figure 3

Examples of equatorial, anisotropic SANS intensities from spruce samples subjected to different conditions. The curves for the samples in \(\hbox {D}_2\hbox {O}\) (blue and orange) overlap almost completely

Full size image
Table 1 Results of fitting the WoodSAS model (Eq. 1) to equatorial, anisotropic SANS intensities from spruce samples subjected to different conditions (means from two or more samples, with error margin equal to standard deviation); see Table S1 for all results
Full size table

The level of the equatorial, anisotropic intensity was lower in samples measured in \(\hbox {H}_2\hbox {O}\) than in \(\hbox {D}_2\hbox {O}\) (Fig. 3), which is due to the lower scattering length density contrast between the crystalline cellulose and \(\hbox {H}_2\hbox {O}\). The nanostructural parameters resulting from fits to samples in \(\hbox {H}_2\hbox {O}\) and \(\hbox {D}_2\hbox {O}\) were similar, without any difference between never-dried and dried/rewetted samples. Only the microfibril diameter was slightly smaller in \(\hbox {D}_2\hbox {O}\) than in \(\hbox {H}_2\hbox {O}\) (Table 1), both in the never-dried and dried/rewetted samples, which could be an effect of the deuteration of surface OH groups in the microfibrils.

The samples dried from \(\hbox {H}_2\hbox {O}\) and \(\hbox {D}_2\hbox {O}\) showed no difference in their equatorial, anisotropic SANS intensities, except that the intenstities of samples dried from \(\hbox {D}_2\hbox {O}\) were systematically higher than those of samples dried from \(\hbox {H}_2\hbox {O}\) (Fig. 3). This difference in the intensity scaling could be explained by residual OD groups remaining after the drying from \(\hbox {D}_2\hbox {O}\), which were also detected by FTIR both before and after the SANS experiments (Fig. S2). Nevertheless, the fitting results (Table 1) indicated no difference in the nanostructural parameters of the samples dried from \(\hbox {H}_2\hbox {O}\) and \(\hbox {D}_2\hbox {O}\). Both followed the previously reported trends of decreasing interfibrillar distance (Penttilä et al. 2019) and microfibril bundle diameter (Penttilä et al. 2020a) as a result of drying.

Time-resolved SANS

In order to follow the exchange of water at the level of cellulose microfibrils and microfibril bundles, time-resolved SANS experiments were conducted immediately after taking a wood sample from a solution with 65% \(\hbox {H}_2\hbox {O}\)/35% \(\hbox {D}_2\hbox {O}\) and immersing it to 100% \(\hbox {D}_2\hbox {O}\). The former condition corresponds to the matching point of crystalline cellulose, at which the contrast between cellulose microfibrils and the surrounding water-accessible matrix is decreased to minimum and the contribution from the microfibrils disappeares from the data (Figs. 2b, 4a). On the other hand, the contrast is maximized in 100% \(\hbox {D}_2\hbox {O}\), leading to a correlation peak from the regular packing distance between individual microfibrils to appear around \(q=0.15\) Å\(^{-1}\). Therefore, the emerging of features originating from the cellulose microfibrils in the SANS patterns provides direct means to quantify the kinetics of water exchange at this particular level of the hierarchical cell wall structure.

Fig. 4
figure 4

Results from time-resolved SANS experiments: a Equatorial SANS intensity from a spruce sample before and after solvent exchange, with the two-dimensional scattering patterns of the contrast match condition and the first (5 min) and last (30 h) time-resolved measurement shown as insets. b Time-dependent change of parameters determined from the SANS data (symbols), fitted with Eq. 2 (solid lines). The equatorial integration sectors used to obtain the one-dimensional data in a and for fitting the WoodSAS model (green) and the radial integration ranges used in the analysis of the azimuthal intensity profiles (purple and orange) are indicated in the lowermost two-dimensional pattern in a. See Fig. S1 for the sample codes in the legend of b and Figs. S4, S5 for more detailed results of the kinetics analysis

Full size image

Similarly to the analysis of the SANS data from samples at equilibrium, the equatorial, anisotropic intensities from the time-resolved experiments were fitted using the WoodSAS model (Eq. 1). However, in this case the power law term and Gaussian term were omitted from the fitting due to the limited q-range and their low contribution at high q. In the results of the fitting (Fig. S4), a significant change with time was observed only in the scaling factor of the microfibril contribution (A in Eq. 1), whereas the other parameters remained constant. The increase in the scaling factor was strongest during the first 30 min of the experiment, which we interpret as a time limit within which most water was exchanged in the interfibrillar spaces. The kinetics of water exchange at the microfibril-level was further analyzed by fitting Eq. 2 to the time-dependence of the scaling factor (Figs. 4b, S4). As no systematic differences were observed between the never-dried and dried/rewetted samples in the analysis, the results can be averaged over all four samples to yield the kinetic parameter \(k_1 = 5.4 \pm 1.2\) h\(^{-1}\) (mean ± standard deviation).

With the aim of investigating the water-exchange kinetics at different hierarchical levels and without any pre-assumed model, time-dependent changes in the azimuthal SANS intensity profiles were analyzed (Fig. S5). This was done by averaging the SANS intensities over two q-ranges, corresponding to length scales of 2 to 5 nm and 6 to 10 nm, and fitting a Gaussian function to the resulting intensity vs. azimuthal angle profile. The time-dependence of the Gaussian peak height was quantified by the kinetic model of Eq. 2 (Figs. 4b, S5), which yielded similar values for \(k_1\) (\(6.0 \pm 1.4\) h\(^{-1}\)) as obtained with the WoodSAS model. A kinetic analysis of the isotropic background below the azimuthal Gaussian peak, using the model of Eq. 3 (Fig. S5), yielded slightly larger values for \(k_2\) (\(6.7 \pm 1.2\) h\(^{-1}\)) than those of \(k_1\). As the isotropic background includes the incoherent scattering, which is sensitive to the ratio of all H and D on the neutron beam path, this difference could be related to a faster exchange of free water in the cell lumina as compared to water at the microfibril-level.

Regardless of the way of analysing the time-resolved SANS data from the water-exchange experiments, no systematic differences were observed due to drying. The large deviation between the kinetics of individual samples is more likely explained by their heterogeneity, including earlywood/latewood proportion, density differences etc. (see Table S2 for sample masses). However, in the azimuthal profile analysis (Fig. S5), the coefficients \(k_1\) and \(k_2\) corresponding to the larger structures (6 to 10 nm) were either larger or the same (within margins of error) in comparison with those corresponding to the smaller structures (2 to 5 nm). As the size of individual cellulose microfibrils lies roughly at the cross-over of these two length scales, this observation could possibly indicate a marginally faster exchange of water around the microfibril bundles than between the individual microfibrils in some of the samples. This difference could not be captured by the WoodSAS model, because the lower limit of the q range of the time-resolved experiments did not allow reliable fitting of all the components of the WoodSAS model. Nevertheless, the overall kinetics analysis of the SANS data, at the level of both the microfibrils and microfibril bundles, pointed at a fast exchange of water during approximately the first 30 min after solvent exchange, with coefficients \(k_1\) and \(k_2\) (Eqs. 2 and 3) in the order of 5–7 h\(^{-1}\), and no observable differences between never-dried and dried/rewetted wood samples.

OD/OH re-exchange experiments

As an approach complementary to the time-resolved SANS experiments, experiments with ATR FTIR were carried out to follow the time-dependent re-exchange of OD groups into OH. This was done by immersing wood samples equilibrated in \(\hbox {D}_2\hbox {O}\) into liquid \(\hbox {H}_2\hbox {O}\) for durations of 20 min, 1 h, 8 h, 24 h, 3 days, 7 days, and 28 days, after which the samples were dried in vacuum oven and FTIR spectra were measured. The complete ATR FTIR spectra (Figs. 5a, S6) showed time-dependent changes mostly in the spectral regions corresponding to the OH and OD group stretching modes around wavenumbers 3300 cm\(^{-1}\) and 2500 cm\(^{-1}\), respectively. Small differences were also observed in the spectral region below 1800 cm\(^{-1}\), especially in the range 850–900 cm\(^{-1}\), and some of these could be related to the OH and OD bending modes (Driemeier et al. 2015). The results were analyzed by integrating the spectral intensities below the OH and OD group stretching bands, and determining the relative amount of OD groups \(X_{OD/(OD+OH)}\) at different times t (Fig. S7). The kinetics were analyzed based on the re-exchanged fraction of the accessible OD groups \(1-X_{OD/(OD+OH)}(t)/X_{OD/(OD+OH)}(0)\) (Fig. 5b), where the accessible OD groups refer to those present in the reference sample dried directly from the \(\hbox {D}_2\hbox {O}\) solution (\(X_{OD/(OD+OH)}(0)\)). This type of analysis was chosen in order to minimize any inaccuracies originating from interaction of the partially deuterated samples with ambient air (Tarmian et al. 2017). The data were fitted with the model of Eq. 4 as presented in Fig. 5b and with more details in Fig. S8.

Fig. 5
figure 5

Results from OD/OH re-exchange experiments with FTIR: a Example ATR FTIR spectra measured from wood samples taken from \(\hbox {D}_2\hbox {O}\) and immersed in liquid \(\hbox {H}_2\hbox {O}\) for a specific time (reference sample taken directly from \(\hbox {D}_2\hbox {O}\)), with the inset showing the contributions from OH and OD groups after linear background subtraction and normalization by the total area under the curves. b Time-dependence of the re-exchanged fraction of accessible OD groups (\(1-X_{OD/(OD+OH)}(t)/X_{OD/(OD+OH)}(0)\)), with the fits of Eq. 4 drawn with solid lines and the inset presenting the data between time points 20 min and 28 days on double logarithmic scale. See Fig. S1 for the sample codes in the legend of b, Fig. S6 for the ATR FTIR spectra of all samples, Fig. S7 for \(X_{OD/(OD+OH)}\) of all samples, and Fig. S8 for more detailed results of the kinetics analysis

Full size image

The kinetics of the re-exchanged fraction of the accessible OD groups (Fig. 5b) showed a fast increase during the first minutes of the immersion in \(\hbox {H}_2\hbox {O}\), which was similar to what was observed with SANS (Fig. 4b). However, the OD/OH re-exchange was not completed during the experiment but continued even after 4 weeks. This was assigned to a slowly exchanging fraction of OD groups that has been reported for various celluloses in the literature (Jeffries 1963; Mann and Marrinan 1956; Hofstetter et al. 2006; Altgen and Rautkari 2020; Thybring et al. 2017). Notably, a small but systematic difference can be seen between the never-dried and dried/rewetted samples, which indicates that the proportion of the slowly replacing OD groups increased by the drying/rewetting procedure. The fitting of a power law model according to Eq. 4 gave the parameters \(c_4=0.861\pm 0.008\) h\(^{-\kappa }\) and \(\kappa =0.0176\pm 0.0005\) for the never-dried samples and \(c_4=0.810\pm 0.004\) h\(^{-\kappa }\) and \(\kappa =0.0197\pm 0.0004\) for the dried/rewetted samples. Based on these results, the rate of exchange described by \(\kappa\) (slope in the double-logarithmic plot, inset in Fig. 5b) was rather similar in both types of samples, but the level reached before the considerable slowing down (approximately the crossing point of y-axis in the double-logarithmic plot, inset in Fig. 5b), described by the pre-factor \(c_4\), was lower in the dried/rewetted samples.

Discussion

Irreversible changes due to drying are a considerable hindrance for the applications of many cellulosic materials. Tighter, irreversible association of microfibrils has been suggested as the primary cause of such “hornification” in pulps (Pönni et al. 2012). Also in native woods, particularly softwoods, drying decreases the distance between cellulose microfibrils, making the aggregates or bundles more compact and resulting in a considerable decrease in the thickness of the entire cell wall (Penttilä et al. 2021; Plaza et al. 2016). In the light of the current SANS results from unmodified spruce wood, however, this change can be reversible, given the presence of liquid water and sufficient time even at ambient conditions. This result is different from the conclusion of Penttilä et al. (2020b), where SANS data obtained after drying wood samples at room temperature and immersion in liquid \(\hbox {D}_2\hbox {O}\) for 5 days indicated 2–3% smaller interfibrillar distance as compared to the never-dried state. The different results might be explained by the shorter time of reimmersion in liquid \(\hbox {D}_2\hbox {O}\) in Penttilä et al. (2020b), which possibly did not allow a full recovery of the structure. It is also noted that the interfibrillar distance obtained for the water-saturated Norway spruce samples in the current study (3.9–4.0 nm, Table 1) is slightly smaller than previously obtained for the same species using SANS and the WoodSAS model (4.2–4.4 nm) (Penttilä et al. 2019, 2020b), which could be due to biological variation between individual trees and types of tissue. More generally, the values are in agreement with the interfibrillar distances of 4.0–4.2 nm reported for different softwoods in the literature (Fernandes et al. 2011; Jakob et al. 1996; Plaza et al. 2016).

One purpose of the time-resolved SANS experiments was to observe any differences in the water-accessibility of different structures among those contributing to the SANS intensities. In the results analysed with the WoodSAS model (Fig. S4), a change with time was observed only in the scaling factor of the microfibril contribution, whereas the other parameters remained constant. This would be expected when water is evenly exchanged in the spaces between individual microfibrils, regardless of the size of the gap separating them. Therefore, the interfibrillar spaces contributing to the SANS intensities did not significantly differ in their water-accessibility. If water in spaces between widely separated fibrils would have exchanged first, the WoodSAS fits should have shown a time-dependent alteration of the interfibrillar distance or its polydispersity.

Furthermore, the time-resolved SANS showed no indications of significantly different exchange rates of water in pores at different levels of the hierarchical structure, such as inside or between microfibril bundles. Such variation in the water-accessibility would be expected to lead to differences in the rate of changes at different q ranges. For instance, if the water in larger domains between aggregates of microfibrils (corresponding to range 6 to 10 nm) would be exchanged faster than water in between individual microfibrils (corresponding to range 2 to 5 nm), a difference in the kinetics of the SANS data corresponding to the two different length scales would be expected. No clear evidence for such behaviour was detected in the data. We therefore conclude that all sites in the water-saturated wood cell wall that are accessible to sufficient amounts of liquid water to create contrast for SANS, are interconnected and have similar accessibility to water molecules. Importantly, this applies also to wood that has been fully dried before immersing back in water.

FTIR experiments with samples subjected to OD/OH re-exchange for different durations were carried out to obtain a complementary view to the accessibility of interfibrillar spaces to water. The re-exchange in liquid \(\hbox {H}_2\hbox {O}\) started with a rapid phase, which was followed by a slower phase still continuing after 4 weeks (Fig. 5b). This behaviour is similar to what has been reported before for OH/OD exchange in various celluloses exposed to liquid or vapour \(\hbox {D}_2\hbox {O}\) (Frilette et al. 1948; Jeffries 1964; Mann and Marrinan 1956). In these studies, it is assumed that the exchange of deuterium or hydrogen between water and the carbohydrates happens almost instantly and in a random manner. Therefore, the rapid phase is typically assigned to the deuteration of the highly accessible, less ordered structural components, which is mainly limited by the diffusion of water. The regions of slower accessibility would then correspond to surface layers of cellulose crystals (Mann and Marrinan 1956), “accessible crystalline regions” (Jeffries 1964), or other regions in the supramolecular structure which the water molecules have difficulties penetrating (Hishikawa et al. 1999). Based on the current results with time-resolved SANS, and assuming that no extensive “amorphous” segments exist along the microfibril (Nishiyama et al. 2003), we can safely attribute the initial rapid phase to the diffusion of water in spaces between the individual cellulose microfibrils. Differences in the sample size and mixing in the time-resolved SANS and FTIR experiments affect the exact rate of diffusion, but in both cases, this phase was over within the first 20–30 min.

The FTIR results also allowed us to recognize a resistant fraction of OD groups in both never-dried and dried/rewetted samples. Previous studies addressing the re-exchange of OD into OH by \(\hbox {H}_2\hbox {O}\), both in liquid and vapour forms, have also identified a fraction of OD groups that is highly resistant to re-exchange (Jeffries 1963; Mann and Marrinan 1956; Hofstetter et al. 2006; Altgen and Rautkari 2020; Thybring et al. 2017). The relative amount of these resistant OD groups is typically only 1–3% of all hydroxyl groups, and it was found to be slightly higher in dried as compared to never-dried spruce samples (Altgen and Rautkari 2020). In our results, this fraction diminished with the time that the samples were immersed in liquid \(\hbox {H}_2\hbox {O}\), but remained still at the end of the 4-week-long experiment series. The analysis with the power-law model (Eq. 4) allows us to estimate the time scale required for a full re-exchange of the resistant OD groups. Assuming that the model is valid throughout the re-exchange process, it would be completed after 7 months in the never-dried samples and 5 years in the dried/rewetted samples. Although these durations are only rough estimates, extrapolated from data gathered on a relatively short time interval at the beginning of the process, the non-negligible values of \(X_{OD/(OD+OH)}\) obtained for samples immersed in \(\hbox {H}_2\hbox {O}\) for 14-15 weeks (Fig. S2) show that the resulting time scale is realistic.

The drying-related changes in the amount of resistant OD groups in the FTIR data clearly showed that drying affects the accessibility of OD groups in the wood material. However, based on the SANS results, these changes are not related to the spaces between microfibrils that contribute to the SANS intensities. An explanation for the different observations could be, in principle, that the drying-related irreversible changes take place outside of the microfibril bundles, for instance in the lignified areas. In this way, they would not contribute to the SANS intensities that mainly originate from the microfibrils and their regular packing in the bundles. However, this scenario is unlikely to be true, because similar resistant OD groups have been observed also in pure celluloses and materials having diverse fibrillar morphologies (Jeffries 1963; Mann and Marrinan 1956; Hofstetter et al. 2006). Therefore, we infer that the differences in OD group accessibility caused by drying should be related to some kind of molecular-level changes on the microfibril surfaces, which do not affect the moisture-dependent opening of microfibril bundles. This could be, for instance, tightening of contact points between adjacent microfibrils or other type of closer association of microfibrils or microfibril segments that are aggregated already in the water-saturated state. We note also that such processes may not necessarily involve crystallization but a reorganization of the non-crystalline polysaccharides, such as previously detected in cellulose films (Hishikawa et al. 1999; Mohan et al. 2012). Nevertheless, these structural features would be present even in fresh, never-dried wood, because the resistant OD groups were observed also in never-dried samples, both in the current work and elsewhere (Altgen and Rautkari 2020; Thybring et al. 2017). Further light on the mechanism could be provided by methods capable of detecting molecular-level order, possibly in combination with molecular simulations. Another approach would be to promote the opening of the microfibril aggregates and exposure of the resistant OD groups by specific chemical or enzymatic treatments.

Conclusions

We showed that SANS is suitable for time-resolved studies of water-accessibility at specific levels of the hierarchical plant cell wall structure. However, SANS was not able to distinguish between never-dried and dried/rewetted wood samples based on the aggregation state of cellulose microfibrils. Time-resolved experiments with SANS and FTIR showed that the diffusion-driven exchange of water in between cellulose microfibrils takes place relatively fast and rather homogeneously. A slowly re-exchanging portion of OD groups was observed with FTIR and its amount increased as a consequence of drying. This observation suggests that understanding the structural origin of the slowly accessible microfibril surfaces could be the key to overcome the challenges related to drying of cellulosic materials.