Introduction

In almost every pulping and papermaking process the flexibility of highly anisotropic cellulose fibres is of high importance. It plays an important role for the quality during the formation of paper where complex flow patterns and interaction between the fibres takes place.

In addition, the flexibility is important during the fractionation of pulps into different lengths, diameters and strengths. Knowledge about this flexibility parameter is thus vital for the papermaking processes.

A beam model of cellulose fibres will be used in this article. The flexibilty (F) of a short part dx of a beam is the reciprocal of the beam cross-section bending stiffness (Pilkey 1994), by definition:

$$ F \, = \, \frac{1}{S} \, = \, \frac{1}{MR} $$
(1)

where S is the stiffness, M the cross-section bending moment, 1/R the curvature of the part dx and R the curvature radius. An in-plane bending of a homogenous, symmetrical and linear elastic cross-section is described by the conventional Bernoulli/Euler beam theory:

$$ F \, = \, \frac{1}{EI} $$
(2)

where E is the modulus of elasticity in the direction of the beam and I the moment of inertia of the beam cross section. The moment of inertia for a hollow cylinder with the outer and inner diameters (Do and Di) is given by:

$$ I \, = \, \frac{\pi }{ 6 4}\left( {{\text{D}}_{\text{o}}^{ 4} - {\text{D}}_{\text{i}}^{ 4} } \right) $$
(3)

Similar for a beam with a rectangular cross section with the width (b) and height (h), the moment of inertia is given by:

$$ I \, = \, \frac{{bh^{3} }}{ 1 2} $$
(4)

The moment of inertia parameter is therefore very sensitive to the geometrical dimensions of the sample. The flexibility of a sample can be calculated from Eq. (1) if the geometrical dimensions and the modulus of elasticity of the sample are known.

When a homogeneous linear elastic beam with a length L and a constant cross-section stiffness (EI) is subjected to a point load (P) on one end while fixed at the other (Fig. 1), the deflection δB is according to the conventional beam theory given by:

$$ \delta_{\text{B}} \, = \, \frac{{PL^{3} }}{{ 3 {\text{EI}}}} $$
(5)
Fig. 1
figure 1

Deflection of a beam subjected to a point load (P) at a distance (L). (A fixed position, B loading position)

Full size image

The conventional beam theory only considers a deflection change in the beam bending curvature which is assumed to be very small (δB ≪ L).

For a slender beam the deflection due to a bending of the beam is dominating. In most structural engineering applications, the conventional theory gives fairly good deflection predictions for a cantilever beam if the ratio between the beam length and the cross-section height is high, approximately greater than 5 for isotropic materials and greater than 10 for an orthotropic material like wood.

Provided that the beam length, force and deflection can be measured, the flexibility can be calculated from Eq. (5). If additionally the cross-section geometry and thereby the moment of inertia can be determined, the modulus of the elasticity can be calculated by Eq. (2).

Literature survey

Forgacs et al. (1958) and Arlov et al. (1958) were among the first to discuss the flexibility of single cellulose fibres and their flow behaviour in shear flow fields. The results were based on qualitative observations of individual cellulose fibres flowing between two cylinders that were rotating in opposite directions. The variation in fibre flexibility was achieved by varying the yields using a sulphite pulp from Douglas fir. The tested samples had an average fibre length of 2 mm and the fluid between the cylinders was a corn syrup with a viscosity of 6 kg/ms (e.g. 6000 times the viscosity of ordinary water).

Four different types of motions were observed by taking pictures with two microscopes:

  1. 1.

    Rigid rotation, the fibres rotate as rigid rods.

  2. 2.

    Springy rotation, starts like a rigid rod but at 45° bends like a leaf spring and flicks back to rigid rotation at 135°.

  3. 3.

    Flexible rotation, the fibre performs an undulation along the fibre from the front to the back until the fibre has rotated 180°. After rotation the fibre is again aligned in the direction of the flow field. This is also called a snake turn or a loop turn.

  4. 4.

    Complex orbit, when the fibre is sufficiently flexible it can undergo a snake turn but never straightens completely in the flow field.

Forgacs et al. (1958) and Arlov et al. (1958) showed that the percentages of fibres in motions types III and IV increased when the yield was decreased, while the flexibility increased with both increased fibre length and beating. The laminar shear flow field between the two cylinders is a well-defined flow field but with limited practical applications. The fluid in the shear flow experiment was a corn syrup mixture, thus the fibre wall was not swollen to the same extent as the fibres are in water suspensions within the pulp or paper mill.

Samuelsson (1963) placed the fibres in a flow channel (0.4 × 6 cm) with a laminar flow of water using a microscope to observe the bending of the fibres. The fibres were placed in a clamp with a sawtooth design and suspended 2 mm into the flow. The fibre stiffness was calculated from the velocity profile, the forces on each segment of the fibre and the deflection of the fibre. The method showed reasonably good agreement when comparing the measured modulus of elasticity with literature data for glass fibres. The flexibilities of two spruce sulphite pulps with kappa numbers of 34 and 43 were measured as 1.25 and 1.43 × 1011 N−1 m−2, respectively. One drawback of the presented method is the difficult estimation of the velocity profile of the flow which leads to difficulties in calculating the drag force which is depending on the shape of the fibre. In spite of all the practical problems flexibility data were presented for wet cellulose fibres.

Mohlin (1975) used a technique to measure a parameter called conformability of single fibres as being a measure of the flexibility. It was performed by placing wet fibres over a single glass fibre with a diameter of 0.06 mm and the distance between the two contact points on the glass plate was measured after drying the fibre. The conformability was calculated as the reciprocal of this distance. The results showed that an increasing yield of the pulping resulted in lower values for the conformability of the fibres. Since the distance between the contact points was of the same magnitude as the length of the fibres, the fibre length could have been a parameter that influenced the results. The method has been further developed for measuring the flexibilities of almost dry or dry fibres (Steadman and Luner (1985); Yan and Li (2008)). Since the fibre dimensions could be measured (Yan and Li 2008) the moment of inertia and the elastic modulus could be calculated. The elastic modulus was varying by a factor of 80, from 0.22 GPa for a refined pulp to 17.17 GPa for an aspen CTMP pulp.

Kerekes and Tam Doo (1985) and Tam Doo and Kerekes (1981) have presented a technique where a fibre is placed in a V-shaped notch of a glass holder. A small 1.5 mm capillary through the holder allows a water flow, creating a hydrodynamic force to bend the fibre which was measured using a microscope. Advantages of this design are that the maximum bending moment was shifted from the support points to the centre of the fibre and that the testing time was reduced to about 2 min. The results showed that the flexibilities for mechanical TMP and SGW pulps were in the range of 0.11–0.38 × 1011 N−1 m−2. Chemical pulps in contrast were more flexible with higher flexibility values in the range 0.85–9.6 × 1011 N−1 m−2. The method is similar to the method that was used by Samuelsson (1963) and the results are in good agreement. They also showed that the flexibility decreased with higher pulp yield but increased with sulphite treatment. The main advantage is that a quantitative value for the flexibility can be obtained but the requirement of a minimum fibre length of 2 mm excludes a number of hardwood pulps. The flow field around the tip of the capillary and the fibre is rather complex and changes with the deflection of the fibre and is not constant along the length which makes it difficult to calculate the drag force on the fibre. It is expected that the method will allow a good relative comparison between different pulps but without calculations of the elastic moduli. A large number of flexibility measurements have been presented using this method (Hattula and Niemi 1988; Paavilainen 1993).

Techniques using digital video systems for measuring the deformation of fibres in flow fields have also been developed (Kuhn et al. 1995; Eckhart et al. 2008, 2009). The results were in good agreement with previous data (Kerekes and Tam Doo 1985) but to our knowledge the principles have not yet been developed into an industrial instrument for measurement of fibre flexibilities.

Tchepel et al. (2006) used a more direct method based on axial loading of cellulose fibres to determine the elastic modulus and confocal laser scanning microscopy to determine the size of single cellulose fibres. The experiments were performed for dry TMP pulp fibres from black spruce refined using 1100 kWh/t and they reported flexibility values between 0.049 × 1011 and 0.083 × 1011 N−1 m−2. These values are slightly lower than the values reported by Tam Doo and Kerekes (1982), in spite of using a dry fibres and a completely different method.

Saketi et al. (2010) measured the flexibility of individual fibres in a microrobotic platform by holding them with two microgrippers while applying a force in the centre of the fibre and calculating the flexibility from the force over deflection data. The fibres were initially wet but after being picked up by the microgrippers they were held at a temperature of 25 °C and a relative humidity of 27%. With this information it is expected that the fibre will dry during the measurement but no data about this was given in the paper. The flexibilities for a bleached pine kraft pulp and a bleached hardwood pulp were reported as 0.094 × 1011 N−1 m−2 and 2.05 × 1011 N−1 m−2, respectively. There are comparable to other data for dry fibres (Yan and Li 2008; Tchepel et al. 2006). One alternative which has been used for dry fibres is to fix them on a support by gluing them with an epoxy resins or other types of super glue (Tchepel et al. 2006; Kompella and Lambros 2002).

Navaranjan et al. (2008) used an atomic force microscope (AFM) to measure the flexibility of earlywood and latewood kraft pine fibres. The fibres were initially wet and placed in a glass holder over a groove with a width of 0.6 mm, the deflection of the fibre was then measured by applying a load on the fibre with a cantilever in the AFM. The average flexibility for the earlywood and latewood fibres was reported as 5.49 × 1011 and 0.73 × 1011 N−1 m−2, respectively. The authors state that the fibres were kept wet above the fibre saturation point during testing but were not immersed in water. Wagner et al. (2016) used contact resonance atomic force microscopy to measure the transverse elastic modulus of three different types of carbon nanomaterials, one of them being cellulose nano fibrils. Cheng and Wang (2008) used an AFM to measure the elastic modulus of dry lyocell fibrils using a three point bending test where the fibrils were positioned on a grooved silica wafer. They recorded tip penetration into the fibril with a diameter of 170 nm and the elastic modulus was calculated as 93 GPa. A similar three point bending method was used by Iwamoto et al. (2009) to determine the elastic modulus of cellulose microfibrils from tunicate. The microfibrils had a dimension of 8 × 20 nm and the results for two different preparation methods,TEMPO-oxidation and acid hydrolysis, were around 145 and 150 GPa, respectively.

This work

The reported flexibilities vary over a wide range depending on the used method, the different origins of the fibres and depending on whether measurements were performed for dry or wet fibres. The data reported by Kerekes and Tam Doo (1985) and Tam Doo and Kerekes (1981, 1982) appear to be the most reliable. However, the force calculations in the flow field appear to be difficult. No method has been introduced which is based on direct measurement of the force that is causing a bending of an individual fibre immersed in water.

When determining the flexibility of single cellulose fibres, three approaches are possible:

  1. A.

    A typical engineering approach would be to measure the flexibility as the combined parameter 1/EI. This requires force and deflection measurements but no measurement of the individual fibre dimensions.

  2. B.

    Determine both the modulus of elasticity E and the moment of inertia I. From a more theoretical position it is interesting to separate these parameters. The first is a typical material constant while the second is a geometrical parameter given by the size and shape of the material. As shown above other data for the modulus of elasticity show that it varies with the type of fibres, type of delignification, amount of beating, etc. This is a truly fundamental issue but also of high engineering relevance.

  3. C.

    Determine the modulus of elasticity from tensile stiffness experiments by measuring the stress and strain curves. For the moment the authors are not aware if such data are available for wet fibres. One advantage using this method is that the calculated stress is proportional to the area of the sample or the square of the fibre dimensions while the moment of inertia is proportional to the fourth power of the fibre dimensions. In this sense it would be easier to measure the modulus of elasticity with tensile experiments than bending experiments.

The main goal of the work presented in this article is to perform direct measurements of the flexibility and modulus of elasticity of single cellulose fibres in water to enable measurements for never dried pulp. AFM is used to measure the force and the displacement which are used to calculate the flexibility of the fibres. Fibres of different origin and treatment are tested. Provided that the cross section of the fibres can be determined with the AFM optical viewing system, it will allow calculation of the modulus of elasticity and how this parameter varies for different pulps. These data will be a starting point for proposing separating schemes for fibres with different flexibility in aqueous solution.

Materials and methods

A MultiMode III AFM with PicoForce extention from Veeco Instruments with a top view optical microscope was used and adopted for the measurements (BioScope II, Veeco Instrument has also been tested and gives comparable results). Individual fibres were mounted in liquid over an edge in the AFM liquid cell where a tipless cantilever was used to bend (deflect) the fibres in a controlled way. The force is detected as cantilever deflection via a laser reflected on the free end of the cantilever into a position sensitive photodiode.

Holding the fibre over an edge in water when performing these deflection measurements is one of the challenges in this project. A number of different methods were investigated such as using microgrippers, grooves covered with a plate and different glues. The microgripper method was not possible to use due to the space limitations in the AFM when manoeuvring the cantilever to different positions along the fibre, even considering usage of larger AFM platforms. The gluing method was abandoned since it was not possible to find glue that worked well in water without the risk for the glue to migrating and spreading along the length of the fibre. Another challenge was to find a cantilever with a suitable geometry (allowing the cantilever to move freely without touching the clamp that is holding the fibres) and a spring constant that allows both the fibre and cantilever to deflect during the measurement. If the spring constant is too weak only the cantilever deflects without bending the fibre. On the other hand, if the spring constant is too stiff only the fibre will bend without deflecting the cantilever. To get a reliable measurement both the cantilever and the fibre needs to be bend. For the wet pulp fibre measurements, a rectangular MLCT-OW cantilever (Bruker Nano Inc, CA) with a length of 200 µm was used. Prior to the fibre bending measurements the cantilever spring constant (k z ) was calibrated in air with the method based on thermal noise and hydrodynamic damping (Sader et al. 1999). The inverse optical lever sensitivity (α 0 ) (Thormann et al. 2009) which is used to convert the detector response into a force signal was determined by measuring force curves between the tipless cantilever and a glass surface in water.

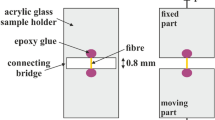
The final method to mount fibres is based on holding the fibre between a thin magnet and a thin steel slab on top of the thin magnet. The magnet was a magnetic tape with a thickness of 0.35 mm (G-0100-1 from Svenska magnetfabriken). The used steel slab was 0.02 mm thick. The magnetic tape was glued to a cover glass placed on the bottom of a petri dish and the fibre was manipulated in water when viewed under a stereo microscope from the solution to the magnetic tape using a pair of tweezers followed by gently placing the steel slab on top of magnet and clamping the fibre. The holder was completely submerged in water and the fibres were covered with water when transferred to the water in the liquid cell in the AFM. The principle for the design and the deflection measurements are shown in Fig. 2 where P 2 is the load on the fibre, L 2 the length of the fibre and δ 2 the deflection of the fibre.

Fig. 2
figure 2

Principle for the deflection measurements in the AFM

Full size image

The fibre was aligned perpendicular to the edge of the magnetic tape and the cantilever load applied perpendicular to the fibre, one experiment is shown in Fig. 3, the distance L 2 is measured from the optical images.

Fig. 3
figure 3

Illustrative optical image as an example of a fibre bending experiment

Full size image

Flexibility calculations

The bending of the fibre has been calculated as bending of a homogenous beam from a point load as shown in Fig. 2. The load (P 1 ) at the end of the magnetic tape for a given load (P 2 ) can be calculated with Eq. (6). Together with the measured deflection (δ 2 ) the flexibility (F) is calculated from Eq. (7).

$$ P_{ 1} \, = {\text{ P}}_{ 2} \left[ {\frac{{\left( {L_{1} + L_{2} } \right)^{3} }}{{L_{1}^{3} }}{ - }\frac{{\left( {L_{1} + L_{2} } \right)^{2} }}{{2L_{1}^{3} }}\left( {3L_{2} { - }\frac{{{\text{L}}_{ 2}^{3} }}{{\left( {L_{1} + L_{2} } \right)^{2} }}} \right)} \right] $$
(6)
$$ F \, = \, \frac{ 1}{\text{EI}} \, = \, \delta_{ 2} \left[ {\frac{{P_{2} \left( {L_{1} + L_{2} } \right)^{3} }}{3}{ - }\frac{{{\text{P}}_{ 1} L_{1}^{3} }}{ 3}{ - }\frac{{{\text{P}}_{ 1} L_{1}^{2} L_{2} }}{ 2}} \right]^{ - 1} $$
(7)

Deflection due to shear stresse of the beam was shown to be less than 3% of the total deflection of the fibre and was not included. Also deflection due to the weight of the beam was shown to be of no importance.

The distance (L 1 ) in Fig. 2 was very small for all measurements and therefore set to zero. For the case where L 1  = 0 the flexibility is directly calculated from Eq. (5):

$$ F \, = \, \frac{1}{\text{EI}} \, = \, \frac{{3\delta_{2} }}{{{\text{P}}_{2} L_{2}^{3} }} $$
(8)

Typically, the load was in the order of nN and the fibre deflection varied between 11 and 800 nm depending on the cantilever spring constant and the flexibility of the fibre.

Indentation experiments on a fibre immersed in water and placed on a solid glass substrate were also performed with the AFM and a cantilever having a tip with a radius of about 10 nm. This indentation was assumed linear and was subtracted from the measured deflection in Eq. (8) before the calculation of the flexibility. For most of the fibres this influence on the result was only marginal but for the experiments with small deflections it was relevant for the obtained results. The indentation of single cellulose fibres is complex and depends on many parameters for the fibres and the method can be seen as a first estimation to account for this.

The software used to evaluate the force data, AFM Force IT v2.6, ForceIT (Sweden) has built in functions for calculating the slope (α) of the raw data when the cantilever and sample are moving together e.g. the invers optical lever sensitivity (α 0 ) when pressed towards a hard surface. By using the spring constant (k z ), slope (α) and the inverse optical lever sensitivity (α 0 ) the ratio between P 2 and δ 2 can be obtained using the following equation:

$$ \frac{{dP_{2} }}{{d\delta_{2} }} \, = \, \frac{{{\text{k}}_{\text{z}} \alpha_{0} }}{{\alpha - \alpha_{0} }} $$
(9)

By using Eq. (9) the flexibility can be calculated without knowing the individual values of P 2 and δ 2 . Using the ratio from Eq. (9) the flexibility is obtained by a linear fit over a large set of data to improve the precision of the calculated flexibility. Additionally, when measuring forces in liquid in some cases long range repulsive forces can be present which makes it hard to determine the position of contact and therefore introduce an uncertainty in the δ 2 value. By using the ratio in Eq. (9) a better signal to noise ratio for the measurements can be achieved. However, values for δ 2 can be calculated for a given value of P 2 , which has been done for illustrative purpose in Table 1 in the result section.

Table 1 Flexibilities and moduli of elasticity for the investigated pulps
Full size table

Materials studied

The following 2 pulps were evaluated in this article:

  • Bleached softwood (60% spruce, 40% pine) kraft pulp with a kappa number of 1.2 from the Södra Cell plant at Mörrum, Sweden (BSW).

  • Unbleached TMP pulp (100% spruce) from the final refiner using about 2000 kWh/t from the Stora Enso plant at Hyltebruk, Sweden (TMP).

The pulps were taken out from the process lines as a liquid solution and diluted to a 2–8% dry matter content and then kept in a cold storage at 7 °C. Before being used for the measurements the samples were further diluted to allow an easy handling of individual cellulose fibres. Four fibres were analysed from each pulp. The fibre outer and inner diameter that gives the wall thicknesses and the lengths (L 1 and L 2 ) were measured by the optical microscope (using a 10× lens) connected to the AFM.

Calculations of moment of inertia

Figure 4 shows one example of the variation found for a softwood pulp. The variation in fibre structure is large but in this article the moment of inertia was calculated assuming a fibre geometry with an elliptical cross section and an approximately constant wall thickness having equal thickness in the vertical and horizontal directions. The ratio between the major and minor axes for the larger ellipse is assumed to be 2, the principle is shown in Fig. 5.

Fig. 4
figure 4

SEM picture of a cross-section of polymer embedded softwood pulp fibres

Full size image
Fig. 5
figure 5

Elliptical fibre structure model with a constant wall thickness

Full size image

With these assumptions the wall thickness (t) and the moment of inertia is given by:

$$ t = \frac{{D_{o} - D_{i} }}{2} $$
(10)
$$ I \, = \, \frac{{\pi \, D_{o}^{4} }}{512} \, \left( {1 - \left( {1 - \frac{2t}{{D_{o} }}} \right)\left( {1 - \frac{4t}{{D_{o} }}} \right)^{3} } \right) \, $$
(11)

where D o is the total width of the fibre and D i the width of the lumen. The moment of inertia from Eq. (11) was used to calculate the modulus of elasticity from the flexibility data.

Validation of method

The used method was validated by performing measurements on glass fibre rods which were manually drawn in a glass workshop from standard borosilicate laboratory glass similar to Pyrex. The used rods had a circular cross section with a diameter of 41 μm. The deflection of the glass fibre was measured in air, not in water. The modulus of elasticity was calculated from the deflection measurements and the calculated moment of inertia. The literature data for the modulus of elasticity for this material is 64 GPa (Corning 2017).

For the measurements of the elasticity of glass rods stiffer cantilevers (HQ:NSC35/tipless/Cr–Au, MikroMasch, CA) were used. The modulus of elasticity for the glass rod measured at the distances 758 and 882 µm were calculated as 70 and 62 GPa. This must be considered in good agreement with the literature value of 64 GPa.

Figure 6 shows a typical AFM bending measurements on pulp fibres. Figure 6a shows the raw data of the measurements that are transformed by an algorithm into force versus separation (e.g. force curve). The used algorithm is well described by Senden (2001) using the optical lever sensitivity (α 0 ) and the spring constant. Typically for elasticity calculations a value for indentation and the corresponding force is picked from the final force curve and used for the calculation of the flexibility. In contrast, by using Eq. (9) the transformation into force versus separation is not needed, e.g. linear fit is done over the linear part of the curve during the bending of the fibre. The deviation from zero in force before contact which is visible in the figures is due to an optical interference and does not affect the contact measurement during a bending of the fibre.

Fig. 6
figure 6

a Raw data from the AFM fibre bending measurement showing the cantilever deflection versus sample stage height position (Z). By using the slope in hard contact (α 0 ), when the cantilever deflects the same amount as the sample motion, the raw data is transformed into force versus separation curve as presents for the same data in b where negative separation corresponds to bending of the pulp fibre. Figure 6 shows a typical AFM bending measurements on pulp fibres

Full size image

Results

Cellulose fibres

Four fibres from each pulp were measured and deflection data were recorded at different positions on each fibre. The results for the different fibres and the different positions are shown in Table 1.

The flexibilities for the BSW fibres are in the range of 4–38 × 1012 N−1 m−2 while the flexibilities for the TMP fibres are about one order of magnitude lower. This can be reasonable since the TMP process does not involve chemical treatment at high temperatures which can be assumed to soften the fibres due to the removal of lignin. The ratio of fibre length to half the width was for most fibres tested greater than 10, suggesting that the contribution from shear deformation to total deflection was small, making it reasonable to neglect the shear deformation in the test result evaluation. For two out of 16 measured data the deflection did not increase with increased length for the same fibre and there is no other than experimental uncertainty to explain this result. For a constant moment of inertia, the deflection should according to Eq. (5) be proportional to the power of 3 of the length and this correlation is not evident in the data. There can be several reasons for this explained by the difference made in the derivation of Eq. (5) and the reality that the cellulose fibres do not have a constant elliptical cross section along the length, they can twist along the length and have deformations, kinks, at some positions due to mechanical treatment.

The results can be compared with the data from Kerekes and Tam Doo (1985) and Tam Doo and Kerekes (1982). Their results for kraft pulp flexibilities were in the range of 0.085–0.96 × 1012 N−1 m−2 which is one to two orders of magnitude lower than our data for the BSW fibres. It is also interesting to compare with the AFM data reported by Navaranjan et al. (2008), showing that these data are also one to two orders of magnitude smaller. Navaranjan et al. (2008) state that the fibres were kept wet during the measurements but they were clearly not immersed in water. The results for close to dry fibres from Yan and Li (2008) for the kraft pulp fibres are close to the data obtained in the present article.

Discussion

The reported flexibilities in this article are higher and consequently the modulus of elasticity lower than most of the previous reported data for cellulose fibres. It should be pointed out that a direct method using an AFM was used and that the measurements were performed using wet and never dried fibres. The method has been validated with good accuracy by measuring the modulus of elasticity of a glass rod with similar size.

The measured flexibility is much larger than previously published results (Kerekes and Tam Doo 1985; Tam Doo and Kerekes 1982; Navaranjan et al. 2008) and reasons for the differences could be due to the different measurement methods used and the different pulp treatments. If the lumen in the fibre is collapsed the moment of inertia at this point will be lower and the bending of the fibre will be more easy. Our never dried pulp fibres were taken directly from the industrial process lines and were not produced in the laboratory as it was the case for the data presented by Kerekes and Tam Doo (1985) and Tam Doo and Kerekes (1981, 1982). Most probably the pulping process has been modified since the results were published in the 1980s by Kerekes and Tam Doo, resulting in a cooking down to lower kappa numbers and thus more flexible fibres. Also our method is based on measuring on the final 200–500 μm of the fibre which can differ from the average over the total length of the fibre.

The flexibility varies with the dimensions (diameter and lumen size) of the fibres. The effect of the dimensions of the fibres is eliminated by calculating the modulus of elasticity from Eq. (2) using Eq. (11) for the moment of inertia. These results are also shown in Table 1.

For BSW the modulus of elasticity ranges from 1 to 12 MPa and for TMP the data are about one order of magnitude larger. These data are very low and comparable to a soft rubber band. The modulus of elasticity is not constant but shows some variation for the two pulps. This is not surprising considering that cellulose fibres can have a varying cross section and have structural changes along the length of the fibre. The flexibility is not depending on Do and Di but a variation will change the moment of inertia and thus the modulus of elasticity. The error of the diameter measurements is estimated to be ±5% and this will result in ±20% in the calculated modulus of elasticity.

No comparable data are available for wet fibres but Ganser et al. (2014) presented nanoindentation data for the hardness and reduced modulus for pulp fibres at varying humidities and also immersed in water. The hardness and the reduced modulus decreased with increasing humidity and when the fibres were immersed in water the reduced modulus was reduced by a factor of 100 compared to a relative humidity of 5%. This supports our results that the modulus of elasticity for fibres immersed in water is much lower than the corresponding value for dry fibres. For dry fibres Yan and Li (2008) report data that are at least one order of magnitude larger. For dry wood a value of 10 GPa is normally reported and for moist cellulose Salmén (2009) gives a value for the longitudinal modulus of elasticity of 134 GPa and only 40 MPa for moist hemicellulose. Our values are lower than the data for cellulose but in the range of the data for hemicellulose.

Conclusions

In this article we report flexibility and modulus of elasticity data for two types of wet never dried cellulose fibres using a direct force–displacement method with an AFM. To our knowledge this is the first data reported for wet never dried fibres immersed in water. The flexibilities for the BSW fibres are in the range of 4–38 × 1012 N−1 m−2 while the flexibilities for the TMP fibres are about one order of magnitude lower. The modulus of elasticity was calculated by using the measured size of the fibres and a model for the moment of inertia. For BSW the modulus of elasticity ranges from 1 to 12 MPa and for TMP the data ranges from 15 to 190 MPa. These data are lower than most other data and comparable to a soft rubber band or a cooked spaghetti. Reasons for the difference can be that our measurements were performed with fibres immersed in water, while other groups have used indirect methods and pulp fibres with different treatments. The measured data are of high importance when describing flow phenomena and separation of fibres in technical applications.