Invariant manifolds near $L_1$ and $L_2$ in the quasi-bicircular problem

Abstract

The quasi-bicircular problem (QBCP) is a periodic time-dependent perturbation of the Earth–Moon restricted three-body problem (RTBP) that accounts for the effect of the Sun. It is based on using a periodic solution of the Earth–Moon–Sun three-body problem to write the equations of motion of the infinitesimal particle. The paper focuses on the dynamics near the $L_1$ and $L_2$ points of the Earth–Moon system in the QBCP. By means of a periodic time-dependent reduction to the center manifold, we show the existence of two families of quasi-periodic Lyapunov orbits around $L_1$ (resp. $L_2$) with two basic frequencies. The first of these two families is contained in the Earth–Moon plane and undergoes an out-of-plane (quasi-periodic) pitchfork bifurcation giving rise to a family of quasi-periodic Halo orbits. This analysis is complemented with the continuation of families of 2D tori. In particular, the planar and vertical Lyapunov families are continued, and their stability analyzed. Finally, examples of invariant manifolds associated with invariant 2D tori around the $L_2$ that pass close to the Earth are shown. This phenomenon is not observed in the RTBP and opens the room to direct transfers from the Earth to the Earth–Moon $L_2$ region.

1 Introduction

The comprehension of the natural dynamics of a spacecraft in the Earth–Moon system is key to develop mission design. Researchers from different areas have contributed to push the boundaries of common knowledge, and dynamical systems theory has been proved to be a powerful tool to understand the relevant factors that determine the motion of a probe under the gravitational attraction of Earth (E) and Moon (M). This is usually fulfilled by using simplified models.

The restricted three-body problem (RTBP) is one of the simplest, well-known and vastly used model to describe the motion of a test particle in the Earth–Moon system (see, for instance, Szebehely 1967; Broucke 1968). In this model, the Earth and the Moon are assumed to move along circular orbits about their common barycenter. By using suitable units and frame, the motion of the particle is described by an autonomous three-degrees-of-freedom Hamiltonian system. The RTBP, even though extremely useful, only takes into account the gravitational pull of the Earth and the Moon. The next step to a more complete model (but still simple) is to include the direct effect of the Sun on the spacecraft. This can be done in a number of ways. Perhaps, the simplest one is the bicircular problem (BCP) [see also Scheeres (1998) for an alternative approach and Lian (2013) for a discussion on high-fidelity models]. The BCP completes the RTBP by considering also the Sun (S), moving together with the E-M barycenter in a circular orbit about the (E+M)-S center of masses. Written down with the same units and coordinates as the RTBP, the model is a periodic time-dependent Hamiltonian system. In fact, the effect of Sun’s gravity can be regarded as a periodic perturbation to the RTBP. This perturbative effect is strong enough to produce relevant changes on several dynamical aspects of the RTBP.

The BCP, though, only takes into account the direct effect of the Sun, i.e., the Earth and the Moon do not feel the presence of the Sun. The model is, therefore, not coherent in the sense that the motion of Earth, Moon and Sun does not verify Newton’s laws.

The quasi-bicircular problem (QBCP) is a coherent version of the BCP, meaning that it is designed to remove the lack of coherence by considering the Earth, the Moon and the Sun to move in a trajectory of the three-body problem.

Both, the BCP and the QBCP can be regarded as periodic perturbations of the RTBP (notice that the period of the vectorfields of the BCP and the QBCP is the same one). To perturb periodically a Hamiltonian system is to, informally speaking, periodically shake the phase space. For instance, due to the non-autonomous character of the vectorfield, the Lagrangian points are no longer equilibria. One can use the implicit function theorem to show that they are replaced by periodic orbits with the same period as the perturbation. The same is true, but much more complicated, for periodic orbits and invariant tori (see Jorba and Villanueva 1997). Those objects, generically, gain a frequency (the one of the perturbation). Therefore, when the perturbing effect is included (for instance, considering the BCP or the QBCP), each invariant object of the RTBP (equilibria, periodic orbits, invariant tori...) is replaced by a higher dimension object. Usually, these replacements are called dynamical equivalents.

The goal of this paper is to complete previous studies on the effect of Sun’s gravity on the dynamics of a test particle near the $L_1$ and $L_2$ Earth–Moon collinear points. Those previous works use the BCP as a model. In Jorba et al. (2020), the dynamics near $L_1$ is analyzed by means of the reduction to the center manifold. In Rosales et al. (2021a), the dynamics near $L_2$ is analyzed by computing the dynamical equivalents of the Lyapunov and Halo orbits. In Rosales et al. (2021b), it is demonstrated that taking into account Sun’s gravity allows for direct transfer orbits from the Earth to the translunar point (this, as far as we know, is not possible to be done ignoring Sun’s gravity). This paper carries out the same analysis as in Jorba et al. (2020) and Rosales et al. (2021a, 2021b) but for the case of the QBCP. Here, we also use the center manifold approach to study $L_2$ as the QBCP has a similar qualitative behavior to the RTBP (while the BCP has not). Notice that this behavior is also observed in the high-fidelity model used in Lian (2013). The center manifold of $L_2$ in the QBCP has also been analyzed in Le Bihan et al. (2017b) by means of the parameterization method. And in Andreu (1998, 2002), using the same approach as in this work: A normal form approach based on the Lie transformation method. However, the normal form constructed in the present paper is slightly different, allowing a different representation and capturing the qualitative behavior shown in Lian (2013). Moreover, by computing the families of dynamical equivalents of the Lyapunov and Halo orbits, we have also provided numerical evidence of a conjecture appearing in Andreu (1998).

This paper is structured as follows: The remaining subsections of this introduction describe more precisely the models and discuss some known facts. In Sect. 2, we provide an insight on the dynamics in the center manifolds related to the (dynamical equivalents of the) collinear points $L_1$ and $L_2$. In Sect. 3, we describe the dynamical equivalents of the Lyapunov and Halo orbits in the QBCP. In Sect. 4, we compute one-maneuver transfers from Halo invariant tori related to the translunar point to the Earth. Finally, in Sect. 5 we provide the conclusions of the work.

1.1 The restricted three-body problem

The restricted three-body problem is a model that describes the dynamics of a massless particle under the influence of two massive bodies called the primaries. This model has been extensively studied, although a lot of questions still remain unanswered. Besides its simplicity, it has been used to plan space missions using as primaries the Sun and the Earth (for example, the missions ISEE-C, SOHO, Gaia, DSCOVR, or JWST), or the Earth and the Moon (for example, the missions Chang’e 5-T1 or Queqiao). Hence, it has both academic and practical interest.

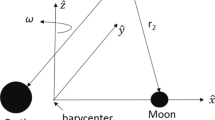
This model assumes that the two primaries orbit in circular motion around their common barycenter following the Newton’s law and that the third body does not influence the motion of the other two bodies. It is convenient to use a rotating frame, with an angular rate equal to the orbital angular rate of the primaries, and scale the time such that the period equals to $2\pi$. This way, the two primaries are fixed on the x-axis. Moreover, it is convenient to chose the unit of distance equal to the constant distance between the two primaries. Finally, the unit of mass is chosen such that the gravitational constant is 1, and then, in these units, the total mass of the system is also 1. Let us denote by $\mu$ the mass of the smallest primary. Then, the primary of mass $1-\mu$ (resp. $\mu$) is at $x=\mu$ (resp. $x=\mu -1$). Hence, the model is fully characterized by the value of $\mu$. Some approximate typical parameters for different systems are listed in Table 1. For the sake of simplicity, from now on we focus discussion in the Earth–Moon system.

Table 1 Some $\mu$ parameters from different systems

Note that this reference frame, often referred to as a synodic reference frame, is not inertial. Details on the construction of the model can be found in Szebehely (1967). In the synodic frame, the dynamics of the RTBP can be expressed in the Hamiltonian formalism,

$$\begin{aligned} H_\textrm{RTBP} = \dfrac{1}{2}(P^{2}_X+P^{2}_Y+P^{2}_Z) + YP_X - XP_Y - \dfrac{1-\mu }{R_{PE}} - \dfrac{\mu }{R_{PM}}. \end{aligned}$$

(1)

Here, $R^{2}_{PE} = (X-\mu )^2 + Y^2 + Z^2$ is the distance of the particle P to the Earth and $R^{2}_{PM} = (X-\mu +1)^2 + Y^2 + Z^2$ is the distance of P to the Moon. Defining the momenta $P_X = {\dot{X}} - Y$, $P_Y = {\dot{Y}} + X$ and $P_Z = {\dot{Z}}$,

In the synodic reference frame, it is well known that the RTBP has five equilibrium points, three of them on the horizontal axis (usually called collinear or $L_{1,2,3}$) and two of them forming equilateral triangles with the primaries (usually called triangular, equilateral or $L_{4,5}$), see Fig. 1. In this paper, we focus on the neighborhood of $L_{1,2}$. In this line, Jorba and Masdemont (1999) studies the dynamics around the collinear Lagrange points in the RTBP. One of the results of this paper is a qualitative description of the stable motions around the Earth–Moon $L_2$ Lagrange point. This is accomplished by means of a reduction to the center manifold around the Earth–Moon $L_2$ point and by generating Poincaré sections for different energy levels. These results were expanded in Gómez and Mondelo (2001) providing a comprehensive description of the dynamics around all the collinear points in the Earth–Moon system. Note that these results do not account for other effects such as the eccentricity of the Moon or the gravitational influence of the Sun. None of these effects are negligible. The following sections describe models that account for the effect of the Sun’s gravity.

1.2 The bicircular problem

The Earth–Moon BCP is a model that describes the motion of a massless particle (P) under the influence of the Earth, the Moon, and the Sun. The Earth and the Moon are defined as the primaries. The dynamics of the Earth, Moon and Sun is simplified considering that the three bodies move in the same plane. Also, it is assumed that the Earth and the Moon follow circular orbits around their barycenter (B) and that B is orbiting around the S-E/M barycenter. Note that this model is not coherent, in the sense that the motion of the three massive bodies is not described by the Newton’s equations.

As in the RTBP, it is standard to take synodic coordinates with respect to the Earth–Moon center, with the origin centered at their respective center of mass. Units of mass, length and time are taken such that the sum of the primaries masses (Earth and Moon), the gravitational constant, and the period of motion of the primaries are 1, 1 and $2\pi$, respectively. Again, the parameter $\mu$ (resp. $1-\mu$) is the normalized mass of the Moon (resp. Earth), and it is located at $(\mu -1, 0,0 )$ (resp. $(\mu , 0,0 )$), the parameters $m_S$, and $a_S$ are the mass of the Sun and its distance to the Earth–Moon barycenter, respectively. The frequency of the Sun around the Earth–Moon barycenter is $\omega _s$, and $\vartheta = \omega _st$, $(X_S,Y_S) = (a_S\cos \vartheta ,-a_S\sin \vartheta )$ is the Sun position vector, $R^{2}_{PE} = (X-\mu )^2 + Y^2 + Z^2$ is the distance of the particle P to the Earth, $R^{2}_{PM} = (X-\mu +1)^2 + Y^2 + Z^2$ is the distance of P to the Moon, and $R^{2}_{PS} = (X-X_S)^2 + (Y-Y_S)^2 + Z^2$ is the distance of P to the Sun. The values of the parameters are shown in Table 2.

Fig. 1

Sketch of the bicircular problem. The points $L_{1,...,5}$ are the Lagrangian (equilibrium) points of the Earth–Moon RTBP

Table 2 Parameters of the BCP

Note that in this reference system the Sun moves around the origin in a circular motion (see Fig. 1). A derivation of these equations of motion can be found in Gómez et al. (2001). Earlier formulations of the BCP can be found in Huang (1960) and Cronin et al. (1964).

Defining the momenta $P_X = {\dot{X}} - Y$, $P_Y = {\dot{Y}} + X$ and $P_Z = {\dot{Z}}$, the dynamics of the BCP can be expressed in Hamiltonian form,

$$\begin{aligned} H_\textrm{BCP}= & {} \dfrac{1}{2}(P^{2}_X+P^{2}_Y+P^{2}_Z) + YP_X - XP_Y - \dfrac{1-\mu }{R_{PE}} - \dfrac{\mu }{R_{PM}} \\{} & {} - \dfrac{m_S}{R_{PS}} - \dfrac{m_S}{a^{2}_S}(Y\sin \vartheta - X\cos \vartheta ). \end{aligned}$$

This Hamiltonian can be expressed as a time-dependent perturbation of the RTBP,

$$\begin{aligned} H_\textrm{BCP} = H_\textrm{RTBP} + H_{S} \end{aligned}$$

where $H_\textrm{RTBP}$ is the Hamiltonian of the RTBP, see Eq. (1), and

$$\begin{aligned} H_{S} = - \dfrac{m_S}{R_{PS}} - \dfrac{m_S}{a^{2}_S}(Y\sin \vartheta - X\cos \vartheta ) \end{aligned}$$

is the perturbation due to the Sun. Let us define

$$\begin{aligned} H^{\varepsilon } = H_\textrm{RTBP} + \varepsilon H_{S} \end{aligned}$$

(2)

Note that $H^{\varepsilon =0} = H_\textrm{RTBP}$, and $H^{\varepsilon =1} = H_\textrm{BCP}$. When $\varepsilon =0$, the Lagrange points ($L_i$, $i=1,...,5$) are equilibrium points of the system (2). When $\varepsilon >0$ and small enough, the implicit function theorem (Lynn 1990) implies that, under generic non-resonant conditions, these equilibrium points become periodic orbits with the same period as the perturbation (in this case, $T_s = 2\pi /\omega _s$).

Remark 1

The frequency $\omega _s$ is the mean angular velocity of the Sun written in the Earth–Moon RTBP units. Notice from Table 2 that it is a little bit smaller than 1; therefore, the period $T_s$ of the vectorfield (for both the BCP and QBCP) is about 30 days.

1.2.1 Known facts on the BCP

The dynamics near the collinear points of the BCP has been analyzed in a number of papers; the direct effect of Sun’s gravity has shown to have a remarkable dynamical impact on the motion of a probe in the Earth–Moon system. Hereafter, we provide a review of results that will help understand the rest of this work.

The motion around $L_1$ in the BCP is analyzed in Jorba et al. (2020). There, the authors provide a description of the center manifold of $L_1$. In particular, it is shown that the bifurcation that leads to the creation of the Halo orbits in the RTBP has a counterpart in the BCP: the horizontal family of Lyapunov of invariant tori undergoes a 1:1 resonance and bifurcate producing a Halo family of invariant tori.

When it comes to $L_2$, in Jorba-Cuscó et al. (2018) it is shown that there is no dynamical equivalent of $L_2$ in the BCP. Indeed, the dynamical equivalent of $L_2$ merges with a 1:2 resonant horizontal Lyapunov orbit. However, at some distance of $L_2$ the model displays common features with the RTBP. In Rosales et al. (2021a), the counterparts of Lyapunov and Halo families (in this case, families of 2-dimensional invariant tori) are described. Particularly, it focus on Halo-like orbits: Two different families, labeled as Type I and Type II, are analyzed in more detail. Type I is the family that plays the role of the classical Halo family. Type II is a family of quasi-Halo orbits which is in 1:2 resonance with the Sun. Due to this resonance, this quasi-Halo family persists as a family of two dimensional tori in the BCP, and it is connected with some (Lyapunov type) horizontal families. In Rosales et al. (2021b), some invariant tori of Type I and Type II Halo families are used to produce direct transfers from the Earth. This kind of transfers has not been found in the RTBP.

The motion near $L_3$ in the BCP is described in Jorba and Nicolás (2020). There, invariant manifolds of invariant tori near $L_3$ are shown to organize the transport of some meteorites from the Moon (lunar ejecta) to the Earth. It is remarkable that these results are also valid for a high-fidelity model. These manifolds also allow to enter/exit the Earth–Moon system and can be used to capture some near-Earth asteroids (Jorba and Nicolás 2021).

The motion around the triangular points ($L_4$ and $L_5$) in the BCP was firstly described in Simó et al. (1995). There the authors show that the dynamical equivalents of the triangular points are three periodic orbits: One of them mildly unstable and the remaining two, stable. These periodic orbits are consequences of a broken pitchfork bifurcation. The lack of symmetry that leads to the pitchfork breaking comes from higher-order terms of Sun’s gravitational potential (see Jorba-Cuscó et al. 2018). In Jorba (2000) and Castellà and Jorba (2000), it is shown that, despite the presence of an unstable periodic orbits, there exist out-of-plane regions of effective stability near $L_4$ and $L_5$.

1.3 The quasi-bicircular problem

The quasi-bicircular problem (QBCP) is also time-periodic perturbation of the RTBP that accounts for the effect of the Sun’s gravity. The difference with the BCP is how the motion of the primaries is modeled. Contrary to the case of the BCP, in the QBCP the motion of the primaries is coherent; this is, their motion follows Newton’s laws and it is a solution of the three-body problem for the Sun–Earth–Moon case. To have a simple model, the chosen solution is the simplest periodic solution close to the true motion of Earth, Moon and Sun.

This model was first introduced by C. Simó (see Andreu 1998), and the reader is referred there for a detailed construction of the model (see also Gabern and Jorba 2001). In this section, we provide an overview of the basic steps to construct the model. The first step is to compute a quasi-bicircular solution that models the motion of the Sun, the Earth, and the Moon under each other’s gravitational influence. This is accomplished by expressing the three-body problem in the Jacobi formulation. Then, an approximation to the Jacobi decomposition of the three-body problem is obtained as Fourier series, solving for the coefficients. The details are in Andreu (1998).

With this solution, the origin of the (inertial) reference frame is translated from the center of masses of the Sun, Earth, and Moon to the Earth–Moon barycenter. Then, the reference frame is rotated such that the x-axis contains both the Earth and the Moon. A third change is a time-dependent transformation that keeps the Earth and the Moon fixed on the x-axis. This defines a pulsating reference frame with period equal to one revolution of the Earth and the Moon around their common barycenter.

Also, the unit of distance is scaled such that the distance between the Earth and the Moon is equal to one, the time is scaled such that one revolution of the pulsating reference frame is equal to $2\pi$, and the unit of mass is scaled such that $m_E+m_M = 1$, where $m_E$ (resp. $m_M$) is the mass of the Earth (resp. Moon). With these transformations, the Earth is located at $(\mu , 0, 0)$ and the Moon at $(1-\mu , 0, 0)$. These are the same scalings and transformations done in the RTBP and the BCP.

With this, the Hamiltonian of the system is:

$$\begin{aligned} \begin{aligned} H_\textrm{QBCP}&= \frac{1}{2}\alpha _1(P_X^2+P_Y^2+P_Z^2) + \alpha _2(P_XX+P_YY+P_ZZ) + \alpha _3(P_XY-P_YX) \\&\quad + \alpha _4X + \alpha _5Y - \alpha _6\Big (\dfrac{1-\mu }{R_{PE}} - \dfrac{\mu }{R_{PM}} - \dfrac{m_S}{R_{PS}}\Big ) \end{aligned} \end{aligned}$$

(3)

where

• $R^{2}_{PE} = (X-\mu )^2 + Y^2 + Z^2$ is the distance of the particle P to the Earth

• $R^{2}_{PM} = (X-\mu +1)^2 + Y^2 + Z^2$ is the distance of P to the Moon

• $R^{2}_{PS} = (X-\alpha _7)^2 + (Y-\alpha _8)^2 + Z^2$ is the distance of P to the Sun

The coefficients $\alpha _i, i=1,..., 8$ are $2\pi$-periodic real functions of the form:

$$\begin{aligned} \alpha _i(\vartheta ) = a_0^i + \sum _{k\ge 0} a_k^i \cos (k\vartheta ) + \sum _{k\ge 0} b_k^i \sin (k\vartheta ) \end{aligned}$$

(4)

The values for the coefficients $a_k^i, b_k^i$ can be found in Andreu (1998). A property of the coefficients $\alpha _i, i=1,...,8$, is that they are odd functions for $i=1, 3, 4, 7$ and even for the rest. These properties imply that the following symmetry holds:

$$\begin{aligned} H_\textrm{QBCP}(\vartheta , X, Y, Z, P_X, P_Y, P_Z) = H_\textrm{QBCP}(-\vartheta , X, -Y, Z, -P_X, P_Y, -P_Z) \end{aligned}$$

Also, the physical interpretation of these coefficients is:

• $\alpha _1(\vartheta )$, $\alpha _2(\vartheta )$, $\alpha _3(\vartheta )$, and $\alpha _6(\vartheta )$ capture instantaneous distance between the Earth and the Moon

• $\alpha _4(\vartheta )$ and $\alpha _5(\vartheta )$ are the instantaneous Coriolis effect due to the rotating reference frame

• $\alpha _7(\vartheta )$ and $\alpha _8(\vartheta )$ capture the instantaneous position of the Sun within its plane of motion.

The values used in this work are in Table 3.

Table 3 This table shows the specific values of the parameters used in this work

Section 1.3.1 reviews the connection between the collinear libration points in the RTBP, and their dynamical equivalents in the QBCP. These results are known (see, for example, Andreu 1998; Jorba-Cuscó et al. 2018), but due to their relevance it was considered that they deserve their own section in this paper.

1.3.1 Dynamical substitutes of the collinear points

In the QBCP, the collinear points in the RTBP are replaced by small periodic orbits with the same period as the perturbation, $T_s = 2\pi /\omega _s$. These orbits are computed by continuation from the RTBP to the QBCP. The formulation of the problem is defined in Andreu (1998) and reproduced here for completeness. We consider the family of Hamiltonians $H^\varepsilon$, where $\varepsilon \in [0, 1]$ is a parameter:

$$\begin{aligned} H^\varepsilon = H_\textrm{RTBP} + \varepsilon (H_\textrm{QBCP}-H_\textrm{RTBP}), \quad \varepsilon \in [0, 1] \end{aligned}$$

(5)

Fig. 2

Dynamical substitutes of the RTBP collinear points in the QBCP ($L_1$, top row and $L_2$, bottom row). The first column represents in the x-axis the first component of the periodic orbit’s position at $t=0$, and the y-axis its associated value of $\varepsilon \in [0, 1]$. The second column contains the dynamic substitutes in the QBCP (this is, the periodic orbits obtained for $\varepsilon =1$)

Note that in Eq. (5), $H^0 = H_\textrm{RTBP}$, and $H^1 = H_\textrm{QBCP}$. The process is the following: we start the continuation scheme from a collinear equilibrium point ($L_i, i=1, 2$) and $\varepsilon =0$, then the value of $\varepsilon$ is increased until it reaches $\varepsilon =1$ (this is, the QBCP model). For each value of $\varepsilon \in [0, 1]$, there is a $T_s$-periodic orbit. The result of this continuation process is illustrated in the first column of Fig. 2 for the collinear libration points, and the second column shows their dynamic substitutes in the QBCP. The first row corresponds to $L_1$ and the second row to $L_2$.

In all two cases, there is a direct connection between the starting point and the final periodic orbit. We recall that, in the BCP, where $L_2$ is connected with a 1:2 resonant planar Lyapunov orbit (see Jorba-Cuscó et al. 2018). We remark that this does not happen for the QBCP.

Also, in the QBCP there are no changes of stability, and throughout the continuation process the stability type of the periodic orbits is $\text {saddle}\!\times \!\text {center}\!\times \!\text {center}$ for all values of $\varepsilon \in [0, 1]$. For completeness, the initial conditions at $t=0$ and the eigenvalues of the monodromy matrices associated with the dynamical substitutes for the collinear points are listed in Tables 4  and 5, respectively.

Table 4 Initial conditions at $t=0$ of the dynamical substitutes for $L_i, i=1, 2$. ($L_1$, top and $L_2$, bottom)

Table 5 Monodromy matrix eigenvalues $\lambda _{i, j}, i=1,2, j=1, 2, 3$ of the dynamical substitutes for $L_i, i=1, 2$. ($L_1$, top and $L_2$, bottom)

2 Center manifold around the collinear points $L_1$ and $L_2$

In this section, the dynamics in a vicinity of the collinear Earth–Moon $L_i, i=1, 2$ points in the QBCP model are studied by means of a reduction to the center manifold. The center manifold has been computed for the dynamic equivalents of the $L_1$ and $L_2$ collinear points. Recall that, these are the $T_s$-periodic orbits presented in Fig. 2. From now on, we will refer to the dynamic equivalent of $L_1$ as POL1 and $L_2$ as POL2.

The implementation of the reduction to the center manifold follows the algorithm described in Gómez et al. (2001), Andreu (2002) and Jorba et al. (2020), see also Gabern and Jorba (2001). In this algorithm, the Hamiltonian expansion is arranged, order by order, up to a certain degree N. As a summary, this process consists in the following steps:

$N=1$::

An affine time-dependent change of coordinates such that in the new variables the periodic orbit becomes an equilibrium point centered at the origin, plus a scaling to make the unit of distance equal to the distance between the libration point studied and the closest primary. We call this distance $\gamma _i, i=1, 2$, and the values used are listed below:

i	$\gamma _i$
1	0.1509342729900642
2	0.1678327317370704

Notice that the scaling is not a canonical transformation. Therefore, it has to be performed on the vectorfield. This results in a (non-autonomous) Hamiltonian with no linear components.

$N=2$::

A symplectic time-dependent (Floquet) change of coordinates such that in the new variables the second-order components of the (non-autonomous) Hamiltonian obtained in the previous step are in normal form and time-independent. There is a certain freedom in choosing the frequencies corresponding to the elliptic eigenspace of the periodic orbit. See Jorba et al. (2020) for more details. The normal frequencies chosen in each case are:

Case	$\kappa _1$	$\omega _1$	$\omega _2$
POL1	2.93720564115629	2.27316022488810	2.33661946019073
POL2	2.16306748237037	1.79017018257069	1.86386291350378

where in both cases $\kappa _1$ corresponds to the hyperbolic part, and $\omega _1$ and $\omega _2$ to the elliptical parts. Note that, for each case, these normal frequencies are very similar to their associated equilibrium points counterparts in the RTBP. We define for convenience the following vector $\omega = (\kappa _1, i\omega _1, i\omega _2)$.

$N>2$::

An expansion of the Hamiltonian with second-order terms in an autonomous normal form, and other nonlinear terms expanded as a series of homogeneous polynomials. (see Gabern et al. 2004; Jorba et al. 2020 for details on this expansion). A symplectic and time-dependent change of variables to transform the non-autonomous Hamiltonian in an autonomous one up to certain degree N with the hyperbolic and the central part decoupled. The Lie transformation method is used to compute this change.

The last step is done such that the resulting expansion of the Hamiltonian has the elliptic and hyperbolic dynamics decoupled. In other words, that we have a description of the neutral dynamics (this is, the center manifold) around the periodic orbit of choice. Note that for dynamical equivalents of $L_i, i=1, 2$, the center manifold has dimension four. A consequence of removing time dependence of the Hamiltonian is the presence of small divisors during the process. Small divisors do not appear in the center manifold reduction of the RTBP. See Jorba et al. (2020) for a comparison between the radius of convergence of the center manifold with small divisors (removing time dependence) and without small divisors (not removing time dependence).

The coefficients of the Hamiltonian restricted to the central manifold around POL1, and POL2 have been computed up to degree $N=16$. During this process, the following indicators have been calculated:

• The presence of small divisors

• Estimated radius of convergence of the series for different values of $N \le 16$

A proxy to measure the presence of small divisors are the denominators of the form

$$\begin{aligned} \delta _D(j, K^0, K^1) = j\omega _s\sqrt{-1}-\langle \omega , K^1-K^0\rangle , \end{aligned}$$

that appear in the generating functions as defined in the Lie transformation. For the center manifold reduction computation around $L_1$, the smallest value for $\delta _D$ was $\delta _D \approx 0.011$, and for the $L_2$ case, $\delta _D \approx 0.013$.

Let $H = H_2+\cdots +H_N$ be a Hamiltonian approximating the center manifold. The radius of convergence is computed as:

$$\begin{aligned} r_n = \frac{1}{\root n \of {\Vert H_n\Vert _1}} \end{aligned}$$

where $\Vert H_n\Vert _1 = \sum \nolimits _{|k|=n}|a_k|, 3\le n\le N$. The radius of convergence for different values of n for POL1 and POL2 is shown in Table 6. Notice that due to the scaling applied at order 1, the distance from the origin of the center manifold to the closest primary is one. The radius of convergence is a fraction of this this distance. For instance, for the case of POL2, $r_{16}\approx 0.5$ means that the center manifold radius of convergence is (more or less) half the distance from $L_2$ to the Moon.

Table 6 Radius of convergence for some values of n for the center manifold around POL1 (left) and POL2 (right)

2.1 Testing the software

Besides the transformed Hamiltonian, we store the symplectic change as it is useful to compute good approximations of invariant objects in the original system. Moreover, the change can be used to test the accuracy of the center manifold (see Jorba 1999). Let us explain briefly how this can be done: We select a point $u_0$ in the center manifold close to the origin (which is a fixed point and corresponds to POL1 or POL2 in the original system). Then, we integrate (in the center manifold) $u_0$ from $t=0$ to $t=t_{f}$. We call the resulting point $u_1$. We use the change to send the points $u_0$ and $u_1$ back to the coordinates of the QBCP. Let us call the transformed points $v_0$ and $v_1$, respectively. Now we integrate $v_0$ the same time (in QBCP units), and let $v_{0}^{1}$ be the result of this computation. If the change of variables were exact, then $v_{0}^{1}$ would be equal to $v_{1}$. In practice, this is not the case due to several sources of error (floating point representation, numerical integration and the truncation order of the center manifold). Therefore, a metric to estimate the error is $e_1 = \Vert v_1 - v_{0}^{1} \Vert$. This error is expected to be smaller as $v_0$ is selected to be close to the origin and to grow as it gets far away from it. Let us name $\Vert u_{0}\Vert _{2}=\lambda _0$, and N is the truncation order. If we neglect the accumulation of errors due to the arithmetic and the numerical integration, the error is expected to behave like $c \lambda _{0}^{N}$ where c is some constant. Repeating this experiment for several initial conditions $u_i$, $i=0,\dots ,m$ at increasing distances to the origin $\lambda _{0}< \dots < \lambda _{m}$ the order of the error can be approximated by

$$\begin{aligned} N_{j}=\frac{\ln (e_{j})-\ln (e_{j+1})}{\ln (\lambda _{j})-\ln (\lambda _{j+1})}, ~~~j=0,\dots ,m-1. \end{aligned}$$

(6)

Then, it is expected that $N_{j} \approx N.$

2.2 Center manifold around $L_1$

The expansion of the center manifold is a Hamiltonin $H_{CM} = H_2+\cdots +H_N$ where $H_k, k=2,..., N$ are homogeneous polynomials of degree k. Each $H_k$ is an expression of the form

$$\begin{aligned} H_k = \sum _{k_1 + k_2 + k_3 + k_4 = k} a_{(k_1, k_2, k_3, k_4)}Q_1^{k_1}P_1^{k_2}Q_2^{k_3}P_2^{k_4}, \quad k_i\in {\mathbb {N}}, i=1,...,4 \end{aligned}$$

(7)

where $(Q_1,Q_2)$ are the positions, and $(P_1,P_2)$ the conjugated momenta. The coefficients, up to degree 6, of the Hamiltonian of the center manifold corresponding to the periodic orbit POL1 are captured in “Appendix A”, Table 14.

After the computation of the center manifold, the test described in Sect. 2.1 (see also Jorba 1999) was executed to check the software implementation and that, numerically, the computed center manifold behaves as expected. The initial condition integrated was of the form $x_0=(\lambda _0, \lambda _0, \lambda _0, \lambda _0)/2$, where $\lambda _0\in \mathbb {R^+}$. Note that $x_0$ is divided by 2. This is done so the value $\lambda _0$ is equal to the distance of the initial condition from the origin (i.e., $\Vert x_0\Vert _2=\lambda _0$). The integration timespan was from $t=0$ to $t_{f}=1$.

For the $L_1$ case (orbit POL1), the results of the test for $N=16$ are in Tables 7 and 8. The data in Table 7 illustrate how as the distance of the initial condition $x_0$ from the origin increases, the error also increases. Table 8 shows good agreement between the degree of the center manifold approximation and the order of the truncation of the ODE. Hence, it is safe to conclude that the center manifold has been properly computed.

Table 7 Differences between the POL1 center manifold predictions and a numerical integration for $N=16$

Table 8 Estimations of the truncation order for the reduction to the center manifold around POL1 for $N=16$

For the sake of completeness, the same test has been applied to several truncation orders. This process to estimate the accuracy is the same as in Andreu (2002), and similar to the one applied in Le Bihan et al. (2017b)

The results of this new test are plotted in Fig. 3a and b. In Fig. 3a, the logarithm of the error is plotted against the distance to the origin, and in Fig. 3b with respect to the energy for different degrees. As before, these results have been obtained by integrating an initial condition $x_0$ of the form $x_0=(\lambda _0, \lambda _0, \lambda _0, \lambda _0)/2$. The data show that increasing the degree of the expansion does not necessarily translate in a better accuracy around a distance of the origin. This behavior is expected, since the series is not in general convergent in any open set. Finally, the relationship between the distance from the origin and the energy is depicted in Fig. 3c for different values of N. It can be seen that for different degrees there is good agreement. Note that the analysis described is limited to the subspace defined by $Q_1=Q_2=P_1=P_2$, but is still a good indicator.

One of the main takeaways of the accuracy analysis is that, if we pick an orbit on the center manifold and apply the change of coordinates to transform it to the synodic frame, the resulting object may not be (quantitatively) representative. In some cases, it may be a good initial condition for a refinement algorithm. However, the benefit of the center manifold is that qualitatively it provides a good picture of the dynamics. For the validity of the qualitatively analysis, the radius of convergence (see Table 6, left column, for POL1) is the right metric to use. Finally, quantitative description on how some families of objects are organized in a vicinity of $L_1$ will be discussed in Sect. 3.1.

Fig. 3

Accuracy of the center manifold around POL1. See text for details

Fig. 4

Poincaré section $Q_1=0$ of the center manifold around POL1 for different energy levels with $N=16$

Fig. 5

Poincaré section $Q_2=0$ of the center manifold around POL1 for different energy levels with $N=16$

To obtain a qualitative description of the dynamics, the (truncated up to degree $N=16$) Hamiltonian reduced to the center manifold has been integrated. Note that the Hamiltonian integrated has two degrees of freedom. This means that the phase space has dimension four. To visualize the center manifold, one can fix an energy level and take a Poincaré section so the dynamics is restricted to a plane. This is the same approach used in Jorba and Masdemont (1999). Let $(Q_1, P_1, Q_2, P_2)$ be the coordinates of the Hamiltonian reduced to the center manifold. The starting point is the selection of the 3D Poincaré section $Q_2=0$. Then, an energy level $h_0$ is fixed to obtain a 2D section. Note that the Hamiltonian is autonomous up to order N. Hence, the energy $h_0$ is conserved for the truncated Hamiltonian. Using this fact, and that $Q_2=0$, if values $(Q_1, P_1)$ are picked, the component $P_2$ is constrained by the energy level and can be computed numerically. (There are two solutions for $P_2$, one negative and one positive; we used the positive one.) This gives an algorithm to compute initial conditions. These initial conditions are integrated numerically, storing the points that have $Q_2=0$ and $P_2>0$. To have a wider perspective, it is useful to consider also the Poincaré section $Q_1=0$ and $P_1>0$ (the process to obtain this second section is the same one as in the first).

The Poincaré sections for different energy levels using $Q_1=0$ are shown in Fig. 4. Similarly, the Poincaré sections for different energy levels for $Q_2=0$ are shown in Fig. 5. In Fig. 4, it is observed that for low energy levels ($h=0.2$), there is a fixed point that corresponds to a periodic orbit. It is observed that this orbit is surrounded by invariant curves that correspond to 2D invariant tori for the reduced Hamiltonian. Note that for the original QBCP Hamiltonian in synodical coordinates, these objects are 3D invariant tori. If the energy level is increased ($h=0.4, 0.7, 0.9$ in Figs. 4, 5), the space phase undergoes a pitchfork bifurcation. This is more clear from Fig. 5. The interpretation in the synodic reference is the following: the fixed point close to the origin corresponds to a quasi-periodic vertical Lyapunov in the synodic reference frame. These are invariant tori with two basic frequencies. The quasi-periodic orbit surrounding the origin correspond to quasi-periodic Lissajous orbits with three basic frequencies. The fixed points that appear after the bifurcation takes place correspond to the northern and southern families of quasi-periodic Halo orbits with two basic frequencies. The quasi-periodic orbits around them correspond to quasi-Halo orbits with three basic frequencies.

This is qualitatively similar to the dynamics in around the $L_1$ region in the BCP (see Jorba et al. 2020), and to the results obtained by Le Bihan et al. (2017b) in the QBCP using the parametrization method to compute the center manifold.

2.3 Center manifold around $L_2$

The same process described in Sect. 2.2 is repeated for the $L_2$ case. Table 15 in “Appendix A” contains the coefficients, up to degree 6, of the reduced Hamiltonian of the center manifold. Also, the same tests described in Sect. 2.2 are done for the present case. Again, the initial condition is of the form $x_0=(\lambda _0, \lambda _0, \lambda _0, \lambda _0)/2$, with $\lambda _0\in \mathbb {R^+}$, and the integration timespan is from $t=0$ to $t=1$. The results are captured in Table 9 and in Table 10. In this case, because the radius of convergence is not as good as in the $L_1$ case, the degree of the expansion used is $N=12$. The results in Table 7 show that as the distance of the initial condition $x_0$ from the origin increases, the error increases, too. This behavior is expected. Table 8 shows that the error increases consistently with the degree of the expansion, as explained in Sect. 2.2.

Table 9 Differences between the POL2 center manifold predictions and a numerical integration for $N=12$

Table 10 Estimations of the truncation order for the reduction to the center manifold around POL2 for $N=12$

The same analysis of accuracy has been done in this scenario, and the main takeaway is the same as for the $L_1$ case. The results are captured in Fig. 6a for the evolution of the logarithm of the error with respect to the distance of the initial condition from the origin, and in Fig. 6a its evolution with respect to the energy for different degrees of the expansion of the center manifold. The main difference is that initially, for low energies, the error is approximately two orders of magnitude smaller that in the $L_1$ case. This is consistent with what is observed in Le Bihan et al. (2017b). Finally, the distance with respect to the energy is in Fig. 6c, and again it is shown good agreement for different degrees.

Fig. 6

Accuracy of the center manifold around POL2. See text for details

Finally, following the same procedure as for the $L_1$ case, the Poincaré sections $Q_1=0$ and $Q_2=0$ at different energy levels have been plotted. These are represented in Fig. 7 for the section ${Q_1=0}$, and in Fig. 8 for the section ${Q_2=0}$. The qualitative behavior and its interpretation are equivalent to the $L_1$ described in Sect. 2.2, and it will not be repeated here. As for the $L_1$ case, in this scenario the results are also qualitatively consistent with Le Bihan et al. (2017a). We remind that in Le Bihan et al. (2017a) the center manifold was constructed using the parametrization method, and not the Lie transform.

As mentioned in Sect. 1.3, the center manifold around $L_2$ in the QBCP was also studied (see Andreu 2002). It is important to note that in Andreu (2002) the construction of the center manifold is different from the one presented here. The reason is that it follows different criteria. First, the choice of the normal frequencies used in the Floquet transformation for the terms of degree two is different from the ones used here. In Andreu (2002), the author uses the following values:

$$\begin{aligned} {{\tilde{\omega }}}_1= & {} \texttt { 1.34709425E-02}\\ {{\tilde{\omega }}}_2= & {} \texttt { 2.16306748E+00}\\ {{\tilde{\omega }}}_3= & {} -\texttt {6.02217885E-02} \end{aligned}$$

where, in this case, ${{\tilde{\omega }}}_1$ and ${{\tilde{\omega }}}_3$ correspond to the elliptical parts, and the ${{\tilde{\omega }}}_2$ to the hyperbolic part. The differences in the normal frequencies of the elliptical part are due to the multiple determination of the complex logarithm as explained in Jorba et al. (2020). The relationship between the values used here and the ones used in Andreu (2002) is:

$$\begin{aligned} {{\tilde{\omega }}}_1= & {} \omega _1 - 2\omega _s\\ {{\tilde{\omega }}}_3= & {} \omega _2 - 2\omega _s \end{aligned}$$

The rationale behind using the values ${{\tilde{\omega }}}_i, i=1, 2, 3$ for the Floquet transformation as opposed to those close to the natural frequencies of $L_2$ is, as argued in Andreu (2002), to improve the radius of convergence.

Second, the criteria to kill monomials is also slightly different in Andreu (2002). In that case, the center manifold is computed removing the time dependency (up to certain order), killing all the monomials associated with the hyperbolic part, and those monomials where $K^0=K^1$ ($K^{0}=(k_1, \dots , k_{3})$ and $K^{1}=(k_{4},\dots , k_{6})$) as long as the denominators in the creation of the generating function are not smaller than the threshold $\varepsilon = 0.05$.

However, the penalty of constructing the center manifold as in Andreu (2002) is that it only provides information for low energy levels. With the criteria used to compute the center manifold in this work, the expression obtained is good enough to provide a good qualitatively description of the dynamics around the $L_2$ point. Overall, both approaches are valid and offer a different perspective on how the dynamics is organized.

Fig. 7

Poincaré section $Q_1=0$ of the center manifold around POL2 for different energy levels with $N=12$

Fig. 8

Poincaré section $Q_2=0$ of the center manifold around POL2 for different energy levels with $N=12$

3 Families of 2D invariant tori

In this section, we compute some of the families of 2D invariant tori that exist in a vicinity of the $L_1$ and $L_2$ collinear points. We show by using numerical continuation that, in the QBCP, there exist horizontal and vertical families parametrized by its frequency of invariant tori near $L_1$ and $L_2$. These families are the dynamical equivalents of the well-known Lyapunov families of periodic orbits in the RTBP. In addition to that, in the continuation of the planar Lyapunov family for each $L_1$ and $L_2$ we identify bifurcation points. At those bifurcation point, we find and continue families that have an out-of-plane component. Finally, we show that a big set of Halo orbits in the RTBP survive when continued to the QBCP. The computation and continuation of tori and their stability in this section are computed with the algorithms described in Jorba (2001) and Rosales et al. (2021a).

3.1 Families around $L_1$

This section starts with the analysis of the vertical family of quasi-periodic orbits around $L_1$. This is the family born from the dynamic equivalent of the $L_1$ (see Fig. 2), following the vertical component. This family would be the quasi-periodic counterpart in the QBCP of the vertical Lyapunov family that appear in the RTBP. The result of continuing this family is shown in Fig. 9. The x-axis is the third component of the position vector (the vertical component) when the invariant curve is evaluated at $\theta =0$. The y-axis is the rotation number of the invariant curve on the Poincaré section. We note that the lower-right part of Fig. 9, between $x=0.13$ and $x=0.14$ there is sharp turn. This reminds to the branch a pitchfork bifurcation obtained by symmetry breaking. We attempted to verify this hypothesis, but we were not successful. This is left as future work.

The stability of this family has been computed for a selected subset of tori. Because of the Hamiltonian character of the system (and the consequent fact that tori lie in families), 1 is always an eigenvalue with multiplicity two. Hence, there are two pairs of non-trivial eigenvalues. The analysis showed that there is always a real eigenvalue (and its inverse). The largest eigenvalue starts with a value of the order of $10^8$ and decreases with the rotation number until a value of the order of $10^6$. The other pair is formed by a complex value of norm 1 and its conjugate. This is represented in Fig. 9 (right panel). Thus, this family is formed by partially elliptic tori. As a final remark, note that no bifurcations were identified. However, based on the results from Sect. 2.2 and specifically shown in Fig. 4, at least one bifurcation exists. One hypothesis is that the step size used to generate this family probably jumped over the bifurcation. Another explanation may be that the family was not continued long enough.

Fig. 9

Left panel: Quasi-periodic vertical Lyapunov family in the QBCP around $L_1$. Right panel: Stability of the quasi-periodic vertical Lyapunov family in the QBCP around $L_1$. See text for details

The following figures are representative tori of this family, and provided here just to illustrate how their shape and size evolve with the rotation number. The first example, in Fig. 10, is a torus with rotation number $\rho = \texttt {2.8710835247657562}$. This torus is very small, and close to the periodic orbit that replaces $L_1$. The second example is in Fig. 11, and it is a representative of the family with rotation number $\rho = \texttt {1.7158771247657665}$. This is similar to the vertical Lyapunov orbit found in the RTBP around $L_1$ but “shaken” due to the effect of the periodic time-dependent perturbation. Finally, an example of a large invariant tori with rotation number $\rho = \texttt {1.0158771247657681}$ is illustrated in Fig. 12. It can be seen that all three tori are very different in size and shape.

Next, the family of horizontal quasi-periodic orbits around $L_1$ born from the planar frequency was computed. This family is the quasi-periodic equivalent to the planar Lyapunov periodic orbits that appear in the RTBP. In addition to the quasi-periodic planar Lyapunov orbits, others families were found during the process. These are captured in Fig. 13. The x-axis is the first component of the position vector when the invariant curve is evaluated at $\theta =0$. The y-axis is the rotation number of the invariant curve. The quasi-periodic planar Lyapunov family is colored in green and labeled as L1-HLy. It can be seen that a new family, colored in red and labeled as L1-QV, is born from it. The L1-QV family is born from a bifurcation of the L1-HLy. This bifurcation was identified during the stability analysis of the family L1-HLy. As for the quasi-periodic vertical Lyapunov family, two eigenvalues are real, and the largest one has an order of magnitude between $10^6$ and $10^8$. Then, there is the eigenvalue equal to one with multiplicity two. The last pair of eigenvalues is shown in Fig. 14, where the x-axis is the rotation number, and the y-axis is the absolute value of the eigenvalue. At the beginning of the family, this pair of eigenvalue is complex with norm equal to one. Then, a bifurcation occurred, and the pair of eigenvalues becomes real. From this bifurcation, the family L1-QV is born. Recall that this bifurcation was observed in the center manifold analysis done in Sect. 2.2, where Fig. 5 captures the present case.

The first tempting (and natural) thought is to claim that this family corresponds to the Halo orbits in the RTBP. To test this hypothesis, a few Halo orbits in the RTBP were continued from the RTBP to the QBCP. Then, this initial orbit was continued in the QBCP. This is the family colored in purple and labeled as L1-Halo seen in Fig. 13. Numerical evidences suggest that these two families are not connected. We stress that the fact that the purple and red curves in Fig. 13 are projections so that their crossings do not mean that they are connected. It is important to stress the representation of the these families in the figures has its limitations: from one point of a 6-dimensional object, we are picking one component and plotting it against the rotation number. A lot of information is missed during this process, but it is still useful to for a first analysis.

One check done to see whether the families L1-Halo and L1-QV are the same is to pick two representatives with similar rotation number and plot them. A member of the family L1-Halo with rotation number $\rho = \texttt {3.4622727594120977}$ and a member of L1-QV with rotation number $\rho = \texttt {3.4623791625106679}$ are shown in Fig. 15. Both orbits are different in size and position. It is interesting to see that the representative of the L1-Q1 family is a Halo-like orbit so, from a practical standpoint it is useful and could be a candidate for a mission. The main difference comes when the stability of these families is analyzed. Leaving aside the big real eigenvalue and its inverse and the unit eigenvalue with multiplicity two, it can be seen that they have differnt stability types. For example, Fig. 16 shows the stability of the Halo family. The x-axis shows the rotation number, and the y-axis, the absolute value of the eigenvalues. The majority of the eigenvalues are complex and have norm equal to one, with very few exceptions. On the other hand, following the same convention for the axes, Fig. 17 characterizes the stability of the QV family, and it can be seen that it undergoes a bifurcation that changes its stability from elliptic to hyperbolic. Hence, the numerical evidence and data gathered in this study do not indicate that these two families are connected, but it is important to remark that this is a local analysis, and hence, the results are not conclusive.

Fig. 10

Example of small vertical torus around $L_1$. Note that the axes have been scaled to appreciate the details

Fig. 11

Example of medium vertical torus around $L_1$

Fig. 12

Example of a big vertical torus around $L_1$

Fig. 13

Families of 2D invariant tori in the QBCP around $L_1$. See text for details

Fig. 14

Stability of the horizontal Lyapunov family in the QBCP around $L_1$. See text for details

Fig. 15

Example of representative of the Halo and QV families with similar rotation numbers. See text for details

Fig. 16

Stability of the Halo family in the QBCP around $L_1$. See text for details

Fig. 17

Stability of the QV family in the QBCP around $L_1$. See text for details

3.2 Families around $L_2$

For the $L_2$ case, we start analyzing the vertical family. The starting point is again the dynamical equivalent of the $L_2$ point in the QBCP. This is, the periodic orbit that replaces the $L_2$ equilibrium point shown in Fig. 2. By continuing along the vertical direction, the family of quasi-periodic orbits illustrated in Fig. 18 (left panel) is obtained. Like in the $L_1$ case, this family is the quasi-periodic counterpart of the vertical Lyapunov periodic orbits that appear in the RTBP.

The stability of these tori was also computed, and the results for the pair of eigenvalues that are not real or equal to one are shown in Fig. 18 (right panel). The x-axis is the rotation number, and the vertical axis is the argument of the eigenvalue. This pair of eigenvalues are complex with norm one, and Fig. 18 (right panel) shows how the argument evolves with respect to the rotation number. In this case, it is observed that at the end of the family (rotation number $\rho \approx \texttt {-1.0179}$) it seems that the two eigenvalues become real, leading to a change in the stability type. This may be the bifurcation observed in Fig. 7 from Sect. 2.3. For completeness, we mention that the large real eigenvalue starts at value on the order of $10^6$ and decreases with the rotation number to a value on the order of $10^5$.

Fig. 18

Left panel: Quasi-periodic vertical Lyapunov family in the QBCP around $L_2$. Right panel: Stability of the quasi-periodic vertical Lyapunov family in the QBCP around $L_2$. See text for details

As is the $L_1$ case in Sect. 3.1, we plotted some representatives of the family with different rotation numbers. Starting from the beginning of the family, Fig. 19 shows a torus with rotation number $\rho = -\texttt {0.4089841068128386}$. This torus is very close to the reference periodic orbit, and its shape and size are influenced by it. Another example is illustrated in Fig. 20. This example has as a rotation number $\rho = -\texttt {0.8717553068128412}$. This case, as in the $L_1$ scenario, portrays an orbit that resembles those found in the RTBP, but under the influence of the periodic perturbation. Finally, the last example is a torus with rotation number $\rho = \texttt {-1.0173803068128409}$. The same comments made for the $L_1$ case apply here (Fig. 21).

The next step is to continue the family of planar invariant 2D tori. As in the $L_1$ case, other families were found and are plotted together in Fig. 22 (left panel. Starting from the dynamical substitute of $L_2$, we start continuing the family along the horizontal frequency to find a family of planar quasi-periodic orbits. This family is quasi-periodic counterpart of the planar Lyapunov that appear in the RTBP. Is it shown in red in Fig. 22 and labeled as L2-HLy. Proceeding as in Sect. 3.1, we computed the stability of this family and found a bifurcation. This is shown in Fig. 23, where a change of stability can be seen. From this bifurcation, a new family is born. This family was computed, and it is illustrated in Fig. 23 as the purple curve labeled as L2-QV. This is the bifurcation obtained in the analysis of the center manifold from Sect. 2.3 and shown in Fig. 8. Note that this bifurcation was also identified in Andreu (1998). However, in Andreu (1998) three other small bifurcations were found. These were not noticed here, probably because the step size used to continue the family was not small enough.

Fig. 19

Example of small vertical torus around $L_2$. Note that the axes have been scaled to appreciate the details

Fig. 20

Example of medium vertical torus around $L_2$

Fig. 21

Example of big vertical torus around $L_2$

Again, it is tempting to claim that the family L1-QV is the equivalent to the Halo family coming from the RTBP. Following the previous argument made in Sect. 3.1, we continued a Halo orbit from the RTBP to the QBCP. Once in the QBCP, we continued the resulting torus to see how its evolves and to check for any connection with other families. The result of this continuation is the family plotted in Fig. 22 in color green and labeled as L2-Halo.

Figure 22 (right panel) is an amplification of the area around the bifurcation of the planar quasi-periodic Lyapunov orbits. There are two observations to be made: the first one is that the family L2-QV and L2-Halo are not connected. The second comment is that the L2-Halo family connects to another family of 2D tori resonant with the frequency of the Sun. This is seen around the point $(-1.12, -0.05)$ in Fig. 22 (right panel). This connection was conjectured in Andreu (1998), and the numerical evidence provided here seems to prove it.

Fig. 22

Families of 2D invariant tori in the QBCP around $L_2$. Left panel: General plot. Right panel: zoom about the bifurcation giving rise to the Halo family. See the text for more details

Now, let us show some examples of the different tori computed. Figure 24 shows three examples of orbits from the L2-Halo family. The rotation numbers are listed in Table 11.

It can be seen that, as expected, the orbits in Fig. 24 resemble the Halo orbits from the RTBP. An orbit from the Halo-L2 family with a rotation number close to the point where the family L2-Halo meets the family of 2D resonant tori was intentionally chosen for comparison purposes. A representative of the family of 2D resonant tori with rotation number $\rho = -\texttt {0.0774976152458405}$ is shown in Fig. 25. It can be seen that the L2-Halo is “thinner” than the 2D resonant torus from Fig. 25. To end this short catalog of orbits, examples of two representatives of the L2-QV family are plotted in Figs. 26 and 26. The rotation numbers are $\rho = \texttt {-0.0721362180958642}$ for Fig. 26 and $\rho = -\texttt {0.2449362180958645}$ for Fig. 27. It can be seen that this family is not Halo-like.

Finally, the stability of the L2-Halo family and the 2D resonant tori family that continues from it, and L2-QV family has been computed. The results are plotted in Figs. 28 and 29. The x-axis is the rotation number, and the y-axis is the absolute value of the eigenvalues. It can be seen in Fig. 28 that the tori from the L2-Halo family have an elliptical direction, with some small pockets of real eigenvalues. On the other hand, the stability for the L2-QV tori computed have all real eigenvalues, as shown in Fig. 29. For both families, the other two eigenvalues are real, with a range between $10^2$ and $10^6$ for the L2-Halo family, and between $10^5$ and $10^6$ for the L2-QV family and the family of 2D resonant tori that meet the L2-Halo family.

Fig. 23

Stability of the quasi-periodic horizontal Lyapunov family in the QBCP around $L_2$. See text for details

Fig. 24

The representatives of the family L2-Halo. Rotation numbers are in Table 11. See text for details

4 Transfers in the QBCP

In this section, we take advantage of the invariant manifolds of three Halo quasi-periodic orbits in the QBCP to design direct transfers from the translunar point (the Earth–Moon $L_2$ equilibrium point) to a 200-km Earth parking orbit. This kind of transfers where already found in the BCP in Rosales et al. (2021b). Here, we repeat a similar analysis for the case of the QBCP. The main idea to construct the transfers is to take initial conditions for a test particle on the unstable manifold of the tori and propagate them until some event takes place. The integration time is set to 6$T_{s}$, which corresponds approximately to 180 days (see Remark 1). This limit is set motivated by looking for transfers that operationally could be interesting. The authors acknowledge that this limit is arbitrary, but provide a valid insight potential transfer candidates.

Those possible events are:

• 1. The particle’s distance to the center of the Earth is less than $R_{E}+200$ km, where $R_{E}=6400$ km is the radius of the Earth. (The sphere centered at the center of the Earth and radius equal to the radius of the Earth plus 200 km is referred as the LEO sphere from now on.)

• 2. The particle collides with the Moon.

• 3. The particle leaves the Earth–Moon system. We set as a criterion for this case that the distance of the particle to the Earth–Moon barycenter is larger than 6 times the distance between the Earth and the Moon.

• 4. None of the above happens after integrating $6T_{s}$ units of time in the normalized frame (the orbits with this behavior will be referred as wandering trajectories).

Also, and as in Rosales et al. (2021b), for transfers, for each transfer, we evaluate three different cost functions. These three cost functions are:

• Minimum $\Delta v$: $J_1(\theta , h) = \Delta v(\theta , h)$

• Minimum transfer time $\Delta t$: $J_2(\theta , h) = \Delta t(\theta , h)$

• Minimum norm of ($\Delta v, \Delta t$): $J_3(\theta , h) = \sqrt{{\Delta v(\theta , h)}^2 + {\Delta t(\theta , h)}^2}$

Finally, the observations in Rosales et al. (2021b) about how the $\Delta v$ and the transfer time are computed apply to this analysis.

Table 11 Rotation numbers of the orbits plotted in Fig. 24

Fig. 25

Representative of the family of 2D resonant tori that meets the L2-Halo family. See text for details

Fig. 26

Representative of the QV family at the beginning of the family. See text for details

Fig. 27

Representative of the QV family away from the bifurcation point. See text for details

Fig. 28

Stability of the Halo family in the QBCP around $L_2$. See text for details

Fig. 29

Stability of the QV family in the QBCP around $L_2$. See text for details

To produce initial conditions on the unstable manifold of the tori, it is suitable to regard them as invariant curves of the stroboscopic map. Then, if $x, \psi _{u}:[0,2\pi ) \mapsto {\mathbb {R}}^{6}$ are the invariant curve of rotation number $\rho$ for the stroboscopic map and $\psi _{u}$ the eigenfunction related to the unstable eigenvalue $\lambda _{u}$, a linear approximation of the invariant manifold is given by:

$$\begin{aligned} \Lambda _{0}^{u}(\theta ,h)=x(\theta ) + h \psi _{u}(\theta ). \end{aligned}$$

Here, h is a small displacement. Take into account that the error of this linear approximation behaves as ${\mathcal {O}}(h^{2})$. Notice that h can be negative. The initial conditions $(\theta , h)$ are taken in the so-called fundamental cylinder given by $[0,2\pi )\times [h_{0}, h_{0}\lambda _{u}]$ where $h_{0}$ is to be chosen so the following quantity

$$\begin{aligned} \Vert P_{T_{s}}(\Lambda _{0}^{u}(\theta , h_0))-\Lambda _{0}^{u}(\theta + \rho , \lambda _{u} h_0)\Vert , \end{aligned}$$

is small enough. (Notice that $h_0$ depends on the invariant curve.) These initial conditions are of the form $(\theta _j, h_k), j=0,..., N-1, k=0,....,M-1$, where $\theta _j = 2\pi j/N, j=0,...,N-1$ and $h_k = h_0((M-k) + \lambda _u k)/M, k=1,...,M-1$. The values for N and M used in this paper are $N=M=1000$.

We have selected three (Halo like) invariant curves: ICQ1, ICQ2, and ICQ3 to preform the experiment. Their characteristics are given in Table 12. The unstable eigenvalues are also of the same order of magnitude. Different projections of the three invariant curves associated with the orbits used in this analysis are plotted in Fig. 30.

Figure 31 shows the results of the analysis for the selected QBCP Halo orbits. The first row corresponds to the invariant curve ICQ1, the second to curve ICQ2, and the third one to ICQ3. The first column corresponds to the negative side of the unstable manifold, and the second one to the positive side. In the ICQ1 case, the distance to the invariant curve has been chosen equal to $2.5\times 10^{-7}$ units of distance in the normalized frame (or approximately 100 m), $7.5\times 10^{-7}$ (or approximately 290 m) for the ICQ2 case, and $7\times 10^{-7}$ (or approximately 270 m) in the ICQ3 case. The color code is as follows: successful transfers are colored in red (this is, at some point the distance of the particle is less than $R_E+200$ km), collisions with the Moon are shown green, yellow shows trajectories where a particle leaves the Earth/Moon system, and none of the previous cases in black. As mentioned before, the maximum integration time is set to 6$T_s$ units of time in the normalized frame.

In all three cases, we observe regions were direct transfers exists, although they are not prominent. It is also observed that the collisions with the Moon are mainly concentrated in the cases ICQ2 and ICQ3, positive sides (these are the sides between the Halo orbit and the Moon). On the other hand, and also for the cases ICQ2 and ICQ3, the negative sides show that a significant number of trajectories leave the influence of the Earth–Moon gravity.

Looking at specific transfers that minimize the cost functions $J_i, i=1, 2, 3$, we see that the total costs in terms of $\Delta v$ and transfer time are consistent with the results described in Rosales et al. (2021b). These results are captured in Table 13. We see that the cheapest transfer in terms of total $\Delta v$ is the case {ICQ2, –, $J_1$} with a cost of 3.1517 km/s. This case, however, spends a total of approximately 125.4 days to complete. In terms of total travel time, the shortest transfer is the case {ICQ3, –, $J_2$}, with a total of approximately 104 days. In this case, the $\Delta v$ is approximately 3.3 km/s, which is comparable to the cheapest transfer. It is worth noting that there are other interesting trade-offs between total $\Delta v$ and travel time, like {ICQ2, –, $J_3$}.

Figure 32 shows the trajectory followed by the transfer {ICQ3, –, $J_2$}. This trajectory corresponds to the stable manifold of the target orbit ICQ3; this is the trajectory that a spacecraft would follow from the Earth to the target orbit. Note that the trajectory circles two times the Earth and the Moon before converging to the target Halo orbit. This “bending” of the invariant manifold is due to the direct gravitational effect of the Sun and it was also observed in the BCP (see Rosales et al. 2021b). Figure 33 shows different projections of the transfer when arriving to the target orbit. Again, the black circle corresponds to the radius of the Moon, and blue circle to the LEO sphere. It can be seen that for the ICQ3 orbit there is no Moon occultation.

Finally, it is worth looking at how the total transfer time changes with the $\Delta v$, and how the $\Delta v$ changes as a function of the latitude of the intersection with the LEO sphere. These are shown in Fig. 34a and b, respectively.

It can be observed in Fig. 34a that the total maneuver cost is between 3.1517 km/s (the minimum computed in this case) and slightly more than 13 km/s. The total $\Delta v$ as function of the latitude LEO sphere latitude is shown in Fig. 34b. The same qualitatively behavior as for the BCP case analyzed is seen here, where the majority of the transfers less than 4 km/s are concentrated between a latitude of $-20$ deg and 40 deg. Overall, the behavior of the cases studied in the QBCP are pretty similar to their counterparts in the BCP (see Rosales et al. 2021b).

Table 12 Characteristics QBCP Halo orbits invariant curves

Fig. 30

Invariant curves ICQ1, ICQ2 and ICQ3 of the QBCP

5 Conclusions and further work

In this paper, we explored some aspects of the dynamics around the Earth–Moon $L_1$ and $L_2$ regions in the context of the QBCP. The QBCP is dynamical system that models the motion of a massless particle under the influence of the Sun, the Earth, and the Moon. One of the main features of the QBCP is that the motion of the Sun, the Earth, and the Moon is coherent. This model can be written in the Hamiltonian formalism as periodic time-dependent perturbation of the RTBP. To study this Hamiltonian, we used numerical tools to get an insight on the phase space. The two techniques used were the reduction to the center manifold and the computation and continuation of 2D tori, their stability, and their associated invariant manifolds.

We first revisited the dynamical substitutes of the RTBP Earth–Moon $L_1$ and $L_2$ points in the QBCP. These dynamical substitutes are periodic orbits with the same period as the perturbation, and it is around these objected where we focused our analyses.

We showed that the reduction to the center manifold around the dynamical substitutes provides relevant qualitative information about the dynamics around $L_1$ and $L_2$. The main takeaway was that $L_1$ and $L_2$ had a similar qualitative behavior. In both cases, there were two families of quasi-periodic Lyapunov orbits, one planar and one vertical. It was also shown that the quasi-periodic planar Lyapunov family underwent a (quasi-periodic) pitchfork bifurcation, giving rise to two families of quasi-periodic orbits with an out-of-plane component. Between them, there was a family of Lissajous quasi-periodic orbits, with three basic frequencies.

Fig. 31

Fundamental cylinders, $(\theta , h)$, for QBCP orbits. Valid transfers are colored in red, trajectories where a particle leaves the Earth/Moon system are colored in yellow, collisions with the Moon are green, and none of the previous cases in black. First row corresponds ICQ1, second row to ICQ2, and third row to ICQ3. The first column corresponds to the negative side of the unstable manifold, and the second one to the positive side. See text for details

Table 13 Transfer cost to QBCP Halo orbits

Fig. 32

Trajectory followed by the transfer {ICQ3, –, $J_2$}

Fig. 33

Zoom around the target orbit showing the trajectory followed by the transfer {ICQ3, –, $J_2$}

Fig. 34

Plots of transfer time against total $\Delta V$ (left) and $\Delta V$ against latitude in the LEO Sphere (right)

In addition to the reduction to the center manifold, we also computed families of invariant 2D tori around $L_1$ and $L_2$. In these cases, the quasi-periodic planar and vertical families were continued. The bifurcations of the quasi-periodic planar Lyapunov were identified. A conclusion from this exercise was that the family of out-of-plane orbits born from the bifurcation seemed not to be the RTBP Halo counterparts in the QBCP. The RTBP Halo orbits do survive in the QBCP, but do not seem to be connected to the quasi-periodic planar Lyapunov family. Another conclusion for the $L_2$ case is about a conjecture enunciated in Andreu (1998). This conjecture stated that the family of Halo orbits in the QBCP obtained from direct continuation of the RTBP Halo orbits is connected to another family of 2D tori resonant with the frequency of the Sun is true. The numerical evidence seemed to indicate that this conjecture is true.

Finally, and also in the context of the QBCP, numerical simulations to study transfers from a parking orbit around the Earth to a Halo orbit around the Earth–Moon $L_2$ point were studied. The main conclusion is that, contrary to the RTBP, the invariant manifolds of the target orbits studied intersect with potential parking orbits around the Earth. This opens the room to potentially planning one-maneuver transfers from a vicinity of the Earth to Earth–Moon $L_2$ Halo orbits. In terms of $\Delta v$ cost and total transfer time, the results are comparable to other techniques requiring two or more maneuvers.

Future research focuses on showing whether or not the objects computed in the context of the QBCP survive in a full ephemeris model. This is especially relevant in the case of invariant manifold used for transfers. If these transfers persist in a full ephemeris model, this could pave the way for efficient ways to reach Halo orbits around the Earth–Moon $L_2$ point.

A Coefficients of the center manifolds

See Tables 14 and 15.

Table 14 Hamiltonian reduced to the central manifold up to order 6 around POL1

Table 15 Hamiltonian reduced to the central manifold up to order 6 around POL2