Determination of the doubly symmetric periodic orbits in the restricted three-body problem and Hill’s lunar problem

Abstract

We review some recent progress on the research of the periodic orbits of the N-body problem, and numerically study the spatial doubly symmetric periodic orbits (SDSPs for short). Both comet- and lunar-type SDSPs in the circular restricted three-body problem are computed, as well as the Hill-type SDSPs in Hill’s lunar problem. Double symmetries are exploited so that the SDSPs can be computed efficiently. The monodromy matrix can be calculated by the information of one fourth period. The periodicity conditions are solved by Broyden’s method with a line-search, and some numerical examples show that the scheme is very efficient. For a fixed period ratio and a given acute angle, there exist sixteen cases of initial values. For the restricted three-body problem, the cases of “Copenhagen problem” and the Sun–Jupiter–asteroid model are considered. New SDSPs are also numerically found in Hill’s lunar problem. Though the period ratio should be small theoretically, some new periodic orbits are found when the ratio is not too small, and the linear stability of the searched SDSPs is numerically determined.

1 Introduction

Many versions of the n-body problems are studied within the theme of periodic orbits or KAM tori, as periodic orbits and quasi-periodic orbits are important in celestial mechanics and very useful in understanding the motions of celestial bodies. For the aspects of the applications of the KAM theories on celestial mechanics, one may refer to Celletti and Chierchia (2006), Biasco and Coglitore (2008), Meyer et al. (2011), Zhao (2014) and the references therein. Here, we mainly discuss the periodic orbits. For the non-integrable dynamical systems, periodic orbits determine the skeleton of the phase space, and stable ones usually accumulate onto the KAM tori.

The problem on the periodic orbits of the three-body problem is intractable ever since (Poincaré 1892). Symmetric periodic orbits are prior to be studied, as symmetries can usually reduce the complexity. Some earlier work on the periodic orbits can be referred to Hadjidemetriou (1984). Three classical families of periodic orbits of the three-body problem are of Euler–Lagrange type (Meyer and Schmidt 1986; Sicardy 2010; Hu and Sun 2010; Zhou and Long 2017), figure-eight type (Chenciner and Montgomery 2000; Muñoz-Almaraz et al. 2007; Chen and Lin 2009; Hu and Sun 2009; Galan-Vioque et al. 2014; Yu 2017) and “Broucke-Hénon”,“Schubart-like” type (Hénon 1974, 1976; Martínez 2013; Ortega and Falconi 2016; Voyatzis et al. 2018; Kuang et al. 2019). It is summarized in Li and Liao (2019) that only these three families and a few more new periodic orbits are numerically calculated before a series of their work, and more than 2000 families of periodic orbits are found by taking use of the “clean numerical simulation” (CNS) technique, the grid search and the Newton-Raphson method on a supercomputer. The CNS is based on the arbitrary order of Taylor series method with a convergence check (Jorba and Zou 2005; Liao and Li 2019). The periodicity conditions are based on the difference of two solutions at different times, and the permissible error is set to be less than $10^{-6}$.

The restricted three-body problem (RTBP) and Hill’s lunar problem are well known as two basic mathematical models, in which many families of periodic orbits have been shown to exist, analysed and calculated. Periodic orbits of a nearly integrable Hamiltonian system with a small parameter are usually shown to exist by Poincaré’s continuation method or Arenstorf’s implicit function theorem, combinating several techniques such as canonical transforms, symplectic scaling, averaging, symmetry reduction and so on (Meyer et al. 2009; Cors et al. 2005). If there exist orbits very far away from the primaries, these orbits are classified as the comet-type. If there exist orbits around and very close to one primary, these orbits are of Hill-type. Howison and Meyer (2000a, 2000b) showed the existence of both the comet- and Hill-type spatial doubly symmetric periodic orbits (SDSPs) in the circular RTBP (CRTBP) and the Hill-type SDSPs in Hill’s lunar problem. Howison and Meyer’s results were generalized to the cases of the restricted (n+1)-body problem with general homogeneous potential successively by Llibre and Roberto (2009) and Llibre and Stoica (2011), where n bodies form a regular polygon or a nested central configuration. Xu (2019, 2020) showed that there exists a class of Hill-type SDSPs around one oblate primary in a generalized CRTBP and in Hill’s lunar problem. According to the known results (Palacián and Yanguas 2006; Meyer et al. 2011), there exist spatial comet-type KAM tori in the elliptic RTBP. For the lunar three-body problem, which is also called the hierarchal triple system, Zhao (2014) showed that there exist families of periodic orbits accumulating onto several KAM tori by applying Féjoz’s finer version of KAM theorem. These analytical results reveal that some SDSPs exist and stable when the small perturbation parameter is sufficiently small.

In Broer and Zhao (2017), only one linearly stable family is shown to exist though there are 16 families of Keplerian periodic orbits of De Sitter. This enlightens us to numerically study Howison and Meyer’s SDSPs with different initial values. If the initial values of SDSPs of the full system can be numerically continued from those of the circular SDSPs of the approximate system, the SDSPs of the full system will be of multiple revolutions and nearly circular. According to Poincaré’s classification, these orbits in the CRTBP can be classified as the third sort of the first species, while these orbits in Hill’s lunar problem can be classified as the third sort of the third species. However, we don’t know the cases when the perturbation is not too small, thus the numerical work on these periodic orbits is necessary and interesting. The purpose of this paper is to study the numerical calculation and stability of the SDSPs in the CRTBP and Hill’s lunar problem.

The readers who are interested in the related history and more aspects are encouraged to refer to Hénon (1969, 1997, 2003), Bruno and Varin (2006), Frauenfelder and van Koert (2018) and the citations. In the earlier stage, solutions of the periodicity conditions are continued based on Newton’s method. Macris et al. (1975) calculated four families of SDSPs of the elliptic RTBP with one fixed mass $\mu =0.4$ and the eccentricity as the small parameter, but all of the 107 orbits are unstable. With the mass ratio of the Sun–Jupiter case, Kazantis (1979) calculated 7 families of SDSPs which bifurcate from the vertical-critical symmetric families a, g$_{1}$, g$_{2}$, h, i, l and m. Family a goes from the Euler collinear libration point $L_{2}$. Families g$_{1}$ and g$_{2}$ are branches of the family g which begins as direct circular orbits of Hill-type around the Jupiter. Families h and i begin from the retrograde and direct circular orbits of Hill-type around the Sun, respectively. Families l and m are retrograde nearly circular periodic orbits of comet-type with positive and negative Jacobi constants, respectively. In addition, families b and c begin from the infinitesimal orbits around $L_{3}$ and $L_{1}$, respectively. Family f begins from the infinitesimal orbits around the primary with a mass tending to zero. Robin and Markellos (1980) dealt with the vertical branches of planar families in the CRTBP and found some linearly stable SDSPs. The accuracy of the initial values for those orbits is $10^{-6}$. The relation between the multiplicity and the symmetry is discussed, and eight vertical branches of retrograde family $f$ around Jupiter with multicity from 5 to 8 are taken as examples. Antoniadou and Libert (2019) studied the stability of some spatial symmetric resonant periodic orbits with resonances 3/2, 2/1, 5/2, 3/1, 4/1, 5/1 for both prograde and retrograde motions. They used the detrended Fast Lyapunov Indicator (DFLI) as a tool to study the maps of dynamical stability (DS map) around some resonant periodic orbits. With similar tools, Kotoulas et al. (2022) focused on the spatial symmetric retrograde periodic orbits of asteroids moving in low order interior mean resonances with Jupiter. A review paper about the resonant periodic orbits can be referred to Pan and Hou (2022).

Lara and Peláev (2002) implemented an intrinsic predictor-corrector algorithm with the help of the Frenet frame. The computations of some periodic orbits of the CRTBP show the robust of this algorithm, although it is a little difficult to implement. Kalantonis et al. (2003) transformed the solving problem of the nonlinear equations into an unconstrained optimization problem and calculated some periodic orbits of Robe’s CRTBP within accuracy $10^{-8}$. Robe’s RTBP considers the motion of an infinitesimal body inside one primary, which is a rigid spherical shell filled with a homogeneous incompressible fluid (Hallan and Rana 2001). Xu (2022) independently applied Broyden’s method with a line-search (Press et al. 1992) to the periodicity conditions and implemented the scheme with the accuracy generally no greater than $10^{-10}$.

The interests on the RTBP come from the non-integrability and a lot of useful research targets, including three species of periodic orbits, elemental periodic orbits, invariant manifolds, homoclinic and heteroclinic orbits, bifurcations and transit orbits. For the interests on the elemental periodic orbits emanating from five librations and homoclinic orbits of the CRTBP, one may refer to Doedel et al. (2007). The transit orbits between an interior region and an exterior region can be studied by the symbolic dynamics. Based on the values for the Sun–Jupiter–Oterma system, Wilczak and Zgliczynski (2003) showed the existence of a homo- and heteroclinic cycle between two Lyapunov orbits, and also showed the existence of a symbolic dynamics on four symbols. Barrabés and Mikkola (2005) computed families of symmetric periodic horseshoe orbits both in the planar RTBP and the spatial RTBP. Bengochea et al. (2013) studied the numerical continuation of the doubly symmetric horseshoe orbits in the general planar three-body problem. Fitzgerald and Ross (2022) demonstrated the phase space geometry of the transit and non-transit orbits of the bicircular problem and the elliptic RTBP by linearing the Hamiltonian differential equations about the collinear Lagrange points. For more numerical aspects on the homo- and heteroclinic orbits, one may refer to Koon et al. (2000), Kalantonis et al. (2006), Papadakis (2006) and Zhang (2022).

Periodic orbits of some special versions of RTBP are studied recently. Sitnikov problem is a special RTBP which considers the vertical motions of the infinitesimal body along a straight line perpendicular to the orbital plane of the primaries. A brief view of the Sitnikov problem is stated in Abouelmagd et al. (2020), and the first- and second-order approximated analytical periodic orbits of the circular Sitnikov problem are constructed without the secular terms via the multiple scales method. With the background of the earth-moon-spacecraft system, Zaborsky (2020) considered the generating solutions of the problem of two fixed attracting masses and derived 7 spatial families by continuing the angular velocity of rotation of the primaries around their center of masses.

Spatial Hill’s problem is important for the study on the motions of small bodies near one primary. Zagouras and Markellos (1985) constructed the fourth-order expressions for the periodic orbits originating at two Euler libration points near the smaller primary by the Lindstedt–Poincaré technique. Gómez et al. (2005) combined the semi-analytical and numerical techniques to study the invariant manifold of the spatial Hill’s problem associated to two Euler libration points. For a brief introduction to the recent progress on the periodic orbits of Hill’s problem, one may refer to Kalantonis (2020). By computing the linear stability of the basic planar families, Kalantonis determined twelve vertical-self-resonant (VSR) periodic orbits bifurcating from planar ones, and found each VSR orbit generates two branches where the multiplicity and symmetry depend on the stability. In the numerical results, the periods of the spatial ones are of three or four times of the periods of the planar ones. The quantized Hill problem can be considered as an equation system derived under the effects of quantum corrections. The periodic orbits emerging from the equilibrium points of the spatial quantized Hill problem are evaluated by the averaging theory in Abouelmagd et al. (2022).

The secular behaviors of the orbits in the RTBP are important. Prokopenya et al. (2015) considered a new version of RTBP when the masses of the primaries vary isotropically with different rates, and the total mass changes according to the joint Meshcherskii law. They studied the secular perturbations of the quasi-elliptic orbits by the averaging method and Hill’s approximation. Qi and Xu (2015) considered the long-term behavior of the spatial orbits near the Moon in the earth-moon-spacecraft CRTBP and calculated some spatial periodic orbits. Cheng and Gao (2022) studied the lognormal distribution of the mass of Saturn’s regular moons by the nonparameter test method in statistics, and obtained the analytical expression of the approximate periodic orbit near the Lagrangian point $L_{3}$ by the Lindstedt–Poincaré technique. Also, the influence of some parameters on the periodic orbits is also discussed.

Although some SDSPs have been calculated before, we draw attention to the fact that our research is new, including the algorithm and results. First, we use the numerical continuation scheme supplied in Xu (2022). We get the desired periodicity conditions of the SDSPs of the autonomous CRTBP by the integration and Hermite interpolation, and then take use of Broyden’s method with a line-search to acquire the roots as the initial values. The key program codes can be found in Press et al. (1992), which is not referenced by Kalantonis et al. (2003). Second, we consider the continuation of the SDSPs of the spatial Kepler problem in a rotating frame without the restriction on the mass ratio of the primaries, and the periods of the comet- and Hill-type SDSPs are quite different from the known ones. As far as we know, the SDSPs before our work were found as vertical branches of some planar families or the Lyapunov orbits near the Euler equilibrium points. Third, we find 16 initial conditions for each comet-type or Hill-type resonant period ratio, and do the numerical research on the SDSPs systematically.

The paper is organized as follows. In Sect. 2, the equations of motion and the Hamiltonian dynamical systems for the CRTBP and Hill’s lunar problem are introduced. In Sect. 3, we introduce the concept of double symmetry and some related lemmas. In Sect. 4, the geometric way to understand the comet- and Hill-type SDSPs of the approximate system is discussed. In Sect. 5, the numerical way to study the linear stability of the SDSPs is supplied. In Sect. 6, some numerical examples are given. This article ends with the discussion section.

2 Equations and Formulation

In this section, the equations of the CRTBP for describing the comet-type orbits are introduced both in the inertial frame and the rotating frame, with the origin at the center of masses. Besides, move the origin to the center of one primary, the Hamiltonian for the Hill-type motions is also introduced. In order to get a clear relation between the rectangular coordinates and the canonical elliptic variables, the orbital elements, Delaunay elements and Poincaré–Delaunay elements are introduced.

2.1 Rectangular coordinates

Consider the CRTBP in the center-of-mass inertial frame. Two primaries are denoted as $m_{1}$ and $m_{2}$, while their masses are also denoted as $m_{1}$ and $m_{2}$, respectively. The primaries move in a fixed plane which is set as the reference plane. The inertial Cartesian coordinate frame $O-u_{1}u_{2}u_{3}$ is established by choosing O as the center of masses and fixing one direction from O as the $u_{1}$ axis. Denote the vector from $m_{2}$ to $m_{1}$ as ${\varvec{d}}$ and the length d is a constant. The angular velocity $n^{\prime }$ of the vector ${\varvec{d}}$ satisfies $(n^{\prime })^{2}d^{3}=\texttt{G}(m_{1}+m_{2})$, where $\texttt{G}$ is the gravitational constant. Set the normalized units of mass, distance and time, $[\texttt{M}]=m_{1}+m_{2}$, $[d]=d$ and $[T]=d^{1/2}(\texttt{G}\texttt{M})^{-1/2}$. In such units, $\mu =m_{2}/\texttt{M}$, $\texttt{G}=1$, $n^{\prime }=1$, $d=1$, and ${\varvec{d}}=(\cos t, \sin t, 0)^{\texttt{T}}$, where the upper $\texttt{T}$ represents transposition. Let the position of the infinitesimal body be ${\varvec{x}}=(x_{1},x_{2},x_{3}) \in \mathbb {R}^{3} {\setminus }\{\mu {\varvec{d}}, (\mu -1){\varvec{d}}\}$. The corresponding conjugate momentum of ${\varvec{x}}$ is $\dot{{\varvec{x}}}$. The differential equation system for the motion of the infinitesimal body is

$$\begin{aligned} \ddot{{\varvec{x}}}=-\frac{(1-\mu )({\varvec{x}}-\mu {\varvec{d}})}{r_{1}^{3}}-\frac{\mu \left( {\varvec{x}}+ (1-\mu ){\varvec{d}}\right) }{r_{2}^{3}}. \end{aligned}$$

(1)

The Hamiltonian is composed of the kinetic energy and the potential energy (Frauenfelder and van Koert 2018),

$$\begin{aligned} \mathcal {H}^{\texttt {iner}}= \frac{1}{2}\Vert \dot{{\varvec{x}}}\Vert ^{2}- \frac{1-\mu }{r_{1}}-\frac{\mu }{r_{2}} , \end{aligned}$$

(2)

where the upper “iner" represents “inertial", and $\Vert \cdot \Vert$ is the Euclidean norm,

$$\begin{aligned}&\Vert \dot{{\varvec{x}}}\Vert ^{2}= \dot{x}_{1}^{2}+\dot{x}_{2}^{2} +\dot{x}_{3}^{2}, \\&r_{1}^{2}=\Vert {\varvec{x}}-\mu {\varvec{d}}\Vert ^{2}= \left( x_{1}-\mu \cos t \right) ^{2}+ \left( x_{2}-\mu \sin t \right) ^{2}+x_{3}^{2} ,\\&r_{2}^{2}=\Vert {\varvec{x}}+(1-\mu ){\varvec{d}}\Vert ^{2}= \left( x_{1}+(1-\mu )\cos t \right) ^{2}+ \left( x_{2}+(1-\mu )\sin t \right) ^{2}+x_{3}^{2} . \end{aligned}$$

Consider the CRTBP in the center-of-mass rotating frame $O-q_{1}q_{2}q_{3}$. The vector direction of ${\varvec{d}}$ is fixed as the $q_{1}$ axis. Denote the position vector of the infinitesimal body in this rotating frame as $\xi$. Substitute the formulas into the differential equations (1), module the rotation, then the differential equations in the rotating frame are acquired (Meyer et al. 2009),

$$\begin{aligned}&\left( \begin{array}{c} \ddot{\xi }_{1}-2 \dot{\xi }_{2} \\ \ddot{\xi }_{2}+2 \dot{\xi }_{1} \end{array}\right) = \left( \begin{array}{c} \xi _{1} \\ \xi _{2} \end{array}\right) -\frac{1-\mu }{r_{1}^{3}} \left( \begin{array}{c} \xi _{1}-\mu \\ \xi _{2} \end{array}\right) -\frac{\mu }{r_{2}^{3}} \left( \begin{array}{c} \xi _{1}+1-\mu \\ \xi _{2} \end{array}\right) , \nonumber \\&\ddot{\xi }_{3}=-\frac{\mu \xi _{3}}{r_{1}^{3}} -\frac{(1-\mu )\xi _{3}}{r_{2}^{3}} . \end{aligned}$$

(3)

Denote $\eta _{1}=\dot{\xi }_{1}-\xi _{2}$, $\eta _{2}=\dot{\xi }_{2}+\xi _{1}$, and $\eta _{3}=\dot{\xi }_{3}$. The Hamiltonian system in the rotating system can be checked out as follows,

$$\begin{aligned} \mathcal {H}^{\texttt {rot}}=\frac{1}{2}\Vert \eta \Vert ^{2} - (\xi _{1}\eta _{2}-\xi _{2}\eta _{1})-\frac{1-\mu }{r_{1}} -\frac{\mu }{r_{2}} , \end{aligned}$$

(4)

where $r_{1}^{2}=(\xi _{1}-\mu )^{2}+\xi _{2}^{2}+\xi _{3}^{2}$, and $r_{2}^{2}=(\xi _{1}+1-\mu )^{2}+\xi _{2}^{2}+\xi _{3}^{2}$.

2.2 Canonical elements

In order to better describe the nearly circular motions, canonical Poincaré elements are usually used. It is convenient to replace the rectangular coordinates by the instantaneous orbital elements firstly, then convert the orbital elements to the Delaunay elements, and finally use the Poincaré–Delaunay elements.

Define two three-dimensional anticlockwise-rotating matrices $\mathcal {R}_{1}$ and $\mathcal {R}_{2}$ as

$$\begin{aligned} \mathcal {R}_{1}(\theta )=\left( \begin{array}{cc} 1 &{} \text {0} \\ \text {0} &{} \exp (-{\varvec{J}}\theta ) \end{array}\right) , \quad \mathcal {R}_{2}(\theta )=\left( \begin{array}{cc} \exp (-{\varvec{J}}\theta ) &{} \text {0} \\ \text {0} &{} 1 \end{array}\right) , \end{aligned}$$

where the skew-symmetric matrix ${\varvec{J}}$ and the two-dimensional orthogonal matrix $\exp (-{\varvec{J}}\theta )$ are, respectively, defined as

$$\begin{aligned} {\varvec{J}}=\left( \begin{array}{cc} 0 &{} 1 \\ -1 &{} 0 \end{array}\right) , \quad \exp (-{\varvec{J}}\theta )=\left( \begin{array}{cc} \cos \theta &{} -\sin \theta \\ \sin \theta &{} \cos \theta \end{array}\right) . \end{aligned}$$

The orbital elements contain six variables, which are semi-major axis a, eccentricity e ($0\le e <1$), inclination i ($0\le i<\pi$), longitude of ascending node $\varOmega$ ($0\le \varOmega <2\pi$), argument of pericenter $\omega$ ($0\le \omega <2\pi$) and mean anomaly $\ell \in \mathbb {R}$. The eccentric anomaly and the true anomaly are $E=E(e,\ell )$ and $f=f(e,\ell )$, respectively. Note that

$$\begin{aligned} r=\Vert {\varvec{x}}\Vert =\Vert \xi \Vert =a(1-e\cos E)= a(1-e^{2})\left( 1+e\cos f\right) ^{-1} . \end{aligned}$$

Let n denote the mean motion and n is positive for the prograde motion while negative for the retrograde motion. For the unperturbed system, if the mass of the central primary is $\mu$, then we have $n^{2}a^{3}=\mu$. The angular momentum is denoted as $\varTheta =\pm \sqrt{ma(1-e^{2})}$, where the “$+$” represents the prograde motion while “−" represents the retrograde motion. The rectangular coordinates of the position can be expressed by

$$\begin{aligned} {\varvec{x}}=\mathcal {R}_{2}(\varOmega ) \mathcal {R}_{1}(i) \mathcal {R}_{2}(f+\omega ) \left( r,0,0\right) ^{\texttt{T}} . \end{aligned}$$

In the sense of instantaneous, the velocity is about the derivative of the anomalies,

$$\begin{aligned} \dot{{\varvec{x}}}=\mathcal {R}_{2}(\varOmega ) \mathcal {R}_{1}(i) \mathcal {R}_{2}(f+\omega ) \left( \dot{r},r\dot{f},0\right) ^{\texttt{T}}, \end{aligned}$$

where $\dot{r}= e\sin (f)/\varTheta$, $r\dot{f}= (1+e\cos f)/\varTheta$. According to the formulas below, the anomalies can be converted to each other,

$$\begin{aligned} E-e\sin E=\ell , \quad r\cos f=a(\cos E -e), \quad r\sin f=a\sqrt{1-e^{2}}\sin E . \end{aligned}$$

The Delaunay elements are

$$\begin{aligned}{} & {} L = \sqrt{ \mu a}, G = L\sqrt{1-e^{2}}, H = G\cos i, \\{} & {} \ell = n t+\ell _{0}, g = \omega , h = \varOmega , \end{aligned}$$

and the Poincaré–Delaunay elements are

$$\begin{aligned} \begin{array}{ccccccccc} P_{1} &{}=&{} L-G+H, &{} P_{2} &{}=&{} \sqrt{2(L-G)}\cos (g+h), &{} P_{3} &{}=&{} G-H , \\ Q_{1} &{}=&{} \ell +g+h, &{} Q_{2} &{}=&{} -\sqrt{2(L-G)}\sin (g+h), &{} Q_{3} &{}=&{} \ell +g . \end{array} \end{aligned}$$

2.3 Perturbed system

Consider the comet-type motion of the infinitesimal body, so 1/r is small. Let $\{\mathcal {P}_{k}\}_{k=0}^{\infty }$ be the Legendre polynomials, and $\mathcal {P}_{0}=1$, $\mathcal {P}_{1}(\xi _{1})=\xi _{1}$, $\mathcal {P}_{2}(\xi _{1})=\frac{3}{2}\xi _{1}^{2} -\frac{1}{2}$, $\mathcal {P}_{3}(\xi _{1})= \frac{5}{2}\xi _{1}^{3}-\frac{3}{2}\xi _{1}$. According to the Legendre expansion technique,

$$\begin{aligned} \frac{1-\mu }{r_{1}}+\frac{\mu }{r_{2}}&= \frac{1-\mu }{\sqrt{r^{2}+\mu ^{2}-2\mu \xi _{1}}} +\frac{\mu }{\sqrt{r^{2}+(1-\mu )^{2}+2(1-\mu ) \xi _{1}}} \\&=\frac{1}{r}+\frac{1-\mu }{r}\sum _{j=2}^{\infty } \mathcal {P}_{j}\left( \frac{\xi _{1}}{r}\right) \left( \frac{\mu }{r}\right) ^{j}+ \frac{\mu }{r}\sum _{k=2}^{\infty } \mathcal {P}_{k}\left( -\frac{\xi _{1}}{r}\right) \left( \frac{1-\mu }{r}\right) ^{k} . \end{aligned}$$

If 1/r is sufficiently small, the Hamiltonian $\mathcal {H}^{\texttt {rot}}$ can be written in the perturbed form as $\mathcal {H}^{\texttt {rot}}=\mathcal {H}_{0}^{\texttt {rot}} +\mathcal {O}(1/r^{3})$ by the canonical elements, where

$$\begin{aligned} \mathcal {H}_{0}^{\texttt {rot}}= -\frac{1}{2L^{2}}-H=-\frac{1}{2(P_{1}+P_{3})^{2}} -\left( P_{1}-\frac{P_{2}^{2}+Q_{2}^{2}}{2}\right) . \end{aligned}$$

(5)

If the infinitesimal body is very close to primary $m_{2}$, it is convenient to move the origin to the center of $m_{2}$. Let $m_{2}-q_{1}q_{2}q_{3}$ denote the $m_{2}$ centered rotating frame. Let the position ${\varvec{q}}=\xi +(1-\mu ,0,0)^{\texttt{T}}$, the conjugate momentum ${\varvec{p}}=\eta + (0,1-\mu ,0)^{\texttt{T}}$. Note that $\Vert {\varvec{q}}\Vert \ll 1$. The Hamiltonian for the Hill-type motion around $m_{2}$ can be written as

$$\begin{aligned} \mathcal {H}^{\texttt {mtwo}}&=\mathcal {H}_{0}^{\mu } +(1-\mu ) q_{1}-\frac{1-\mu }{\sqrt{1-2q_{1} +\Vert {\varvec{q}}\Vert ^{2}}} -\frac{(1-\mu )^{2}}{2} , \\ \mathcal {H}_{0}^{\mu }&=\frac{1}{2}\Vert {\varvec{p}}\Vert ^{2}- (q_{1}p_{2}- q_{2}p_{1})-\frac{\mu }{\Vert {\varvec{q}}\Vert } . \end{aligned}$$

Expand the potential function by Legendre expansion technique, neglect the constant $-(1-\mu )-(1-\mu )^{2}/2$, and write the part of the integrable Hamiltonian in the canonical elements, we get

$$\begin{aligned} \mathcal {H}^{\texttt {mtwo}}=\mathcal {H}_{0}^{\mu } -(1-\mu ) \left( \frac{3}{2}q_{1}^{2}-\frac{1}{2} \Vert {\varvec{q}}\Vert ^{2}\right) -(1-\mu ) \cdot \mathcal {O}(\Vert {\varvec{q}}\Vert ^{3}) , \end{aligned}$$

(6)

where $\mathcal {H}_{0}^{\mu }=-\frac{\mu }{2L^{2}}-H$ and the canonical elements change with $L= \sqrt{ \mu a}$.

Hill’s lunar problem can be derived by the following way. Make symplectic scaling ${\varvec{q}}\rightarrow \mu ^{1/3}{\varvec{q}}$ and ${\varvec{p}}\rightarrow \mu ^{1/3}{\varvec{p}}$, then scale the Hamiltonian by $\mu ^{-2/3}$, afterwards make $\mu \rightarrow 0$, the Hamiltonian becomes

$$\begin{aligned} \mathcal {H}^{\texttt {Hill}}=\mathcal {H}_{0}^{\texttt {rot}} -\left( \frac{3}{2}q_{1}^{2}-\frac{1}{2} \Vert {\varvec{q}}\Vert ^{2}\right) . \end{aligned}$$

(7)

In the following, the integrable system like $\mathcal {H}_{0}^{\texttt {rot}}$ and $\mathcal {H}_{0}^{\mu }$ is usually referred as the approximate system.

3 Double symmetries and SDSPs

The double symmetries exist in the RTBP and Hill’s lunar problem, because these systems satisfy two time-reversing symmetries. One is with respect to the syzygy (the line containing both primaries), the other is about the vertical plane containing the primaries. The differential equation system (3) is invariant under the two anti-symplectic reflections (Kazantis 1979; Robin and Markellos 1980; Howison and Meyer 2000a, b; Llibre and Roberto 2009; Llibre and Stoica 2011; Bengochea et al. 2013; Xu 2019, 2020; Antoniadou and Libert 2019; Kotoulas et al. 2022).

$$\begin{aligned} \mathscr {R}_{1}:&(\xi _{1},\xi _{2},\xi _{3}, \dot{\xi }_{1}- \xi _{2}, \dot{\xi }_{2}+ \xi _{1}, \dot{\xi }_{3}) \rightarrow (\xi _{1},-\xi _{2},-\xi _{3}, -\dot{\xi }_{1}+ \xi _{2}, \dot{\xi }_{2}+ \xi _{1}, \dot{\xi }_{3}), \\ \mathscr {R}_{2}:&(\xi _{1},\xi _{2},\xi _{3}, \dot{\xi }_{1}- \xi _{2}, \dot{\xi }_{2}+ \xi _{1}, \dot{\xi }_{3}) \rightarrow (\xi _{1},-\xi _{2},\xi _{3}, -\dot{\xi }_{1}+ \xi _{2}, \dot{\xi }_{2}+ \xi _{1}, -\dot{\xi }_{3}). \end{aligned}$$

The two time reversing symmetries can be explained geometrically. $\mathscr {R}_{1}$ denotes the symmetry about the $\xi _{1}$ axis, while $\mathscr {R}_{2}$ denotes the symmetry about the $\xi _{1}\xi _{3}$ plane. It is difficult to know directly the rectangular initial values for the SDSPs, but there is one way to get the precise initial values by numerically continuing the approximate initial values, which can be achieved by determining the SDSPs of the approximate system.

Though the Hamiltonians of the comet and Hill-type motions are different, the corresponding approximate systems are similar to $\mathcal {H}_{0}^{\texttt {rot}}$. The SDSPs of the approximate system can be determined according to the following three lemmas (Howison and Meyer 2000a; Xu 2019).

Lemma 1

If one orbit of the Hamiltonian (4) starts from a Lagrangian subplane $\mathscr {L}_{1}^{(0)}$ (or $\mathscr {L}_{2}^{(0)}$), and intersects $\mathscr {L}_{2}^{(0)}$ (or $\mathscr {L}_{1}^{(0)}$) after time $T/4>0$, then the orbit is periodic with period T and doubly symmetric, where

$$\begin{aligned} \mathscr {L}_{1}^{(0)}&=\{(\xi ,\eta )|\xi =(\xi _{1},0,0), \eta =(0,\dot{\xi }_{2}+\xi _{1},\dot{\xi }_{3})\}, \nonumber \\ \mathscr {L}_{2}^{(0)}&=\{(\xi ,\eta )|\xi =(\xi _{1},0,\xi _{3}), \eta =(0,\dot{\xi }_{2}+\xi _{1},0) \} . \end{aligned}$$

(8)

The Hamiltonian systems (5), (6), (7) also satisfy this proposition.

Proof

Consider one solution starts from $\mathscr {L}_{1}^{(0)}$. Let $\phi (t,X_{0},Y_{0})$ be a solution of (3) with the initial values $X_{0}=(\xi _{1},0,0)$ and $Y_{0}=(0,\eta _{2},\eta _{3})$ at the time $t=0$. The differential equation system satisfies the double symmetries $\mathscr {R}_{1}$ and $\mathscr {R}_{2}$. After time T/4, the solution intersects with the set $\mathscr {L}_{2}^{(0)}$ at $X_{1}=(\tilde{\xi }_{1},0, \tilde{\xi }_{3})$, $Y_{1}=(0,\tilde{\eta }_{2},0)$. One has

$$\begin{aligned} \phi _{T/4}=\phi (T/4,X_{0},Y_{0})=(\tilde{\xi }_{1},0, \tilde{\xi }_{3}, 0,\tilde{\eta }_{2},0) . \end{aligned}$$

As the solution satisfies the symmetry $\mathscr {R}_{1}$, one has

$$\begin{aligned} \mathscr {R}_{1} \phi _{T/4} =\phi (-T/4,X_{0},Y_{0}) =(\tilde{\xi }_{1},0,-\tilde{\xi }_{3}, 0,\tilde{\eta }_{2},0) . \end{aligned}$$

It takes T/2 for this orbit from $\mathscr {L}_{2}$ to $\mathscr {L}_{2}$ again. The solution also satisfies the symmetry $\mathscr {R}_{2}$, so one has

$$\begin{aligned} \phi (T/4+T/2,X_{0},Y_{0})=\mathscr {R}_{2}\phi _{-T/4} =(\tilde{\xi }_{1},0,-\tilde{\xi }_{3}, 0,\tilde{\eta }_{2},0) =\phi (-T/4,X_{0},Y_{0}) . \end{aligned}$$

So the solution $\phi (t,X_{0},Y_{0})$ is periodic with period T and doubly symmetric. For the case that one solution starts from $\mathscr {L}_{2}^{(0)}$, the proof is the same as above. $\square$

Lemma 2

The Lagrangian subplane $\mathscr {L}_{k}^{(0)}$ is equivalent to $\mathscr {L}_{k}^{(1)}$, to $\mathscr {L}_{k}^{(2)}$ and to $\mathscr {L}_{k}^{(3)}$ for $k=1, 2$, where

$$\begin{aligned} \mathscr {L}_{1}^{(1)}&=\{(f=0 \mod \pi , \ \ \omega =0 \mod \pi , \ \ \varOmega =0 \mod \pi )\}, \nonumber \\ \mathscr {L}_{2}^{(1)}&=\{(f=0 \mod \pi , \ \ \omega =\frac{\pi }{2} \mod \pi , \ \ \varOmega =\frac{\pi }{2} \mod \pi ) \}. \end{aligned}$$

(9)

$$\begin{aligned} \mathscr {L}_{1}^{(2)}&=\{(\ell =0 \mod \pi , \ \ g=0 \mod \pi , \ \ h=0 \mod \pi )\}, \nonumber \\ \mathscr {L}_{2}^{(2)}&=\{(\ell =0 \mod \pi , \ \ g=\frac{\pi }{2} \mod \pi , \ \ h=\frac{\pi }{2} \mod \pi ) \}. \end{aligned}$$

(10)

$$\begin{aligned} \mathscr {L}_{1}^{(3)}&=\{ (Q_{1}=0 \mod \pi , \ \ Q_{2}\equiv 0, \ \ Q_{3}=0 \mod \pi )\}, \nonumber \\ \mathscr {L}_{2}^{(3)}&=\{ (Q_{1}=0 \mod \pi , \ \ Q_{2}\equiv 0, \ \ Q_{3}=\frac{\pi }{2} \mod \pi )\}. \end{aligned}$$

(11)

Lemma 3

The SDSPs of the approximate system $\mathcal {H}_{0}^{\texttt {rot}}$ can only be the circular orbits.

Proof

The rectangular coordinates $\xi$ and $\eta$ can be expressed by the orbital elements,

$$\begin{aligned} \xi =\mathcal {R}_{2}(-n^{\prime }t){\varvec{x}} =r\alpha _{1}, \quad \eta =\mathcal {R}_{2}(-n^{\prime }t)\dot{{\varvec{x}}} =\dot{r}\alpha _{1}+r\dot{f}\alpha _{2}, \end{aligned}$$

where $\mathcal {A}=\mathcal {R}_{2} (\varOmega -n^{\prime }t) \mathcal {R}_{1}(i) \mathcal {R}_{2}(f+\omega ) =(\alpha _{1},\alpha _{2},\alpha _{3})$ is a $3\times 3$ matrix,

$$\begin{aligned} \alpha _{1}&=\left( \begin{array}{c} \cos (f+\omega )\cos (\varOmega -t)-\cos i \sin (f+\omega ) \sin (\varOmega -t) \\ \cos (f+\omega )\sin (\varOmega -t)+\cos i \sin (f+\omega ) \cos (\varOmega -t) \\ \sin (f+\omega )\sin i \end{array}\right) , \\ \alpha _{2}&=\left( \begin{array}{c} -\sin (f+\omega )\cos (\varOmega -t)-\cos i \cos (f+\omega ) \sin (\varOmega -t) \\ -\sin (f+\omega )\sin (\varOmega -t)+\cos i \cos (f+\omega ) \cos (\varOmega -t) \\ \cos (f+\omega )\sin i \end{array}\right) , \end{aligned}$$

and $\alpha _{3}=\left( \sin (\varOmega -t)\sin i, -\cos (\varOmega -t)\sin i, \cos i \right) ^{\texttt{T}}$. Let the initial values of one orbit be $X_{0},Y_{0}$ as above. Suppose that after time T/4, the solution intersect $\mathscr {L}_{2}^{(0)}$ at $X_{1},Y_{1}$. According to the two boundary conditions, the solution satisfies $f=\omega =\varOmega =0 \mod \pi$ at $t=0$, and $f=0 \mod \pi$, $g=\pi /2 \mod \pi$, $h=\pi /2 \mod \pi$ at $t=T/4$. However, $\dot{g}=0$ in the approximate system. There exists a conflict if the orbit is elliptic. So the doubly symmetric periodic orbit can only be circular. $\square$

4 Approximate system and SDSPs

Let us recall three theorems proved by Howison and Meyer (2000a, 2000b) in order to make the readers to understand what kinds of SDSPs to be calculated in this paper.

Theorem 1

(Howison and Meyer 2000a, b) (1) There exist doubly symmetric periodic solutions of the spatial restricted three-body problems for all values of the mass ratio parameter $\mu$ with large inclination which are arbitrarily far away from the primaries. (2) There exist doubly symmetric periodic solutions of the spatial restricted three-body problems for all values of the mass ratio parameter $\mu$ with large inclination which are arbitrarily close to one of the primaries. (3) There exist doubly symmetric periodic solutions of the spatial Hill’s lunar problems with large inclination which are arbitrarily close to the primary.

The existence of the SDSPs is shown by the continuation method, which needs a small parameter. The small parameter is introduced by the symplectic scaling method (Howison and Meyer 2000a). Theoretically, the small parameter is small enough, however, it is not necessarily to be too small in the numerical research.

4.1 Symplectic scaling

In order to understand the small parameter and estimate the order of magnitude of the perturbation to the approximate system, we recall the symplectic scaling procedure (Meyer et al. 2009; Howison and Meyer 2000a; Xu 2019, 2020). For the comet-type orbits, the coordinate frame is the rotating frame with the origin at the center of masses. The symplectic transformation is $\xi \rightarrow \varepsilon ^{-2}\xi , \quad \eta \rightarrow \varepsilon \eta$, and the new Hamiltonian is equal to the old Hamiltonian multiplied with $\varepsilon$. The small parameter $\varepsilon ^{2}$ represents the inverse of the great distance of the infinitesimal body from the origin 1/r. The symplectic scaled new Hamiltonian is $\tilde{\mathcal {H}}^{\texttt {rot}} =\tilde{\mathcal {H}}_{0}^{\texttt {rot}} +\mathcal {O}(\varepsilon ^{7})$, where $\tilde{\mathcal {H}}_{0}^{\texttt {rot}}= -\varepsilon ^{3}/(2\tilde{L}^{2})-\tilde{H}$, $L=\sqrt{a}$, $\tilde{L}=\varepsilon L$ and $\tilde{H}=\varepsilon H$.

While for the Hill-type orbits, the origin is set to locate at the center of one primary $m_{2}$. This symplectic transfromation is $\xi \rightarrow \varepsilon ^{2}\xi , \quad \eta \rightarrow \varepsilon ^{-1}\eta$, and the new Hamiltonian is equal to the old Hamiltonian multiplied with $\varepsilon ^{-1}$. Here the small parameter $\varepsilon ^{2}$ represents the degree of closeness to the primary $m_{2}$. $\mathcal {H}^{\texttt {mtwo}}$ is transformed to $\hat{\mathcal {H}}^{\texttt {mtwo}}= \hat{\mathcal {H}}_{0}^{\mu }+\mathcal {O}(\varepsilon ^{3})$, where $\hat{\mathcal {H}}_{0}^{\mu } =-\frac{\varepsilon ^{-3}\mu }{2\hat{L}^{2}}-\hat{H}$, $L=\sqrt{\mu a}$, $\hat{L}=\varepsilon ^{-1} L$ and $\hat{H} =\hat{L}\sqrt{1-e^{2}}\cos i$. If $\mu \rightarrow 0$, we use $\hat{L}= \mu ^{1/3}\check{L}$, and have $\check{\mathcal {H}}^{\texttt {Hill}}= \check{\mathcal {H}}_{0}^{\texttt {rot}}+\mathcal {O} (\varepsilon ^{3})$, where $\check{\mathcal {H}}_{0}^{\texttt {rot}} = -\varepsilon ^{-3}/(2\check{L}^{2})-\check{H}$.

4.2 Sixteen cases of the initial values

In order to do the numerical study, it is convenient to use the usual rectangular coordinates to represent the initial values. Consider the initial values of the comet-type SDSPs of the approximate system. Let $\phi (t,X_{0},Y_{0})$ be one solution and satisfy $(X_{0},Y_{0}) \in \mathscr {L}_{1}^{(0)}$. According to Lemma 2 and Lemma 3, the initial values at $t=0$ can be written as

$$\begin{aligned} X_{0}=(\pm a\cos \varOmega _{0},0,0), \quad Y_{0} =\pm (0, n a\cos i\cos \varOmega _{0}, n a\sin i) . \end{aligned}$$

Suppose $\phi (\frac{T}{4},X_{0},Y_{0}) =(X_{1},Y_{1})$ $\in \mathscr {L}_{2}^{(0)}$. Let $\varOmega _{1}=\varOmega _{0}-T/4$, and we have again

$$\begin{aligned} X_{1}=a\left( \mp \cos i\sin (\varOmega _{1}), 0, \pm \sin i \right) , \quad Y_{1}=\left( 0, \pm n a \sin (\varOmega _{1}), 0\right) . \end{aligned}$$

Usually, $\dot{X}_{k}=Y_{k}-(0,a,0)$ for $k=1, 2$ are used instead of $Y_{0}, Y_{1}$, respectively.

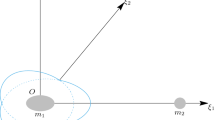
Let $\textrm{sgn}(n)=1$ if the infinitesimal body moves prograde (anticlockwise) and $\textrm{sgn}(n)=-1$ if the infinitesimal body moves retrograde (clockwise). Given an acute angle $i_{0}<\pi /2$, the inclination is supposed to be $i_{0}$. If the orbit starts from $\mathscr {L}_{1}^{(0)}$, each parameter in $(\xi _{1},\dot{\xi }_{2},\dot{\xi }_{3})$ has a possibility to be positive or negative, so there are eight cases of the initial values. There are also eight cases for the signs of $(\xi _{1}, \xi _{3},\dot{\xi }_{2})$ if the orbit starts from $\mathscr {L}_{2}^{(0)}$. As we can see in Fig. 1, there are three orbital planes with different dihedral angles. The first two sketch maps represent that the orbits start from $\mathscr {L}_{1}^{(0)}$, and the third sketch map represents that the orbits start from $\mathscr {L}_{2}^{(0)}$. There are eight cases of initial values in each Lagrangian subplane. The signs of $(\xi _{1},\dot{\xi }_{2},\dot{\xi }_{3})$ or $(\xi _{1},\xi _{3},\dot{\xi }_{2})$ are applied to represent a set of initial values. For example, $(1,+,+,+)$ means that the orbit starts from $\mathscr {L}_{1}^{(0)}$ and $\xi _{1}=a>0$, $\dot{\xi }_{2}>0$, $\dot{\xi }_{3}>0$, while $(2,+,+,+)$ represents that the orbit starts from $\mathscr {L}_{2}^{(0)}$ and $\tilde{\xi }_{1}=a\cos i_{0}>0$, $\tilde{\xi }_{3}>0$,$\dot{\tilde{\xi }}_{2}>0$. In all, there can be 16 possibilities of initial values of SDSPs for a fixed period ratio in the approximate system. For more details, the readers can refer to the caption of the Fig. 1.

Fig. 1

Three sketch maps are supplied for describing the initial values for the SDSPs of the approximate system. The included angle between the initial orbital plane $\mathscr {L}_{1}^{(0)}$ and the $\xi _{2}$ axis is no greater than $90^{\circ }$ for the first sketch (upper left) and greater than $90^{\circ }$ for the second sketch (upper right). There are four cases of initial values in each of the first two sketch maps. In the third sketch map (lower middle), the included angle between the initial orbital plane $\mathscr {L}_{2}^{(0)}$ and the $\xi _{2}$ axis is $90^{\circ }$, and there are also eight cases of initial values. The signs of $(\xi _{1},\dot{\xi }_{2}, \dot{\xi }_{3})$ are marked in the upper two sketch maps, while the signs of $(\tilde{\xi }_{1},\tilde{\xi }_{3}, \dot{\tilde{\xi }}_{2})$ are marked in the third sketch map. There are totally sixteen cases of initial values for the SDSPs of the approximate system

4.3 Initial values

According to the Hamiltonian $\mathcal {H}_{0}^{\texttt {rot}}$ of the approximate system in Eq. (5), the longitude of the ascending node satisfies the differential equation $\dot{h}=\frac{\partial \mathcal {H}_{0}^{\texttt {rot}}}{\partial H}=-1$, so $h(t)=h(0)-t$ and the line of apsides moves retrograde. Let $\mathbb {Z}^{+}$ denote all the non-negative integers. One fourth period is set to be $\frac{T_{0}}{4}=\frac{\pi }{2}+k\pi$ ($k\in \mathbb {Z}^{+}$), such that $h(\frac{T_{0}}{4})=h(0)-\frac{T_{0}}{4}$ satisfies $\mathscr {L}_{2}^{(2)}$ if $h(0)=0 \mod \pi$ and satisfies $\mathscr {L}_{1}^{(2)}$ if $h(0)=\frac{\pi }{2} \mod \pi$. In addition, we have the differential equation $\dot{Q}_{3}(t)=\dot{\ell }(t)+\dot{g}(t)= \textrm{sgn}(n) L^{-3}$, so $Q_{3}(t)=Q_{3}(0)\pm L^{-3}t$. We must have $L^{-3}\frac{T_{0}}{4}=\frac{\pi }{2}+j\pi$ with $j\in \mathbb {Z}^{+}$, such that $Q_{3}(\frac{T_{0}}{4})$ satisfies $\mathscr {L}_{2}^{(3)}$ if $Q_{3}(0)=0 \mod \pi$ and satisfies $\mathscr {L}_{1}^{(3)}$ if $Q_{3}(0)=\frac{\pi }{2} \mod \pi$. Because the argument of perigee g is of no definition in the circular orbit, and we redefine $\ell (\frac{T_{0}}{4}) =\ell (0)+\textrm{sgn}(n)j\pi$ and $g(\frac{T_{0}}{4})=\textrm{sgn}(n)\frac{\pi }{2}$ such that this definition keeps in coincident with the Poincaré–Delaunay elements for the symmetries. Then $T_{0}=2\pi +4k\pi$ is set as the period of a SDSP of the approximate system. In the inertial frame, during the period that the primaries revolve $2k+1$ turns around each other, the projection of infinitesimal body in the $\xi _{1}\xi _{2}$ plane revolve $2j+1=\frac{T_{0}}{2\pi }|n|$ turns.

The mean anomaly can be determined by the period ratio, that is $|n|=\frac{2j+1}{2k+1}$. For the comet-type orbits, the semi-major axis a is much longer than $d=1$ and is determined by $a=L^{2}=\left[ (2k+1)/(2j+1)\right] ^{2/3}$ with $k\gg j\ge 0$. We can check that the Kepler’s third law $n^{2}a^{3}=1$ is satisfied for the comet-type SDSPs. The small parameter $\varepsilon$ is also determined by the period ratio as $\varepsilon ^{3}=\left[ (2j+1)/(2k+1)\right]$ with $\tilde{L}=1$. We conclude that $n a=\textrm{sgn}(n) \varepsilon =a^{-1/2}$. Suppose $a=a_{0}$ when j and k are fixed. The initial orbital inclination is $i_{0}<\frac{\pi }{2}$ or $\pi -i_{0}$. Then the initial values of a SDSP starting from $\mathscr {L}_{1}^{(0)}$ can be written as

$$\begin{aligned} (\xi _{1},0,0,0,\dot{\xi }_{2},\dot{\xi }_{3})= (\pm a_{0},0,0,0,\pm a_{0}^{-1/2}\cos i_{0} -a_{0}, \pm a_{0}^{-1/2}\sin i_{0}). \end{aligned}$$

(12)

While the initial values of a SDSP starting from $\mathscr {L}_{2}^{(0)}$ can be written as

$$\begin{aligned} (\tilde{\xi }_{1},0,\tilde{\xi }_{3},0,\dot{\tilde{\xi }}_{2},0)= (\pm a_{0}\cos i_{0}, 0, \pm a_{0}\sin i_{0}, 0, \pm a_{0}^{-1/2} -a_{0}, 0). \end{aligned}$$

(13)

The initial values $({{\varvec{q}}},\dot{{\varvec{q}}})$ of a Hill-type SDSP of $\mathcal {H}_{0}^{\mu }$ in (6) are formally the same as (12) or (13). For the Hill-type orbits, the semi-major axis $a_{1}$ is much shorter than $d=1$, and $a_{1}=\left( \frac{\mu }{n^{2}}\right) ^{\frac{1}{3}} =\mu ^{1/3}\left[ (2k+1)/(2j+1)\right] ^{2/3}$ with $j \gg k \ge 0$. Denote the initial orbital inclination as $i_{1}<\frac{\pi }{2}$ or $\pi -i_{1}$. The initial parameters of a Hill-type SDSP starting from $\mathscr {L}_{1}^{(0)}$ can be expressed as

$$\begin{aligned} (q_{1},\dot{q}_{2},\dot{q}_{3})= (\pm a_{1}, \pm \sqrt{\mu /a_{1}}\cos i_{1} -a_{1}, \pm \sqrt{\mu /a_{1}}\sin i_{1}) . \end{aligned}$$

(14)

If a Hill-type SDSP starts from $\mathscr {L}_{2}^{(0)}$, the set of initial parameters is given by

$$\begin{aligned} (\tilde{q}_{1},\tilde{q}_{3},\dot{\tilde{q}}_{2})= (\pm a_{1}\cos i_{1}, \pm a_{1}\sin i_{1}, \pm \sqrt{\mu /a_{1}}-a_{1}) . \end{aligned}$$

(15)

The initial values for the Hill-type SDSPs of the approximate system of Hill’s lunar problem can be calculated by Eqs.(12) and (13) for $j \gg k \ge 0$.

4.4 Periodicity conditions

The integration procedure and the periodicity conditions are based on the rectangular coordinates. Consider the comet-type case and let j and k be fixed as $k\gg j \ge 0$. Suppose that the initial values are chosen as $(X_{0},\dot{X}_{0}) \in \mathscr {L}_{1}^{(0)}$. There are three undetermined values $\xi _{1},\dot{\xi }_{2}, \dot{\xi }_{3}$, and three periodicity conditional equations are as follows,

$$\begin{aligned} \tilde{\xi }_{2}(T/4,\xi _{1},\dot{\xi }_{2}, \dot{\xi }_{3})=0, \quad \dot{\tilde{\xi }}_{1}(T/4,\xi _{1},\dot{\xi }_{2}, \dot{\xi }_{3})=0, \quad \dot{\tilde{\xi }}_{3}(T/4,\xi _{1},\dot{\xi }_{2}, \dot{\xi }_{3})=0 . \end{aligned}$$

As T is also unknown, the integration time can be determined by the orbit’s $(k+j+2)$-th passing of the $\xi _{1}\xi _{3}$ plane. The parameter T can be exported as a global variable. One can also try to add the period as one undetermined parameter to the conditional equations, like $T/4=T_{0}/4+\xi _{2}(T_{0}/4)/\dot{\xi }_{2}(T_{0}/4)$, and T can be calculated iteratively. However, it may fail when the precision of $T_{0}$ is poor for the full system, or say when the ratio j/k is not small enough.

A SDSP starts from the $x_{1}x_{3}$ plane, which is also the $\xi _{1}\xi _{3}$ plane at the initial epoch. During the time span $T_{0}/4$, as the line of syzygy rotates $(k+0.5)\pi$, the orbit of the infinitesimal body hits the $x_{2}x_{3}$ plane perpendicularly at the $(j+k+1)$-th passing. Meanwhile, the $\xi _{1}\xi _{3}$ plane rotates in the inertial frame anticlockwise with the angular velocity $n^{\prime }=1$, and coincides with the $x_{2}x_{3}$ plane at $T_{0}/4$. The infinitesimal body passes the $\xi _{1}\xi _{3}$ plane $j+k+2$ times containing the beginning and the ending within one fourth period. We use the interpolation method to get the $(k+j+2)$-th intersection with the $\xi _{1}\xi _{3}$ plane so as to get the periodicity conditional equations.

Suppose that the initial values are chosen as $(X_{1},\dot{X}_{1}) \in \mathscr {L}_{2}^{(0)}$. Three parameters $(\tilde{\xi }_{1}$, $\tilde{\xi }_{3}$,$\dot{\tilde{\xi }}_{2})$ are needed to be determined. Then the periodicity conditions are as follows,

$$\begin{aligned} \xi _{2}(T/4,\tilde{\xi }_{1},\tilde{\xi }_{3}, \dot{\tilde{\xi }}_{2})=0, \quad \xi _{3}(T/4,\tilde{\xi }_{1},\tilde{\xi }_{3}, \dot{\tilde{\xi }}_{2})=0, \quad \dot{\xi }_{1}(T/4,\tilde{\xi }_{1},\tilde{\xi }_{3}, \dot{\tilde{\xi }}_{2})=0 . \end{aligned}$$

For example, the $(k+j+2)$ passings can be counted from how many times that $\xi _{2}(t)\xi _{2}(t+\varDelta t)\le 0$ is satisfied, where $\varDelta t$ is the integration step. And the $(k+j+2)$-th intersection can be precisely acquired if we use the Hermite interpolation (or cubic spline interpolation).

5 Linear stability

Consider the linear variation of the differential equations (3), which can be rewritten as $\dot{\xi }= \partial \mathcal {H}^{\texttt {rot}}/\partial \eta$, $\dot{\eta }=- \partial \mathcal {H}^{\texttt {rot}}/\partial \xi$. Then the linear variations satisfy

$$\begin{aligned} \delta \dot{\xi }=\delta \eta + (\delta \xi _{2},-\delta \xi _{1},0)^{\texttt{T}}, \quad \delta \dot{\eta }\approx -\frac{\partial ^{2} \mathcal {H} ^{\texttt {rot}}}{\partial \xi \partial (\xi ,\eta )} \left( \begin{array}{c} \delta \xi \\ \delta \eta \end{array}\right) , \end{aligned}$$

(16)

the formulas can be referred to Lara and Peláev (2002) or one can calculate them by one symbol algebra software.

Suppose $\left( \xi (T),\eta (T)\right) =\left( \xi (0),\eta (0)\right)$, this means that a solution starts from $(\xi _{0},\eta _{0})$ and comes back after time T. Along this periodic solution, the coefficient matrix $-\frac{\partial ^{2} \mathcal {H} ^{\texttt {rot}}}{\partial \xi \partial (\xi ,\eta )}$ is periodic. According to the Floquet theorem, the stability depends on the eigenvalues of the monodromy matrix, which is a fundamental solution matrix taking the value after a period. The eigenvalues of $\frac{\partial (\xi (T),\eta (T))}{\partial (\xi (0),\eta (0))}$ are the same as those of $\frac{\partial (\xi (T),\dot{\xi }(T))}{\partial (\xi (0),\dot{\xi }(0))}$ as there exists only elementary matrix transforms between these two monodromy matrices.

Consider $\zeta = (\delta \xi _{1},\cdots ,\delta \eta _{1},\cdots , \delta \eta _{3})^{\texttt{T}} \in \mathbb {R}^{6}$. The differential equation can be derived as (16). The standard fundamental solution matrix about $\zeta$ can be denoted as $\mathcal {Z}(t)=\mathcal {Z}(t,0)=\left( \frac{\partial \zeta _{i}(t,0)}{\partial \zeta _{j}(0)} \right) _{1\le i,j\le 6}$ and satisfies $\mathcal {Z}(0)=\textbf{I}_{6\times 6}$, where $\textbf{I}_{6\times 6}$ is a $6\times 6$ identical matrix, so the monodromy matrix $\mathcal {Z}(T)$ can be integrated numerically. Some Lemmas can be referred to Meyer et al. (2009).

Lemma 4

If $\mathcal {Z}(t)$ is a fundamental solution matrix of a linear differential system with a T-periodic coefficient matrix, then $\mathcal {Z}(t+T)=\mathcal {Z}(t) \mathcal {Z}(T)$.

Theorem 2

The fundamental solution matrix $\mathcal {Z}(t)$ is symplectic for all $t\in \mathbb {R}$. The eigenvalues of $\mathcal {Z}(T)$ (characteristic multipliers) are symmetric with respect to the real axis and the unit circle.

According to the double-symmetry property, the $\mathcal {Z}(T)$ can be calculated by just integrating T/4 (Robin and Markellos 1980).

Theorem 3

Let $\mathcal {Z}(t)$ be defined as above. If a SDSP starts from $\mathscr {L}_{1}^{(0)}$, and $\mathcal {Z}(T/4)=\mathcal {Z}_{(0,T/4)}$ is known, then the monodromy matrix of this SDSP can be calculated by

$$\begin{aligned} \mathcal {Z}(T)=\left( \mathcal {N}\left( \frac{T}{2}\right) \mathscr {R}_{1}\right) ^{2}, \quad \mathcal {N}\left( \frac{T}{2}\right) =\mathcal {Z}\left( \frac{T}{4}\right) \mathscr {R}_{2}\mathcal {Z}^{-1} \left( \frac{T}{4}\right) , \end{aligned}$$

(17)

where $\mathscr {R}_{1}=$ $\texttt{diag}$ $(1, -1, -1, -1, 1, 1)$ and $\mathscr {R}_{2}=\texttt{diag}( 1, -1, 1, -1, 1, -1)$. If the solution starts from $\mathscr {L}_{2}^{(0)}$ and $\tilde{\mathcal {Z}}(T/4)$ is known, then

$$\begin{aligned} \mathcal {Z}(T)=\left( \tilde{\mathcal {N}}\left( \frac{T}{2}\right) \mathscr {R}_{2}\right) ^{2}, \quad \tilde{\mathcal {N}}\left( \frac{T}{2}\right) = \tilde{\mathcal {Z}}\left( \frac{T}{4}\right) \mathscr {R}_{1}\tilde{\mathcal {Z}}^{-1}\left( \frac{T}{4}\right) . \end{aligned}$$

Proof

According to Liouville’s theorem, the trace of the periodic coefficient matrix equals zero, so the determinant of $\mathcal {Z}(t)$ equals 1. According to the property of the fundamental solution matrix, we have $\mathcal {Z}(T) =\mathcal {Z}(T/2)\mathcal {Z}_{(T/2,T)}$. For the symmetry $\mathscr {R}_{1}$, we can find that $\mathcal {Z}_{(T/2,T)} =\mathscr {R}_{1}\mathcal {Z}^{-1}(T/2)\mathscr {R}_{1}$. For the symmetries $\mathscr {R}_{1}$ and $\mathscr {R}_{2}$, we have

$$\begin{aligned} \mathcal {Z}(T)&= \mathcal {Z}\left( \frac{T}{2}\right) \left( \mathscr {R}_{1} \mathcal {Z}^{-1}\left( \frac{T}{2}\right) \mathscr {R}_{1}\right) , \\ \mathcal {Z}\left( \frac{T}{2}\right)&=\mathcal {Z}\left( \frac{T}{4}\right) \left( \mathscr {R}_{2} \mathcal {Z}^{-1}\left( \frac{T}{4}\right) \mathscr {R}_{2}\right) . \end{aligned}$$

We derive

$$\begin{aligned} \mathcal {Z}^{-1}\left( \frac{T}{2}\right) =\mathscr {R}_{2}\mathcal {Z}\left( \frac{T}{4}\right) \mathscr {R}_{2} \mathcal {Z}^{-1}\left( \frac{T}{4}\right) =\mathscr {R}_{2}\mathcal {N}\left( \frac{T}{2}\right) \mathscr {R}_{2}. \end{aligned}$$

Then $\mathcal {Z}(T)$ for the SDSP can be calculated by $\mathcal {Z}(T/4)$. The proof for the other case of $\mathcal {Z}(T)$ is similar if the SDSP starts from $\mathscr {L}_{2}^{(0)}$. $\square$

The characteristic multipliers of (16) measures the stability of periodic solutions. For the three-dimensional CRTBP, there are six characteristic multipliers which are in pairs of reciprocals. In fact, these multipliers can be complex conjugate on a circle or can be real reciprocals. Denote one multiplier as $\lambda$, if there exists a $|\lambda |>1$, then the periodic solution is not linearly stable. The six multipliers can be represented as $\lambda _{i},\frac{1}{\lambda _{i}}$ ($i=1,2,3$). We refer to the well-known index for the linear stability in Hénon (1969), Lara and Peláev (2002), and define

$$\begin{aligned} \rho =\sum _{i=1}^{3}\left( |\lambda _{i}|+ \frac{1}{|\lambda _{i}|}\right) \ge 6 \end{aligned}$$

(18)

as the linear stability index for the spatial periodic orbits. The trace of $\mathcal {Z}(T)$ can be firstly used to judge the stability. If $\rho \ge \textrm{Tr}(\mathcal {Z}(T))>6$, the orbit is linearly unstable. While if $\textrm{Tr}(\mathcal {Z}(T))\le 6$, we will use $\rho$ to help understand the linear stability. When all the multipliers are on the unit circle, one has $\rho =6$, and such a periodic solution is linearly stable. In fact, for the numerical errors, we cannot get the precise $\rho =6$, so we retain 6 significant digits for convenience to characterize the stability. The monodromy matrix $\mathcal {Z}(T)$ can be calculated by the integration of linear variational equations together with the corresponding differential equations, and by the application of Theorem 3. The eigenvalues are calculated by the elimination method and the QR algorithm. The Fortran subroutines “elmhes" and “hqr" can be referred to in Press et al. (1992). “elmges" transforms a matrix to the upper Hessenberg form, and “hqr" solves the eigenvalues by a sequence of Householder transformations.

6 Numerical Examples

All the numerical experiments are carried out in a Linux system on a personal computer with Intel Core i7-6500U CPU @ 2.50GHz $\times$ 4 and 7.7 GiB memory. If the maximal numerical deviation of the periodicity conditions at one fourth period is no greater than $10^{-9}$, a symmetric periodic orbit is supposed to be found. The time consuming for the continuation can be controlled by the maximum number of loops. The symmetric periodic orbits with the designated k and j are found by Broyden’s method with a line-search, which is globally convergent. The Fortran subroutines “broyden”, “lnsrch” and so on can be referred in Press et al. (1992). Although Kalantonis et al. (2003) have pointed out this method, we haven’t realized their work until very recently.

6.1 Case $\mu =1/2$

The special case of equal masses in the RTBP known as the “Copenhagen problem". This case has been studied with the generalized force potential. Here, we confine our experiment on the Newtonian potential. Generally speaking, it is necessary for the perturbation to be small if one wants to continue the periodic orbits from the approximate system to the full system. In order to estimate the order of the magnitude of the perturbation on the approximate system, we compare the first-order perturbation term with $\mathcal {H}_{0}^{\texttt {rot}}$. The first-order perturbation term is $\mathcal {H}_{1}^{\texttt {rot}}= -(1-\mu )\mu \mathcal {P}_{2}(\xi _{1}/r)/r^{3}$. For the nearly circular orbits near the infinity, the line of syzygy moves much faster than the mean motion of the big orbit of the infinitesimal body. During one orbit period of the infinitesimal body, the averages of $\cos 2\varOmega$ and $\sin 2\varOmega$ equal zeros. We refer to Xu (2019) for the necessary terms and have

$$\begin{aligned} \frac{1}{2\pi }\int _{0}^{2\pi }\mathcal {P}_{2} (\xi _{1}/r) r^{-3} \textrm{d}\ell /n =\frac{1}{8}(3\cos ^{2}i-1)\varTheta ^{-3} . \end{aligned}$$

It seems that the first-order averaged perturbation equals zero when $\cos ^{2} i=1/3$ though the first-order perturbation does not vanish.

One set of initial values for the planar RTBP can be referred to Lara and Peláev (2002) as follows,

$$\begin{aligned} (x_{0},y_{0},z_{0},\dot{x}_{0},\dot{y}_{0},\dot{z}_{0}) =(0, 4, 0, 4.5, 0, 0)\in \mathscr {L}_{2}^{(0)}, \quad T_{0}=5.585 . \end{aligned}$$

(19)

The periodic orbits continued from this set of values belong to family m, in which the periodic orbits are usually stable. Our numerical experiment shows that there are a lot of symmetric periodic orbits near this approximate solution. The results achieved by our algorithm are more close to the initial values. In Fig. 2, there are four near circular retrograde periodic orbits. The outer orbit is symmetric with respect to the y axis. The initial values of the outer orbit is $y_{1}=4.00021433614826$, $\dot{x}_{1}=4.50254016243978$, and the period is $T_{1}=5.5815257432169$. There are two orbits in the middle and almost coincide. One orbit is determined by the double symmetries, and the other orbit is determined by the second perpendicular crossing of the positive y axis. The initial values are $(y_{2},\dot{x}_{2})$ $=$ $(3.99876390419082$, 4.50118225570633), and $(y_{3},\dot{x}_{3})$ $=$ $(3.99857131110253$, 4.50100195228139), respectively. The periods are $T_{2}=5.5811840743002$ and $T_{3}=5.58113868599737$, respectively. The accuracy of the three periodic orbits is within 1.1E-13.

Fig. 2

Planar symmetric period orbits of family m continued from the same initial values in Eq. (19) with $\mu =0.5$. The initial values of the inner periodic orbit are $(x,y,\dot{x},\dot{y})=(0,3.96199469992294, 4.46677589984367,0)$, and the period is 5.57243120610132. The outer periodic orbits are continued by the optimization method in this paper. Part of the left-side sketch map is enlarged as the right-side sketch map. Primaries are represented by dots

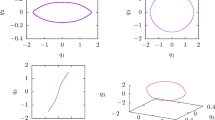
For $\mu =0.5$ and $\cos i_{0}=\sqrt{3}/3$, we vary integers k, j, as well as the directions, and numerically find many SDSPs. Some examples are listed in Table 1. For $k=30,j=0$, we get $a_{0}=61^{2/3}\approx 15.496$, $T_{0}= 30.5\pi \approx 95.819$. It takes about several minutes to get the continued initial values. For the $(1,+,+,+)$ case, we have $\xi _{1}=15.5061254882711$, $\dot{\xi }_{2}= -\,15.7370477222493$, $\dot{\xi }_{3}=0.105884508957052$, $T/4=95.81968944276656$. The accuracy is within $10^{-10}$ by the program. As we can see, the approximate initial values approximate the true values, as the small parameter satisfies $\epsilon ^{3}=1/61\approx 0.0164$. This periodic orbit is nearly linear stable, as maximum absolute value for the six multipliers is 1.000188. In order to show robust of the program, a bigger $\varepsilon \approx 0.101$ with $k=15,j=0$ is taken. The corresponding initial values for the SDSPs can be calculated as $a_{0}\approx 9.868$, $n_{0}=1/31$ and $i_{0}\approx 0.9553$. More continuation results are listed in Table 1, and the corresponding characteristic multipliers are listed in Table 2. In order to have a better view of the SDSPs, an example for the case $k=9,j=0$ is shown in Fig. 3, and four interesting sketch maps are shown in Fig. 4.

Fig. 3

An orbit diagram of comet-type SDSPs in case $(1,+,-,-)$ with $\mu =0.5$, $k=9$, $j=0$, $\cos i=\sqrt{3}/3$. The initial values and the period can be found in Table 1. The characteristic multipliers can be found in Table 2

Fig. 4

Four sketch maps of SDSPs with $\mu =0.5$ calculated in Table 1. The upper left one describes the $(1,0)(1,+,-,-)$ type orbit, which is retrograde. The upper right one is continued from the $(1,0)(1,+,-,+)$ type orbit, and the orbit is of Hill-type and retrograde. The lower left one is continued from the $(2,0)(1,-,+,-)$ type orbit, and the orbit is planar retrograde comet-type. The fourth one is interesting and continued from the $(10,0)(1,-,+,-)$ type orbit

Table 1 A list of initial values of the comet-type SDSPs in the $O-q_{1}q_{2}q_{3}$ frame with $\mu =0.5$, $\cos ^{2} i=1/3$

Table 2 Characteristic multipliers of the comet-type SDSPs in the Table 1

6.2 Sun–Jupiter case

The mass of the Sun is about 1.988500E+30 kg, while the mass of the Jupiter is about 1.89813E+27 kg, so we derive the mass ratio $1-\mu \approx$ 9.5364E-4. However, if the masses of the satellites and the rings are included in the Jupiter system, the mass ratio $1-\mu$ may approximate 9.5388E-4 according to Bruno and Varin (2006). Consider the calculation of the Hill-type SDSPs around the Sun. We use our numerical scheme to check some SDSPs calculated by Kazantis (1979). One example is shown in Fig. 5. The orbit is found to be in the $O-q_{1}q_{2}q_{3}$ frame, and the accuracy of the initial values given in Kazantis (1979) is of order $10^{-4}$ at a fourth period. This orbit has two nearly perpendicular crossing to the $q_{2}$ axis during the time T/4. Our numerical experiment with $k=j=0$ convinced this result by the accuracy $10^{-6}$. However, this SDSP is not linearly stable, as the index $\rho \approx$ 2.0E+18. Our improved initial information is $\tilde{\xi }_{1}=$0.47926856385, $\tilde{\xi }_{3}=$5.000000496E-3, $\dot{\tilde{\xi }}_{2}=$0.962741651771, and $T=$1.569831796427. In addition, some more examples are supplied in Table 3.

If we fix $\mu =0.06$ and $k=0,j=10$, then the small parameter $\varepsilon$ satisfies $\varepsilon ^{3}=1/21$. Let $a_{1}=\varepsilon ^{2}= 1/(21)^{2/3}\approx 0.13138$, then $|n|=\mu ^{1/2} \varepsilon ^{-3} =21 \sqrt{\mu }$. There is no restriction on the inclination i, so we can suppose $i_{1}=\pi /4$. A SDSP under this case can be calculated as is shown in Fig. 6. The orbit is of multiple revolutions and linearly stable. The Hill-type SDSPs in Hill’s lunar problem can also calculated, as many examples are shown in Table 4.

Fig. 5

An unstable SDSP in the i$_{3v}$ family found by Kazantis (1979). The orbital information includes $1-\mu =0.00095$, $\tilde{\xi }_{01}\approx$0.47926860, $\tilde{\xi }_{03}\approx$0.005, $\dot{\tilde{\xi }}_{2}$ $\approx$0.96274159, $T/4\approx$1.56983, and the Hamiltonian $\mathcal {H}^{\texttt {rot}}\approx -1.733535$

Fig. 6

One example of Hill-type SDSP around $m_{2}$ in the case $(1,+,+,+)$ with $m_{2}=\mu =0.06$, $k=0,j=10$, $\cos i=\sqrt{2}/2$ is supplied. The integration time span is 20 and its period T is 4 times of 1.568164286834137. The initial values $(\xi _{1}$,$\dot{\xi }_{2}$,$\dot{\xi }_{3})$ are 0.12098046779638547, 2.24272842162778E-3,1.4780876804155E-3, respectively

Table 3 A list of initial information of the SDSPs in the $m_{2}-q_{1}q_{2}q_{3}$ frame with $m_{1}=1-\mu =0.00095388$ and $\cos i=\sqrt{2}/2$

Table 4 A list of initial values of the Hill-lunar-type of SDSP with $\cos ^{2} i=1/2$

7 Discussion

This paper considers the numerical continuation of the comet- and Hill-type SDSPs of the approximate system to the full system. The full system can be the CRTBP or Hill’s lunar problem. There are few numerical results about Howison and Meyer’s SDSPs. The numerical results reveal that SDSPs exist even if the small symplectic scaled parameters are not necessarily too small. Classical continuation method based on the implicit function theorem which just has a local convergence may fail in continuing the approximate initial values to the exact values for the SDSPs. Broyden’s method with a line-search is taken in use to solve the nonlinear periodicity conditions expressed in the rectangular coordinates. The algorithm and related Fortran programs can be referred to Press et al. (1992). Numerically, different approximate initial values are continued to different initial values for the SDSPs, and we use sixteen cases to continue the known initial values of the Keplerian orbits. Some cases even fail because of the strong perturbation or the essential instability. Many successful examples in Tables 1, 3, 4 and in the Figures show that our numerical scheme behaves well in determining the SDSPs.

For a periodic orbit with double symmetry, only one fourth period information is needed to determine the whole orbit, and the reason is well explained. Some questions are raised at the end of this paper. First, numerical method has its advantages and shortcomings. If the perturbation is sufficiently small, the period ratio between the inner orbit and the outer orbit is also very small and the integration time will be long. If the perturbation is mild strong, the stability of the orbit starting from the beginning initial values affects the numerical integration and the continuation results. The grid search, Poincaré section method, the optimization method, the Lyapunov indicator method and so on can be integrated in order to give a better understanding of the three-dimensional phase structure. If the energy is fixed, then there are only two unknown initial parameters, and the families of periodic orbits can be tracked. The bifurcation of the families will be interesting for analysis. Second, there may exist invariant torus around the linearly stable periodic orbits. The linear stability may be settled with the help of Floquet theory and some perturbation methods. At last, as there exist singularities, so the regularization may be used in order to find more spatial periodic orbits in these problems with a background of real astronomy.