Different perspectives on the b-plane: perturbation effects and use for resonant flyby design

Abstract

Orbital resonances can be leveraged in the mission design phase to target planets at different energy levels. On the other side, precise models are needed to predict possible threatening returns of natural and artificial objects closely approaching a target planet. To this aim, we propose a semi-analytic extension of the b-plane resonance model to account for perturbing effects inside the planet’s sphere of influence. We compute the actual values of the perturbing coefficients by means of precise numerical simulations, whereas their expression stems from the properties of hyperbolic trajectories and asymptotic planetocentric velocity vectors. We apply the proposed b-plane model to design ballistic resonant flybys by solving a multilevel mixed-integer nonlinear optimization problem.

1 Introduction

The condition for two orbiting bodies to be in orbital resonance with each other is conceptually simple and is met when the two orbital periods are in a ratio that equals that of two integers. Such a physical phenomenon has been widely explored and exploited in the past two decades.

Orbital resonances can be used to further characterize the planetary protection analysis, which in general poses a constraint on the design of end of life and disposal maneuvers. The impact probability of human-crafted objects with specified planets or celestial bodies must remain below a certain threshold, under a certain confidence level up to some epoch forward in time. For instance, European Space Agency (ESA)’s planetary protection requirements (Kminek 2012) impose a planet-dependent maximum impact probability for the 100 upcoming years, accurate at 95$\%$ confidence level. Any of the mission disposal objects must be considered, as well as any perturbing effects on the two-body dynamics, uncertainties on maneuvers or initial conditions and possible failures of the propulsion systems must also be accounted for. An uncontrolled close approach of a disposal object with a given body is therefore a potential impact threat; studying orbital resonances allows the extension of the planetary protection analysis considering also future returns at the moment of first encounter.

Colombo et al. (2016) made some work in this direction developing the SNAPPshot suite, a tool that performs the planetary protection compliance analysis according to the just mentioned requirements (Kminek 2012). SNAPPshot’s original version estimates the impact probabilities performing a full Monte Carlo simulation, by sampling the state probability distribution that stems from either the uncertainty on the initial condition, the interplanetary injection maneuver or the failure of the propulsion system. SNAPPshot also represents possible resonant returns that may arise from the uncertainty sampling, using the b-plane formalism (Valsecchi et al. 2003). Romano (2020) improved the SNAPPshot suite by extending the pool of available numerical integration schemes and implementing a line sampling procedure, a Monte Carlo-based technique that improves the accuracy of the impact probability estimation and lowers the overall computational burden of the analysis.

Planetary defense is another direct application of orbital resonance theory, aiming to understand whether a near-Earth asteroid returns and threatens the planet again. Valsecchi et al. (2003) showed the b-plane potential for the resonance analysis, using the asteroid orbit characterization as principal application in their work. They also modeled the so-called keyholes (Chodas 1999), which are the counter-image of the Earth at the consequent resonant return mapped onto the b-plane of the current close encounter (Valsecchi et al. 2003). Keyholes identify the regions of the current b-plane that lead to future impacts, not simply to new crossings of the sphere of influence. Petit (2018) exploited the keyhole definition to design asteroid deflection maneuvers so that a consequent impact and resonance is avoided. The variety of works on the asteroid identification and characterization is extremely wide on its own, and it is beyond the scopes of this work to deepen the topic. Here, we focus on the b-plane model and its planetary protection and flyby design applications.

Orbital resonances are exploited in mission design applications, and repeated flybys over the same body can allow complex and composed trajectory deflections with low fuel consumption that could not be achieved with a single gravity assist maneuver. Most recent works explore the concept in the three-body problem and different moon systems.

Within the Earth–Moon system, Topputo et al. (2005) showed that a low-energy transfer to the L1 libration point is similar to a 5/2 resonance with the Moon. Topputo et al. (2008) studied a peculiar Earth–Moon resonance with a Poincare map approach to show its close link with weak capture into Moon orbits. Then, they also showed that such resonant orbits may lead to escape toward heliocentric trajectories, accounting for solar gravity within the four-body environment. Ceriotti and McInnes (2014) investigated the resonance exploitation for continuous polar observation missions, using the resonance with the Moon particularly for a ballistic flip of line of apsides. Vaquero and Howell (2014b) exploited the design of resonant arcs to target the libration points in the Earth–Moon system in the circular restricted three-body problem. Vaquero and Howell (2014a) also proposed a solution for targeting the libration point L5 exploiting dynamical systems theory and unstable invariant manifolds together with Moon-resonant orbits. Yárnoz et al. (2016) showed that the Sun gravitational perturbation can be used as free acceleration within multiple gravity assist trajectories in the Earth–Moon system, and applied the concept to design transfers to the Earth–Moon L2 point and toward the asteroid Phaethon. Oshima et al. (2017) searched for low-thrust transfers to the Moon in the circular restricted three-body problem, showing that repeated high-altitude lunar flybys reduce the total fuel consumption.

The other major set of works on orbital resonance exploitation regards the design of missions within Jupiter’s and Saturn’s moon systems. A proper trajectory choice is crucial, as major constraints on payload and fuel consumption are present. Johannesen and D’Amario (2000) designed the endgame of the Europa Orbiter mission within the Jovian system as a series of nearly resonant orbits with the Jovian moon Europa itself. Within the framework of the circular restricted three-body problem, Ross and Scheeres (2007) studied possible multiple gravity assist trajectories for quasi-ballistic captures and escapes in low-energy orbits. Campagnola and Russell (2010) introduced the Tisserand–Poincare graph for the study of ballistic endgames, showing the important role of resonant orbits patched with high-altitude flybys in the low fuel consumption and applying it to transfers between the Jupiter’s moons Europa and Ganymede and between halo orbits from the Jupiter-Ganymede to the Jupiter-Europa system. Woolley and Scheeres (2011) showed that, albeit the most efficient strategy for a cheap capture would require infinite flybys, fuel savings up to 50% can be achieved performing repeated gravity assists for v-infinity leveraging, without requiring excessive times of flight. Lantoine et al. (2011) used the Tisserand–Poincare graph to target trajectories in the patched three-body problem to optimize the fuel consumption in a transfer between a close resonant orbit of Ganymede to a close resonant orbit of Europa. Campagnola and Kawakatsu (2012) studied 3-D resonant hopping strategies to connect resonant orbits over Jupiter’s moons, for JAXA’s Jupiter Magnetospheric Orbiter mission. Vaquero and Howell (2013) exploited dynamical systems theory, invariant manifolds and Poincare maps to design ballistic transfers between libration point and resonant trajectories in the Saturn–Titan system to target the moon Hyperion. Campagnola et al. (2014) introduced the Tisserand-leveraging transfers to design low energy and applied them to ESA’s JUICE mission to Ganymede. They also used low-thrust models within Tisserand-leveraging transfers to explain the lunar resonances of the Moon orbiter SMART-1.

In this work, we use orbital resonances for trajectory design purposes in a different framework compared to what mentioned above, sticking to interplanetary resonant transfers and adopting the b-plane formalism, that allows the study of orbital resonances at the moment of first close encounter (Valsecchi et al. 2003). The theory is based on Opik’s variables (Opik 1976) and continues the work on the geometry and the modeling of close encounters initiated by Carusi et al. (1990) and Valsecchi et al. (1997). The formalism has been further developed in the past years by Valsecchi (2006) and Valsecchi et al. (2015) providing better insight on the geometry of close encounters and quasi-collision conditions (Valsecchi 2006). Valsecchi et al. (2015) obtained a fully analytic solution for the post-encounter orbital parameters, for a given entry condition to the sphere of influence (Valsecchi et al. 2015), under the assumptions of two-body zero-radius sphere of influence theory and conservation of the Tisserand parameter $\mathcal {T}$. A specified post-encounter semi-major axis is described by a circle in the b-plane (Valsecchi et al. 2003), tightly connected to the resonance definition because of its relation with the orbital period.

This work refines the b-plane model for a given post-encounter semi-major axis accounting for general perturbing effects. This is a direct consequence of better modeling the rotation of the planetocentric velocity vector experienced during gravity assists. The standard b-plane theory is summarized in Sect. 2. Section 3 presents a perturbed model for the b-plane circles, the loci of points of common post-encounter semi-major axis. We obtain the key physical quantities to extend the b-plane circle model to the general perturbed case with numerical simulations. The circular locus of point is extended to a belt-shaped one, also considering almost perfectly phased returns among the possibly threatening ones for planetary protection applications. We validate the model against a Monte Carlo simulation of Solar Orbiter’s upper stage of launcher, visualizing which subset of the simulated cloud on the b-plane is in actual, i.e., simulated, resonance with Venus. We finally apply the proposed b-plane model to the design of interplanetary resonant orbits in Sect. 4. We study the case of Solar Orbiter (SolO) (EADS-Astrium 2011; European Space Agency (ESA) 2011) with its repeated flybys of Venus aimed at rising the orbit inclination. An optimization problem is formulated and solved, designing resonant interplanetary trajectories with ballistic gravity assist maneuvers. We obtain a solution already close to ESA’s optimized resonant trajectory in a few seconds only.

2 B-plane deflection and resonance theory

2.1 Deflection and b-plane reference frame

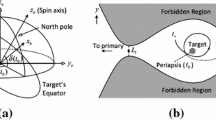
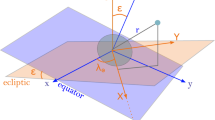
By assuming that the planet follows a circular orbit around the Sun, the reference frame of analysis (Fig. 1) was first introduced by Carusi et al. (1990). The system is centered on the planet’s center of mass, and the (x, y, z) axes are directed as the heliocentric position, velocity ${\textbf {v}}_{p}$ and orbital angular momentum of the planet, respectively.

Fig. 1

Graphical representation of the reference frame of analysis. Picture from Carusi et al. (1990)

The remaining quantities stand for the planetocentric velocities ${\textbf {U}}$ and ${\textbf {U}}'$ before and after the close approach, the spherical angles $\theta$ and $\theta '$ with respect to the planet’s velocity. The angles $\phi$ and $\phi '$ locate the maximum circles identified by the y-axis passing through the ${\textbf {U}}$ and ${\textbf {U}}'$ directions, respectively, measured from the maximum circle of the plane (y, z). $\gamma$ identifies the deflection magnitude (i.e., the turn angle of the flyby) and $\psi$ its direction, given as the internal angle between the sides $\gamma$ and $\theta$ of the spherical triangle $\theta \gamma \theta '$, formed by the vectors ${\textbf {U}}$, ${\textbf {U}}'$ and ${\textbf {v}}_{p}$ (Carusi et al. 1990; Valsecchi et al. 2003). The flyby effect is modeled as an instantaneous rotation of the vector ${\textbf {U}}$ without magnitude change.

First defined in Appendix of Greenberg et al. (1988) as $(x',y',z')$ in the framework of Öpik’s theory (Opik 1976) and corresponding to the $(\xi ,\eta ,\zeta )$ frame of Valsecchi and Manara (1997) and Valsecchi et al. (2003), the axes $(\hat{\xi },\hat{\eta },\hat{\zeta })$ of the b-plane reference frame are defined as:

(1)

The impact parameter b is defined in the b-plane as (Milani et al. 2002)

$$\begin{aligned} \begin{aligned} \xi ^2+\zeta ^2=b^2. \end{aligned} \end{aligned}$$

(2)

Recalling Fig. 1, from an interplanetary point of view the flyby can be modeled as an instantaneous rotation of ${\textbf {U}}$ into ${\textbf {U}}'$. The resulting velocity deflection can be determined by solving the spherical triangle $(\theta ,\gamma ,\theta ')$, with $\psi$ acting as internal angle, obtaining the new orientation $\theta '$. The cosine law for spherical geometry gives (Valsecchi et al. 2003):

$$\begin{aligned} \begin{aligned} \cos \theta ' = \cos \theta \cos \gamma + \sin \theta \sin \gamma \cos \psi . \end{aligned} \end{aligned}$$

(3)

2.2 Resonant circles

The b-plane coordinates and the impact parameter provide a straightforward definition of the deflection direction angle $\psi$ (Carusi et al. 1990; Valsecchi et al. 2003):

$$\begin{aligned} \begin{bmatrix} \xi \\ \zeta \end{bmatrix} = \begin{bmatrix} b\sin \psi \\ b\cos \psi \end{bmatrix} \end{aligned}$$

(4)

and introducing the quantity $c=m/U^2$, where m is the planet’s mass expressed in solar masses, $\gamma$ can be identified as (Valsecchi et al. 2003):

$$\begin{aligned} \tan \frac{\gamma }{2} = \frac{m}{bU^2} = \frac{c}{b} \end{aligned}$$

(5)

or

$$\begin{aligned} \cos \gamma= & {} \frac{b^2 - c^2}{b^2 + c^2} \nonumber \\ \sin \gamma= & {} \frac{2bc}{b^2+c^2}. \end{aligned}$$

(6)

We introduce the resonance definition, i.e., that a flyby leads to a resonant return when the new small object’s interplanetary orbit (with superscript $'$) satisfies the condition (Valsecchi et al. 2003)

$$\begin{aligned} h T'_{obj}=k T_{pl} \end{aligned}$$

(7)

with T to identify the orbital periods for the planet (pl) and of the small object (obj) and (k, h) positive integers, respectively, the number of orbits of planet and small object until the next close approach. In the adopted unit system (Valsecchi et al. 2003), the planet’s orbital period is $T_{pl} = 2\pi$ and the small object’s one is linked to the new interplanetary orbit semi-major axis by $T'_{obj} = 2\pi a'^{3/2}$. Therefore, a resonant post-encounter semi-major axis can be determined just by k and h (Valsecchi et al. 2003). The subscript R is added to remark the resonance feature of this new orbit:

$$\begin{aligned} a'_R = \bigg (\frac{k}{h}\bigg )^{2/3}. \end{aligned}$$

(8)

The resonant condition is fully determined by the angle $\theta '_R$ (Valsecchi et al. 2003):

$$\begin{aligned} \cos \theta '_R = \frac{1 - 1/a'_R - U^2}{2U}. \end{aligned}$$

(9)

This post-encounter angle must satisfy the deflection equation (Equation (3)). The resonant circle equation proposed in Valsecchi et al. (2003) is then:

$$\begin{aligned} \xi ^2 + \zeta ^2 -\frac{2c\sin \theta }{\cos \theta '_R-\cos \theta }\zeta + \frac{c^2(\cos \theta '_R + \cos \theta )}{\cos \theta '_R-\cos \theta } = 0, \end{aligned}$$

(10)

which is equivalent to

$$\begin{aligned} \xi ^2 + \zeta ^2 -2D\zeta + D^2 = R^2 \end{aligned}$$

(11)

with

$$\begin{aligned} D = \frac{c\sin \theta }{\cos \theta '_R-\cos \theta } \qquad R = \bigg |\frac{c\sin \theta '_R}{\cos \theta '_R-\cos \theta }\bigg |. \end{aligned}$$

(12)

3 Perturbed semi-analytic extension

We semi-analytically extend the b-plane resonance model, considering also non-perfectly phased returns as resonant ones (Sect. 3.1) and accounting for perturbation effects inside the sphere of influence (Sect. 3.2).

3.1 Resonant belts

Recalling Equations (7) and (8), as in Colombo et al. (2016) we introduce a quasi-resonance definition, i.e., an object is considered in resonance with a given planet whether the condition for a generic resonance k/h

$$\begin{aligned} \bigg |\frac{T_{object}/T_{planet} - k/h}{k/h}\bigg |\le \Delta ^* \end{aligned}$$

(13)

is satisfied, with the quantity $\Delta ^*$ to be an arbitrary value identifying the quasi-resonance threshold. We can be conceptually revert the definition, in order to obtain the values of k/h that correspond to the quasi-resonance boundaries:

$$\begin{aligned} \frac{k}{h}^{\pm } = \frac{k}{h}(1\pm \Delta ^*). \end{aligned}$$

(14)

Re-applying Equation (8), we obtain two new quasi-resonant post-encounter semi-major axes:

$$\begin{aligned} a_{R}^{'\pm } = \bigg (\frac{k}{h}^{\pm }\bigg )^{2/3}, \end{aligned}$$

(15)

which in turn result in two new values for $\cos \theta '_R$ (as in Eq. (9)) and the parameters of two new resonant circles (as in Eq. (12)).

3.2 Perturbed deflection

Some work to model perturbing effects in hyperbolic trajectories has already been made. For example, Anderson and Giampieri (1999) present an analytic solution for perturbing angles in a formalism close to Öpik’s variables (Opik 1976), by means of the Born approximation (Fowler et al. 1927). A few of the geometrical considerations made in Anderson and Giampieri (1999) remain valid in this work, even though we assume no specific expression of the perturbing force and do not apply superposition of effects.

Starting with the perturbing effects, inside the sphere of influence any perturbation acts by modifying the classical spherical triangle introduced by Carusi et al. (1990) and Valsecchi et al. (2003) for the angles:

$$\begin{aligned} \begin{aligned} \gamma ^*&= \gamma + \Delta \gamma \\ \psi ^*&= \psi + \Delta \psi \\ \theta ^{'*}&= \theta ' + \Delta \theta ' \end{aligned} \end{aligned}$$

(16)

with the superscript $^*$ to identify the real quantities after the flyby and the clean symbols to denote the analytic ones, from the usual resonance theory (Valsecchi et al. 2003). Such angles are relative to the single planetocentric trajectory, i.e., in general different variations appear for different trajectories undergoing the same perturbations. Then, we model perturbing effects as the angular displacements given by $(\Delta \gamma ,\Delta \psi ,\Delta \theta ')$, which modify the two-body asymptotic velocity deflection given by $(\gamma ,\psi ,\theta ')$.

Modeling the variation in the deflection $\gamma ^*$ and $\theta ^{'*}$ is straightforward:

(17)

Re-arranging Equation (16) and with the definition of $\gamma$ from Equation (6), $\Delta \gamma$ becomes

$$\begin{aligned} \Delta \gamma = \gamma ^* - \gamma = \gamma ^* - \arccos \bigg (\frac{b^2-c^2}{b^2+c^2}\bigg ) \end{aligned}$$

(18)

and $\Delta \theta '$, with the expression for $\theta '$ as in Equation (9)

$$\begin{aligned} \begin{aligned} \Delta \theta ' = \theta ^{'*} - \theta ' = \theta ^{'*} - \arccos \bigg (\frac{1-1/a^{'}-U^{2}}{2U}\bigg ) \end{aligned} \end{aligned}$$

(19)

with the symbol $a^{'*}$ to denote the actual post-encounter semi-major axis, without the resonance subscript to preserve for now the generality of the definition. Following the definition in Equation (19), possible variations of the asymptotic velocity magnitude U can be included in $\Delta \theta '$.

The computation of the perturbation $\Delta \psi$ requires some observations on the encounter geometry. By definition, the b-plane is perpendicular to the vector ${\textbf {U}}$, which identifies the $\hat{\eta }$ direction (Equation (1)) and is common to both the simulated and the theoretical deflections. Particularly, we observe that:

• The angle $\psi$ is measured clockwise on the b-plane and counterclockwise on the three-dimensional reference frame of Fig. 1 (Carusi et al. 1990; Valsecchi et al. 2003).

• The vector ${\textbf {U}}\times {\textbf {U}}'^{*}$ identifies the principal rotation direction of ${\textbf {U}}$ into ${\textbf {U}}'^{*}$ and must lie on the b-plane, because of the cross-product properties.

We denote with $\psi$ and $\psi ^*$ the deflection direction angles, theoretical and actual, respectively, according to the definition by Carusi et al. (1990) and Valsecchi et al. (2003). $\psi ^*$ is related but not equal to the angle identified by the vector ${\textbf {U}}\times {\textbf {U}}'^{*}$ and the $+\hat{\zeta }$ direction. If we define $\tilde{\psi }^*$ as the counterclockwise angle measured from the $-\hat{\zeta }$ direction to the vector ${\textbf {U}}\times {\textbf {U}}'^{*}$, we have that

$$\begin{aligned} \begin{aligned} |\tilde{\psi }^*|= |\psi ^*|+ \pi /2. \end{aligned} \end{aligned}$$

(20)

Similarly, switching to a counterclockwise measure from the $-\hat{\zeta }$ direction also for the angle $\psi$ allows us to introduce the related angle $\tilde{\psi }$. Its definition is similar to Equation (4) and also stems from the b-plane coordinates $\xi$ and $\zeta$:

$$\begin{aligned} \begin{aligned} \cos (\tilde{\psi }-\pi /2)&= -\frac{\zeta }{b}\\ \sin (\tilde{\psi }-\pi /2)&= \frac{\xi }{b}. \end{aligned} \end{aligned}$$

(21)

Figure 2 shows a graphical representation of these handle angles $\tilde{\psi }$ and $\tilde{\psi }^*$.

Fig. 2

Graphical representation of the rotation convention used for the computation of $\Delta \psi$

These handle angles allow us to retrieve the value of $\Delta \psi$ because they still refer to the rotation direction vector and the chosen b-plane point $(\xi ,\zeta )$. To obtain $\tilde{\psi }^*$, we first express the vector ${\textbf {U}}\times {\textbf {U}}'^{*}$ in the b-plane reference frame with¹

$$\begin{aligned} \begin{aligned} {\textbf {U}}\times {\textbf {U'}}|^*_{b-plane} = \big [\hat{\xi },\hat{\eta },\hat{\zeta }\big ]^T {\textbf {U}}\times {\textbf {U'}}|^*_{Cartesian} \end{aligned} \end{aligned}$$

(22)

and then, observing the geometry of Fig. 2, we retrieve $\tilde{\psi }^*$ using its cosine:

$$\begin{aligned} \begin{aligned} \cos \tilde{\psi }^* = \frac{\big [{\textbf {U}}\times {\textbf {U'}}|^*_{\hat{\xi }},{\textbf {U}}\times {\textbf {U'}}|^*_{\hat{\zeta }}\big ]^T\cdot [0,-1]^T}{|{\textbf {U}}\times {\textbf {U'}}||^*}. \end{aligned} \end{aligned}$$

(23)

Since both the angles $\tilde{\psi }$ and $\tilde{\psi }^*$ are measured counterclockwise on the b-plane, we add a change of sign to finally comply with the original b-plane description (Carusi et al. 1990; Valsecchi et al. 2003), obtaining:

$$\begin{aligned} \begin{aligned} \Delta \psi = -(\tilde{\psi }^*-\tilde{\psi }). \end{aligned} \end{aligned}$$

(24)

3.3 Perturbed circle parameters

The perturbing angles $(\Delta \gamma ,\Delta \psi ,\Delta \theta ')$ modify the circle parameters presented in Equation (12), since their definition has a direct impact on the variables that mathematically define the circles. Consequently, the resonant circle equations need to be re-derived. The spherical triangle equation highlighting the perturbations is then

$$\begin{aligned} \begin{aligned} \cos \theta ^{'*}_R = \cos \theta \cos (\gamma +\Delta \gamma )+\sin \theta \sin (\gamma +\Delta \gamma )\cos (\psi +\Delta \psi ). \end{aligned} \end{aligned}$$

(25)

Since the perturbing effects must be small compared to the main two-body effect, the overall shape should be still identified by circles centered on the $\hat{\zeta }$ axis. Then, we find the two intersections of such circles with the b-plane $\hat{\zeta }$ axis, linked to the new circle parameters as:

$$\begin{aligned} \begin{aligned} \zeta _{1,2} = D\pm R, \end{aligned} \end{aligned}$$

(26)

which correspond to the solution of the quadratic equation that is obtained by setting $\xi = 0$ and exploiting $b^2 = \zeta ^2+\xi ^2$ in Equation (25), after introducing the b-plane definition of the trigonometry functions of $\gamma$ and $\psi$. The full derivation is reported in Appendix A. The trigonometry function properties lead to the definition of the following perturbed circle parameters:

$$\begin{aligned} \begin{aligned} D&= \frac{c(\sin \theta \cos \Delta \gamma \cos \Delta \psi - \cos \theta \sin \Delta \psi )}{\cos \theta ^{'*}_R - \cos \theta \cos \Delta \gamma - \sin \theta \sin \Delta \gamma \cos \Delta \psi }\\ R&= \bigg |\frac{c\sqrt{\sin ^2\theta ^{'*}_R-\sin ^2\theta \sin ^2\Delta \psi }}{\cos \theta ^{'*}_R - \cos \theta \cos \Delta \gamma - \sin \theta \sin \Delta \gamma \cos \Delta \psi }\bigg |. \end{aligned} \end{aligned}$$

(27)

If the angles $\Delta \gamma$, $\Delta \psi$ and $\Delta \theta '$ were all zero, the original solution of Equation (12) from Valsecchi et al. (2003) would be obtained.

3.4 Validation: SolO’s upper stage of launcher planetary protection

A test case taken from a study conducted in Colombo et al. (2016) over Solar Orbiter’s (SolO) upper stage of launcher is shown in Fig. 3, the same presented for the planetary protection analysis in Fig. 5. The original analysis and data reported in Colombo et al. (2016) were referred to a mission profile with launch on October 2018 (European Space Agency (ESA) 2011), while the actual launch eventually took place in February 2020.

The nominal initial condition is (J2000 reference frame, centered on the Sun)²:

(28)

and the covariance matrix ${\textbf {C}}$ used for the sample generation (Colombo et al. 2016) for the Monte Carlo simulation expressed in an inertial Cartesian reference frame is reported in Table 1.

Table 1 SolO’s covariance matrix unique elements at the initial epoch, inertial reference frame (Colombo et al. 2016)

The simulated nominal condition features a resonant close approach (resonance condition $k/h = 5/4$) with Venus at epoch April 6, 2019, 12:40:58.214 UTC. We used the flyby entry nominal condition as basis for the validation of the deflection model in Fig. 3, where we held the entry velocity constant and equal to:

$$\begin{aligned} \begin{aligned} {\textbf {U}}_0 = \begin{Bmatrix} 3.79322995886949 \\ -8.13551531308769 \\ -2.1091357908664 \end{Bmatrix} \text {km/s}. \end{aligned} \end{aligned}$$

(29)

We multiplied the same initial velocity by a factor 0.1 to generate the low-velocity case presented in Fig. 4.

3.4.1 B-plane deflection model

We have obtained the b-plane region presented in Figs. 3 and 4, simulating with Matlab a fine grid of points, all with the planetocentric velocity of the respective nominal conditions but with different initial positions. We generated the samples in b-plane polar coordinates and divided the whole domain in several regions; for the sake of conciseness, we present only the low- and high-altitude results, for a limited b-plane region. We compute the deflection as the rotation of the planetocentric velocity due to the angles $\gamma$ and $\psi$, and we then compare it to the results from numerical simulations in the relativistic N-body environment. In the corrected b-plane model, the angles $\Delta \gamma$ and $\Delta \psi$ introduce the perturbing effects, computed from the simulation of the nominal sample. We then apply the same numerical values of $\Delta \gamma$ and $\Delta \psi$ to the whole cloud of simulated b-plane points. The perturbation on $\Delta \theta '$ affects the circles for a specified post-encounter semi-major axis only; thus, we show it directly on the planetary protection analysis.

In the SolO case, the implemented correction (Fig. 3b and d) improves the deflection model, obtaining exact deflections at the point where the perturbations are computed and highly accurate results nearby, although the error obtained with the standard deflection is already small (Fig. 3a and c). High-altitude flybys are less affected by errors, because of the lower time spent within the planet’s sphere of influence and the lower nominal deflection, which introduces some error amplification itself.

Fig. 3

Relative errors against full numerical simulation, SolO-like close approach

The low-speed case shown in Figure 4 partly exposes the singularity of the b-plane formalism visible in the definition of $\cos \theta$ (Equation (9)). The error becomes large at both low and high altitudes (Fig. 4a and c), and despite enormously improved by the perturbed model (Fig. 4b and d), the reliability of the proposed approach becomes extremely localized. This is due to the b-plane theory itself, not suited to handle low-energy cases where the three-body problem would better describe the dynamical regime. Still, the simulation-based computation of the perturbing angles keeps the deflection error small nearby the reference where such angles are computed.

Fig. 4

Relative errors against full numerical simulation, low-speed close approach

3.4.2 Perturbed resonant belts

We obtained the results presented in this subsection using SNAPPshot to perform a planetary protection analysis for SolO’s upper stage of launcher. We generated the cloud of points shown in Fig. 5a and b using the Monte Carlo analysis and consequent b-plane representation of the resonances already available in SNAPPshot. We computed the perturbing coefficients $(\Delta \gamma ,\Delta \psi ,\Delta \theta ')$ only at the barycenter of the simulated cloud, expecting accurate results near it. This is mainly due to SNAPPshot’s current features that allow the user to retrieve the full propagation data only of a single specified sample of the cloud (Colombo et al. 2016). We present a visual check in Fig. 5a and b, whereas the numerical values for the relative error are available in Table 2. We show directly the resonant belts, both for a better visualization of the results and to check the compliance of the size of the modeled belts with the amplitude of the proportion of the cloud in actual orbital resonance.

Fig. 5

Visual accuracy improvement of the b-plane circle model. The analytical belts are bounded by the black circles, the yellow dots represent the numerically detected resonances, and the gray dots represent the numerically simulated non-resonant close approaches

The error drastically drops nearby the reference point and it increases the farther the cloud’s samples get from it, as expected from the deflection model validation and as the numerical values in Table 2 show. Figure 5a and b also offers a visual feeling of the improvement reached: The yellow dotted loci of points, being the b-plane representation of numerically simulated resonances, are now almost perfectly predicted by the analytical belts, drawn in black. Furthermore, the neat separation from the non-resonant close approaches (dark gray dots) is also precisely predicted.

4 Ballistic resonant flyby design

In a planetary protection application, one wishes to identify orbital resonances in order to minimize the probability of a resonant return. Here, instead, we exploit the resonant circle concept in the opposite way, using the degree of freedom left in the patched conics approximation³ to force resonant flybys, trying to achieve a total ballistic deflection unfeasible for a single flyby.

About the perturbed b-plane model proposed in this work, we are not aware of any application of this kind in the literature, particularly dealing with open interplanetary resonances. The model is yet to be completed to the most general extent, i.e., it still relies on the patched conics approximation for the definition of resonance. In other words, even though there we can already semi-analytically refine the deflection of the planetocentric velocity vector, constraining the corresponding modified resonant circles does not provide the same $\Delta {\textbf {v}}$ of their two-body parents and therefore does not correspond to the $\Delta {\textbf {v}}$ required for that specified resonance to happen. In any case, the innermost structure of the algorithm we present remains unchanged, since only the interfaces with the interplanetary environment will be adapted in future works.

Table 2 SolO case, relative error for standard and corrected belt models with respect to the simulated resonances

The proposed algorithmic method features a modular structure, where at the highest level the resonant flybys are designed by solving a global optimization problem, under a fully two-body patched conics approximation. At a lower level, the perturbed resonant deflections are designed to minimize their difference against each correspondent optimal two-body $\Delta {\textbf {v}}$. Some work in a similar direction, even though not specifically meant for the optimal trajectory design purposes of this work, was already done in Valsecchi (2006) and Valsecchi et al. (2015), where the authors developed an analytic solution for the post-encounter Keplerian parameters implementing the b-plane deflection formalism. In Valsecchi (2006) and Valsecchi et al. (2015), a fully b-plane and Keplerian description was enough to achieve a fully analytic solution. In this work, we propose instead a hybrid Cartesian, b-plane and Keplerian approach, in order to exploit the b-plane flyby design properties, the Keplerian description of the orbital parameters and the simplicity of the Cartesian coordinates, where the flyby deflections become simple vector summations.

4.1 Assumptions

First of all, a major limitation appears when using the b-plane formalism for design purposes: The deflections can be described in this framework only if fully natural. An artificial maneuver modifies the outgoing asymptote, the hyperbolic excess velocity magnitude and consequently the geometry described in Carusi et al. (1990). The design is limited to initial and final orbits featuring the same Tisserand parameter $\mathcal {T}$. Recalling the relation in Carusi et al. (1990) and Valsecchi et al. (2003):

$$\begin{aligned} \begin{aligned} U = \sqrt{3 - \mathcal {T}}. \end{aligned} \end{aligned}$$

(30)

The two-body patched conics definition of orbital resonance naturally embeds another assumption: Under a Cartesian description of the two orbits, the position remains fixed for all the resonant flybys designed, with only the heliocentric velocity ${\textbf {v}}$ to change according to some $\Delta {\textbf {v}}$ to have consequent resonant returns. This new velocity ${\textbf {v}}+\Delta {\textbf {v}}$ becomes the incoming condition of the consequent flyby. In this way, at least part of the combinatorial nature of the multi-flyby design problem can be neglected; having the encounter position always fixed in time and space reduces the problem to identifying the velocities only.

Even when dealing with resonances some combinatorial issues exist, i.e., what actual resonance to choose at each flyby. Once a specified resonance is selected, there are again infinite possible solutions that satisfy such a resonance condition, which represent the degree of freedom exploited in the presented algorithm.

Apart from the gravitational constants, the reference frame and the ephemerides data, the algorithm requires:

• A set of admissible resonances $S=\big \{k/h|_i\big \}$.

• An initial orbit $({\textbf {r}}_0,{\textbf {v}}_0)$.

• An ultimate target orbit $({\textbf {r}}_f,{\textbf {v}}_f)$.

• The number of close approaches N to be designed to reach such a final trajectory.

Figure 6 shows a block scheme diagram of the overall algorithm, described in detail in the following sections.

Fig. 6

Block scheme diagram of the overall design algorithm

4.2 Optimization levels

4.2.1 Highest level

A sub-$\Delta {\textbf {v}}$ target is assigned to each flyby, and the planetocentric trajectory is selected in order to minimize the difference between its own deflection and the specified sub-target. The highest optimization level determines the best set of sub $\Delta {\textbf {v}}$ targets that eventually minimizes the artificial contribution needed to match the final orbit. We can formulate the optimization problem as:

$$\begin{aligned}&{\mathop {\hbox {minimize}}\limits _{\Delta {\textbf {v}}^{(i)}}}\quad {|\Delta {\textbf {v}}_{residual}(\Delta {\textbf {v}}^{(i)},(k/h)_i,{\textbf {v}}_0,{\textbf {v}}_f)|}\nonumber \\&\hbox {subject to}\quad {\mathop {\sum }\limits _{i}} \Delta {\textbf {v}}^{(i)} = \Delta {\textbf {v}}_{target}, \quad i = 1,...,N,\nonumber \\&(k/h)_i\; {\in S, \quad i = 1,...,N}. \end{aligned}$$

(31)

Three remarks arise from the possible ways of computing $|\Delta {\textbf {v}}_{residual}|$:

• The summation of the sub-targets $\Delta {\textbf {v}}^{(i)}_{target}$ must lead to the global $\Delta {\textbf {v}}_{target}$, but the optimal solution could still feature some residual at each flyby. The resonance condition is a constraint on the $\Delta {\textbf {v}}$ to ensure consequent return; matching the global deflection does not require anything specific on the single flybys.

• We should expect some residuals arising because of the resonance constraint; in spite of this, the summation of all the actual $\Delta {\textbf {v}}$-s given must still lead to the final target.

• The last flyby may not be resonant and should match the final orbit, allowing a much more flexible design of the last deflection.

A possible design choice is then splitting evenly the residual $\Delta {\textbf {v}}$ of the current flyby over all the next sub-targets. This allows the design of resonant flybys up to and including the penultimate one, without any artificial $\Delta {\textbf {v}}$, optimizing the last and more flexible deflection to reach the final target.

For N flybys, we can write the sub-target update as:

$$\begin{aligned} \begin{aligned} \Delta {\textbf {v}}^{(i)}_{target, \, new} = \Delta {\textbf {v}}^{(i)}_{target, \, old} + \sum _{j = 1}^{i - 1} \frac{\Delta {\textbf {v}}^{(j)}_{residual}}{N-j} \qquad i = 2,...,N. \end{aligned} \end{aligned}$$

(32)

The sub-targets are a sort of guidance for the design of each flyby. Here lies the drastic reduction in the combinatorial nature of the problem, replaced by the solution of a non-smooth optimization leading to the optimal set of brute-force designed resonant deflections. Figure 7 shows a summary of the algorithm flow for the presented optimization level.

Fig. 7

Block scheme diagram of the higher optimization level

4.2.2 Resonant flyby optimization

Given a set S of resonances, for a specified sub $\Delta {\textbf {v}}$ the algorithm finds the best resonant trajectory whose deflection gets the closest to the sub-target. We perform this with another two-level local optimization algorithm:

• 1. Select one of the resonances in S.

• 2. Find the point on the resonant circle that gives the best $\Delta {\textbf {v}}$.

• 3. Loop over all the admissible resonances and pick the best $\Delta {\textbf {v}}$.

• 4. Store the data the selected resonant trajectory.

We still need to introduce some constraints to bound the trajectories in a feasible region (i.e., the impact parameter must be at the same time not too low and not too high, $b_{min}\le b \le b_{max}$). Figure 8 summarizes the algorithm flow.

Fig. 8

Block scheme diagram of the circle-level optimization

4.3 Deflection models

4.3.1 Unperturbed case

We model each deflection using the b-plane formalism. A distinction between resonant and free flybys is required for the first step: A specific resonance acts similarly to imposing a constraint on the position on the b-plane; the point must belong to a circle of center’s $\hat{\zeta }$ coordinate D and radius R. Identifying with $\alpha$ a counterclockwise angle measured from the $\hat{\xi }$ direction (exactly as the angle in simple polar coordinates), given D and R a generic point is identified by:

$$\begin{aligned} \begin{aligned} \xi&= R\cos \alpha \\ \zeta&= D + R\sin \alpha \end{aligned} \end{aligned}$$

(33)

and the impact parameter is defined as

$$\begin{aligned} \begin{aligned} b^2 = \xi ^2 + \zeta ^2, \end{aligned} \end{aligned}$$

(34)

whereas for a non-resonant case we obtain $\xi$ and $\zeta$ by

$$\begin{aligned} \begin{aligned} \xi&= b\cos \alpha \\ \zeta&= b\sin \alpha , \end{aligned} \end{aligned}$$

(35)

where b acts directly as the radius variable in b-plane polar coordinates. The non-resonant case removes the resonant circle constraint, introducing one more degree of freedom on b.

We compute the deflection angle $\gamma$ as in Valsecchi et al. (2003):

$$\begin{aligned} \begin{aligned} \cos \gamma = \frac{b^2-c^2}{b^2+c^2}. \end{aligned} \end{aligned}$$

(36)

The rotation direction lies on the b-plane, and its orientation is strictly linked to the angle $\psi$, defined as:

$$\begin{aligned} \begin{aligned} \cos \psi&= \frac{\zeta }{b}\\ \sin \psi&= \frac{\xi }{b}. \end{aligned} \end{aligned}$$

(37)

Particularly, the planetocentric velocity points toward the b-plane and the angle $\psi$ measures a clockwise rotation from the $\hat{\zeta }$ direction to the b-plane point itself. In addition, we observe that the velocity vector is always rotated toward the center of the plane. Consequently, a possible deflection direction computation strategy rotates the direction $-\hat{\zeta }$ counterclockwise of an angle $\psi +\pi /2$. Then, the rotation of the Cartesian incoming planetocentric velocity ${\textbf {U}}_i$ into the outgoing one ${\textbf {U}}'_i$ at the ith flyby follows these steps:

• 1. Rotate $-\hat{\zeta }$ counterclockwise of $\psi +\pi /2$.

• 2. Represent this new vector in the Cartesian reference frame, applying a vector rotation whose matrix arises from the b-plane axes definition (Equation (1)).

• 3. Include $\gamma$ to build the principal rotation vector in the Cartesian reference frame.

• 4. Apply the rotation to ${\textbf {U}}_i$.

• 5. Compute $\Delta {\textbf {v}}^{(i)} = {\textbf {U}}'_i - {\textbf {U}}_i$.

Defining the residual of flyby i as

$$\begin{aligned} \begin{aligned} \Delta {\textbf {v}}^{(i)}_{residual} = \Delta {\textbf {v}}^{(i)}_{target} - \Delta {\textbf {v}}^{(i)} \end{aligned} \end{aligned}$$

(38)

at the lowest level, the optimization process finds a solution where the quantity $|\Delta {\textbf {v}}^{(i)}_{residual}|^2$ is minimized. For the last free flyby, the algorithm selects the best coordinates $(b,\alpha )$, whereas for a resonant flyby the choice is limited to the coordinate $\alpha$ and the correspondent circle parameters.

4.3.2 Perturbed case

We rely on a fine b-plane mapping of $\Delta \gamma$, $\Delta \psi$ and $\Delta \theta '$ to account for perturbing effects. We report the interpolation and mapping strategies we adopted in this concept validation in Appendix B, as well as the way to compute the perturbed resonant circles from a map of perturbing angles.

Since the resonance definition is still strictly two-body patched conics, the current implementation of the algorithm targets these resonant orbits. We expect some residuals given the circle modification, i.e., because we compute the perturbed $\Delta {\textbf {v}}$s so that their difference with respect to the already optimized two-body deflections is minimized. We do not mean these $\Delta {\textbf {v}}$s to be maneuvers to be implemented, and our current purpose is only to show the difference between the perturbed and the unperturbed cases.

For the resonant case, we apply the same optimization process, constraints and deflection presented in the unperturbed application. The only difference lies on including the perturbing angles $\Delta \gamma$ and $\Delta \psi$ in the deflection computation. The perturbed last free flyby is again free of any constraint, and solution is free to comply with the last deflection required. Yet again the deflection model remains the same, but having both b and $\alpha$ as optimization variables and including the perturbing effects.

4.4 Validation:SolO-like resonant orbit design

We performed the optimization with Matlab and JPL ephemerides through the SPICE toolkit (Acton 1996), using the function patternsearch.m at the highest level (optimal $\Delta {\textbf {v}}$ target search) and a multi-start fmincon.m for the unperturbed b-plane deflections, since the formulation is non-convex albeit smooth enough to allow the convergence of descent methods if starting from a good enough initial guess. In general, for the perturbed model the interpolation of the perturbing parameters makes the problem non-smooth even at the planetocentric design; thus, we implemented a patternsearch.m optimization at this level as well, with an fmincon.m refinement performed on the direct search optimal solution.

We ask the resonant trajectory design algorithm to search for an optimal solution similar to SolO’s flybys of Venus (EADS-Astrium 2011), where resonant gravity assists raise the orbit’s ecliptic inclination with low-cost maneuvers. We expect the solution to slightly differ from ESA’s optimized one, since the algorithm for now designs ballistic flybys only. In any case, reaching a solution similar to SolO’s mission profile would give a strong proof of the proposed design approach.

The reference case is the solution proposed with launch in January 2017 in European Space Agency (ESA) (2011), even though the actual launch has eventually happened in February 2020. We report the just mentioned optimized trajectory in Fig. 9. We use our algorithm to reproduce the resonant flybys only, i.e., to find a solution similar to the trajectory between the close approaches marked as V2 and V6.

Fig. 9

Optimized, final orbit sequence for the January 2017 Solar Orbiter’s mission plan. Picture from European Space Agency (ESA) (2011)

We report the main features of the four resonant orbits in Table 3, with the first flyby to happen on May 22, 2020 (European Space Agency (ESA) 2011). The resonances are also available in European Space Agency (ESA) (2011), (3/4, 3/4, 2/3, 3/5) in that order. We use the same notation introduced in European Space Agency (ESA) (2011) to identify the different close approaches, with Vi standing for the ith flyby of Venus and $Vi-Vj$ referring to the heliocentric orbit between the flybys i and j. The orbits are uniquely defined, since the position of Venus at each specified time adds the three remaining parameters.

Table 3 Orbital parameters of the resonant orbits for SolO’s January 2017 mission profile (European Space Agency (ESA) 2011)

4.4.1 Unperturbed (interplanetary) level

For the sake of testing the fully ballistic design algorithm, we remove some of the mission constraints, especially keeping perihelion and aphelion altitudes within specified boundaries. Therefore, we ask the solver to perform the specified change in inclination in the same number of flybys, letting all the parameters adjust autonomously. Given the optimal resonances mentioned above, the algorithm selects (k, h) values only within the range 1 to 5. We report the initial and final orbits for a Solar Orbiter-like resonant phase with Venus in Table 4.

Table 4 Initial and final orbit parameters given as input to the optimization algorithm

The total deflection required is

$$\begin{aligned} \begin{aligned} \Delta {\textbf {v}}_{tot} = \begin{Bmatrix} -10.544\\ -7.553\\ 13.381 \end{Bmatrix} \text {km/s}. \end{aligned} \end{aligned}$$

(39)

The algorithm converged to a ballistic optimal solution, obtaining a $\Delta {\textbf {v}}_{residual}$ after the last flyby whose norm is on the order of $10^{-8}$ km/s. The four deflections are

(40)

We report the orbits designed in Fig. 10 and their parameters in Table 5. The intermediate orbits feature resonances (3/4, 2/3, 3/5) and the last orbit complies with the final inclination, albeit the last orbit reported in Table 3 is still in a 3/5 resonance. As a visual check, the algorithm has produced orbits that are similar to the optimized ones (Fig. 9) available in European Space Agency (ESA) (2011). Also, the orbital parameters obtained are similar, apart from the perihelion distance which appears to be the main objective of control maneuvers, given also the purposes of the mission itself (EADS-Astrium 2011).

Fig. 10

Interplanetary trajectory computed by the optimization algorithm

Table 5 SolO-like interplanetary orbital parameters for the trajectories computed by the optimization algorithm

Only the first one out of three resonances corresponds to the ones designed in European Space Agency (ESA) (2011). This may be due to the absence of maneuvers and mission constraints in the optimization algorithm, which, for instance, leads to perihelion distances too low compared to the constraints specified in European Space Agency (ESA) (2011). Also the Cartesian formulation of the objective function that features an automatic $\Delta {\textbf {v}}$ split might affect the obtained solution, since the optimization does not include user-specified intermediate orbital parameters.

4.4.2 Perturbed b-plane level

Figure 11 shows the perturbed b-plane points that are chosen for achieving a deflection that gets the closest to the unperturbed interplanetary target. Visually, their distance from the optimal unperturbed b-plane coordinates seems to be minimized, and this may be due to the higher difference between the b-plane circle shapes than the actual $\Delta {\textbf {v}}$ deflections, as it is discussed in Sect. 3.4.1. For the sake of conciseness, all the resonant flybys are reported in the same plot, although the b-plane reference frame itself has a different orientation for each close approach.

Fig. 11

B-plane coordinates and circles of the resonant close approaches

All the resonant deflections feature some residual, shown in Equation (41), which is explained by the constraint of lying on their b-plane perturbed circles. The residual on the last free flyby is in the order of $10^{-6}$ km/s:

(41)

Providing a further and final check to the deflection model, we obtain the maximum error on the third flyby, equal to $0.628\%$ with respect to the simulated trajectory.

4.4.3 Performances

In the unperturbed design, the heaviest part from the computational point of view is the target selection. patternsearch.m implements an intelligent direct search method that needs to perform several function evaluations at each algorithm iteration. For large domains and small tolerances, this results in a rather high computational time, due to the optimal targets not known at all. Instead, we obtain an extremely small computational time when the algorithm is executed again for retrieving the complete solution, of only 1.5 seconds on a single core of a CPU Intel Core$^{{\textsc {tm}}}$ i5-5200U running at 2.20 GHz.

About the perturbed design, in order to underline the performances of the deflection model itself we focus on the performance of the local computations, whose time mentioned below includes the numerical simulation of the selected trajectory. The heaviest part is the map generation, with higher computational time required for higher resolution. For a given map, we obtain again an extremely fast convergence, for about 2.7 seconds in the last free flyby and 1.9 seconds for the resonant close approaches, with the same CPU and machine settings of the unperturbed case. Considering the pair precision level reached and software used, a full transition to better programming languages could easily tackle these design problems with higher precision and even lower computational times.

5 Conclusion

The precise identification of the resonant loci of point in the b-plane reference frame successfully brought a semi-analytic modification of the current model. We obtained an exact solution, in terms of simulation compliance, at the b-plane point where the perturbing coefficients have been computed, achieving a highly reliable approximation in the nearby b-plane regions. The immediately next developments already comply with the planetary protection application needs, i.e., showing a full Monte Carlo simulation on the same b-plane. The model should eventually detach from the patched conics approximation: The proposed semi-analytic solution should be generalized to account for the variations of the perturbing parameters among different b-plane regions. To this extent, some focus should be put toward both exploring optimal mapping strategies and new analytic solutions, preserving the efficiency features and ensuring an in-b-plane precise impact/resonance probability computation.

Finally, we have shown the deflection modeling capabilities of the b-plane formalism by implementing an efficient ballistic resonant trajectory design algorithm. The algorithm could already be used for preliminary mission analysis purposes, given that a good enough guess for the resonant deflection is known. The main outcome is perhaps having shown how embedding and connecting different orbital representations could enhance the algorithm performances, using the b-plane features for the deflection design, the traditional Keplerian elements for the objective definition and the simple Cartesian representation to perform simple computations. The results achieved by the algorithm, in terms of precision and required computational resources, suggest keeping developing both the model and the method. On the one hand, the restriction to resonant flybys drastically reduced the number of degrees of freedom left to the problem, which is the main reason for such low computational costs. This also highlights that proper analytic or semi-analytic developments, such as optimal perturbation mapping strategies and in-b-plane maneuver design, could lead to application extensions to the non-resonant case. On the other hand, optimal trajectory design techniques already exist; thus, our method could contribute to increasing the functionality of the current procedures.

Appendices

Appendix A: Perturbed resonant circles derivation details

From

$$\begin{aligned} \begin{aligned} \cos \theta ^{'*}_R = \cos \theta \cos (\gamma +\Delta \gamma )+\sin \theta \sin (\gamma +\Delta \gamma )\cos (\psi +\Delta \psi ) \end{aligned} \end{aligned}$$

(A1)

with the trigonometry relations

$$\begin{aligned} \begin{aligned} \cos (A+B)&= \cos A \cos B - \sin A \sin B \\ \sin (A+B)&= \sin A \cos B + \cos A \sin B, \end{aligned} \end{aligned}$$

(A2)

we obtain an equation of the following form

$$\begin{aligned} \begin{aligned} \cos \theta ^{'*}_R =&a_1\cos \gamma + a_2\sin \gamma + a_3 \sin \gamma \cos \psi + a_4 \cos \gamma \cos \psi + \\&a_5\sin \gamma \sin \psi + a_6\cos \gamma \sin \psi \end{aligned} \end{aligned}$$

(A3)

with the $a_i$ coefficients not to depend on the b-plane variables, particularly:

$$\begin{aligned} \begin{aligned} a_1&= \cos \theta \cos \Delta \gamma \\ a_2&= \cos \theta \sin \Delta \gamma \\ a_3&= \sin \theta \cos \Delta \gamma \cos \Delta \psi \\ a_4&= \sin \theta \sin \Delta \gamma \cos \Delta \psi \\ a_5&= -\sin \theta \cos \Delta \gamma \sin \Delta \psi \\ a_6&= -\sin \theta \sin \Delta \gamma \sin \Delta \psi . \end{aligned} \end{aligned}$$

(A4)

By replacing the trigonometric functions of $\gamma$ and $\psi$ with their b-plane definitions, Equation (A3) becomes

$$\begin{aligned} \begin{aligned} (b^2+c^2)\cos \theta ^{'*}_R =&a_1(b^2-c^2) + 2a_2bc + 2a_3c\zeta + a_4 (b^2-c^2)\zeta /b + \\&2a_5c\xi + a_6(b^2-c^2)\xi /b. \end{aligned} \end{aligned}$$

(A5)

The two intersections with the $\zeta$ axis are:

$$\begin{aligned} \begin{aligned} \zeta _{1,2} = D\pm R, \end{aligned} \end{aligned}$$

(A6)

which correspond to the solution of the quadratic equation that is obtained by setting $\xi = 0$ and $b = \zeta$ in Equation (A5):

$$\begin{aligned} \begin{aligned} (\zeta ^2+c^2)\cos \theta ^{'*}_R = a_1(\zeta ^2-c^2) + 2a_2c\zeta + 2a_3c\zeta + a_4 (\zeta ^2-c^2) \end{aligned} \end{aligned}$$

(A7)

and therefore

$$\begin{aligned} \begin{aligned} \zeta ^2 -2c\frac{B}{A}\zeta + c^2\frac{C}{A} = 0 \end{aligned} \end{aligned}$$

(A8)

where, writing explicitly the coefficients $a_i$,

$$\begin{aligned} \begin{aligned} A&= \cos \theta ^{'*}_R - \cos \theta \cos \Delta \gamma - \sin \theta \sin \Delta \gamma \cos \Delta \psi \\ B&= \sin \theta \cos \Delta \gamma \cos \Delta \psi - \cos \theta \sin \Delta \psi \\ C&= \cos \theta ^{'*}_R + \cos \theta \cos \Delta \gamma + \sin \theta \sin \Delta \gamma \cos \Delta \psi . \end{aligned} \end{aligned}$$

(A9)

The solutions to Equation (A8) are

$$\begin{aligned} \begin{aligned} \zeta _{1,2} = \frac{2c(B\pm \sqrt{B^2-AC})}{2A}. \end{aligned} \end{aligned}$$

(A10)

Simplifying the square root argument, some of the terms become:

$$\begin{aligned} \begin{aligned} B^2&= \sin ^2\theta \cos ^2\Delta \gamma \cos ^2\Delta \psi - 2\sin \theta \cos \Delta \gamma \cos \Delta \psi \cos \theta \sin \Delta \psi \\&\quad + \cos ^2\theta \sin ^2\Delta \psi \\ AC&= \cos ^2\theta ^{'*}_R - (\cos \theta \cos \Delta \gamma + \sin \theta \sin \Delta \gamma \cos \Delta \psi )^2 \\&= \cos ^2\theta ^{'*}_R + \cos ^2\theta \cos ^2\Delta \gamma + 2\cos \theta \cos \Delta \gamma \sin \theta \sin \Delta \gamma \cos \Delta \psi \\&\quad + \sin ^2\theta \sin ^2\Delta \gamma \cos ^2\Delta \psi , \end{aligned} \end{aligned}$$

(A11)

thus

$$\begin{aligned} \begin{aligned} B^2-AC =&\sin ^2\theta \cos ^2\Delta \gamma \cos ^2\Delta \psi + \cos ^2\theta \sin ^2\Delta \psi - \cos ^2\theta ^{'*}_R + \\&\cos ^2\theta \cos ^2\Delta \gamma + \sin ^2\theta \sin ^2\Delta \gamma \cos ^2\Delta \psi \end{aligned} \end{aligned}$$

(A12)

and using the identity $\sin ^2\Delta \gamma = 1 - \cos ^2\Delta \gamma$

$$\begin{aligned} \begin{aligned} B^2-AC = \cos ^2\theta - \cos ^2\theta ^{'*}_R + \sin ^2\theta \cos ^2\Delta \psi \end{aligned} \end{aligned}$$

(A13)

finally the use of $\cos ^2\Delta \psi = 1 - \sin ^2\Delta \psi$ yields the desired solution form $\zeta _{1,2} = D\pm R$, where

$$\begin{aligned} \begin{aligned} D&= \frac{c(\sin \theta \cos \Delta \gamma \cos \Delta \psi - \cos \theta \sin \Delta \psi )}{\cos \theta ^{'*}_R - \cos \theta \cos \Delta \gamma - \sin \theta \sin \Delta \gamma \cos \Delta \psi }\\ R&= \bigg |\frac{c\sqrt{\sin ^2\theta ^{'*}_R-\sin ^2\theta \sin ^2\Delta \psi }}{\cos \theta ^{'*}_R - \cos \theta \cos \Delta \gamma - \sin \theta \sin \Delta \gamma \cos \Delta \psi }\bigg |. \end{aligned} \end{aligned}$$

(A14)

Appendix B Perturbation and mapping strategy for flyby design

We map perturbing effects onto the b-plane before designing the flyby, with a finer mesh close to the planet, and then interpolate to obtain the perturbing values not exactly at the map nodes, exploiting the deflection model to avoid numerical propagations within the optimization process.

We perform a set of simulations at the beginning of the design itself: We describe the starting conditions with the b-plane polar coordinates $(b_{min}\le b \le b_{max}, 0 \le \alpha < 2\pi )$, thus with their correspondent $(\xi ,\eta ,\zeta )$ positions at the entrance of the sphere of influence, and the incoming planetocentric velocity of the current flyby. All these points together build a mesh (Fig. 12), whose propagation brings the following set of parameters at each node:

• The perturbation $\Delta \gamma$ on the deflection magnitude.

• The perturbation $\Delta \psi$ on the deflection direction.

• The perturbation $\Delta \theta '$ on the outgoing angle between the planet’s and the object’s planetocentric velocities.

• Mesh-related handle quantities for the interpolation.

Fig. 12

Quartic mesh representation example, polar (top) and b-plane (bottom) coordinates

The different $\alpha$ angles are linearly spaced, whereas b features a quartic distribution between $b_{min}$ and $b_{max}$. As shown in Fig. 12, we arbitrarily chose the quartic distribution on b to reach a finer mapping nearby the lower limit, where the difference between two values of b has an higher impact on the deflection error.

Despite the reason of mapping, the whole domain is fully evident in the free flyby case; we would not necessarily need to propagate the whole mesh for the resonant close approaches. If we knew the b-plane region of a specified resonance, we could restrict the domain to the interest areas only. Nevertheless, in the current application, not only is the position of the resonant circles at a specified close approach not known, but also all the configurations of the intermediate encounters are let free, leading to even more uncertainties than the sole circle location. For the current implementation, the optimal two-body result could cut some computational cost, identifying the interest areas in the N-body analysis. However, aiming to detach from the patched conics approximation, a complete mapping is anyway needed to include the perturbing effects, since we would run the optimization already at the perturbed level.

The interpolation strategy is similar to a bi-linear Lagrange polynomials, interpolating over b and the arc $b\alpha$. The four interpolation coefficients are

$$\begin{aligned} \begin{aligned} l_{ij}(b,\alpha ) = \frac{b - b_i}{b_j - b_i}\frac{b\alpha - b_i\alpha _i}{b_j\alpha _j - b_i\alpha _i} \end{aligned} \end{aligned}$$

(B15)

with i, j the indexes identifying the nodes of the cell enclosing b and $\alpha$.

Being in a design phase and having mapped the perturbing effects on the b-plane, we do not need to pick one node only as the reference to draw the perturbed resonant circles, whose approximation looses accuracy far from the reference. Since in general the position of the circle intersection with the $\hat{\zeta }$ axis is not known, some iteration method is required. We propose a fixed-point-iteration-like algorithm:

• 1. Initialize the search by computing the unperturbed circle parameters D and R.

• 2. Compute the highest magnitude intersection b with the $\hat{\zeta }$ axis (accounting for both positive and negative intersections with $\hat{\zeta }$).

• 3. Get the interpolated perturbing angles $\Delta \gamma$, $\Delta \psi$ and $\Delta \theta '$ on this point.

• 4. Compute the perturbed circle parameters $D_p$ and $R_p$ and get the updated intersection $b_{new}$ with the $\hat{\zeta }$ axis.

• 5. If the difference between the current $b_{new}$ and the previous iteration’s one (equal to b when initializing the algorithm with the unperturbed case) is lower than some tolerance stop the algorithm, otherwise return to step 1.

We expect a fast convergence, given the map resolution and the deflection model validation results. In fact, despite having set a rather strict tolerance of $10^{-6}km$ for the difference between two iterations and a maximum of 1000 steps, this number was never reached and convergence happened in all the test cases analyzed.

This model does not take into account possible different values of the perturbation $\Delta \theta '$ and still assumes the resonant loci of points to be described by circles. A possible generalization performs the optimization over both the variables $(b,\alpha )$ of the free flyby and relaxes the circle approximation of the perturbed resonances, but still makes use of the perturbing coefficients to insert the following nonlinear constraint based on the perturbed resonant geometric deflection:

$$\begin{aligned} \begin{aligned}&\cos \theta ^{'*}_R - \cos (\gamma +\Delta \gamma )\cos \theta ^* - \sin (\gamma +\Delta \gamma )\sin \theta ^*\cos (\psi +\Delta \psi ) = 0. \end{aligned} \end{aligned}$$

(B16)

We are removing the assumption that such a deflection must bring a circular locus of points in the b-plane, accounting for possible different angles $\Delta \gamma$, $\Delta \psi$ and $\Delta \theta$ in the various b-plane positions to be obtained via map interpolation. We attempted to optimize the deflection with this generalized resonance, although the new setup has not converged to an optimal solution. The results reported in the main body involve only the circular resonance model, and a further analysis to find a suitable method for the generalized resonance optimization is required.