Overlong simulations of the solar system dynamics with two alternating step-lengths

Abstract

We compare the performance of four symplectic integration methods with leading order symplectic corrector in simulations of the Solar System. These simulations cover 10 Gyr. They are longer than the astrophysical predicted future of the present-day Solar System, thus this work is mainly a study of the integration methods. For the outer Solar System simulation, where the used stepsize was 100 days, the energy errors do not show any secular evolution. The maximum errors show a dependence on the method. The simulations of the full Solar System from Mercury, and including Pluto as a test particle, were calculated with a stepsize of 7 days. The energy errors behave somewhat differently having a small secular behavior. This may due to the short timestep and the short period of the planet Mercury or some small round off error produced by the code. Comparison of the eccentricity evolution’s within simulations show that some planets are dynamically strongly coupled. Venus and Earth form a dynamical pair, also Jupiter and Saturn form a dynamical pair. The FFT of the analysis of the simulations suggests that all the giant planets form a single dynamical quadruple system. The orbit of Mercury is possibly unstable. Each simulation is stopped when Mercury is expelled. All the methods show similar results for times less than $30\,$Myr in the way that the results for orbital elements are same within plotting precision. Inclusion of Mercury in simulations shortens the Solar System e-folding time to $3.3\,$Myr. It is clear that chaos has a strong effect in the evolution of orbital elements, especially eccentricities. This is easily seen in Mercury’s orbit when the simulation time exceeds at least $30\,$ Myr. Our low-order simulations seem to match high-order methods over long timescales.

1 Introduction

We compare the performance of four different symplectic integration methods (Mikkola and Palmer 2000). The integrations, using Jacobian coordinate system, were extended to the very long time of 10 billion years. The methods used were the basic Wisdom–Holman, the Gaussian two-point formula, the alternating stepsize WH-method and the modified potential method (Wisdom and Holman 1991; Mikkola and Palmer 2000). The leading order symplectic corrector (Wisdom, Holman, Touma 1997; Mikkola and Palmer 2000) was used in these models, except for the Gaussian method because in that the leading order corrector expression becomes zero.

The Solar System does not survive in reality for the whole simulation time due to the Sun evolving into a red giant. We ignore the solar evolution and fix the Sun to present-day Sun. We stop a simulation when Mercury instability occurs and it is ejected from the Solar System or it collides with Venus or Earth.

Other studies of the long-term dynamical evolution of the solar system have been published suggesting also a possibility in the instability in the orbit of Mercury (Ito and Tanikawa 2002), (Batygin and Laughlin 2008; Mogavero and Laskar 2021) and (Laskar and Gastineau 2009). These papers have applied other computational methods than ours. The aim in this paper is not to compare our calculations to these simulations, but rather to compare the earlier named four symplectic integrators only.

Our first attempt to investigate symplectic methods for the derivations of their results and precision is discussed in Mikkola and Palmer (2000). We studied only these methods although there are higher-order ones (Farrés et al. 2013; Rein et al. 2019).

For initial conditions, we used the initial setup of DE234 (Standish 1991) which were given for the time $TDB=2440400.5\ =\ 1969\ 06\ 28.00\$. Earlier Laskar (1994) investigated the stability of the Solar System by using a large number of a little different initial conditions. We found recently that the results were quite similar to our conclusions. In addition, Mogavero and Laskar (2021) and Brown and Rein (2020) mentioned in these recent papers similar results, although they were interested in the Solar System and not much in different methods.

2 Integration methods

The integration methods we use in the calculations are symplectic methods using alternating stepsize with a mean step size noted by h. Having the same mean stepsize in all of the methods causes them to evaluate perturbations equally frequently. The first method noted as 00 is the basic Wisdom and Holman (1991) method. The method noted as 10 is the two-step method (Mikkola and Palmer 2000), and 11 with a modified perturbation force (Wisdom, Holman, Touma 1997). In the three cases above, the $O(h^2)$ errors are removed by the leading order symplectic corrector (Mikkola and Palmer 2000; Wisdom, Holman, Touma 1997). Finally, the method 20 uses the two point Gaussian stepsizes, which eliminates second-order $O(h^2)$ errors.

Let us write the Hamiltonian as

$$\begin{aligned} H=K(\mathbf{p},\mathbf{r})+R(\mathbf{r}), \end{aligned}$$

(1)

where K is the Keplerian part and R means the planet–planet attractions which perturb the Keplerian motions. The $\mathbf{p}$ and $\mathbf{r}$ represent the impulse vectors and the radius vectors of the planets. The order of magnitude of the perturbation is

$$\begin{aligned} O(R)\approx \varepsilon , \end{aligned}$$

where $\varepsilon$ denotes the small perturbation acting on the Keplerian motions.

According to Mikkola and Palmer (2000), the Wisdom and Holman (1991) midpoint method, the two-point Gaussian method and a higher-order scheme MWH can be described using a unified formalism where the perturbation evaluations are taken at intervals of $(1\pm q)h$. If we write $h_1=(1-q)h$ and $h_2=(1+q)h$ then the algorithms can be explained as follows.

Let the operator $\mathbf{{\widehat{K}}}(\tau )$ signify motion according to the Keplerian Hamiltonian, i.e., just the Kepler motion and $\mathbf{{\widehat{R}}}(\tau )$ the motion under the Hamiltonian $R(\mathbf{r}),$ which causes linear motion of the velocities by the amount $\delta \mathbf{v}=-\tau {{\partial {R}}\over {\partial {\mathbf{r}}}}=\tau \mathbf{F}$. A double step can then be written as

$$\begin{aligned} \mathbf{{\widehat{K}}}(h_1/2) \mathbf{{\widehat{R}}}(h) \mathbf{{\widehat{K}}}(h_2) \mathbf{{\widehat{R}}}(h) \mathbf{{\widehat{K}}}(h_1/2), \end{aligned}$$

and longer integrations as

$$\begin{aligned} \mathbf{{\widehat{S}}} =\mathbf{{\widehat{K}}}(h_1/2)\mathbf{{\widehat{R}}}(h) \left( \mathbf{{\widehat{K}}}(h_2)\mathbf{{\widehat{R}}}(h)\mathbf{{\widehat{K}}}(h_1)\right) ^{n-2}\mathbf{{\widehat{K}}}(h_2) \mathbf{{\widehat{R}}}(h) \mathbf{{\widehat{K}}}(h_1/2)),\end{aligned}$$

(2)

which represent integration over time (t) interval of $\Delta t=n h$ between outputs. When the time interval between outputs ($\Delta t$) is given, one must adjust the stepsize a little such that the number of steps between outputs become an, often large, integer. The accuracy of the results can be improved applying a symplectic corrector (Wisdom, Holman, Touma 1997). According to Mikkola and Palmer (2000), the leading order corrector can be written as

$$\begin{aligned} \delta \mathbf{r}= & {} -h^2 C_0 \mathbf{F}, \end{aligned}$$

(3)

$$\begin{aligned} \delta \mathbf{v}= & {} +h^2 C_0 {{\dot{\mathbf{F}}}}, \end{aligned}$$

(4)

where

$$\begin{aligned} C_0 = \frac{1}{24} (1-3 q (q+2)), \end{aligned}$$

(5)

which removes the $O(h^2)$ error terms. The correctors are to be added to coordinates and velocities at output, but they are not used to affect the integration. However, before starting the integration one must find the values in other ways, i.e., one finds initial values that give the true values after application of the correction. A simple explanation is as follows: Let $\mathbf{q}$ contain the coordinates and momenta and $\mathbf{c}(\mathbf{q})$ be the symplectic corrector. At the starting point, we must have

$$\begin{aligned} \mathbf{q}+\mathbf{c}(\mathbf{q})=\mathbf{q}_0, \end{aligned}$$

where $\mathbf{q}_0$ is the correct starting point and $\mathbf{q}$ the quantities to be used in the computation. It is easy to obtain $\mathbf{q}$ by iteration with the equation

$$\begin{aligned} \mathbf{q}=\mathbf{q}_0-\mathbf{c}(\mathbf{q}), \end{aligned}$$

where one sets initially $\mathbf{q}_0$ for $\mathbf{q}$ and then repeats the iteration as many times as the result changes. This is done only once and so the iteration is a minor effort.

The integration methods of type (2) give correct results for a surrogate Hamiltonian

$$\begin{aligned} H_s=H+a_2(q)h^2H_2+a_4(q)h^4H_4+a_6(q)h^6H_6+.., \end{aligned}$$

(6)

where H is the true Hamiltonian and the functions $H_k$ can be derived from equation (2) using the Baker–Campbell–Hausdorff equation (Yoshida 1990).

The error estimate of the method may thus be written as

$$\begin{aligned} Error\approx \sum _{k=2,4,6,..} a_k(q) h^k H_k, \end{aligned}$$

where the coefficients $a_k(q)$ are

$$\begin{aligned} a_2(q)= & {} \frac{1}{24} (1-3 q (q+2)) \end{aligned}$$

(7)

$$\begin{aligned} a_4(q)= & {} -\frac{1}{5760} (15 q (q+2) (q (q+2)-6)+7) \end{aligned}$$

(8)

$$\begin{aligned} a_6(q)= & {} \frac{21 q (q+2) (q (q+2) (q (q+2)-17)+75)-31}{967680}. \end{aligned}$$

(9)

If we modify the potential by including its gradient:

$$\begin{aligned} {{\widetilde{R}}} = R(\mathbf{r}+2 \chi h^2 {{\partial {R(\mathbf{r},t)}}\over {\partial {\mathbf{r}}}},t), \end{aligned}$$

(10)

or modify the force to approximate it as:

$$\begin{aligned} \mathbf{F}(\mathbf{r}+ \chi h^2 \mathbf{F}(\mathbf{r},t),t), \end{aligned}$$

(11)

where $\mathbf{F}=\bigtriangledown {R}$ and

$$\begin{aligned} \chi =(1+3q^2)/12, \end{aligned}$$

then we get improved precision.

We remove the leading contribution of the second-order terms having the order $\varepsilon ^2h^2$ so that there remains error $O(\varepsilon ^3h^2)$.

When the perturbation size can be written to be $R\approx \varepsilon$ the following list of the error terms in the different methods can be symbolized as

• Method 00 = Wisdom and Holman (1991) with symplectic corrector [WH]. $q=0$, Error$=O(\epsilon h^4 )$

• Method 10 = Modified Wisdom–Holman (Mikkola & Palmer (2000) [MWH]. $a_4(q)=0 =>\ q=2 \sqrt{1-2 \sqrt{{2}/{15}}}-1,$  Error$=O(\epsilon h^6)+O( \epsilon ^2 h^2)$

• Method 11 = MWH with modified perturbation force. =$F(X)\rightarrow F( X +\chi h^2 F(X))$ $\chi =(1+3q^2)/12$, with $q=2 \sqrt{1-2 \sqrt{{2}/{15}}}-1$ , as above. Error is supposed to be smaller (of order $\varepsilon ^2 h^4$), but this is slower by a factor of 1.5 and therefore often not used. Dividing the stepsize by 1.5 gives often more additional accuracy in other methods with the same computing time. According to Wisdom, Holman, Touma (1997), the error may be written as Error$=O(\epsilon h^6)+O( \epsilon ^2 h^4)$

• Method 20 = Gaussian two-point formula. $a_2(q)=0,\ =>\ q={2}/{\sqrt{3}}\ \,-1,$ Error$=O(\epsilon h^4 )$

The leading order symplectic corrector was used in all of these methods, with the exception that in the Gaussian (20) method the corrector becomes equal to zero, since the corrector coefficient is in fact $a_2(q)=0$, so (20) is an $O(h^4)$ algorithm without symplectic corrector.

3 Outer solar system

We computed first the results for the outer Solar System with 100 days stepsize using Jacobian coordinates. Figure 1 shows the maxima of the absolute values of the relative energy errors.

The errors fluctuate so densely that only maximal errors are shown. The maximal values were computed over a million year segment in this 10 Gyr plot. The respective one million year averages were in all cases under $10^{-10}$. One notes the effects of the used methods, but the values in the figure tell mostly about the fluctuation of the errors and there is no visible secular effect. The largest energy fluctuation is produced by the Gaussian method (designated 20). Here also the MWH (designated 11) produces smallest energy errors as expected. However, the small error value is partly due to the use of the symplectic corrector which does not change the actual integration but only output.

Fig. 1

Energy errors in outer Solar System integrations show the maximal values of the absolute values of relative energy errors in million year segments over the 10 Gyr timescale

Fig. 2

Evolution of $\log (|d\mathbf{r}|)$ in the outer Solar System integrations. All the methods seem to give similar result. The e-folding time is close to 13 Myrs

The variational equation solutions grow exponentially even in the outer Solar System. These are plotted in the Fig. 2. The system gives a 13 Myr e-folding time for the outer Solar System. This e-folding time is much larger than the one obtained for the entire Solar System. The reason is the slow variation of that system while in the entire system there are much higher frequencies which makes the true system more sensitive, in fact more chaotic. It is clear that the different methods give very similar values for chaos, i.e., for the e-folding time of the growth of the variational equation solutions.

Fig. 3

The effect of the Great Inequality (GI) in the eccentricities of Jupiter and Saturn. The GI is visible here as the tiny fluctuation shown in this figure. The long wave is due to secular effects and it is clearly enormous compared with the GI. The length of the long sinusoidal wave is 54000 years

When the outer Solar System dynamics is discussed it is common that the so-called ‘Great Inequality’ (GI) resonance between Jupiter and Saturn motions is considered to be important. This phenomenon is mainly visible in the main motions of the planets. However, Fig. 3 shows the GI as a fast tiny fluctuation in the eccentricity values of Jupiter and Saturn. After all, it seems to be an almost negligible effect on long timescales and thus may not affect the orbits of the big planets very strongly. On the other hand, it has been found to affect the motion of asteroids (Ferraz-Mello et al. 1998). The long wave in Fig. 3 has a length of about 54000 years and the height is about 0.1 in the eccentricity of Saturn. These values are much larger and longer than those in the traditional (GI) and they are in fact the leading terms in the secular system. Similar dynamical connections are visible between some other planets, see Sect. 5.  

4 Entire Solar System

The full Solar System from Mercury and including Pluto was calculated with a step size of 7 days with an output interval of 1000 years.

4.1 Energy errors with the different methods

Figure 4 shows the energy errors (maxima over a million year intervals) in the different simulations. One sees that three of the methods fail to continue at some point of time. This is because Mercury becomes unstable in those simulations (most likely due to the chaos in the system). Because the used codes integrated the Jacobian coordinates the entire simulation lost precision when Mercury escaped causing a runaway effect in the energy error. The possible instability of Mercury was suggested earlier by (Laskar and Gastineau 2009; Mogavero and Laskar 2021). The mean energy errors are less that $10^{-10},$ except close to the Mercury discontinuities.

Fig. 4

Maxima of the relative energy errors in the integrations of the entire system with different methods. The curves represent the maxima of the errors in one million year segments. The system disruptions due to Mercury’s instability are visible as energy runaway in the different integrations except simulation 10

Fig. 5

Eccentricity of Mercury up to 35 Myr with different methods. We see same results within plotting accuracy

Here, the errors have clear secular effects. The small stepsize ($7\,$days) makes the number of steps big. That difference with the outer Solar System integrations is thus due to round-off errors (or due to the surrogate Hamiltonian effects). However, it is likely that the reason for secular error is in the programming of the code as found out by Rein and Tamayo (2015). One notes that the first system disruption (with the (20) method) occurs near $3\,$Gyr. In this simulation, Mercury’s eccentricity grows to a large value at that time. Corresponding results were also obtained by Mogavero and Laskar (2021). As long as the system remains stable the errors in the 20 integration are clearly largest like it was for the outer Solar System integration. The 10 and 11 cases the errors are similar, but here 00 the basic WH method makes it most accurately. The reason may be that in these alternating stepsize methods we must consider the real stepsize to be $=2h$ except for the WH method where the steps are fixed $=h$.

4.2 Mercury’s eccentricities

We used the eccentricity to characterize the effects of the instability in Mercury’s orbit.

Fig. 6

Differences of the eccentricities of Mercury, with respect to their mean values, up to 60 Myr with all the tested methods. The different methods are plotted in different colors

Fig. 7

Maximal eccentricities of Mercury with different methods. Here, the maxima are taken over segments of one million years. The initial 30 Myr time in which the orbital element evolution’s are equal with the different methods is here essentially a negligible short interval

Mercury’s eccentricities behave in the same way in all the simulations for over more than 30 Myr (Fig. 5). One can see that the evaluations start to separate after about 30 Myr. The different integration methods induce differences between the integrations, thus the exponential divergence visible after 30 Myr is due to the chaotic nature of the dynamics.

The curves in Fig. 6 were obtained by first computing the mean values over the different simulation results and then the difference of each simulation to the mean value. In that it is easy to see that the results were almost the same up to the time of 30 Myr after which the curves start separating slowly. However, the separation is so slow that in Fig. 5 it is still difficult to see the differences.

The evolution of the eccentricities of Mercury in our different simulations is shown in Fig. 7. Only the maximum values over one million year intervals and close approaches to Venus are shown.

From this illustration, one can note that very long integrations indicate a behavior which is clearly different from shorter simulations. The stability of the orbit of planet Mercury is questionable. Not much can be concluded about the reasons for the possible instability of Mercury’s orbit. It is anyway likely to be caused by high eccentricities and close approach to Venus.

The stepsize of 7 days could be a reason too for the divergent calculations. That means about 12.6 integration steps per Mercury’s period, but it should be sufficient for a period and 30 Myr long good behavior. One possible reason is that the surrogate Hamiltonians are a bit different for the different methods, and symplectic integrations follow the orbits defined by those Hamiltonians. Another likely reason is the chaos in the entire system (Laskar 1990).

4.3 Chaos time in the Solar System

The e-folding time of chaos in the Solar System has been traditionally estimated to be $6\,$Myr (Mikkola and Innanen 1995), but our results suggest that including Mercury shortens it to about $3.3\,$Myr. To obtain these results, our code was differentiated line by line, so we get real correct results for the variations of the algorithm, as explained in Mikkola and Innanen (1999).

Fig. 8

Evolution of $\log (|d\mathbf{r}|)$ in the entire Solar System integration. The e-folding time is about  3.3 Myr

Fig. 9

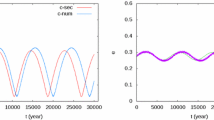
Eccentricities of Venus and Earth in the beginning. These complicated curves are obviously results from several sinusoidal waves. The lengths were estimated to be about 422700, 211374, 123972 and 95728 years (See Sect. 6)

Fig. 10

Eccentricities of Venus and Earth in the end of simulation

Fig. 11

Eccentricities of Jupiter and Saturn in the beginning. Clearly, these two planets form a kind of dynamical double just as Venus and Earth. The major waves here have about constant length, i.e., about 5400 years like in Fig. 3

As can be seen in Fig. 8, all the different methods in our simulations give the same result for the e-folding time. This suggests that the resulting value is correct. One cannot see any increase of $\log (|d\mathbf{r}|)$ near the times when Mercury escapes, but this may be due to the 1000 year output interval. The close approach with Venus may have happened in shorter time and lead to escape (which may be partly due to integration errors during the close approach). Only in one of the methods, in the MWH (i.e., 10) Mercury stays circling the Sun for the entire integration up to $10\,$Gyears. The fact that the e-folding time is only  3.3 Myr, tells that chaos in the Solar System is stronger than estimated in the past.

5 Coupling of planets

Figures 9 and 10 show the evolution of the eccentricities of Venus and Earth in the first and the last million years of the 10 billion year integration. It is clear that Venus and Earth are dynamically coupled.

Figures 11 and 12 show the eccentricities of Jupiter and Saturn during the first and last million years in the 10 Gyr integration, respectively. One can see that these planets are also coupled dynamically over really long times.

Fig. 12

Eccentricities of Jupiter and Saturn in the end of simulation. Clearly, the dynamical behavior has remained the same during the whole 10 Gyr simulation

As the figures starting from Figs. 9, 10, 11, 12, 13 suggest the planet pairs seem to exchange angular momenta, so that pairwise the sums of the momenta remain (at least almost) constant. For Uranus–Neptune pair, the situation is not so clear and it may be that Jupiter and Saturn affect those planets and that effect may be partly visible in the figures of the eccentricity evolution.

Fig. 13

Eccentricities of Uranus and Neptune in the beginning. Even here one can see resonant like behavior, although it is not as clear as in the other cases. When determined using the maximums of the Uranus eccentricity, the length of the major wave was obtained to be 1.03 million years

Fig. 14

Eccentricities of Uranus and Neptune in the end of simulation. Even here it seems that the dynamical coupling continues over all times

Fig. 15

The eccentricities of the Earth with the different methods

As one can see from Figs. 13 and 14, also the planets Uranus and Neptune form a pair with same time eccentricity variations. It is possible that the outer planets form a quadruple dynamic system. In Fig. 15, we demonstrate the clear phase separation in the different integration methods. This seems to happen more clearly in shorter oscillations, but very long ones survive for a longer time. The most likely reason for this behavior is that the surrogate Hamiltonian (which really moves the system in the different integrations) is a bit different in the various methods. The time interval in Fig. 15 is a million years after a billion years integration. Here already the curves are different, although one may get an impression that long (roughly half a million years) waves are still quite similar.

6 FFT results

Here, we present only a small part of our analyzing work. Due to the extensive amount of results, presenting them entirely must be done in a separate publication. We compared the four simulations 00, 10, 11 and 20. In the data, the time interval in coordinates was 1000 years. We analyzed this data for each of the simulations with FFTs using $2^{20}=1048576$ points, starting from point 524288, thus roughly covering the time interval from 0.5Gyr to 1.5Gyr. The selections of the data have standard limits for the oscillatory periods to be investigated.

A signal is present in all outer planets at $54026.7\pm 1.4$ years. Jupiter and Neptune are in phase and Saturn and Uranus are in the opposite phase. Based on FFT phase determinations, all four outer planets form a dynamic connected system. The errors presented here are the deviations between outer planets periods determined from the FFTs.

A second strong signal $1108500\pm 500$ years is shown in the eccentricities of all larger planets. All the planets and the simulations are in phase here.

The inner planets Earth and Venus form a pair, they are almost locked to each other. The similarity in the FFTs is obvious in Figs. 9 and 10. (Similar results were reported in Laskar (1990, 1994).) Many periods are present in all the inner planets, such as the $\tilde{4}22000$ year period. A broad peak at 95000 period is also shown for all inner planets but it is weak for Mercury.

A section of the FFTs is represented showing a log of amplitude squared as a function of period for the Earth simulations only. It is clear from Figs. 16 and 17 that the FFT peaks are broadened possibly due to slight instability in the oscillation periods which, when accumulated by time, cause small phase difference in the eccentricity curves between the results of the different integration methods. These results explain the fact that in Fig. 15 the curves clearly have a different phase after a billion years, or in fact after 300 Myr. These phenomena may have an explanation in Hoang et al. (2021).

It is clear that the different simulations produce different results by about $\pm 1\% .$ The position of the maximum of the peak period varies, and thus the internal frequency of oscillation, yet the synchronicity of Venus and Earth remains in all the simulations.

Fig. 16

FFT analysis of Earth eccentricity by means of the different methods. Here, the obtained periods are between 95,000 and 96,000 years

Fig. 17

Earth eccentricity with periodicity signals around 420,000 to 425,000 years

7 Some curiosities in the dynamics of terrestrial planets.

In Fig. 18, the curves are not from the actual Solar System dynamics but point partly to an earlier result published in Innanen et al. (1998), where the effect of various planets was attempted to study. In those early times, it was normal to put the Sun and Mercury together in their center of mass because it was assumed that Mercury is negligibly small. This short computation results here suggest that Mercury is far from being negligible. If the Earth was neglected, the Venus eccentricity started growing to the large value of $\approx 0.6$.

Here, we simply did not neglect Mercury (but the Earth was removed). The variations of Mercury’s eccentricity became significantly smaller. This obviously suggests that Mercury is not negligible in any Solar System simulations. This result is somewhat curious.

Fig. 18

A curiosity in Venus orbit. If Mercury and Earth are removed the eccentricity of Venus increases up to the value $e=0.6$. If Mercury is included then the Venus eccentricity varies only little. Is this phenomenon due to the coupling of Mercury with Venus and Earth orbits?

8 Discussion and conclusions

First, the outer Solar System was calculated with a 100 days step. No secular trends are observable in the energy plots of the four symplectic analysis methods over $10^9$ years. The e-folding time is 13 Myr.

In computing the entire Solar System, we used 7 days stepsize, for Mercury this means about 12.6 steps/period. The energy error in the method that made it up to 10Gyr, with altogether $5.2\times 10^{11}$ integration steps, causes apparently enough roundoff errors to produce some secular error. The energy error is anyway only $dE/E=2.*10^{-21}$ per step, which is surprisingly small. It is not clear if any of the used methods are preferable. The basic Wisdom–Holman method seems to be satisfactory, in fact it produced smallest energy error as long as Mercury remained stable. Thus, a side result was the confirmation of the possible instability of the orbit of Mercury. This happened in three of the methods and only in one case the planetary system survived the big time of $10^{10}$ years. One notes that the system becomes unstable at intervals of about 3 Gyr. Although this happens in different methods, it probably means that this chaotic system has almost unstable situations at those intervals, and the different methods make it unstable at one or another of those situations. The e-folding time of the divergence of energies is 3 Myrs.

In all four methods, the orbital elements behave in the same way within the plotting precision for about 30 Myr. The differences in longer times are likely due to the surrogate Hamiltonians which are somewhat different in these methods.

Venus and Earth form a couple, Jupiter and Saturn also form a couple, and based on the FFT analysis Uranus and Neptune are included in the dynamically quadruple system. Mercury is clearly unstable according to our simulation and this was earlier found out by Laskar (2008); Laskar and Gastineau (2009) and Batygin et al. (2015). This is the case at least in simulations without general relativity terms.

8.1 Final remarks

• 1. All the methods seem to work quite well. Same results for 30 Myr. The differences in the stability of planet Mercury proves nothing about the methods, but is likely a property of the Solar System, i.e., chaos.

• 2. In systems with long e-folding times, like in the outer Solar System, the analytical error estimates are correct at least in the sense that errors behave according to the $O(h^n)$ estimates. This is true at least in our simulations.

• 3. In systems with eccentric orbits and short periods, like the entire Solar System, it is not so clear if the higher-order methods are any better. This may be because it is customary to use as long a stepsize as possible to save computing time.

• 4. It seems that the basic WH-method is very useful, even one of the best because it has essentially stepsize $=h$, while in all the other methods the stepsize is $=2h$. In any case, the WH method is good and simplest among all methods.

• 5. The planet pairs Venus and Earth, Jupiter and Saturn form a dynamical couple and very likely with Uranus and Neptune.

• 6. Mercury’s orbit is unstable as found out in earlier studies.