High precision symplectic integrators for the Solar System

Abstract

Using a Newtonian model of the Solar System with all 8 planets, we perform extensive tests on various symplectic integrators of high orders, searching for the best splitting scheme for long term studies in the Solar System. These comparisons are made in Jacobi and heliocentric coordinates and the implementation of the algorithms is fully detailed for practical use. We conclude that high order integrators should be privileged, with a preference for the new $(10,6,4)$ method of Blanes et al. (2013).

Appendices

Appendix A: On the compensated summation

Using any of the symplectic integrating schemes described in this article, we require successive evaluations of $\exp (a_i\tau A)$ and $\exp (b_i\tau B)$. Each of these evaluations slightly modifies the position and velocity of each planet. For $\tau$ small, we will have a loss in accuracy due to round-off errors. The Compensated Summation is a simple trick that is commonly used to reduce the round-off error. In a general framework, when we consider a numerical method for solving an ODE, we require a recursive evaluation of the form:

$$\begin{aligned} y_{n+1} = y_n + \delta _n, \end{aligned}$$

(26)

where $y_n$ is the approximated solution and $\delta _n$ is the increment to be done. Usually $\delta _n$ will be smaller in magnitude than $y_n$. In this situation, the rounding errors caused by the computation of $\delta _n$ are in general smaller that those to evaluate Eq. 26. The algorithm that can be used in order to reduce this round-off error is called the “Compensated Summation” (Kahan 1965).

Compensated summation algorithm: Let $y_0$ and $\{\delta _n\}_{n\ge 0}$ be given and put $e=0$. Compute $y_1,y_2, \ldots$ from Eq. 26 as follows:

$$\begin{aligned} \begin{array}{l} for\,n = 0, 1, 2, \ldots \ do \\ \,\quad \quad a = y_n \\ \,\quad \quad e = e + \delta _n \\ \,\quad \quad y_{n+1} = a + e \\ \quad \quad e = e + (a - y_{n+1})\\ end do \end{array} \end{aligned}$$

This algorithm accumulates the rounding errors in $e$ and feeds them back into the summation when possible. At each time-step of the integration, when we evaluate $\exp (a_i\tau A)$ or $\exp (b_i\tau B)$, the increment in position and velocity is done using the compensated summation. In Fig. 8 we show the results for the $\mathcal{ABA }(2n,2)$ schemes for $n = 1,2,3,4$ using double (left) and extended precision (right). In both cases we gain almost one order of magnitude in precision when we take into account the compensated summation.

Fig. 8

Comparison between the $\mathcal{ABA }$ schemes of order $(2n,2)$ for $n=1,2,3,4$ applied to the Sun-Jupiter-Saturn three body problem. With (CS) and without (noCS) the compensated summation. The $x$-axis represent the cost $(\tau /n)$ and the $y$-axis the maximum energy variation for one integration with constant step-size $\tau$. Left using a double precision arithmetics; Right using an extended precision arithmetics (decimal log scales)

Appendix B: Integration schemes (some help on the practical coding)

In this paper we have reviewed many splitting symplectic integrating schemes, all of them of the form:

$$\begin{aligned} \mathcal{S }(\tau ) = \exp (a_1\tau A) \exp (b_1\tau B) \, \ldots \, \exp (b_1\tau B) \exp (a_1\tau A), \end{aligned}$$

(27)

where $\exp (\tau A)$ and $\exp (\tau B)$ can be computed explicitly. They correspond to the integrals of the two different parts of the original Hamiltonian. In this section we show how to compute explicitly $\exp (\tau A)$ and $\exp (\tau B)$ for the particular case of the N-body problem in Jacobi and heliocentric coordinates. We note that from now on: ${\tilde{\mathbf{u}}}$ stands for the momenta associated to $\mathbf{u}$ and $\mathbf u^{\prime }$ stands for $d\mathbf{u}/dt$.

1.1 B.1 Keplerian motion $(H_{K})$

We recall that in Jacobi coordinates,

$$\begin{aligned} H_{K} = \sum _{i=1}^{n} \left( \frac{1}{2} \frac{\eta _i}{\eta _{i-1}}\frac{||{\tilde{\mathbf{v}}}_\mathbf{i}||^2}{m_i} - G\frac{m_i \eta _{i-1}}{||\mathbf{v_i}||} \right) , \end{aligned}$$

(28)

whereas in heliocentric coordinates,

$$\begin{aligned} H_{K} = \sum _{i=1}^{n} \left( \frac{1}{2} ||{{\tilde{\mathbf{r}}}_\mathbf{i}}||^2 \left[ \frac{m_0 + m_i}{m_0 m_i}\right] - G\frac{m_0 m_i}{||\mathbf{r_i}||} \right) . \end{aligned}$$

(29)

In both cases $H_K$ is a sum of independent Keplerian motions. In Jacobi coordinates each planet follows an elliptical orbit around the centre on mass of the Sun and the planets that are closer to the Sun, the mass parameter of the system is $\mu _J = G\eta _i$. While in heliocentric coordinates each planet follows an elliptical orbit around the planet-Sun centre of mass, and the mass parameter of the system is $\mu _H = G(m_0+m_i)$.

It is well known that Kepler problem is integrable, but the solution from time $t = t_0$ to $t = t_0 + \tau$ is expressed in a simple form if we consider action-angle variables. To compute $\exp (\tau L_{H_K})$ we need to be able to compute $\mathbf (r(t_0+\tau ),v(t_0+\tau ))$ from $\mathbf (r(t_0), v(t_0))$.

An option is to change to elliptical coordinates, advance the mean anomaly and then return to Cartesian coordinates. But this can accumulate a lot of numerical errors as well as it is very expensive in terms of computational cost. Instead we use a similar idea as the Gauss $f$ and $g$ functions (Danby 1992), where we use an expression for the increment in position and velocities for a given step-size $\tau$, without having to perform any change of coordinates. Let us give some details on how to derive these expressions.

In elliptical coordinates the motion of the two body problem is given by $(a,e,i, \varOmega , \omega , E)$, where all of the elements remain fixed except for $E$ that varies following Kepler equation $(n(t -t_p) = M = E - e\sin E)$. Using a reference frame where the orbital plane is given by $Z=0$, the $X$-axis is the direction of the perihelion and the $Y$-axis completes an orthogonal reference system on the orbital plane, the position $(X, Y, 0)$ and velocity $(X^{\prime }, Y^{\prime }, 0)$ are given by:

$$\begin{aligned} \begin{array}{rclcrcl} X &{}=&{} a(\cos E - e), &{} &{} Y &{}=&{} a\sqrt{1-e^2} \sin E, \\ X^{\prime } &{}=&{} -\displaystyle \frac{na^2}{r}\sin E, &{} &{} Y^{\prime } &{}=&{} \displaystyle \frac{na^2}{r}\sqrt{1-e^2} \cos E, \end{array} \end{aligned}$$

(30)

where $r = a(1 - e \cos E)$ and $n = \mu ^{1/2}a^{-3/2}$. The position and velocities on a fixed reference frame are given by:

$$\begin{aligned} \left( \begin{array}{cc} x &{} x^{\prime } \\ y &{} y^{\prime }\\ z &{} z^{\prime } \end{array}\right) = \mathcal{R }_3(\varOmega )\times \mathcal{R }_1(i)\times \mathcal{R }_3(\omega ) \times \left( \begin{array}{cc} X &{} X^{\prime } \\ Y &{} Y^{\prime }\\ 0 &{} 0 \end{array}\right) , \end{aligned}$$

(31)

where

$$\begin{aligned} \mathcal{R }_1(\theta ) = \left( \begin{array}{c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0 \\ 0 &{} \cos \theta &{} \sin \theta \\ 0 &{} -\sin \theta &{} \cos \theta \end{array}\right) , \text{ and } \mathcal{R }_3(\theta ) = \left( \begin{array}{c@{\quad }c@{\quad }c} \cos \theta &{} \sin \theta &{} 0 \\ -\sin \theta &{} \cos \theta &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array}\right) \end{aligned}$$

Notice that

$$\begin{aligned} \mathcal{R }_3(\varOmega )\times \mathcal{R }_1(i)\times \mathcal{R }_3(\omega ) = \mathcal{R } \times \mathcal{R }_3(\varpi ), \end{aligned}$$

where $\varpi = \varOmega + \omega$ and $\mathcal{R }= \mathcal R _3(\varOmega )\times \mathcal{R }_1(i)\times \mathcal{R }_3(-\varOmega )$. Given that $\mathcal{R }_1(i) = \mathcal{R }_1(i/2)\mathcal{R }_1(i/2)$ we have that:

$$\begin{aligned} \mathcal{R } =\left( \begin{array}{c@{\quad }c@{\quad }c} 1 - 2\mathbf{p}^2 &{} 2\mathbf{p q} &{} 2\mathbf{p} \chi \\ 2\mathbf{p q}&{} 1 - 2\mathbf{q}^2&{} -2\mathbf{q} \chi \\ -2\mathbf{p} \chi &{} 2\mathbf{q} \chi &{} 1 - 2\mathbf{p}^2 - 2\mathbf{q}^2 \end{array}\right) , \end{aligned}$$

(32)

where $\mathbf{p} = \sin i/2 \sin \varOmega , \mathbf{q} = \sin i/2 \sin \varOmega ,$ and $\chi = \sqrt{1- \mathbf{p}^2 - \mathbf{q}^2} = \cos i/2$. From Eq. 31 we have,

$$\begin{aligned} \mathbf{[\,r(t_0),\ v(t_0)\,]}&= \mathcal{R }\times \mathcal{R }_3(\varpi ) \times \left[ \begin{array}{cc} X_0 &{} X_0^{\prime } \\ Y_0 &{} Y_0^{\prime } \\ 0 &{} 0 \end{array}\right] \end{aligned}$$

(33)

$$\begin{aligned} \mathbf{[\,r(t_0+\delta t),\, v(t_0 + \delta t)\,]}&= \mathcal{R }\times \mathcal{R }_3(\varpi ) \times \left[ \begin{array}{cc} X_1 &{} X_1^{\prime } \\ Y_1 &{} Y_1^{\prime } \\ 0 &{} 0 \end{array}\right] . \end{aligned}$$

(34)

Hence,

$$\begin{aligned} \mathbf{[\ r(t_0 + \delta t),\ v(t_0+\delta t)\ ]}&= \mathbf{[\ r(t_0), v(t_0)\ ]} \left[ \begin{array}{cc} X_0 &{} X_0^{\prime } \\ Y_0 &{} Y_0^{\prime } \end{array}\right] ^{-1}\left[ \begin{array}{cc} X_1 &{} X_1^{\prime } \\ Y_1 &{} Y_1^{\prime } \end{array}\right] \end{aligned}$$

(35)

$$\begin{aligned}&= \mathbf{[\ r(t_0), v(t_0)\ ]} \left[ \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{array}\right] . \end{aligned}$$

(36)

One can check that,

$$\begin{aligned} a_{11}&= \displaystyle 1 + (\cos (E_1 - E_0) - 1)\frac{a}{r_0}, \nonumber \\ a_{21}&= \displaystyle \frac{a^{3/2}}{\mu ^{1/2}}\sin (E_1 - E_0) - e\sin E_1 + e\sin E_0,\nonumber \\ a_{12}&= \displaystyle -\frac{\sqrt{a}}{r_0r_1}\sin (E_1 - E_0), \nonumber \\ a_{22}&= \displaystyle 1 + (\cos (E_1 - E_0) - 1)\frac{a}{r_1}, \end{aligned}$$

(37)

where $r_{i} = a(1 - e\cos E_{i})$ for $i=0,1$. We use Kepler’s equation to compute $\delta E = E_1-E_0$ from $\delta t = t_1 - t_0$. Taking $M_{i} = n(t_{i} - t_p)$ for $i=0,1$, we have that $\delta E$ is the solution of

$$\begin{aligned} x - e \cos E_0 \sin x - e \sin E_0 \cos x + e \sin E_0 - n\delta t = 0. \end{aligned}$$

(38)

Calling $C = \cos \delta E,\ S = \sin \delta E$ and $ce = e \cos E_0,\ se = \sin E_0$ we have that $r_1 = a(1 - ce\cdot C + se\cdot S)$. Now we can rewrite Eq. 37 as:

$$\begin{aligned} a_{11}&= \displaystyle 1 + ( C - 1)\frac{a}{r_0}, \nonumber \\ a_{21}&= \displaystyle \delta t + ( S - \delta E )\frac{a^{3/2}}{\mu ^{1/2}}, \nonumber \\ a_{12}&= \displaystyle - \frac{S}{r_0\sqrt{a}(1 - ce\cdot C + se\cdot S)}, \nonumber \\ a_{22}&= \displaystyle 1 + \frac{C - 1}{1 - ce\cdot C + se\cdot S}. \end{aligned}$$

(39)

To summarise, given $\mathbf{r = r(t_0), v = v(t_0)}$ and defining $r_0 = ||\mathbf{r}||$ and $v_0 = ||\mathbf{v}||$, we find

$$\begin{aligned} a = r_0/(2 - r_0v_0^2), \quad \quad ce = e \cos E_0 = r_0 v_0^2 - 1, \quad \quad se = e \sin E_0 = \langle \mathbf{r}, \mathbf{v}\rangle /\sqrt{\mu a}. \end{aligned}$$

Then we take $\delta t$ and we use Eq. 38 to find $\delta E$. Finally we use Eqs. 35 and 39 to find $\mathbf{r(t_0 + \delta t), v(t_0 + \delta t)}$.

1.2 B.2 Jacobi coordinates

We recall that in this set of coordinates the perturbation part is given by:

$$\begin{aligned} H_{I} = U_1 = G \left[ \sum _{i=1}^{n}m_i\left( \frac{\eta _{i-1}}{||\mathbf{v_i}||} - \frac{m_0}{||\mathbf{r_i}||}\right) - \sum _{0 < i < j\le n}\left( \frac{m_i m_j}{||\mathbf{r_i - r_j ||}} \right) \right] . \end{aligned}$$

(40)

1.2.1 B.2.1 Computing $\exp (L_{H_{I}})$

$U_1$ depends only on the position, hence the equations of motion are given by,

$$\begin{aligned} \frac{d}{dt}\mathbf{v_k} = \frac{\partial U_1}{\partial \,{\tilde{\mathbf{v}}}_\mathbf{k}}, \quad \quad \quad \quad \frac{d}{dt}{{\tilde{\mathbf{v}}}_\mathbf{k}} = -\frac{\partial U_1}{\partial \, \mathbf v_k}. \end{aligned}$$

Using ${{\tilde{\mathbf{v}}}_\mathbf{i}} = \displaystyle \frac{\eta _{i-1}m_i}{\eta _i}{\dot{\mathbf{v}}}_i$ we have

$$\begin{aligned} \mathbf{v_k}(\tau ) = \mathbf{v_k}(\tau _0), \quad \quad \quad \quad {\dot{\mathbf{v}}}_k(\tau ) = {\dot{\mathbf{v}}}_k(\tau _0) - \tau \frac{\eta _i}{\eta _{i-1}m_i}\frac{\partial U_1}{\partial \mathbf{v_k}}. \end{aligned}$$

As the expressions for ${\partial U_1}/{\partial \mathbf{v_k}}$ can be a little cumbersome, we compute them separately. When we derive $H_{I}$ with respect to $\mathbf{v_k}$ we must derive 3 main expressions: ${1}/{||\mathbf{v_i}||},\,{1}/{||\mathbf{r_i}||}$ and ${1}/{||\mathbf{r_i - r_j}||}$ for $i<j$. We first give the derivatives of these factors with respect to $\mathbf{v_k}$ and then we will deduce ${\partial H_{I}}/{\partial \mathbf{v}_\mathbf{k}}$ for $k = 1, \ldots , n$.

$$\begin{aligned} \begin{array}{lcl} \displaystyle \frac{\partial }{\partial \mathbf{v}_\mathbf{k}} \left( \frac{1}{||\mathbf{v}_\mathbf{i}||}\right) = -\frac{\mathbf{v}_\mathbf{i}}{||\mathbf{v}_\mathbf{i}||^3}\cdot \delta _{i,k}, &{}\text{ where }&{} \delta _{i,k} = \left\{ \begin{array}{ccl} 0 &{} \text{ if } &{} i \ne k, \\ 1 &{} \text{ if } &{} i = k.\end{array}\right. \\ \displaystyle \frac{\partial }{\partial \mathbf{v}_\mathbf{k}} \left( \frac{1}{||\mathbf{r}_\mathbf{i}||}\right) = -\frac{\mathbf{r}_\mathbf{i}}{||\mathbf{r}_\mathbf{i}||^3}\cdot \xi _{i,k}, &{} \text{ where } &{} \xi _{i,k} = \left\{ \begin{array}{ccl} 0 &{} \text{ if } &{} i < k, \\ 1 &{} \text{ if } &{} i = k, \\ \displaystyle \frac{m_k}{\eta _k} &{} \text{ if } &{} i > k.\end{array}\right. \\ \displaystyle \frac{\partial }{\partial \mathbf{v}_\mathbf{k}} \left( \!\frac{1}{||\mathbf{r}_\mathbf{i} \!-\! \mathbf{r}_\mathbf{j}||}\!\right) \!=\! \!-\!\frac{\mathbf{r}_\mathbf{i} \!-\! \mathbf{r}_\mathbf{j}}{||\mathbf{r}_\mathbf{i} \!-\! \mathbf{r}_\mathbf{j}||^3}\cdot \psi _{i,j,k}, &{}\!\! \text{ where } &{} \psi _{i,j,k} \!=\! \left\{ \begin{array}{ccl}\!\! \displaystyle \frac{\eta _{k-1}}{\eta _k} &{} \text{ if } &{} k = i < j, \\ -\displaystyle \frac{m_{k}}{\eta _k} &{} \text{ if } &{} i < k < j, \\ -1 &{} \text{ if } &{} i < j = k, \\ 0 &{}\!\!\! \text{ else } &{} (k \!<\! i \!<\! j, \ \ i \!<\! j \!<\! k). \end{array}\right. \end{array} \end{aligned}$$

To compute ${\partial U_1}/{\partial \mathbf v_k}$ for $k = 1, \ldots , n$, we consider separately the cases $k = 1$ and $k > 1$:

$$\begin{aligned} \frac{\partial U_1}{\partial \mathbf{v}_\mathbf{1}}&= G \frac{m_0m_1}{\eta _1}\left[ \sum _{i=2}^{n} m_i \frac{\mathbf{r}_\mathbf{i}}{||\mathbf{r}_\mathbf{i}||^3} + \sum _{i=2}^n m_i \frac{\mathbf{r}_\mathbf{1}-\mathbf{r}_\mathbf{i}}{||\mathbf{r}_\mathbf{1} - \mathbf{r}_\mathbf{i}||^3}\right] .\\ \frac{\partial U_1}{\partial \mathbf{v}_\mathbf{k}}&= Gm_k\left[ -\eta _{k-1}\frac{\mathbf{v}_\mathbf{k}}{||\mathbf{v}_\mathbf{k}||^3} + m_0\frac{\mathbf{r}_\mathbf{k}}{||\mathbf{r}_\mathbf{k}||^3} + \frac{m_0}{\eta _k}\sum _{i=k+1}^{n}m_i \frac{\mathbf{r}_\mathbf{i}}{||\mathbf{r}_\mathbf{i}||^3}\right. \\&\!+\! \left. \frac{\eta _{k-1}}{\eta _k} \sum _{j=k+1}^n m_j\frac{\mathbf{r}_\mathbf{k} \!-\! \mathbf{r}_\mathbf{j}}{||\mathbf{r}_\mathbf{k} \!-\! \mathbf{r}_\mathbf{j}||^3} \!-\! \sum _{i=1}^{k-1} m_i \frac{\mathbf{r}_\mathbf{i} \!-\! \mathbf{r}_\mathbf{k}}{||\mathbf{r}_\mathbf{i} \!- \!\mathbf{r}_\mathbf{k}||^3} \!-\!\frac{1}{\eta _k} \sum _{i=1}^{k-1}\sum _{j=k+1}^n m_im_j \frac{\mathbf{r}_\mathbf{i}-\mathbf{r}_\mathbf{j}}{||\mathbf{r}_\mathbf{i} - \mathbf{r}_\mathbf{j}||^3}\right] . \\ \end{aligned}$$

1.2.2 B.2.2 Computing the corrector: $\exp (L_{\{\{A,B\},B\}})$

In Sect. 5.2.1 we described a splitting symplectic schemed where a corrector term was added at the beginning and at the end of each step-size. The corrector term is given by,

$$\begin{aligned} \exp \left( -\tau ^3\varepsilon ^2\frac{c}{2}L_C\right) , \end{aligned}$$

with $L_C = L_{\{\{A,B\},B\}}$ and $c$ a constant coefficient that depends on the order of the $\mathcal{ABA }$ scheme.

In Jacobi coordinates $A$ is quadratic in $p$ and $B$ only depends on $q$ so $\{\{A,B\},B\}$ only depends on $q$ and $\{\{A,B\},B\}$ is integrable. We recall that $A = H_{Kep} = T_0 + U_0$ and $B = H_{pert} = U_1$. Hence,

$$\begin{aligned} \{\{T_0 + U_0, U_1\}, U_1\} = \{\{T_0, U_1\}, U_1\}. \end{aligned}$$

Given that $T_0 = \displaystyle \mathop {\sum }\nolimits _{i=1}^{n} \frac{\eta _i}{\eta _{i-1}m_i} \frac{||{\tilde{\mathbf{v}}}_\mathbf{i}||^2}{2}$, we have,

$$\begin{aligned} \{T_0, U_1\}&= \sum _{i=1}^{n} \frac{\eta _i}{\eta _{i-1}m_i} {\tilde{\mathbf{v}}}_\mathbf{i} \frac{\partial U_1}{\partial \mathbf v_i}, \\ \{\{T_0, U_1\}, U_1\}&= \sum _{i=1}^{n} \frac{\eta _i}{\eta _{i-1}m_i} \left( \frac{\partial U_1}{\partial \mathbf v_i} \right) ^2. \end{aligned}$$

Then the equations of motion for $L_C$ are given by:

$$\begin{aligned} \mathbf{v_k} (\tau )&= \mathbf{v_k}(\tau _0), \\ \displaystyle {{\tilde{\mathbf{v}}}_\mathbf{k}} (\tau )&= {{\tilde{\mathbf{v}}}_\mathbf{k}}(t_0) + \tau \sum _{i=1}^{n} 2 \gamma _i \frac{\partial U_1}{\partial \mathbf v_i} \frac{\partial ^2 U_1}{\partial \mathbf v_i \partial \mathbf v_k }, \end{aligned}$$

where $\gamma _k = \frac{\eta _k}{\eta _{k-1}m_k}$. As before, using ${{\tilde{\mathbf{v}}}_\mathbf{i}} = \displaystyle \frac{\eta _{i-1}m_i}{\eta _i}{\dot{\mathbf{v}}}_\mathbf{i}$ we have

$$\begin{aligned} {\dot{\mathbf{v}}}_\mathbf{k} (\tau ) = {\dot{\mathbf{v}}}_\mathbf{k}(t_0) + \tau \gamma _k \sum _{i=1}^{n} 2 \left( \gamma _i \frac{\partial U_1}{\partial \mathbf v_i} \right) \frac{\partial ^2 U_1}{\partial \mathbf v_i \partial \mathbf v_k}. \end{aligned}$$

Again the expressions for $\displaystyle \frac{\partial ^2 U_1}{\partial \mathbf v_i \partial \mathbf v_k}$ are a little cumbersome and we first show how to derive the different parts in $\displaystyle \frac{\partial U_1}{\partial \mathbf v_k}$: $\mathbf{v_i}/{||\mathbf{v_i}||^3},\,\mathbf{r_i}/{||\mathbf{r_i}||^3}$ and $\mathbf{r_i - r_j}/{||\mathbf{r_i - r_j}||^3}$.

$$\begin{aligned} \displaystyle \frac{\partial }{\partial \mathbf{v}_\mathbf{k}} \left( \frac{\mathbf{v}_\mathbf{i}}{||\mathbf{v}_\mathbf{i}||^3}\right)&= \displaystyle \left( \frac{\langle {\mathbf{h, k}}\rangle }{||\mathbf{v}_\mathbf{i}||^3} -3\frac{\langle {\mathbf{v}_\mathbf{i}, \mathbf{h}}\rangle \langle {\mathbf{v}_\mathbf{i}, \mathbf{k}}\rangle }{||\mathbf{v}_\mathbf{i}||^5}\right) \cdot \delta _{i,k},\\ \displaystyle \frac{\partial }{\partial \mathbf{v}_\mathbf{k}} \left( \frac{\mathbf{r}_\mathbf{i}}{||\mathbf{r}_\mathbf{i}||^3}\right)&= \displaystyle \left( \frac{\langle {\mathbf{h, k}}\rangle }{||\mathbf{r}_\mathbf{i}||^3} -3\frac{\langle {\mathbf{r}_\mathbf{i}, \mathbf{h}}\rangle \langle {\mathbf{r}_\mathbf{i}, \mathbf{k}}\rangle }{||\mathbf{r}_\mathbf{i}||^5} \right) \cdot \xi _{i,k},\\ \displaystyle \frac{\partial }{\partial \mathbf{v}_\mathbf{k}} \left( \frac{\mathbf{r}_\mathbf{i} - \mathbf{r}_\mathbf{j}}{||\mathbf{r}_\mathbf{i} - \mathbf{r}_\mathbf{j}||^3}\right)&= \displaystyle \left( \frac{\langle {\mathbf{h}, \mathbf{k}}\rangle }{||\mathbf{r}_\mathbf{i} - \mathbf{r}_\mathbf{j}||^3} \right. \displaystyle \left. -3\frac{\langle {\mathbf{r}_\mathbf{i} - \mathbf{r}_\mathbf{j}, \mathbf{h}}\rangle \langle {\mathbf{r}_\mathbf{i} - \mathbf{r}_\mathbf{j}, \mathbf{k}}\rangle }{||\mathbf{r}_\mathbf{i} - \mathbf{r}_\mathbf{j}||^5} \right) \cdot \psi _{i,j,k}. \end{aligned}$$

From now on we call $\mathbf{Acc}(i) = \gamma _i \displaystyle \frac{\partial U_1}{\partial \mathbf v_i}$, and

$$\begin{aligned} \varLambda _s&= \mathbf{Acc}(s) \displaystyle \left( \frac{\langle \mathbf{h, k}\rangle }{||\mathbf{v_i}||^3} -3\frac{\langle \mathbf{v_i, h}\rangle \langle \mathbf{v_i, k}\rangle }{||\mathbf{v_i}||^5}\right) ,\\ \varTheta _{i,s}&= \mathbf{Acc}(s) \displaystyle \left( \frac{\langle \mathbf{h, k}\rangle }{||\mathbf{r_i}||^3} -3\frac{\langle \mathbf{r_i, h}\rangle \langle \mathbf{r_i, k}\rangle }{||\mathbf{r_i}||^5} \right) ,\\ \varPsi _{i,j,s}&= \mathbf{Acc}(s) \displaystyle \left( \frac{\langle \mathbf{h, k}\rangle }{||\mathbf{r_i - r_j}||^3} -3\frac{\langle \mathbf{r_i - r_j, h}\rangle \langle \mathbf{r_i - r_j, k}\rangle }{||\mathbf{r_i - r_j}||^5} \right) .\\ \end{aligned}$$

We can now give the expressions for $\displaystyle \frac{\partial ^2 U_1}{\partial \mathbf v_i \partial \mathbf v_k}\,\forall j, k$

$$\begin{aligned} \frac{\partial ^2 U_1}{\partial \mathbf{v_1} \partial \mathbf{v_1}}&= G\frac{m_0m_1}{\eta _1} \left[ \sum _{j = 2}^n m_j\left( \varTheta _{j,1}\frac{m_1}{\eta _1} + \varPsi _{1,j,1}\frac{m_0}{\eta _1}\right) \right] .\\ \frac{\partial ^2 U_1}{\partial \mathbf{v_1} \partial \mathbf{v_k}}&= G\frac{m_0m_1m_k}{\eta _1} \left[ \varTheta _{k,s} - \varPsi _{1,k,s} + \frac{1}{\eta _k} \sum _{j = k+1}^n m_j( \varTheta _{j,s} - \varPsi _{1,j,s})\right] . \\ \frac{\partial ^2 U_1}{\partial \mathbf{v_k} \partial \mathbf{v_k}}&= G m_k \left[ -\eta _{k-1} \varLambda _k + m_0 \varTheta _{k,k} + \frac{m_0m_k}{\eta _k^2}\sum _{i = k+1}^{n} m_i \varTheta _{i,k} + \frac{\eta _{k-1}^2}{\eta _k^2} \sum _{i = k+1}^{n} m_i \varPsi _{k,i,k} \right. \\&\left. + \sum _{i = 1}^{k-1} m_i \varPsi _{i,k,k} + \frac{m_k}{\eta _k^2} \sum _{i = 1}^{k-1}\sum _{j = i+1}^n m_im_j \varPsi _{i,j,k}\right] . \\ \frac{\partial ^2 U_1}{\partial \mathbf{v_k} \partial \mathbf{v_l}}&= G\frac{m_k m_l}{\eta _k}\left[ m_0 \varTheta _{l,s}- \eta _{k-1}\varPsi _{k,l,s}+ \frac{1}{\eta _l}\sum _{i = l+1}^{n} m_i (m_0\varTheta _{i,s} - \eta _{k-1}\varPsi _{k,i,s}) \right. \\&\left. + \sum _{i = 1}^{k-1} m_i \varPsi _{i,l,s} + \frac{1}{\eta _l} \sum _{i = 1}^{k-1}\sum _{j = l+1}^n m_im_j \varPsi _{i,j,k}\right] . \\ \end{aligned}$$

1.3 B.3 Heliocentric coordinates

We recall that in this set of coordinates the perturbation part is given by:

$$\begin{aligned} H_{I} = T_{1} + U_{1} = \sum _{0 < i < j\le n} \frac{{\tilde{\mathbf{r}}}_\mathbf{i} \cdot {\tilde{\mathbf{r}}}_\mathbf{j}}{m_0} - G\sum _{0 < i < j\le n} \frac{m_i m_j}{\varDelta _{ij}}, \end{aligned}$$

(41)

1.3.1 B.3.1 Computing $\exp (\tau L_{T_{1}})$

Notice that $T_{1}$ depends only on the momenta $({{\tilde{\mathbf{r}}}})$. Hence, the equations of motion are given by,

$$\begin{aligned} \displaystyle \frac{d}{dt}\mathbf{r_k}&= \frac{\partial T_{1}}{\partial \ {\tilde{\mathbf{r}}}_\mathbf{k}} = \sum _{j = 1, j \ne k} \frac{{\tilde{\mathbf{r}}}_\mathbf{j}}{m_0} = \sum _{j = 1, j \ne k} \frac{m_j {\dot{\mathbf{r}}}_\mathbf{j}}{m_0},\\ \displaystyle \frac{d}{dt}{{\tilde{\mathbf{r}}}_\mathbf{k}}&= \frac{\partial T_{1}}{\partial \, \mathbf r_k} = 0. \end{aligned}$$

Finally,

$$\begin{aligned} \mathbf{r_k}(\tau ) = \mathbf{r_k}(\tau _0) + \tau \sum _{j = 1, j \ne k} \frac{m_j {\dot{\mathbf{r}}}_\mathbf{j}}{m_0}, \quad \quad \quad \quad {\dot{\mathbf{r}}}_\mathbf{k}(\tau ) = {\dot{\mathbf{r}}}_\mathbf{k}(\tau _0). \end{aligned}$$

1.3.2 B.3.2 Computing $\exp (\tau L_{U_{1}})$

Notice that $U_{1}$ depends only on the positions $(\mathbf{r})$. Hence, the equations of motion are given by,

$$\begin{aligned} \displaystyle \frac{d}{dt}{{\tilde{\mathbf{r}}}_\mathbf{k}}&= \frac{\partial U_{1}}{\partial \, \mathbf r_k} = 0,\\ \displaystyle \frac{d}{dt}{{\tilde{\mathbf{r}}}_\mathbf{k}}&= -\frac{\partial U_{1}}{\partial \, \mathbf r_k} = -G \left( \sum _{j = 1}^{k-1} \frac{m_k m_j}{\varDelta _{kj}^3}(\mathbf{r_k - r_j}) - \sum _{j = k+1}^{n} \frac{m_k m_j}{\varDelta _{jk}^3}(\mathbf{r_j - r_k}) \right) . \end{aligned}$$

Given that ${\tilde{\mathbf{r}}}_\mathbf{k} = m_k {\dot{\mathbf{r}}}_\mathbf{k}$, we have:

$$\begin{aligned} \mathbf{r_k}(\tau ) = \mathbf{r_k}(\tau _0), \quad \quad {\dot{\mathbf{r}}}_\mathbf{k}(\tau ) = {\dot{\mathbf{r}}}_\mathbf{k}(\tau _0) - \tau \ G \left( \sum _{j = 1}^{k-1} \frac{m_j}{\varDelta _{kj}^3}(\mathbf{r_k - r_j}) + \sum _{j = k+1}^{n} \frac{m_j}{\varDelta _{kj}^3}(\mathbf{r_k - r_j}) \right) . \end{aligned}$$

Appendix C: Heliocentric coordinates (alternatives for the set of equations)

The canonical heliocentric (CH) coordinates used in Sect. 6 are canonical and the position of each body is taken with respect to the position of the Sun. The position and their associated momenta are given by:

$$\begin{aligned} \left. \begin{array}{rcl} \mathbf r_0 &{}=&{} \mathbf u_0 \\ \mathbf r_i &{}=&{} \mathbf u_i - u_0 \end{array}\right\} , \quad \quad \quad \quad \left. \begin{array}{rcl} {\tilde{\mathbf{r}}}_\mathbf{0} &{}=&{} {\tilde{\mathbf{u}}}_\mathbf{0} + \cdots + {\tilde{\mathbf{u}}}_\mathbf{n} \\ {\tilde{\mathbf{r}}}_\mathbf{i} &{}=&{} {\tilde{\mathbf{u}}}_\mathbf{i} \end{array}\right\} . \end{aligned}$$

The main difference between Jacobi and heliocentric coordinates is that in the second set of coordinates the kinetic energy is not diagonal in the momenta. Instead we have:

$$\begin{aligned} T = \displaystyle \frac{1}{2}\sum _{i=0}^{n}\frac{||{{\tilde{\mathbf{u}}}_\mathbf{i}}||^2}{m_i}=\frac{1}{2}\sum _{i=1}^{n}\frac{||{{\tilde{\mathbf{r}}}_\mathbf{i}}||^2}{m_i}+\frac{1}{2}\frac{|| \sum _{i=1}^n{{\tilde{\mathbf{r}}}_\mathbf{i}} ||^2}{m_0}, \end{aligned}$$

(42)

which can be rewritten as:

$$\begin{aligned} T = \displaystyle \frac{1}{2}\sum _{i=0}^{n}\frac{|| {{\tilde{\mathbf{u}}}_\mathbf{i}} ||^2}{m_i} = \frac{1}{2} \sum _{i=1}^{n}{|| {{\tilde{\mathbf{r}}}_\mathbf{i}} ||^2} \left[ \frac{1}{m_0} + \frac{1}{m_i}\right] + \sum _{0<i<j} \frac{{\tilde{\mathbf{r}}}_\mathbf{i} \cdot {\tilde{\mathbf{r}}}_\mathbf{j}}{m_0}. \end{aligned}$$

(43)

The extra term due to the momenta of the Sun is added to the perturbation part and makes it depend on both position and velocities. In Sect. 3 we used Eq. 43 to derive the Hamiltonian expression, as in Laskar (1990b, 1991), Koseleff (1993a). Duncan et al. (1998) used Eq. 42 instead, and a Keplerian approximation in which the planets orbits around a fixed Sun (Eq. 48). Following Laskar (1991) we will call the first set of equations CH, and following Duncan et al. (1998) we will call the second set of equations democratic canonical heliocentric (DCH). Here we discuss the main differences between the two sets of equations and compare the performance of the integrators presented in this paper for both expressions.

1.1 C.1 Two different expressions for Heliocentric coordinates

As we know in heliocentric coordinates the Hamiltonian for an n-planetary system takes the form:

$$\begin{aligned} H = H_{K} + T_1 + U_1, \end{aligned}$$

a sum of Keplerian parts, a quadratic term in the momenta and the gravitational interaction between the other planets. Using Eq. 43 we have, for CH decomposition

$$\begin{aligned} H_{K}&= \sum _{i=1}^{n} \left( \frac{1}{2} ||{{\tilde{\mathbf{r}}}_\mathbf{i}}||^2 \left[ \frac{m_0 + m_i}{m_0 m_i}\right] - G\frac{m_0 m_i}{||\mathbf{r_i}||} \right) ,\end{aligned}$$

(44)

$$\begin{aligned} T_1&= \sum _{0 < i < j\le n} \frac{{\tilde{\mathbf{r}}}_\mathbf{i} \cdot {\tilde{\mathbf{r}}}_\mathbf{j}}{m_0},\end{aligned}$$

(45)

$$\begin{aligned} U_1&= - G \sum _{0 < i < j\le n} \frac{m_i m_j}{\varDelta _{ij}}. \end{aligned}$$

(46)

The main advantage of this way to split the equations is that Kepler’s third law is satisfied for the individual planets: $n^2a^3 = G(m_0 + m_i)$. But $H_I = T_1 + U_1$ is not integrable and $\{T_1, U_1\} \ne 0$.

Using Eq. 42 we have the DCH splitting introduced by Duncan et al. (1998), and used later on by Chambers (1999) and Wisdom (2006)

$$\begin{aligned} H_{K}^*&= \sum _{i=1}^{n} \left( \frac{1}{2} \frac{||{{\tilde{\mathbf{r}}}_\mathbf{i}}||^2}{m_i} - G\frac{m_0 m_i}{||\mathbf{r_i}||} \right) ,\end{aligned}$$

(47)

$$\begin{aligned} T_1^*&= \frac{1}{2} \frac{|| \sum _{i=1}^n {{\tilde{\mathbf{r}}}_\mathbf{i}} ||^2}{m_0},\end{aligned}$$

(48)

$$\begin{aligned} U_1^*&= - G \sum _{0 < i < j\le n} \frac{m_i m_j}{\varDelta _{ij}}. \end{aligned}$$

(49)

With this way to split the equations the mass parameter for the Keplerian orbits is $\mu = Gm_0$ for all of the planets. On the other hand, $T_1^*$ and $U_1^*$ (Eqs. 48–49) commute, i.e. $\{T^*_1, U^*_1\} = 0$ and this is a advantage when we build high order splitting schemes. For simplicity let us consider $H_B = T_1$ and $H_C = U_1$ for both expressions. We recall that in heliocentric coordinates we need to integrate $\exp (\tau (B + C))$. Using DCH splitting (Eqs. 48–49) we have:

$$\begin{aligned} \exp (\tau (B + C)) = \exp (\tau B)\exp (\tau C), \end{aligned}$$

(50)

which can be computed exactly and does not introduce any extra error terms to the splitting schemes discussed in Sect. 5. Instead, using CH variables (Eqs. 45–46) we used

$$\begin{aligned} \exp (\tau (B + C)) \approx \exp \left( \frac{\tau }{2} C\right) \exp (\tau B)\exp \left( \frac{\tau }{2} C\right) , \end{aligned}$$

(51)

and introduced error terms of order $\varepsilon ^3\tau ^2$. To deal with this in Sect. 6 derived splitting schemes where an extra stage was added to get rid of these extra error terms.

1.2 C.2 Comparisons between the expressions

We recall that when we use DCH variables (Eqs. 47–49) we use the splitting schemes discussed in Sect. 5 with

$$\begin{aligned} \mathcal{S }(\tau ) = \prod _{i = 1}^n \exp (a_i\tau L_{H_{K^*}}) \exp (b_i\tau L_{T_1^*})\exp (b_i\tau L_{U_1^*}). \end{aligned}$$

(52)

While when we use the classical CH variables (Eqs. 44–46) we use the splitting schemes discussed in Sect. 6 with

$$\begin{aligned} \mathcal{S }(\tau ) = \prod _{i = 1}^n \exp (a_i\tau L_{H_{Kep}}) \exp \left( b_i\frac{\tau }{2} L_{T_1}\right) \exp (b_i\tau L_{U_1})\exp \left( b_i\frac{\tau }{2} L_{T_1}\right) . \end{aligned}$$

(53)

We compare the $\mathcal{ABA }$ schemes of orders $(8,2), (8,4)$ and $(10,6,4)$ for both splitting expressions. We recall that the schemes of order $(8,4)$ and $(10,6,4)$ that use CH variables (Eqs. 44–46) have one more stage than the schemes used with DCH variables (Eqs. 47–49).

Fig. 9

Comparison between the two expressions for heliocentric coordinates: the classical CH expressions (Eqs. 44–46) continuous lines and the DCH expressions (Eqs. 47–49) discontinuous lines. For the schemes $\mathtt{ABA82 }$ (red), $\mathtt{ABA84 }$ (green) and $\mathtt{ABA1064 }$ (blue). From left to right the 4 inner planets, the 4 outer planets and the whole Solar System. The $x$-axis represents the cost $(\tau /s)$ of the method and the $y$-axis the maximum energy variation for one integration with constant step-size $\tau$ (decimal log scales)

Figure 9 summarise the performance of the different integrating schemes presented in Sects. 5 and 6. From left to right we have the results for the inner planets, the outer planets and the whole Solar System. The red lines show the performance of the $\mathtt{ABA82 }$ scheme, the green lines are for the $\mathtt{ABA84 }$ schemes and the blue lines are for the $\mathtt{ABA1064 }$ schemes. We use continuous lines when we consider CH variables and discontinuous lines for DCH variables.

As we can see, there is no significant difference between using one splitting or the other. In some cases one is better that the other. The main advantage that the splitting DCH introduced by Duncan et al. (1998) is that we do not require an extra stage for a high-order scheme.

Appendix D: Comparison in quadruple precision

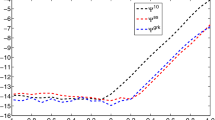
As we have discussed throughout the article, in many cases we have seen that despite taking higher order methods no significant improvement on the performance of the schemes was observed. This is the case of the 4 inner planets in the Solar System, where the size of the perturbation is so small that the extra stages to increase the order of the schemes are useless. Here the round-off error dominates the terms in $\varepsilon ^2$ and $\varepsilon ^4$. Similar results are also observed when we consider the whole Solar System. In order to see an improvement we need to use higher precision arithmetics. Here we have repeated the test from Sects. 5 and 6 for the different integrating schemes using quadruple precision arithmetics. We want to illustrate that the different schemes of orders $(8,6,4)$ and $(10,6,4)$ perform better that those of order $(8,4)$.

In Figs. 10 and 11 we show the results for the same test models used throughout the article for Jacobi and heliocentric coordinates, respectively using quadruple precision arithmetics. For Jacobi coordinates (Fig. 10) we compare the $\mathtt{ABA82 },\,\mathtt{ABA84 },\,\mathtt{ABA104 }, \mathtt{ABA864 }$ and $\mathtt{ABA1064 }$ schemes. For heliocentric coordinates (Fig. 11) we compare the $\mathtt{ABAH82 },\,\mathtt{ABAH84 },\,\mathtt{ABAH864 }$ and $\mathtt{ABAH1064 }$. As we can see in Fig. 10 for Jacobi coordinates, the $\mathtt{ABA864 }$ and $\mathtt{ABA1064 }$ (Blanes et al. 2013) do improve the performance of the $\mathtt{ABA84 }$ (McLachlan 1995). Notice also that for the 4 inner planets (Fig. 10 left) and the whole Solar System (Fig. 10 right) the improvement is achieved for small step-sizes, where the energy variation is below the machines epsilon for extended arithmetics precision. In Fig. 11 similar results are observed for heliocentric coordinates.

Fig. 10

Comparison using Jacobi coordinates between the $\mathtt{ABA82 },\,\mathtt{ABA84 },\,\mathtt{ABA104 },\,\mathtt{ABA864 }$ and $\mathtt{ABA1064 }$ schemes using quadruple precision arithmetics. From left to right the 4 inner planets, the 4 outer planets and the whole Solar System. The $x$-axis represents the cost $(\tau /s)$ and the $y$-axis the maximum energy variation for one integration with constant step-size $\tau$ (decimal log scales)

Fig. 11

Comparison using heliocentric coordinates between the $\mathtt{ABAH82 },\,\mathtt{ABAH84 },\,\mathtt{ABAH864 }$ and $\mathtt{ABAH1064 }$ schemes using quadruple precision arithmetics. From left to right the 4 inner planets, the 4 outer planets and the whole Solar System. The $x$-axis represents the cost $(\tau /s)$ and the $y$-axis the maximum energy variation for one integration with constant step-size $\tau$ (decimal log scales)

From these experiments we see how the $\mathcal{ABA }$ splitting methods of orders $(8,6,4)$ and $(10,6,4)$ for both sets of coordinates improve the performance of the McLachlan (1995) $\mathtt{ABA84 }$ and the Laskar and Robutel (2001) $\mathtt{ABA82 }$.