Brouwer’s satellite solution redux

Abstract

Brouwer’s solution to the artificial satellite problem is revisited. We show that the complete Hamiltonian reduction is rather achieved in the plain Poincaré’s style, through a single canonical transformation, than using a sequence of partial reductions based on von Zeipel’s alternative for dealing with perturbed degenerate Hamiltonian systems. Beyond the theoretical interest of the new approach as regards the complete reduction of perturbed Keplerian motion, we also show that a solution based on a single set of corrections may yield computational benefits in the implementation of an analytic orbit propagator.

1 Introduction

Brouwer’s (1959) analytical solution to the artificial satellite problem based on von Zeipel’s (1965) partial reduction method for dealing with perturbed degenerate Hamiltonians fiercely resists obsolescence sixty years after publication. Indeed, in spite of the spectacular increase of the computational power, widespread software packages for approximate ephemeris prediction still rely on Brouwer’s seminal results (Hoots and Roehrich 1980; Vallado et al. 2006). Furthermore, the success of Brouwer’s closed-form solution among practitioners as well as the reputation gained among theorists by Brouwer’s stepwise normalization makes that the technique is designated these days as either “the Brouwer–von Zeipel method” (Vinti 1998) or “the von Zeipel–Brouwer theory” (Ferraz-Mello 2007).

Since then, the merits of Brouwer’s decomposition of the solution of perturbed Keplerian motion into secular, long-, and short-period effects seem not to have been questioned. Moreover, after the invention of Hamiltonian simplification methods (Deprit 1981), it was suggested that carrying out additional decompositions, thus increasing the number of canonical transformations, could be the proper way to success in the search for separable perturbation Hamiltonians of celestial mechanics problems (Deprit and Miller 1989). Conversely, it has been recently pointed out that the use of Hamiltonian simplification procedures could be merely optional in the construction of higher-order analytical approximations to the satellite problem (Lara 2020). Then, it emerges the question of which is the real value of splitting a normalization procedure, either partial or complete, into several different stages, a topic that may well deserve additional study.

We walk a step in that direction and, in the classical style of Poincaré’s (1893) “new method,” undertake the construction of Brouwer’s second-order completely reduced Hamiltonian of the main problem in the artificial satellite theory (the $J_2$ problem) by means of a single canonical transformation. The difficulties stemming from the degeneracy of the Kepler Hamiltonian, who has two null frequencies, are easily overcome with the addition of suitable integration constants to the generating function of the transformation that yields the complete Hamiltonian reduction.

The use of arbitrary functions in the construction of perturbation solutions is not new at all (Morrison 1966). In fact, it can be traced back to Poincaré’s efforts in approaching degenerate perturbation problems (Poincaré 1893, Chap. XI). They also play a fundamental role in a reverse partial normalization process in which the angular momentum is normalized in first place (Alfriend and Coffey 1984; San-Juan et al. 2013; Lara et al. 2014; Lara 2020). On the other hand, in spite of average perturbation Hamiltonians do not exist in general (Ferraz-Mello 1999), the use of arbitrary constants to guarantee the purely periodic nature of the generating function became customary in attempts to bring the mean elements dynamics as close as possible to the true average dynamics (Métris and Exertier 1995; Steichen 1998; Lara et al. 2011).

To the first order, the construction of Brouwer’s closed-form solution by means of a single transformation amounts to the direct sum of the two transformations computed by Brouwer for the short- and long-period elimination. This is due to the linearization provided by the first-order truncation of a perturbation theory. In view of no differences arise between Brouwer’s and the current approach when the periodic corrections are constrained to first-order effects, we feel compelled to supplement Brouwer’s analytical solution with second-order periodic corrections, yet limited to the $J_2$ contribution. We compare our results with corresponding corrections obtained in the traditional way, in which the normalization is split into the elimination of the parallax, the elimination of the perigee, and the Delaunay normalization (Coffey and Alfriend 1984; Lara 2019b).

At the second order the single transformation is no longer the addition of the different canonical transformations. As expected, the (single) periodic corrections are now much more involved than those corresponding to each of the partial reductions or simplifications and are also more intricate than the sequence formed by of all of them. However, the length of the series defining the solution is only a part of the whole picture, and we found clear computational advantages in the evaluation of the single transformation. The improvements stem from the fact that many inclination polynomials pertaining to the periodic corrections admit factorization. Because common factors repeat many times throughout the corrections, the compiler is able to perform a higher optimization of the code in the case of the single transformation than in the case in which the transformation is split in different stages.

In addition, when used in the implementation of an analytic orbit propagator, the new approach shows additional merits derived from the Poisson series structure of the periodic corrections. Indeed, in the case of a single set of periodic corrections, the eccentricity and inclination polynomials defining the coefficients of the trigonometric terms of the Poisson series remain constant in mean elements. Therefore, they only need to be evaluated once, which is done immediately after the initialization of the constants of the perturbation theory. Hence, repeated ephemeris evaluation only requires the update of the trigonometric terms and, therefore, is radically simplified. On the contrary, the sequence of periodic corrections in which traditional methods rely requires the update of all orbital elements at each evaluation step.

Because of the algebraic properties of Lie transforms (Henrard 1970), there is no doubt that the periodic corrections provided by our approach are the same as those that would be obtained if properly composing the different transformations involved in any of the schemes in the literature based on the traditional splitting. This property has been used to check that the periodic terms of our single-transformation approach are free from errors. That the new approach provides comparable accuracy to previous published solutions for the same truncation orders becomes then evident. It could not be otherwise save for programming errors or numerical evaluation issues stemming for the different arrangement of the periodic corrections in the variety of available solutions, or for the use of different sets of canonical or non-canonical variables. Nonetheless, these computational aspects may have in practice actual effects regarding the implementation of an analytic orbit propagator.

In the process of computing the second-order corrections, we will recognize how artificial the controversy created about the integration of the equation of the center was. Indeed, difficulties confronted by researchers involved in the automatization of celestial mechanics computations were, in fact, derived from their own programming strategies (Deprit and Rom 1970; Jefferys 1971). On the contrary, the trouble had been easily sidestepped by celestial mechanicians relying on traditional hand computations (Kozai 1962b; Aksnes 1971). We will show that standard integration by parts reduces the equation of the center issue to the well known integration of cosine functions in elliptic motion (Deprit and Ferrer 1987; Kelly 1989; Ahmed 1994). We hasten to say that the controversy was in no way futile since it provoked the appearance of Hamiltonian simplification methods and led to the development of sophisticated computational strategies (Healy 2000).¹

To fully determine the second-order term of the generating function of Brouwer’s theory, the third-order term of the completely reduced Hamiltonian needs to be previously specified. The use of higher-order secular terms should improve further the long-term performance of Brouwer’s solution. However, to be effective in the propagation of an initial state vector, the initialization constants of the analytical solution, and, in particular, the secular frequencies, must be computed within comparable accuracy to that of the secular terms. Rather than carrying out the long and tedious computations required in the determination of the third-order generating function, we take the clever shortcut proposed by Breakwell and Vagners (1970). That is, we limit the computation of third-order corrections to the case of the secular mean motion, which, besides, is directly obtained from the secular Hamiltonian. With this effortless procedure, the addition of third-order secular terms clearly improves the performance of Brouwer’s solution.

Beyond the $J_2$ perturbation term that we took as a toy model for the description of the new method, Brouwer’s theory incorporates the first few zonal harmonics of the Geopotential. These additional terms produce quantitative variations that are clearly observed in short-term propagations of circumterrestrial orbits with rotating periapsis. Higher-order zonal harmonics produce also qualitative modifications in the artificial satellite problem dynamics (Coffey et al. 1994; Lara 2018), yet these modifications basically affect the perigee-oscillation regime, a region of phase space in which Brouwer’s solution does not apply. Therefore, these terms need to be mandatorily included in an analytic orbit propagator program. From the nature of Legendre polynomials, the higher-order harmonics can be arranged formally in the same way as we discuss here for the second zonal harmonic to ease integration by parts. Based on the single periodic corrections approach, the implementation of an analytical orbit propagator dealing with the full Brouwer’s solution has been undertaken by the author. Initial results are promising and seem to support the advantages observed in the much simpler main problem. If confirmed, results in this regard will be published elsewhere.

2 Brouwer’s complete reduction at once

Constraining the dynamical model of the artificial satellite problem to the $J_2$ perturbation (main problem), Brouwer’s (1959) gravitational Hamiltonian takes the form

$$\begin{aligned} {\mathcal {H}}=-\frac{\mu }{2a}+\frac{\mu }{r}\frac{R_\oplus ^2}{r^2}\frac{1}{2}C_{2,0}\left[ 1-\frac{3}{2}s^2+\frac{3}{2}s^2\cos (2f+2\omega )\right] , \end{aligned}$$

(1)

where the Earth’s gravitational field is materialized by the physical constants $\mu$, the gravitational parameter, $R_\oplus$, the equatorial radius, and $C_{2,0}=-J_2$, the non-dimensional oblateness coefficient.² The symbols a, r, f and $\omega$ stand for semi-major axis, radius from the Earth’s center of mass, true anomaly, and argument of the perigee, respectively, whereas $s\equiv \sin {I}$ abbreviates the sine of the inclination I. Since we are dealing with Hamiltonian mechanics, these symbols must be understood as functions of some set of canonical variables. In particular we assume, with Brouwer, that the Hamiltonian is written in terms of the Delaunay coordinates $\ell$, the mean anomaly, $g=\omega$, and h, the longitude of the ascending node, and their conjugate momenta $L=\sqrt{\mu {a}}$, $G=L(1-e^2)^{1/2}$, with e denoting the eccentricity, and $H=G\cos {I}$, standing for the Delaunay action, the total angular momentum, and the projection of the angular momentum vector along the Earth’s rotation axis, respectively. That H is an integral of Eq. (1) becomes evident from the cyclic character of h. Besides, the Hamiltonian itself is constant because the time does not appear explicitly in it.

The small value of the Earth’s $J_2$ coefficient identifies Eq. (1) like a case of perturbed Keplerian motion, which, therefore, can be reduced to a separable Hamiltonian by perturbation methods. This is achieved by finding a canonical transformation ${\mathcal {T}}:(\ell ,g,h,L,G,H,\epsilon )\mapsto (\ell ',g',h',L',G',H')$, from osculating to mean variables, depending on the small parameter $\epsilon \sim {J}_2$, such that the transformed Hamiltonian in mean (prime) variables becomes a function of only the momenta, namely ${\mathcal {H}}\circ {\mathcal {T}}={\mathcal {K}}(-,-,-,L',G',H';\epsilon )$. The transformation ${\mathcal {T}}$, we learned from Poincaré (1893), is derived from a determining function that is solved in the form of a Taylor series up to some truncation order of the small parameter $\epsilon$.

Brouwer, for his part, after introducing the method of solution, seems to refuse approaching the direct computation of the transformation ${\mathcal {T}}$ since the beginning, by simply declaring that

“[...] it is more convenient to choose a determining function in such a manner that the mean anomaly is not present in the transformed Hamiltonian while the argument of the perigee is permitted to appear.”

Next, after invoking von Zeipel, he proceeded stepwise by partial reduction, first computing a canonical transformation that only removes the short-period terms from the Hamiltonian, and then carrying out a second canonical transformation that removes the long-period terms. In this way Brouwer outstandingly achieves the complete Hamiltonian reduction in closed form.

Conversely, we ignore the presumed convenience of Brouwer’s procedure and approach the perturbation problem searching for a single determining function in the original style of Poincaré, yet we better rely on the equivalent but more functional method of Lie transforms (Hori 1966; Deprit 1969; Deprit and Deprit 1999). Thus, we write Eq. (1) in the usual form of a perturbation Hamiltonian ${\mathcal {H}}=\sum _{m\ge 0}(\epsilon ^m/m!){\mathcal {H}}_{m,0}$, with

$$\begin{aligned} {\mathcal {H}}_{0,0}=-\frac{\mu }{2a}, {\mathcal {H}}_{1,0}=-\frac{\mu }{r}\frac{R_\oplus ^2}{r^2}\frac{1}{2}\left[ 1-\frac{3}{2}s^2+\frac{3}{2}s^2\cos (2f+2\omega )\right] , \end{aligned}$$

${\mathcal {H}}_{m,0}=0$ for $m\ge 2$, and $\epsilon \equiv {J}_2=-C_{2,0}$. Recall that all the symbols are functions of the Delaunay canonical variables, in which the Lie operator ${\mathcal {L}}_0=\{\quad ;{\mathcal {H}}_{0,0}\}$, where the curly brackets stand for the Poisson brackets operator, takes the simple form ${\mathcal {L}}_0=n\partial /\partial \ell$, where $n=\mu ^2/L^3$ is the mean motion. This allows us to compute the determining function ${\mathcal {W}}=\sum _{m\ge 0}(\epsilon ^m/m!){\mathcal {W}}_{m+1}$ from the sequence given by the homological equation

$$\begin{aligned} {\mathcal {W}}_m=\frac{1}{n}\int (\widetilde{{\mathcal {H}}}_{0,m}-{\mathcal {H}}_{0,m})\mathrm {d}\ell +{\mathcal {C}}_m. \end{aligned}$$

(2)

At each step m, terms $\widetilde{{\mathcal {H}}}_{0,m}$ in Eq. (2) are known, coming either from the original Hamiltonian or stemming from intermediate computations at previous orders. Terms ${\mathcal {H}}_{0,m}$ are selected in such a way that they cancel those terms of $\widetilde{{\mathcal {H}}}_{0,m}$ pertaining to the kernel of the Lie operator. Finally, the integration “constants” ${\mathcal {C}}_m$—arbitrary functions of the Delaunay variables fulfilling the condition $\partial {\mathcal {C}}_m/\partial \ell =0$—will be chosen like such trigonometric functions of g that they prevent the appearance of purely long-period terms at the next order of the perturbation approach, in this way making feasible the complete normalization at once. The method is standard these days, and the required details can be found in textbooks as, for instance (Meyer et al. 2009; Boccaletti and Pucacco 2002).

In preparation of the solution, the equivalence

$$\begin{aligned} \frac{1}{r^j}=\frac{1}{r^2}\left( \frac{1+e\cos {f}}{p}\right) ^{j-2}, \end{aligned}$$

(3)

where $p=a\eta ^2$ is the orbit parameter and $\eta =(1-e^2)^{1/2}$, is applied to the instances $j>2$ in $\widetilde{{\mathcal {H}}}_{0,1}={\mathcal {H}}_{1,0}$, which is then written in the convenient form

$$\begin{aligned} \widetilde{{\mathcal {H}}}_{0,1}={\mathcal {H}}_{0,0}\frac{R_\oplus ^2}{r^2}\frac{1}{\eta ^2} \sum _{i=0}^1B_i(s)\sum _{j=i}^{2i+1}(2-j^\star )^ie^{|j-2i|}\cos (jf+2ig), \end{aligned}$$

(4)

where $B_0=1-\frac{3}{2}s^2$, $B_1=\frac{3}{4}s^2$, and we abbreviate $j^\star \equiv {j}\bmod 2$. On account of $j\ge {i}$ in Eq. (4), we immediately verify that $\widetilde{{\mathcal {H}}}_{0,1}$ is not affected of purely long-period terms. Then, the complete reduction is achieved at the first order by choosing the new Hamiltonian term ${\mathcal {H}}_{0,1}$ like the average of ${\mathcal {H}}_{1,0}$ over the mean anomaly.

The average is obtained in closed form with the help of the Keplerian differential relation between the true and mean anomalies $\eta {a}^2\mathrm {d}\ell =r^2\mathrm {d}f$. It is equivalent to removing all the terms with $j>0$ from Eq. (4) after multiplied by the factor $r^2/(a^2\eta )$. We trivially obtain the usual result

$$\begin{aligned} {\mathcal {H}}_{0,1}=\langle \widetilde{{\mathcal {H}}}_{0,1}\rangle _\ell \equiv {\mathcal {H}}_{0,0}\frac{R_\oplus ^2}{p^2}\eta \left( 1-\frac{3}{2}s^2\right) , \end{aligned}$$

(5)

which is, of course, the same expression obtained by Brouwer. Then, Eq. (2) is rearranged in the form

$$\begin{aligned} {\mathcal {W}}_1=\frac{1}{n}\left[ {\mathcal {H}}_{0,1}\phi +\int \left( \widetilde{{\mathcal {H}}}_{0,1}\frac{r^2}{a^2\eta }-{\mathcal {H}}_{0,1}\right) \mathrm {d}f\right] +{\mathcal {C}}_1, \end{aligned}$$

(6)

where $\phi =f-\ell$ denotes the equation of the center, and the integrand in Eq. (6) only embraces periodic functions of f. We obtain

$$\begin{aligned} {\mathcal {W}}_1=-G\frac{R_\oplus ^2}{p^2}\frac{1}{2}\bigg [B_0\phi + \sum _{i=0}^1B_i\sum _{j=1}^{2i+1}\frac{(2-j^\star )^i}{j}e^{|j-2i|}\sin (jf+2ig)\bigg ]+{\mathcal {C}}_1, \end{aligned}$$

(7)

where the first term of the right-hand member is the same as Brouwer’s first order determining function of the short-period elimination, and ${\mathcal {C}}_1$ is an integration constant that is left undetermined by the time being.

On account of ${\mathcal {H}}_{2,0}\equiv 0$, the known terms at the second order of the Lie transforms approach are $\widetilde{{\mathcal {H}}}_{0,2}=\{{\mathcal {H}}_{1,0};{\mathcal {W}}_1\}+\{{\mathcal {H}}_{0,1};{\mathcal {W}}_1\}$, from which the terms pertaining to the kernel of the Lie operator must be canceled by the adequate selection of ${\mathcal {H}}_{0,2}$. The usual choice is ${\mathcal {H}}_{0,2}=\langle \widetilde{{\mathcal {H}}}_{0,2}\rangle _\ell$, yet additional terms could be left in the new Hamiltonian in particular cases (Deprit 1981; Lara 2019a). However, this process would leave purely long-period terms in the new Hamiltonian in addition to the secular terms, both certainly pertaining to the kernel of the Lie operator. Since this is against the total normalization criterion, purely long-period terms should vanish identically in $\widetilde{{\mathcal {H}}}_{0,2}$, a requirement that is achieved with the proper selection of ${\mathcal {C}}_1$, whose partial derivatives with respect to g, G, and L appear formally in $\widetilde{{\mathcal {H}}}_{0,2}$.

We attack the computation of the second order of the perturbation theory by parts. To that effect, we make $\widetilde{{\mathcal {H}}}_{0,2}=\widetilde{{\mathcal {H}}}'_{0,2}+\widetilde{{\mathcal {H}}}^*_{0,2}$ with $\widetilde{{\mathcal {H}}}'_{0,2}=\{{\mathcal {H}}_{1,0}+{\mathcal {H}}_{0,1};{\mathcal {V}}_1\}$ and $\widetilde{{\mathcal {H}}}^*_{0,2}=\{{\mathcal {H}}_{1,0}+{\mathcal {H}}_{0,1};{\mathcal {C}}_1\}$. Straightforward evaluation of the Poisson brackets, followed by the use of Eq. (3) and standard trigonometric reduction, yields

$$\begin{aligned} \widetilde{{\mathcal {H}}}'_{0,2}= & {} {\mathcal {H}}_{0,0}\frac{R_\oplus ^4}{p^4}\frac{a^2}{r^2}\frac{3}{64}\frac{\eta ^2}{1+\eta } \sum _{i=0}^2s^{2i}\sum _{j=(-1)^ii}^{i+4}\sum _{k=0}^{3-|2i-j|}B_{i,j,k}\eta ^ke^{|j-2i|}\cos (jf+2ig)\nonumber \\&+\,{\mathcal {H}}_{0,0}\frac{R_\oplus ^4}{p^4}\frac{3}{8}\eta \bigg [\eta (3s^2-2)^2 +3(5s^2-4)s^2\sum _{j=1}^3\frac{2-j^\star }{j}e^{j^\star }\cos (jf+2g)\bigg ]\nonumber \\&+\,{\mathcal {H}}_{0,0}\frac{R_\oplus ^4}{p^4}\frac{9}{8}\left( 5 s^2-4\right) s^2 \frac{p^2}{r^2}\frac{1}{\eta ^2}\phi \sum _{j=1}^3(2-j^\star )e^{j^\star }\sin (jf+2g), \end{aligned}$$

(8)

where the needed coefficients $B_{i,j,k}(s)$ are listed in Table 1.

Table 1 Inclination polynomials $B_{i,j,k}$ in Eq. (8)

We intentionally split $\widetilde{{\mathcal {H}}}'_{0,2}$ into three different blocks. Namely, all the terms on the first row of Eq. (8) are free from the equation of the center and factored by $a^2/r^2$, hence being of trivial integration in the true anomaly. Terms of the second row are free from both $\phi$ and r; the integration of terms of this type reduces to the well-known case of the integration of cosine functions in elliptic motion (Deprit and Ferrer 1987; Kelly 1989; Ahmed 1994). Terms on the third row are of the form $(p/r)^2\phi \sin (mf+\alpha )$, with m integer, and are readily integrated by parts. That is, on account of $\mathrm {d}(\cos {mf})/\mathrm {d}\ell =-(m/\eta ^3)(p/r)^2\sin {mf}$,

$$\begin{aligned} \frac{m}{\eta ^3}\int \frac{p^2}{r^2}\phi \sin {mf}\,\mathrm {d}\ell =-\phi \cos {mf}+\frac{\sin {mf}}{m}-\int \cos {mf}\,\mathrm {d}\ell , \end{aligned}$$

(9)

in this way leading to the previous case of integration of cosine functions. Particularization for definite integration follows from the fundamental theorem of calculus. Alternatively, the needed quadratures can be obtained from known expressions (Brouwer 1959; Kozai 1962a; Tisserand 1889).

On the contrary, it is worth noting that unnecessary complications may arise if the third row of Eq. (8) is organized in the form of a Fourier series. Indeed, if we replace r by the conic equation in the third row of Eq. (8), we obtain

$$\begin{aligned} {\mathcal {H}}_{0,0}\frac{R_\oplus ^4}{p^4}\frac{9}{8}(5s^2-4)s^2 \phi \sum _{j=-1}^5q_{|j-2|}e^{|j-2|}\sin (jf+2g), \end{aligned}$$

with $q_0=3e^2+2$, $q_1=\frac{3}{4}(e^2+4)$, $q_2=\frac{3}{2}$, and $q_3=\frac{1}{4}$, then the equation of the center shows as an isolated function of the mean anomaly when the summation index takes the value $j=0$. This arrangement brings no problem in the computation of definite integrals, which can be carried out using the general rules for computing $\langle \phi \sin {mf}\rangle _\ell$ and $\langle \phi \cos {mf}\rangle _\ell$ provided by Métris (1991). On the contrary, while indefinite integration is still possible, it requires the sophisticated use of special functions, which could make notably difficult to progress in the perturbation approach (Osácar and Palacián 1994).

On the other hand, the evaluation of the Poisson brackets involving the integration constant ${\mathcal {C}}_1$ yields

$$\begin{aligned} \widetilde{{\mathcal {H}}}^*_{0,2}= & {} {\mathcal {H}}_{0,0}\frac{R_\oplus ^2}{p^2}\frac{1}{L}\frac{\partial {\mathcal {C}}_1}{\partial {g}}\frac{3}{2}\bigg [4-5s^2+\frac{a^2\eta }{r^2} \sum _{i=0}^1\sum _{j=-i}^{2i+3}\sum _{k=0}^{j^\star }b_{i,j,k}\eta ^{2k}e^{j'}\cos (jf+2ig)\bigg ]\nonumber \\&-\,{\mathcal {H}}_{0,0}\frac{R_\oplus ^2}{p^2}\frac{\partial {\mathcal {C}}_1}{\partial {G}}\frac{3}{2}\eta {s}^2\frac{a^2\eta }{r^2} \sum _{j=1}^{3}[1+(j+1)^\star ]e^{j^\star }\sin (jf+2g)\nonumber \\&+\,{\mathcal {H}}_{0,0}\frac{R_\oplus ^2}{p^2}\frac{\partial {\mathcal {C}}_1}{\partial {L}}\frac{3}{16\eta ^2}\frac{a^2\eta }{r^2} \sum _{i=0}^1b_i\sum _{j=-i}^{2i+3}q_{i,j}e^{j^\star }\sin (jf+2ig), \end{aligned}$$

(10)

where $j'=(|j-2i|-2)j^\star$, $(j+1)^\star \equiv (j+1)\bmod 2$, and the inclination polynomials $b_{i,j,k}(s)$ and the eccentricity polynomials $q_{i,j}(e)$ are provided in Table 2.

Table 2 Non-null inclination $b_{i,j,k}$ and eccentricity polynomials $q_{i,j}$ in Eq. (10)

In the same way as we did in the first order, we choose ${\mathcal {H}}_{0,2}=\langle \widetilde{{\mathcal {H}}}_{0,2}\rangle _\ell =\langle \widetilde{{\mathcal {H}}}'_{0,2}\rangle _\ell +\langle \widetilde{{\mathcal {H}}}^*_{0,2}\rangle _\ell$ to guarantee that it cancels all the terms of $\widetilde{{\mathcal {H}}}_{0,2}$ pertaining to the kernel of the Lie derivative. Firstly, we compute $\langle \widetilde{{\mathcal {H}}}'_{0,2}\rangle _\ell$ as follows. To average the first row of Eq. (8) over the mean anomaly, it is first multiplied by the factor $r^2/(a^2\eta )$ to carry out the integration in the true anomaly, and then those terms that are free from f, which are those with $j=0$, are selected. The term free from f in the second row averages to itself while the remaining terms in this row are averaged using the rule

$$\begin{aligned} \frac{1}{2\pi }\int _0^{2\pi }\cos (mf+\alpha )\,\mathrm {d}\ell =\left( \frac{-e}{1+\eta }\right) ^m(1+m\eta )\cos \alpha , \end{aligned}$$

(11)

cf. Kozai (1962a). Finally, the terms on the third row of Eq. (8) are averaged by parts with the help of Eqs. (9) and (11). We finally obtain,

$$\begin{aligned} \langle \widetilde{{\mathcal {H}}}'_{0,2}\rangle _\ell= & {} {\mathcal {H}}_{0,0}\frac{R_\oplus ^4}{p^4}\frac{3}{32}\eta \left[ 5(7s^4-16s^2+8) +\eta (6s^2-4)^2+\eta ^2(5 s^4+8s^2-8)\right] \nonumber \\&+\,{\mathcal {H}}_{0,0}\frac{R_\oplus ^4}{p^4}\frac{3}{16}\eta (15s^2-14)s^2e^2\cos 2g, \end{aligned}$$

(12)

which is precisely Brouwer’s second-order Hamiltonian after the elimination of short-period terms. The average of Eq. (10) is readily obtained with analogous procedures, to obtain

$$\begin{aligned} \langle \widetilde{{\mathcal {H}}}^*_{0,2}\rangle _\ell = -{\mathcal {H}}_{0,0}\frac{R_\oplus ^2}{p^2}3(5s^2-4)\frac{1}{L}\frac{\partial {\mathcal {C}}_1}{\partial {g}}. \end{aligned}$$

(13)

Visual inspection of Eqs. (12) and (13) immediately shows that if we complete the computation of the first-order term of the generating function in Eq. (7) choosing

$$\begin{aligned} {\mathcal {C}}_1=G\frac{R_\oplus ^2}{p^2}\frac{15s^2-14}{32(5s^2-4)}s^2e^2\sin 2g, \end{aligned}$$

(14)

then Eq. (13) turns into the opposite of the term in the last row of Eq. (12), the only one that depends on g, thus mutually canceling out. Hence,

$$\begin{aligned} {\mathcal {H}}_{0,2}={\mathcal {H}}_{0,0}\frac{R_\oplus ^4}{p^4}\frac{3}{32}\eta \left[ 5(7s^4-16s^2+8)+\eta (6s^2-4)^2+\eta ^2(5 s^4+8s^2-8)\right] , \end{aligned}$$

(15)

which is the same as the second-order term of Brouwer’s Hamiltonian after the elimination of long-period terms. In this way we have achieved Brouwer’s total Hamiltonian reduction of the main problem at once, with a single canonical transformation.

It is not a big surprise that ${\mathcal {C}}_1$ is the same integration constant obtained in the so-called elimination of the perigee (Alfriend and Coffey 1984; Lara et al. 2014) or in the author’s reverse normalization of the angular momentum (Lara 2020), because the motion in the orbital plane is decoupled from the rotation of that plane in each case.

The computation of first-order periodic corrections is now straightforward from the simple evaluation of Poisson brackets, namely $\xi -\xi '=J_2\Delta \xi$, where $\Delta \xi \equiv \{\xi ,{\mathcal {W}}_1\}$ and $\xi$ denotes either a canonical variable or some wanted function of the canonical variables (Deprit 1969). For instance, for the first-order periodic corrections to the semi-major axis we obtain

$$\begin{aligned} \Delta {a}=a\frac{R_\oplus ^2}{p^2}\frac{1}{4\eta ^2} \sum _{i=0}^1B_i(s)\sum _{j=-i}^{3+2i}A_{i,j}(\eta )e^{|j-2i|}\cos (jf+2ig), \end{aligned}$$

(16)

where $A_{0,0}=10-6\eta ^2-4\eta ^3$, $A_{0,1}=A_{1,1}=A_{1,3}=15-3\eta ^2$, $A_{0,2}=A_{1,0}=A_{1,4}=6$, $A_{0,3}=A_{1,-1}=A_{1,5}=1$, and the coefficients $B_i$ are the same as those in Eq. (4). Recall that Eq. (16) must be evaluated in mean (prime) variables in the direct transformation from mean elements to osculating ones, and in original (unprimed) variables in the inverse transformation from osculating to mean variables.

Table 3 Non-null inclination polynomials $\beta _{i,j,k}$ in Eq. (17)

3 Second-order periodic corrections

The second-order term of the generating function is now computed making $m=2$ in Eq. (2). Namely

$$\begin{aligned} {\mathcal {W}}_2={\mathcal {V}}_2+{\mathcal {C}}_2, \quad \mathrm {with} \quad {\mathcal {V}}_2=\frac{1}{n}\int (\widetilde{{\mathcal {H}}}_{0,2}-{\mathcal {H}}_{0,2})\mathrm {d}\ell . \end{aligned}$$

In view of Eqs. (8), (10), and (15), the needed integrals in the computation of ${\mathcal {V}}_2$ are either trivial, solved with the help of Eq. (9) for those terms involving the equation of the center, or using the differential relation between the mean and true anomalies for those other that are free from $\phi$ but depend on trigonometric functions of f. Straightforward computations yield

$$\begin{aligned} {\mathcal {V}}_2= & {} G\frac{R_\oplus ^4}{p^4}\frac{3}{64}\phi \bigg [ -\eta ^2(5s^4+8s^2-8)-5(7s^4-16s^2+8) \nonumber \\&-\,(15s^2-14)e^2s^2\cos 2g +12s^2(5s^2-4)\sum _{j=1}^3\frac{2-j^\star }{j}e^{j^\star }\cos (jf+2g)\bigg ]\nonumber \\&+\,G\frac{R_\oplus ^4}{p^4}\frac{1}{512}\sum _{i=0}^2\sum _{j=j_\mathrm {min}}^{j_\mathrm {max}}\sum _{k=0}^3 \frac{\beta _{i,j,k}(s)\eta ^ks^{2i}e^{j^\star }\sin (jf+2ig)}{(5s^2-4)^{2-i^\star }(1+\eta )^{\lfloor \frac{1}{2}(3-i)\rfloor }}, \end{aligned}$$

(17)

where $j_\mathrm {min}=2(i+1)^\star -1$, $j_\mathrm {max}=4+i+\lfloor \frac{1}{2}(i-1)\rfloor$, and the inclination polynomials $\beta _{i,j,k}$ are listed in Table 3.

It is worth to remark that, in spite of ${\mathcal {V}}_2$ is made only of short-period terms, the appearance of the critical divisor $5s^2-4$ in Eq. (17) makes more than evident the important differences between ${\mathcal {V}}_2$ and the second-order generating function of Brouwer’s short-period elimination. As it is well known, there are no offending divisors in Brouwer’s approach for the removal of short-period terms, and the critical inclination divisors only stem with the elimination of long-period terms.

On the other hand, the attentive reader will have noticed that the exponents of the offending divisors are exactly the same as those of equivalent solutions in the literature. So, in theory, the fact that they now affect both the short- and long-period terms of the periodic corrections should not harm the new formulation. In this regard, differences between the variety of existing formulations should remain below the accuracy expected from the truncation of the series that comprise the perturbation solution. Extensive numerical computations would be required to fix accurately the bounds of specific regions of the rotating-perigee phase space in which any of the existing theories—basically, the current approach, Brouwer’s method, reverse normalization, and Hamiltonian simplification alternatives based on the elimination of the parallax—present the higher accuracy. This kind of numerical campaign falls out of the scope of the current investigation. If this challenging endeavor is eventually attacked, it should take into account the effect that may have in different regions of phase space the use of the variety of canonical or non-canonical, singular or non-singular variables, in which the periodic corrections can be formulated. The fact that a single winner of the contest is not expected should not be of worry for a practitioner. At the end, beyond the simplified model used in this paper to illustrate the author’s findings, actual analytical orbit propagators are composed of different solutions, each of which applying to different orbital regimes—like SGP4 best exemplifies (Hoots and Roehrich 1980; Vallado et al. 2006); see also Coffey et al. (1996) .

As before, the integration constant ${\mathcal {C}}_2$ will be determined by imposing to the known terms of the next order

$$\begin{aligned} \widetilde{{\mathcal {H}}}_{0,3}=\{{\mathcal {H}}_{0,2}+{\mathcal {H}}_{1,1},{\mathcal {W}}_1\}+\{{\mathcal {H}}_{0,1}+2{\mathcal {H}}_{1,0},{\mathcal {W}}_2\}, \end{aligned}$$

where ${\mathcal {H}}_{1,1}={\mathcal {H}}_{0,2}+\{{\mathcal {H}}_{0,1},{\mathcal {W}}_1\}$, the condition of being free from pure long-periodic terms. Again, the known terms are split into terms directly computable and those depending on the arbitrary function ${\mathcal {C}}_2$. That is, $\widetilde{{\mathcal {H}}}_{0,3}=\widetilde{{\mathcal {H}}}'_{0,3}+\widetilde{{\mathcal {H}}}^*_{0,3}$, where

$$\begin{aligned} \widetilde{{\mathcal {H}}}'_{0,3}= & {} \{{\mathcal {H}}_{0,2}+{\mathcal {H}}_{1,1},{\mathcal {W}}_1\} +\{{\mathcal {H}}_{0,1}+2{\mathcal {H}}_{1,0},{\mathcal {V}}_2\}, \\ \widetilde{{\mathcal {H}}}^*_{0,3}= & {} \{{\mathcal {H}}_{0,1}+2{\mathcal {H}}_{1,0},{\mathcal {C}}_2\}. \end{aligned}$$

It follows the customary computation of ${\mathcal {H}}_{0,3}$ so that it cancels the terms of $\widetilde{{\mathcal {H}}}_{0,3}$ pertaining to the kernel of the Lie operator; namely

$$\begin{aligned} {\mathcal {H}}_{0,3}=\langle \widetilde{{\mathcal {H}}}_{0,3}\rangle _\ell =\langle \widetilde{{\mathcal {H}}}'_{0,3}\rangle _\ell +\langle \widetilde{{\mathcal {H}}}^*_{0,3}\rangle _\ell . \end{aligned}$$

After straightforward evaluation of the Poisson brackets, we obtain

$$\begin{aligned} \langle \widetilde{{\mathcal {H}}}'_{0,3}\rangle _\ell ={\mathcal {H}}_{0,0}\frac{R_\oplus ^6}{p^6}\frac{9}{512}\eta \sum _{i=0}^{2}\sum _{k=0}^{4-2i+i^\star }\frac{\beta _{i,k}(s)\eta ^ks^{2i}e^{2i}}{(5s^2-4)^{2-i^\star }(1+\eta )^{i^\star }}\cos 2ig, \end{aligned}$$

(18)

where $i^\star =i\bmod 2$ and the inclination polynomials $\beta _{i,k}$ are given in Table 4. Analogously,

$$\begin{aligned} \langle \widetilde{{\mathcal {H}}}^*_{0,3}\rangle _\ell =-{\mathcal {H}}_{0,0}\frac{R_\oplus ^2}{p^2}\frac{9}{2}(5 s^2-4)\frac{1}{L}\frac{\partial {\mathcal {C}}_2}{\partial {g}}. \end{aligned}$$

(19)

In this process, we only found integrals of the same type as we did at the second order, and hence, there were no special difficulties in solving them, yet in this case we needed to deal with notably longer series than in previous orders.

Table 4 Inclination polynomials $\beta _{i,k}$ in Eq. (18)

Once more, the simple inspection of Eqs. (18) and (19) shows that if we now choose³

$$\begin{aligned} {\mathcal {C}}_2=G\frac{R_\oplus ^4}{p^4}\frac{1}{256}\sum _{i=1}^2\sum _{k=0}^{4-2i+i^\star }\frac{\beta _{i,k}(s)\eta ^ks^{2i}e^{2i}}{(5s^2-4)^{i+1}(1+\eta )^{i^\star }}\frac{\sin 2ig}{2i}, \end{aligned}$$

(20)

then Eq. (19) cancels the terms of Eq. (18) depending on the argument of the perigee out, to yield

$$\begin{aligned} {\mathcal {H}}_{0,3}={\mathcal {H}}_{0,0}\frac{R_\oplus ^6}{p^6}\frac{9}{512}\frac{\eta }{(5s^2-4)^{2}}\sum _{k=0}^{4}\beta _{0,k}(s)\eta ^k, \end{aligned}$$

(21)

which is completely reduced as desired.

Equations (5), (15), and (21) show that differentiation of the secular Hamiltonian with respect to L brings the mean motion n as a coefficient with power 1 at each order. That this kind of coefficient also appears at higher orders of the secular terms is expected, and has been confirmed at least up to the order 6 using reverse normalization [see Lara 2020, Eqs. (45)–(47)]. Therefore, it may be expected that a m-th-order truncation of the perturbation approach would yield an error $\Delta \approx {n}J_2^{m+1}t$ in the computation of the secular terms after a propagation time t.

As verification of our solution, we checked that the secular terms obtained with the new approach match those provided by alternative solutions in the literature. In particular, up to third-order terms, we found the expected full agreement with the secular terms of our own implementations of Brouwer’s classical algorithm (Brouwer 1959), Deprit’s parallax–Delaunay–perigee approach (Coffey and Deprit 1982), Alfriend and Coffey’s parallax–perigee–Delaunay variant (Coffey and Alfriend 1984), and the author’s reverse normalization (Lara 2020). Besides, we also checked that the proper composition (Henrard 1970) of the separate Lie transformations involved in each of these perturbation theories relying in a sequential partial reduction, either without or with additional Hamiltonian simplifications, yields corresponding generating functions that match term for term the generator of the new single Lie transformation constructed in Poincaré’s original style.

Beyond the first order, direct and inverse transformations are no longer opposite. At the second order, the direct transformation is given by $\xi =\xi '+J_2\Delta \xi +\frac{1}{2}J_2^2\delta '\xi$, where $\delta '\xi =\{\Delta \xi ,{\mathcal {W}}_1\}+\{\xi ,{\mathcal {W}}_2\}$ is evaluated in prime variables. The inverse transformation is $\xi '=\xi -J_2\Delta \xi +\frac{1}{2}J_2^2\delta \xi$, where $\delta \xi =\{\Delta \xi ,{\mathcal {W}}_1\}+\{\xi ,-{\mathcal {W}}_2\}$ is evaluated in the original variables. For instance, replacing $\xi$ by a we obtain the inverse second-order periodic correction to the semi-major axis

$$\begin{aligned} \delta {a}= & {} a\frac{R_\oplus ^4}{p^4}\frac{1}{4^4\eta ^4}\bigg [ 24\eta ^7(5s^4+8s^2-8) +48\eta ^5(15 ^2-14)s^2e^2\cos 2g\nonumber \\&+\,\sum _{i=0}^2\sum _{j=-i-3i^\star }^{6+2i}\sum _{k=0}^{6-|j-2i|} (3s^2-2)^{i^\star }s^{2i}A_{i,j,k}(s)\eta ^ke^{|j-2i|}\cos (jf+2ig) \bigg ], \end{aligned}$$

(22)

where the inclination coefficients $A_{i,j,k}$ are provided in Table 5.

Table 5 Non-null inclination coefficients $A_{i,j,k}$ in Eq. (22)

4 Initialization of the secular constants and performance tests

Soon after Brouwer’s solution appeared in print, different reports pointed out an apparent contradiction between the accuracy expected from the series truncation order and the comparatively large in-track errors obtained in a variety of tests against numerical integrations (Bonavito et al. 1969). The issue, however, did not happen when fitting Brouwer’s solution to observational data.⁴ Hence, the apparent discrepancy was easily identified with an inconsistency in the use of Brouwer’s theory. Indeed, to get the expected accuracy provided by the secular terms, the initialization of the constants of Brouwer’s solution should be done with comparable accuracy. However, Brouwer only provided the periodic corrections up to the first order of $J_2$, and hence, the direct initialization of the secular mean motion for given initial conditions yields equivalent accuracy. The trouble is, of course, solved when the inverse periodic corrections are computed up to the same order of the secular terms.

On the other hand, since the trouble arises from an inaccurate computation of the secular mean motion, the theory can be patched by supplementing Brouwer’s first-order corrections only with the inverse second-order correction to the semi-major axis, either using Eq. (22) or in the different much shorter formulation given by Lyddane and Cohen (1962). Alternatively, the errors in the initialization procedure can be palliated by fitting the secular frequencies to data obtained from a preliminary numerical integration over several revolutions, or by a calibration of the secular mean motion $n'=\mu ^2/L'^3$ from the energy equation (Breakwell and Vagners 1970).

The latter approach is particularly appealing because it totally avoids the need of carrying out additional computations to those already carried out by Brouwer. Thus, for given initial conditions $(\ell _0,g_0,h_0,L_0,G_0,H_0)$, the initial Hamiltonian in osculating elements evaluates to ${\mathcal {H}}(\ell _0,g_0,-,L_0,G_0,H_0)=E_0$. On the other hand, after the complete Hamiltonian reduction

$$\begin{aligned} E_0=-\frac{\mu ^2}{2L'^2}+\sum _{m=1}^k\frac{J_2^m}{m!}{\mathcal {H}}_{0,m}(L',G',H)+{\mathcal {O}}(J_2^{k+1}). \end{aligned}$$

(23)

However, the constants $L'$ and $G'$ are computed from the osculating initial conditions through the inverse periodic corrections only up to ${\mathcal {O}}(J_2^{k-1})$. While this fact does not compromise the accuracy of Eq. (23) in what respects to the terms ${\mathcal {H}}_{0,m}$ ($m\ge 1$) because they are multiplied by corresponding factors $J_2^m$, it certainly does in the case of the Keplerian term. What Breakwell and Vagners (1970) propose is then to replace $L'$ by the calibrated value

$$\begin{aligned} \widehat{L}=\frac{\mu }{\sqrt{2}\left[ -E_0+\sum _{m=1}^k(J_2^m/m!){\mathcal {H}}_{0,m}(L',G',H)\right] ^{1/2}}, \end{aligned}$$

(24)

obtained by solving the Keplerian term from Eq. (23). If now $L'$ is replaced in Eq. (23) by the calibrated value $\widehat{L}$ then the energy equation will remain certainly accurate to ${\mathcal {O}}(J_2^{k+1})$. Therefore, the initialization of the secular frequencies is notably improved using the values

$$\begin{aligned} n_\ell =\frac{\mu ^2}{\widehat{L}^3}+\sum _{m=1}^k\frac{J_2^m}{m!}\frac{\partial {\mathcal {H}}_{0,m}}{\partial {L'}}, \quad n_g=\sum _{m=1}^k\frac{J_2^m}{m!}\frac{\partial {\mathcal {H}}_{0,m}}{\partial {G'}}, \quad n_h=\sum _{m=1}^k\frac{J_2^m}{m!}\frac{\partial {\mathcal {H}}_{0,m}}{\partial {H}}. \end{aligned}$$

Obviously, the use of Breakwell and Vagners’ calibration procedure is not constrained to the second order of Brouwer’s theory and also applies to any truncation order. In our particular case, in which we had already computed the second-order direct and inverse periodic corrections of Brouwer’s theory, the calibration of the (mean) Delaunay action allowed us to improve the accuracy of Brouwer’s secular terms to the third order of $J_2$ without need of computing the long series that comprise the third-order term of the generating function.

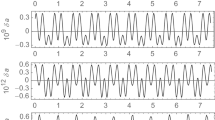
The accuracy obtained with different truncations of both the single-transformation approach and the classical parallax + perigee + Delaunay is illustrated in Fig. 1 for three test cases. The first is a TOPEX-type orbit with approximate orbital elements $a=7707.270$ km, $e=0.0001$, $I=66.04^\circ$, $\Omega =180^\circ$, $\omega =270^\circ$, and $\ell _0=90^\circ$, which is close to, yet far away enough from the critical inclination (top row of Fig. 1). The second is a PRISMA-type orbit with $a=6878.14$ km, $e=0.001$, $I=97.42^\circ$, $\Omega =168.2^\circ$, $\omega =20^\circ$, and $\ell _0=30^\circ$ (center row of Fig. 1). The third is a GTO orbit with $a=24460$ km, $e=0.73$, $I=30^\circ$, $\Omega =170.1^\circ$, $\omega =280^\circ$, and $\ell _0=0$ (bottom row of Fig. 1). The exact initial conditions in polar variables used in the simulations are given in Table 6, where corresponding mean elements obtained after second-order corrections of the different theories are also provided. In the latter, “Brouwer at once” denotes the theory of this paper, and “Hamiltonian simplification” that constructed by successive eliminating the parallax and the perigee, and carrying out the final Delaunay normalization. The units of length and time are km and s, respectively.

Fig. 1

Root sum square error of the Cartesian coordinates (in m) provided by different truncations $\{I,S,D\}$ (for Inverse, Secular, Direct) of the two tested versions of Brouwer’s $J_2$ solution; numbers on the right side of the labels denote the maximum error. From top to bottom: TOPEX, PRISMA, and GTO orbits. Abscissas are days

Table 6 Osculating elements and corresponding mean elements after second-order corrections

We remark that both analytical solutions were derived by the author in Delaunay variables. This includes the computation of Deprit’s elimination of the parallax as well as Alfriend and Coffey’s elimination of the perigee (cf. Lara et al. 2014). However, to avoid possible singularities in the propagation of almost-circular orbits, the secular terms have been reformulated in the semi-equinoctial elements that materialize the eccentricity vector in the nodal frame (Cook 1966; Deprit and Rom 1970; Konopliv 1991). For the same reason, but also for efficiency purposes, the required direct and inverse transformations have been computed in polar variables (Izsak 1963; Aksnes 1972; Lara 2015a, b).

Needless to say that different perturbations solutions to the same problem must present comparable accuracy level for the same truncation order of the solution series, independently of the approach used in their computation. As expected, it was certainly the current case.

Each plot of Fig. 1 depicts the time history of the root sum square (RSS) of the position errors of the analytical solution. The RSS errors are computed for different truncations of the analytical solutions when compared with the “true” solution along one-month propagation. To guarantee the accuracy of the latter, the reference orbits were obtained from the numerical integration of the differential equations of the main problem in Cartesian coordinates using extended precision. The integrations were carried out with the reputed, public code DOPRI 853 of Hairer et al. (2008), which implements an explicit Runge–Kutta method of order 8(5, 3) due to Dormand and Prince (1980). The code was compiled in Fortran quadruple precision, and the propagations were performed with tolerance $10^{-22}$ in order to guarantee that the reference orbits preserve at least 16 exact digits. Additionally, it has been checked that the 16-digit truncation of the reference orbits preserves both the energy integral and the third component of the angular momentum with a minimum of 14 digits (most commonly 15 digits).

Labels {I:S:D} in the plots denote the truncation order of the Inverse corrections, Secular terms, and Direct corrections of the orbital theory. The notation {I+:S:D} means that the inverse corrections are improved in Breakwell and Vagners’ style. Thus, the label {1:2:1} denotes the truncations of the original Brouwer’s approach. At the end of one month, the {1:2:1} theory accumulates a RSS error of about 2.5 km for TOPEX, about 13 km in the case of PRISMA, and $\sim 50$ km for the GTO. The simple calibration of the secular mean motion using Eq. (24) clearly bends the RSS errors curve toward the meter level with a negligible increase of the computational burden. Thus, at the end of the propagation period, the RSS errors of the {1+:2:1} solution reach about 15 m for TOPEX, or $\sim 50$ m for both PRISMA and the GTO. Figures are further improved when the orbit is propagated with the full second-order theory, in which the second-order transformation is used both in the initialization of the constants of Brouwer’s secular terms (inverse periodic corrections) and in the ephemeris computation (direct periodic corrections). Now, RSS errors fall to about 10 m at day 30 for TOPEX and the GTO, or 30 m for PRISMA, curve labeled {2:2:2}, yet the computational burden increases by about one third due to the evaluation of second-order direct corrections, contrary to the lighter first-order corrections. Finally, supplementing Brouwer’s theory with third-order secular terms and the consequent calibration of the secular mean motion, case {2+:3:2}, keeps the RSS errors of all the cases tested to the level of just a few cm along the whole propagation interval, with negligible increase of the computational burden with respect to the {2:2:2} case.

The accuracy of the results obtained in our tests is in clear agreement with which one may expect from the nature of a perturbation solution. Thus, a truncation error ${\mathcal {O}}(J_2^m)$ of the series comprising the perturbation solution is expected to yield an error ${\mathcal {O}}(J_2^{m+1})$ in the evaluation of these series. More precisely, absolute errors of ${\mathcal {O}}(J_2^{m+1})$ in radians are expected for the angle variables, whereas relative errors of the action variables should be proportional to $J_2^{m+1}$. Analogously, the proper initialization of the constants of the perturbation theory would yield errors in the secular frequencies proportional to their values. In particular, $\Delta {n}=n\times {J}_2^{m+1}$ radians per unit of time for the secular mean motion. The estimation of corresponding errors in a different set of variables is obtained from the usual properties of the propagation of errors. For instance, errors in the eccentricity must be divided by the eccentricity value itself, thus being notably increased in the case of low-eccentricity orbits; analogously, inclination errors are divided by the sine of the inclination and hence are more apparent in the case of low-inclination orbits. Expanded discussions on the topic may be consulted in §6.5 of Lara (2021).

Thus, for instance, the initialization of the secular constants of the {2+:3:2} theory would yield an error of ${\mathcal {O}}(J_2^4)$ in the secular terms, which, on account of $J_2=1.082634\times 10^{-3}$ for the Earth, yields $\approx 1.37\times 10^{-12}$. In the case of TOPEX, with a period of 112 minutes, this truncation error would produce a concomitant error $\Delta {n}\approx (2\pi /6720)\times 1.37\times 10^{-12}=1.3\times 10^{-15}$ rad/s in the secular mean motion. Then, after one-month propagation of the secular terms $t=2.592\times 10^{6}$ s, and the error in the mean anomaly due to the truncation of the perturbation solution would reach roughly $\Delta {n}t=3.3\times 10^{-9}$ radians. Due to the almost-circular character of the TOPEX orbit, this error will result in an in-track error of $7707.270\times \Delta {n}t$ km—or about 3 cm. In addition, the truncation of the direct periodic corrections to the second order would yield an error ${\mathcal {O}}(J_2^3)\approx 1.27\times 10^{-9}$ radians in the periodic corrections, which for TOPEX means position errors of amplitude $\Delta {r}\approx 7707.270\times 1.27\times 10^{-9}$ km—or about one cm. The combination of both errors still constrains the total error at the end of the one-month propagation to the cm level. And this is exactly what we have obtained, as clearly noted in the two upper plots of Fig. 1.

Analogous rough estimations for the different truncations and orbits provide figures that are consistent with the observed errors displayed in Fig. 1. Nevertheless, one should be aware that the actual errors may depend on the particular orbital configuration to which the perturbation solution is applied. However, in those regions of phase space in which the perturbation theory is expected to converge, the actual errors should be of the order of the forecasted value. In this respect one should not be confused by the apparent high value of a single coefficient of some inclination polynomial. On the contrary, the whole double summation comprising the coefficient of the men motion term (see Eqs. (45) and (17) of Lara (2020), for reference) should be evaluated instead. We illustrate these facts in Fig. 2 for the third-order coefficient of the mean motion and the orbital parameters of the TOPEX orbit. As shown in the left plot of Fig. 2, except for the vicinity of the critical inclination, where the perturbation theory does not apply, the worst case happens for the lower inclination orbits. Still, the size of the coefficient that multiplies $nJ_2^3$ is roughly of order 1. The right plot of Fig. 2 shows that this coefficient also remains bounded for the TOPEX orbit inclination and variations of the eccentricity. While the error estimator is based on the higher-order term, which is not computed, it seems reasonable to assume that it will also remain of order one. Needless to say that these considerations apply to any perturbation solution and are not a particular feature of the new approach.

Fig. 2

Evolution of the mean motion coefficient multiplying $nJ_2^3$ for the TOPEX orbital configuration. Left: $e=0.001$. Right: $I=66.04^{\circ }$

A variety of additional test cases have been carried out for other orbit configurations finding always analogous accuracy levels, which, besides, agree with previous reported results using other perturbation solutions of the $J_2$ problem (Lara 2020).

For efficiency in the evaluation of perturbation solutions, arrangement of the series that comprise the periodic corrections for optimal evaluation is an important consideration (Coffey and Deprit 1980; Healy and Travisano 1998). In this task, we limited our efforts to minor arrangements of the code, like the factorization of the inclination polynomials involved in the different summations and the following use of Horner’s algorithm, and left the code optimization job to the compiler. Because we did the same for both analytical solutions (Brouwer’s with single periodic corrections, and the traditional parallax–perigee–Delaunay solution), even if optimal evaluation is not achieved, the comparisons are not expected to be biased toward a particular theory.

After repeated evaluation of the periodic corrections for a variety of initial conditions, we found that the evaluation of the periodic corrections of the traditional analytical solution spends roughly twice the time needed by the single-transformation approach in the evaluation of the periodic corrections. This result was a priori unexpected because the series comprising the corrections of the new approach, which only involves a single transformation, are clearly longer than the combination of those involved in the three transformations needed in the traditional approach. The improved evaluation efficiency is then attributed to the fact that the compiler is able to carry out a better optimization of the code in the case of the single-transformation approach. This fact may be understood when taking into account that, for instance, the coefficient $(5s^2-4)$ appears about 300 times in our arrangement of the periodic corrections of the single transformation, but only 73 times in the classical parallax–perigee–Delaunay transformation arranged with the same factorization criterion, where, in particular, this factor only appears in the corrections related to the elimination of the perigee. Thus, canceling this common factor by the compiler is roughly four times more efficient in the first case.

The original code was developed in Wolfram Mathematica 12 programming environment and compiled with the option CompilationTarget $\rightarrow$ “C.” In this computing system, calling three compiled functions by the interpreter, contrary to just one, might be penalizing the classical parallax–perigee–Delaunay approach. Hence, we exported the Wolfram Mathematica code to Fortran and performed additional tests using 64-bit compiled code and the robust -O2 optimization of the Absoft Pro Fortran 16.0.2 compiler. In spite of the execution time now balances significantly, the new, single transformation approach always ran at least 6% faster than the classical parallax–perigee–Delaunay implementation in all our tests. Execution times were obtained after averaging the repeated evaluation of the mean to osculating transformations. The DO loops were iterated up to one million times in the case of Wolfram Mathematica 12 and up 100 million times in the Fortran simulations. For Wolfram Mathematica 12 simulations, the user’s time was obtained through the Timing[] function, which includes only CPU time spent in the Wolfram Language kernel. The UNIX’s time command was used in the case of Fortran runs.

Undeniably, making a smarter organization of the code before sending it to the compiler might modify the reported figures. The author’s periodic corrections of the single mean to osculating transformation are available upon request for those programming wizards interested in further digging in this issue.

On the other hand, improvements achieved with the single-transformation approach become more relevant when the new analytical solution is implemented in a typical ephemeris generator. Indeed, in that case the eccentricity and inclination polynomials of the mean to osculating transformation remain constant along the whole mean elements propagation. In consequence, they only need to be evaluated once, which is done at the same time of the initialization of the constants of the analytical theory. Therefore, the mean to osculating corrections reduce to extremely simple expressions that only need the update of the angle variables at each ephemeris evaluation. Obviously, analogous simplifications apply when the orbit propagator is based on equivalent solutions obtained by the stepwise elimination of the different periodic effects. However, the simplification level achieved with this strategy is shallower in the latter case. For instance, when using the classical parallax–perigee–Delaunay theory, the eccentricity polynomials only remain constant in the transformation of the Delaunay normalization. The inclination polynomials remain constant in the transformation equations of both the Delaunay normalization and the elimination of the perigee, but neither the eccentricity nor the inclination polynomials remain constant in the elimination of the parallax transformation. In consequence, the action variables must be updated at each ephemeris evaluation in addition to the angles. This fact furnishes the single-transformation approach with an additional advantage. In particular, for a dense output of 3000 points, our simulations of the $J_2$ problem showed that the formulation based on a single set of periodic corrections always ran at least 20% faster than the parallax–perigee–Delaunay competitor. Similar advantages are expected with respect to the other formulations based on splitting the periodic corrections in different stages.

5 Conclusions

Experience gained through the use of Hamiltonian simplification methods prompted us to question Brouwer’s splitting normalization strategy. The convenience of dividing a normalization process into different stages has been taken for granted since the initial efforts in fully automatizing the computation of perturbation theories. Needless to say that we agree in which this way of proceeding may ease the construction of the perturbation solution. However, what is not so obvious is that the evaluation of the solution constructed this way must necessarily yield the less computational burden. On the contrary, results in this paper seem to point in the direction that the claimed benefits of partial normalization as well as Hamiltonian simplification procedures can be counterbalanced by other type of considerations, at least for the lower orders of normalization that suffice in many practical cases. Prospective application of the strategy proposed here to other instances of perturbed Keplerian motion, or to the computation of higher orders of the main problem of artificial satellite theory, should contribute to make clear the issue.

Brouwer’s closed-form approach and full automatization of the computation of perturbation theories seem two legitimate aims in this epoch of computational plenty. However, as demonstrated by the equation of the center controversy, rather than running perturbation algorithms in batch processes, one should not disregard the power of modern hand computations carried out with the help of existing software tools. Indeed, as far as mathematical simplification remains in the category of arts, inspection of intermediate expressions turns into a convenient practice that may eventually lead the user to straightforward simplifications that make feasible or just simpler the next step of a partially automated procedure. Like chess players, celestial mechanicians are rarely able to anticipate more than a few moves in the outcome of a perturbation approach. On the contrary, they need to wait for the opponent’s reaction in order to implement a winning strategy, which, in addition, is most times settled on an empirical basis. It was, in particular, the case of the current research, in which the help provided by the computer algebra system converted into a simple task the critical inspection of the seminal solution provided by Brouwer.