Abstract
To validate an established breast cancer incidence model in an independent prospective data set. After aligning time periods for follow-up, we restricted populations to comparable age ranges (47–74 years), and followed them for incident invasive breast cancer (follow-up 1994–2008, Nurses’ Health Study [NHS]; and 1995–2009, California Teachers Study [CTS]). We identified 2026 cases during 540,617 person years of follow-up in NHS, and 1,400 cases during 288,111 person years in CTS. We fit the Rosner–Colditz log-incidence model and the Gail model using baseline data. We imputed future use of hormones based on type and prior duration of use and other covariates. We assessed performance using area under the curve (AUC) and calibration methods. Participants in the CTS had fewer children, were leaner, consumed more alcohol, and were more frequent users of postmenopausal hormones. Incidence rate ratios for breast cancer showed significantly higher breast cancer in the CTS (IRR = 1.32, 95 % CI 1.24–1.42). Parameters for the log-incidence model were comparable across the two cohorts. Overall, the NHS model performed equally well when applied in the CTS. In the NHS the AUC was 0.60 (s.e. 0.006) and applying the NHS betas to the CTS the performance in the independent data set (validation) was 0.586 (s.e. 0.009). The Gail model gave values of 0.547 (s.e. 0.008), a significant 4 % lower, p < 0.0001. For women 47–69 the AUC values for the log-incidence model are 0.608 in NHS and 0.609 in CTS; and for Gail are 0.569 and 0.572. In both cohorts, performance of both models dropped off in older women 70–87, and later in follow-up (6–12 years). Calibration showed good estimation against SEER with a non-significant 4 % underestimate of overall breast cancer incidence when applying the model in the CTS population (p = 0.098). The Rosner–Colditz model performs consistently well when applied in an independent data set. Performance is stronger predicting incidence among women 47–69 and over a 5-year time interval. AUC values exceed those for Gail by 3–5 % based on AUC when both are applied to the independent validation data set. Models may be further improved with addition of breast density or other markers of risk beyond the current model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
For over a decade since developing and expanding the Rosner–Colditz model for breast cancer incidence [1, 2], we have sought approaches to estimating performance in an independent validation data set. Although we have conducted internal validation using split sample approaches [3], we have not previously used an independent data set to assess performance. This has largely been due to the need for data on age at each birth for women, an input to spacing of births that directly relates to breast cancer risk in early studies [4] and is confirmed in our model [5] and by others [6]. The closer births are together, the more rapidly breast tissue-aging decreases and the lower total risk accumulates through premenopausal years [7]. In addition, details on age at menopause and type of menopause as well as type and duration of postmenopausal hormone therapy (HT) are important risk factors.
Our approach then is to use an independent data set to estimate performance following the principles outlined in literature addressing validation and application of prediction models in medicine [8, 9]. To date, no model of breast cancer incidence has been implemented as part of routine clinical care where risk estimates might guide level of screening, genetic counseling, or chemoprevention.
As previously noted, the Rosner–Colditz model includes a range of established reproductive factors, body mass index (BMI), and alcohol intake in its basic form [2]. This is one of a large number of breast cancer risk prediction models. In a systematic review and meta-analysis, Meads et al. [10] identified 17 breast cancer risk models with differing sets of modifiable and non-modifiable risk factors, with many omitting age at menopause, type of menopause, and use of postmenopausal hormones, all factors strongly related to future breast cancer risk. Only four models had validation in potentially independent data sets. These models included Gail [11] and also the Rosner–Colditz model [1, 2, 12]. The performance of the Gail model summarized as AUC in a previous validation within the NHS data was 0.58, though both have not been compared in a common independent data set.
Moons and others emphasize a sequence of model development, validation, application, and assessment of performance in application/clinical setting [8, 9]. To date, we find no reports on the last aspect of breast cancer model performance in routine clinical settings. Here we focus on the conduct of validation in an independent data set.
We collaborated with California Teachers Study (CTS) investigators to draw on an independent prospective data set and assess the performance of the Rosner–Colditz model, which was developed and refined in the Nurses’ Health Study (NHS). We also compare model performance against the Gail model when both are fit to the independent data set.
Methods
As noted above, a key issue in identifying an independent prospective study with appropriate risk factor collection included the need for details of age at each pregnancy, a refinement of usual reporting of age at first birth and number of births typical of epidemiologic studies. Details on age and type of menopause were also important since this is omitted from the Gail model despite a long record of being established as a modifier of future breast cancer risk [5, 13, 14]. Other key risk factors not included in the Gail model are duration and type of postmenopausal HT used [15], BMI [16], and alcohol intake [17]. These are all in the Rosner–Colditz log-incidence model.
CTS This cohort contains the necessary data collected at baseline in 1995 for the cohort. The CTS approach to questionnaire follow-up, after 2 years, then after 3 more years, then at varying intervals each updating some exposures, together with case ascertainment ongoing annually through the California tumor registry, meant we use baseline data only. We limit the population to women who were postmenopausal at baseline. To compare incidence during common follow-up time periods we use the time frame for CTS from baseline 1995 to 2009.
NHS This cohort of women followed from 1976 has routinely updated information every 2 years on reproductive risk factors for breast cancer, family history of breast cancer, use of postmenopausal hormones, and from 1980 onwards alcohol intake. The original Rosner–Colditz model was developed in the broader NHS cohort [1, 2, 5]. For comparability with data available from the CTS, we limit the population for this analysis to women who were postmenopausal at baseline in 1994. Thus the corresponding time available for the NHS is 1994–2008. In 1994, NHS participants were 47–74. Hence, we limit the CTS participants included in the analysis to a comparable age range, excluding their older cohort members.
Model fitting issues
Limited only to baseline data from the CTS, we modified the Rosner–Colditz model to omit updating. Because this differs from our standard approach of updating exposure information every 2 years [2], we estimate the impact of this modification on overall performance.
Duration of current use of postmenopausal HT is significantly related to incidence of breast cancer [2, 18], and to type of menopause, age at menopause, and time since menopause. These factors are all importantly related to postmenopausal breast cancer incidence. We, therefore, used imputation methods to estimate future duration of use for postmenopausal HT in the CTS [19]. We used a two-step process to estimate use according to type of hormone used currently, and duration of use. We first fit a model to NHS data to estimate the duration of hormone use from 1994 to the return of the 2006 follow-up questionnaire for each type of HT (estrogen, E, alone and estrogen plus a progestin, E&P). Predictors included menopause type and time since menopause, and duration of use of HT among current users (see Tables 8 and 9). In addition to these characteristics of menopause, parity was positively related to ever use of E alone but not E&P, and positively to duration of use of estrogen alone, but inversely to duration of estrogen plus progestin. BMI was inversely related to ever use of E and E&P, but was unrelated to duration of use of either. Alcohol use was inversely related to ever use of E alone and to ever use of E&P, but not to duration of use of either formulation. We developed this model separately for use of E alone and for use of E&P. We then used this model with baseline CTS data to impute future use by type and duration for participants, taking the average of 5 imputations for each participant. (See Tables 8 and 9 for the imputation models and Appendix 2 for a summary of the imputation strategy.)
Time frame
To compare incidence of breast cancer in the two cohorts over a common time frame, we identified common subsets from the two cohorts. We use the CTS baseline in 1995 and 1994 as the start point for inclusion of NHS follow-up. We then draw on the age range of the NHS participants to define a comparable age range for CTS participants. Thus we limit NHS follow-up data to the interval 1994–2008. CTS data for the corresponding years are included with follow-up from 1995 to 2009.
During follow-up of the NHS cohort from 1994 to 2008, we identified 2,026 invasive breast cancer diagnoses among postmenopausal women during 540,617 person years. In the CTS, we identified 1,400 incident invasive breast cancer diagnoses among postmenopausal women during 288,111 person–years.
Description of the log-incidence model of breast cancer
We assume that the incidence of breast cancer at time t (I t ) is proportional to the number of cell divisions accumulated throughout life up to age t (i.e., I t = kC t ).
C t is obtained from
Thus, \(\lambda_{i} = \frac{{C_{i + 1} }}{{C_{i} }} =\) the rate of increase in \(C_{t}\) from age \(i\) to age \(i + 1\).
Log (\(\lambda_{i} )\) is assumed to be a linear function of risk factors that are relevant at age \(i.\) The set of relevant risk factors and their magnitude and/or direction may vary according to the stage of reproductive life. We fit PROC NLIN of SAS to estimate the parameters of the model with breast cancer risk factors including (1) duration of premenopause, (2) duration postmenopause, (3) type of menopause, natural or surgical (4) parity, (5) age at each birth, (6) current, past HRT use, (7) duration of HT use by type, (8) BMI, premenopause ≡ BMI1, (9) BMI, postmenopause ≡ BMI2, (10) height, (11) benign breast disease (BBD), (12) alcohol intake, (13) family history of breast cancer.
We fit the base model using baseline variables and imputed HT duration without updating exposures and assessed covariates using the CTS comparing their magnitude and direction to the variables in the NHS. We assess the performance of the model from the NHS in the CTS by fitting the NHS model and averaging five imputations of HT use. We fit the Gail model [11] using the formula from page 1880, with the caveat that in each cohort the number of previous biopsies is scored 0 or 1 and the number of relatives with family history is scored 0 or 1. We compare the c-statistic for Gail versus Rosner–Colditz log-incidence using the Wilcoxon rank sum test [20].
To assess calibration, we use the NHS model to estimate relative risks for individual women in the CTS and combine these with SEER data to estimate absolute risk. We then group the CTS participants by decile of estimated absolute risk and compare observed and expected counts of incident breast cancers and test for trend using Poisson regression approaches (for additional details, see Appendix 1).
To assess calibration, we apply the NHS risk model to the CTS population using imputed data for HRT use over 12 years. Suppose there are N subjects in the CTS population who are followed for T person–years. We divide the T person–years into L age strata and let T l = number of person–years in the lth age stratum. Based on the NHS risk model, we compute the relative risk for the ith person at the jth person–year given by RR ij compared to a hypothetical person at baseline risk where all covariate values are 0. Let h *1 (l) be the age-specific incidence rate for the lth age group from SEER 1995–2006. We use the methods of Gail (1989) to combine the RR ij from the NHS model with h *1 (l) to estimate h 1(l) = baseline incidence rate for the lth age group of CTS. An estimate of the incidence rate for the ith subject in the jth person–year is then given by
where \(\delta_{ijl} = { 1}\) if the ith subject is in age group l at the jth person–year, = 0 otherwise.
The corresponding estimate of cumulative incidence for the ith subject over t i person–years is given by
Let O i = 1 if the ith subject develops breast cancer over t i person–years, = 0 otherwise.
If the NHS model is well calibrated in the CTS population, then O i should follow a Poisson distribution with mean = \(E_{i}\). To test this we let \(\mu_{i} = E(O_{i} )\) and consider the Poisson regression model
A test of the calibration of the model at the individual level is
which we can perform using a Poisson regression model with intercept only and offset given by \({ \ln }(E_{i} )\).
We also can group the subjects into deciles by cumulative incidence per year (or \(E_{i}^{*} = E_{i} /t_{i}\)) and compute the observed (O (d)) and expected (E (d)) number of cases in the dth decile and run a Poisson regression at the aggregate level of the form:
where \(\mu^{(d)} = E(O^{(d)} ).\)
The individual and aggregate Poisson regression models are actually equivalent. The Poisson regression approach should be a more sensitive model of goodness of fit than the Hosmer–Lemeshow statistic given by
which is more similar to a test of hetereogeneity than the test for trend approach given by Poisson regression.
Finally, to combine inferences over several imputed data sets, multiple imputation approaches are used to obtain an overall test of calibration based on averaging estimates of \(\alpha\) over several imputations. More detail on the calibration methodology is given in Table 8.
Results
Risk factor prevalence differences (Tables 1, 2)
Baseline data for the NHS and CTS are presented in Table 1, for women 47–59 years at baseline, and Table 2, for women 60–74 years of age. The mean age, age at menarche, and age at menopause were comparable in the cohorts as were the prevalence of biopsy confirmed BBD and family history of breast cancer. The CTS included more nulliparous women (25 %) versus 6 % in the NHS for women 47–59 years, and 18 versus 6 % for women 60–74 years. CTS cohort members versus women in the NHS had an average of 1 fewer births per woman; more current postmenopausal hormone use (age 47–59 years: 70 vs. 56 %, age 60–74 years: 53 vs. 35 %) and longer duration of use; leaner current BMI (age 47–59 years: 25.3 vs. 26.6, age 60–79 years: 25.3 vs. 26.1) and higher current alcohol intake (age 47–59: 7.9 g/day vs. 5.0 g/day, 60–79: 8.2 g/day vs. 5.1 g/day).
Incidence rates (Table 3)
Age-specific and age-adjusted incidence rates show breast cancer incidence rates are higher in the CTS for women over age 60 years (Table 3). Across all ages, 47–87 years, the age-adjusted incidence rate ratio shows that the CTS has significantly higher incidence (age-adjusted IRR 1.32, 95 % CI 1.24–1.42).
Comparing parameter estimates in each cohort (Table 4)
The modified model using only baseline data and imputed HT duration of use was fit separately to the NHS and then to the CTS cohort data to compare coefficients side by side (see Table 4). We note a number of important similarities across the two independent cohort studies supporting favorable performance. The magnitude of the coefficient for age at first birth (gynecologic age at first birth) is comparable, being positive in both cohorts. The associated birth index (a summary of total years from each birth to minimum [age, or age at menopause], summed over all births in parous women and = 0 for nulliparous women) shows a strong inverse association of comparable magnitude in both cohorts (−0.0032 in NHS vs. −0.0026 in CTS). Thus, for a typical woman with menarche at age 13, menopause at 50, births at 20, 23, 26, 29, (giving a birth index 102), this translates to a RR 0.72 for the NHS and 0.77 for the CTS. Terms for BBD and family history are comparable as are the association for alcohol and for height and BMI among women not taking HT (estrogen negative time).
We also note some differences between the two cohorts. The magnitude of the association for duration of E&P has a larger magnitude in the CTS, b = 0.035 versus 0.015 in NHS. The term for current use is weaker in the CTS, giving a combined relative risk for a current user with 5 years of use of e0.202+ 5(0.035) = e0.377 = 1.46 compared to a never user for the CTS and e0.368+5(0.015) = e0.443 = 1.56 for the NHS. For current users with 10 years of use, the RRs are 1.74 for the CTS and 1.68 for the NHS. Thus, the overall associations for current users are comparable at longer durations of use. The association for BMI is somewhat weaker during estrogen negative time (postmenopause, non-use of postmenopausal hormones) in the CTS compared to the NHS (0.00038 vs. 0.00195 per BMI unit per year).
Summary model performance in NHS and CTS cohorts (Table 5)
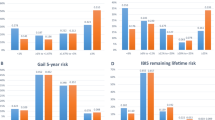
We fit model coefficients from Table 4 to NHS and applied the coefficients from NHS to CTS data for follow-up from 1995 to 2009 as an external validation of the NHS model (see Table 5). The overall performance in the NHS was 0.597 for the full follow-up and 0.586 in CTS. For the first 5-year follow-up interval among women 47–69 years, the risk prediction performance was comparable in both cohorts (0.608 in NHS and 0.609 in CTS) supporting validity of the model. We also observed that in NHS during the first 5-year follow-up period, 1994–1999, performance was higher in women 47–69 years (c = 0.608) than in those 70–87 years (c = 0.587). For the second follow-up interval from 2000 to 2008 the model again performed better in younger women c = 0.599 compared to older women c = 0.577, but in each group performance was lower than in the first time interval. This pattern of performance was also observed when the Gail model was applied to the NHS cohort performance was higher in younger women and in the first versus second follow-up interval.
Applying the NHS log-incidence model to the CTS data, a similar pattern emerged; the performance was better during the first 5 years of follow-up in younger than older women (c = 0.609 for 47–69 year old women vs. 0.564 for 70–87 year old women). During the later follow-up, 2001–2009, the performance was further reduced. The Gail model applied to the CTS data also showed this pattern in the first follow-up interval.
Comparing the Gail model to the log-incidence model in the independent CTS data, the AUC for the Gail model performance was 4 % lower overall (c = 0.547 vs. 0.586, p < 0.0001); during the first follow-up period for women 47–69 years (c = 0.572 vs. 0.609, difference in AUC = 0.037, p = 0.008), and in women 70–87 years (c = 0.516 vs. 0.564, difference in AUC = 0.048, p = 0.09). In the later follow-up from 2001 to 2009 these differences persisted.
Comparison of c statistic for actual NHS data versus the use of imputed values in that cohort (Table 6)
To assess the drop off in model performance induced by not updating exposure variables, we next fit the model to NHS data using first imputed and then updated values for HT duration (see Table 6). Fitting the model to NHS updated data from 1994 through 2008 (right hand panel of Table 6) we observe an AUC c statistic value of 0.616 (s.e. 0.006). If instead of using observed updated data, we impute future duration of HT after menopause, the AUC c statistic is reduced modestly to 0.600 (s.e. 0.006). When assessing performance in the early follow-up from baseline and later follow-up—again the actual data were comparable to imputed data for the first 5 years, but showed reduced performance in the 2000–2008 interval. For example, for women 47–69, the AUC decreased from 0.641 with actual updated data to 0.595 using imputed data.
Calibration observed and expected counts in CTS by decile of risk, predicted with NHS betas
Finally, we use five imputations to estimate the expected number of cases of breast cancer according to the NHS model stratifying the CTS participants by decile of risk. As shown in Table 7, the observed count was slightly lower than the predicted case count. Poisson regression across all women allows estimation of the adjustment factor (α) = −0.048, s.e. (α) = 0.027, p = 0.074. Overall the model fit is not significantly different from SEER, O/E = 0.96 a 4 % underestimate. Thus applying the NHS model with its rich use of exposure across the life course for established breast cancer risk factors, and accounting for the risk factor profile of individual women in the CTS, we fully account for breast cancer incidence in this independent population.
Discussion
We identified an independent large data set with 1,400 incident invasive breast cancer cases, that allowed evaluation of a breast cancer incidence risk prediction models using a common definition of incident invasive breast cancer, over common time periods, and age groups. Age-standardized breast cancer incidence in the CTS was significantly higher than in NHS. Overall performance of the Rosner–Colditz log-incidence model shows AUC consistent with performance in the original NHS, supporting external validity of the model. In the external validation data set the model outperformed the Gail model by 3–5 % for differing age groups and follow-up intervals based on the AUC. Although adaptations had to be made using only baseline data, this approach is comparable to using the tool in clinical practice to predict risk and stratify women to guide prevention interventions. Assessment of the lack of updating but use of imputed duration of hormone use among postmenopausal women showed modest attenuation over a 5-year follow-up interval in the NHS. Calibration against SEER showed good performance and close agreement of predicted with observed incidence.
General issues on validating
Data availability on key reproductive variables including age at first birth, age at each birth, menopause and type of menopause, as well as history of biopsy confirmed BBD and family history of breast cancer, height, weight, and history of alcohol intake supported use of a common model in comparable data that had been collected with similar methods and would reflect approaches in clinical and epidemiologic practice. Because HT modifies risk of breast cancer, imputing future use among current users was necessary as the CTS does not update data every 2 years as NHS does, and in clinical practice future use is unknown but is important for risk prediction. Summary imputation models are provided that may be of use for clinical application in other settings where future use of hormones will be estimated given past history ascertained at a clinic visit without any updating going forward. As seen in Tables 8 and 9 the imputation performed well in terms of ever use (c statistic 0.87) and duration of use of estrogen alone and estrogen plus progestin. Assessment indicates such imputation is robust for 5 years, though predictive performance may attenuate over longer follow-up or prediction time intervals.
To fit the Gail model we used a common approach in both cohorts and used family history positive without the added detail of more than one relative. An extremely small fraction of all cohort members have more than one relative with breast cancer, limiting the impact of this truncation of data.
Review of evidence shows many models of breast cancer incidence have been developed, but few are validated, and perhaps even fewer evaluated for performance in clinical settings. This applies more broadly than just breast or other cancer prediction—with limited validation and evaluation of clinical impact of prediction models on disease outcomes. For breast cancer, Meads [10] show the range of variables included is substantial with many models not including menopause, type of menopause, or use of postmenopausal HT, or alcohol intake. Other than the Rosner–Colditz model based on NHS data, only Boyle includes alcohol [21], a known carcinogen for breast cancer [17], and age at menopause is only included by Rosner–Colditz and Tyrer [22]. Parity and BMI are more broadly included across models [10]. The most complete of the 17 models summarized by Meads is the Rosner–Colditz model with external validity now established in this independent data set. Several models were assessed for performance by Amir et al. [23] in a UK population of 4,536 women attending a “family history and hereditary screening programme”, among whom 52 developed breast cancer. The Tyrer–Cuzick model [22] had the best performance based on c statistic, though the O/E performance was at the level of 0.8 for this model compared to 0.9 for Gail [23]. While Amir and Tyrer–Cuzick have been evaluated in high-risk populations where they are likely to perform better, such a comparison in the general population has not been reported.
For CHD on the other hand, Van Dieren et al. [24] review evidence on model development and evaluation—45 prediction models reported in the literature, 12 specific for patients with diabetes; 31 % validated in independent population of diabetics, and only one evaluated in clinic for its effect on patient management.
Calibration
While age-standardized incidence rates differ between NHS and CTS the coefficients for risk factors when fitted to the Rosner–Colditz breast cancer incidence model are quite comparable and evaluation of predicted incidence in the calibration analysis shows no significant deviation from SEER incidence, with O/E of 0.96. The range of incidence expected in the SEER calibration study reveals approximately fourfold difference in expected values between lowest and highest decile. This is a non-trivial spread in risk across deciles and is evaluated by the Poisson regression to assess trend in difference between O and E over deciles of risk. The observed lower incidence in NHS may reflect cohort follow-up procedures that do not fully capture incident breast cancers as efficiently as the surveillance through the state tumor registry in California, a state with historically low out migration. As all women should have access to Medicare after age 65, differential screening and access to care should not be an issue when comparing these two cohorts.
Future issues
Future applications in routine clinical settings will add further modeling issues. For example, as approximately one-third of women report hysterectomy in the United States and because age at menopause is an important risk factor in our model, we will need to impute estimated age at menopause among women with hysterectomy before menopause. We have previously derived an algorithm for use in this setting [25]. Other missing data will also need to be addressed, likely using NHANES data as has been implemented in clinical applications of a risk model for progression of age-related macular degeneration using demographic, genetic, environmental, and ocular factors [26]. Other clinical application data come from the United Kingdom where Evans and colleagues have collected breast risk data in a routine breast screening setting, and report evaluation of the Tyrer and Cuzick breast risk model at the level of distributions of 10-year risk and also assess SNPs in a subset of women. Approximately 34 % of women attending breast screening enrolled and risk estimates were returned to those with 10-year risk above 8 % (107 women). Performance assessment of the tool is ongoing in this routine mammography setting [27]. The breast cancer surveillance consortium generated a risk prediction model among more than 1 million women undergoing mammography [28]. They began with age, race, ethnicity, and breast density (measure with BI-RADS) and adjusted estimates of family history and history of breast biopsy. The model was developed in 60 % of the population and validated in the remaining 40 %, and is well calibrated, though it does not include any reproductive or lifestyle predictors of breast cancer. While these two examples indicate that risk factors and prediction can be incorporated into mammography services, issues of missing data and real time estimation of risk have yet to be addressed, and the impact of risk presentation on clinical decision making and outcomes of care has not been evaluated.
Conclusion
Through validation in an independent data set, we have shown that the Rosner–Colditz model performs consistently when applied in that independent setting. Performance is stronger predicting incidence among women 47–69 years and over a 5-year time interval. AUC values are significantly higher than the Gail model in the independent validation data set, and may be further improved with addition of breast density or other markers of risk beyond the current model. Further refinement may be needed to handle missing data in routine clinical settings.
References
Rosner B, Colditz GA (1996) Nurses’ health study: log-incidence mathematical model of breast cancer incidence. J Natl Cancer Inst 88(6):359–364
Colditz G, Rosner B (2000) Cumulative risk of breast cancer to age 70 years according to risk factor status: data from the Nurses’ Health Study. Am J Epidemiol 152(10):950–964
Colditz G, Rosner B, Chen WY, Holmes M, Hankinson SE (2004) Risk factors for breast cancer: according to estrogen and progesterone receptor status. J Natl Cancer Inst 96:218–228
Trichopoulos D, Hsieh CC, MacMahon B et al (1983) Age at any birth and breast cancer risk. Int J Cancer 31(6):701–704
Rosner B, Colditz GA, Willett WC (1994) Reproductive risk factors in a prospective study of breast cancer: the Nurses’ Health Study. Am J Epidemiol 139(8):819–835
Lambe M, Hsieh C-c, Trichopoulos D, Ekbom A, Pavia A, Adami H-O (1994) Transient increase in risk of breast cancer after giving birth. N Engl J Med 331:5–9
Colditz GA, Rosner BA (2006) What can be learnt from models of incidence rates? Breast Cancer Res 8(3):208
Moons KG, Kengne AP, Grobbee DE et al (2012) Risk prediction models: II. External validation, model updating, and impact assessment. Heart 98(9):691–698
Moons KG, Kengne AP, Woodward M et al (2012) Risk prediction models: I. Development, internal validation, and assessing the incremental value of a new (bio)marker. Heart 98(9):683–690
Meads C, Ahmed I, Riley RD (2012) A systematic review of breast cancer incidence risk prediction models with meta-analysis of their performance. Breast Cancer Res Treat 132(2):365–377
Gail MH, Brinton LA, Byar DP et al (1989) Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst 81:1879–1886
Rosner B, Colditz GA, Iglehart JD, Hankinson SE (2008) Risk prediction models with incomplete data with application to prediction of estrogen receptor-positive breast cancer: prospective data from the Nurses’ Health Study. Breast Cancer Res 10(4):R55
Lilienfeld AM (1956) The relationship of cancer of the female breast to artificial menopause and marital status. Cancer 9:927–934
Trichopoulos D, MacMahon B, Cole P (1972) Menopause and breast cancer risk. J Natl Cancer Inst 48(3):605–613
International Agency for Research on Cancer (2008) Monograph on the evaluation of carcinogenic risk to humans: combined estrogen/progestogen contraceptives and combined estrogen/progestogen menopausal therapy. Combined estrogen-progestogen contraceptives and combined estrogen-progestogen menopausal therapy, vol 91. IARC Press, Lyon.
International Agency for Research on Cancer (2002) Weight control and physical activity, vol 6. International Agency for Research on Cancer, Lyon
IARC Working Group on the Evaluation of Carcinogenic Risks to Humans (2007) Alcohol consumption and ethyl carbamate. International Agency for Research on Cancer, Lyon (Distributed by WHO Press, 2010)
Colditz GA, Hankinson SE, Hunter DJ et al (1995) The use of estrogens and progestins and the risk of breast cancer in postmenopausal women. N Engl J Med 332:1589–1593
Bernstein L, Allen M, Anton-Culver H et al (2002) High breast cancer incidence rates among California teachers: results from the California Teachers Study (United States). Cancer Causes Control 13:625–635
Rosner B, Glynn RJ (2009) Power and sample size estimation for the Wilcoxon rank sum test with application to comparisons of C statistics from alternative prediction models. Biometrics 65(1):188–197
Boyle P, Mezzetti M, La Vecchia C, Franceschi S, Decarli A, Robertson C (2004) Contribution of three components to individual cancer risk predicting breast cancer risk in Italy. Eur J Cancer Prev 13(3):183–191
Tyrer J, Duffy SW, Cuzick J (2004) A breast cancer prediction model incorporating familial and personal risk factors. Stat Med 23(7):1111–1130
Amir E, Evans DG, Shenton A et al (2003) Evaluation of breast cancer risk assessment packages in the family history evaluation and screening programme. J Med Genet 40(11):807–814
van Dieren S, Beulens JW, Kengne AP et al (2012) Prediction models for the risk of cardiovascular disease in patients with type 2 diabetes: a systematic review. Heart 98(5):360–369
Rosner B, Colditz GA (2011) Age at menopause: imputing age at menopause for women with a hysterectomy with application to risk of postmenopausal breast cancer. Ann Epidemiol 21(6):450–460
Seddon JM, Reynolds R, Yu Y, Daly MJ, Rosner B (2011) Risk models for progression to advanced age-related macular degeneration using demographic, environmental, genetic, and ocular factors. Ophthalmology 118(11):2203–2211
Evans DG, Warwick J, Astley SM et al (2012) Assessing individual breast cancer risk within the U.K. National Health Service Breast Screening Program: a new paradigm for cancer prevention. Cancer Prev Res 5(7):943–951
Tice JA, Cummings SR, Smith-Bindman R, Ichikawa L, Barlow WE, Kerlikowske K (2008) Using clinical factors and mammographic breast density to estimate breast cancer risk: development and validation of a new predictive model. Ann Intern Med 148(5):337–347
Acknowledgments
This work was supported by the National Cancer Institute, National Institute of Health (PO1 CA87969). G.A.C. is also supported by an American Cancer Society Clinical Research Professorship and the Breast Cancer Research Foundation. LB, JVL, and JSH are supported by RO1 CA077398. LB is also supported by K05 CA136967. We also acknowledge insightful comments from our colleagues Drs. Tamimi and Willett, programming support of Marion McPhee and Rong Chen and secretarial support of Virginia Piaseczny.
Conflict of interest
The authors declare they have no conflict of interest.
Ethical standards
All data collection was conducted with approval of appropriate institutional review boards to protect human subjects with consent and data protection systems in place. Data analysis for this manuscript was conducted on de-identified data sets.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Calibration procedure—CTS validation study
We follow the general calibration procedure of Gail (1989).
Procedure for the mth imputation
-
1.
We wish to apply the NHS risk model to the CTS population, where the incidence model is of the form:
$$\ln \left( I \right) = \alpha + \mathop \sum \limits_{k = 1}^{K} \beta_{k} x_{k}$$ -
2.
Suppose there are N subjects in the CTS population who are followed collectively for T person–years.
-
3.
Suppose the ith subject is followed for t i person years, where:
$$\mathop \sum \limits_{i = 1}^{N} t_{i} = T,$$and that m ij = age of the ith subject at the jth person–year.
-
4.
We divide the T person–years into L age strata and let T l = number of person–years in the lth age stratum, where
$$T = \mathop \sum \limits_{q = 1}^{L} T_{q} ,$$and
$$\begin{aligned} q & = 1 \quad {\text{if}} \ {\text{a}}_{ 1} \le {\text{ m}}_{\text{ij}} < {\text{ a}}_{ 2} , \\ & = 2 \quad {\text{if}} \ {\text{a}}_{2} \le \, m_{ij} < {\text{a}}_{3} , \\ & \ldots \\ & = l \quad {\text{if}} \ {\text{a}}_{l} \le \, m_{ij} < {\text{a}}_{l + 1,} \\ & \ldots \\ & = L \quad {\text{if}} \ {\text{a}}_{L} \le \, m_{ij} < {\text{a}}_{L + 1} . \\ \end{aligned}$$In this case, L = 8 and the age groups are defined by 45–49, 50–54, 55–59, 60–64, 65–69, 70–74, 75–79, 80–87.
-
5.
We define a person as being at baseline risk in the lth age stratum if x = 0.
-
6.
We define covariate values for the ith person in the jth person–year by x ij1,…, x ijK, and let
$$RR_{ij} = exp\left( {\mathop \sum \limits_{k = 1}^{K} \hat{\beta }_{k} x_{ijk} } \right), \quad i = 1, \ldots, \, N; \ j = 1, \ldots, \; t_{i} .$$ -
7.
Let
$$\begin{aligned} {\text{Y}}_{l} & = {\text{observed number of cases in age group}}\;l, \\ & \quad l = 1, \ldots ,{\text{ L}}; \\ O_{{ij}} & = 1{\text{ if the }}i{\text{th subject becomes a case in the }} \\ & \quad j{\text{th person}} - {\text{year}}, = 0{\text{ otherwise}}. \\ \delta _{ijl} & = 1{\text{ if }} a_{l} \le {\text{ m}}_{{ij}} < a_{l} + {\text{1}}, = 0 {\text{ otherwise}}, \\ & \quad i = {\text{1}},\, \ldots ,{\text{ }}N;{\text{ }}j = {\text{1}},\, \ldots \,t_{i}; \ l = {\text{1}},\, \ldots ,{\text{ }}L. \\ \end{aligned}$$ -
8.
Let
$$F_{l} = \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{{t_{i} }} \frac{{O_{ij} \delta_{ijl} /Y_{l} }}{{RR_{ij} }}, \quad l = 1, \ldots , L.$$ -
9.
Let
\(h_{1}^{*} (l) = {\text{age-specific incidence rate from SEER }} 1995{-}2006, \; l = 1, \, \ldots ,{\text{ L}}.\)
-
10.
Let
$$\begin{aligned} h_{1} \left( l \right) =\, & h_{1}^{*} \left( l \right)F_{l} , \\ & = {\text{baseline incidence rate in the }}l{\text{th age stratum of CTS}}, \, l=1,\,\ldots\,,L. \\ \end{aligned}$$ -
11.
An estimate of the incidence rate for the ith subject in the jth person–year is given by:
$$\hat{I}_{ij} = \mathop \sum \limits_{l = 1}^{L} h_{1} \left( l \right)\delta_{ijl} RR_{ij} , \quad i = 1, \ldots ,N;\ j = 1, \ldots ,t_{i}$$ -
12.
An estimate of the cumulative incidence for the ith subject over t i person–years is given by:
$$E_{i} = 1 - exp\left( { - \mathop \sum \limits_{j = 1}^{{t_{i} }} \hat{I}_{ij} } \right), \quad i = 1, \ldots,\;N$$ -
13.
Let
$$\begin{aligned} O_{i} & = {\text{ }}1{\text{ if the }}i{\text{th subject is a case over }}t_{i} {\text{ person{-}years}}, \\ & = 0{\text{ if the }}i{\text{th subject is a control over }}t_{i} {\text{ person{-}years}},{\text{ }}i{\text{ }} = {\text{ }}1,\, \ldots ,{\text{ }}N. \\ \end{aligned}$$ -
14.
Compute
\(E_{i}^{*} = E_{i} /t_{i} = {{{\text{cumulative}}\; {\text{incidence}} \; {\text{per}} \; {\text{person}}}} - {{{\text{year}} \; {\text{for}} \; {\text{the}} \; i{\text{th}}\; {\text{subject}}}}, \ i = 1, \ldots ,{\text{ N}}\) and rank subjects by decile of \(E_{i}^{*}.\)
-
15.
Let
$$\begin{aligned} \lambda _{{id}} = & 1{\text{ if subject}}\;i\;{\text{is in the}}\;d{\text{th}}\;{\text{decile of}}\;E_{i}^{*} , \\ = & 0{\text{ otherwise}}, \ i = 1,\, \ldots ,{\text{ N}};{\text{ d}} = 1,\, \ldots ,10.{\text{ }} \\ \end{aligned}$$ -
16.
Compute
$$\begin{aligned} O^{{(d)}} & = \sum\limits_{{i = 1}}^{N} {O_{i} } \lambda _{{id}} = {\text{observed number of cases in the }}d{\text{th}}\;{\text{decile of }}E_{i}^{*} , \\ E^{{(d)}} & = \sum\limits_{{i = 1}}^{N} {E_{i} } \lambda _{{id}} = {\text{expected number of cases in the }}d{\text{th}}\;{\text{decile of }}E_{i}^{*} \\ \end{aligned}$$ -
17.
Poisson regression at the aggregate level
Run Poisson regression of O (d) using ln(E (d)) as the offset based on the model:
$$\ln \left( {\mu_{d} } \right) = \alpha + \ln \left( {E^{\left( d \right)} } \right), \quad {\text{where }}\mu_{d} = E\left( {O^{\left( d \right)} } \right)$$or equivalently \(\mu_{d} = { \exp }({{\upalpha}})E^{\left( d \right)}\)
Note in the above model, α = 0 implies that μ d = E (d).
-
18.
Poisson regression at the individual level
Run Poisson regression of O i using ln(E i ) as the offset based on the model:
$$\ln \left( {\mu_{i} } \right) = \alpha + \ln \left( {E_{i} } \right),$$or
$$O_{i} = { \exp }\left( \alpha \right)E_{i} ,$$where
$$\mu_{i} = E\left( {O_{i} } \right).$$Note α = 0 implies that μ i = E i . Also, the models in steps 17 and 18 are equivalent because O (d) is a sum of Poisson distributions which is also Poisson, where
$$\mu_{d} = \mathop \sum \limits_{i = 1}^{N} \mu_{i} \lambda_{id} = { \exp }(\alpha )\mathop \sum \limits_{i = 1}^{N} E_{i} \lambda_{id} = \exp \left( \alpha \right)E^{\left( d \right)} .$$ -
19.
If we average SEER incidence rates for white women from 1995 to 2000 and 2000 to 2006, we obtain:
Age | SEER incidence rate (per 105 person–years) | CTS incidence rate (per 105 person–years) | CTS number of cases |
|---|---|---|---|
45–49 | 253.3 | 64.2 | 1 |
50–54 | 336.8 | 269.2 | 47 |
55–59 | 417.0 | 407.1 | 173 |
60–64 | 494.2 | 493.2 | 297 |
65–69 | 538.8 | 534.6 | 328 |
70–74 | 579.3 | 540.4 | 268 |
75–79 | 592.6 | 582.0 | 166 |
80–87 | 517.4 | 476.1 | 55 |
Overall inference over m imputations
-
20.
For step 16, let
\(O_{m}^{\left( d \right)} , E_{m}^{\left( d \right)} , T_{m}^{\left( d \right)} =\) observed count, expected count and person–years for the dth risk decile in the mth imputation. The overall estimates of \(O^{\left( d \right)}\), \(E^{\left( d \right)}\) and \(T^{\left( d \right)}\) are given by:
$$O^{\left( d \right)} = \mathop \sum \limits_{m = 1}^{M} O_{m}^{\left( d \right)} /M,E^{\left( d \right)} = \mathop \sum \limits_{m = 1}^{M} E_{m}^{\left( d \right)} /M,T^{\left( d \right)} = \mathop \sum \limits_{m = 1}^{M} T_{m}^{\left( d \right)} /M.$$For steps 17 and 18, we obtain the estimate:
\(\hat{\alpha }^{(m)}\) for the mth imputation and associated estimate
\({\text {var}}[\hat{\alpha }^{(m)} ]\). The overall point estimate is:
$$\hat{\alpha } = \mathop \sum \limits_{m = 1}^{M} \hat{\alpha }^{\left( m \right)} /M,$$with associated variance given by:
$${\text {var}}\left( {\hat{\alpha }} \right) = \mathop \sum \limits_{m = 1}^{M} {\text {var}}[\hat{\alpha }^{\left( m \right)} ]/M + \left[ {\left( {M + 1} \right)/M} \right]\mathop \sum \limits_{m = 1}^{M} \left[ {\hat{\alpha }^{\left( m \right)} - \hat{a}} \right]^{2} /(M - 1),$$and test statistic
$$\begin{aligned} & z_{{\hat{\alpha }}} = \hat{\alpha }/\left[ {{{\text {var}}} \left( {\hat{a}} \right)} \right]^{{1/2}} \sim N\left( {0,1} \right){\text{ under }}H_{0} {\text{ that }} \alpha = 0, \\ & p{\text{-value}} = 2 \times \left[ {1 - \Phi |z_{\alpha } |} \right]. \\ \end{aligned}$$
Appendix 2: Imputation strategy for ever use and duration of use of postmenopausal hormone therapy
-
1.
Let
$$\begin{gathered} ln\left( {\frac{{P_{i1} }}{{1 - P_{i1} }}} \right) = \alpha_{1} + \mathop \sum \limits_{k = 1}^{K} \beta_{k1} x_{ik} \hfill \\ ln\left( {\frac{{P_{i2} }}{{1 - P_{i2} }}} \right) = \alpha_{2} + \mathop \sum \limits_{k = 1}^{K} \beta_{k2} x_{ik} \hfill \\ \end{gathered}$$(1)where p i1 = Prob(duration estrogen alone > 0, 1994-2006) for the ith NHS woman, i = 1,…, 45742, p i2 = Prob(duration E&P > 0, 1994–2006) for the ith NHS woman, I = 1,…, 45742, x ik = kth breast cancer risk factor for the ith subject, I = 1,…, 45742, k = 1,…, K and let \(\hat{p}_{i1} ,\hat{p}_{i2}\) be the corresponding estimated probabilities obtained by substituting the estimated parameters \(\hat{\alpha }_{1} ,\hat{\alpha }_{2}\) and \(\hat{\beta }_{k1} ,\hat{\beta }_{k2}\), k = 1, …, K for the true parameters in Eq. 1.
-
2.
$$\begin{aligned} {\text{Let }}y_{i1} & = \ln ({\text{duration of use of estrogen alone for the }}i {\text{th NHS woman, where }}, y_{i1} > 0 \\ y_{{i{\text{2}}}} \\ \quad y_{i2} & = \ln{\text{duration of use of E }} \& {\text{P for the }}i{\text{th NHS woman, where }} y_{i2} > 0. \\ \end{aligned}$$
-
3.
-
(a)
Let
$$\begin{gathered} z_{i1} = \alpha_{1}^{*} + \mathop \sum \limits_{k = 1}^{K} \beta_{k1}^{*} x_{ik} + e_{i1}^{*} , \hfill \\ z_{i2} = \alpha_{2}^{*} + \mathop \sum \limits_{k = 1}^{K} \beta_{k2}^{*} x_{ik} + e_{i2}^{*} \hfill \\ \end{gathered}$$(2)where
$$z_{i1} = \ln \left( {y_{i1} } \right),z_{i2} = \ln \left( {y_{i2} } \right),e_{i1} \sim N\left( {0,\sigma_{i1}^{2} } \right),e_{i2} \sim N(0,\sigma_{i2}^{2} )$$be linear regressions of \(z_{i1}\) and \(z_{i2}\) on \(\tilde{x}_{i}\), respectively.
-
(b)
Let
$$\begin{gathered} \hat{z}_{i1}^{*} = \hat{\alpha }_{1}^{*} + \mathop \sum \limits_{k = 1}^{K} \hat{\beta }_{k1}^{*} x_{ik} , \hfill \\ \hat{z}_{i2}^{*} = \hat{\alpha }_{2}^{*} + \mathop \sum \limits_{k = 1}^{K} \hat{\beta }_{k2}^{*} x_{ik} \hfill \\ \end{gathered}$$be the corresponding predicted values of z i1 and z i2, respectively.
-
(c)
Let \(\hat{\sigma }_{1}^{2} ,\hat{\sigma }_{2}^{2}\) be the estimated residual variances corresponding to z i1 and z i2, in Eq. 2, respectively.
-
(a)
-
4.
Let U i1, U i2 be U(0,1) random variables and let u i1, u i2 be the realization of these random variables generated using the RANUNI function of SAS.
Let V i1, V i2 be corresponding N(0,1) random variables and let v i1, v i2 be the realization of these random variables generated using the RANNOR function of SAS.
-
5.
Let \(\hat{y}_{i1} ,\hat{y}_{i2}\) = imputed estimate of duration of estrogen alone and duration of E&P, respectively, for the ith NHS woman.
-
(a)
If \(\hat{p}_{i1} < u_{i1}\), then \(\delta_{i1} = 1, {\text{else }}\delta_{i1} = 0.\)
-
(b)
If \(\hat{p}_{i2} < u_{i2}\), then \(\delta_{i2} = 1, {\text{else }}\delta_{i2} = 0.\)
-
(c)
Let \(\begin{aligned} \hat{w}_{{i1}} & = \hat{z}_{{i1}}^{*} + \hat{\sigma }_{1} {\text{v}}_{{i1}} , \\ \hat{w}_{{i2}} & = \hat{z}_{{i2}}^{*} + \hat{\sigma }_{2} {\text{v}}_{{i2}} . \\ \end{aligned}\)
-
(d)
(i) If \(\delta_{i1} = \delta_{i2} = 0, {\text{then }}\hat{y}_{i1} = \hat{y}_{i2} = 0,\)
(ii) If \(\delta_{i1} = 1 \; {\text{and }}\delta_{i2} = 0, {\text{then }}\hat{y}_{i1} = \hbox{min} \left[ {\exp \left( {\hat{w}_{i1} } \right),12} \right],\hat{y}_{i2} = 0,\)
(iii) If \(\delta_{i1} = 0 \; {\text{and }}\delta_{i2} = 1, {\text{then }}\hat{y}_{i1} = 0, \hat{y}_{i2} = { \hbox{min} }\left[ {\exp \left( {\hat{w}_{i2} } \right),12} \right],\)
(iv) If \(\delta_{i1} = 1 \; {\text{and }}\delta_{i2} = 1, {\text{and }}\hat{w}_{i1} > \hat{w}_{i2} , {\text{then }}\hat{y}_{i1} = { \hbox{min} }\left[ {\exp \left( {\hat{w}_{i1} } \right),12} \right],\hat{y}_{i2} = 0,\)
(v) If \(\delta_{i1} = 1 {\text{ and }}\delta_{i2} = 1, {\text{ and }}\hat{w}_{i1} < \hat{w}_{i2}, {\text{ then }}\hat{y}_{i1} = 0, \; \hat{y}_{i2} = \hbox{min} \left[ {\exp \left( {\hat{w}_{i2} } \right),12} \right].\)
-
(a)
-
6.
-
(a)
Based on steps 1–5, we estimate duration of estrogen alone and duration of E&P for all NHS women and fit the log-incidence model described in step 1, assuming that duration of HT is continuous starting in 1994 and ceases after duration \(\hat{y}_{i1} \; {\text{or}} \; \hat{y}_{i2}\), respectively.
-
(b)
We repeat (a) five times and obtain five separate estimates of α and β, respectively. Let \(\hat{\alpha }_{m} ,\hat{\beta }_{k,m}\) be the estimates of and β k for the mth imputation, k = 1,…, K.
The overall estimates are given by:
$$\hat{\alpha } = \mathop \sum \limits_{m = 1}^{5} \hat{\alpha }_{m} /5,\hat{\beta }_{k} = \mathop \sum \limits_{m = 1}^{5} \hat{\beta }_{k,m} /5,$$with
$$\begin{aligned} {\text {var}}\left( {\hat{\alpha }} \right) & = \mathop \sum \limits_{m = 1}^{5} {\text {var}}(\hat{\alpha }_{m} )/5 + (6/5)\mathop \sum \limits_{m = 1}^{5} \left( {\hat{\alpha }_{m} - \hat{\alpha }} \right)^{2} /4, \\ {\text {var}}\left( {\hat{\beta }_{k} } \right) & = \mathop \sum \limits_{m = 1}^{5} {\text {var}}(\hat{\beta }_{k,m} )/5 + (6/5)\mathop \sum \limits_{m = 1}^{5} \left( {\hat{\beta }_{k,m} - \hat{\beta }_{k} } \right)^{2} /4. \\ \end{aligned}$$
-
(a)
-
7.
A similar strategy as in step 6 is used to obtain multiple imputation estimates of AUC based on imputed data, where \(Va\hat{r}(AUC)\) is obtained using the methods in Rosner and Glynn [20].
-
8.
For imputation with the CTS data, we use the NHS prediction equations in (1) and (2) and proceed as in steps 5 and 6 to obtain overall estimates of α and β for CTS as given in Table 4.
-
9.
Estimates of AUC are obtained for CTS based on the coefficients \(\hat{\alpha }{\text{ and }}\hat{\beta }\) obtained from NHS data in step 6. The AUC estimates were obtained for five imputed CTS datasets and combined using the methods in step 6.
-
10.
Similarly, calibration of the NHS model based on the coefficients \(\hat{\alpha }{\text{ and }}\hat{\beta }\) in step 6 were applied to five imputed CTS datasets. Separate estimates of observed counts, expected counts and Poisson regression parameters were obtained for each imputed CTS dataset and combined using multiple imputation methods described in Appendix 1.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Rosner, B.A., Colditz, G.A., Hankinson, S.E. et al. Validation of Rosner–Colditz breast cancer incidence model using an independent data set, the California Teachers Study. Breast Cancer Res Treat 142, 187–202 (2013). https://doi.org/10.1007/s10549-013-2719-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10549-013-2719-3