1 Introduction

The mixed-layer similarity is often used to describe turbulence statistics within the fair-weather convective boundary layer (CBL), (e.g. Stull 1988; Wyngaard 2010). This scaling applies to the asymptotic state of free convection, i.e. in the limit of zero mean wind and associated wind shear. Hence, the turbulence shear production is negligible compared to the turbulence buoyant production (e.g. Stull 1988; Wyngaard 2010). The corresponding relevant velocity and time scales are defined by Deardorff (1970):

$$\begin{aligned} w_*\equiv \left( \frac{g}{\theta }Hz_i\right) ^{\frac{1}{3}}\text {, and }t_*\equiv \frac{z_i}{w_*}, \end{aligned}$$
(1)

where g is the acceleration due to gravity, \(\theta \) is the mean potential temperature of the CBL, H is the surface kinematic heat flux, and \(z_i\) is the CBL depth. Hereafter \({w_*}\) will be called the convective velocity scale, \(t_*\) the convective eddy-turnover time scale, and “the surface heat flux” will be used to refer to the surface kinematic heat flux.

The earliest numerical and observational studies on the applicability of the mixed-layer similarity (Deardorff 1972; Kaimal et al. 1976; Caughey and Palmer 1979) already recognized that it does not account for the influence of entrainment. This is especially the case for scalar statistics, when fluctuations originating from entrainment dominate over those from the surface (Wyngaard 1992, 2010). The mixed-layer similarity may also not hold in complex terrain because of the mechanical turbulence induced by the terrain (Kustas and Brutsaert 1987; Wyngaard 1992). The mixed-layer similarity becomes less applicable during the late afternoon transition, which motivates this work.

Despite the shortcomings of the mixed-layer similarity briefly outlined above, it remains a useful framework that allows to compare and interpret measurements collected in different parts of the world during low-wind conditions (e.g. Kaimal et al. 1976; Caughey and Palmer 1979; Lenschow et al. 1980), measurements from laboratory experiments (e.g. Willis and Deardorff 1974; Deardorff and Willis 1985; Fedorovich et al. 1996) and results from numerical simulations (e.g. Schmidt and Schumann 1989; Moeng and Sullivan 1994; Sullivan and Patton 2011). Dispersion models for air-quality assessment utilize the mixed-layer scales for the parametrization of convective turbulence (e.g. Hanna and Paine 1989; Cimorelli et al. 2005). Large-scale models of atmospheric circulation also benefit from the mixed-layer scales in terms of the parametrization of surface fluxes (e.g. Miller et al. 1992; Beljaars 1995).

The mixed-layer similarity relies on the assumption that the CBL is in a quasi-equilibrium or quasi-steady state. Qualitatively, it means that “even though the CBL evolves in response to the roughly sinusoidal variation of surface heating, there is justification for treating its midday structure as if it were in steady state. The time scale characteristic of convectively driven turbulence [...] is much smaller than the time scale of changes in \(Q_0\) and \(z_i\), or changes in the pressure field that drives the flow. Thus, we expect that near midday the mixed layer quickly adjusts its structure in response to the slowly varying boundary conditions and keeps itself in a condition of moving equilibrium or quasi-steady state.” (\(Q_0\) refers to the surface heat flux) (Kaimal et al. 1976). In other words, “the turbulence follows a continuum of equilibrium states—that it tracks the “changes” perfectly” (Wyngaard 1973). Quantitatively, it means that the turbulence statistics become time independent when normalized by \(w_*(t)\) and \(z_i(t)\), with the same value as the normalized statistics resulting from situations where the surface heat flux is constant (Wyngaard 1973; Kaimal et al. 1976). Similar ideas were also used by Momen and Bou-Zeid (2017) to investigate the quasi-equilibrium of Ekman boundary layers. From the perspective of the turbulence kinetic energy (TKE) budget, the term “quasi-stationary” refers to the state where the TKE tendency is much smaller than the other budget terms (Nieuwstadt and Brost 1986; Nilsson et al. 2016). We do not consider this perspective in this study.

The quasi-equilibrium assumption becomes questionable in the late afternoon transition when the surface heat flux decays rapidly, a topic to be investigated in this study. For convenience, “the afternoon transition” will hereafter refer to the stage of the diurnal cycle when the surface heat flux gradually decays between its maximum value around midday and a zero value shortly before sunset (Nadeau et al. 2011). The duration of the afternoon transition is typically denoted as \(\tau _f\), which is also sometimes called “the external time scale controlling the surface heat flux changes”, or “the forcing time scale” (Sorbjan 1997).

More specifically, the present work aims to characterize the departure from mixed-layer similarity while the quasi-equilibrium assumption gradually breaks down. We aim to show how the scales, \(z_i(t)\) and \(w_*(t)\), can still be used to describe the velocity-variances profiles, even after the breakdown of quasi-equilibrium. Thereby, we also address “a question that is still poorly understood [...]: how long does the CBL remain quasi-stationary during the afternoon transition, or, equivalently, for how long does the convective scaling apply as the surface flux decreases?” (Lothon et al. 2014).

Based on a brief analysis of the boundary-layer averaged TKE in the free-convective CBL from large-eddy simulation (LES) experiments, Elguernaoui et al. (2019) suggested an empirical threshold of approximately 0.7\(\tau _f\) (with \(\tau _f\) = 2, 4, 6, and 10 h in that study) for locating the time when the TKE normalized with \(w_*(t)\) gradually departs from mixed-layer similarity. In the present study, we carry out a more detailed analysis of the profiles of the vertical and horizontal velocity variances in simulations with different shapes of the surface heat flux decay. We find that within the descriptive frame where the timeline is tracked by fractions of \(\tau _f\), the departure from mixed-layer similarity is dependent on the shape of the surface heat flux decay, suggesting that \(\tau _f\) is not particularly useful for characterizing the departure from mixed-layer similarity. We will show that the forcing time scale introduced by Wyngaard (1973):

$$\begin{aligned} \widetilde{\tau }_f(t)\equiv \left| \frac{1}{H}\frac{dH}{dt}\right| ^{-1}, \end{aligned}$$
(2)

which is time dependent, and characterizes the rate of change in the surface heat flux relative to its magnitude, is more relevant than the constant forcing time scale \(\tau _f\).

Furthermore, motivated by the two following facts,

  1. 1.

    The quasi-equilibrium underlying the mixed-layer similarity requires the convective eddy-turnover time scale being much smaller than the forcing time scale (Wyngaard 1973; Kaimal et al. 1976).

  2. 2.

    As the surface heat flux decays, the convective eddy-turnover time scale gradually increases (see Eq. 1), and approaches the forcing time scale. Note that in our study, the slight increase of the boundary-layer depth during the surface heat flux decay also contributes to the increase of the convective eddy-turnover time scale.

we will consider the convective eddy-turnover time scale (\(t_*\)), in addition to the forcing time scale, for characterizing the departure from mixed-layer similarity.

This work reflects a basic research. It does not aim to investigate the effects of processes associated with radiation, clouds, entrainment, or surface heterogeneity for examples, as recommended by Angevine et al. (2020). The reason is that elementary scaling aspects of the turbulence decay in the CBL are still not sufficiently well understood, as shown by the following results.

2 Description of the LES Model and the Numerical Experiments

The PALM model has been widely used in its LES mode to study various flow regimes in the convective (e.g. Raasch and Harbusch 2001; Gehrke et al. 2021), the neutral (e.g. Gronemeier et al. 2021; Krutova et al. 2022), and the stable boundary layer (e.g. Schwenkel and Maronga 2020; Maronga and Li 2022). The equations solved by the PALM model in this study are the filtered Navier–Stokes equations within the Boussinesq approximation, together with the filtered transport equation for potential temperature. The discretization of the model equations is carried on a Cartesian C-type staggered grid using finite differences. The second-order advection scheme (Piacsek and Williams 1970) and the third-order Runge-Kutta timestep scheme (Williamson 1980) are used. The subgrid-scale closure uses a 1.5-order flux-gradient scheme after Deardorff (1980). More details about the model can be found in Maronga et al. (2015). We used revision 2663 of the model.

The CBL in our simulations is driven by a prescribed homogeneous surface heat flux. A non-slip condition is imposed at the bottom boundary, while constant velocity and potential temperature gradients are imposed at the top boundary towards the free atmosphere. The lateral boundary conditions are cyclic. At the model top boundary, the reflection of the gravity waves formed at the interface between the boundary layer and the free atmosphere can affect the boundary layer. To prevent those potentially adverse effects, a damping layer is added to the highest levels of the modelling domain. The potential temperature at the initial time equals 300 K at the surface, and increases from there with a rate of 3 K km\(^{-1}\). We set the geostrophic wind speed to zero, because we do not aim to investigate its effect on the departure from mixed-layer similarity as the quasi-equilibrium breaks down. Thus, the following results should be considered as valid in the asymptotic state of vanishing geostrophic wind, assuming that this asymptotic state is not singular.

The surface kinematic heat flux is maintained constant with a value of 0.1 K m s\(^{-1}\), during the 5-h spin-up time. Thereafter, the surface heat flux decays following either a sinusoidal or an exponential decay function (Fig. 1a). The sinusoidal decay is in line with previous modelling and/or observational studies (e.g. Nadeau et al. 2011; Rizza et al. 2013; Darbieu et al. 2015). Further considering an exponential decay is useful to gain more confidence in the generalizability of our results in this idealized study, where we aim to characterize the response of the free-convective boundary layer to vastly different surface heat flux decay-shapes. In reality, the exponential decay might be associated with the onset of clouds blocking downwelling solar radiation. The duration between the maximum and the zero surface heat flux, \(\tau _f\), is chosen as 6 h or 2 h. Observations suggest that \(\tau _f\) = 6 h is a common value (Nadeau et al. 2011; Lothon et al. 2014), while \(\tau _f\) = 2 h can be considered as a lower-bound value (Lothon et al. 2014, Fig. 8). The analytical expressions for the prescribed decaying kinematic heat flux are:

$$\begin{aligned} H(t) = 0.1\ cos\left( \frac{\pi }{2}\ \frac{t-18{,}000}{3600\tau _f}\right) \text {, or } H(t) = 0.1\ \bigg ( \frac{e^{-\left( \dfrac{t-18{,}000}{3600\tau _f}\right) }-1}{1-e^{-1}}+ 1\bigg ), \end{aligned}$$
(3)

with \(t\in \) [18,000 s, 25,200 s] or [18,000 s, 39,600 s]. Note that we also perform a reference run with a simulation time of 11 h, driven by a constant surface heat flux value of 0.1 K m s\(^{-1}\) as during the spin-up period of our decay simulations (H_constant). We assume no water-vapor flux.

Fig. 1
figure 1

a Time series of the prescribed surface heat flux in the runs H_constant, \(\tau _f6\)_cos, \(\tau _f2\)_cos, \(\tau _f6\)_exp, and \(\tau _f2\)_exp. b Time series of the resulting boundary-layer height defined here as the height of the capping inversion

Full size image

The horizontal extent of the model domain is 12.8 km in both x and y directions. The domain height is 4400 m and 3210 m for experiments with \(\tau _f\) = 6 h and 2 h, respectively. As the domain size in the vertical (horizontal) is more than two (five) times larger than the maximum boundary-layer height (which is shown in Fig. 1b), the largest turbulent eddies can evolve freely, independent of the periodic sidewall effects (de Roode et al. 2004). The grid spacing is 12.5 m in all three directions. A sensitivity test of our results to the grid spacing has been carried out and is presented in the discussion section. For the analysis of our results, we define the CBL depth as the height of the capping inversion, where the vertical gradient of the mean potential temperature reaches its maximum, following the recommendation of Sullivan et al. (1998). This criterion is relevant during fair-weather conditions, because the CBL is then often capped by a temperature inversion (e.g. Kaimal et al. 1976; LeMone et al. 2019). In the discussion section, we will explore the sensitivity of our results to the definition of the CBL height.

For estimating the vertical profiles of turbulence statistics, we apply space averaging over horizontal cross-sections, time averaging over 1-min intervals, as well as ensemble averaging over eight realisations of the flow. Each realisation is obtained by imposing at the initial time random perturbations to the surface heat flux field, and to the horizontal-velocity field in the vertical range extending from the near-surface up to a height of one third of the domain height. Statistical homogeneity in the x and y directions justifies the use of horizontal averaging. Time-averaging over 1-min intervals does not conflict with the turbulence being non-stationary because the time-dependent convective eddy-turnover time (\(t_*\)) remains much larger than 1 min for all the simulations. Starting from a value of 14 min at the end of the spin-up time, the convective eddy-turnover time increases as the surface heat flux decays, reaching values on the order of 100 min before the surface heat flux becomes zero (see also Fig. 5a in the Results section). A sensitivity test of our results to the averaging length has been carried out and is presented in the discussion section.

Hereafter, we refer to each experiment by the value of \(\tau _f\) followed by the shape of the decay function for the surface heat flux. In run \(\tau _f\)6_cos for example, the surface heat flux decay is sinusoidal, with a 6-h duration between its maximum and zero value.

3 Results

3.1 The Self-Similar Profiles from the Case with Constant Heat Flux

The profiles of the sum of the resolved and the subgrid-scale vertical and horizontal velocity variances, as well as the profiles of the resolved w skewness, are presented in Fig. 2a–c respectively, at times between 5 and 11 h of simulation time for the run H_constant. The boundary-layer depth increases by approximately 600 m during the 6-h period, and the velocity variances increase for both the vertical and horizontal component. Clearly, a steady state is not reached during 11 h of simulation time, even though the surface heat flux is kept constant. Nevertheless, the developing profiles remain in a quasi-steady state, or a moving equilibrium with the constant surface heat flux and the increasing boundary-layer depth. Indeed, the profiles collapse when the height and the velocity variances are normalized with the actual \(z_i(t)\) and \(w_*(t)\), respectively (see Fig. 2d–f), indicating that the mixed-layer similarity applies.

Fig. 2
figure 2

Time change during [5 h, 11 h] of the profiles of the sum of the resolved and the subgrid-scale velocity variances, and the resolved w skewness for the run H_constant. Dimensional variables in (a), (b), and (c). Normalized variables in (d), (e), and (f). Average is done over space, time (1 min), and eight ensemble runs. The green curves are estimates of the self-similar profiles calculated by averaging over the [5 h, 11 h] time interval. At each height in the interval [0.1\(z_i\), 0.8\(z_i\)], more than 94% of the values used for calculating the average are within ± two standard deviations indicated by the error-bars. The dotted curves are the self-similar profiles for the most convective cases reported in Lenschow et al. (2012). The dashed curves are the self-similar profiles reported in Sullivan and Patton (2011). The variance of the horizontal velocity is calculated as the average of the velocity variances in the x and y directions

Full size image
Fig. 3
figure 3

Time change during [5 h, 11 h] of the profiles of the velocity variances and the w skewness for the run \(\tau _f6\)_cos. Average is done over space, time (1 min), and eight ensemble runs. Dimensional variables in (a), (b), and (c). Normalized variables in (d), (e), and (f). The green curves are estimates of the mixed-layer similarity profiles. The variance of the horizontal velocity is calculated as the average of the velocity variances in the x and y directions

Full size image
Fig. 4
figure 4

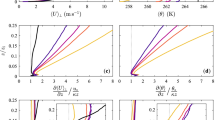
a–e The departure of the vertical-velocity variance profiles from the mixed-layer similarity profile, in the runs \(\tau _f6\)_cos, \(\tau _f2\)_cos, \(\tau _f6\)_exp, and \(\tau _f2\)_exp. The time is tracked by fractions of \(\tau _f\). f–j Same as in (a)–(e), but for the horizontal-velocity variances

Full size image

As the normalized profiles of the velocity variances from different times collapse (see Fig. 2d, e), the time development of the velocity variances illustrated in Fig. 2a, b is self-similar, and those self-similar profiles can be described as:

$$\begin{aligned} \hat{\sigma }_{w,u}^2\left( \frac{z}{z_i(t)}\right) \equiv \frac{\sigma _{w,u}^2(t,z)}{w_*^2(t)}, \end{aligned}$$
(4)

with the function \(\hat{\sigma }_{w,u}^2\) depending on a single variable, the normalized boundary-layer height \({z}/{z_i(t)}\). In particular, \(\hat{\sigma }_{w,u}^2\) is not a function of time. For more details about the concept of self-similarity, see Pope (2000). The self-similar profiles from our simulations are in good agreement with the field-experiment results reported by Lenschow et al. (2012) (Fig. 2d, f). The data used by Lenschow et al. (2012) were collected over a relatively flat and uniform agricultural surface during the Lidars-in-Flat-Terrain (LIFT) experiment in 1996 (Angevine et al. 1998), from about 13:00 to 16:00 local time, using a high resolution Doppler lidar. The profiles from Lenschow et al. (2012) shown in Fig. 2d, f are actually an average over the 5 most convective cases with a global stability parameter, \(-z_i/L\) (L is the Obukhov length), greater than 30. The self-similar profiles from our simulations are also in good agreement with the LES results reported by Sullivan and Patton (2011) (Fig. 2d–f). Around the entrainment zone, the magnitude of the horizontal velocity variance from Sullivan and Patton (2011) is slightly higher (see Fig. 2e), most likely because Sullivan and Patton (2011) prescribe a 1 ms\(^{-1}\) geostrophic flow, while our simulations are performed without background wind. Even if no geostrophic wind is prescribed in our study, the horizontal return flow of the large scale convective cells near the surface and the entrainment zone will generate horizontal wind fluctuations and thus variances. The presented self-similar profiles will be used thereafter as the reference for investigating the departure from mixed-layer similarity.

3.2 The Departure from Mixed-Layer Similarity

In the next step, we investigate the boundary-layer response to the decaying surface heat flux. An example for the run \(\tau _f6\)_cos is presented in Fig. 3. The velocity variances do not decay immediately after the surface heat flux starts declining at the end of the 5-h spin-up time (see Fig. 3a, b), they keep further increasing for approximately 45 min because the boundary-layer depth is still growing and the decay rate of the surface heat flux remains very small (Fig. 1a, b). Later on, the velocity variances decay (see Fig. 3a, b), despite the continuing increase of the boundary-layer depth (Fig. 1b), reflecting the decreasing ability of the surface-driven convective elements to maintain high turbulence levels.

The departure from mixed-layer similarity for the run \(\tau _f6\)_cos is illustrated in Fig. 3d, e: while the profiles of the normalized velocity variances collapse with the self-similar profiles during the early times, a gradual and monotonic departure from the self-similar profiles can be observed after around 0.7\(\tau _f\). In contrast to the velocity variances, the w skewness profiles within the approximate height interval [0.2\(z_i\), 0.6\(z_i\)] remain almost indistinguishable from the self-similar profile (Fig. 3f). This suggests, for the times presented, the preservation of the typical cellular structure with narrow updraft regions surrounded by broad areas of downdraft, although the velocity-variances profiles depart from the self-similar profiles.

3.3 What Controls the Departure from Mixed-Layer Similarity?

As alluded to in the introduction, Elguernaoui et al. (2019) suggested an empirical time threshold of approximately 0.7\(\tau _f\), for locating the time when the boundary-layer averaged TKE departs from mixed-layer similarity. To apply this criterion to the profiles of the vertical and horizontal velocity variances in runs with different shapes of the surface heat flux decay, we investigate the collapse of the profiles through time with the timeline tracked by fractions of \(\tau _f\). The result is shown in Fig. 4 for increasing times of 0.4\(\tau _f\), 0.6\(\tau _f\), 0.7\(\tau _f\), 0.8\(\tau _f\), and 0.9\(\tau _f\). The corresponding actual times are reported in Table 1. We find that the profiles of the velocity variances from these different runs all depart from the self-similar profiles after 0.7\(\tau _f\). More importantly, the spread among the runs increases with time from the time 0.7\(\tau _f\) and onward (Fig. 4c–e, and h,i,j). These results suggest that the departure from the self-similar profiles is not only time-dependent within the descriptive frame where the time is tracked by fractions of \(\tau _f\) (note that for each experiment \(\tau _f\) is a constant), but also dependent on the shape of the surface heat flux decay.

Table 1 Actual times in [h] corresponding to 0.4\(\tau _f\), 0.6\(\tau _f\), 0.7\(\tau _f\), 0.8\(\tau _f\), and 0.9\(\tau _f\) for all the runs
Full size table

Even though \(\tau _f\) is a characteristic time scale of the surface heat flux decay, one might have expected that it is not the correct scale for characterizing the effect of the forcing on the departure from self-similarity, because \(\tau _f\) does not encode information regarding the time-dependence of a given decay shape. For illustration, the runs \(\tau _f6\)_cos and \(\tau _f6\)_exp have the same \(\tau _f\) but very different decay shapes (Fig. 1a). Instead of the constant forcing time scale \(\tau _f\), considering the time-dependent forcing time scale \(\widetilde{\tau }_f\) (Eq. 2) (Wyngaard 1973) might be more helpful for describing the departure from self-similarity, because \(\widetilde{\tau }_f\) describes the time-dependent, relative changes in the surface heat flux, and hence, \(\widetilde{\tau }_f\) includes information about the time-dependence of a given decay shape

Given the definition of \(\widetilde{\tau }_f\) as the relative time-change of the surface heat flux (Eq. 2), one might easily conclude that \(\widetilde{\tau }_f\) decreases in time for the sinusoidal decay because the heat-flux magnitude decreases while the decay rate increases in absolute value (Fig. 1a). But this qualitative observation could not have been anticipated for the exponential decay, in which case both the heat-flux magnitude and the decay rate decrease in absolute value (Fig. 1a). Using Eqs. 2 and 3, we calculated the time derivative of \(\widetilde{\tau }_f\) and found it to be negative, consistent with the monotonic decrease of \(\widetilde{\tau }_f\) illustrated in (Fig. 5a), which means that the relative decay-rate becomes faster.

Fig. 5
figure 5

a Time series of the characteristic time scale of the surface heat flux decay, \(\widetilde{\tau }_f\) (solid lines), and the eddy-turnover time, \({t_*}\) (dashed lines). b Time series of the ratio \(r \equiv \frac{\tau _f}{t_*}\). c Time series of the ratio \(\widetilde{r} \equiv \frac{\widetilde{\tau }_f}{t_*}\). The horizontal lines in c indicate values of \(\widetilde{r}\) of 2, 1, and 0.4, which are used later on to illustrate the relevance of \(\widetilde{r}\). The time in the horizontal axes is normalized by \(\tau _f\) for convenience, because the duration between the maximum and the zero heat flux varies from one run to another

Full size image

To examine the results in the descriptive frame where the time is tracked by \(\widetilde{\tau }_f(t)\), for a given value \(\widetilde{\tau }_f(t)\) we locate the corresponding time (t) for each run. These times are listed in Table 2, for \(\widetilde{\tau }_f\) taking the successively decreasing values of 6, 3, 1, 0.5, and 0.2 h. Each panel in Fig. 6 shows the velocity variances profiles from different runs, which correspond to different t but the same value of \(\widetilde{\tau }_f(t)\). For \(\widetilde{\tau }_f\) smaller than 1 h, Fig. 6c–e, and h–j, shows a gradually increasing departure from the self-similar profiles for both the vertical and horizontal velocity variances. Furthermore, as time progresses, i.e. when \(\widetilde{\tau }_f\) decreases and the relative changes in the forcing become faster, the spread among the profiles from different runs increases. In other words, this descriptive frame also reveals a dependency of the departure from mixed-layer similarity on the shape of the surface heat flux decay.

Table 2 Actual times in [h] corresponding to the decreasing values of \(\widetilde{\tau }_f\) (6, 3, 1, 0.5, and 0.2 h) for all the runs
Full size table
Fig. 6
figure 6

a–e The departure of the vertical-velocity variance profiles from the mixed-layer similarity profile, in the runs \(\tau _f6\)_cos, \(\tau _f2\)_cos, \(\tau _f6\)_exp, and \(\tau _f2\)_exp. The time is tracked by \(\widetilde{\tau _f}\)(t), so \(\widetilde{\tau _f}^{-1}\)(X) corresponds to the time when \(\widetilde{\tau _f}\) equals X hours. f–j Same as in (a)–(e), but for the horizontal-velocity variances

Full size image

The underlying cause of the departure from mixed-layer similarity is the breakdown of the quasi-equilibrium. As discussed in the introduction, the quasi-equilibrium is maintained as long as the adjustment time scale of the largest eddies (i.e. the convective eddy-turnover time scale) is much (e.g., an order of magnitude) smaller than the characteristic time scale of the surface heat flux decay. Motivated by this, we turn to the ratio of the time scale of the surface heat flux decay and the convective eddy-turnover time scale, instead of the time scale of the surface heat flux decay alone. In the following, we again try both \(\tau _f\) and \(\widetilde{\tau }_f\) as candidates for the characteristic time scale of the surface heat flux decay.

Using \(\tau _f\) as the time scale of the surface heat flux decay, we define the parameter r:

$$\begin{aligned} r(t) \equiv \frac{\tau _f}{t_*(t)} \end{aligned}$$
(5)

and use it for characterizing the departure. The parameter r monotonically decreases in time because \(\tau _f\) is constant and \(t_*\) increases (Fig. 5a, b). Considering values of r of 20, 16, 12, 8, and 5, we plot together the velocity variances from different runs, which correspond to different t but the same r. These times are listed in Table 3 for each value of r and for all the runs. Similarly to the analysis with \(\tau _f\) and \(\widetilde{\tau }_f\), the result in Fig. 7 shows an increasing spread among the profiles from different runs as they depart from the self-similar profile. This result suggests that when the time is tracked by the parameter r, the departure from self-similarity is dependent on the shape of the surface heat flux decay.

Table 3 Actual times in [h] corresponding to the decreasing values of r (20, 16, 12, 8, and 5) for all the runs
Full size table

Note that the values of r used in Table 3 are in fact on the order of 10, namely, the convective eddy-turnover time scale remains nearly an order of magnitude smaller than the characteristic time scale of the surface heat flux decay. If \(\tau _f\) was the correct time scale that characterizes the surface heat flux decay, then the quasi-equilibrium conditions would have prevailed for these r values. The fact that the departure from the self-similar profiles is observed as early as \(r = 12\) implies that \(\tau _f\) is not the correct time scale for characterizing the effect of the surface heat flux decay on the departure from self-similarity for the velocity variances.

Fig. 7
figure 7

a–e The departure of the vertical-velocity variance profiles from the mixed-layer similarity profile, in the runs \(\tau _f6\)_cos, \(\tau _f2\)_cos, \(\tau _f6\)_exp, and \(\tau _f2\)_exp. The time is tracked by r(t), so \(r^{-1}\)(X) corresponds to the time when r equals X. f–j Same as in (a)–(e), but for the horizontal-velocity variances

Full size image
Fig. 8
figure 8

a–e The departure of the vertical-velocity variance profiles from the mixed-layer similarity profile, in the runs \(\tau _f6\)_cos, \(\tau _f2\)_cos, \(\tau _f6\)_exp, and \(\tau _f2\)_exp. The time is tracked by \(\widetilde{r}\)(t), so \(\widetilde{r}^{-1}\)(X) corresponds to the time when \(\widetilde{r}\) equals X. f–j Same as in (a)–(e), but for the horizontal-velocity variances

Full size image

Now we substitute the constant forcing time scale \(\tau _f\) by the time dependent forcing time scale \(\widetilde{\tau }_f(t)\) and repeat the analysis with the ratio \(\widetilde{r}\) defined as

$$\begin{aligned} \widetilde{r}(t) \equiv \frac{\widetilde{\tau }_f(t)}{t_*(t)}. \end{aligned}$$
(6)

As \(\widetilde{\tau }_f\) decreases and \(t_*\) increases with time, \(\widetilde{r}\) decreases with time (Fig. 5a, c). Considering values of \(\widetilde{r}\) of 10, 4, 2, 1, and 0.4, we plot in Fig. 8 the velocity variances from different runs, which correspond to different t (listed in Table 4) but the same \(\widetilde{r}\). The results are shown in Fig. 8. There are two important features of this figure that need to be highlighted. First, when \(\widetilde{r}\) is equal to 10 (Fig. 8a,f), no departure from the self-similar profile is observed. This is consistent with the discussion earlier that when the convective eddy-turnover time scale is an order of magnitude smaller than the characteristic time scale of the surface heat flux decay, the quasi-equilibrium assumption is satisfied.

Table 4 Actual times in [h] corresponding to the decreasing values of \(\widetilde{r}\) (10, 4, 2, 1, and 0.4) for all the runs
Full size table

Second, in contrast to the results in Figs. 4, 6, and 7, Fig. 8 shows that the profiles from different runs collapse as they depart from the self-similar profile, meaning that the departure from mixed-layer similarity is independent of the shape of the surface heat flux decay when the time is tracked by the parameter \(\widetilde{r}\). As a consequence of this collapse, we argue that the scales \(z_i(t)\) and \(w_*(t)\) can still be used to describe the velocity-variances profiles during the late afternoon transition, even though mixed-layer similarity and the underlying quasi-equilibrium are no longer valid. The knowledge of \(\widetilde{r}\) is sufficient to predict the velocity variances and evaluate their departure from the quasi-steady state, irrespective of the shape of the surface heat flux decay. For illustration, considering the times when \(\widetilde{r}\) takes the values 2, 1, and 0.4 (these values are also indicated by the horizontal lines in Fig. 5c), the vertical-velocity variance at a height of 0.3 \(z_i\) departs from its self-similar magnitude by 13%, 23%, and 51% respectively.

4 Discussion

4.1 Sensitivity of Our Results to the Grid Spacing and to the Averaging Length

Figure 9 shows results from the simulations carried out with a grid spacing of 25 m (effective grid spacing of \(\approx \) 50 m), in which case the averaging is also done over space, time (1 min), and eight-ensemble runs. Comparing this figure with Fig. 8 where the grid spacing is 12.5 m, we conclude that a grid spacing of 25 m is sufficient to reveal the relevance of the parameter \(\widetilde{r}\) for predicting the departure of the velocity-variances profiles from mixed-layer similarity, regardless of the shape of the surface heat flux decay. Furthermore, comparing Fig. 9 where the span of ensemble averaging extends to eight realizations, with Fig. 10 where only four realizations are used, we conclude that our results will not change if more than eight realizations are used for averaging. Hence, our initial choice of averaging length made up of horizontal averaging, time averaging, and further averaging over eight-ensemble runs, is sufficient for characterizing the departure from mixed-layer similarity.

Fig. 9
figure 9

Same as in Fig. 8, but for the runs with 25-m grid spacing. To further simplify the comparison with Fig. 8, we show the self-similar profiles from the run with 12.5-m grid spacing (dotted lines), and the average (dashed lines) over the four runs with different shapes of H-decay (blue, orange, green, and red lines in Fig. 8)

Full size image
Fig. 10
figure 10

Same as in Fig. 9 except for the span of ensemble averaging, which is limited to four realisations here, instead of eight realisations in Fig. 9. To further simplify the comparison with Fig. 9, we show the average (dashed lines) over the four runs with different shapes of H-decay (blue, orange, green, and red lines in Fig. 9)

Full size image

4.2 Sensitivity of Our Results to the Definition of the CBL Depth

Despite the complexity in defining and estimating the CBL depth from observations and models, it is safe to state that for any of those definitions, the CBL depth characterizes the layer with significant turbulence, as compared with the free atmosphere (e.g. Seibert et al. 2000; Dai et al. 2014). If the quasi-steady fair-weather CBL is capped by an inversion with a well-defined increase of potential temperature, and if the surface heat flux is sufficiently strong to drive energetic thermals extending up to that capping inversion, then the layer of significant turbulence is confined to the height of the capping inversion. For these specific, yet common conditions in the quasi-steady fair-weather CBL, the inversion height can be defined using different criteria, and estimated from data collected with different measurements systems (see the review from Seibert et al. (2000) and references therein, and Bennett et al. (2010)). The resulting relative differences are mostly below 10% (Seibert et al. 2000). For those conditions with weak inversion and/or not well-mixed CBL, the corresponding relative differences might exceed 25% (Seibert et al. 2000).

As the surface buoyancy source fueling the thermals weakens, does the height of significant turbulence still coincides with the capping-inversion height? According to the profiles of the velocity variances shown at different times during the surface heat flux decay (Fig. 11), the answer is yes. Indeed, even at the time \(\tau _f\) when the surface heat flux becomes zero, one can still see in each panel of Fig. 11 that the height level of the capping inversion, \(z_i\), is a reasonable separation between the region of significant turbulence, and the free atmosphere above. This result is in line with the idealized LES studies of Sorbjan (1997) (his Figs. 11 and 12), van Driel and Jonker (2011) (their Fig. 4), and van Heerwaarden and Mellado (2016) (their Fig. 7e, f). The field observational studies of Grimsdell and Angevine (2002) and Lothon et al. (2014) suggest, however, a separation between the top of the layer of significant turbulence and the capping-inversion height.

Fig. 11
figure 11

a–d Profiles of the vertical-velocity variance in the runs \(\tau _f6\)_cos, \(\tau _f2\)_cos, \(\tau _f6\)_exp, and \(\tau _f2\)_exp, at the times 0.2\(\tau _f\), 0.4\(\tau _f\), 0.6\(\tau _f\), 0.8\(\tau _f\), and \(\tau _f\). e–h Same as in (a)–(d), but for the horizontal-velocity variance

Full size image
Fig. 12
figure 12

The departure of the vertical-velocity variance profiles from the mixed-layer similarity profile, in the runs \(\tau _f6\)_cos, \(\tau _f2\)_cos, \(\tau _f6\)_exp, and \(\tau _f2\)_exp. The time is tracked by \(\widetilde{r}\)(t), so \(\widetilde{r}^{-1}\)(X) corresponds to the time when \(\widetilde{r}\) equals X. In (a)–(e), the CBL-depth is defined as the height of the capping inversion (\(z_i\)), while in (f)–(j), the CBL-depth is defined as the height of the minimum heat flux (\(z_i'\))

Full size image
Fig. 13
figure 13

Same as in Fig. 12, but for values of \(\widetilde{r}\) of 0.6, 0.5, 0.4, 0.3, and 0.2

Full size image
Fig. 14
figure 14

Time series of the CBL-depth defined as the height of the capping inversion (\(z_i\)) (a), or the height of the minimum heat flux (\(z_i'\)) (b). c–d Close-up view on the latest times. The crosses indicates the times corresponding to Fig. 13

Full size image

Even though the definition of the CBL depth as the height where the heat flux reaches its minimum value (\(z_i'\)) is not practical for the observed CBL (LeMone et al. 2019), idealized LES studies of the quasi-steady CBL often use this definition for the CBL depth (e.g. Nieuwstadt et al. 1993; Conzemius and Fedorovich 2006; Salesky et al. 2017). Hence, we examine the sensitivity of our results if this CBL-depth definition is considered instead of the height of the capping inversion. The collapse of the profiles in Figs. 12 and 13 shows that the use of \(z_i\) gives better results than \(z_i'\) at the late times. The reason for that might go back to the differences in the qualitative time-variability observed in Fig. 14a, b. Consistent with the previous LES study of Sullivan et al. (1998), \(z_i'(t)\) has more short time fluctuations than \(z_i(t)\) (Fig. 14a, b). Furthermore, the amplitude of these fluctuations seems to increase during late times as compared to early times (Fig. 14c, d), which might explain the deviations observed in the profiles collapse depending on the CBL-depth definition. The increasing amplitude of \(z_i'\)-fluctuations during late times might be due to a change in the vertical scale of the thermals. Indeed, during the early afternoon when the surface heat flux is large, most of the largest thermals originating at the surface have sufficient buoyancy to reach the interfacial layer and induce entrainment. Hence a relatively well defined minimum negative heat flux, and relatively small amplitudes of variation in \(z_i'\). However, during the late afternoon when the surface heat flux is small and varying substantially, only a few thermals originating at the surface might reach the interface, so the minimum heat flux is less well defined in this case.

5 Conclusion

Motivated by the importance of mixed-layer similarity for evaluating the turbulence strength in the free-convective boundary layer, we aim to characterize the departure from this similarity framework during the afternoon decay of turbulence, and investigate the departure’s dependence on the shape of the surface heat flux decay in the absence of geostrophic wind.

We run LES experiments with prescribed sinusoidal and exponential surface heat flux decay, with two values of \(\tau _f\), 6 and 2 h. \(\tau _f\) equals the duration between the maximum and the zero surface heat flux, it is a constant characteristic time scale of the decaying forcing surface heat flux (Sorbjan 1997). An additional run with prescribed constant surface heat flux is performed in order to retrieve the mixed-layer similarity profiles of the vertical and horizontal velocity variances. These self-similar profiles describe the reference quasi-steady state. The departure from mixed-layer similarity occurs as the normalized profiles with the actual mixed-layer scales, \(z_i(t)\) and \(w_*(t)\), gradually depart from the self-similar profiles.

The dimensional time when the departure gradually occurs changes from one run to another, because the shape of the forcing surface heat flux changes. One might then reasonably anticipate that if the departure is described within a frame where the timeline is tracked by some time scale controlling the surface heat flux changes, then the departure would no longer be dependent on the characteristics of the surface heat flux decay. For that purpose, we successively use the constant forcing time scale \(\tau _f\), and the time-dependent forcing time scale \(\widetilde{\tau }_f(t)\equiv \left| \frac{1}{H}\frac{dH}{dt}\right| ^{-1}\) (Wyngaard 1973). Within these descriptive frameworks, the velocity-variances profiles from different runs do not collapse as they depart from the self-similar profile, indicating that the departure from mixed-layer similarity is dependent on the particularities of the decaying surface heat flux.

Recalling that, the quasi-equilibrium assumption (or quasi-steady state) underlying the mixed-layer similarity requires the adjustment time scale of the largest eddies (i.e. the convective eddy-turnover time scale, \(t_*(t)\)) being much smaller than the characteristic time scale of the surface heat flux decay, we consider the ratio of both these characteristic time scales, instead of the forcing time scale alone, in order to characterize the departure. As the ratios \(r(t)\equiv \frac{\tau _f}{t_*(t)}\) and \(\widetilde{r}(t)\equiv \frac{\widetilde{\tau }_f(t)}{t_*(t)}\) monotonically decrease in time, they both can be used for tracking the time and characterizing the departure. While the profiles from different runs depart from the self-similar profiles, we find them to collapse, only in the descriptive frame where the parameter \(\widetilde{r}(t)\) is used for tracking the time, supporting the independence of the shape of the surface heat flux decay.

This result emphasizes the importance of considering both, the time-dependent characteristic time scale describing the changes in the surface heat flux decay, and the time dependent convective eddy-turnover time scale, in order to systematically describe the departure from mixed-layer similarity independently from the particularities of the surface heat flux decay. Furthermore, this result suggests that with the knowledge of \(\widetilde{r}(t)\), the scales \(z_i(t)\) and \(w_*(t)\) might still be used to describe the magnitude of the velocity-variances even after the breakdown of the quasi-equilibrium, irrespective of the shape of the surface heat flux decay.

This work is limited by the assumption of zero geostrophic wind. Beside the time scale describing the variability of the surface heat flux, the often observed time variability of the background wind during the afternoon transition of the CBL introduces an additional time scale describing the variability of the mechanical forcing. We address this added complexity in a future work. This study also prompts a follow-up study for confronting our model results to field observations.