Abstract
The heterogenous structure of urban environments impacts interactions with radiation, and the intensity of urban–atmosphere exchanges. Numerical weather prediction (NWP) often characterizes the urban structure with an infinite street canyon, which does not capture the three-dimensional urban morphology realistically. Here, the SPARTACUS (Speedy Algorithm for Radiative Transfer through Cloud Sides) approach to urban radiation (SPARTACUS-Urban), a multi-layer radiative transfer model designed to capture three-dimensional urban geometry for NWP, is evaluated with respect to the explicit Discrete Anisotropic Radiative Transfer (DART) model. Vertical profiles of shortwave fluxes and absorptions are evaluated across domains spanning regular arrays of cubes, to real cities (London and Indianapolis). The SPARTACUS-Urban model agrees well with the DART model (normalized bias and mean absolute errors < 5.5%) when its building distribution assumptions are fulfilled (i.e., buildings randomly distributed in the horizontal). For realistic geometry, including real-world building distributions and pitched roofs, SPARTACUS-Urban underestimates the effective albedo (< 6%) and ground absorption (< 16%), and overestimates wall-plus-roof absorption (< 15%), with errors increasing with solar zenith angle. Replacing the single-exponential fit of the distribution of building separations with a two-exponential function improves flux predictions for real-world geometry by up to half. Overall, SPARTACUS-Urban predicts shortwave fluxes accurately for a range of geometries (cf. DART). Comparison with the commonly used single-layer infinite street canyon approach finds SPARTACUS-Urban has an improved performance for randomly distributed and real-world geometries. This suggests using SPARTACUS-Urban would benefit weather and climate models with multi-layer urban energy balance models, as it allows more realistic urban form and vertically resolved absorption rates, without large increases in computational cost or data inputs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Given their high concentrations of both people and infrastructure, cities are places of high vulnerability to variations in weather, climate, and air quality (Baklanov et al. 2018). Currently, limited-area numerical-weather-prediction (NWP) models have spatial resolutions such that cities span multiple model grid boxes (e.g., Hagelin et al. (2017)). In addition, global NWP models generally have poor representation of urban structure and energy exchanges, for example the European Centre for Medium-Range Weather Forecasts IFS (Integrated Forecasting System) model with 9–18 km resolution, with no urban model (Hogan et al. 2017). As NWP spatial resolution increases, smaller-scale processes will need to be resolved. Alongside this, global population and urban land cover are expected to increase, bringing about a need for greater understanding of energy exchanges between the surface and the atmosphere (Loridan and Grimmond 2012).
Cities have complex three-dimensional structures, with varying building heights, densities, materials, arrangements, shapes, and surroundings. These affect the radiative exchanges and heat storage within the urban surface (Grimmond et al. 2010; Yang and Li 2015; Ao et al. 2016), e.g., altering the effective shortwave albedo due to multiple reflections in the street canyon (Aida and Gotoh 1982). Given that shortwave radiation is the most important contribution to the surface energy balance, it is vital to understand how it is absorbed within urban areas (Fortuniak 2008).
Models have been developed to account for the three-dimensional nature of urban surfaces. A common approach is to simplify the urban form as a canyon of infinite length between buildings that are of equal height with a fixed height-to-width (H/W) ratio (Nunez and Oke 1977). This urban-canyon approach is fast enough for NWP, and has been applied to urban radiation specifically (e.g., Aida 1982; Arnfield 1982a, 1988; Harman et al. 2004) and other energy balance fluxes (e.g., Masson 2000; Kusaka et al. 2001a; Lee and Park 2008). This approach subdivides the canyon into three facets: walls, roof, and ground. Advancements of this approach include models subdividing facets further into sunlit and shaded, with varying canyon orientation (e.g., Oleson et al. 2008a, b), accounting for different building heights (Martilli et al. 2002), and the interactions between neighbouring canyons (Schubert et al. 2012). Some models have added vegetation, both at ground level and in the vertical plane (e.g., street trees) (Lemonsu et al. 2012; Krayenhoff et al. 2014; Redon et al. 2017).
These improvements in the vertical structure of urban form have led to improvements in the prediction of shortwave fluxes onto roofs (Schubert et al. 2012). Despite this, many models still make the unrealistic assumption of an infinitely long urban canyon. This leads to models neglecting key features of the urban form, such as intersections, building height variations, courtyards, and clusters of buildings. Ignoring these features impacts building shadowing, radiation trapping between buildings, and increased penetration of shortwave radiation to the surface in open areas such as parking areas, hence impacting the overall energy balance.
Building-resolving models, with details of each individual building and facet, are suitable for microscale research applications but not NWP, given their high data and computational demands (e.g., Krayenhoff and Voogt 2007; Krayenhoff et al. 2015; Resler et al. 2017). These models simulate radiative interactions between individual buildings, requiring detailed three-dimensional (3D) geometry and material data, which are hard to obtain for large areas (Ghandehari et al. 2018; Masson et al. 2020). Gastellu-Etchegorry et al. (2012) suggested a key application for complex building-resolving models is both to calibrate and evaluate simpler radiative transfer models (e.g., suitable for NWP). However, very few urban radiative transfer models have been evaluated against these models. One exception is the evaluation of shortwave radiation in the Town Energy Balance (TEB) model against the SOLENE explicit radiative transfer model, considering vertical vegetation (Redon et al. 2017), although an infinite street canyon is used in both the TEB and SOLENE models. Other urban radiative transfer models suitable for NWP could (or should) be calibrated and/or evaluated using explicit 3D models.
Here, we evaluate the shortwave performance of the SPARTACUS (Speedy Algorithm for Radiative Transfer through Cloud Sides) radiative transfer model for urban areas, SPARTACUS-Urban (Hogan 2019a), with respect to the more detailed explicit 3D Discrete Anisotropic Radiative Transfer (DART) model (Gastellu-Etchegorry 2008). The SPARTACUS-Urban model resolves the vertical structure of the urban canopy and exploits the recent finding that wall-to-wall separation distances in an urban area fit an exponential distribution well (Hogan 2019b). It can account for atmospheric absorption, emission, and scattering in the urban environment, rather than assuming a vacuum, as is done by most urban radiation models (e.g., Masson 2000; Harman et al. 2004), while being fast enough for use in NWP. Although it can represent vertical profiles of vegetation, this capability is not evaluated here. We examine SPARTACUS-Urban’s ability to predict the vertical profile of the clear-air downwelling and upwelling fluxes, and the absorption into walls and roofs, across a range of urban forms: from simple cuboid ‘buildings’ to highly realistic structures.
The methods include a description of the SPARTACUS-Urban (Sect. 2) and DART (Sect. 3) models, and of the evaluation techniques (Sect. 4). After an investigation of the underpinning assumptions that SPARTACUS-Urban makes about the urban form (Sect. 5), the results of the evaluation are presented (Sect. 6). Finally, a comparison of SPARTACUS-Urban with DART is made with respect to the Harman et al. (2004) method for radiation within an urban street canyon (Sect. 7).
2 Description of the SPARTACUS-Urban Model
The SPARTACUS-Urban model (Hogan 2019a) uses an approach that originates from the SPARTACUS model for simulating 3D radiative transfer in complex cloud fields (Hogan and Shonk 2013; Hogan et al. 2016) and SPARTACUS-Vegetation for 3D interaction of radiation in forest-type vegetation (Hogan et al. 2018). These algorithms share a common mathematical approach for treating radiative transfer in the presence of objects that are randomly distributed in the horizontal. The SPARTACUS-Surface open-source software package (Hogan 2021) combines the capabilities of SPARTACUS-Urban and SPARTACUS-Vegetation, but since vegetation is not considered here we refer to the algorithm as SPARTACUS-Urban.
The SPARTACUS-Urban model is underpinned by the one-dimensional discrete ordinate method (Stamnes et al. 1988), which assumes that diffuse radiation travels in 2N streams of different elevations, with N streams per hemisphere. As N increases, the radiation field is described more accurately, but with increased computational cost. Here 16 streams (N = 8) are used. The SPARTACUS-Urban model splits a scene (defined here as any combination of building geometry, solar zenith angle, and albedo) vertically by height, z, into n horizontal layers above an assumed flat ground level. Each layer is split horizontally into ‘regions’ of clear sky, vegetation, or buildings. As with other urban models, SPARTACUS-Urban computes the interaction of radiation with three urban facets (wall, roof, ground) and optionally vegetation.
Through the process of this work, we have found that two modifications to SPARTACUS-Urban are needed. Section 2.1 describes how to treat the more common occurrence of large open spaces such as parking areas and parks than predicted by the exponential model of urban geometry used by SPARTACUS-Urban. Section 2.2 describes a correction to account for fine structure in the building perimeters.
2.1 Modification to Treat Non-Exponential Building Separations
To characterize urban geometry, SPARTACUS-Urban takes building plan area fraction (λp) and the normalized building perimeter length (L) as a function of z for the city area of interest (hereafter “domain”). Thus, L(z) is the total building perimeter normalized by the horizontal area of the domain (units m−1). The SPARTACUS-Urban model discretizes the vertical profile into n layers where layer i has thickness Δzi and normalized perimeter length Li. Following this, the normalized wall area (AW) is
which is proportional to the frontal area index (λf) or projected wall area for a particular azimuthal direction (Raupach and Shaw 1982; Grimmond and Oke 1999; Sützl et al. 2020). The SPARTACUS-Urban model assumes that walls face in all azimuthal directions with equal probability.
Based on analysis of the geometry in real cities (Hogan 2019b), SPARTACUS-Urban assumes that the probability distribution of wall-to-wall horizontal separation distances, pww(x), and the distribution of ground-to-wall separations, pgw(x), each follow an exponential distribution:
where x is the horizontal wall-to-wall distance in any azimuthal direction, and X is the mean wall-to-wall distance, or ‘e-folding’ distance (Hogan 2019a, b). This exponential distribution allows the direct and diffuse streams of radiation to be attenuated according to the Beer–Lambert law (Hogan 2019a).
The assumption that buildings are randomly distributed horizontally has two other important consequences. First, the horizontal distribution of radiation between buildings (or vegetation, if included) need not be explicitly simulated; rather the horizontal-mean radiation field in each direction is computed as a function of height alone. Second, at a given height, the rate of interception of radiation by buildings is proportional the total building perimeter. However, in real cities Eq. 2 tends to underpredict the frequency of large building separations such as parks, parking-areas, and plazas (e.g., Fig. 6, Hogan (2019b)). Hence, the penetration of direct shortwave radiation to street level tends to be underpredicted when the sun is low in the sky, leading to an overprediction in absorption of shortwave radiation by walls. To address this, we replace Eq. 2 with the sum of two exponentials, with a weighting between them (Gww):
where X1 and X2 are the e-folding distance of each exponential. The weighting function (Eq. 3) better predicts the frequency of large building separations by up to three times that of Eq. 2, in theory improving the prediction of radiative fluxes. Applying Eq. 1 of Hogan (2019b) leads to an equation for pgw(x) with both the same form as Eq. 3 and the same X1 and X2 values, but a different weighting coefficient Ggw
To use the two-exponential model within SPARTACUS-Urban, we modify L(z) so that it varies with θ0, where θk is the zenith angle of a stream k, where k = 0 indicates the solar zenith angle, defining an effective normalized perimeter length, \(\hat{L}\), given by
This is identical to Eq. 8 of Hogan (2019b) except for the use of an effective e-folding building separation (\(\hat{X})\) in place of the e-folding building separation used to characterize the horizontal distribution of urban geometry. To derive an analytical relation between \(\hat{L}\) and the two-exponential fit coefficients (Ggw, X1 and X2), we assume that if all buildings had the same height, H, the fraction of direct solar radiation penetrating to street level (F0g) can be predicted exactly using Eq. 3 of Hogan (2019b)
where x0 = H tan θ0. As buildings are typically not all the same height, we use the mean building height (\(\overline{H})\). Substituting our Eq. 3 (but for pgw) in Eq. 6 gives
However, as SPARTACUS-Urban follows an exponential building distribution (Eq. 2) we apply Eq. 6, leading to
This is equal to Eq. 20 of Hogan (2019b), but using the effective e-folding building separation, \(\hat{X}\). Combining this with Eq. 5 gives
where \(\hat{L}\) 0 is \(\hat{L}\) at the surface. This can be applied to any city with building footprint data, but probability distributions can only be computed using the Hogan (2019b) method near the surface for building densities, λp > 0.01. Using \(\hat{L}\) 0 we scale L(z) at each height using the building cover fraction at that height
This leads to the scaling factor to L(z) (Eq. 10) having a greater impact near the surface where λp is larger, and a reduced impact as buildings thin out towards the top of any urban canopy, where \(\hat{L}\) tends toward L. The appropriateness of the single- and two-exponential methods in describing urban environments is discussed in Sect. 5, and their use in calculating fluxes is assessed in Sect. 6.3.
2.2 Modification to Treat Building Concavity
From SPARTACUS-Urban’s use of L to describe the rate of interception of radiation by building walls, it follows that the width of the shadow cast by any building (WS), averaged over all azimuthal illumination directions, is assumed to be equal to \(P/\pi\) where P is the building’s perimeter length. This is true for convex shapes such as cylinders and cuboids, but not for many real-world buildings, which have fine structure in their perimeters, and so the shadows cast in SPARTACUS-Urban tend to be wider than reality. We therefore define the “concavity parameter” C as the ratio of the true perimeter length to the perimeter length of the equivalent convex hull, which for an individual building is given by
Values of C are found to be 1 or greater, and to vary with height (Appendix 1, Fig. 12 and Online Resource 7). The effective concavity parameter of all the buildings at a particular height can be calculated by replacing the numerator and denominator of Eq. 11 each by the average over all buildings. In this work, the median of C at all heights above \(\overline{H}\) for each domain is used as a scaling factor to L(z) at all heights (i.e., \(L\left( z \right)/C\)).
3 Description of the Discrete Anisotropic Radiative Transfer Model
The three-dimensional DART model (Gastellu-Etchegorry et al. 2015; Landier et al. 2018) simulates radiation propagation for heterogenous scenes that can include vegetation, buildings, a within-canopy atmosphere, and variations in ground height (i.e., topography). The latter can be imported using 3D vector models. The DART model has been evaluated using observations and other 3D radiative transfer models for vegetation (Sobrino et al. 2011; Widlowski et al. 2015), and has been applied in urban areas (e.g., Landier et al. 2018; Chrysoulakis et al. 2018; Morrison et al. 2020a).
Radiative fluxes are calculated iteratively, with radiation tracked and emitted along a number of discrete directions within angular cones (Gastellu-Etchegorry et al. 2015) using a 3D array of voxels to facilitate radiation tracking. Radiation interacts with the scene elements in each voxel. Per-voxel scattered, absorbed, emitted, upwelling and downwelling radiative fluxes are updated after each iteration, with upwelling and downwelling fluxes for each voxel stored in the top face of each voxel. Here, we use DART’s ability to calculate the radiative budget to assess the SPARTACUS-Urban emission and absorption of shortwave radiation.
4 Evaluation Methods
4.1 Model Domains
Four types of urban form (F) (Table 1) are used in the evaluation, from simplest to most complex:
-
(1)
Regular array of cubes that repeat on a regular grid (FREG1 and FREG2, Table 1). Cubes are often used to approximate urban processes (e.g., Aida 1982; Kondo et al. 2005; Kanda et al. 2005; Kanda 2007; Morrison et al. 2018) as they create a regular grid street pattern that occurs in many cities in the U.S. and China (Figueiredo and Amorim 2007; Han et al. 2020).
-
(2)
Random cuboids (FRAND) where building centroids are randomly located within a domain with random building heights, widths, and orientations. Twelve domains are used, but four are focussed on, with building fraction at the surface (λp,0) and \(\overline{H }\) values spanning those found in areas of real cities (FRAND1–FRAND4, Table 1) based on prior studies (Loridan and Grimmond 2012). This form type tests situations where the SPARTACUS-Urban building layout assumptions are met. These might be more typical of European cities, where street orientation is more random.
-
(3)
Low level-of-detail (LOD) real-world geometry using building footprint data, with one height per building creating flat roofs and walls that do not taper, and flat ground (Fig. 1a, d). Building footprints used are for part of central London (FLon,L, Table 1).
-
(4)
High LOD real-world geometry where heights can vary across a building (Fig. 1b, e). Parts of two cities are analyzed: a dense European megacity London (FLon,H)—and an open low-density U.S. grid-city—Indianapolis (FInd,H).
Real-world domains in parts of (a, b, d–e) London, and (c, f) Indianapolis; for the following LOD: (a, d) low, and (b, c, e, f) high; with building height for (a–c) SPARTACUS-Urban—rasterized building footprints, (d–f) DART- 3D building model. Data sources are given in Table 1
The three real-world domains (i.e., 3 and 4) are 2000 × 2000 m2, to sample a wide range of streets with different widths, orientation, intersections, parking areas, plazas, and parks.
The DART model uses vector 3D building models to describe the urban form. For the low LOD, a raster digital surface model (DSM) and digital elevation model (DEM) are used to determine the building roof and ground level from the “Virtual London” building footprint dataset (Evans et al. 2006), using the 25th percentile of the DEM height, and the 75th percentile of the DSM height. Each building is assigned one height value from these building footprints. The 3D building models in the high LOD domains are created using the Morrison et al. (2020a, b) method from Google Earth imagery (Google Inc. 2019) and building footprints (Evans et al. 2006; Heris et al. 2020).
For SPARTACUS-Urban, profiles of λp and L are calculated from rasterized (1 m resolution) building heights derived from the 3D building models. As SPARTACUS-Urban assumes no topographic variation within an individual NWP grid cell (i.e., flat), the DART 3D array of voxels is re-gridded to give heights relative to local ground level for high LOD scenes (Morrison and Benjamin 2021). To balance computational time and simulation resolution, the DART voxel resolution used is 1 m vertically and 15 m horizontally for both the real-world and FRAND scenes. For FREG, a vertical resolution of 0.5 m is used. In all scenes, SPARTACUS-Urban uses the same vertical resolution as DART.
As the real-world 3D building models are found to not conserve energy in DART, primarily because of periodic boundary conditions, the energy loss (always < 2%) needs to be redistributed. The rationale and method are explained in Appendix 2.
Fluxes from the DART model for FREG (Table 1) scenes are offset by the voxel vertical resolution, as DART provides the fluxes at the ‘top face’ of each voxel and all roofs are at 5 m, so at the top of a voxel. As SPARTACUS-Urban outputs wall absorption profiles between height intervals, DART wall absorption for FREG scenes is offset by 0.25 m. All data used and code are archived at https://zenodo.org/10.5281/zenodo.5145851.
4.2 Sun Angles and Albedos
Both the DART and SPARTACUS-Urban models require solar zenith angle, θ0, to be provided for a simulation. For computational simplicity we use three: directly overhead (0°, although unrealistic when out of the tropics), 45°, and low-sun conditions (75°). Incoming radiation at the top of the canopy is assumed to be directly from the sun; diffuse incoming radiation is set to zero. Similarly, a material albedo (α) is needed. We use two values: low (0.1) as observed in dense urban areas (e.g., 0.11, Kotthaus and Grimmond 2014) and high (0.5) as typical of ‘cool’ materials (e.g., Santamouris 2014; Santamouris et al. 2018; Jandaghian and Akbari 2018).
As SPARTACUS-Urban assumes that the azimuthal orientation of buildings is random, solar azimuth angle (Ω) is not specified by the model, whereas for DART the value of Ω is specified. Thus, DART has varying shadow patterns with Ω used. The DART simulations use four values for the simpler FRAND and FREG cases, and eight (at 45° intervals) for the real-world cases. The final DART fluxes for comparison use the mean across all Ω intervals.
4.3 Evaluation Statistics
To quantify SPARTACUS-Urban performance, we compare SPARTACUS-Urban and DART profiles of: mean shortwave upwelling (SW↑) and downwelling clear-air (SW↓) fluxes, and mean wall (aWall) and roof shortwave absorption (aRoof). The fluxes have units of watts per square metre (W m−2) of the entire horizontal scene (rather than per square metre of the clear-air region excluding buildings), while the absorptions have units of W m−3, since we divide the absorption in a layer by the layer thickness to obtain a resolution-independent quantity. Thus, the vertical integral of aWall and aRoof provide the total wall and roof absorptions (again per unit area of the entire horizontal scene). Unlike the vertical walls assumed by SPARTACUS-Urban for all domains, for the high LOD geometry in DART there is no simple way to distinguish or define roofs and walls. Hence, we combine the wall and roof absorption (aWall+Roof) for the evaluation of the high LOD scenes. All fluxes and absorptions are normalized by the bottom of atmosphere (BOA) shortwave flux (SW↓,BOA). This is defined as the incoming shortwave flux across a horizontal plane above the tallest roughness elements in a scene (Gastellu-Etchegorry et al. 2015; Wang et al. 2020).
Profiles of aWall and aRoof are compared using the normalized mean-absolute error (nMAE) and normalized mean-bias error (nMBE) expressed as a percentage of the mean DART absorption
where aSU and aDART are the flux at each height from SPARTACUS-Urban or DART, respectively. The metrics nMAE and nMBE are calculated at scene resolution (e.g., 1 m) vertically from 1 m to the maximum height in DART (Hmax). The SW↑ flux profiles are evaluated using the normalized bias error at a specified height (nBE), expressed as a percentage of the DART flux:
The scene albedo is evaluated using SW↑ at the top of the canopy (Hmax in DART). We also use the metric nBE to evaluate the total ground absorption (aGround).
5 Test of the SPARTACUS-Urban Geometry Assumptions
We examine the underpinning SPARTACUS-Urban assumption—that urban buildings are randomly distributed, or equivalently their horizontal separations follow an exponential distribution (Eq. 2)—by analyzing probability distributions from real cities and domains containing randomly placed cuboids (Table 1).
For the high density FRAND3 domain, the ‘true’ probability density of wall-to-wall (pww) and ground-to-wall (pgw) separations (Fig. 2) are calculated following Hogan (2019b) with 1 × 1 m2 resolution building rasters, analyzed in four azimuthal directions 45° apart. Both the pww and pgw distributions fit a single-exponential well (Fig. 2b, c) for separations up to 200 m, indicating FRAND3 satisfies SPARTACUS-Urban’s assumption of randomly distributed buildings. This behaviour is seen for all FRAND domains. Here we use Eq. 2, where X is obtained from Eq. 5 with the surface value of L (denoted L0).
Randomly placed cuboid buildings (FRAND3, Table 1) within a 2 × 2 km2 domain with a plan area fraction at the surface, (λp,0) of 0.5 and a mean height (\(\overline{H }\)) of 7 m: a Plan view, randomly placed cuboid buildings and probability density with a single-exponential (Eq. 2) fits to the b wall-to-wall and c ground-to-wall probability distributions
Figures 3 and 4 present similar analyses for London and Indianapolis respectively, although here eight azimuthal directions are used to determine pgw and pww, but offset by 22.5° to not align with major streets orientations (e.g., north–south or east–west in Indianapolis, Fig. 1c). Comparison of the calculated probability distribution to both the single- and two-exponential fits for central London indicates that the latter is a better fit for FLon,L (Fig. 3) and FLon,H (Online Resource 1). For FLon,L, the single-exponential fit diverges from the pww distribution at approximately 200 m and from the pgw distribution at approximately 100 m (Fig. 3b, c), whereas for FInd,H (Fig. 4) the single-exponential fits diverge at slightly greater distances (these numbers increasing to around 300 and 200 m, respectively). By contrast, the two-exponential (Eq. 3) predicts the larger building-separations much better than the single-exponential in both cities.
For a 2 × 2 km2 area of central London at low LOD (FLon,L): a wall-to-wall and b ground-to-wall probability distribution, with single- (Eq. 2, blue) and two-exponential fit (Eq. 3 where X1 = 21.6 m, X2 = 57.4 m and Ggw = 0.534, red), and c corresponding effective normalized perimeter length at the surface as a function of solar zenith angle, \({\hat{L}_{0}}\)(θ0), as predicted by Eq. 9 when applied to the actual data (black) and fitted (red) ground-to-wall probability distributions, and the true perimeter length at the surface (blue)
As Fig. 3, but for Indianapolis at high LOD (FInd,H)
For FLon,L the effective normalized building perimeter length, \({\widehat{L}}_{0}\), decreases when θ0 > 30° (black line Fig. 3c). This is computed using Eq. 5 with the true ground-to-wall probability distribution (i.e., Fig. 3b), the mean building height (\(\overline{H }\) = 25.5 m), and F0g (Eq. 6). This shows that more direct solar radiation reaches the surface when the sun is low in the sky (i.e., less chance of wall interception) compared to purely randomly distributed buildings. Using the actual normalized perimeter of 0.055 m−1 (blue, Fig. 3c), equivalent to the single-exponential assumption, would be expected to lead to an overpredicted interception of direct solar radiation by walls for larger θ0. The \(\widehat{L}\) value obtained from Eq. 9 with the two-exponential method agrees well with \(\widehat{L}\) obtained using the true probability (Fig. 3c), and the same behaviour is seen for Indianapolis (Fig. 4c) (\(\overline{H }\) = 17.9 m). Thus, we expect that the two-exponential fit should improve SPARTACUS-Urban simulations for real-world cities. This is tested in Sect. 6.
6 Evaluation of SPARTACUS-Urban Shortwave Fluxes
6.1 Regular Cubes
Comparison of shortwave radiative flux profiles simulated with DART and SPARTACUS-Urban (single-exponential, Eq. 2) in a low-density regular array of cubes (FREG1) shows that SW↓ decreases closer to the surface when the zenith angle θ0 = 75° (Fig. 5) because more radiation is intercepted by buildings. Hence, less shortwave radiation penetrates to ground level. For all θ0 values, the roof absorption, aRoof, remains constant, with nMAE = 0 (i.e., machine precision). As the buildings are all the same height, aRoof can be computed exactly from the building fraction and albedo. Maximum values of aWall increase with θ0 (Fig. 5c, g, k), with aWall increasing with height due to building shadowing at the surface (as θ0 increases). Azimuth angle (Ω) variations change shadow patterns and alter the wall area exposed to shortwave radiation. Hence, the aWall vertical profiles differ between DART and SPARTACUS-Urban. The DART model’s fluxes are averaged across four Ω values (Sect. 4.2). The SPARTACUS-Urban model’s aWall profiles are within the DART range arising from Ω (Fig. 5c, g, k shading) when θ0 = 0° and 45°, but not when θ0 = 75° and α = 0.1 near the surface (approximately 1 m). Errors in aWall are lowest when θ0 = 45° (nMAE between 9.9 and 17%, nMBE between −7.5 and 1.8%). For the scene albedo the nBE are < 1.2%, with values highest if the sun is overhead (θ0 = 0°). When α = 0.1, nBE in SW↑ and SW↓ increase, but are still < 2% (Online Resource 2). These results are better than expected, given the grid arrangement of the buildings do not have an exponential distribution of building separations (i.e. as SPARTACUS-Urban assumes, Sect. 2.1).
Fluxes for a regular repeated array of 5 × 5 × 5 m3 cubes (FREG1, Table 1) normalized by the BOA flux (SW↓,BOA) with height, simulated with SPARTACUS-Urban (orange) and DART (blue), for two albedos (α: 0.1, 0.5) and three solar zenith angles (θ0: 0°, 45°, 75°): (a, e, i) downwelling clear air flux (SW↓), (b, f, j) upwelling clear air flux (SW↑), (c, g, k) wall absorption (aWall), (d, h, l) roof absorption (aRoof) with solar azimuth angle (Ω) dependence in DART (shading)
The larger plan area index of FREG2 (Table 1) causes SW↓ to decrease more as height decreases (for high θ0) (Fig. 6a, e, i). The form FREG2 also increases mutual building shadowing, reducing the shortwave radiation penetrating to the surface. With less shortwave radiation escaping, the scene albedo decreases with increasing θ0. The metric nBE is larger (up to 10%, Table 2b) cf. FREG1. Maximum values of aWall increase as θ0 increases (Fig. 6c, g, k). However, aWall decreases more rapidly as height decreases than in FREG1, due to the increased shadowing from the buildings/cubes. The value of nMAE is larger (cf. FREG1) for aWall (up to 35%, Table 2b). The peak in aRoof remains at 5 m, as all buildings are of equal height. The SPARTACUS-Urban model generally overpredicts the SW↑ and SW↓ profiles, and underestimates aWall at the top of the canopy (Fig. 6) in FREG2. Similarly to FREG1, when α = 0.1 nMAE in aWall can be up to 35% when θ0 > 45° (Online Resource 2).
As Fig. 5, but for FREG2
6.2 Random Cubes
Four FRAND domains (FRAND1 to FRAND4) are intended to test SPARTACUS-Urban performance across the λp,0 and \(\overline{H }\) extreme combinations, with more results for eight other FRAND domains given in Online Resource 3. All FRAND simulations use the single-exponential model (Eq. 2), as it fits the building distribution data well (Fig. 2).
Figure 7 shows the agreement between DART and SPARTACUS-Urban for each θ0 and α for profiles of aWall, aRoof, and SW↓ for FRAND3. Overall, for FRAND1–FRAND4, the nBE and nMAE are less than 6% for all quantities (Table 3), as SPARTACUS-Urban’s urban form assumptions (Sect. 5) are fulfilled. The SPARTACUS-Urban model agrees better with DART when λp,0 and \(\overline{H }\) are small, as buildings are further apart so there is less within-canyon scattering and building shadowing. The largest differences between DART and SPARTACUS-Urban are seen for aWall between 1 and 5 m for θ0 = 45°, 75°. The SPARTACUS-Urban model underestimates SW↑ for θ0 = 0° and 45°. In FRAND1-2, when λp,0 = 0.05, nBE < 0.7% compared to nBE = 3.4–5.0% when λp,0 = 0.5 (FRAND3-4). When λp,0 = 0.05, nMAE < 1%, except for aWall in FRAND1, where nMAE = 2.1%. Although performance becomes poorer as λp,0 increases, FRAND3-4 errors do not exceed 5.5% when θ0 = 75° and α = 0.5. The differences in nBE and nMAE magnitudes are larger with an increase in λp,0 (FRAND1–FRAND3), compared with an increase in \(\overline{H }\) (FRAND1–FRAND2). This is also seen in the additional scenes in Online Resource 3.
As Fig. 5, but for FRAND3
6.3 Real-World Geometry
For the real-world urban form in SPARTACUS-Urban, both the single- (Eq. 2) and two-exponential (Eq. 3) fits are used, allowing assessment of the impact of the building layout assumptions on shortwave radiative fluxes. Although errors are discussed here, the range of C values in real-world cities (Appendix 1) means that the SPARTACUS-Urban flux calculations could be adjusted based on the exact value of C used.
Building height distribution profiles have spikier patterns for FLon,L than FLon,H (blue and orange, Online Resource 4c), with the largest differences between 25 and 50 m. These spikes occur because individual buildings in the FLon,L domain each have only one height, and are aggregated per 1 m interval. Despite this, the vertical profiles of aRoof in SPARTACUS-Urban and DART are still close (Fig. 8d, h, l).
As Fig. 5, but for London with low LOD (FLon, L) and SPARTACUS-Urban using single- (dashed) and two-exponential (solid) fits
The SPARTACUS-Urban model has good agreement to DART for FLon,L vertical flux profiles (Fig. 8), although the agreement is generally poorer with increasing θ0. The SPARTACUS-Urban model always underestimates SW↑, with nBE values within 7% of DART (Table 4a). In the SPARTACUS-Urban model, aGround is overestimated but with nBE < 6%. The SPARTACUS-Urban model is generally in better agreement to the DART model for both SW↑ and aGround when using the two-exponential method. This is most evident as θ0 increases. Neither nMAE nor nMBE exceed 7.3% for aWall. Generally, the SPARTACUS-Urban model underestimates aRoof, with nMAE < 12%, and nMBE up to −4.3% (increases to 13% and −6.3% for the single-exponential method). When α = 0.1 for the two-exponential, the maximum magnitudes of nBE for SW↑ increases (10%, Online Resource 5) but nBE for aGround, and nMAE for aRoof are similar (cf. α = 0.5).
The vertical absorption profiles (aWall, aRoof, aWall+Roof) for the London scenes are well captured by SPARTACUS-Urban (Figs. 8 and 9). The aWall+Roof maxima between DART and SPARTACUS-Urban (Fig. 9f, i) disagree mainly because of the need to adjust for intra-scene local topography heights in DART, in contrast to SPARTACUS-Urban where the ground is assumed to be flat. The SPARTACUS-Urban model fluxes for FLon,H are within 12% of DART, except for aGround when θ0 = 45° and 75° (nBE = −22%, −27%, Table 4b). Both scene albedo and transmission to the surface (Table 4b) are underestimated at all θ0. SPARTACUS-Urban overestimates the aWall+Roof profiles (Fig. 9c, f, i) leading to less shortwave radiation at ground level (with reduced SW↓ with decreasing height as θ0 increases). This leads to less shortwave reflected to the top of the canopy, reducing the scene albedo. The largest differences between the single- and two-exponential results occurs when θ0 = 75° (Table 4b). Simulations for FLon,H using α = 0.1 (cf. 0.5) have higher nBE magnitudes for both SW↑ (3.0–5.7%), and aGround (7.5–36%, Online Resource 5). Error metrics (nBE, nMAE, nMBE) are notably larger when using the single-exponential.
Fluxes normalized by the BOA flux (SW↓,BOA) for a high LOD 2 × 2 km2 domain in central London (FLon, H, Table 1), using SPARTACUS-Urban (orange) and DART (blue) for two albedos (α: 0.1 and 0.5) and three solar zenith angles (θ0: 0°, 45°, 75°) with solar azimuth angle (Ω) variation in DART (shading): (a, d, g) downwelling clear air flux (SW↓), (b, e, h) upwelling clear air flux (SW↑), (c, f, i) wall-plus-roof absorption (aWall+Roof). The SPARTACUS-Urban model’s radiative fluxes are computed using both single (Eq. 2, orange solid) and two- (Eq. 3, orange dashed) exponential fits
Both FInd,H SW↑ and aGround (hence SW↓) are generally underestimated, with nBE increasing with θ0 (0.32 to −3.7%, and −4.5 to −16% respectively, Table 4c). The SPARTACUS-Urban model overestimates aWall+Roof for all θ0 and α (Fig. 10c, f, i), with nMAE and nMBE between 6.3 and 15% (Table 4c) when using the two-exponential, with similar errors using the single-exponential. Using α = 0.1 increases the nBE in both SW↑ and aGround to −7% and −21% respectively (Online Resource 5).
As Fig. 9, but for Indianapolis with a high level of detail (FInd,H)
7 Comparison to the Single-Layer Infinite-Street-Canyon Assumption
Given the current urban models within NWP models commonly assume an urban form consisting of an infinite canyon with buildings of the same height and flat roofs, we assess SPARTACUS-Urban relative to one model of this type, Harman et al. (2004). This solves a small system of linear equations to treat any number of reflections within the canyon. Previously, Hogan (2019a) compared SPARTACUS-Urban to the Harman et al. (2004) longwave radiation by modifying the configuration, so assumptions are met for both, viz.: buildings all the same height, and exponential model of urban geometry (Hogan 2019b). Hogan (2019a) found excellent agreement between SPARTACUS-Urban using eight streams, supporting the use of the discrete ordinate method for urban radiative transfer.
Here, for shortwave radiation, we compare SPARTACUS-Urban and Harman et al. (2004) against DART for cases when the assumptions of the two models are not necessarily satisfied. The Harman method is used with its usual configuration (i.e., exchange coefficients consistent in a single-layer infinite street canyon as in Sect. 3 of Hogan (2019b)), and we implement the 2 × 2 matrix inversion approach of Harman et al. (2004), as outlined in Sect. 4.2 and Eq. 4 of Hogan (2019a). This approach assumes two parallel infinite length buildings have constant height, H, separated by street of constant width, W, with a fixed H/W.
Care is taken to ensure that in all comparisons, the total area of ground, wall, and roof is equal between the three models. For the Harman simulations, the height H is set equal to \(\overline{H }\) (Table 1), and the building fraction equal to λp,0. The value of H/W is calculated using the operational method in Eq. 3 of Hertwig et al. (2020),
where λf is calculated for each domain using Eq. 1 with the true wall area of the domain calculated from Δz and L(z). From Eq. 15 we obtain W using \(\overline{H }\). For SPARTACUS-Urban, we use the two-exponential form. Analysis is undertaken for both random cuboid and real-world scenes.
Unlike SPARTACUS-Urban, the Harman et al. method cannot predict vertical profiles, so the comparison of wall and roof absorptions is limited to vertically integrated quantities. Values of SW↑ at the top of the canopy are calculated for the Hmax in each scene for DART and SPARTACUS-Urban. These are compared using nBE (Eq. 14). We expand on results for an albedo of 0.5 here, with results of the comparison for an albedo of 0.1 in Online Resource 6. Run times for five SPARTACUS-Urban configurations are compared. These have varying numbers of diffuse streams per hemisphere (N = 1 to 8) and layers: n = 1 (i.e., as Harman et al. (2004)) to 6 (e.g., reasonable for operational NWP), to 151 (i.e., this work). The computer time of a single-threaded run for a SPARTACUS-Urban profile with the most basic configuration (N = 1, n = 1) is fast (12 μs) but six times longer than for the Harman model (Table 5). The FLon,L scenes (Sect. 6.3; SPARTACUS-Urban configuration: N = 8, n = 151) have a much longer run time (9.2 ms) but SPARTACUS-Urban is ~ 2.5 million times faster than DART despite DART using 14 parallel threads (Table 5).
Overall, Harman et al. (2004) has the best agreement with DART SW↑ (nBE < 6.3%, Fig. 1) but generally overestimates aWall, aRoof, and aWall+Roof. The best agreement between Harman et al. (2004) and DART is found for FRAND scenes (Fig. 11), however, SPARTACUS-Urban performs better (cf. Harman). Harman absorption errors increase with θ0, with nBE up to 18% or 32% (aWall and aRoof respectively), compared with nBE for SPARTACUS-Urban (up to 13.7% or 0.8%).
Comparison of SPARTACUS-Urban, Harman et al. (2004) and DART values for real-world scenes at low and high LOD (FLon, L, FLon,H, FInd,H), and random cuboid scenes (FRAND) for three solar zenith angles (θ0: 0°, 45°, 75°) and an albedo of 0.5: upwelling clear air flux at the top of the canopy (SW↑), and total wall, roof, and ground absorption (aWall, aRoof, aGround). For high LOD scenes aWall and aRoof are combined (aWall+Roof) for evaluation. Numbers on each bar are the nBE (Eq. 14) between the SPARTACUS-Urban model/Harman approach and the DART model. Error bars for DART span the range between if no correction for the energy imbalance is made, and if double this correction is made (Appendix 2)
For real-world domains, SPARTACUS-Urban performs better than the Harman approach, particularly for low θ0 (Fig. 11). The nBESPARTACUS values are in the range 1.3–14.3% for aRoof, aWall, and aWall+Roof, while nBEHarman is 0.3–31% for the same quantities. The value of aRoof is overestimated by both models in all cases, except for the SPARTACUS-Urban model for FLon,L at 45° and 75° (magnitudes of nBESPARTACUS < 4.3%, Fig. 11, cf. nBEHarman < 21.8%), which is expected for the Harman approach as roof shadowing is neglected. Both models predict SW↑ well (nBE all < 7%), but the SPARTACUS-Urban model almost always performs better (Fig. 11). The worst performance for both models is for aGround, with both models generally underestimating it (nBE of 0.4–26.6% for SPARTACUS-Urban and 1.2–56.4% for the Harman method). Overall, using SPARTACUS-Urban has a smaller nBE (cf. Harman) when evaluated using DART. For scenes where nBEHarman (cf. DART) are lower than nBESPARTACUS (i.e., better performance), the differences in nBE are < 5%.
8 Conclusions
Evaluation of the multi-layer SPARTACUS-Urban shortwave fluxes is undertaken using reference calculations from the explicit 3D radiative transfer model DART. The SPARTACUS-Urban model computes the vertical profiles of fluxes and absorption rates in urban scenes, which is crucial for vertically resolved urban energy balance models. A range of urban geometries were considered: regular arrays of cubes, cuboids with random placement and heights, to real city complexity (London and Indianapolis).
The SPARTACUS-Urban approach performs well when the SPARTACUS-Urban assumption of randomly distributed buildings is fulfilled. This is particularly evident for low building densities (λp,0 = 0.05) where the normalized bias error (nBE) and normalized mean absolute error (nMAE) < 1%. The SPARTACUS-Urban model and the DART model agree less well as building fraction increases (λp,0 = 0.5, nBE and nMAE < 5.5%). The largest nBE and nMAE occur when the solar zenith angle is highest (θ0 = 75°). For all random cuboid scenes presented, all nBE and nMAE are below 6%.
The shortwave radiative fluxes for real cities (London and Indianapolis) have nBE magnitudes of less than 7% for effective scene albedo, and nBE generally less than 15% for ground absorption. Exceptions to the latter occur for the high level of detail London domain when θ0 = 45° and 75°. Errors (nMAE) for the wall and roof absorption (low LOD) are less than 7% and 12%, respectively. The combined wall and roof absorption (high LOD domains) is always overestimated by SPARTACUS-Urban (nMAE < 15%), which leads to underestimation in the effective albedo of the scene, and underestimation in the transmission of shortwave radiation at the surface. However, the structure of the vertical profiles of fluxes and absorptions are captured well by SPARTACUS-Urban. Overall, upwelling profiles are best predicted by SPARTACUS-Urban. For the low LOD London domain, shortwave downwelling is typically overestimated, and roof absorptions are generally underestimated, in contrast to the high LOD domains. The performance of SPARTACUS-Urban in Indianapolis is slightly worse than for London scenes, which could be related to the grid-like street layout being further from the random building distribution assumed by SPARTACUS-Urban. Nonetheless, the Indianapolis domain used here still contains parks and diagonally oriented streets, which make the domain and building separations sufficiently random enough that SPARTACUS-Urban still performs well.
Regular cube arrays tested have a similar form to earlier urban radiation studies. The roof absorptions modelled in SPARTACUS-Urban are exact (cf. DART), as all buildings have the same height. The smallest differences between SPARTACUS-Urban and DART are found in scene albedo and ground absorption, where nBE < 2.2%. This increases to < 18% for denser cube arrays. Across all scenes, the largest differences between DART and SPARTACUS-Urban are found in wall absorption, with nMBE between 1.8 and −22% (nMAE 9.9% and 31%) depending on cube density. These errors in wall absorption are greater than in the real scenes, which given the regular spacing does not meet the randomly distributed buildings SPARTACUS-Urban assumption, this result is not unexpected. It is plausible the low nMAE and nBE results may be associated with the open cube spacing reduces building shadowing effects.
A modification to the original SPARTACUS-Urban method is introduced here, relaxing the strict assumption that the distribution of building separations fits a single-exponential (Eq. 2). This is replaced with a two-exponential method, allowing for effective building edge length to vary with θ0 (Eq. 3). This new method is proposed because Eq. 2 underpredicts the frequency of large building separations, and thus underpredicts the fraction of solar radiation reaching ground level. Using the two-exponential method both improves the predicted probability distributions (cf. ‘true’ distributions for London and Indianapolis) and reduces the SPARTACUS-Urban model’s radiative flux errors by up to a factor of a half. A further correction is applied to both the single- and two-exponential methods to account for the concavity of real buildings, leading to better representation of the width of building shadows. The range of possible concavity values in real-world cities means that SPARTACUS-Urban simulations could be calibrated to fit DART simulations. For NWP, the concavity value uncertainty for an individual domain is smaller than the uncertainty in L(z) itself.
There is scope to further refine SPARTACUS-Urban, including adjusting building shadowing. As SPARTACUS-Urban assumes the shadow cast by a building falls onto neighbouring buildings, or on gaps between buildings, is proportional to the roof area, this means shadows are randomly overlapped with roofs that they fall on. However, buildings often have roofs at low and high heights that are effectively next to each other when viewed from overhead. So, higher parts of a building can shadow lower roofs, rather than the street-level. Correcting this could improve the SPARTACUS-Urban performance further.
Comparison to the Harman et al. (2004) single-layer infinite street canyon model for randomly distributed cuboid, and real-world geometries found it performs best (c.f. DART) for random cuboid scenes. However, SPARTACUS-Urban generally performs better and notably in real-world scenes. The model results are most similar in their effective scene albedo predictions (nBE generally < 7%). The Harman approach overestimates the roof absorption, which is expected as the single-layer infinite street approach neglects roof shadowing.
Overall, our results show the SPARTACUS multi-layer approach to modelling radiative transfer in urban areas agrees well with the more complex and computationally demanding radiative transfer model DART when modelling real-world cities. The SPARTACUS-Urban model is the first multi-layer urban radiation model to achieve this, whilst being computationally cheap enough to be incorporated into weather and climate models (Hogan 2019a). This work surpasses previous evaluations that compare radiative transfer models to small scale observations or to more simplistic radiative transfer models (e.g., Harman et al. 2004; Krayenhoff and Voogt 2007; Aoyagi and Takahashi 2012; Krayenhoff et al. 2014). The single-exponential distribution that underpins SPARTACUS-Urban performs well but can be improved by using a two-exponential method. It is not yet certain if the extra complexity of implementing this two-exponential is justified, given the uncertainty in urban morphology datasets. Such datasets are required to compute required model inputs for SPARTACUS-Urban to describe the urban form (i.e., vertical descriptions of the urban canopy), which would be required if SPARTACUS-Urban is to be applied into a large-scale model.
Further investigation is needed to ascertain the amount of data required to describe building geometry worldwide, and how this impacts radiative fluxes. Further evaluation should be completed with SPARTACUS-Urban in the longwave, as this is a significant term in the urban surface energy balance (Oke 1988). As SPARTACUS-Urban can be integrated within existing urban surface energy budget models, the results of this shortwave evaluation provide a promising start to improving the treatment of the complex urban structure in NWP models.
References
Aida M (1982) Urban albedo as a function of the urban structure—A model experiment—Part I. Boundary-Layer Meteorol. https://doi.org/10.1007/BF00116269
Aida M, Gotoh K (1982) Urban albedo as a function of the urban structure—A two-dimensional numerical simulation—Part II. Boundary-Layer Meteorol. https://doi.org/10.1007/BF00116270
Ao X, Grimmond CSB, Liu D et al (2016) Radiation fluxes in a business district of Shanghai, China. J Appl Meteorol Climatol. https://doi.org/10.1175/JAMC-D-16-0082.1
Aoyagi T, Takahashi S (2012) Development of an urban multilayer radiation scheme and its application to the urban surface warming potential. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-011-9679-0
Arnfield AJ (1982) An approach to the estimation of the surface radiative properties and radiation budgets of cities. Phys Geogr. https://doi.org/10.1080/02723646.1982.10642221
Arnfield AJ (1988) Validation of an estimation model for urban surface albedo. Phys Geogr. https://doi.org/10.1080/02723646.1988.10642360
Baklanov A, Grimmond CSB, Carlson D et al (2018) From urban meteorology, climate and environment research to integrated city services. Urban Clim 23:330–341. https://doi.org/10.1016/J.UCLIM.2017.05.004
Chrysoulakis N, Grimmond S, Feigenwinter C et al (2018) Urban energy exchanges monitoring from space. Sci Rep. https://doi.org/10.1038/s41598-018-29873-x
Evans S, Hudson-Smith A, Batty M (2006) 3-D GIS; virtual London and beyond: an exploration of the 3-D GIS experience involved in the creation of virtual London. CyberGeo. https://doi.org/10.4000/cybergeo.2871
Figueiredo L, Amorim L (2007) Decoding the urban grid: or why cities are neither trees nor perfect grids. In: 6th International space syntax symposium
Fortuniak K (2008) Numerical estimation of the effective albedo of an urban canyon. Theor Appl Climatol. https://doi.org/10.1007/s00704-007-0312-6
Gastellu-Etchegorry JP (2008) 3D modeling of satellite spectral images, radiation budget and energy budget of urban landscapes. Meteorol Atmos Phys. https://doi.org/10.1007/s00703-008-0344-1
Gastellu-Etchegorry JP, Grau E, Lauret N (2012) DART: A 3D Model for Remote Sensing Images and Radiative Budget of Earth Surfaces. In: Modeling and Simulation in Engineering
Gastellu-Etchegorry JP, Yin T, Lauret N et al (2015) Discrete anisotropic radiative transfer (DART 5) for modeling airborne and satellite spectroradiometer and LIDAR acquisitions of natural and urban landscapes. Remote Sens. https://doi.org/10.3390/rs70201667
Ghandehari M, Emig T, Aghamohamadnia M (2018) Surface temperatures in New York City: geospatial data enables the accurate prediction of radiative heat transfer. Sci Rep. https://doi.org/10.1038/s41598-018-19846-5
Google Inc. (2019) Google Earth Pro. Geospatial Solut. 16
Grimmond CSB, Blackett M, Best MJ et al (2010) The International urban energy balance models comparison project: first results from phase 1. J Appl Meteorol Climatol 49:1268–1292. https://doi.org/10.1175/2010JAMC2354.1
Grimmond CSB, Oke TR (1999) Aerodynamic properties of urban areas derived from analysis of surface form. J Appl Meteorol. https://doi.org/10.1175/1520-0450(1999)038%3c1262:APOUAD%3e2.0.CO;2
Hagelin S, Son J, Swinbank R et al (2017) The Met Office convective-scale ensemble, MOGREPS-UK. Q J R Meteorol Soc. https://doi.org/10.1002/qj.3135
Han B, Sun D, Yu X et al (2020) Classification of urban street networks based on tree-like network features. Sustain. https://doi.org/10.3390/su12020628
Harman IN, Best MJ, Belcher SE (2004) Radiative exchange in an urban street canyon. Boundary-Layer Meteorol. https://doi.org/10.1023/A:1026029822517
Heris MP, Foks NL, Bagstad KJ et al (2020) A rasterized building footprint dataset for the United States. Sci Data. https://doi.org/10.1038/s41597-020-0542-3
Hertwig D, Grimmond S, Hendry MA et al (2020) Urban signals in high-resolution weather and climate simulations: role of urban land-surface characterisation. Theor Appl Climatol. https://doi.org/10.1007/s00704-020-03294-1
Hogan R, Ahlgrimm M, Balsamo G, et al (2017) Radiation in numerical weather prediction. ECMWF Tech Memo
Hogan RJ (2021) Spartacus-surface. GitHub Repos
Hogan RJ (2019a) Flexible treatment of radiative transfer in complex urban canopies for use in weather and climate models. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-019-00457-0
Hogan RJ (2019b) An exponential model of urban geometry for use in radiative transfer applications. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-018-0409-8
Hogan RJ, Quaife T, Braghiere R (2018) Fast matrix treatment of 3-D radiative transfer in vegetation canopies: SPARTACUS-Vegetation 1.1. Geosci Model Dev 11:339–350. https://doi.org/10.5194/gmd-11-339-2018
Hogan RJ, Schäfer SAK, Klinger C et al (2016) Representing 3-D cloud radiation effects in two-stream schemes: 2. Matrix formulation and broadband evaluation. J Geophys Res 121:8583–8599. https://doi.org/10.1002/2016JD024875
Hogan RJ, Shonk JKP (2013) Incorporating the effects of 3D radiative transfer in the presence of clouds intol two-stream multilayer radiation schemes. J Atmos Sci. https://doi.org/10.1175/JAS-D-12-041.1
Jandaghian Z, Akbari H (2018) The effect of increasing surface albedo on urban climate and air quality: a detailed study for Sacramento, Houston, and Chicago. Climate. https://doi.org/10.3390/cli6020019
Kanda M (2007) Progress in urban meteorology: a review. J Meteorol Soc Japan 85:363–383
Kanda M, Kawai T, Nakagawa K (2005) A simple theoretical radiation scheme for regular building arrays. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-004-8662-4
Kondo H, Genchi Y, Kikegawa Y et al (2005) Development of a multi-layer urban canopy model for the analysis of energy consumption in a big city: structure of the urban canopy model and its basic performance. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-005-0905-5
Kotthaus S, Grimmond CSB (2014) Energy exchange in a dense urban environment—Part II: impact of spatial heterogeneity of the surface. Urban Clim. https://doi.org/10.1016/j.uclim.2013.10.001
Krayenhoff ES, Christen A, Martilli A, Oke TR (2014) A multi-layer radiation model for urban neighbourhoods with trees. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-013-9883-1
Krayenhoff ES, Santiago JL, Martilli A et al (2015) Parametrization of drag and turbulence for urban neighbourhoods with trees. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-015-0028-6
Krayenhoff SE, Voogt JA (2007) A microscale three-dimensional urban energy balance model for studying surface temperatures. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-006-9153-6
Kusaka H, Kondo H, Kikegawa Y, Kimura F (2001) A simple single-layer urban canopy model for atmospheric models: Comparison with multi-layer and slab models. Boundary-Layer Meteorol. https://doi.org/10.1023/A:1019207923078
Landier L, Gastellu-Etchegorry JP, Al Bitar A et al (2018) Calibration of urban canopies albedo and 3D shortwave radiative budget using remote-sensing data and the DART model. Eur J Remote Sens. https://doi.org/10.1080/22797254.2018.1462102
Lee SH, Park SU (2008) A vegetated urban canopy model for meteorological and environmental modelling. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-007-9221-6
Lemonsu A, Masson V, Shashua-Bar L, et al (2012) Inclusion of vegetation in the Town Energy Balance model for modelling urban green areas. Geosci Model Dev. https://doi.org/10.5194/gmd-5-1377-2012
Loridan T, Grimmond CSB (2012) Characterization of energy flux partitioning in urban environments: Links with surface seasonal properties. J Appl Meteorol Climatol 51:219–241. https://doi.org/10.1175/JAMC-D-11-038.1
Martilli A, Clappier A, Rotach MW (2002) An urban surface exchange parameterisation for mesoscale models. Boundary-Layer Meteorol 104:261–304. https://doi.org/10.1023/A:1016099921195
Masson V (2000) A physically-based scheme for the urban energy budget in atmospheric models. Boundary-Layer Meteorol 94:357–397. https://doi.org/10.1023/A:1002463829265
Masson V, Heldens W, Bocher E et al (2020) City-descriptive input data for urban climate models: model requirements, data sources and challenges. Urban Clim. 31:100536
Morrison W, Benjamin K (2021) daRt. GitHub Repos
Morrison W, Kotthaus S, Grimmond CSB et al (2018) A novel method to obtain three-dimensional urban surface temperature from ground-based thermography. Remote Sens Environ. https://doi.org/10.1016/j.rse.2018.05.004
Morrison W, Yin T, Lauret N et al (2020a) Atmospheric and emissivity corrections for ground-based thermography using 3D radiative transfer modelling. Remote Sens Environ. https://doi.org/10.1016/j.rse.2019.111524
Morrison W, Yin T, Lauret N et al (2020b) Atmospheric and emissivity corrections for ground-based thermography using 3D radiative transfer modelling. Remote Sens Environ. https://doi.org/10.1016/j.rse.2019.111524
Nunez M, Oke TR (1977) Energy balance of an urban canyon. J Appl Meteorol. https://doi.org/10.1175/1520-0450(1977)016%3c0011:TEBOAU%3e2.0.CO;2
Oke TR (1988) The urban energy balance. Prog Phys Geogr. https://doi.org/10.1177/030913338801200401
Oleson KW, Bonan GB, Feddema J et al (2008a) An urban parameterization for a global climate model. Part II: sensitivity to input parameters and the simulated urban heat island in offline simulations. J Appl Meteorol Climatol 47:1061–1076. https://doi.org/10.1175/2007JAMC1598.1
Oleson KW, Bonan GB, Feddema J et al (2008b) An urban parameterization for a global climate model. Part I: formulation and evaluation for two cities. J Appl Meteorol Climatol 47:1038–1060. https://doi.org/10.1175/2007JAMC1597.1
Raupach MR, Shaw RH (1982) Averaging procedures for flow within vegetation canopies. Boundary-Layer Meteorol. https://doi.org/10.1007/BF00128057
Redon EC, Lemonsu A, Masson V et al (2017) Implementation of street trees within the solar radiative exchange parameterization of TEB in SURFEX v8.0. Geosci Model Dev 10:385–411. https://doi.org/10.5194/gmd-10-385-2017
Resler J, Krč P, Belda M, et al (2017) A new urban surface model integrated in the large-eddy simulation model PALM. Geosci Model Dev Discuss. https://doi.org/10.5194/gmd-2017-61
Santamouris M (2014) Cooling the cities—A review of reflective and green roof mitigation technologies to fight heat island and improve comfort in urban environments. Sol Energy. https://doi.org/10.1016/j.solener.2012.07.003
Santamouris M, Haddad S, Saliari M et al (2018) On the energy impact of urban heat island in Sydney: climate and energy potential of mitigation technologies. Energy Build. https://doi.org/10.1016/j.enbuild.2018.02.007
Schubert S, Grossman-Clarke S, Martilli A (2012) A double-canyon radiation scheme for multi-layer urban canopy models. Boundary-Layer Meteorol 145:439–468. https://doi.org/10.1007/s10546-012-9728-3
Sobrino JA, Mattar C, Gastellu-Etchegorry JP et al (2011) Evaluation of the DART 3D model in the thermal domain using satellite/airborne imagery and ground-based measurements. Int J Remote Sens. https://doi.org/10.1080/01431161.2010.524672
Stamnes K, Tsay S-C, Wiscombe W, Jayaweera K (1988) Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl Opt. https://doi.org/10.1364/ao.27.002502
Sützl BS, Rooney GG, van Reeuwijk M (2020) Drag distribution in idealized heterogeneous urban environments. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-020-00567-0
Wang Y, Lauret N, Gastellu-Etchegorry JP (2020) DART radiative transfer modelling for sloping landscapes. Remote Sens Environ 247:111902. https://doi.org/10.1016/j.rse.2020.111902
Widlowski JL, Mio C, Disney M et al (2015) The fourth phase of the radiative transfer model intercomparison (RAMI) exercise: actual canopy scenarios and conformity testing. Remote Sens Environ. https://doi.org/10.1016/j.rse.2015.08.016
Yang X, Li Y (2015) The impact of building density and building height heterogeneity on average urban albedo and street surface temperature. Build Environ 90:146–156. https://doi.org/10.1016/j.buildenv.2015.03.037
Acknowledgements
The authors acknowledge the funding and support from the Scenario NERC Doctoral Training Partnership Grant, EPSRC 2130186,EPRSC DARE (EP/P002331/1), ERC urbisphere (855005), and Newton Fund/Met Office CSSP China NGC. All data and code have been archived at https://zenodo.org/10.5281/zenodo.5145851.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix 1: Building Concavity in Real-World Cities
As outlined in Sect. 2.2, a correction is made in SPARTACUS-Urban to account for the building concavity in real-world cities. Real-world buildings tend to not be convex, which means the relation between the building perimeter length given to SPARTACUS-Urban and the rate of radiation exchange is not correct. Therefore, we correct for this concavity by applying a constant scaling factor to L at each height level using a concavity parameter (C, Eq. 11). This allows us to approximately obtain the perimeter of the convex hull of each building. Here, three real-world domains are analyzed (in London and Indianapolis) at two levels of detail (LOD, low and high) (FLon,L, FLon,H, FInd,H, Table 1), derived from building footprints (Table 1).
For the London domains, C ranges between 1.04 and 1.66 at each height interval, with smaller values for the low (FLon,L) than high (FLon,H) LOD domain (Fig.
12). Generally, C decreases with height in real cities (Fig. 12, Online Resource 7), because individual buildings in an area of the city may be short and wide, or tall and narrow, and so cast different sized shadows. Cross-sections of the high LOD London domain support this, with low height levels, where the building density is high, having a larger C (cf. higher heights where smaller, taller building occur) (Online Resource 7d). Given this, we calculate C at all heights, and use median C from all heights above \(\overline{H }\), applying this as the scaling factor to L(z) (black, Fig. 12). Values below \(\overline{H }\) are excluded given both the presence of courtyards, and that taller buildings will shadow shorter buildings (rather than vice versa).
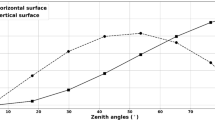
We examine the impact on the shortwave fluxes, with C from 1.1 to 1.7 but constant with height (Sect. 4.3). Across the three solar zenith angles (Fig.
13), the C value has the greatest impact on the SW↑ profiles for the FLon,H domain, and less impact on the SW↓ and aWall+Roof profiles.
Appendix 2: Redistribution of Lost Energy in the DART Model Output
We calculate energy imbalance (Ε, W m−2/W m−2) for each DART run, using
where the total wall, ground and roof absorption are given by aWall, aGround and aRoof, respectively and SW↑,top is the shortwave upwelling clear air flux at the top of the canopy. Ε = 0 for a perfectly conserving model.
The DART energy imbalance is always less than 2%, and usually less than 1% (Fig.
14b). Generally, energy conservation is highest for overhead sun conditions (θ0 = 0°) and decreases with geometry complexity to be lowest for the real-world domains (FLon, FInd). FREG (Table 1) domains have a lower voxel resolution, so do not follow this relation, as DART energy conservation tends to improve as voxel resolution increases (e.g. 1 m → 0.5 m).
Processes identified that contribute to energy loss are (Fig.
Energy lost in DART occurs at the edge of periodic model domains (grey) if there is a unmatched topography, and/or b buildings missing external walls. To distribute the energy through the c ground (EGround), and d walls (EWall), where the purple arrows (i) represent the extra energy into the ground and walls, and the red (ii) and green (iii) represent the first and second reflections of shortwave radiation, to determine the total extra shortwave radiation into the walls, ground, and upwelling (aWall,extra, aGround,extra, and SW↑,extra)
15):
-
(1)
rays passing ‘underground’ of the domain when there are holes in the 3D building model,
-
(2)
rays hitting internal walls of buildings
Both can occur from the domain periodic boundary conditions, if buildings and topography are cut at the domain edge (Wang et al. 2020). The FRAND, FLon,H and FInd,H (Table 1) 3D building models contain some buildings that cross the domain edge. As the domain cuts though it creates ‘open’ buildings allowing rays to pass directly underneath the building footprint model or interact with the ‘internal’ walls of the buildings (Fig. 15b). With non-flat topography (e.g., FLon,H and FInd,H) the periodic boundary conditions create gaps through which rays can pass (Fig. 15a). FREG scenes have neither of these features, whereas FRAND scenes have only building split, hence energy loss increases with increasing domain complexity. As the real-world scenes have the largest energy loss, the DART missing energy is assumed to be lost through the building walls and the ground, attributed to processes (1) and (2) above.
For high LOD scenes, we redistribute lost energy into the walls (Fig. 15b, d) first as a ratio of total AW to total aWall. The approximated (AW,edges) wall area missing at the edge of the domain is used to calculate the average wall absorption
We note AW,edges is an overestimate, as building walls in the repeated units may overlap. We assume aWall,edges is the amount of energy absorbed by these extra walls. The amount of total energy available for exchange by the wall processes (EWall) in Fig. 15d is equal to \({a}_{\mathrm{Wall},\mathrm{edges}}/\left(1-\alpha \right)\). This energy is split between SW↑, aWall, and aGround (Fig. 15d). The remainder of the lost energy is attributed to the ground process (EGround) (Fig. 15a), and is redistributed (Fig. 15c) into aGround, aWall, and SW↑, where the two-thirds of the radiation reflected from the ground is distributed into aWall. Combining these processes (Fig. 15) leads to the total added energy.
This is distributed at all height levels using a scaling factor (e.g., \({a}_{\mathrm{Wall}}/{a}_{\mathrm{Wall},\mathrm{extra}}\)). For FLon,L, the buildings at the edge of the domain have complete walls with flat topography, so we distribute lost energy through both the wall and ground processes (Fig. 15) equally, assuming EWall = EGround. Although we redistribute the energy through these processes, we note this may not match the true DART results if external walls and topography are corrected. The uncertainty in these numbers is less than the range if solar azimuth angle is varied, and so it not shown in the vertical flux profiles compared in Sect. 6. In Sect. 7, this uncertainty is shown by an error bar across: the fluxes if no correction for the energy imbalance is made, and the fluxes if double the correction is made.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stretton, M.A., Morrison, W., Hogan, R.J. et al. Evaluation of the SPARTACUS-Urban Radiation Model for Vertically Resolved Shortwave Radiation in Urban Areas. Boundary-Layer Meteorol 184, 301–331 (2022). https://doi.org/10.1007/s10546-022-00706-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-022-00706-9