1 Introduction

Both fog and mist are water droplets suspended in the near-surface air that result in reduced visibility. The Glossary of Meteorology (AMS 2020) defines fog as when visibility is less than 1 km, while visibility in mist is greater than 1 km. An upper limit of visibility to define mist or light fog was set at 5 km (Meyer et al. 1980), above which the reduction of visibility is attributed to haze with dry or activated aerosols. The commonly-used variables to describe the physical characteristics of fog/mist include the droplet size spectra, total droplet number concentration, liquid water content (LWC), and characteristics of droplet size parameters such as effective or mean droplet diameters. The thickness of the fog layer is also used as one of the macroscopic properties of the hygrometer layer. In this work, the term ‘fog’ is sometimes used loosely when we refer to the attenuation media. The focus on the range of visibility is between 0 and 5 km.

The most prominent impact of fog on human activities is visibility degradation, a common problem that poses safety and efficiency issues to all transportation systems. Other systems relying on visible and infrared transmissions, such as those related to defense or communication systems, also experience performance degradation caused by fog attenuations. For example, free-space optical (FSO) communication systems are leveraging bands in shorter wavelengths of the electromagnetic wave spectrum, which are outside of ever-increasing congestion in the radio and microwave frequencies (Bouchet et al. 2006, Arnon et al. 2012). The FSO link is affected by the various weather conditions, such as fog, rain, dust, snow, etc., with fog having a particularly consequential impact because it can attenuate signals up to 480 dB km−1 (Demers et al. 2011). This high attenuation reduces the link availability and causes link outage. The attenuation of visible signals through fog is also a major concern for high-energy-laser (HEL) weapon systems with direct intensive narrow light beams propagating through the atmosphere. Despite apparent advantages, effects of propagation impairments, such as fog attenuation, can adversely affect the HEL weapon performance. As both FSO and HEL systems gain broader use, accurate forecasts of fog events and their impact on optical systems have become crucial.

In aviation applications, visibility, represented by the meteorological optical range (MOR), is used to represent the intensity of fog (Gultepe et al. 2009). Visibility is directly related to the atmospheric extinction coefficient through the Koschmieder equation

$$ m = \frac{c}{{\sigma_{e} }}, $$
(1)

where m represents MOR, \(c = \ln \left( {\frac{1}{0.05}} \right) = 2.996\) and extinction coefficient, \(\sigma_{e}\), is in units of km−1. Visibility hence can be used to represent the atmospheric attenuation of optical signals in general and is not limited to aviation use.

Visibility is derived diagnostically from numerical weather prediction (NWP) model output variables such as the LWC or droplet number concentration (\({N}_{d},\) if available) based on an empirically determined visibility-fog property relationship. The accuracy of the derived visibility depends on two factors: (1) the accuracy of the model forecast variables (LWC, \({N}_{d}\), or both) as input to MOR calculations, and (2) the adequacy of the visibility algorithms depicting visibility as a function of model predicted fog properties such as the LWC and/or \({N}_{d}\). Both factors are equally important for producing accurate depictions of the impact of fog on optical signal propagation. For the latter, the relationship between MOR and the fog properties needs to be tested, which requires simultaneous measurement of attenuation and fog microphysics. The visibility-fog relationship is also important to improve the numerical prediction of LWC by assimilating visibility data into forecast models (Clark et al. 2008; Kim et al. 2020).

There is a long history of research relating visibility to fog properties. Since LWC is the most common output variable from NWP models to represent warm clouds and fog, it is used most frequently to calculate visibility (e.g., Kunkel 1984, hereafter K84, Gultepe et al. 2006, hereafter G06). K84 analyzed 11 advective fog cases totaling 90 h of data, which led to the K84 relationship. However, later studies by G06 found the K84 relationship insufficient for NWP models using aircraft measurements from 16 flights in low-level clouds with various mass origins. Meyer et al. (1980) identified functional relationships between visibility and the droplet number concentration. Their approach was tested by G06 based on aircraft measurements in low-level clouds where large variability in the cloud droplet number concentration at a given LWC was identified. They further suggested that the droplet number concentration should be included in addition to LWC to form a ‘fog index’ (the product of LWC and \({N}_{d}\)), which is a more appropriate parameter to obtain better accuracy in visibility parametrization. Later studies by Gultepe and collaborators further evaluated the visibility-fog index relationship for various case studies (Gultepe and Milbrandt 2007; Gultepe et al. 2009, 2020).

Although the various visibility-fog microphysics relationships fit the original data with good statistics, there is a lack of ‘universal’ formulation as the coefficients differ from case to case (see Table 4 Gultepe et al. 2021). Such inconsistency may result from multiple reasons. Kunkel (1984) pointed out the differences in the lower and upper limit of the different droplet spectrometers that generated the visibility data for the curve fit, resulting in uncertainties in the estimated LWC and \({N}_{d}\). Similar uncertainties may exist in later research efforts when the fog properties were obtained from different sensors. Inconsistency in the visibility measurements is also a possibility. Most importantly, due to the extremely large spatial and temporal variability in fog, the number of cases used to generate the empirical relationship is likely a key factor.

In this paper, we intend to understand the impact of fog on visibility by examining the visibility-fog relationship from 15 cases of observed fog events from two field campaigns in distinctively different locations. The key instruments and the experiment set-up in both field campaigns were nearly identical so that there were no systematic differences in the measurements. In Sect. 2, the measurements from the two field campaigns are introduced. The methodology used to obtain key fog parameters and visibility is described in Sect. 3 followed by results in Sect. 4. The results include the thermodynamic and microphysical characteristics of the observed fog from the two locations, a comparison of visibility data between point and path-integrated sensors as well as those derived from Mie scattering theory, and an evaluation of the several visibility parametrizations used in current NWP models or proposed by previous work. In Sect. 5, we present initial analyses on precipitation in reducing visibility. Summary and discussions are given in Sect. 6.

2 Observations

The field campaigns that obtained the data used in this work are briefly discussed in this section. Since the two campaigns used the same instrument and set-up, they are described in the same section with differences noted wherever applicable.

2.1 Field Campaigns for Data Collections

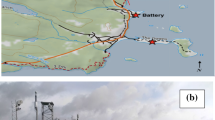
Measurements from two field campaigns are used in this study: the High Energy Laser propagation in Fog (HELFOG) and the Toward Improving Coastal Fog Prediction (C-FOG) projects. The HELFOG project conducted an observational study in two collection sites in the central Monterey Bay area (Fig. 1). Site 1, located at the Salinas River Wildlife Refuge (Fig. 1, red dot), about 1.3 km east of the coastline, was used during 13–15 July 2018. Collection site 2 (Fig. 1 orange dot), located at Marina Municipal Airport, about 5 km from the shore, was used during 15–24 July 2018. Both sites afforded approximately 600 m of a usable path with site 1 (Fig. 1a) located along a dirt road in a lettuce field and site 2 (Fig. 1b) located over the airport taxiway and ramp. These site locations and periods of the experiment warranted the best chance of collecting data in fog while site 2 presented a secure site for 24-h operations. Daniels (2019) gave detailed descriptions of the two sites. His analyses found few systematic differences between the observed microphysics of fog events from the two nearby locations of HELFOG. Hence, we do not separate the data by specific sites from HELFOG here.

Fig. 1
figure 1

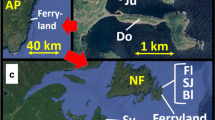
a The HELFOG sites at the Monterey Bay and b The Downs supersite at Ferryland during C-FOG. The red arrows denote the two-ended transmission paths by a transmissometer and a scintillometer in HELFOG and by a scintillometer only in C-FOG. The inset in red and orange frames show the details of the land use over sites 1 and 2 in HELFOG

Full size image

A C-FOG overall summary is given in Fernando et al. (2021); its microphysical observations are described in Gultepe et al. (2021). The project was conducted near the coasts of Avalon Peninsula, Newfoundland, and Nova Scotia, Canada as part of a multidisciplinary team effort to explore coastal fog over land and at sea during August–October 2018. In this work, the measurements from the C-FOG supersite at The Downs of Ferryland, Newfoundland were used. The thin peninsula protruding into the Atlantic hosted a large suite of meteorological sensors to characterize the dynamics, thermodynamics, and microphysics of fog with auxiliary measurements from the nearby C-FOG sites. For details of the overall C-FOG set-up and microphysics measurements and main results, the readers are referred to Fernando et al. (2021) and Gultepe et al. (2021).

2.2 Instrumentation

The key instrument for fog droplet-size distribution is a forward-scattering droplet-size spectrometer, the Cloud Droplet Probe 2 (CDP-2, Droplet Measurement Inc., Boulder, Colorado). The CDP-2 utilizes a 658 nm laser to illuminate droplets and the intensity of forward-scatter is measured to quantify the droplet or particle size. The 30 user-defined diameter size bins range from 2 to 50 μm and the CDP-2 outputs a size distribution spectrum at 1 Hz. In both projects, the modified CDP-2 was set on top of a trailer (Fig. 2f) with the sensing volume at about 4 m above ground.

Fig. 2
figure 2

Relevant instruments used in HELFOG and C-FOG measurements. a Transmitter for BLS900 (left) and beacon for the wide angle teteradiometric transmissometer (WATT, right) in HELFOG, b BLS900 transmitter at The Downs supersite in C-FOG, c the modified CDP-2 inside the cowling, d the tripod mast set-up in C-FOG for meteorological measurements, e the BLS900 (left) and WATT (right) receivers in HELFOG and f the modified CDP-2 deployed on top of a trailer hosting the Naval Postgraduate School (NPS) Aerosol Sampling Unit (NASU) at The Downs supersite in C-FOG

Full size image

The CDP-2, originally designed for research aircraft deployment, was modified for land-based static use. The sensor was housed in a cowling with one open end and a fan on the opposing side to provide forced aspiration through the CDP-2 sampling volume. A mechanical ‘flip-flop’ flowmeter that measures the airspeed is housed within the cowling and below the sampling volume, shown in Fig. 2c. As air flows through, the flip-flop swings back and forth caused by the restoring force of the fin. A small arm extends between a light-emitting diode and photodiode path, which blocks and unblocks the light, exciting a periodic square wave signal on the output of the photodiode as air flows through the cowling. The flip-flop anemometer can be modelled as a second-order system; hence, the square wave signal frequency is directly proportional to the flow speed. The flip-flop flowmeter frequency was calibrated against a hot wire anemometer before deployment. The CDP-2 and flip-flop photodiode signals are synchronously measured with a data acquisition system (CR3000, Campbell Scientific Inc., Logan, Utah). Combining the raw droplet number size spectra, flow speed, and known sampling volume yields the droplet size spectra. Figure 3 shows the variation of the flow speed measured by the flow meter at the sampling volume during HELFOG. Although we oriented the cowling with the predominant wind direction, the flow speed still varied considerably. Since the CDP-2 is the key instrument that quantified the fog droplets, the addition of the flow speed measurements ensures the quality of the measured droplet spectra.

Fig. 3
figure 3

The flow speed measured close to the sampling volume of the modified CDP-2. The data shown are 10-min averages

Full size image

In HELFOG, optical transmission is quantified using two methods: a direct extinction measurement from a two-terminal transmissometer, the Wide Angle Teteradiometric Transmissometer (WATT, custom-built, Naval Air Warfare Center Weapons Division, China Lake, U.S.), and a Vaisala Present Weather and Visibility Sensor (PWD10, Helsinki, Finland). In C-FOG, only the Vaisala Present Weather and Visibility Sensor (PWD22, Helsinki, Finland) was used. The PWD sensors use a light source at 875 nm and obtain the scattering coefficients of the droplets by detecting light scattered at an angle of 45o. This angle is considered to produce a stable response in various types of fog droplets (Vasaila, PWD manual) in a sampling volume of about 0.1 L (100 cm3). The PWD sensors output visibility at 1- and 10-min intervals. The WATT instrument is used to measure optical transmission along the path between the transmitter and the receiver. It is composed of a power-stabilized near-infrared 1.064 μm laser beacon and custom-designed optical telescope with a rear-mounted charged-coupled device (CCD) sensor. Using image-processing methods, the WATT instrument measures the attenuated signal of the beacon transmitter by calculating the path-averaged extinction, which should include attenuation through scattering and absorption by molecules, droplets, and particulates along the path. For fog/mist conditions, the main attenuation for the wavelength at 1.064 μm are the results of droplet scattering in the Mie scattering regime. In HELFOG, the WATT transmitter and receiver were separated by about 600 m. The measurements ended on 21 July 2018 while the rest of the measurements continued until 25 July 2018. It is noted that the two sensors measure atmospheric extinction differently. The PWD is considered a point measurement while the WATT instrument provides a path-integrated measurement. In the case of spatial inhomogeneity, the difference in the volumes of the sampled air may be a direct cause of some inconsistency in the results. To develop the parametrization, a volume average in the model grid is ideal but not realistically feasible for any existing sampling approaches. Consequently, significant representation errors must be considered for visibility observations used for model evaluation.

The tripod mast (Fig. 2d) utilized a three-dimensional ultrasonic wind anemometer and infrared gas analyzer combination sensor (IRGASON, Campbell Scientific, Logan, Utah). The IRGASON measured water vapour density and CO2 concentration, three-dimensional wind velocity, and temperature derived from the speed of sound within the same sampling volume and sampled synchronously at 50 Hz. Slower response sensors were deployed along the mast to measure the bulk air temperature, relative humidity, barometric pressure, ground temperature, net irradiance, and wind speed and direction, which are used to support the analyses on fog evolution and microphysics. Rawinsonde launches were also made during both HELFOG and C-FOG using Vaisala RS41 sondes (Radiosonde RS4, Vaisala, Helsinki, Finland) to measure vertical variations of temperature, humidity, pressure, wind speed, and wind direction.

3 Method of Study

3.1 Cloud Microphysical Relationship

The key microphysical variables used in visibility parametrization are LWC \((q_{l} )\) and total droplet number concentration (Nd). The droplet sizes can be represented using several variables, namely, the mean droplet radius (Rm), the effective droplet radius (Re), and the mean volume radius (MVR, Rv). The raw measured droplet number count in each size bin was converted to a droplet size spectrum, \(n\left( r \right)\) in the units of cm−3 μm−1 in each bin by dividing the volume of the flow based on the measured flow speed, the CDP-2 sampling area, and the bin width. Here, \(r\) is the radius of a fog droplet. All microphysical variables can be obtained from the CDP-2 droplet spectra, originally sampled at 1 Hz, through Eq. 2

$$ \begin{aligned} & N_{d} = \int {n\left( r \right)dr} ,\quad q_{l} = \int {\frac{4}{3}\pi \rho_{w} n\left( r \right)r^{3} dr} \\ & R_{m} = \frac{{\int {n\left( r \right)rdr} }}{{\int {n\left( r \right)dr} }},\quad R_{e} = \frac{{\int {n\left( r \right)r^{3} dr} }}{{\int {n\left( r \right)r^{2} dr} }},\quad R_{v} = \left( {\frac{{\int {n\left( r \right)r^{3} dr} }}{{\int {n\left( r \right)dr} }}} \right)^{1/3} \\ \end{aligned} $$
(2)

The effective radius, defined as a ratio of the third moment to the second moment of the size spectra, is considered the best single parameter describing the scattered light (Hansen and Travis 1974) and has been examined extensively to study the effects of cloud droplets on cloud albedo known as the indirect effects of aerosols through cloud processes (e.g., Reid et al. 1999; Peng et al. 2002). This area-weight droplet size is hence the most relevant variable associated with the radiative properties of the droplets. On the other hand, the MVR \((R_{v} )\) is directly related to LWC and Nd by

$$ q_{l} = \int {\frac{4}{3}\pi \rho_{w} n\left( r \right)r^{3} dr} = \frac{4}{3}\pi \rho_{w} R_{v}^{3} \int {n\left( r \right)dr} = \frac{4}{3}\pi \rho_{w} R_{v}^{3} N_{d} . $$
(3)

Equation 3 suggests that there are only two independent variables among LWC, the number of droplets and the droplet size. This is an important point to keep in mind when deriving visibility parametrizations.

3.2 Optical Attenuation

Radiative energy propagating through the atmosphere is affected by absorption and scattering by air molecules and suspended particles, such as aerosol and fog. Based on Beer–Lambert’s law, the received irradiance \((E_{R} )\) at a distance L from the light source (transmitter) is related to the transmitted irradiance \((E_{T} )\) at the source by Eq. 4

$$ \tau \left( {\lambda ,L} \right) = \frac{{E_{R} }}{{E_{T} }} = {\text{exp}}\left( { - \sigma_{e} \left( \lambda \right)L} \right), $$
(4)

where \(\sigma_{e}\) is the extinction coefficient (m−1) as in Eq. 1, and \(\tau \left( {\lambda ,L} \right)\) is the transmittance of the atmosphere at wavelength \(\lambda\) for the given propagation path length L. The total extinction coefficient is the sum of the absorption \((\sigma_{a} )\) and the scattering \((\sigma_{s} )\) coefficients \((\sigma_{e} = \sigma_{s} + \sigma_{a} )\). These coefficients are functions of the molecular constituents, physical and chemical properties of suspended hydrometers/aerosols, and the wavelength of incident irradiance. In the case of fog, the extinction is dominated by scattering by fog droplets and is insensitive to the incident wavelength up to approximately1.55 μm (Isaac et al. 2001).

Optical attenuation was obtained from three independent methods using different measurements: the WATT instrument, the PWD sensors, and calculated from the Mie theory based on measured fog droplet spectra. For the first method, the WATT transmissometer-measured transmittance was used to derive transmittance based on the definition in Eq. 4. The result is the extinction coefficient along the given path length. It is hence a path-averaged scattering coefficient assuming negligible absorption (Isaac et al. 2001). The MOR from the WATT measurements is further obtained from Eq. 1.

In the second method, optical attenuation was obtained through the visibility measurement by the PWD-10 (HELFOG) or the PWD-22 (C-FOG). The PWD sensors directly measure the scattering coefficient from a sampling volume of 0.1 L (100 cm3), and hence are essentially point measurements. The same assumptions of dominant water droplet scattering and negligible absorption allow the calculation of MOR directly from Eq. 1. Note that the built-in conversion of the PWD sensors is the Koschmieder relationship in Eq. 1, although using a slightly different c value of 3. This subtle difference in the choice of c is ignored in the analyses. The MOR is used consistently here to represent optical attenuation.

The third method for calculating optical attenuation is to use the full Mie theory applied to a medium with distributions of scatterers (Petty 2004), in which the scattering coefficient is given by

$$ \sigma_{s} = \mathop \int \limits_{{r_{1} }}^{{r_{2} }} \pi r^{2} Q_{sct} \left( {mr,\frac{r}{\lambda }} \right)n\left( r \right)dr, $$
(5)

where \(mr\) is the real part of the refractive index, and \(Q_{sct}\) is the scattering efficiency. The water droplet refractive index was calculated at 20 °C and a density of 1000 kg m−3 following the formulation in IAPWS (1997) and programmed by Schaarsberg (2021). The droplet size spectrum \(n\left( r \right)\) was obtained from the CDP-2 droplet spectra measurements. The limits of the integration (\(r_{1}\) and \(r_{2}\)) cover the full range of the CDP-2 spectrometer measurements (2 to 50 μm in diameter). The calculation of of the scattering coefficient \(\sigma_{s}\) uses the Mie code developed by Matzler (2002) based on the formulation in Bohren and Huffman (1983). Again, assuming dominant scattering by fog droplets, the coefficient \(\sigma_{s}\) is used in Eq. 1 in place of \(\sigma_{e}\) to obtain MOR.

3.3 Data Processing

Extensive data quality control was made throughout and data consistency checks. Some spurious data points such as an extremely large number of droplets at a single time instance were removed in this step. To remove the noise floor in the data, all statistics of fog shown in Eq. 2 were calculated by removing data points with \(N_{d} < 1\) cm−3 or \(q_{l} < 0.001 \) gm−3 to stay within the reasonable range for fog following Gultepe et al. (2006). However, the LWC used to derive the fog-visibility relationship included the full measurements. Because of the strong spatial and temporal variability in fog and the associated visibility and the large range of variation of droplet number, different averaging approaches may produce significantly different results. Since the PWD provides 1-min data, when deriving the fog-visibility relationship, 1-min averaging was applied to obtain the fog microphysics variables. The fog spectra were averaged over the entire fog period. In some of the figures, the data were decimated for presentation purposes to avoid too many data points clustering in the figure. The statistical results, however, were calculated using the full range of the respective data.

4 Results

The results are displayed here in two subsections: (1) a comparison of fog microphysics and thermodynamic properties from two geographic locations; (2) the relationship between fog microphysics properties and visibility. Preliminary results in rain/fog are presented in Sect. 5.

4.1 Fog Microphysics and Environmental Conditions

A total of eight fog events in HELFOG and seven in C-FOG were identified and their mean properties are summarized in Table 1. The start and end of each fog event were nominally determined based on the presence of detectable droplets in the CDP-2 measurements of \({N}_{d}\). The HELFOG events lasted between 3.2 and 17.3 h, while the C-FOG events range from 5.6 to 31.3 h in duration. The data analyzed in this study contains 89/96 h of measurements in fog and/or mist during HELFOG/C-FOG projects. Figure 4a shows the temporal variation of LWC (\({q}_{l}\)), total number concentration (\({N}_{d}\)), and the effective radius (\({R}_{e}\)). All fog events are denoted at the top panel of Fig. 4 preceded with letters H and C denoting HELFOG and C-FOG events, respectively. For presentation purposes, all microphysical quantities in Fig. 4 were 5-min averaged to reduce the noise while retaining the correct magnitude for each variable. The statistical fog properties for each event are shown in the columns of Table 1 where the fog events are restricted to those data points with \({N}_{d}\) >1 cm-3 and \({q}_{l}\) > 0.001 g m-3.

Table 1 General characteristics of the observed fog events
Full size table
Fig. 4
figure 4

An overview of the observed fog properties. All variables shown were derived from the CDP-2 measurements averaged over a moving window of one minute. a HELFOG, and b C-FOG. Plotted is the LWC (\(q_{l}\), g m−3), droplet number concentration (\(N_{d}\), cm−3), and effective radius (\(R_{e}\), μm). The names for all fog events are shown at the top panels. Some non-fog periods were removed from (b) to allow sufficient space for the fog events on the time axis

Full size image

Some distinct differences in fog characteristics in the two geographic locations are seen in Fig. 4 and Table 1. Figure 4 shows that the LWC of the fog events from both locations is low and comparable in magnitude. The fog events observed from the same location can vary substantially especially in C-FOG where the vertical axis for \({N}_{d}\) needs to be plotted in logarithmic scale. Fog properties from the two locations are significantly different in droplet number concentration. The HELFOG cases show the mean droplet number concentration to be less than 10 cm−3 (except for the event H8) in general (Table 1), whereas in C-FOG, all identified fog events had a significantly larger number in the range of O(10) cm−3. The effective radius in HELFOG, on the other hand, is much larger than those in C-FOG.

The HELFOG fog events were consistently observed in weak westerly or south-westerly onshore flow, denoting their marine origin. Most of the fog events started in the late evening or later (H1, 3, and 6–8, local time = UTC –7 h) and the remaining initiated in the afternoon (H2, 4, and 5). All HELFOG fog events dissipated in the morning, with the latest (H1) at around 1100 LT. The last event, H8, has the highest LWC and \({N}_{d}\) and is a stark deviation from the other events. The wind direction and droplet size show this event may not be of marine origin, which is usually advection fog with larger droplets (Muhammad et al. 2007; Duthon et al. 2019). The C-FOG events do not show any correlation with a diurnal variation or associated specific wind direction. Aside from the variability in LWC, the C-FOG events show drastic variations in the mean droplet number concentration ranging between 8.3 and 63.2 cm−3 (Table 1). Despite the diversity in droplet number concentration, the mean effective radius of the droplets is consistently small at around 4.5–7.5 μm compared to the HELFOG droplets at 9.1–12.4. Overall, the variation of droplet size in each location is relatively small while there are large differences between HELFOG and C-FOG. The fog water at the same location is hence loosely determined by the droplet number concentration.

Mean droplet size spectra from all the fog events in Table 1 are shown in Fig. 5. Each spectrum in Fig. 5 is obtained by averaging each bin over the identified fog period. The HELFOG spectra show a bimodal distribution in six of the eight events with two local peaks at about 4-μm and 10-μm diameter, respectively. Overall, the 10 μm peak dominates the spectra. The H8 event was the dense fog event from HELFOG with a significantly large value of \({N}_{d}\). It shows a single peak around 10 μm and large number of droplets between 6 and 28 μm. The H7 event was the other event that did not follow the bi-modal distribution, but with a single peak at 4 μm, consistent with the other HELFOG events. Notably, this was also the most short-lived fog event in all observed cases. The C-FOG spectra are just as diverse as their number concentration. In general, for most of the events, small size droplets dominate the spectra, except for the C1 and C3 events. Interestingly, these are the two events without observed drizzle/rain, which were often found in the C-FOG fog events. The C5 and C6 events were under the influences of persistent rainfall (Sect. 5, Figs. 13 and 15). These two events had the highest number concentration in the small size range (Fig. 5b). However, the size distribution does not indicate measurable enhanced droplet concentration beyond 25 μm, likely because of the low sensor height above the ground (about 4 m). It is also possible that the rain/drizzle was from the saturated layer (cloud) above the fog layer, which was often present in C-FOG. Note Fig. 5 shows the size distribution as a function of droplet diameter. All droplet sizes discussed from this figure refer to diameter in μm.

Fig. 5
figure 5

Mean droplet size distribution measured by the modified CDP-2 probe from (a) HELFOG and (b) C-FOG. The legends correspond to the fog events in Table 1. Each spectrum was obtained by averaging over the entire period for each event given in Table 1

Full size image

A time-series view of a single fog event from C-FOG is shown in Fig. 6 to illustrate the temporal variability of the microphysical properties of fog and visibility. Table 1 shows that the C3 event was a dense fog event compared to the others in C-FOG, with a mean LWC close to 0.04 g m−3. The mean droplet number concentration from the C3 event also tops all other fog events with peak values exceeding 100 cm−3, a significant contrast to the advection fog observed in HELFOG. Figure 6 shows that the C3 event is composed of two fog patches with a short break in between. The two patches are different in their droplet size, about 5 μm of the effective radius during 0130 to 0240 UTC (first patch), and about 7 μm between 0300 and 0450 UTC (the second patch). The mean over the entire fog patch is about 6.4 μm (Table 1). It is interesting to note that the non-fog periods before and after each fog patch have a large droplet effective radius at about 11 μm, indicating the presence of mainly large droplets. The processes leading to the non-existence of the small droplets are worth exploring in future research with more data samples. Figure 6 also shows strong temporal variation within each fog patch. The short-lived sub-patches can be identified in both LWC and Nd plots, each lasting between 10 and 25 min.

Fig. 6
figure 6

Temporal variation of a LWC (g m−3), b droplet number concentration (# cm−3), c effective radius (μm); and d visibility (km) from the C3 event in C-FOG between 2338 Sept 13 and 0542 Sept 14, 2018, from The Downs, Ferryland, Newfoundland. The red dash line in (d) denotes visibility at 1 km. The two green double-arrow lines denote a fog period when visibility is less than 1 km

Full size image

The mean meteorological and turbulence conditions during the same fog event are shown in Fig. 7. As expected, the relative humidity is very close to 100% around the fog period and decreases slightly before and after, while there was no discernible variability of temperature associated with the event (Fig. 7a). The downward longwave radiation (Fig. 7b) was nearly constant except during the short break between the two fog patches with a slight decrease and variable downward longwave radiative flux. Both wind speed and the vertical velocity component (Fig. 7c, d) show reduced variability during the fog event, signalling reduced turbulence as suggested by many previous studies (e.g., Gultepe et al. 2021).

Fig. 7
figure 7

Temporal C-FOG C3 event shown in Fig. 6. a Temperature (T, °C) and relative humidity (RH, %), b downward infrared radiation (LWd, W m−2), c wind speed (WS, m s−1), and d the vertical velocity component (w, m s−1). The green double arrows denote periods of fog when visibility was lower than 1 km

Full size image

The temporal evolution of the vertical variation of temperature, humidity, and winds during the fog events can be seen from the time-height plots in Fig. 8 using data from multiple soundings. The thermodynamics of the low-level atmosphere have distinctive characteristics during the two field campaigns in different geographic locations. The HELFOG period covering the events H2 and H3 and C4 in C-FOG were selected because of the availability of multiple soundings. They also represent the typical vertical variations seen in each respective project.

Fig. 8
figure 8

Time-height plots of potential temperature, relative humidity, and wind speed from radiosonde measurements. The top panels are results from HELFOG covering H2 and H3 periods. The bottom panels are from the period C4 of C-FOG. The red downward triangles denote the fog layer top, the green downward and the blue upward triangles denote the cloud top and bottom, respectively, above the fog layer, all identified from the soundings by comparison of temperature and dewpoint temperature. The time of soundings used in the plots is shown as the short vertical magenta dash lines at the top of each subplot (14 soundings from HELFOG and six from C-FOG). The turquoise line on the potential temperature plot from C-FOG denotes the measured rainfall rate (R) from PWD-22 shown in centimeter per day (left axis). Fog/mist microphysical properties from the CDP-2, namely LWC \((q_{l} )\), droplet number concentration \((N_{d} )\), and effective radius \((R_{e} )\) are shown on the right axes (brown lines on each plot). All microphysical data shown were 10-min averaged to smooth out the short period variability solely for clarity purposes

Full size image

Figure 8 shows that the fog layer observed in HELFOG is quite uniform with a top at about 400 m persistently within each event. The layer is capped by a strong temperature inversion and a moisture lapse, and both the events H2 and H3 were in a relatively low wind speed of 2–4 m s−1. On the microscale, we still observed strong temporal variation of fog LWC and \({N}_{d}\), while the effective radius varied between 7 and 15 μm. Similar measurements from Newfoundland show strong temporal variability in the layers above. Event C4 shown in Fig. 8 was preceded by two rain events, each lasting for about an hour. The rain was no longer detectable when fog LWC and number concentration started to ramp up after 1430 UTC. The event C4 fog was always topped by a cloud layer. During the fog development stage, the cloud layer and the fog layer could not be distinguished from relative humidity alone as the entire layer was saturated. However, the temperature, wind speed, and direction (not shown) indicated the presence of two layers, which is evident in Fig. 9b (right panels) as an example. Figure 9b shows a shallow layer that is relatively well-mixed in potential temperature with the weak northerly wind at about 5 m s−1. This is the layer identified as the fog layer. The cloud layer aloft is stably stratified with respect to potential temperature and with significant wind shear. Although this cloud layer is also capped by an inversion, the inversion and moisture lapse strength are significantly weaker than the HELFOG case (Fig. 9a, left panels). The layering is vaguely present in the colour contours in Fig. 8. The fog layer top seemed to follow the 287 K potential temperature contour, while the cloud layer was slightly warmer. The clear region between the fog and the cloud layer aloft is very close to saturation if it existed. The C-FOG case also indicates that the fog layer dissipated quickly when the dry air mass (about 60% relative humidity) approached the area. The cloud base also lowered substantially resulting in a low ceiling at approximately 190 m above the surface towards the end of the fog event. It is also interesting to note that the C-FOG sounding on 26 September 2018 also shows two more layers above the cloud layer: each has correlated signals in potential temperature, relative humidity, and wind speed. This observation reveals the complexity of low-level airmass origin in this region, which may be one of the reasons for the large variation in fog microphysics observed in C-FOG. The evolution of the fog layers is likely tightly associated with mesoscale forcing and the associated horizontal advection.

Fig. 9
figure 9

Examples of the vertical profiles of wind and thermodynamic variables in (left) HELFOG (0755 UTC 17 July 2018), and (right) C-FOG (1935 UTC, 16 Sept 2018). The multi-layered vertical structure is shown in the C-FOG sounding in all variables

Full size image

4.2 Optical Attenuation and Fog Microphysics

Figure 6 shows an example of the variability of visibility with fog microphysical properties such as the LWC, number concentration, and effective radius. In this section, measurements from all 14 fog events are used to statistically evaluate the dependence of visibility on fog properties.

4.2.1 Visibility from Point and Path-integrated Measurements and Mie Theory

As discussed in Sect. 3.2, optical attenuation was obtained from three methods using different sampling principles. They each result in different variables to describe attenuation: transmittance (WATT) or scattering coefficients (PWD sensors, and Mie calculation based on measured droplet spectra). For comparison, results from all three methods are reduced to MOR based on Eq. 1 and shown in Fig. 10a using the HELFOG data. Note that the Vaisala PWD-10 has an upper limit of 2 km in its visibility measurements. The period with light fog/mist where visibility is larger than 2 km was made by WATT transmittance measurements. The WATT transmissometer was not available after 21 July 2018 during HELFOG; luckily, the fog events in the remaining days resulted in low visibility within the PWD-10 sampling range. The transmission data from HELFOG are hence a combination of the two sensors.

Fig. 10
figure 10

Variation of visibility (MOR) with LWC \((q_{l} )\) from a HELFOG, and b C-FOG fog events. Results from the C6 event are shown in the inset. The blue dots are from the PWD sensors, red from WATT (HELFOG only) and all green dots are results from the Mie calculation. Data shown here are 1-min averages

Full size image

Visibility is significantly affected by the scattering phase function of the air/particle/hydrometeor distribution and is thus directionally dependent (Petty 2004, Sect. 11.5.2). Both PWD-10 and PWD-22 measure light from forward scattering particles, which means the shape of the scattering phase function affects the measurements. The WATT transmissometer is affected by multiple scattering which also can be directionally dependent. This directional dependence in the intensity of light, even in conditions that seem isotropic to the human, could be the cause of some of the differences seen in the different types of MOR quantifications. Nevertheless, Fig. 10a shows that the MOR derived from the WATT and the PWD-10 were consistent when they overlap although their principle of measurements are different and they operate at different frequencies (875 nm for PWD-10 and 1064 nm for WATT). This result supports the notion that fog scattering is insensitive to wavelength (Isaac et al. 2001) in the visible/near-infrared wavelength range and the effects of multiple scattering are likely small or about equivalent in both sensors. We further compared the scattering coefficients using the Mie scattering calculation at the two wavelengths and found negligible differences. The combination of the WATT and PWD-10 measurements hence make up the ‘observed’ MOR for HELFOG without the need to differentiate the source of measurements.

The MOR–LWC plots in Fig. 10 show significant scattering, but a general trend of MOR decreasing with LWC is evident in data from both HELFOG and C-FOG. In HELFOG, a well-defined relationship between LWC and MOR is clearly seen, particularly in fog and mist conditions when MOR is less than 2 km. Substantial scattering is seen in high visibility conditions. These results are consistent with the dominant effects of liquid hygrometers in the ‘fog’ condition as defined by MOR < 1 km and the increasing role of aerosol attenuation as fog LWC decreases. The aerosol attenuation thus is one of the sources of the apparent scatters in the measured data points. An increased level of variability in the corresponding data from C-FOG is observed for six of the seven events: the correlation between MOR and LWC is weak in all visibility conditions although one still sees the general trend of increasing visibility with decreasing LWC. An added cause for the scatter of data points in C-FOG is precipitation, which tends to result in enhanced visibility attenuation. The inset in Fig. 10b depicts the case of C6 where the strongest impact of rain was found. The low visibility in this case seems to be independent of fog LWC. This case is further examined in Sect. 5.

Figure 10 also shows the comparison of the MOR from the two optical sensors with those calculated by the Mie theory based on the measured 1-min averaged droplet spectra. The Mie results follow the general trend of the observed MOR well, albeit with clear differences. In HELFOG, the MOR from the Mie calculation does not show significant variabilities compared to the C-FOG data, a consequence of larger variations in the fog droplet spectra in C-FOG. In visibility regimes dominated by fog and mist, nominally when MOR < 2 km, the Mie calculation represents the WATT/PWD-derived MOR well in HELFOG although Mie tends to underestimate MOR when LWC exceeds 0.02 g m−3 (Fig. 10a). It is not clear whether multiple scattering (not included in the Mie calculation) can explain this difference as the sampling volume of the PWD-10 is quite small and most of the HELFOG measurements occurred at night (weak effects of the ambient light source). Another possibility is the difference in the scattering phase function at different angles. However, testing this hypothesis is practically challenging.

In cases of MOR > 2 km, the same magnitude of MOR was observed in a broad range of LWC, many were lower than what is normally considered to have meaningful liquid water as fog/mist. Aerosols in haze must have contributed to the reduced visibility in the absence of precipitation detected in the HELFOG cases. Aerosol scattering/absorption becomes critical in determining visibility when MOR is greater than 5 km (Meyer et al. 1980). However, the CDP-2 measurements do not cover the small-sized dry and/or swollen aerosols. Therefore, scattering by aerosols is not included in the Mie calculation, resulting in Mie depicting the upper bound of the measured MOR seen in Fig. 10.

Interestingly, the overestimation of visibility by Mie calculation when MOR is above 2 km and the underestimate when MOR is below 2 km are both consistent with a similar study by Kunkel (1981) where droplet spectra were measured by an aspirated FSSP-100 on a tower. Hence, the result in Fig. 10 not only provides a better understanding of the MOR from different measurement sources but also provides confidence in our droplet measurements using the modified CDP-2.

4.2.2 Optical Attenuation and Liquid Water Content

The HELFOG data show a good correlation between LWC and visibility to allow the establishment of an empirical relationship. An exponential least-squares fit was made to the observed MOR–LWC data shown as the thick turquoise line (W21ql) in Fig. 11. The combined measurements of WATT and PWD-10 from HELFOG are shown as blue dots, and the PWD-20 measurements from C-FOG during the two non-precipitating fog cases (C1 and C3) are shown in red. The empirical best-fit function for the HELFOG data can be expressed as

$$ m = aq_{l}^{b} $$
(6)

where \(a = 0.146\) and \(b = - 0.63,\) the MOR m is in km and \(q_{l}\) in g m−3. The root-mean-square error (r.m.s.e.) for the fit is 0.95 km. Note this fitted function is for the MOR range up to about 7 km, much larger than the MOR range for fog/mist. The r.m.s.e. should be much smaller if the relationship is obtained for the fog/mist regime. For comparison, the results derived from K84 and G06 are also shown in Fig. 11. K84 provided an empirical relationship between the scattering extinction coefficient and LWC based on measurements in several fog events given as \(\sigma_{s} = 0.1447q_{l}^{0.88}\) where \(\sigma_{s}\) and \(q_{l}\) are in units of km−1 and g m−3. The resultant values of \(\sigma_{s}\) was converted to m through Eq. 1 using \(c = 3.0\). The K84 formulation has been widely used for visibility calculations based on fog LWC forecast (e.g., Stoelinga and Warner 1999) in mesoscale model simulations. Our results from HELFOG seem to depict a steeper increase of visibility with decreasing LWC in the fog/mist regime compared to the other parametrizations. As a result, K84 and G06 both seem to underestimate MOR in fog/mist conditions while G06 predicts a similar relationship of MOR with ql above 4 km in MOR. Recent work by Gultepe et al. (2021, hereafter G21) proposed MOR as a function of the fog index defined as the inverse product of LWC and Nd using the C-FOG measurements from the ship or at a coastal site close to the Downs at Ferryland. The G21 parametrization is not directly comparable with the parametrization in the discussion here because only the LWC factor is considered in Eq. 6. However, using our measurements from C-FOG non-precipitating fog cases (C1 and C3), we fitted a relationship of Nd as a function of the observed LWC. Hence, the function in G21 can be empirically converted to a MOR–LWC relationship shown also in Fig. 11. We can see that the G21 parametrization is very similar to K84, with both tending to underestimate visibility for a given LWC in the HELFOG cases. Note both K84 and G21 used measurements from the east coast with similar mean volume diameter (See Table 3 in K84 and compare to Table 1 for C-FOG here). The data used in G06 were also collected on the east coast, by a research aircraft mostly from low-level clouds. All three previous results from the east coast show similar parametrizations especially in fog cases (m < 1 km). Compared to all three parametrizations based on the east coast fog/cloud data, the west coast HELFOG data and parametrization (W21ql) show a stronger dependence of MOR on LWC in fog/mist conditions.

Fig. 11
figure 11

Visibility and LWC relationship with the HELFOG (blue dot) and C-FOG (red dot) data. The thick turquoise line (W21ql) denotes the fitted relationship from this study using the HELFOG data only. K84, G06, and G21 denote results from Kunkel (1984), Gultepe et al. (2006), and Gultepe et al. (2020), respectively

Full size image

Results of visibility variation with LWC from in C-FOG non-precipitating fog events are also shown in Fig. 11 (red dots). Here the C-FOG data points are very scattered in all visibility regimes. At LWC greater than 0.02 g cm−3, visibility was significantly reduced in most cases and appears to be consistent with the observations in HELFOG. However, there were also some instances with much larger MOR, which is not well-explained. Overall, the MOR–LWC relationship in C-FOG is not well defined even in cases with no detectable precipitation. We thus did not attempt to derive an empirical fit to this dataset. Nevertheless, all empirical relationships previously derived from the east coast measurements seem to fit the C-FOG measurements better than W21ql derived from the west coast fog with a larger droplet diameter. Hence, the MOR–LWC parametrization works well in general, but one should still explore an improved parametrization that is capable of representing MOR in a broad range of fog conditions.

4.2.3 Optical Attenuation and Droplet Number Concentration

Another category of visibility parametrization in foggy conditions relates MOR or scattering extinction \((\sigma_{s} )\) to the fog droplet number concentration \((N_{d} )\). This is expected given that LWC and \(N_{d}\) are linearly related with a factor of \(R_{v}^{3}\) (Eq. 3). Based on this relationship, MOR and \(N_{d}\) should follow the same power relationship as in the MOR–LWC relationship in Eq. 5 except with \(R_{v}^{3}\) in the coefficient

$$ m = aq_{l}^{b} = a\left( {\frac{4}{3}\pi R_{v}^{3} N_{d} } \right)^{b} = a\left( {\frac{4}{3}\pi \rho_{w} R_{v}^{3} } \right)^{b} N_{d}^{b} $$
(7)

Equation 7 indicates that MOR can be represented as a function of \(N_{d}\) only if the values of \(R_{v}\) stays relatively constant. Indeed, the fog events observed in the same geographic region have similar droplet sizes, although the regional differences can be quite large, as seen in Table 1 between HELFOG and C-FOG. As such, one can expect some success using the MOR–Nd parametrization, but such a relationship is limited to fog cases with similar \(R_{v}\), and prior knowledge of \(R_{v}\) is needed. The related variables that should go into the visibility parametrization have been extensively discussed in Gultepe et al. (2006, 2009, 2021).

Of course, one can still derive an empirical relationship between MOR and \(N_{d}\) from the measured data points using a direct empirical power relationship

$$ m = \alpha N_{d}^{\beta } . $$
(8)

With the HELFOG data, \(\alpha = 5.089\) and \(\beta = - 0.57\) with an r.m.s.e. of about 0.9 km when the input \(N_{d}\) is in cm−3, and m in km. The consistency between this method and that in Eq. 7 is examined next.

Figure 12 shows the measured MOR–\({N}_{d}\) relationship from both HELFOG (blue dots) and C-FOG (red dots) and the various parametrizations. The direct fitted line (Eq. 8) is shown as the thick black line. And the ones derived from the MOR–LWC relationship (Eq. 7 and the turquoise line in Fig. 11) are shown in turquoise lines: solid line for HELFOG and dash line for C-FOG using their respective MVR. In addition, selected formulations from previous work such as Meyer et al. (1980) and Gultepe et al. (2006) are shown in Fig. 12 as well.

Fig. 12
figure 12

Measured and modelled relationship between visibility and droplet number concentration. The measurements are shown in blue (HELFOG) and red (C-FOG) dots. The thick black line is the direct power function fit Eq. 8 using the HELFOG data. The W21ql_Nd lines follow Eq. 7 using the MVR from HELFOG (solid turquoise line) and C-FOG (dotted turquoise line). See text for discussions on the other model parametrizations

Full size image

Figure 12 again shows the larger scatter of data points in the C-FOG data compared to the HELFOG data. In general, the C-FOG fog layers resulted in less attenuation and hence higher visibility compared to those in HELFOG measurements, although the differences are less prominent in foggy conditions. The results from different locations do not collapse into a similar relationship, suggesting a slim chance of identifying a single formulation of the MOR–\({N}_{d}\) relationship that can fit various datasets. This is an expected outcome that can be explained by Eq. 7, where the coefficients from the power relations are dependent on the MVR. Note that the mean MVR is 8.9 μm in HELFOG averaged over all identified HELFOG events. In contrast, the value of \({R}_{v}\) from the event C1 and C3 averages to about 5.4 μm.

It is also seen in Fig. 12 that the two approaches expressed in Eqs. 7 and 8 provide similar results (thick turquoise and black lines) for the HELFOG data. Equation 7 applied to the C-FOG data using the averaged MVR qualitatively match the data from C-FOG data well, but there is too much scatter in the observed data to warrant any further quantitative analyses.

Meyer et al. (1980) analyzed measurements from nine cases of haze and fog over a large grassy area at Albany, New York. The encountered fog days were mostly radiation fog. In searching for the MOR–\({N}_{d}\) relationship, they found a marked discontinuity occurred in the 1–2 km region and provided the relationships for mist/haze and fog conditions separately. Their fitted functions are given in Fig. 12. Their relationship for the fog cases (m < 1 km) qualitatively matches the C-FOG observations well, but the mist/haze region is represented poorly, again the expected outcome since aerosol and haze are not included in our measurements. The fitted function from the G06 parameterization does not seem to represent the C-FOG or the HELFOG data. One needs to keep in mind, though, that G06 was based on data through the low-level-cloud environment. Since \({N}_{d}\) alone cannot fully represent the MOR variation with fog, the G06 formulation may have been derived from a population of cloud droplets with different droplet size properties.

5 Observed Precipitation Fog

The C-FOG measurements uniquely captured several fog events with concurrent measurable rainfall. During C-FOG, the rain was observed on and off throughout the period and accompanied by five of the seven fog events. Persistent rain and dense fog were measured from 28 September through the morning of 30 September (C5 and C6 periods). This period is shown in Fig. 13 as an example of mixed fog/rain events.

Fig. 13
figure 13

An example of fog and rain events observed during C-FOG. The double green arrows cover the period of mixed fog/rain (C5 and C6) and the red double arrows highlight the period with rain only without significant fog droplets. The blue vertical arrow points to an extremely light fog event resulting in significant visibility reduction. The blue and red vertical dash lines represent the start and end of the C5 and C6 periods, respectively. The units are mm h−1, g m−3, cm−3, μm, and km for rain rate (R), LWC \((q_{l} )\), total number concentration \((N_{d} )\), effective radius \((R_{e} )\), and visibility (m), respectively

Full size image

Several important observations can be made in Fig. 13. First, although two major fog events were identified during this period, the presence of a small number of water droplets is often seen in other periods. The extremely light fog period without rain between 1630– 2016 UTC on 28 September (blue downward arrow, not included as a fog event in Table 1) also resulted in significantly reduced visibility. Second, the measurable fog droplets seem to be associated with periods of rain, either during or right after the rain event. However, the fog liquid water and droplet number concentration do not seem to be correlated with the rain rate shown in Fig. 13a. And third, a substantial reduction in visibility occurred in both fog and rain events or a mixed rain/fog event. In Fig. 13, the two fog events are highlighted by green double arrows while the two rain-only events are also highlighted with red double arrows. The same notations are also shown in Fig. 13e to highlight their impact on visibility. These events plus the very light fog period make up the periods of all reduced visibility.

The temporal variation of the atmospheric conditions at The Downs site during the periods C5 and C6 is shown in Fig. 14 to illustrate the evolution of temperature, relative humidity, wind speed, and wind direction associated with the fog/rain event. During the period C5, the lowest 2 km of the atmosphere was nearly saturated at all levels. However, the individual sounding taken around 0230 UTC on 28 September 2018 during period C5 still shows a multi-layered structure with two saturated layers, one below 500 m, which is the fog layer, another between 900 and 1220 m (individual sounding not shown). It is not clear if the precipitation was generated by the fog layer or from the cloud layer above. The CDP-2 measurements were taken at about 4 m above the surface. Its measured spectra are likely different from the upper fog layer, particularly in the large-size bins. The atmospheric conditions during the C6 event are very different. There was a single saturated layer at the surface with depth varied between 200 and 800 m. The precipitation was hence generated by the fog layer itself, although the droplet spectra near the surface still show few droplet sizes above the 20 μm bin. This long-lasting event (31 h in duration) has strong wind shear immediately above the fog layer top and strong wind extending to above 3 km above the surface at the end of the event. Figure 14d shows period C6 ended with a drastic change of the wind direction to northerly wind, reduction of mid-level wind speed (Fig. 14c), and cooling of the low levels (Fig. 14a), accompanied by much stronger rainfall and a deeper saturated layer above 3 km level (Fig. 14b). These are all indicative of mesoscale forcing in the evolution of the fog event involving precipitations.

Fig. 14
figure 14

Vertical variability of a potential temperature, b relative humidity, c wind speed, d wind direction from soundings during the periods C5 and C6. The right axes are for fog droplet properties. All other notations are the same as in Fig. 8

Full size image

Representing visibility in the rain/fog condition is challenging, as shown in Fig. 15 using a single rain/fog event (C5) highlighted on the background of all C-FOG data. Here, we find that the Mie theory and the derived MOR–LWC parametrization in Eq. 5 represent the upper limits of visibility at a given LWC. In fog with moderate LWC, the Mie theory still does a decent job in predicting MOR, suggesting that fog is the dominant factor for reducing visibility even when it is during the rain period. When fog LWC is low, other factors significantly reduced visibility from the Mie- or Eq. 5-predicted values. The low visibility completely uncorrelated with LWC, normally at small LWC, shows the impact of rain. These results are some initial observations from a single case. Unfortunately, insufficient concurrent and collocated rain microphysics data were collected to allow further investigation. However, comparing the observed MOR and rain rate in rain only conditions (Fig. 13, red double-arrow periods), the magnitude of visibility reduction seem to match those from Gultepe and Milbrandt (2010, Fig. 6) for drizzle conditions where visibility greater than 10 km is expected for the larger droplets of rain at the same rain rate.

Fig. 15
figure 15

Visibility variation with LWC in a precipitating fog event (C5). All C-FOG data are shown in the background as grey dots

Full size image

6 Summary and Conclusions

In this work, we analyzed measurements from two field campaigns, HELFOG and C-FOG, to investigate the characteristics of fog microphysics, thermodynamics, and the impact of fog and rain on optical propagation through the lower atmosphere. In both field campaigns, fog microphysics were measured by a CDP-2 droplet spectrometer modified to include forced aspiration and flow-speed measurements near the sampling volume. The modification was intended to improve the accuracy of droplet spectra measurements by capturing the instantaneous flow rate through the sampling volume. Concurrent measurements of optical attenuations were also made by visibility meters (PWD10 and PWD22) as well as a path-integrated transmissometer (WATT). Our main findings can be summarized as the following:

  1. (1)

    The fog events in HELFOG, mostly advected marine fog, are characterized by low number concentration and relatively large droplet diameter compared to those in C-FOG. Bimodal distributions of the size spectra were frequently observed in HELFOG. Many of the C-FOG fog events were accompanied by precipitation at the surface and are characterized by small droplets and comparatively high number concentration.

  2. (2)

    The low-level atmosphere in the C-FOG region shows a multi-layered vertical structure in wind, temperature, and humidity, a direct result of the advection of air from different origins at different altitudes. Mesoscale disturbances may have played an important role in the fog development in this coastal region, particularly associated with low-level convective events leading to enhanced low-level water vapour and precipitation.

  3. (3)

    In HELFOG, the attenuation measurements from PWD10 based on droplet forward scattering are consistent with the total transmittance measurements from WATT, suggesting the dominant role of scattering in fog attenuation. The results also confirmed that fog scattering is insensitive to wavelength within the visible to near-infrared range. Since the propagation path was relatively short (600 m), the difference between the point measurements of PWD10 and the path-integrated measurements of the WATT is small. This may not be true in the case of strong heterogeneity within the fog.

  4. (4)

    MOR based on Mie scattering calculation using the measured droplet spectra compares well in general with the optically measured MOR. However, there may be an underestimate of MOR through the fog. On the other hand, Mie theory overestimates MOR in light fog/mist because the aerosol effects are neglected.

  5. (5)

    While the MOR–LWC parametrizations in the literature derived from measurements on the east coast of the U.S. fit the C-FOG data better, they all slightly underestimate the measured MOR from HELFOG. Meanwhile, the large scattering of datapoints in C-FOG points to impacts from other variables in addition to LWC. For improved accuracy of such representation, more data from different regions are needed to further evaluate the differences seen in this study.

  6. (6)

    The MOR–\({N}_{d}\) parametrization cannot realistically represent MOR without the droplet size information. This is confirmed using measured fog properties in different locations. However, the MOR–\({N}_{d}\) relationship is well-defined for a given population of fog with known mean droplet size.

  7. (7)

    Precipitation in the fog was frequently observed on the Newfoundland coast and affects optical propagation differently from fog droplets as also indicated by Gultepe and Milbrandt (2010). Future research on the topic of optical attenuation in fog should include a full characterization of precipitation microphysics.

It is noted that the dataset based on which the visibility parametrization was derived shows a very large scatter. This is an indication that factors other than LWC or \({N}_{d}\) are affecting optical propagation and the inference of visibility from LWC or \({N}_{d}\) are at best be crude estimates. Nevertheless, the merit of such parametrization is the general trend in the results. The presence of a general relationship between the two variables (MOR–LWC or MOR–\({N}_{d}\)) is indicative of the dominant effects of LWC or \({N}_{d}\) on visibility. Our results suggest that the two types of relationship are not independent because LWC and \({N}_{d}\) are proportional with a factor proportional to MVR cubed. If the MOR–LWC relationship holds for all fog cases, the MOR–\({N}_{d}\) relationship is still dependent on the droplet size. Hence, a universal MOR–\({N}_{d}\) relationship does not exist. In fact, in the original paper by Koschmieder (1924), the impact of mean droplet size, represented by the root-mean-square diameter squared, on the visual range was also discussed. Meyer et al. (1980) also examined the MOR-root-mean-square diameter relationship and identified a clear relationship between MOR and the droplet size in cases of fog. As a result, both number concentration and droplet size should affect visibility, which points to LWC as a combination of both variables. The next logical question would be: is LWC the most appropriate combination of droplet number and size to represent optical attenuation? Gultepe et al. (2021) and several previous papers suggested the fog factor that brings less scatter to the data points than LWC or \({N}_{d}\). This is likely a solution, although other likely alternatives based on physical arguments should also be explored. Above all, more observations in a broad range of fog events should be most beneficial.