Abstract
In the stable boundary layer, thermal submesofronts (TSFs) are detected during the Shallow Cold Pool experiment in the Colorado plains, Colorado, USA in 2012. The topography induces TSFs by forming two different air layers converging on the valley-side wall while being stacked vertically above the valley bottom. The warm-air layer is mechanically generated by lee turbulence that consistently elevates near-surface temperatures, while the cold-air layer is thermodynamically driven by radiative cooling and the corresponding cold-air drainage decreases near-surface temperatures. The semi-stationary TSFs can only be detected, tracked, and investigated in detail when using fibre-optic distributed sensing (FODS), as point observations miss TSFs most of the time. Neither the occurrence of TSFs nor the characteristics of each air layer are connected to a specific wind or thermal regime. However, each air layer is characterized by a specific relationship between the wind speed and the friction velocity. Accordingly, a single threshold separating different flow regimes within the boundary layer is an oversimplification, especially during the occurrence of TSFs. No local forcings or their combination could predict the occurrence of TSFs except that they are less likely to occur during stronger near-surface or synoptic-scale flow. While classical conceptualizations and techniques of the boundary layer fail in describing the formation of TSFs, the use of spatially continuous data obtained from FODS provide new insights. Future studies need to incorporate spatially continuous data in the horizontal and vertical planes, in addition to classic sensor networks of sonic anemometry and thermohygrometers to fully characterize and describe boundary-layer phenomena.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Submesoscale motions, called ‘submeso motions’ hereafter, are defined by their typical temporal and spatial scales, and due to their significance are added to the classification established by Orlanski (1975). According to this definition, a range of motions fall into this category including meandering, solitary waves, gravity waves, wave-like motions, and microfronts. The detection of submeso motions is usually performed based on tower data by analyzing case studies of meandering (Cava et al. 2019a), by using the Haar-wavelet (Mahrt 2019), by analyzing spectra and thus their temporal scale (Stiperski and Calaf 2018), by identifying meandering with autocorrelation functions (Anfossi et al. 2005), or by using autocorrelation functions to determine oscillations within several parameters, like horizontal and vertical wind speed, temperature, and other scalars (Kang et al. 2014, 2015; Mortarini et al. 2017; Stefanello et al. 2020).
Submeso motions usually occur during weak large-scale flow and are distinctive features of the stable boundary layer (SBL) (e.g., Mortarini et al. 2019). Because the turbulence structure and vertical exchange in the SBL are altered during the occurrence of submeso motion, such phenomena are worth investigating in detail. Stiperski and Calaf (2018) found that submeso motions are likely to significantly alter the isotropy of turbulence and thus require different scaling methods within the SBL. Further, a follow-up study of Vercauteren et al. (2019) related this anisotropy to the activity of submeso motions. Meandering within the SBL influences horizontal and vertical exchange processes (Cava et al. 2019a), and affects scalar dispersion, flux patterns, and the surface energy balance (Stefanello et al. 2020). Usually the short-term variability of the near-surface temperature during the presence of submeso motions significantly exceeds the nocturnal trend (Mahrt et al. 2020). Submeso motions may be related to low-level jets and corresponding turbulent down-bursts (Mortarini et al. 2017; Cava et al. 2019b).
As described in Part 1 (Pfister et al. 2021), we were able to detect and track the propagation of a specific submeso motion, which we call a thermal submesofront (TSF). Here we focus on the vertical exchange processes during the presence of TSFs, as vertical exchange processes are important for determining when z-less scaling cannot be applied in the SBL. To date, most studies have used tower or vertical profile observations to investigate submeso motions. We therefore define our first objective as setting the occurrence of TSFs in the context of existing studies by focusing on the vertical exchange while the fibre-optic distributed sensing (FODS) technique offers a much richer set of information. As additional objectives, we further investigate the implications of TSFs on the SBL, as well as their relation to commonly used alternative approaches to classify the boundary layer, including wind regimes defined by the relation of wind speed to a turbulence statistic (Sun et al. 2012), or thermal regimes defined by the relation of the Obukhov length to the sensible heat flux (Mahrt 1998).
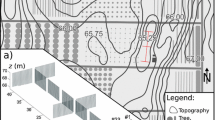
The use of the FODS technique enables the detection and tracking of the propagation of TSFs in time and space (cf. Sect. 2). Thermal submesofronts consist of two contrasting air layers, as shown in a conceptual drawing in Fig. 1. A summary of Part 1 is given in Sect. 3. As FODS was an essential tool, we compare the spatial continuous FODS measurements with point observations (Sect. 4.1). Utilizing multiple observations from a tower, the layered structure of TSFs is further investigated with regard to vertical exchange processes (Sect. 4.2). For clarifying the forcings of TSFs, which create the two distinctly different air layers, parameters such as topography, the near-surface and synoptic velocity field, static stability, and radiative forcing are investigated (Sect. 4.3). The manuscript closes with a discussion on the implications of TSFs for the SBL (Sect. 4.4), recommendations for further studies (Sect. 4.5), and the conclusion (Sect. 5).
Conceptual drawing (cf. Pfister et al. 2021) of a TSF (not to scale) within the valley (grey areas) consisting of a warm-air layer (red) and a cold-air layer (blue). Coloured arrows indicate the different flow direction of the air layers, while black swirls indicate the topographically-induced mixing. At the transition area, where the air layers merge, the warm-air layer is pushed upwards (black arrow) as the cold-air layer acts as a barrier
2 Field Site and Methods
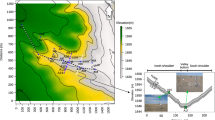
The data from the Shallow Cold Pool (SCP) experiment are used in our analysis (please see Pfister et al. 2021 for a complete overview). The experiment was conducted in north-east Colorado, U.S.A., over semiarid grassland at approximately 1660 m above mean sea level from 1 October to 1 December 2012 (https://www.eol.ucar.edu/field_projects/scp). Measurements incorporating FODS (Ultima SR, Silixa, London, UK) make it a unique study, while other more traditional observations include a network of ultrasonic anemometers (Model CSAT3, Campbell Scientific, Logan, Utah, U.S.A.) with 19 stations at 1 m above ground level (a.g.l.) and eight stations on a 20-m tower, and an acoustic wind profiler (sodar, PCS2000-24, Metek GmbH, Elmshorn, Germany). FODS measurements were conducted from 16 November until 27 November. This study analyzes the nine nights with FODS data without observational gaps from 1900 LT (local time = UTC − 7 h) until 0500 LT. A topographical overview with the instrumentation is shown in Fig. 2. There is open access to the data of the network through the Earth Observatory Laboratory of the National Center for Atmospheric Research, while the FODS technique, and wind profiler are published on Zenodo (Pfister et al. 2020).
Left: Topographical overview of field site with ultrasonic anemometer stations (A1−A19), the 20-m main tower (M), and the FODS transect (white line). Right: Cross-valley view of the fiber-optic transect showing its length and elevation (after Pfister et al. 2021)
Reynolds decomposition is applied to determine temporal and spatial perturbations with a perturbation time scale of 60 s (Pfister et al. 2021). To determine turbulence characteristics, the friction velocity \(u_* = \left( \overline{u_s'w_s'}^2 + \overline{v_s'w_s'}^2 \right) ^{0.25}\) and sensible heat flux \(Q_\mathrm{H} = \rho ~c_p~\overline{w_s'T'}\) are computed from the ultrasonic-anemometer measurements with \(u_s\), \(v_s\), and \(w_s\) being the west, south, and vertical velocity components of the velocity, T the temperature as measured by each ultrasonic-anemometer station, \(\rho \) the air density, and \(c_p\) is the specific heat at constant pressure. The meteorological sign convention is used with a negative sign representing a flux towards the surface, while a positive sign indicates a flux away from the surface. The Obukhov length L is defined as \( L~=~ - u_*^3 ~~ \left( \kappa ~~\overline{w_s'T'}~~g~T^{-1} \right) ^{-1}\), where \(\kappa \) is the von Karman constant, g is the acceleration due to the gravity, and T is the reference air temperature.
The third-order moment (TOM) of the vertical velocity component \(\overline{w'^3}\) and the sensible heat flux \(\overline{w'T'w'}\) are computed with the same perturbation time scale and compared with their second-order moment (SOM) to determine the direction of turbulent transport. Accordingly, TOM shows how efficient and in which direction turbulence was transported, while SOM shows how strong the turbulence quantity was. The unrotated values of \(w_s\) are used for the computation of TOM and SOM to ensure a consistent coordinate systems, which enabled a comparison of observations from all heights on the main tower.
Mean values and the standard deviation of the wind direction \(\varphi \) are computed by the method of Yamartino (1984). For conditional averaging, any parameter \(\phi \) is averaged over all samples fulfilling a specific condition and is marked by angular brackets \([\phi ]\).
The bulk Richardson number \(Ri_\mathrm{B} = \frac{g~~\Delta \theta \Delta z^{-1}}{{\overline{\theta }}~~(\Delta u \Delta z^{-1})^2}\) is computed for the FODS transect, with \({\overline{\theta }}\) being the mean layer temperature and \(\Delta \theta \Delta z^{-1}\) and \(\Delta u \Delta z^{-1}\) being the vertical potential temperature and wind-speed gradients at each measurement point within the FODS transect, respectively. \([Ri_B]\) is calculated based on the conditionally-averaged quantities of \([{\overline{\theta }}]\), \([\Delta \theta \Delta z^{-1}\)], and \([\Delta u \Delta z^{-1}]\).
To analyze topographical effects on the flow, the Froude number \(F_\lambda \equiv v_{20}~N^{-1}~\lambda ^{-1}\) is computed by using the Brunt−Väisälä frequency \(N = \sqrt{g \theta _0^{-1} \Delta \theta (\Delta z)^{-1}}\), with \(v_{20}\) being the north−south component of the velocity at 20 m a.g.l. (which is assumed to be the advection speed for flows over the north shoulder), \(\lambda \) a characteristic length scale of the topography (here defined as the distance between the valley shoulder and the main tower in the valley), \(\theta _0\) the layer mean temperature, and \(\Delta \theta (\Delta z)^{-1}\) the vertical temperature gradient. The Froude number \(F_\lambda \) decreases during conditions with a higher impact of topography on the flow.
3 Summary of Thermal Submesofronts from Part 1
Thermal submesofronts were detected using the spatially continuous FODS technique (cf. Pfister et al. 2021 and Sect. 4.1). The main characteristic of TSFs are the two air masses with contrasting characteristics (Figs. 1, 5a). We refer to those air masses as layers as they are vertically stacked above the valley bottom, and hence were detected as such at the main tower. In contrast, on the north shoulder of the valley the air layers are in contact with the ground and converge (Fig. 1). As the horizontal scale of the TSFs was on the order of 200−300 m (Fig. 5) and lasted between 40s and 1 h, they classify as submesoscale motions. Thermal submesofronts had a mean advective velocity of 0.2 m s\(^{-1}\). The mean temperature decrease from the warm to the cold air was 3.4 K (Fig. 3a). The cold-air layer most likely originates from non-local cold-air advection as a result of radiative cooling, and has enough momentum to move uphill of the north shoulder of the valley. At this location, the warm-air layer is formed by topographically-induced turbulence which increases near-surface temperatures. Consequently, the topography plays a dominant role in forming TSFs (Sect. 4.3.1). At the TSF boundary, the warm air is forced upwards as the cold-air layer with high density acts as a barrier. Further on, we refer to the interface where the TSF air layers converge as a transition area. TSF mostly occur during weak flows at 20 m a.g.l. with a mean wind speed of 3.5 m s\(^{-1}\) and are absent during a strong and spatially homogeneous near-surface flow when the cold-air layer is presumably eroded by the intense mixing. The presented mean statistics do not give insights into the time evolution of TSFs, thus, vanishing TSFs actually represents TSFs that suddenly disappear or do not form at all.
The main analytical feature of Part 1 is the conditional averaging of various parameters depending on the distance of the measurement location to the TSF boundary. In Fig. 3, we present the most important conditionally averaged parameters leading to the description of TSFs as summarized above and used in the discussion below.
4 Results and Discussion
4.1 Comparison of Detection Techniques for Thermal Submesofronts
As TSFs are formed by two competing air layers (Sect. 3), a passing TSF generates abrupt changes in point observations, such as of temperature, wind speed and direction, as well as of turbulence characteristics (Fig. 3). Accordingly, TSFs have a significant impact on near-surface flow statistics and need to be detected precisely.
A frequently passing TSF may cause meandering, which was observed in the time series of two case studies (Fig. 14a, b). For example, Eulerian autocorrelation functions might be used to determine the occurrence of TSFs as they use the change in wind direction in combination with scalars such as temperature or gas concentration to detect meandering (Mortarini et al. 2019; Stefanello et al. 2020). But even though near-surface meandering is connected to TSFs, meandering at higher levels or within other field campaigns can also be caused by other types of motions such as gravity waves. Another option for detecting TSFs might be a clustering method as presented by Vercauteren and Klein (2015), as the slow moving TSFs enhance the variance of the vertical velocity component \(\overline{w'w'}\) (not shown). Other studies, including Lang et al. (2018), investigated the propagation of structures between towers by a cross-correlation function method, however, their sampling was done on 20-min time scales and are much longer compared to this study.
Most important parameter describing TSFs (1-min averages) which are conditionally averaged depending on their distance to the boundary of the fronts from Part 1 (Pfister et al. 2021). Fibre-optic measurements of a spatial temperature perturbation \([{\widehat{\theta }}]\) and, b the bulk Richardson number \([Ri_\mathrm{B}]\) derived from the ratio of the buoyancy gradient \([\Delta \theta ~\Delta z^{-1}]\) to the wind shear \([\Delta u~\Delta z^{-1}]\) as well as ultrasonic anemometer measurements showing, c the mean wind direction \([\varphi ]\), d mean wind speed [V], e sensible heat flux \([Q_\mathrm{H}]\) and, f friction velocity \([u_*]\)
Irrespective of the method used to detect a submesoscale motion such as TSFs, knowing its location in the context of the topography is important. To give an example: for the SCP experiment, all observations on the south shoulder as well as stations near the valley bottom and the 20-m tower missed TSFs completely or most of the time, as the TSF did not pass them or passed the tower so slowly that instationarities usually caused by the passage became negligible. For 16% of all occurrences with TSFs, either station A15 or A17 was within the transition area of TSFs but not every station was necessarily passed by the TSF. As a TSF is only detected by a station when passing, the actual detection of TSFs from each point observation is even lower. Even though the SCP experiment featured an extraordinarily dense classical sensor network, TSFs were mostly invisible even when using all point observations. Further, tracking the propagation and movement of TSFs between the stations is aggravated or impossible as the minimum station spacing was 40 m, thus the actual location of TSFs remains unknown until the TSFs pass the next station. Accordingly, the semi-stationary uphill and downhill motions of TSFs cannot be tracked as the TSF is most of the time between stations.
Consequently, spatially continuous observations from FODS are ideally suited to detecting TSFs.
4.2 Vertical Structure of Thermal Submesofronts
Thermal submesofronts occur during lower wind speeds resulting in weaker turbulent transport. This could be observed at the main tower by the strength and sign of SOM and TOM of the vertical velocity component and the sensible heat flux (Fig. 4, green). The lowest two levels have very limited vertical transport of vertical variance as shown by \(\overline{w'^3}\) (Fig. 4a) as well as low vertical mixing \(\overline{w'w'}\) (Fig. 4b), both indicating a decoupled layer as turbulence intensity is small and turbulence is not transported downwards. At 2−5 m a.g.l. SOM and thus the turbulence intensity increased with height, while TOM and thus the downward transport of SOM decreased. We conclude that these levels are affected by downward mixing of warm air eroding the cold-air layer. Accordingly, the cold-air layer has a vertical extent between 1 and 3 m depending on forcing conditions and is decoupled from the layers above inhibiting vertical exchange. This is in concordance with the estimation of the cold-air layer within Part 1 (Pfister et al. 2021).
Profiles of the third-order moment of the a vertical velocity component \(\overline{w'^3}\) and c sensible heat flux \(\overline{w'T'w'}\) on the main tower and the corresponding profiles of the second-order moments b \(\overline{w'w'}\) and d \(\overline{w'T'}\) during the occurrence and absence of TSFs. Areas: inter-quartile range (IQR)
The 10-m level shows no preferential transport direction for the low values of \(\overline{w'w'}\), while for \(\overline{w'T'w'}\) the opposite is the case with peak values of \(\overline{w'T'}\) and \(\overline{w'T'w'}\) as shown with green colours (Fig. 4). At the 20-m level SOM and TOM of the momentum and sensible heat flux are close to zero, hence not transport of turbulence. We conclude that at 10 m a.g.l. the flow is adjusting to the regional flow, while at 20 m a.g.l. an equilibrium is reached with the regional flow. Given this interpretation, the warm-air layer is located approximately between 2 and 20 m a.g.l. depending on forcing conditions.
Thermal submesofronts vanish during a strong and spatially-homogeneous near-surface flow during which the cold-air layer is presumably eroded (Sect. 3), which could be confirmed by TOM and SOM (Fig. 4, black). The turbulent transport terms \(\overline{w'^3}\) and \(\overline{w'T'w'}\) have a s-shaped profile with an inflection point at \(z \approx 4\) m. Above \(z = 4\) m, the transport of \(\hbox {SOM}\) is directed upwards for continuity reasons as the absolute values of \(\overline{w'w'}\) and \(\overline{w'T'}\) decrease dramatically from 10 m to 20 m. The strongly negative value of \(\overline{w'^3}\), especially near the ground, reveals the efficient downward transport of turbulence. As \(\overline{w'T'}\) near the surface is relatively high and negative, the positive values of \(\overline{w'T'w'}\) also indicate an efficient downward transport of the sensible heat flux. Consequently, during the absence of TSFs, the cold-air layer is eroded and the boundary layer is well connected with the surface.
4.3 Forcings of Thermal Submesofronts
4.3.1 Topography
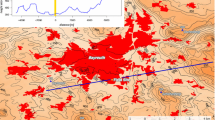
Existing studies confirm that topography can induce mixing and thus enhances near-surface temperatures, on the one hand (Turnipseed et al. 2004) but on the other hand, the topography also plays an important role for cold-air drainage and pooling (Soler et al. 2002; Vosper and Brown 2008). During the occurrence of TSFs, the warm-air layer is formed mechanically by topographically-induced turbulent mixing on the north shoulder, while the cold-air layer is formed thermodynamically by radiative cooling and corresponding cold-air drainage within the valley (Sect. 3). This is confirmed by the mean location of TSFs within the network (Fig. 5a) as well as by the elevated turbulence statistics at the plateau edge on the north shoulder (Fig. 5b). The air layers of TSFs move in different directions (Fig. 3c) as the cold air follows the topography while the flow within the warm-air layer is aligned with the regional flow (Fig. 5).
Overview of field site with elevation shown by contour lines (dark blue). a The mean spatial temperature perturbation, \([{\widehat{\theta }}]\), and b the mean friction velocity, \([u_*]\), during the occurrence of TSFs is added by filled contour lines (see colour scale). Black arrows show flow direction and strength
The role of topography on the near-surface flows is quantified using the Froude number \(F_\lambda \). During the occurrence of TSFs, \(F_\lambda \) is lower with a mean of 0.2\(~\pm ~\)0.1, while during there absence \(F_\lambda \) is larger (0.7\(~\pm ~\)1.4). Similarly, the median of \(F_\lambda \) is only half as high during the occurrence than during the absence of TSFs. As lower \(F_\lambda \) values are expected for a flow strongly affected by topography, we conclude that during conditions in which TSFs form, the topographical effects on the flow are strong, and that even gentle terrain has a significant impact on the near-surface temperature and on the flow.
In summary, even for gentle terrain topographical effects are significant. Any field site with a similar geometry featuring a valley deep enough to provide some mechanical sheltering and with a relatively pronounced elevation change of 6\(^\circ \) at the shoulder can potentially form TSFs. As an example, Mahrt (2019) describes submeso motions at three different field sites including TSFs within the SCP experiment.
4.3.2 Near-Surface Wind Speed
A minimum required wind speed was expected for the topographically-induced turbulent mixing forming the warm-air layer, as well as for the erosion of TSFs. However, no minimum wind speed for the generation of the warm-air layer could be detected. Nevertheless, the maximum wind speed for which TSFs persisted is 3.4\(~\pm ~\)0.3 m s\(^{-1}\) as determined by averaging over the maximum of all 1-m stations except A9. Contrary to the network mean, this station, which is located on the north shoulder, detects wind speeds up to 4.6 m s\(^{-1}\), most likely because of the reduced sheltering compared with the stations within the valley. Above 3.4 m s\(^{-1}\), the cold air within the valley and thus TSFs are presumably eroded due to mixing. Below this threshold, the wind-speed distribution during the occurrence and absence of TSFs is similar (not shown); hence, TSFs can, but do not necessarily, occur at moderate wind speeds. Consequently, TSFs are related to, but not dominated by, the strength of the near-surface flow and most likely further forcings are involved in forming TSFs.
Thermal submesofronts do not move with the mean flow as their advective velocity and thus propagation is an order of magnitude lower (cf. Sect. 3). Nevertheless, TSFs barely protruded into the valley during low wind speeds at station A9, while they protruded far into the valley during high wind speeds at A9 (Fig. 13). Consequently, the location of the TSF boundary is modulated by the magnitude of the near-surface wind speed. We assume that the horizontal extent of the warm-air layer and thus the TSF movement is influenced by the near-surface flow pushing the TSF boundary down the north shoulder during increasing wind speeds. To test this hypothesis, the correlation between the fluctuation of the north−south component, \(v_s - \overline{v_s}\), and the change in the TSF location, \(x_\mathrm{TSF} - \overline{x_\mathrm{TSF}}\), is evaluated during each TSF event (Fig. 6a, b). The bar in this case indicates temporal averaging over the TSF duration. The vectorial component \(v_s\) is chosen for this analysis as it is aligned with the FODS transect and represents the TSF dislocation better than the mean wind speed. The stations A9 and A15 are chosen for this analysis as both were located on the north shoulder. For both stations, a change in the value of \(v_s\) and thus wind speed was substantially correlated to a change in the value of \(x_\mathrm{TMF}\) representing the dislocation of TSFs. The data from the station A15 had higher coefficient of determination \(R^2\) and a smaller slope than the data at station A9. We suspect that the correlation at A9 is smaller because this station was further away from the FODS transect where TSFs were detected and thus it does not represent the TSF movement as well as A15. From this, we conclude TSFs do not advect with the flow, but their location responds to a change in wind speed, which agrees well with Lang et al. (2018).
Variation of the north–south component of the velocity \(v_s - \overline{v_s}\) plotted against the variation of the TSF boundary location \(x_\mathrm{TSF} - \overline{x_\mathrm{TSF}}\) determined during each TSF event for, a station A9 on north shoulder, and b station A15 half-way uphill on the north shoulder. c Duration of TSF events plotted against the mean wind speed at A9
As the TSF location is correlated to the wind speed, we also checked if a similar relationship existed for the duration of TSFs (Fig. 6c). Different stations were evaluated, however, the relation between the TSF duration and wind speed is rather obscure.
In summary, moderate wind speeds cause topographically-induced mixing and thus generate the warm-air layer and force the TSF boundary further down the shoulder. We conclude that, especially for the warm-air layer, the near-surface wind speed plays a role particularly for the TSF boundary location, while it is unrelated to the TSF duration.
4.3.3 Synoptic Wind Speed and Direction
Larger-scale forcings for the formation of TSFs were analyzed with the wind profiler and the 20-m high main tower. During TSFs, the maximum wind speeds in the lowest levels from 0.5 to 100 m range from 2.4 up to 12.4 m s\(^{-1}\), but TSFs vanished for wind speeds higher than 12.4 m s\(^{-1}\) in the lowest 100 m. However, there was no clear wind-speed threshold for TSFs at any level as the inter-quartile ranges of the wind speed V during the occurrence and absence of TSFs overlapped (Fig. 7a). While some studies (e.g. Cava et al. 2019b) showed that submeso motions are related to low-level jets, during the occurrence of TSFs no low-level jets were observed.
Conditional averaging of a wind speed [ V ] and b wind direction \([~\varphi ~]\) during the occurrence (green) and absence of TSFs (black). Inverted triangles and crosses: 20-m tower; triangles and stars: wind profiler; shaded areas: inter-quartile range (IQR) of [ V ] and standard deviation of \([~\varphi ~]\)
During the absence of TSFs, the wind-speed profile indicates a coupled boundary layer as it had an exponential shape with matching speeds at the main tower and the lowest wind profiler gates (Fig. 7a, black line) even though they were 100 m apart. This finding suggests that the wind speed and direction were spatially homogeneous. Besides, the larger-scale flow changed direction from west to north-west near the surface, which is probably caused by the regional topography being oriented north-west and thus forcing the near-surface flow into this direction.
Usually an exponential wind-speed profile is assumed for the boundary layer, however, during TSFs, wind speeds from 50 to 100 m a.g.l. were constant and only gradually increased at higher levels (Fig. 7a, green line). Further, the mean wind speed at all levels was lower during the occurrence than during the absence of TSFs. Significant wind-directional shear was evident, as the wind direction turned from south-west at levels higher than 155 m, to north-west at 20 m, and then to west near the surface (Fig. 7b). Furthermore, wind speed and direction were spatially inhomogeneous as the tower and sodar data did not match.
From these findings and Sect. 4.2, we conclude that the boundary layer is separated into four vertical layers during the occurrence TSFs. The near-surface layer below \(\approx \) 2 m is influenced by the cold-air layer following the topography. Between 2 and 10 m, the warm-air layer is detected with wind directions from north-west following the regional topography. A transition layer is established between 10 and 150 m where the wind direction shifts from north-west to south-west with a spatially homogeneous wind speed. Finally, for heights greater than 150 m, the synoptically-forced layer is found with wind directions from south-west.
4.3.4 Radiation and Static Stability
The radiation balance is investigated assuming the formation of the TSF cold-air layer during low incoming longwave radiation, \(L{\downarrow }\), or high net radiative longwave loss, \(\Delta L\). But again, no clear threshold for the formation of TSFs could be determined. For the same \(L{\downarrow }\) or \(\Delta L\), instances with and without TSFs could be identified (Fig. 8a). Nevertheless, TSFs most likely occur for \(L{\downarrow }~\approx ~-\,\)250 W m\(^{-2}\), and TSFs mostly vanished for \(L{\downarrow }<-\,\)280 W m\(^{-2}\) (Fig. 8a). For \(\Delta L\), TSFs mostly occur around 58 W m\(^{-2}\), while for values exceeding 76 W m\(^{-2}\), no TSF could be detected (Fig. 8b).
Static stability \(\Delta _z \theta \) as derived from the temperature difference between 15 and 0.5 m at the main tower plotted against a incoming longwave radiation \(L{\downarrow }\) and b net longwave radiation \(\Delta L\). Equally sized bin averages were added for the occurrence and absence of TSFs
Static stability \(\Delta _z \theta \) is derived from the temperature difference between 15 and 0.5 m at the main tower. Since \(\Delta _z \theta \) is a response of the boundary layer rather than a forcing, we use \(\Delta _z \theta \) as a diagnostic for TSFs. Static stability was elevated during TSFs due to their vertical structure with the cold-air layer at the bottom and warm-air layer on top. We expect a correlation between radiative forcing and static stability with increasing stability for small \(L{\downarrow }\) or strong \(\Delta L\). However, neither is the case regardless of the occurrence or absence of TSFs. We therefore conclude that the source of cold air within the valley is non-local. Cold air could be advected from outside the valley with sufficient momentum to force cold air uphill against the buoyancy force. Similar observations were made by Mahrt (2010) during the Fluxes Over a Snow Surface II (FLOSSII) field campaign and described in detail for a case study during the SCP experiment where the cold-air advection is described as a south-westerly flow (Mahrt et al. 2020). This mechanism would also explain why the TSF boundary is mainly found halfway uphill on the north shoulder, and why the coldest air is found next to the TSF boundary. The source of the cold air could not be identified as it is located outside of the observational domain. However, it seems likely that the nearby terrain towards the south featuring a tall and broad hill could provide enough cold-air formation resulting in drainage flows.
4.4 Implications for the Stable Boundary Layer
4.4.1 Static Stability and Near-surface Sensible Heat Flux
The SBL is usually classified by the inversion strength, which can in a very simple fashion be described by \(\Delta _z \theta \). Another commonly applied concept involve wind regimes as introduced by Sun et al. (2012), which are defined by the relation of the friction velocity \(u_*\) and wind speed V in our case for night-time data. During the SCP experiment, \(\Delta _z \theta \) showed distinct differences for the occurrence and absence of TSFs in contrast to the near-surface wind regime (Fig. 9a), or radiation (Fig. 8), or their combination (Fig. 15a, b). Static stability within each wind regime was roughly similar (Fig. 9a), while the occurrence and absence of TSFs created subsets even within each wind regime with higher \(\Delta _z \theta \) during TSFs. The high value of \(\Delta _z \theta \), especially within the strong-wind regime but also within the weak-wind regime, is most likely caused by the distinct vertical structure of TSFs with the vertically stacked cold-air and warm-air layers (Fig. 1 and Sect. 4.2). This is counter-intuitive as the high correlation between the wind speed and turbulence during the strong-wind regime usually suggests a well-coupled boundary layer with neutral conditions. In contrast, the opposite appears to be true in the case of TSFs with the decoupled cold-air layer and strong stratification. Consequently, a near-surface strong-wind regime does not necessarily reflect a well-coupled boundary layer.
Boxplots of a static stability \(\Delta _z \theta \) and b sensible heat flux \(Q_\mathrm{H}\) for the 1-m station on the main tower. The boxplots are classified by the occurrence of TSFs as well as wind regimes introduced by Sun et al. (2012) (cf. x-axis)
Choosing the levels over which to calculate bulk parameters such as \(\Delta _z \theta \) is critical when describing the boundary layer, especially when determining the static stability between two stations being separated by several metres instead of examining the complete temperature profile. We arbitrarily chose two levels for the computation of \(\Delta _z \theta \) which sampled the two air layers of TSFs with opposing characteristics. Due to this decision, \(\Delta _z \theta \) had high values, but for our experiment it does not indicate a cold-air pool with significant stratification, it indicates the occurrence of TSFs. In other field studies there could be more vertical layers, especially when having a more complex geometry of the topography, making the correct choice for determining \(\Delta _z \theta \) even more important.
The near-surface static stability changed depending on the station above which the air layer of the TSFs was located, and even showed peak values when a TSF was passing (Fig. 3b). Accordingly, TSFs affect the near-surface static stability, but mainly on the north shoulder. We conclude that, besides choosing the right levels for computing meaningful values of \(\Delta _z \theta \), the station location is also important.
Parameters for determining dynamic stability including \(Ri_\mathrm{B}\) do not offer an alternative for \(\Delta _z \theta \) due to the impact of TSFs on the near-surface static stability. Thermal submesofronts altered \(Ri_\mathrm{B}\) (Fig. 3b) and its relationship to \(Q_\mathrm{H}\) (Fig. 10). The relationship between dynamic stability and \(Q_\mathrm{H}\) is commonly used for prescribing turbulent exchange in land models (Lapo et al. 2019) or other studies (Brotzge and Crawford 2000). Within the transition area of TSFs, the air layers converged and created strong static stability as well as a low wind shear leading to high \(Ri_B\), hence a strong dynamic stability (Fig. 3b). High positive values of \(Ri_B\) usually indicates low values of \(Q_\mathrm{H}\) due to the strong dynamic stability restricting vertical turbulent exchange, which in land models or stability functions leads to the adjustment of \(Q_\mathrm{H}\) towards lower values. In contrast, our findings demonstrated peak values in \(u_*\) and \(Q_\mathrm{H}\) (Fig. 3e, f). Consequently, the concept of dynamic stability misleads the interpretation of the flux when a TSF is passing.
The slow moving TSFs altered the near-surface sensible heat flux within a few minutes and led to a mean decrease of 30 W m\(^{-2}\) when passing (Fig. 3e). As TSFs were semi-stationary moving uphill and downhill the valley shoulder, they enhanced or reduced the sensible heat flux intermittently. Consequently, TSFs dictate the behaviour of near-surface fluxes, highlighting their importance for the SBL. Surprisingly, the sensible heat flux at 1 m a.g.l. on the main tower did not show distinct differences even when using the information about the occurrence or absence of TSFs (Fig. 9b). The boxplots do not differ depending on TSF presence as \(Q_\mathrm{H}\) ranges from low values within the cold-air layer up to high values within the warm-air layer and even peak values within the transition area. As a consequence, especially for the near-surface value of \(Q_\mathrm{H}\), it is important to not only know whether TSFs occur, but to know which air layer of the TSF is sampled by the point observation, which requires location-specific, and ideally spatially continuous, observations.
In summary, it is insufficient for models to prescribe surface temperature as suggested by others (e.g. Basu et al. 2008) especially for sites where thermal submesofronts occur. Thermal submesofronts and their effect on turbulent exchange are not distinctly described by the common metrics \(\Delta _z \theta \) or \(Ri_B\). Models struggle to represent intermittent turbulence as generated by TSFs, providing strong motivation for investigating submeso motions using spatially continuous observations.
4.4.2 Boundary-Layer Regimes During Thermal Submesofronts
As shown in the introduction, there are many approaches to characterizing the boundary layer by regimes. Here we want to see if the occurrence of TSFs is related to a specific boundary-layer regime.
The approach of Pfister et al. (2019), which combined radiative forcing, wind regime, and static stability to form specific boundary-layer regimes, is tested. However, since TSFs are not influenced solely by radiative forcing or by the wind regime as shown in the previous sections, their combination and resulting boundary-layer regimes could not successfully predict the occurrence of TSFs. Instead, TSFs occur throughout all boundary-layer regimes with statically stable conditions (not shown). We summarize four possible reasons why this approach fails. First, the formation of the TSF air layers is mostly independent from each other. Topographically-induced turbulence is generated irrespective of the radiative forcing, while vice versa the cold-air layer can form within the valley independently from the wind speed as long as it is not eroding the cold-air layer. Second, the warm-air layer can persist for an unknown duration during low wind speeds. Similarly, the cold-air layer can persist even into periods with less radiative cooling, for example created by broken cloud cover, especially when being advected. Third, as explained earlier, one observational point cannot reveal a threshold for the occurrence of TSFs as they consist of two distinct air layers. Depending on the location of a measurement, a station was either within the warm-air or cold-air layer, implying the sampling of only one layer at any moment while missing the TSF structure. Due to this, there is a mismatch between bulk and point statistics that becomes obvious when looking at static stability and the wind regime. The static stability is a bulk measure between two levels. In our case, like in many other field studies, it was determined at the main tower at the valley bottom in the centre of the network. At the same time, the wind regime is determined locally for a specific height and location, and hence, is a point measure. As TSFs move across the network, the relation between V and \(u_*\) and thus the wind regime can change suddenly at a point measurement depending on which TSF air layer is sampled, and independent of the bulk static stability, which remained strong throughout the occurrence of TSFs. A final point of consideration, which was not further investigated in this study, is the adjustment time scale between the change in bulk forcing to a change in turbulence (Mahrt and Thomas 2016). Maybe a more careful investigation of the relationship between, for example, synoptic flow and the occurrence of TSFs may emerge when accounting for an adjustment time scale.
An established and commonly used method to characterize the boundary layer uses near-surface wind regimes, as introduced by Sun et al. (2012). But due to the rather broad wind-speed range for which TSFs occur (Sect. 4.3.2), TSFs are not related to one specific wind regime. Nevertheless, we wanted to set the air layers of TSFs into the context of these wind regimes. For instance, it is conceivable that the warm-air layer with high values of V and \(u_*\) (Fig. 3d, f) could be confined to the strong-wind regime, while the cold-air layer with cold-air drainage could be confined to the weak-wind regime. If this assumption applies, maybe even the TSF structure and location of TSF layers within the network could be determined when analyzing the wind regimes of each point observation. We further chose to investigate if the TSF transition area falls into a specific regime.
The relation of wind speed to friction velocity \(u_*\) following Sun et al. (2012). Vertical lines show the wind-speed threshold separating the weak-wind from the strong-wind regime for a all night-time data, b weak static stability during the absence of TSFs, and c elevated static stability during the occurrence of TSFs. Further, equally sized bin averages are added (lines with dots) as well as the linear correlation lines for a the air layer of the TSFs or b, c each wind regime. a Each air layer of the TSF is coloured differently and the polygons show the range of the 10–90% percentile of \(u_*\)
Following Sun et al. (2012), a threshold value of 1.6 m s\(^{-1}\) is found for the night-time 1-min data at station A15 (2 m a.g.l.) irrespective of the occurrence of TSFs as described in detail in Pfister et al. (2019). The warm-air layer has a wind-speed range from 0.5 m s\(^{-1}\) up to 4.4 m s\(^{-1}\), while for the cold-air layer ranges from 0.3 up to 2.5 m s\(^{-1}\) (Fig. 11a). Hence, the TSF air layers are not confined to a single wind regime. For the warm-air layer, 91% of the data occurs within the strong-wind regime, while for the cold-air layer, 47% fall into the same regime, which is higher than expected. Due to this overlap, we conclude that a simple threshold cannot separate the air layers from each other.
Further, the warm-air and cold-air layer each showed a distinct relationship between the parameters V and \(u_*\) with a higher slope for the warm-air layer than for the cold-air layer. We speculate that, within the cold-air layer, thermodynamics supersede the mechanical generation of turbulence and thus \(u_*\) only slowly increases with V. In contrast, the well-mixed warm-air layer was characterized by a strong correlation between V and \(u_*\) persisting even during rather low wind speeds. Particularly the cold-air layer occurred for wind speeds by far exceeding the wind-speed threshold, underlining our conclusion that the air layers cannot be separated by a simple wind-speed threshold.
The transition area of TSFs revealed a slope similar to that of the warm-air layer, but with a higher offset, as expected from peak values in \(u_*\) for this area (Fig. 3f). Within the transition area, \(u_*\) was also intermittently enhanced during a passing TSF as observed within the time series of two case studies (Fig. 14c, d). The conditions within the transition area of TSFs could be compared with regime 3 of Sun et al. (2012), however, the transition area spans both the weak-wind and strong-wind regime equally, and not only the weak-wind regime. The intermittent turbulence within the transition area was caused by the convergence of both air layers, and as a conclusion we argue that the turbulence within the transition area is a bottom-up process and not an intermittent down-mixing of turbulence by larger-scale eddies.
The above described wind regimes do not incorporate a specific thermal regime for determining the threshold separating the wind regimes. Some studies report a change in minimum wind speed needed to sustain shear-generated turbulence near the surface (Van de Wiel et al. 2017; Maroneze et al. 2019). More specifically, the wind-speed threshold separating the weak-wind from the strong-wind regime changes depending on the thermal regime (Sun et al. 2020). As elevated static stability was observed during TSFs (Figs. 8, 9a), we separated the dataset into stronger static stability during the occurrence of TSFs and weaker static stability during the absence of TSFs and compared the resulting wind-speed thresholds.
However, even when choosing a specific thermal regime as it occurred during TSFs, the wind-speed threshold did not change (Fig. 11b, c). This finding supports our earlier interpretation that the relationship of a bulk measure such as static stability and a point measure such as the wind regime is poorly defined or arbitrary during TSFs. So even when considering static stability for the determination of wind regimes, we could not determine a specific wind regime for TSFs.
One could argue that the parameter for inferring the static stability was biased by the choice of using the occurrence of TSFs. To test this potential bias, the thermal regimes as commonly defined by Mahrt (1998) are evaluated separating the SBL into weakly and very stable. Here, we assume that the cold-air layer with a low correlation between V and \(u_*\) represents the very stable regime, while the warm-air layer with a stronger relationship represents the weakly stable regime. If the air layers mostly fall within one thermal regime, which in turn modifies the wind-speed threshold for regime transition, the separation of the two distinct TSF air layers should be possible.
Thermal regimes as defined by Mahrt (1998) separating the boundary layer into the weakly and very stable regime by using the Monin−Obukhov stability parameter, z/L, and kinematic sensible heat flux \(\overline{w'T'}\). Equally sized bin averages (dotted lines) are computed for the different air layers of TSFs. Vertical lines and text indicate the regime change from weak to very stable
The air layers forming TSFs were not confined to one thermal regime, but show different correlations between z/L and \(\overline{w' T'}\) (Fig. 12). Substantial scatter around the bin averages were observed, which is most likely caused by differences in radiative or non-local forcings such as the regional flow or varying and unknown adjustment time scales. We acknowledge that the cold-air layer had more points within the very stable regime while the warm-air layer was mostly within the transition regime, but the air layers were not characteristic of just one regime. Even though the cold-air layer showed a constant low slope between V and \(u_*\), the cold-air layer did not exclusively represent the very stable regime. Vice versa the same finding applied to the warm-air layer and weakly stable regime. Out of curiosity, we also investigated the relationship between z/L and \(\overline{w'T'}\) depending on the occurrence of TSFs and depending on the wind regime. The relation changed during the occurrence of TSFs and the weakly stable regime had a broader range (not shown). For the strong-wind regime most points were detected within the weakly stable and transition regimes, while the weak-wind regimes had most points within the transition and very stable regime (not shown), but there was no clear pattern. From this we conclude that at least at the SCP site, the wind regime change does not co-occur with a change from the weakly stable to the very stable regime. Further, we think that, even if the thermal regimes change the wind-speed threshold, this process cannot be represented by a regime change determined from the parameter z/L or static stability determined by a bulk parameter as many confounding and interdependent factors are at work creating substantial scatter around mean values.
In summary, due to the specific and antagonistic characteristics of the air layers of TSFs causing strong spatial perturbations, it is unlikely that even a combination of thermal and wind regimes is able to determine a regime which is characteristic of TSFs. Near-surface features measured by a point observation can only reflect either one of the TSF air layers or the transition area between them when applying a time-series analysis. Dependent on the physical location within the valley, a point observation spends most of the time in either one layer or has a few occasions when a TSF passes. But, as shown here, most of the time the location of the TSF boundary or front is unknown unless spatially continuous observations are used. Thermal submesofronts affect the SBL characteristics significantly, and thus need to be considered when characterizing the boundary layer. Unless spatial perturbations can be added to the surface-layer condition or non-local forcing like cold-air advection added to the regime definition, we conclude that no point-based boundary-layer regime or classification is capable of correctly predicting the occurrence of TSFs.
4.5 Recommendations and Thoughts for Further Studies
While the SCP observational network was very dense and provided good coverage, we were missing observations from outside the valley to the north and south which would, for example, determine the source for cold-air advection. At the same time, not all stations within the valley would have been necessary. For future SBL studies, we recommend the following:
-
Nested networks observing the boundary layer in the best possible quasi-three-dimensional way by using a combination of, for example, wind profiler with tower data (both as high as possible), with an instrument density dependent on location: the highest density shall be located along main topographical features (cross-valley, down-valley, vertical), and decreasing density outside the valley.
-
Short pilot campaigns prior to the main experiment shall determine the topographical features that influence the boundary layer. If TSFs were modified locally or if cold-air advection occurred for the formation of TSFs could not be identified here due to the lack of spatially continuous data outside of the valley. Adding more stations or spatially continuous observations from, for example, FODS outside the valley should enable an investigation of the evolution of TSFs. Such insights could be beneficial for both experimentalists and modellers.
-
If possible, spatially continuous data should be collected horizontally and vertically and combined with sonic anemometer measurements as done in Pfister et al. (2021).
-
Spatially continuous data as measured by FODS are also limited in their application. While even a dense quasi-three-dimensional set-up such as in Zeeman et al. (2015) can track cold-air motions, it fails in capturing the origin of the cold air, which is likely to be non-local. Furthermore, even the FODS technique is limited in its spatial observational extent with a maximum length of fibre-optic cables of 5–10 km. This limitation needs to be kept in mind when trying to use FODS to its full potential.
-
For modelling the SBL, we recommend focusing on incorporating topographical effects like mixing at edges and local as well as non-local cold-air drainage.
5 Conclusion
Thermal submesofronts are detected during the SCP experiment, which is a unique field study featuring a near-surface network combining 27 ultrasonic anemometer stations, a wind profiler, and FODS. Thermal submesofronts frequently occur within the SBL and are generated by the gentle topography, creating two contrasting air layers. The warm-air layer is mechanically generated by topographically-induced mixing consistently elevating near-surface temperatures at the plateau edge, while the cold-air layer is thermodynamically driven by radiative cooling and corresponding topographically-induced cold-air drainage decreasing near-surface temperatures in the valley. Accordingly, even in the gentle SCP terrain, the impact of topography is much larger than usually anticipated. Further, TSFs can be expected at any field site with a similar topographical architecture.
We could not identify a single local forcing or combination of several common forcing metrics that successfully determine the occurrence of TSFs. Similarly, we are unable to find a clear connection between synoptic flow and TSFs. Our analyses demonstrate a significant impact of TSFs on SBL behaviour, as follows:
-
the advective velocity of TSFs is an order of magnitude lower than the mean wind speed which renders ergodicity assumptions invalid.
-
Thermal submesofronts can cause sudden decreases of 30 W m\(^{-2}\) in the near-surface \(Q_\mathrm{H}\) within a minute or less when passing a station and thus cause intermittent turbulence.
-
the vertical structure of TSFs increases the static stability beyond the capability of radiative forcing.
-
the decoupled boundary layer during TSFs renders the use of flux−gradient similarity theory invalid within the valley where the warm-air layer lies atop of the cold-air layer. The same applies to the transition area of TSFs.
-
the occurrence of TSFs is unrelated to a specific wind or thermal regime.
The boundary-layer community so far usually classifies the SBL by flow conditions (e.g., Low-level jeh or geostrophic wind speed), thermal regimes, radiative forcing, or a combination of these. In these approaches, the boundary layer is assumed to be a bottom-up or top-down controlled column. However, the vertically-layered structure of TSFs in conection with their semi-stationary location tied to topography invalidates this vertical conceptualization. As a result, point observations need to be put into the spatial context of the surrounding topography as well as the type of submeso motions. The use of a network of point observations is insufficient as they are likely to miss submeso motions most of the time. We recommend the use of spatially continuous observations in the horizontal as well as vertical in combination with nested networks of stations inside and outside the investigated topographical feature. Future studies need to consider the limitations of point observations when spatially continuous measurements are unavailable.
References
Anfossi D, Oettl D, Degrazia G, Goulart A (2005) An analysis of sonic anemometer observations in low wind speed conditions. Boundary-Layer Meteorol 114(1):179–203. https://doi.org/10.1007/s10546-004-1984-4
Basu S, Holtslag AAM, Van De Wiel BJH, Moene AF, Steeneveld GJJ, Wiel BJ, Moene AF, Steeneveld GJJ (2008) An inconvenient truth about using sensible heat flux as a surface boundary condition in models under stably stratified regimes. Acta Geophys 56(1):88–99. https://doi.org/10.2478/s11600-007-0038-y
Brotzge JA, Crawford KC (2000) Estimating sensible heat flux from the Oklahoma Mesonet. J Appl Meteorol 39(1):102–116
Cava D, Mortarini L, Anfossi D, Giostra U (2019a) Interaction of Submeso motions in the antarctic stable boundary layer. Boundary-Layer Meteorol 171(2):151–173. https://doi.org/10.1007/s10546-019-00426-7
Cava D, Mortarini L, Giostra U, Acevedo O, Katul G (2019b) Submeso motions and intermittent turbulence across a nocturnal low-level jet: a self-organized criticality analogy. Boundary-Layer Meteorol 172(1):17–43. https://doi.org/10.1007/s10546-019-00441-8
Kang Y, Belušić D, Smith-Miles K (2014) Detecting and classifying events in noisy time series. J Atmos Sci 71(3):1090–1104. https://doi.org/10.1175/JAS-D-13-0182.1
Kang Y, Belušić D, Smith-Miles K (2015) Classes of structures in the stable atmospheric boundary layer. Q J R Meteorol Soc 141(691):2057–2069. https://doi.org/10.1002/qj.2501
Lang F, Belušić D, Siems S (2018) Observations of wind-direction variability in the nocturnal boundary layer. Boundary-Layer Meteorol 166(1):51–68. https://doi.org/10.1007/s10546-017-0296-4
Lapo K, Nijssen B, Lundquist JD (2019) Evaluation of turbulence stability schemes of land models for stable conditions. J Geophys Res Atmos 124(6):3072–3089. https://doi.org/10.1029/2018JD028970
Mahrt L (1998) Nocturnal boundary-layer regimes. Boundary-Layer Meteorol 88(2):255–278. https://doi.org/10.1023/A:1001171313493
Mahrt L (2010) Common microfronts and other solitary events in the nocturnal boundary layer. Q J R Meteorol Soc 136(652):1712–1722. https://doi.org/10.1002/qj.694
Mahrt L (2019) Microfronts in the nocturnal boundary layer. Q J R Meteorol Soc 145(719):546–562. https://doi.org/10.1002/qj.3451
Mahrt L, Thomas CK (2016) Surface stress with non-stationary weak winds and stable stratification. Boundary-Layer Meteorol 159(1):3–21. https://doi.org/10.1007/s10546-015-0111-z
Mahrt L, Pfister L, Thomas CK (2020) Small-scale variability in the nocturnal boundary layer. Boundary-Layer Meteorol 174(1):81–98. https://doi.org/10.1007/s10546-019-00476-x
Maroneze R, Acevedo OC, Costa FD, Puhales FS, Demarco G, Mortarini L (2019) The nocturnal boundary layer transition from weakly to very stable, part II: numerical simulation with a second-order model. Q J R Meteorol Soc 145(725):3593–3608. https://doi.org/10.1002/qj.3643
Mortarini L, Cava D, Giostra U, Acevedo O, Nogueira Martins LG, Soares de Oliveira PE, Anfossi D (2017) Observations of submeso motions and intermittent turbulent mixing across a low level jet with a 132-m tower. Q J R Meteorol Soc 144(710):172–183
Mortarini L, Cava D, Giostra U, Costa FD, Degrazia G, Anfossi D, Acevedo O (2019) Horizontal meandering as a distinctive feature of the stable boundary layer. J Atmos Sci 76(10):3029–3046. https://doi.org/10.1175/JAS-D-18-0280.1
Orlanski I (1975) A rational subdivision of scales for atmospheric processes. Bull Am Meteorol Soc 56(5):527–530
Pfister L, Lapo K, Sayde C, Selker J, Mahrt L, Thomas CK (2019) Classifying the nocturnal atmospheric boundary layer into temperature and flow regimes. Q J R Meteorol Soc 145(721):1515–1534. https://doi.org/10.1002/qj.3508
Pfister L, Lapo K, Mahrt L, Thomas CK (2021) Thermal submeso-scale motions in the nocturnal stable boundary layer—part 1: detection and mean statistics. Boundary-Layer Meteorol
Pfister L, Sayde C, Selker JS, Thomas CK (2020) Fiber-optic distributed temperature sensing and wind profiler data during the shallow cold pool experiment. Dataset on Zenodo. https://doi.org/10.5281/zenodo.4290254
Soler M, Infante C, BuenestadoP Mahrt L (2002) Observations of nocturnal drainage flow in a shallow gully. Boundary-Layer Meteorol 105(2):253–273. https://doi.org/10.1023/A:1019910622806
Stefanello M, Cava D, Giostra U, Acevedo O, Degrazia G, Anfossi D, Mortarini L (2020) Influence of submeso motions on scalar oscillations and surface energy balance. Q J R Meteorol Soc 146(727):889–903. https://doi.org/10.1002/qj.3714
Stiperski I, Calaf M (2018) Dependence of near-surface similarity scaling on the anisotropy of atmospheric turbulence. Q J R Meteorol Soc 144(712):641–657. https://doi.org/10.1002/qj.3224
Sun J, Mahrt L, Banta RM, Pichugina YL (2012) Turbulence regimes and turbulence intermittency in the stable boundary layer during CASES-99. J Atmos Sci 69(1):338–351. https://doi.org/10.1175/JAS-D-11-082.1
Sun J, Takle ES, Acevedo OC (2020) Understanding physical processes represented by the Monin–Obukhov bulk formula for momentum transfer. Boundary-Layer Meteorol 177(1):69–95. https://doi.org/10.1007/s10546-020-00546-5
Turnipseed AA, Anderson DE, Burns S, Blanken PD, Monson RK (2004) Airflows and turbulent flux measurements in mountainous terrain. Agric For Meteorol 125(3–4):187–205. https://doi.org/10.1016/j.agrformet.2004.04.007
Van de Wiel BJH, Vignon E, Baas P, van Hooijdonk IGS, van der Linden SJA, Antoon van Hooft J, Bosveld FC, de Roode SR, Moene AF, Genthon C (2017) Regime transitions in near-surface temperature inversions: a conceptual model. J Atmos Sci 74(4):1057–1073. https://doi.org/10.1175/JAS-D-16-0180.1
Vercauteren N, Klein R (2015) A clustering method to characterize intermittent bursts of turbulence and interaction with submesomotions in the stable boundary layer. J Atmos Sci 72(4):1504–1517. https://doi.org/10.1175/JAS-D-14-0115.1
Vercauteren N, Boyko V, Faranda D, Stiperski I (2019) Scale interactions and anisotropy in stable boundary layers. Q J R Meteorol Soc 145(722):1799–1813. https://doi.org/10.1002/qj.3524
Vosper SB, Brown R (2008) Numerical simulations of sheltering in valleys: the formation of nighttime cold-air pools. Boundary-Layer Meteorol 127(3):429–448. https://doi.org/10.1007/s10546-008-9272-3
Yamartino RJ (1984) A comparison of several “Single-Pass” estimators of the standard deviation of wind direction. J Clim Appl Meteorol 23(9):1362–1366
Zeeman MJ, Selker JS, Thomas CK (2015) Near-surface motion in the nocturnal, stable boundary layer observed with fibre-optic distributed temperature sensing. Boundary-Layer Meteorol 154(2):189–205. https://doi.org/10.1007/s10546-014-9972-9
Acknowledgements
This project received support from awards AGS-1115011, AGS-1614345, and AGS-0955444 by the National Science Foundation and contracts W911NF-10-1-0361 and W911NF-09-1-0271 by the Army Research Office. We acknowledge the Earth Observing Laboratory of the National Center for Atmospheric Research for collecting the sonic anemometer measurements for the SCP experiment. This project has received funding from the European Research Council under the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 724629, project DarkMix. Many thanks to Otávio Acevedo and the other three anonymous reviewers whose comments and suggestions helped improve and clarify this manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1
Appendix 1
The wind-speed distribution at station A9 on the north shoulder (cf. Fig. 2) is different depending on how far the warm-air layer of TSFs protrude down the north shoulder into the valley (Fig. 13). A TSF is defined as barely protruding if A15 (half way uphill the north shoulder) was within the cold-air layer while a TSF is far protruding if the station A15 is within the warm-air layer. This shows that wind speeds were usually greater when the warm-air layer with in TSFs protrudes far into the valley.
a Incoming longwave radiation \(L{\downarrow }\) and b net longwave radiation \(\Delta L\) plotted against static stability \(\Delta _z \theta \) as derived from the temperature difference between 15 and 0.5 m at the main tower during night-time. Equally sized bin averages were added for the weak-wind and strong-wind regime introduced by Sun et al. (2012)
Case studies in Fig. 14a, b show that TSFs can induce meandering as well as intermittently enhanced turbulence (Fig. 14c, d) when passing a station.
Static stability \(\Delta _z \theta \) is similar for different wind-speed regimes (Fig. 15), but has the lowest values during the strong-wind regime. Static stability also shows no relationship to the incoming longwave radiation \(L\downarrow \) nor the net radiation \(\Delta L\). Accordingly, also the combination of radiative forcing and wind regimes cannot give a meaningful classification for the boundary layer (cf. Sect. 4.4).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pfister, L., Lapo, K., Mahrt, L. et al. Thermal Submeso Motions in the Nocturnal Stable Boundary Layer. Part 2: Generating Mechanisms and Implications. Boundary-Layer Meteorol 180, 203–224 (2021). https://doi.org/10.1007/s10546-021-00619-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-021-00619-z