Understanding Physical Processes Represented by the Monin–Obukhov Bulk Formula for Momentum Transfer

Abstract

Physical processes represented by the Monin–Obukhov bulk formula for momentum are investigated with field observations. We discuss important differences between turbulent mixing by the most energetic non-local, large, coherent turbulence eddies and local turbulent mixing as traditionally represented by K-theory (analog to molecular diffusion), especially in consideration of developing surface-layer stratification. The study indicates that the neutral state in a horizontally homogeneous surface layer described in the Monin–Obukhov bulk formula represents a special neutrality regardless of wind speed, for example, the surface layer with no surface heating/cooling. Under this situation, the Monin–Obukhov bulk formula agrees well with observations for heights to at least 30 m. As the surface layer is stratified, stably or unstably, the neutral state is achieved by mechanically generated turbulent mixing through the most energetic non-local coherent eddies. The observed neutral relationship between $u_*$ (the square root of the momentum flux magnitude) and wind speed V at any height is different from that described by the Monin–Obukhov formula except within several metres of the surface. The deviation of the Monin–Obukhov neutral $u_*-V$ linear relation from the observed one increases with height and contributes to the deteriorating performance of the bulk formula with increasing height, which cannot be compensated by stability functions. Based on these analyses, estimation of drag coefficients is discussed as well.

1 Introduction

The Monin–Obukhov similarity theory (MOST) was established more than 70 years ago (Monin and Obukhov 1954), and its historical impacts on the atmospheric boundary layer have been reviewed extensively (e.g., Foken 2006). Part of the popularity of MOST is its derivation of the Monin–Obukhov bulk formula for momentum (hereinafter, the bulk formula), which can approximately describe observed wind profiles near the surface. Nonetheless, Foken (2006) concluded that even under ideal conditions, the theory has an accuracy of about 10–20%. Measurement uncertainties and deviations of various assumptions implicitly assumed in the derivation of the bulk formula from observations could contribute to its performance. However, physical processes that are implicitly assumed in the derivation of the formula have not been fully investigated. In this study, we investigate the physical process represented in the bulk formula only, recognizing that the contribution of Monin and Obukhov is not limited to momentum transfer.

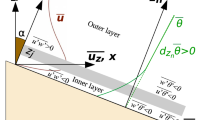
Recently, observational analyses of the relationship between turbulent momentum fluxes and wind speed over a variety of surface types have raised questions on the physical representation of the bulk formula. Sun et al. (2012) analyzed the relationship between $V_{TKE} =\sqrt{e} \equiv [(\overline{u'}^2+\overline{v'}^2+\overline{w'}^2)/2]^{1/2}$ and wind speed $V=\sqrt{{\bar{u}}^2+{\bar{v}}^2}$ at an observation height [u, v, and w are the zonal, latitudinal, and vertical wind components, the bar represents 5-min block averages and the prime represents perturbations from the block averages, and e represents turbulence kinetic energy (TKE) per unit mass] using night-time observations from the 60-m tower over the short grass site of the Cooperative Atmosphere-Surface Exchange Study in 1999 (CASES-99). They found that over this relatively homogeneous flat site, the transition of $V_{TKE}$ between the stable and the neutral regimes as a function of V at a given height z (hereinafter, z refers to a height above the surface unless otherwise specified) resembles a hockey stick. That is, $V_{TKE}$ increases linearly with V under neutral conditions associated with strong winds and gradually with V under weak winds due to the influence of the stable stratification. Because $V_{TKE}$ is approximately linearly related to any turbulence-intensity-related variable such as the standard deviations of any wind component and $u_*=(\overline{w'u'}^2+\overline{w'v'}^2)^{1/4}$ (Here we use $u_*$ to represent momentum fluxes observed at any z, the friction velocity would be $u_*$ observed near the surface.), the linear relationship between $V_{TKE}$ and V at z suggests that under neutral conditions, $u_*$ at z increases linearly with the bulk shear V/z instead of local vertical shear $\partial V/\partial z$ at z suggested in MOST (here $\partial V/\partial z=\sqrt{(\partial u/\partial z)^2+(\partial v/\partial z)^2}$; differences between wind-speed and vector shear are discussed in Sun 2011). Sun et al. (2016) extended the night-time analysis presented in Sun et al. (2012) to include the daytime analysis, and found that because of the unique linear relationship between $u_*$ and V for the neutral regime, a hockey-stick transition between the unstable and the neutral regimes exists as well. Sun et al. (2016) named the transition the HOckey-Stick Transition (HOST) and proposed the HOST hypothesis to explain the observation. The HOST hypothesis states that most energetic coherent turbulence eddies near the surface are large, i.e., non-local, and the turbulence intensity is determined by energy conservation. The contribution of such large non-local eddies to turbulent mixing is schematically illustrated in Fig. 1 and is further explained below.

Since the publication of Sun et al. (2012), the relationship between $u_*$ or $V_{TKE}$ vs. V has been examined over various surfaces, including sea surfaces (e.g., Andreas et al. 2012; Sun and French 2016), over open pasture (van de Wiel et al. 2012), over thick vegetation (Martins et al. 2013), over patchy agricultural fields (Bonin et al. 2015), within a conifer forest (Russell et al. 2016), over Amazon forests (Dias-Júnior et al. 2017), over the Antarctic plateau (Vignon et al. 2017), over gentle rolling terrain (Mahrt et al. 2015), over complex terrain (Acevedo et al. 2016), over a valley floor (Mahrt et al. 2013), and over urban canopies (Huang et al. 2017; Liang et al. 2018). They found similar HOST patterns with deviations at some sites, which is discussed herein.

Fig. 1

Schematics of any observed TKE-related variable including $u_*$, $V_{TKE}$, $\sigma _{V}$ and $\sigma _{w}$ at an observation height z (top row) and contribution of the most energetic non-local coherent eddies (represented by pairs of arrows) to the atmospheric stratification (represented by the layers with different colours) within the surface layer between the surface and z (middle row) as a function of the atmospheric stratification associated with wind speed V. The stratified (night-time: left column; daytime: right column) and the near-neutral regimes correspond to weak winds and strong winds, respectively and are separated by the vertical dotted line at the threshold wind speed $V_s$ at z. The temperature standard deviation, $\sigma _{\theta }$, which is linearly correlated with $|\theta _* \equiv -\overline{w'\theta '}/u_*|$, is schematically illustrated as a function of V for the night-time stable stratification (bottom left), and as a function of the vertical potential temperature difference $\delta \theta = \theta (z)-\theta (z \approx 0)$ for the daytime unstable stratification (bottom right). The thick dashed curves in the top row mark the variation of any TKE-related variable in the stratified regime and the thick straight lines in the top row mark the neutral $u_*-V$ relationship. At night, the most energetic non-local coherent eddies generated by weak wind shear between z and the surface are relatively small and mix the surface cold air up in formation of a thin cold layer between z and the surface (dark blue), leading to the stable layer between z and the surface. During daytime, the most energetic non-local coherent eddies under convective conditions associated with weak winds are relatively large and are maintained by the warmer and lower density air (red) near the surface, leading to the unstable surface layer between z and the surface. As V increases, mechanically generated large non-local coherent eddies lead to the well-mixed, near-neutral surface layer between z and the surface (the blue and the orange layers on the right side of the dotted vertical line for the night-time and the daytime, respectively)

The significance of the observed HOST pattern is that the observational evidence challenges some physical concepts implicitly assumed in MOST as the observed HOST is different from what the bulk formula describes, even at observation heights as low as 10 m. In addition, an increasing number of discussions on the self-correlation issue in the similarity approach of MOST also challenge the implicit physical process that MOST represents (e.g., Hicks 1978; Klipp and Mahrt 2004; Baas et al. 2006; Mahrt 2008; Sun et al. 2016). Validity of the bulk formula is commonly justified by a circular argument, that is, the bulk formula is valid in the surface layer, which is commonly defined as the region in which the bulk formula is valid. No clear physical processes for its validity near the surface and its departure from observations with increasing z have been discussed in the literature. As a result, validity of the bulk formula in the surface layer is often approximated to be the bottom 10% of the atmospheric boundary layer.

In this study, we analyze performance of the bulk formula transfer at a given z with focus on the physical process that MOST represents in the air layer between z and the surface. We first discuss the bulk formula briefly, especially the relationship between $u_*$ and V at a given z under neutral conditions (Sect. 2). We then explain differences between turbulent mixing and molecular diffusion with special emphases on the most energetic non-local coherent turbulence eddies at z, impacts of the size of these eddies on the stratification of the air layer between z and the surface, and the critical role of wind speed in generating mechanical turbulent mixing in achieving a neutral atmospheric surface layer (Sect. 4). We then compare observed neutral $u_*-V$ relationships with that based on the bulk formula (Sect. 5) using field observations over a relatively homogeneous and flat surface as well as over complex terrain (Sect. 3). We then discuss why the bulk formula is commonly observed to be valid near the surface but not for turbulence observations high above the surface and the role of the Monin–Obukhov stability function for momentum in modifying turbulent momentum transfer in the stratified atmosphere (Sect. 6). Because observed surface drag coefficients or surface roughness lengths rely on the $u_*-V$ relationship, we also discuss impacts of our analyses on estimating the surface drag coefficient and roughness length (Sect. 7). Major results are summarized in Sect. 8.

2 Monin–Obukhov Similarity Theory

Based on dimensional analysis and laboratory observations of a turbulent layer near a surface, Prandtl and von Kármán developed the relationship between $u_*$ and V in the 1920s as

$$\begin{aligned} \frac{\kappa z}{u_{*0}}\frac{\partial V}{\partial z}=1, \end{aligned}$$

(1)

where $\kappa$ is the von Kármán constant, and $u_{*0}$ is the $u_*$ value at the surface (e.g., Tennekes and Lumley 1972; Davidson et al. 2011). Realizing the atmosphere is characterized with the atmospheric stratification, Obukhov (1946) introduced the atmospheric stability function $\phi$ to modify the above relationship such that

$$\begin{aligned} \frac{\kappa z}{u_{*0}}\frac{\partial V}{\partial z}=\phi (Ri). \end{aligned}$$

(2)

In (2), $Ri=(g/\theta _0)\partial \theta /\partial z/(\partial V/\partial z)^2$ (g is the acceleration due to gravity, $\theta$ is the potential temperature, $\theta _0$ is a reference temperature) is the local gradient Richardson number, and $\phi (Ri=0)=1$ under neutral conditions. The original usage of Ri was influenced by the early study of the critical Richardson number. The stability function was then expressed as a function of z/L (L is the Obukhov length) by Obukhov (1946), which was further investigated by Monin and Obukhov (1954). In addition, they assumed that $u_*$ is approximately invariant with height in the surface layer, that is, $u_* (z) \approx u_{*0}$, and the atmospheric stratification does not deviate significantly from its neutral state. Under these conditions, the relationship between $u_*$ and V for z near the surface can be obtained by vertically integrating (2) as (Monin and Obukhov 1954)

$$\begin{aligned} u_*(z)=\frac{\kappa V(z)}{\ln (z/z_o) - \varPsi (Ri)}, \end{aligned}$$

(3)

where $\varPsi (Ri)$ is the vertically integrated $\phi (Ri)$, and $z_o$ is the aerodynamic roughness length. Equation 3 is the Monin–Obukhov bulk formula.

Essentially the Monin–Obukhov bulk formula is based on dimensional analysis of (1) for the neutral value of $u_*$ and the stability function obtained by empirically fitting the observed function $\phi$ in (2) as a function of a stability parameter, Ri or z/L. The bulk formula, (3), describes two aspects of $u_*$ over a horizontally homogeneous surface: how the neutral $u_*-V$ relationship varies with z, and how the stability function modifies $u_*$ when the atmosphere is stratified for a given V and z. When the atmospheric stability varies with z, $u_*$ would vary significantly with z. In this study, we use only the functions $\phi$ and $\varPsi$ to describe the general stability effect on $u_*$ regardless of whether the stability parameter z/L or Ri is used, knowing the specific forms of $\phi$ and $\varPsi$ depend on the choice of the stability parameter.

Under neutral conditions, i.e., $\varPsi (Ri=0)=0$, (3) becomes

$$\begin{aligned} u_*=\frac{\kappa V }{\ln (z/z_o)}. \end{aligned}$$

(4)

That is, the neutral $u_*$ at a given z varies linearly with V for a given $z_o$, the Monin–Obukhov neutral $u_*-V$ line goes through the zero point, $(u_*,V)=(0,0)$ for any z, and its slope, $u_*/V=\kappa /\ln (z/z_o)$, decreases with increasing z. Equation 4 provides a clear description of how V changes with z for a given $u_*$ under neutral conditions, as shown in Fig. 2. Even though $u_*$ may be invariant with z in the surface layer between some height z and the surface under neutral conditions, its value at z depends on the value of V at z. The bulk formula derived by vertical integrating MOST implicitly captures the contribution of the most energetic non-local coherent eddies with the scale of z to turbulent mixing proposed by Prandtl and von Kármán (more in Sect. 4).

Fig. 2

Comparison of an observed neutral wind profile during CASES-99 (red), for which the vertical temperature difference between 0.2 m and 58.1 m is less than 0.4$^{\circ }$C, with the one estimated from the Monin–Obukhov bulk formula using the vertically-averaged observed $u_*$ at the time of the wind observation and the observed $z_o=0.05$ m (black). All the observations are 5-min averaged

3 Observations and Methodology

We use two field datasets in this study: one set taken for flow over a relatively homogeneous flat surface, CASES-99 (UCAR/NCAR-Earth Observing Laboratory 2016), and the other taken over a basin surrounded by mountains, Fluxes over Snow-covered Surfaces II (FLOSS-II) (UCAR/NCAR-Earth Observing Laboratory 2017). Although FLOSS-II is more complex than CASES-99, the most important difference between the two datasets relevant here is that CASES-99 has strong thermal diurnal variations during the one-month field campaign in October; FLOSS-II has a variety of thermal diurnal variations during a period of six months from November to April.

Fig. 3

Fractions of the daily maximum net radiation ($R_n$) at each 50 W $\hbox {m}^{-2}$$R_n$ bin during the entire field campaigns of CASES-99 and FLOSS-II

3.1 CASES-99

CASES-99 was conducted in October 1999, within a site that is relatively flat with short senescent grass. The detailed field campaign, the instrument set-up, and the data processing for CASES-99 were described in Poulos et al. (2002), Sun et al. (2002, (2003, (2013). Here we only briefly describe the observations used in this study. There were eight three-dimensional sonic anemometers (CSAT version 3, Campbell Scientific, USA ) on a 60-m tower (55, 50, 40, 30, 20, 10, and 5 m for the top seven ones), and the lowest one was moved to 0.5 m from 1.5 m on 20 October. Downward and upward solar (PSP, The Eppley Laboratory, Inc., USA) and longwave radiative flux (PIR, The Eppley Laboratory, Inc., USA ) components were observed at 2 m above the surface at six satellite stations surrounding the 60-m tower. We used those measurements at station 1, which is the closest one to the 60-m tower (about 100 m away). High vertical-resolution air temperatures were observed by thermocouple sensors (E-type, Chromel-Constantan, 0.0254 mm diameter) at 0.23 m, 0.6 m, and every 1.8 m above 0.6 m up to the top of the 60-m tower. Air pressure measurements (quartz-based microbarographs, Paroscientific, Inc., USA) at the lowest sonic anemometer level, 30 m, and 50 m were also used (Cuxart et al. 2002).

The entire field campaign was predominantly sunny with only one cloudy day and no significant rain (Fig. 3). Drizzle was reported on 8 October but no increase of soil moisture at 25 mm below the surface was observed. Dew was reported in the morning of 10 and 12 October, which was consistent with the relatively high water-vapour concentration at 2 m observed at all the satellite stations. Local time at the CASES-99 site is six hours behind UTC.

3.2 FLOSS-II

FLOSS-II was conducted from November 2002 to April 2003 with significant weather variations (Mahrt and Vickers 2006; Acevedo et al. 2016). Turbulence observations (CSAT, Campbell Scientific, USA ) were made at seven levels on the tower (1, 2, 5, 10, 15, 20, and 30 m), and air temperature was observed at nine levels (0.5, 1, 2, 5, 10, 15, 20, 25, 30 m) by thermocouple sensors (E-type, Chromel-Constantan, 0.0254 mm diameter). Air pressure (PTB220, Väisälä, Finland) was observed at 1 m above ground. The surface radiation temperature $T_s$ (Everest Interscience, Inc.,USA) was estimated from the hemispheric upward longwave radiative flux $L^{\uparrow }$ (PIR, The Eppley Laboratory, Inc., USA) at 2 m with $L^{\uparrow }= \epsilon \sigma T_s^4$, where $\epsilon$ is the surface emissivity, assumed to be 0.98, and $\sigma$ is the Stefan–Boltzmann constant. Similar to CASES-99, the net radiation $R_n$ from the upward and downward solar (PSP, The Eppley Laboratory, Inc., USA ) and longwave (PIR, The Eppley Laboratory, Inc., USA) radiative flux components was observed at 2 m above the surface. In contrast to the CASES-99 flat terrain, the FLOSS-II site was in the centre of a meadow area surrounded by mountains at a distance of about 30 km or more (Fig. 4). Local time at the FLOSS-II site is seven hours behind UTC.

Fig. 4

The elevation map for FLOSS-II, where the 30-m flux tower is marked in the middle

3.3 Methods

We calculate turbulent fluxes using the eddy-correlation method with 5-min block averages for both field experiments, which, on average, have no systematic differences from 30-min fluxes throughout the diurnal variation. This result implies that on average, the 5-min block averages capture the most energetic eddies that contribute to turbulent momentum fluxes at the observation heights. We use $u_*$ measured at each observation height z to represent the turbulent momentum flux at the height. The bulk formula describes the surface $u_*$ because of the approximate invariance of $u_*$ with z assumed in the bulk formula and as is approximately observed from CASES-99 under neutral conditions. The vertical variation of the observed $u_*$ under neutral conditions was examined with the CASES-99 dataset in Sun et al. (2013). We apply the bulk formula to all observation heights to determine the height at which it starts to deviate from observations.

To examine the $u_*-V$ relationship, we apply the bin-averaged method to illustrate the general pattern without being overwhelmed by many data points. The median $u_*$ value of all the data within each wind speed bin is obtained as the bin-averaged value.

Potential temperatures are calculated with air temperatures measured by thermocouples and air pressures from the 60-m tower. We seldom observe zero vertical air-temperature difference between z and the surface $|\delta \theta |$ for $z \approx O(10)$ m even under strong winds because the air temperature in the surface layer is strongly influenced by surface heating/cooling and $|\delta \theta |$ increases with z even if $|\partial \theta /\partial z|$ is small. The neutral surface layer in this study refers to when $|\delta \theta |$ is small enough such that the characteristic linear relationship between $u_*$ and V at a given z is approximately unchanged with further increasing V.

Various stability functions for the bulk formula have been developed in the literature (e.g., Högström 1988); we use the one developed by Beljaars and Holtslag (1991) for the stable regime and the Businger stability function for the unstable regime (Businger 1966). The conclusion about stability effects is based on general characteristics of stability functions, and is independent of specific stability functions. The local gradient Richardson number Ri at a given z is calculated using the observations above and below z.

4 Non-local Coherent Eddies

One of the important roles of turbulent mixing in the atmosphere is its role in the transport of momentum, scalars, and energy through its most energetic non-local coherent turbulence eddies (e.g., Green 1995; Davidson 2015) forced by either positive buoyancy or vertical wind shear in changing mean atmospheric thermodynamics. Turbulent mixing generated by active forcing is much more effective in transporting energy and scalars than molecular diffusion. Molecular diffusion passively relies on molecule movements; its transfer of a scalar is related to the local gradient of the scalar. In contrast, the size of the most energetic non-local coherent turbulence eddies is determined by the scale of their forcing. For example, when the wind shear at height z is $\delta V/\delta z$ ($\delta$ represents a finite change), the most energetic eddies at z would have the scale of $\delta z$. That is, the turbulence intensity at z is not related to local shear $\partial V/\partial z$ at the point, which is often assumed for parametrizing turbulent transfer. As the most energetic turbulent eddies cascade to small eddies through eddy interactions due to air viscosity, turbulent mixing consists of turbulence eddies with a range of sizes. However, contribution of small eddies to the turbulence intensity are much less than contributions from the most energetic eddies due to their reduced coherence and relatively small variances (evident in comparison of the w coherence between two levels for different Obukhov length L associated with V in Fig. 11, Sun et al. 2016).

4.1 Role of the Most Energetic Non-local Coherent Eddies in Turbulent Mixing

The concept of non-local coherent turbulence eddies is based on the relationship between turbulence eddies and the turbulence generation mechanism; thus, the most energetic turbulence eddies are non-local. When the forcing scale approaches zero, that is, $\delta z \rightarrow 0$, $\delta V/\delta z \rightarrow \partial V/\partial z$, turbulent mixing is through local turbulence eddies. This may happen when the observation height approaches the surface (i.e., $z \rightarrow 0$) or in turbulence cascades where the size of the most energetic eddies becomes smaller while still having scales larger than Brownian motion. Turbulent mixing adjacent to the surface is technically non-local, but mathematically, the difference between non-local and local turbulent mixing is relatively small. Practically, whether turbulence is local or not depends on whether variations of the turbulence intensity are related to local forcing gradients such as local wind shear, which can be application dependent. The concept of non-local coherent turbulence eddies in the atmospheric boundary layer (e.g., Stull 1988), especially in wall turbulence (e.g., Jiménez 2013; Marusic et al. 2013), has been discussed in the literature.

It is critical to understand characteristics of the most energetic turbulence eddies that dominate the turbulence intensity in the atmosphere. The size of the most energetic non-local coherent turbulence eddies, which is defined as the size of turbulence eddies with the maximum vertical velocity variance at height z, was investigated by Sun et al. (2016) using the CASES-99 observation on the 60-m tower. Based on the spectral analyses, they found that the scale of the most energetic coherent turbulence eddies at any height z is about the length of z under neutral conditions, is slightly larger than the length of z under convective conditions, and is less than the length of z under stable conditions, as shown in Fig. 5. The confined scale for convective eddies is due to mass conservation with air motions constrained by the surface. Under neutral conditions at a given height z, which are observed to occur for $V>V_s$, where $V_s$ is the threshold wind speed, $u_*$ at height z is controlled by wind shear V/z, leading to the observed linear relationship between $u_*$ and V at a given z. The observed neutral $u_*-V$ line demonstrates not only the significant contribution of the most energetic non-local coherent turbulence eddies to $u_*$ but also the non-local shear forcing V/z in their generation even though V at height z is local. The importance of the finite scale of turbulence eddies was also implicitly showed in field data analyses (e.g., Wyngaard 2004; Klipp 2014).

Fig. 5

Normalized vertical velocity power spectra $S_w(z)$, $2 \pi f S_w(z)/\sigma _w^2(z)$, as functions of normalized frequency $2 \pi fz/V(z)$ at eight observation heights from CASES-99 for three stability conditions (a, b, and c) represented by the Obukhov length ($L=-3.9$ m from 1600–2000 UTC on 10 October, $L=1561$ m from 0400–0800 UTC on 17 October, and $L= 4.4$ m from 0000–0400 UTC on 5 October), where $\sigma _w(z)$ is the standard deviation of w. The spectra are calculated using the data recorded at 20 samples $\hbox {s}^{-1}$ at all observation heights. No sonic anemometer data are available at 20 m. Note that b and c are selected for $V(z) > V_s(z)$ and $V(z) < V_s(z)$, respectively. The vertical dashed line marks $2 \pi fz/V(z)=2$ when the neutral regime is observed at all the heights and $2 \pi f S_w(z)/\sigma _w^2(z)$ reaches its maximum in b. Adapted from Sun et al. (2016)

Existence of the most energetic non-local coherent turbulence eddies in turbulent mixing is also evident in temperature perturbations at the scale of these eddies in the stratified atmosphere (Sun et al. 2012, 2016). Under convective conditions, the temperature standard deviation at height z, $\sigma _{\theta }$, is found to be linearly proportional to $|\theta _*|$, where $\theta _* \equiv -\overline{w'\theta '}/u_*$, $\overline{w'\theta '}$ represents kinematic heat fluxes. In addition, $\sigma _{\theta }$ is found to be well correlated with $\delta \theta =\theta (z)-\theta (z_s)$ (Here $z_s$ represents a height at which air temperature can be practically measured as close to the surface as possible.) instead of proportional to local vertical temperature gradients, $\partial \theta /\partial z$ (Fig. 7c in Sun et al. 2016, which is schematically illustrated at the bottom right in Fig. 1). In the stable surface layer, the scale of the most energetic non-local coherent eddies increases with V toward the length scale of z and $\sigma _{\theta }$ is observed to increase with V for $V<V_s$ due to turbulent mixing with increasing eddy sizes and increasing vertical temperature differences that those eddies encounter. Further increasing V for $V>V_s$ would increase the strength and the coherence of the most energetic non-local coherent turbulence eddies with the scale of z, which would effectively mix the air layer between the surface and height z and decrease the atmospheric stratification within this layer to near zero. Therefore, the relationship between $\sigma _{\theta }$ and V would decrease with V for $V>V_s$ until the air layer is completely neutral when $\sigma _{\theta }$ approaches zero (Fig. 7a in Sun et al. 2016, which is schematically illustrated at the bottom left of Fig. 1).

4.2 Energy Transfers in Generation of the Most Energetic Non-local Coherent Eddies

To understand the most energetic non-local coherent eddies, we also need to understand energy contribution to generation of these eddies governed by total energy conservation (Sun 2019).

4.2.1 Unstable Stratification

The most unstable condition occurs during daytime when the surface is heated by the sun and wind speed is small. As the air temperature near the heated surface increases as a result of molecular thermal conduction near the surface, the air layer experiences thermal expansion, resulting in the warmer and lower density air near the surface than the overlying air and formation of the unstable surface layer. The positive buoyancy associated with a vertical increase of air density would lead to the warmer and lower density air moving upward, which forces the colder and higher density air downward as constrained by mass conservation, leading to negative vertical density flux, which is out of the hydrostatic balance. The negative vertical density flux, not just the heat flux, decreases air potential energy, which in turn increases TKE based on TKE conservation as evident in commonly observed thermal plumes. These non-local coherent thermal plumes originate from the surface heating and contribute to turbulent momentum, energy, and trace gas transfers under convective conditions.

4.2.2 Stable Stratification

Energy that forms the most energetic non-local coherent eddies under stable conditions is derived from wind shear through mechanically generated turbulent mixing. At night, molecular thermal conduction leads to the cold air near the radiatively cooled surface, which in turn leads to air compression near the surface, the colder and denser air below the warmer and low-density air above, and formation of the stable surface layer. As shear-generated non-local coherent turbulence eddies develop, they must lift the cold and high-density air upward and push the relatively warm and low-density air downward. The positive vertical density flux enhances air potential energy, which consumes shear generated TKE. As a result of the energy consumption for increasing air potential energy, TKE under stable conditions is relatively small in comparison with TKE under neutral conditions, that is, the scale of the most energetic non-local coherent eddies under stable conditions is less than the length of z.

4.2.3 Neutral Stratification

Neutrality of the air layer between height z and the surface achieved from either stable or unstable stratification requires mechanical mixing to redistribute the vertical variation of air density such that the air density within the layer becomes vertically invariant when height z is near the surface or the air layer between z and the surface is hydrostatically balanced when z is large. To achieve the neutral surface layer, the size of the most energetic non-local coherent eddies has to be about the scale of z. Buoyancy generated turbulence eddies cannot lead to the neutral atmosphere as positive buoyancy is supported by a vertical increase of air density. Due to the approximate invariance of the air density with height within the neutral layer below height z (more in Sect. 5), further increasing wind speed at z would generate TKE directly through wind shear between z and the surface without being used to vertically redistribute air density, leading to the observed linear relationship between $u_*$ and V at a given z (Sect. 5).

4.3 Contribution of the Most Energetic Non-local Coherent Eddies to Turbulence Surface Coupling

The scale of the most energetic non-local coherent turbulence eddies in turbulent mixing at z also determines the coupling of the air between z and the surface. If the scale of the most energetic coherent eddies at height z is larger than or equal to the length of z, the turbulent mixing at z is coupled with the surface. The turbulent mixing at z can be coupled to the surface while the air above z is not if the size of the most energetic eddies above z is less than its height. A clear example of the air layer that is coupled to the surface but the air above is not is the daytime convective boundary layer underneath the stable troposphere. If the atmosphere at z is coupled with the surface, the air layer between the surface and any level below z is well mixed by the most energetic non-local coherent eddies that are cascaded down to the scale of the height as suggested by the spectral analysis in Fig. 5; thus, the air layer at any level below z has to be coupled with the surface. If the scale of the most energetic coherent eddies at z is less than the length of z such as in the stable surface layer, the air at z is not fully coupled to the surface. Therefore, the atmospheric boundary depth, which is the maximum height of the atmosphere that is coupled with the surface, depends on the forcing for generation of the most energetic non-local coherent turbulence eddies.

4.4 Representation of Non-local Coherent Eddies in Numerical Models

Understanding contributions of the most energetic non-local coherent eddies to turbulent mixing has an important implication in turbulence parametrization. Maroneze et al. (2019) tested impacts of turbulence parametrization on establishment of the stable boundary layer by posting different ways in dealing with turbulent momentum and heat transfers in a simple numerical model. The traditional turbulence parametrization with the K theory implicitly assumes local turbulent mixing, that is, turbulent mixing is analogous to molecular diffusion and follows the Fick’s diffusion law. Maroneze et al. (2019) found that without adding constraints to the scale of the most energetic coherent turbulence eddies that dominate the turbulence intensity as imposed through local turbulent mixing schemes and allowing turbulent heat and momentum transfers as independent variables, the numerical model can capture observed relationships between environmental forcing such as wind speed and turbulence intensity such as $u_*$ and $\sigma _{\theta }$.

4.5 Surface Layer Relevant to Turbulent Mixing at a Given Height

As we focus on turbulent mixing at a given z, where turbulence intensity is dominated by the most energetic non-local coherent turbulence eddies and their size is constrained by the distance between z and the surface, the relevant air layer for turbulent mixing at z is the surface layer between the surface and height z. Thus, the surface layer relevant to turbulence observations at height z in this study refers to the air layer between the surface and height z. Because the most energetic non-local coherent eddies generated by strong shear not positive buoyancy can effectively eliminate the atmospheric stratification (schematically illustrated in the middle row of Fig. 1), the atmospheric stratification underneath z and its transition to a neutral layer are closely related to V at height z. The close relationship between turbulence intensity and the bulk Richardson number of this surface layer has been demonstrated in Vickers and Mahrt (2004), Mahrt (2008) and Vickers et al. (2015).

5 Development of Neutral Surface Layers

In this section, we compare the dependence of the Monin–Obukhov estimated $u_*$ on V with observations at a given z under neutral conditions. Although technically, (1) and (4) were developed by Prandtl and von Kármán , we refer to (4) as the Monin–Obukhov neutral $u_*-V$ relationship here due to familiarity of the Monin–Obukhov bulk formula to the boundary-layer community.

5.1 Development of the Neutral Regime Under Strong Diurnal Variations

We first study the observed transition of a strongly stratified surface layer underneath height z to a neutral layer over a homogeneous flat terrain by examining the $u_*-V$ relationship at z in comparison with the Monin–Obukhov neutral $u_*-V$ relationship (Fig. 6). Because of the overwhelming number of clear sky days during CASES-99, the diurnal variation of the atmospheric stratification in the surface layer is significant. As our focus is on the neutral surface layer, which is characterized with nearly invariant vertical air density within the bottom 60-m surface layer and a unique relationship between $u_*$ and V for a given surface regardless of whether it is transitioned from the unstable or the stable surface layer through strong mechanical mixing under strong wind conditions, we focus on the night-time CASES-99 observation here.

The observation indicates that because of the correlation between the stable stratification and weak winds when the surface is cooled, the bin-averaged $u_*$ at a given z under weak winds is relatively small in comparison with any neutral $u_*$ associated with strong winds and increases with V at the height gradually (Fig. 6a). When V at height z is larger than the threshold wind speed $V_s$, $u_*$ is observed to increase approximately linearly with V even though the vertical temperature difference between z and 0.2 m is not exactly zero and decreases slightly with V along the $u_*-V$ line (Fig. 6a). The observed variation of $u_*$ with V at a given z for the range of the observed V demonstrates the transition of the surface layer between the stable and the neutral regimes, which resembles a hockey stick, or HOST as shown in Fig. 6a and schematically at the top left of Fig. 1.

As explained in Sect. 4, the observed HOST pattern at night indicates the contribution of the most energetic non-local coherent turbulence eddies to $u_*$, the connection between the generation of these eddies and non-local wind shear, and the significant role of non-local wind shear in the atmosphere stratification. Similarly, the same neutral linear $u_*-V$ relationship can be transitioned from an unstable surface layer, forming a similar HOST pattern with relatively larger convective $u_*$ compared to stable $u_*$ under weak winds depending on the magnitude of the vertical temperature difference $\delta \theta$ (Fig. 8 in Sun et al. 2016, which is schematically illustrated as the thick dashed curve in the upper right of Fig. 1). If V at z is reduced from $V>V_s$ to $V<V_s$ at night, the cold air near the surface would start to accumulate as a result of the continuous cooling surface; the stable surface layer would be established again. Sun et al. (2015) found that the HOST pattern of $u_*$ explains intermittent turbulence when the background flow is enhanced and reduced periodically by internal gravity waves relative to $V_s$ and the turbulence regime switching between stable and neutral.

Fig. 6

Bin-averaged $u_*$ as a function of wind speed V at nine observation levels from CASES-99 based on a all the night-time data and b all the neutral data when the vertical air temperature difference between each observation height z and 0.2 m is less than 0.7–1.3 $^{\circ }$C. The MOST neutral line at each z with $z_0=0.05$ m is marked as the dashed line with the colour of the height for comparison. The vertical lines in each panel mark the standard deviations of $u_*$ in each wind-speed bin, which increases towards high winds at the high levels mainly due to the insufficient number of strong-wind observations, resulting in fluctuations of the $u_*-V$ lines at the high wind end. Further investigation on the $u_*-V$ relationship with increasing z is needed

The threshold wind $V_s$ at any z represents the averaged V beyond which $u_*$ increases linearly and more rapidly with V. Physically, the value of $V_s$ depends on the strength of the stratification between z and the surface and effectiveness of mechanical generation of turbulent mixing. The magnitude of the stratification (either stable or unstable) depends on the rate and the total amount of heat gained or lost in the surface layer in relation to the heat content of the overlying air (e.g., van de Wiel et al. 2012) under weak winds when mechanically generated turbulent mixing is relatively weak. As a stable layer develops slowly near the surface due to the slow molecular diffusion process, episodes of weak to moderate wind speed reduce the rate of development of a strong stable layer leading to a reduced $V_s$ value for the development of a neutral surface layer. A deeper surface layer requires a greater $V_s$ to vertically mix the surface layer between z and the surface towards neutral. Furthermore, $V_s$ also depends on the effectiveness of wind shear in turbulence generation, which is related to surface roughness (e.g., Mahrt et al. 2013).

Clearly, the observed neutral $u_*-V$ line at z under strong diurnal variations in Fig. 6 is shifted away from the zero point of $(u_*, V)=(0,0)$ towards strong winds with the slope of the neutral $u_*-V$ line remaining approximately unchanged (more in Sect. 7). Evidently, the characteristics of the neutral $u_*-V$ line at a given z achieved by strong mechanically generated turbulent mixing in the surface layer with a strong diurnal variation are different from the one described by the bulk formula. When z is close to the surface such as at 0.5 m in Fig. 6a, the surface layer below z is so thin that V at 0.5 m can be really small to generate the most energetic non-local coherent eddies to well mix the thin surface layer. Consequently, the surface layer below 0.5 m is practically near neutral day or night, $V_s$ at 0.5 m is near zero, and the neutral $u_*-V$ line does not shift much away from the zero point as described by the bulk formula.

5.2 Development of the Neutral Regime Under Varying Diurnal Variations

We then examine development of the neutral surface layer under weather conditions ranging from clear to precipitation days during FLOSS-II, which is reflected in the widespread frequency distribution of the 5-min averaged maximum daily net radiation, $R_n$ (Fig. 3). Because the surface heating or cooling is the major contributor for development of the surface-layer stratification, reduced diurnal solar radiation such as on cloudy or precipitation days would reduce the surface-layer stratification. If the air−land temperature difference is approximately zero, the surface layer would be neutral with zero $V_s$. Thus, the neutral $u_*-V$ line would approximately pass through the zero point as described by the Monin–Obukhov bulk formula. Because FLOSS II includes a significant fraction of days with low net radiation, the bin-averaged $u_*-V$ relationships at the observation heights over the entire period of FLOSS-II do not have the strong HOST pattern as observed in CASES-99, especially for the observation heights below 10 m (Fig. 7a) due to the overall weak stratification, either stable or unstable. For this reason, the observed variation of the HOST pattern over a wide range of surface conditions described in Sect. 1 could be due to variations of the strength of the diurnal variation of the surface-layer stratification besides variations of surface roughness through their impacts on $V_s$.

Fig. 7

The bin-averaged night-time relationships between $u_*$ and wind speed V at seven observation heights from FLOSS-II based on a all the night-time data, b the nights following the daytime maximum surface radiation temperature ($T_s$) that exceeds the air temperature 0.5 m ($T_a$) by less than 2 K, i.e., $[T_s-T_a]^{max} <2$ K, c the nights with $[T_s-T_a]^{max} >5$ K, and d the nights with the vertical air temperature difference between z and 0.5 m less than 0.5 K. The Monin–Obukhov neutral relationships at the seven heights are plotted with dashed lines and in the colours of the corresponding heights in b, c and d for comparison

To distinguish relatively strong from weak diurnally varying stratification and validate the above interpretation of the development of the neutral surface layer, we conditionally sample the FLOSS-II nights based on strong and weak daytime surface heating prior to sunset as the daytime heating impacts the temperature of the residual air layer overlying the cold surface air at night (Fig. 7b). The night following a strong surface heating day is defined as the maximum daytime surface radiative temperature larger than the air temperature at 0.5 m by 5$^{\circ }$C , i.e., $[T_s-T_a]^{max} > 5^{\circ }$C (Fig. 7c); the night following a weak surface-heating day is defined as $[T_s-T_a]^{max}< 2^{\circ }$C. Clearly, the night-time $u_*-V$ relationship at a given z following the strong surface heating days resembles the HOST pattern from CASES-99 (Fig. 7c), and the night-time $u_*-V$ relationship following the weak surface heating days resembles the pattern described by the bulk formula (Fig. 7b). The analyses in Fig. 7 indicate that without strong temperature advection, synoptic systems, or surface heterogeneity, the daytime surface heating plays an important role in determining the night-time stratification. That is, the warmer the residual air above the surface is, the more stable the surface layer would be due to the vertical air temperature difference in the surface layer as the surface cools at night. If we constrain the night-time vertical stratification to be nearly neutral, that is, $|\varDelta T_a|=|T_a(z)-T_a(z=0.5$ m$)|<0.5 ^{\circ }$C, the neutral $u_*-V$ line is observed to go through the zero point at all the observation levels during FLOSS-II and the slope of the neutral $u_*-V$ line decreases with increasing z (Fig. 7d), which is consistent with the bulk formula, (4). As the signal of surface heating/cooling to the atmosphere through molecular diffusion is better observed under weak winds when the atmosphere is less influenced by mechanically generated turbulent mixing, the independence of the atmospheric stratification on wind speed observed in Fig. 7d suggests that the neutral surface layer implicitly assumed in the bulk formula is a special neutral condition when the surface does not contribute to any atmospheric stratification. This special neutral condition can occur regardless of surface complexity and heterogeneity.

6 Physical Processes Represented by the Monin–Obukhov Bulk Formula

As demonstrated in Sect. 5, the Monin–Obukhov neutral regime represents a special situation in the atmosphere. This occurs when the surface layer is initially not stratified, such as under heavy cloudy conditions when the air–surface temperature difference is approximately zero or at sunset or sunrise when the surface net radiation is approximately zero. That is, the vertical air density distribution in the surface layer is independent of mechanical turbulent mixing or wind speed. Under this neutral condition, the bulk formula describes the $u_*-V$ relationship well, as observed during FLOSS-II. The observed linear increase of $u_*$ with V at a given z indicates that the increasing contribution of the most energetic non-local coherent turbulence eddies to $u_*$ with increasing V results from enhanced bulk shear with increasing V at the given z. The decreasing slope of the neutral $u_*-V$ line with z reflects the decreasing contribution of the surface drag to turbulent momentum transfer with increasing z (more in Sect. 7). The implication of the Monin–Obukhov neutral regime in the atmosphere may seem obvious, its modification with the influence of the atmospheric stratification is significant and leads to the applicability of the bulk formula.

6.1 Differences Between the Monin–Obukhov and the Observed Neutral Relationships

Commonly, the air density adjacent to the surface constantly changes by the surface heating or cooling such as during CASES-99. The most effective way to achieve the neutral regime in the atmospheric surface layer is through mechanically generated non-local coherent turbulent eddies, which mix air vertically until the atmospheric surface layer is neutral. Because mechanically mixing the entire surface layer between the surface and z to the neutral state requires energy generated by strong wind shear associated with strong wind speed at z, the Monin–Obukhov neutral $u_*-V$ line at z has to be shifted towards strong winds regardless of whether the surface layer is unstable or stable to start with. As the energy required to mix a stratified surface layer to a neutral layer increases with the surface layer depth, the threshold wind for turning the stratified to the neutral surface layer increases with z, and the HOST pattern shifts towards strong winds with increasing z.

In this study, we call the surface layer with no atmospheric stratification under any wind condition for which the Monin–Obukhov neutral $u_*-V$ relationship is valid the MOST surface layer; we call the surface layer that is stratified under weak wind conditions and reaches neutral through strong mechanically generated turbulent mixing the HOST surface layer. Thus, the MOST neutral surface layer represents a special situation of the HOST surface layer when the surface influence on the surface layer stratification becomes neglible. Specifically, the most important difference between the MOST and the HOST surface layers is reflected in their neutral $u_*-V$ lines: (1) the MOST neutral line goes through the zero point, while the HOST neutral line does not except when z is adjacent to the surface; (2) the slope of the MOST neutral line varies with z, while the slope of the HOST neutral line is approximately invariant (more in Sect. 7) and agrees reasonably well with the MOST neutral line when z is below several metres above the surface. That is, there is no difference between the MOST and the HOST surface layers when the surface layer is thin, such as at 0.5 m.

Fig. 8

a Schematic illustrations of the observed night-time $u_*-V$ relationship at a given height z above the surface in a HOST surface layer and the corresponding $u_*-V$ relationships at z described by the Monin–Obukhov bulk formula. The solid green line represents the HOST neutral $u_*-V$ line, and the area surrounded by dashed green curves represents the observed stable regime. The dashed black line represents the MOST neutral $u_*-V$ line at z, and the area surrounded by the dotted black curves represents the stable regime described by a Monin–Obukhov stability function. b The same as a with the neutral drag coefficients derived from the slopes $(u_*/V)_n$ of the corresponding neutral $u_*-V$ lines. At z away from the surface, the neutral drag coefficient estimated from the Monin–Obukhov bulk formula, $C_{dn}^{MO}$ (orange), is less than the observed one $C_{dn}^{HOST}$ (magenta). As z approaches the surface, the surface layer below z is always neutral, and the MOST and HOST neutral $u_*-V$ lines converge (solid black line). The stability regime where the estimated $u_*$ at z deviates from the observed one most is marked with a blue circle in a

6.2 Monin–Obukhov Stability Functions in Representing the Stratified to the Neutral Atmosphere

An important dilemma in the Monin–Obukhov bulk formula is the role of the Monin–Obukhov stability function in describing $u_*$ when the surface layer is stratified, or is the HOST surface layer. Essentially, the Monin–Obukhov stability function for momentum is developed by empirical fitting of observed $u_*$ in the HOST surface layer under weak winds associated with stratification and returns $u_*$ to the MOST neutral line under strong winds associated with the neutral layer. As the Monin–Obukhov neutral line is significantly different from the HOST neutral line, except for very small z as illustrated in Fig. 8a, naturally, the bulk formula would perform well near the surface and deteriorate with increasing z mainly because the deviation of the MOST $u_*-V$ neutral line from the HOST neutral line increases with z.

Fig. 9

Relationships between the 5-min wind speed V and $u_*$ at the indicated heights, where the observed daytime and night-time, and the ones estimated by the bulk formula with the observed Ri at the given height and the stability functions described in Sect. 3.3 are marked in red, dark blue, and cyan. The performance of the bulk formula can be evaluated as whether cyan dots are over red or dark blue dots. The MOST neutral line at each height is marked with the black solid line for reference. The transition between the stable and the neutral regimes, where the difference between the MOST and HOST neutral $u_*-V$ lines is largest, is marked with a dashed magenta circle from 30 to 50 m

Using the CASES-99 and FLOSS-II observations, we examine the performance of the bulk formula with a special focus on where the MOST and the HOST neutral lines differ in the $u_*-V$ framework. As demonstrated in Sect. 5, the surface layer is more stratified during CASES-99 than during FLOSS-II. We find that overall, the estimated $u_*$ tends to follow the MOST neutral $u_*-V$ line throughout the diurnal cycle during CASES-99. This is due to our usage of the observed Ri at each z in the stability function, which underestimates either stable or unstable stratification in the surface layer between the surface and z, and the MOST neutral relationship implicitly assumed in the bulk formula. Because the difference between the MOST and the HOST neutral $u_*-V$ lines is small when z is near the surface, both the Monin–Obukhov neutral $u_*-V$ line and the stability function described in Sect. 3 capture the observed $u_*-V$ relationship reasonably well from $z=1.5$ m to $z=10$ m in CASES-99 (estimated $u_*$’s in cyan overlap observed ones marked in red and dark blue for daytime and night-time, respectively, in Fig. 9). As z increases, the largest deviation between the Monin–Obukhov estimated and the observed $u_*$ is at night when V approaches the night-time threshold wind speed $V_s$ (dark blue points below the cyan points in dashed magenta circles at 30 m to 50 m in Fig. 9), where the MOST and the HOST neutral lines become significantly different. The disagreement between the bulk formula estimate and the observation at 0.5 m in comparison with the agreement between the two at 1.5 m is discussed in Sect. 7.

Due to a significant fraction of cloud and precipitation days during FLOSS-II, the observed $u_*-V$ points approximately follow the MOST neutral line (the left column in Fig. 10 with red and dark blue dots for daytime and night-time, respectively). However, we do see a clear HOST pattern for the night-time $u_*-V$ relationship at $z=10$ m (the blue dots in the bottom left panel in Fig. 10), indicating the impact of the increasing bulk stratification between the surface and height z with increasing z on $u_*$. We apply the stability functions described in Sect. 3 for $|Ri|<3$ only to the FLOSS-II dataset for better estimating the $u_*-V$ relationship using the bulk formula (the right column in Fig. 10). Clearly, the estimated $u_*-V$ relationship with the observed stability parameter agrees reasonably well with the observed $u_*-V$ at $z=1$ m. As z increases, for example, at z = 10 m, the estimated $u_*$ for a given observed V tends to underestimate the observed $u_*$ under stable conditions, especially at the transition between the stable and the neutral regimes. The underestimation is due to the nearly neutral environment associated with clouds and precipitation during FLOSS-II while the stability function is developed for “normal” stable conditions under weak winds. Again, the local Richardson number is used in the stability function here, which tends to underestimate the stable stratification of the surface layer.

Fig. 10

Relationships between observed wind speed V and $u_*$ for the daytime (red) and night-time (dark blue) for FLOSS-II (left column) and between the estimated $u_*$ from the Monin–Obukhov bulk formula and observed V (right column) for $|Ri|<3$ (including day and night-time data) at the indicated observation heights

6.3 Differences Between the Monin–Obukhov and the Observed Neutral Wind Profiles

Fundamentally, the physical process for achieving neutrality in the atmospheric surface layer is critically important in understanding validity of the Monin–Obukhov bulk formula. The performance of the bulk formula is related to the implicitly assumed Monin–Obukhov neutral regime. When the surface layer is approximately neutral, even under weak winds as during FLOSS-II, the neutral Monin–Obukhov $u_*-V$ relationship would estimate the observation reasonably well. When the bulk stratification below z is large, the MOST neutral line deviates from the observed HOST neutral line, and the difference between the two lines increases with z, especially when V approaches $V_s$, and the transition from the stratified to the neutral regimes is abrupt. Even if the stability function is developed based on the HOST surface layer, the performance of the bulk formula would still deteriorate with z because the correction of the stability function for the stratification has to increase with z. Consequently, the bulk formula performs reasonably well for small z but not for large z, which is well known but not well explained physically in the literature.

Based on the observations demonstrated in this study, the HOST neutral $u_*-V$ line can be approximately expressed as

$$\begin{aligned} u_*(z) = \alpha (z) V(z) + \beta (z), \end{aligned}$$

(5)

as suggested by Sun et al. (2016), where $\alpha (z)$ is the slope of the HOST neutral $u_*-V$ line, and $\beta (z)$ in m $\hbox {s}^{-1}$ is the intercept of the HOST neutral line associated with $V_s$. Because the shift of the HOST neutral line is towards large V under stable conditions, $\beta (z)$ is normally negative and decreases with z.

Comparison between the HOST neutral line, (5), and the MOST neutral line, (4), indicates that to represent the turbulent mixing in the HOST surface layer, the bulk formula needs to be generalized to include $\beta (z)$ such that $u_* - \beta (z)$ instead of $u_*$ is linearly related to V and the linear relationship between $u_* - \beta (z)$ and V goes through the zero point. When $V_s=0$, $\beta (z)=0$ only occurs at $z=0$. Thus, the MOST neutral line is a special case of the HOST neutral line. Without consideration of the negative $\beta (z)$ when the surface layer is actually a HOST surface layer, the bulk formula would underestimate wind-speed profiles in the HOST surface layer, and the difference between the observed and the Monin–Obukhov estimated wind speeds would increase with z. Using the vertically-averaged $u_*$ and $z_o$ observed from CASES-99, the described deviation of the Monin–Obukhov wind profile from the observed one is indeed observed in Fig. 2. Decreasing $z_o$ for estimating the wind profile with the bulk formula in Fig. 2 may increase the estimated V at a relatively larger z but would overestimate V near the surface. Because physically $\beta (z)$ represents the extra momentum transfer needed to transition the stratified surface layer into the neutral layer, it should depend on the strength of the stratification of the surface layer prior to the neutral surface layer obtained through strong mechanically generated non-local coherent turbulence eddies. The wind-profile comparison in Fig. 2 indicates that invalidity of the bulk formula is not because of the approximation of vertical invariant $u_*$ under neutral conditions, but the deviation of the MOST neutral $u_*-V$ line from the HOST neutral line when the surface layer is stratified.

7 Surface Drag Coefficient

Surface drag coefficients are used to describe impacts of characteristics of surfaces on air–surface interactions for momentum transfer. Derivation of surface drag coefficients has been reported extensively in the literature. Garratt (1977) thoroughly reviewed surface drag coefficients over sea and land. Raupach (1992) theoretically investigated how surface drag coefficients vary with surface roughness elements. Mahrt et al. (2001) examined how complication of the natural environment can influence calculations of turbulent momentum transfer and estimates of surface drag coefficients.

Drag coefficients are commonly defined as,

$$\begin{aligned} C_d(z)=[u_*(z)/V(z)]^2, \end{aligned}$$

(6)

which is the square of the slope of the $u_*-V$ relationship. To obtain surface drag coefficients, which describe impacts of a surface on turbulent momentum transfer, the turbulent momentum transfer at z needs to be fully coupled with the surface. Thus, impacts of the atmospheric stratification on the turbulent momentum transfer need to be excluded such that the turbulent momentum transfer is only influenced by the surface. Therefore, the surface drag coefficient has to be estimated with the neutral $u_*-V$ line at z.

Based on the bulk formula, (4), the neutral drag coefficient, $C_{dn}^{MO}$, can be expressed with (6) as

$$\begin{aligned} C_{dn}^{MO}=\left[ \frac{\kappa }{\ln (z/z_o)}\right] ^2. \end{aligned}$$

(7)

As expected, $C_{dn}^{MO}$ increases with roughness length $z_0$ and decreases with z (more later in this section). Based on (7), both $C_{dn}^{MO}$ and $z_o$ are aerodynamic variables. The value of $z_o$ reflects the net dynamic effect of the surface on the atmospheric momentum transfer, relies on validity of the log-linear wind profile near the surface, and may not be the averaged value of the physical heights of surface roughness elements (e.g., Lettau 1969; Raupach 1992, 1994; Sozzi et al. 1998; Sun 1999; Nakai et al. 2008).

In contrast to the MOST surface layer, the surface drag coefficient in the HOST surface layer cannot be estimated with (6), even when $u_*$ at z reaches its neutral value. This is because the surface-layer stratification affects $u_*$ under weak winds and the HOST neutral $u_*-V$ line does not go through the zero point, $(u_*,V)=(0,0)$ when z is not close to the surface. Using (6) would lead to the variation of the neutral drag coefficient with V for a given surface (Sun and French 2016), which has puzzled the air–sea-interaction community for a long time and led the community to scrutinize the role of water waves on turbulent momentum transfer as water waves are also related to V and $z_o$. The observed variation of $C_d$ with V has been discussed, for example, in Tennekes and Lumley (1972), Garratt (1977) and Marusic et al. (2010).

The neural drag coefficient in the HOST surface layer that is comparable with $C_{dn}^{MO}$ can be estimated using the HOST neutral $u_*-V$ line only as

$$\begin{aligned} C_{dn}^{HOST} \approx \left[ \frac{u_{*n}(z)-u_{*s} (z)}{V_n(z)-V_s(z)}\right] ^2, \end{aligned}$$

(8)

where $u_{*s}(z)$ and $u_{*n}(z)$ are the values of $u_*$ at any two wind speeds $V_s$ and $V_n$ on the HOST neutral $u_*-V$ line at z. Here we use one of the two points at the threshold wind $V_s(z)$ for convenience. Note that (8) relies on the variation of $u_*$ with V along the HOST neutral line at a given z, not the vertical variation of $u_*$. Because the well-defined slope of the neutral $u_*-V$ line as shown in Fig. 6a even though there is uncertainty for estimating $u_*$ at a given z and a given V, the uncertainty in estimating $C_{dn}^{HOST}$ should be relatively small.

As $C_{dn}^{HOST}$ is estimated when turbulent mixing at z is fully coupled with the surface, it represents the surface drag coefficient for a given surface type. Sun et al. (2016) found that $C_{dn}^{HOST}$ is approximately invariant at the CASES-99 site while $C_{dn}^{MO}$ decreases with z. The dependence of the slope of the HOST neutral $u_*-V$ line on surface roughness variations was indeed observed by Mahrt et al. (2013). Decreasing $C_{dn}^{MO}$ with z implies differences in the surface coupling between the MOST and the HOST surface layers because the MOST surface layer is neutral without mechanically generated turbulence eddies to vertically mix the entire air layer below z. Based on CASES-99, Sun et al. (2016) noted that $C_{dn}^{HOST}$ is observed to decrease with z slightly below 10 m (Fig. 13a of Sun et al. 2016), which is consistent with the observed decrease of bulk shear V/z with z in this layer (Fig. 14 of Sun et al. 2016). The sharper vertical decrease of $C_{dn}^{MO}$ with z near the surface in comparison with the observed $C_{dn}^{HOST}$ explains the overestimation of $u_*$ at 0.5 m in Fig. 9. Further investigation of $C_{dn}^{HOST}$ below 10 m is needed.

Essentially using the neutral $u_*-V$ line only, regardless of how the neutral surface layer is achieved, would ensure correct estimates of surface drag coefficients. If all we need to know is the net dynamic impact of the surface on atmospheric momentum transfer, not the impact of the surface on detailed wind profiles, using $C_{dn}^{HOST}$ instead of $z_o$ can avoid issues such as how to relate physical heights of all the roughness elements to $z_o$, finding displacement heights, and validity of the Monin–Obukhov bulk formula in a relatively deep surface layer.

8 Summary

We investigate the physical processes that contribute to the observed turbulent momentum transfer and implicitly assumed in the Monin–Obukhov bulk formula. The observations from two field experiments are used: CASES-99 is overwhelmed by clear sky days in October with strong thermal diurnal variations, and FLOSS-II is with a significant percentage of cloudy and precipitation days from late autumn to spring resulting in weak diurnal variations in the surface layer. As a result, CASES-99 is associated with strong diurnal variations of the surface layer stratification; FLOSS-II with relatively weak ones on average. We summarize the important understandings of the turbulent transfer of momentum below.

Turbulence intensity is dominated by the most energetic non-local coherent turbulence eddies generated by non-local shear or positive buoyancy. The scale of the most energetic non-local coherent turbulence eddies observed at a given height z is about the length of z for the unstable and the neutral surface layers and less than the length of z in the stable surface layer. Therefore, the atmospheric stratification near the surface is related to the scale of the most energetic non-local coherent turbulence eddies, and the surface layer relevant to the turbulence intensity at z is the air layer between the surface and z. Additionally, turbulence intensity is not related to local shear $\partial V/\partial z$ unless the observation height z is near the surface, such as $z = 0.5$ m, where the difference between the bulk shear V/z and $\partial V/\partial z$ is negligible. Only mechanically generated turbulent mixing can lead to a neutral surface layer, while thermally generated turbulent mixing has to be supported by a vertical decrease of air density associated with positive buoyancy. Thus, variations of wind speeds at z are closely related to the surface-layer stratification.

The Monin–Obukhov bulk formula under neutral conditions is valid for a special neutral surface layer between the surface and height z, which remains neutral under any wind conditions. This neutrality implies that the surface heating/cooling has to be zero. The MOST neutral surface layer has been observed during FLOSS-II with relatively weak atmospheric stratification. The Monin–Obukhov bulk formula agrees well with observations at least up to 30 m when this neutral surface layer is observed.

When the surface heating/cooling is strong, especially under weak winds, the surface layer stratification is relatively strong. The neutrality of the surface layer is achieved through mechanically generated non-local turbulent mixing under strong wind conditions and is observed during CASES-99. The observed transition between the stratified and the neutral $u_*$ as a function of V at z forms the observed HOST. The Monin–Obukhov linear $u_*-V$ relationship at z goes through the zero point, $(u_*,V)=(0,0)$ for any z, while the neutral $u_*-V$ line achieved through strong shear-generated turbulent mixing while the surface heats/cools the air above shifts towards strong winds and only goes through the zero point when z is near the surface. Physically, the Monin–Obukhov bulk formula describes $u_*$ variations at z by fitting the observed $u_*$ in the stratified surface layer and returning the Monin–Obukhov neutral $u_*-V$ line instead of the neutral one resulted from the strong mechanically generated turbulent mixing under strong winds. Consequently, the Monin–Obukhov bulk formula performs reasonably well near the surface and deviates from the observed $u_*-V$ relationship with increasing z in a stratified surface layer. The poor performance of the Monin–Obukhov bulk formula in a stratified surface layer is due to the deviation of its neutral state implicitly assumed for a special neutral surface layer and cannot be improved by fitting stability functions. Further investigation of the vertical variation of the most energetic non-local coherent turbulence eddies, especially near the surface, is needed.

Understanding the physical processes responsible for differences between the observed HOST $u_*-V$ relationship when the surface layer is stratified and the $u_*-V$ relationship described by the Monin–Obukhov bulk formula provides guidance to capture important physical processes in numerical models. These processes involve the correct description of the development of the stratified surface layer including surface molecular diffusion and capture of non-local forcing for generation of the most energetic non-local coherent turbulence eddies. Development of the most energetic non-local coherent turbulence eddies is constrained by conservation laws of momentum and energy. MOST is a theory for describing the relationship between turbulent mixing and mean states in the air layer near the surface, which is only observed under a special neutral condition. HOST represents the observed $u_*-V$ relationship in a stratified surface layer and reveals important physical processes in turbulent mixing that cannot be fully described by MOST. An example of simulating the transition between the stable and the neutral regimes based on conservation laws for capturing observed physical processes has been demonstrated in Maroneze et al. (2019).

To estimate the surface drag coefficient for a given surface type, the neutral relationship between $u_*$ and V near the surface should be used when the observed turbulent mixing for $u_*$ at a given z is fully coupled with the surface and the stratification between z and the surface is eliminated. When the level z is near the surface such as at 0.5 m, turbulent mixing at 0.5 m is practically coupled with the surface all the time, there are no significant differences between the MOST and the HOST neutral $u_*-V$ relationships within the thin layer below 0.5 m. If an observation height z is further away above the surface and the surface layer below z is stratified, the surface drag coefficient cannot be estimated using the traditionally defined drag coefficients $C_{d}(z)=[u_*(z)/V(z)]^2$ even after the surface layer below z is transitioned from the stratified to the neutral layer. This is because the relationship between $u_*$ and V under weak winds is influenced by the stratification, which deviates away from the neutral $u_*-V$ line. In this situation, the surface drag coefficient can be estimated with the observed HOST neutral $u_*-V$ relationship resulting from the full coupling of the air between height z and the surface through mechanically generated non-local coherent turbulence eddies.

This study is mainly based on observations over two relatively bare surfaces. The concepts of the physical processes described in the study should be valid over other types of surfaces. Scales of the most energetic non-local coherent turbulence eddies under a variety of conditions need to be further investigated.