Thermal Submesoscale Motions in the Nocturnal Stable Boundary Layer. Part 1: Detection and Mean Statistics

Abstract

Submesoscale motions within the stable boundary layer were detected during the Shallow Cold Pool Experiment conducted in the Colorado plains, Colorado, U.S.A. in 2012. The submesoscale motion consisted of two air layers creating a well-defined front with a sharp temperature gradient, and further-on referred to as a thermal submesofront (TSF). The semi-stationary TSFs and their advective velocities are detected and determined by the fibre-optic distributed-sensing (FODS) technique. An objective detection algorithm utilizing FODS measurements is able to detect the TSF boundary, which enables a detailed investigation of its spatio–temporal statistics. The novel approach in data processing is to conditionally average any parameter depending on the distance between a TSF boundary and the measurement location. By doing this, a spatially-distributed feature like TSFs can be characterized by point observations and processes at the TSF boundary can be investigated. At the TSF boundary, the air layers converge, creating an updraft, strong static stability, and vigorous mixing. Further, the TSF advective velocity of TSFs is an order of magnitude lower than the mean wind speed. Despite being gentle, the topography plays an important role in TSF formation. Details on generating mechanisms and implications of TSFs on the stable boundary layer are discussed in Part 2.

Introduction

Atmospheric processes cover a broad range of temporal and spatial scales as introduced by Orlanski (1975), to which the submeso scale was later added. These processes range from the macroscale (cyclones), mesoscale (orographic effects, urban heat island, thunderstorms) to the microscale (convection, turbulence). Here we focus on atmospheric processes on the submeso scale with a spatial scale of several hundred metres and temporal scales up to one hour, which means higher temporal and spatial scales than small-scale turbulence, but lower spatial scales than deep convection.

Understanding the formation of submesoscale motions within the stable boundary layer (SBL) as well as their connection to turbulent fluxes is important as such motions affect near-surface transport processes and thus ecosystems and humans. Submesoscale motions, such as cold-air drainage within the SBL, may alleviate urban heat islands (Kuttler et al. 1996; Sachsen et al. 2014) and affect the formation of fog (Izett et al. 2019). The formation of cold-air layers can trap contaminants and other gases that cause health hazards (Silcox et al. 2012). Further, turbulent fluxes, which are influenced by submesoscale motions, affect hydrological cycles by determining the timing of snow melt (Pohl et al. 2006; Mott et al. 2011; Burns et al. 2012) and the sublimation of snow (MacKay et al. 2006; Reba et al. 2012).

Investigating submesoscale motions was the objective of the Shallow Cold Pool (SCP) experiment in the Colorado plains, Colorado, U.S.A. in 2012. Within this experiment, a very dense network of stations were deployed within the valley in addition to acoustic remote sensing. Publications analyzing data of the SCP experiment so far focused on investigating stably stratified flow (Mahrt et al. 2014b; Mahrt 2017c), the structure of the nocturnal boundary layer (Geiss and Mahrt 2015; Mahrt and Heald 2015; Mahrt 2017b), and the response of the boundary layer to shear (Mahrt et al. 2014a; Mahrt 2017a). Further, the relation between horizontal wind speed, turbulence characteristics, and stratification was investigated in detail (Mahrt and Thomas 2016). As noted in some of these publications, transitory modes or microfronts were observed to cause intermittently increased turbulence during cold-air drainage and pooling, further raising questions about their formation and interaction with the SBL. While Mahrt (2017b) investigated this to some extent, these questions are explored in more detail below.

The detailed investigation into nocturnal submesoscale motions necessitates a measurement technique that offers high spatial resolution of temperature measurements, such as the fibre-optic distributed-sensing (FODS) technique. Every few decimetres along a fibre-optic cable, the spatially-distributed air temperature and wind speed can be measured up to a frequency of 1 Hz. The FODS technique has been applied previously in the atmospheric boundary layer (Keller et al. 2011; Thomas et al. 2012; Sayde et al. 2015; Sigmund et al. 2017), leading to unique results such as the tomography of a cold-air current (Zeeman et al. 2015), the invalidation of Taylor’s hypothesis in the atmospheric surface layer (Cheng et al. 2017), and the determination of temperature and flow regimes (Pfister et al. 2017, 2019). While the FODS technique is especially useful for tracking submesoscale motions in space and time, it does not yet provide flux measurements as are made at ultrasonic-anemometer stations.

During the SCP experiment, measurements with the FODS technique were conducted along a 240-m-long cross-valley transect. Fibre-optic distributed sensing  provided spatially continuous measurements of temperature and, for the first time also wind speeds (Sayde et al. 2015) using the actively-heated fibre-optic-cable approach. Even though the sonic anemometer and thermohygrometer network used during the SCP experiment is considered dense, it was unable to track nocturnal submesoscale motions (Mahrt 2017b). In contrast, the animation of FODS data (Online Resource 1) does show a specific submesoscale motion. Here, the interaction between a warm-air layer and cold-air layer forming a thermal front was observed moving up and down the northern valley side wall. We name these motions thermal submesofronts (TSF), similar to Mahrt (2010).

In Part 1 of our study, we develop the detection algorithm for the TSF boundary and compute unique spatiotemporal statistics. The novelty is the ability to detect the presence and precise location of the TSF boundary used for conditional averaging by placing point observations from ultrasonic anemometry into the spatial context of the near-surface temperature field derived from the FODS technique. This approach combines the strengths of both measurement techniques. Mean statistics are given, revealing the horizontal extent as well as the vertical structure of the boundary layer during the occurrence of TSFs, their advective velocity, and characteristics of the two air layers forming TSFs.

Field Site and Methods

Shallow Cold Pool Experiment

The SCP Experiment was designed to investigate shallow cold pools in gentle terrain. It was conducted in north-east Colorado, U.S.A., over semi-arid grassland at approximately 1660 m above mean sea level from 1 October to 1 December 2012 (https://www.eol.ucar.edu/field_projects/scp). Ancillary measurements with the FODS technique makes it a unique field study. These measurements were conducted in the period 16–27 November, though we only consider the nine nights with FODS data without observational gaps from 1900 LT (local time = $\hbox {UTC} - 7$ h) until 0500 LT. A detailed description of the field site and all instrumentation can be found in Mahrt and Thomas (2016).

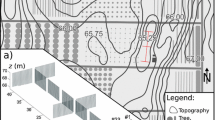
The valley can be described as gentle terrain with a height difference of $\approx$ 27 m from north-west to south-east along a distance of $\approx$ 1.2 km for a maximum inclination of 1.4$^\circ$ (https://www.eol.ucar.edu/system/files/files/field_project/SCP/SCP-RIC.kmz). On average, the valley slopes rise about 12 m over a horizontal distance of about 130 m; the width of the flat valley bottom averages to about 5 m. The north side of the valley is characterized by a small plateau followed by a smooth hill into the valley with an inclination of $\approx$ 6$^\circ$ (Fig. 1). Inclination and heights were determined with a hand-held Global Positioning System instrument.

The experiment consisted of a near-surface network of 19 ultrasonic anemometer (Model CSAT3, Campbell Scientific, Logan, UT, U.S.A.) stations (A1–A19) at 1 m above ground level (a.g.l.), except A15 at 2 m and A17 at 0.5 m a.g.l., and a 20-m tower with eight ultrasonic anemometer stations (0.5 m, 1–5 m, 10 m, 20 m a.g.l.) were set up. Data from the 3-m station had to be discarded due to errors. At the tower, ventilated thermohygrometers operated by the National Center for Atmospheric Research (NCAR) (https://www.eol.ucar.edu/rtf/facilities/isff/sensors/ncar_trh.pdf) were installed at several heights of which the 0.5-m and 15-m measurements on the main tower (M) were used to estimate the static stability.

Fig. 1

Left: Topographical overview of field site with ultrasonic anemometer stations (A1–A19), the 20-m high main tower (M), and the fibre-optic distributed-sensing (FODS) transect (white line). Chosen stations for down-valley transect (dashed black line) and cross-valley transect (dashed purple line) for Fig. 4 (cf. Sect. 3.2). Right: Cross-valley view of the fiber-optic transect showing its length and elevation

The fibre-optic transect sampled by the FODS instrument (Ultima SR, Silixa, London, UK) was 240-m long and was constructed from a cable duplet: an unheated optical glass-fibre cable with an outer diameter of 0.9 mm to measure air temperatures, and an actively heated stainless-steel fibre-optic-cable (1.3 mm outer diameter) for measurements of the velocity component orthogonal to the fibre-optic cable. Each fibre-optic-cable duplet was installed at heights of 0.5 m, 1 m, and 2 m a.g.l. (cf. Fig. 1). The temporal and spatial resolution of the FODS measurements were 5 s and 0.25 m, respectively. Artefacts from the fibre holders causing additional heating or cooling of the fiber-optic cable were removed and filled using spatial linear interpolation for each timestep. For further information on the FODS set-up and the wind-speed measurements, refer to Sayde et al. (2015) and Pfister et al. (2019).

Ancillary to the 20-m tower, a ground-based acoustic wind profiler (sodar, PCS2000-24, Metek GmbH, Elmshorn, Germany) was installed at the valley bottom (1640 m above mean sea level) between stations A18 and A19. The wind profiler had an observational range of 10 m to 320 m a.g.l. measuring the wind speed as well wind direction every 10 m. Measurements were averaged to 5 min. For the analysis, we use the cluster data output of the wind profiler, which is quality-controlled by the internal-data-processing software.

There is open access to the data of the network through the Earth Observatory Laboratory of NCAR, while the FODS technique, and wind-profiler details are published on Zenodo (Pfister et al. 2020).

Averaging Operators and Computed Fluxes

We applied Reynolds decomposition to determine temporal and spatial perturbations, by which an arbitrary variable $\phi$ is divided into a mean and a fluctuating part,

$$\begin{aligned} \phi= & {} \overline{\phi }+\,\phi ' , \end{aligned}$$

(1)

$$\begin{aligned} \phi= & {} <\phi >~+\,\widehat{\phi } , \end{aligned}$$

(2)

with $\overline{\phi }$ representing the temporal and $<\phi>$ the spatial mean, while $\phi '$ and $\widehat{\phi }$, respectively, are the corresponding fluctuating parts. An averaging time scale of 60 s was chosen. For this time scale, the fast Fourier transform spectra and cospectra of temperature and velocity components agree well in comparisons between an ultrasonic-anemometer station and the nearest FODS measurement. A variety of spatial scales was used for computing $<\phi>$ depending on the involved stations and which transect or area was investigated.

To determine turbulence characteristics, the friction velocity $u_*$ and sensible heat flux $Q_H$ were computed from the measurements of each ultrasonic anemometer as

$$\begin{aligned} u_*= & {} \left( \overline{u_s'w_s'}^2 + \overline{v_s'w_s'}^2 \right) ^{0.25} , \end{aligned}$$

(3)

$$\begin{aligned} Q_H= & {} \rho ~c_p~\overline{w_s'T_s'}, \end{aligned}$$

(4)

with $u_s$, $v_s$, and $w_s$ being the west, south, and vertical velocity components, $T_s$ the temperature, $\rho$ the air density, and $c_p$ the specific heat at constant pressure. The meteorological sign convention is used with a negative sign representing a net flux towards the surface, while a positive sign indicates a flux away from the surface.

For conditional averaging, any parameter $\phi$ was averaged over all samples fulfilling a specific condition and is written with angular brackets $[\phi ]$. Mean values and the standard deviation of the wind direction are computed according to Yamartino (1984). The bulk Richardson number is computed from the FODS transect as

$$\begin{aligned} Ri_B= & {} \frac{g}{\overline{\theta }} \frac{\Delta \theta \Delta z^{-1}}{(\Delta u \Delta z^{-1})^2} , \end{aligned}$$

(5)

with $\overline{\theta }$ being the mean layer temperature, and $\Delta \theta \Delta z^{-1}$ and $\Delta u \Delta z^{-1}$ being the vertical potential temperature and wind-speed gradients at each measurement point within the FODS transect. The conditionally-averaged $[Ri_B]$ is calculated from the conditionally-averaged quantities of $[\overline{\theta }]$, $[\Delta \theta \Delta z^{-1}$], and $[\Delta u \Delta z^{-1}]$.

Comparison of Fibre-Optic and Ultrasonic-Anemometer Measurements

The FODS and ultrasonic anemometer measurements were compared to ensure high data quality and to test if both devices can be used interchangeably for conditional averaging. A scatter-plot of temperature reveals a high linear 1:1-correlation ($R^2 = 0.996$) between the FODS and ultrasonic anemometer measurements at an offset of − 0.4 K for A15 (2 m a.g.l.) at the north shoulder and − 0.2 K for A17 (0.5 m a.g.l.) at the valley bottom (see “Appendix 1”, Fig. 9a, b). This offset of both ultrasonic anemometers was accounted for in the complete field campaign to match the FODS measurements, which reduced the disagreement between these techniques to 5–6%. Analysis of the spatial and temporal temperature perturbations demonstrates a close match between the devices (Fig. 9c, d). We therefore conclude that both devices represent the mean and turbulent temperature field equally well, enabling their use for conditional averaging.

Evaluating the FODS wind-speed measurements showed a dependence on the angle of attack to the fibre (Sayde et al. 2015; Pfister et al. 2019; van Ramshorst et al. 2019). As expected, the velocity component parallel to the fibre orientation is generally underestimated by FODS. But FODS wind-speed measurements were not adjusted for this angular dependence as there were not enough ultrasonic anemometers next to the FODS transect to correct for it. Nonetheless, FODS can be used to determine the vertical wind-speed gradient assuming wind directions within 2 m a.g.l. are constant with height given the topography.

Detection of Thermal Submesofronts and Conditional Averaging

A detection algorithm was developed for the TSF boundary using the sharp horizontal temperature difference $\Delta _x \theta$ between the warm air on the north shoulder and the adjacent cold air (cf Fig. 2b). The spatially-continuous FODS data were used to determine the exact location of the non-stationary TSF boundary in a three-step process.

Fig. 2

a Length of fibre-optic transect and elevation in metres showing the cross-valley topography. b Potential fibre-optic temperatures $\theta _f$ (colourbar) within the valley in a space-time diagram. Two examples are given to illustrate how the distance from the thermal submesofront (black lines) to each ultrasonic anemometer station (grey crosses and vertical lines) is assigned as indicated by black arrows and $+/-$ signs for the distance to the thermal submesofront

First, the optimal separation distance needs to be determined for computing the spatial temperature difference $\Delta _x \theta$ between two measurement bins of the FODS measurements. We used a fixed separation distance between bins and then computed the difference $\Delta _x \theta$ for all bin-pairs of the fibre-optic transect for each transect level. The physical location of the difference $\Delta _x \theta$ is the centre between the bins. For each timestep, the location of the maximum $\Delta _x \theta$ value should reveal the location of the TSF boundary. Different separation distances ranging from 0.5 m up to 16 m were tested and their results evaluated visually. A separation distance of 4 m was optimal as it provides large $\Delta _x \theta$ values while being considered precise enough to represent a TSF boundary.

Second, if temperatures are spatially homogeneous, the difference $\Delta _x \theta$ should diminish to very small values and fall below a certain threshold, which is defined as the uncertainty of temperature differences $\delta _T$ measured by the FODS technique. This quantity is defined as $\delta _T = \sqrt{2\sigma _\mathrm{FODS}^2}$ with $\sigma _\mathrm{FODS}$ being the root-mean error of the temperature difference between a reference platinum-wire thermometer and the FODS cable in a thermally controlled calibration bath. We discarded any values for $\Delta _x \theta <$ 0.73 K.

In a last step, two further measures are applied: TSFs are required to persist for at least 40 s, and are discarded if their advective velocity within 5 s is higher than the maximum wind speed detected at 2 m a.g.l. for the analyzed nights. We assumed that TSFs do not move faster than this maximum wind speed at any time. The outcome of this detection algorithm is shown in Fig. 2b as a solid black line.

The uniqueness of our study is the use of conditional averaging for placing any measurement location into the spatial context of the TSF boundary. Therefore, a relative distance between the TSF boundary and the measurement location of an arbitrary parameter $\phi$ is defined with the sign indicating the air layer in which $\phi$ was measured. A negative sign indicates the warm-air layer, while a positive sign indicates the cold-air layer  (cf. Fig 2b). A relative distance could only be determined for the FODS measurements and two ultrasonic anemometer stations, namely A15 and A17 of the sensor network (Figs. 1, 2a), as they were adjacent to the FODS transect. For all other measurements, including the SODAR measurements, conditional averaging was applied only depending on the occurrence of TSFs.

Results and Discussion

Mean Statistics and Conditions during the Occurrence of Thermal Submesofronts

The main TSF characteristic is the sharp horizontal temperature gradient max$(\Delta _x~\theta )$ between the warm and cold air with a mean value of 3 K ranging up to 13 K (cf. Fig. 2b). A TSF is formed by the interface created by warm air entering the valley from the north and cold air being present primarily at the valley bottom, but occasionally reaching up to the valley’s sidewall. Thermal submesofronts are a consistent feature on the north shoulder of the valley moving up and down; therefore, the TSFs in our study are semi-stationary. They occur 31% of the time and during most nights of statically stable conditions with a duration between 40 s up to 1 h. Their spatial scales ranged from 200 to 300 m as determined from the complete ultrasonic anemometer network (Sect. 3.2). Hence, we classify TSFs as submesoscale motions, following (Orlanski 1975), which occur frequently in the SBL. Accordingly, the name TSF refers to the scale and the front, which is the boundary between two air masses of different density due to their different thermal properties. So we note that the motion or other characteristics of TSF do not follow the commonly used definition for fronts on the synoptic scale to prevent confusion.

The advective velocity of TSFs, defined as the spatial change in TSF boundary location over time, was 0.2 m s$^{-1}$ on average with maxima reaching up to 5.5 m s$^{-1}$. Thermal submesofronts move very slowly, roughly an order of magnitude lower than the mean wind speed. This is in concordance with Lang et al. (2018), which concluded that flow perturbations of microfronts are not transported by the local flow.

Fig. 3

Wind roses showing the frequency of wind speed V and direction for the 20-m station on the main tower during the occurrence and absence of TSFs (cf. titles)

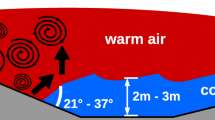
The TSF boundary was detected at all three levels of the FODS transect simultaneously, allowing for the derivation of the tilt of the TSF boundary, defined as the angle between the TSF boundary and the surface (cf. Fig. 8). The interquartile range of this tilt angle is $21-37^\circ$, with the warm air being aloft of the cold air and tilting towards the valley bottom. If the tilt is close to the inclination of the valley shoulders, we would expect a fully developed cold-air pool with warmer air flowing on top. As the tilt is much higher than 6$^\circ$, the tilt of the TSF boundary is created by the convergence of the warm-air and cold-air layers.

During the SCP experiment the main wind direction was from the north-west and did not change during the occurrence of TSF events, as shown by the 20-m measurement on the main tower (Fig. 3). Thermal submesofronts preferably occur during low wind speeds (3.5 m s$^{-1}$) compared to slightly higher wind speeds during their absence (4.8 m s$^{-1}$).

Spatial Extent of Thermal Submesofronts at Field-Site Scale

Conditional averaging based on the occurrence of TSFs was applied to the parameter $\widehat{\theta }$ and $u_*$ for each ultrasonic anemometer station of the network, and is presented as spatially-interpolated contour plots. Figure 4 represents the average location of the TSF boundary as the conditional average computed over all incident TSFs without considering their actual location. Three views were chosen (cf. Fig. 1) for a quasi-three-dimensional presentation of TSFs: overhead view, down-valley view (dashed black line), and cross-valley view (dashed purple line). In addition to the near-surface stations, the down-valley view incorporates all stations of the main tower, while the cross-valley view only includes the 20-m station.

Fig. 4

Spatial temperature perturbations $[\widehat{\theta }]$ (a–c) and friction velocity $[u_*]$ (d–f) during the occurrence of thermal submesofronts as an overhead view of the field site (a, d), as a down-valley view (b, e), and as a cross-valley view (c, f). Stations included for each view are shown in Fig. 1. Black crosses: ultrasonic anemometer station. Blue contourlines: elevation in m above mean sea level. Arrows: mean wind speed (cf. legend). Arrows of the overhead view (a, d) show the flow direction

For computation of the friction velocity $u_*$, height-independent fluxes are assumed to be in equilibrium with the surface. Since one knows from the FODS technique that cold-air and warm-air layers were in contact with the surface, the use of $u_*$ appears justified for all 1-m stations, while on the main tower it is only justified for the stations within the cold-air layer.

Two air layers can clearly be distinguished in Fig. 4a. For the warm-air layer, near-surface temperatures (Fig. 4a), as well as the magnitude of $[u_*]$ (Fig. 4d) were increased across the entire plateau edge on the north shoulder. While at the same time on the valley bottom, the parameters $[\widehat{\theta }]$ and $[u_*]$ were low for all near-surface stations as they were located within the cold-air layer. The air layers also had different flow directions as illustrated by arrows in Fig. 4a, d. Stations within the warm-air layer detected a strong flow from the north-west, which was aligned with the flow at 20 m a.g.l. on the main tower (Fig. 3), while stations within the cold-air layer detected a weaker terrain-following flow corresponding to that of the 1-m station on the main tower (Fig. 10).

Here we discuss the role of topography to form both air layers. The main wind direction is from the north-west, accordingly the air flows over the small plateau at the north shoulder. Due to the elevation change on the north shoulder, the flow detaches from the ground, creates a cavity region, and then reconnects with the surface where increased turbulence and mixing are observed, hence, this turbulence is topographically induced. This interpretation is supported by observations at the stations at the opposite side of the valley at identical elevation, which did not show similarly high values of $[\widehat{\theta }]$ (Fig. 4c) and $[u_*]$ (Fig. 4e) compared with observations on the north shoulder. For the valley bottom, the topography provides shelter for cold-air drainage and pooling as indicated by the terrain-following flow of low temperatures. This interpretation is supported by the occurrence of TSFs, and cold-air drainage persisting during topographically-induced mixing and relatively high wind speeds. Hence, topography plays a major role in forming TSFs even though this process is usually not anticipated for gentle terrain and high wind speeds.

From the preceding section, we recall that the mean horizontal extent of TSF boundary is approximately 200–300 m and thus TSFs classify as submesoscale motions. To determine their vertical extent, the profile of $u_*$ is analyzed (Fig. 4e) as $\widehat{\theta }$ only indicates a SBL profile without revealing specific air layers further aloft (Fig. 4b). The friction velocity $u_*$ was smallest in the lowest 2 m a.g.l., while at 4 m and 5 m a.g.l. peak values were observed. We conclude that the cold-air layer characterized by low turbulence had a mean thickness ranging between 2 m and 3 m topped by warm air. The cross-valley view confirms this configuration (Fig. 4c, f). The vertical structure of TSFs and their impact on the SBL are discussed in Part 2 (Pfister et al. 2021).

When TSFs were absent (not shown), $u_*$ and $\widehat{\theta }$ were spatially homogeneous and the wind direction was uniform across all stations, as shown at the 20-m and 1-m stations on the main tower (Figs. 3, 10). We therefore conclude that TSFs are eroded by the intense turbulent mixing in a coupled boundary layer and are marked by a uniform flow direction.

Thermal Submesofront Characteristics from Spatially-Distributed Sensing

A more detailed view of the TSF boundary can be derived from conditionally averaging the FODS data using the relative distance to the TSF boundary. The mean temperature decrease from warm to cold air was 3.4 K over a horizontal distance of approximately 20 m (Fig. 5a).

Fig. 5

Conditional averaging of fibre-optic data depending on the distance to the thermal submesofront: a spatial temperature perturbation $\left[ \widehat{\theta }\right]$, b temporal temperature perturbation $\left[ \overline{\theta '^2}\right]$, c spatial wind-speed perturbation $\left[ \widehat{u}\right]$, and d bulk Richardson number $\left[ Ri_B\right]$

When defining the transition area from warm to cold air at the TSF boundary as the location of the sign change between the 10% and 90% percentiles of $[\widehat{\theta }]$, its width amounts to 11 m (cf. Fig. 5). The transition area may appear very narrow, but it substantially affects temporal temperature perturbations (Fig. 5b), the wind field (Fig. 5c), as well as static stability and wind shear (Fig. 5d). Peak values in the transition area were 0.8 K$^2$ for $[\overline{\theta '^2}]$, winds speeds decreased by 0.5 m s$^{-1}$, static stability was maximum at 1.3 K m$^{-1}$, and the wind shear $\left[ \Delta u\,\Delta z^{-1}\right]$ decreased by 0.2 m s$^{-1}$ m$^{-1}$ (Fig. 5d). In the transition area, warm air pushes against and slides over the cold air creating strong static stability as well as the peak in $[\overline{\theta '^2}]$. Considering the size of the transition area and the advective velocity of TSFs as determined earlier, the transition from cold to the warm air takes on average 55 s at a fixed location. This finding confirms our earlier choice of an averaging time scale of 60 s. The decrease in wind shear is due to the convergence of the air layers creating similar velocities in the lowest 2 m a.g.l. Therefore, peak values in $Ri_B$ are found at the transition area due to the peak in temperature gradient and minimum in wind shear.

When the warm air flows over the cold-air layer, it can create a ripple-like structure of the interfacial boundary. This modulation is not further investigated but can be seen for example in Fig. 2b, and thus is added to the conceptual summary given in Fig. 8.

Flow and Turbulence Characteristics of Thermal Submesofronts from Single-Point Measurements

The contrasting flow characteristics of the two competing air layers of the TSF are investigated in detail by conditional averaging the observations from the two ultrasonic anemometer stations A15 and A17 next to the FODS measurements. Here, we present statistics on the wind speed, V, the velocity component along the FODS transect, $v_s$, the vertical velocity component, $w_s$, wind direction, $\varphi$, friction velocity, $u_*$, and sensible heat flux, $Q_H$.

Wind speeds in the warm-air layer were higher by almost 2 m s$^{-1}$ compared with those in the cold air (Fig. 6a). The north–south component, $v_s$, changed sign within the transition area with strong negative values within the warm-air layer and small positive values within the cold-air layer (Fig. 6b), which highlighted the opposite flow direction of the air layers and their convergence at the interfacial boundary. The warm air entered the valley from north-north-west while the cold air followed the terrain with wind directions from west-south-west (Fig. 6d), creating a mean wind directional shear of 90$^\circ$ between the air layers.

Fig. 6

Conditional averaging of ultrasonic anemometer data depending on the distance to the TSF boundary: a wind speed [V], b north–south component of the velocity $[v_s]$, c vertical velocity component $[w_s]$, and d mean wind direction $[\varphi ]$. Bars: 10% and 90% percentile. Colours: location of ultrasonic anemometer station. Grey area: transition area

In the transition area, an upward motion was observed with the sign of $w_s$ changing from negative to positive (Fig. 6c), and was already detected a few metres in advance of the station on the north shoulder, while at the valley bottom $w_s$ was also positive, but rather weak. We conclude that the dense cold air acts as a barrier for the warm air, hence, instead of eroding the cold-air layer it flows on top and is forced upwards. This effect is weaker at the valley bottom because the warm-air layer only reaches the valley bottom during higher wind speeds and corresponding strong turbulence, which most likely erodes the cold air, hence, the upward motion of the warm air is weaker or negligible.

Note that the value of $[\widehat{u}]$ computed from FODS (Fig. 5d) does not show the same results as for the value of [V] from the ultrasonic anemometer measurements. This difference is likely caused by the flow direction deviating from being perpendicular to the optical-fibre orientation in the warm-air layer compared with that in the cold-air layer (cf. Fig. 6d). This systematic directional change leads to an underestimation of the wind speed for the actively-heated FODS technique (Pfister et al. 2019). We were unable to compensate for this observational artefact due to the lack of a sufficient number of reference stations next to the FODS transect, which would have allowed for applying an angularly dependent correction.

Turbulence characteristics strongly differed for the contrasting air layers of the TSF. In the warm air, $u_*$ as well as $Q_H$ is elevated (Fig. 7), as can be expected from high wind speeds and topographically-induced turbulent mixing. In contrast, $u_*$ and $Q_H$ were very low in the cold air, as can be expected for cold-air drainage and pooling with reduced vertical turbulent exchange. In summary, TSFs caused a rapid change in the values of $u_*$ and $Q_H$ of 0.1 m s$^{-1}$ and − 30 W m$^{-2}$, respectively, during passage.

Fig. 7

Conditional averaging of ultrasonic anemometer data depending on the distance to the TSF boundary: a friction velocity $[u_*]$, and b sensible heat flux $[Q_H]$. Bars and colours as in Fig. 6

Fig. 8

Conceptual drawing of a TSF (not to scale) within the valley (grey areas) consisting of a warm-air layer (red) and a cold-air layer (blue). Coloured arrows indicate the different flow directions of the air layers, while black swirls indicate the topographically-induced mixing. At the transition area, where the air layers merge, the warm-air layer is forced upwards (black arrow) as the cold-air layer acts as a barrier

Conclusion

The SCP experiment is a unique study combining the observational strengths of the FODS technique with a near-surface network of ultrasonic anemometer stations to investigate TSFs within the nocturnal boundary layer in gentle terrain.

Thermal submesofronts occurred frequently in the SBL and were generated by the gentle topography, creating two air layers with distinctly different characteristics: the warm-air layer is mechanically generated by topographically-induced turbulence, consistently elevating near-surface temperatures at the plateau edge, while the cold-air layer is thermodynamically driven by topographically induced cold-air drainage and pooling, with low near-surface temperatures in the valley bottom caused by radiative cooling. A key feature of our resukits is the conditional averaging revealing the vertical and horizontal structure of TSFs as well as processes at the TSF boundary.

Our main findings are best summarized in a conceptual cross-section of a TSF (Fig.  8). Implications of TSFs for the SBL are discussed in Part 2 (Pfister et al. 2021).

Appendix 1

Figure 9a, b compares the temperature measurements by FODS and by ultrasonic anemometer at station A15 at 2 m a.g.l. on the north shoulder and at station A17 at 0.5 m a.g.l. at the valley bottom. The computed offset or bias was corrected for the ultrasonic anemometer measurements. To verify a reasonable correction, the spatial as well as temporal temperature perturbation conditionally averaged depending on the distance to the TSF boundary is compared between the fibre-optic and ultrasonic anemometer data in Fig. 9c, d.

Fig. 9

Comparison of fibre-optic and ultrasonic anemometer temperature measurements (a) at 2 m a.g.l. on the north shoulder and (b) at 0.5 m a.g.l. at the valley bottom revealing the offset between measurements. The offset was adjusted for the ultrasonic anemometer measurements. After the correction, the spatial (c) and temporal temperature perturbation (d) show the match between all measurement devices

Wind roses show the wind speed and direction at the 1-m station on the main tower during the absence and occurrence of TSFs (Fig. 10). During the absence of TSFs, the wind speed was higher and wind directions were mainly from the north-west, while during occurrence of TSFs, the wind speed was lower and wind directions were from the west.

Fig. 10

Wind roses showing the frequency of wind speed and direction for the 1-m station on the main tower during the absence and occurrence of TSFs