Wind-Tunnel Simulation of Approximately Horizontally Homogeneous Stable Atmospheric Boundary Layers

Abstract

Two cases of an overlying inversion imposed on a stable boundary layer are investigated, extending the work of Hancock and Hayden (Boundary-Layer Meteorol 168:29–57, 2018; 175:93–112, 2020). Vertical profiles of Reynolds stresses and heat flux show closely horizontally homogeneous behaviour over a streamwise fetch of more than eight boundary-layer heights. However, profiles of mean temperature and velocity show closely horizontally homogeneous behaviour only in the top two-thirds of the boundary layer. In the lower one-third the temperature decreases with fetch, directly as a consequence of heat transfer to the surface. A weaker effect is seen in the mean velocity profiles, curiously, such that the gradient Richardson number is invariant with fetch, while various other quantities are not. Stability leads to a ‘blocking’ of vertical influence. Inferred aerodynamic and thermal roughness lengths increase with fetch, while the former is constant in the neutral case, as expected. Favourable validation comparisons are made against two sets of local-scaling systems over the full depth of the boundary layer. Close concurrence is seen for all stable cases for z/L < 0.2, where z and L are the vertical height and local Obukhov length, respectively, and over most of the layer for some quantities.

1 Introduction

Wind-tunnel simulations of the atmospheric boundary layer should, obviously, exhibit features that are characteristic of full-scale flows. Moreover, from a practical point of view, where the study is of the effect of a simulated flow on some ‘body’ or surface disturbance, the undisturbed conditions should change slowly in the direction of the flow. That is, the flow should be at least approximately horizontally homogeneous. The present interest concerns the wakes of large offshore wind turbines where, to be representative, the flow away from the turbine and wake should be at least approximately constant in the streamwise direction, as in the case of a naturally-arising atmospheric boundary layer.

Two previous studies have systematically investigated the simulation of weakly or moderately stable boundary layers, drawing on well-established wind-engineering techniques for wind-tunnel studies in neutral flow. These techniques use a system of tall generators and surface roughness in order to create profiles of mean velocity and turbulence quantities that have the desired characteristics of a deep ($\approx$ 1 m) boundary layer, which offers practical experimental benefits associated with model size and instrumentation. In the first investigation, Hancock and Hayden (2018) give results leading to the simulation of a boundary layer that had approximately horizontally homogeneous characteristics,¹ with profiles of mean and second-order turbulence quantities that compare favourably with the field measurements of Caughey et al. (1979), and with the local-scaling frameworks of Nieuwstadt (1984) and Sorbjan (2010). In that study, the temperature above the boundary layer was constant (as also in Caughey et al. 1979). In the second investigation, Hancock and Hayden (2020) give results for the effect of imposing an overlying inversion compared with the case of no inversion (as in the 2018 paper). These, too, compare favourably with the scaling frameworks of Nieuwstadt (1984) and Sorbjan (2010). The inversion was imposed by means of heaters at the working-section inlet, and was imposed in four different ways. It was imposed to one or other of two depths, denoted ‘mid’ and ‘deep’ as also used here, and to one or other of two values of temperature gradient ${\text{d}}\Theta /{\text{d}}z$, where ${\Theta }$ is the temperature and z is the vertical distance from the wind-tunnel floor. However, all these measurements were made at only a single streamwise station; the extent to which each case was horizontally homogenous was not investigated.

In Hancock and Hayden (2018), the profiles of mean velocity and second-order moments show little variation over a steamwise fetch of 9h, including the turbulent heat flux (see their Fig. 10f), where h is the boundary-layer height as inferred from the mean velocity profile. However, the mean temperature profiles show two distinct features (their Fig. 10e). For heights $z \gtrsim h/3$ the temperature profiles exhibit little variation with streamwise fetch, but for $z \lesssim h/3$ there is a clear reduction of temperature with increasing fetch at constant z. Hancock and Hayden (2020) found that imposing an inversion has, in fact, no more than a minor effect on the flow for $z \lesssim h/3$. Most striking was no change in the heat-flux profiles. They also found that changing the near-surface temperature difference has no effect on the flow for $z \gtrsim h/3$. This lack of vertical interaction is referred to here as ‘blocking’.

The present study complements those of Hancock and Hayden (2018, 2020). The streamwise development of two cases of a stable boundary layer with an overlying inversion is investigated, with baseline cases of no inversion and neutral flow. Given that Hancock and Hayden (2020) found that the depth or ‘penetration’ to which the inversion is imposed has a much greater effect than the strength of the inversion (of 20 K m⁻¹ and 40 K m⁻¹), only one inversion gradient is employed here (of 20  K m⁻¹). The only other systematic study of the effect of an overlying inversion, as far as we are aware, is that of Ohya and Uchida (2003). This, though, was for a conventionally-tripped (rough-surface) turbulent boundary layer, and measurements were made at only one streamwise station.

The wind-engineering techniques that use artificially thickened boundary layers were originally developed for investigating wind loads on structures such as bridges and towers, and so the primary interest was in high-wind-speed conditions, for which the effects of stability are regarded as negligible. For a brief recent review of the technique for neutral flow, see Hohman et al. (2015). Counihan was one of the first to review relevant atmospheric-boundary-layer data, and to develop wind-tunnel-simulation methods (Armitt and Counihan 1968; Counihan 1969, 1970, 1973, 1975). More recently, the Engineering Science Data Unit produced a number of reports documenting neutral-stability characteristics (e.g. ESDU 2001, 2002). Counihan’s preferred method comprises a barrier fence upstream of a number of tall generators in the shape of a quarter ellipse (Counihan 1969). However, Irwin (1981) showed that generators formed from flat plates can be used equally well, and have the attraction of being much easier to manufacture. Generating prescribed vertical profiles of mean velocity and turbulence quantities requires (if at all possible) iterative adjustment of the spire shape and lateral spacing, combined with control of the aerodynamic roughness on the wind-tunnel floor. Hancock and Pascheke (2014) obtained a close match to the mean velocity and turbulence intensity profiles according to ESDU (2001, 2002) after a large number of trials. Hohman et al. (2015), using Counihan’s method, did not get such close a match. Artificially-thickened boundary layers are also used in wind-tunnel studies of atmospheric dispersion of pollutants, for example, that by Robins et al. (2001). For this type of study, it is usually required that the simulated flow changes as little as possible in the streamwise direction as the pollutant disperses, while for a wind-loading study this is less important.

The particular application to which both the previous and present work is directed is that of wakes of large wind turbines in offshore wind farms, where the aerodynamic roughness is much smaller than for land surfaces (see e.g. Stull 1988; ESDU 2002). The work of Hancock and Hayden (2018) has been extended to that of rougher surfaces for studies of the urban environment in stable boundary layers (Marucci et al. 2018). In Hancock and Hayden (2018), it was noted that there is, it appears, no particular measure by which horizontal homogeneity is judged to have been achieved, and is dependent on the application in question. The degree to which a simulation is regarded as ‘constant’ is one of pragmatic judgement. Here, we take it that profiles of mean velocity and other quantities change only slowly over the fetch of interest of, say, 10h. From our experience, it is relatively easy to generate various stable boundary layers that change rapidly in the flow direction, but rather more difficult to generate ones that do not. In the dispersion experiments of Robins et al. (2001), closely constant conditions were obtained for at least five nominal boundary-layer heights, or 50 source lengths, in a neutrally buoyant flow. From the objective of investigating turbine wakes, it is highly desirable that the undisturbed boundary layer does not change significantly over a streamwise fetch of at least 10 turbine rotor diameters (or a fetch > 7h as found in Hancock and Hayden 2018, 2020).

2 Wind Tunnel and Instrumentation

The wind-tunnel set-up and the instrumentation were essentially identical to that employed by Hancock and Hayden (2018, 2020). The EnFlo wind tunnel has a working section that is 20 m in length, 3.5 m in width, and 1.5 m in height. Stratification is achieved by means of 15 sets of heating elements at the working-section inlet, combined with cooled floor panels for stable stratification, supplied by a chilled-water system. The deep boundary layer was generated by means of 13 flat-plate spires mounted 0.5 m from the working-section inlet, together with sharp-edged rectangular roughness elements mounted on the floor. The spires were slightly truncated triangles with a base width of 60 mm, tip width of 4 mm, and height of 600 mm, spaced laterally at intervals of 266 mm. The roughness elements consisting of blocks 50 mm wide, 16 mm high, and 5 mm thick, and made of low-thermal-conductivity material, standing on the 50 mm × 5 mm face, were placed over the whole of the floor in a staggered arrangement with streamwise and lateral pitches of 360 mm and 510 mm, respectively, giving a very low plan-area density of 0.14%. Hancock and Pascheke (2014) showed there to be no detectable Reynolds-number dependence in neutral flow, and argued that there should be no dependence in a stable flow because the element height is much less than the height of the boundary layer, but high enough to avoid Reynolds-number dependence (see also Stull 1988). Figure 1 of Hancock and Hayden (2018) shows the spires and roughness elements. In the first part of the working section, the highly three-dimensional flow generated by the spires mixes laterally, and settles to the closely two-dimensional state in the measurement section. Hancock and Hayden (2018) concluded that the surface cooling should be started at a distance of 5 m from the working-section inlet. Further upstream, the surface was adiabatic.

Fig. 1

Working-section inlet-temperature profiles

Measurements of mean velocity and Reynolds stresses were made using a two-component, frequency-shifted laser-Doppler-anemometry (LDA) system (FibreFlow, Dantec, Denmark) with the probe head held by a three-dimensional traversing system that hung from rails mounted beneath the wind-tunnel roof. The measuring volume of the 300-mm focal-length probe was 0.14 mm in diameter and 5.5 mm long (in the lateral direction), and spatial positioning errors were negligible. Only the streamwise and vertical velocity components were measured, with u and w denoting the fluctuating parts, respectively, and U the mean streamwise velocity component. Mean temperatures were measured using thermistor probes and the fluctuating temperature by means of a cold-wire, fast-response probe held 4 mm behind the LDA measurement volume, where the advection time was calculated using the instantaneous streamwise velocity component $\left( {U + u} \right)$ to correct for the displacement, in order to measure the turbulent heat flux (Heist and Castro 1998). The cold wire was calibrated against a thermistor, itself calibrated against a standard calibration; differences between thermistors are < 0.1 °C. Sample durations were 3 min at a sampling frequency of typically 100 Hz for the LDA system, and at 1 kHz for the cold-wire probe, where linear interpolation between the nearest (time-shifted) temperature samples were used for the turbulent heat-flux measurements. Time-averaged quantities such as Reynolds stresses and heat flux are denoted by an overbar. As in Hancock and Hayden (2018), statistical errors are within about ± 0.5% for the mean velocity and within ± 5% for the second-order momentum and thermal moments, to a 95% confidence level. Surface values of shear stress and heat flux were determined from linear extrapolation of the corresponding profiles, over about the lower third of the boundary layer, with extrapolation expected to be within about ± 6% for both. The lowest measurement point was at z = 49 mm; this and the next at 57 mm were within the roughness sublayer, and hence discounted in the extrapolation for surface shear stress and heat flux. The viscous and thermal-conduction contributions over the measured profiles do not exceed about 3.5% and 7%, respectively. The reference mean wind-tunnel speed $U_{{{\text{Ref}}}}$ = 1.5 m s⁻¹ was measured using an ultrasonic anemometer mounted in a standard upstream position, at X = 5 m, Y = 1 m, z = 1 m, where X is the distance from the working-section inlet in the streamwise direction, Y is the lateral distance from the working-section centreline, and z is the vertical distance from the wind-tunnel floor. The Reynolds number ${{Re}}_{h} = U_{{{\text{Ref}}}} h/\nu$ = 56 × 10³, where ν is the kinematic viscosity evaluated at the surface. In each case, $h$ ≈ 0.55 m, to within ± 5% of a height based on 99% of the local freestream mean streamwise velocity U_e (except for the downstream-most profile of the neutral flow, at 11%). The pressure-gradient parameter $\left( {\nu /U_{{\text{e}}}^{2} } \right)\left( {{\text{d}}U_{{\text{e}}} /{\text{d}}X} \right)$ < 5 × 10⁻⁸, and U_e is about 8% higher than $U_{{{\text{Ref}}}}$ in magnitude.

3 Results and Discussion

As mentioned in the Introduction, two inversion cases were investigated (denoted cases 3–4) along with two baseline cases, one for neutral flow (case 1) and one for stable flow (case 2) with no inversion, as summarized in Table 1. The working-section inlet-temperature profiles $\Theta_{{{\text{IN}}}} \left( z \right)$ for cases 2–4 are shown in Fig. 1, where $\Theta_{0}$ is the surface temperature for X ≥ 5 m. Note that case 2 corresponds to the ‘final case’ example given in Hancock and Hayden (2018) and cases 3–4 correspond to cases 3 and 5 in Hancock and Hayden (2020). The inlet profiles $\Theta_{{{\text{IN}}}} \left( z \right)$ for cases 3–4 are defined by a linearly increasing increment $\Delta \Theta_{{{\text{IN}}}}$ above that of the no-inversion profile (case 2) as follows: $\Delta \Theta_{{{\text{IN}}}}$ increases by 2 K for each interval $\Delta z$ = 100 mm (the distance between the centres of the inlet heater units), where these increments begin at the origins of z = 250 mm and z = 50 mm, and are denoted as ‘mid’ and ‘deep’ inversions, respectively. The inversion gradient above the boundary layer is 20 K m⁻¹. Measurements were made at the streamwise stations of X = 9.2, 10.0, 12.1, and 14.2 m.² Unless otherwise stated, all measurements were made on the wind-tunnel centreline. Summary details for all four cases are given in Table 1.

Table 1 Summary of the cases investigated and the salient parameters

3.1 First- and Second-Order Moments of Velocity and Temperature

Figure 2 shows profiles of mean streamwise velocity and Reynolds stresses for the neutral flow (case 1) normalized by the reference flowspeed (rather than, say, the friction velocity) as the interest is in the independence of these quantities from the streamwise coordinate X (c.f. Robins et al. 2001). The profiles of mean streamwise velocity differ most noticeably from one to the next in the freestream, reflecting the slightly favourable pressure gradient in the (constant cross-section) working section. Broadly, the Reynolds stresses compare closely, except for the most downstream station, X = 14.2 m.

Fig. 2

Profiles of mean streamwise velocity and Reynolds stresses for neutral flow, normalized by the reference flowspeed. Symbols as in a

In that the primary attention here is stable flow, time was not spent ‘fine-tuning’ the spires to give profiles of mean velocity and turbulence intensities that closely match the neutral flow described in ESDU (2001, 2002). As already noted, Hancock and Hayden (2018) obtained profiles of mean and second-order turbulence quantities that compare favourably with those reported by Caughey et al. (1979). Also, from ESDU (2001), the shear stress varies with height according to $\left( {1 - z/h} \right)^{2}$, implying an asymptotic variation with height near the surface according to $\left( {1 - 2z/h} \right)$. The profiles of Fig. 2d closely follow this behaviour, and there is no nominal constant-stress layer. Note that in ‘engineering’ zero-pressure-gradient boundary layers, the gradient is less steep, as seen in Schultz and Flack (2007), for example.

Figure 3 shows the mean streamwise velocity and mean temperature profiles for the three stable cases (2–4). Consistent with what was observed in Hancock and Hayden (2018, 2020), the mean streamwise velocity profiles appear closely similar in shape, and only slightly affected by the inversion. The height h is about the same in each case, to within the measurement resolution, though slightly larger for the no-inversion flow. The mean temperature profiles all show a similar feature in that there is little streamwise variation for $z \gtrsim$ 200 mm, but a clear variation for $z \lesssim$ 200 mm, as observed previously. This pattern, consistent in each case, shows a decrease in temperature at constant z with increasing X, which differs from that seen in turbulent boundary layers with heat transfer but for a negligible influence of stability, as described in, for instance, Hoffmann and Perry (1979), where the whole of the boundary layer is affected. The temperature profiles also differ fundamentally from that seen in the unstable simulation of Hancock et al. (2013) where the positive surface heat flux and the associated increased level of turbulent mixing led to a streamwise increase of mean temperature across the whole depth of the layer (except in the limit $z \to 0$). The behaviour seen here is a direct consequence of stability and blocking.

Fig. 3

Profiles of mean streamwise velocity normalized by the reference flow speed, and mean temperature. Top row: no inversion; middle row: mid inversion; bottom row: deep inversion. Symbols as in a

Figure 4 shows profiles of Reynolds stresses and turbulent heat flux where, for convenience (as previously), the latter is given in dimensional terms. For each parameter, the profiles are broadly consistent, though with some residual streamwise development, most noticeable for profiles of the vertical Reynolds stress $\overline{{w^{2} }}$. Slower convergence of $\overline{{w^{2} }}$ profiles was also seen in the results reported by Hancock and Pascheke (2014) and Hancock and Hayden (2018). Note that the trends are opposite to those in the neutral case, shown in Fig. 2, where the stresses tend to increase with the streamwise distance X, rather than decrease, but the prime consideration here is the behaviour in the stable simulation cases. As observed in Hancock and Hayden (2020), the stresses in the centre of the layer decrease with the imposition of an inversion, more so for the deep inversion. Although there is some change in the profiles of shear stress and heat flux, the surface values vary little with either streamwise fetch or with the imposition of an overlying inversion. The latter aspect was, as already noted, reported by Hancock and Hayden (2020). The surface fluxes, denoted respectively by $- \left( {\overline{uw} } \right)_{0}$ and $\left( {\overline{w\theta } } \right)_{0}$, are given in Table 1. Overall, the second-order moments converge to approximate horizontal homogeneity over the whole boundary layer in each case, and the effect of imposing an inversion has not adversely affected the degree of horizontal homogeneity seen in Hancock and Hayden (2018). But, in that the mean temperature profiles clearly show a streamwise development for $z \lesssim$ 200 mm, the mean temperature is clearly not horizontally homogeneous in the lower one-third of the layer.

Fig. 4

Profiles of Reynolds stresses and turbulent heat flux. Top row: no inversion; middle row: mid inversion; bottom row: deep inversion. Symbols as in a

A partial explanation for the streamwise change in the mean temperature profiles now presents itself: the heat flux to the surface is predominantly provided by the advection of mean-flow heat flux. Hancock and Hayden (2020) observed that changing the near-surface condition—by changing the near-surface mean temperature difference—has no effect on the flow for $z \gtrsim h/3$. Therefore, heat transfer through the surface can be expected to lead to a change in successive temperature profiles, with a negative $\partial \Theta /\partial X$ amounting to a change in the near-surface mean temperature difference. But, as a result of what we describe as ‘blocking’, the flow for $z \gtrsim h/3$ is unaffected. It is, though, a curious feature that the profiles of turbulent heat flux are seemingly unchanged. It also poses a question about how far such behaviour might be maintained in the flow direction; it is supposed the flow must at some stage depart from a state of approximate horizontal homogeneity.

Another point can also be made at this juncture. Ideally, the boundary layer would be perfectly two-dimensional, and it would be possible from an energy balance to calculate the change of heat flux between, say, z = 0 and 200 mm from the change of the mean-flow advection. However, as discussed in the Appendix, such a calculation is ill-conditioned.

Profiles of mean streamwise velocity and mean temperature are shown again in Fig. 5, but here each set of profiles has been normalized by averaged values of the friction velocity $u_{*}$ or the temperature scale $\theta_{*}$, where $u_{*} = \surd \left( { - \overline{uw} } \right)_{0}$ and $\theta_{*} = - \left( {\overline{w\theta } } \right)_{0} /u_{*}$. As can be seen from Table 1, these surface-layer values do not vary much with X in each case, and are within the level of uncertainty from the extrapolation. The profiles in each panel coincide very closely for $z \gtrsim$ 200 mm, but below this height, the temperature profiles show the streamwise development discussed above. Though not clear from Fig. 3, there is also a corresponding development in the mean streamwise velocity, but markedly weaker than that seen in the mean temperature. Figure 5e includes the profiles for the neutral flow, where no significant streamwise change is evident; the development seen in the stable cases is therefore taken to be a consequence of stability. Both the mean streamwise velocity and mean temperature profiles could be seen as showing the growth of an internal layer, with successive profiles differing progressively from the first in each case. However, it is argued in Hancock and Hayden (2020) that the flow in the lower one-third of the layer is not like that of a conventional internal layer because a change in the upper part by the imposition of an inversion does not lead to a change in the near-surface flow. This lack of influence is attributed here to a mechanism of blocking; changes in the near surface condition do not influence the flow for $z \gtrsim h/3$, and changes in the overlying inversion do not influence the flow for $z \lesssim h/3$.

Fig. 5

Profiles of mean streamwise velocity and mean temperature in the lower part of the boundary layer, normalized by surface-layer variables. Top row: no inversion; middle row: mid inversion; bottom row: deep inversion. Full lines correspond to Eqs. 1 or 2. Panel e also shows the mean streamwise velocity profiles for the neutral flow, case 1. Symbols as in a

Figure 5 also shows curves according to the surface-layer functions given by (Högström 1988, 1996)

$$ U = \frac{{u_{*} }}{\kappa }\left[ {\ln \left( {\frac{z}{{z_{0} }}} \right) + \beta_{{\text{m}}} \frac{{z - z_{0} }}{{L_{0} }}} \right] $$

(1)

and

$$ {\Theta } - {\Theta }_{0} = \frac{{\theta_{*} }}{\kappa }\left[ {0.95 {\text{ln}}\left( {\frac{z}{{z_{0\theta } }}} \right) + \beta_{\theta } \frac{{z - z_{0\theta } }}{{L_{0} }}} \right], $$

(2)

where $\kappa$ = 0.4 is the von Kármán constant, $\beta_{{\text{m}}}$ = 8, and $\beta_{\theta }$ = 16, as employed in Hancock and Hayden (2018, 2020). The aerodynamic and thermal roughness lengths, $z_{0}$ and $z_{0\theta }$, are given in Table 2. As found by Hancock and Hayden (2018, 2020) and Hancock and Pascheke (2014), and supported by the results of Beljaars and Holtslag (1991) and Duynkerke (1999), the thermal roughness length is orders of magnitude smaller than the aerodynamic roughness length. Here, the surface Obukhov length $L_{0} = - \left( {{\Theta }_{0} u_{*}^{2} } \right)/\left( {\kappa g\theta_{*} } \right)$, where $g$ is the acceleration due to gravity.

Table 2 Surface-layer roughness lengths, at X = 9.2, 10.0, 12.1, and 14.2 m, respectively

The measured profiles follow Eqs. 1 or 2 fairly well up to at least z ≈ 100 mm, corresponding to $z \approx 0.17h$, as typically observed for neutral boundary layers above smooth or rough surfaces (Placidi and Ganapathisubramani 2015; Schultz and Flack 2007; Hoffmann and Perry 1979). Now, given the changes seen in both the mean streamwise velocity and temperature profiles in Fig. 5, and assuming the surface scales $u_{*}$ and $\theta_{*}$ to be constant, it follows that neither of the roughness lengths can stay constant, but must increase with X in order for U and $\Theta$ to decrease with X (at constant z), as indeed is observed (Table 2, and by Hancock and Hayden 2018).

Figure 6 shows the dimensionless gradients for momentum and temperature, respectively $\phi_{{\text{m}}}$ and $\phi_{\theta }$, defined by

$$ \phi_{{\text{m}}} = \frac{\kappa z}{{u_{*} }}\frac{\partial U}{{\partial z}}, $$

(3)

$$ \phi_{\theta } = \frac{\kappa z}{{\theta_{*} }}\frac{{\partial {\Theta }}}{\partial z}, $$

(4)

Fig. 6

Dimensionless gradients for momentum and temperature $\phi_{{\text{m}}}$ and $\phi_{\theta }$. Top row: no inversion; middle row: mid inversion; bottom row: deep inversion. Full lines correspond to Eqs. 5 or 6. Symbols as in a

as well as the surface-layer forms (Högström 1988, 1996)

$$ \phi_{{\text{m}}} = 1 + \beta_{{\text{m}}} \frac{z}{{L_{0} }}, $$

(5)

$$ \phi_{\theta } = 0.95 + \beta_{\theta } \frac{z}{{L_{0} }}. $$

(6)

Here, we have used the fact that the surface Obukhov length is very nearly constant in each case; the lines shown in Fig. 6 are based on mean values. A particularly notable feature in these profiles is that they fall close together for $z \gtrsim 300$ mm, and fairly close together for $z \lesssim 100$ mm, but differ markedly in between. The pattern of change is broadly consistent, with both $\phi_{{\text{m}}}$ and $\phi_{\theta }$ increasing with X at constant z. For $z \lesssim 100$ mm, the profiles fall moderately close to Eq. 5 or 6, though less so for the deep-inversion case, presumably because of the greater influence of the deep inversion near the surface. The correspondence of profiles for $z \gtrsim$ 300 mm, in contrast to the earlier observation that profiles concur for $z \gtrsim 200$ mm, is a consequence of $\phi_{{\text{m}}}$ and $\phi_{\theta }$ being defined in terms of gradients of U and ${\Theta }$ (rather than U, ${\Theta } - {\Theta }_{0}$, and z). That is, small departures in the profiles of U and ${\Theta }$ can be accompanied by large changes in their gradients. The concurrence of profiles for $z \gtrsim 300$ mm is not to be interpreted as $u_{*}$ and $\theta_{*}$ being the relevant scales in this region, since the use of the scales $U_{e}$ and ${\Theta }\left( h \right) - {\Theta }_{0}$ would also give concurrence.

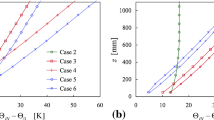
Given the changes seen in the profiles of U and ${\Theta }$, it is interesting to note the variation of the gradient Richardson number, ${{Ri}} = (g/{\Theta })\left( {\partial {\Theta }/\partial z} \right)/\left( {\partial U/\partial z} \right)^{2}$, shown in Fig. 7a (where ${\Theta }$ is the absolute temperature). Curiously, the profiles show no clear streamwise variation in each of the three cases, and also that all three cases concur for $z \lesssim 150$ mm, where ${{Ri}} \approx$ 0.1. There is no obvious reason why the gradient Richardson number should be unchanging with X when U and ${\Theta }$ and their vertical gradients are changing.

Fig. 7

Profiles of gradient Richardson number and local Obukhov length. Broken lines in panels b–d are for $z/L$ = 0.2, and dash-dotted lines are for $z/L$ = 2. Symbols as in a

Figure 7 also shows profiles of the local Obukhov length, $L = - \left( {\Theta_{0} \left( { - \overline{uw} } \right)^{3/2} } \right)/\left( {\kappa g\left( {\overline{w\theta } } \right)} \right)$. Again, the profiles within each case coincide in the upper part of the boundary layer, though the height at which this starts varies, decreasing from roughly z = 400 mm, to z = 300 mm, to z = 200 mm for the no-, mid- and deep-inversion cases, respectively. Below these heights, the profiles differ markedly from each other, except for the deep-inversion case where the variation is relatively small, though with a qualitatively similar systematic change with increasing X. Near the surface, the values are close to the corresponding surface value $L_{0}$, as is to be expected. Broadly, over the depth of the boundary layer, the value of L decreases as the effect of stability increases (from no inversion to mid to deep inversion), as is to be anticipated. In the deep-inversion case, the profiles are roughly horizontally homogeneous over the whole of the boundary layer, but clearly not in the other cases.

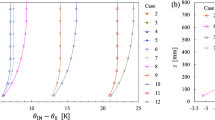
The dimensionless gradients of Eqs. 3 and 4 can be more generally defined in terms of local velocity and temperature scales

$$ \phi_{{\text{m}}}^{\prime } = \frac{\kappa z}{{u_{*}^{\prime } }}\frac{\partial U}{{\partial z}}, $$

(7)

$$ \phi_{\theta }^{\prime } = \frac{\kappa z}{{\theta_{*}^{\prime } }}\frac{{\partial {\Theta }}}{\partial z}, $$

(8)

where $u_{*}^{\prime } = \left( { - \overline{uw} } \right)^{1/2 }$ and $\theta_{*}^{\prime } = \left( {\overline{w\theta } } \right)/u_{*}^{\prime }$, and are shown in Fig. 8 as functions of the stability parameter $z/L$. In contrast with Figs. 6 and 7, all the cases fall closely coincident up to at least $z/L$ = 0.3, and closely so for $\phi_{{\text{m}}}^{\prime }$ over the entire layer. For $\phi_{\theta }^{\prime }$, the scatter is larger for $z/L$ > 0.4. In that $\phi_{{\text{m}}}^{\prime }$ and $\phi_{\theta }^{\prime }$ are ill-conditioned near the top of the boundary layer, these quantities have not been plotted when either $\left| {{-}\overline{uw} } \right|$ or $\left| {\overline{w\theta } } \right|$ is less than 10% of the respective surface value.

Fig. 8

Local-scaling functions, $\phi_{{\text{m}}}^{\prime }$ and $\phi_{\theta }^{\prime }$. All stable cases. Green: no inversion; red: mid inversion; blue: deep inversion. Symbols as in a

3.2 Comparisons with the Local-Scaling Analyses of Nieuwstadt and Sorbjan

As in Hancock and Hayden (2018, 2020), we compare the present measurements with the local-scaling analyses of Nieuwstadt (1984) and Sorbjan (2010). However, here, for comparison with Nieuwstadt’s analysis, $z/L$ is shown on a logarithmic axis in Fig. 9, which allows the near-surface behaviour to be seen in more detail. All stable cases are shown together, and the measurements presented in Hancock and Hayden (2018) are shown as single trend lines. Figure 9 shows the following non-dimensional groups:

$$ {{Ri,}}\, \frac{{\overline{{w^{2} }}^{1/2} }}{{\left( { - \overline{uw} } \right)^{1/2} }}, \frac{{ - \left( {\overline{{\theta^{2} }} \left( { - \overline{uw} } \right)} \right)^{1/2} }}{{\overline{w\theta } }},\frac{{ - \overline{u\theta } }}{{\overline{w\theta } }},\frac{{K_{{\text{m}}} }}{{L\left( { - \overline{uw} } \right)^{1/2} }},\frac{{K_{\theta } }}{{L\left( { - \overline{uw} } \right)^{1/2} }}, $$

Fig. 9

Parameters according to Nieuwstadt’s (1984) local scaling. Green: no inversion; red: mid inversion; blue: deep inversion. Full lines show Nieuwstadt’s (1984) analytical results; broken lines, the field-measurement trend lines, and the dash-dot lines show Hancock and Hayden’s (2018) trend lines. Thick lines in c and d show error bands—see text. Symbols as in a

where the momentum and heat exchange coefficients $K_{{\text{m}}} = - \overline{uw} /\left( {\partial U/\partial z} \right)$ and $K_{\theta } = - \overline{w\theta } /\left( {\partial {\Theta }/\partial z} \right)$, respectively, and shows Nieuwstadt’s predictions along with his trend lines from the Cabauw field data. These groups are also ill-conditioned near the top of the boundary layer and so the same criteria have been applied as for Fig. 8.

It is clearly noticeable that all the profiles fall together for $z/L \lesssim 0.2$, and in most cases fall close to Nieuwstadt’s (1984) results in this range. In two cases, Fig. 9b, e, the profiles fall close together over most of the layer. In the other four cases, there is no comparably clear single trend for $z/L \gtrsim 0.2$, though their general trends are comparable with Nieuwstadt’s field data. The scatter is emphasized by the logarithmic scale for z/L, and for some quantities it is somewhat larger than that seen by Hancock and Hayden (2018, 2020). Figure 9c, d, which exhibits the larger levels of scatter, shows error bars at the cut-off height (as given above). These are based on the worst-case combinations with errors of ± 1% of the surface values of shear stress and heat flux, and of the maxima in the mean-square temperature fluctuations and horizontal heat flux (not shown). A single trend line could reasonably be drawn in each of the two panels, since there is no clear distinction between the cases.

Now, a threshold of z/L = 0.2 provides a useful way to consider the measurements presented in Fig. 7b–d; as will have been noticed, these panels show the line z = 0.2L, which passes through the spread of the profiles already discussed. All points below the line are for z/L < 0.2, while all those above are for z/L > 0.2. That is, all those points below the line correspond to the coalescence of all cases seen in Fig. 9, and all those above to where (in most of the parameters) the profiles do not coalesce. Furthermore, by noting where the line z = 0.2L cuts the various profiles (in Fig. 7), it can be seen that the coalescence in Nieuwstadt’s framework occurs between about z = 100 mm and z = 200 mm for the no-inversion and mid-inversion cases, and between about z = 90 mm and z = 130 mm for the deep-inversion case. These ranges of z clearly lie where the profiles shown in Figs. 5 and 6 do not coincide in their respective sets. Thus, local similarity is seen to occur in the parameters of Nieuwstadt’s (1984) framework, while the mean-flow profiles of Figs. 5 and 6 do not show concurrence. Figure 7b–d also shows a line $z = 2L$; where this line cuts the various profiles, the profiles of each case broadly concur.

Figure 10 gives the measurements in terms of Sorbjan’s (2010) ‘master’ scaling, which employs a length scale $\kappa z$, a velocity scale, $U_{{\text{S}}} = \kappa zN$, and a temperature scale, ${\Theta }_{{\text{S}}} = \kappa z\partial {\Theta }/\partial z$, where $N^{2} = \left( {g/{\Theta }} \right)\left( {\partial {\Theta }/\partial z} \right)$. Four of the non-dimensional groups for Sorbjan’s scaling are

$$ \frac{{ - \overline{uw} }}{{U_{{\text{S}}}^{2} }},\frac{{ - \overline{w\theta } }}{{U_{{\text{S}}} \Theta_{{\text{S}}} }}, \frac{{\left( {\overline{{w^{2} }} } \right)^{1/2} }}{{U_{{\text{S}}} }},\frac{{\left( {\overline{{\theta^{2} }} } \right)^{1/2} }}{{\Theta_{{\text{S}}} }}, $$

Fig. 10

Non-dimensional groups resulting from Sorbjan’s (2010) local scaling. Green: no inversion; red: mid inversion; blue: deep inversion. Lines with no symbols show Sorbjan’s fitted curves. Symbols as in a

and are shown in Fig. 10, together with Sorbjan’s empirical trend lines for these functions, based on data from the Surface Heat Budget of the Arctic Ocean (SHEBA) study. The same constraint near the top of the boundary layer has been applied to these quantities as those given in Figs. 8 and 9. The trends in the present data follow the same trends in relation to Sorbjan’s curves as those found in Hancock and Hayden (2018, 2020). Within the spread, a slight difference might be inferred, with the no-inversion case sitting a little below the others, for ${{Ri}} \gtrsim 0.2$. However, no difference between the cases was seen in Hancock and Hayden (2020).

4 Further and Concluding Comments

All three stable cases show the mean streamwise velocity and mean temperature profiles to be closely horizontally homogeneous in about the top two-thirds of the boundary layer, over a streamwise distance of about eight boundary-layer heights, and it is assumed this behaviour may have persisted over a greater distance still. In the lower part of the boundary layer, the temperature profiles show a clear streamwise development that is like that of an inner layer, but may not be an inner layer in the usual sense, for reasons given by Hancock and Hayden (2020). The streamwise development is as seen in the temperature profiles of Hancock and Hayden (2018). The turbulent heat flux is decreased to about 15% of the surface value at z = h/3 in each case. It is inferred that the heat flux to the surface is largely provided by mean advection, which necessarily requires a streamwise reduction in temperature³ at constant z. The weaker streamwise development in the case of Hancock and Pascheke (2014) is consistent with the lower surface heat flux in their case.

The mean streamwise velocity profiles (Fig. 5) also exhibit streamwise development in the lower one-third of the boundary layer, though the change is weaker than that seen in the temperature profiles. Any such development is absent (or much smaller) in the neutral flow; the development in the stable cases is, therefore, a consequence of stability. The influence of buoyancy forces on the mean streamwise velocity has to be through the influence on the Reynolds shear stress. The effects of the inversion are seen in the shear-stress profiles (Fig. 4), but only weakly in the lower one-third of the boundary layer (Hancock and Hayden 2020). Curiously, the gradient Richardson number shows no significant variation with streamwise distance over the whole depth of the boundary layer. It is also perhaps significant to note that Ri is below the classical limit of 0.2 over most of the layer in the no-inversion case, but is not so for the inversion cases (Fig. 7a).

In each stable case, the profiles of Reynolds stresses and heat flux show approximately horizontally homogeneous behaviour, with very little variation in the inferred surface shear stress and heat flux. However, assuming standard forms for surface-layer mean streamwise velocity and mean temperature (Eqs. 1 and 2) leads to aerodynamic and thermal roughness lengths that increase with streamwise distance in the stable cases. In the neutral case, there is no significant variation in the aerodynamic roughness length. The physical height of the roughness elements is less than 0.03h, amounting to only 8% of the lower one-third of the layer. The former is well within the range covered by Placidi and Ganapathisubramani (2015), up to $z \approx 0.1h$, where a consistent logarithmic law-of-the-wall behaviour for $z \lesssim 0.2h$ was observed for twelve different roughness patterns. Although the present (plan-view) area density of the roughness elements, at 0.14%, is much smaller than in their investigation, it seems unlikely that a much lower density would lead to a different behaviour in this regard. The behaviour seen here must be an effect of the stability, and leads to the conclusion that one or more of the assumptions behind the standard forms for stable flow, though well established, do not adequately represent the flow for $z \lesssim 0.2h$.⁴ Conventional arguments for the logarithmic law-of-the-wall require a change in both the inner and outer layers (see, for example, Townsend 1976). Note that a re-evaluation of the values attributed to the surface shear stress and heat flux in order to force constant roughness lengths is not appropriate as the trends are repeated in the stable cases, and $z_{0}$ is constant in the neutral case.

While by some measures it is the lower one-third of the layer that is much less horizontally homogeneous than the flow above, departure in some quantities is seen to exist over the lower half. This is true for the dimensionless gradients $\phi_{{\text{m}}}$ and $\phi_{\theta }$, and for the local Obukhov length L for the no- and mid-inversion cases, but not for the deep-inversion, where slight departure only arises for $z \lesssim h/3$. The lack of influence of an imposed overlying inversion on the flow for $z \lesssim h/3$ seen here is as also seen in Hancock and Hayden (2020). This, together with the lack of influence they observed for a change in the near-surface condition on the flow for $z \gtrsim h/3$, is denoted here by the term ‘blocking’. The effect of stability is to inhibit vertical influence across a height that is roughly one-third of the boundary-layer height, but reaching for some quantities to about one-half the boundary-layer height.

In contrast, the local-scaling framework of Nieuwstadt (1984) shows concurrence of all cases for $z/L \lesssim 0.2$ (and over the whole layer for two of the six quantities examined). A ratio of z/L = 0.2 amounts to a physical height of up to $z \approx h/3$. For $z/L > 0.2$ the profiles show less concurrence, but broadly exhibit consistent trends. Increasing scatter with height is to be anticipated simply because each of the quantities in the non-dimensional ratios decreases with height. Increasing scatter with height was also seen by Hancock and Hayden (2018, 2020) and by Nieuwstadt (1984). The local similarity parameters, $\phi_{{\text{m}}}^{\prime }$ and $\phi_{\theta }^{^{\prime}}$, exhibit high concurrence as functions of z/L for all cases at least up to about z/L = 0.3, with $\phi_{{\text{m}}}^{\prime }$ showing this same close behaviour over nearly the whole boundary layer. The non-dimensional groups of Sorbjan’s (2010) framework differ from those of Nieuwstadt in that they each tend to zero with increasing height, rather than (in terms of the latter’s theory) to ‘z-less’ constant values. All the profiles in the framework of Sorbjan follow the same trend, with a scatter comparable to that in the field data presented by Sorbjan, though with shallower slopes as also seen in Hancock and Hayden (2018, 2020).

Finally, it is worth making perhaps an obvious point about field studies over large, horizontally homogenous planes, free from significant upstream influences of topographical features (though upstream conditions would not be like those in the early part of the wind-tunnel working section, of course). These results suggest that vertical profiles of temperature and some other quantities, if they were obtained at a number of stations separated in the wind direction, would differ over the lower one-third or half of the boundary-layer depth. However, as shown here, local scaling would still apply, and, moreover, apparently be unaffected by blocking.

Appendix: Flow Two-Dimensionality

The temperature profiles change in shape in the lower part of the boundary layer because of the heat transfer to the surface. It would appear therefore that an energy and mass balance could be used in order to provide a consistency check on the measured change in heat flux over the lower part of the boundary layer. However, the calculation is ill-conditioned and very sensitive to slight convergence of the boundary layer, as will have arisen from the growth of the boundary layers on the working-section side walls, as is always the case in wind-tunnel boundary-layer experiments unless special care is taken to avoid it. A convergence of only about ± 1.7° at a lateral distance in Y of ± 0.6 m (i.e. a width ≈ 2h) is sufficient to account for the difference in surface heat flux obtained from profiles of $\overline{w\theta }$ and that obtained from profiles of mean streamwise velocity and mean temperature.

Figure 11 shows profiles of mean streamwise velocity, mean temperature, and second-order moments at five lateral positions, Y =  ± 400 mm, ± 700 mm and 0 mm, at X = 9.2 m, for the deep-inversion case. While the profiles do not fall precisely on top of each other, there is satisfying concurrence. This is so, even though the wind tunnel (in order to provide the stratification required) does not have the usual devices of a contraction or a settling chamber ahead of the working section in order to improve flow uniformity.

Fig. 11

Profiles of mean streamwise velocity and temperature, Reynolds stresses, and heat flux, at five lateral positions at X = 9.2 m, for the deep-inversion case. Symbols as in a