Some Further Aspects of Stable Boundary-Layer Simulation in a Stratified-Flow Wind Tunnel

Abstract

It is demonstrated that the vertical profile of gradient Richardson number, Ri, can be shaped by control of the working-section inlet temperature profile. In previous work (Hancock and Hayden in Boundary-Layer Meteorol 168:20–57, 2018; 175:93–112, 2020; 180:5–26, 2021) the inlet temperature profile had been specified but without control of the profile of $Ri$ in the developed-flow region of the working section. Control of the inlet temperature profile is provided by 15 inlet heaters (spread uniformly across the height of the working section), allowing control of the temperature gradient over the bulk of the boundary layer, and the overall temperature level above that of the surface. The bulk Richardson number for the 11 cases covers the range 0.01–0.17 (there is no overlying inversion). In the upper $\approx$ 2/3 of the boundary layer the Reynolds stresses and turbulent heat flux are controlled by the gradient in mean temperature, while in the lower $\approx$ 1/3 they are controlled both by this gradient and by the level above the surface temperature. In three examples, $Ri$ is approximately constant at 0.07, 0.10 and 0.13 across the bulk of the layer. The previous observation of horizontally homogenous behaviour in the temperature profiles in the top $\approx$ 2/3 of the boundary layer but not in the lower $\approx$ 1/3 is repeated here, except when, tentatively, Ri does not exceed 0.05 over the bulk of the boundary layer. Favourable validation comparisons are made against two sets of local scaling systems and field data over the full depth of the boundary layer, over the range 0.006 $\le Ri \le$ 0.3, or, in terms of height and local Obukhov length, 0.005 $\le z/L \le$ 1.

1 Introduction

Simulation of a stably stratified atmospheric boundary layer in a wind tunnel requires a (potential) temperature rising with height in a direction opposite to that of the gravitational vector. In the EnFlo wind tunnel this is achieved by means of a cooled floor and a system of heaters at the working-section inlet. In addition, a system of ‘flow generators’ is employed in order to provide vertical profiles of mean velocity and Reynolds stresses that are characteristic of an atmospheric boundary layer, and to a greater height than would otherwise naturally occur (with the concurrent advantages of Reynolds number and model scale). If the maximum temperature difference $\Delta \vartheta$ between freestream edge of the boundary layer and the floor is sufficiently small the effects of buoyancy must be negligible. In this instance, the temperature of the flow acts like a passive scalar. The vertical distribution of temperature will be influenced by turbulent mixing, so that the temperature profile at the inlet of the working section will not be the same as that at downstream stations, but nevertheless a change in the vertical profile at inlet would be expected to lead to a corresponding change in the profile shape downstream. As $\Delta \vartheta$ is increased, all else constant such as the flow speed, buoyancy effects come into play. Now, it is to be expected that the heat flux to the surface is at least related to the temperature difference $\delta \vartheta$ between the flow near the surface and the surface itself.¹ In the top part of the boundary layer, we can expect (or suppose) that buoyancy effects will only arise if there is a vertical gradient in temperature, but that the actual temperature above the surface is not important, at least for weak to moderate stability. The point here is to distinguish between that that would in effect specify the surface Obukhov length, and characterize the surface layer, and that that would characterize the flow higher in the boundary layer.

In earlier work, Hancock and Hayden (2020, 2021) found that an increase in the temperature gradient in the bulk of the boundary layer above the surface layer, reduced the Reynolds stresses in this region, but had little effect nearer the surface and no measurable influence on surface heat flux. They also found that, increasing $\delta \vartheta$ while not changing the temperature gradient higher up in the boundary layer, slightly reduced Reynolds stresses, but significantly increased the surface and near surface heat flux, concluding that the surface heat flux was controlled only by the temperature across the surface layer. The implied lack of vertical interaction was termed ‘blocking’. In terms of surface Obukhov length, $L_{0}$, Hancock and Hayden (2020) found the surface heat flux to be given by $h/L_{0} = 20 Ri_{SL}$, where h is the height of the whole boundary layer and $Ri_{SL}$ is the bulk Richardson number over the surface layer (see Hancock and Hayden 2020). The lack of vertical interaction had a distinctive effect on the vertical profile of temperature. Above $z \approx h/3$, where z is the distance above the surface, there was no significant streamwise development of temperature, but below this height the temperature decreased in the flow direction. A decrease is consistent with heat flux to the surface, but this occurred only in the lower approximately 1/3 of the boundary layer. This is in contrast to an unstable simulation where the whole of the boundary layer is affected (Hancock et al. 2013), or where there is heat transfer but negligible effect of buoyancy (e.g. Hoffmann and Perry 1979).

The characteristics of the whole boundary layer are not determined just by surface-layer conditions, but by conditions advected from upstream. In Hancock and Hayden (2018) the working-section inlet temperature profile was specified so as to give a ‘reasonable’ temperature profile over the whole boundary layer in the developed flow. It was found, for example, that if a fully uniform inlet profile (above the surface temperature) was imposed, the top part of boundary layer remained in a neutral state, stable conditions being confined to the bottom part (roughly one half of the boundary layer depth). In the subsequent work (Hancock and Hayden 2020, 2021), the main concern was to investigate the effect of an overlying inversion (imposed at the working section inlet). In these cases, the gradient Richardson number became large in the upper half of the boundary layer, exceeding 1 above $z/h \approx 0.8$.

In Hancock and Hayden (2018, 2020, 2021) we did not address a question such as ‘what temperature profile should be employed at the inlet in order to give a specified profile of gradient Richardson number over the whole of the developed boundary layer?’. The present paper complements the earlier ones by focusing on three things. Firstly, can a desired profile of gradient Richardson number prescribed for the developed flow be used to define the working-section inlet temperature profile? Secondly, can this be done separately from specifying the near-surface condition? Thirdly, is the phenomenon of blocking seen in the vertical temperature profiles related to the gradient Richardson number? As far as we are aware, no other attempts have been made to address these questions.

The results presented in Hancock and Hayden (2018) showed reasonable agreement with vertical profiles of mean and turbulence quantities given by Caughey et al. (1979). In the earlier work of Hancock and Pascheke (2013), extensive effort was made in order to give a close match to prescribed profiles of mean velocity and Reynolds stresses in neutral flow, by iterative adjustment of the generator shape and lateral separation. A further refinement of the present simulations would be a similar iterative adjustment, coupled with iterative adjustment of the inlet temperature profile, to bring measured vertical profiles close to a prescribed set of mean and turbulence quantities.

Wind-tunnel experiments in stable flow are small in number, but include those of Arya and Plate (1969), Arya (1975), Ogawa et al. (1981, 1985), Meroney and Melbourne (1992), Fedorovitch et al. (1996), Ohya et al. (1996, 1997, 2008), Ohya (2001), Robins et al. (2001), Ohya and Uchida (2003), Ross et al. (2004), Chomorro and Porté-Agel (2010), Hancock and Pascheke (2014), Williams et al. (2017) and Van Buren et al. (2017), Hancock and Hayden (2018, 2020, 2021), Marucci et al. (2016, 2018), Maricci and Carpentieri (2020), where these latter three contributions were also made in our laboratory using the same techniques. In several cases, the boundary layer was made turbulent by means of a boundary layer ‘trip’, small in height compared with the boundary layer height at the measurement station or stations, and maintained in some cases by surface roughness, and made stably stratified by means of a difference between the surface temperature and a uniform upstream temperature. Ohya and Uchida (2003) however, imposed a nonuniform inlet temperature, as did Ross et al. (2004), Hancock and Pascheke (2014), Hancock and Hayden (2018, 2020, 2021), Marucci et al. (2018), Marucci and Carpentieri (2020). In the cases of Robins et al. (2001), Hancock and Pascheke (2014), Hancock and Hayden (2018, 2020, 2021), Marucci et al. (2018), Marucci and Carpentieri (2020), the application areas are dispersion in urban environments and wind power. In these studies, other than that of Ohya and Uchida (2003), tall flow generators about equal in height with the developed boundary layer, coupled with surface roughness, were used, drawing on well-established wind engineering practice for studies in neutral flow. For further details see Hancock and Hayden (2018). A particular issue of concern in wind power and dispersion studies is that the simulated boundary layer should be at most slowly varying in the flow direction (and ideally constant—i.e. horizontally homogeneous), representing constant external conditions to a turbine wake, for example, or a streamwise row of turbines.

The present experiments cover a gradient Richardson number range of 0.006 $\le Ri \le$ 0.3, or equivalently, 0.005 $\le z/L \le$ 1, where $z/L$ is the ratio of height above the surface to the local Obukhov length. In these, $R_{i} = \left( {g/{\Theta }} \right)\left( {d{\Theta }/dz} \right)/\left( {dU/dz} \right)^{2}$ and $L = - {\Theta }\left( { - \overline{uw} } \right)_{{}}^{3/2} /\left( {\kappa g\left( {\overline{w\theta } } \right)} \right)$, where ${\Theta }$ is the absolute temperature, $U$ is the mean streamwise velocity, $\kappa$ is the von Kármán constant (= 0.40), $g$ is the acceleration due to gravity, and $- \overline{uw}$ and $\overline{w\theta }$ are the local kinematic shear stress and heat flux, respectively. There is no single, widely accepted classification of degree of stability. We quote just two. Basu et al. (2006) give five bands for $z/L$: 0 – 0.10, 0.10 – 0.25, 0.25 – 0.50, 0.50 – 1.0, and > 1, covering from ‘near neutral’ to ‘very stable’. Sorbjan (2012) gives four bands for $Ri$: 0 $< Ri <$ 0.02, 0.02 $< Ri <$ 0.12, 0.12 $< Ri <$ 0.7, and $Ri > 0.7$, respectively described as ‘nearly neutral, stable, very stable and extremely stable’. Validation against field data is made by using the analysis and scaling frameworks of Nieuwstadt (1984) and Sorbjan (2010, 2012).

2 Inlet Temperature Profile

From the definition of gradient Richardson number it follows that:

$$ \theta \left( z \right) - \theta_{0} = \frac{1}{g}\mathop \int \limits_{0}^{z} {\Theta }\left( {\frac{{{\text{d}}U}}{{{\text{d}}z}}} \right)^{2} Ri\left( z \right) {\text{dz}}, $$

(1)

where $\left( z \right)$ is the temperature and $\theta_{0}$ is the surface temperature. A number of simplifications were made in order to progress. Firstly, the right-hand side of Eq. (1) was split into two parts:

$$ \theta \left( z \right) - \theta_{0} = \frac{1}{g}\mathop \int \limits_{0}^{z1} {\Theta }\left( {\frac{{{\text{d}}U}}{{{\text{d}}z}}} \right)^{2} Ri\left( z \right) {\text{dz}} + \frac{1}{g}\mathop \int \limits_{{z_{1} }}^{z} {\Theta }\left( {\frac{{{\text{d}}U}}{{{\text{d}}z}}} \right)^{2} Ri\left( z \right) {\text{dz}}. $$

(2)

The first integral represents the temperature difference at height $z_{1}$, that is $\theta_{z1} - \theta_{0}$. While forms could be assumed for the elements of the first integrand, this was not done. Instead, we used the observation in the previous work (Hancock and Hayden 2020, 2021) that flow conditions near the surface, nominally over the surface layer, were little affected by conditions further out, and we therefore took the measured temperature (from the measurements of Hancock and Hayden 2021) at height $z_{1}$ above that of the surface.² The right-hand side of Eq. (2) was then written as:

$$ \theta \left( z \right) - \theta_{0} = \left( {\theta \left( {z_{1} } \right) - \theta_{0} } \right)_{measured} + \frac{1}{g}\mathop \int \limits_{{z_{1} }}^{z} {\Theta }\left( {\frac{{{\text{d}}U}}{{{\text{d}}z}}} \right)^{2} Ri\left( z \right){\text{d}}z. $$

(3)

For the integral in Eq. (3), $U\left( z \right)$ was also taken as previously measured, and the absolute temperature taken as constant. $Ri\left( z \right)$ was prescribed as constant, or according to Eq. (4) below, when less than this constant value, near the surface. This led to a new temperature profile above $z_{1}$, and the difference in temperature between old and new profiles was then simply subtracted from the original working-section inlet temperature profile, to give a new inlet temperature profile.³ In principle, this process could be repeated iteratively to refine the temperature profiles at the measurement stations, though this was not done in this investigation, and was not needed. If logarithmic forms are assumed for $U\left( z \right)$ and $\theta \left( z \right)$, such as those given by Eqs. (1) and (2) of Hancock and Hayden (2021), then a specific variation of $Ri\left( z \right)$, increasing with z, is implied, namely:

$$ Ri\left( z \right) = z/L_{0} \frac{{0.95 + 16\left( {z/L_{0} } \right)}}{{\left( {1 + 8\left( {z/L_{0} } \right)} \right)^{2} }}, $$

(4)

(see Appendix) where the constants are as given in Hancock and Hayden (2021). The surface Obukhov length $L_{0} = - {\Theta }_{0} \left( { - \overline{uw} } \right)_{0}^{3/2} /\left( {\kappa g\left( {\overline{w\theta } } \right)_{0} } \right)$, where ${\Theta }_{0}$ is the absolute temperature at the surface, and $\left( { - \overline{uw} } \right)_{0}$ and $\left( {\overline{w\theta } } \right)_{0}$ denote the surface kinematic shear stress and surface heat flux, respectively. In passing, it is interesting to note that neither aerodynamic nor thermal roughness lengths appear in this equation. The height $z_{1}$ was taken as 79 mm, $L_{0}$ as 790 mm, (where h was 550 mm, based on 99% of the local freestream mean streamwise velocity), though this height is not critical. Temperature profiles obtained in this way, leading to 11 stable cases, are shown in Fig. 1 and will be discussed in Sect. 4.

Fig. 1

Working-section inlet mean temperature profiles for the 11 stable cases

3 Wind Tunnel and Instrumentation

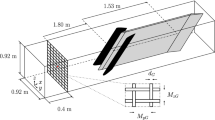
The wind-tunnel set-up and the instrumentation are essentially identical to that employed by Hancock and Hayden (2018, 2020, 2021). The EnFlo wind tunnel has a working section that is 20 m in length, 3.5 m in width, and 1.5 m in height. Thermal stratification is achieved by means of 15 sets of heating elements at the working-section inlet, combined with cooled floor panels, supplied by a chilled-water system. The deep boundary layer was generated by means of 13 flat-plate spires mounted 0.5 m from the working-section inlet, together with sharp-edged rectangular roughness elements mounted on the floor. The spires were slightly truncated triangles with a base width of 60 mm, tip width of 4 mm, and height of 600 mm, spaced laterally at intervals of 266 mm (centre-to-centre). The roughness elements consisting of blocks 50 mm wide, 16 mm high, and 5 mm thick, and made of low-thermal-conductivity material, standing on the 50 mm × 5 mm face, were placed over the whole of the floor in a staggered arrangement with streamwise and lateral pitches (centre-to-centre) of 360 mm and 510 mm, respectively, giving a very low plan-area density of 0.14%. Hancock and Pascheke (2014) showed there to be no detectable Reynolds-number dependence in neutral flow, and argued that there should be no dependence in a stable flow because the element height is much less than the height of the boundary layer, but high enough to avoid Reynolds-number dependence (see also Stull 1988). Figure 1 of Hancock and Hayden (2018) shows the spires and roughness elements. In the first part of the working section, the highly three-dimensional flow generated by the spires mixes laterally, and settles to the closely two-dimensional state in the measurement section (Hancock and Hayden 2021). Hancock and Hayden (2018) concluded that the surface cooling should be started at a distance of 5 m from the working-section inlet. Further upstream, the surface was adiabatic.

Measurements of mean velocity and Reynolds stresses were made using a two-component, frequency-shifted laser-Doppler anemometry (LDA) system (FibreFlow, Dantec, Denmark) with the probe head held by a three-axis traversing system that hung from rails mounted beneath the wind-tunnel roof. The measuring volume of the 160-mm focal-length probe was 0.074 mm in diameter and 1.6 mm long (in the flow’s lateral direction). Spatial positioning errors were negligible. Only the streamwise and vertical velocity components were measured, with u and w denoting the fluctuating parts, respectively, and U the mean streamwise velocity component. Mean temperatures were measured using thermistor probes and the fluctuating temperature by means of a cold-wire, fast-response probe held 4 mm behind the LDA measurement volume so that the probe’s upstream influence was negligible. The instantaneous advection time was calculated using the instantaneous streamwise velocity component $\left( {U + u} \right)$ to correct for the displacement, in order to measure the turbulent heat flux (Heist and Castro 1998). The cold wire was calibrated against a thermistor, itself calibrated against a standard calibration; differences between thermistors are < 0.1 °C. Sample durations were 3 min at a sampling frequency of typically 100 Hz for the LDA system, and at 1 kHz for the cold-wire probe, where linear interpolation between the nearest (time-shifted) temperature samples was used for the turbulent heat-flux measurements. Time-averaged quantities such as Reynolds stresses and heat flux are denoted by an overbar. As in Hancock and Hayden (2018), statistical errors are within about ± 0.5% for the mean velocity and within ± 5% for the second-order momentum and thermal moments, to a 95% confidence level. Surface values of shear stress and heat flux were determined from linear extrapolation of the corresponding profiles, over about the lower third of the boundary layer, with extrapolated values expected to be within about ± 6% for both. The lowest measurement point was at z = 49 mm; this and the next at 57 mm were within the roughness sublayer, and hence discounted in the extrapolation for surface shear stress and heat flux. The viscous and thermal-conduction contributions over the measured profiles do not exceed about 3.5% and 7%, respectively. The reference mean wind-tunnel speed $U_{{{\text{Ref}}}}$ = 1.5 m s⁻¹ was measured using an ultrasonic anemometer mounted in a standard upstream position, at X = 5 m, Y = 1 m, z = 1 m, where X is the distance from the working-section inlet in the streamwise direction, Y is the spanwise direction measured from the centreline, and z is the vertical distance from the wind-tunnel floor. Measurements were made on the centreline at either a single station, X = 10 m, or at five stations: X = 9.2, 10, 12.1, 14.2 and 16.2 m. The height, $h$ is in the range 0.53 m to 0.68 m, based on 99% of the local freestream mean streamwise velocity U_e. The Reynolds number $Re_{h} = U_{{\text{e}}} h/\nu$ is in the range 57 × 10³ to 65 × 10³, at X = 10 m, where ν is the kinematic viscosity evaluated at the surface. The acceleration parameter $\left( {\nu /U_{e}^{2} } \right) \left( {{\text{d}}U_{e} /{\text{d}}X} \right)$ < 5 × 10^–8.

4 Results and Discussion

4.1 Inlet Temperature Profiles—The Cases

Figure 1 shows the profiles of the inlet temperature, $\theta_{{{\text{IN}}}}$ in two ways: in Fig. 1a, with respect to the surface temperature $\theta_{0}$, and in Fig. 1b with respect to the inlet freestream temperature, $\theta_{e}$. A baseline (stable) case, denoted here as case 10, was taken as the no-inversion case 2 of Hancock and Hayden (2021), from which four further cases where initially defined, but only one of these is presented here, case 9. More cases were defined simply by subtracting an offset from the inlet temperature profiles, cases 3, 4, 5, 6, and 8, or adding an offset, cases 11 and 12, leaving the temperature differences between adjacent inlet heaters unchanged. It was expected that this would leave the temperature gradient ${\text{d}}\theta /{\text{d}}z$ unchanged in the upper region of the developed boundary layer, and thereby leave the gradient Richardson number unchanged in that region, but varied nearer the surface. Case 7 is an intermediate case between case 6 and case 8. Cases 3, 4, 5, 6, 9, and 11 differ from each other only by differing offsets with respect to $\theta_{0}$. Similarly, cases 8, 10, and 12 differ from each other only by differing offsets. Case 2, differs from all these, having the smallest temperature difference, $\theta_{e} - \theta_{0}$, with a much reduced gradient, and is termed ‘very nearly neutral’ as stability effects are very small. Case 1 is isothermal.

In Hancock and Hayden (2018) it was found that a perfectly uniform inlet temperature profile (above $\theta_{0}$) led to the upper part of the developed boundary layer remaining neutral. At that time it was inferred that the inlet temperature profile had to be rising across the whole depth of the boundary layer. However, the present results show that this constraint is not in fact necessary, and provided a rising temperature exists over a sufficient part of the boundary layer there is sufficient vertical mixing in the development region of the working section for a rising temperature profile to then develop over the whole depth of the boundary layer.

For all cases, measurements were made at X = 10 m, and for cases 1, 2, 3, 7, 8, 9, and 10 measurements were also made at X = 9.2, 12.1, 14.2, and 16.2 m.⁴ In presenting the results, we start with the weaker stability cases. Details of salient parameters are given in Table 1. $Ri_{h} = gh\left( {\theta_{e} - \theta_{0} } \right)/{\Theta }_{0} U_{e}^{2}$ is the bulk Richardson number for the boundary layer as a whole.

Table 1 Summary of the cases investigated and the salient parameters at X = 10 m

4.2 Cases 1, 2, 3, 4, and 5

Cases 2–5 are the mildest stability cases. Figure 2 shows profiles of mean streamwise velocity and Reynolds stresses, normalized by the reference flow speed, and profiles of mean temperature, vertical heat flux, mean-square temperature fluctuation, and gradient Richardson number, at X = 10 m. As observed previously (Hancock and Hayden 2020, 2021), the profiles of U are closely coincident. At the working section inlet the gradient in temperature provided by the heaters is the same for cases 3, 4, and 5; only that of case 2 differs. At the X = 10 m station, the mean temperature profiles (Fig. 2e) have closely similar gradients in the upper half of the boundary layer, while near the surface the temperature (above $\theta_{0}$) is close for cases 2 and 3. The profiles of vertical heat flux (Fig. 2f) show concurrence in the upper half of the boundary layer for cases 3, 4, and 5, showing that the heat flux in this region is governed by the mean temperature gradient, and not by the temperature above the surface. For case 2, the temperature gradient and heat flux are both lower. Near the surface though, the heat fluxes for cases 2 and 3 are close to each other. In all these cases, the near-surface heat flux increases with near-surface temperature difference, as already observed in Hancock and Hayden (2018, 2020). The pattern seen in the vertical heat flux is also seen in the profiles of mean-square temperature fluctuation, Fig. 2g.

Fig. 2

Profiles of a mean streamwise velocity, b–d Reynolds stresses, e mean temperature, f heat flux, g mean-square temperature fluctuation and h gradient Richardson number, for stable cases 2–5. Case 1 is isothermal. Symbols as in a

Comparing the Reynolds stresses, Fig. 2b–d, those for case 2 are very close to those of the neutral flow, case 1, implying negligible effect of stability. The larger mean temperature gradient for cases 3, 4, and 5 lead to a small but clear reduction in these stresses in the upper half of the boundary layer, and a fractionally smaller reduction lower down.

The gradient Richardson number, by definition, is ill-conditioned near the top of the boundary layer; points above z = 471 mm ($\approx 0.85h)$ are shown but ignored in further comment here, Fig. 2h. The profiles for cases 3, 4, and 5 are roughly linearly varying with z over the bulk of the boundary layer, but with differing levels near the surface, consistent with the difference in near-surface temperature. As with other profiles of gradient Richardson number presented here, they are the result of a first iteration. We note from case 2 that $Ri$ of 0.02 corresponds to negligible effect of stability, tying up with Sorbjan’s (2012) band of nearly neutral.

4.3 Cases 1, 5, 6, 8, and 10

Profiles for the quantities shown in Fig. 2 are shown in Fig. 3 for cases 1, 5, 6, 8, and 10, though note that the abscissa scales for thermal quantities differ. Again, the profiles of mean streamwise velocity are closely comparable. Case 8 has the same temperature gradient at the inlet heaters as that of case 10 (see Fig. 1b); only the near-surface temperature differs, with a corresponding difference in vertical heat flux in the lower part of the boundary layer (Fig. 3f). In the upper part, the vertical heat flux profiles of these two cases fall close together, as do the profiles for cases 5 and 6, which similarly have equal temperature gradients at the inlet heaters. In the lower $\approx$ 1/3 of the boundary layer, the profiles for cases 6 and 8 fall near each other, arising from the closeness in $\theta - \theta_{0}$ (Fig. 3f, e). The mean-square temperature fluctuation profiles also pair together in the upper $\approx$ 2/3 and lower $\approx$ 1/3, according to the mean temperature profiles.

Fig. 3

Profiles of a mean streamwise velocity, b–d Reynolds stresses, e mean temperature, f heat flux, g mean-square temperature fluctuation and h gradient Richardson number, for stable cases 5, 6, 8, and 10. Symbols as in a

The Reynolds stresses, Fig. 3b–d, exhibit larger changes than seen in Fig. 2. A larger mean temperature gradient in the upper part of the boundary layer leads to a larger reduction in the stresses in the upper $\approx$ 2/3 of the boundary layer. In the lower $\approx$ 1/3 different behaviours are observed. The profiles of cases 5 and 6 are closely coincident, as they are in the upper part, but this is not so for cases 8 and 10, where the latter exhibits a slightly lower level compared with the former, and is attributable to the larger mean temperature difference (Fig. 3e). However, near the surface, where the temperatures for cases 6 and 8 are close, the Reynolds stresses are also close. These results for momentum and thermal quantities are consistent with those presented in Sect. 4.2.

The temperature profiles of cases 8 and 10 lead to approximately coincident profiles of gradient Richardson number in the upper part of the boundary layer, but to differences in the lower part, consistent with the near-surface temperature difference. Cases 5 and 6 show a lower level of $Ri$ in the centre of the boundary layer, one higher than the other near the surface, consistent with the different mean temperature profiles.

4.4 Cases 1, 6, 8, 9, 10, 11, and 12

These cases (except for case 1) form pairs of cases, as can be seen by the mean temperature profiles in Fig. 4c. The comparisons in Fig. 4 omit the measurements involving the fluctuating vertical velocity, because there was a likely instrument error for the highest temperature cases (11 and 12).⁵ As previously observed, the profiles of mean streamwise velocity have closely the same shape, and the streamwise Reynolds stress is reduced by the influence of stability. In the upper $\approx$ 2/3 of the boundary layer, the stress profiles for cases 8, 10, and 12 concur, as do those for cases 6, 9, and 11. That is, as seen in Sect. 4.3, the level of the stress is controlled by the gradient of the mean temperature, not by its level.

Fig. 4

Profiles of a mean streamwise velocity, b streamwise Reynolds stress, c mean temperature, d mean-square temperature fluctuation, e–f gradient Richardson number and g local Obukhov length, for cases 6, 8, 9, 10, 11 and 12. Symbols as in a

In the lower $\approx$ 1/3, a feature seen in Sect. 4.3 is also seen here, in that the Reynolds stress is also affected by the near-surface mean temperature difference. For cases 8, 10, and 12 close examination shows that the higher temperature differences for cases 10 and 12 leads to a slightly larger reduction in the stress compared with case 8, but that there is little difference in the stress profiles for cases 10 and 12 (and over the whole boundary layer). The same features are seen for cases 6, 9, and 11. Near the surface the Reynolds stress profiles fall close to each other for cases 6 and 8, even though the gradients differ in the upper $\approx$ 2/3. Cases 9 and 10 and cases 11 and 12, though, indicate an influence of the temperature gradient. Profiles of mean-square temperature fluctuation pair together according to the mean temperature profiles (Fig. 4c–d).

The gradient Richardson number is presented in two panels in Fig. 4e–f corresponding to the ‘small’ and ‘large’ mean temperature gradients in the upper half of the boundary layer. In Fig. 4e $Ri$ is approximately constant in the middle of the boundary layer in each case, with levels of 0.07, 0.1, and 0.13 in cases 6, 9, and 11, respectively. They demonstrate the success of controlling the working-section inlet temperature profile to control the gradient Richardson number in the developed boundary layer. These levels of $Ri$ vary linearly with respect to the near-surface temperature difference (whether taken at z = 57 mm or 152 mm, for example), and monotonically from neutral flow. The profiles of Fig. 4f are close in the upper half of the boundary layer, consistent with control by the mean temperature gradient, but differ in the lower part according to the near-surface temperature difference. Though not shown directly, the gradient Richardson number profiles concur near the surface in each pair (defined by Fig. 4c).

The local Obukhov length is shown in Fig. 4g, for two pairs. As anticipated, cases 2 and 7 concur in the upperpart of the boundary layer, as do cases 6 and 10. Near the surface the respective pairs concur: 7 and 10, and 2 and 6, also concurring with the surface values.

4.5 Cases 2, 3 and 7—Variations with X

Three cases, respectively 2, 3 and 7, are presented in Figs. 5, 6, 7, each with profiles at five streamwise stations, from X = 9.2 m to 16.2 m, thereby showing the boundary layer development with streamwise distance in each set (over about 12 boundary-layer heights). As the primary interest here is in the development with X – or, rather, ideally, the absence of development with X – the profiles of mean streamwise velocity and Reynolds stresses are again normalized with respect to the reference speed, rather than the local freestream speed, for example. Thermal quantities are given in dimensional terms as in the previous figures.

Fig. 5

Profiles of a mean streamwise velocity, b–d Reynolds stresses, e mean temperature, f heat flux, g mean-square temperature fluctuation and h gradient Richardson number, at five stations in X. Case 2. Symbols as in a

Fig. 6

Profiles of a mean streamwise velocity, b–d Reynolds stresses, e mean temperature, f heat flux, g mean-square temperature fluctuation and h gradient Richardson number, at five stations in X. Case 3. Symbols as in a

Fig. 7

Profiles of a mean streamwise velocity, b–d Reynolds stresses, e mean temperature, f heat flux, g mean-square temperature fluctuation and h gradient Richardson number, at five stations in X. Case 7. Symbols as in a

Several features are as observed previously by Hancock and Hayden (2021), such as the small increase in mean freestream streamwise velocity, arising from the constant cross-sectional area of the wind tunnel (and associated slightly favourable pressure gradient). The small streamwise development of the profiles of U is very comparable in each case (Figs. 5a, 6a and 7a), and is not discussed further here. The details of the mean temperature profiles are, of course, different in each set (Figs. 5e, 6e and 7e), the case of Fig. 5 being the very nearly neutral case. Now, the profiles of mean temperature in Fig. 7e (case 7) show characteristics previously seen in Hancock and Hayden (2018, 2021), of streamwise development in the lower half of the boundary layer but no significant variation in the upper half. The development differs from that in Figs. 5e and 6e, where there is no observable comparable development seen only in the lower half. In these two cases there is a trend of slight decrease across the whole depth of the layer, diminishing to zero only at the boundary layer edge. It appears, therefore, that the change in streamwise development of the mean temperature profile is associated with the local strength of stability, characterized here in terms of the gradient Richardson number (compare Figs. 5h, 6h and 7h). At a height of z = 300 mm, $Ri \approx$ 0.05 for case 3 (Fig. 6h) and $\approx$ 0.1 for case 7 (Fig. 7h). However, there may be no simple threshold criterion for the change in characteristics seen between Fig. 6e and Fig. 7e. Case 9, as already discussed in Sect. 4.3, has an approximately constant value of Ri $\approx$ 0.1 over the bulk of the boundary layer, and this case also shows the temperature-profile characteristics seen in in Fig. 7e.⁶ Unfortunately, streamwise development was not investigated for cases 4, 5, and 6. Tentatively, it is suggested the threshold, if there is a simple one, may be Ri $\approx$ 0.05.

Comparing the Reynolds stresses of cases 2, 3, and 7 (Figs. 5, 6, 7), case 7 is closest to exhibiting horizontally homogeneous flow (a sought-after feature), while case 2 is the least closest of the three. These examples might be used to suggest that the closeness seen in the upper half of the boundary layer in case 3 is attributable to $Ri$ ${ \gtrsim }$ 0.05. In Fig. 5 the stresses are rising with streamwise distance. It is supposed that the influence of stability, in addition to reducing the levels of turbulent activity, is also to slow down the development with X, to leave nearly constant levels over the fetch covered. (Achieving a comparable lack of streamwise variance in a neutral flow would require a change in the spires, though this is not pursued here.)

4.6 Comparisons with the Local-Scaling Arguments of Nieuwstadt and Sorbjan

In Hancock and Hayden (2018, 2020, 2021) comparisons were made with the local-scaling frameworks and field data given by Nieuwstadt (1984) and Sorbjan (2010), and so the present results are also compared with these, and Sorbjan (2012). See also Gracheve et al. (2013). In Nieuwstadt’s analysis the following non-dimensional groups are functions alone of $z/L$:

$$ Ri,\frac{{\overline{{w^{2} }}^{1/2} }}{{\left( { - \overline{uw} } \right)^{1/2} }},\frac{{ - \left( {\overline{{\theta^{2} }} \left( { - \overline{uw} } \right)} \right)^{1/2} }}{{\overline{w\theta } }},\frac{{ - \overline{u\theta } }}{{\overline{w\theta } }},\frac{{K_{m} }}{{L\left( { - \overline{uw} } \right)^{1/2} }},\frac{{K_{\theta } }}{{L\left( { - \overline{uw} } \right)^{1/2} }}, $$

(5)

where the momentum and heat exchange coefficients are respectively $K_{m} = - \overline{{\left( {uw} \right)}} /\left( {\partial U/\partial z} \right)$ and $K_{\theta } = - \overline{{\left( {w\theta } \right)}} /\left( {\partial {\Theta }/\partial z} \right)$. These six quantities are shown in Fig. 8 for cases 3–10, but each case with a single symbol where there is more than one measurement station.⁷ In order to clearly show the weaker cases $z/L$ is shown on a logarithmic scale. Trend lines of results from Nieuwstadt (1984) and Hancock (2018) are also given. Basu et al. (2006) define five stability regimes, S1 to S5, where S1 is for $0 \le z/L \le 0.1$, S2 for $0.1 \le z/L \le 0.25$, S3 for $0.25 \le z/L \le 0.5$, S4 for $0.5 \le z/L \le 1.0$ and S5 for $z/L > 1$. The present results cover the first four of the five regimes, and assuming a single trend line in Fig. 8a, given by $Ri = 0.31\left( {z/L} \right)^{0.73}$, the boundaries between these five regimes correspond to $Ri \approx$ 0.06, 0.11, 0.19 and 0.31.

Fig. 8

Parameters according to Nieuwstadt’s (1984) local scaling, for cases 3–10, all stations in X. Full lines show Nieuwstadt’s analytical results; dashed line, Nieuwstadt’s field results; dash-dot lines show Hancock and Hayden’s (2018) trend lines; dotted line in c is Caughey et al. (1979) from Nieuwstadt (1984). Symbols as in a

Overall, the data in five of the six quantities given in Fig. 8 exhibit single trends, although cases 3, 4, and 5 lie slightly to one side of the trends of the other cases in some instances. A clear departure from a single trend is seen in the ratio of the heat fluxes, in Fig. 8d, with cases 3, 4, 5, 6, and 7 differing from 8, 9, and 10. For cases 3 and 7, the earlier stations in X follow the lower ‘fork’, while the later stations follow the trend set by the upper fork, a feature that is attributed to a residual streamwise development of this ratio for these milder stable cases. It is assumed that cases 4–6 would have shown similar behaviour had measurements been made at stations beyond that at X = 10 m. It is perhaps arguably significant to note that greater concurrence is seen when Fig. 8 is replotted, but with Ri as the independent variable rather than $z/L$, as shown in Fig. 9. A particular point to note is that all the parameters are purely local variables; z is not involved except in the derivatives for $R$i, $K_{m}$, and $K_{\theta }$.

Fig. 9

Parameters according to Nieuwstadt’s (1984) local scaling, for cases 3–10, all stations in X, but as functions of Ri. Symbols and lines as in Fig. 8

Nieuwstadt’s (1984) theoretical predictions show all the quantities in Fig. 8 to approach asymptotic levels, and to be close to these levels by $z/L \approx 2$. Some quantities in Fig. 8 are still clearly rising at $z/L = 1$, implying that, if asymptotes exist, they are reached more slowly.

Four of the non-dimensional groups for Sorbjan’s (2010) ‘master’ scaling, functions of Ri, are:

$$ \frac{{ - \overline{uw} }}{{U_{S}^{2} }}, \,\frac{{ - \overline{w\theta } }}{{U_{S} {\Theta }_{S} }}, \,\frac{{\left( {\overline{{w^{2} }} } \right)^{1/2} }}{{U_{S} }}, \,\frac{{\left( {\overline{{\theta^{2} }} } \right)^{1/2} }}{{{\Theta }_{S} }}, $$

(6)

and are shown in Fig. 10 for cases 3–10, where the velocity scale, $U_{S} = \kappa zN$, the temperature scale, ${\Theta }_{S} = \kappa z\partial {\Theta }/\partial z$, and $N^{2} = \left( {g/{\Theta }} \right)\left( {\partial {\Theta }/\partial z} \right)$. This figure also shows the empirical trend lines given by Sorbjan (2010) based on data from the Surface Heat Budget of the Arctic Ocean (SHEBA) study. Overall, there is less concurrence between the different cases of the present measurements than that seen in Nieuwstadt’s scaling framework. Cases 6, 7, 8, 9, and 10 concur, as do cases 3, 4, and 5, but the trends in the latter fall consistently below the trends in the former, for all four ratios. However, the above velocity and temperature scales can only be expected (at most) to properly apply in the surface layer where the length scale varies linearly with z. Sorbjan (2012), extended the above framework for the whole of depth of the boundary layer by supposing a mixing-length type of variation of length scale: $\ell = \kappa z/\left( {1 + \kappa z/\ell_{0} } \right)$, originally proposed by Blackadar (1962) for neutral flow, where $\ell_{o}$ is a length scale associated with the flow above the surface layer (sometimes termed the outer layer), and is of order of the boundary layer height, h. This more general scaling was validated against CASES-99 (Cooperative Atmospheric-Surface Exchange Study, 1999; see e.g. Poulos et al. 2002) which concurred with the earlier validation against the SHEBA study for the surface layer. Figure 11 shows the measurements of Fig. 10 but with $U_{S} = \ell N$ and ${\Theta }_{S} = \ell \partial {\Theta }/\partial z$, where $\ell_{o}$ has been taken as 0.45 h for each case. This value is very comparable with that employed by Williams et al. (2017), where they equated $\ell_{o}$ to the streamwise integral length scale. In contrast to the profiles in Fig. 10, those in Fig. 11 fall close to single curves in each panel. In Fig. 10, the cases form one or other of two distinct trends, the weaker cases 3, 4 and 5 forming the lower trend line in each panel. The physically more realistic length scale, $\ell$, has a significant effect on the velocity and temperature scales in the flow above the surface layer, such as to bring all cases to concurrence. (It is not obvious why in Fig. 10 the cases should fall into two largely distinct trends rather than a spread of cases.) Nevertheless, it seems unlikely, though, that $\ell_{o}$ as a fraction of h, or an integral length scale, would be unchanging as stability increases; inhibited vertical interaction would suggest a reduction of $\ell_{o} /h$.

Fig. 10

Parameters according to Sorbjan’s (2010) local scaling, for cases 3–10, all stations in X. Full lines show Sorbjan’s fitted curves. Symbols as in Fig. 8a

Fig. 11

Parameters according to Sorbjan’s (2012) local scaling, for cases 3–10, all stations in X. Full lines show Sorbjan’s fitted curves. Symbols as in Fig. 8a

The trends in Fig. 11a, c are nearly linear, lying close to Sorbjan’s (2010, 2012) consensus curves for $Ri{ \lesssim }0.09$, but above this they do not fall as steeply as his consensus curves. The trends in Fig. 11b, d are fairly linear, but that for $\left( {\overline{{\theta^{2} }} } \right)^{1/2} /\left( {{\Theta }_{S} } \right)$ differs markedly from the consensus curve. Although $\left( {\overline{{\theta^{2} }} } \right)^{1/2}$ is normalized in a different way in the framework of Nieuwstadt (1984), the level of $\left( {\overline{{\theta^{2} }} } \right)^{1/2}$ does not differ from his measured data or his theoretical curve by nearly as much. In fact, at Ri = 0.01 for example, the consensus field-data curves of Figs. 11a, b, d give a value of $- (\left( {\theta^{2} } \right)\left( { - \overline{uw} } \right))^{1/2} /\overline{w\theta }$ that is twice as large as that in Fig. 9b. Figure 9b includes a trend line of the measurements by Caughey et al. (1979), taken from Nieuwstadt (1984), which also compares well with the present measurements. (A similar comparison for the consensus field-data curves of Figs. 11a, c compare much more closely with the field-data curves and present measurements of Fig. 9a.)

5 Concluding Comments

Results have been presented for 11 stable boundary-layer simulations covering the range of 0.006 $\le Ri \le$ 0.3, or, equivalently, the range 0.005 $\le z/L \le$ 1.0.⁸ The vertical profile of $Ri$ was imposed by controlling the profile of the working-section inlet temperature provided by the inlet heaters. This included three cases in which $Ri$ was constant (approximately 0.07, 0.1 and 0.13) over the bulk of the boundary layer depth. The level and shape of the profile of $Ri$ was determined primarily by controlling (i) the near-surface temperature above that of the surface itself and (ii) the gradient in the inlet temperature profile in the region above this. Here, ‘near-surface’ refers to the bottom $\approx$ 20% of the boundary layer—and so may be equated with the surface layer—and the near-surface temperature difference was controlled primarily by the temperatures of the lowest two inlet heaters.

The streamwise decrease in temperature in the lower 1/3 of the boundary layer, accompanied by negligible change in the upper 2/3, attributed by Hancock and Hayden (2020) to a blocking of vertical interaction, was seen here but not in all cases. It was not seen in the nearly-neutral case (case 2), nor in the next stronger case (case 3). Further measurements will be needed in order to establish a criterion or criteria at which blocking starts. Tentatively, it is suggested that the threshold, if there is a simple one, may be Ri $\approx$ 0.05 in the bulk of the boundary layer.

The Reynolds stresses in each case are reduced by stability, but in differing ways in two parts of the boundary layer. In the upper $\approx$ 2/3 of the boundary layer, they are controlled by the gradient of mean temperature, while in the lower $\approx$ 1/3 they are controlled by the level in the upper $\approx$ 2/3 and by the temperature difference across the near-surface layer.

All the measurements collapse in the scaling framework of Nieuwstadt (1984), with the exception of the ratio of heat fluxes $\overline{u\theta } /\overline{w\theta }$ in weaker stability cases, where there is some residual streamwise development in the earlier stations, the later stations falling in line with bulk of the profiles. This dependence looks to be weaker if Nieuwstadt’s ratios are expressed as a function of $R$i rather than $z/L$, where $Ri$ is of course a fully local parameter. Overall, the measurements concur with the field measurements presented by Nieuwstadt. In the framework of Sorbjan (2010, 2012), the measurements only fully collapse if the adopted length scale is of mixing-length form with $\ell = \kappa z/\left( {1 + \kappa z/\ell_{0} } \right)$ rather than $\ell = \kappa z$, where $\ell_{o}$ is of order the boundary layer height, and taken here as 0.45 h. There is near agreement with the consensus field data given by Sorbjan, for the vertical velocity fluctuation intensity and the Reynolds shear stress for $Ri { \lesssim }0.1$; above this the consensus field data decreases more strongly. The concurrence is least good for the temperature fluctuation, though the consensus given by Sorbjan (2010, 2012) is twice that given by Nieuwstadt (1984, and Caughey et al. 1979, cited there in).

Appendix: Equation (4)

From Eqs. (1) and (2) in Hancock and Hayden (2021) the mean velocity and mean temperature gradients are given by, respectively,

$$ \frac{\partial U}{{\partial z}} = \frac{{u_{*} }}{\kappa }\left[ {\frac{1}{z} + 8\frac{1}{{L_{o} }}} \right]\; {\text{and}}\;\, \frac{{\partial {\Theta }}}{\partial z} = \frac{{\theta_{*} }}{\kappa }\left[ {0.95\frac{1}{z} + 16\frac{1}{{L_{o} }}} \right], $$

where $u_{*} = \left( { - \overline{uw} } \right)_{0}^{1/2}$ and $\theta_{*} = - \left( {\overline{w\theta } } \right)_{0} /u_{*}$. Equation (4) follows straightforwardly from the definition of Ri.