Thermal Stratification Effects on Turbulence and Dispersion in Internal and External Boundary Layers

Abstract

A synthetic-turbulence and temperature-fluctuation-generation method is developed and embedded in large-eddy simulations to investigate the effects of weak stable stratification (i.e. Richardson number $Ri\le 1$) on turbulence and dispersion following a simulated rural-to-urban transition. The modelling approach is validated by comparing predictions of mean velocity, turbulent stresses, and point-source dispersion against data from a wind-tunnel experiment that simulates a stable atmospheric boundary layer ($Ri=0.21$) approaching a regular array of uniform rectangular blocks. The depth of the internal boundary layer (IBL) that develops from the leading edge of the block array is determined using the wall-normal turbulent stress method proposed by Sessa et al. (J Wind Eng Ind Aerodyn 182:189–291, 2018). This shows that the depth and growth rate of the IBL are sensitive to the thermal stability and the turbulence kinetic energy (TKE) prescribed at the inlet, such that the IBL depth reduces as the TKE of the inflow is reduced while maintaining the same Ri, or as the Ri is increased while maintaining the same inflow TKE. When a ground level line source is introduced it is found that increasing Ri evidently reduces the vertical scalar fluxes at the canopy height, while increasing the mean concentrations within the streets. Furthermore, as with IBL development it is found that for a given value of Ri the effect of stratification becomes more pronounced as the inflow level of TKE is reduced, affecting scalar fluxes within and above the canopy, and volume-averaged mean concentrations within the streets.

1 Introduction

Nearly two decades ago Britter and Hanna (2003) suggested that urban flows may be considered as neutral or nearly neutral in urban dispersion models. However, the topic of thermal stratification in urban areas has recently received renewed attention (e.g. Boppana et al. 2013; Kanda and Yamao 2016), from which it has been concluded that non-neutral atmospheric stratification frequently occurs in urban areas, and neutral conditions may be the exception rather than the rule (Wood et al. 2010). It has been documented that unstable thermal conditions occur three times more frequently than stable and six times more than neutral conditions over the city of London during the daytime. Furthermore, at night the number of unstable cases was almost equal to the number of stable cases and four times greater than the number of neutral cases because of radiative cooling of the surface.

In stable conditions, pollutant concentration may increase and air quality may decrease within the urban canopy because of reduced dispersion in the vertical direction. Despite the increasing concerns regarding air quality, only a few experimental studies have examined the effects of stable stratification on turbulent structures over smooth, rough (e.g. Ohya 2001; Williams et al. 2017), and very rough (e.g. Marucci and Carpentieri 2018; Marucci et al. 2018) surfaces, and the impact on passive scalar dispersion (e.g. Yassin et al. 2005; Kanda and Yamao 2016). Not surprisingly, only a very few numerical studies (e.g. Cheng and Liu 2011; Boppana et al. 2013; Xie et al. 2013; Tomas et al. 2016) have examined turbulence and dispersion in stably stratified flows over very rough surfaces. Two key problems remain to be addressed.

The first problem relates to identifying the critical level of stratification, which can be interpreted as signalling the start of a ‘strongly’ stratified region. Williams et al. (2017) reported that the critical bulk Richardson number (Ri)—based on the boundary-layer thickness, the freestream velocity, and the temperature difference across the boundary layer—was 0.10 for a smooth surface, while the critical bulk Richardson number was 0.15 for a rough surface with roughness length $< 4$ in wall units ($z_0^+$, based on the roughness length and friction velocity). This confirms that a rough surface reduces the stratification effect compared to a smooth wall, and also suggests that for a very rough urban surface, which is likely to have a much greater roughness length, the critical Richardson number is likely to be greater than 0.15.

The second problem is that the urban surface is always heterogeneous. The change in surface roughness associated with a flow crossing from a rural area into an urban area, or from an area of low-rise-buildings into a central business district with high-rise buildings, leads to a region of transitional flow as the turbulent boundary adapts to the new wall condition (e.g. Cheng and Castro 2002; Hanson and Ganapathisubramani 2016; Tomas et al. 2016; Marucci et al. 2018; Sessa et al. 2018). This transitional flow results from the development of an internal boundary layer (IBL) from the interface of the different roughness. To understand how air quality may be affected, it is necessary to determine to what extent the step change of roughness and the thermal stratification combine to affect flow and dispersion.

Tomas et al. (2016) investigated the effect of stable stratification on flow and line-source dispersion by simulating a smooth-wall boundary layer entering a generic urban area using large-eddy simulation (LES). Although they only considered a weakly stable condition with a bulk Richardson number of 0.147, they found that the IBL was $14\%$ shallower than that in neutral conditions, and the turbulence kinetic energy (TKE) was reduced by $21\%$. It should be noted that the approaching flow was developed over a smooth-wall surface so that the inflow turbulence intensity and integral length scales were not representative of a typical rural boundary layer. This implies that the subsequent turbulence and dispersion predictions downstream of the step change in surface roughness are not representative of a genuine rural-to-urban surface.

The effects of stable stratification on turbulence and dispersion are not negligible even under weakly stable conditions (e.g. Xie et al. 2013; Boppana et al. 2014). The consumption of buoyant energy in such conditions damps turbulence, which affects ventilation and the concentration of pollutants at the pedestrian level. When Cheng and Liu (2011) investigated stability effects at bulk Richardson numbers of 0.18 and 0.35 on the dispersion in two-dimensional street canyons using LES, they found that for a bulk Richardson number greater than 0.25, turbulence was strongly suppressed at ground level. This meant that the pollutant tended to reside longer at the pedestrian level than in the upper street canyon. Tomas et al. (2016) showed that for a bulk Richardson number of 0.147 the area-averaged street concentration of a line source was $17\%$ higher than in neutral conditions due to decreased streamwise advection and trapping of pollutant by the IBL. Similar conclusions were reached in the LES study conducted by Xie et al. (2013), who found that the stability effects induced at a bulk Richardson number of 0.21 increased mean concentrations by up to an order of magnitude when compared to neutral conditions. Moreover, Xie et al. (2013) also found that turbulent fluctuations and mean velocities were not substantially affected either by a change of mean temperature profile below the canopy or inlet temperature fluctuations for a given Richardson number.

As far as we are aware, very few studies have examined the effects of stable stratification on dispersion within an IBL, and those that have have only considered weakly stable conditions. In this paper we consider the effects of various stratification conditions up to a Richardson number of 1 on turbulence and dispersion following a rural-to-urban transition. The objective was to a LES model to answer the following three questions:

• 1. To what extent are stratification effects on flow and dispersion following a step change in roughness length dependent on the inflow turbulence intensity?

• 2. To what extent does increasing stratification affect the IBL thickness for bulk Ri numbers below 1?

• 3. To what extent does increasing stratification affect the ventilation of pollutant within and above the canopy for bulk Ri numbers below 1?

The governing equations are briefly described in Sect. 2. Details of numerical settings including geometry, mesh, and inflow conditions are given in Sect. 3, and LES validation, sensitivity tests on the ground temperature, and TKE at the inlet are reported in Sect. 4. Stratification effects on the IBL are discussed in Sect. 5, and the analysis of scalar fluxes and mean concentration results are reported in Sect. 6. Finally, the conclusions are summarized in Sect. 7.

2 Governing Equations

In a LES model the filtered continuity and momentum equations for a buoyancy-driven flow are written as follows,

$$\begin{aligned} \frac{\partial {{u}_i}}{\partial x_i}= & {} 0, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial {{u}_i}}{\partial t}+\frac{\partial {{u}_i {u}_j}}{\partial x_j}= & {} -\frac{1}{\rho }\frac{\partial {{p}}}{\partial x_i}+ f\delta _{i2}+\frac{\partial }{\partial x_j}\left( \frac{\tau _{ij}}{\rho }+\nu \frac{\partial {u}_i}{\partial x_j}\right) , \end{aligned}$$

(2)

where the filtered velocity and pressure fields are ${u}_i$ and p respectively, $\nu$ is the kinematic molecular viscosity, and $\rho$ is the density. The term $\tau _{ij}$ is the subgrid-scale (SGS) Reynolds stress, which was determined by using the mixed time-scale subgrid eddy viscosity model (Inagaki et al. 2005); $f\delta _{i2}$ is the body force due to thermal buoyancy and is calculated using the Boussinesq approximation.

The filtered transport equation for a passive scalar is

$$\begin{aligned} \frac{\partial {C}}{\partial t}+\frac{\partial {u}_j{C}}{\partial x_j}=\frac{\partial }{\partial x_j}\left[ (K+K_r)\frac{\partial {C}}{\partial x_j}\right] +S, \end{aligned}$$

(3)

where C is the filtered scalar concentration and S is a source term. The second term on the left-hand side (l.h.s.) is the advection term and the first term on the right-hand side (r.h.s.) is the diffusion term. K is the molecular diffusivity and $K_r$ is the SGS turbulent diffusivity computed as

$$\begin{aligned} K_r=\frac{\nu _r}{Sc_r}, \end{aligned}$$

(4)

where $\nu _r$ is the SGS viscosity and $Sc_r$ is the subgrid Schmidt number. A constant Schmidt number of $Sc_r=0.7$ is assumed.

The filtered transport equation of temperature is

$$\begin{aligned} \frac{\partial {T}}{\partial t}+\frac{\partial {u}_j{T}}{\partial x_j}=\frac{\partial }{\partial x_j}\left[ (D+D_r)\frac{\partial {T}}{\partial x_j}\right] , \end{aligned}$$

(5)

where T is the resolved-scale temperature. D is the molecular diffusivity of temperature, $D_r$ is the subgrid turbulent diffusivity and is given by $\nu _r/Pr_r$, where $Pr_r$ is the subgrid Prandtl number, set to 0.9.

3 Numerical Settings

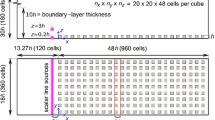
The LES model was implemented within the open-source CFD package OpenFOAM version 2.1.1. A second-order backward implicit scheme in time and second-order central difference scheme in space were applied for the discretization of the terms in Eqs. 2, 3, and 5. The domain was set as a half channel. An efficient inflow turbulence generation method (Xie and Castro 2008) was used at the inlet, with periodic conditions at the lateral boundaries and a stress-free condition at the top of the domain ($y=12h$, where $h = 70\hbox { mm}$ is the uniform height of the array element). The Reynolds number based on h and the freestream velocity $u_{\mathrm{ref}}=1.35$ m $\hbox {s}^{-1}$ at $y=12h$ was approximately 8000. The average CFL number was 0.2, and based on a timestep of 0.0007 s. Flow and second-order statistics were initialized for 20 flow passes and then averaged over 150 flow passes.

For the purpose of validating the baseline study, the numerical settings (e.g. the geometry of the array, the point source, the approaching boundary layer, and the thermal stratification conditions) were made consistent with experiments (Castro et al. 2017; Hertwig et al. 2018; Marucci et al. 2018; Marucci and Carpentieri 2018). The wind-tunnel experiments were conducted using the meteorological wind tunnel at the University of Surrey, UK, which has a test section 20 m (length) $\times$ 3.5 m (width) $\times$ 1.5 m (height). A ‘simulated’ atmospheric boundary layer representative of stable and unstable conditions was generated by using Irwin’s spires at the inlet, two-dimensional roughness elements on the floor, and adjusting the inlet and floor temperature. Propane was used as a passive tracer and its concentration was measured by using a fast flame ionization detector (FFID) system. Velocities were measured by using two-component laser Doppler anemometry LDA. Mean temperature and its fluctuations were measured using a fast-response cold-wire probe. The numerical settings applied to simulate the flow and point source dispersion in neutral conditions were consistent with those experimental settings in Castro et al. (2017) and Hertwig et al. (2018), respectively. For the studies in stable conditions, the numerical settings applied to the flow and point source dispersion were consistent with those in Marucci et al. (2018) and Marucci and Carpentieri (2018), respectively. More specific details are given below.

Fig. 1

Plan view of the array configuration showing dimensions of buildings and streets, coordinate system, flow direction, and locations of line source S1 and point source S2

3.1 Geometry, Mesh, and Resolution

The array of regular cuboid elements modelled herein represents part of a larger array used in the wind-tunnel experiments of Castro et al. (2017) and Marucci and Carpentieri (2018). The modelled array was designed to simulate a neighbourhood scale region in which statistical homogeneities are assumed. The basic obstacle layout was identical to those described in Sessa et al. (2018) and in Fuka et al. (2018).

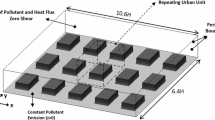
A plan view of the modelled array is shown in Fig. 1 where the street units parallel to the x axis are 1h long and referred to as ‘short streets’ hereinafter. Street units parallel to the z axis are 2h long and referred to as ‘long streets’. The rectangular array comprised 48 aligned blocks with h spacing, which leads to a plan area density of $\lambda _p=0.33$ when considering the single block unit.

The dimensions of the modelled domain are $31.5h\times 12h\times 12h$ within a uniform Cartesian grid of resolution $\bigtriangleup =h/16$. The top boundary is placed at $y=12h$ to be very close to the experimental boundary-layer top (Marucci et al. 2018). In order to ensure the zero-gradient outflow boundary condition, the domain size is extended by 2.5h in the x-direction compared to the domain used in Sessa et al. (2018). Computations were made for the zero degree wind direction by assuming that the mean flow is perpendicular to the front face of the cuboid elements as indicated in Fig. 1.

3.2 Scalar Sources

A passive scalar is released from a ground-level point source (S2) and a ground-level line source (S1) within the array of cuboid elements. Because of the finite size of the grid, the shape of the point source only approximated the source used in the experiment. The shape and size of the point source are identical to those reported in Fuka et al. (2018). The diameter is represented by four cells and so measured 0.25h, while the height is one cell (h/16). The point source is positioned in the middle of a short street within the seventh row of blocks (Fig. 1) in accordance with the experimental set-up of Marucci and Carpentieri (2018).

The line source is positioned on the ground between the fifth and sixth rows of blocks. The lateral extent of the line source is set equal to the entire width of the domain (12h) while the height and width of the line source are one cell (h/16) and four cells (4h/16) respectively. A constant scalar-flux release rate is set for each cell inside the volume of both the point source and the line source.

3.3 Temperature Inlet Conditions for Large-Eddy Simulation

In order to analyze the effects of thermal stratification on flow and dispersion, large-eddy simulations were conducted for various bulk Richardson numbers Ri, defined as

$$\begin{aligned} Ri=\frac{g H ({\overline{T}}_{\mathrm{ref}}-{\overline{T}}_0)}{{\overline{T}}_0 {\overline{u}}_{\mathrm{ref}}^2}, \end{aligned}$$

(6)

where ${\overline{u}}_{\mathrm{ref}}$ is the mean freestream velocity at the inlet, g is the acceleration due to gravity, H is the domain height. ${\overline{T}}_{0}$ and ${\overline{T}}_{\mathrm{ref}}$ are the mean temperature on the ground and the mean freestream temperature. Large-eddy-simulation comparisons for increasing stable stratification are achieved in a similar manner to Boppana et al. (2013), by fixing ${\overline{T}}_{\mathrm{ref}}$ and ${\overline{T}}_0$ and changing the value of g as shown in Table 1. The upstream boundary-layer height is kept fixed at $H=12h$ in the LES simulations for all values of Ri, as in the wind-tunnel experiments of Marucci et al. (2018) in which the tendency towards reducing boundary-layer height with increasing stability is overcome by the level of turbulence generated by the inlet spires.

Table 1 Variation of g with Ri in the LES model

The LES requires a continuous specification of turbulence in time at the inlet to simulate an evolving turbulent boundary layer. This was achieved by using the inflow turbulence method developed by Xie and Castro (2008) to generate a synthetic turbulent inflow with exponential-form correlations in time and space. This inflow method has been shown to provide a high fidelity reconstruction of the turbulence characteristics in both the energy-containing region and inertial sublayer of the spectra. Moreover, recent work by Bercin et al. (2018) has shown that the exponential-form correlations provide a better approximation than the Gaussian ones.

Fig. 2

Vertical profiles of prescribed integral length scales at the LES inlet $x=-2.5h$

The turbulence generated by the inflow method satisfies the prescribed integral length scales and Reynolds stress-tensor values. The integral length scales $L_x$, $L_y$, and $L_z$ prescribed in the streamwise, vertical, and lateral directions, respectively, are shown in Fig. 2. These were estimated from data presented in Marucci et al. (2018) for an experiment simulating $Ri=0.21$.

The estimated integral length scales can have considerable uncertainties due to the complexity of the autocorrelation function and the selection of its cut-off point for the integration. Xie and Castro (2008) performed numerical sensitivity tests using different length scale combinations imposed at inlet (i.e. $L_x$, $L_y$, and $L_z$ factored by 0.5, 1, or 2). They found that the mean velocities and turbulent stresses within or immediately above the canopy were not sensitive to these variations provided the baseline length scales are not too different from the ‘true’ values. This suggests that it is not necessary to consider the effect of integral length scales in the current work.

The inflow turbulence method of Xie and Castro (2008) is also used to generate temperature fluctuations. The integral length scale of turbulence in the vertical direction $L_y$ (Fig. 2) is chosen as the integral length scale of temperature fluctuations. Xie et al. (2013) and Okaze and Mochida (2017) used similar approaches to generate flow temperature fluctuations, whereas Xie et al. (2013) did not carry out a validation and Okaze and Mochida (2017) considered temperature a passive scalar. The mean temperature (Fig. 3a) and temperature variance (Fig. 3b) obtained from the wind-tunnel experiment at $Ri=0.21$ reported in Marucci et al. (2018) are prescribed at the inlet assuming a lateral homogeneity. Marucci et al. (2018) fitted the mean temperature profile (Fig. 3a) for $Ri=0.21$ in the usual log-linear form,

$$\begin{aligned} {\overline{T}}(y)-{\overline{T}}_0=\frac{T_*}{\kappa }\left[ \ln (\frac{y-d}{y_{0h}})+16\frac{y-d-y_{0h}}{L}\right] , \end{aligned}$$

(7)

where the von Kármán constant $\kappa =0.41$, the roughness displacement height $d=0$, the ratio of the boundary-layer thickness to the Obukhov length H/L = 1.13, the scaling temperature $T_* =0.34$ K, the thermal roughness length $y_{0h}=0.021$ mm, and the maximum temperature difference $\varDelta {\overline{T}}$ between the cooled floor ${\overline{T}}_0$ and the free stream flow ${\overline{T}}_{\mathrm{ref}}$ was fixed as 16 K. Because of the experimental uncertainty in measuring temperature values close to the ground, Marucci et al. (2018) applied the least-squares fitting procedure to estimate the ground temperature $\overline{T_0}$ shown in Hancock and Hayden (2018).

Figure 3b shows the prescribed temperature variance at the LES inlet and the experimental values. A constant temperature variance is prescribed in the vicinity of the floor $(y/h \le 1)$ where we assume the existence of a surface layer. The building walls, the streets, and the ground are assumed to be adiabatic, as the inlet wind speed is high, the air pass-through time over the array is short, and the local heat transfer over the block surfaces is negligible. In Sect. 4, this assumption is confirmed to be reasonable by comparing the LES data against the measurements of Marucci and Carpentieri (2018).

3.4 Velocity Inlet Conditions for Large-Eddy Simulation

Figure 4a, b shows vertical profiles of experimental data (Marucci et al. 2018) and numerically (Sessa et al. 2018) prescribed inlet mean velocity and turbulent stresses for $Ri=0$, respectively. Figure 4c, d shows vertical profiles of experimental data (Marucci et al. 2018) and numerically prescribed inlet mean velocity and turbulent stresses respectively, at $Ri=0.21$. The prescribed inlet mean velocity and turbulent stresses for the cases $Ri=0.5$, 0.7, 1 (Table 1) are the same as those for the case $Ri=0.21$. This is useful for quantifying to which extent the thermal stratification alone impacted turbulence and dispersion, as in Xie et al. (2013).

Fig. 3

Prescribed a mean temperature and b temperature-fluctuation variance at the LES inlet and the corresponding experimental data. $\varDelta {\overline{T}}$ is the maximum temperature difference between the cooled floor ${\overline{T}}_0$ and the freestream flow ${\overline{T}}_{\mathrm{ref}}$

Fig. 4

Prescribed mean velocity and turbulent stresses at the LES inlet and the corresponding experimental data. a Mean velocity, $Ri=0$; b turbulent stresses, $Ri=0$; c mean velocity, $Ri=0.21$; d turbulent stresses, $Ri=0.21$

The case $Ri=1^*$ (Table 1) is designed to quantify the effect of inlet TKE. The inlet mean velocity profile is prescribed to be the same as that of $Ri=1$, while the turbulent stresses are estimated using a simple method. The ratios of the friction velocity to the freestream velocity $u_*/u_{\mathrm{ref}}$ at $Ri=0$, 0.14, 0.21, 0.33 reported in Marucci et al. (2018) are normalized by that at $Ri=0.21$, and fitted to an exponential function of Ri (Fig. 5).

Marucci et al. (2018) found that the ratio of turbulent stresses to the friction velocity (i.e. $\overline{u'u'}/u^2_*$) did not change significantly in the vicinity of the wall in various weakly stable conditions. We therefore assume that this ratio is constant between $Ri=1$ and $Ri=0.21$. The turbulent stresses for $Ri=1^*$ at the inlet are determined from the estimated friction velocity $u_*$ obtained from Fig. 5. The estimated TKE prescribed at inlet for $Ri=1^*$ is about $10\%$ of that for $Ri=0.21$.

4 Validation and Verification of Large-Eddy Simulation

4.1 Validation

Predictions of turbulence, dispersion, and mean temperature at $Ri=0.21$ are validated against the wind-tunnel data reported in Marucci et al. (2018) and Marucci and Carpentieri (2018). The standard error of the experimental measurements is around $\pm 1\%$ for mean velocity, $\pm 5\%$ for mean concentration and turbulent variances (Marucci et al. 2018; Marucci and Carpentieri 2018). Mean velocity and temperature, streamwise and lateral turbulent stresses, mean concentration, and concentration variance from the point source S2 are compared with wind-tunnel data measured at $x=16h$ and $z=0$.

Fig. 5

The exerimental (Expt) data of $u_*/u_{\mathrm{ref}}$ at $Ri=0$, 0.14, 0.21, 0.33 in Marucci et al. (2018) fitted to an exponential function of Ri number, normalized by that at $Ri=0.21$

Fig. 6

A comparison between LES and experimental data. Vertical profiles of laterally-averaged a mean velocity, b mean temperature, c streamwise turbulent stress, and d lateral turbulent stress at $x=16h$. Vertical profiles of e mean concentration, and f concentration variance measured at $x=16h$ and $z=0$ for the point source S2

Mean velocity (Fig. 6a) and mean temperature (Fig. 6b) from LES are spatially averaged over four identical street intersections at $x=16h$, whereas the experimental data are averaged in time only. The LES predictions of mean velocity are found to be in good agreement with experimental values below and immediately above the canopy (Fig. 6a). Similarly, the experimental profile of mean temperature is well captured by LES, although the experimental uncertainty in temperature measurements close to the ground is not negligible.

Figure 6c, d presents comparisons between LES predictions of the mean streamwise and lateral turbulent stresses again averaged over four identical street intersections at $x=16h$ with the corresponding experimental data. The small differences between the second-order statistics in the LES and wind-tunnel data in the figures demonstrate the success of the validation. The differences may reasonably be attributed to comparing spatial averages from the LES with a single sampling station in the experimental data.

The scalar concentration from the point source S2 is normalized following the method of Sessa et al. (2018) and Fuka et al. (2018),

$$\begin{aligned} \overline{C^*}={\overline{C}}\frac{u_{\mathrm{ref}}L_{\mathrm{ref}}^2}{Q}, \end{aligned}$$

(8)

where ${\overline{C}}$ is the mean scalar concentration, the characteristic length $L_{ref}$ is the building height h, and Q is the emission rate. Similarly, the scalar variance is normalized as

$$\begin{aligned} \overline{c'c'^*}=\left[ \frac{\sqrt{\overline{c'c'}}u_{\mathrm{ref}}L_{\mathrm{ref}}^2}{Q}\right] ^2, \end{aligned}$$

(9)

where $c'$ is the scalar concentration fluctuation.

The LES mean concentration (Fig. 6e) and scalar variance (Fig. 6f) data were sampled at the main street intersection ($x=16h$, $z=0$) and compared with the experimental data. It can be seen that the LES accurately predicts the experimental mean concentration for $y\ge 0.5h$. The close agreement suggests that the predicted mean concentration at ground level should also be accurate. Figure 6f shows that the concentration variance is also well predicted above the canopy, but underestimated within it. This difference may well be due to the uncertainties in measuring the concentration variance in the wind tunnel, and the source shape/size differences that affect the results in the near field (Sessa et al. 2018).

4.2 Ground Temperature Sensitivity Test

As discussed in Sect. 3.3, Marucci et al. (2018) used the least-square fitting method of Hancock and Hayden (2018) to obtain the upstream mean temperature profile and the temperature at the surface. From this they determined a good fit close to the ground. They then determined that the stability level in the wind tunnel was $Ri=0.21$ by considering the maximum temperature difference $\varDelta {\overline{T}}=16$ K between the cooled floor $\overline{T_0}$ and the free stream flow ${\overline{T}}_{\mathrm{ref}}$.

Although the temperature comparison was acceptable, the sensitivity of the derived value of Ri to this must be assessed because of the experimental uncertainty in determining the surface temperature. A ground-temperature sensitivity assessment was therefore conducted to assess to what extent turbulence and dispersion within and above the canopy were affected by a small change in ground temperature at the inlet. One case was simulated using the inlet mean temperature profile shown in Fig. 3a but changing the temperature profile in the vicinity of the ground (i.e. for $y/h\le 0.125$) to be a constant, which was 2K lower than ${\overline{T}}_0$ in Sect. 4.

The normalized total heat flux, $\psi ^{u_*}_{h,tot}$, in the direction of flow resulting from the prescribed inlet temperature profile (Fig. 3a) can be estimated

$$\begin{aligned} \psi ^{u_*}_{h,tot}=\int _{y/h\in (0,12)}\frac{({\overline{U}}\,{\overline{T}}+\overline{u'T'})}{u_*T_*}\text{ d }\left( \frac{y}{h}\right) , \end{aligned}$$

(10)

where $u'$ and $T'$ are the velocity and temperature fluctuations, respectively. As discussed above, the temperature in the vicinity of the ground was changed between the two LES cases for $y/h\le 0.125$ only. This meant that the incoming heat flux was only expected to change below $y/h=0.125$. It is to be noted that close to the ground the turbulent flux component $\overline{u'T'}$ in Eq. 10 is always very small or negative compared to the advective part ${\overline{U}}\,{\overline{T}}$ (Fuka et al. 2018; Goulart et al. 2019). Similarly, the advective component ${\overline{U}}\,{\overline{T}}$ in the vicinity of the ground is also very small as the mean flow speed is nearly zero.

Vertical profiles of mean velocity and turbulent stresses were sampled at $x=16h$ and laterally averaged over 60 locations. The mean concentration from point source S2 was sampled in the lateral direction at $x=16h$ and $y=0.5h$ below the canopy, and normalized as in Eq. 8. As expected, the mean velocity, turbulent stresses, and normalized concentration values for the two cases were found to be in close agreement. This confirmed that small differences in incoming heat flux due to the measurement errors in ground temperature had a negligible effect on the downstream turbulence and dispersion within and above the canopy.

4.3 Sensitivity to the Prescribed Inlet Turbulence Kinetic Energy

Vertical profiles of mean velocity (Fig. 7a) and normalized mean concentration (Fig. 7b) were sampled at $x=16h$ and laterally averaged over 60 locations. The effect of applying an inflow with a much lower TKE (i.e. $Ri=1^*$) on the mean velocity profile at $x=16h$ was negligible. This suggests that the difference between the mean velocity $x=16h$ for $Ri=0$ and the stable cases was mainly due to the small difference in the velocity profiles at the inlet (Fig. 4).

Fig. 7

Vertical profiles of laterally-averaged a mean velocity, and b normalized concentration measured at $x=16h$ for the line source S1

Figure 7b shows vertical profiles of laterally-averaged mean concentration at $x=16h$ for the line source S1 at various stratification levels. It is to be noted that dispersion from the line source is a quasi-two-dimensional problem where the plume is laterally homogeneous. Increasing stability yielded higher concentrations within the canopy and lower concentrations above it. These effects were found to be more pronounced as the inflow level of TKE was reduced. The increase in concentration with the streets also suggests a reduced vertical mixing at the canopy height.

Fig. 8

Vertical profiles of laterally-averaged, a streamwise, and b vertical turbulent stresses at $x=16h$

Figure 8a, b respectively shows vertical profiles of streamwise and vertical turbulent stresses laterally averaged over 60 points at $x=16h$. The effects of inflow TKE and thermal stability are clearly visible on both quantities. For $Ri=0.2$, 0.5, 0.7, 1, both the streamwise and the vertical stresses were found to be reduced within and above the canopy by increasing stability. For the cases $Ri=0.2$, 0.5, 0.7, 1, the differences approximately above $y/h=6h$ were negligible due to the same inflow turbulence conditions being imposed at the inlet. On the contrary, for the cases $Ri=0$ and $Ri=1^*$, the different turbulence conditions imposed at the inlet led to substantial differences in turbulent stresses at $x=16h$ above the height 6h compared to the other cases. The evident differences in the $Ri=0$, 1, and $1^*$ profiles demonstrate the importance of applying the correct inflow TKE for a chosen stability level.

We have also analyzed the laterally-averaged vertical profiles of lateral normal turbulent stress and turbulent shear stress at $x=16h$. Similarly to the profiles of streamwise and vertical turbulent stresses in Fig. 8, both the lateral normal turbulent stress and turbulent shear stress profiles showed no visible differences approximately above $y/h=6$ for $Ri=0.2$, 0.5, 0.7, 1, while within and immediately above the canopy increasing stability damped the lateral normal turbulent stress and turbulent shear stress. For the $Ri=1^*$ case, both the turbulent stresses were lower than those for $Ri=1$, due to the much lower TKE prescribed at the inlet, which was nearly zero above 4h.

5 Effects of Stability on the Internal Boundary Layer

The transition from the rough surface upstream of the array to the much higher roughness of the array itself causes an IBL to develop from the leading edge of the array. In neutral stratification conditions, the IBL increases in depth as it develops downstream over the array, and the flow within it has greater turbulence kinetic energy than that in the external boundary layer (e.g. Sessa et al. 2018). Given that an IBL develops at rural-to-urban transitions and affect the dispersion in urban areas, it is important to understand their characteristics and how these affect the dispersion of pollutants at various stability levels.

Fig. 9

Q-criterion contours at $z=-1.5h$ for various stratification conditions and same inflow turbulence conditions. $Ri=0.21$ (a), $Ri=0.5$ (b), $Ri=0.7$ (c), $Ri=1$ (d)

The Q criterion is useful for highlighting flow regions in which rotation is dominant over the shear, and is defined as

$$\begin{aligned} Q=0.5(\varOmega _{ij}\varOmega _{ij}-S_{ij}S_{ij}), \end{aligned}$$

(11)

where $\varOmega _{ij}=0.5(\frac{\partial u_i}{\partial x_j}-\frac{\partial u_j}{\partial x_i})$ and $S_{ij}=0.5(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})$. Figure 9 shows the results of Q-criterion analyses for $Ri=0.2$ (Fig. 9a), $Ri=0.5$ (Fig. 9b), $Ri=0.7$ (Fig. 9c), and $Ri=1$ (Fig. 9d) cases. The IBL in greater thermal stratification is shallower and of a lower growth rate compared to weaker thermal stratification. The Q-criterion analyses were repeated for several cross-sections in the lateral direction with similar results.

Fig. 10

Laterally-averaged wall-normal turbulent stress $\overline{v'v'}^+$ at a$x=6h$, and b$x=18h$

The method described in Sessa et al. (2018) was used to process the data from each lateral street downstream of the array leading edge to determine the height of the IBL interface for various stability cases (Fig. 10). This involves deriving laterally-averaged vertical profiles of dimensionless wall-normal turbulent stress $\overline{v'v'}^+$ above the canopy. It is easy to implement and provides a reasonable indication of the IBL development. Figure 10 shows vertical profiles of wall-normal turbulent stress immediately above the canopy, and evident discontinuities in these profiles. Linearly fitting these profiles to two straight lines yielded intersections (i.e. “knee” points). These were identified as the interface of the internal and external boundary layers, which was consistent with the Q-criterion analyses shown in Fig. 9. This approach is similar to the methods of Antonia and Luxton (1972) and Efros and Krogstad (2011). The vertical stress profiles in the external and internal boundary-layer regions were linearly fitted to a residual error of less than $2\%$ in all cases.

Figure 10 shows that for the case $Ri=1^*$ the wall-normal turbulent stress was much smaller than for the other cases. This was because less TKE was prescribed at the inlet. On the contrary, for the $Ri=0$ case, the wall-normal turbulent stress was greater than for the other stable cases because of the greater level of TKE defined at the inlet.

In Fig. 10a for $x=6h$ the intersection of the two straight lines shows the height of the IBL interface is approximately the same for all the LES cases. This is due to a strong recirculation bubble formed at the leading edge, whose size is relatively insensitive to the inflow turbulence and thermal stability. At $x=10h$, and farther downstream $x=14h$ and 18h (Fig.10b), the effects of thermal stability on the depth of the IBL are more evident and the IBL is found to be shallower as the stratification is increased from $Ri=0$ to $Ri=1$. These results confirm that increasing the thermal stratification damped the turbulence and mixing, and leads to a thinner IBL. It is to be noted that the local mean temperature gradient within the IBL is much greater than that above it (Fig. 3a), resulting in a greater local stratification effect on the turbulence and mixing in the IBL and a virtual step-change in normal Reynolds stress at the interface.

Figure 10a, b shows that under the same stratification, lower incoming turbulence (i.e. $Ri=1^*$) yields a shallower IBL compared to greater incoming turbulence (i.e. $Ri=1$). This suggests that an approaching boundary layer with lower turbulence intensity is more susceptible to the effect of local thermal stratification over an urban area. This is consistent with Williams et al. (2017) who found that the critical Richardson number for a rough wall is greater than for a smooth wall. This also emphasizes the importance of modelling the non-linear interaction between the incoming turbulence and locally generated turbulence in thermally stratified conditions.

Fig. 11

IBL height $\delta$ for different stratification conditions derived using the method of Sessa et al. (2018) based on vertical profiles of wall-normal turbulent stress $\overline{v'v'}^+$; $x_{LE}$ is the streamwise coordinate of the leading edge of the array

Figure 11 shows the IBL height $\delta$ for different stratification conditions derived by using the method of Sessa et al. (2018) based on vertical profiles of wall-normal turbulent stress $\overline{v'v'}^+$. It can be seen that the overall depth and growth rate of the IBL are sensitive to both the thermal stability and inflow turbulence conditions. Increasing stratification leads to a reduced IBL depth and a lower growth rate. A reduced TKE at the inlet ($Ri=1^*$) enhances these effects further compared to the case $Ri=1$. The depth of the IBL varies by up to $30\%$ within the studied range of thermal stratification conditions. Given that the present work has only considered weakly stably-stratified conditions, we conclude that both the depth of the IBL and the turbulence intensity below and above it following a change in surface roughness are significantly affected by even small changes in thermal stratification.

6 Pollutant Dispersion

The effects of stable stratification on pollutant dispersion are investigated by considering the emission of a passive scalar from a line source S1 (Fig. 1). This set-up is useful for studying the effect of stratification on scalar concentration and scalar fluxes. As the periodic boundary conditions are used in the lateral direction, dispersion from the line source is a quasi-two-dimensional problem, and the the scalar plume is considered laterally homogeneous.

6.1 Stability Effects on Scalar Fluxes

The total vertical flux $\psi ^{v*}_{tot}=\psi ^{v*}_{adv}+\psi ^{v*}_{turb}$ includes contributions from both advective (Eq. 12) and turbulent (Eq. 13) scalar fluxes. The advective and turbulent vertical concentration fluxes transport pollutants from the canopy flow to the boundary layer above. The dimensionless advective and turbulent vertical flux components are defined as follows (Fuka et al. 2018),

$$\begin{aligned} \psi ^{v*}_{adv}= & {} {\overline{V}}\,{\overline{C}}\frac{h^2}{Q}, \end{aligned}$$

(12)

$$\begin{aligned} \psi ^{v*}_{turb}= & {} \overline{v'c'^*}=({\overline{VC}}-{\overline{V}}\,{\overline{C}})\frac{h^2}{Q}, \end{aligned}$$

(13)

where $v'$ and $c'$ are the vertical velocity and concentration fluctuations respectively, and ${\overline{V}}$ and ${\overline{C}}$ are the mean vertical velocity and mean concentration respectively.

Similarly, the total streamwise flux in the streamwise direction is defined as follows,

$$\begin{aligned} \psi ^{u*}_{tot}=({\overline{U}}\,{\overline{C}}+\overline{u'c'})\frac{h^2}{Q}, \end{aligned}$$

(14)

where $u'$ is the streamwise velocity fluctuation, and ${\overline{U}}$ is the mean streamwise velocity component.

Fig. 12

Integrated a turbulent, and b advective vertical concentration flux over horizontal planes $2h\times 12h$ at $y=1h$, and at 7 streamwise locations in various stratification conditions for the line source S1

The vertical turbulent (Fig. 12a) and advective (Fig. 12b) concentration fluxes from the line source S1 are integrated at the canopy height $y=1h$ across the entire span 12h, between two x coordinates a and b separated by 2h,

$$\begin{aligned} \psi ^{a,b}=\int \int _{x/h\in (a,b), y/h=1}\psi ^{v*}\text{ d }\left( \frac{x}{h}\right) \text{ d }\left( \frac{z}{h}\right) . \end{aligned}$$

(15)

Large positive turbulent and advective fluxes are found over the first interval ($x=8.5h-10.5h$) because the horizontal plane is above the source street ($x=10h$). Further downstream, the turbulent and advective concentration flux components decrease significantly. Figure 12a, b shows that the turbulent flux is generally greater in magnitude than the advective flux.

Both the turbulent and the advective fluxes generally decrease as Ri is increased from 0.2 to 1.0, given the same turbulent inflow conditions. This confirms that increasing stratification reduces vertical transport of pollutant due to decreasing both the turbulent and advective scalar fluxes in the vertical direction. For $Ri=0$, because of higher TKE prescribed at the inlet, the general pattern is slightly different. For example, at the third downstream interval from the line source ($x=14.5h-16.5h$), the turbulent scalar flux (Fig. 12a) is found to be lower than that for $Ri=0.2$. This was due to higher TKE near the source, which yields greater vertical transport above the canopies than that for $Ri=0.2$. For $Ri=1^*$, the much lower TKE at the inlet causes significantly lower turbulent and advective scalar fluxes over the source street ($x=8.5h-10.5h$). As a result, the scalar plume for $Ri=1^*$ is strongly advected into the following lateral street ($x=10.5h-12.5h$), producing a so-called virtual secondary source. Figure 12a, b shows that over the first two lateral streets both the turbulent and advective scalar fluxes for $Ri=1^*$ have almost the same magnitude. This again confirms the existence of the virtual secondary source in the second street.

Fig. 13

Total streamwise flux over a$1h\times 12h$,  and b$2h\times 12h$, vertical planes at seven streamwise locations downstream for the line source S1

The streamwise total concentration flux (Eq. 14) of the line source S1 is integrated over vertical planes with dimensions ($1h\times 12h$) as shown in Fig. 13a and ($2h\times 12h$) as shown in Fig. 13b. The integration is performed between two constant y coordinates across the entire span. For example, at $x=10.5h$, the total flux is computed as follows,

$$\begin{aligned} \psi ^{a,b}=\int \int _{y/h\in (a,b), x/h=10.5}\psi ^{u*}\text{ d }\left( \frac{y}{h}\right) \text{ d }\left( \frac{z}{h}\right) . \end{aligned}$$

(16)

Figure 13a shows the amount of pollutant transported in the streamwise direction below the canopy top. Near the line source, approximately $60\%$ of the total emission Q for $Ri=0$ is transported in the streamwise direction while approximately $40\%$ of the emission Q is transported vertically through the horizontal plane above the source street. Further downstream, the amount of pollutant transported in the streamwise direction decreases less than $20\%$ of the total flux for $x\ge 20h$.

From $Ri=0.2$ to $Ri=1$ a similar amount of pollutant is transported downstream at $x=10.5h$ because the kinetic energy close to the source is similar in all cases. Away from the source, greater stability traps more pollutant within the canopy layer. In the range $Ri=0.2$ to $Ri=1$ the total concentration flux below the canopy increases by more than $50\%$ at $x/h=20$, which is five rows of blocks downstream from the line source. For the case $Ri=1^*$ with lower incoming TKE, the stratification effect is evidently stronger compared to the case $Ri=1$.

Figure 13b shows the amount of pollutant transported through the vertical plane below $y=2h$ in the streamwise direction. All of the profiles show a peak value at approximately $x=12.5h$. The vertical plane at $x=10.5h$ was very close to the line source at $x=10h$, where the gradient of total streamwise flux, and consequently the error in integrated total streamwise flux through the plane is greatest. This might explain why the integrated total streamwise flux at $x=10.5h$ shown in Fig. 13b is not 100%. Further downstream, the total streamwise flux through the vertical plane $y=0-2h$ increases monotonically as the stratification level increases for the same incoming turbulence intensity, confirming again that the spreading of the plume is evidently affected by the stability level. Furthermore, reducing incoming turbulence intensity results in an increase in total streamwise flux through the vertical plane $y=0-2h$ at the same stratification.

6.2 Stability Effects on Mean Concentration

As stated earlier in Sect. 6, within the LES model the dispersion from a ground-level constant line source can be considered to be laterally homogeneous, with spreading of the plume constrained in the lateral direction. The previous sections show that increasing Ri decreases the vertical scalar transport above the canopy and leads to higher concentrations close to the ground. In this section, we quantify these effects on mean concentration.

Fig. 14

Volume-averaged normalized mean concentration within lateral streets, from the ground to the canopy height $y=1h$. The lateral source street is defined at $x=9.5-10.5h$

The volume-averaged concentration is calculated within each lateral street up to the canopy height, starting from the source street, which is located between $x=9.5h$ and $x=10.5h$. Mean concentration from the line source S1 is normalized in accordance with Eq. 8, and averaged over a volume with dimensions $1h\times 1h\times 12h$ to give the volume-averaged concentration,

$$\begin{aligned} {<\overline{C^*}>}^{a,b}=\int _{x/h\in (a,b)} \int _{y/h\in (0,1)} \int _{z/h\in (-6,6)}\overline{C^*} \text{ d }\left( \frac{x}{h}\right) \text{ d }\left( \frac{y}{h}\right) \text{ d }\left( \frac{z}{h}\right) . \end{aligned}$$

(17)

Figure 14 shows that the volume-averaged concentration increases monotonically in all of the streets as the thermal stability is increased, and decreased with distance from the source at all stratification conditions. This is because increases stability suppresses turbulence, resulting in reduced vertical mixing within and above the canopy (see Fig. 10). Figure 14 also shows that the volume-averaged concentration is increased when a lower TKE is prescribed at the inlet in the case $Ri=1^*$ compared to that in the case $Ri=1$. This is consistent with a reduction in vertical scalar flux in the case $Ri=1^*$ compared to that in the case $Ri=1$ (Sect. 6.1).

Fig. 15

Increase in volume-averaged concentration $<\overline{C^*}>$ for cases at $Ri\ge 0.2$ compared to $Ri=0$ within lateral streets up to the canopy height

Figure 15 shows a monotonic increase in volume-averaged concentration within each lateral street for cases at $Ri\ge 0.2$ compared to that within the same street for case $Ri=0$. This again confirms the effect of increasing thermal stratification, and the lower TKE in the approaching flow for the $Ri=1^*$ case shows a 20% increase in volume-averaged concentration.

7 Discussion and Conclusions

We have rigorously examined the effects of various levels of weakly stable stratification ($0\le Ri\le 1$) on turbulence and dispersion over a rural-to-urban transition region using a high-fidelity large-eddy simulation (LES) approach. First, we validated the LES predictions against wind-tunnel measurements on a stratified boundary layer approaching a regular array of cuboid elements at $Ri = 0.21$. This showed that the LES with the synthetic inflow generation method was able to accurately predict mean velocities, turbulent stresses, mean concentration, and concentration fluctuations from a ground-level point source in weakly stratified flows over a rough-to-very-rough transition region.

A numerical sensitivity test was conducted to assess whether a small change of ground temperature upstream of the step change in roughness affected turbulence and dispersion further downstream. This was required to assess the potential impact of the non-negligible errors in measuring the ground temperature upstream of the step change in the experiments. We found that the effect of small changes to the ground temperature on the incoming heat flux were negligible, and speculated that this was because the mean streamwise velocity component was nearly zero in the vicinity of the ground. From this we conclude that the turbulence and dispersion downstream of the step change in roughness was insensitive to small changes of ground temperature upstream of the step change.

The transition from a rough surface to a much rougher surface composed of an array of regular cuboids generated an IBL from the leading edge of the array. The method developed in Sessa et al. (2018) was used to evaluate the depth of the IBL for the different stratification conditions simulated (i.e. $0\le Ri\le 1$) and different inflow TKE. We found that the IBL became shallower as the thermal stratification was increased. The greater local vertical temperature gradient within the IBL than in the external boundary layer led to a greater local stratification effect within the IBL, and consequently an evident step change of the normal Reynolds stress at the interface of the IBL.

When the level of TKE was reduced in the approaching flow for the same stratification condition, we found that the IBL height was reduced. This suggests that an approaching boundary layer with a smaller turbulence intensity is more susceptible to the effect of local thermal stratification over an urban area. This also indicates the importance of accurately modelling the non-linear interaction between the incoming turbulence and locally generated turbulence in thermal stratification.

The dispersion and scalar fluxes from a ground-level line source placed behind the fifth row of elements downstream of the leading edge were analyzed extensively in various stratification conditions ($0\le Ri\le 1$). The total vertical flux decreased above the lateral streets whereas the horizontal total flux increased within the lateral streets as the thermal stratification was increased. This led to larger volume-averaged concentrations within streets with increasing stratification. We conclude that if the TKE in the approaching boundary layer is reduced while maintaining the same level of thermal stratification, the effect on the total vertical scalar fluxes at the canopy height, and on the volume-averaged mean concentration within the streets, is greater.

Overall, we conclude that even weakly stable stratification ($0\le Ri\le 1$) in a boundary layer approaching a simulated rural-to-urban transition significantly changes the concentration levels that result from material dispersing from point or line sources within the urban array. This is because of the suppression of the turbulence in the IBL, and of the reduced vertical transport of pollutant above the canopy.