Large-Eddy Simulation of Neutrally-Stratified Turbulent Flow Within and Above Plant Canopy Using the Central-Moments-Based Lattice Boltzmann Method

Abstract

A central-moments-based lattice Boltzmann model for large-eddy simulation of neutrally-stratified turbulent flows is described. Through comparative simulations of the airflow within and above a homogeneous plant canopy, the performance of the model is evaluated with respect to a conventional large-eddy-simulation model based on the incompressible Navier–Stokes equations. Simulated turbulence statistics, such as the mean velocity, velocity variances, velocity skewness, and power spectra, are shown to be almost identical between the two models. The spatial structure of coherent eddies and their maintenance processes are also confirmed to be properly represented by the lattice Boltzmann method through analysis of the turbulence kinetic energy budget and spatial two-point correlation functions. Using the simulated results, the energetics of the streamwise-elongated streaky structures commonly observed over vegetation and urban canopies are examined. While the short-wavelength components of the shear-generated streamwise kinetic energy are redirected rapidly by pressure to the lateral and vertical velocity components, long-wavelength energy tends to remain in the streamwise velocity component, which is dissipated in relatively slower processes. Consequently, the streaky structures persist in the streamwise velocity component.

1 Introduction

The exchange of momentum, heat, water vapour, carbon dioxide and other gasses, and particles between vegetation and the atmosphere, is one of the main processes in land–atmosphere interactions. Turbulent eddies promote vegetation–atmosphere exchange by transferring these quantities through the plant canopy layer, in which individual sources and sinks are spatially distributed below plant height, to and from the roughness sublayer above the canopy.

In neutrally-stratified conditions, turbulence both in the roughness sublayer and in the canopy layer originally stems from strong mean shear, which is the consequence of the reduction of wind speed in the canopy layer due to the drag force exerted by canopy elements. Turbulence kinetic energy (TKE) produced near the canopy top is then transported by eddies into the canopy layer, where it is dissipated substantially in the wake of canopy elements (Raupach and Thom 1981). The spatial length scale of most energetic shear-generated eddies is typically a few times larger than the canopy height (Raupach et al. 1996). These phenomenological characteristics explain a number of well-documented features of canopy turbulence that differ from those of ordinary boundary-layer turbulence. Such features include large values of skewness in the streamwise and vertical velocity components, which are consistent with the dominance of sweep motions near the canopy top, velocity flatness factors that greatly exceed the Gaussian value, the marked contribution of vertical transport in the budgets of second-order moments, and counter-gradient flux phenomena, indicating the inadequacy of the local gradient-diffusion model for representing the fluxes of momentum and scalars in the canopy layer (Shaw 1977; Wilson and Shaw 1977; Raupach and Thom 1981; Denmead and Bradley 1985; Watanabe 1993; Raupach et al. 1996; Katul et al. 2013). All these features are consistent with the fact that tall, coherent eddies make essential contributions to the vertical fluxes (Denmead and Bradley 1985; Bergstöm and Högström 1989; Gao et al. 1989), and constitute the majority of turbulent structures within and above the canopy layer (Shaw et al. 1995; Finnigan and Shaw 2000).

In addition to field observations, flume or wind-tunnel experiments, and theoretical considerations, numerical analysis using large-eddy simulation (LES) has received increasing attention in the previous three decades. Since Shaw and Schumann (1992) and Kanda and Hino (1994) first conducted LES investigations of turbulent flows within and above plant canopies, many other authors have published reports on numerical analyses of canopy turbulence in homogeneous plant canopies (e.g., Dwyer et al. 1997; Shen and Leclerc 1997; Su et al. 1998; Patton et al. 1998; Fitzmaurice et al. 2004; Watanabe 2004, 2009; Yue et al. 2007; Finnigan et al. 2009; Shaw et al. 2013), heterogeneous plant canopies (Dupont and Brunet 2009; Bohrer et al. 2009), and a homogeneous plant canopy under the influence of convective motions in the atmospheric boundary layer (Patton et al. 2016). The LES approach has also been applied to urban canopies in pioneering work by Kanda et al. (2004), Kanda (2006), and Coceal et al. (2006), followed by Inagaki et al. (2012) and others, and LES is now established as an indispensable tool for investigation of the nature of canopy turbulence.

The LES models used in previous studies have generally been based on the Navier–Stokes equations and the incompressible continuity equation, which is indeed the most orthodox method in computational fluid dynamics. As these equations directly express macroscopic conservation laws, it is straightforward to compile simulation code that conserves momentum and mass. Kinetic energy can also be conserved if the non-linear advection terms are treated properly. Therefore, such models are superior in terms of property conservation, which is desirable for the reliable simulation of turbulence.

The lattice Boltzmann method (hereafter, the "Boltzmann approach") is a recently advanced method of computational fluid dynamics (e.g., Chen and Doolen 1998; Aidum and Clausen 2010), which, instead of considering macroscopic velocities and density, describes fluid motions by the spatiotemporal variations of the discrete velocity-distribution function of microscopic fluid particles (Krüger et al. 2017). In an Eulerian framework, the temporal evolution of the distribution function at a given node in a regular grid (lattice) system is governed by the discretized Boltzmann equation, which incorporates particle streaming, collision, and forcing processes as the key physics. Macroscopic variables (velocities and density) are evaluated as low-order moments of the distribution function. It can be shown mathematically that the derived macroscopic variables satisfy the weakly compressible Navier–Stokes equations within the limit of a low Mach number (Chen and Doolen 1998; Krüger et al. 2017). The lattice Boltzmann method has several advantages over the incompressible Navier–Stokes models. Solving the Poisson equation is not necessary for evaluation of the pressure, which is calculated simply from an equation of state, i.e., pressure is related linearly to density in an isothermal condition. Advection of macroscopic variables can be simulated with high accuracy because the streaming process in the method is expressed exactly as a translation of the distribution function during one timestep to a neighbouring grid point in the direction of the prescribed constant microscopic velocities. Collision and forcing processes are expressed in a local manner, in which reference is only to a set of variables defined at a single grid point. With these features, together with its simple algorithm and the ease of implementing boundary conditions, the lattice Boltzmann method is feasible for application to high-resolution simulations of atmospheric-boundary-layer flows using advanced parallel-processing machines.

Application of the lattice Boltzmann method to the atmospheric-boundary-layer flow was initiated only recently. Onodera et al. (2013) compiled a LES code by incorporating an eddy-viscosity model (Kobayashi 2005) into a lattice Boltzmann algorithm, and conducted a precise numerical simulation of airflow within and above an actual urban canopy. Through using a massively parallelized supercomputer, the authors simulated the detailed wind field at 1-m resolution over individual buildings in an area of approximately 10 km × 10 km in the city of Tokyo, Japan. Ahmad et al. (2017) and Inagaki et al. (2017) used the same code to perform simulations of the spatial development of a neutral boundary layer over an actual urban geometry near Tokyo with 2-m resolution in a domain of 19.2 × 4.8 × 1.0 km³. The latter simulation allowed the authors to conduct simultaneous analysis of the aerodynamic properties both of boundary-layer-scale eddies and of gusty motions in street canyons. These studies demonstrated the potential of the lattice Boltzmann approach to be a powerful tool for simulations of turbulent flows in the atmospheric boundary layer.

This paper describes the development of a new LES code based on the lattice Boltzmann method for the simulation of canopy turbulence in neutrally-stratified conditions, presents the validation of the code with respect to a conventional LES model based on the Navier–Stokes equations, and briefly discusses the maintenance process of the large-scale eddies that dominate canopy turbulence.

2 Model Description

We adopt a Cartesian coordinate system in which $x$ denotes the streamwise direction, $y$ represents the lateral direction, and $z$ represents the vertical direction. Velocity components in these three directions are $u$, $v$, and $w$, respectively. Tensor notation such as (${x}_{1}$, ${x}_{2}$, ${x}_{3}$) = ($x$, $y$, $z$) and (${u}_{1}$, ${u}_{2}$, ${u}_{3}$) = ($u$, $v$, $w$) is also used.

2.1 Navier–Stokes-Based Model

A LES model described by Watanabe (2004, 2009) is used for the reference simulation, and is based on the Navier–Stokes equations and the incompressible continuity equation. The subgrid-scale (SGS) TKE is modelled using a separate prognostic equation. The SGS TKE is used to model the eddy viscosity, which relates the strain-rate tensor of resolved velocities to the SGS momentum fluxes. Horizontal derivatives are represented by a pseudo-spectral method with the 2/3 dealiasing rule, while a fourth-order Padé scheme is adopted for vertical differencing. Time advancement is performed by the third-order Runge–Kutta scheme. At each step in the Runge–Kutta scheme, the Poisson equation for pressure is solved in Fourier space to satisfy the constraint of incompressible continuity. The plant canopy is modelled as homogeneously distributed sinks for momentum and SGS TKE. The instantaneous sink strengths are described by the plant area density, an isotropic drag coefficient, and the resolved velocity components. The numerical set-up for the reference simulation is the same as that of the lattice Boltzmann method (described later), except that the exact value of the external driving force is different and a longer streamwise domain (1500, 400, and 81 nodes in the streamwise, lateral, and vertical directions, respectively) is adopted because this simulation is conducted for the further purpose of inspecting the longest streamwise modes of the velocity fluctuations. However, an appropriate normalization described in Sect. 3 enables a proper comparison of turbulence statistics presented here. The influence of the domain size is reported elsewhere (Watanabe 2004, 2009).

2.2 Lattice Boltzmann Method

General and detailed descriptions of the lattice Boltzmann method can be found in published reviews (e.g., Chen and Doolen 1998; Aidum and Clausen 2010), textbooks (e.g., Mohamad 2011; Krüger et al. 2017), and references therein. Only the essence adequate for reproducing the present model is given here.

The basic structure of our lattice Boltzmann method is a three-dimensional 27-velocity (D3Q27) lattice model, which is considered suitable for simulations of high Reynolds number flows in terms of numerical stability and accuracy (Suga et al. 2015). In this model, the distribution functions ${f}_{ijk}\left(x,y,z,t\right)$ at position $\mathbf{x}$ and time $t$ of discrete microscopic velocities $\left(ic,jc,kc\right)$ are considered. The indices $i,j,k\in \left\{-{1,0},1\right\}$ represent the direction of the discretized velocities (thus 27 velocities in total), and $c=\Delta x/\Delta t$ is the lattice velocity unit defined with lattice spacing $\Delta x$ and timestep $\Delta t$. The main part of the lattice Boltzmann algorithm consists of three steps: collision, forcing, and streaming. The collision step represents the tendency of distribution functions towards equilibrium (with respect to macroscopic velocities and density) due to collisions between particles. The forcing step calculates temporal variations of distribution functions induced by external and internal forces. The streaming step describes the translation of fluid particles in the direction of the discrete microscopic velocities. The equations involved in each step are shown below. Following the convention in the literature, the equations are written using the lattice-unit system in which all variables are normalized, such that $\Delta x=\Delta t=c=1$ should result and the mean fluid density should be equal to unity. Therefore, the differences $\Delta x$ and $\Delta t$ are eliminated from most of the following equations for brevity.

The collision process is modelled using a central-moment-based multi-relaxation-time model (Geier et al. 2006, 2015; Premnath and Banerjee 2009, 2011), which is known to have higher numerical accuracy and stability compared with more commonly used single-relaxation-time models and other multi-relaxation-time models based on raw moments (Geier et al. 2015). A cumulant-based multi-relaxation-time model (Geier et al. 2015; 2017) is another possible candidate if a few more computations can be devoted for the collision step. The central moments of the distribution function, ${\kappa }_{pqr}$, are defined as

$${\kappa }_{pqr}\left({\varvec{x}},{\varvec{t}}\right)=\sum_{i=-1}^{1}\sum_{j=-1}^{1}\sum_{k=-1}^{1}{\left(ic-u\right)}^{p}{\left(jc-v\right)}^{q}{\left(kc-w\right)}^{r}{f}_{ijk}\left({\varvec{x}},{{t}}\right),$$

(1)

where the indices $p,q,r\in \left\{{0,1},2\right\}$ are the directional orders of moment, and the sum of the indices ($p+q+r$) defines the formal order of moment (e.g., ${\kappa }_{200}$, ${\kappa }_{110}$, and other moments with permutated indices are of the second order).

In the lattice Boltzmann algorithm, the distribution functions and the macroscopic variables (density, velocities, and pressure) are updated through the following procedure. At every timestep, the distribution functions are transformed by Eq. 1 into the central-moment space, where the collision and forcing steps proceed as

$${\kappa }_{pqr}^{*}\left(\mathbf{x},t\right)={\kappa }_{pqr}\left(\mathbf{x},t\right)+{\Omega }_{pqr}^{\upkappa }\left(\mathbf{x},t\right)+{S}_{pqr}^{\upkappa }\left(\mathbf{x},t\right).$$

(2)

Here, the asterisk indicates the state after the collision and forcing steps (hereafter, the “post-collision state”), and ${\Omega }_{pqr}^{\upkappa }$ and ${S}_{pqr}^{\upkappa }$ respectively denote the collision and forcing terms described later. The post-collision central moments are then transformed back to the distribution function space by

$${\mathbf{f}}^{*}\left(\mathbf{x},t\right)={C}^{-1}{{\varvec{\upkappa}}}^{*}\left(\mathbf{x},t\right),$$

(3)

where ${C}^{-1}$ represents the inverse transform of Eq. 1. In the streaming step, the post-collision distribution functions are translated to adjacent grid points as

$${f}_{ijk}\left(x+ic\Delta t, y+jc\Delta t,z+kc\Delta t,t+\Delta t\right)={f}_{ijk}^{*}\left(x, y,z,t\right).$$

(4)

After the streaming step, which is followed by application of appropriate boundary conditions, the macroscopic variables at the next timestep are calculated from the low-order raw moments of the distribution function as

$$\rho =\sum_{i=-1}^{1}\sum_{j=-1}^{1}\sum_{k=-1}^{1}{f}_{ijk},$$

(5)

$$\rho u=\sum_{i=-1}^{1}\sum_{j=-1}^{1}\sum_{k=-1}^{1}{\left(ic\right)f}_{ijk}+{F}_{x}/2,$$

(6a)

$$\rho v=\sum_{i=-1}^{1}\sum_{j=-1}^{1}\sum_{k=-1}^{1}\left(jc\right){f}_{ijk}+{F}_{y}/2,$$

(6b)

$$\rho w=\sum_{i=-1}^{1}\sum_{j=-1}^{1}\sum_{k=-1}^{1}\left(kc\right){f}_{ijk}+{F}_{z}/2,$$

(6c)

$$p=\rho /3,$$

(7)

where $p$ is the macroscopic static pressure.

As explained, the collision step describes the tendency of the velocity distribution towards equilibrium. The continuous Maxwell–Boltzmann distribution ${f}^{{\rm M}}$ defined as

$${f}^{{\rm M}}\left(\rho ,\mathbf{u},{\varvec{\upxi}}\right)=\rho {\left(\frac{3}{2\pi }\right)}^{3/2}{{\rm exp}}\left[-\frac{3{\left|{\varvec{\upxi}}-\mathbf{u}\right|}^{2}}{2}\right],$$

(8)

where ${\varvec{\upxi}}=\left({\xi }_{{x}},{\xi }_{{y}},{\xi }_{{z}}\right)$ denotes the microscopic particle velocity, is adopted as the equilibrium distribution to which the velocity distribution is relaxed. The continuous central moments of the equilibrium distribution, ${\kappa }_{pqr}^{{\rm eq}}$, are defined as

$${\kappa }_{pqr}^{{\rm eq}}=\underset{-\infty }{\overset{+\infty }{\iiint }}{\left({\xi }_{{x}}-u\right)}^{p}{\left({\xi }_{{y}}-v\right)}^{q}{\left({\xi }_{{z}}-w\right)}^{r}{f}^{{\rm M}}{\rm d}{\xi }_{{x}}{\rm d}{\xi }_{{y}}{\rm d}{\xi }_{{z}},$$

(9)

and are shown analytically to have non-zero values only for the moments for which the directional orders (p, q, r) are all even (Geier et al. 2006; Premnath and Banerjee 2011), i.e.,

$$ \begin{aligned} & \kappa_{000}^{{{{\rm eq}}}} = \rho , \\ & \kappa_{200}^{{{{\rm eq}}}} = \kappa_{020}^{{{{\rm eq}}}} = \kappa_{002}^{{{{\rm eq}}}} = \rho /3, \\ & \kappa_{220}^{{{{\rm eq}}}} = \kappa_{022}^{{{{\rm eq}}}} = \kappa_{202}^{{{{\rm eq}}}} = \rho /9, \\ & \kappa_{222}^{{{{\rm eq}}}} = \rho /27. \\ \end{aligned} $$

(10)

The forcing processes are also considered in the central-moment space. Defining $\mathbf{F}=\left({F}_{\mathbf{x}},\boldsymbol{ }{F}_{\mathbf{y}},\boldsymbol{ }{F}_{\mathbf{z}}\right)$ as a force vector, the temporal rate of the distribution function attributable to that force can be approximated as

$$\Delta f/\Delta t=(3/\rho) \left[\left({\xi }_{x}-u\right){F}_{{x}}+\left({\xi }_{y}-v\right){F}_{{y}}+\left({\xi }_{z}-w\right){F}_{{z}}\right]{f}^{{\rm M}},$$

(11)

based on the assumption that the particle-velocity distribution is generally near the equilibrium state represented by the Maxwell–Boltzmann distribution (He et al. 1998b; Premnath and Banerjee 2009). The forcing term ${S}_{pqr}^{\upkappa }$ is given the continuous central moments of Eq. 11, which can also be derived analytically and the non-zero values are written as

$$ \begin{aligned} & S_{100}^{{\upkappa }} = F_{{{x}}} ,\quad S_{010}^{{\upkappa }} = F_{{{y}}} ,\quad S_{001}^{{\upkappa }} = F_{{{z}}} , \\ & S_{120}^{{\upkappa }} = S_{102}^{{\upkappa }} = F_{x} /3, \\ & S_{210}^{{\upkappa }} = S_{012}^{{\upkappa }} = F_{y} /3, \\ & S_{021}^{{\upkappa }} = S_{201}^{{\upkappa }} = F_{z} /3, \\ & S_{122}^{{\upkappa }} = F_{x} /9,\quad S_{212}^{{\upkappa }} = F_{y} /9,\quad S_{221}^{{\upkappa }} = F_{z} /9. \\ \end{aligned} $$

(12)

Using these expressions, the collision term is basically modelled as

$${\Omega }_{pqr}^{\upkappa }=-{\omega }_{pqr}\left({\kappa }_{pqr}+\frac{1}{2}{S}_{pqr}^{\upkappa }-{\kappa }_{pqr}^{{\rm eq}}\right),$$

(13)

where ${\omega }_{pqr}$ denotes the collisional relaxation coefficients for the individual moments. Equation 13 represents that the central moments after the half forcing is relaxed towards the equilibrium moments ${\kappa }_{pqr}^{{\rm eq}}$, which are associated with the macroscopic density and velocities (Eqs. 8 and 9) that are also affected by the same amount of forcing, as implied by Eq. 6. By adopting this representation, the overall numerical accuracy can be maintained at the second order in both space and time (Guo et al. 2002; Krüger et al. 2017). However, as applying Eq. 13 independently to each of the moments may break the rotational invariance, some moments are linearly combined and classified into 10 groups for which the same relaxation coefficients (${\omega }_{1}, {\omega }_{2},\dots , {\omega }_{10}$) are assigned (Geier et al. 2015). The equations actually implemented for the calculation of the post-collision moments are fully described in Appendix.

2.3 Subgrid-Scale Viscosity and Relaxation Coefficients

The macroscopic velocities predicted by the lattice Boltzmann method are defined at discrete nodes of the lattice system and therefore correspond to the resolved-scale components. The SGS stress is modelled by the eddy-viscosity model as

$${\tau }_{\alpha \beta }=-{\upsilon }_{{\rm SGS}}\left(\frac{\partial {u}_{\alpha }}{\partial {x}_{\beta }}+\frac{\partial {u}_{\beta }}{\partial {x}_{\alpha }}\right)+\frac{2}{3}{k}_{{\rm SGS}}{\delta }_{\alpha \beta },$$

(14)

where $\alpha$ and $\beta$ are indices for spatial coordinates, ${\tau }_{\alpha \beta }$ is the SGS stress, ${\upsilon }_{{\rm SGS}}$ is the SGS eddy viscosity, ${k}_{{\rm SGS}}$ is the SGS kinetic energy, and ${\delta }_{\alpha \beta }$ is the Kronecker delta. A Smagorinsky-type parametrization is used for the subgrid eddy viscosity,

$${\upsilon }_{{\rm SGS}}={C}_{{\rm SGS}}{\Delta }^{2}\sqrt{2{S}_{\alpha \beta }{S}_{\alpha \beta }},$$

(15)

where ${C}_{{\rm SGS}}$ is a parameter that depends on time and space, Δ is the grid spacing, and ${S}_{\alpha \beta }$ is the resolved strain-rate tensor; the repetition of indices implies summation over all three components unless otherwise stated. The strain-rate tensor in Eq. 15 is evaluated using local information (Eqs. 48 and 49 in Appendix) rather than finite differences that refer to the macroscopic velocities at neighbouring grid points. In accordance with the coherent-structure Smagorinsky model proposed by Kobayashi (2005), the parameter ${C}_{{\rm SGS}}$ is evaluated by

$${C}_{{\rm SGS}}={C}_{1}{\left|\frac{Q}{E}\right|}^{3/2},$$

(16)

where C₁ = $\sqrt{3}/20$ is a model parameter optimized to reproduce the velocity spectra well above the canopy in preliminary simulations, Q is the second invariant of the velocity gradient tensor, and E is the magnitude of the velocity gradient tensor,

$$Q=\frac{1}{2}\left({W}_{\alpha \beta }{W}_{\alpha \beta }-{S}_{\alpha \beta }{S}_{\alpha \beta }\right),$$

(17)

$$E=\frac{1}{2}\left({W}_{\alpha \beta }{W}_{\alpha \beta }+{S}_{\alpha \beta }{S}_{\alpha \beta }\right),$$

(18)

with ${W}_{\alpha \beta }$ being the resolved vorticity tensor. Only for the evaluation of the tensors $Q$ and $E$ in these equations are the velocity gradients estimated using the second-order centred difference. As the value of ${C}_{{\rm SGS}}$ given by Eq. 16 automatically vanishes on a solid wall (Kobayashi 2005), wall-damping functions are not introduced.

In the framework of the lattice Boltzmann approach, the SGS eddy viscosity is incorporated into the relaxation coefficient ${\omega }_{1}$ for a group of the second-order moments (see Appendix) as (Aidum and Clausen 2010)

$$\upsilon +{\upsilon }_{{\rm SGS}}= \frac{1}{3}\left(\frac{1} {{\omega }_{1}}-\frac{1} {2}\right),$$

(19)

where $\upsilon$ is the kinematic shear viscosity. Relaxation coefficients for other groups of the moments are practically free parameters in the range of $0<\omega <2$, because they do not appear in the Navier–Stokes equations recovered from the lattice Boltzmann equations (see below) and thus have no primary influence on the simulated velocity fields. The values used here are ${\omega }_{2}={\omega }_{6}={\omega }_{7}={\omega }_{8}={\omega }_{10}={\omega }_{1}$ and ${\omega }_{3}={\omega }_{4}={\omega }_{5}={\omega }_{9}=1$, which are determined through preliminary simulations to achieve suitable numerical stability as simple as possible. It should be noted that, although the parameter $\upsilon$ is included in Eq. 19 for generality, the effect of shear viscosity is negligible in the present simulation of a well-developed turbulent flow with a Reynolds number of Re ~ 10⁵ (based on the canopy height and the friction velocity defined later).

To account correctly for the second term on the right-hand side of Eq. 14, the SGS kinetic energy ${k}_{{\rm SGS}}$ must be evaluated. Following Inagaki et al. (2010) and Suga et al. (2015), the value of ${k}_{{\rm SGS}}$ is estimated by

$${k}_{{\rm SGS}}=\rho {c}_{{k}}\sum_{\alpha =1}^{3}{\left({u}_{\alpha }-\langle {u}_{\alpha }\rangle \right)}^{2},$$

(20)

where ${c}_{{k}}$ (= 1) is a model constant and $\langle {u}_{\alpha }\rangle$ is a filtered velocity component given by

$$\langle {u}_{\alpha }\rangle =\frac{1}{12}\left({u}_{\alpha }^{{\rm B}}+{u}_{\alpha }^{{\rm S}}+{u}_{\alpha }^{{\rm W}}+{6u}_{\alpha }+{u}_{\alpha }^{{\rm E}}+{u}_{\alpha }^{{\rm N}}+{u}_{\alpha }^{{\rm T}}\right),$$

(21)

in which ${u}_{\alpha }^{{\rm B}}, {u}_{\alpha }^{{\rm S}},\dots$ denote velocities at the six surrounding grid points. By adding the term $-\left(2/3\right)\partial {k}_{{\rm SGS}}/\partial {x}_{\alpha }$ to all the force components (${F}_{\alpha }$) in the above equations, the effects of the normal components of the SGS stress are included properly.

With these parametrizations, the present lattice Boltzmann model predicts the macroscopic density and velocities that satisfy the filtered continuity equation,

$$\frac{\partial \rho }{\partial t}+\frac{\partial \rho {u}_{\alpha }}{\partial {x}_{\alpha }}=0,$$

(22)

and the filtered Navier–Stokes equations,

$$\frac{\partial \rho {u}_{\alpha }}{\partial t}+\frac{\partial \rho {u}_{\alpha }{u}_{\beta }}{\partial {x}_{\beta }}=-\frac{\partial p}{\partial {x}_{\alpha }}+\frac{\partial }{\partial {x}_{\beta }}\left[\rho \left(\upsilon +{\upsilon }_{{\rm SGS}}\right)\left(\frac{\partial {u}_{\alpha }}{\partial {x}_{\beta }}+\frac{\partial {u}_{\beta }}{\partial {x}_{\alpha }}\right)-\frac{2}{3}{k}_{{\rm SGS}}{\delta }_{\alpha \beta }\right]+{F}_{\alpha }.$$

(23)

2.4 Set-Up for the Canopy-Turbulence Simulation

The lattice Boltzmann simulation is performed for a turbulent flow within and above a homogeneous plant canopy in a computational domain of 1024, 512, and 80 nodes in the streamwise, lateral, and vertical directions, respectively. The lowest 10 nodes comprise the canopy layer, in which the effect of plant elements is considered a spatially distributed momentum sink. The grid spacing therefore corresponds to 0.1 $h$, with $h$ being the canopy height.

The airflow in the computational domain is driven by a streamwise external force ${F}^{{\rm ext}}$, which is fixed constant at ${F}^{{\rm ext}}/\left(\rho \Delta x/{\left(\Delta t\right)}^{2}\right)={10}^{-7}$. Horizontal boundaries are periodic, while the top boundary is a rigid free-slip wall. The bottom boundary (i.e., the ground surface) is a rigid wall with friction that is represented by including an instantaneous frictional force in the horizontal force terms at the lowest fluid nodes. The rigid (and free-slip) boundaries are represented by means of halfway specular reflection, in which particle-velocity components that move inwards from the wall are given by

$${f}_{ij\overline{k}}\left(x,y,{z}_{{\rm b}},t+\Delta t\right)={f}_{ij{k}^{^{\prime}}}^{*}\left(x-ic,y-jc,{z}_{{\rm b}},t\right),$$

(24)

where ${z}_{{\rm b}}$ is the height of the highest or lowest fluid node, and $\overline{k}$ denotes an inwards direction opposite to the direction towards the wall (${k}^{^{\prime}}$). This implies that the actual wall boundaries are located one-half grid spacing beyond the highest or lowest fluid node (Lallemand and Luo 2003); all variables ($f$, $u$, $v$, $w$,$\rho$, $p$) are collocated at each grid node.

The instantaneous drag force exerted by the plant elements is conventionally modelled using a product of the leaf area density $a$, isotropic drag coefficient ${c}_{{\rm d}}$, and instantaneous macroscopic velocity $\mathbf{u}$ as

$${\mathbf{F}}_{{\rm d}}=-\rho {c}_{{\rm d}}a\left|\mathbf{u}\right|\mathbf{u}.$$

(25)

These canopy parameters are given as $ah=2$ (i.e., the leaf area index LAI = 2) and ${c}_{{\rm d}}=0.2$. Similarly, the frictional force of the underlying ground is given by the bulk relation,

$${\mathbf{F}}_{{\rm g}}=-\rho {C}_{{\rm M}}\left|{\mathbf{u}}_{{\rm b}}\right|{\mathbf{u}}_{{\rm b}},$$

(26)

where ${C}_{{\rm M}}$ is the bulk transfer coefficient of momentum and ${\mathbf{u}}_{{\rm b}}$ is the instantaneous macroscopic velocity at the lowest nodes. The coefficient ${C}_{{\rm M}}$ is calculated assuming a logarithmic wind profile with a prescribed aerodynamic roughness length ${z}_{0{\rm g}}$, which is prescribed as ${z}_{0{\rm g}}/h={10}^{-3}$ throughout the bottom boundary. The drag force depends on the square of the macroscopic velocity (Eq. 25). However, as the definition of macroscopic velocity includes the drag force (Eq. 6), the macroscopic velocity is evaluated as a solution of the resulting quadratic equation (Guo and Zhao 2002),

$$\mathbf{u}=\frac{{\mathbf{u}}_{0}}{\frac{1}{2}+\sqrt{\frac{1}{4}+\frac{1}{2}{c}_{{\rm d}}a|{\mathbf{u}}_{0}|}},$$

(27)

where ${\mathbf{u}}_{0}$ denotes the macroscopic velocity calculated without the drag force from Eq. 6. At the lowest nodes, ${c}_{{\rm d}}a$ in the above equation is replaced by $\left({c}_{{\rm d}}a+ {C}_{{\rm M}}\right)$ to account for the frictional force of the ground.

Each simulation is initialized with a uniform streamwise velocity component with a small amount of random perturbations in the vertical velocity component and the distribution functions that represent equilibrium to the given velocities. After the turbulence statistics reach a steady state, three-dimensional data of the macroscopic variables and the distribution functions are collected at a constant time interval of 0.66 $h/{u}_{*}$. In total, 450 samples are used for the analysis described in the next section.

2.5 Implementation of the Lattice Boltzmann Method

In the actual implementation, the distribution functions pre-conditioned by subtracting constant values are used as suggested by Geier et al. (2015, 2017) to minimize round-off errors. Moreover, the corresponding transformations to/from the central-moment space are performed using a factorized fast procedure described by Geier et al. (2017). The model, coded using the Compute Unified Device Architecture (CUDA) C language, runs on a desktop PC (CPU: Intel Core i7-4790K) equipped with a graphics processing unit (NVIDIA Quadro GV100). Double-precision (64 bit) arithmetic is used. As suggested by Rinaldi et al. (2012) and Delbosc et al. (2014), a streaming–collision combined kernel is adopted to reduce the number of accesses to the global memory and thereby to improve overall computational efficiency.

3 Results and Discussions

The results are presented non-dimensionalized using the friction velocity ${u}_{*}$ and canopy height $h$. In a horizontally homogeneous steady airflow driven by a constant volumetric force, the mean shear stress above the canopy should decrease linearly with height to zero at the free-slip top boundary. The shear stress at the canopy top ${\tau }_{{\rm h}}$ can be predicted theoretically as

$${\tau }_{{\rm h}}={F}^{{\rm ext}}\left({z}_{{\rm top}}-h\right),$$

(28)

where ${z}_{{\rm top}}$ is the top-boundary height ($=8h$). The friction velocity in the present simulations is therefore defined by ${u}_{*}=\sqrt{{\tau }_{{\rm h}}/\rho }$. In what follows, an overbar ($\overline{\phantom{x}}$) denotes a mean value obtained by averaging over horizontal planes at a given height in all samples, while a prime (${^{\prime}}$) indicates deviations from the mean.

3.1 One-Dimensional Profile

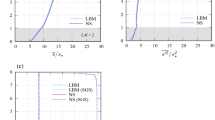
Vertical profiles of the mean wind speed, turbulent momentum flux, resolved velocity variances, and resolved velocity skewness are shown in Fig. 1. The mean wind speed decreases exponentially with depth into the canopy and increases near-logarithmically with height above the canopy. An inflection point of the profile is thus located near the canopy top. As expected, the magnitude of the vertical momentum flux decreases linearly with height above the canopy, while it decreases quickly within the canopy because of the existence of a momentum sink. Velocity variances have maxima at $z/h=$ 1.2–1.8 and their relative magnitudes are $\overline{u^{\prime}u^{\prime}} > \overline{v^{\prime}v^{\prime}} > \overline{w^{\prime}w^{\prime}}$. Velocity skewness in the canopy layer is positive for the streamwise velocity component and negative for the vertical velocity component, and the signs become reversed at a distance well above the canopy. The skewness of the lateral velocity component is essentially zero at all heights. All these characteristics share common well-known features of turbulent flows within and above plant canopies (Kaimal and Finnigan 1994; Raupach et al. 1996). While the profiles for these quantities are similar to those from the Navier–Stokes model, a remarkable difference can be seen in Fig. 1c, in which the Navier–Stokes $\overline{u{^{\prime}}u{^{\prime}}}$ profile exhibits an oscillation near the canopy top. Because of the stepwise change given in the leaf area density, the velocity varies sharply across the canopy top. In such a circumstance, vertical advection near the canopy top is approximated less accurately by the finite-difference method adopted in this Navier–Stokes model (Watanabe 2004, 2009) and dispersive errors grow around this point; a similar result was found by Ouwersloot et al. (2017). To reduce such errors, a higher-order less dispersive scheme must be used. Conversely, streaming of the distribution functions in the lattice Boltzmann method is always performed by an exact upstream scheme with a Courant number of unity (Eq. 4), which enables the model to simulate three-dimensional advection with almost no numerical error. In general, this is one of the remarkable advantages of the lattice Boltzmann method in simulating airflow within and above canopies with complex geometries.

Fig. 1

Vertical profiles of a mean wind speed, b momentum flux, c resolved velocity variances, and d resolved velocity skewness calculated from the lattice Boltzmann method (LBM) (mark and line) and the Navier–Stokes (NS) model (line). Broken lines in the (b) represent the SGS components of the momentum flux, and grey shading indicates the canopy layer in which the leaf area is distributed homogeneously

3.2 Turbulence Kinetic Energy Budget

Figure 2 shows vertical profiles of the individual terms in the budget equation of the TKE,

$$\frac {\partial \overline{\rho e}}{\partial t}=0=-\frac{\partial \overline{{\rho w}^{^{\prime}}e}}{\partial z}-\frac{\partial \overline{\rho {u}_{\alpha }^{^{\prime}}{\tau {^{\prime}}}_{\alpha 3}}}{\partial z}-\frac{\partial \overline{{p}^{^{\prime}}{w}^{^{\prime}}}}{\partial z}-\overline{\rho u{^{\prime}}w{^{\prime}}}\,\frac{\partial \overline{u}}{\partial z}-{c}_{d}a\overline{\rho \left|\mathbf{u}\right|{{u}_{\alpha }u}_{\alpha }^{^{\prime}}}-\overline{\rho \varepsilon },$$

(29)

where $\rho$e denotes the resolved TKE with $e={u}_{\alpha }^{^{\prime}}{u}_{\alpha }^{^{\prime}}/2$, and $\rho \varepsilon$ is the loss of TKE due to the production of SGS motion. The terms on the right-hand side of Eq. 29 represent (from left to right) turbulent transport, SGS transport, pressure transport, shear production, loss of TKE due to the production of small-scale turbulence in the wakes of canopy elements, and SGS production, respectively. The vertical fluxes in this equation are calculated at the same grid points as the velocities, while the vertical gradients are evaluated at the grid boundaries. The SGS production term for the Navier–Stokes model is calculated directly from

$$\varepsilon ={\tau {^{\prime}}}_{\alpha \beta }\partial {u}_{\alpha }^{^{\prime}}/\partial {x}_{\beta },$$

(30)

whereas the same term for the lattice Boltzmann method is evaluated as the residual of Eq. 29. In Fig. 2, the Navier–Stokes results are smoothed by a vertical 1–2–1 filter to reduce numerical oscillations and to facilitate comparison with the lattice Boltzmann results. The figure implies that TKE is injected by the mean shear and consumed by the SGS productions above the canopy and the wake production within the canopy. Vertical transfer by the resolved turbulence, SGS turbulence, and pressure work in tandem to redistribute TKE to deep inside the canopy layer. Although these features are well known in relation to canopy turbulence (Wilson and Shaw 1977; Raupach et al. 1986; Meyers and Baldocchi 1991; Dwyer et al. 1997), this figure clearly indicates that the method is as capable as the Navier–Stokes model of reproducing the key processes of production, dissipation, and transport of TKE.

Fig. 2

Vertical profiles of the terms in the TKE budget equation simulated by the lattice Boltzmann (lines) and the Navier–Stokes (marks) models. ${P}_{{\rm s}}$: shear production, ${T}_{{\rm t}}$: turbulent transport, ${T}_{{\rm p}}$: pressure transport, ${D}_{{\rm c}}$: loss by canopy drag, ${T}_{{\rm SGS}}$: SGS transport, ${D}_{{\rm SGS}}$: SGS production. A non-zero ${D}_{{\rm c}}$ value for the Navier–Stokes model above the canopy is attributable to the 1–2–1 filtering

Certain differences between the two models can be seen in terms of the pressure transport and SGS production near the canopy top, with the difference in pressure transport presumably attributable to the differences of the model equations. The Navier–Stokes model is based on the incompressible continuity equation, whereas the lattice Boltzmann equation possesses a weakly compressible nature (Eqs. 22 and 23), which permits the propagation of pseudo sound waves. The reason why the difference in SGS production cannot be determined explicitly is that this term in the lattice Boltzmann equation is a residual of the TKE budget. One possible factor might be the aforementioned dispersion error associated with the Navier–Stokes model used here. If so, the numerical dispersion locally increases the spatial derivatives of velocities near the canopy top, thereby producing a local peak of SGS production at that point.

3.3 Spectra

Streamwise and lateral one-dimensional power spectra of the velocity components $u$, $v$, and $w$ at selected levels are shown in Fig. 3. Spectra at levels above the canopy ($z/h$ = 3.05, 2.05) generally follow the $-5/3$ power law in the inertial subrange, whereas spectra within the canopy ($z/h$ = 0.55) have steeper gradients due to the so-called short-circuiting process of the inertial energy cascade caused by the drag of canopy elements (Raupach and Shaw 1982; Finnigan 2000). As obstacles such as stems and branches of a particular length scale are not represented in the model, a secondary peak in the inertial subrange that is sometimes observed inside canopy layers (Seginer et al. 1976; Raupach et al. 1986; Poggi et al 2004; Cava and Katul 2008; Dupont et al. 2012) is not seen in Fig. 3. High-performance simulations that resolve small-scale eddies shed by canopy elements may provide direct representation of the short-circuiting processes. Overall, the spectra from both models are almost identical for the range of the longest wavelengths down to a wavelength of approximately $(2/3)h$.

Fig. 3

One-dimensional power spectra at four different heights of $z/h$ = 3.05 (a, b), 2.05 (c, d), 1.05 (e, f), and 0.55 (g, h). a, c, e, and g are streamwise spectra, while b, d, f, and h are lateral spectra. Lines represent the lattice Boltzmann results and marks denote the results of the Navier–Stokes model; ${L}_{x}$ and ${L}_{y}$ are the streamwise and lateral dimensions of the computational domain; ${\lambda }_{x}$ and ${\lambda }_{y}$ are the streamwise and lateral wavelengths

3.4 Two-Point Correlation Function

The mean spatial structure of coherent motions in canopy turbulence can be deduced by examining spatial two-point correlation functions (Shaw et al. 1995; Su et al. 2000; Finnigan and Shaw 2000), such as that between flow variables obtained at arbitrary heights and a reference height,

$${R}_{ab}\left({r}_{x},{r}_{y},z,{z}_{r}\right)=\frac{\overline{a{^{\prime}}\left(x+{r}_{x}, y+{r}_{y},z\right) b{^{\prime}}\left(x, y,{z}_{r}\right)}}{{\left[ \overline{{a{^{\prime}}}^{2}\left(z\right)}\,\, \overline{{b{^{\prime}}}^{2}\left({z}_{r}\right)} \right]}^{1/2}},$$

(31)

where $a$ and $b$ are one of the flow variables (e.g., velocity, pressure), ${r}_{x}$ and ${r}_{y}$ are streamwise and lateral separations, respectively, and ${z}_{r}$ is the reference height, which is fixed at a height just above the canopy as ${z}_{r}/h=1.05$. In the periodic domain used in the present simulations, the covariance and variances in the above equation can be calculated via the Fourier transform,

$$\overline{a{^{\prime}}\left(x+{r}_{x}, y+{r}_{y},z\right) b{^{\prime}}\left(x, y,{z}_{r}\right)}={\mathcal{F}}^{-1}\left[ \widehat{a}\left({k}_{x}, {k}_{y},z\right){\widehat{b}}^{*}\left({k}_{x}, {k}_{y},{z}_{r}\right)\right]/{N}_{x}{N}_{y},$$

(32)

where $\widehat{a}$ and $\widehat{b}$ are the Fourier transform of ${a}^{^{\prime}}$ and $b{^{\prime}}$, respectively, ${k}_{x}$ and ${k}_{y}$ are horizontal wavenumbers, ${\mathcal{F}}^{-1}\left[\, \right]$ represents the inverse Fourier transform (the asterisk * denotes the complex conjugate), and ${N}_{x}{N}_{y}$ is the total number of horizontal grid points.

As the power spectra are almost identical in the range of low wavenumbers where the spectra have significant power (Fig. 3), the two-point autocorrelation functions of the velocity components can be foreseen as similar between the two models, as confirmed in Fig. 4. In this figure, the lattice Boltzmann results are shown by line contours and the Navier–Stokes results are represented by coloured shading. As expected, the two-point correlation functions from both almost coincide. The autocorrelation of streamwise velocity component exhibits a streamwise-elongated (Fig. 4c) and vertically tilted large-scale structure, in which the 0.1 contour reaches higher than 6 $h$ and extends downstream beyond the figure (Fig. 4a). Such spatial coherence in the vertical velocity component is much more compact in a horizontal slice (Fig. 4d) and it is nearly in phase at all levels from the ground to the height 2–3 h (Fig. 4b). As these figures are similar to what has been reported following earlier studies using wind-tunnel experiments (Shaw et al. 1995) and an LES analysis (Su et al. 2000) of flows within and above different plant canopies, the key features of the coherent structures depicted here are considered not strongly affected by the details of canopy morphology. Similarly to Su et al. (2000), a region of negative correlations in the function ${R}_{uu}$ is seen near the ground in Fig. 4a. The occurrence of such a region is probably attributable to an adverse pressure gradient induced by large-scale sweep motions impinging on the canopy constrained by solid ground. For more discussions, the readers should refer to Su et al. (2000) and Shaw et al. (2013).

Fig. 4

Spatial distribution of two-point autocorrelation functions of the streamwise (a, c) and vertical (b, d) velocity components in a vertical–streamwise cross-section (a, b) and a horizontal cross-section (c, d) at the height $z/h$ = 1.05. Line contours with an interval of 0.1 denote the lattice Boltzmann results and coloured shading represents the Navier–Stokes results

As suggested by Finnigan and Shaw (2000) and supported by the positive streamwise skewness shown in Fig. 1d, sweep motions generally have greater kinetic energy than ejection motions near the canopy top. Hence, the distribution of two-point correlations, with the reference point near the canopy top, tends to reflect the structure of sweep motions selectively. Conducting a conditional sampling analysis on the LES results, Watanabe (2004, 2009) reported that sharp streamwise gradients of the streamwise velocity component near the canopy top, associated with a scalar micro-front between an upstream sweep and a downstream ejection, are observed most often with the passage of a streamwise-elongated and vertically-tilted structure similar to that shown in Fig. 4. Similar spatial structures were also detected in the LES results of Fitzmaurice et al. (2004), who used an occurrence of a positive pressure pulse near the canopy top as a trigger of conditional sampling. As the combination of an upstream sweep and a downstream ejection causes streamwise convergence (i.e., $\partial u/\partial x<0$) near the canopy top, a positive pressure zone that develops there gives rise to divergent flow in both lateral and vertical directions. An intense positive pressure perturbation can thus be used as an indicator of the presence of the sweep–ejection system that also causes the scalar micro-front. Therefore, although the detection method was different between Fitzmaurice et al. (2004) and Watanabe (2004, 2009), the sweep part of the spatial patterns shown by these authors essentially represent the common structure that induces the most energetic perturbations in the streamwise velocity component, of which the spatial structure is depicted by the two-point autocorrelation ${R}_{uu}$ in Fig. 4.

As shown in Fig. 4c, d, the horizontal distribution of the two-point correlation functions exhibits lateral symmetry attributable to the statistical homogeneity in the lateral direction. However, this picture is not quite representative because individual eddies generally have asymmetric shapes with different orientations. To obtain averaged images of such asymmetrical spatial structure of the dominant eddies, the two-point correlation functions are recalculated using only a part of the Fourier components in the first (${k}_{x}$ > 0, ${k}_{y}$ > 0) and third (${k}_{x}\hspace{0.17em}$< 0, ${k}_{y}\hspace{0.17em}$< 0) quadrants in the horizontal wavenumber plane, thereby summing only the components that have negative inclination angles of wave crest line with respect to the streamwise direction.

Horizontal distributions of the recalculated functions ${R}_{uu}$, ${R}_{vu}$, ${R}_{wu}$ are shown in Fig. 5, with only the lattice Boltzmann results shown for brevity. Figure 5a reveals that the symmetric pattern seen in the streamwise velocity component (Fig. 4c) is comprised of the superposition of laterally meandering structures that are much longer streamwise than shown in Fig. 4c. It should be noted that the unused Fourier components in the second and fourth quadrants would produce mirrored patterns (with respect to the horizontal axis at ${r}_{y}=0$) of Fig. 5 and the summation of all components would reduce to Fig. 4. The cross-correlation functions ${R}_{vu}$ and ${R}_{wu}$ (Fig. 5b, c) indicate that high values of the streamwise velocity component are accompanied not only by the negative values of the vertical velocity component corresponding to sweep motions but also by excursions of the lateral velocity component. The lateral motions are directed systematically towards the region of low values of the streamwise velocity component from the high-speed counterparts. Similar results were reported by Perret and Ruiz (2013), who conducted conditional sampling of sweep and ejection motions from wind-tunnel particle-image-velocimetry data using a biased threshold towards positive values of the lateral velocity component. Moreover, compared with the streamwise-elongated feature of the streamwise velocity component, the lateral and vertical velocity components generally have shorter oblique structures that concentrate near the meandering core of the streamwise velocity component. Thus, the most energetic sweep event, in the meandering field of streamwise velocity component, corresponds to the oblique front where a fast-moving high-speed perturbation overtakes and pushes aside low-speed perturbations that move more slowly; this finding is consistent with Watanabe (2009).

Fig. 5

Horizontal distribution at $z/h$ = 1.05 of the two-point correlation functions a${R}_{uu}$, b${R}_{vu}$, and c${R}_{wu}$ recalculated using a limited number of Fourier components. Only the lattice Boltzmann results are shown and the contour interval is 0.1

3.5 Spectral Energy Budget of the Streamwise Structure

Although the mechanism leading to the occurrence of the streaky structures mentioned above remains a matter of debate (Raupach et al. 1996; Finnigan et al. 2009; Watanabe 2009; Shaw et al. 2013) and beyond the scope here, some insights into the process that maintains such structures can be obtained by examining the TKE budget in more detail. Figure 6a shows the pre-multiplied spectral distribution of the terms in the budget equation for the variance $\overline{{u}^{{^{\prime}}2}}/2$ calculated just above the canopy ($z=1.1h$). The pre-multiplied versions of the streamwise one-dimensional power spectra of the $u$ and $w$ components are also shown in Fig. 6b for comparison.

Fig. 6

Streamwise one-dimensional spectral distribution. a Pre-multiplied distribution of individual terms in the budget equation of $\overline{u{^{\prime}}u{^{\prime}}}/2$. ${P}_{{\rm s}}$: shear production, ${T}_{{\rm t}}$: turbulent transport, ${R}_{{\rm p}}$: pressure–strain-rate correlation, ${T}_{{\rm SGS}}$: SGS transport, ${D}_{{\rm SGS}}$: SGS production. b Pre-multiplied power spectra of the $u$ and $w$ velocity components. c Vertical coherence length for the $u$ and $w$ velocity components. Data shown in (a) and (b) are evaluated just above the canopy ($z/h\hspace{0.17em}$= 1.1). The horizontal axis is the streamwise wavelength normalized by the canopy height. Only the lattice Boltzmann results are shown

As has been widely accepted, the kinetic energy is first injected into the streamwise energy through shear production, i.e., streamwise fluctuation is induced by the vertically advected (displaced) mean velocity. The peak of shear production $-{\rm Re}\left[{\widehat{u}}^{*}\widehat{w}\right]{\rm d}\overline{u}/{\rm d}z$ (Re denotes the real part) is located in between the peaks of the pre-multiplied power spectra of the $u$ and $w$ components. Thus, the fundamental source of TKE includes both long- and short-wavelength components. In fact, the long components (wavelengths > 10$h$) are responsible for 46% of the total shear stress $\overline{{u}^{^{\prime}}{w}^{^{\prime}}}$ at the canopy top. However, the kinetic energy induced by shortwave components is redistributed largely to the lateral and vertical components of TKE through the action of pressure, as indicated by the pressure–strain-rate correlation term ${\rm Im}\left[{k}_{x}\widehat{p}{\widehat{u}}^{*}\right]$ (Im denotes the imaginary part) in Fig. 6a. This is attributable to the sharp streamwise gradients in the shortwave fluctuations of the streamwise velocity component, which induce intense pressure perturbations to satisfy the constraint of flow continuity. One may recall that the pressure-strain-rate correlation is the only substantial source in the budget of lateral and vertical components of TKE, and the sum of the terms in all three components almost vanishes because of the flow continuity. As a result, the power spectra of the $v$ and $w$ components have significant values only in the short-wavelength or large-wavenumber range (Figs. 3 and 6b), while the longwave energy tends to remain in the streamwise velocity component. The shear production to a longwave component is balanced by the turbulent transport, which is composed of the vertical transport towards the canopy layer and the energy cascade to shortwave components, and, to a lesser extent, direct consumption for SGS production. Because these non-linear processes involve the higher-order interactions between the turbulent velocity fluctuations, these processes are slower than the pressure-redistribution process, which is dominated by the linear rapid pressure that responds instantaneously to the shear production (Pope 2000). Consequently, longwave structures in the streamwise velocity component persist for longer.

The spectral distribution of the vertical coherence length (Fig. 6c) indicates that streamwise-elongated structures are generally tall. The coherence length, which is a spectral analogue of the integral length scale, is calculated as

$${L}_{z}^{\alpha \alpha }\left({k}_{x},{z}_{r}\right)={\int }_{h}^{{z}_{{\rm top}}}{C}_{\alpha \alpha }\left({k}_{x},z, {z}_{r}\right){\rm d}z,$$

(33)

where ${C}_{\alpha \alpha }$ is the coherence function between individual Fourier modes obtained at arbitrary heights and the reference height, i.e.,

$${C}_{\alpha \alpha }\left({k}_{x},z, {z}_{r}\right)=\frac{\overline{{\stackrel{\sim }{u}}_{\alpha }\left({k}_{x},y, z\right){{\stackrel{\sim }{u}}_{\alpha }^{*}\left({k}_{x},y,{z}_{r}\right)}}}{{\left[ \overline{{\left|{\stackrel{\sim }{u}}_{\alpha }\left({k}_{x},y,z\right)\right|}^{2}} \,\,\overline{{\left|{\stackrel{\sim }{u}}_{\alpha }\left({k}_{x},{y,z}_{r}\right)\right|}^{2}} \right]}^{1/2}}.$$

(34)

Here, ${\stackrel{\sim }{u}}_{\alpha }$ is the streamwise one-dimensional Fourier transform of ${u}_{\alpha }$, and repeated indices in Eqs. 33 and 34 do not imply summation. The reference height is set to ${z}_{r}/h=1.05$, and the integral in Eq. 33 is calculated only in the region above the canopy. It should be noted that the above definition is based on the “coherence height” used by Jiménez et al. (2004) but differs slightly from the original definition. Figure 6c clearly indicates that the vertical length scales for both the streamwise and vertical velocity components increase with the streamwise wavelength ${\lambda }_{x}$ in the shorter range (${\lambda }_{x}\le 10h$), where the structure of the vertical velocity component is generally taller than that of the streamwise velocity component. For longer wavelengths (${\lambda }_{x}>10h$), however, the length scale of the vertical velocity component levels off, whereas the length scale of the streamwise velocity component continues to grow to the dimension of 2–3 $h$ at the longest wavelengths. Thus, the longest modes of the streamwise velocity component are coherent across the roughness sublayer, which is considered to extend to a height of roughly $3h$.

Taken altogether, the larger contribution of longwave components to the streamwise velocity component (Fig. 6b) results in a more streamwise-elongated, taller coherent structure (Fig. 4a) in comparison with the compact structure of the vertical velocity component (Fig. 4b).

4 Conclusions

We have described a central-moments-based lattice Boltzmann method for the simulation of neutrally-stratified turbulent flows with the LES approach. By conducting comparative simulations of the airflow within and above a homogeneous plant canopy, the performance of the model was evaluated against a conventional LES model based on the Navier–Stokes equations. The simulated turbulence statistics such as mean velocity, velocity variances, velocity skewness, and power spectra are almost identical between the two models. The spatial structure of the coherent eddies and their maintenance processes were confirmed properly represented by the lattice Boltzmann approach through analysis of the TKE budget and the spatial distribution of two-point correlation functions.

As already shown by previous studies, the most prominent spatial structures in the streamwise velocity component present a streaky form in the roughness sublayer over both vegetation and urban canopies. An examination of the spectral TKE budget shows that the difference in the pressure-redistribution process between short- and long-wavelength components of the shear-generated streamwise energy plays a role in the maintenance of the streaky structures. Although the turbulent pressure rapidly redirects short-wavelength components of streamwise energy to the lateral and vertical velocity components, long-wavelength components of energy tend to remain in the streamwise velocity component because the pressure-redistribution process works only marginally because of the small streamwise gradients in the long-wavelength components.

Based on our experience, the lattice Boltzmann algorithm is quite simple and its coding is straightforward. Its particulate nature and local dynamics are suitable for high-performance computations of the atmospheric-boundary-layer flows. Although we only dealt with a neutrally stratified flow, the method can be applied to non-neutral conditions by including the buoyancy in the forcing terms, with the aid of a coupled solver for (potential) temperature. The temperature solver could also use a lattice Boltzmann approach for predicting the distribution function of the internal energy (e.g., He et al. 1998a; Wang et al. 2018) or a conventional finite-difference approach for the macroscopic thermodynamic equation.

Appendix: Equations for the Collision and Forcing

The post-collision central moments are generally calculated by Eq. 2 with the collision process parametrized as a relaxation towards equilibrium (Eq. 13). However, to maintain the rotational invariance, some moments need to be rearranged before relaxation, and some relaxation coefficients must be assigned the same value (Geier et al. 2015). The actually implemented equations are described here.

For the conservative moments (i.e., the zeroth- and first-order moments, related to the mass and momentum conservations, respectively), the relaxation coefficients must be zero, and the post-collision moments are given as

$${\kappa }_{000}^{*}={\kappa }_{000},$$

(35)

$${\kappa }_{100}^{*}={\kappa }_{100}+{F}_{{\rm x}}=-{\kappa }_{100},$$

(36a)

$${\kappa }_{010}^{*}={\kappa }_{010}+{F}_{{\rm y}}=-{\kappa }_{010},$$

(36b)

$${\kappa }_{001}^{*}={\kappa }_{001}+{F}_{{\rm z}}={-\kappa }_{001}.$$

(36c)

The second-order moments are rearranged to correctly recover the traceless and trace components of the momentum flux tensor, to which the coefficients ${\omega }_{1}$ and ${\omega }_{2}$ are applied respectively,

$${\kappa }_{110}^{*}=\left(1-{\omega }_{1}\right){\kappa }_{110},$$

(37a)

$${\kappa }_{011}^{*}=\left(1-{\omega }_{1}\right){\kappa }_{011},$$

(37b)

$${\kappa }_{101}^{*}=\left(1-{\omega }_{1}\right){\kappa }_{101},$$

(37c)

$${\kappa }_{200}^{*}-{\kappa }_{020}^{*}=\left(1-{\omega }_{1}\right)\left({\kappa }_{200}-{\kappa }_{020}\right)-3\rho \left(1-\frac{{\omega }_{1}}{2}\right)\left({u}^{2}\frac{\partial u}{\partial x}-{v}^{2}\frac{\partial v}{\partial y}\right),$$

(38a)

$${\kappa }_{200}^{*}-{\kappa }_{002}^{*}=\left(1-{\omega }_{1}\right)\left({\kappa }_{200}-{\kappa }_{002}\right)-3\rho \left(1-\frac{{\omega }_{1}}{2}\right)\left({u}^{2}\frac{\partial u}{\partial x}-{w}^{2}\frac{\partial w}{\partial z}\right),$$

(38b)

$${\kappa }_{200}^{*}+{\kappa }_{020}^{*}+{\kappa }_{002}^{*}=\left(1-{\omega }_{2}\right)\left({\kappa }_{200}+{\kappa }_{020}+{\kappa }_{002}\right)+{\omega }_{2}\rho -3\rho \left(1-\frac{{\omega }_{2}}{2}\right)\left({u}^{2}\frac{\partial u}{\partial x}+{v}^{2}\frac{\partial v}{\partial y}+{w}^{2}\frac{\partial w}{\partial z}\right).$$

(39)

Final terms in Eqs. 38 and 39 are partial corrections for the lack of Galilean invariance of the original lattice Boltzmann equation (Geier et al. 2015), and the velocity gradients used in these terms are calculated by Eq. 48 shown below. Similarly, the post-collision values of the higher-order moments are calculated by the rearranged equations as

$${\kappa }_{120}^{*}+{\kappa }_{102}^{*}=\left(1-{\omega }_{3}\right)\left({\kappa }_{120}+{\kappa }_{102}\right)+\left(1-\frac{{\omega }_{3}}{2}\right)\frac{2{F}_{{x}}}{3},$$

(40a)

$${\kappa }_{210}^{*}+{\kappa }_{012}^{*}=\left(1-{\omega }_{3}\right)\left({\kappa }_{210}+{\kappa }_{012}\right)+\left(1-\frac{{\omega }_{3}}{2}\right)\frac{2{F}_{{y}}}{3},$$

(40b)

$${\kappa }_{201}^{*}+{\kappa }_{021}^{*}=\left(1-{\omega }_{3}\right)\left({\kappa }_{201}+{\kappa }_{021}\right)+\left(1-\frac{{\omega }_{3}}{2}\right)\frac{2{F}_{{z}}}{3},$$

(40c)

$${\kappa }_{120}^{*}-{\kappa }_{102}^{*}=\left(1-{\omega }_{4}\right)\left({\kappa }_{120}-{\kappa }_{102}\right),$$

(41a)

$${\kappa }_{210}^{*}-{\kappa }_{012}^{*}=\left(1-{\omega }_{4}\right)\left({\kappa }_{210}-{\kappa }_{012}\right),$$

(41b)

$${\kappa }_{201}^{*}-{\kappa }_{021}^{*}=\left(1-{\omega }_{4}\right)\left({\kappa }_{201}-{\kappa }_{021}\right),$$

(41c)

$${\kappa }_{111}^{*}=\left(1-{\omega }_{5}\right){\kappa }_{111},$$

(42)

$${\kappa }_{220}^{*}-2{\kappa }_{202}^{*}+{\kappa }_{022}^{*}=\left(1-{\omega }_{6}\right)\left({\kappa }_{220}-2{\kappa }_{202}+{\kappa }_{022}\right),$$

(43a)

$${\kappa }_{220}^{*}+{\kappa }_{202}^{*}-2{\kappa }_{022}^{*}=\left(1-{\omega }_{6}\right)\left({\kappa }_{220}+{\kappa }_{202}-2{\kappa }_{022}\right),$$

(43b)

$${\kappa }_{220}^{*}+{\kappa }_{202}^{*}+{\kappa }_{022}^{*}=\left(1-{\omega }_{7}\right)\left({\kappa }_{220}+{\kappa }_{202}+{\kappa }_{022}\right)+{\omega }_{7}\frac{\rho }{3},$$

(44)

$${\kappa }_{211}^{*}=\left(1-{\omega }_{8}\right){\kappa }_{211},$$

(45a)

$${\kappa }_{121}^{*}=\left(1-{\omega }_{8}\right){\kappa }_{121},$$

(45b)

$${\kappa }_{112}^{*}=\left(1-{\omega }_{8}\right){\kappa }_{112},$$

(45c)

$${\kappa }_{221}^{*}=\left(1-{\omega }_{9}\right){\kappa }_{221}+\left(1-\frac{{\omega }_{9}}{2}\right)\frac{{F}_{z}}{9},$$

(46a)

$${\kappa }_{212}^{*}=\left(1-{\omega }_{9}\right){\kappa }_{212}+\left(1-\frac{{\omega }_{9}}{2}\right)\frac{{F}_{{y}}}{9},$$

(46b)

$${\kappa }_{122}^{*}=\left(1-{\omega }_{9}\right){\kappa }_{122}+\left(1-\frac{{\omega }_{9}}{2}\right)\frac{{F}_{{x}}}{9},$$

(46c)

$${\kappa }_{222}^{*}=\left(1-{\omega }_{10}\right){\kappa }_{222}+{\omega }_{10}\frac{\rho }{27},$$

(47)

where ${\omega }_{{3,4},5}$ are the relaxation coefficients for the third-order moments, ${\omega }_{{6,7},8}$ are those for the fourth-order moments, and ${\omega }_{9}$ and ${\omega }_{10}$ are those for the fifth- and the sixth-order moments, respectively. The forcing terms in the higher-order moments are included in Eqs. 40 and 46, as suggested by Fei and Luo (2017) and Fei et al. (2018). The velocity gradients in Eqs. 38 and 39 are evaluated from the second-order central moments as (Geier et al. 2017)

$$\frac{\partial u}{\partial x}=-\frac{{\omega }_{1}}{2\rho }\left(2{\kappa }_{200}-{\kappa }_{020}-{\kappa }_{002}\right)-\frac{{\omega }_{2}}{2\rho }\left({\kappa }_{200}+{\kappa }_{020}+{\kappa }_{002}-\rho \right),$$

(48a)

$$\frac{\partial v}{\partial y}=\frac{\partial u}{\partial x}+\frac{3{\omega }_{1}}{2\rho }\left({\kappa }_{200}-{\kappa }_{020}\right),$$

(48b)

$$\frac{\partial w}{\partial z}=\frac{\partial u}{\partial x}+\frac{3{\omega }_{1}}{2\rho }\left({\kappa }_{200}-{\kappa }_{002}\right).$$

(48c)

Other components of the strain rates are similarly evaluated as

$$\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}=-\frac{3{\omega }_{1}}{\rho }{\kappa }_{110},$$

(49a)

$$\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}=-\frac{3{\omega }_{1}}{\rho }{\kappa }_{101},$$

(49b)

$$\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}=-\frac{3{\omega }_{1}}{\rho }{\kappa }_{011}.$$

(49c)

The final three relationships are used in the evaluation of the subgrid eddy viscosity (Eq. 15).