Abstract
Profiles of the sensible heat flux are key to understanding atmospheric-boundary-layer (ABL) structure and development. Based on temperature profiling by a remotely-piloted aircraft system (RPAS), the Small Unmanned Meteorological Observer (SUMO) platform, during the Boundary Layer Late Afternoon and Sunset Turbulence (BLLAST) field campaign, 108 heat-flux profiles are estimated using a simplified version of the prognostic equation for potential temperature \(\theta \) that relates the tendency in \(\theta \) to the flux divergence over the time span between two consecutive flights. We validate for the first time RPAS-based heat-flux profiles against a network of 12 ground-based eddy-covariance stations (2–60 m above ground), in addition to a comparison with fluxes from a manned aircraft and a tethered balloon, enabling the detailed investigation of the potential and limitations related to this technique for obtaining fluxes from RPAS platforms. We find that appropriate treatment of horizontal advection is crucial for obtaining realistic flux values, and present correction methods specific to the state of the ABL. Advection from a mesoscale model is also tested as another correction method. The SUMO heat-flux estimates with appropriate corrections compare well with the reference measurements, with differences in the performance depending on the time of day, since the evening period shows the best results (94\(\%\) within the spread of ground stations), and the afternoon period shows the poorest results (63\(\%\) within the spread). The diurnal cycle of the heat flux is captured by the SUMO platform for several days, with the flux values from the manned aircraft and tethered balloon coinciding well with those from the SUMO platform.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The turbulent sensible heat flux is, due to its direct connection to the buoyancy production in the budget for turbulence kinetic energy (TKE), one of the main drivers of energy and mass transport in the atmospheric boundary layer (ABL) (e.g. Stull 1988; Wyngaard 2010). The availability of accurate heat-flux profiles is thus key to the understanding of the structure and diurnal development of the ABL over land, which affects a wide range of practical meteorological applications, such as the concentration and distribution of aerosols and other pollutants (Zhang and Rao 1999; Schäfer et al. 2006), and the prediction of air temperature close to the surface, in particular for the stable boundary layer (SBL) (Holtslag et al. 2013; Bosveld et al. 2014).
Turbulent fluxes close to the ground are typically measured directly, either in situ using eddy-covariance (EC) systems on masts (Foken 2017) or towers (Kaimal and Gaynor 1983; Neisser et al. 2002; Monna and Bosveld 2013), or remotely using scintillometers (Hartogensis et al. 2002). Measurements higher up in the atmosphere require airborne platforms with multi-hole probes and fast temperature sensors on manned (Crawford and Dobosy 1992; Lothon et al. 2007) or unmanned (van den Kroonenberg et al. 2008; Thomas et al. 2012; Reineman et al. 2013; Martin and Bange 2014; Wildmann et al. 2017; Calmer et al. 2018; Bärfuss et al. 2018) aircraft, or towed by a manned helicopter as in the case of the Helipod (Bange and Roth 1999). More experimental approaches include the operation of turbulence sensor packages tethered beneath balloons (Canut et al. 2016) and kites (Muschinski et al. 2001) or beneath an unmanned helicopter (Giebel et al. 2011). Very recently, various groups have also flown sonic anemometers on small to medium-sized multi-copter systems (Palomaki et al. 2017). However, to our knowledge, none of the latter attempts have so far produced reliable heat-flux profiles. For example, disturbances of the ambient conditions related to flow distortion and rotor-induced downwash hamper the precise measurement of turbulent fluctuations.
The airborne approaches described above provide fluxes either averaged over straight flight legs at specific altitudes in the case of aircraft observations or temporally averaged for the tethered balloon, but endurance constraints limit the achievable vertical resolution. Continuous heat-flux profiles can be estimated from the evolution of mean temperature profiles based on a range of techniques (e.g. Deardorff et al. 1980; Bange et al. 2007) by utilizing the integrating and averaging capacity of the ABL, and thus linking ground-based flux measurements from masts and towers (2 m to below 100 m) with airborne observations, which are typically taken up to, or slightly above, the mixed-layer depth h. A quasi-Lagrangian integral method has been applied to temperature profiles taken at different distances from the coast by the remotely-piloted aircraft system (RPAS) Aerosonde (Holland et al. 2001) in strong katabatic outflows from the Antarctic continent (Knuth and Cassano 2014). A heating-rate method has been presented using measurements from the unmanned Multi-purpose Airborne Sensor Carrier (MASC) system (Wildmann et al. 2014) during the morning transition (Wildmann et al. 2015). The very first application of an RPAS platform using a profile-integration method based on the evolution of mean temperature profiles was based on measurements by the SMARTSonde unmanned aircraft (Chilson et al. 2011) taken during the afternoon transition period (Bonin et al. 2013).
Our main objective is to quantify the potential and limitations of the profile-integration method using the RPAS platform by utilizing a large flight-based dataset collected with the Small Unmanned Meteorological Observer (SUMO) platform (Reuder et al. 2009) during the Boundary Layer Late Afternoon and Sunset Turbulence (BLLAST) campaign in southern France (Lothon et al. 2014; Reuder et al. 2016a), which represents a considerable extension of previous studies (Bonin et al. 2013; Knuth and Cassano 2014; Wildmann et al. 2015). The BLLAST campaign offered the unique opportunity of estimating heat-flux profiles from a large number of SUMO flights covering a variety of synoptic situations and a range of diurnal ABL developments. The method is tailored to consider the growing convective boundary layer (CBL), the fully-developed CBL, and the developing SBL in the evening transition, including estimation of the uncertainties of the resulting fluxes. The results are also validated against ground-based EC flux measurements at altitudes between 2 and 60 m above ground level (a.g.l.) over various surface types (Lothon et al. 2014; De Coster and Pietersen 2011), against direct flux measurements obtained with the manned-research aircraft Piper Aztec (Saïd et al. 2005), and against data from an experimental flux-measurement system based on a sonic anemometer carried by a tethered balloon (Canut et al. 2016). Finally, we also present a first test to investigate the incorporation of advection based on model simulations.
Below, the BLLAST field campaign is described in Sects. 2 and 3 gives a description of the SUMO temperature-profile dataset and the algorithms used to estimate the corresponding sensible heat flux based on consecutive temperature profiles. We also describe the supplementary datasets and discuss the sensitivity of the SUMO heat-flux estimates. Section 4 gives examples of the resulting flux profiles for different atmospheric states and the various methods to account for the effect of advection, after which a case study is presented showing the diurnal heat-flux development. We then present and discuss the overall statistics for a comparison of the 108 SUMO heat-flux profiles to the surface measurements from the EC stations, and end the section with a case study of the potential for incorporating advection from a mesoscale model. Section 5 summarizes the main conclusions and presents a short outlook for future work.
2 The Boundary Layer Late Afternoon and Sunset Turbulence Field Campaign
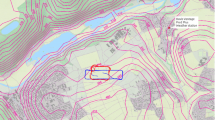
Data were collected as a part of the international field campaign BLLAST in Lannemezan in southern France in June and July 2011 (Lothon et al. 2014; Reuder et al. 2016a). The overall campaign objective was the investigation of the development of the CBL over heterogeneous surface conditions (see Fig. 1), with the focus on the afternoon and evening transition period and, in particular, the decay of turbulence. The campaign included 11 intensive observational periods (IOP) (see Table 1), with data collected from a 60-m tower, distributed EC surface stations, various remote-sensing profilers, tethered balloons, radiosondes, manned aircraft and different RPAS platforms (Lothon et al. 2014). Site selection ensured the EC stations cover a wide range of relevant surface types for the experiment area, such as wheat, corn, moorland, forest, and grass, making it suitable to study the effects of surface heterogeneity on turbulent exchange.
Land-use map for the experiment area around Lannemezan in southern France based on the dataset compiled by Hartogensis (2015). The blue dot and red triangle mark the locations of site 1 and site 2, respectively. The purple rectangle indicates the boundaries of a \(10~\hbox {km}\times 10~\hbox {km}\) box used for averaging of the mesoscale-model output
The synoptic situation during the main campaign period (15 June–5 July 2011) is generally characterized by fair-weather conditions with mainly weak horizontal pressure gradients, temporarily disrupted by a few weaker frontal passages (Lothon et al. 2014). The frequent situations with weak synoptic background flow favoured the development of thermally-driven flow in the region. As Lannemezan is located on a plateau at the foothills of the Pyrenees, slightly sloping towards the north-east and about 10 km from the exit of the Vallée d’Aure, locally and regionally generated upslope (downslope), plain–mountain (mountain–plain) circulations and up-valley (down-valley) flow strongly influence the diurnal (nocturnal) ABL features (Jiménez and Cuxart 2014; Jiménez et al. 2019), and must be taken into account in any estimation of large-scale temperature advection for the area (Cuxart et al. 2016). Each IOP was conducted on a fair-weather day in order to sample the afternoon transition of convective turbulence. However, depending on the weather conditions on the day or days prior to the actual IOP, different amounts of moisture were available at the surface. As a result, the Bowen ratio varied strongly, and the CBL developed differently for the individual IOP. For instance, the maximum depth of the boundary-layer during the campaign ranged from about 1000–1600 m a.g.l., and may be classified into three main groups (Lothon et al. 2014). For several days, the ABL developed for about 4 h, before a slight lowering of the capping inversion, while other days showed a rapid ABL growth in the morning, and a levelling of the inversion in the afternoon. The last group of days was characterized by a slow ABL growth, followed by a steep decrease of the inversion level. The sunrise, solar noon and sunset times were around 0420 UTC (0620 local time; LT), 1200 UTC (1400 LT), and 1940 UTC (2140 LT), respectively. For more information on the BLLAST campaign set-up, see Lothon et al. (2014).
3 Data and Methods
3.1 SUMO Profiles
A central contribution of the University of Bergen team during the BLLAST campaign was the frequent profiling of the ABL up to about 1500–1600 m a.g.l. using the SUMO platform (Reuder et al. 2016a), which is a small and lightweight (0.65 kg) RPAS platform based on a fixed-wing airframe with length and wingspan of approximately 0.8 m (Reuder et al. 2009, 2012b). The system was originally developed as a recoverable radiosonde for the measurement of vertical profiles of basic meteorological parameters, such as temperature, humidity, and pressure, for bridging the gap between ground-based meteorological stations and radiosonde or manned-aircraft observations. In addition, wind speed and direction have been estimated using a “no-flow-sensor” algorithm (Mayer et al. 2012). The SUMO platform has previously been used for numerous such profiling missions (Reuder et al. 2012a; Cassano 2014; Jonassen et al. 2015; Kral et al. 2018), as well as the mapping of surface-temperature development by horizontal survey missions (Reuder et al. 2016a) and the effect on local advection (Cuxart et al. 2016), and the investigation of turbulence in wind-turbine wakes (Reuder et al. 2016b).
The SUMO aircraft system is based on the Paparazzi autopilot (Brisset et al. 2006), and is equipped with an inertial measurement unit for attitude information, and a GPS sensor for navigation and position. The SUMO sensor package during the BLLAST campaign included the Sensirion SHT75 temperature and humidity sensor (2-Hz sampling frequency, \(\pm \,0.3^\circ \)C accuracy), a PT1000 Heraeus M222 sensor (8.5 Hz) for additional higher frequency temperature measurements, a MS 5611 sensor (4 Hz) for pressure, and a Melexis MLX90614 sensor (8.5 Hz) for surface temperature. The temperature sensor used for the sensible-heat-flux determination has a time constant of about 5 s for the ambient-temperature range during the BLLAST campaign. Additionally, an Aeroprobe 5-hole probe (100 Hz) was operated for direct turbulence measurements during specific flights (Båserud et al. 2016; Reuder et al. 2016a). For more detailed information on the SUMO platform and the sensors used during the BLLAST campaign, see Reuder et al. (2016a).
Of a total of 299 SUMO flight missions during the BLLAST campaign, 168 were dedicated profile flights, from which 124 profiles could be used for the flux estimation (see Table 1). The remaining 44 profiles were discarded for a range of reasons, such as test flights (26, including the 19 sensor-comparison flights from the last three days of the campaign), incomplete temperature, humidity or GPS data (7), missing pressure data (6), profiles not capturing the whole ABL (3), and very large differences between the ascent and descent parts of the profiles (2). The time interval between the subsequent profiles used for the flux estimation differs considerably, as the SUMO aircraft was operated in a variable schedule throughout each day, alternating between profile, survey and turbulence-transect missions. For most of the cases, the time difference is between 30 min and 1.5 h, with about 15 min and 4.5 h as the extremes. The 124 available profiles result in a total of 108 sensible-heat-flux estimates, as we need two consecutive profiles for the flux determination, resulting in one flux determination less than the profiles measured during a given measurement day.
All SUMO operations were carried out during the daytime, as the reserved airspace for this campaign was only between 0500 and 2100 UTC, while the available battery capacity at the time allowed for total flight durations of the order of 25 min. The SUMO profiles were flown in an ascending and descending helical pattern of diameter 120 m; thus, the results represent the average conditions over an atmospheric column of these dimensions. For the ascent, the SUMO platform climbed at a higher rate of 7–10 m s\(^{-1}\) to maximize the vertical extent of the profiles. During descent, the engine was turned off and the platform descended in a glide path at a vertical speed of 2–3 m s\(^{-1}\). In the following, only the descending part of the profiles is used for analysis to minimize the influence of the sensor time constants on the measured profiles (Jonassen 2008; Reuder et al. 2016a; Corominas Del Hoyo 2018).
The SUMO data were quality controlled and cleared for spikes before the potential temperature profiles were calculated from temperature and pressure measurements. The descent profiles were then averaged over 20-m vertical bins to obtain smoother profiles on a regularly-spaced vertical grid. All SUMO timestamps presented hereafter correspond to the start of the corresponding descent profile.
3.2 Supplementary Datasets
3.2.1 Eddy-Covariance Flux Stations
Several EC flux stations on masts and towers at heights between 2 m and 60 m a.g.l. were deployed over various surface types to monitor the effects of surface heterogeneity on the turbulent fluxes recorded during the BLLAST campaign (see Table 2 for the basic information of the masts and towers used here). At the main site (site 1), surface-flux stations were placed over wheat, grass, the border between wheat and grass, the prairies, and different mixed surfaces. At a second site (site 2), EC stations were located over corn and moorland. Site 1 was located approximately 4 km to the north of site 2 with a forest station half-way in between (see Lothon et al. 2014 for a map of the experimental area and all ground-based flux stations).
The EC-station sensors were mounted at heights > 3–5 times the height of the roughness elements of each surface cover to ensure the instruments were situated inside the constant-flux layer (Lothon et al. 2014). The corresponding measurement height for each station and surface type is listed in Table 2. All ground-based flux measurements during the BLLAST campaign have been processed and quality controlled by De Coster and Pietersen (2011) using the software package “EC-pack” (Dijk et al. 2004) with the planar-fit correction. The turbulent fluxes are calculated from either 10-Hz or 20-Hz raw data based on an averaging interval of 30 min, which is usually considered acceptable for a fixed EC station to capture the typical range of eddy sizes in the surface layer over the whole day (e.g. Foken 2017; Vesala et al. 2008).
For the comparison with the heat-flux estimates derived from the SUMO profiles, we use 12 out of a total of 18 EC measurement points deployed during the BLLAST campaign. The key characteristics of the chosen measurement sites are summarized in Table 2. Multiple measurement levels at relatively low masts, for example, at the divergence site, have been omitted to avoid over-representation of single surface types when averaging over the different stations for the comparison. The flux value from the lowest height level of each SUMO profile to be compared to the EC surface measurements is situated at 10 m a.g.l., and can be seen as representative for the surface layer.
With respect to temporal averaging when comparing the sensible-heat-flux estimates from the SUMO platform with the EC measurements, the EC-based heat-flux value for each station is calculated as the mean over the time period between the two SUMO flights used for the flux estimation. One example from 2 July can be seen in Fig. 2 showing the relevant EC flux values for the time period 1222–1425 UTC, which are marked by additional symbols in the time series. The heat-flux estimate from the SUMO platform is compared here to the mean of the EC flux values at 1230, 1300, 1330, 1400 and 1430 UTC.
Figure 2 shows that the 12 flux stations can be divided in two groups. Most of the stations, including the tower measurements at 30, 45 and 60 m, reach noon sensible heat fluxes of between 100 and \(200~\hbox {W m}^{-2}\). The two measurements above forest and the one above wheat, however, are by about a factor of two higher and range between 300 and \(400~\hbox {W m}^{-2}\), which is consistent throughout the campaign for the forest site, having previously been identified and described (Lothon et al. 2014; Darbieu et al. 2015). The canopy is a Douglas Fir coniferous forest of 20–25-m height, and the instruments were placed at around 20 and 30 m a.g.l. (i.e. inside or only slightly above the tree tops). Thus, the higher values of sensible heat flux measured here are not surprising, as the low albedo and the trapping of shortwave radiation due to the geometry of the trees lead to a considerable warming of the crown area during the daytime, with corresponding enhanced heat fluxes. For the wheat site, the high sensible heat fluxes only occur towards the end of the campaign starting around 27 June (Lothon et al. 2014), which is related to the full ripening and drying of crops in that period.
In comparing the SUMO sensible-heat-flux estimates to the average over the EC measurements at the surface in the following sections (Sects. 4.2–4.4), the wheat and forest stations have not been included in the calculation of the mean. For the wheat site, this choice is motivated by the changing behaviour over the course of the campaign and the relatively small abundance of the corresponding surface type surrounding the SUMO profile flights (see Fig. 1 and Seidl 2017), while the forest measurements are taken at levels unrepresentative for the corresponding constant-flux layer.
The observations at the EC stations described above give us the unique possibility to compare the lowermost part of the flux-profile estimates from the SUMO platform with direct measurements from well-established and well-maintained ground-based instrumentation.
3.2.2 The Manned Twin-Engine Aircraft Piper Aztec
The manned twin-engine aircraft Piper Aztec is operated by the French facility for airborne research, SAFIRE (www.safire.fr), and is equipped for thermodynamic and turbulence measurements (Saïd et al. 2005). The kinematic heat flux is computed with the EC method along straight and level runs. The time series of the vertical wind velocity component and potential temperature are computed at a rate of 25 Hz. As the airspeed of the aircraft is approximately \(60~\hbox {m s}^{-1}\), the smallest turbulence scales sampled are 2.4 m. The temperature, which is measured with a Rosemount 102E2AL probe installed in a dedicated housing, is corrected for adiabatic heating due to the airspeed assuming a recovery factor of the probe close to unity (Lenschow 1986). The three components of the wind velocity are computed according to Lenschow (1986) as the sum of the groundspeed vector (measured by the IXblue inertial platform coupled to a Bancomm GPS receiver) and the airflow vector of the aircraft. The latter is computed from the true airspeed (measured with a Pitot system) and the attack \(\alpha \) and sideslip \(\beta \) angles, which are computed from the differential pressure between the upper and lower, and the left and right ports, respectively, at the tip of a 2.5-m long boom in front of the aircraft nose. The projection of the airflow vector from the aircraft-based to the Earth-based frame is calculated using the pitch, roll and yaw angles measured by the inertial platform. The data processing is quite similar to that described in Saïd et al. (2010) for the ATR-42 SAFIRE airplane. In particular, time series are high-pass filtered to remove mesoscale structures before flux computation. The choice of the filter wavelength is guided by a compromise between competing effects: reducing (increasing) the cut-off wavelength increases (reduces) the systematic error whereas the random error is simultaneously reduced (increased) (Lenschow et al. 1994); the chosen cut-off value (4.5 km) is in agreement with previous studies of airborne flux estimates (e.g. Grunwald et al. 1996; Lambert and Durand 1998).
The flights, which were performed in the early-to-late-afternoon period, consist of stacked straight and level runs. The targeted measurement heights were chosen according to the estimated boundary-layer top just before each flight based on ultra-high-frequency wind profilers and/or SUMO and radiosonde profiles. A Degreane PCL 1300 ultra-high-frequency radar measured continuously the wind-speed profile between 200 m and 3000 m a.g.l., as well as the reflectivity, which enabled computation of the time series of the daytime boundary-layer height (Angevine et al. 1994). Meteomodem M2K2 radiosondes were launched during IOP days at least every 6 h starting from 0600 UTC. The manned flights were oriented east–west or north–south. For the flight analyzed below in Sect. 4.1.2 (flight #23 on 2 July), stacked legs were flown in an L-shaped pattern, with the corner close to site 1, from which two 25-km branches extended towards the west and the north. Given the topography of the area, the height a.g.l. varied considerably during a flight (see also the inset in Fig. 8b in Sect. 4.1.2). The heat fluxes were, therefore, computed over both the entire 25-km legs, and the 2.5-km non-overlapping sub-legs to relate local flux estimates to the corresponding height a.g.l. A study on the contribution of different scales to the overall heat flux has shown that the sub-legs miss around 20% of the flux with respect to the complete legs. On flight #23, the fluxes computed over the entire legs coincide remarkably well with the average over the sub-legs, which gives confidence in the local flux estimates.
3.2.3 The Mesoscale Non-Hydrostatic Model
Simulations were performed with the mesoscale non-hydrostatic (MesoNH) model (Lafore et al. 1998) for several, but unfortunately not all, IOP days during the BLLAST campaign; IOP simulations are available for days with thermally-driven flow during the night-time (IOP 3, 5, 6, 9, 10 and 11). Two nested domains are used: the outer domain has a \(2~\hbox {km}~\times ~2~\hbox {km}\) resolution (domain size \(500~\hbox {km}~\times ~480~\hbox {km}\) covering the Garonne river basin), and the inner domain has a \(400~\hbox {m}~\times ~400~\hbox {m}\) resolution (domain size \(80~\hbox {km}~\times ~120~\hbox {km}\) centered on Lannemezan). The vertical resolution is 3 m close to the surface and stretched with height above (e.g. 135 m at 1600 m a.g.l.) to properly capture the physical processes in the lower atmosphere. The simulations extend over 30 h, starting at 0600 UTC of the corresponding IOP and finishing at 1200 UTC the next day. Further details of the model set-up and the simulations are presented in Jiménez and Cuxart (2014) and Jiménez et al. (2019), respectively.
One of our working hypotheses is that mesoscale-model simulations are capable of quantifying the advection conditions over the experiment area and, thus, may have the potential to improve our sensible-heat-flux profiles derived from the SUMO platform. The three-dimensional temperature advection is computed from the model fields over an area of \(10~\hbox {km}~\times ~10~\hbox {km}\) centered on Lannemezan. Here, we utilize only the horizontal component of advection, since the vertical component in the CBL is dominated by the thermally-driven motion of turbulent eddies, which masks the effects of subsidence of interest here.
The horizontal components of the temperature advection are estimated as
and
where \({\overline{u}}\) (\({\overline{v}}\)) is the horizontally-averaged u-component (v-component) of the velocity vector over the box of length \(L=10^4\) m indicated in Fig. 1. The second term is computed from the difference between the potential temperature at the eastern (northern) and western (southern) edges of the box for any given latitude (longitude) and then averaged over all latitudes (longitudes) included in the box. This computation is applied for all vertical model levels, resulting in average profiles of the horizontal components of temperature advection.
3.3 Sensible-Heat-Flux Estimation
The heat flux is calculated with the profile-integration method based on an algorithm developed for the SMARTSonde aircraft and used for the first time on RPAS data by Bonin et al. (2013). The general technique, which originates from Deardorff et al. (1980), is based on a simplified version of the prognostic equation for the potential temperature \(\theta \) relating the change of the mean quantity with time to the flux divergence. After horizontally averaging and vertically integrating from the height z to \(h_{F0}\), where \(h_{F0}\) is the height at which the flux is zero, assuming horizontal homogeneity, and neglecting diabatic processes, mean vertical motion and molecular diffusivity, then the sensible heat flux
Each pair of RPAS profiles of temperature T, potential temperature \(\theta \), and pressure p are linearly interpolated from the 20-m bins to a common vertical grid of \({\varDelta } z=\) 1 m prior to integration.
Two consecutive profiles are combined to calculate the temperature changes \({\varDelta }\theta \) over the time period \({\varDelta } t\) between the flights using the specific heat at constant pressure \(c_p\) and the density \(\rho \) (calculated from profiles of T and p). The sensible heat flux is obtained by summation from each height level z to the top of the profiles where the flux should be zero (\(h_{F0}\)) above the entrainment zone as
Visualization of the method to determine the mixed-layer depth h for flight # 88 at 1217 UTC on 20 June (a–c) and the SBL depth \(h_{SBL}\) for flight # 259 at 1935 UTC on 4 July (d–f) using the information from the profiles of \(\theta \), \(\theta '\), and \(\theta ''\) (a, d), the profiles of q, \(q'\), and \(q''\) (b, e), and the profiles of wind speed u and wind direction \(\phi \) (c, f) obtained from the SUMO platform
The heat-flux-estimation algorithm assumes that any change in temperature is due to vertical turbulent heat transport, implying no advection and subsidence, and no diabatic radiative heating/cooling or condensation/evaporation processes within the air column. Since these assumptions are not necessarily fulfilled in real-world situations, we use this simplified estimate with caution. Model output from the MesoNH simulations clearly show radiative effects \(<2.8\times 10^{-5}~\hbox {K}~\hbox {s}^{-1}\) up to 2000–2200 UTC, implying a negligible contribution for our profiles, as the flux profile from each pair is calculated for times earlier than 2010 UTC. With respect to advection, we propose different correction methods to obtain more realistic heat-flux profiles described below (Sects. 3.3.1–3.3.3). Cases that potentially violate the assumptions behind Eq. (4), or cannot be treated properly with the proposed advection corrections, are marked correspondingly.
3.3.1 Correction Method 1: Constant Advection at All Levels
The constant-advection correction (referred to as method 1) relates the mean change in the value of \({\varDelta }\theta /{\varDelta } t\) in the free atmosphere to the large-scale advection, which is assumed to be independent of height, and, therefore, representative for the ABL (the method was developed and applied by Bonin et al. 2013).
The first step requires objectively determining the mixed-layer depth h by finding the maximum and minimum values of the terms \(\partial ^2\theta /\partial z^2=\theta ''\) and \(\partial ^2q/\partial z^2=q''\) in the second profile in each pair, where q is the specific humidity [g kg\(^{-1}\)]; the method may be visualized in Fig. 3a–c. Since some cases need additional information to determine the value of h, a flag (1–3) has been added to all profiles in Table 4 in Appendix 1, Electronic Supplementary Material denoting the following approaches: (1) the maximum/minimum values of the second derivative as described above, (2) using a prominent secondary maximum of the second derivative, and (3) manually inspecting the temperature, humidity, wind speed u, and wind-direction \(\phi \) profiles to find the most reasonable h value.
We then determine the level above which temperature advection is dominant and there are no longer ABL or entrainment effects. This level, which is typically several tens to a few hundred meters higher than the mixed-layer top itself, is the entrainment-zone top at \(z=h_{EZT}\). We assume that the instantaneous inversion zone separating the mixed layer and the free atmosphere is quite thin for a snap-shot profile (Deardorff et al. 1980), and define \(h_{EZT}=1.2h\) as a compromise between being sure to be out of the entrainment zone, but still have a substantial part of the free atmosphere covered. Above this height, we expect to find a steady change in temperature over time, and typically also distinct wind direction and/or wind-speed changes.
In a second step, the mean temperature change between two consecutive profiles (i.e. the mean \({\varDelta }\theta /{\varDelta } t\) value) above the height \(z=h_{EZT}\) is calculated and subtracted from the original \({\varDelta }\theta /{\varDelta } t\) profile before the sensible heat flux is recalculated based on Eq. (4). An example of applying the constant-advection correction can be seen in Fig. 4b where the average \({\varDelta }\theta /{\varDelta } t\) value of the original profile (dashed line) in the free atmosphere is \(-0.5\times 10^{-4}\) K s\(^{-1}\), which is then subtracted over the entire column to give the advection-corrected \({\varDelta }\theta /{\varDelta } t\) profile (solid line). Using method 1, the integration height is set to the top of the profile to make the resulting flux estimate as robust as possible. In this way, the flux in the free atmosphere functions as a check of the advection correction, as it should be zero after the integration.
The constant-advection method is used for cases with a fully-developed CBL, corresponding to the time when the mixed layer of the second profile has outgrown the capping inversion of the residual layer (determined by manual inspection). By this constraint, we avoid using the method during complex stratification with residual-layer structures. We mark the heat-flux estimates subject to subsidence, height-dependent advection, or having very small regions of the free atmosphere included in the RPAS profiles (see Appendix 1, Electronic Supplementary Material).
Examples of corrected \({\varDelta }\theta /{\varDelta } t\) profiles (thick solid red lines) using a correction method 2 for a growing CBL with constant advection below the entrainment zone top at \(z=h_{EZT}\) (flight # 172–175, 27 June, 0835–0936 UTC), b correction method 1 for a fully-developed CBL with constant advection at all levels (flight # 266–267, 5 July, 1035–1218 UTC), and c correction method 2 for a developing SBL with constant advection below \(z=h_{SBL}\) (flight # 258–259, 4 July, 1905–1937 UTC). The original \({\varDelta }\theta /{\varDelta } t\) profiles for the whole column (dashed red lines) and the integration range of method 2 (thin solid red lines) are shown for comparison. The potential-temperature profiles are shown as dashed (first profile) and solid (second profile) blue lines. The levels h, \(h_{EZT}\) and \(h_{SBL}\) are marked by dotted horizontal lines
3.3.2 Correction Method 2: Constant Advection Below a Specific Level
Method 1 is significantly challenged in any situation where the surface forcing is decoupled from the capping inversion and thus the free atmosphere, which is the case for both the growing CBL in the morning and the developing SBL in the evening. In both cases, the residual layer from the previous day is still present above, separating the free atmosphere from the direct influence of the surface forcing. Thus, we propose the correction method 2 of integrating the flux only between the surface and \(z=h_{EZT}\) for profiles with a growing CBL in the morning, and only between the surface and \(z=h_{SBL}\) for profiles with an SBL forming at the surface in the evening. As for the fully-developed CBL cases, these profile types are determined by manual inspection.
The advection correction here is based on the assumption that all observed temperature changes at the corresponding levels \(z=h_{EZT}\) for the growing CBL and \(z=h_{SBL}\) for the developing SBL are caused by advection that is representative of the whole layer below. Consequently, we correct for advection by shifting the profile of \({\varDelta }\theta /{\varDelta } t\) to equal zero at the heights \(z=h_{EZT}\) and \(z=h_{SBL}\). The mixed-layer depth for the growing CBL is detected based on the criteria already presented in Sect. 3.3.1, with \(h_{EZT}=1.1h\) following a suggestion by Foken (2017). The SBL depth \(h_{SBL}\) is detected as the top of the surface inversion where the values of \(\theta '\) and \(\theta ''\) become constant as shown in Fig. 3d–f. As for method 1, a flag (for the SBL, 1–2) has been added to Table 4 in Appendix 1, Electronic Supplementary Material to make it clear when additional inspection of the profiles of q, \(\theta \), u, and \(\phi \) is needed to determine the value of \(h_{SBL}\).
Figure 4a, c shows examples of a growing CBL in the morning and a SBL forming at the surface, respectively. The solid thick lines correspond to the advection-corrected profile by integrating between the surface and the heights \(z=h_{EZT}\) or \(z=h_{SBL}\), respectively, for calculation of the sensible-heat-flux profile using Eq. (4). The original uncorrected \({\varDelta }\theta /{\varDelta } t\) profiles are shown for the whole column as dashed lines, and within the relevant integration range, i.e. the boundary layer, as solid lines. In both cases, advection has a cooling effect leading to too low positive heat-flux values for the growing CBL case, and too large negative heat-flux values for the SBL case if not appropriately corrected.
3.3.3 Correction Method 3: Height-Dependent Advection from a Mesoscale Model
Mesoscale simulations with high spatial and temporal resolution (described in detail in Sect. 3.2.3) are available for several IOP during the BLLAST campaign, offering an opportunity to test the use of advection calculated by the model as a correction for the temperature profiles measured by the SUMO platform. This approach is referred to as correction method 3.
Potential-temperature \(\theta \) profiles (a–c) and sensible-heat-flux H sensitivity (d–f) to the entrainment-zone top at \(z=h_{EZT}\) when estimating the flux with the advection-correction method 1 for the three cases of low (a, d), medium (b, e), and high (c, f) sensitivity. The original flux estimate (dashed red line) is shown together with the corrected flux estimate using method 1 (thick solid red line), and estimates using a range (\(\pm 140\) m in 20-m steps) of adjacent \(h_{EZT}\) levels (dashed coloured lines from blue to yellow). The horizontal dotted lines show the value of \(z=h_{EZT}\), and the mixed-layer top at \(z=h\). Corresponding fluxes from the EC surface stations (symbols) are plotted for reference (see Sect. 3.2.1 for more information on the fluxes from the EC stations)
The MesoNH model advection in the x- and y-directions (calculated from Eqs. (1) and (2), respectively) are combined as \(Adv\theta _{hor} = Adv\theta _x + Adv\theta _y\) to provide the total horizontal-advection profile, which is available every 30 min. The advection estimates from several profiles covering the time period between two consecutive SUMO profiles for the flux determination are added together. The first and last 30-min profiles have been weighted with respect to the number of relevant minutes to fit the exact time period between the two SUMO profiles.
To incorporate the advection from the model into the RPAS flux estimation, we add the \(Adv\theta _{hor}\) profile to the \({\varDelta }\theta /{\varDelta } t\) profile calculated between the two consecutive SUMO flights, which results in a modified \({\varDelta }\theta /{\varDelta } t\) profile for calculation of the sensible heat flux using Eq. (4). Using method 3, the integration level \(z=hF0\) is placed in accordance with method 1 and method 2 for each case.
3.4 Sensitivity of the Heat-Flux Estimation
The important height levels for a robust heat-flux estimation are \(z=h_{EZT}\) and \(z=h_{SBL}\). The importance of accurately determining the vertical range over which the fluxes are integrated has also been highlighted by previous studies (Knuth and Cassano 2014; Wildmann et al. 2015). By the nature of the correction methods presented here, method 1 is potentially sensitive to the value of \(z=h_{EZT}\), and method 2 may be strongly dependent on the value of \(z=h_{EZT}\) for the growing CBL or the value of \(z=h_{SBL}\) for the developing SBL. To investigate the robustness of the resulting flux profiles, we performed a systematic sensitivity test of all profiles to be used below for an uncertainty estimate of the calculated flux profiles from the SUMO platform. Using method 1, the level \(z=h_{EZT}\) determines the lower boundary of the atmospheric column for calculation of the mean value of \({\varDelta }\theta /{\varDelta } t\) for the advection correction. Uncertainties in \(z=h_{EZT}\) can lead to corresponding inaccuracies in the heat-flux profiles. The potential effect depends on the sensitivity of the calculated flux profile to an inaccurate determination of the value of \(h_{EZT}\). The magnitude of the effect varies individually, mainly dependent on the vertical structure of \({\varDelta }\theta /{\varDelta } t\) profiles in the free atmosphere. In cases with well-defined and height-invariant advection, slightly adjusting \(z=h_{EZT}\) does not make a significant difference. The correction is especially robust if a large part of the free atmosphere is captured by the RPAS profile, as the calculated mean is rather unaffected by the chosen lower boundary. For the sensitivity test on profiles using the advection-correction method 1, we recalculate the flux profiles by varying \(z=h_{EZT}\) in 20-m steps in an interval of \(\pm 140\) m around the originally chosen height.
Figure 5 shows three examples of the flux sensitivity to the value of \(z=h_{EZT}\) using correction method 1, representing low, medium and high sensitivities. The low-sensitivity case (5 July 0923–1035 UTC) has a well-defined steady positive change in the free atmosphere of about 1 K from the first to the second profile, implying the correction by method 1 changes little unless \(z=h_{EZT}\) is unrealistically low (i.e. \(<h\)). The intermediate-sensitivity case (2 July 1105–1222 UTC) shows a slightly-variable and positive change of around 0.5 K between the two profiles. The captured region of the free atmosphere is additionally shallower, so the correction of method 1 is more affected by a change in \(z=h_{EZT}\). The highly-sensitive case (27 June 1253–1357 UTC) represents a situation where the top of the entrainment zone is very close to the ceiling of the SUMO profile, leaving only about 20 m for the calculation of the average value of \({\varDelta }\theta /{\varDelta } t\). Below \(z=h_{EZT}\) down to \(\approx \)1200 m, there is a layer of distinct temperature difference between the two profiles, indicating a strong mixed-layer growth in between their recording. This and similar cases have been flagged as having captured a small region of the free atmosphere and should be interpreted with care.
Using the approach of method 2, the flux is integrated up to the height \(z=h_{EZT}\) for a growing CBL or up to the height \(z=h_{SBL}\) for a developing SBL. Changing this level, therefore, gives different advection corrections to the \({\varDelta }\theta /{\varDelta } t\) profile in the boundary layer, yielding different results for the calculated flux profiles. However, the heat-flux estimates based on the correction by method 2 are generally less sensitive to the values of \(z=h_{EZT}\) or \(z=h_{SBL}\) than the sensitivity of method 1 to the value of \(z=h_{EZT}\), since the overall integration by Eq. (4) extends over a considerably shallower layer for the developing morning CBL or any SBL. Again, the sensitivity was investigated by varying the chosen integration height in 20-m steps (see the Supplementary Electronic Material).
4 Analysis of Sensible-Heat-Flux Profiles
In the following, we first present examples of individual sensible-heat-flux profiles for a growing morning CBL (using correction method 2 up to the top of the entrainment zone at \(z=h_{EZT}\)), a fully-developed CBL (using correction method 1), and a developing SBL in the evening (using correction method 2 up to the top of the SBL at \(z=h_{SBL}\)). The lowermost values of all of those profiles are compared to flux values from EC stations close to the ground and at different altitudes of the 60-m mast. For one case, direct airborne-flux measurements from a manned research aircraft and from a sonic system on a tethered balloon are also available for validation. Thereafter, we present a case study showing the diurnal evolution of the sensible heat flux for a day with numerous SUMO profile flights combining the correction methods 1 and 2. The near-surface values of all SUMO heat-flux profiles during the campaign are then compared to the corresponding flux values from the EC stations, which enables a robust statistical evaluation and analysis of the proposed method. Finally, we present a second case study exploring the potential of incorporating advection information from the MesoNH model (using correction method 3) in improving the performance of our flux-estimation algorithm.
4.1 Flux Profiles for Different Atmospheric States
4.1.1 Developing Morning Convective Boundary Layer
Figure 6 shows the \(\theta \) profiles, their change \({\varDelta }\theta /{\varDelta } t\), and the sensible-heat-flux estimate between 0627–0740 UTC from 5 July. The SBL below 190 m from 0627 UTC develops into a CBL with a mixed-layer depth of 210 m at 0740 UTC. The residual layer, which is still present above from the previous day, extends to about 700 m and efficiently decouples the developing CBL from the higher levels, showing a slight, but rather variable increase in temperature with height. Above, there is almost no change in the value of \(\theta \) between 800 and 1200 m, before a clear increase occurs with height above 1200 m, most likely indicating large-scale horizontal advection and/or subsidence.
Sensible-heat-flux H estimation for a growing CBL, applying the correction method 2 between the SUMO profiles at 0627 UTC (black) and 0740 UTC (blue) on 5 July. The \(\theta \) profiles, the \({\varDelta }\theta /{\varDelta } t\) profile, and the flux profile are given in (a), (b), and (c), respectively. The original profile of \({\varDelta }\theta /{\varDelta } t\) is shown for the whole column (dashed red line), for the integration range of correction method 2 (thin solid red line), and after correction (thick solid red line). The mean flux values from the different EC stations over the corresponding time period are plotted for reference. The symbols and colours identifying the EC stations are listed in Table 2. The inset on the top right is magnified over the lowest 80 m of the heat-flux profile
The method of integrating up to the height \(z=h_{EZT}\) (method 2) is, therefore, used to capture the physical constraints as a result of the decoupling between this growing ABL from the higher levels. Advection effects in the developing CBL are, in this case, rather weak, as indicated by the near-zero change in the value of \({\varDelta }\theta /{\varDelta } t\) at the height \(h_{EZT}\) (\(-0.25\times 10^{-4}\) K s\(^{-1}\)) applied for the advection correction.
The resulting corrected flux profile is slightly negative at the top of the CBL before increasing in magnitude towards the surface. The EC flux measurements at the surface range between \(20~\hbox {W}~\hbox {m}^{-2}\) and \(36~\hbox {W}~\hbox {m}^{-2}\), with an average of \(30~\hbox {W}~\hbox {m}^{-2}\). The corrected heat-flux estimate from the SUMO platform is \(29~\hbox {W}~\hbox {m}^{-2}\) and is clearly within the observed spread. The stations over forest and wheat show considerably higher values (55–73\(~\hbox {W}~\hbox {m}^{-2}\)). Within the uncertainty interval of well-maintained EC stations of the order of \(10~\hbox {W}~\hbox {m}^{-2}\) (e.g. Oncley et al. 2007), the SUMO flux profile also agrees well with the tower measurements. The original uncorrected SUMO heat flux integrated over the relevant range (i.e. up to \(z=h_{EZT}\)) is lower (at \(23~\hbox {W}~\hbox {m}^{-2}\)) than the corrected one (but still within the spread of the EC stations), and also less in agreement with the 60-m tower values (see the inset in Fig. 6).
4.1.2 Fully-Developed Convection Boundary Layer
Figure 7 shows the \(\theta \) profiles, their change \({\varDelta }\theta /{\varDelta } t\), and the sensible-heat-flux estimate for the period 1222–1425 UTC on 2 July. The CBL is fully developed in both profiles, and reaches 1050 m at 1425 UTC, after having grown by about 100 m since 1222 UTC. The uncorrected flux profile calculated from Eq. (4) has a value of 176 W m \(^{-2}\) at the surface, which is considerably higher than the average over the main group of EC-station measurements (104 W m \(^{-2}\)). A constant positive change of \(0.33\times 10^{-4}\) K s\(^{-1}\) is visible in the \(\theta \) and \({\varDelta }\theta /{\varDelta } t\) profiles above 1260 m in the free atmosphere, which is used to correct the original profile of \({\varDelta }\theta /{\varDelta } t\) by applying the constant-advection correction method 1.
As for Fig. 6 but for SUMO profiles at 1222 UTC (black) and 1425 UTC (blue) on 2 July. Method 1 is now applied to correct for the effect of the advection in the temperature profiles for this fully-developed CBL. The original profiles of \({\varDelta }\theta /{\varDelta } t\) and the sensible heat flux are shown as dashed red lines, while the corrected are shown in thick solid red lines
As expected, method 1 works well for this case, which is a textbook CBL profile of the sensible heat flux: close to zero in the free atmosphere, slightly negative in the entrainment zone, and increases linearly towards the surface in the boundary layer. The heat flux from the SUMO platform (\(103~\hbox {W}~\hbox {m}^{-2}\)) matches the average flux value for the main group of EC stations (\(104~\hbox {W}~\hbox {m}^{-2}\)), and is also in good agreement with the three levels from the 60-m tower, with measurements from the EC stations over forest and wheat again showing much higher values (280–320\(~\hbox {W}~\hbox {m}^{-2}\)).
The SUMO sensible-heat-flux H profile for the period 1222–1425 UTC on 2 July plotted against the flux from transects by the manned aircraft in the period 1253–1357 UTC (a), and the position of the transects with reference to site 1 (b). The original SUMO profile is shown as a dashed red line, and the advection-corrected (method 1) profile as a thick solid red line. The position of each manned aircraft 2.5-km sub-leg is shown as an open circle and corresponds to one circle for the flux. The colours represent the four pressure levels of the aircraft tracks. The filled circles represent flux values calculated over the entire 25-km east–west (yellow) or north–south (cyan) branch of the aircraft track. The inset in b shows the relation to topography of all sub-legs. The black diamonds show flux values from a tethered balloon equipped with a sonic-anemometer system at 1300 UTC taken from Canut et al. (2016). The mean sensible heat flux from the different EC stations are again plotted for reference at the surface. The symbols and colours identifying the stations are listed in Table 2
As for Fig. 6 but for the SUMO profiles at 1759 UTC (black) and 2002 UTC (blue) on 20 June. Method 2 is applied to correct the effect of the advection in the temperature profiles for this developing SBL
The SUMO sensible-heat-flux profile presented in Fig. 7 can also be compared to direct flux measurements from the manned aircraft operated in the area during the time period 1253–1357 UTC between the two SUMO profiling missions in Fig. 8. The right panel shows the projection of the corresponding flight pattern consisting of level straight legs in the north–south and east–west directions at four different pressure altitudes on this day, corresponding to levels between approximately 300 m and 1000 m above the elevation of measurement site 1 (see inset in Fig. 8b for information on the topography along the tracks). Each red open circle in the left panel of Fig. 8 corresponds to one of the red circles along the flight track, and represents a flux value averaged over a 2.5-km leg. The filled, coloured symbols give the flux when calculated over the full 25-km leg, whose values are in excellent agreement with the advection-corrected SUMO profiles. The flux data over the individual 2.5-km legs show some variability, but are distributed more or less evenly around the flux profile from the SUMO platform. An analysis (not shown) with respect to the position along the flight track, and thus the distance from the location of the SUMO profiles at site 1, reveals no systematic clustering of data points in the scatter plot, indicating that the observed variability is mainly related to internal spatial and temporal variability of the ABL rather than to the surface properties and heterogeneity along the flight track. This is also consistent with the observation that the variability around the SUMO profile has no clear height dependency. In the case of a considerable influence of the surface heterogeneity, one would expect an increase in variability towards the ground. At the level of around 400 m a.g.l., the SUMO heat-flux profile can also be compared to direct flux measurements from a sonic system carried by a tethered balloon (Canut et al. 2016), which are marked as black diamonds in Fig. 8, and coincide well with both the SUMO and the manned-aircraft flux estimates.
4.1.3 Developing Stable Boundary Layer
Figure 9 shows the \(\theta \) profiles, their change \({\varDelta }\theta /{\varDelta } t\), and the sensible-heat-flux estimate in the period 1759–2002 UTC from 20 June. An SBL develops in the evening hours by radiative cooling of the surface as the incoming solar radiation decreases and is no longer able to balance the outgoing longwave radiation. Remaining from the CBL earlier in the day, the residual layer persists above the extent of the SBL of height 140 m. The residual-layer inversion top decreases by about 200 m from 1759 to 2002 UTC, and the whole residual layer has slightly stabilized. There is almost no change between the two profiles in the free atmosphere above 1200 m, indicating the absence of large-scale advection.
All SUMO \(\theta \) profiles (a) and all SUMO sensible-heat-flux H estimates against the mean flux from the EC stations at the surface (b) from 5 July. The \(\theta \) profiles are reported in UTC and in parentheses is reported the flight number. Each flux estimate is marked by the flight numbers of the contributing profiles. The gray asterisk, purple diamond, and purple circle refer to the flux-estimation methods. The error bars show the spread between the EC stations (x-axis) and the SUMO heat-flux sensitivity to a variation in the height \(z=h_{EZT}\) or \(z=h_{SBL}\) of \(\pm \,20\) m around each chosen value (y-axis)
There is a clear stabilization in the developing SBL below 140 m, with a cooling rate exceeding \(3\times 10^{-4}~\hbox {K}~\hbox {s}^{-1}\) close to the surface. Integrating the original heat-flux estimate through just the SBL yields \(-\,28~\hbox {W}~\hbox {m}^{-2}\), but a still considerable cooling \(>1\times 10^{-4}~\hbox {K}~\hbox {s}^{-1}\) occurs at \(z=h_{SBL}\), which is either caused by local advection or longwave-radiation divergence, and needs to be corrected for a proper estimation of the turbulent heat flux. Assuming no temperature change at \(z=h_{SBL}\) by applying the correction method 2 leads to SUMO flux estimates much closer to the values produced by the EC stations. The sensible heat flux from the SUMO platform is reduced to \(-11~\hbox {W}~\hbox {m}^{-2}\) at the surface, which is clearly within the spread of the EC values, and close to the EC flux average of \(-\,8~\hbox {W}~\hbox {m}^{-2}\). Magnifying the lowest levels shows that the corrected SUMO flux profile has a steeper slope than the original profile, and also now matches the EC measurements for all three height levels on the tower.
4.2 Daily Sensible-Heat-Flux Evolution: 5 July
So far we have only presented selected situations to exemplify the flux-estimation method under different boundary-layer conditions and the effect of the applied advection-correction methods 1 and 2. Here, we analyze the evolution of the ABL and the corresponding flux profiles over the course of 5 July. Figure 10 shows the development of the potential temperature \(\theta \) and the derived heat flux based on SUMO profiles from the morning at 0627 until the late afternoon at 1731 UTC.
The mixed-layer depth increased slowly initially, and then more rapidly around midday, before reducing considerably in the afternoon/evening. This ABL development falls under category three of observed ABL developments (see also Sect. 2) during the BLLAST campaign (Lothon et al. 2014) as also discussed in Blay-Carreras (2013) and Nilsson et al. (2016).
The potential temperature at the surface increased from 295 K at 0627 UTC (SBL) to a maximum of 304 K in the afternoon. The new developing CBL grows through the residual layer, at that time extending to about 550 m, during the time period 0923–1035 UTC, which also marks the transition from applying the advection-correction method 2 in the growing CBL to the use of method 1 in the now fully-developed CBL. The maximum extension of the mixed layer was reached at 1556 UTC with a depth slightly above 1000 m.
Figure 10b shows that the advection correction clearly improves the flux estimates for each pair of profiles during that day, as indicated by the shift of the purple symbols (advection corrected) closer towards the 1:1 line compared with the corresponding grey symbols (raw values). The largest improvements are seen for the pairs 264–265 (from 285 to \(118~\hbox {W}~\hbox {m}^{-2}\)), 265–266 (from 416 to \(126~\hbox {W}~\hbox {m}^{-2}\)), and 266–267 (from \(-2\) to \(127~\hbox {W}~\hbox {m}^{-2}\)), with the uncorrected SUMO flux estimates for the first two time periods even located outside the range of the y-axis. After advection correction, all SUMO flux estimates fall inside the range of values from the EC surface stations.
4.3 Systematic Comparison with the Eddy-Covariance Measurements
In the previous sections, we only presented selected examples for the proposed flux-estimation method. The distributed network of EC stations deployed over a range of surface types allows us, however, to conduct a more systematic and statistically-robust analysis of the potential and limitations of our flux-estimation algorithm.
The SUMO sensible-heat-flux H estimates for the surface layer (y-axes) plotted against the average flux from the EC surface stations (x-axes). The data are grouped into the morning (MOR; 0500–1000 UTC; (a, e)), midday (MID; 1000–1400 UTC; (b, f)), afternoon (AFT; 1400–1800 UTC; (c, g)), and evening (EVE; 1800–2100 UTC; (d, h)) periods. The panels (a–d) contain all data points, including clear outliers, while the panels (e–h) have magnified axes to focus on the realistic fluxes. The symbols denote the advection-correction method used for each case: method 1 (circles) and method 2 (diamonds). The error bars show the spread of the EC stations (x-axes) and the sensitivity of the SUMO estimates to a variation in \(z=h_{EZT}\) or \(z=h_{SBL}\) of \(\pm 20\) m around the chosen value (y-axes). Data shown in purple are not expected to have increased uncertainty. The other colours denote flux estimates of higher uncertainty due to the effects of either subsidence (red), highly variable \({\varDelta }\theta /{\varDelta } t\) values (yellow), only a small part of the free atmosphere being captured (blue), and the presence of scattered or broken clouds (black triangles or squares, respectively) as potential indicators for diabatic effects
Figure 11 and Table 3 summarize a comparison of all 108 SUMO surface-layer sensible-heat-flux estimates with the flux data from the EC stations. The EC measurements on the x-axes represent the average flux over all stations at the surface (see also Table 2), except for wheat as discussed in Sect. 3.2.1. The error bars indicate the spread between the minimum and maximum value of the average station values. The values on the y-axes show the advection-corrected heat-flux estimates from the SUMO platform, where the correction methods 1 and 2 have been applied based on the criteria described in Sects. 3.3.1 and 3.3.2. The error bars represent the sensitivity of the SUMO flux estimates to a variation in the height \(z=h_{EZT}\) or \(z=h_{SBL}\) of \(\pm \,20\) m around each chosen value. Flagged and marked by the colour coding are heat-flux estimates with expected higher uncertainty because of either subsidence, only a small region of the free atmosphere is captured, or a highly-variable value of \({\varDelta }\theta /{\varDelta } t\). The subsidence flag is activated using method 1 if the mixed-layer depth decreases from one flight to the next. Using method 2, we flag for subsidence in cases where the residual-layer inversion sinks and merges with the growing CBL. The flag for capturing only a small region of the free atmosphere is used for method 1 in situations where \(z=h_{EZT}\) is located at 1400 m or above, leaving < 200 m of the free atmosphere for the determination of the constant-advection correction. The variable \({\varDelta }\theta /{\varDelta } t\) flag is used if the sum of the absolute maximum and minimum change in potential temperature in the free atmosphere, after applying the advection correction, is > 0.9 K. In total, 44 of the 108 cases during the BLLAST campaign have been flagged for one of these reasons (see Table 3 and Appendix 1, Electronic Supplementary Material).
To account for a potential diabatic effect by phase changes in the mixed layer, we included a final flag based on the convective cloud cover over the time period between consecutive flights by manual inspection of the time series of incoming solar radiation in combination with available all-sky camera pictures to distinguish between clear conditions (no flag, corresponding to 0–1 octa of Cu cloud cover), scattered clouds (2–4 octa of Cu cloud cover), and broken cloud cover (5–6 octa of Cu cloud cover) for the time period of corresponding flight pairs (see Appendix 1, Electronic Supplementary Material).
The results are separated into four different time periods representing different typical development states of the ABL to investigate the performance of the heat-flux algorithm in more detail. The chosen time periods are 0500–1000 UTC for the morning, 1000–1400 UTC for the midday, 1400–1800 UTC for the afternoon, and 1800–2100 UTC for the evening. Sunrise and sunset during the IOP periods of the BLLAST campaign varied between 0419 and 0425 UTC and 2140 and 2142 UTC, respectively. While the distribution of our 108 cases over the different periods of the day is not fully homogeneous, with more than 30 cases for the midday and afternoon, and around 20 for the morning and evening, each period has sufficient data for a statistical analysis. The axes limits for the panels to the left (−670–1340\(~\hbox {W}~\hbox {m}^{-2}\)) have been chosen to show all SUMO heat-flux estimates, and show that all extreme outliers can be associated with at least one of the identified uncertainty factors. The four panels on the right have limits between −50 and \(250~\hbox {W}~\hbox {m}^{-2}\) for the morning, midday and afternoon periods, and between \(-50\) and \(10~\hbox {W}~\hbox {m}^{-2}\) for the evening period, with the results in the realistic range of flux values magnified. All (except two during the midday) non-flagged flux estimates (coloured in purple) are found within these limits. The majority of the non-flagged data points, in particular for the morning, midday and evening, are within the uncertainty estimates located on the 1:1 line. For the afternoon, however, there is a systematic underestimation of the heat flux estimated by the SUMO platform in many of the cases.
The results presented in Fig. 11 are quantified in more detail by the results presented in Table 3, showing the number and percentage of cases for the different times of the day for which the different versions of the flux estimates from the SUMO platform are found within the spread of the corresponding EC measurements. Overall, our proposed method for the flux estimation from SUMO profiles when applying one of the advection-correction methods 1 or 2 results in 51\(\%\) of the cases being within the spread of the EC stations (column “H all method 1,2”). Without advection correction, only 25\(\%\) of the data fulfill this criterion. For the various times of the day, the success rate for the advection-corrected values varies between 30\(\%\) (afternoon) and 94\(\%\) (evening). Considering only the non-flagged cases (column “H no-flag method 1,2”), the results improve substantially, with a total of 77\(\%\) of the cases falling within the spread of the EC stations. The highest success rate of 94\(\%\) is reached for the evening followed by the morning with 81\(\%\), the midday with 69\(\%\), followed by the period for the decaying CBL (afternoon) showing the poorest performance, with only 63\(\%\) of the estimates within the spread of the EC stations (Table 3). The heat-flux estimation seems to struggle in situations when the surface flux changes from positive to negative values between the recording of the two SUMO profiles. One possible explanation is that the second SUMO flight rarely observes the exact start of the SBL development, and so the SUMO flux estimate, which is an average flux over this time span, misses the still-positive flux contribution right before the onset of the SBL. The correction by method 2 interprets this part as advection and consequently over-adjusts the \({\varDelta }\theta /{\varDelta } t\) profile. The mean flux of each EC station is based on an average over positive and negative flux values around the time the SBL starts to develop from the ground, resulting in a higher flux value from the EC stations compared with the value from the SUMO platform, and is a common underestimation tendency for the transition period for all days. The magnitude of the error in each individual case is linked to how much of the boundary-layer change was missed over the time period between the two consecutive profiles. The vertical error bars, indicating the sensitivity of the heat-flux estimates from the SUMO platform to a variation in the height \(z=h_{EZT}\) or \(z=h_{SBL}\) of \(\pm 20\) m around the chosen value, vary to a large extent, but are clearly smallest during the afternoon for the convective situations. For the vast majority of the situations, this uncertainty is also considerably lower than the spread of flux values from the EC stations.
For the interpretation, it should be kept in mind the challenge of comparing flux estimates from a moving RPAS platform to ground-based measurements fixed at one location. One cannot expect a perfect match, since the difference in the measurement principles results in largely different footprints over heterogeneous terrain. The EC stations close to the surface have small footprints, with each station representing their respective surface cover. The tower has increasingly larger footprints from the levels of 30 m to 45 m to 60 m, becoming more affected by a mixture of the surface types found over a larger area. The flux from the SUMO platform is influenced by an even larger footprint area as the aircraft ascends to nearly 1600 m. The footprint area is additionally affected by atmospheric stability (e.g. Kljun et al. 2002) and the background wind speed. An analysis with the bulk CBL model CLASS (Vilà-Guerau de Arellano et al. 2015) for the IOP of the BLLAST campaign indicates that a footprint region of the order of 2–3 km upstream seems to be a realistic guess (Seidl 2017). Comparing the fluxes from the SUMO platform to the average flux over all EC stations over the time span between the flights ensures that the integrating capacity of the CBL is taken into account, and that the EC-based heat-flux measurements are not dominated by a single surface type.
Phase changes and latent-heat release may be one of the reasons for the failure of the sensible-heat-flux-estimation techniques to give realistic flux values, as it is clear from Table 1 that several of the days have at least partially-cloudy conditions. For a more detailed investigation of this hypothesis, we introduced two flags indicating scattered or broken cloud cover by convective clouds. These two flags indicate 37 of the convective cases as potentially affected by diabatic effects related to phase changes, with 27 of those, however, already marked by one of the previously-defined flags for either subsidence, a small region of free atmosphere or variable advection. The overlap of 75% (12 out of 16) is particularly large for the latter condition, indicating the close connection in changes of humidity and temperature profiles in the case of condensation, and a potential misinterpretation of this effect as a change in horizontal advection with height. Figure 11a–c shows that the application of the diabatic flags indicated by the squared or triangular boxes around the corresponding data points removes not all but a considerable amount of the heavy outliers from the dataset, which is also evident in the magnified panels Fig. 11e–g where the diabatic flags again predominantly mark data points further removed from the 1:1 line.
The variability of the time difference for each pair of temperature profiles presented in Sect. 3.1 was not found to have any systematic effect on the resulting fluxes, but such effects should be investigated in detail by future targeted experiments where one intentionally alters \({\varDelta } t\) under more constant atmospheric conditions.
4.4 Potential for Using Model Advection (method 3): 1 July
The treatment of advection is further investigated for the case of 1 July (IOP 9) by using correction method 3, because this day was one of the most intensively-studied and analyzed IOP of the BLLAST campaign (Cuxart et al. 2016; Román-Cascón et al. 2015). The trial is motivated by the fact that the correction methods 1 and 2 are unable to appropriately handle all situations. Exact and timely advection estimates taken from model simulations may help to reduce the uncertainties in the correction algorithm related to the assumption of height-independent advection, or in the cases with an inflated mixed-layer depth with respect to the highest altitude of the SUMO profiles.
Sensible-heat-flux H estimates from the SUMO platform corrected by height-dependent advection from the mesoscale model MesoNH for all flights from 1 July plotted against the average flux from the EC stations at the surface. All \(\theta \) profiles (a) are reported in UTC together with the flight number, whereas all profiles of model advection (b), \({\varDelta }\theta /{\varDelta } t\) (c) and H (d) are marked by the two relevant flight numbers. The \({\varDelta }\theta /{\varDelta } t\) profiles are shown before and after correction by the model data as dashed lines and solid thin (entire profile) and thick (relevant integration range) lines, respectively. The colours of the model-advection profiles and the \({\varDelta }\theta /{\varDelta } t\) profiles correspond to the colour of the first of the two relevant \(\theta \) profiles. The error bars show the spread of the flux values from the EC stations
The flux profiles estimated from the SUMO platform are corrected by the horizontal temperature advection forecasted by the MesoNH model as described in Sect. 3.3.3 and shown in Fig. 12. This day is strongly influenced by advection due to the thermally-driven flow present in the region (Jiménez et al. 2019). The SUMO profiles of potential temperature show a growth of the ABL during the morning transition up to about 1200 m a.g.l. at around noon, after which it remains nearly stationary (well-mixed CBL) until 1830 UTC when a shallow SBL develops from the ground (Fig. 12a).
The observed temperature change between the SUMO profiles (dashed lines in Fig. 12c) indicates warm-air advection until the early afternoon, changing slowly into cold-air advection towards the evening. The strong positive temperature advection around midday is clearly associated with thermally-driven plain-to-mountain circulations and northerly upslope flow over Lannemezan. The subtraction of the advection predicted by the model is shown by the solid lines in Fig. 12b. The warm air predicted by the model during the large parts of the day reduces the temperature change as seen by the shift to the left of the solid lines. As a result, the sensible-heat-flux estimates from the SUMO platform are reduced and move closer to the values reported by the surface stations. As no advection is predicted by the model towards the evening, the original flux estimates remain unchanged. During the evening transition, the effect of the temperature advection in the \({\varDelta }\theta /{\varDelta } t\) profile is reduced because the wind speed, and consequently advection, is weaker. During the night-time, a southerly flow prevails, indicating the influence of thermally-driven flow at the foothills of the Pyrenees.
Including the advection contribution from the model in the estimates of the SUMO heat fluxes for this day distinctly improves the results compared with the EC stations (Fig. 12d), with most of the corrected data (purple) now much closer to the 1:1 line compared with the raw estimates (grey). This improvement is not seen for the last two estimates, where the original and corrected values are practically identical and underestimated by the SUMO platform in both cases, and is probably related to the inability of the model to adequately capture the change in wind direction and reduction of wind speed associated with the onset of katabatic flow during the evening transition; similar results were reported by Jiménez et al. (2016) for a morning transition case. Our hypothesis is supported by the fact that the increasing stability at the ground observed by the SUMO platform is not as evident in the model profiles.
The number of cases to test method 3 was limited as the MesoNH simulations are only available for IOP with a clear thermally-driven circulation during the night-time (see Sect. 3.2.3). The clear improvement of the flux estimates for the whole day presented for 1 July in Fig. 12 cannot be seen to the same extend for the other days simulated with the MesoNH model, which may be related to model uncertainties, leading to either a vertical structure of the ABL not matching the real situation or a time shift with respect to the observations. Models have their limitations in reproducing the evolution of the ABL, particularly in complex terrain, which can be related to the inadequate representation of the topography, the surface characteristics, and the soil conditions. The physical parametrizations may also not be valid under certain conditions (see Jiménez and Cuxart 2014; Jiménez et al. 2019 for more details). As a result, the improvements in the computation of the heat flux from the SUMO flights only occur when the model results are realistic.
Another important factor to take into account when applying model advection to the SUMO profiles are the scales of temperature advection involved. Cuxart et al. (2016) found that different spatial scales contribute to the temperature advection in Lannemezan, with increasing relative importance towards smaller scales, and those at the hectometre scale the most important locally. These scales are included in the SUMO measurements but are only partially represented in the estimates of the modelled advection (computed from the temperature fields at the edge of the 10 km \(\times \) 10 km box and the averaged flow within the box using the model outputs at 400-m resolution).
5 Conclusions and Outlook
The SUMO profile measurements made during the BLLAST campaign, together with the comprehensive reference datasets from ground-based EC stations and two airborne flux systems, provide a unique possibility for investigating the potential and limitations of the profile-integration technique for sensible-heat-flux determination using RPAS platforms. The analyzed dataset consists of 108 flux profiles recorded during 11 intensive observation periods covering a variety of diurnal ABL developments.
The quality of the SUMO flux estimates depends on the validity of the assumptions required for the appropriate use of Eq. (4). In particular, advection introduces considerable uncertainty, and a straightforward calculation without corresponding corrections results in flux profiles outside the range of the selected EC stations for a majority (\(\approx \) 75%) of the SUMO profile pairs from the BLLAST campaign. The pure application of an appropriate advection correction reduces this portion to < 50%. Improving the success rate to 77\(\%\) is achieved by additionally excluding the cases where we expect other violations of our assumptions, such as in the case of subsidence, advection dependent on height, or situations where the vertical extension of the free atmosphere for the estimation of the advection in the SUMO profiles is too small. The best fit is found for the evening period with 94\(\%\) of the corrected SUMO flux estimates within the variability of the individual EC stations.
We also show the importance of choosing the correct advection-correction method and the vertical area of integration. The constant-advection approach (method 1) works well for classic textbook cases of the fully-developed CBL with steady temperature changes with height detectable in the free atmosphere between two consecutive profiles. Integrating the flux only up to the top of the entrainment zone or to the top of the SBL (method 2) and taking the value of \({\varDelta }\theta /{\varDelta } t\) at that level as representative advection for the whole boundary layer yields promising results for the developing CBL and SBL in the presence of residual-layer structures above. The SUMO flux estimates are sensitive to the height \(z=h_{EZT}\) for correction method 1 and to the height \(z=h_{EZT}\) or \(z=h_{SBL}\) for correction method 2, depending on several features, such as the overall depth of the integration (for both methods 1 and 2) and the depth of the captured free atmosphere (for method 1). A reliable determination of the depth of the ABL is an important part of obtaining realistic sensible-heat-flux estimates. The overall flux sensitivity for the convective cases is lowest for the afternoon period, and in general distinctly lower than the variations in flux values between the different EC surface stations. The poorest results are found for the afternoon period, where the SUMO platform underestimates the flux values during the transition period from the CBL to the SBL. The profile-integration method struggles when the ABL undergoes transition from positive to negative flux values. One explanation is that the value of \({\varDelta } t\) between two consecutive flights is too long, so that method 2 misses the positive flux contribution just before SBL formation, with the positive flux contribution inferred as advection, and the result that method 2 overcompensates for this effect. Therefore, approximately continuous profiling is important for future use of the profile-integration technique during the afternoon transition to avoid underestimating the flux in this way.
By combining the correction methods 1 and 2 depending on the state of the ABL, the profile-integration method can be used to investigate the flux evolution over the diurnal cycle. We present the case of 5 July when the whole diurnal cycle is captured by the SUMO platform, which shows the best results for the daily evolution when compared with the EC-based heat-flux measurements. However, certain differences between the SUMO flux estimates close to the ground and the measurements from the EC stations have to be expected (as discussed in Sect. 4.3). While the differences in measurement footprint between the RPAS platform and the EC technique affect the flux values, by having a large network of EC surface stations over different surface types, we can capture the range of flux conditions for the campaign area. A comparison should, therefore, be possible by judging the heat flux from the SUMO platform with respect to the average and the spread of the EC-based flux values. Wildmann et al. (2015) mentions that having a network of EC surface stations would be an important validation for flux estimations from RPAS platforms over a patchy heterogeneous surface.
We also tested the possibility of incorporating information on height-dependent horizontal advection from a mesoscale model for the correction, which improves the results for 1 July, but no clear improvement could be obtained during the other five IOP with the MesoNH simulations tested here. The success of this method strongly depends on the accuracy of the model with respect to both the exact timing and the accurate prediction of the magnitude and vertical structure of the temperature advection. Therefore, while it would be difficult to use this on a forecast basis, it may be feasible to incorporate information on height-dependent advection for a detailed analysis based on hindcast simulations. Another pragmatic analytical approach for obtaining flux profiles from RPAS platforms could be to constrain the variation of the parameter set used for estimating the flux profiles by physical reasoning, and then pick the best value with respect to the ground-based measurement(s).
Future improvements in sensor technology, in particular with respect to the response time, would significantly benefit the flux-estimation approach. A shorter response time means, for example, that the temperature gradients of an inversion are resolved, which enables a more accurate determination of the depth of the mixed-layer or the SBL. Faster humidity sensors would additionally enable the determination of profiles of specific humidity in sufficient quality to also allow for a meaningful application of the profile-integration method for the latent heat flux, since the vertical structure of humidity profiles in the ABL is typically more complex than for temperature. The appropriate probing of these features requires humidity sensors to be considerably faster than those used in the SUMO system with a time constant on the order of 5 s at a temperature of \(25\,^{\circ }\hbox {C}\) (Jonassen 2008; Corominas Del Hoyo 2018). A recently presented family of fast humidity sensors with response times far below 1 s, manufactured by U.P.S.I. in France, shows a promising potential in this direction.
Data Availability
Data from the BLLAST field campaign are available at http://bllast.sedoo.fr/.
References
Angevine W, White A, Avery SK (1994) Boundary-layer depth and entrainment zone characterization with a boundary-layer profiler. Boundary-Layer Meteorol 68(4):375–385. https://doi.org/10.1007/BF00706797
Bange J, Roth R (1999) Helicopter-borne flux measurements in the nocturnal boundary layer over land—a case study. Boundary-Layer Meteorol 92(2):295–325. https://doi.org/10.1007/s10546-006-9106-0
Bange J, Spiess T, van den Kroonenberg A (2007) Characteristics of the early-morning shallow convective boundary layer from Helipod Flights during STINHO-2. Theor Appl Climatol 90(1–2):113–126. https://doi.org/10.1007/s00704-006-0272-2
Bärfuss K, Pätzold F, Altstädter B, Kathe E, Nowak S, Bretschneider L, Bestmann U, Lampert A (2018) New setup of the UAS ALADINA for measuring boundary layer properties, atmospheric particles and solar radiation. Atmosphere 9(1):28. https://doi.org/10.3390/atmos9010028
Båserud L, Reuder J, Jonassen MO, Kral ST, Paskyabi MB, Lothon M (2016) Proof of concept for turbulence measurements with the RPAS SUMO during the BLLAST campaign. Atmos Meas Tech 9(10):4901–4913. https://doi.org/10.5194/amt-9-4901-2016
Blay-Carreras E (2013) Day-by-day description of the IOPs. Tech. Rep. http://bllast.sedoo.fr/documents/
Bonin T, Chilson P, Zielke B, Fedorovich E (2013) Observations of the early evening boundary-layer transition using a small unmanned aerial system. Boundary-Layer Meteorol 146(1):119–132. https://doi.org/10.1007/s10546-012-9760-3
Bosveld FC, Baas P, van Meijgaard E, de Bruijn EIF, Steeneveld GJ, Holtslag AAM (2014) The third GABLS intercomparison case for evaluation studies of boundary-layer models. Part A: case selection and set-up. Boundary-Layer Meteorol 152(2):133–156. https://doi.org/10.1007/s10546-014-9917-3
Brisset P, Drouin A, Gorraz M, Huard Ps, Tyler J (2006) The Paparazzi solution. In: MAV2006 2nd US-European competition and workshop on micro air vehicles, pp 1–15. https://hal-enac.archives-ouvertes.fr/hal-01004157/document
Calmer R, Roberts GC, Preissler J, Sanchez KJ, Derrien S, O’Dowd C (2018) Vertical wind velocity measurements using a five-hole probe with remotely piloted aircraft to study aerosol-cloud interactions. Atmos Meas Tech 11(5):2583–2599. https://doi.org/10.5194/amt-11-2583-2018
Canut G, Couvreux F, Lothon M, Legain D, Piguet B, Lampert A, Maurel W, Moulin E (2016) Turbulence fluxes and variances measured with a sonic anemometer mounted on a tethered balloon. Atmos Meas Tech 9(9):4375–4386. https://doi.org/10.5194/amt-9-4375-2016
Cassano JJ (2014) Observations of atmospheric boundary layer temperature profiles with a small unmanned aerial vehicle. Antarct Sci 26(02):205–213. https://doi.org/10.1017/S0954102013000539
Chilson PB, Bonin TA, Zielke BS, Kirkwood S (2011) The small multi-function autonomous research and teaching sonde (Smartsonde): relating in-situ measurements of atmospheric parameters to radar returns. In: Ouwehand L (ed) 20th Symposium on European rocket and balloon programmes and related research, ESA Communications ESTEC, Noordwijk, The Netherlands, pp 387–394. http://adsabs.harvard.edu/full/2011ESASP.700..387C
Corominas Del Hoyo A (2018) Estimation of the time constants for the temperature and relative humidity sensors used on the SUMO aircraft during the Hailuoto campaign. Master thesis, University of Barcelona
Crawford TL, Dobosy RJ (1992) A sensitive fast-response probe to measure turbulence and heat flux from any airplane. Boundary-Layer Meteorol 59(3):257–278. https://doi.org/10.1007/BF00119816
Cuxart J, Wrenger B, Martínez-Villagrasa D, Reuder J, Jonassen MO, Jiménez MA, Lothon M, Lohou F, Hartogensis O, Dünnermann J, Conangla L, Garai A (2016) Estimation of the advection effects induced by surface heterogeneities in the surface energy budget. Atmos Chem Phys 16(14):9489–9504. https://doi.org/10.5194/acp-16-9489-2016
Darbieu C, Lohou F, Lothon M, Vilà-Guerau de Arellano J, Couvreux F, Durand P, Pino D, Patton EG, Nilsson E, Blay-Carreras E, Gioli B (2015) Turbulence vertical structure of the boundary layer during the afternoon transition. Atmos Chem Phys 15(17):10,071–10,086. https://doi.org/10.5194/acp-15-10071-2015
De Coster OMY, Pietersen HP (2011) BLLAST—uniform processing of Eddy-Covariance data. Tech. Rep., Université de Toulouse. http://bllast.sedoo.fr/documents/
Deardorff JW, Willis GE, Stockton BH (1980) Laboratory studies of the entrainment zone of a convectively mixed layer. J Fluid Mech 100(01):41. https://doi.org/10.1017/S0022112080001000
Dijk A, Moene AF, de Bruin H (2004) The principles of surface flux physics: theory, practice and description of the ECPACK library. Tech. Rep. http://library.wur.nl/WebQuery/wurpubs/334734
Foken T (2017) Micrometeorology. Springer, Berlin. https://doi.org/10.1007/978-3-642-25440-6
Giebel G, Schmidt Paulsen U, Bange J, la Cour-Harbo A, Reuder J, Mayer S, van den Kroonenberg A, Mølgaard J (2011) Autonomous aerial sensors for wind power meteorology—a pre-project. Tech. Rep. http://orbit.dtu.dk/fedora/objects/orbit:110631/datastreams/file_7726678/content
Grunwald J, Kalthoff N, Corsmeier U, Fiedler F (1996) Comparison of areally averaged turbulent fluxes over non-homogeneous terrain: results from the EFEDA-field experiment. Boundary-Layer Meteorol 77(2):105–134. https://doi.org/10.1007/BF00119574
Hartogensis O (2015) Land-use map http://bllast.sedoo.fr/database/source/displayDataset.php?repertoire=../data/AUTH/Area-averaged_surface_flux_maps/&fichier=Land-usemap.xml
Hartogensis OK, De Bruin HAR, Van De Wiel BJH (2002) Displaced-beam small aperture scintillometer test. Part Ii: Cases-99 stable boundary-layer experiment. Boundary-Layer Meteorol 105(1):149–176. https://doi.org/10.1023/A:1019620515781
Holland GJ, Webster PJ, Curry JA, Tyrell G, Gauntlett D, Brett G, Becker J, Hoag R, Vaglienti W (2001) The aerosonde robotic aircraft: a new paradigm for environmental observations. Bull Am Meteorol Soc 82(5):889–901
Holtslag AAM, Svensson G, Baas P, Basu S, Beare B, Beljaars ACM, Bosveld FC, Cuxart J, Lindvall J, Steeneveld GJ, Tjernström M, Van De Wiel BJH (2013) Stable atmospheric boundary layers and diurnal cycles: challenges for weather and climate models. Bull Am Meteorol Soc 94(11):1691–1706. https://doi.org/10.1175/BAMS-D-11-00187.1
Jiménez MA, Cuxart J (2014) A study of the nocturnal flows generated in the north side of the Pyrenees. Atmos Res 145–146:244–254. https://doi.org/10.1016/j.atmosres.2014.04.010
Jiménez MA, Simó G, Wrenger B, Telisman-Prtenjak M, Guijarro JA, Cuxart J (2016) Morning transition case between the land and the sea breeze regimes. Atmos Res 172–173:95–108
Jiménez MA, Cuxart J, Martinez-Villagrasa D (2019) Influence of a valley exit jet on the nocturnal atmospheric boundary-layer at the foothills of the Pyrenees. Q J R Meteorol Soc 145:356–375. https://doi.org/10.1002/qj.3437
Jonassen MO (2008) The small unmanned meteorological observer (SUMO)—characterization and test of a new measurement system for atmospheric boundary layer research. Master thesis, University of Bergen
Jonassen MO, Tisler P, Altstädter B, Scholtz A, Vihma T, Lampert A, König-Langlo G, Lüpkes C (2015) Application of remotely piloted aircraft systems in observing the atmospheric boundary layer over Antarctic sea ice in winter. Polar Res 34:1–15. https://doi.org/10.3402/polar.v34.25651
Kaimal JC, Gaynor JE (1983) The boulder atmospheric observatory. J Appl Meteorol Clim 22(5):863–880
Kljun N, Rotach MW, Schmid HP (2002) A three-dimensional backward lagrangian footprint model for a wide range of boundary-layer stratifications. Boundary-Layer Meteorol 103(2):205–226. https://doi.org/10.1023/A:1014556300021
Knuth SL, Cassano JJ (2014) Estimating sensible and latent heat fluxes using the integral method from in situ aircraft measurements. J Atmos Ocean Technol 31(9):1964–1981. https://doi.org/10.1175/JTECH-D-14-00008.1
Kral ST, Reuder J, Vihma T, Suomi I, O’Connor E, Kouznetsov R, Wrenger B, Rautenberg A, Urbancic G, Jonassen MO, Båserud L, Maronga B, Mayer S, Lorenz T, Holtslag AAM, Steeneveld GJ, Seidl A, Müller M, Lindenberg C, Langohr C, Voss H, Bange J, Hundhausen M, Hilsheimer P, Schygulla M (2018) Innovative strategies for observations in the arctic atmospheric boundary layer (ISOBAR)—the Hailuoto 2017 campaign. Atmosphere 9(7):1–29. https://doi.org/10.3390/atmos9070268
Lafore JP, Stein J, Asencio N, Bougeault P, Ducrocq V, Duron J, Fischer C, Héreil P, Mascart P, Masson V, Pinty JP, Redelsperger JL, Richard E, Vilà-Guerau De Arellano J (1998) The Meso-NH atmospheric simulation system. Part I: adiabatic formulation and control simulation. Ann Geophys 16(1):90–109. https://doi.org/10.1007/s005850050582
Lambert D, Durand P (1998) Aircraft to aircraft intercomparison during SEMAPHORE. J Geophys Res Ocean 103(C11):25,109–25,123. https://doi.org/10.1029/97JC02199
Lenschow DH (1986) Aircraft measurements in the boundary layer. In: Lenschow DH (ed) Probing the atmospheric boundary layer. American Meteorological Society, Boston, pp 39–55
Lenschow DH, Mann J, Kristensen L (1994) How long is long enough when measuring fluxes and other turbulence statistics. J Atmos Ocean Technol 11:661–673
Lothon M, Couvreux F, Donier S, Guichard F, Lacarrère P, Lenschow DH, Noilhan J, Saïd F (2007) Impact of coherent eddies on airborne measurements of vertical turbulent fluxes. Boundary-Layer Meteorol 124(3):425–447. https://doi.org/10.1007/s10546-007-9182-9
Lothon M, Lohou F, Pino D, Couvreux F, Pardyjak ER, Reuder J, Vilà-Guerau de Arellano J, Durand P, Hartogensis O, Legain D, Augustin P, Gioli B, Lenschow DH, Faloona I, Yagüe C, Alexander DC, Angevine WM, Bargain E, Barrié J, Bazile E, Bezombes Y, Blay-Carreras E, van de Boer A, Boichard JL, Bourdon A, Butet A, Campistron B, de Coster O, Cuxart J, Dabas A, Darbieu C, Deboudt K, Delbarre H, Derrien S, Flament P, Fourmentin M, Garai A, Gibert F, Graf A, Groebner J, Guichard F, Jiménez MA, Jonassen M, Van den Kroonenberg A, Magliulo V, Martin S, Martinez D, Mastrorillo L, Moene AF, Molinos F, Moulin E, Pietersen HP, Piguet B, Pique E, Román-Cascón C, Rufin-Soler C, Saïd F, Sastre-Marugán M, Seity Y, Steeneveld GJ, Toscano P, Traullé O, Tzanos D, Wacker S, Wildmann N, Zaldei A (2014) The BLLAST field experiment: Boundary-Layer late afternoon and sunset turbulence. Atmos Chem Phys 14(20):10,931–10,960. https://doi.org/10.5194/acp-14-10931-2014
Martin S, Bange J (2014) The influence of aircraft speed variations on sensible heat-flux measurements by different airborne systems. Boundary-Layer Meteorol 150(1):153–166. https://doi.org/10.1007/s10546-013-9853-7
Mayer S, Hattenberger G, Brisset P, Jonassen M, Reuder J (2012) A ‘no-flow-sensor’ wind estimation algorithm for unmanned aerial systems. Int J Micro Air Veh 4(1):15–30. https://doi.org/10.1260/1756-8293.4.1.15
Monna W, Bosveld F (2013) In Higher Spheres: 40 years of observations at the Cabauw Site. Tech. Rep.. KNMI, http://www.cesar-observatory.nl/publications/reports/knmipub232.pdf
Muschinski A, Frehich R, Jensen M, Hugo R, Hoff A, Eaton F, Balsley B (2001) Fine-scale measurements of turbulence in the lower troposphere: an intercomparison between a kite- and balloon-borne, and a helicopter-borne measurement system. Boundary-Layer Meteorol 98(2):219–250. https://doi.org/10.1023/A:1026520618624
Neisser J, Adam W, Beyrich F, Leiterer U, Steinhagen H (2002) Atmospheric boundary layer monitoring at the Meteorological Observatory Lindenberg as a part of the “Lindenberg Column”: facilities and selected results. Meteorol Z 11(4):241–253. https://doi.org/10.1127/0941-2948/2002/0011-0241
Nilsson E (2014) Day-by-day analysis of synoptic and meteorological conditions. Tech. Rep. http://bllast.sedoo.fr/documents/
Nilsson E, Lohou F, Lothon M, Pardyjak E, Mahrt L, Darbieu C (2016) Turbulence kinetic energy budget during the afternoon transition. Part I: Observed surface TKE budget and boundary layer description for 10 Intensive Observation Period days. Atmos Chem Phys 16:8849–8872. https://doi.org/10.5194/acp-16-8849-2016
Oncley SP, Foken T, Vogt R, Kohsiek W, DeBruin HAR, Bernhofer C, Christen A, Ev Gorsel, Grantz D, Feigenwinter C, Lehner I, Liebethal C, Liu H, Mauder M, Pitacco A, Ribeiro L, Weidinger T (2007) The energy balance experiment ebex-2000. Part i: overview and energy balance. Boundary-Layer Meteorol 123(1):1–28. https://doi.org/10.1007/s10546-007-9161-1
Palomaki RT, Rose NT, van den Bossche M, Sherman TJ, De Wekker SFJ (2017) Wind estimation in the lower atmosphere using multirotor aircraft. J Atmos Ocean Technol 34:1183–1191. https://doi.org/10.1175/JTECH-D-16-0177.1
Reineman BD, Lenain L, Statom NM, Melville WK (2013) Development and testing of instrumentation for UAV-based flux measurements within terrestrial and marine atmospheric boundary layers. J Atmos Ocean Technol 30(7):1295–1319. https://doi.org/10.1175/JTECH-D-12-00176.1
Reuder J, Brisset P, Jonassen M, Müller M, Mayer S (2009) The small unmanned meteorological observer SUMO: a new tool for atmospheric boundary layer research. Meteorol Z 18(2):141–147. https://doi.org/10.1127/0941-2948/2009/0363
Reuder J, Ablinger M, Ágústsson H, Brisset P, Brynjólfsson S, Garhammer M, Jóhannesson T, Jonassen MO, Kühnel R, Lämmlein S, de Lange T, Lindenberg C, Malardel S, Mayer S, Müller M, Ólafsson H, Rögnvaldsson Ó, Schäper W, Spengler T, Zängl G, Egger J (2012a) FLOHOF 2007: an overview of the mesoscale meteorological field campaign at Hofsjökull. Central Iceland. Meteorol Atmos Phys 116(1):1–13. https://doi.org/10.1007/s00703-010-0118-4
Reuder J, Jonassen M, Ólafsson H (2012b) The small unmanned meteorological observer SUMO: recent developments and applications of a micro-UAS for atmospheric boundary layer research. Acta Geophys 60(5):1454–1473. https://doi.org/10.2478/s11600-012-0042-8
Reuder J, Båserud L, Jonassen MO, Kral ST, Müller M (2016a) Exploring the potential of the RPA system SUMO for multipurpose boundary-layer missions during the BLLAST campaign. Atmos Meas Tech 9(6):2675–2688. https://doi.org/10.5194/amt-9-2675-2016
Reuder J, Båserud L, Kral ST, Kumer V, Wagenaar JW, Knauer A (2016b) Proof of Concept for Wind Turbine Wake Investigations with the RPAS SUMO. Energy Proc 94(1876):452–461. https://doi.org/10.1016/j.egypro.2016.09.215
Román-Cascón C, Yagüe C, Mahrt L, Sastre M, Pardyjak GJ, van de Boer A, Hartogensis O (2015) Interactions among drainage flows, gravity waves and turbulence: a BLLAST case study. Atmos Chem Phys 15:9031–9047
Saïd F, Corsmeier U, Kalthoff N, Kottmeier C, Lothon M, Wieser A, Hofherr T, Perros P (2005) ESCOMPTE experiment: intercomparison of four aircraft dynamical, thermodynamical, radiation and chemical measurements. Atmos Res 74(1–4):217–252. https://doi.org/10.1016/J.ATMOSRES.2004.06.012
Saïd F, Canut G, Durand P, Lohou F, Lothon M (2010) Seasonal evolution of boundary-layer turbulence measured by aircraft during the AMMA 2006 Special Observation Period. Q J R Meteorol Soc 136:47–65. https://doi.org/10.1002/qj.475
Schäfer K, Emeis S, Hoffmann H, Jahn C (2006) Influence of mixing layer height upon air pollution in urban and sub-urban areas. Meteorol Z 15(6):647–658. https://doi.org/10.1127/0941-2948/2006/0164
Seidl A (2017) Investigations on the external forcings acting on the convective boundary layer during the BLLAST Campaign by the CLASS Model. Master thesis, University of Bergen
Stull RB (1988) An introduction to boundary layer meteorology. Springer, Berlin. https://doi.org/10.1007/978-94-009-3027-8
Thomas RM, Lehmann K, Nguyen H, Jackson DL, Wolfe D, Ramanathan V (2012) Measurement of turbulent water vapor fluxes using a lightweight unmanned aerial vehicle system. Atmos Meas Tech 5(1):243–257. https://doi.org/10.5194/amt-5-243-2012
van den Kroonenberg A, Martin T, Buschmann M, Bange J, Vörsmann P (2008) Measuring the wind vector using the autonomous mini aerial vehicle M2AV. J Atmos Ocean Technol 25(11):1969–1982. https://doi.org/10.1175/2008JTECHA1114.1
Vesala T, Kljun N, Rannik Ü, Rinne J, Sogachev A, Markkanen T, Sabelfeld K, Foken T, Leclerc MY (2008) Flux and concentration footprint modelling: state of the art. Environ Pollut 152(3):653–666. https://doi.org/10.1016/j.envpol.2007.06.070
Vilà-Guerau de Arellano J, van Heerwaarden CC, van Stratum BJ, van den Dries K (2015) Atmospheric boundary layer: integrating chemistry and land interactions. Cambridge University Press, Cambridge
Wildmann N, Hofsäss M, Weimer F, Joos A, Bange J (2014) MASC: a small remotely piloted aircraft (RPA) for wind energy research. Adv Sci Res 11(1):55–61. https://doi.org/10.5194/asr-11-55-2014
Wildmann N, Rau GA, Bange J (2015) Observations of the early morning boundary-layer transition with small remotely-piloted aircraft. Boundary-Layer Meteorol 157(3):345–373. https://doi.org/10.1007/s10546-015-0059-z
Wildmann N, Bernard S, Bange J (2017) Measuring the local wind field at an escarpment using small remotely-piloted aircraft. Renew Energy 103:613–619. https://doi.org/10.1016/j.renene.2016.10.073
Wyngaard JC (2010) Turbulence in the atmosphere. Cambridge University Press, Cambridge
Zhang J, Rao ST (1999) The role of vertical mixing in the temporal evolution of ground-level ozone concentrations. J Appl Meteorol 38(12):1674–1691
Acknowledgements
The BLLAST field experiment was made possible thanks to the contribution of several institutions and support: INSU-CNRS (Institut National des Sciences de l’Univers, Centre national de la Recherche Scientifique, LEFE-IDAO program), Météo-France, Observatoire Midi-Pyrénées (University of Toulouse), EUFAR (EUropean Facility for Airborne Research) and COST ES0802 (European Cooperation in Science and Technology). The field experiment would not have occurred without the contribution of all participating European and American research groups, which all have contributed a significant amount. The BLLAST field experiment was hosted by the instrumented site of Centre de Recherches Atmosphériques, Lannemezan, France (Observatoire Midi-Pyrénées, Laboratoire d’Aérologie). The BLLAST data are managed by SEDOO from Observatoire Midi-Pyrénées. The participation of the Meteorology Group of the Geophysical Institute, University of Bergen was facilitated by contributions of the Geophysical Institute and the Faculty of Mathematics and Natural Sciences under the “små driftsmidler” scheme, a travel stipend by the Meltzer Foundation in Bergen, and the Short Term Scientific Mission (STSM) scheme within the COST Action ES0802 ”Unmanned Aerial Vehicles in Atmospheric Research”. The authors are grateful to Anak Bhandari for the technical assistance in the preparation of the campaign, and to Christian Lindenberg, the SUMO chief pilot during the campaign. Without his passion, determination and patience we would never have achieved this large number of flights. ECMWF and AEMET are thanked for the access to computing time and the Meso-NH team in Météo France and Laboratoire d’Aérologie for their support. Simulations have been supported by the CGL2015-65627-C3-1-R research project of the Spanish Government supplied by the European Regional Development Fund (FEDER). The SAFIRE (CNES-CNRS-Météo-France) and CNRM (Météo-France) teams operated the Piper-Aztec aircraft and processed the data. We also would like to thank Oscar Hartogensis for the provision of the database for the land-use map and Andrew Seidl for creating the corresponding figure for the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix 1
Appendix 1
A detailed table (Table 4) describing all flights from the SUMO platform used in this analysis is presented as Supplementary Electronic Material. Information on the flight number, date, time, boundary-layer type, depth of the mixed layer and the top of the entrainment zone, the SBL depth, uncertainty flags, and advection changes with height are shown for all cases.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Båserud, L., Reuder, J., Jonassen, M.O. et al. Potential and Limitations in Estimating Sensible-Heat-Flux Profiles from Consecutive Temperature Profiles Using Remotely-Piloted Aircraft Systems. Boundary-Layer Meteorol 174, 145–177 (2020). https://doi.org/10.1007/s10546-019-00478-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-019-00478-9