Abstract
Tower-based measurements from within and above the urban canopy in two cities are used to evaluate several existing approaches that parametrize the vertical profiles of wind speed and temperature within the urban roughness sublayer (RSL). It is shown that current use of Monin–Obukhov similarity theory (MOST) in numerical weather prediction models can be improved upon by using RSL corrections when modelling the vertical profiles of wind speed and friction velocity in the urban RSL using MOST. Using anisotropic building morphological information improves the agreement between observed and parametrized profiles of wind speed and momentum fluxes for selected methods. The largest improvement is found when using dynamically-varying aerodynamic roughness length and displacement height. Adding a RSL correction to MOST, however, does not improve the parametrization of the vertical profiles of temperature and heat fluxes. This is expected since sources and sinks of heat are assumed uniformly distributed through a simple flux boundary condition in all RSL formulations, yet are highly patchy and anisotropic in a real urban context. Our results can be used to inform the choice of surface-layer representations for air quality, dispersion, and numerical weather prediction applications in the urban environment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
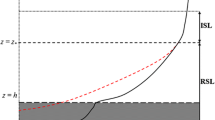
When modelling urban meteorological processes, it is crucial to represent the exchange of momentum and scalars such as temperature and humidity between the surface and overlying atmosphere. Although much progress has been made (e.g., Masson 2000; Martilli et al. 2002; Harman et al. 2004; Krayenhoff et al. 2015; Simón-Moral et al. 2017), modelling wind speed and scalars within and above the heterogeneous urban surface in a one-dimensional approach, without explicitly resolving buildings, poses significant challenges. Urban obstacles (e.g., buildings and trees) disturb the flow and in turn cause vertical divergence of turbulent fluxes, modifying the turbulent exchange (Rotach 1995; Christen et al. 2007). The layer in which the flow and turbulent fluxes are disturbed by obstacles is one definition of the roughness sublayer (RSL); this layer can be two to five times the mean canopy height (Raupach et al. 1991; Grimmond and Oke 1999; Kastner-Klein and Rotach 2004; Grimmond et al. 2004). Above the RSL is the inertial sublayer (ISL), and for surfaces with small roughness elements the RSL is very shallow and the ISL exchanges of momentum and scalars can be modelled using Monin–Obukhov similarity theory (MOST). MOST relates momentum and scalars over horizontally-homogeneous surfaces, i.e. where the point fluxes or means measured are representative of the spatially-averaged fluxes or means, and assumes that height above the ground is the only relevant length scale. Flux-gradient relations based on MOST apply in the ISL (Roth and Oke 1995; Wood et al. 2010), but not in the RSL. Within the RSL the MOST relations must be modified through use of an influence function that represents, in a simple analytical form, the RSL effects [Sect. 2.1, Eqs. (1) and (2)]. In practice, the RSL effects on measurements and model calculations are only significant above surfaces such as tall crops and forests, and above the urban canopy layer (UCL).
Modelling the exchange of heat and momentum for numerical weather prediction (NWP) models is important in the urban RSL, but is conceptually challenging as transport of momentum is typically parametrized using MOST and not resolved explicitly. Although several types of MOST “corrections” have been proposed for the horizontally-averaged RSL above forest canopies (e.g., Physick and Garratt 1995; Harman and Finnigan 2007, 2008; De Ridder 2010), these are untested for the urban RSL. Alternatively, momentum profile parametrizations within the RSL using local scaling (e.g., Macdonald 2000; Coceal and Belcher 2004; Kastner-Klein and Rotach 2004) have been proposed. However, most of the latter approaches only consider neutral atmospheric conditions and are derived from idealized wind-tunnel and computational fluid dynamics (CFD) approaches.
There have been several observational campaigns aimed at understanding and generalizing mean flow, turbulence, and scalar exchange in the urban RSL in several cities around the world (e.g., Nakamura and Oke 1988; Rotach 1993; Feigenwinter et al. 1999; Feigenwinter and Vogt 2005; Dobre et al. 2005; Rotach et al. 2005; Eliasson et al. 2006; Nelson et al. 2007; Christen et al. 2009; Zou et al. 2017). Most of these studies show similarities in the profiles of wind speed, and momentum exchange (e.g., an inflection point above the mean canopy height and presence of sweeps and ejections). However, few studies measure wind speed and fluxes simultaneously at several heights in and above the UCL. Here, we use data from two sites that include turbulent quantities in and above the UCL (i.e Basel and Gothenburg: Rotach et al. 2005; Eliasson et al. 2006).
In the present study, we compare approaches that estimate profiles of wind speed and temperatures in the RSL using observations from ultrasonic anemometers and thermometers at multiple heights in two real-world urban canopies under a range of near-neutral to highly unstable conditions. Momentum and heat-flux measurements are analyzed for 7.5 months located within (three levels) and above (three levels) the UCL as part of the Basel Urban Boundary Layer Experiment (BUBBLE, Rotach et al. 2005). Similarly for Gothenburg, Sweden, within (five levels) and above the canopy (three levels) observations over 14 months are analyzed (Eliasson et al. 2006; Offerle et al. 2007). The objective is to test and assess different existing approaches used in urban canopy parametrizations to describe the horizontally-averaged profiles of wind speed and temperature in the urban RSL. In addition, we assess the errors made when considering aerodynamic roughness properties to be horizontally averaged and not directionally dependent (Kent et al. 2017). When these parametrizations are applied in NWP models, most use a single value as an average for a given grid cell or even larger areas such as land-cover classes.
The equations and the parametrizations used (Sect. 2) and the observations from two urban sites are described in Sect. 3. The performance of the parametrizations for wind speed is evaluated and the sensitivity of model input parameters tested (Sect. 4). Next, temperature profiles (Sect. 5) and turbulent fluxes of momentum and heat (Sect. 6) are evaluated. Finally, the results are discussed in Sect. 7 and summarized in Sect. 8.
2 Methods
2.1 Governing Equations
The wind speed and potential temperature profiles are based on the flux-gradient relations that follow from the adaptation of MOST to the RSL (Garratt 1980),
where z is the height above ground level (see Table 1 for notation), \(z_{d}\) is the zero-plane displacement, \(z_*\) is the depth of the RSL, \(\kappa \) is the von Kármán constant (=0.4), \(u_*\) is the friction velocity, \(\theta _{*}\) is the temperature scale, L is the Obukhov length, \(\varPhi _{M}\) and \(\varPhi _{H}\) are the MOST functions for momentum and heat respectively, and \({\hat{\phi }}_{M}\) and \({\hat{\phi }}_{H}\) are the RSL profile functions for momentum and heat, respectively.
Through integration (Appendix 1), we find for wind speed,
and similarly, for potential temperature,
where \(z_{a}\) is a level within the ISL and thus above the RSL, \(z_0\) is the aerodynamic roughness length, \(\psi _{M}\) and \(\psi _{H}\) are the stability functions (Garratt 1992), and \({\hat{\psi }}_{M}(z)\) and \({\hat{\psi }}_{H}(z)\) represent RSL effects (Physick and Garratt 1995),
where \(z'\) is the height used for the integration. For Eqs. (5) and (6) several relations exist for vegetation canopies (e.g., Harman and Finnigan 2007; De Ridder 2010; Arnqvist and Bergström 2015), some of these are discussed in Sect. 2.2.
2.2 Parametrizations for Wind Speed and Temperature Profiles
Tables 2 and 3 summarize the approaches used to calculate wind-speed and temperature profiles, with the equations, and their implementation. Of the six momentum methods evaluated, two are designed for neutral conditions: logarithmic law (LL) and Kastner-Klein and Rotach (2004) (KK&R). The former applies above the RSL and the latter is for neutral conditions in the horizontally-averaged urban RSL.
Since the wind speed in the surface layer is influenced by buoyancy, two methods are analyzed to correct for atmospheric stability effects: MOST (Eq. 9) and MOST+, MOST with a stability correction to the aerodynamic roughness length applied (Eq. 10, see Appendix 1 for derivation). Herein, the Macdonald et al. (1998) aerodynamic roughness parameters (\(z_0\) and \(z_{d}\)) are used, following many urban canopy models (e.g., Kusaka et al. 2001; Coceal and Belcher 2004; Harman et al. 2004; Oleson et al. 2008). The derivation for the stability dependent \(z_0\) is given in Appendix 1.
The two other approaches evaluated are based on MOST but have RSL corrections: De Ridder (2010) (dR) and Harman and Finnigan (2007) (H&F). The former provides a simple approximation to \({\hat{\psi }}_{m}(z)\) with one additional equation to MOST+ (Eq. 11) and uses the RSL depth (\(z_*\)) as a known parameter. However, this height will vary depending on the direction of the flow and the measurements are not always above \(z_*\); therefore it is set to the highest measurement level. The H&F method is a more complex, physically-based method (Eq. 12). As both RSL corrections were derived for the RSL within and above forest canopies, the theory the models are based on does not necessarily apply in the urban RSL. The RSL approaches assume (1) a negligible volume fraction taken up by the canopy, (2) no directional shear, (3) isotropic drag coefficient and no preference of canopy element orientation, and (4) quadratic drag aligned with the mean wind vector. Those assumptions are not met in urban canopies, where the sharp-edged, anisotropic (i.e. varying with wind directions), impermeable and inflexible roughness elements (buildings) occupy a significant volume fraction.
Three methods to predict vertical profiles of temperatures are evaluated: MOST (Eq. 13), De Ridder (2010) (Eq. 14), and Harman and Finnigan (2008) (Eq. 15).
3 Observational Data
3.1 Basel
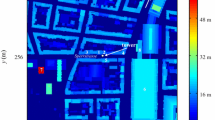
As part of the Basel Urban Boundary Layer Experiment (BUBBLE, Rotach et al. 2005) in Basel, Switzerland, sonic anemometer observations at six levels in and above the UCL were collected on a 32-m tall vertical lattice tower located in a street canyon and are used for the evaluation of the different parametrizations. The street canyon [called, Sperrstrasse, “Ue1” in Rotach et al. (2005)] had a height (H) to width (W) ratio of about 1, and was located within the densely built-up city centre with no vegetation in the canyon (Fig. 1a, Table 4). The orientation of the street canyon where the instrument mast was located is approximately west-south-west to east-north-east (Christen and Vogt 2004; Rotach et al. 2005). The period analyzed is 1 December 2001–15 July 2002. Site and measurements details can be found in Rotach et al. (2005), Christen et al. (2007), and Christen et al. (2009).
Height of the buildings in the surroundings above ground level (a.g.l.) of the a Basel-Sperrstrasse tower (Chrysoulakis et al. 2018) in Basel, Switzerland, and b Gothenburg tower, Sweden, with tower location (red dot), and radius of 250 m (black, dotted) and 500 m (black, solid)
3.2 Gothenburg
Momentum and sensible heat fluxes were observed in and above a deep street canyon (\(H/W = 2.1\)) in a densely built-up part of Gothenburg, Sweden with no vegetation in the street canyon. The orientation of the street canyon with the instruments is approximately north–south (Fig. 1b). The period analyzed is 23 June 2003 to 24 August 2004. More details about the site and instrumental set-up are given in Table 4, Eliasson et al. (2006), and Offerle et al. (2007).
3.3 Data Analysis
The analysis of both datasets uses 60-min averages of scalars and fluxes. For the fluxes, this averaging period is used to ensure that a representative range of eddies sizes are sampled (Finnigan et al. 2003). The observed \(u_*\) and \(\theta _*\) used to parametrize the wind speed and temperature (Eqs. 3 and 4, respectively) should be in the ISL. Therefore, we use the highest measurement level throughout the analysis (\(z_{m} = 2.2 z_{h}\) Basel and \(z_{m} = 1.8 z_{h}\) Gothenburg).
From the data \(u_*\) is calculated as,
where \(\overline{u'w'}\) and \(\overline{v'w'}\) are the north–south and east–west turbulent shear stress components, respectively, at \(z_{m}\). The temperature scale \(\theta _*\) is
where \(\overline{w'\theta '}\) is the vertical flux of potential temperature at \(z_{m}\). The stability is calculated using the Obukhov length L,
where \({\overline{\theta }}\) is the mean absolute potential temperature at \(z_{m}\).
Hours classified as stable (\(z_{h}/L>0.1\) at \(z_{m}\)) are excluded (Basel: 5.1% and Gothenburg: 3.5% of all hourly data). The majority of these hours are not locally stable just above the UCL (i.e. the heat flux becomes positive at lower heights). The conditions became dynamically neutral or unstable due to the heat release in the canopy, thus the stability may not be the same throughout the RSL.
4 Wind-Speed Profiles
4.1 Variation with Wind Direction
As the selected urban surfaces have predominantly aligned bluff bodies rather than porous roughness elements (e.g., trees) it is anticipated that the building arrangement affects results, as roughness elements encountered vary with wind direction. Figure 2a, e shows the wind-direction dependence of wind-speed profiles normalized using the friction velocity at \(z_{m}\) for the two sites. The wind-speed profiles clearly vary for different wind directions. Large differences are observed between wind directions perpendicular (000–030\(^{\circ }\), 120–200\(^{\circ }\), 290–360\(^{\circ }\) in Basel and 020–110\(^{\circ }\), 210–290\(^{\circ }\) for Gothenburg), and parallel (050–080\(^{\circ }\), 220–260\(^{\circ }\) for Basel and 140–180\(^{\circ }\), 320–360\(^{\circ }\) for Gothenburg) to the street canyon where the instruments are located. When the flow is perpendicular to the street canyon, an increased velocity gradient is detected and shows an inflection point just above the roof level. When the flow is parallel to the street canyon, the wind speed in the UCL is higher, and the inflection point is less pronounced.
Variations by wind direction at a–c Basel-Sperrstrasse and d–f Gothenburg measured a, d wind speed normalized by the median friction velocity at \(z_{m}\). b, e Number of 60-min intervals (green area, left y-axis) and building height (right y axis) within 500-m (solid black line) and 250-m (dotted black line) radius. c, f Median friction velocity normalized by the friction velocity measured at \(z_{m}\). All the data are 60-min averages and the median of each bin (\(5^\circ \)). a, c, d, f Wind directions perpendicular to the street canyon with the instruments are indicated by blue (pitched roofs) and green (flat roofs) lines, and parallel to the street canyon by red lines, the mean building height is indicated by grey dashed lines
For the Basel site, the vertical wind-speed gradient is largest when the wind direction is perpendicular to a street canyon with pitched roofs (between 120 and \(200^\circ \)) with a gable height of 21 m. During these conditions there is an acceleration of the flow close to the surface within the canopy. The wind direction in the canopy changes to be parallel to the street canyon orientation, associated with channeling flow. The increase of the wind speed close to the surface when the flow is over flat roofs is mostly associated with a recirculation vortex, the wind direction is reversed in the canopy compared to the wind direction measured at \(z_{m}\).
In Gothenburg the building heights are more uniform with wind direction (Fig. 2e) and the inflection point is just above the mean building height for all directions. The wind speed rarely increases close to the surface, while Eliasson et al. (2006) showed there to be recirculation vortices developing in the urban canopy. However, as the height-to-width ratio of this canyon is higher (2.1 compared to 1 in Basel), the median wind speed in the canopy is lower than at the Basel site.
The friction velocity normalized by the friction velocity at \(z_{m}\) reduces closer to the surface, especially within the canopy (Fig. 2c, f) similar to Rotach (1993). However, variability with direction is evident; for example, in Basel between 100 and \(150^\circ \) the fluxes increase above the mean building height, implying the situation is non-homogeneous or non-steady in the horizontal. The wind direction coincides with the location of taller pitched roofs (21 m) along the adjacent canyon. Pitched roofs and tall buildings are known to enhance the momentum flux and thus the friction velocity (e.g., Rafailidis 1997; Kastner-Klein and Rotach 2004; Kellnerová et al. 2012; Fuka et al. 2017). In the median, a similar local increase in the momentum flux does not occur in the data for the Gothenburg site.
The variation of the wind-speed and friction-velocity profiles with wind direction in mesoscale models is rarely considered, as models often assume homogeneous or isotropic conditions. In order to assess the impact of this assumption, the observations are split by wind sectors (defined by wind direction at \(z_{m}\)) with flow parallel and perpendicular to the street canopy (Fig. 2). For Basel, data are further subdivided into flow that is perpendicular to pitched and flat roofs, given their distinctly different behaviour (Fig. 2a).
4.2 Wind-Speed Profile Evaluation
Median normalized wind-speed profiles (Fig. 3) for flow sectors that are perpendicular to the street canyon with the instrument tower are analyzed. The six methods (Table 2) are evaluated for each 60-min time interval and compared to the tower data. As with assumptions made for most NWP models the building height, plan area index, and frontal area index are homogeneous. In this case, the horizontal average in a 250-m radius is used, and in-canopy methods assume the obstacles in the canopy are of negligible volume (Sect. 2.2). As this is not a reasonable assumption in the urban canopy, the measurements below the mean building height are corrected to reflect the assumed spatial mean wind speed \(\langle u\rangle \) by
where \(u_{c}\) is the canopy wind speed, assumed to be equal to the measurements, and \(u_{b}\) the wind speed within the volume of the buildings, assumed to be zero. This is a simple correction where we assume \(\lambda _{p}\) is constant with height in the UCL and is negligible above the mean building height. In reality, the building height surround the tower is variable and \(\lambda _{p}\) changes gradually with height.
Wind speed normalized by friction velocity at \(z_{m}\) for Basel-Sperrstrasse stratified by wind direction over a–c flat-roof buildings (000–030\(^{\circ }\) and 290–360\(^{\circ }\)), d–f over pitched-roof buildings (120–200\(^{\circ }\)), and g–i for the Gothenburg site perpendicular to the street canyon (020–110\(^{\circ }\) and 210–290\(^{\circ }\)) for different stabilities a, d, g very unstable \(-4>z_{h}/L> -0.5\)b, e, h unstable \(-0.5 z_{h}/L> -0.1\)c, f, i near-neutral \(-0.1>z_{h}/L> 0.1\). Observations median (dots) interquartile range (IQR) (bars) and wind-speed measurements corrected for in-canopy volume (grey dots Eq. 19). The median and IQR (shading) of the wind-speed estimate using six methods (Table 2). In near-neutral conditions, flow perpendicular to pitched roofs the horizontal mean wind speed modelled by Giometto et al. (2016) (LES) is shown (purple thick line). Filtered for times when \(u_*/u(z_{h})<1.0\), \({\hat{\phi }}_{M}(z=z_{h})<1.0\), and wind direction change between the top four sonics \(<20^{\circ }\). Grey shaded area indicates the heights below the mean building height within a 250-m radius. Horizontally-averaged morphometric parameters in a 250-m radius are used
Giometto et al. (2016) analyzed 1-m resolution LES data for a domain surrounding the Basel tower (512 m \(\times \) 512 m \(\times \) 160 m centred on the tower) and found the tower location to not necessarily be representative of the spatial mean flow for all wind sectors (Giometto et al. 2016). The fluid averaged wind-speed profiles of the u and v components are plotted for neutral conditions when flow is perpendicular to pitched roofs (156\(^{\circ }\)) (Fig. 3f). The spatial mean above the canopy is within the interquartile ranges of the measurements; however, in the UCL the LES spatial mean modelled profiles are different from the observations at the tower site. This difference between the LES results and observations is likely related to local flow patterns observed at the tower site (e.g., recirculation zones and channelling) averaging out in the spatial mean. Therefore, the different approaches are evaluated above the mean building height. The applicability of exponential models for wind speed (Eqs. 11 and 12) in the UCL is discussed in Sect. 7.
When the wind speed is normalized by friction velocity and stratified by stability (\(z_{h}/L\), L calculated at \(z_{m}\)) and wind direction (Fig. 3), the largest temporal variability (shading in Fig. 3) appears when using the Harman and Finnigan (2007) method. This is a consequence of the \(\beta \)-parameter in Eq. 12 being calculated from \(u_*(z_{m})\) and \(u(z_{h})\) observations. The H&F method agrees well with the observations for the majority of the profiles, especially when the flow is over the flat roofs in Basel and Gothenburg (Fig. 3a–c, g–i) (median absolute error 0.15–0.5m s\(^{-1}\)). During very unstable conditions at the Basel site, the wind-speed gradient is small and the difference between the methods is within the temporal variability of the data.
The dR RSL correction performs well given its simplicity, particularly in the upper part of the RSL. This method (empirically-fitted approximation to Eq. (5)) requires only one additional equation to be solved. Comparing MOST and MOST+ reveals that the wind-speed profiles in non-neutral cases require a stability correction to be added to the aerodynamic roughness length of Macdonald et al. (1998), but with only a small effect on the calculated wind speed.
Previous studies of flow over pitched roofs indicate the top of the roof height should be used for turbulent dynamics, rather than the mean building height (e.g., Neto 2015; Llaguno-Munitxa et al. 2017). Therefore, we increase the building height to the gable height of 21 m (Fig. 3d–f). For these wind directions, most models show similar results in the RSL, only in very unstable conditions do the wind-speed profiles deviate, giving an underestimation of the wind speed for MOST-based approaches and an overestimation for the LL and KK&R methods. These results indicate that it is possible to improve upon MOST by using a RSL correction.
4.3 Sensitivity Analysis
4.3.1 Aerodynamic Parameters
Figure 4 shows the sensitivity of the wind-speed error at the Gothenburg site above the canopy using different values of the morphometric parameters ( \(\lambda _{p}\), \(\lambda _{f}\), \(z_{h}\)), which modify the Macdonald et al. (1998) \(z_{d}\) and \(z_0\). Morphometric parameters averaged over \(5^{\circ }\) sectors in a radius of 250 and 500 m from the tower were tested. Using a radius of 500 m has the best agreement with wind speed observed above roof height, and in all cases, the H&F method has the lowest median absolute error (varying for parallel or perpendicular flow, 0.25 and \(0.5\hbox { m s}^{-1}\)). Using anisotropic morphometric parameters to calculate \(z_{d}\), \(z_0\), and \(L_{c}\) improves the results for most methods, especially those that do not include a RSL correction and for flow perpendicular to the street canyon.
Median absolute error of the wind speed at the Gothenburg site for all measurement heights above the canopy (1.2, 1.5, and \(1.9z_{h}\)) using hourly averages with wind direction perpendicular (Perp.) and parallel (Par.) to the street canyon. Table 2 gives the methods used. Morphometric parameters for a 500-m radius are used. A refers to isotropic, B to isotropic with Harman and Finnigan (2007) \(z_0\) and \(z_{d}\), C to all anisotropic, D to only \(\lambda _{p}\) anisotropic, E to only \(z_{h}\) anisotropic, and F to only \(\lambda _{f}\) anisotropic
Separating the effect of each individual morphometric parameter on \(z_{d}\) and \(z_0\) and on the wind speed, \(\lambda _{p}\) has the most impact, both when the flow is parallel and perpendicular to the street canyon.
Figure 4 also demonstrates that using the correct method to calculate \(z_{d}\) and \(z_0\) is of crucial importance (Kent et al. 2017). When \(z_{d}\) and \(z_0\) are calculated using Harman and Finnigan (2007) (Eq. 12) the median absolute error of the MOST and LL methods decreases by 0.9–1.2 m s\(^{-1}\). The dR method does not improve when \(z_0\) is calculated using the H&F method as this RSL correction already takes into account the effect of additional surface drag in the RSL. The H&F method accounts for the influences of the canopy height and varying stabilities on the drag at the surface by calculating a varying \(z_{d}\) and \(z_0\), which is clearly critical to evaluating momentum in urban areas. Results for the Basel site show similar behaviour.
4.3.2 “Tuneable” Parameters
The H&F-model \(\beta \)-parameter is used to calculate the wind-speed profile in the RSL,
For the RSL within and above forest canopies, Harman and Finnigan (2007) found \(\beta \) to vary between about 0.1 and 0.6. In the current dataset \(\beta \) can be slightly larger and varies with wind direction (Fig. 5). The generally larger \(\beta \) for Basel compared to Gothenburg is attributable to a lower wind speed at the inflection point (\(u(z_{h})\)) in Basel. In Gothenburg, the mean \(\beta \) for flow perpendicular to the street canyon is 0.46, and 0.31 for parallel flow. For Basel when the flow is parallel to the canyon (0.36), \(\beta \) is similar to the spatial mean LES profiles (0.40). In Basel, when the flow approaches perpendicular to the canyon over flat roofs \({\overline{\beta }} = 0.43\), when flow approaches perpendicular over the pitched roofs \({\overline{\beta }} =0.54\). The high \(\beta \)-coefficient over pitched roofs is due to the low wind speed at the mean building height related to the upward shift of the inflection point (Fig. 2a), because of locally taller buildings in this wind direction. For the H&F method to be used in NWP models, we parametrize \(\beta \) based on stability (\(\phi _{M}(L_{C}/L)\)) and \(\beta \) during neutral conditions, \(\beta _{N}\) (Harman 2012). Although \(\beta _{N}\) has considerable spread, especially at the Basel site, the spatial mean based on LES shows \(\beta _{N}\) is the same for both modelled flow directions (0.40). Using \(\beta _{N}\) as 0.4 gives a slight overestimation of \(u_*\) during moderately unstable conditions (\(-1<z_{h}/L<-0.1\)), especially in Gothenburg. The H&F-method prediction of an increasing value of \(\beta \) with increasingly unstable conditions (\(z_{h}/L<-1.0\)) is not supported by the observations at either Basel or Gothenburg. However, this is expected, as in these conditions the shear-driven dynamics embodied in the H&F RSL model are less relevant (see Harman and Finnigan (2007) and Harman (2012) for further discussion). Following Bonan et al. (2018) we limit \(\beta \) to values below 0.5, and hereafter \(\beta \) is parametrized using Harman (2012) with \(\beta _{N} = 0.4\).
Observed \(\beta \)-parameter (Eq. 20) from hourly data with stability at the highest measurement level for, a Basel-Sperrstrasse stratified for perpendicular to flat roofs (light green), pitched roofs (blue), and parallel to the street canyon (red), with \(\beta \) calculated in the LES (triangles, Giometto et al. 2016), and b Gothenburg. Data are stratified in 13 \(z_{h}/L\) bins, showing the median (dots) and the interquartile ranges (error-bars). The grey lines indicate the \(\beta \)-fit from Harman (2012) using different \(\beta \) in neutral conditions \(\beta _{N}\)
Median absolute error of the wind speed at 17.9 m (1.2\(z_{h}\)) using all 60-min averages when varying the dR-model constants a\(\lambda \) versus \(\mu _{M}\), b\(\lambda \) versus \(\nu \), and c\(\mu _{M}\) versus \(\nu \) from De Ridder (2010) Eq. (11) (Table 2). The black dots indicate the default values of each parameter. Notations given in Table 1
As the three empirical constants in the dR model (\(\lambda \), \(\mu _{M}\), and \(\nu \) Eq. 11) were optimized for an RSL within and above forest canopies (De Ridder 2010) we perform a sensitivity analysis for the Basel site. The dR method shows the highest sensitivity to \(\lambda \) (Fig. 6), which is not surprising as \({\hat{\psi }}_{M}(z)\) is mostly inversely proportional to \(\lambda \) (Eq. 11). For small \(\lambda \), the model performance is also sensitive to \(\mu _{M}\), as \({\hat{\psi }}_{M}(z)\) generally becomes larger. The median absolute error varies very little with \(\nu \).
Figure 6 shows the median absolute error at \(1.2z_{h}\) from all wind directions but does not account for the variation of \(\lambda \), \(\mu _{M}\), and \(\nu \) with wind direction or street-canyon orientation. Taking all measurement levels above the mean canopy height, based on the median absolute error the best fit of the parameters for Basel are: \(\lambda =0.9\), \(\mu _{M}=1.3\), and \(\nu =0.2\).
4.4 Spatial Representativeness
The parametrizations are derived for spatially-averaged vertical profiles of wind speed, whereas, the tower measurements allow wind sectors from which an average wind-speed profile can be calculated (Fig. 7). The averaged vertical wind-speed profile calculated for each wind direction bin from observations and the H&F model weighted (by direction frequency) and unweighted means with the standard deviation are shown in Fig. 7. The difference between the frequency weighted and unweighted means is minor for the H&F method in Basel in neutral conditions and increases only slightly in more unstable conditions. However, the differences are too small to draw any meaningful conclusions.
The H&F modelled and observed (Basel-Sperrstrasse) normalized wind-speed profiles; mean and standard deviation (shaded and bars) from \(10^{\circ }\) wind direction bins, weighted by frequency of occurrence (red markers and lines) and equal weights (black markers and lines). Modelled wind-speed profiles are calculated using the isotropic \(L_{c}\) and \(z_{h}\) (solid lines) and \(L_{c}\) and \(z_{h}\) varying for each bin, for each stability class (a, d very unstable \(-4>z_{h}/L> -0.5\)b, e unstable \(-0.5>z_{h}/L> -0.1\), and c, f near-neutral \(-0.1>z_{h}/L> 0.1\)) a–c histograms and d–f profiles are shown. Bins analyzed where more than 10 h of data is available. \(\beta \) is parametrized using Harman (2012) with \(\beta _{N} = 0.4\)
5 Temperature Profiles
5.1 Variation with Wind Direction
Temperature profiles at the Basel site allow for analysis (Sect. 3) of the dependence of the observed normalized potential temperature and heat-flux profiles with wind direction (Fig. 8). Temperature generally increases into the urban canopy when we assume mostly unstable conditions (\(\theta _*(z_{m})<0\)). As with to the wind-speed profiles (Fig. 2a), the temperature profiles have the largest vertical variation with wind direction over pitched roofs.
Across the flat roofs, there is a strong inflection point just above the mean roof level. The temperature in the RSL and in the UCL remain near constant, while the temperature gradient is large only near the canopy top. This probable skimming-flow inflection point is also seen in momentum profiles (wind speed and friction velocity, Fig. 2) and has been observed previously (e.g., Rotach 1995; Castro et al. 2006; Christen et al. 2009). Skimming flow can lead to a decoupling of the UCL from the atmosphere above, which causes the larger temperature gradients when the flow is perpendicular to pitched roofs. Therefore, as with modelling the wind speed, the temperature in the canopy layer has to be modelled using a separate expression. For forest canopies, Harman and Finnigan (2008) use an exponential function dependent on the mixing length \(\ell _{M}\), \(\beta \), and the Prandtl number (\(P_{r}\)). This is applied to the Basel data in Sect. 5.2.
Urban environments have anthropogenic heat emissions (e.g., venting through windows, air conditioning systems, traffic) and spatial variations of shading that are hypothesized to be important. The variation in the normalized turbulent sensible heat flux with height and wind direction (Fig. 8c) is larger than the friction velocity (Fig. 2d). In particular, between 090 and \(140^{\circ }\) there is a large increase in the sensible heat flux at \(1.5 z_{h}\). However, from this analysis we are unable to distinguish between heat flux enhancement caused by turbulence generated by the tall, pitched roof buildings, and from (anthropogenic) heat sources. Data analysis shows that the strongest peaks in the turbulent sensible heat flux between 090 and \(140^{\circ }\) are found during the night, suggesting that solar heating is an unlikely cause for the maximum in the flux.
With flow approaching the street canyon over the flat roofs, the profiles of the normalized turbulent heat flux have a more consistent pattern. The heat flux increases (cf. the ISL flux) just above the canopy top, related to the heat release (e.g., radiation) emitted by roofs. In the canopy the heat flux decreases and is smaller than the heat flux at the top of the RSL.
5.2 Temperature Profile Evaluation
As expected, the modelled normalized temperature stratified by stability and direction of the approaching flow have similar results between the different methods, with the largest difference between the schemes near roof level (Fig. 9). Generally, the RSL models underpredict the temperature gradients, in particular the dR model, with the dR-model constants expected to differ for urban areas (Sec. 4.3). For most of the cases in Fig. 9 it is reasonable to use MOST above the canopy. For flow directions perpendicular to the pitched roofs, the temperature gradient, especially inside the UCL, is captured well by the exponential equation of Harman and Finnigan (2007). In these wind directions, the temperature gradient is larger as a result of the decoupling of the UCL and the lower wind speeds in this layer (Fig. 2). This suggests that the canopy parametrization might be more applicable to canopies with a higher building height to street canyon width ratio, but requires testing at more measurement sites.
As Fig. 3, but for temperature profiles scaled with the temperature scale at \(z_{m}\) at the Basel-Sperrstrasse site. Filtered to exclude \(|\theta _*|<0.02 \hbox {K}\), \(u_*/u(z_{h})>1.0\), and \({\hat{\phi }}_{M}(z=z_{h})<1.0\)
The poor performance of the H&F method when the flow is perpendicular to the flat roofs (Fig. 9a–c) is probably related to the idealized source/sink within the canopy, effectively setting the length scale for temperature. This has some justification for certain scalars but is likely inappropriate for heat, especially in an urban area where the length scale should reflect processes such as shading. It is possible to connect a model for a different scalar source/sink distribution into the H&F approach as applied by Bonan et al. (2018). This affects the magnitude of the temperature perturbations and the gradients, therefore affecting the above canopy solution as well.
As the Prandtl number at the canopy top is crucial in the H&F method (Eq. 15) it is useful to analyze the values determined by observations (Kays 1994),
with those from the empirical equation derived in Harman and Finnigan (2008) and Harman (2012),
The binned median Prandtl numbers (Fig. 10) calculated using Eq. (21) are similar to those derived at the forest canopy top (Eq. 22). The general trend is similar but values observed at the canopy top (\(1.1z_{h}\)) are 10% higher than modelled. Figure 10 shows all flow directions, including those perpendicular to pitched roofs, where large values for the H&F \(\beta \)-coefficient were measured (Fig. 5). When excluding these wind sectors, the median Prandtl numbers decrease towards the Harman and Finnigan (2007) derived fit.
6 Turbulent Fluxes
To parametrize the turbulent fluxes Eqs. (3) and (4) can be rewritten to calculate the friction velocity and the turbulent heat flux,
a Sensible heat, and b momentum flux e.g. within the RSL at 22.4 m (\(1.5z_{h}\)) at Basel-Sperrstrasse for a period of 10 days (3–13 April 2002) and c momentum flux at 32.3 m (\(1.8z_{h}\)) at Gothenburg (31 July–10 August 2004); observations (dots) and modelled using MOST, the dR model, and the H&F model using 30-min averages. The parameter \(\beta \) is parametrized using Harman (2012) with \(\beta _{N} = 0.4\)
Figure 11 compares modelled above-canopy fluxes excluding \({\hat{\psi }}_{M,H}\) and parametrizing \({\hat{\psi }}_{M,H}\) using the dR (Eqs. 11 and 14) and H&F (Eqs. 12 and 15) methods for 10 days in April 2002 in Basel and 10 days in August 2004 at the Gothenburg site. MOST underpredicts the friction velocity, and the modelled values can be half the observed friction velocity. Including a RSL correction increases the friction velocity, with values based on the H&F method being the same order of magnitude as the observations (Fig. 11b, c).
The RSL corrections do not improve the sensible heat flux calculated from MOST. These are largely overestimated in the RSL, which is consistent with the underestimation of the temperature gradient (Sect. 5.2), where MOST has a better representation of heat transfer in the RSL. This is again related to the lumped nature of sources and sinks of heat that are formulated in all RSL approaches (Sect. 5.2).
7 Discussion
Tower-mounted instruments are point measurements and cannot fully capture the horizontally-averaged wind-speed profiles in the urban RSL, especially UCL measurements under conditions when flow is perpendicular to the street, which are clearly not representative for the spatial average (Giometto et al. 2016). However, DNS, LES, and wind-tunnel data with better spatial coverage are typically restricted to neutral conditions. The tower provides measurements that converge towards the spatial averages above the UCL, and in the UCL when the flow is parallel to the street canyon (Giometto et al. 2016).
In both the urban and forest RSL, obstacles disturb the flow. Momentum is absorbed not at the surface but at a finite depth, with sweeps and ejections as well as inward and outward interactions (Gao et al. 1989; Christen et al. 2007). However, urban bluff bodies are known to cause stronger locked circulations and channeling effects (Nakamura and Oke 1988), an example of this being the recirculation zones and vortexes created in skimming flow regimes. In addition, urban environments have anthropogenic heat sources. Chimneys on roofs or traffic in the street canyon act as additional sources of heat and turbulence (Eskridge and Rao 1983). Additionally, the change in the volume of air and the variation in the mixing length (\(\ell _{M}\)) in the UCL are not negligible, in contrast to the forest canopy layer (Coceal and Belcher 2004). From DNS and LES, Coceal et al. (2006) and Castro (2017) both found \(\ell _{M}\) to vary with height in the street canyon, with a minimum near the canopy top and a maximum at \(\approx 0.5 z_{h}\). Assuming a non-constant mixing length, the classical mixing length relation between the shear stress and wind gradient (assuming this is valid) will no longer yield an exponential profile for wind speed in the canopy. However, the presence of finite obstacles and varying \(\ell _{M}\) does not preclude that the majority of the flux being carried by motions at scales associated with the canopy instabilities (e.g., Böhm et al. 2013).
8 Conclusions
Monin–Obukhov similarity theory (MOST) is often used to scale velocity and scalars (e.g., temperature and humidity) in the inertial sublayer. However, this theory assumes homogeneous surface conditions. In this study, the complexities associated with modelling the exchange of momentum and scalars in the urban roughness sublayer (RSL) are explored. The performance of methods that assume MOST and have a correction for the RSL are evaluated with tower measurements at two sites with little vegetation (Basel, Switzerland and Gothenburg, Sweden), considering a range of stabilities from neutral to strongly unstable.
As urban flow varies with wind direction, flow characteristics parallel and perpendicular to a street canyon differ. When urban areas have large spatial variability in morphometric properties (e.g., variable building height), these details at a given location may become important when interpreting measurements as spatial averages. For example, by accounting for the gable height of a pitched roof height rather than the mean building height. Taking the mean height of the building causes the modelled momentum inflection point to be lower than that observed in the wind-speed profiles.
Roughness sublayer corrections based on forest canopy theory lead to an improvement in the prediction of the profiles for momentum, and assume constant fluxes with height in the RSL. A constant momentum flux in the RSL is only seen with flow approaching the towers from directions with flat roofs in Basel and Gothenburg. In these cases, the Harman and Finnigan (2007) RSL parametrization performs remarkably well. The RSL parametrizations require empirical constants that should be optimized for urban environments to allow for a more general application in numerical weather prediction.
The RSL parametrizations do not improve the performance of a stand-alone MOST approach in the modelling of temperature profiles above the canopy. However, the Harman and Finnigan (2008) approach allows for the possibility of estimating the in-canopy temperature.
Using site-specific characteristics by wind direction improves results through \(z_0\) and \(z_{d}\), although the method of determining \(z_0\) and \(z_{d}\) is more crucial than directionally-dependent morphometric parameters. Modelling a varying \(z_0\) and \(z_{d}\) by stability greatly improves the parametrized momentum.
Insights help guide the representation of the urban RSL for numerical weather prediction and indicates the uncertainties related to the assumptions made. The results can be used to quantify the reliability to which any representation of the urban RSL can aspire.
References
Arnqvist J, Bergström H (2015) Flux-profile relation with roughness sublayer correction. Q J R Meteorol Soc 141(689):1191–1197
Böhm M, Finnigan JJ, Raupach MR, Hughes D (2013) Turbulence structure within and above a canopy of bluff elements. Boundary-Layer Meteorol 146(3):393–419
Bonan GB, Patton EG, Harman IN, Oleson KW, Finnigan JJ, Lu Y, Burakowski EA (2018) Modeling canopy-induced turbulence in the earth system: a unified parameterization of turbulent exchange within plant canopies and the roughness sublayer (CLM-ml v0). Geosci Model Dev 11(4):1467–1496
Castro IP (2017) Are urban-canopy velocity profiles exponential? Boundary-Layer Meteorol 164(3):337–351
Castro IP, Cheng H, Reynolds R (2006) Turbulence over urban-type roughness: deductions from wind-tunnel measurements. Boundary-Layer Meteorol 118(1):109–131
Christen A, Vogt R (2004) Energy and radiation balance of a central european city. Int J Climatol 24(11):1395–1421
Christen A, van Gorsel E, Vogt R (2007) Coherent structures in urban roughness sublayer turbulence. Int J Climatol 27(14):1955–1968
Christen A, Rotach MW, Vogt R (2009) The budget of turbulent kinetic energy in the urban roughness sublayer. Boundary-Layer Meteorol 131(2):193–222
Chrysoulakis N, Grimmond S, Feigenwinter C, Lindberg F, Gastellu-Etchegorry JP, Marconcini M, Mitraka Z, Stagakis S, Crawford B, Olofson F et al (2018) Urban energy exchanges monitoring from space. Sci Rep 8(1):11498
Coceal O, Belcher SE (2004) A canopy model of mean winds through urban areas. Q J R Meteorol Soc 130(599):1349–1372
Coceal O, Thomas TG, Castro IP, Belcher SE (2006) Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Boundary-Layer Meteorol 121(3):491–519
De Ridder K (2010) Bulk transfer relations for the roughness sublayer. Boundary-Layer Meteorol 134(2):257–267
Dobre A, Arnold S, Smalley R, Boddy J, Barlow J, Tomlin A, Belcher S (2005) Flow field measurements in the proximity of an urban intersection in London, UK. Atmos Environ 39(26):4647–4657
Eliasson I, Offerle B, Grimmond CSB, Lindqvist S (2006) Wind fields and turbulence statistics in an urban street canyon. Atmos Environ 40(1):1–16
Eskridge RE, Rao ST (1983) Measurement and prediction of traffic-induced turbulence and velocity fields near roadways. J Clim Appl Meteorol 22(8):1431–1443
Feigenwinter C, Vogt R (2005) Detection and analysis of coherent structures in urban turbulence. Theor Appl Climatol 81(3–4):219–230
Feigenwinter C, Vogt R, Parlow E (1999) Vertical structure of selected turbulence characteristics above an urban canopy. Theor Appl Climatol 62(1–2):51–63
Finnigan JJ, Clement R, Malhi Y, Leuning R, Cleugh HA (2003) A re-evaluation of long-term flux measurement techniques part I: averaging and coordinate rotation. Boundary-Layer Meteorol 107(1):1–48
Fuka V, Xie ZT, Castro IP, Hayden P, Carpentieri M, Robins AG (2017) Scalar fluxes near a tall building in an aligned array of rectangular buildings. Boundary-Layer Meteorol 162(2):207–230
Gao W, Shaw RH, Paw UKT (1989) Observation of organized structure in turbulent flow within and above a forest canopy. In: Munn RE (ed) Boundary layer studies and applications. Springer, Dordrecht
Garratt JR (1980) Surface influence upon vertical profiles in the atmospheric near-surface layer. Q J R Meteorol Soc 106(450):803–819
Garratt JR (1992) The atmospheric boundary layer. Cambridge University Press, Cambridge
Giometto MG, Christen A, Meneveau C, Fang J, Krafczyk M, Parlange MB (2016) Spatial characteristics of roughness sublayer mean flow and turbulence over a realistic urban surface. Boundary-Layer Meteorol 160(3):425–452
Grimmond CSB, Oke TR (1999) Aerodynamic properties of urban areas derived from analysis of surface form. J Appl Meteorol 38(9):1262–1292
Grimmond CSB, Salmond JA, Oke TR, Offerle B, Lemonsu A (2004) Flux and turbulence measurements at a densely built-up site in Marseille: heat, mass (water and carbon dioxide), and momentum. J Geophys Res Atmos 109:D24
Harman IN (2012) The role of roughness sublayer dynamics within surface exchange schemes. Boundary-Layer Meteorol 142(1):1–20
Harman IN, Finnigan JJ (2007) A simple unified theory for flow in the canopy and roughness sublayer. Boundary-Layer Meteorol 123(2):339–363
Harman IN, Finnigan JJ (2008) Scalar concentration profiles in the canopy and roughness sublayer. Boundary-Layer Meteorol 129(3):323–351
Harman IN, Barlow JF, Belcher SE (2004) Scalar fluxes from urban street canyons part II: model. Boundary-Layer Meteorol 113(3):387–410
Kastner-Klein P, Rotach MW (2004) Mean flow and turbulence characteristics in an urban roughness sublayer. Boundary-Layer Meteorol 111(1):55–84
Kays WM (1994) Turbulent Prandtl number—Where are we? J Heat Transf 116(2):284–295
Kellnerová R, Kukačka L, Jurvcáková K, Uruba V, Jaňour Z (2012) PIV measurement of turbulent flow within a street canyon: detection of coherent motion. J Wind Eng Ind Aerodyn 104:302–313
Kent CW, Grimmond CSB, Barlow J, Gatey D, Kotthaus S, Lindberg F, Halios CH (2017) Evaluation of urban local-scale aerodynamic parameters: implications for the vertical profile of wind speed and for source areas. Boundary-Layer Meteorol 164(2):183–213
Krayenhoff ES, Santiago JL, Martilli A, Christen A, Oke TR (2015) Parametrization of drag and turbulence for urban neighbourhoods with trees. Boundary-Layer Meteorol 156(2):157–189
Kusaka H, Kondo H, Kikegawa Y, Kimura F (2001) A simple single-layer urban canopy model for atmospheric models: comparison with multi-layer and slab models. Boundary-Layer Meteorol 101(3):329–358
Llaguno-Munitxa M, Bou-Zeid E, Hultmark M (2017) The influence of building geometry on street canyon air flow: validation of large eddy simulations against wind tunnel experiments. J Wind Eng Ind Aerodyn 165:115–130
Macdonald RW (2000) Modelling the mean velocity profile in the urban canopy layer. Boundary-Layer Meteorol 97(1):25–45
Macdonald RW, Griffiths RF, Hall DJ (1998) An improved method for the estimation of surface roughness of obstacle arrays. Atmos Environ 32(11):1857–1864
Martilli A, Clappier A, Rotach MW (2002) An urban surface exchange parameterisation for mesoscale models. Boundary-Layer Meteorol 104(2):261–304
Masson V (2000) A physically-based scheme for the urban energy budget in atmospheric models. Boundary-Layer Meteorol 94(3):357–397
Nakamura Y, Oke TR (1988) Wind, temperature and stability conditions in an east-west oriented urban canyon. Atmos Environ (1967) 22(12):2691–2700
Nelson MA, Pardyjak ER, Klewicki JC, Pol SU, Brown MJ (2007) Properties of the wind field within the Oklahoma City Park Avenue street canyon. Part I: mean flow and turbulence statistics. J Appl Meteorol Climatol 46(12):2038–2054
Neto WN (2015) The dependence of urban climate on building layout and design. PhD thesis, University of Reading, Reading, UK
Offerle B, Eliasson I, Grimmond CSB, Holmer B (2007) Surface heating in relation to air temperature, wind and turbulence in an urban street canyon. Boundary-Layer Meteorol 122(2):273–292
Oleson KW, Bonan GB, Feddema J, Vertenstein M, Grimmond CSB (2008) An urban parameterization for a global climate model. Part I: formulation and evaluation for two cities. J Appl Meteorol Climatol 47(4):1038–1060
Physick WL, Garratt JR (1995) Incorporation of a high-roughness lower boundary into a mesoscale model for studies of dry deposition over complex terrain. Boundary-Layer Meteorol 74(1–2):55–71
Rafailidis S (1997) Influence of building areal density and roof shape on the wind characteristics above a town. Boundary-Layer Meteorol 85(2):255–271
Raupach MR, Antonia RA, Rajagopalan S (1991) Rough-wall turbulent boundary layers. Appl Mech Rev 44(1):1–25
Rotach MW (1993) Turbulence close to a rough urban surface part I: Reynolds stress. Boundary-Layer Meteorol 65(1–2):1–28
Rotach MW (1995) Profiles of turbulence statistics in and above an urban street canyon. Atmos Environ 29(13):1473–1486
Rotach MW, Vogt R, Bernhofer C, Batchvarova E, Christen A, Clappier A, Feddersen B, Gryning SE, Martucci G, Mayer H et al (2005) BUBBLE—an urban boundary layer meteorology project. Theor Appl Climatol 81(3–4):231–261
Roth M, Oke TR (1995) Relative efficiencies of turbulent transfer of heat, mass, and momentum over a patchy urban surface. J Atmos Sci 52(11):1863–1874
Simón-Moral A, Santiago JL, Martilli A (2017) Effects of unstable thermal stratification on vertical fluxes of heat and momentum in urban areas. Boundary-Layer Meteorol 163(1):103–121
Stewart ID, Oke TR (2012) Local climate zones for urban temperature studies. Bull Am Meteorol Soc 93(12):1879–1900
Wood CR, Lacser A, Barlow JF, Padhra A, Belcher SE, Nemitz E, Helfter C, Famulari D, Grimmond CSB (2010) Turbulent flow at 190 m height above London during 2006–2008: a climatology and the applicability of similarity theory. Boundary-Layer Meteorol 137(1):77–96
Zou J, Zhou B, Sun J (2017) Impact of eddy characteristics on turbulent heat and momentum fluxes in the urban roughness sublayer. Boundary-Layer Meteorol 164(1):39–62
Acknowledgements
This research was funded as part of the NWO Rubicon grant number 019.161LW.026 (Theeuwes), EU H2020 URBANFLUXES (Grimmond, Theeuwes), and Newton Fund/Met Office CSSP China (Grimmond, Theeuwes). The core measurements during BUBBLE were funded by the Swiss Federal Office for Education and Science (Grant C00.0068). We acknowledge Roland Vogt, Mathias Rotach, and Eberhard Parlow for their contributions to setting-up and collecting the tower measurements in Basel. For the tower measurements in Gothenburg, we thank Ingegärd Eliasson, Brian Offerle, and Fredrik Lindberg for collecting and processing the data. In addition, we would like to thank Marco Giometto for providing the LES data and Janet Barlow, Jordi Vilà-Guerau de Arellano, and Metodija Shapkalijevski for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Modifications to Monin–Obukhov Similarity Theory in the Roughness Sublayer
Appendix 1: Modifications to Monin–Obukhov Similarity Theory in the Roughness Sublayer
The notation for the variables used herein is given in Table 1. Integrating Eq. (1) from \(z_0+z_{d}\) to height z leads to
which can be rewritten as
The first term on the right-hand side (r.h.s.) of Eq. (26) yields the traditional integral form of the flux-gradient relations in the surface layer, i.e the MOST relations in the ISL. The second r.h.s. term of Eq. (26) is the correction for the wind-speed profile in the RSL. Integrating yields
It can be expected that far from the surface where \(z>> z_0\), the RSL effects become minor and Eq. (27) approaches the traditional MOST,
Reconciling Eqs. (28) and (27) yields the following expression for the wind speed at \(z_0+z_{d}\),
Inserting Eq. (29) in Eq. (27) yields the following relation for the wind-speed profile within the RSL, as provided in Eqs. (3) and (5),
To calculate the roughness length as given in Eq. (30) we follow Macdonald et al. (1998), and assume that the total friction force caused by the bluff bodies (\(F_{D}\)) that form the urban canopy is given by,
where \(\rho \) is the air density, \(C_{dh}\) is a height-integrated drag coefficient and \(A_{f}\) the frontal surface area of all bluff bodies in the area of analysis (\(A_{d}\)). The average friction force generated by the bluff bodies leads to the flux of momentum flux towards the surface,
where \(\tau \) is the momentum towards the surface. Rewriting Eqs. (31) and (32) to find an expression for the wind speed at roof level yields,
where \(A_{f}/A_{d}=\lambda _{f}\). Combining Eqs. (30) and (33) to derive an implicit expression for \(z_0\) yields,
Deriving and expression for \(z_0\) following Eq. (34) requires us to solve a non-linear equation. Therefore we assume \(\psi _{M}\left( z_0/L\right) \) to be small enough to be negligible compared to the other terms. This assumption yields an expression for \(z_0\),
Macdonald et al. (1998) defined the roughness length under neutral conditions as,
and assumed \(C_{dh} = 1.2\) for cuboids.
This way of computing the roughness length using Eq. (35) is used in the De Ridder (2010) approach. In the MOST+ approach the RSL term (i.e. the last term of Eq. (35)) is neglected.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Theeuwes, N.E., Ronda, R.J., Harman, I.N. et al. Parametrizing Horizontally-Averaged Wind and Temperature Profiles in the Urban Roughness Sublayer. Boundary-Layer Meteorol 173, 321–348 (2019). https://doi.org/10.1007/s10546-019-00472-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-019-00472-1