Abstract
The capabilities of nine atmospheric dispersion models in predicting near-field dispersion from puff releases in an urban environment are addressed under the Urban Dispersion INternational Evaluation Exercise (UDINEE) project. The model results are evaluated using tracer observations from the Joint Urban 2003 (JU2003) experiment where neutrally-buoyant puffs were released in the downtown area of Oklahoma City, USA. Sulphur hexafluoride concentration time series measured at ten sampling locations during four daytime and four night-time puff releases are used to evaluate how the models simulate the puff passage at the measurement locations. The neutrally-buoyant puff releases in the JU2003 experiment are the closest scenario to radiological dispersal device (RDD) releases in urban areas, and therefore, UDINEE is a first step towards improving the emergency response to an RDD explosion in the urban environment. We investigate for each puff and sampler the model capability of simulating the peak concentration; the peak and puff arrival times; and time duration, defined as the period over which concentrations exceed 10% of the peak concentration. This analysis points out differences on the performance of models: the fraction within a factor-of-two values ranges from 0.10 to 0.6 for peak concentration, from 0 to 1 for the peak and arrival times, and from 0 to 0.8 for the time duration. The results reveal that the characteristics of the release site largely influence the model simulation as it affects initial puff size and the initial downwind spread of the puff.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Atmospheric dispersion models (ADMs) are used for assisting emergency management planning and response associated with the release of hazardous materials in the atmosphere (e.g. Bradley 2007; Benamrane et al. 2013; Benamrane and Boustras 2015). The dispersion of radioactive material from a radiological dispersal device (RDD) (e.g. Andersson et al. 2009; Di Lemma et al. 2014), for example, due to its likely use in urban environments, poses a challenge for ADMs. It is in populated areas where a proper estimation of the radioactive dispersion is indispensable to minimize possible health risks associated with RDD explosions (e.g. Jonsson et al. 2013).
Understanding the transport and dispersion of pollutants in urban environments is difficult (e.g. Hosker 1984), as it largely depends on the city-scale flows above and within the urban canopy layer, and the urban atmospheric boundary-layer characteristics. Britter and Hanna (2003) review mean flow, turbulence and dispersion in urban areas. Advancements in computing resources during the last few years have improved the simulation by atmospheric models of urban flow and its short time-scale variability (e.g. Blocken 2015). Because of this progress, a wide range of ADMs can now simulate air pollution dispersion in cities (e.g. Baklanov et al. 2009; Lateb et al. 2016; Wingstedt et al. 2017).
To support decision making dealing with the atmospheric dispersion of airborne harmful materials, predictions of ADMs must be able to provide adequate description of the atmospheric processes (Ribeiro et al. 2014). To increase the confidence in decision making based on ADM predictions requires establishing the ADM capabilities and limitations. The variability between model predictions should also be characterized and quantified (COST ES1006 2015). Both purposes are achieved through comparison of model predictions to tracer and meteorological observations provided by field campaigns (e.g. Rao 2005).
Model evaluation criteria depend on the context in which models are used (Steyn and Galmarini 2008). Moreover, observations from field campaigns must fulfil certain requirements to be used for evaluating urban ADMs (Schatzmann and Leitl 2002), so as to resolve the short time-scale variability in meteorological conditions and pollutant concentrations inside the urban canopy layer (Britter and Hanna 2003). The meteorological and tracer observations measured during the Joint Urban 2003 (JU2003) field campaign (Allwine and Flaherty 2006) perfectly fulfil these requirements. In addition, during the JU2003 experiment, 40 instantaneous puff releases (25 daytime and 15 nocturnal) were performed.
Under the Urban Dispersion INternational Evaluation Exercise (UDINEE) project, nine ADMs have been evaluated using the subset of the observations from the JU2003 database measured during the set of puff releases performed over ten intensive operational periods. The puff releases in the JU2003 experiment (Clawson et al. 2005) were chosen because one of the UDINEE objectives is to better understand modelling capabilities for RDD scenarios. A radiological dispersal device is typically associated with the explosive dispersal of radiological materials in urban areas, and due to the heat associated with the explosion, these explosive releases are characterized by buoyancy (e.g. Sharon et al. 2012). The instantaneous non-buoyant puff releases at ground level in the JU2003 experiment are the closest scenario to RDD releases in urban areas, and therefore, the JU2003 database based on puff releases is an excellent resource for evaluating the application of ADMs in RDD-like releases in urban environments.
From the basis of this exceptional field experiment, UDINEE with its multi-model approach provides an important contribution towards the study of RDD explosions and the associated emergency response in urban environments. Under the UDINEE project, observations and model predictions were made available to all participants through the ENSEMBLE web-based platform (http://ensemble.jrc.ec.europa.eu/), hosted at the European Commission Joint Research Centre (Bianconi et al. 2004; Galmarini et al. 2004, 2012).
In our study, we examine how the models simulate the puff passage at the measurement locations (a companion study is devoted to the comparison of observed and predicted concentration levels, see Hernández-Ceballos et al. 2019). We evaluate for each puff and sampler the model capability to match the peak concentration, the peak and puff arrival times, and the time duration (the period over which concentrations exceed 10% of the peak concentration). Predictions of the dispersion coefficients (σt, σx) and their spatial and temporal variability are also evaluated. To achieve this purpose, simulations from the nine ADMs participating in the UDINEE project are compared with sulphur hexafluoride (SF6) time series measured from eight puff releases. The impact of modelling thermal effects (day–night stability differences or neutral atmospheric conditions) on the performance of models is also discussed.
2 Methodology
2.1 Observed Time Series
A comprehensive description and technical details of the JU2003 experiment are given in Clawson et al. (2005). In this field campaign, SF6 concentration time series with a temporal resolution of 0.5 s were measured for each puff by fast-response tracer gas analyzers. In this analysis, and in agreement with Hernández-Ceballos et al. (2019), we take as reference the SF6 concentrations from the four puffs released during the third and eighth intensive operating periods (IOP3 and IOP8), which were carried out during daytime and night-time respectively. The selection of both intensive operating periods is based on the large availability of predictions (eight out of the nine models simulated the dispersion of the four puffs each released in IOP3 and IOP8), and tracer measurements in each one, thus guaranteeing the largest statistical sample.
Clawson et al. (2005) show a summary of the meteorological conditions during the July 2003 study period, calculated over all fixed anemometers at street level and on building tops, mean wind direction was 196° during IOP3 and 157° during IOP8, whilst a relative narrow range of wind speeds was also encountered in both intensive operating periods (3.7 m s−1 in IOP3 and 3.8 m s−1 in IOP8) (Zhou and Hanna 2007). During the JU2003 experiment, there were no large diurnal differences in urban boundary-layer stability. Hanna et al. (2007) reported that slightly unstable conditions prevailed during both day and night intensive operating periods, while Hertwig (2007) indicated that differences in stability existed between the daytime and night-time releases during the JU2003 experiment. A detailed characterization of the mean and turbulent atmospheric parameters governing the observed tracer distributions in each intensive operating period is addressed in Brown (2004) and Hanna et al. (2007).
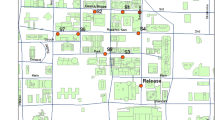
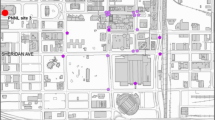
Each puff was released at a height of about 2 m above street level by popping a balloon containing a known mass of SF6 (Fig. 1), which is a highly inert tracer gas and has relatively low background levels (about 5 pptv, see Martin et al. 2011). The release times range from 0900 to 1000 CDT (Central Daylight Time) for IOP3 and from 0500 to 0600 CDT for IOP8 (CDT = UTC − 5 h). To ensure that SF6 concentrations in each sampling location were from the latest puff released, the puffs were released every 20 min in each IOP. Figure 1 shows the locations of the release points and the nine fast-response tracer gas analyzers that remained stationary in IOP3 and IOP8 (the number 5 was mobile and it is not considered in our study). As can be seen van-mounted fast-response tracer gas analyzers were deployed at about 2 m above ground level (a.g.l.), in different configurations depending on the release location and wind direction. The fast-response tracer gas analyzers were positioned to the north–north–east of the release point in IOP3 and to the north-west in IOP8. The distance from the release points ranges from 183 (L13) to 539 m (L17) in IOP3 and from 176 (L8) to 600 m (L3) in IOP8 (Fig. 1).
View of SF6 source and the fast-response tracer gas analyzers on the UDINEE modelling domain during IOP3 and IOP8. In brackets and in each table are indicated the number of puffs analyzed in each measurement location in each intensive operating period (maximum observed > 400 pptv). Below, concentration time series from fast-response sampler L15 during IOP3 release 4 and L1 during IOP8 release 2 are shown
Clawson et al. (2005) provide information on the calibration of fast-response tracer gas analyzers, with eight calibration standards used ranging in concentration from pure air to over 10,000 pptv SF6. The calibration standards had a manufacturer-listed concentration uncertainty of ± 5%. Considering this value, it is reasonable to expect accuracy variations up to ± 10%. All of the average recovery values are within this range. The standard deviations for all of the groups reported were less than 9%, which should be a reasonable estimate of instrument precision.
Following the criterion applied in Hernández-Ceballos et al. (2019), a SF6 concentration of 400 pptv is assumed to account for the minimum threshold in the observations. For an equal comparison, we wished to use only those puff and sampler data in each intensive operating period when a clear concentration signal is available, and observed maximum concentration is above 400 pptv. This value agrees with the typical limit of quantitation (LOQ) for each intensive operating period and fast-response tracer gas analyzer reported in Clawson et al. (2005), and at the same time, it limits the presence of residual tracer from an earlier puff, which is of vital importance in order to correctly identify the main puff passage at each sampler.
2.2 Participating Models and Modelling Input Variables
In the context of UDINEE, six modelling groups from Europe and two modelling groups from North America simulated the dispersion of the puff releases that occurred during the JU2003 experiment. The nine ADMs, listed below, have been evaluated; for more information see Hernández-Ceballos et al. (2019).
-
Emergency Source Term Evaluation—Chemical, Biological, Radiological and Nuclear (ESTE CBRN) (ABmerit (Slovakia); Čarný et al. 2015).
-
Canadian Urban Flow and Dispersion System (CUDMS) (Meteorological Service of Canada (Canada); Benbouta 2007; Hogue et al. 2009).
-
Parallel-Micro-SWIFT-SPRAY (PMSS) (France Atomic and Alternative Energies Commission (France); Oldrini et al. 2017).
-
Micro SWIFT-SPRAY (MSS) (L’Istituto di Scienze dell’Atmosfera e del Clima (Italy), Anfossi et al. 2010; Tinarelli et al. 2012).
-
Numerical atmospheric-dispersion modelling environment (NAME) (UK National Weather Service (United Kingdom); Jones et al. 2007).
-
NAME-Urban (UK National Weather Service (United Kingdom); Jones et al. 2007).
-
Quick Urban and Industrial Complex (QUIC) (National centre for Nuclear Research (Poland); Pardyjak and Brown 2001, 2002).
-
ADREA-HF (National Centre for Scientific Research “Demokritos” (Greece); Bartzis 1991; Venetsanos et al. 2010).
-
Urban dispersion model (UDM)/second-order closure Integrated Puff (SCIPUFF) (Defense Threat Reduction Agency (United States); Hall et al. 2003; DTRA 2008; Sykes et al. 2016).
We need to consider that a single model realization cannot reproduce a single realization of one puff dispersion in a turbulent flow, as measured in the JU2003 experiment. Considering this, part of the bias is unavoidable and arises from the very stochastic nature of the turbulent flow. An observed ensemble average should be obtained from a group of puffs released under identical (or similar) conditions. However, a large number of such puffs is required for a statistically stable ensemble, but is impossible to achieve in a field program (Chang and Hanna 2004).
UDINEE does not aim at an identification of the best or worst model, as different urban geometries, meteorological conditions, set of models, boundary conditions, and diffusion schemes, should be taken into account. UDINEE aims at evaluating the overall performance of the models analyzed and the state-of-the-art in urban dispersion modelling, as well as explaining the differences between the model results and the dependence on input assumptions made by the project participants. With this aim, each model is identified hereafter by an anonymous code (M1–M10). For more information on the characteristics and performance of each model, see other articles in this special issue.
The information provided to all modellers participating in the UDINEE project to simulate the SF6 dispersion resulting from each puff releases was:
-
Source location and height (2 m a.g.l.), release times and mass released (Fig. 1);
-
Meteorological information: 10-s average time series of wind direction and speed, temperature and relative humidity measurements by the Portable Weather Information Display System (PWIDS) sensor No. 15. This sensor was located 10 m above the roof of the Post Office (40 m a.g.l.) and 1 km upwind of central business district. Also available are 10-min average time series of wind direction and speed for the 20 DPG sonic anemometers, all located in the downtown street canyons at heights of 8 m a.g.l. on small towers and sited above 5 m or more from the nearest building. All participating models were run using the meteorological time series from the PWIDS sensor (Hernández-Ceballos et al. 2019).
-
Geographical information System (GIS) shapefiles of the Oklahoma City centre, which contains building heights and coordinates. The urban canopy of Oklahoma City was highly inhomogeneous. The tallest building in the urban core during the JU2003 experiment was approximately 152 m (Burian et al. 2003).
The simulations were conducted for an urban domain covering the downtown Oklahoma City area (1.6 km × 1.4 km2 in size and from zero to 402 m a.g.l.). The horizontal grid size selected is 5 × 5 m2 and 57 vertical levels are defined according to exponential grid spacing. There were modelling groups performing the simulations in different grid spacing (see Table 1 in Hernández-Ceballos et al. 2019), and model data were interpolated onto the common grid. The simulation domain and the complex of buildings in the area are shown in Fig. 1.
2.3 Definition of Puff Parameters
Modelled time series of SF6 concentrations with temporal resolution of 0.5 s were requested at the measurement locations (blue dots in Fig. 1) from each UDINEE participant. We note that the ADMs used in this context provide ensemble-averaged concentrations at the time resolution of the meteorological input variables. Thus, the ADM predictions cannot be representative of the intrinsic atmospheric variability at a frequency of 0.5 s from the single realization given by measurements. Several of the Lagrangian models do not directly calculate time series with a temporal resolution of 0.5 s. To fulfil the UDINEE requirements, these models produced averaged time series at the sampling sites with a lower temporal resolution (20 s or 1 min), and the corresponding 0.5-s time series are obtained by interpolation. The Eulerian models, in contrast, provide instantaneous ensemble-averaged values at the time instances every 0.5 s.
Figure 2 is an observed concentration time series (in logarithmic scale) illustrating the parameters that are used in the current study to characterize the puff passage at each measurement location. We note that peak concentrations are calculated using normalized concentrations to the release mass (Q) of each puff (Fig. 1). The rest of parameters are invariant to normalization. As defined by Zhou and Hanna (2007):
-
Peak concentration (Cmax) is the 0.5-s maximum concentration in each time series (red cross in Fig. 2);
-
Peak time is the difference between the time when the peak concentration is reached and the release time of each puff (red dot in Fig. 2);
-
Arrival time is the time difference between the release time and the time when the concentration is greater than or equal to 0.1 Cmax for the first time;
-
Time duration (Dt) is the time period over which concentrations exceeds 10% of the peak concentration (Cmax).
Based on the previous parameters, the following dispersion coefficients have also been estimated,
-
Standard deviation of the concentration time series (σt), based on the approach used by Hanna and Franzese (2000) for non-Gaussian distributions (e.g. time series with outliers and/or two or more peaks). Thus, σt is calculated as
where 4.3 is the width of a normal distribution at 0.1 of its maximum value (Doran et al. 2007; Zhou and Hanna 2007).
-
Along-wind dispersion coefficient (σx) is the standard deviation of spatial concentration distribution (Hanna and Franzese 2000), and is calculated as
where u indicates the effective puff speed at which the puff is moving; u is not the instantaneous puff speed, but the average puff speed over its trajectory from the source position to the sampler position. The speed is calculated as the straight-line distance from the source to the sampler, x (Fig. 1) divided by the peak time (Zhou and Hanna 2007).
2.4 Metrics for Evaluating Model Performance
Quantitative comparisons assess whether the simulation of the aforementioned parameters at receptors points can match the observed ones, and the degree of scatter. The primary quantitative performance measures used to assess the prediction skill of the models are the geometric mean (MG), geometric variance (VG), fraction of predictions within a factor-of-two and a factor-of-five of observations (FAC2 and FAC5), and its use was suggested by Hanna and Chang (2012) for ADM evaluation. These measures are generic and apply to any kind of data pairings, including paired in space (sampler) and time (puff), and any kinds of variables, including peak concentration, the peak and puff arrival times and time duration. According to Chang and Hanna (2004), MG and VG values may be more suitable for dispersion modelling because of concentrations spanning many orders of magnitude. These measures have been used in the statistical evaluation of other dispersion models (e.g. Hendricks et al. 2007; Schatzmann et al. 2010). A perfect model has values of MG, VG, FAC2 and FAC5 = 1. To evaluate and compare how models simulate the variability of the derived parameters with distance and time, the coefficient of determination (R2) is used. This coefficient is a statistical measure of how close the data are to the fitted regression line, which ranges from zero (none of the variability explained) to 1 (all variability explained).
3 Results
Tables 1 and 2 present quantitative performance measures for the nine models used in UDINEE, with concentrations paired in space and time. Table 1 has been generated using the complete set of sampling data for each model and for the four release periods during IOP3 and IOP8 respectively. The total number of samplers for each intensive operating period is 36 (nine fast-response tracer gas analyzers and four puffs during each intensive operating period) (Clawson et al. 2005). The Table includes samplers where either maximum observed (CO,max) or predicted (CP,max) concentration is less than the minimum threshold (400 pptv) used in this analysis (Sect. 2.1). Hence, Table 1 includes a listing of the number of samplers for each model that indicate acceptable (CO,max > 400 pptv; CP,max > 400 pptv), false negative (CO,max > 400 pptv; CP,max < 400 pptv), false positive (CO,max < 400 pptv; CP,max > 400 pptv) and zero-zero (CO,max = 0; CP,max = 0) pairs of values.
The number of modelled SF6 time series with acceptable samplers varies between models and intensive operating periods (Table 1). These differences arise because several models simulated zero concentration values during the sampling period (20 min) at some samplers in which puffs were actually measured. There are only “zero–zero” cases for IOP3, mostly due to the fact that the observed and predicted plumes (models M1, M5 and M6) were shifted to the east after the release, and hence were off of some samplers located to the north of the release point (Hernández-Ceballos et al. 2019). The zero–zero category has no cases for IOP8, due to the observed plumes stayed over the sampler network, and the predicted plumes were either relatively broad (models M3 and M5) or spread laterally much more to the west than the observed plume (models M4 and M9) (Hernández-Ceballos et al. 2019). IOP8 has many more false negative than false positive pairs. In contrast, the number of false negative and false positive is similar in IOP3, because both observed and predicted plumes were broad in the east-north-east direction.
Clawson et al. (2005) explains that the samplers were occasionally saturated (i.e., concentrations exceeded the maximum concentration measurement capability). Figure 1 shows two examples of this behaviour from sampler L15 during IOP3 and sampler L1 during IOP8. We have removed these time series in the results shown in Table 2, which only considered those samplers (N value) where the observed and predicted SF6 maximum concentrations exceed the minimum threshold of 400 pptv and the maximum is properly measured. In total, 13 and 18 SF6 time series in IOP3 and IOP8 (see the samplers analyzed in Fig. 1) are used to evaluate how the models simulate the puff passage at the measurement locations.
The results of this multi-model quantitative comparison are organized in two subsections. In Sect. 3.1, we show the performance of models in simulating the peak concentrations, the peak and puff arrival times and the time duration, while Sect. 3.2 is dedicated to displaying how the models simulate the temporal and spatial variability of the dispersion coefficients (σt, σx).
3.1 Simulation of Observed Puff Parameters
Two panels are shown for each parameter, with each being the corresponding scatter plot with the observed (horizontal axis) and predicted (vertical axis) values for each intensive operating period (Fig. 3a–d for IOP3 and Fig. 3e–h for IOP8). Each point represents the observed-modelled pair for a given puff and sampler. In the scatter plots, straight lines corresponding to FAC2 and FAC5 (without FAC2) agreement are also plotted. The model performance metrics for each puff parameter are shown in Table 2 (FAC2 and FAC5) and in Fig. 4 (VG vs MG).
Scatter plots for, a peak concentrations (in pptv kg−1), b peak time (in seconds), c arrival time (in seconds), and d time duration (in sec) predicted and observed paired in space (same sampling location) for IOP3. Scatter plots for, (e) peak concentrations (in pptv kg-1), (f) peak time (in seconds), (g) arrival time (in seconds) and (h) time duration (in seconds) predicted and observed paired in space (same sampling location) for IOP8. The axes of the plots are logarithmic for concentrations and linear for the times. Points are plotted for individual models under the condition that observed and predicted peak concentrations must both exceed the threshold of 400 pptv
3.1.1 Peak Concentration Normalized by the Emission Mass
Figure 3 shows the two panels of the maximum 0.5-s concentrations for each intensive operating period. The scatter plots reveal differences between models based on the large and different spread of the points around the main diagonal. Visual inspection shows more spread during night-time (IOP8) than during daytime (IOP3).
In general, several potential factors, such as transport distance, wind speed and direction, and turbulence patterns can potentially account for the range of observed maximum concentrations. Flaherty et al. (2007) reported the critical influence of the wind direction on the variability in the concentrations measured for different release periods, and how the highest concentrations measured at the crane site occurred when the wind direction was within 20° of the ideal transport direction. For deviations greater than 20°, concentrations drop off rapidly as only the far edges of the plume are observed, or the plume misses the receptor completely.
On average, there are also differences between the daytime and night-time normalized maximum concentrations. Observed peaks average about 8 pptv kg−1 during daytime and about 16 pptv kg−1 at night. Not all of the models match these day–night differences in the normalized maximum concentrations. Models M4, M6, M3 and M5 present higher mean peaks during night-time and models M8, M9 and M10 during daytime. These differences between models can be attributed to the consideration of day–night thermal differences in the simulations (e.g., the tracer vented upwards, with upward motions more intense during daytime, and therefore favour lower concentration levels during daytime puffs). Flaherty et al. (2007) and Finn et al. (2010) reported, from enhanced dispersion during convective conditions, that the daytime vertical profiles of the SF6 tracer generally show a lower magnitude and exhibit a more uniform vertical distribution than the night-time profiles. In contrast, if day–night stability differences are not considered, the differences between modelling predictions can be associated with the changes in the release location and flow dynamics in the urban area.
Low FAC2 values are obtained in both intensive operating periods, with a range from 0.15 (M8) to 0.61 (M3) during daytime, and from 0.10 (M6) to 0.38 (M5) at night (Table 2). There are more points largely underpredicting (> FAC5) the observed peak values in IOP8 than in IOP3. In addition, the largest overprediction in IOP3 is seen on both the lowest and the highest observed peak concentrations, while the largest overprediction is concentrated at low peak concentrations in IOP8.
On average, peak concentrations are overestimated in both intensive operating periods (MG values average about 1.3 in IOP3 and 1.9 in IOP8, Fig. 4). Three models (M4, M8 and M9) underestimate and two models (M6 and M3) overestimate the observed peak concentrations in both intensive operating periods. A change in the behaviour of models M5 and M10 between daytime and night-time is observed. With the exception of model M6 in IOP8, VG values < 100 in both intensive operating periods (Fig. 4). The large bias obtained for M6 is mainly caused by the large overprediction registered in three measurement locations in IOP8 respectively (Fig. 3e–h).
3.1.2 Peak Time
The scatter plots for the peak times are shown in Fig. 3a–d (IOP3) and Fig. 3e–h (IOP8). Based on the scatter diagrams, there are large differences between them. On average, all models present larger peak times during night-time, which is in agreement with the average values from observations (about 201 s in IOP3 and 224 s in IOP8).
Despite the different scatter, most of the predictions fall within a factor-of-two of observations in both intensive operating periods, pointing out the FAC2 values (100% of the predicted samplers) of models M4, M1, M8 and M9 during daytime, and of models M9 and M10 during night-time (Table 2). In contrast, models M10 and M3 in IOP3 and model M6 in IOP8 have the highest percentage of points falling within a factor-of-five. Looking at Table 2, and with the exception of model M10 in IOP3 and model M6 in IOP8, predicted peak times are mainly below FAC5 of the observations (above 95% of the points).
The MG values (Fig. 4) indicate that the models overestimate or underestimate the peak times independently of the intensive operating period. The MG values show that six out of eight models clearly overderpredict the observed peak times (MG > 1) in IOP3, with a maximum MG value of 1.9 (M6). The maximum VG value in IOP3 is 6.1 (M10), while the rest of the models keep VG values below 2.4 (Fig. 4). In IOP8, seven out of eight models overpredict the observed peak times (MG > 1), with a maximum value of 3.2 (M6). IOP8 presents low VG values, with an average of about 2, which indicates that the spread is limited to a small number of pairs.
Comparing the scatter, model M6 is highlighted, since many predictions are flat and high in both intensive operating periods (Fig. 3). In the case of IOP8, this model largely overestimates the peak times at eight samplers (peak concentration is predicted just at the end of the sampling period). Analyzing the observed time series at these samplers (puffs 1, 2, 3, 4 from L06, puffs 1, 3, 4 from L02, and puff 3 from L08), the common characteristic is the presence of more than one peak and a relatively long time duration of the time series. Zhou and Hanna (2007) identify some of these outliers in the peak time, which were associated with the location of the samplers near to and/or behind large buildings. Considering this information, model M6 could therefore have difficulties in simulating the physical processes determining the puff dispersion in these specific samplers.
3.1.3 Arrival Time
Figures 3 shows the scatter plots for predicted and observed arrival times for each intensive operating period. Visually, the distribution of the points is completely different in each one. The scatter also points out how the agreement looks better below 180 s in both, which suggests a better representation of the small puff arrival times, i.e. fast puffs and/or nearby samplers to the release point. This result is in agreement with the increase in the complexity of matching the observed puff concentrations with increasing the distance of the sampling site from the release point. Hernández-Ceballos et al. (2019) report that the models tend to increasingly underestimate concentration as the puff moves away from the source. This behaviour is strongly influenced by the complex circulations and turbulence patterns generated by the buildings in the built-up urban area.
In IOP3, and with the exception of M3 and M10, the models present high agreement with observations [FAC2 values range from 0.8 (M6) to 1.0 (M4, M5, M9)] (Table 2). In the case of M3 and M10, there are many points underestimating the observed values above a factor-of-five (77% of the points for M3 and 46% for M10), which consequently causes the minimum FAC2 value (FAC2 is zero for models M3 and M10). In IOP8, although the spread of the points is larger, most of them fall within a factor-of-two of observations, in a range from 0.45 (M6) to 1.0 (M9) (Table 2). Only M6 shows a larger percentage of points (≥ 50%) within or above a factor of five of observed arrival times.
On average, the MG values show different trends in IOP3 (MG = 0.8) and in IOP8 (MG = 1.2). In IOP3, with the exception of M6 and M5 (MG > 1.0), the models underestimate the arrival time (MG < 1) in a range from 0.1 (M3) to 0.9 (M4) (Fig. 4). In the case of IOP8, while three models (M2, M3 and M10) underestimate the arrival of the plume (MG values average about 0.5), there are five models overestimating its arrival (MG values average about 1.8). Model M6 reaches the maximum MG value (2.9).
The VG value is below 10 in most of the models and in both intensive operating periods (Fig. 4). The highest VG values (VG > 100) correspond to M3 in IOP3 and M2 in IOP8. These large values relates to the large underestimation of the arrival time at most of the receptors in the case of model M3 in IOP3, and in five receptors in the case of model M2 in IOP8.
3.1.4 Time Duration
Scatter plots for the time duration are depicted in Fig. 3. We note the large spread in both plots and how models tend to largely overpredict the observed time duration during IOP8 (night-time), whilst there appears to be more balance between the points around the line of best fit during IOP3 (daytime hours). According to the meaning of this parameter, i.e. time period over which concentrations exceed the 10% of the peak concentration, these results suggest day–night stability differences, if thermal effects are taken into account. Differences can be, for instance, in the simulation of building wake effects, which contribute to the puff elongation by retaining and then releasing tracer over the city. This mechanism contributes to the asymmetry of the puff about their maximum values (Doran et al. 2007).
On average, the FAC2 value is higher in IOP3 (0.5) than in IOP8 (0.3), and it is important to point out that all models present improved FAC2 values during IOP3 (daytime) (Table 2). The majority of points in most of the models are within a factor-of-five in both intensive operating periods and an increase in the number of predicted values above the FAC5 value is registered overnight. This result reveals how the characteristics of the sampler location inside the urban canopy can affect the agreement between observed and predictions at a particular receptor (given that they are placed in different locations for the different intensive operating periods). In this sense, the location of the sampler can cause it to be affected either by the edges or by the middle of the spreading cloud of tracer material.
In terms of MG values, seven out of eight models overpredict the time duration in IOP8, with values in a range from 1.2 (M6) to 4.0 (M2) (Fig. 4). In contrast, model M9 underpredicts the observed time duration, with an MG value of 0.9. In the case of IOP3, three models predict a shorted puff duration at the receptors (MG values are 0.4 for M10 and 0.8 for M3) while the rest of them predict a longer duration with an average value of 2.1 and a maximum value of 3.7 (M8). On average, the VG value is larger during IOP8 (it averages about 10) than during IOP3 (it averages about 3), in agreement with the large scatter shown. The highest VG value is obtained for M6 in IOP8 (at around 20) and the lowest for M1 and M9 (VG = 1.2) (Fig. 4), for which most of the points fall along the perfect agreement line.
3.2 Dispersion Coefficients
The purpose here is to evaluate how models capture the relationships between, (i) σt and peak time, and (ii) σx and downwind distance from the release point in IOP3 and IOP8. We apply a linear relationship to quantify the association between these variables. However, we need to keep in mind that due to the effect of buildings and street canyons on urban dispersion, these relationships may not actually be linear in an urban environment, as they are in open fields (e.g. Hanna and Franzese 2000). Many studies have been carried out to investigate the influence of buildings on the airflow and concentration fields (e.g. Zhang et al. 2015, Ricci et al. 2017). The wind field within the street canyons can look very different from the average wind field with along-street flow and large-scale turbulent eddies. In this sense, Flaherty et al. (2007) show how the presence of buildings channels the plume, shifts its transport direction, and makes it wider than a non-channelled plume.
By analyzing these relationships, and according to Zhou and Hanna (2007), we also investigate the model predictions about the initial size and spread of the puff. The intercept value of the linear relation between σt and peak time (at peak time = 0) represents the measure of the initial puff size (in seconds), while in the relationship between σx and downwind distance, the intercept value (at distance from the release = 0) represents the initial downwind plume spread (in metres).
The value of both intercept values relates to the influence of buildings around the source location. In this sense, the four puffs were released in the midst of tall buildings (on the east side of Broadway across from the Westin Hotel) during IOP8, while they were released in a park upwind of the area of tall buildings (near the Myriad Botanical Gardens) during IOP3 (see Fig. 1, and Clawson et al. 2005). Figures 5 and 6 show the graphical relationship between variables, and Table 3 summarizes the values obtained for the elements of each linear relation (slope, y-intercept and R2 values). The observed values have been generated using the complete set of samplers (Fig. 1), while for each model, we have considered the number of samplers where each model made predictions above 400 pptv (N value in Table 2).
3.2.1 Variation of the Standard Deviation of the Concentration Time Series with Peak Times
The observed relationship between these two variables is different in each intensive operating period (Fig. 5). From observations, while σt values seem to increase with peak times during IOP3 (daytime—positive linear correlation with R2 = 0.43), σt values are more spread out and seem to decrease drastically as peak time increases in IOP8 (overnight—negative linear correlation with R2 = 0.18). Some of the models (Table 3) also catch these differences between intensive operating periods. In IOP3, the models present a positive linear correlation between these two variables and four of them (models M6, M9, M5, M10) improve the coefficient of determination between the observed values. In the case of IOP8, there are four models (M6, M8, M3, M10) following the negative linear correlation obtained from observations, and the R2 values range from 0.05 (M8) to 0.59 (M10).
The observed and predicted intercept values (Table 3) reflect the impact of the release site characteristics on the initial puff size. In all of the models, the linear relationship presents a larger intercept value in IOP8 than in IOP3, in line with the different characteristics of the release sites. In IOP3, six out of eight models have a larger intercept value than with the observations (5.08 s), with the maximum value reached by M8 (about 160 s). It should be pointed out that two models (M4 and M9) present a negative intercept value, i.e., initial puff size. A possible cause of this result could be in the simulation of the puff hold-up in the wakes of large buildings upwind of the sampler locations, which influence the effective intercept term (Zhou and Hanna 2007). In IOP8, only one model (M3 with − 2.70 s) presents a negative intercept value while the rest of the models give an average initial puff size of about 113 s, with a maximum value of 231 s (model M10) and a minimum one of 48 s (model M9), while the observations yield 78.3 s.
3.2.2 Variation of the Along-Wind Dispersion Coefficient with Downwind Distance
The set of observed σX values present rather small differences with distance in both intensive operating periods (Fig. 6). There is a positive and low-slope linear relation with increasing downwind distance from the release point in both (0.23 in IOP3 and 0.09 in IOP8), with R2 values of 0.42 during IOP3 (daytime) and 0.04 during IOP8 (overnight). Differences between models and between intensive operating periods (day–night) results are pointed out. In IOP3, most of the points from models are close to the observed values with the exception of M8, which clearly provides bigger σX values than those found from observations at the same distances. In the case of IOP8, there is a large amount of scatter around observations. In general, the variance between these two parameters is captured and better explained by most of the models in each intensive operating period, with the exception of models M4, M1, M8 and M3 in IOP3 and of model M8 in IOP8 (Table 3). These differences between models can be partly justified by the relationship between duration time and σx (Sect. 2.3) and so, the large scatter obtained in the simulation of the time duration in each IOP.
The intercept term of this linear relation represents the initial downwind plume spread (in metres). The intercept value calculated from observations is 1.4 m in IOP3 and 50 m in IOP8. It is necessary to point out that the derived initial σx obtained for IOP3 is similar to the initial puff size (1 m) in the JU2003 experiment. In contrast, for IOP8, the intercept value (51.1 m) is in the line with the one obtained in Zhou and Hanna (2007) of about 40 m and therefore, much larger than the physical puff size of the JU2003 experiment. Most of the models present a non-zero and positive intercept value, which suggest the simulation of the “hold-up” effect caused by the retention and subsequent release of airborne material by the buildings (Doran et al. 2007). Five out of eight models present larger intercept values in IOP3, in a range from 30 (M5) to 309 m (M8), and 6 out of 8 in IOP8, with values from 55 m (M2) to 342 m (M10). There are models predicting negative intercept values in each intensive operating period, M6 and M9 in IOP3 and M4 in IOP8. This negative value indicates the simulation of more upwind dispersion of the puff in the early phase of the dispersion.
4 Influence of Atmospheric Stability
As in Hernández-Ceballos et al. (2019), the statistical measures presented in the previous sections show variability among different models in the simulation of the puff dispersion. As expected in complex built environments and in agreement with COST ES1006 (2015), the performance of models is influenced significantly by the location of sources (e.g. open space such in IOP3, and inside a complex building structure in IOP8) and receptor points.
The impact of using fixed or time-varying inflow conditions on the performance of models was addressed in Hernández-Ceballos et al. (2019). Another key factor contributing to differences between models is if and how they treat the effect of atmospheric stability on puff dispersion. Many studies have reported the significant effect of atmospheric stability on pollutant dispersion in the urban environment (e.g. Kumar et al. 2006; Yassin 2013). In urban areas, during the day, surfaces are more reflective and become hotter and thus, producing more convective eddies. As a result, urban areas are rarely as stable, and hence, the performance of models could change in case stable or unstable atmospheric stratification is considered in their computations. Significant day–night differences in puff dispersion and concentration variability have also been reported (e.g. Finn et al. 2010; Franzese and Huq 2011). Marked differences of about a factor of three or four between concentrations data during day and night releases have been observed, as well as, night-time plumes are more likely to have reduced concentration fluctuation intensities relative to daytime plumes. In contrast, Hanna et al. (2007) concludes that the effects of atmospheric stability are minimal in the downtown area.
Table 4 shows whether models simulating IOP3 and IOP8 assumed day–night stability differences or neutral atmospheric conditions. Whilst there are four models (M9, M3, M5, M10) assuming different stability between day and night intensive operating periods, there were five models (M1, M2, M4, M8, M6) in which neutral atmospheric conditions without any thermal effect were established for simulating both IOPs. We need to point out that M2 and M1 simulated only one intensive operating period respectively (see Sect. 2.1).
Looking at the results shown in Table 3, the model simulations using day–night stability differences are acceptable (> 400 pptv) for 84% and 82% of the total simulated samplers in IOP3 and IOP8 respectively, while the percentage is lower for those using neutral stability (67% and 66% of the simulated samplers in IOP3 and IOP8). In addition, considering the percentage of false negative samplers predicted by each group of models, those applying day–night stability differences present a lower percentage than those using neutral stability in each intensive operating period. It is for 3% and 8% of the total simulated samplers in IOP3, and for 21% and 25% in IOP8 respectively.
Considering the performance measures of MG and VG obtained simulating the maximum concentrations (Sect. 3.1), differences are also observed between both groups of models. In IOP3 (daytime) and applying neutral stability conditions, MG values average about 0.7, which suggests a mean underprediction bias of about a factor of 2, and it has range from 0.30 to 1.87. In contrast, the average of MG values is 1.35, which suggests mean overprediction bias of about a factor of 2, and the range is 0.32–2.25 considering day–night stability differences. The range of VG values is higher for neutral, between 5.0 and 97.2, than for day–night stability conditions, between 3.4 and 39.2. In IOP8 (night-time), MG values average about 0.9 for neutral and 1.2 for day–night stability differences, while the average of VG values decreases about three orders of magnitude using day–night atmospheric conditions. These results suggest that there is a change between underestimation and overestimation by using neutral conditions or day–night stability differences, and that the largest modelled bias in the simulation of maximum concentrations tend to appear simulating the puff dispersion using neutral atmospheric conditions.
Taking as reference the coefficient of determination calculated between σt and peak time, and σx and downwind distance from the release point in IOP3 and IOP8, we have also found that models using day–night stability differences improve the percentage of explained variance. For σt vs peak time, the mean R2 is 0.30 for neutral and 0.56 for day–night differences in IOP3, while it is 0.16 and 0.29 respectively in IOP8. In the case of σx versus downwind distance, models using day–night stability differences improve largely the mean R2 value in IOP3, from 0.24 to 0.61, while IOP8 is the only case in which the neutral models present a mean R2 (0.42) higher than those applying day–night differences (0.24). The latter obtain the highest R2 value in each intensive operating period, with the exception of IOP8 and of σx versus downwind distance. These results, hence, suggest that those models applying day–night stability differences tend to yield a better fit than neutral ones.
It is often assumed when simulating transport and dispersion in the urban environment that stability conditions are neutral. Lundquist and Chan (2007) indicated that for long-duration releases under moderate wind conditions and within a built-up area the assumption of neutral stability is accepted. The results shown in this analysis looks contradictory with this suggestion, and point out the need to consider even slight unstable conditions in the simulation of daytime and night-time releases. To achieve this, there is a need to have sufficient meteorological input variables and data to address atmospheric stability to model urban dispersion.
5 Conclusions
Under the UDINEE project, nine ADMs of different levels of complexity were evaluated and compared with tracer measurements from the subset of instantaneous puff releases performed during the Oklahoma City Joint Urban 2003 field experiment. This study has investigated the model capability in simulating the characteristics (concentrations and timing) of the fast-response time series, as well as how models simulate the initial dispersion phase of the puff dispersion. To this purpose, we have compared observed and modelled SF6 concentrations, with time resolution of 0.5 s and concentrations above 400 pptv, corresponding to four puff releases each in IOP3 (daytime) and IOP8 (night-time).
Overall, the point-by-point quantitative comparison of the simulated and observed parameters has shown that models better capture the arrival and peak times. There are specific samplers in which puff parameters were poorly simulated, showing how the characteristics of the sampler location inside the urban canopy can affect the agreement between observations and predictions. Within this mean behaviour, it should be pointed out that there were noticeable differences between models, both in simulating the parameters and between day and night predictions. These differences are also observed in the results obtained for the dispersion coefficients. It is important to emphasize that the evaluation results here are based on two out of 10 intensive operating periods of the JU2003 experiment.
UDINEE has highlighted differences in ADMs and in the parametrization schemes, in simulating the propagation of the plume from an instantaneous source of release in an urban environment. Our analysis demonstrates that knowledge of concentration variability is potentially very significant for urban emergency-response planning. In this sense, and in the present framework, the impact of atmospheric stability on the performance of models has also been investigated. An improvement in the performance of models (e.g. increase the percentage of acceptable samplers, a decrease in the percentage of false negative samplers, an improvement in the simulation of maximum concentrations, and in the relationships between dispersion coefficients with time and distance) has been observed by using day–night stability differences. This result indicates the need to have sufficient meteorological input variables and data to quantify atmospheric stability in simulating urban dispersion.
It appears that there is still need for more work to further improve the present modelling tools, and the UDINEE project has been proven to be a good platform to foster collaborations among modelling groups. The large amount of data produced under the UDINEE project and already stored in the ENSEMBLE system should support detailed studies of urban dispersion models. By building on the current experience and promoting community work, it is expected that additional analysis can be efficiently conducted to improve the currently available modelling systems. This dispersion dataset is a valuable asset, not only for developing advanced tools for emergency-response situations in the event of a toxic release, but also for refining air-quality models. More work is needed to investigate the sensitivity of the model results to different modelling options, different urban geometries and different meteorological conditions.
References
Allwine KJ, Flaherty J (2006) Joint Urban 2003: study overview and instrument locations. Pacific Northwest National Lab., Richland, WA. PNNL-15967
Andersson KG, Mikkelsen T, Astrup P, Thykier-Nielsen S, Jacobsen LH, Hoe SC, Nielsen SP (2009) Requirements for estimation of doses from contaminants dispersed by a ‘dirty bomb’ explosion in an urban area. J Environ Radioact 100:1005–1011
Anfossi D, Tinarelli G, Trini Castelli S, Nibart M, Olry C, Commanay J (2010) A new Lagrangian particle model for the simulation of dense gas dispersion. Atmos Environ 44:753–762
Baklanov A, Grimmond S, Mahura A, Athanassiadou M (2009) Meteorological and air quality models for urban areas. Springer, Berlin, Heidelberg, p 183. https://doi.org/10.1007/978-3-642-00298-4
Bartzis JG (1991) ANDREA-HF: a three dimensional finite volume code for vapour cloud dispersion in complex terrain. CEC JRC Ispra Report EUR 13580 EN, Ispra: EC Joint Research Centre
Benamrane Y, Boustras G (2015) Atmospheric dispersion and impact modeling systems: how are they perceived as support tools for nuclear crises management? Saf Sci 71:48–55
Benamrane Y, Wybo J-L, Armand P (2013) Chernobyl and Fukushima nuclear accidents: what has changed in the use of atmospheric dispersion modeling? J Environ Radioact 126:239–252
Benbouta N (2007) Canadian urban flow and dispersion model (CUDM): developing Canadian capabilities for CBRN hazard dispersion in urban areas. CMOE Dorval TR 2007-001 technical report. Environment Canada
Bianconi R, Galmarini S, Bellasio R (2004) Web-based system for decision support in case of emergency: ensemble modelling of long-range atmospheric dispersion of radionuclides. Environ Model Softw 19:401–411
Blocken B (2015) Computational fluid dynamics for urban physics: importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build Environ 91:219–245
Bradley MM (2007) NARAC: an emergency response resource for predicting the atmospheric dispersion and assessing the consequences of airborne radionuclides. J Environ Radioact 96:116–121
Britter RE, Hanna SR (2003) Flow and dispersion in urban areas. Annu Rev Fluid Mech 35:1–496
Brown MJ (2004) Urban dispersion-challenges or fast response modelling. In: Fifth conference on urban environment, Vancouver, BC, Canada. Amerian Meteorological Society, J5, p 1
Burian S, Han W, Brown M (2003) Morphological analyses using 3D building databases: Oklahoma City, Oklahoma. Technical Report LA-UR-05-1821, LANL, Los Alamos, NM, USA
Čarný P, Lipták Ľ, Smejkalová E, Krpelanová M (2015) Protective measures based on the state of reactor and source term predicted (ESTE tool). International Experts’ Meeting on Assessment and Prgonosis in Response to a Nuclear or Radiological Emegency. Vienna, 20–24 April 2015 (Org: IAEA)
Chang J, Hanna SR (2004) Air quality model performance evaluation. Meteorol Atmos Phys 87:167–196
Clawson KL, Carter RG, Lacroix DJ, Biltoft CJ, Hukari NF, Johnson RC, Rich JD, Beard SA, Strong T (2005) Joint Urban 2003 (JU2003) SF6 atmospheric tracer field tests, NOAA tech memo OAR ARL-254. Air Resources Lab., Silver Spring, MD, 162 pp
COST ES1006 (2015) Best practice guidelines, COST action ES1006 “Evaluation, improvement and guidance for the use of local-scale emergency prediction and response tools for airborne hazards in build environments”. ISBN: 987-3-9817334-0-2, © COST Office, 2015, April 2015
Defense Threat Reduction Agency (2008) HPAC version 5.0 SP1 (DVD containing model and accompanying data files), DTRA, 8725 John J. Kingman Road, MSC 6201, Ft. Belvoir, VA 22060-6201
Di Lemma FG, Colle JY, Ernstberger M, Rasmussen G, Thiele H, Konings RJM (2014) RADES an experimental set-up for the characterization of aerosol release from nuclear and radioactive materials. J Aerosol Sci 70:36–49
Doran JC, Allwine KJ, Flaherty JE, Clawson KL, Carter RG (2007) Characteristics of puff dispersion in an urban environment. Atmos Environ 41:3440–3452
Dugway Proving Ground (2005) Data archive for JU2003. https://ju2003-dpg.dpg.army.mil
Finn D, Clawson KL, Carter RG, Rich JD, Biltoft C, Leach M (2010) Analysis of urban atmosphere plume concentration fluctuations. Boundary-Layer Meteorol 136:431–456
Flaherty JE, Lamb B, Allwine KJ, Allwine E (2007) Vertical tracer concentration profiles measured during the Joint Urban 2003 dispersion study. J Appl Meteorol Clim 46:2019–2037
Franzese P, Huq P (2011) Urban Dispersion modelling and experiments in the daytime and nighttime atmosphere. Boundary-Layer Meteorol 139:395–409
Galmarini S, Bianconi R, Klug W, Mikkelsen T, Addis R, Andronopoulos S, Astrup P, Baklanov A, Bartniki J, Bartzis JC, Bellasio R (2004) Ensemble dispersion forecasting—part I: concept, approach and indicators. Atmos Environ 38:4607–4617
Galmarini S, Bianconi R, Appel W, Solazzo E, Mosca S, Grossi P, Moran M, Schere K, Rao ST (2012) ENSEMBLE and AMET: two systems and approaches to a harmonized, simplified and efficient facility for air quality models development and evaluation. Atmos Environ 53:51–59
Hall D, Spanton A, Griffiths I, Hargrave M, Walker S (2003) The urban dispersion model (UDM): version 2.2 technical documentation, release 1.1. Tech. Rep. DSTL/TR04774, Defence Science and Technology Laboratory, Porton Down, United Kingdom, 106 pp
Hanna S, Chang J (2012) Acceptance criteria for urban dispersion model evaluation. Meteorol Atmos Phys 116:133–146
Hanna SR, Franzese P (2000) Along wind Dispersion—a simple similarity formula compared with observations at 11 field sites and in one wind tunnel. J Appl Meteorol 39:1700–1714
Hanna S, White J, Zhou Y (2007) Observed winds, turbulence, and dispersion in built-up downtown areas of Oklahoma City and Manhattan. Boundary-Layer Meteorol 125:441–468
Hendricks EA, Diehl SR, Burrows DA, Keith R (2007) Evaluation of a fast-running urban dispersion modeling system using Joint Urban 2003. J Appl Meteorol Climatol 46:2165–2179
Hernández-Ceballos MA, Hanna S, Bianconi R, Bellasio R, Mazzola T, Chang J, Andronopoulos S, Armand P, Benbouta N, Čarný P, Ek N, Fojcíková E, Fry R, Huggett L, Kopka P, Korycki M, Lipták L, Millington S, Miner S, Oldrini O, Potempski S, Tinarelli G, Trini Castelli S, Venetsanos A, Galmarini S (2019) UDINEE: evaluation of multiple models with data from the JU2003 puff releases in Oklahoma City. Part I: comparison of observed and predicted concentrations. Boundary-Layer Meteorol. https://doi.org/10.1007/s10546-019-00433-8
Hertwig D (2007) Dispersion in an urban environment with a focus on puff releases. Studienarbeit, Universitat, Fachbereich Meteorologie, Hamburg
Hogue R, Benbouta N, Mailhot J, Belair S, Lemonsu A, Yee E, Lien FS, Wilson JD (2009) The development of a prototype of Canadian urban flow and dispersion modeling system. In: AMS 89 annual conference. Joint session 19 urban transoprt and dispersion modeling. January 2009. (Phoenix, AZ)
Hosker RP Jr (1984) Flow and diffusion near obstacles. Atmospheric science and power production, DOE/TIC-27601. In: Randerson D (ed) Ch. 7. U.S. Dept. of Energy, Wash, pp 241–326
Jones AR, Thomson DJ, Hort M, Devenish B (2007) The U.K. Met Office’s next-generation atmospheric dispersion model, NAME III. In: Borrego C, Norman AL (eds) Air pollution modeling and its application XVII (proceedings of the 27th NATO/CCMS international technical meeting on air pollution modelling and its application). Springer, pp 580–589
Jonsson L, Plamboeck AH, Johansson E, Waldenvik M (2013) Various consequences regarding hypothetical dispersion of airborne radioactivity in a city center. J Environ Radioact 116:99–113
Kumar A, Dixit S, Varadarajan C, Vijayan A, Masuraha A (2006) Evaluation of the AERMOD dispersion model as a function of atmospheric stability for an urban area. Air Pollut 25:141–151
Lateb M, Meroney RN, Yataghene M, Fellouah H, Saleh F, Boufadel MC (2016) On the use of numerical modelling for near-field pollutant dispersion in urban environments. Environ Pollut 208:271–283
Lundquist JK, Chan ST (2007) Consequences of urban stability conditions for computational fluid dynamics simulations of urban dispersion. J Appl Meteorol Climatol 46:1080–1097
Martin D, Petersson KF, Shallcross DE (2011) The use of cyclic perfluoroalkanes and SF6 in atmospheric dispersion experiments. Q J R Meteorol Soc 137:2047–2063
Oldrini O, Armand P, Duchenne C, Olry C, Moussafir J, Tinarelli G (2017) Description and preliminary validation of the PMSS fast response parallel atmospheric flow and dispersion solver in complex built-up areas. Environ Fluid Mech 17:997–1014
Pardyjak E, Brown M (2001) Evaluation of a fast response urban wind model—comparison to single building wind-tunnel data. In: International symposium on environmental hydraulics, Tempe, AZ, LA-UR-01-4028, 6 pp
Pardyjak E, Brown M (2002) Fast response modeling of a two building urban street canyon. In: 4th AMS symposium on urban environment, Norfolk, VA, LA-UR-02-1217
Rao KS (2005) Uncertainty analysis in atmospheric dispersion modeling. Pure Appl Geophys 162:1893–1917
Ribeiro I, Valente J, Amorim JH, Miranda AI, Lopes M, Borrego C, Monteiro A (2014) Air quality modelling and its applications. In: Cao G, Orrú R (eds) Current environmental issues and challenges. Springer, Dordrecht
Ricci A, Kalkman I, Blocken B, Burlando M, Freda A, Repetto MP (2017) Local-scale forcing effects on wind flows in an urban environment: impact of geometrical simplifications. J Wind Eng Ind Aerodyn 170:238–255
Schatzmann M, Leitl B (2002) Validation and application of obstacle resolving urban dispersion models. Atmos Environ 36:4811–4821
Schatzmann M, Olesen H, Franke J (2010) COST 732 model evaluation case studies: approach and results. COST Office, Brussels. ISBN 3-00-018312-4
Sharon A, Halevy I, Sattinger D, Yaar I (2012) Cloud rise model for radiological dispersal devices events. Atmos Environ 54:603–610
Steyn DG, Galmarini S (2008) Evaluating the predictive and explanatory value of atmospheric numerical models: between relativism and objectivism. Open Atmos Sci J 2:38–45
Sykes RI, Parker S, Henn D, Chowdhury B (2016) SCIPUFF version 3.0 technical documentation. Sage Management, 15 Roszel Road, Suite 102, Princeton, NJ 08540, 403 pp
Tinarelli G, Mortarini L, Trini Castelli S, Carlino G, Moussafir J, Olry C, Armand P, Anfossi D (2012) Review and validation of microspray, a Lagrangian particle model of turbulent dispersion, in Lagrangian modeling of the atmosphere in geophysical monograph series 200, 2012. American Geophysical Union, pp 311–327
Venetsanos AG, Papanikolaou E, Bartzis JG (2010) The ADREA-HF CFD code for consequence assessment of hydrogen applications. Int J Hydrog Energy 35:3908–3918
Wingstedt EMM, Osnes AN, Åkervik E, Eriksson D, Pettersson Reif BA (2017) Large-eddy simulation of dense gas dispersion over a simplified urban area. Atmos Environ 152:605–616
Yassin MF (2013) A wind tunnel study on the effect of thermal stability on flow and dispersion of rooftop stack emissions in the near wake of a building. Atmos Environ 65:89–100
Zhang H, Wang Y, Li S, Tang H, Liu X, Wang Y (2015) Study on the influence of the street side buildings on the pollutant dispersion in the street canyon. Procedia Eng 121:37–44
Zhou Y, Hanna SR (2007) Along-wind dispersion of puffs released in a built-up urban area. Boundary-Layer Meteorol 125:469–486
Acknowledgements
We gratefully acknowledge the European Commission Directorate General for Migration and Home Affairs (DG HOME) for their support to the Urban Dispersion International Evaluation Exercise (UDINEE) activity. Authors want to acknowledge the contribution of various groups to UDINEE. The following agencies have prepared the data sets used in this study: U.S Army Dugway Proving Group as manager of the JU2003 database (Dugway Proving Ground 2005); data from tracer monitoring stations were provided by the National Oceanic and Atmospheric Administration (NOAA) Air Resources Laboratory Field Research Division; data from meteorological monitoring stations were provided by Dugway Proving Ground.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hernández-Ceballos, M.A., Hanna, S., Bianconi, R. et al. UDINEE: Evaluation of Multiple Models with Data from the JU2003 Puff Releases in Oklahoma City. Part II: Simulation of Puff Parameters. Boundary-Layer Meteorol 171, 351–376 (2019). https://doi.org/10.1007/s10546-019-00434-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-019-00434-7