Abstract
In a complex environment such as an urban area, accurate prediction of the atmospheric dispersion of airborne harmful materials such as radioactive substances is necessary for establishing response actions and assessing risk or damage. Given the variety of urban atmospheric dispersion models available, evaluation and inter-comparison exercises are vital for assessing quantitatively and qualitatively their capabilities and differences. To that end, the European Commission/Directorate General Joint Research Centre with support from the European Commission/Directorate General-Migration and Home Affairs, and with the contribution of the U.S. Defense Threat Reduction Agency, launched the Urban Dispersion INternational Evaluation Exercise (UDINEE) project. Within UDINEE, nine atmospheric dispersion models are evaluated and intercompared. Sulphur hexafluoride concentrations from puffs released near the ground during the Joint Urban 2003 (JU2003) field experiment are used in UDINEE to evaluate atmospheric dispersion models. The JU2003 experiment is chosen because UDINEE aims at the better understanding of modelling capabilities for radiological dispersal devices in urban areas, and the neutrally-buoyant puff releases performed in the JU2003 experiment are the closest scenario to this purpose. The present study evaluates the capability of models at simulating the presence and concentration levels of the tracer at sampling locations. The fraction of predicted concentrations and time-integrated concentrations within a factor-of-two of observations are less than 0.36 and 0.4 respectively. The analysis reveals an improvement in the performance of models by using time-varying inflow conditions. Since the simulation of the dispersion of puff release is particularly challenging, the results of UDINEE could constitute a benchmark for future model developments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The use of a radiological dispersal device (RDD), comprising a combination of conventional explosives and radioactive material, is considered a likely malevolent act at the disposal of terrorist groups (Medalia 2004, 2011). The potential use of radiological dispersal devices would probably not produce a large number of casualties, but could certainly produce panic and chaos in the population, including fear of the long-term contamination of facilities and places where people live and work (e.g. Rosoff and von Winterfeldt 2007; Kamboj et al. 2009).
The intended impacts are therefore maximized should the RDD explosion occur in an urban area. In such a complex environment, the intent of minimizing health, environmental, and economic impacts of an RDD event (e.g. Ansari 2010) implies the selection and implementation of effective countermeasures that would largely rely on adequate knowledge of the dispersion patterns and the potential levels of radioactive contamination (e.g. Shin and Kim 2009; Jonsson et al. 2013). This information can be estimated using atmospheric dispersion models (ADM) (e.g. Rentai 2011).
Urban features (e.g., sizes of buildings and overall morphology, distribution of streets, total dimension of urban area) affect low-level atmospheric flow and hence influence turbulence and the dispersion of airborne pollutants and their deposition (Baklanov et al. 2009). The simulation of airflow distribution constitutes a challenge whenever ADMs are used to better understand and/or predict the pollutant dispersion in an urban environment (e.g. Thiessen et al. 2009). A wide range of approaches developed to include urban characteristics and the subsequent simulation of airflow in and around the urban canopy has resulted in a wide range of ADMs and, consequently, variability in the model results (see e.g., Britter and Hanna 2003; Schatzmann and Leitl 2011; COST ES1006 2015a, b).
Because of the inherent uncertainty in ADM results, models are evaluated and, at a practical level, based on acceptance criteria i.e. performance thresholds are identified as “acceptable” and “unacceptable” for a specific application. Hanna and Chang (2012) suggest acceptance criteria for rural and urban applications. Basically, the better that models match the quantitative criteria for model acceptance, the more reliable are their results in support of emergency management and remediation actions. Thus, it is important to understand and to assess the qualitative and quantitative differences between model results. In this sense, a large modelling effort and related evaluation on puff releases has been performed in the framework of the COST Action ES1006 research activity, both for wind-tunnel experiments and real field emissions (Baumann-Stanzer et al. 2015; Efthimiou et al. 2017).
Meteorological and tracer observations from atmospheric tracer dispersion experiments that are representative of the physical processes that models simulate are necessary to evaluate the capabilities of ADMs (e.g. Britter et al. 2000; Cooke et al. 2000; Neophytou et al. 2011). However, such observations are very difficult to collect in the case of dispersion in urban areas. The URBAN 2000 experiment in Salt Lake City (Allwine et al. 2002), the Joint Urban 2003 (JU2003) experiment in Oklahoma City (Allwine and Flaherty 2006), the London Dispersion of Air Pollutants and their Penetration into the Local Environment (DAPPLE) experiment (Arnold et al. 2004), and the Madison Square Garden (MSG05) and the Midtown Manhattan (MID05) experiments in New York City (Allwine and Flaherty 2007) are urban-tracer dispersion experiments of significance to the further development and evaluation of urban dispersion models, since they fulfil the requirements indicated in Schatzmann and Leitl (2002).
The Urban Dispersion INternational Evaluation Exercise (UDINEE) project is one of the first evaluation exercises involving a considerable number of ADMs used for emergency preparedness and response in the case of a radiological release in an urban environment. The study was led by the European Commission Directorate General Joint Research Centre (EC/DG JRC) with the support of the United States Defence Threat Reduction Agency (U.S. DTRA). As part of this inter-agency collaboration, and to evaluate the model results, U.S. DTRA made available meteorological and tracer observations collected during the JU2003 field campaign. An overview of the JU2003 experiments is presented in Allwine and Flaherty (2006) and a comprehensive description and technical details are given in Clawson et al. (2005).
Ten intensive operating periods were organized during the JU2003 experiment, and in each intensive operating period, puff releases were made close to the ground. For each release, a known amount of the non-toxic and inert atmospheric tracer sulphur hexafluoride (SF6), a passive gas that can be detected at concentrations as low as 10 pptv (Clawson et al. 2005), was instantaneously injected into the atmosphere by exploding balloons filled with the gas. Tracer concentration data collected after each puff release are used to evaluate nine ADMs under the UDINEE project. These data can be seen as representative of the dispersion process following an RDD explosion. The observations and model results were uploaded and made available to all participants through the ENSEMBLE web-based platform (http://ensemble.jrc.ec.europa.eu/), hosted at the EC/DG JRC (Bianconi et al. 2004; Galmarini et al. 2004, 2012).
The goal of our study is to evaluate the capability of models to simulate puff passage and concentration levels of the tracer at sampling locations (while a companion study is devoted to the analysis of puff parameters used to characterize the puff passage at each sampler, see Hernández-Ceballos et al. 2019). The simulation of the time-integrated air concentrations for each puff and sampler is also evaluated. In the framework of our study, the effect of different boundary conditions, such as fixed or time-varying inflow conditions, on the dispersion and concentration field predicted by models is discussed.
2 Materials and Methods
2.1 List of Participants and Models
Table 1 summarizes the models and groups that participated in the UDINEE project; six modelling groups from Europe and two from North America have applied their modelling systems. The nine models participating in this exercise are documented in the scientific literature referenced in Table 1. Differences in the model results are due to the use of different meteorological inputs or physical parametrizations (e.g. Hanna et al. 2006; Neophytou et al. 2011). It is beyond our scope to identify the individual causes of the similarities or differences between observations and model results. For more information on the characteristics of each model, see other articles in this special issue.
Since the project aims at identifying the overall performance of the models analyzed and the state-of-the-art in urban dispersion modelling, each model is identified hereafter by an anonymous code (M1 – M10).
2.2 Observations
The JU2003 database fulfils the requirements for evaluating urban dispersion models, as described in the COST ES1006Action documents (COST ES1006 2015c). The database resolves the short-time-scale variability in meteorological variables and pollutant concentrations occurring in the urban canopy layer. In our study, and after review of all release trials and model predictions under UDINEE, we work with two subsets of tracer concentrations, namely intensive operating period 3 (IOP3) and 8 (IOP8). This selection is based on the availability of results from all models participating in UDINEE and on the abundance of collected tracer measurements in each intensive operating period (Clawson et al. 2005), thus guaranteeing the largest statistical sample.
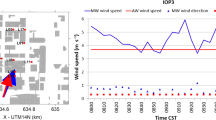
Figure 1 shows the location of the release points (red stars) and of the fast-response tracer gas analyzers (blue dots)—for IOP3 and IOP8 (Clawson et al. 2005). At alcan be seen, locations of the nine SF6 analyzers are different in the two intensive operating periods so that changes in the wind direction could be accommodated. The releases were performed near the Myriad Botanical Gardens in IOP3 (Fig. 1a), and near the Westin Hotel in IOP8 (Fig. 1b). The samplers were deployed downwind from the release points at distances that ranged from less than 200 m to as much as 1 km.
View of SF6 source (red star) and samplers (blue points) on the UDINEE modelling domain during a IOP3, and b IOP8. In brackets is indicated the number of puffs analyzed in each location in each intensive operating period. c Observed concentration time series from fast response sampler L17 during IOP3. Red dots on the x axis indicate the release time of each puff in IOP3
Meteorological synopses of both intensive operating periods can be consulted in Clawson et al. (2005). The weather in IOP3 was mostly cloudy during the morning puff releases and surface wind directions were southerly at 7–10 m s−1 for the entire intensive operating period. In contrast, the weather in IOP8 was characterized by clear skies and consistent wind directions from the south-east through south at 4–5 m s−1. The analysis carried out in Hanna et al. (2007), using analyses of stability parameters such as the Obukhov length, indicated that predominantly neutral conditions prevailed in the downtown area during both intensive operating periods.
The fast-response tracer gas analyzers measured atmospheric concentrations of SF6 with a response time of 0.5 s. The start of each sampling period (20 min) coincided with the release of each puff (red circles in Fig. 1c), where Fig. 1 shows an example of three SF6 concentration time series (in logarithmic scale) from sampler L17 during IOP3. The measurements for the three puffs differ significantly. This fact clearly illustrates the variability of individual puff concentration time traces measured at the same tracer gas analyzers following successive puffs under similar meteorological conditions (same intensive operating period). These three time series are, therefore, a good example of the high complexity of the dispersion processes in an urban environment. Figure 1a, 1b also shows the number of puffs analyzed in each measurement location for IOP3 and IOP8 (number between brackets). Table 2 indicates the set of fast-response tracer gas analyzer measurements analyzed for each intensive operating period and puff. In total, 24 (IOP3) and 26 (IOP8) SF6 concentration time series are used for model evaluation. Clawson et al. (2005) also explain that the samplers were occasionally saturated (i.e., concentrations exceeded the maximum concentration measurement capability), but we have retained these samplers because they include measurements that definitely exceed 10,000 or 23,000 pptv. We need to indicate that these high and uncertain values can affect the quantitative performance metrics (see Sect. 2.3) calculated to compare the performance of models.
2.3 Modelling Input Variables
UDINEE participants were provided with the meteorological and SF6 instantaneous release information mentioned below to perform the simulation of each puff dispersion. Eight out of these nine models simulated the dispersion of the four puffs released in IOP3 and IOP8, whilst models M2 and M1 did not simulate IOP3 and IOP8 respectively.
2.3.1 Source Location and Release Time
In the JU2003 field campaign, all puffs were released at 2 m above ground level (a.g.l.). Table 2 shows the release time, location and mass of each one in IOP3 and IOP8.The released quantity of SF6 was from 1.000 to 1.005 kg in IOP3 and from 0.305 to 0.5 kg in IOP8, with puffs released at intervals of 20 min in each intensive operating period. This time delay allowed the transport of SF6 out of the area and a return to background concentration level (about 5 ppt, see Martin et al. 2011; Hanna et al. 2011), thus avoiding the contamination of the sampling field by overlapping the puffs in time.
2.3.2 Domain and Grid Size
Figure 1 shows the urban domain defined for the simulations, the domain covering largely downtown Oklahoma City and 1.6 × 1.4 km2 in size. The horizontal grid size selected is 5 × 5 m2 and 57 vertical levels are defined (from zero to 402 m a.g.l. according to exponential grid spacing). As indicated in Table 1, most of the model simulations used this horizontal grid size. However, other modelling groups applied different grid spacing, and to facilitate the cross-comparison between models, model data were interpolated onto the common grid. Building heights and building coordinates of the Oklahoma City (Burian et al. 2003) centre were also provided to the UDINEE modelling community to perform the simulations.
2.3.3 Meteorology
All participating models were run using the meteorological time series from the Portable Weather Information Display System (PWIDS) sensor No. 15, which was located 10 m above the roof of the Post Office (40 m a.g.l.) and 1 km upwind of the central business district. The meteorological data comprised 10-s average time series of wind direction and speed, temperature and relative humidity.
2.4 Method of Evaluating of Model Predictions
This model evaluation exercise is based on the set of measured and simulated SF6 concentration time series (temporal resolution of 0.5 s) at the measurement locations indicated in Table 2. In this sense, we need to consider that models reproduce the ensemble-averaged flow and dispersion, but not a single realization of a puff dispersion in a turbulent flow. A single puff, as measured in the JU2003 experiment, is a single realization and there is always an unavoidable bias in any model due to the stochastic nature of the turbulent flow. A statistically stable ensemble should be obtained from a large number of puffs released under identical (or similar) conditions, which is impossible to achieve in the field (Chang and Hanna 2004).
We also note that the ADMs used under UDINEE provide ensemble-averaged concentrations in the samplers at the time resolution of the meteorological input variables. Thus, the ADM outputs are not representative of the intrinsic atmospheric variability at a frequency of 0.5 s from the single realization given by the measurement. While the Eulerian models provide instantaneous ensemble-averaged values at the time instances every 0.5 s, several of the Lagrangian models do not directly calculate time series with the temporal resolution of 0.5 s. To fulfil the UDINEE requirements, they produce averaged time series at the sampling sites with a lower temporal resolution (20 s or 1 min), and the corresponding 0.5-s time series are obtained by interpolation.
The comparison of the measured and modelled concentrations has to account for the existence of a threshold that defines, with a degree of confidence, the minimum measurable concentration value. In the JU2003 experiment, the tracer concentrations defined as “above the threshold” were based on the limit of quantitation (LOQ). This is the level at which the tracer concentration is determined with an accuracy of ± 30%, and it changes for each sampler and intensive operating period (Clawson et al. 2005). For example, LOQ values range from 34 pptv (L13) to 151 pptv (L8) in IOP3, and from 16 pptv (L16) to 96 pptv (L5) in IOP8. Applying these thresholds to model predictions, many simulated maximum concentrations are below 100 pptv, while the observed maxima generally are not less than 400 pptv. This contrast between observed and modelled maximum concentrations leads us to use a higher threshold to even up the comparison and to achieve reasonable conclusions the model evaluation exercise. The use of this threshold (400 pptv) removes the outlying concentration values before and after the puff passage at each measurement location (Fig. 1c), thus ensuring that the concentrations sampled correspond to a clear portion of the puff at each receptor.
The following quantitative performance metrics have been used for evaluating the performance of models (e.g. Hanna and Chang 2012): the “threshold-based” normalized absolute difference (NAD), the geometric mean (MG), the geometric variance (VG) and the fraction of predictions within a factor-of-two (FAC2) and factor-of-five (FAC5) of observations. We need to emphasize that the Hanna and Chang (2012) urban model acceptance criteria were determined for continuous releases, so the present results should not be compared with them. In the following definitions, it is assumed that P and O denote model predictions and observations respectively, and an overbar is the arithmetic mean:
where AF is the average number of false negative and false positive pairs, and AOV is the number of valid pairs (we refer to Sect. 3.2 for details).
Threshold-based NAD values give information on the capability of the models to reproduce the observations independently from the level of the concentrations, while the other metrics focus on the reproducibility of the observed values. A perfect model has a threshold-based NAD = 0 and MG, VG, FAC2 and FAC5 = 1.
In addition, Pearson’s correlation coefficient (PCC) was used to score the individual performance of models in simulating the associativity between two variables, where PCC between two vectors is (e.g. Mu et al. 2018),
where cov (αiαj) is the covariance, var (αi) is the variance of αi and var (αj) is the variance of αj. The PCC results range from − 1 (perfect negative relationship) and + 1 (perfect positive relationship); PCC = 0 implies no relationship between the variables.
Quantile–quantile plots have also been used to determine whether a model can generate a concentration distribution similar to that observed in each intensive operating period. Scatter plots providing visual information of the relationship between simulations and observations have helped to better understand the quantitative differences between models (e.g. Chang and Hanna 2004).
3 Results
3.1 Observed Versus Modelled Concentration Values
The predicted concentrations are assessed against the observed concentrations in box-and-whisker plots in Fig. 2, where the plots are based on the set of non-zero pairs (observations and predictions above zero pptv) obtained for each model. Pairs in which either observation or prediction is zero are not included in order to calculate the MG and VG values, since logarithms are taken. For each model and intensive operating period, the figure illustrates the distribution of observed (in blue) and simulated (in grey) SF6 concentrations normalized to the release mass (Q) of each puff. The Q values for each puff are given in Table 2.
Observed (blue) and modelled (grey) box plots for SF6 concentrations pairing in space and time in IOP3 and IOP8 under the condition that observed and predicted concentrations must both be above zero pptv. Predicted (Pi) and observed (Oi) concentrations are normalized to the release mass (Q) in each puff (C/Q). The centre of each box denotes the 50% (P50), and the bottom and top of the box correspond to the 25% (P25) and 75% (P75) values, respectively. The squares indicate the P90 and the circles the P10 values, while the extremes of the box represent the P95 and P5 values
In general, the distributions of simulated SF6 concentrations are larger than those obtained for observed values (e.g. models M3, M6 and M10 in IOP3, and models M6 and M10 in IOP8). The comparison also shows how the 50th percentile (P50) values from simulated SF6 concentrations are higher than those from observations in M5 and in both intensive operating periods. The opposite behaviour is found in M4, M9 and M10 for both periods. In contrast, M3 and M6 overpredict the observed P50 in IOP3 and underpredict in IOP8. Most of the models show a good representation of the smallest and highest SF6 concentrations, slightly overestimating or underestimating the 5th percentile (P5) and the 90th and 95th percentile (P90 and P95) values from observations. The largest differences are found for the smallest concentrations, in which P5 is largely underestimated (e.g. models M3, M6 and M10 in IOP3, and models M6 and M10 in IOP8 are more than two orders of magnitude lower than those observed). In contrast, observed and modelled P90 and P95 values usually remain in the same order of magnitude, with M1 and M8 having the largest overestimation in IOP3, and M6 and M2 in IOP8. Considering these results, there is a trend to overestimate the measurements, but the concentration bias varies significantly from model to model, being necessary to highlight the largest concentration bias observed in M10 and in both intensive operating periods.
Table 3 presents the quantitative performance metric results (FAC2, MG and VG) for each model. The FAC2 performance measures are low and slightly improved during night-time (ranging from 0.09 (M2) to 0.36 (M8), with an average of 0.20) than during daytime (ranging from 0.06 (M10) to 0.34 (M9), with an average of 0.18). These results, together with the high VG value obtained in most of the models, confirm the large spread of the simulated concentrations. Three models present higher VG values during daytime (models M3, M8 and M10) and three during night-time (models M5, M6 and M9). The models overestimate, on average, the observed concentrations, with MG values of 1.59 during daytime and 2.37 during night-time. However, and in agreement with Fig. 2, there are models with a MG value close to zero, such as M3 (MG = 0.08) in IOP3 and M6 (MG = 0.17) in IOP8. M10 has the lowest MG value in both intensive operating periods (zero in IOP3 and 0.09 in IOP8).
3.2 Spatial Overlapping Between Observations and Simulations
The histograms in Fig. 3 show the percentages of valid, false positive, false negative and zero-zero pairs for each model in each intensive operating period. The threshold-based NAD values for each model in each intensive operating period is listed under the histograms. This analysis uses the complete set of observed and simulated tracer concentrations paired in space and time for each model regardless of the fact that they belong to different puff releases. By considering the 400 pptv threshold (Sect. 2.3), we identify as “acceptable” values the observed and modelled concentrations above 400 pptv and those below this value are treated as zero. Pairing the observed and modelled concentrations in space and time, if the observed concentration (Oi) is equal to zero and the predicted concentration (Pi) > 400 pptv, this is a false negative. If Oi> 400 pptv and Pi = 0, this is a false positive. If both Pi and Oi = 0, this is a zero–zero, while if both > 400 pptv, this is a valid pair.
We would like to point out the minimal percentage of time (1% in IOP3 and zero in IOP8) in which the observed concentrations and all eight model-simulated SF6 concentrations at the sampling locations are above the concentration threshold of 400 pptv. This minimal overlapping between observations and all eight model predictions is a proof of the time and space variations in the predictions provided by the dispersion models available. This variability is associated with boundary conditions, formulations and/or approaches used to model dispersion in an urban environment (e.g. the flow dynamics over and within urban topography and the building configurations).
Figure 3 displays the significant percentage of zero-zero pairs obtained in most of the models. The percentage of zero-zero pairs ranges from 47% (M5) to 70% (M4), with an average of 59% during daytime (IOP3), and from 9% (M5) to 68% (M4), with an average of 49% during night-time (IOP8). One reason for the large percentage of zero-zero pairs is the difference between the duration of each sampling period (20 min) and the puff passage at each measurement location (see Fig. 1c as an example of this difference). Another explanation relates to the design of the sampling networks in field experiments, which are always planned to be broad to be sure to capture the puff dispersion, but in contrast, they can contribute to large numbers of samplers with observed and predicted zero concentrations. In addition, changes between day–night percentages can also be due to differences in the duration of puff passages during daytime (it averages at about 203 s) and night-time (it averages at about 237 s).
On average, the percentage of valid pairs is similar during daytime (about 12%) and night-time (about 11%). However, there are large differences within each intensive operating period regarding the model percentages. In IOP3, the percentage of valid pairs ranges from 1% (M10) to 25% (M5), with six models presenting a percentage of valid pairs above 10%. In contrast, in IOP8, five out of eight models have percentages of valid pairs below 7%, and there are three models (M2, M3 and M5) with percentages in a range from 22 to 27%. There are four models (M4, M6, M8 and M9) with higher percentages of valid pairs during daytime and three (M3, M5, M10) during night-time. Model M3, with 20% (IOP8 > IOP3), is the model with the highest difference in percentage of valid pairs between daytime and night-time puff releases.
Figure 3 shows a large variation in the percentage of false negatives and positives between models in the same and between day–night intensive operating periods. On average, the percentages of false negatives and positives are higher during night-time. During daytime, false negatives and positives average at about 14% and 10% respectively, while the percentages of false negatives and positives are about 19% and 20% at night. Atmospheric dispersion models with high percentages of false negatives have a more detrimental effect for establishing response actions and assessment of risk, because they would predict little or no risk while receptors are measuring high concentrations (e.g. Dennis et al. 2010). Models M3 and M8 are those with the highest percentages of false negatives in IOP3 and IOP8 respectively, while models M4, M9 and M10 are those with higher percentages of false negatives than false positives in both intensive operating periods.
The accuracy of the predicted spatial position of the puff for each model has been addressed using the threshold-based NAD performance metric. The lower the threshold-based NAD value, the better the model is from an emergency-response perspective (Warner et al. 2004). The NAD values vary widely from model to model in the same and between intensive operating periods. NAD ranges from 0.23 (M1) to 0.96 (M10), with an average of 0.52 during daytime, while it ranges from 0.38 (M3) to 0.95 (M4), with an average of 0.73 during night-time. These results indicate large modelling differences in the simulation of the puff dispersion in the same intensive operating period and under day–night meteorological conditions. Based on the comparison of threshold-based NAD values between intensive operating periods, five models (M4, M6, M8, M9, M5) are more effective in simulating the puff dispersion during daytime, and less during night-time.
To finalize this analysis, Table 4 shows the Pearson correlation coefficient (PCC) between the percentage of pairs of each model for each puff and sampler and the downwind distance of each sampler to the source in IOP3 and IOP8. Our purpose is to analyze whether the distance from the source influences the simulation of the puff passage at the measurement locations.
The results show two clear types of behaviour. The models present a positive correlation of the distance and the percentage of false negative and zero–zero pairs, and a negative correlation with the false positive and valid pairs. In the light of these results, it is possible to indicate which models better catch the presence of the puff in samplers located near to release points, and those that have more difficulties with increasing distance from the source. In terms of emergency response, these results imply consideration of a conservative approach to reporting the model results with increasing distance from the release point following a RDD explosion in this kind of complex environment.
Positive PCC values of the FN percentage with downwind distance implies that models tend to increasingly underestimate concentrations as the distance from the source increases. Therefore, the models predict a faster dilution of the puff than that actually observed. These results are attributable to the fact that, in an urban scenario, the more distance from the source, the more buildings affect the complex nature of urban flows and turbulence patterns, and hence, the more difficult it is to capture the observed propagation of the puff. In addition, differences in the PCC values between models represent the use of different approaches to simulate the impact of urban features on the puff dispersion (e.g. Hanna et al. 2011).
3.3 Time-Integrated Concentration (Dosage)
For radiological pollutants, the dosage (the time-integrated concentration) is the determining factor for health effects. Underestimating the dosage can be misleading in decision-making for countermeasures, and in contrast, its overestimation in areas where significant dosages are not reached would lead to countermeasures in oversized areas in the case of RDD events. Due to its importance, it is one of the key parameters taken as a reference to evaluate the reliability of ADMs used for emergency preparedness and response in case of a radiological release in an urban environment (e.g. Efthimiou et al. 2011, 2017).
The observed and modelled time-integrated concentrations for each puff and sampler are calculated from the corresponding SF6 time series as the sum of the product of each “acceptable” value (C > 400 pptv) by the timestep of the time series (0.5 s). Hence, for the present comparison, differences between observed and predicted time-integrated concentrations do not depend on how models match the times at which single 0.5-s concentrations above 400 pptv occur within the sampling period.
Figure 4 shows the scatter plots of predicted and observed time-integrated concentrations for each intensive operating period; SF6 concentrations were normalized to the release mass (Q) of each puff. These figures point out differences in the observed dosage values at the same measurement location within the same intensive operating period, which is in agreement with Harms et al. (2011) who indicate a large variability of the time-integrated concentration values at the same sampling site.
In each figure (IOP3 and IOP8), there is one point for each sampler in which the corresponding model simulated the puff passage. The total number of points varies from model to model in the same intensive operating period as there were models predicting zero SF6 concentrations at measurement locations during the whole sampling period. For an equal comparison, we wished to use only those puffs and samplers in each intensive operating period when both observed and predicted concentrations were above 400 pptv. Table 5 shows, below the model code, the number of samplers in each intensive operating period (N value) in which each model simulated the puff passage. The ratio between the N value of each model and the total number of samplers analyzed (24 in IOP3 and 26 in IOP8) indicates that there are few models simulating correctly the horizontal dispersion of the puff in both intensive operating periods. During daytime (IOP3), there are four models (M8, M3, M5, M10) predicting concentrations above 400 pptv in all 24 samplers, M4 and M1 predict for 83% of these samplers, and M6 and M9 predict for 58% of them. During night-time, M5, M2 and M3 models predict concentrations above 400 pptv for 98% of the 26 samplers, while the rest of the models are in a range from 42% (M6) to 30% (M4, M9, M10) of the samplers.In Sect. 3.4 we intend to clarify this variability between models by showing the space distribution of the modelled SF6 concentrations.
In general, there is much scatter in each plot shown in Fig. 4, as is typical of model comparisons in urban scenarios (Hanna et al. 2011). The scatter of simulated values is larger during night-time (0.6 to 2.4 × 105 pptv s kg−1) than during daytime (1.6 to 3.4 × 104 pptv s kg−1). Visual inspection shows more points above the 1:1 line in the IOP8 scatter plot than in the IOP3, which indicates a greater overprediction of the observed values.
The number of samplers with a simulated time-integrated concentration within a factor-of-two of observations is less than 40% and limited in all models and in both intensive operating periods (Table 5). For most of the models, the largest percentage of simulated values is within or above a factor-of-five of the observations (above 60% during the daytime and above 50% overnight). On average, the MG value is higher overnight (MG = 4.52) than during daytime (MG = 3.91). According to the MG values, there are models consistently overpredicting (M6, M5, M3) or underpredicting (M4, M8) the time-integrated concentrations in both intensive operating periods.
To complement our analysis, we have investigated if models match the sampler in which the maximum dosage was measured for each puff. The success rate of samplers is low in each intensive operating period, and only models M4, M8, M9, M3, M5 and M10 in puff 4 during daytime, and model M2 in puff 3, and models M5 and M10 in puff 4 during night-time, are able to simulate the maximum dosage at the corresponding sampler.
3.4 Modelling SF6 Dispersion Patterns
Under the UDINEE project, six out of eight models in IOP3 and five out of eight in IOP8 have produced the forecast of 1-min averaged SF6 concentrations over the simulation domain and at different heights after each puff release commences. We have used this information to analyze the quantitative differences between models (e.g. Kumar and Feiz 2016). Figures 5 and 6 display the 1-min averaged concentrations of SF6 over the whole domain predicted by each model at certain times after the first puff release in each intensive operating period. In both Figs. 5 and 6, the time after release varies from model to model to visually identify the characteristics of the simulated dispersion pattern of each model. Concentrations above 400 pptv at a height of 2 m a.g.l are shown.
M1 and M3 1-min averaged SF6 concentrations 2 min after IOP3 puff release 1 starts, M4 1-min averaged SF6 concentrations 3 min after IOP3 puff release 1 commences, M5 and M9 1-min averaged SF6 concentrations 4 min after IOP3 puff release 1 commences and M6 1-min averaged SF6 concentrations 6 min after IOP3 puff release 1 commences. The six models are using the same colour contour legend. Unit: pptv. Height: 2 m a.g.l. CDT: Central Daylight Time (5 h behind UTC). Blue dots are sampler locations (fast-response tracer gas analyzers) and the red star is the release location
M3, M4, M5 and M9 1-min averaged SF6 concentrations 6 min after IOP8 puff release 1 commences and M2 1-min averaged SF6 concentrations 9 min after IOP8 puff release 1 commences. The five models are using the same colour contour legend. Unit: pptv. Height: 2 m a.g.l. Blue dots are sampler locations (fast-response tracer gas analyzers) and star is the release location
IOP3 release 1 was made at 0900 CDT with the local wind speed equal to 3.7 m s−1 and wind direction of 196° (from the south-west). The wind speed and direction are observed averages over all fixed anemomenters calculated in Hanna et al. (2007). The puff release was approximately 50 m from the nearest building with a park upwind of the area of tall buildings. Four modelling data (M1, M4, M6, M9) “look similar” in the cloud shape and in the main dispersion pathway, and predict downwind transport to the north-east and high concentrations extending further downwind within the first minutes after the release. Model M6 predicts a large area to the east under high concentrations, model M4 simulates maximum SF6 concentrations close to the release point, while models M1 and M9 predict the maximum between buildings. Model M3 simulates a downwind movement of the puff to the north-east, with broader horizontal extension, and it also predicts little upwind dispersion of the puff close to the release point. Model M5 simulates a large and circular spread pattern of the puff from the release point.
In the case of IOP8 release1 (0500 CDT), local wind speed was 3.8 m s−1 with wind direction from the south-east (157°) (Hanna et al. 2007); the release location was placed in the midst of the buildings. According to Fig. 6, models M3 and M5 predict the largest spread of the puff, simulating, in both cases, a circular dispersion pattern of the puff from the release point. The main difference between them is that model M3 predicts a slight movement of the puff to the west. Models M9 and M4 forecast the dispersion of the puff to the west, while model M2 simulates a broader cloud being transported to the north-west.
According to these results, most of the simulated patterns are in a good qualitatively agreement, with the exception of models M3 and M5. Most of the models predict in both intensive operating period a similar dispersion direction, to the north-east in IOP3 and to the west-north-west in IOP8. However, some differences in the simulation of the puff dispersion stand out from model to model, e.g. the simulated puff varies largely in size in IOP8. In the case of models M3 and M5, the excessive dispersion is probably because these models do not resolve for airflow between the buildings but they consider the city as a collection of roughness elements. Another difference between models can be found in IOP3 (Fig. 5), by considering the dispersion predicted by models M6 and M9. Both models present a shift of the plume to the east and the dispersion is wider than others simulated dispersion patterns. This predicted pattern is in agreement with Flaherty et al. (2007) which demonstrated that for a release from the botanical gardens and with wind directions highly oblique to the street direction, the plume centreline was offset from the wind direction transport location and the plume width was enhance by dispersion from a line source from the channelled plume.
Differences between space distributions of SF6 concentrations expose the diversity of ADMs used within this project, and, hence, the variety of approaches and assumptions to simulate the short time-scale variability in wind direction and speed, and turbulence, and the effects of buildings on the transport and dispersion of pollutant within the urban boundary layer (e.g. Brown 2004). In urban areas, in which there is a wide range of building heights and sizes, differences between predictions can be associated, for instance, with the order in which models parametrize the wakes of buildings (Hanna et al. 2011). As an example, and considering the location of the measurement location, Figs. 5 and 6 help to identify that M6 and M9 models seem to miss the western fast-response tracer gas analyzers in IOP3, while M4 and M9 are not able to simulate the northern transport of the puff along the avenue in IOP8. Therefore, they do not predict concentrations in the samplers deployed more to the north.
Differences between models are also observed comparing day–night puff dispersions. There are models (e.g. M4 and M9) simulating broader clouds during daytime than overnight. In addition, differences between the times in which each model simulates the arrival of the puff to the borders of the simulation domain in each intensive operating period (between 2–6 min in IOP3 and 6–9 min in IOP8) would indicate the simulation of faster puff dispersion during daytime than during night-time. Both results are qualitatively consistent with the behaviour of daytime releases in urban environments where the presence of buildings is expected to enhance both vertical and lateral mixing (Britter and Hanna 2003). More analysis about each model can be found elsewhere in this special issue.
4 Influence of the Meteorological Input Data
Previous sections endeavour to give a general assessment concerning the present use of urban atmospheric dispersion models. These sections have pointed out a large spread on the modelling predictions. In this sense, we recall that under UDINEE the three alternative approaches are used, the Eulerian, the Lagrangian, and the Gaussian (Zannetti 2005, 2010), and the individual performance of each approach in application to the JU2003 experiment can be consulted in this special issue.
The larger part of differences between model predictions is due to the simulation of the flow dynamics and turbulence that drives the dispersion (COST ES 1006 2015a). Other factors contributing to differences are: boundary conditions (e.g. fixed or time-varying inflow conditions during dispersion of each puff), modelling of thermal effects (day vs. night and if and how is this modelled), assumptions made by each modelling group (e.g. aerodynamic roughness of surfaces). In addition, in urban areas, the simulation of the wind direction and speed in street channels in which building heights vary is another factor in order to account for flow distortion and deflection by building layout (Brown 2004).
UDINEE does not intend to promote or downgrade any modelling system or to identify the most appropriate for predicting concentrations in an urban environment. To overcome this limitation and in the framework of our analysis, the effect of different boundary conditions on the dispersion and concentration field predicted by models can be discussed, with the purpose of making recommendations on the selection and procedures of data inputs to limit the uncertainty associated to this selection dealing with urban dispersion events.
Predicted concentrations are still highly dependent upon the inflow conditions used as input variable, as concentrations are primary controlled by wind direction and speed (for transport) and turbulence (for dispersion). Therefore, it must be treated as a critical input variable in any modelling study. To simulate the dispersion in an urban canopy layer, the average wind speed and the prevailing wind direction, measured by weather stations, are usually used in determining the inflow conditions. However, this neglects the main properties of the natural background flow dynamics, due to the time-varying characteristics of wind speeds and directions. The variation of inflow conditions is one of the primary factors that influencing the transport efficiency of pollutants in an urban environment (e.g. Zhang et al. 2018). Differences in wind direction and speed have a substantial influence on the airflow pattern in urban street canyons, and hence, on dispersion patterns (e.g. Li et al. 2017). Zhang et al. (2011) compared the simulated results under time-varying wind conditions and averaged wind conditions, and shows significant differences in dispersion patterns using both inflow conditions.
Under UDINEE, wind measurements on a single site (PWIDS 15) were used to sustain the inflow condition (Sect. 2.2.3). However, and as Table 6 shows, whilst there are models (M9, M4, M2, M6) using constant-in-time incoming wind as input, others (M1, M3, M5, M8, M10) use time-varying wind speed and direction at the boundary of the computations domain to simulate the dispersion of each puff. Time-varying wind data ranged from 1 to 5-min averages at PWIDS15 meteorological station, while in the case of models M3 and M5, it is 0.1 s but with very little change at each step time due to the long interpolation period (1 h) considered.
Grouping the NAD values of Sect. 3.2, NAD ranges in similar values, 0.23–0.96 for time varying and 0.39–0.94 for constant time. However, time-varying models obtain the lowest NAD values during daytime (model M1) and night-time (model M3) respectively, which suggest that the use of time-varying transport properties improves the performance of models. This improvement is also registered, on average, in the simulation of the time-integrated concentrations. First, the number of receptors matched by models using time-varying wind speed and direction is higher than for models using constant wind speed and direction in both intensive operating periods. While for IOP3, the average of false negative samplers is 1 for time-varying and 8 for constant wind, for IOP8 it is 9 and 13 respectively. Secondly, the percentage of samplers within a factor-of-two and factor-of-five of observations increases considering using time-varying wind, and finally, the average values of MG and VG improve in IOP3 by using time-varying wind speed and direction. In IOP8, VG values improve and MG values are higher for constant wind models (4.7 against 4.3). Hence, these results also suggest how the use of time-varying wind speed and direction data as input variable reduces the uncertainty in the time-integrated predictions, which is representative of a dose estimate and it is among the most important impact parameters for population protection.
Flaherty et al. (2007) also report the importance of changes in wind direction in the variations in tracer concentrations observed in the time series between different release periods. The results of our study reveal the importance of carrying out simulations under time-varying wind conditions. In this sense, we can draw that the usage of complex models (as those that were mostly used under UDINEE) would require the use of time-varying input wind data in order to produce much more meaningful predictions to assist emergency management in case of the release of airborne hazardous substances in a densely built-up region.
5 Conclusions
An evaluation and intercomparison of ADM capabilities in simulating the dispersion of SF6 puff releases in an urban environment has been conducted in the context of the UDINEE project. Nine ADMs have simulated the transport and dispersion of the set of puff releases performed during the JU2003 field experiment. Although UDINEE is a model evaluation study using tracer data representative of the dispersion process following neutrally-buoyant puff releases in the urban environment, it is also an important step towards the simulation of RDD explosions in built-up areas.
In the present study, simulated concentration time series, from the nine models with a temporal resolution of 0.5 s, are compared using a subset of the observations to investigate the model capabilities in simulating the presence of the contaminant, the concentrations and the time-integrated air concentrations at the sampling locations. Data from eight puff releases (four during daytime and four during night-time) are used. We have considered as “acceptable” those pairs of observed and modelled concentrations where both were above 400 pptv.
The results have shown large differences among models in the simulation of the puff passage at the measurement locations under the same or different meteorological conditions. The comparison of the modelled and observed concentration distributions shows that most of the models capture, reasonably well, the smallest concentrations (< 10th percentile) and the largest ones (> 90th percentile) in both intensive operating periods. In contrast, there are two models presenting large underestimates of the smallest concentrations. The predicted concentrations within a factor of two of observations are similar and ranged between 1–34% during daytime and 1–36% during night-time. The percentage of valid pairs ranged from 1 to 25% during daytime and from 1 to 27% during night-time. The percentage of false-negative pairs (underpredictions) increases with the distance from the release location. The models present higher percentages of false positive and false negative pairs overnight, and this may have implications for emergency management and the taking of counter-measures. The analysis of the time-integrated concentrations for each puff and sampler reports that models tend to overestimate the observed values and present better performance during daytime than night-time.
Most of the models are capable of reproducing the transport direction of SF6 in this urban area, but, they show significant differences between day–night puff dispersions, e.g. lower agreement between the number of sampling sites in which the tracer was observed and simulated during night-time, and the simulation of faster puff dispersion during daytime. There are two models simulating a circular dispersion of the tracer during daytime and overnight, without considering the influence of the urban environment on the puff dispersion. In both models, the wind direction appears not to be considered, since the tracer spreads excessively.
These results should not be considered as solely the difference between models in predicting certain observations. We have investigated the impact of differences in using constant or time-varying incoming wind direction on the predictions. In this sense, an improvement in the performance of models by using time-varying wind speed and direction, as the average of several minutes from in situ measurements, is obtained. This result is a valuable asset for emergency-response situations as it suggests the importance for having sufficient information to assess this input variable in order to improve the reliability of the predictions.
The large amount of data already generated under UDINEE and stored in the ENSEMBLE system is valuable not only for developing advanced tools for emergency –response situations but also for refining urban dispersion models. By building on the present database, future work on the comparison of modelled and observed concentrations will help to further improve the present modelling tools to match these good quality experimental data.
To proceed to more realistic simulations of the consequences from RDD explosions, experimental data on dispersion and deposition of particles (of different sizes) are needed. However, it is difficult to obtain such experimental data to evaluate models. To this purpose, new experiments should be organized in urban areas to collect meteorological and concentration fields following deliberate releases. These experiments should include many different release scenarios to establish the sensitivity of model predictions for different urban geometries and under different meteorological conditions.
The JU2003 observations showed a rather large variability in the dispersion of puffs released under very similar meteorological conditions (in the same intensive operating period). This has been observed in other experimental campaigns too, and even in wind tunnels. Therefore, future studies should consider ensemble statistics in both experimental and model data, requiring, of course, experiments involving a large number of puffs released under the “same” conditions to derive a stable ensemble.
References
Allwine KJ, Flaherty J (2006) Joint urban 2003: study overview and instrument locations. Pacific Northwest National Lab., Richland, WA. PNNL-15967
Allwine KJ, Flaherty J (2007) Urban dispersion program overview and MID05 field study summary. Pacific Northwest National Lab., Richland, WA. PNNL-16696
Allwine KJ, Shinn JH, Streit GE, Clawson KL, Brown M (2002) Overview of Urban 2000. Bull Am Meteorol Soc 83:521–536
Anfossi D, Tinarelli G, Trini Castelli S, Nibart M, Olry C, Commanay J (2010) A new Lagrangian particle model for the simulation of dense gas dispersion. Atmos Environ 44:753–762
Ansari A (2010) Radiation threats and your safety: a guide to preparation and response for professionals and community. Taylor & Frances Group, Abingdon. ISBN 978-1-4200-8361-3
Arnold SJ, ApSimon H, Barlow J, Belcher S, Bell M, Boddy JW, Britter R, Cheng H, Clark R, Colvile RN, Dimitroulopoulou S, Dobre A, Greally B, Kaur S, Knights A, Lawton T, Makepeace A, Martin D, Neophytou M, Neville S, Nieuwenhuijsen M, Nickless G, Price C, Robins A, Shallcross D, Simmonds P, Smalley RJ, Tate J, Tomlin AS, Wang H, Walsh P (2004) Introduction to the DAPPLE air pollution project. Sci Total Environ 332:139–153
Baklanov A, Grimmond S, Mahura A, Athanassiadou M (2009) Meteorological and air quality models for urban areas. Springer, Berlin, p 183. https://doi.org/10.1007/978-3-642-00298-4
Bartzis JG (1991) ANDREA-HF: a three dimensional finite volume code for vapour cloud dispersion in complex terrain. CEC JRC Ispra Report EUR 13580 EN, EC Joint Research Centre, Ispra
Baumann-Stanzer K, Andronopoulos S, Armand P, Berbekar E, Efthimiou G, Fuka V, Gariazzo C, Gasparac G, Harms F, Hellsten A, Jurcakova K, Petrov A, Rakai A, Stenzel S, Tavares R, Tinarelli G, Trini Castelli S (2015) COST ES1006—model evaluation case studies: approach and results, COST Action ES1006, April 2015, ISBN: 987-3-9817334-2-6, © COST Office
Benbouta N (2007) Canadian urban flow and dispersion model (CUDM): developing Canadian capabilities for CBRN hazard dispersion in urban areas. CMOE Dorval TR 2007-001 technical report. Environment Canada
Bianconi R, Galmarini S, Bellasio R (2004) Web-based system for decision support in case of emergency: ensemble modelling of long-range atmospheric dispersion of radionuclides. Environ Model Softw 19:401–411
Britter RE, Hanna SR (2003) Flow and dispersion in urban areas. Annu Rev Fluid Mech 35:1–496
Britter RE, Caton F, Di Sabatino S, Cooke KM, Simmonds PG, Nickless G (2000) Dispersion of a passive tracer within and above an urban canopy. In: Proceedings of the third symposium on the urban environment. American Meteorological Society, pp 30–31
Brown MJ (2004) Urban dispersion-challenges or fast response modelling. In: Fifth conference on urban environment. Amerian Meteorological Society, Vancouver, BC, Canada, J5, 1
Burian SJ, Han WS, Brown MJ (2003) Morphological analyses using 3D building databases: Oklahoma City, Oklahoma. Los Alamos National Laboratory Rep. LA-UR-02-0781
Čarný P, Lipták Ľ, Smejkalová E, Krpelanová M (2015) Protective measures based on the state of reactor and source term predicted (ESTE tool). International Experts’ meeting on assessment and prognosis in response to a nuclear or radiological emegency. Vienna, 20–24 April 2015 (Org: IAEA)
Chang J, Hanna SR (2004) Air quality model performance evaluation. Meteorol Atmos Phys 87:167–196
Clawson KL, Carter RG, Lacroix DJ, Biltoft CJ, Hukari NF, Johnson RC, Rich JD, Beard SA, Strong T (2005) Joint urban 2003 (JU2003) SF6 atmospheric tracer field tests, NOAA Tech Memo OAR ARL-254. Air Resources Lab, Silver Spring
Cooke KM, Di Sabatino S, Simmonds P, Nickless G, Britter RE, Caton F (2000) Tracer and dispersion of gaseous pollutants in an urban area. Birmingham tracer experiments. Technical Paper CUED/A-AERO/TR.27. Department of Engineering, Cambridge University
COST ES1006 (2015a) Model evaluation case studies, COST action ES1006 “evaluation, improvement and guidance for the use of local-scale emergency prediction and response tools for airborne hazards in build environments”. ISBN 987-3-9817334-2-6
COST ES1006 (2015b) Best practice guidelines, COST action ES1006 “evaluation, improvement and guidance for the use of local-scale emergency prediction and response tools for airborne hazards in build environments”. ISBN 987-3-9817334-0-2
COST ES1006 (2015c) Model evaluation protocol, COST action ES1006 “evaluation, improvement and guidance for the use of local-scale emergency prediction and response tools for airborne hazards in build environments”. ISBN 987-3-9817334-1-9
Defense Threat Reduction Agency (2008) HPAC version 5.0 SP1 (DVD containing model and accompanying data files), DTRA, 8725 John J. Kingman Road, MSC 6201, Ft. Belvoir, VA 22060-6201
Dennis R, Fox T, Fuentes M, Gilliland A, Hanna S, Hogrefe C, Irwin J, Rao ST, Scheffe R, Schere K, Steyn D, Venkatram A (2010) A framework for evaluation of regional-scale numerical photochemical modeling systems. Environ Fluid Mech 10:471–489
Efthimiou GC, Bartzis JG, Koutsourakis N (2011) Modelling concentration fluctuations and individual exposure in complex urban environments. J Wind Eng Ind Aerodyn 99:349–356
Efthimiou GC, Andronopoulos S, Bartzis JG (2017) Prediction of dosage-based parameters from the puff dispersion of airborne materials in urban environments using the CFD RANS methodology. Meteorol Atmos Phys. https://doi.org/10.1007/s00703-017-0506-0
Flaherty JE, Lamb BK, Allwine KJ, Allwine EJ (2007) Vertical tracer concentration profiles measured during the joint urban 2003 dispersion study. J Appl Meteorol Climatol 46:2019–2037
Galmarini S, Bianconi R, Klug W, Mikkelsen T, Addis R, Andronopoulos S et al (2004) Ensemble dispersion forecasting—part I: concept, approach and indicators. Atmos Environ 38:4607–4617
Galmarini S, Bianconi R, Appel W, Solazzo E, Mosca S, Grossi P et al (2012) ENSEMBLE and AMET: two systems and approaches to a harmonized, simplified and efficient facility for air quality models development and evaluation. Atmos Environ 53:51–59
Hall D, Spanton A, Griffiths I, Hargrave M, Walker S (2003) The urban dispersion model (UDM): version 2.2 technical documentation, release 1.1. Technical report DSTL/TR04774. Defence Science and Technology Laboratory, Porton Down, UK
Hanna SR, Chang J (2012) Acceptance criteria for urban dispersion model evaluation. Meteorol Atmos Phys 116:133–146
Hanna SR, Brown MJ, Camelli FE, Chan ST, Coirier WJ, Hansen OR et al (2006) Detailed simulations of atmospheric flow and dispersion downtown Manhattan: an application of five computational fluid dynamics models. Bull Am Meteorol Soc 87:1713–1726
Hanna SR, White J, Zhou Y (2007) Observed winds, turbulence and dispersion in built-up downtown areas in Oklahoma city and Manhattan. Boundary Layer Meteorol 125:441–468
Hanna SR, White JM, Troiler J, Vernot R, Brown M, Kaplan H et al (2011) Comparisons of JU2003 observations with four diagnostic urban wind flow and Lagrangian particle dispersion models. Atmos Environ 45:4073–4081
Harms F, Leitl B, Schatzmann M, Patnaik G (2011) Validating LES-based flow and dispersion models. J Wind Eng Ind Aerodyn 99:289–295
Hernández-Ceballos MA, Hanna S, Bianconi R, Bellasio R, Chang J, Mazzola T, Andronopoulos S, Armand P, Benbouta N, ˇCarný P, Ek N, Fojcíková E, Fry R, Huggett L, Kopka P, Korycki M, Lipták L, Millington S, Miner S, Oldrini O, Potempski S, Tinarelli G, Trini Castelli S, Venetsanos A, Galmarini S (2019) UDINEE: evaluation of multiple models with data from the JU2003 puff releases in Oklahoma City. Part II: simulation of puff parameters. Bound Layer Meteorol https://doi.org/10.1007/s10546-019-00434-7
Hogue R, Benbouta N, Mailhot J, Belair S, Lemonsu A, Yee E, Lien F-S, Wilson JD (2009) The development of a prototype of Canadian urban flow and dispersion modeling system. In: AMS 89 annual conference. Joint Session 19 Urban transport and dispersion modeling
Jones AR, Thomson DJ, Hort M, Devenish B (2007) The U.K. Met Office’s next-generation atmospheric dispersion model, NAME III. In: Borrego C, Norman A-L (eds) Proceedings of the 27th NATO/CCMS international technical meeting on air pollution modelling and its application air pollution modeling and its application XVII. Springer, pp 580–589
Jonsson L, Plamboeck AH, Johansson E, Waldenvik M (2013) Various consequences regarding hypothetical dispersion of airborne radioactivity in a city center. J Environ Radioact 116:99–113
Kamboj S, Cheng J-J, Yu C, Domotor S, Wallo A (2009) Modeling of the EMRAS urban working group hypothetical scenario using the RESRAD-RDD methodology. J Environ Radioact 100:1012–1018
Kumar P, Feiz A-A (2016) Performance analysis of an air quality CFD model in complex environments: numerical simulation and experimental validation with EMU observations. Build Environ 108:30–46
Li C, Zhou ST, Xiao YQ, Huang Q, Li LX, Chan PW (2017) Effects of inflow conditions on mountainous/urban wind environment simulation. Build Simul 10:573–588
Martin D, Petersson KF, Shallcross DE (2011) The use of cyclic perfluoroalkanes and SF6 in atmospheric dispersion experiments. Q J R Meteorol Soc 137:2047–2063
Medalia J (2004) Terrorist ‘Dirty Bombs’: a brief primer. Congressional Research Staff Report for Congress. Order Code RS21528, April 1. http://www.fas.org/spp/starwars/crs/RS21528.pdf
Medalia J (2011) “Dirty Bombs”: technical background, attack prevention and response, issues for congress. Technical report, Congressional Research Service, Washington, DC
Mu Y, Liu X, Wang L (2018) A Pearson’s correlation coefficient based decision tree and its parallel implementation. Inf Sci 435:40–58
Neophytou M, Gowardhan A, Brown M (2011) An inter-comparison of three urban wind models using Oklahoma City joint urban 2003 wind field measurements. J Wind Eng Ind Aerodyn 99:357–368
Oldrini O, Armand P, Duchenne C, Olry C, Moussafir J, Tinarelli G (2017) Description and preliminary validation of the PMSS fast response parallel atmospheric flow and dispersion solver in complex built-up areas. Environ Fluid Mech. https://doi.org/10.1007/s10652-017-9532-1
Pardyjak E, Brown M (2001) Evaluation of a fast response urban wind model—comparison to single building wind-tunnel data. In: International society of environment hydraulics, Tempe, AZ, LA-UR-01-4028
Pardyjak E, Brown M (2002) Fast response modeling of a two building urban street canyon. In: 4th AMS symposium urban environment, Norfolk, VA, LA-UR-02-1217
Rentai Y (2011) Atmospheric dispersion of radioactive material in radiological risk assessment and emergency response. Prog Nucl Sci Techonol 1:7–13
Rosoff H, Von Winterfeldt D (2007) A risk and economic analysis of dirty bombAttacks on the ports of Los Angeles and Long Beach. Risk Anal 27:533–546
Schatzmann M, Leitl B (2002) Validation and application of obstacle resolving urban dispersion models. Atmos Environ 36:4811–4821
Schatzmann M, Leitl B (2011) Issues with validation of urban flow and dispersion CFD models. J Wind Eng Ind Aerodyn 99:169–186
Shin H, Kim J (2009) Development of realistic RDD scenarios and their radiological consequence analyses. Appl Radiat Isot 67:1516–1520
Sykes RI, Parker S, Henn D, Chowdhury B (2016) SCIPUFF version 3.0 technical documentation. Sage Management, 15 Roszel Road, Suite 102, Princeton, NJ 08540
Thiessen KM, Anderson KG, Batandjieva B, Cheng J-J, Hwang WT, Kaiser JC, Kamboj S, Steiner M, Tomás J, Trifunovic D, Yu C (2009) Modelling the long-term consequences of a hypothetical dispersal of radioactivity in an urban area including remediation alternatives. J Environ Radioact 100:445–455
Tinarelli G, Mortarini L, Trini Castelli S, Carlino G, Moussafir J, Olry C, Armand P, Anfossi D (2013) Review and validation of MicroSpray, a Lagrangian particle model of turbulent dispersion, in Lagrangian modeling of the atmosphere in geophysical monograph series 200, American Geophysical Union, 311–327. ISBN 978-0-87590-490-0
Venetsanos AG, Papanikolaou E, Bartzis JG (2010) The ADREA-HF CFD code for consequence assessment of hydrogen applications. Int J Hydrog Energy 35:3908–3918
Warner S, Platt N, Heagy J (2004) User-oriented two-dimensional measure of effectiveness for the evaluation of transport and dispersion models. J Appl Meteorol 43:58–73
Zannetti P (ed) (2005) Air quality modeling theories, methodologies, computational techniques, and available databases and software. Vol I and II fundamentals. The EnviroComp Institute and the Air & Waste Management Association, Pittsburgh
Zannetti P (ed) (2010) Air quality modeling—theories, methodologies, computational techniques, and available databases and software. Vol IV—advances and updates. The EnviroComp Institute and the Air & Waste Management Association, Pittsburgh
Zhang YW, Gu ZL, Cheng Y, Lee SC (2011) Effect of real-time boundary wind conditions on the airflow and pollutant dispersion in an urban street canyon-large eddy simulations. Atmos Environ 45:3352–3359
Zhang Y, Gu Z, Yu CW (2018) Review on numerical simulation of airflow and pollutant dispersion in urban street canyons under natural background wind condition. Aerosol Air Qual Res 18:780–789
Acknowledgments
We gratefully acknowledge the European Commission Directorate General for Migration and Home Affairs (DG HOME) for their support to the Urban Dispersion International Evaluation Exercise (UDINEE) activity. Authors want to acknowledge the contribution of various groups to UDINEE. The following agencies have prepared the data sets used in this study: U.S Army Dugway Proving Group as manager of the JU2003 database. Data from tracer monitoring stations were provided by the National Oceanic and Atmospheric Administration (NOAA) Air Resources Laboratory Field Research Division; Data from meteorological monitoring stations were provided by Dugway Proving Ground.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hernández-Ceballos, M.A., Hanna, S., Bianconi, R. et al. UDINEE: Evaluation of Multiple Models with Data from the JU2003 Puff Releases in Oklahoma City. Part I: Comparison of Observed and Predicted Concentrations. Boundary-Layer Meteorol 171, 323–349 (2019). https://doi.org/10.1007/s10546-019-00433-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-019-00433-8