Abstract
The representation of a neutral atmospheric flow over roughness elements simulating a vegetation canopy is compared between two large-eddy simulation models, wind-tunnel data and recently updated empirical flux-gradient relationships. Special attention is devoted to the dynamics in the roughness sublayer above the canopy layer, where turbulence is most intense. By demonstrating that the flow properties are consistent across these different approaches, confidence in the individual independent representations is bolstered. Systematic sensitivity analyses with the Dutch Atmospheric Large-Eddy Simulation model show that the transition in the one-sided plant-area density from the canopy layer to unobstructed air potentially alters the flow in the canopy and roughness sublayer. Anomalously induced fluctuations can be fully suppressed by spreading the transition over four steps. Finer vertical resolutions only serve to reduce the magnitude of these fluctuations, but do not prevent them. To capture the general dynamics of the flow, a resolution of 10 % of the canopy height is found to suffice, while a finer resolution still improves the representation of the turbulent kinetic energy. Finally, quadrant analyses indicate that momentum transport is dominated by the mean velocity components within each quadrant. Consequently, a mass-flux approach can be applied to represent the momentum flux.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Canopies, both natural and anthropogenic, act as aerodynamically rough surfaces and consequently significantly affect the atmospheric flow inside and aloft, and the resulting vertical exchange (Thom et al. 1975; Finnigan and Shaw 2000; Harman and Finnigan 2007; Finnigan et al. 2009). The drag induced by the canopy leads to deviations from the classical characterizations such as Monin–Obukhov similarity theory (MOST), which describe the non-dimensionalized properties of atmospheric flow near the surface. In order to represent the inertial sublayer (ISL) over canopies, the flux-gradient relationships therefore need to be adapted to account for this influence.
The region above the canopy where turbulence and associated transport are altered, the so-called roughness sublayer (RSL) below the ISL, is of special interest. Over the past decades, studies made use of observations, turbulence resolving numerical models and theory to increase understanding of this atmospheric layer (e.g., Brunet et al. 1994; Su et al. 1998; Patton et al. 2003; Harman and Finnigan 2007; Bohrer et al. 2009; Finnigan et al. 2009; Maurer et al. 2015). Combined, an effort is made to understand the processes in the canopy layer and RSL and develop the necessary adaptations to the traditional surface-layer relationships, i.e. MOST, focusing on horizontally homogeneous vegetation canopies.
Using field observations (e.g., Katul and Albertson 1998) and wind-tunnel studies (e.g., Brunet et al. 1994), properties of the flow in the canopy layer and RSL were described and quantified. These studies were completed by using the three-dimensional data fields generated by numerical large-eddy simulation (LES) models. Finnigan et al. (2009), representing a similar flow as in Brunet et al. (1994), identified that the sweeps and ejections that govern turbulent transport are generated by pairs of hairpin vortices. The effects of horizontal transitions in plant-area density were studied by investigating the effects of heterogeneous canopy distributions (Bohrer et al. 2009) and the processes near forest edges (Cassiani et al. 2008). Additionally flow characteristics were compared for different vertical plant-area density profiles (Dupont and Brunet 2008), which mainly confirmed the similar characteristics for turbulent flows over canopies. However, none of these studies characterized the effect of the vertical plant-area density transition at canopy top. The effect of the canopy on the dispersion of particles such as spores was recently investigated by Pan et al. (2014), who furthermore identified that applying a drag coefficient that depends on wind speed improves the resemblance between LES data and field observations.
Recently, advances have been made in the representation of the deviations in the canopy layer and RSL from traditional flux-gradient relationships due to the canopy (Harman and Finnigan 2007, 2008; de Ridder 2010). An advantage of these new expressions over older, purely empirical corrections (Garratt 1983; Raupach 1992; Cellier and Brunet 1992; Mölder et al. 1999) is that they incorporate both the canopy layer and RSL, result in continuous profiles throughout the various atmospheric layers, and are based on physical considerations. These relationships can be used to improve the interpretation of observational and numerical data, as we will demonstrate for the LES momentum-flux profiles.
In this study we extend previous research by comparing the normalized first- and second-order momentum profiles that follow from wind-tunnel observations, two state-of-the-art LES models and the adapted empirical theory for a neutral flow over roughness elements simulating a horizontally homogeneous vegetation canopy. The evaluated conditions are based on the wind-tunnel observations of Brunet et al. (1994). To the authors’ knowledge, this is the first time that the similarity of all these different representations has been evaluated. By doing so, the consistency and validity of the independent representations can be confirmed. After validation of the canopy representation in the LES models, we further our understanding by investigating the sensitivities of the model results to vertical transitions in the plant-area density profile near canopy top and to numerical grid resolution, as recommended by Su et al. (1998). Furthermore, the momentum flux is analyzed in more detail using quadrant analyses (e.g., Lu and Willmarth 1973). To test our hypothesis that transport is driven by organized structures, we contrast the contributions to the total flux within the various quadrants, differentiating between turbulent and advective terms. The presented case study acts as a standardized basis for future comparison and sensitivity studies, and can be expanded to study the impact of canopies on the vertical exchange of inert and reactive atmospheric compounds.
2 Methods
Profiles of flow characteristics (first- and second-order moments) are compared between various data sources and conditions. The specific case that serves as the basis of this study has been discussed in the literature using methods summarized in Sect. 2.1. In Sect. 2.2, we describe the applied version of the Dutch Atmospheric Large-Eddy Simulation (DALES) model and the numerical set-up for the various comparisons. Finally, the theoretical profiles that follow from empirical relationships are recapped in Sect. 2.3.
2.1 Previously Published Data
The neutral flow over a canopy investigated herein is based on a wind-tunnel experiment performed by Brunet et al. (1994). This experiment was designed to represent a scaled down atmospheric flow over real vegetation, using flexible cylindrical stalks of monofilament nylon fishing line, mimicking waving wheat, with a diameter of \(0.25\,\mathrm{mm}\), a height of \(50\,\mathrm{mm}\) and a grid spacing of \(5\,\mathrm{mm}\) on a smooth surface in an 11-m long wind tunnel. Since the stalks bend, the average canopy height was \(47\,\mathrm{mm}\). Velocity observations of the flow in the streamwise and vertical directions were obtained using triple-hot-wire probes.
Using the National Center for Atmospheric Research’s (NCAR’s) LES code (Patton et al. 2005) and scaling up the dimensions to arrive at a canopy height, \(h_\mathrm{c}\), of \(10\,\mathrm{m}\), Finnigan et al. (2009) performed numerical simulations to represent this flow. While details can be found in Finnigan et al. (2009), it is worthwhile to note that, although the canopy drag coefficient varied with height in the wind-tunnel experiment (Brunet et al. 1994), a fixed value was chosen for the NCAR LES study. Furthermore, the one-sided plant-area density (PAD), prescribed at interface levels \(z = n {\varDelta } z\) and interpolated in between, was generally set to \(a = 5.32 \times 10^{-2}\,\mathrm{m}^2\,\mathrm{m}^{-3}\) below canopy top, half that base value at the uppermost interface level below canopy top and zero above that, resulting in a frontal plant area index (PAI, i.e. vertically integrated PAD) of \(\textit{PAI} = 0.479\). This adapted plant-area density profile compared to Brunet et al. (1994) was applied to remedy spurious oscillations and results in a slight departure from the original PAI (0.47).
For the intercomparison, we make use of the original wind-tunnel data of Brunet et al. (1994) and updated NCAR LES data. The provided NCAR LES data was updated to rectify settings in Finnigan et al. (2009). In short, the drag coefficient is revised to \(C_\mathrm{d} = 0.675\) and the roughness length is set to \(z_0 = 3.8 \times 10^{-3}\,\mathrm{m}\). Furthermore, the PAD profile is further smoothed near the canopy top to inhibit spurious oscillations in the flow, as discussed in Sect. 3.2. The value of a at the interface levels directly above and below the uppermost interface level below canopy top are \(\frac{1}{8}\) and \(\frac{7}{8}\) of the base value, respectively.
2.2 DALES
2.2.1 Model Description
We perform numerical experiments with an adapted version 4.0 of the DALES model, which originates from Nieuwstadt and Brost (1986) and is described in detail for version 3.2 in Heus et al. (2010). Later updates served to e.g. account for heterogeneous land surfaces (Ouwersloot et al. 2011), update the land-surface submodel to incorporate photosynthesis processes (Vilà-Guerau de Arellano et al. 2014) and introduce an anelastic approximation for height-dependent air density (Böing et al. 2014). As with the NCAR LES model, the DALES model resolves processes on scales larger than the grid spacing. However, in contrast the DALES model uses fifth-order discrete differences in the horizontal directions to represent advection, rather than pseudospectral differences. Sub-filter scale transport is parametrized following Deardorff (1980) using 1.5-order closure with mixing length \(\varDelta = \root 3 \of {\varDelta x \varDelta y \varDelta z}\).
The applied boundary conditions and forcings are identical to those of the NCAR LES model. A frictionless rigid lid (\({\partial u}/{\partial z}\), \({\partial v}/{\partial z}\), \({\partial e}/{\partial z}\) and w set to 0) is assumed for the upper boundary and periodic boundary conditions are applied in the horizontal directions. To account for the drag induced by the canopy elements, tendencies to the three velocity components, \(u_i\), and subgrid turbulent kinetic energy, e, are prescribed in the current version of the DALES model according to
where \(C_\mathrm{d}\) is the dimensionless canopy drag coefficient and a is the one-sided plant-area density in \(\mathrm{\mathrm m}^2\,\mathrm{m}^{-3}\). The relative \(\textit{PAD}\) profile is prescribed and, combined with the integrated one-sided plant-area index, determines the value of a at any given level.
In Eqs. 1 and 2, turbulent kinetic energy (TKE) production by wake generation is not considered, since it only has a small effect on the total TKE (Shaw and Patton 2003; Dupont and Brunet 2008; Bohrer et al. 2009). A spatially-invariant external pressure gradient was used as additional velocity tendency, \(\left. \frac{\partial u_i}{\partial t}\right| _{\mathrm{ext.}}\), to ensure that at every timestep the average velocity over the entire grid is maintained at \(\mathbf {u}=\left( 6,0,0\right) \mathrm{m} \,\hbox {s}^{-1}\). Note that this pressure-gradient driven acceleration yields slightly different results from the neutral flow over a canopy in the wind tunnel, where the acceleration of the flow is caused by entrainment of the freestream velocity into the developing boundary layer. To consider a pure neutral flow, the effects of buoyancy and the Coriolis force were ignored.
Furthermore, the statistical routines of the DALES model are expanded to include quadrant-hole analyses (Lu and Willmarth 1973; Su et al. 1998). In short, data are sampled in four bins, based on the quadrant in the u,w plane. The four quadrants are (Q1) outward interactions with \(u'>0, w'>0\), (Q2) ejections with \(u'<0, w'>0\), (Q3) inward interactions with \(u'<0, w'<0\) and (Q4) sweeps with \(u'>0, w'<0\), where primes denote deviations from horizontal slab-averaged data.
Finally, the DALES model is adapted to enable 2D parallelization, since the original 1D parallelization in the y-direction did not suffice for these numerical experiments. By dividing the domain over \(N_x\) and \(N_y\) processor cores in the respective horizontal directions, more processors can be used than in the case of 1D parallelization, while at the same time reducing the computational overhead related to communication between the different cores. As a result, we are able to handle the computationally intensive numerical experiments. Note that parallelization in the original direction is still faster than in the perpendicular direction, so that it is advised to prescribe \(N_y \ge N_x\).
2.2.2 Model Set-Up
As in Finnigan et al. (2009), a \(1024 \times 1024 \times 128\) grid with a resolution of \(0.1 \,h_\mathrm{c} \times 0.1\,h_\mathrm{c} \times 0.1\,h_\mathrm{c}\) is used for the base numerical experiment, where \(h_\mathrm{c} = 10\,\mathrm{m}\) is the height of the canopy. Similarly, the flow is simulated for \(2400\,\mathrm{s}\) of which the last \(900\,\mathrm{s}\) are considered for statistics. To consider a pure neutral flow, no specific humidity is present and the atmospheric vertical gradient and surface flux of potential temperature are set to zero. The initial velocity is set equal to the background velocity, which is \(\mathbf {u}= \left( 6,0,0\right) \,\mathrm{m}\, \hbox {s}^{-1}\) for the base numerical experiment. In accordance with the updated NCAR LES data, we prescribe \(z_0 = 3.8 \times 10^{-3}\mathrm{\mathrm m}\) and \(C_\mathrm{d} = 0.675\). For all numerical experiments, the PAI of the canopy is set equal to the value that results from the applied plant-area density profile in Finnigan et al. (2009), i.e. 0.479. Every numerical experiment is performed three times with different random seeds after which we ensemble average the statistics. However, differences between the flow statistics from the three realizations are minimal.
In the DALES experiments, in general three different relative PAD profiles are prescribed for our sensitivity analyses, listed in Table 1: four steps is the standard configuration based on the updated NCAR LES experiment, two steps corresponds to the configuration as used in Finnigan et al. (2009) and the sharp transition considers a uniform distribution of PAD at the interface levels within the canopy. The absolute value of a is obtained by multiplying the profile with a base value that results in the prescribed PAI. In case of \(\textit{PAD}\) transitions in multiple steps, the canopy top is defined as the first interface layer where a is less than \(50~\%\) of the base value.
Relative one-sided \(\textit{PAD}\) profiles compared to their maximum value for a vertical resolution of \(0.1 h_\mathrm{c}\) for the sharp transition, two steps and four steps profiles (solid lines) and a vertical resolution of \(0.05 h_\mathrm{c}\) for the interpolated profile (dotted line). The canopy top is indicated by a thin black dotted line
Next to the standard configuration (STD) and the different \(\textit{PAD}\) distributions, we vary the resolution and the u component of the background velocity to investigate the sensitivity of the resolved flow. For a proper comparison between simulations with different resolutions, in general a sharp transition in PAD is prescribed. However, to obtain the most accurate result a set of LES experiments, COMB, is run with a grid spacing of \(0.5\,\mathrm{m}\) in all directions and a fourth relative PAD profile: the interpolated profile that is based on the four steps transition using cubic splines. This results in relative \(\textit{PAD}\) values of 1, 0.971, 0.875, 0.7076, 0.5, 0.2924, 0.125, 0.029 and 0, from \(i_h - 6\) to \(i_h + 2\). For comparison, the resulting relative \(\textit{PAD}\) profiles are depicted in Fig. 1 for the standard vertical resolution of \(0.1 h_\mathrm{c}\) for the sharp transition, two steps and four steps profiles and for a vertical resolution of \(0.05 h_\mathrm{c}\) for the interpolated profile. While checking the influence of u the simulation time, and the start and end time of sampling are scaled inversely proportional with the wind speed. Since our tests confirm that scaled results are nearly identical for different background wind speeds, these numerical experiments are not further discussed. An overview of the different configurations is given in Table 2.
2.3 Empirical Profiles of Wind Velocity
The vertical profile of the normalized mean wind velocity is compared to the theoretical profile within the canopy and RSL aloft that was derived in Harman and Finnigan (2007) for dense canopies. Their theoretical profile, summarized in this section for a neutral flow, was validated by observations from three forest sites, but has not been corroborated by numerical methods as of yet.
Next to a canopy height, a canopy penetration depth is defined as
where we substitute a by the average a that is calculated as \(\left. {\textit{PAI}}/{h_\mathrm{c}}\right. \), considering the evaluated non-uniform \(\textit{PAD}\) distribution. This results in \(L_\mathrm{c} \approx 3.09 h_\mathrm{c}\). Inside the canopy
where \(\beta \), the ratio between \(u_*\) and u at the top of the canopy, is assumed to be equal to 0.3, based on observations. Above the canopy an integral needs to be solved (Eq. 15 of Harman and Finnigan (2007)) to infinite height, which we do numerically in steps of \(\mathrm{\mathrm{d}}z = 0.01 \,\mathrm{m}\) with an upper height of 150 m.
Streamwise velocity component scaled by the friction velocity at canopy top as a function of scaled height, comparing data from the wind-tunnel experiment, the NCAR LES and DALES models, as well as the theoretical profile of Harman and Finnigan (2007). For the DALES data, numerical experiment STD is evaluated. The grey area covers the range between minima and maxima during the evaluated time frame for the STD experiment. The canopy top is indicated by a dotted line
3 Results
3.1 Comparison
The first objective of our comparison study is to analyze whether different representations of a neutral flow over a canopy match each other and observational data collected from a laboratory experiment. To this end, the scaled streamwise velocity component profile is depicted in Fig. 2 for the wind-tunnel data, the empirical profile and the flows simulated by the NCAR LES and DALES models. Results are scaled by the friction velocity, \(u_*\), determined at canopy top and height is scaled by the geometric canopy height, \(h_\mathrm{c}\). The profiles are depicted up to the top of the roughness sublayer, which is estimated at a height of \(3 h_\mathrm{c}\) (Harman and Finnigan 2007). In the velocity profile, the inflection point between the in-canopy flow and the RSL, which is characteristic for this type of flow (Brunet et al. 1994; Raupach et al. 1996), is clearly visible at \(z\approx h_\mathrm{c}\).
While differences are discernible, the profiles match each other remarkably well, even though there are various factors that lead to differences between the individual representations. The canopy elements in the wind-tunnel experiment were designed to represent waving wheat rather than (more rigid) trees (Brunet et al. 1994). Moreover, \(\beta \) (i.e. \({u_*}/{u}\) at canopy top) and a constant for integration had to be prescribed a priori for the theoretical profile (\(c_2\) in Harman and Finnigan 2007). Furthermore, the non-uniform \(\textit{PAD}\) distribution in the LES experiments, leading to a height-dependent canopy penetration depth scale, is not consistent with the assumptions of Harman and Finnigan (2007) and affects the displacement height. As a result, the aerodynamically effective canopy height, \(h_\mathrm{e}\), which is defined as the height of the velocity inflection point (Bohrer et al. 2009), is only \(0.9 h_\mathrm{c}\) in the LES experiments, due to the small \(\textit{PAD}\) value at the interface layer at canopy top. That the profiles still match well first confirms the validity of the parametrizations in the LES models. Moreover, the LES profiles are indistinguishable from each other, especially compared to the depicted temporal spread in the DALES results. Second, this figure further corroborates the theoretical profile that was only tested with observational data until now. Even though observational data should be closer to reality, it is also characterized by larger spreads than simulated flows without external disturbances due to e.g. non-stationary conditions and non-uniform canopies. Furthermore, Eq. 4, which is demonstrated here to be valid, demonstrates that, even for a uniform \(\textit{PAD}\) distribution, in the canopy and RSL the depth \(h_\mathrm{c}\) is not the only relevant length scale. The canopy penetration depth determines how rapidly u falls descending from canopy top.
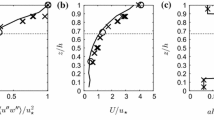
Standard deviations of a u, b v and c w, and d the mean kinetic energy as a function of scaled height. All variables are scaled by the friction velocity at canopy top. Depicted data originates from the wind-tunnel experiment and the NCAR LES and DALES models. For the DALES data, numerical experiment STD is evaluated. The grey areas cover the ranges between minima and maxima during the evaluated time frame for the STD experiment. The canopy top is indicated by a black dotted line. In panels a–c, colored dotted lines denote the explicitly resolved standard deviations
Next to the mean profile, the second-order moments are evaluated. To this end, the scaled standard deviations and mean kinetic energy (MKE) are shown in Fig. 3 up to a height of \(6 h_\mathrm{c}\), which is the highest altitude for which wind-tunnel data are available. Note that the theoretical expression of Harman and Finnigan (2007) only treats the mean u profile and is therefore absent from this figure. For the wind-tunnel data the cross-wind velocity component, v, was not measured. Qualitatively, the two LES experiments compare well to each other and the wind-tunnel data, although, as is common for LES studies (Su et al. 1998; Finnigan et al. 2009), the scaled wind-tunnel data show higher standard deviations than the numerical experiments, especially in the RSL. All standard deviations of \(u_i\) are slightly higher in the NCAR LES experiment than in the base DALES experiment, STD. Differences are small, but significant compared to the temporal spread within the DALES data. We hypothesize that these are due to the contrasting numerical methods. The pseudospectral differences solver for \(u_i\) of the NCAR LES model could retain more fluctuations than the dissipative discrete differences solver of the DALES model due to the more accurate representation of the turbulent cascade in the energy spectra. This hypothesis is tested in Sect. 3.3 by checking whether a finer resolution yields second-order moments that are closer to the NCAR LES results. As the differences between the two LES experiments are small and the profiles are similar to those observed in the wind-tunnel experiment, we conclude that both numerical models capture the neutral flow over a canopy well.
a Momentum flux scaled by the friction velocity at canopy top as a function of scaled height, comparing data from the wind-tunnel experiment and the NCAR LES and DALES models. For the DALES data, numerical experiment STD is evaluated. Additionally, the approximation within the canopy from Eq. 6 is depicted. b The related scaled TKE production by shear. The canopy top is indicated by a dotted line
The momentum flux and associated TKE production by shear is very similar between the NCAR LES model and the STD experiment as well, as shown in Fig. 4a. In the atmospheric boundary layer, momentum is transported down to the canopy, where it is mainly consumed by drag from the canopy elements. For our PAI values, less than 1 % of the momentum flux reaches the surface where the momentum is destroyed by surface drag. In the LES under steady-state conditions, the momentum-flux divergence compensates the source and sink terms for momentum, such as surface drag, canopy drag and external pressure gradients,
where the overbar denotes a horizontal slab-averaged quantity and the weak influence of viscous stress is ignored. Above the canopy, only the external pressure gradient is present, which is spatially invariant, so it follows that \(\overline{u_i'w'}\) increases linearly with height. This increase continues up to the top of the domain on which the external pressure gradient is applied. In the case of the NCAR LES and DALES models, this is equal to the total domain height, i.e. 128 m (\(12.8 h_\mathrm{c}\)). Note that, as a result, the boundary-layer height is imposed by the numerical design of the experiments. Since in the LES model a similar domain height is chosen with respect to \(h_\mathrm{c}\) as the actual boundary-layer height in the wind-tunnel experiment, the simulated and observed flows are still comparable. It is important to note that, even though we scale the height of the profiles by \(h_\mathrm{c}\), in total two other length scales are relevant in the canopy and the flow aloft, i.e. \(L_\mathrm{c}\) and \(z_i\). Therefore, the depicted profiles in characterizations as these are only representative for situations with similar \({L_\mathrm{c}}/{h_\mathrm{c}}\) and \({z_i}/{h_\mathrm{c}}\).
The minimum momentum flux in the LES experiments is not located at the defined geometric (\(h_\mathrm{c}\)) or aerodynamically effective (\(h_\mathrm{e}\)) canopy height, as might be expected, but rather at one interface level above, \(1.1 h_\mathrm{c}\). Due to the four steps transition, a very sparse canopy is present in the grid boxes centered at \(1.05 h_\mathrm{c}\) (i.e. between levels \(i_h\) and \(i_h+1\)) with an a value of 0.0625 times the value within the lower canopy. Even though this sparse canopy extension does not significantly affect the mean wind profile, the resulting negative momentum tendency due to canopy drag is still greater than the positive tendency related to the external pressure gradient. In steady-state conditions, these contributions are therefore compensated by a weak but negative momentum-flux gradient. This interpretation is further corroborated in Sect. 3.2.
In the wind tunnel, in contrast to the LES experiments, the acceleration of the flow is due to the entrainment of air from the freestream, which is characterized by higher momentum. This entrained air does not reach down completely, resulting in a layer of near-constant momentum flux at \(h_\mathrm{c}< z < 2 h_\mathrm{c}\). Above this region, the momentum flux decreases with height. Since the scaled boundary layer is slightly lower in the wind-tunnel experiment and the decrease in magnitude begins at a higher location, the positive momentum-flux gradient above the roughness sublayer is stronger than in the LES numerical experiments.
Within the canopy, the momentum flux increases roughly exponentially in magnitude with height, which is confirmed by evaluating the theoretical profiles and the steady-state momentum balance. The momentum-flux divergence mainly compensates for the canopy drag. Combined with Eqs. 3 and 4 this results in
if a is considered to be constant with height. This exponential profile, labelled Approximation in Fig. 4a, is similar to the momentum-flux profiles of the NCAR LES model and the STD numerical experiment. Note that small deviations are mainly due to the height-dependent a in the LES experiments.
3.2 Canopy Transition
When prescribing a \(\textit{PAD}\) distribution, one has to take into account that sharp transitions from canopy to unobstructed air lead to spurious oscillations that are expressed in fluctuations in the vertical profiles of the velocity components and their standard deviations near canopy top, as mentioned in Sect. 2.1. The influence of the fluctuations is strongest for u and weakest for w. Because of these oscillations, although not explicitly mentioned, Finnigan et al. (2009) already presented their results for a \(\textit{PAD}\) profile according to two steps instead of sharp transition (Table 1). While it remedied most of the fluctuations, their influence can still be discerned in e.g. their Fig. 1b. The updated NCAR LES experiment therefore makes use of the four steps \(\textit{PAD}\) profile, which successfully removes the remaining fluctuations. Here we explore the necessity of deviating from a desired \(\textit{PAD}\) profile by this smoothing of transitions.
a Mean and b standard deviation of the streamwise velocity component, c TKE and d skewness of w, all as a function of scaled height and scaled by the friction velocity at canopy top. Shown are the differences between different PAD transitions (Tables 1, 2). Insets zoom in on the region \({z}/{h_\mathrm{c}} \in \left[ 0.9,1.3\right] \). The canopy top is indicated by a dotted horizontal line. Dotted profiles in panel b denote the explicitly resolved standard deviations
In Fig. 5a,b the effect of the different \(\textit{PAD}\) transitions in the DALES model is presented for the scaled streamwise velocity component and its standard deviation. While the profiles are generally the same for the different configurations, it is confirmed that stronger fluctuations are introduced by more abrupt transitions in the \(\textit{PAD}\) profile. Since this is a numerical effect, only the magnitude and not the occurrence of these fluctuations is dependent on resolution, which will be confirmed in Sect. 3.3. For the sharp transition (experiment TR1) fluctuations are present in both u and \(\sigma _u\), while the inset of Fig. 5b shows that weaker fluctuations remain for \(\sigma _u\) for a transition in two steps (experiment TR2). The more gradual transition in four steps fully remedies the induced fluctuations. For total TKE (Fig. 5c), oscillations are less pronounced than for \(\sigma _u\) and the transition of experiment TR2 results in a smooth, albeit underpredicted, profile in the RSL. Figure 5d shows that the skewness of the vertical velocity component is affected to a lesser degree by the \(\textit{PAD}\) transition and in all cases is similar to NCAR LES data. For atmospheric flows over a canopy in numerical experiments, we conclude the following. One could stay close to any desired \(\textit{PAD}\) distribution to represent the mean velocity profile and the skewness of w, which is related to sweeps and ejections. However, to properly capture second-order moments, including TKE, it is advised to smooth \(\textit{PAD}\) transitions in more than two steps.
As a drawback, the \(\textit{PAD}\) transition smoothing also affects the vertical momentum-flux profile. The momentum flux reaches its minimum at \(z = h_\mathrm{c}\) in the TR1 and TR2 experiments, while it reaches its minimum at the interface layer aloft (\(1.1 h_\mathrm{c}\)) in the STD experiment (\(\overline{u'w'} ({1.1 h_\mathrm{c}}) \approx 1.03 \, \overline{u'w'} ({h_\mathrm{c}})\), not shown). These levels correspond to the lowest level where the prescribed one-sided \(\textit{PAD}=\hbox {zero}\). This corroborates the deduction of Sect. 3.1 that for the evaluated case study a net negative vertical momentum-flux gradient is maintained over the grid cells where a canopy is present, even if very sparse. Additionally the vertical position of the inflection point in u (Fig. 5a) depends on the \(\textit{PAD}\) transition. For experiment TR1, it is located at canopy top, but for the smoothed transitions in experiments TR2 and STD it is located one interface layer below. Considering the magnitudes of the gradients at adjoining levels, the inflection point is positioned slightly above the vertical position where a is half its base value.
a Mean and b standard deviation of the streamwise velocity component scaled by the friction velocity at canopy top as a function of scaled height. Shown are the differences between different resolutions (Table 2). Insets zoom in on the region \({z}/{h_\mathrm{c}} \in \left[ 0.9,1.3\right] \). The canopy top is indicated by a dotted horizontal line. Dotted profiles in panel b denote the explicitly resolved standard deviations
3.3 Resolution
We furthermore evaluate the impact of different vertical and horizontal grid resolutions on the resolved atmospheric flow. To enable a fair comparison with a single consistently applied \(\textit{PAD}\) profile for all vertical resolutions, the sharp transition is prescribed. Note that, because the sharp transition in a occurs between canopy top and the underlying interface layer, a finer (coarser) vertical resolution results in a slightly higher (lower) PAD value in the upper 1 m of the canopy, resulting in lower (higher) normalized values of u and \(\sigma _u\).
Figure 6 shows that in general the differences between the standard resolution of \(0.1 h_\mathrm{c}\) (experiment TR1) and the fine resolution of \(0.05 h_\mathrm{c}\) (experiment RESH) are small. For the finer resolution, the predicted \(\sigma _u\) is slightly higher, which is more consistent with the NCAR LES results (Fig. 3a), but the standard resolution suffices to capture the characteristics of the atmospheric flow. This is confirmed by checking whether inertial subrange scaling is obeyed (Sullivan and Patton 2011), which is the case if \(\frac{\root 3 \of {\varDelta }}{\sqrt{e}}\) is independent of resolution. Here, \(\varDelta = \root 3 \of {\varDelta x \varDelta y \varDelta z}\) and e is the subgrid TKE. Above the canopy, this relation is indeed fulfilled, indicating that the dissipation of TKE is independent of the grid resolution (Sullivan and Patton 2011). Inside the canopy, there is a dependence of the dissipation on grid resolution, but since the destruction of TKE is dominated by canopy drag there, this does not lead to large deviations.
On the other hand, the use of a coarser resolution (\(0.2 h_\mathrm{c}\); experiment RESL) results in strong deviations and a noticeably worse performance. The intermediate solution between the coarse and standard solution, an anisotropic grid with a \(0.2 h_\mathrm{c}\) spacing in the horizontal directions and a \(0.1 h_\mathrm{c}\) spacing in the vertical direction (experiment RESA), does not remedy these deviations. In the roughness sublayer above the canopy, the profiles of u and \(\sigma _u\) even deviate considerably more from the profiles of the RESH experiment than for the coarse resolution. We conclude that it is ill advised to apply anisotropic grids in this numerical model for this type of atmospheric flows.
The spurious oscillations, as discussed in Sect. 3.2, are similar in magnitude for numerical experiments RESA and TR1, while they are weaker and stronger in numerical experiments RESH and RESL, respectively. This indicates that, although the fluctuations are manifest in the horizontal wind components, only the vertical resolution determines their amplitude. This corroborates that the fluctuations originate from the numerical artefacts.
As hypothesized in Sect. 3.1, a finer resolution yields second-order moments that are higher and thus closer to the NCAR LES results, confirming that the differences in simulated TKE are due to the contrasting numerical methods. Therefore, to even better reproduce the NCAR LES second-order moments than with the STD experiment, one would have to apply a finer resolution, while prescribing an equivalently smooth \(\textit{PAD}\) profile. This is corroborated by numerical experiment COMB, whose resulting u and \(\sigma _u\) profiles are shown in Fig. 7. Indeed, even though u is higher in the RSL, the resulting \(\sigma _u\) profile is more similar to the NCAR LES data than the STD numerical experiment. However, note that in LES experiments in general skewness is affected by resolution (e.g., Sullivan and Patton 2011), in the evaluated case leading to more negative skewness in the canopy layer (not shown).
a Mean and b standard deviation of the streamwise velocity component scaled by the friction velocity at canopy top as a function of scaled height. NCAR LES data is compared to DALES simulations with the finest PAD transition and the two finest resolutions (Table 2). Insets zoom in on the region \(\frac{z}{h_\mathrm{c}} \in \left[ 0.9,1.3\right] \). The canopy top is indicated by a dotted horizontal line. Dotted profiles in panel b denote the explicitly resolved standard deviations
3.4 Quadrant Analyses
Finally, we investigate how organized the transport of momentum is, by making use of quadrant analyses of the atmospheric flow up to twice the canopy height. Results are presented for the STD numerical experiment, but are similar for the other simulations. Data are sampled into four quadrants based on the signs of \(u'\) and \(w'\) (Sect. 2.2.1). Most frequent (not shown) are periods of ejections (Q2; 30–41 %), followed by the periods of sweeps (Q4; 27–32 %). Less common are outward (Q1; 13–24 %) and inward (Q3; 14–19 %) interactions. These percentages are consistent with previously published frequencies of occurrence in and just above the canopy (e.g., Yue et al. 2007).
To calculate the momentum fluxes within each quadrant the absolute velocities, \(u_i\), or the velocities relative to the horizontal slab average, \(u_{i,r} \equiv u_i'\), could be sampled. The former method stems from splitting the total momentum flux, \(\overline{u\,w}\), into different contributions, while the latter method is based on splitting the turbulent momentum flux, \(\overline{u'\,w'}\). In line with previous studies (Yue et al. 2007), we present the results using \(u_r\) for the fluxes in each quadrant. Within each quadrant, averages of any arbitrary variable, \(\phi \), are denoted by \(\langle \phi \rangle \) and deviations are denoted by \(\phi ''\).
By definition of the quadrants \(\langle u_r w\rangle \) is positive for the interactions quadrants Q1 and Q3 and negative for quadrants Q2 and Q4. The magnitude and contribution of the momentum flux within each quadrant are depicted in Fig. 8. The turbulent momentum fluxes that are sampled during sweeps and ejections individually are greater than the net domain-averaged momentum flux, while the momentum fluxes that are sampled during interactions are only larger than that in the lower part of the canopy. Even though ejections occur more frequently than sweeps, the sweeps contribute more to the total momentum flux in the canopy and lower RSL due to the greater fluxes during those periods. As discussed below, this is mainly caused by the higher \(\left| \langle u_r \rangle \right| \) (20 %) and \(|\langle w \rangle |\) (25 %) during the sweeps compared to the ejections. At canopy top, the ejections make up for 50 % of the total (negative) momentum flux and the sweeps for 65 %. The excess over 100 % is compensated by the (positive) momentum-flux contributions of the inward and outward interactions. These findings are comparable with previous studies (Yue et al. 2007). However, while Yue et al. (2007) suggested that the contributions of the interactions to the total turbulent momentum flux are mainly smaller than those of the sweeps and ejections due to the less frequent occurrence, we find that the lower \(\langle u_r w \rangle \) in the interactions compared to the sweeps and ejections is at least as influential.
Contribution of the advective momentum flux within each quadrant to a the total momentum flux in that quadrant and b the total domain-averaged momentum flux. The purple line depicts the combined contributions of all quadrants (weighted by frequency of occurrence) and is compared in b with the domain-averaged momentum flux. The canopy top is indicated by a dotted horizontal line
Here we compare the momentum flux within each quadrant to the kinematic mass-flux approach (Siebesma and Cuijpers 1995). Within each quadrant, the fluctuations in \(u_r\) and w are well below the fluctuations over all data. As a result, the advective contribution, \(\langle u_r \rangle \langle w \rangle \), makes up for the majority (\(\approx \)80–95 % for sweeps and ejections) of the total momentum flux within a quadrant, \(\langle u_r w \rangle \). This is shown in more detail in Fig. 9a. When only considering the advective fluxes within each quadrant, 84 % of the total turbulent momentum flux is represented at canopy top. Figure 9b suggests that a decomposition similar to the kinematic mass-flux approach could be applied for a first-order estimate of the momentum flux,
by only conditionally sampling mean values for \(u_r\) and w. f is the frequency of occurrence of the respective quadrant. The compensated difference between \(\overline{u'w'}\) and \(\sum _\mathrm{quadrant} f \langle u_r \rangle \langle w \rangle \) is due to the contributions of the turbulent momentum flux within each quadrant, \(\langle u_r''w'' \rangle \), which are all negative.
4 Conclusions
We have compared different representations of a neutral atmospheric flow over roughness elements simulating a vegetation canopy. Special attention was dedicated to analyzing the consistency between the state-of-the-art portrayals based on wind-tunnel observations, empirical flux-gradient relationships and LES modelling. After establishing the validity of the depiction by the Dutch Atmospheric Large-Eddy Simulation (DALES) model, sensitivity analyses have been performed with this model to different conditions in order to check the robustness of the representation and to determine the requirements for these conditions to capture this flow. The evaluated case is based on data from a wind-tunnel experiment (Brunet et al. 1994) and our results can be used as a standard for future comparison studies on neutral flows over vegetation canopy. By selecting a neutral flow, the effects of vegetation on the turbulence and velocity profiles are not masked by buoyancy-induced destruction or generation of TKE.
Even though the representation in the LES models and the adaptations to the empirical flux-gradient relationships were derived independently and different assumptions were made, the resulting normalized velocity profiles are nearly identical to both each other and the wind-tunnel data. This strengthens confidence in the validity of using either one to represent the effects of vegetation on a neutral atmospheric flow and demonstrates that normalizing by the canopy height and friction velocity at canopy top results in universally applicable profiles if the ratios of the canopy penetration depth and boundary-layer height compared to the canopy height are kept the same. Moreover, the interpretation of features that are diagnosed in a specific representation can be supported by analyzing the alternative representations. As an example, the simulated shape of the momentum-flux profile in the canopy layer can be explained and reproduced by considering the relevant contributions to the momentum budget and the empirical velocity profile.
Furthermore, the velocity variances and vertical momentum flux were compared between wind-tunnel and LES data only, since these are not explicitly predicted by the available flux-gradient relationships. While the profiles are very similar in the canopy layer, aloft noteworthy deviations appear for the wind-tunnel data, which is most likely caused by the differently applied forcing to accelerate the flow. The numerical LES experiments employ a height-independent horizontal pressure gradient, whereas the flow is accelerated by entrainment from the freestream in the wind tunnel. Between the two different LES codes, the momentum flux is nearly identical, while above the canopy the standard deviations of the different velocity components are slightly higher for the pseudospectral code of the NCAR LES model than for the finite-volume code of the DALES model. This minor discrepancy, related to the distinct numerical differences schemes, can be resolved by applying a finer resolution to the DALES model.
In the numerical models the transition in the one-sided plant-area density profile from canopy to unobstructed air affects the flow. Sharp transitions result in fluctuations in the streamwise velocity component and its standard deviation. These spurious oscillations cannot be prevented by applying a different resolution, but do scale in magnitude with the vertical resolution. By spreading the transition over four steps, all fluctuations are successfully remedied. The deviation of the applied plant-area density profile from the assumed one for the empirical expressions, i.e. constant within the canopy and zero above, results in shifts in the heights of the inflection point, i.e. aerodynamically effective canopy height, (lower) and minimum momentum flux (higher) compared to the level of the canopy top.
For the evaluated flow, we found that an isotropic resolution of \(0.1 h_\mathrm{c}\) suffices to capture the most relevant dynamics in and above the canopy. A finer resolution does contribute to remedy the differences in wind velocity standard deviations between the two evaluated numerical models, but does not affect the mean flow properties. Applying an anisotropic grid, with coarser resolution in the horizontal directions, is not recommended as it does not yield better results than applying the coarse resolution in all directions.
The quadrant analyses of the vertical profiles were consistent with previous studies and confirmed the importance of organized structures, i.e. sweeps and ejections, for vertical exchange. Moreover, they resulted in the new insight that most momentum transport is associated to the mean properties (i.e. advective flux) within each quadrant, while the turbulent contributions within each quadrant make up for less than 20 % of the total vertical momentum flux at canopy top. As a result, similar to the kinematic mass-flux approach, sampled mean velocities in each quadrant could be used to approximate the total vertical momentum flux. Considering the link to the relaxed eddy accumulation technique (e.g., Businger and Oncley 1990), we recommend this to be further investigated in future studies, including as well the vertical exchange of heat and atmospheric constituents.
References
Bohrer G, Katul GG, Walko RL, Avissar R (2009) Exploring the effects of microscale structural heterogeneity of forest canopies using large-eddy simulations. Boundary-Layer Meteorol 132:351–382. doi:10.1007/s10546-009-9404-4
Böing SJ, Jonker HJJ, Nawara WA (2014) On the deceiving aspects of mixing diagrams of deep cumulus convection. J Atmos Sci 71:56–68. doi:10.1175/JAS-D-13-0127.1
Brunet Y, Finnigan JJ, Raupach MR (1994) A wind tunnel study of air flow in waving wheat: single-point velocity statistics. Boundary-Layer Meteorol 70:95–132. doi:10.1007/BF00712525
Businger JA, Oncley SP (1990) Flux measurement with conditional sampling. J Atmos Ocean Technol 7:349–352. doi:10.1175/1520-0426(1990)007<0349:FMWCS>2.0.CO;2
Cassiani M, Katul GG, Albertson JD (2008) The effects of canopy leaf area index on airflow across forest edges: large-eddy simulation and analytical results. Boundary-Layer Meteorol 126:433–460. doi:10.1007/s10546-007-9242-1
Cellier P, Brunet Y (1992) Flux–gradient relationships above tall plant canopies. Agric For Meteorol 58:93–117. doi:10.1016/0168-1923(92)90113-I
de Ridder K (2010) Bulk transfer relations for the roughness sublayer. Boundary-Layer Meteorol 134:257–267. doi:10.1007/s10546-009-9450-y
Deardorff JW (1980) Stratocumulus-capped mixed layers derived from a three dimensional model. Boundary-Layer Meteorol 18:495–527. doi:10.1007/BF00119502
Dupont S, Brunet Y (2008) Influence of foliar density profile on canopy flow: a large-eddy simulation study. Agric For Meteorol 148:976–990. doi:10.1016/j.agrformet.2008.01.014
Finnigan JJ, Shaw RH (2000) A wind-tunnel study of airflow in waving wheat: an EOF analysis of the structure of the large-eddy motion. Boundary-Layer Meteorol 96:211–255. doi:10.1023/A:1002618621171
Finnigan JJ, Shaw RH, Patton EG (2009) Turbulence structure above a vegetation canopy. J Fluid Mech 637:387–424. doi:10.1017/S0022112009990589
Garratt JR (1983) Surface influence upon vertical profiles in the nocturnal boundary layer. Boundary-Layer Meteorol 26:69–80. doi:10.1007/BF00164331
Harman IN, Finnigan JJ (2007) A simple unified theory for flow in the canopy and roughness sublayer. Boundary-Layer Meteorol 123:339–363. doi:10.1007/s10546-006-9145-6
Harman IN, Finnigan JJ (2008) Scalar concentration profiles in the canopy and roughness sublayer. Boundary-Layer Meteorol 129:323–351. doi:10.1007/s10546-008-9328-4
Heus T, van Heerwaarden CC, Jonker HJJ, Siebesma AP, Axelsen S, van den Dries K, Geoffroy O, Moene A, Pino D, de Roode SR, Vilà-Guerau de Arellano J (2010) Formulation of the Dutch Atmospheric Large-Eddy Simulation (DALES) and overview of its applications. Geosci Model Dev 3:415–444. doi:10.5194/gmd-3-415-2010
Katul GG, Albertson JD (1998) An investigation of higher-order closure models for a forested canopy. Boundary-Layer Meteorol 89:47–74. doi:10.1023/A:1001509106381
Lu SS, Willmarth WW (1973) Measurements of the structure of the reynolds stress in a turbulent boundary layer. J Fluid Mech 60:481–511. doi:10.1017/S0022112073000315
Maurer KD, Bohrer G, Kenny WT, Ivanov VY (2015) Large-eddy simulations of surface roughness parameter sensitivity to canopy-structure characteristics. Biogeosciences 12:2533–2548. doi:10.5194/bg-12-2533-2015
Mölder M, Grelle A, Lindroth A, Halldin S (1999) Flux-profile relationships over a boreal forest—roughness sublayer corrections. Agric For Meteorol 98–99:645–658. doi:10.1016/S0168-1923(99)00131-8
Nieuwstadt FTM, Brost RA (1986) The decay of convective turbulence. J Atmos Sci 43:532–545. doi:10.1175/1520-0469(1986)043<0532:TDOCT>2.0.CO;2
Ouwersloot HG, Vilà-Guerau de Arellano J, van Heerwaarden CC, Ganzeveld LN, Krol MC, Lelieveld J (2011) On the segregation of chemical species in a clear boundary layer over heterogeneous land surfaces. Atmos Chem Phys 11:10,681–10,704. doi:10.5194/acp-11-10681-2011
Pan Y, Chamecki M, Isard SA (2014) Large-eddy simulation of turbulence and particle dispersion inside the canopy rougness sublayer. J Fluid Mech 753:499–534. doi:10.1017/jfm.2014.379
Patton EG, Sullivan PP, Davis KJ (2003) The influence of a forest canopy on top-down and bottom-up diffusion in the planetary boundary layer. Q J R Meteorol Soc 129:1415–1434. doi:10.1256/qj.01.175
Patton EG, Sullivan PP, Moeng CH (2005) The influence of idealized heterogeneity on wet and dry planetary boundary layers coupled to the land surface. J Atmos Sci 62:2078–2097. doi:10.1175/JAS3465.1
Raupach MR (1992) Drag and drag partition on rough surfaces. Boundary-Layer Meteorol 60:375–395. doi:10.1007/BF00155203
Raupach MR, Finnigan JJ, Brunet Y (1996) Coherent eddies and turbulence in vegetation canopies: the mixing-layer analogy. Boundary-Layer Meteorol 78:351–382. doi:10.1007/BF00120941
Shaw RH, Patton EG (2003) Canopy element influences on resolved- and subgrid-scale energy within a large-eddy simulation. Agric For Meteorol 115:5–17. doi:10.1016/S0168-1923(02)00165-X
Siebesma AP, Cuijpers JW (1995) Evaluation of parametric assumptions for shallow cumulus convection. J Atmos Sci 52:650–666. doi:10.1175/1520-0469(1995)052<0650:EOPAFS>2.0.CO;2
Su HB, Shaw RH, Paw UKT, Moeng CH, Sullivan PP (1998) Turbulent statistics of neutrally stratified flow within and above a sparse forest from large-eddy simulation and field observations. Boundary-Layer Meteorol 88:363–397. doi:10.1023/A:1001108411184
Sullivan PP, Patton EG (2011) The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation. J Atmos Sci 68:2395–2415. doi:10.1175/JAS-D-10-05010.1
Thom AS, Stewart JB, Oliver HR, Gash JHC (1975) Comparison of aerodynamic and energy budget estimates of fluxes over a pine forest. Q J R Meteorol Soc 101:93–105. doi:10.1002/qj.49710142708
Vilà-Guerau de Arellano J, Ouwersloot HG, Baldocchi D, Jacobs CMJ (2014) Shallow cumulus rooted in photosynthesis. Geophys Res Lett 41:1796–1802. doi:10.1002/2014GL059279
Yue W, Meneveau C, Parlange MB, Zhu W, van Hout R, Katz J (2007) A comparitive quadrant analysis of turbulence in a plant canopy. Water Resour Res 43(W05):422. doi:10.1029/2006WR005583
Acknowledgments
Open access funding provided by Max Planck Institute for Chemistry. The authors gratefully acknowledge Dr. E. G. Patton for inspiring discussions and for providing data and numerical code.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ouwersloot, H.G., Moene, A.F., Attema, J.J. et al. Large-Eddy Simulation Comparison of Neutral Flow Over a Canopy: Sensitivities to Physical and Numerical Conditions, and Similarity to Other Representations. Boundary-Layer Meteorol 162, 71–89 (2017). https://doi.org/10.1007/s10546-016-0182-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-016-0182-5