Skip to main content
SpringerLink
Log in

Proximal gradient algorithm for nonconvex low tubal rank tensor recovery

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

Abstract

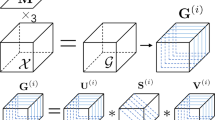
In this paper, we consider the three-order tensor recovery problem within the tensor tubal rank framework. Most of the recent studies under this framework can not handle the tubal rank directly due to its numerical challenges, while approximating it using various surrogate functions. Although the optimization models derived from these approximation methods are relatively easy to solve, their results can be substantially suboptimal. In this study, we discover that the proximal operator of the tubal rank can be explicitly solved. Then, without relaxing the tubal rank, an efficient proximal gradient algorithm is proposed to directly solve the tensor recovery problem. We establish the convergence properties of the proposed method and present an adaptive strategy for parameter selection. Experimental results on synthetic and real-world data demonstrate the superior performance of the proposed method over several widely used state-of-the-art methods in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

Code availability

The code generated during the current study are not publicly available but are available from the corresponding author on reasonable request.

References

  1. Candes, E., Romberg, J., Tao, T.: Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52(2), 489–509 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  2. Donoho, D.: Compressed sensing. IEEE Trans. Inf. Theory 52(4), 1289–1306 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  3. Candès, E., Recht, B.: Exact matrix completion via convex optimization. Found. Comput. Math. 9, 717–772 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  4. Davenport, M., Romberg, J.: An overview of low-rank matrix recovery from incomplete observations. IEEE J. Sel. Top. Signal Process. 10(4), 608–622 (2016)

    Article  Google Scholar 

  5. Bentbib, A., Khouia, A., Sadok, H.: Color image and video restoration using tensor CP decomposition. BIT Numer. Math. 62(4), 1257–1278 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  6. Kapushev, Y., Oseledets, I., Burnaev, E.: Tensor completion via Gaussian process-based initialization. SIAM J. Sci. Comput. 42, 3812–3824 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  7. Jiang, T., Huang, T., Zhao, X., Deng, L.: Multi-dimensional imaging data recovery via minimizing the partial sum of tubal nuclear norm. J. Comput. Appl. Math. 372, 112680 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  8. Qian, C., Fu, X., Sidiropoulos, N., Yang, Y.: Tensor-based channel estimation for dual-polarized massive MIMO systems. IEEE Trans. Signal Process. 66, 6390–6403 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  9. Huang, Y., Liao, G., Zhang, L., Xiang, Y., Li, J., Nehorai, A.: Efficient narrowband RFI mitigation algorithms for SAR systems with reweighted tensor structures. IEEE Trans. Geosci. Remote Sens. 57, 9396–9409 (2019)

    Article  Google Scholar 

  10. Song, G., Ng, M., Zhang, X.: Robust tensor completion using transformed tensor singular value decomposition. Numer. Linear Algebra Appl. 27, 2299 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhou, P., Lu, C.Y., Feng, J.S., Lin, Z.C., Yan, S.C.: Tensor low-rank representation for data recovery and clustering. IEEE Trans. Pattern Anal. Mach. Intell. 43(5), 1718–1732 (2021)

    Article  Google Scholar 

  12. Luo, Y., Zhao, X., Jiang, T., Chang, Y., Ng, M., Li, C.: Self-supervised nonlinear transform-based tensor nuclear norm for multi-dimensional image recovery. IEEE Trans. Image Process. 31, 3793–3808 (2022)

    Article  Google Scholar 

  13. Lu, C., Feng, J., Chen, Y., Liu, W., Lin, Z., Yan, S.: Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 42(4), 925–938 (2020)

    Article  Google Scholar 

  14. Ballani, J., Kressner, D.: Reduced basis methods: from low-rank matrices to low-rank tensors. SIAM J. Sci. Comput. 38(4), 2045–2067 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  15. Kolda, T., Bader, B.: Tensor decompositions and applications. SIAM Rev. 51, 455–500 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  16. Tucker, L.: Some mathematical notes on three-mode factor analysis. Psychometrika 31, 279–311 (1966)

    Article  MathSciNet  Google Scholar 

  17. Oseledets, I.V.: Tensor-train decomposition. SIAM J. Sci. Comput. 33, 2295–2317 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Kilmer, M., Braman, K., Hao, N., Hoover, R.: Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 34, 148–172 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Kilmer, M., Martin, C.: Factorization strategies for third-order tensors. Linear Algebra Appl. 435, 641–658 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kilmer, M., Horesh, L., Avron, H., Newman, E.: Tensor-tensor algebra for optimal representation and compression of multiway data. Proc. Natl. Acad. Sci. U.S.A. 118(28), 2015851118 (2021)

    Article  MathSciNet  Google Scholar 

  21. Kernfeld, E., Kilmer, M., Aeron, S.: Tensor-tensor products with invertible linear transforms. Linear Algebra Appl. 485, 545–570 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Lu, C., Peng, X., Wei, Y.: Low-rank tensor completion with a new tensor nuclear norm induced by invertible linear transforms. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 5989–5997 (2019)

  23. Wang, H., Zhang, F., Wang, J., Huang, T., Huang, J., Liu, X.: Generalized nonconvex approach for low-tubal-rank tensor recovery. IEEE Trans. Neural Netw. Learn. Syst. 33(8), 3305–3319 (2022)

    Article  MathSciNet  Google Scholar 

  24. Soltani, S., Kilmer, M.E., Hansen, P.C.: A tensor-based dictionary learning approach to tomogrephic image reconstruction. BIT Numer. Math. 56, 1425–1454 (2016)

    Article  MATH  Google Scholar 

  25. Rauhut, H., Stojanac, Z.: Tensor theta norms and low rank recovery. Numerical Algorithms 88, 25–66 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang, A., Lai, Z., Jin, Z.: Noisy low-tubal-rank tensor completion. Neurocomputing 330, 267–279 (2019)

    Article  Google Scholar 

  27. Shi, C., Huang, Z., Wan, L., Xiong, T.: Low-rank tensor completion based on Log-Det rank approximation and matrix factorization. J. Sci. Comput. 80, 1888–1912 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  28. Liu, X., Aeron, S., Aggarwal, V., Wang, X.: Low-tutal-rank tensor completion using alternating minimization. IEEE Trans. Inf. Theory 66(3), 1714–1737 (2020)

    Article  MATH  Google Scholar 

  29. Zhang, Z., Aeron, S.: Exact tensor completion using t-SVD. IEEE Trans. Signal Process. 65, 1511–1526 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  30. Li, T., Ma, J.: T-SVD based non-convex tensor completion and robust principal component analysis. In: 2020 25th International Conference on Pattern Recognition (ICPR), pp. 6980–6987 (2021)

  31. Zhang, X., Ng, M.: Low rank tensor completion with poisson observations. IEEE Trans. Pattern Anal. Mach. Intell. 44(8), 4239–4251 (2021)

    Google Scholar 

  32. Zhang, Z., Ely, G., Aeron, S., Hao, N., Kilmer, M.: Novel methods for multilinear data completion and de-noising based on tensor-SVD. In: IEEE Conference on Computer Vision and Pattern Recognition, pp. 3842–3849 (2014)

  33. Chen, L., Jiang, X., Liu, X., Zhou, Z.: Robust low-rank tensor recovery via nonconvex singular value minimization. IEEE Trans. Image Process. 29, 9044–9059 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. Zhao, X., Bai, M., Ng, M.: Nonconvex optimization for robust tensor completion from grossly sparse observations. J. Sci. Comput. 85(2), 46 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  35. Yang, M., Luo, Q., Li, W., Xiao, M.: Multiview clustering of images with tensor rank minimization via nonconvex approach. SIAM J. Imaging Sci. 13, 2361–2392 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  36. Zhang, X., Ng, M.: A corrected tensor nuclear norm minimization method for noisy low-rank tensor completion. SIAM J. Imaging Sci. 12(2), 1231–1273 (2019)

    Article  MathSciNet  Google Scholar 

  37. Beck, A.: First-order Methods in Optimization. SIAM Society for Industrial and Applied Mathematics, Philadelphia, PA (2017)

    Book  MATH  Google Scholar 

  38. Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2, 183–202 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  39. Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Lojasiewicz inequality. Math. Oper. Res. 35, 438–457 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  40. Attouch, H., Bolte, J., Svaiter, B.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Math. Program. 137(1–2), 91–129 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  41. Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146, 459–494 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  42. Newman, E., Kilmer, M.: Nonnegative tensor patch dictionary approaches for image compression and deblurring applications. SIAM J. Imaging Sci. 13(3), 1084–1112 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  43. Golub, G.H., Van Loan, C.F.: Matrix Computation, 4th edn. The Johns Hopkins University Press, Baltimore (2013)

    Book  MATH  Google Scholar 

  44. Martin, D., Fowlkes, C., Tal, D., Malik, J.: A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: 8th IEEE International Conference on Computer Vision (ICCV 2001), vol. 2, pp. 416–423 (2001)

Download references

Funding

This work is supported by the National Natural Science Foundation of China (No. 11701538 and No. 11871444) and the Fundamental Research Funds for the Central Universities (No. 202264006).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Ocean University of China, Qingdao, 266100, China

    Yanhui Liu, Xueying Zeng & Weiguo Wang

Authors
  1. Yanhui Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xueying Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Weiguo Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Yanhui Liu, Xueying Zeng and Weiguo Wang. The first draft of the manuscript was written by Yanhui Liu and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Xueying Zeng.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

All authors agreed with the content and that all gave explicit consent to submit and that they obtained consent from the responsible authorities at the organization where the work has been carried out, before the work is submitted.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Y., Zeng, X. & Wang, W. Proximal gradient algorithm for nonconvex low tubal rank tensor recovery. Bit Numer Math 63, 25 (2023). https://doi.org/10.1007/s10543-023-00964-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10543-023-00964-0

Keywords

Mathematics Subject Classification

Search

Navigation