1 Introduction

In comparison to normal integer derivatives, fractional derivatives include a memory effect, which is advantageous when modeling real materials in mechanics and electronics, as well as in the description of rheological properties of solids [26]. Other applications where this memory effect is important include modeling of speech [6], bioengineering [20], fluid dynamics [16] and finance [29]. There are several formulations of fractional derivatives, and the most common ones are Riemann-Lioville’s, Grünwald-Letnikov’s and Caputo’s formulation [25].

Fractional differential equations (FDEs) extend ordinary differential equations by introducing or replacing the integer order derivatives with fractional derivatives. The Caputo derivative is suitable when modeling real physical problems, since it requires integer (and not fractional) order of the derivative as initial condition in FDEs. Together with a closed quadrature rule (including both end-points), the finite-difference approximation is a common approach for evaluating the Caputo fractional derivative.

High-order methods for the Caputo fractional derivative have been developed in [8, 19] where the order is \(3-\alpha \) and in [22] of order \(4-\alpha \). Another approach for the Caputo fractional derivative based on quadratic interpolation and compact operators, which obtain convergence rates of \(3-\alpha \), is presented in [12]. In [10], a similar procedure for the diffusion-wave equation (\(1< \alpha < 2\)) obtained a convergence rate of \(4-\alpha \). In [24], Odibat presents a modification of the Trapezoidal rule for approximating the fractional integral and Caputo derivative to second order. A convergent scheme for the diffusion-wave equation where the truncation error depends on the fraction of the derivative (usually denoted by \(\alpha )\) was derived in [31]. Similar error estimates are found in [18, 23]. A comprehensive review of finite difference methods and the relation between accuracy, stability and treatment of boundary conditions is provided in [32], where order reduction in numerical approximations is observed at the boundaries.

Fractional derivatives can be used to form FDEs but also stand alone, for example when used in a \(PI^\lambda D^\mu \) controller [26]. FDEs are a special type of Volterra equations with weakly singular kernels [13]. To treat the singularity, different strategies can be employed such as graded meshes or transformations [7, 14, 27] Other numerical methods include non-polynomial spline methods [17], spectral methods [11, 33], piecewise constant approximation or integrabilization methods [3, 4] and the discrete time random walk approach [1, 2, 5]. Yet, another strategy, which we use in this article, is integration by parts. This bypasses the singularity already in the continuous setting, but requires additional smoothness of the integrand.

High-order methods are beneficial when accurate solutions to partial differential equations is the target [15]. They heavily rely on stable and accurate weak boundary and interface conditions, which summation-by-parts operators (SBP) together with the Simultaneous-Approximation-Term technique (SAT) provide for finite differences [9]. We will in this work illustrate that the approximation of the individual components of the fractional derivative (integral, convolution kernel and integrand) by SBP operators yields a concise numerical approximation of the fractional derivative. This enables results from the extensive SBP literature [9] to be employed to fractional order problems.

In this note, we examine a methodology for numerically computing the Caputo fractional derivative of smooth functions with non-singular derivatives by approximating the expression component-wise using a quadrature for the integral and an appropriate discretization of the integrand using SBP operators. Of particular interest is the limitations of the convergence rates for closed quadratures and the influence of the parameter \(\alpha \) as observed in the references above. We do not intend to develop a new numerical method, but rather aim to edify the source of the reduced accuracy obtained from traditional quadrature methods. Moreover, we illustrate the dependence of the convergence rate on the position within the domain, most appreciably so when the quadrature domain approaches the singularity in the integration kernel. Finally we show how to increase accuracy for smooth functions, and compensate for the order dependent loss. The insights provided herein may lead to the development of robust and more accurate quadrature methods for integrals of this nature.

2 Fractional calculus preliminaries

All preliminaries presented here can be found in [26]. The fractional integral is defined as

$$\begin{aligned} I_{0, t}^{\alpha } f(t) = \frac{1}{\Gamma (\alpha )} \int _{0}^{t}(t-\tau )^{\alpha -1} f(\tau ) \textrm{d} \tau , \end{aligned}$$
(2.1)

where \(\Gamma (\alpha ) = \int _{0}^{\infty } z^{\alpha -1} e^{-z} dz\) is the Gamma function. The Caputo derivative is given by

$$\begin{aligned} {}_\textrm{C} D_{0, t}^{\alpha } f(t)=I_{0, t}^{(m-\alpha )} \frac{\textrm{d}^{m}}{\textrm{d} t^{m}} f(t)=\frac{1}{\Gamma (m-\alpha )} \int _{0}^{t}(t-\tau )^{m-\alpha -1} f^{(m)}(\tau ) \textrm{d} \tau , \end{aligned}$$
(2.2)

where \(m-1< \alpha < m\). For \(0< \alpha < 1\), (2.2) simplifies to

$$\begin{aligned} D ^\alpha f(t) = {}_C D_{0,t}^{\alpha } f(t) = \frac{1}{\Gamma (1-\alpha )} \int _{0}^{t}(t-\tau )^{-\alpha } f'(\tau ) \textrm{d} \tau \, , \end{aligned}$$
(2.3)

where the first equality is introduced to ease the notation for the upcoming analysis. In this work we only consider the case of \(m=1\). This is justified by the possibility of decomposing a higher order fractional derivative into a system of first and \(\alpha \)th (\(0< \alpha <1\)) order differential equations.

3 The reduction of accuracy in quadrature

This section illustrates the common reduction of order in quadrature methods when approximating the convolution integral of the fractional derivative. Considering the domain \(\tau \in [0,t]\), with uniform discretisation \({\varvec{\tau }} = \{0, \Delta \tau , \ldots , t- \Delta \tau , t\}\), we show that \(\mathscr {O}(\Delta \tau ^{1-\alpha })\) terms cannot be avoided or cancelled by any Newton–Cotes quadrature. This claim is proved in Sect. 4.

We begin by considering the convolution integral

$$\begin{aligned} \int _{0}^{t}(t-\tau )^{-\alpha } f'(\tau ) \textrm{d} \tau = \int _{0}^{\Delta \tau }(t-\tau )^{-\alpha } f'(\tau ) \textrm{d} \tau + \cdots \int _{t-\Delta \tau }^{t}(t-\tau )^{-\alpha } f'(\tau ) \textrm{d} \tau \, .\nonumber \\ \end{aligned}$$
(3.1)

We parameterise the integration limits and consider an arbitrary ‘sub’ integral subject to the general integration limits \(\tau \in [a,b]\), such that \(b-a = \Delta \tau \). This enables the change in behaviour as \(b \rightarrow t\) to be quantified. Explicitly this integral is

$$\begin{aligned} \int _a^b (t-\tau )^{-\alpha }f'(\tau ) d\tau = \int _a^b g(\tau ) d\tau , \end{aligned}$$
(3.2)

where \(g(\tau ) = (t-\tau )^{-\alpha }f'(\tau )\). We now replace the integrand \(g(\tau )\) with the Taylor series of this function expanded around the midpoint of the integral domain, \(\tilde{\tau } = \frac{a+b}{2}\), yielding

$$\begin{aligned} g(\tau ) = g\left( \tilde{\tau }\right) +\left( \tau -\tilde{\tau }\right) g'\left( \tilde{\tau }\right) +\frac{1}{2} \left( \tau -\tilde{\tau }\right) ^2 g''\left( \tilde{\tau }\right) +\mathscr {O}\left( \left( \tau -\tilde{\tau }\right) ^3\right) . \end{aligned}$$
(3.3)

This expansion is a valid use of the Taylor series since we never explicitly evaluate \(g(\tau )\) (or any derivatives of \(g(\tau )\)) at \(\tau =t\) where we have a singularity. We now compute the integral in (3.2) with \(\Delta \tau = b-a\), to obtain,

$$\begin{aligned} \int _a^b g(\tau ) d\tau&= \Delta \tau g\left( \tilde{\tau }\right) +\frac{1}{24} \Delta \tau ^3 g''\left( \tilde{\tau }\right) +\frac{\Delta \tau ^5}{1920} g^{(4)}\left( \tilde{\tau }\right) +\frac{\Delta \tau ^7 }{322560} g^{(6)}\left( \tilde{\tau }\right) + \cdots , \nonumber \\&= \sum _{i=0}^{\infty } \frac{\Delta \tau ^{2i+1}}{2^{2 i}(2i+1)!} g^{(2 i)}(\tilde{\tau }) \nonumber \\&= \sum _{j\text { even}}^{} \frac{\Delta \tau ^{j+1}}{2^{j}(j+1)!} g^{(j)}(\tilde{\tau }), \end{aligned}$$
(3.4)

noting that the integral of odd derivative terms is zero, due to the expansion around the midpoint of the domain.

We may construct a quadrature (trapezoidal) to cancel the leading term in Eq. (3.4) using

$$\begin{aligned} g(a)&= g\left( \tilde{\tau }\right) -\frac{1}{2} \Delta \tau g'\left( \tilde{\tau }\right) +\frac{1}{8}\Delta \tau ^2 g''\left( \tilde{\tau }\right) +\cdots , \end{aligned}$$
(3.5)
$$\begin{aligned} g(b)&= g\left( \tilde{\tau }\right) +\frac{1}{2} \Delta \tau g'\left( \tilde{\tau }\right) +\frac{1}{8}\Delta \tau ^2 g''\left( \tilde{\tau }\right) +\cdots , \end{aligned}$$
(3.6)

noting that the error, E, is then given by,

$$\begin{aligned} E= & {} \int _a^b g(\tau ) d\tau - \Delta \tau \left( \frac{g(a)+g(b)}{2}\right) \nonumber \\= & {} -\frac{1}{12} \Delta \tau ^3 g''\left( \tilde{\tau }\right) - \frac{1}{480} \Delta \tau ^5 g^{(4)}\left( \tilde{\tau }\right) + \cdots \end{aligned}$$
(3.7)

Now one might be inclined to conclude that \(E = \mathscr {O}(\Delta \tau ^3)\) in all subintervals. However since,

$$\begin{aligned} g(\tau ) = (t-\tau )^{-\alpha }f'(\tau )= K(t-\tau ) f'(\tau ), \end{aligned}$$
(3.8)

where \(K(t-\tau ) = (t-\tau )^{-\alpha }\), the derivatives of \(g(\tau )\) will include increasing derivatives of the kernel \(K(t-\tau )\), due to repeated application of the product rule. Note that,

$$\begin{aligned} g''(\tau )&= f'(\tau ) K''(t-\tau ) -2 f''(\tau ) K'(t-\tau )+ f^{(3)}(\tau ) K(t-\tau ) \nonumber \\&= \alpha (\alpha +1) f'(\tau ) (t-\tau )^{-\alpha -2} + 2 \alpha f''(\tau ) (t-\tau )^{-\alpha -1} + f^{(3)}(\tau ) (t-\tau )^{-\alpha } . \end{aligned}$$
(3.9)

Then the first term in Eq. (3.7) is then given by

$$\begin{aligned} -\frac{1}{12} \Delta \tau ^3 g''\left( \tilde{\tau }\right)&= -\frac{1}{12} \Delta \tau ^3 \left( \alpha (\alpha +1) f'(\tilde{\tau } ) (t-\tilde{\tau } )^{-\alpha -2} \right. \nonumber \\&\quad \left. + 2 \alpha f''(\tilde{\tau } ) (t-\tilde{\tau } )^{-\alpha -1} + f^{(3)}(\tilde{\tau } ) (t-\tilde{\tau } )^{-\alpha } \right) , \nonumber \\&= \mathscr {O}\left( \Delta \tau ^{3} (t-b+\frac{\Delta \tau }{2})^{-\alpha - 2}\right) , \end{aligned}$$
(3.10)

since \(\tilde{\tau } = b - \Delta \tau /2\).

This process can be repeated for every error term in Eq. (3.7) giving the general form,

$$\begin{aligned} \Delta \tau ^{n+1}g^{(n)} = \mathscr {O}\left( \Delta \tau ^{n+1} (t-b+\frac{\Delta \tau }{2})^{-\alpha - n} \right) , \quad n=2,4,\ldots . \end{aligned}$$
(3.11)

The form in (3.11) illustrates that there are two sources of truncation error, and the dominance of one over the other is predicated by the position in the integral, or the value of b. Examining (3.11), when \(b = \Delta \tau \) (corresponding to the first sub integral), or when the quadrature is sufficiently far from the singularity the order, (3.11), is dominated by the \(\Delta \tau ^{n+1}\) since

$$\begin{aligned} \left| (t-\frac{\Delta \tau }{2})^{-\alpha - n}\right| \gg \left| \Delta \tau ^{n+1}\right| , \end{aligned}$$
(3.12)

provided \(\Delta \tau \ll t\). This phenomenon is also observed numerically where, away from the singularity, our quadrature recovers \(\mathscr {O}(\Delta \tau ^3)\) per subinterval, and when N of these errors are summed, we observe error like \(\mathscr {O}(\Delta \tau ^2)\).

When \(b=t\), or when b is sufficiently close to the singularity, then we have relation (3.11) reducing to

$$\begin{aligned} \mathscr {O}\left( \Delta \tau ^{1-\alpha } 2^{n+\alpha } \right) , \quad n=2,4,\ldots . \end{aligned}$$
(3.13)

By observing the convergence behaviour at the lower and upper integration terminals we are able to establish bounds on the order of convergence of the total quadrature scheme. However, we are also interested in how the order of convergence changes across the domain. To assess this, we visualise the convergence in (3.7) as a function of b. We note that the expansions used in (3.5) and (3.6) are centered in the midpoint of each domain, so as to avoid evaluating the integrand at the point of singularity.

Figure 1 illustrates the convergence order of each subinterval, \(\tau \in [b-\Delta \tau ,b]\), as a function of b. As \(b \rightarrow 0\) the integrand exhibits no singular behaviour and recovers the expected convergence rate. However, as \(b\rightarrow t\) the degeneration of convergence rate from \(\mathscr {O}(\Delta \tau ^3)\) to \(\mathscr {O}(\Delta \tau ^{1-\alpha })\) occurs gradually as the quadrature approaches the singularity at \(\tau = t\). More importantly, the leading error for any Newton–Cotes quadrature at \(b=t\) is given by (3.13) and is bound by \(\Delta \tau ^{1-\alpha }\) regardless of the value of n. The natural approach in improving the accuracy of a quadrature is to increase the number of quadrature nodes to cancel increasing error terms. However, as was shown above, this procedure does not reduce the order of leading error term, regardless of how many quadrature nodes are used.

Fig. 1
figure 1

Behaviour of the leading error term with \(m=1\), \(t=1\) and \(\alpha = 1/2\) as a function of b

Full size image

While Fig. 1 illustrates the order of the truncation error of each subdomain, \(\tau \in [b - \Delta \tau , b]\), parameterised by b, we need the accumulated truncation error over all subdomains to quantify the truncation error of the total quadrature.

Considering the sum over all sub-intervals we have,

$$\begin{aligned} E_{tot} = \sum _{i=1}^{N} \Delta \tau ^{2p+1} \left( t-i \Delta \tau -\frac{\Delta \tau }{2}\right) ^{-\alpha - 2p} , \end{aligned}$$
(3.14)

where \(\Delta \tau = t/ N\), and p indicates the error behaviour for the pth term in the Taylor series. The function \(E_{tot}\) is sampled with decreasing values of \(\Delta \tau \) and various values of \(\alpha \), shown in Fig. 2. From this figure we can see that the dynamics of the total quadrature follow \(\mathscr {O}(\Delta \tau ^{1-\alpha })\), an inevitable limitation using this approach. This poor accuracy has been previously observed and can be improved upon using several methodologies [8, 10, 22], however these approaches are not directly related to the Newton–Cotes type quadrature present in this work. Subsequent sections in this work propose a methodology for improving the accuracy.

Fig. 2
figure 2

Theoretical convergence behaviour over all subintervals with \(m=1\) and \(\alpha \) as a function of \(\Delta \tau \), continuous lines denote the slope of \(1-\alpha \)

Full size image

4 Generalisations

This section generalises the results shown in the previous section to an arbitrary order Newton–Cotes quadrature as well as the expected convergence ceiling imposed by a generalised weakly singular kernel in the form \(K(\tau ) = (t-\tau )^{k-\alpha }\), where \(k\in \textbf{N}\). Typically Newton–Cotes quadratures with n nodes in a given stencil will exhibit a convergence rate of \(\mathscr {O}(\Delta \tau ^n)\) for non-singular integrands.

Proposition 1

A Newton–Cotes quadrature of order n for integrals containing a weakly singular kernel of the form

$$\begin{aligned} (t-\tau )^{k-\alpha }, \quad \forall k \in \textbf{N}, \end{aligned}$$

have a convergence rate of

$$\begin{aligned} \mathscr {O}\left( \Delta \tau ^{k+1-\alpha }\right) , \end{aligned}$$

independent of n.

Proof

Consider a discretisation of the domain [a, b] with equally spaced nodes, so that \(\{\tau _0, \tau _1, \ldots , \tau _n\} = \{a,a+\Delta \tau , \dots ,b\}\). Given \(g(\tau ) = K(t-\tau ) f'(\tau )\) and provided \(f(\tau )\) is sufficiently smooth, then we have an nth order Newton–Cotes quadrature defined as

$$\begin{aligned} \int _a^b g(\tau ) d\tau \approx \sum _{i=0}^{n} \omega _i g(\tau _i), \end{aligned}$$
(4.1)

where \(\omega _i\) is obtained from computing (3.5) and (3.6) on each subinterval and collecting the equally sized coefficients. The values for \(\omega _i\)’s are computed to match and cancel the first n terms of (3.4) Hence, this quadrature has error

$$\begin{aligned} E = \int _a^b g(\tau ) d\tau - \sum _{i=0}^{n} \omega _i g(\tau _i) \sim g^{(n)}(\tilde{\tau })\Delta \tau ^{n+1}. \end{aligned}$$
(4.2)

The leading error term in (4.2) contains the nth derivative of \(g(\tilde{\tau })\), \(g^{(n)}(\tilde{\tau })\). Moreover, generalising (3.9) using the generalised Leibniz Rule (product rule of high order derivatives) we have, with \(g(\tau ) = K(t-\tau ) f'(\tau )\),

$$\begin{aligned} g^{(n)}(\tilde{\tau }) = \sum _{j=0}^{n} \left( {\begin{array}{c}n\\ j\end{array}}\right) K^{(j)}(t-\tau )f^{(n-j+1)}(\tau ). \end{aligned}$$
(4.3)

The term in the above summation limits the convergence rate for \(j=n\), is \(K^{(n)}(t-\tau ) f'(\tau )\). We can now more precisely define (4.2) as

$$\begin{aligned} E \sim \Delta \tau ^{n+1} \sum _{j=0}^{n} \left( {\begin{array}{c}n\\ j\end{array}}\right) K^{(j)}(t-\tau )f^{(n-j+1)}(\tau ). \end{aligned}$$
(4.4)

The leading cause of error occurs in the final term of the sum, i.e. for \(j=n\),

$$\begin{aligned} E&= \mathscr {O}\left( \Delta \tau ^{n+1} K^{(n)}(t-\tau ) f'(\tau ) \right) \nonumber \\&= \mathscr {O}\left( \Delta \tau ^{n+1} \frac{(-1)^n \Gamma (k-\alpha +1)}{\Gamma (k-n-\alpha +1)}\left( \frac{\Delta \tau }{2} \right) ^{k-n-\alpha }\right) \nonumber \\&= \mathscr {O}\left( \Delta \tau ^{k+1-\alpha }\right) , \end{aligned}$$
(4.5)

where \(\tau = t - \frac{\Delta \tau }{2}\) is sufficiently close to the singular boundary and the nth derivative of the convolution kernel is given by

$$\begin{aligned} K^{(n)}(t-\tau ) = \frac{(-1)^n \Gamma (k-\alpha +1) }{\Gamma (k-n-\alpha +1)} \left( \frac{\Delta \tau }{2}\right) ^{k-n-\alpha }. \end{aligned}$$
(4.6)

\(\square \)

Remark 4.1

In summary, we highlight that the error result obtained in (4.5) is independent of n, indicating that the source of error inherent in this class of quadrature for weakly singular kernels is independent of the order of the specific quadrature used.

5 Raising the accuracy to compensate for the previously described loss

To obtain a numerical approximation of (2.3), we discretize the domain \(\tau \in [0,t]\) with \(N+1\) equidistant grid points \(\tau _i = ih\), where \(i = 0,1,2, \dots , N\) and \(h = t/N\). Also, let \(P = \text {diag}(\omega _0, \dots , \omega _N)h\) and \(\textbf{f}= (f(x_0), \dots f(x_N))^\top \). If a closed quadrature rule of the form

$$\begin{aligned} \int _0^t f(\tau ) d\tau \approx h \sum _{i = 0}^N \omega _i f(x_i) = \textbf{1}^\top P \textbf{f} \end{aligned}$$
(5.1)

is used, where \(\omega _i > 0\) are weights, then the singularity of the integrand in (2.3) at \(\tau = t\) will lead to a blow-up.

To cure this anomaly, (2.2) is rewritten by using integration by parts which leads to the modified formula

$$\begin{aligned} \begin{aligned} D^\alpha f(t)&= \frac{1}{\Gamma (2-\alpha )} \left[ t^{1-\alpha }f'(0) + \int _0^t (t-\tau )^{1-\alpha } f''(\tau ) d\tau \right] \end{aligned} \end{aligned}$$
(5.2)

and removes the singularity. Approximating (5.2) numerically yields

$$\begin{aligned} D^\alpha f(t) \approx D^\alpha _h \textbf{f}= \frac{1}{\Gamma (2-\alpha )} \left( t^{1-\alpha } (D_1\textbf{f})_0 + \textbf{1}^\top P T^{1-\alpha } D_2 \textbf{f}\right) \, . \end{aligned}$$
(5.3)

In (5.3), \(D_1 \textbf{f}\approx \mathbf {f'}\) and \(D_2 \textbf{f}\approx \mathbf {f''}\) are finite-difference approximations of \(f'\) and \(f''\) evaluated on the grid. The matrix \(D_1\) approximates the first derivative [30], while \(D_2\) generates an approximation of the second derivative [21]. Furthermore, \(T = \text {diag}(t, t-h,\dots ,0)\) and the exponent in \(T^{1-\alpha }\) should be interpreted element-wise.

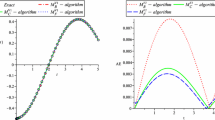
To verify the accuracy of (5.3), we compare the numerical result to a known analytical value. For polynomials of degree n, an analytic expression can be obtained by repeatedly using integration-by-parts: \(D^\alpha t^n = n! t^{n-\alpha }/ \Gamma (n+1-\alpha )\). Given two step-sizes, \(h_1,h_2\), the error in (5.3) is \(e_{h_i} = \big |D^\alpha f(t) - D^\alpha _{h_i} \textbf{f}\big |\), \(i = 1,2\), and the convergence rate is \(r_{h_1} = \log (e_{h_1}/e_{h_2})/\log (h_1/h_2)\). To start, we let \(P_2\) contain the weights of the second order Trapezoidal rule and \(D_{1,21}, D_{2,21}\) be the matrices containing the second order accurate central finite-difference schemes in the interior and appropriate first order forward and backward stencils at the boundaries. The error and convergence rate is presented in Table 1 for \(f(t) = t^3\). We find that the convergence rate approaches \(2-\alpha \), thus we have raised the order of the accuracy by one.

Table 1 Error and convergence rate of \(D^\alpha t^3\) for different values of \(\alpha \)
Full size table

In an ambition to further increase the convergence rate, we use a quadrature matrix P and differentiation matrix D of higher order. Table 2 presents the result for SBP84, where \(P_7\) now is a diagonal and positive definite matrix forming a quadrature of order seven and \(D_{1,84},D_{2,84}\) are eighth order in the interior and fourth order at the boundaries. These operators are sufficiently accurate such that numerical integration and differentiation errors are negligible [21, 30, 32]. However, as for the lower order case, the numerical experiments again suggest a convergence rate of \(2-\alpha \), with no improvement in accuracy. Similar results are obtained for other smooth functions f in the integrand.

Table 2 Error and convergence rate of \(D^\alpha t^3\) for different values of \(\alpha \)
Full size table

The results in Tables 1 and 2 and the previous analysis in Sect. 4 illustrate that there are two factors limiting the accuracy: (1) the natural error source that is related to the fractional kernel and present for all closed quadratures and (2) the order of the specific quadrature. The most significant error source determines the convergence rate.

To verify our claim, we start by integrating (2.2) by parts to get

$$\begin{aligned} D^\alpha f(t) = \frac{t^{1-\alpha }f'(0)}{\Gamma (2-\alpha )} + \frac{1}{\Gamma (3-\alpha )} \left( t^{2-\alpha }f''(0) + \int _0^t (t-\tau )^{2-\alpha } f^{(3)}(\tau ) d\tau \right) \, .\nonumber \\ \end{aligned}$$
(5.4)

Note that (5.4) can only be obtained if f is smooth enough and has non-singular derivatives. A discrete approximation of (5.4) is

$$\begin{aligned} D^\alpha _h \textbf{f}= \frac{t^{1-\alpha }(D\textbf{f})_0}{\Gamma (2-\alpha )} + \frac{1}{\Gamma (3-\alpha )} \left( t^{2-\alpha }(D_2\textbf{f})_0 + \textbf{1}^\top P T^{2-\alpha } D_3 \textbf{f}\right) \, . \end{aligned}$$
(5.5)

In (5.4), \(D_3 \textbf{f}= D_2D_1 \textbf{f} \approx \mathbf {f'''}\) and the quadrature matrices are the same as in Sect. 5. For the fractional kernel \((t-\tau )^{1-\alpha }\), the convergence order of the numerical approximation (5.3) was \(2-\alpha \). Raising the power of the kernel to \(2-\alpha \) as in (5.4), we expect a high-order version of the numerical approximation in (5.5) to generate a convergence of order \(3-\alpha \). The error and convergence rates for the scheme in (5.5) together with \(P_7\) and \(D_{1,84},D_{2,84}\) and \(f(t) = t^3\) are presented in Table 3. As expected, the results suggest a convergence rate of \(3-\alpha \), meaning that (1) is the limiting factor. If P or D are of lower convergence order, then (2) will dominate instead, as seen in Table 4.

Table 3 Error and convergence rate of \(D^\alpha t^3\) for different values of \(\alpha \) for (5.5)
Full size table
Table 4 Error and convergence rate of \(D^\alpha t^3\) for different values of \(\alpha \) for (5.5)
Full size table

In a similar manner, repeatedly using integrating-by-parts results in

$$\begin{aligned} D^\alpha f(t) = \frac{1}{\Gamma (n+1-\alpha )} \int _0^t (t-\tau )^{n-\alpha } f^{(n+1)}(\tau ) d\tau + \sum _{i = 1}^n \frac{t^{i-\alpha }f^{(i)}(0)}{\Gamma (i+1-\alpha )} \, ,\nonumber \\ \end{aligned}$$
(5.6)

which can be used to increase the order. Discretizing (5.6) leads to

$$\begin{aligned} D_h^\alpha f(t) = \frac{1}{\Gamma (n+1-\alpha )} \left( \textbf{1}^\top P T^{n-\alpha } D^{n+1} \textbf{f} \right) + \sum _{i = 1}^n \frac{t^{i-\alpha } (D^i \textbf{f} )_0}{\Gamma (i+1-\alpha )} \, , \end{aligned}$$
(5.7)

where \(D^i \textbf{f} \approx \textbf{f}^{(i)}\) is the i-th derivative evaluated on the grid. The obvious downsides of (5.6) and (5.7) are that the function must be smooth enough with non-singular derivatives and secondly, the necessity of an high-order approximation of a high derivative.

6 The extension to open quadratures

The analysis above carries over to open quadratures as well, which we will illustrate numerically by considering the composite 2nd order midpoint rule and the composite 4th order Milne’s rule [28], denoted by \(P^O_2\) and \(P^O_4\), respectively. For the approximation \(\int _0^t (t-\tau )^{2-\alpha } d\tau \approx \textbf{1}^\top P T^{2-\alpha }\textbf{1}\), we expect that \(P^O_2\) leads to 2nd order convergence and \(P^O_4\) leads to \(3-\alpha \). Tables 5 and 6 presents the results, which agree with our theoretical speculation.

Table 5 Error and convergence rate for the 2nd order quadrature rule
Full size table
Table 6 Error and convergence rate for the 4th order quadrature rule
Full size table

7 Conclusions

We have investigated the numerical approximations of Caputo’s formulation for fractional derivatives for closed quadrature rules. We showed that the convergence rate for such discretization depend naturally on the fractional parameter \(\alpha \). Two different error sources determine the convergence rate: (1) the inherent error associated with the numerical integration of the kernel and (2) the order accuracy of the numerical method used. The most significant one determines the convergence rate. Moreover, we have shown in the case of a general Newton–Cotes quadrature that the leading term in the error expression is limited not by the order of the quadrature but by the degree of the singularity present in the integrand. We have also shown how to increase the order of accuracy by using integration by parts. The present work is general for smooth integrands. In future work we aim to extend the analysis to non-smooth integrands. Lastly, we presented numerical evidence that the theoretical findings carries over to open quadratures as well.