Rank-adaptive dynamical low-rank integrators for first-order and second-order matrix differential equations

Abstract

Dynamical low-rank integrators for matrix differential equations recently attracted a lot of attention and have proven to be very efficient in various applications. In this paper, we propose a novel strategy for choosing the rank of the projector-splitting integrator of Lubich and Oseledets adaptively. It is based on a combination of error estimators for the local time-discretization error and for the low-rank error with the aim to balance both. This ensures that the convergence of the underlying time integrator is preserved. The adaptive algorithm works for projector-splitting integrator methods for first-order matrix differential equations and also for dynamical low-rank integrators for second-order equations, which use the projector-splitting integrator method in its substeps. Numerical experiments illustrate the performance of the new integrators.

1 Introduction

Dynamical low-rank integrators [17, 19] have been designed for the approximation of large, time-dependent matrices which are solutions to first-order matrix differential equations

$$\begin{aligned} A'(t) = F\big (A(t)\big ), \quad t \in [0,T], \quad A(0) = A_0 \in \mathbb {C}^{m\times n}, \end{aligned}$$

(1)

whose solutions can be well approximated by low-rank matrices. The projector-splitting integrator introduced in [19] has particularly favorable properties. It is robust in the presence of small singular values, which appear in the case of over-approximation, i.e.,  when the approximation rank is chosen larger than the rank of the solution A(t) of (1). A variant of this method adapted to strongly dissipative problems was presented in [5]. Another variant for stiff first-order matrix differential equations was introduced in [24].

Recently, a novel dynamical low-rank integrator for second-order matrix differential equations

$$\begin{aligned} A''(t) = F\big (A(t)\big ), \quad t \in [0,T], \quad A(0) = A_0, \quad A'(0) = B_0, \end{aligned}$$

(2)

has been constructed in [12]. Is is based on a Strang splitting of the equivalent first-order formulation and the projector-splitting integrator [19]. This integrator is also robust in the case of over-approximation and shows second-order convergence in time. In particular, with a few amendments it is an effective method for semilinear second-order matrix differential equations, see Sect. 2.3.

In applications, rank-adaptivity turns out to be essential for the efficiency of the algorithms. For first-order equations, in [4] a rank-adaptive variant of the unconventional integrator [5] was proposed. However, the approach from [4] is not applicable to the projector-splitting integrator [19]. In [8], rank-adaptivity for tensor methods for high-dimensional PDEs was based on a functional tensor train series expansion. For the special case of finite-dimensional parametrized Hamiltonian systems modeling non-dissipative phenomena, a rank-adaptive structure-preserving reduced basis method was introduced in [11]. Very recently, in [10] a Predictor–Corrector strategy for adaptivity was proposed, and in [31] the authors developed a rank-adaptive splitting method for the extended Fisher–Kolmogorov equation.

In the present paper, we discuss a general strategy for selecting the rank adaptively in the projector-splitting integrator. Increasing or decreasing the rank from one time step to the next was already proposed in [19] and quite recently in [13]. Our main contribution is a strategy for which the time step of the underlying splitting method, i.e.,  the Lie-Trotter splitting for first-order and the Strang splitting for second-order problems, is the only input parameter. We determine the rank such that the error of the dynamical low-rank approximation does not spoil the order of the underlying splitting method applied to the full matrix differential equation. This is achieved by propagating one additional singular value which is used for accepting or rejecting the current time step and for selecting the rank in the next step. The decision is based on an estimator of the global time-discretization error. This adaptivity control is also applicable to the dynamical low-rank integrators for stiff problems. The new dynamical low-rank integrator for (2) uses the projector-splitting integrator in the substeps of the Strang splitting, which allows to control the rank adaptively also for second-order equations. Moreover, it can be readily combined with the integrator from [5].

The paper is organized as follows: In Sect. 2, we briefly recall the projector-splitting integrator introduced in [19] and the LRLF scheme from [12]. Additionally, we sketch variants of both methods for (stiff) semilinear first-order and second-order differential equations, respectively. Section 3 is devoted to rank-adaptivity. In Sect. 4, numerical experiments illustrate the performance of the new schemes.

Throughout this paper, $m,n$, and $r$ are natural numbers, where w.l.o.g.  $m\ge n\gg r$. If $n> m$, we consider the equivalent differential equation for the transpose. By $\mathscr {M}_r$ we denote the manifold of complex $m\times n$ matrices with rank $r$,

$$\begin{aligned} \mathscr {M}_r= \{ {{\widehat{Y}}}\in \mathbb {C}^{m\times n}~|~{{\,\textrm{rank}\,}}({{\widehat{Y}}}) = r\}. \end{aligned}$$

The Stiefel manifold of $m\times r$ unitary matrices is denoted by

$$\begin{aligned} \mathscr {V}_{m,r}= \{ U \in \mathbb {C}^{m\times r}~|~U^H U = I_r\}, \end{aligned}$$

where $I_r$ is the identity matrix of dimension $r$ and $U^H$ is the conjugate transpose of U.

The singular value decomposition of a matrix $Y \in \mathbb {C}^{m\times n}$ is given by

$$\begin{aligned} Y = U \Sigma V^H, \quad U \in \mathscr {V}_{m,m}, \quad V \in \mathscr {V}_{n,n}, \quad \Sigma = {{\,\textrm{diag}\,}}(\sigma _1,\ldots , \sigma _n) \in \mathbb {C}^{m\times n}, \end{aligned}$$

where $\sigma _1 \ge \cdots \ge \sigma _n\ge 0$ are its singular values. It is well known that for $r< n$, the rank-$r$ best-approximation to Y w.r.t.  the Frobenius norm is

$$\begin{aligned} {{\widehat{Y}}}^\text {best}= U {\widetilde{\Sigma }} V^H = {{\widehat{U}}}{\widehat{\Sigma }} {{\widehat{V}}}^H, \end{aligned}$$

where ${\widetilde{\Sigma }} = {{\,\textrm{diag}\,}}(\sigma _1, \ldots , \sigma _r, 0, \ldots , 0)$ and

$$\begin{aligned} {{\widehat{U}}}= U [I_r ~ 0] \in \mathscr {V}_{m,r}, \quad {{\widehat{V}}}= V [I_r ~ 0] \in \mathscr {V}_{n,r}, \quad {\widehat{\Sigma }}= {{\,\textrm{diag}\,}}(\sigma _1, \ldots , \sigma _r). \end{aligned}$$

The Frobenius norm is denoted by $\Vert \cdot \Vert$, and the Frobenius inner product by $\langle \cdot , \cdot \rangle$. The symbol $\bullet$ denotes the entrywise or Hadmard product of matrices. For a given step size $\tau$ we use the notation $t_k = k \tau$ for any k with $2 k \in \mathbb {N}_0$.

2 Dynamical low-rank integrators with fixed rank

In this section we give a review on various low-rank integrators for first and second-order matrix differential equations.

2.1 First-order differential equations

In the dynamical low-rank approximation of the solution to first-order matrix differential equations (1), the approximation ${{\widehat{A}}}\approx A$ is determined as solution of the projected differential equation

$$\begin{aligned} {{\widehat{A}}}'(t) = P\big ({{\widehat{A}}}(t)\big ) F\big ({{\widehat{A}}}(t)\big ), \quad {{\widehat{A}}}(0) = {{\widehat{A}}}_0. \end{aligned}$$

(3)

Here, $P\big ({{\widehat{A}}}(t)\big )$ denotes the orthogonal projector onto the tangent space of the low-rank manifold $\mathscr {M}_r$ at ${{\widehat{A}}}(t) \in \mathscr {M}_r$, i.e., 

$$\begin{aligned} P\big ({{\widehat{A}}}(t)\big )Z = Z {{\widehat{V}}}(t) {{\widehat{V}}}(t)^H - {{\widehat{U}}}(t) {{\widehat{U}}}(t)^H Z {{\widehat{V}}}(t) {{\widehat{V}}}(t)^H + {{\widehat{U}}}(t) {{\widehat{U}}}(t)^H Z, \end{aligned}$$

cf.  [17, Lemma 4.1], where ${{\widehat{A}}}(t) \in \mathscr {M}_r$ is decomposed in a non-unique fashion resembling the singular value decomposition into

$$\begin{aligned} {{\widehat{A}}}(t) = {{\widehat{U}}}(t) {{\widehat{S}}}(t) {{\widehat{V}}}(t)^H, \quad {{\widehat{U}}}(t) \in \mathscr {V}_{m,r}, \quad {{\widehat{V}}}(t) \in \mathscr {V}_{n,r}, \quad {{\widehat{S}}}(t) \in \mathbb {C}^{r\times r}~\text {invertible}.\nonumber \\ \end{aligned}$$

(4)

For the initial value ${{\widehat{A}}}_0$, typically the rank-$r$ best-approximation to A(0) computed by a truncated SVD is used.

The dynamical low-rank integrator developed in [19], also called the projector-splitting integrator, is constructed by performing a Lie-Trotter splitting on the right-hand side of (3) and solving the three subproblems on the low-rank manifold. This approach yields an efficient time-stepping algorithm for computing the desired low-rank approximations. One time-step of the projector-splitting integrator is given in Algorithm 1.

2.2 Second-order differential equations

For the second-order problem (2), a novel dynamical low-rank integrator named LRLF (low-rank leapfrog) scheme was presented in [12, Section 3]. Given ${r_A},{r_B}\in \mathbb {N}$ and approximations ${{\widehat{A}}}_k\approx A(t_k)$ of rank ${r_A}$ and ${{\widehat{B}}}_{k-\frac{1}{2}}\approx A'(t_{k-\frac{1}{2}})$ of rank ${r_B}$, it computes approximations ${{\widehat{A}}}_{k+1}\in \mathscr {M}_{r_A}$ and ${{\widehat{B}}}_{k+ \frac{1}{2}}\in \mathscr {M}_{r_B}$ with ${{\widehat{A}}}_{k+1}\approx A(t_{k+1})$ and ${{\widehat{B}}}_{k+ \frac{1}{2}}\approx A'(t_{k+ \frac{1}{2}})$, respectively. This integrator is based on the first-order formulation of (2),

$$\begin{aligned} \begin{bmatrix} A \\ B \end{bmatrix}' = \begin{bmatrix} 0 \\ F(A) \end{bmatrix} + \begin{bmatrix} B \\ 0 \end{bmatrix}, \end{aligned}$$

combined with a Strang splitting. The subproblems are first-order matrix differential equations, (5a, 5b)

$$\begin{aligned} A'= & {} B, \quad B' = 0, \end{aligned}$$

(5a)

$$\begin{aligned} B'= & {} F(A), \quad A'= 0, \end{aligned}$$

(5b)

which can be solved exactly. The low-rank matrices ${{\widehat{A}}}_{k+1}$ and ${{\widehat{B}}}_{k+ \frac{1}{2}}$ are obtained by approximating the solutions of (5a) by application of Algorithm 1 to

$$\begin{aligned} {\widetilde{B}}_{k-\frac{1}{2}}'(\sigma )= & {} F( {{\widehat{A}}}_k), \quad {\widetilde{B}}_{k-\frac{1}{2}}(0) = {{\widehat{B}}}_{k-\frac{1}{2}}, \quad \sigma \in [0,\tau ], \\ {\widetilde{A}}_k'(\sigma )= & {} {\widetilde{B}}_{k+ \frac{1}{2}}, \qquad \quad {\widetilde{A}}_k(0) = {{\widehat{A}}}_k, \qquad \quad \!\!\sigma \in [0,\tau ]. \end{aligned}$$

This leads to the dynamical low-rank integrator LRLF shown in Algorithm 2.

2.3 Semilinear problems

A fixed-rank dynamical low-rank integrator for the stiff semilinear first-order problem

$$\begin{aligned} A'(t) = L_1A(t) + A(t) L_2+ f\big (A(t)\big ), \quad t \in [0,T], \quad A(0) = A_0, \end{aligned}$$

(6)

where the norms of $L_1\in \mathbb {C}^{m\times m}$ and $L_2\in \mathbb {C}^{n\times n}$ are large and f is a Lipschitz continuous function with moderate Lipschitz constant, was introduced in [24]. It is based on the subproblems (7a, 7b)

$$\begin{aligned} A'&= L_1A + A L_2, \end{aligned}$$

(7a)

$$\begin{aligned} A'&= f(A). \end{aligned}$$

(7b)

The solution to (7a) is given by

$$\begin{aligned} A(t) = \exp (t L_1) A_0 \exp (t L_2). \end{aligned}$$

(8)

Note that the rank of the initial value is preserved for all times [24, Section 3.2]. In contrast, the rank of the solution to the nonlinear subproblem (7b) may vary in time.

In [24], a low-rank approximation has been computed by applying a Lie-Trotter splitting to (6) and solving the subproblems (7) by the projector-splitting integrator in Algorithm 1. This method is called PSI-stiff in the following.

For semilinear second-order equations of the form

$$\begin{aligned} A''(t) = -\Omega _1^2 A(t) - A(t) \Omega _2^2 + f\big (A\big ), \quad t \in [0,T], \quad A(0) = A_0, \quad A'(0) = B_0,\nonumber \\ \end{aligned}$$

(9)

with Hermitian, positive semidefinite matrices $\Omega _1\in \mathbb {C}^{m\times m}$, $\Omega _2\in \mathbb {C}^{n\times n}$ and f again Lipschitz continuous, a dynamical low-rank integrator named LRLF-semi was proposed in [12, Section 5]. It is based on the equivalent first-order formulation of the second-order problem (9), where the right-hand side is split into

$$\begin{aligned} \begin{bmatrix} A \\ B \end{bmatrix}' = \begin{bmatrix} B \\ -\Omega _1^2 A - A \Omega _2^2 + f\big (A\big ) \end{bmatrix} = \begin{bmatrix} \omega _1^2 B \\ -\Omega _1^2 A \end{bmatrix} + \begin{bmatrix} \omega _2^2 B \\ - A \Omega _2^2 \end{bmatrix} + \begin{bmatrix} \omega _3^2 B \\ f(A) \end{bmatrix}. \end{aligned}$$

(10)

The weights $\omega _{i}\ge 0$, $i=1,2,3$, can be chosen arbitrarily such that $\omega _1^2 + \omega _2^2+\omega _3^2= 1$. A natural choice is $\omega _i^2 = 1/3$. The linear subproblems can be solved exactly. Low-rank approximations to these solutions are obtained by application of the projector-splitting integrator. The nonlinear subproblem is solved approximately with a variant of the LRLF scheme, cf.  [12, Algorithm 3]. Denoting the numerical flows of the linear subproblems by $\phi ^{\Omega _1}_\tau$ and $\phi ^{\Omega _2}_\tau$, and the numerical flow of the nonlinear subproblem as $\phi ^\mathscr {S}_\tau$, respectively, one step of the LRLF-semi scheme reads

$$\begin{aligned} \begin{bmatrix} {{\widehat{A}}}_{k+1}\\ {{\widehat{B}}}_{k+1}\end{bmatrix} = \left( \phi ^{\Omega _1}_\frac{\tau }{2}\circ \phi ^{\Omega _2}_\frac{\tau }{2}\circ \phi ^\mathscr {S}_\tau \circ \phi ^{\Omega _2}_\frac{\tau }{2}\circ \phi ^{\Omega _1}_\frac{\tau }{2}\right) \begin{bmatrix} {{\widehat{A}}}_k\\ {{\widehat{B}}}_k\end{bmatrix}. \end{aligned}$$

3 Rank adaptivity

In many applications, an appropriate rank for computing a low-rank approximation to the exact solution of (2) or (1) is not known a priori and it may also vary with time. If the rank is chosen too small, the low-rank approximation lacks accuracy. Conversely, if the rank is chosen too large, the algorithm becomes inefficient.

In the following, we develop rank-adaptive variants of the projector-splitting integrators PSI and PSI-stiff for first-order problems and for the LRLF and the LRLF-semi schemes for second-order problems.

3.1 Selecting the rank

We first discuss the projector-splitting integrator for the first-order problem (1). The general idea of our rank-adaptive strategy is to approximate the exact solution of (1) by a low-rank solution of rank $r_k$ in the $k$th time step, but to propagate a solution of rank $r_k+1$. The additional information is used as an indicator whether to accept or reject the current time step, and for selecting the rank $r_{k+1}$ for the next time step.

Given ${{\widehat{A}}}_k= {{\widehat{U}}}_k{{\widehat{S}}}_k{{\widehat{V}}}^H_k\in \mathscr {M}_{r_k+1}$, a single step of Algorithm 1 yields the approximation ${{\widehat{A}}}_{k+1}= {{\widehat{U}}}_{k+1}{{\widehat{S}}}_{k+1}{{\widehat{V}}}^H_{k+1}\in \mathscr {M}_{r_k+1}$. We then compute the singular value decomposition of ${{\widehat{S}}}_{k+1}$,

$$\begin{aligned} {{\widehat{S}}}_{k+1}= P_{k+1}\Sigma _{k+1}Q_{k+1}^H, \quad \Sigma _{k+1}= {{\,\textrm{diag}\,}}( {{\widehat{\sigma }}}_1, \ldots , {{\widehat{\sigma }}}_{r_k}, {{\widehat{\sigma }}}_{r_k+1}), \end{aligned}$$

with $P_{k+1},Q_{k+1}\in \mathscr {V}_{r_k+1,r_k+1}$, and ${{\widehat{\sigma }}}_1 \ge \cdots \ge {{\widehat{\sigma }}}_{r_k+1} \ge 0$ so that

$$\begin{aligned} {{\widehat{A}}}_{k+1}= ({{\widehat{U}}}_{k+1}P_{k+1}) \Sigma _{k+1}({{\widehat{V}}}_{k+1}Q_{k+1})^H \end{aligned}$$

is the singular value decomposition of ${{\widehat{A}}}_{k+1}$. Given a tolerance $\texttt{tol}$, we determine $r_k$ such that

$$\begin{aligned} {{\widehat{\sigma }}}_{r_k+1} < \texttt{tol}\le {{\widehat{\sigma }}}_{r_k} \end{aligned}$$

(11)

by distinguishing three cases:

• 1. Augmentation case If ${{\widehat{\sigma }}}_{r_k+1} \ge \texttt{tol}$, the step is rejected and recalculated with rank $r_k+ 2$. The ranks of the initial values ${{\widehat{U}}}_k, {{\widehat{S}}}_k, {{\widehat{V}}}_k$ of the current integration step are increased by adding a zero entry to ${{\widehat{S}}}_k$,

  $$\begin{aligned} S^*= \begin{bmatrix} {{\widehat{S}}}_k&{} 0 \\ 0 &{} 0 \end{bmatrix} \in \mathbb {C}^{(r_k+2) \times (r_k+2)}. \end{aligned}$$

  This choice has been motivated by [19, Section 5.2]. The matrices ${{\widehat{U}}}_k$ and ${{\widehat{V}}}_k$ are augmented by unit vectors $u \in \mathbb {C}^m$ and $v \in \mathbb {C}^n$ such that

  $$\begin{aligned} U^*= \begin{bmatrix} {{\widehat{U}}}_k&u \end{bmatrix} \in \mathscr {V}_{m, r_k+2}, \quad V^*= \begin{bmatrix} {{\widehat{V}}}_k&v \end{bmatrix} \in \mathscr {V}_{n, r_k+2}. \end{aligned}$$

  Numerical tests indicate that choosing u and v as random vectors and orthonormalizing them against ${{\widehat{U}}}_k$ and ${{\widehat{V}}}_k$ is reliable and robust, but other choices are also possible. Clearly, $U^*S^*(V^*)^H = {{\widehat{U}}}_k{{\widehat{S}}}_k{{\widehat{V}}}_k^H = {{\widehat{A}}}_k$, thus the initial value of the current integration step has not changed. However, the numerical approximation has been enabled to evolve to rank $r_k+2$. The step is recomputed with the new initial values $U^*, S^*, V^*$, and it is again checked if the new smallest singular value is sufficiently small for accepting the step. This procedure is repeated until (11) is satisfied and the step is finally accepted, see Algorithm 3 for details.

• 2. Reduction case If ${{\widehat{\sigma }}}_{r_k} < \texttt{tol}$, this indicates that a sufficiently accurate approximation is available with a smaller rank. The step is accepted, but the rank for the next step is set to

  $$\begin{aligned} r_{k+1}= \max \left\{ {{\,\textrm{argmin}\,}}\{ j ~|~{{\widehat{\sigma }}}_{j+1} < \texttt{tol}\}, r_k-2 \right\} , \end{aligned}$$

  i.e.,  the rank is reduced by either 1 or 2. Thus, the rank may only decay slowly. Sudden rank-drops are prohibited. For the initial values in the next time step we use

  $$\begin{aligned} {\widetilde{S}} = {\widetilde{I}} ^T \Sigma _{k+1}{\widetilde{I}}, \quad {\widetilde{U}} = ({{\widehat{U}}}_{k+1}P_{k+1}) {\widetilde{I}}, \quad \widetilde{V} = ({{\widehat{V}}}_{k+1}Q_{k+1}) {\widetilde{I}}, \end{aligned}$$

  where ${\widetilde{I}} = \begin{bmatrix} I_{r_{k+1}+1} \\ 0 \end{bmatrix} \in \mathbb {C}^{(r_k+1) \times (r_{k+1}+1)}$. To prevent rank-oscillations, rank reduction is prohibited within the first 10 steps after an augmentation step.

• 3. Persistent case If ${{\widehat{\sigma }}}_{r_k} \ge \texttt{tol}>{{\widehat{\sigma }}}_{r_k+1}$, the time step is accepted and the same rank $r_{k+1}= r_k$ is used for the next one.

3.2 Choice of tolerance

It remains to find a suitable tolerance parameter $\texttt{tol}$. The global error of our integrator is a combination of a time-discretization error and a low-rank approximation error. We suggest to choose the rank such that the low-rank error is of about the same size as the time discretization error, but does not exceed the latter. If the time discretization error is large, the low-rank error is allowed to be large as well, and hence the approximation rank might be chosen small. If the time discretization error is small, then the approximation rank needs to be sufficiently large for an equally small low-rank error. By this procedure, we hope to ensure that the rank-adaptivity does not impair the convergence order of the integrator.

To balance the low-rank error with the time discretization error, we need to approximate the global time discretization error. This comprises an estimate of the local error and a simple model for the global error. While the error analysis of the projector-splitting integrator [16] and of the LRLF scheme [12, Theorem 6] show exponential error growth w.r.t.  time, numerical experiments indicate that this is a far too pessimistic bound, and that piecewise linear accretion in time is a more realistic scenario. Since the estimation of the local error induces some computational overhead, we keep an estimate for M steps before we recompute it. To be more precise, let $e_\ell$ be an approximation to the local error at time $t_{\ell M + 1}$. Since we assume that the local error is constant for the next M time steps, the global error at time $t_{\ell M + j}$ is approximated by $E_\ell + j e_\ell$, $j=1,\ldots ,M$, where $E_{\ell }$ is defined recursively by

$$\begin{aligned} E_{\ell +1} = E_{\ell } + M e_{\ell }, \quad \ell = 0,1,\ldots , \quad E_{0} = 0. \end{aligned}$$

This simple technique worked very well in numerous numerical simulations. Note that the linear model is a conservative choice in the sense that if the error growth is faster than linear (e.g., quadratic or even exponential), then we underestimate the global error which enforces the integrator to use a larger rank. We thus still compute a numerical solution where the low-rank approximation does not impair the time integration error.

The tolerance threshold $\texttt{tol}$ is then determined heuristically by the following steps:

• 1. Estimation of the local error (every M steps): Starting from an approximation ${{\widehat{A}}}_{\ell M} \approx A(t_{\ell M})$, we compute an approximation ${{\widehat{A}}}_{\ell M+1}$ to $A(t_{\ell M+1})$ by performing one integration step with step size $\tau$ and rank r. Additionally, we perform two time steps with step size $\frac{\tau }{2}$ and the same rank r, starting again from the initial value ${{\widehat{A}}}_{\ell M}$. By this, we obtain an alternative approximation $\breve{A}_{\ell M+1} \approx A(t_{\ell M+1})$. Assuming that the method converges with order $p \in \mathbb {N}$ in time, we apply Richardson extrapolation [9, Section II.4] to estimate the local error $e_{\ell }$ at $t_{\ell M+1}$ as

  $$\begin{aligned} e_{\ell } {:}{=}\frac{2^p}{2^p -1} \Vert {{\widehat{A}}}_{\ell M +1} - \breve{A}_{\ell M +1} \Vert , \end{aligned}$$

  cf.  [7, Section 5]. The global error is modeled as

  $$\begin{aligned} \Vert A(t_{{\ell M}+j}) - {{\widehat{A}}}_{{\ell M}+j} \Vert \approx E_{\ell } + j e_{\ell }, \quad j = 1,2,\dots ,M. \end{aligned}$$

  (13)

• 2. Estimation of the low-rank error: If $\sigma _1 \ge \cdots \ge \sigma _n\ge 0$ are the singular values of the exact solution $A(t_{k+1})$, then the rank-$r_{k+1}$ best-approximation ${{\widehat{A}}}^\text {best}_{k+1}$ to $A(t_{k+1})$ fulfills

  $$\begin{aligned} \frac{\Vert A(t_{k+1}) - {{\widehat{A}}}^\text {best}_{k+1}\Vert ^2}{\Vert A(t_{k+1}) \Vert ^2}&= \frac{ \sigma _{r_{k+1}+1}^2 + \cdots + \sigma _n^2}{\sigma _1^2 + \cdots + \sigma _n^2} \le \frac{(n- r_{k+1}) \sigma _{r_{k+1}+1}^2}{\Vert {{\widehat{A}}}^\text {best}_{k+1}\Vert ^2} , \end{aligned}$$

  so that

  $$\begin{aligned} \Vert A(t_{k+1}) - {{\widehat{A}}}^\text {best}_{k+1}\Vert \le \sigma _{r_{k+1}+1} \frac{\Vert A(t_{k+1}) \Vert }{\Vert {{\widehat{A}}}^\text {best}_{k+1}\Vert } \sqrt{n-r_{k+1}} \approx {{\widehat{\sigma }}}_{r_{k+1}+1} \sqrt{n-r_{k+1}}.\nonumber \\ \end{aligned}$$

  (14)

• 3. Tolerance threshold: The parameter $\texttt{tol}_k$ is set by equating the right-hand sides of (13) and (14) for $k= \ell M + j$, $j=0,\dots ,M-1$. This yields the condition

  $$\begin{aligned} {{\widehat{\sigma }}}_{r_{k+1}+1} \le \frac{ E_{\ell } + j e_{\ell }}{ \sqrt{n- r_{k+1}} } {=}{:}\texttt{tol}_k, \quad k= \ell M + j. \end{aligned}$$

  (15)

• 4. Initial rank: An obvious choice for the initial rank for the integration is $r_0={{\,\textrm{rank}\,}}(A_0)$. However, if the rank of $A_0$ is very small, this may not necessarily hold for the rank of the exact solution A(t), even for small t. On the other hand, if the rank of $A_0$ is large, this choice is also questionable. In our implementation, we first perform $\nu$ integration steps (with $\nu$ small, e.g.,  $\nu = 5$) with an initial rank $r_1$ given by the user (say $r_1=5$). Rank reduction is disabled in this phase. Then let $r^*$ denote the number of singular values of ${\widehat{A}}_\nu$ greater than or equal to $\texttt{tol}_\nu$ defined in (15). If $r^*< r_1$, we continue the integration with $r_{\nu +1} = r^*$. Otherwise, we multiply $r_1$ by 2 and rerun the initializing process, until $r^*< r_1$ holds.

3.3 Rank-adaptive algorithms

The rank-adaptive version of the projector-splitting integrator Algorithm 1 is called RAPSI for r ank-a daptive projector-splitting integrator in the following. A single step of the RAPSI scheme is given in Algorithm 4.

The rank-adaptive version of the LRLF scheme is derived by replacing the PSI routines by the RAPSI routines. We name this new integrator rank-adaptive LRLF (RALRLF) method. It is presented in Algorithm 5.

The rank-adaptive counterpart of the PSI-stiff scheme is named RAPSI-stiff. Since the linear subproblem preserves the rank, rank-adaptivity is only applied in the integration of the nonlinear subproblem (7b).

For semilinear second-order matrix differential equations of the form (9), we equip the integrator LRLF-semi with the adaptivity schemes described above. For the sake of efficiency, rank changes are only implemented in the integration of the nonlinear subproblem, even though the linear subproblems are in general not rank-preserving. Only in the case of rank augmentation in the integration of the nonlinear subproblem, the affected substeps of [12, Algorithm 3] are recomputed. This adaptive integrator is named RALRLF-semi.

4 Numerical experiments

We now report on numerical experiments for matrix differential equations resulting from space discretizations of PDEs on a rectangular domain

$$\begin{aligned} \Omega = [-L_x,L_x] \times [-L_y, L_y] \subset \mathbb {R}^2. \end{aligned}$$

(16)

For simplicity, we use a uniform mesh with n grid points in x- and m grid points in y-direction, i.e., 

$$\begin{aligned} \begin{aligned} \Omega _h&= \{ (x_j, y_i) ~|~x_j = -L_x + jh_x, ~ y_i = -L_y + i h_y, ~ 0 \le j \le n, ~ 0 \le i \le m\}, \\&\text {with} \quad h_x = \frac{2L_x}{n}, \quad h_y = \frac{2L_y}{m}, \quad n, m \in \mathbb {N}. \end{aligned} \end{aligned}$$

(17)

Errors of the low-rank solutions are measured w.r.t.  numerically computed reference solutions. Details are given in the respective subsections. Since we are only interested in the time discretization error, reference solutions and low-rank solutions are computed on the same spatial grid. The computation of the tolerance threshold as explained in Sect. 3.2 is performed with $M = 100$, i.e.,  every 100 steps we perform four additional steps with step size $\frac{\tau }{2}$, so that we increase the computational effort by $4\%$. Coosing a smaller value of M may sometimes be advantageous to reduce the global error.

All algorithms have been implemented in Python and were performed on a computer with an Intel(R) Core(TM) i7-7820X @ 3.60GHz CPU and 128 GB RAM storage. The codes are available from [25].

4.1 Nonlinear fractional Ginzburg–Landau equation

The fractional Ginzburg–Landau equation describes a variety of physical phenomena, cf.  [22, 23, 28]. Here, we consider the problem in two space dimensions [29] and with homogeneous Dirichlet boundary conditions. Discretization in space by the second-order fractional centered difference method [3] yields the stiff semilinear matrix differential equation

$$\begin{aligned} A'(t) = -D_x A(t) - A(t) D_y - (\kappa + \textrm{i}\xi ) A(t) \bullet \overline{A(t)} \bullet A(t) + \gamma A(t) , \quad A(0) = A_0.\nonumber \\ \end{aligned}$$

(18)

Here, $D_x$ and $D_y$ are symmetric Toeplitz matrices [18] with first rows

$$\begin{aligned} \frac{\nu + \textrm{i}\eta }{h^\alpha _x} \big [ g^\alpha _1, g^\alpha _2, \ldots , g^\alpha _{n - 1} \big ] \quad \text {and} \quad \frac{\nu + \textrm{i}\eta }{h^\beta _y} \big [ g^\beta _1, g^\beta _2, \ldots , g^\beta _{m- 1} \big ], \end{aligned}$$

respectively. Further, $\textrm{i}= \sqrt{-1}$, $\nu ,\kappa >0$, $\eta , \xi , \gamma \in \mathbb {R}$, $1< \alpha ,\beta < 2$ denote given parameters, and

$$\begin{aligned} g^\mu _k= \frac{(-1)^{k-1} \varGamma (1+\mu )}{\varGamma (\mu /2 - k +2) \varGamma (\mu /2 + k +2) }, \quad \mu \in \{\alpha , \beta \}, \quad k \in \mathbb {Z}, \end{aligned}$$

where $\varGamma (\cdot )$ denotes the Gamma-function.

In [29], (18) was solved with the linearized second-order backward differential scheme (LBDF2). A fixed-rank dynamical low-rank integrator for (18) was proposed in [32], based on considerations from [24]. We compute low-rank solutions of (18) with PSI-stiff and RAPSI-stiff. The solution to the linear subproblem of (18), which is of form (8), is computed with the Krylov subspace method proposed in [18].

An efficient implementation of products $F({{\widehat{A}}}) E$ of the right-hand side F(A) in (18) with a skinny matrix E is crucial. For the linear part, this is achieved by computing the matrix products in

$$\begin{aligned} -D_x {{\widehat{U}}}{{\widehat{S}}}{{\widehat{V}}}^H E - {{\widehat{U}}}{{\widehat{S}}}{{\widehat{V}}}^H D_y E \end{aligned}$$

successively from the right to the left. The implementation of the cubic nonlinear part of F is more involved, see “Appendix A.2”.

In our first experiment, we use the same parameter values as in [32], namely $L_x = L_y = 10$, $m = n = 512$, $\nu = \eta = \kappa = \xi = \gamma = 1$, $T=1$, $\alpha = 1.2$, $\beta = 1.9$, and the initial value

$$\begin{aligned} (A_0)_{ij} = 2 {{\,\textrm{sech}\,}}(x_j) {{\,\textrm{sech}\,}}(y_i) {{\,\textrm{e}\,}}^{3 \textrm{i}(x_j+y_i)}, \quad i,j=1,\ldots ,m. \end{aligned}$$

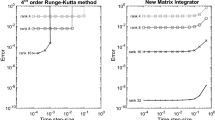
The (full-rank) reference solution is computed with LBDF2 on the same spatial grid, with time step size $\tau = 10^{-4}$. Figure 1 shows the relative global errors

$$\begin{aligned} \textrm{err} = \frac{\Vert A - {{\widehat{A}}}\Vert }{\Vert A \Vert } \end{aligned}$$

between the reference solution A and the respective low-rank solutions ${{\widehat{A}}}$ at $t= T$ for different step sizes $\tau$. Convergence order one is observed for the PSI-stiff scheme. For large step sizes, the approximations computed with the RAPSI-stiff method exhibit large errors. This is explained by the behavior of the singular values, cf.  Fig. 1 (right picture). The time-discretization error is overestimated in this experiment, so that the tolerance threshold becomes so large that the second largest singular value is discarded. The induced low-rank error is then of magnitude $10^{-1}$. If the parameter M is reduced to 10, this unfortunate rank reduction vanishes. However, reducing M increases the workload for the updates of $\texttt{tol}$, while $M=100$ worked well in all other experiments and also in this experiment for smaller step sizes.

Fig. 1

Fractional Ginzburg–Landau equation, first experiment. The left picture shows the relative global error at $T=1$ for $(\alpha ,\beta ) = (1.2, 1.9)$, where the fixed-rank approximation (yellow) is computed with $r=5$. The rank-adaptive approximation was computed with $M=100$ (orange) and $M=10$ (blue). The trajectories of the ten largest singular values of the reference solution (gray), the singular values of RAPSI-stiff ($M=10$) for $\tau = 1\cdot 10^{-3}$ (blue), and the computed tolerance threshold (red, dashed) are displayed on the right (color figure online)

Fig. 2

Fractional Ginzburg–Landau equation, second experiment. The left picture shows the relative global error at $T=1$ for $(\alpha ,\beta ) = (1.2, 1.9)$, where the fixed-rank approximation is computed with $r=8$. The trajectories of the ten largest singular values of the reference solution (gray), the singular values of RAPSI-stiff for $\tau = 10^{-3}$ (orange), and the computed tolerance threshold (red, dashed) are displayed on the right (color figure online)

For our second example, we choose the second parameter set from [32], $L_x = L_y = 8$, $n = m = 512$, $\nu = \kappa = 1$, $\eta = 0.5$, $\xi = -5$, $\gamma =3$, $\alpha = 1.2$, $\beta = 1.9$, and the initial values

$$\begin{aligned} (A_0)_{ij} = {{\,\textrm{e}\,}}^{-2 (x_j^2 + y_i^2)} {{\,\textrm{e}\,}}^{\textrm{i}(S_0)_{ij}}, \quad \text {where} \quad (S_0)_{ij} = ( {{\,\textrm{e}\,}}^{x_j+y_i} + {{\,\textrm{e}\,}}^{-(x_j+y_i)})^{-1}, \end{aligned}$$

for $i=1,\ldots ,m-1$, $j=1, \ldots , n-1$. The relative global errors at $T=1$ are displayed in Fig. 2. In contrast to the previous experiment, order one is observed for both integrators. Now the error curves for the fixed-rank integrator and its rank-adaptive variant align almost perfectly, and the singular values follow nicely the trajectories of the singular values of the reference solution.

Similar results for both experiments were obtained for the parameter values $(\alpha , \beta ) = (1.5,1.5),\, (1.7,1.3)$, and (1.9, 1.2), cf.  [25].

4.2 Nonlinear fractional Schrödinger equation

The nonlinear fractional Schrödinger equation [30] is a special case of the fractional Ginzburg–Landau equation (18) with $\nu = \kappa = \gamma = 0$. For the limit $\alpha , \beta \rightarrow 2$ it becomes the classical Schrödinger equation.

In our experiment, the reference solution to the problem was again computed with the LBDF2 method, using the step size $\tau = 2 \cdot 10^{-5}$. Figure 3 shows the results for the parameter values from [30], $L_x = L_y = 10$, $n = m = 512$, $\eta = 1$, $\xi = -2$, $T=0.2$, $\alpha = 1.2$, $\beta = 1.9$, and the initial value

$$\begin{aligned} (A_0)_{ij} = {{\,\textrm{sech}\,}}(x_j) {{\,\textrm{sech}\,}}(y_i) \exp (\textrm{i}(x_j + y_i)), \quad i,j=1,\ldots ,m-1. \end{aligned}$$

Fig. 3

Fractional Schrödinger equation. The left picture shows the relative global error at $T=0.2$ for $(\alpha ,\beta ) = (1.2, 1.9)$, where the fixed-rank approximation is computed with $r=5$. The trajectories of the ten largest singular values of the reference solution (gray), the singular values of RAPSI-stiff ($M=100$) for $\tau = 4\cdot 10^{-4}$ (orange), and the computed tolerance threshold (red, dashed) are displayed on the right (color figure online)

Again, the relative global error curves match almost perfectly for both low-rank methods, and are also clearly indicating convergence of order one. The results for other choices of $\alpha$ and $\beta$ are available in [25].

4.3 Laser-plasma interaction

As an example for second-order problems, we consider a reduced model of laser-plasma interaction from [14, 15, 26]. It is given by a wave equation with space-dependent cubic nonlinearity on a bounded, rectangular domain $\Omega$ given in (16) with periodic boundary conditions. After space discretization according to [26, Section 4.1.3], we obtain the matrix differential equation

$$\begin{aligned} A''(t) = \mathscr {L}A(t) - 0.3 {\widetilde{\chi }} \bullet \left( A(t) - \frac{1}{2} A(t) \bullet \overline{A(t)} \bullet A(t) \right) = F\big (A(t)\big ), \end{aligned}$$

(19)

with initial values $A(0) = A_0$ and $A'(0) = B_0$ given by

$$\begin{aligned} (A_0)_{ij} = 0.12 \exp \Big ( - \frac{y_i^2}{l^2_0} - \frac{x_j^2}{w^2_0} + \textrm{i}y_i \Big ), \quad (B_0)_{ij} = \Big ( - \frac{2y_i}{l^2_0} - \textrm{i}\Big ) (A_0)_{ij}, \end{aligned}$$

where $x_j,y_i$ are defined in (17) and $i=1,\ldots ,m,~j = 1,\ldots ,n$. The discrete Laplacian $\mathscr {L}$ acts on A(t) via

$$\begin{aligned} \mathscr {L}A(t) = \mathscr {F}^{-1}_{m} D^2_y \mathscr {F}_{m} A(t) + A(t) D_x, \end{aligned}$$

where $D_x \in \mathbb {R}^{n \times n}$ denotes the symmetric Toeplitz matrix with first row

$$\begin{aligned} - \frac{1}{12 h_x^2} \left[ 30,-16,1,0,\ldots ,0,1,-16 \right] , \end{aligned}$$

and

$$\begin{aligned} D_y = \frac{\textrm{i}\pi }{L_y} {{\,\textrm{diag}\,}}\left( 0, \ldots , \frac{m}{2}-1, - \frac{m}{2}, \ldots , -1 \right) . \end{aligned}$$

$\mathscr {F}_{m}$ denotes the discrete Fourier transformation operator for m Fourier modes and $\mathscr {F}^{-1}_{m}$ its inverse. Hence we use fourth order finite differences with n equidistant grid points in transversal direction and a pseudospectral method with m equidistant grid points in longitudinal direction.

Equation (19) describes the propagation of a laser pulse with wavelength $\lambda _0$ in the direction of the positive y-axis through vacuum and through a strongly localized plasma barrier. The plasma is located between $y = 50 \pi$ and $y= 300\pi$ and has constant density 0.3. The localization is modeled by the matrix ${\widetilde{\chi }} \in \mathbb {R}^{m \times n}$ with entries

$$\begin{aligned} {\widetilde{\chi }}_{ij} = {\left\{ \begin{array}{ll} 1, &{} 50\pi \le y_i \le 300 \pi , \\ 0, &{} \text {else.} \end{array}\right. } \end{aligned}$$

(20)

The interaction between the pulse and the plasma is modeled by a cubic nonlinearity. As in [15] we use the parameters $\lambda _0=\pi$, $l_0=10 \pi$, $w_0=100\pi$, $L_x = 300 \pi$, and $L_y = 600 \pi$.

Our numerical experiments were carried out for $t \in [0, 600 \pi ]$ with $n = 1024$ and $m = 8192$ discretization points in transversal and longitudinal direction, respectively. The reference solution was computed with the Gautschi-type method from [26], with step size $\tau _0 = L_y/(80 m)$. For the low-rank solutions we used the step sizes $\tau = 2^k \tau _0$, $k=2,\ldots ,6$. The algorithms LRLF and LRLF-semi were performed with fixed ranks ${r_A}= {r_B}=4$.

In [12] it was obeserved that choosing the weights $\omega _i$ in LRLF-semi according to the direction of motion can improve the approximation significantly. Since the laser pulse moves mainly in longitudinal direction, we therefore used the weights

$$\begin{aligned} \omega ^2_1 = \frac{2}{3}, \quad \omega ^2_2 = 0, \quad \omega ^2_3 = \frac{1}{3} \end{aligned}$$

in (10) for both LRLF-semi and RALRLF-semi.

Fig. 4

Laser-plasma interaction. Relative global error between reference solution and low-rank approximations at $T=600 \pi$ (left), and absolute error in the maximal intensity for $\tau = 4 \tau _0 = L_y/(20m)$ (right). The fixed-rank methods were computed with ${r_A}={r_B}=4$, the rank-adaptive methods with $M=100$

Fig. 5

Laser-plasma interaction. Trajectories of the ten largest singular values of the reference solution (gray) together with the trajectories of the singular values of the rank-adaptive low-rank integrators for $\tau = 4 \tau _0$ (left: RALRLF, right: RALRLF-semi), and the respective computed tolerance thresholds (red, dashed) (color figure online)

The left picture in Fig. 4 shows the relative global error at $T= 600 \pi$ between the reference solution and the different low-rank integrators. Second-order convergence is observed in all cases, and the integrators designed for semilinear problems yield better approximations than the other methods. The accuracy of the rank-adaptive schemes is comparable to those of the fixed-rank integrators, showing nicely that the heuristics works well for this example, cf.  Fig. 5.

In physics, the maximal intensity $\max _{i,j} | A_{ij}(t) |^2$ of the propagating pulse over time is sometimes of higher interest than A itself. In the right picture of Fig. 4, the absolute error between the maximal intensity of the numerical pulse computed with the Gautschi-type integrator and the maximal intensity of the approximations obtained by the low-rank integrators is displayed.

4.4 Sine-Gordon equation

In our last experiment, we consider the two-dimensional sine-Gordon equation on the domain $\Omega$ from (16) with homogeneous Neumann boundary conditions [1]. Using finite differences of second order on the grid (17) with $L_x = L_y = 7$, $n = m = 1001$ in both x- and y-direction, we obtain the semi-discretized matrix differential equation

$$\begin{aligned} A''(t) = D A(t) + A(t) D^T - \Phi \bullet {{\,\mathrm{\underline{\sin }}\,}}\big (A(t)\big ), \quad t \in [0, T], \quad A \in \mathbb {C}^{(m+1)\times (m+1)}. \end{aligned}$$

Here, ${{\,\mathrm{\underline{\sin }}\,}}(A)$ denotes the entrywise evaluation of the sine function. The matrix D is given by

$$\begin{aligned} D = \frac{1}{h^2}\begin{pmatrix} -2 &{} 2 &{} &{} &{} \\ 1 &{} -2 &{} 1 &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} 1 &{} -2 &{} 1 \\ &{} &{} &{} 2 &{} -2 \end{pmatrix} \in \mathbb {R}^{(m+1) \times (m+1)}, \quad h= \frac{1}{m+1}. \end{aligned}$$

The storage-economical evaluation of the products ${{\,\mathrm{\underline{\sin }}\,}}({{\widehat{A}}})E$ and ${{\,\mathrm{\underline{\sin }}\,}}({{\widehat{A}}})^H E$ is presented in “Appendix A”. There is no preferred direction of propagation, so that we used the weights

$$\begin{aligned} \omega ^2_1 = \omega ^2_2 = \omega ^2_3 = \frac{1}{3} \end{aligned}$$

in (10) for the LRLF-semi and RALRLF-semi methods .

First we consider the initial values

$$\begin{aligned} (A_0)_{ij} = 4 \arctan \exp \left( \frac{x_j-3.5}{0.954} \right) , \quad (B_0)_{ij} = 0.629 {{\,\textrm{sech}\,}}\left( \frac{x_j-3.5}{0.954}\right) , \end{aligned}$$

and

$$\begin{aligned} \Phi _{ij} = 1+{{\,\textrm{sech}\,}}^2 \sqrt{x_j^2 + y_i^2}, \end{aligned}$$

$i,j=0,\ldots ,m$, of a line soliton in an inhomogeneous medium [2, Section 3.1.3]. The reference solution is computed by the leapfrog scheme on the same spatial grid with time step size $\tau = 2.5 \cdot 10^{-5}$. Figure 6 shows the relative global errors between the low-rank approximations and the reference solution. Convergence order two is observed for all methods. The fixed-rank integrators are slightly more accurate than their rank-adaptive pendants, probably because they use a higher rank.

Fig. 6

Sine-Gordon equation, first setting. Relative global error at $T=9$ between reference solution and low-rank approximations (left), and rank evolution of the solutions computed with the rank-adaptive integrators over time (right) for $\tau = 10^{-4}$. For the fixed-rank integrators, we used ${r_A}= {r_B}=20$, for the rank-adaptive methods $M=100$ (color figure online)

Fig. 7

Sine-Gordon equation, second setting. Relative global error at $T=11$ between reference solution and low-rank approximations (left), and rank evolution of the solutions computed with the rank-adaptive integrators over time (right) for $\tau = 10^{-4}$. For the fixed-rank integrators, we used ${r_A}= {r_B}=50$, for the rank-adaptive methods $M=100$ (color figure online)

In a second setting, we consider the symmetric perturbation of a static line soliton [2, Section 3.1.2] with $\Phi _{ij}= 1$, $(B_0)_{ij} = 0$, and

$$\begin{aligned} (A_0)_{ij} = 4\arctan \exp \left( x_j + 1 - \frac{2}{\cosh (y_i+7)} - \frac{2}{\cosh (y_i-7)}\right) , \quad i,j = 0,\ldots ,m. \end{aligned}$$

Figure 7 shows a similar behavior of the methods as in the first setting. For the $\textsc {RALRLF}$ scheme however, the initial rank is rather large, and drops significantly after a few steps. This is caused in the routine for determining an appropriate initial rank. As explained in Sect. 3.2, the initial guess $r_1=5$ is doubled repeatedly until the criterion for continuing the integration beyond the first $\nu$ steps is satisfied. In this experiment, an initial rank of $\sim 23$ is adequate. Therefore, the guesses 5, 10, and 20 are rejected, until $r_1 = 40$ is accepted and rank reduction applies in the subsequent integration steps.

5 Conclusion and outlook

In the present paper, we developed adaptive schemes for dynamical low-rank integrators for first and second-order matrix differential equations. The performance of these schemes have been illustrated by numerical experiments.

Both the projector-splitting integrator and the unconventional robust integrator have been successfully adapted to first-order tensor differential equations, cf.  [6, 20, 21] and references therein. We are confident that the strategy for the adaptive algorithm for matrix differential equations also works for the tensor case. This is part of ongoing research and will be reported in the future.

A Evaluation of entrywise functions for low-rank matrices

Let f be a (nonlinear) function that acts entrywise on matrices, let $E \in \mathbb {C}^{n\times r}$ be an arbitrary matrix, and let ${{\widehat{A}}}= {{\widehat{U}}}{{\widehat{S}}}{{\widehat{V}}}^H \in \mathscr {M}_r$ be a low-rank matrix with factors ${{\widehat{U}}},{{\widehat{S}}},{{\widehat{V}}}$ given in (4). For the efficiency of low-rank integrators for nonlinear problems, it is crucial to evaluate the product

$$\begin{aligned} f({{\widehat{A}}})E, \end{aligned}$$

(21)

using the factors ${{\widehat{U}}}$, ${{\widehat{S}}}$, and ${{\widehat{V}}}$ instead of the full matrix ${{\widehat{A}}}$. However, the entrywise computation of all components ${{\widehat{A}}}_{ij}$ of ${{\widehat{A}}}$ can not be avoided in general. Nevertheless, it is not necessary to store the full matrix ${{\widehat{A}}}\in \mathbb {C}^{m\times n}$, but it suffices to compute the rows of ${{\widehat{A}}}$ successively.

1.1 A.1 General functions

The ith row of ${{\widehat{A}}}$ is given by

$$\begin{aligned} (e_i{{\widehat{A}}}) = (e_i \widetilde{U}) {{\widehat{V}}}^H \in \mathbb {C}^{1 \times n}, \quad i = 1,\ldots ,m, \end{aligned}$$

where $\widetilde{U}= {{\widehat{U}}}{{\widehat{S}}}$. The matrix products $(e_i \widetilde{U}) {{\widehat{V}}}^H$ are carried out with complexity $\mathscr {O}(nr)$. We now evaluate f entrywise at $e_i {{\widehat{A}}}$ and multiply the result with E, which gives the ith row of the product (21). This sequence of operations can be performed for each $i = 1, \ldots ,m$ independently and thus in parallel. This allows for a fast computation, even for large $m$. Similarly, the evaluation of

$$\begin{aligned} C = f({{\widehat{A}}})^H E, \quad E \in \mathbb {C}^{m\times r}, \end{aligned}$$

is realized by computing the jth row via

$$\begin{aligned} (e_j C) = f( \widetilde{U}(e_j {{\widehat{V}}})^H)^H E, \quad j = 1,\ldots ,n. \end{aligned}$$

This approach is suitable for any function f acting entrywise on its argument, e.g.,  trigonometric functions. For monomials, the successive computation of the entries of ${{\widehat{A}}}$ can be avoided, which speeds up the computation further.

1.2 A.2 Monomials

Consider a (complex) monomial of degree $p \in \mathbb {N}$, $f(z) = z^p$ for $z \in \mathbb {C}$. The entrywise evaluation of f at ${{\widehat{A}}}\in \mathscr {M}_r$ is defined as $\big (f({{\widehat{A}}})\big )_{ij} = {{\widehat{A}}}^p_{ij}$.

We now show how to compute the product (21) without computing or storing the elements of ${{\widehat{A}}}$ explicitly. Let $\widetilde{U}= {{\widehat{U}}}{{\widehat{S}}}\in \mathbb {C}^{m\times r}$. Then we have

$$\begin{aligned} {{\widehat{A}}}= {{\widehat{U}}}{{\widehat{S}}}{{\widehat{V}}}^H = \widetilde{U}{{\widehat{V}}}^H = \sum ^r_{j=1} \widetilde{U}_j {{\widehat{V}}}^H_j, \end{aligned}$$

(22)

where $\widetilde{U}_j$ is the jth column of $\widetilde{U}$ and ${{\widehat{V}}}_j$ the jth column of ${{\widehat{V}}}$, respectively. The Hadamard product is distributive and satisfies

$$\begin{aligned} (\widetilde{U}_j {{\widehat{V}}}_j^H) \bullet (\widetilde{U}_k {{\widehat{V}}}_k^H) = (\widetilde{U}_j \bullet \widetilde{U}_k) ({{\widehat{V}}}_j \bullet {{\widehat{V}}}_k)^H \end{aligned}$$

for $1 \le j,k \le r$, cf.  [27, Section 2]. Hence, for $E \in \mathbb {C}^{n\times r}$ it holds

$$\begin{aligned} f({{\widehat{A}}}) E&= \left( \left( \sum ^r_{j_1 = 1} \widetilde{U}_{j_1} {{\widehat{V}}}_{j_1}^H \right) \bullet \cdots \bullet \left( \sum ^r_{j_p = 1} \widetilde{U}_{j_p} {{\widehat{V}}}_{j_p}^H \right) \right) E \nonumber \\&= \left( \sum ^r_{j_1,\ldots ,j_p=1} \bigl (\widetilde{U}_{j_1} \bullet \widetilde{U}_{j_2} \bullet \cdots \bullet \widetilde{U}_{j_p}\bigr ) \bigl ({{\widehat{V}}}_{j_1} \bullet {{\widehat{V}}}_{j_2} \bullet \cdots \bullet {{\widehat{V}}}_{j_p}\bigr )^H \right) E \nonumber \\&= \sum ^r_{j_1,\ldots ,j_p=1} (\widetilde{U}_{j_1} \bullet \widetilde{U}_{j_2} \bullet \cdots \bullet \widetilde{U}_{j_p}) \big ( ({{\widehat{V}}}_{j_1} \bullet {{\widehat{V}}}_{j_2} \bullet \cdots \bullet {{\widehat{V}}}_{j_p})^H E \big ). \end{aligned}$$

(23)

For the special case of the cubic nonlinearity which appears in the examples in Sects. 4.1, 4.2, and 4.3,

$$\begin{aligned} f({{\widehat{A}}}) = {{\widehat{A}}}\bullet {\overline{{{\widehat{A}}}}} \bullet {{\widehat{A}}}, \end{aligned}$$

where ${\overline{{{\widehat{A}}}}}$ denotes the complex conjugate of ${{\widehat{A}}}$, (23) reads

$$\begin{aligned} ({{\widehat{A}}}\bullet {\overline{{{\widehat{A}}}}} \bullet {{\widehat{A}}}) E= & {} \sum ^r_{j,k,\ell = 1} \widetilde{U}_{jk\ell } {{\widehat{V}}}_{jk\ell }^H E, \\ {\text {where}}\quad \widetilde{U}_{jk\ell }= & {} \widetilde{U}_j \bullet {\overline{\widetilde{U}}}_k \bullet \widetilde{U}_\ell , \\ {{\widehat{V}}}_{jk\ell }= & {} {{\widehat{V}}}_j \bullet {\overline{{{\widehat{V}}}}}\!_k \bullet {{\widehat{V}}}_\ell . \end{aligned}$$

The computational cost is further reduced by exploiting the symmetry in j and $\ell$,

$$\begin{aligned} ({{\widehat{A}}}\bullet {\overline{{{\widehat{A}}}}} \bullet {{\widehat{A}}}) E= \sum ^r_{k=1} \Bigg [ \sum ^r_{j=1} \big ( \widetilde{U}^2_j \bullet {\overline{\widetilde{U}}}_k \big ) \Big (\big ( {{\widehat{V}}}^2_j \bullet {\overline{{{\widehat{V}}}}}\!_k \big )^H E \Big )+ 2 \sum ^r_{j=1} \sum ^{j-1}_{\ell =1} \widetilde{U}_{jk\ell } ({{\widehat{V}}}^H_{jk\ell } E) \Bigg ]. \nonumber \\ \end{aligned}$$

(24)

The product $({{\widehat{A}}}\bullet {\overline{{{\widehat{A}}}}} \bullet {{\widehat{A}}})^H E$ with $E \in \mathbb {C}^{m\times r}$ can be computed analogously.

Additional simplifications apply to the product $({\widetilde{\chi }} \bullet {{\widehat{A}}}\bullet {\overline{{{\widehat{A}}}}} \bullet {{\widehat{A}}}) E$ with ${\widetilde{\chi }} \in \mathbb {C}^{m\times n}$ given in (20). It satisfies

$$\begin{aligned} {\widetilde{\chi }} = \begin{bmatrix} 0_{(\eta -1) \times n} \\ \mathbb {1}_{(\xi - \eta +1) \times n} \\ 0_{(m- \xi ) \times n} \end{bmatrix} = \begin{pmatrix} 0_{\eta -1} \\ \mathbb {1}_{\xi - \eta + 1} \\ 0 _{m-\xi } \end{pmatrix} \mathbb {1}_{n}^T {=}{:}\widetilde{\mathbb {1}}_{m} \mathbb {1}^T_{n}, \end{aligned}$$

(25)

where $0_n$, $\mathbb {1}_n$ are the vectors of length n filled with zeros and ones, respectively, and $0_{n\times p}$ and $\mathbb {1}_{n \times p}$ the matrices of dimension $n \times p$ with all entries being zeros and ones, respectively. From (22) and (25), we obtain

$$\begin{aligned} ({\widetilde{\chi }} \bullet {{\widehat{A}}}) E&= \Big [ ( {\widetilde{\mathbb {1}}}_{m} \mathbb {1}^T_{n}) \bullet {{\widehat{A}}}\Big ] E = \left[ \sum ^r_{j=1} {{\,\textrm{diag}\,}}({\widetilde{\mathbb {1}}}_{m}) \widetilde{U}_j {{\widehat{V}}}^H_j {{\,\textrm{diag}\,}}(\mathbb {1}_{n}) \right] E \\&= \sum ^r_{j=1} \begin{pmatrix} 0_{\eta -1} \\ \vartheta (\widetilde{U}_j) \\ 0_{m- \xi } \end{pmatrix} ({{\widehat{V}}}^H_j E) = \begin{bmatrix} 0_{(\eta -1)\times r} \\ \sum \limits ^r_{j=1} \vartheta (\widetilde{U}_j) ({{\widehat{V}}}^H_j) E \\ 0_{(m- \xi ) \times r} \end{bmatrix}, \end{aligned}$$

where $\vartheta (\widetilde{U}_j)$ denotes the restriction of $\widetilde{U}_j$ to its $\eta$th to $\xi$th entries. Here, we made use of the following property of the Hadarmard product, cf.  [27, Section 2]: If $A \in \mathbb {C}^{m\times n}$, $x \in \mathbb {R}^m$, and $y \in \mathbb {R}^n$, then

$$\begin{aligned} (x y^T) \bullet A = {{\,\textrm{diag}\,}}(x) A {{\,\textrm{diag}\,}}(y). \end{aligned}$$

Hence, it suffices to compute and sum up the small matrices $\vartheta (\widetilde{U}_j) ({{\widehat{V}}}^H_jE)$. Likewise, using (24), we have

$$\begin{aligned}{} & {} ({\widetilde{\chi }} \bullet {{\widehat{A}}}\bullet \overline{\!{{\widehat{A}}}} \bullet {{\widehat{A}}}) E \\{} & {} =\left[ \begin{array}{cc} &{}0_{(\eta -1)\times r} \\[1ex] &{}\sum \limits ^r_{k=1} \Big [ \sum \limits ^r_{j=1} \big ( \vartheta (\widetilde{U}_j)^2 \bullet \vartheta ({\overline{\widetilde{U}}}_k) \big ) \Big (\big ( {{\widehat{V}}}^2_j \bullet {\overline{{{\widehat{V}}}}}\!_k \big )^H E \Big ) + 2 \sum \limits ^r_{j=1} \sum \limits ^{j-1}_{\ell =1} \vartheta (\widetilde{U}_{jk\ell }) ({{\widehat{V}}}^H_{jk\ell } E) \Big ] \\[1ex] &{} 0_{(m- \xi ) \times r} \end{array}\right] . \end{aligned}$$

The implementation of $({\widetilde{\chi }} \bullet {{\widehat{A}}}\bullet \overline{\!{{\widehat{A}}}} \bullet {{\widehat{A}}})^H E$, $E \in \mathbb {C}^{m\times r}$, is realized in the same manner.