Convergence of Lobatto-type Runge–Kutta methods for partitioned differential-algebraic systems of index 2

Abstract

In this paper a numerical scheme for partitioned systems of index 2 DAEs, such as those arising from nonholonomic mechanical problems, is proposed and its order for a certain class of Runge–Kutta methods we call of Lobatto-type is proven.

1 Introduction

Let $N = \mathbb {R}^n$ and $M \subseteq N$ a submanifold of $\mathrm {codim} M = m$. Let M be defined as the null-set of $\phi : N \rightarrow \mathbb {R}^m$. A generic explicit differential equation on M can be recast into a semi-explicit index 2 differential algebraic equation (DAE) on N taking the form:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{y} = f(y,\lambda )\\ 0 = \phi (y) \end{array}\right. \end{aligned}$$

(1.1)

where $y \in N$ and $\lambda \in V$, with V a vector space such that $\dim V = m$. Studies on the numerical solution of initial value problems (IVP) for such systems can be found in the bibliography that serves as foundation for this paper, such as [2] or [5].

We are interested in a subset of such problems, which will be referred to as partitioned, where $y = (q,p)$, $\dim Q = n_q$, $\dim P = n_p$, and $\lambda \in \mathbb {R}^m$.

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q} = f(q,p)\\ \dot{p} = g(q,p,\lambda )\\ 0 = \phi (q,p). \end{array}\right. \end{aligned}$$

(1.2)

Such is the case of the equations of motion of nonholonomic mechanical systems which motivates our study, where $\dim Q = \dim P = n$ (thus, in this case $\dim N = 2 n$). For a Hamiltonian function $H: N \rightarrow \mathbb {R}$ and linear nonholonomic constraints $\mu _i^{\alpha }(q) \dot{q}^i = 0$, $i = 1,\ldots , n, \alpha = 1,\ldots , m$, we get

$$\begin{aligned} \left\{ \begin{array}{l} \dot{q}^i = \partial _{p_i} H\\ \dot{p}_i = -\partial _{q^i} H + \lambda _{\alpha } \mu ^{\alpha }_i\\ 0 = \mu ^{\alpha }_i \partial _{p_i} H \end{array}\right. \end{aligned}$$

(1.3)

An IVP for this partitioned DAE is defined by an initial condition $(q_0, p_0, \lambda _0) \in \left. N\right| _{M} \times \mathbb {R}^m$.

The development and application of the methods shown here in the case of nonholonomic mechanical systems will be the subject of a follow-up paper where further numerical experiments will be performed [1].

For the remainder of the paper we will assume that f, g and $\phi$ are sufficiently differentiable and that $\left( D_p \phi D_{\lambda } g\right) (q,p,\lambda )$ remains invertible in a neighbourhood of the exact solution. Here $D_p$ means the derivative with respect to the p variables, and similarly with q and $\lambda$.

2 Lobatto-type methods

A numerical solution of an IVP for (1.1) can be found using an s-stage Runge–Kutta (RK) method with coefficients $(a_{i j}, b_{j})$. Writing the corresponding equations is a relatively trivial matter, taking the form:

$$\begin{aligned} y_1&= y_0 + h \sum _{j = 1}^s b_{j} k_j, \quad \lambda _1 = \lambda _0 + h \sum _{j = 1}^s b_{j} l_j \end{aligned}$$

(2.1a)

$$\begin{aligned} Y_i&= y_0 + h \sum _{j = 1}^s a_{i j} k_j, \quad \Lambda _i = \lambda _0 + h \sum _{j = 1}^s a_{i j} l_j \end{aligned}$$

(2.1b)

$$\begin{aligned} k_i&= f(Y_i,\Lambda _i), \quad 0 = g(Y_i). \end{aligned}$$

(2.1c)

Note that these $l_j$ are not given explicitly and must instead be solved for with the help from the constraint equations. In fact, provided the RK coefficients satisfy certain conditions, the second set of equations in (2.1a) and (2.1b) may be discarded.

Now, a numerical solution of an IVP for Eq. (1.2) can also be found using an s-stage partitioned RK method but already the correct application of such a scheme is non-trivial. One could naively write:

$$\begin{aligned} q_1&= q_0 + h \sum _{j = 1}^s b_{j} V_j,\quad p_1 = p_0 + h \sum _{j = 1}^s \hat{b}_{j} W_j,\quad \lambda _1 = \lambda _0 + h \sum _{j = 1}^s \check{b}_j U_j, \end{aligned}$$

(2.2a)

$$\begin{aligned} Q_i&= q_0 + h \sum _{j = 1}^s a_{i j} V_j,\quad P_i = p_0 + h \sum _{j = 1}^s \hat{a}_{i j} W_j,\quad \Lambda _i = \lambda _0 + h \sum _{j = 1}^s \check{a}_{i j} U_j, \end{aligned}$$

(2.2b)

$$\begin{aligned} V_i&= f(Q_i, P_i),\quad W_i = g(Q_i, P_i, \Lambda _i),\quad 0 = \phi (Q_i, P_i). \end{aligned}$$

(2.2c)

Again, $U_j$ are not given explicitly and, as above, in some cases, it may also be possible to discard the third set of equations in (2.2a) and (2.2b). Such a system of equations may have certain issues, both from a solvability and a numerical convergence point of view. This is especially true for the particular case of partitioned RK methods that we will consider.

In [5] the author considers RK methods satisfying the hypotheses:

• H1 $a_{1 j} = 0$ for $j = 1,\ldots , s$;

• H2 the submatrix $\tilde{A} := (a_{i j})_{i,j \ge 2}$ is invertible;

• H3 $a_{s j} = b_j$ for $j = 1,\ldots , s$ (the method is stiffly accurate).

H1 implies that $c_1 =\sum _{j=1}^{s}a_{1j}= 0$ and for Eq. (2.1) $Y_1 = y_0$, $\Lambda _1 = \lambda _0$. H3 implies that $y_1 = Y_s$, $\lambda _1 = \Lambda _s$. Furthermore, if the method is consistent, i.e. $\sum _j b_j = 1$, then H3 implies $c_s = 1$. For Eq. (2.2), if $(\check{a}_{i j},\check{b}_j)$ also satisfies the hypotheses, then $Q_1 = q_0$, $\Lambda _1 = \lambda _0$, $Q_s = q_1$ and $\Lambda _s = \lambda _1$. The most salient example of these methods is the Lobatto IIIA, which is a continuous collocation method.

The Lobatto IIIB is a family of discontinuous collocation methods which are symplectically conjugate to the IIIA methods. Two RK methods, $(a_{i j}, b_j)$ and $(\hat{a}_{i j}, \hat{b}_j)$, are symplectically conjugate if they satisfy:

$$\begin{aligned}&b_i \hat{a}_{i j} + \hat{b}_j a_{j i} = b_i \hat{b}_j \quad \text {for}\quad i,j = 1,\ldots , s, \end{aligned}$$

(2.3)

$$\begin{aligned}&b_j = \hat{b}_j \quad \text {for}\quad j = 1,\ldots , s. \end{aligned}$$

(2.4)

Together they form the Lobatto IIIA-IIIB family of symplectic partitioned Runge-Kutta methods, which is precisely the one we want to study (see also [3, 9]).

Note that Lobatto IIIB methods do not satisfy hypotheses H1, H2 and H3. In fact, any symplectic conjugate method to a method satisfying those hypotheses must necessarily be such that:

H1’:

$\hat{a}_{i s} = 0$ for $i = 1,\ldots , s$;

H2’:

$\hat{a}_{i 1} = \hat{b}_1$ for $i = 1,\ldots , s$.

Obviously, the submatrix $\tilde{\hat{A}} := (\hat{a}_{i j})_{i,j \ge 2}$ is never invertible because of H1’, and this is the culprit of the solvability issues of (2.2).

We shall consider a further compatibility hypothesis:

H*:

$\hat{c}_{i} = c_i$ for $i = 1 ,\ldots , s$.

This hypothesis ensures that the stages of both methods are concurrent. The Lobatto IIIA-IIIB family satisfies H*, but one should note that for $s = 2$, $\hat{c}_i \ne \sum _{j = 1}^2 \hat{a}_{i j}$.

For such methods, we propose the following equations for the numerical solution of the partitioned IVP:

$$\begin{aligned} q_1&= q_0 + h \displaystyle \sum _{j = 1}^s b_{j} f(Q_j, P_j),\quad p_1 = p_0 + h \displaystyle \sum _{j = 1}^s \hat{b}_{j} g(Q_j, P_j, \Lambda _j), \end{aligned}$$

(2.5a)

$$\begin{aligned} Q_i&= q_0 + h \displaystyle \sum _{j = 1}^s a_{i j} f(Q_j, P_j),\quad P_i = p_0 + h \displaystyle \sum _{j = 1}^s \hat{a}_{i j} g(Q_j, P_j, \Lambda _j), \end{aligned}$$

(2.5b)

$$\begin{aligned} L_i&= p_0 + h \displaystyle \sum _{j = 1}^s a_{i j} g(Q_j, P_j, \Lambda _j),\quad 0 = \phi (Q_i, L_i), \end{aligned}$$

(2.5c)

together with $\Lambda _1 = \lambda _0$ and $\Lambda _s = \lambda _1$. From H1, we have that $L_1 = p_0$, and from H3 and Eq. (2.3), $L_s = p_1$. The intuition behind the proposed scheme is that $P_i$ are not as good an approximation to the continuous p as $Q_i$ are to q, and in order to impose the constraint we need a more accurate estimate of p. Such new variables can be added to partitioned non-DAE systems, where they become decoupled and can be computed as a post-processing step to have better approximations of the p variables inside the interval. The auxiliary $L_i$ variables can be eliminated altogether, leading to

$$\begin{aligned} q_1&= q_0 + h \displaystyle \sum _{j = 1}^s b_{j} f(Q_j, P_j), p_1 = p_0 + h \displaystyle \sum _{j = 1}^s \hat{b}_{j} g(Q_j, P_j, \Lambda _j), \end{aligned}$$

(2.6a)

$$\begin{aligned} Q_i&= q_0 + h \displaystyle \sum _{j = 1}^s a_{i j} f(Q_j, P_j), P_i = p_0 + h \displaystyle \sum _{j = 1}^s \hat{a}_{i j} g(Q_j, P_j, \Lambda _j), \end{aligned}$$

(2.6b)

$$\begin{aligned} 0&= \phi \left( q_0 + h \displaystyle \sum _{j = 1}^s a_{i j} f(Q_j, P_j), p_0 + h \displaystyle \sum _{j = 1}^s a_{i j} g(Q_j, P_j, \Lambda _j)\right) , \end{aligned}$$

(2.6c)

It should be noted that, although similar, these methods do not generally coincide with the SPARK methods proposed by L. O. Jay in [7]. (After talking to prof. Jay, he noted the approach suggested here is similar to that of Murua [8] which was not previously known by the author.)

There are several simplifying assumptions that a given RK scheme satisfies:

$$\begin{aligned}&B(p): \sum _{i = 1}^s b_i c_i^{k-1} = \frac{1}{k} \quad \text {for}\quad k = 1,\ldots , p \end{aligned}$$

(2.7a)

$$\begin{aligned}&C(q): \sum _{j = 1}^s a_{i j} c_j^{k-1} = \frac{c_i^k}{k} \quad \text {for}\quad i = 1, \ldots , s,\quad k = 1,\ldots , q \end{aligned}$$

(2.7b)

$$\begin{aligned}&D(r): \sum _{i = 1}^s b_i c_i^{k-1} a_{i j} = \frac{b_j (1 - c_j^k)}{k} \quad \text {for}\quad j = 1, \ldots , s,\quad k = 1,\ldots , r \end{aligned}$$

(2.7c)

When referring to these assumptions for a RK method $(\hat{a}_{i j}, \hat{b}_i)$ we will write them as $\widehat{X}(\hat{y})$. Note that if $(a_{i j}, b_i)$ and $(\hat{a}_{i j}, \hat{b}_i)$ are two symplectically conjugate methods, each satisfying the symplifying assumptions B(p), C(q), D(r) and $\widehat{B}(\hat{p}), \widehat{C}(\hat{q}), \widehat{D}(\hat{r})$ then $\hat{p} = p$, C(q) implies $\hat{r} = q$, and conversely D(r) implies $\hat{q} = r$. Also in the symplectically conjugate case, whenever both $p, r \ge 1$, H* is automatically satisfied.

Apart from these, there are a few more simplifying assumptions that pairs of compatible methods satisfy (see [6]):

$$\begin{aligned}&C\widehat{C}(Q): \sum _{j = 1}^s \sum _{l = 1}^s a_{i j} \hat{a}_{j l} c_l^{k-2} = \frac{c_i^k}{k (k - 1)} \quad \text {for}\quad i = 1,\ldots , s,\quad k = 2,\ldots , Q\\&D\widehat{D}(R): \sum _{i = 1}^s \sum _{j = 1}^s b_i c_i^{k-2} a_{i j} \hat{a}_{j l} = \frac{b_l}{k (k - 1)} \left[ (k - 1) - (k c_l - c_l^k)\right] \\&\qquad \hbox {for}\quad l = 1, \ldots , s,\quad k = 2,\ldots , R \\&\widehat{C} C(\hat{Q}): \sum _{j = 1}^s \sum _{l = 1}^s \hat{a}_{i j} a_{j l} c_l^{k-2} = \frac{c_i^k}{k (k - 1)} \quad \text {for}\quad i = 1, \ldots , s,\quad k = 2,\ldots , \hat{Q}\\&\widehat{D} D(\hat{R}): \sum _{i = 1}^s \sum _{j = 1}^s \hat{b}_i c_i^{k-2} \hat{a}_{i j} a_{j l} = \frac{\hat{b}_l}{k (k - 1)} \left[ (k - 1) - (k c_l - c_l^k)\right] \\&\qquad \hbox {for}\quad l = 1, \ldots , s,\quad k = 2,\ldots , \hat{R} \end{aligned}$$

It can be shown that if both methods are symplectically conjugate, then $Q = R = p - r$ and $\hat{Q} = \hat{R} = p - q$. In particular, Lobatto IIIA and IIIB methods, which will be very important for us, satisfy $B(2 s - 2)$, C(s), $D(s-2)$, $\widehat{B}(2 s - 2)$, $\widehat{C}(s-2)$, $\widehat{D}(s)$, as well as $C\widehat{C}(s), D\widehat{D}(s), \widehat{C}C(s-2), \widehat{D}D(s-2)$ respectively.

Lastly, there is a function associated to a RK method that we need to define. Consider the linear problem $\dot{y} = \lambda y$, and apply one step of the given method for an initial value $y_0$. The function $\mathcal {R}(z)$ defined by $y_1 = \mathcal {R}(h \lambda ) y_0$ is the so-called stability function of the method.

For an arbitrary RK method we have that

$$\begin{aligned} \mathcal {R}(z) = 1 + z b^T (I_s - z A)^{-1} {1_s}, \end{aligned}$$

where $A = \left( a_{i j}\right)$, $b = (b_1,\ldots ,b_s)^T$ and ${1_s} = {\overbrace{(1,\ldots ,1)^T}^s}$. In the particular case of a method satisfying that $a_{s j} = b_j$, i.e. $e_s^T A = b^T$, which is the case of Lobatto methods, this can be reduced to:

$$\begin{aligned} \mathcal {R}(z) = e_s^T (I_s - z A)^{-1} {1_s}, \end{aligned}$$

where $e_s = (\underbrace{0,\ldots ,0}_{s-1}, 1)^T$.

3 Existence, uniqueness and influence of perturbations

Before proceeding, let us introduce the following notational conventions:

$$\begin{aligned} A = \left[ \begin{array}{cc} a_{1 1} &{} \tilde{A}^1\\ \tilde{A}_1 &{} \tilde{A} \end{array} \right] = \left[ \begin{array}{c} A^1\\ \overline{A} \end{array} \right] = \left[ \begin{array}{cc} A_1&\underline{A} \end{array} \right] , \quad \hat{A} = \left[ \begin{array}{cc} \hat{a}_{1 1} &{} \tilde{\hat{A}}^1\\ \tilde{\hat{A}}_1 &{} \tilde{\hat{A}} \end{array} \right] = \left[ \begin{array}{c} \hat{A}^1\\ \overline{\hat{A}} \end{array} \right] = \left[ \begin{array}{cc} \hat{A}_1&\underline{\hat{A}} \end{array} \right] , \end{aligned}$$

where $A_1 = (a_{i 1})$ is a column matrix and $A^1 = (a_{1 j})$ is a row matrix, with $i, j = 1,\ldots , s$. $\tilde{A}_1, \tilde{A}^1$ indicate the elimination of the first component of these vectors. Clearly, if H1 applies then, $A^1 = (a_{1 1},\; \tilde{A}^1) = 0_s^T$, where $0_s = {\underbrace{(0,\ldots ,0)}_{s}} ^T$.

We will mainly be concerned with derivatives of the functions that define our partitioned vector field and the constraint, Eq. (1.2), namely f, g and $\phi$, evaluated at the different stages of our RK methods, (2.5) and (2.5). For this we define:

$$\begin{aligned} D_q f&= \text {blockdiag}(D_q f(Q_1, P_1), D_q f(Q_2, P_2),\ldots , D_q f(Q_s, P_s))\\&= \text {blockdiag}(D_q f_1, D_q \tilde{f}), \end{aligned}$$

where $D_q f_1 = D_q f(Q_1, P_1)$ and the tilde indicates the elimination of the derivative with respect to the first stage. The same applies to derivatives of g and $\phi$, where the latter will be evaluated at $(Q_i, L_i)$. In analogy with our notation for A and $\hat{A}$, we write $\overline{D_q f} = [ 0_{s-1, n} \; D_q \tilde{f} ]$ and $\underline{D_q f} = [ 0_{s-1, n} \; (D_q \tilde{f})^T ]^T$, where $0_{m,n}$ is the zero matrix of dimension m by n.

Similar use of tilde for the elimination of the first stage components applies also to other vectors such as $\delta _Q$, $\delta _P$, $\theta$ in Theorem 3.2.

Theorem 3.1

Let $U \subset N \times \mathbb {R}^m$ be a fixed neighbourhood of $(q_0, p_0, \lambda _0) = (q_0(h),$ $p_0(h), \lambda _0(h))$, a set of h-dependent starting values, and assume:

$$\begin{aligned}&\phi (q_0, p_0) = {\mathcal {O}(h^2)}\\&(D_q \phi \cdot f)(q_0,p_0) + (D_p \phi \cdot g)(q_0,p_0,\lambda _0) = \mathcal {O}(h)\\&(D_p \phi \cdot D_{\lambda } g)(q,p,\lambda ) \text { invertible in }U. \end{aligned}$$

Assume also that the Runge–Kutta coefficients A verify the hypotheses H1 and H2, and that $\hat{A}$ satisfies H1’ and H*. Then, for $h \le h_0$, there exists a locally unique solution to:

$$\begin{aligned} Q_i&= q_0 + h \displaystyle \sum _{j = 1}^s a_{i j} f(Q_j,P_j), \end{aligned}$$

(3.1a)

$$\begin{aligned} P_i&= p_0 + h \displaystyle \sum _{j = 1}^s \hat{a}_{i j} g(Q_j,P_j,\Lambda _j), \end{aligned}$$

(3.1b)

$$\begin{aligned} 0&= \phi \left( q_0 + h \displaystyle \sum _{j = 1}^s a_{i j} f(Q_j,P_j), p_0 + h \displaystyle \sum _{j = 1}^s a_{i j} g(Q_j,P_j,\Lambda _j)\right) , \end{aligned}$$

(3.1c)

with $\Lambda _1 = \lambda _0$, satisfying:

$$\begin{aligned} \begin{array}{rl} Q_i - q_0 &{}= \mathcal {O}(h),\\ P_i - p_0 &{}= \mathcal {O}(h),\\ \Lambda _i - \lambda _0 &{}= \mathcal {O}(h). \end{array} \end{aligned}$$

Proof

The proof of existence differs little from what is already offered in [2] (for invertible A matrix) or [5] (for A satisfying the hypotheses H1 and H2). The idea is to consider a homotopic deformation of the equations which leads to a system of differential equations where the existence of a solution for the corresponding IVP implies the existence of a solution to the original system.

The key of the proof is the use of the invertibility of $D_p \phi (\tilde{A} \otimes I) D_{\lambda } g$, which is a term arising from the constraint equation. As stated in the former section, if the system were described by Eq. (2.2) we would instead have $D_p \phi (\tilde{\hat{A}} \otimes I) D_{\lambda } g$, which is not invertible by H1’, rendering the system unsolvable.

The proof of uniqueness remains essentially the same. $\square$

Theorem 3.2

Under the assumptions of Theorem 3.1, let $Q_i$, $P_i$, $\Lambda _i$ be the solution of system (3.1). Now consider the perturbed values $\hat{Q}_i$, $\hat{P}_i$, $\hat{\Lambda }_i$ satisfying:

$$\begin{aligned} \hat{Q}_i&= \hat{q}_0 + h \displaystyle \sum _{j = 1}^s a_{i j} f(\hat{Q}_j,\hat{P}_j) + h\delta _{Q,i} \end{aligned}$$

(3.2a)

$$\begin{aligned} \hat{P}_i&= \hat{p}_0 + h \displaystyle \sum _{j = 1}^s \hat{a}_{i j} g(\hat{Q}_j,\hat{P}_j,\hat{\Lambda }_j) + h\delta _{P,i} \end{aligned}$$

(3.2b)

$$\begin{aligned} 0&= \phi \left( \hat{q}_0 + h \displaystyle \sum _{j = 1}^s a_{i j} f(\hat{Q}_j,\hat{P}_j) + h\delta _{Q,i}, \right. \nonumber \\&\quad \left. \hat{p}_0 + h \displaystyle \sum _{j = 1}^s a_{i j} g(\hat{Q}_j,\hat{P}_j,\hat{\Lambda }_j) + h\delta _{P,i}\right) + \theta _i \end{aligned}$$

(3.2c)

with $\hat{\Lambda }_1 = \hat{\lambda }_0$, and where $\delta _{Q,i}$, $\delta _{P,i}$ and $\theta _i$ are perturbation terms. Additionally, assume that:

$$\begin{aligned} \begin{array}{rl} \hat{q}_0 - q_0 &{}= \mathcal {O}(h),\\ \hat{p}_0 - p_0 &{}= \mathcal {O}(h),\\ \delta _{Q,i}, \delta _{P,i} &{}= \mathcal {O}(h),\\ \theta _i &{}= \mathcal {O}(h^2). \end{array} \end{aligned}$$

(3.3)

Then, using the notation $\Delta X := \hat{X} - X$ and $\left\| X \right\| := \max _i \left\| X_i \right\|$, for small h we have:

$$\begin{aligned} \left\| \Delta Q_i \right\|&\le C \left( \left\| \Delta q_0 \right\| + h \left\| \Delta p_0 \right\| + h^2 \left\| \Delta \lambda _0 \right\| + h \left\| \delta _Q \right\| + h^2 \left\| \delta _P \right\| + h \left\| \theta \right\| \right) \\ \left\| \Delta P_i \right\|&\le C \left( \left\| \Delta q_0 \right\| + \left\| \Delta p_0 \right\| + h \left\| \Delta \lambda _0 \right\| + h^2 \left\| \delta _Q \right\| + h \left\| \delta _P \right\| + \left\| \theta \right\| \right) \\ \left\| \Delta \Lambda _i \right\|&\le \frac{C}{h} \left( h \left\| \Delta q_0 \right\| + h \left\| \Delta p_0 \right\| + h \left\| \Delta \lambda _0 \right\| + h \left\| \delta _Q \right\| + h \left\| \delta _P \right\| + \left\| \theta \right\| \right) . \end{aligned}$$

Proof

To tackle this problem we first subtract Eq. (3.1) from Eq. (3.2) and linearize. If we temporarily introduce back the auxiliary $L_i$ variables defined in Eq. (2.5), we get:

$$\begin{aligned} \Delta Q_i&= \Delta q_0 + h \sum _{j = 1}^s a_{i j} \left[ D_q f(Q_j,P_j) \Delta Q_j + D_p f(Q_j,P_j) \Delta P_j\right] + h \delta _{Q,i}\\&\quad + \mathcal {O}\left( h \Vert \Delta Q\Vert ^2 + h\Vert \Delta P \Vert ^2 + h \Vert \Delta Q \Vert \Vert \Delta P \Vert \right) \\ \Delta L_i&= \Delta p_0 + h \sum _{j = 1}^s a_{i j} \left[ D_q g(Q_j,P_j,\Lambda _j) \Delta Q_j + D_p g(Q_j,P_j,\Lambda _j) \Delta P_j \right. \\&\quad \left. + D_{\lambda } g(Q_j,P_j,\Lambda _j) \Delta \Lambda _j\right] + h\delta _{P,i} + \mathcal {O}\left( h \Vert \Delta Q \Vert ^2 + h\Vert \Delta P \Vert ^2\right. \\&\quad \left. + h \Vert \Delta Q\Vert \Vert \Delta P \Vert + h \Vert \Delta Q \Vert \Vert \Delta \Lambda \Vert + h \Vert \Delta P \Vert \Vert \Delta \Lambda \Vert \right) \\ \Delta P_i&= \Delta p_0 + h \sum _{j = 1}^s \hat{a}_{i j} \left[ D_q g(Q_j,P_j,\Lambda _j) \Delta Q_j + D_p g(Q_j,P_j,\Lambda _j) \Delta P_j \right. \\&\quad \left. + D_{\lambda } g(Q_j,P_j,\Lambda _j) \Delta \Lambda _j\right] + h\delta _{P,i} + \mathcal {O}\left( h \Vert \Delta Q \Vert ^2 + h\Vert \Delta P \Vert ^2\right. \\&\quad \left. + h \Vert \Delta Q \Vert \Vert \Delta P \Vert + h \Vert \Delta Q \Vert \Vert \Delta \Lambda \Vert + h \Vert \Delta P \Vert \Vert \Delta \Lambda \Vert \right) \\ 0&= D_q\phi (Q_i,L_i) \Delta Q_i + D_p\phi (Q_i,L_i) \Delta L_i + \theta _i\\&\quad + \mathcal {O}\left( \Vert \Delta Q \Vert ^2 + \Vert \Delta L \Vert ^2 + \Vert \Delta Q \Vert \Vert \Delta L \Vert \right) . \end{aligned}$$

We can thus rewrite the system as

$$\begin{aligned} \Delta Q&= {1_s} \otimes \Delta q_0 + h \left[ \delta _Q + (A \otimes I_n) (D_q f \Delta Q + D_p f \Delta P ) \right] \end{aligned}$$

(3.4a)

$$\begin{aligned} \Delta L&= {1_s} \otimes \Delta p_0 + h \left[ \delta _Q + (A \otimes I_n) (D_q g \Delta Q + D_p g \Delta P + D_{\lambda } g \Delta \Lambda ) \right] \end{aligned}$$

(3.4b)

$$\begin{aligned} \Delta P&= {1_s} \otimes \Delta p_0 + h \left[ \delta _Q + (\hat{A} \otimes I_n) (D_q g \Delta Q + D_p g \Delta P + D_{\lambda } g \Delta \Lambda ) \right] \end{aligned}$$

(3.4c)

$$\begin{aligned} 0&= D_q \phi \Delta Q + D_p \phi \Delta L + \theta \end{aligned}$$

(3.4d)

Using hypothesis H1 the first stage components of $\Delta Q$ and $\Delta L$ simplify to

$$\begin{aligned} \Delta Q_1&= \Delta q_0 + h \delta _{Q,1}\\ \Delta L_1&= \Delta p_0 + h \delta _{L,1}\\ D_q\phi (q_0,p_0) \Delta q_0 + D_p\phi (q_0,p_0) \Delta p_0&= \mathcal {O}\left( h \Vert \delta _{Q,1}\Vert + h \Vert \delta _{L,1}\Vert + \Vert \theta _1\Vert \right. \\&\quad \left. + \Vert \Delta q_0\Vert ^2 + \Vert \Delta p_0\Vert ^2 + \Vert \Delta q_0\Vert \Vert \Delta p_0\Vert \right) . \end{aligned}$$

Thus, isolating the rest of the variables, we can rewrite the system as

$$\begin{aligned} \Delta \tilde{Q}&= {1_{s-1}} \otimes \Delta q_0 + h \left[ \tilde{\delta }_Q + (\overline{A} \otimes I_n) D_p f \Delta P + (\tilde{A} \otimes I_n) D_q \tilde{f} \Delta \tilde{Q} + (\tilde{A}_1 \otimes D_q f_1 \Delta Q_1 ) \right] \\ \Delta \tilde{L}&= {1_{s-1}} \otimes \Delta p_0 + h \left[ \tilde{\delta }_P + (\overline{A} \otimes I_n) D_p g \Delta P + (\tilde{A} \otimes I_n) ( D_q \tilde{g} \Delta \tilde{Q} + D_{\lambda } \tilde{g} \Delta \tilde{\Lambda })\right. \\&\quad +\left. (\tilde{A}_1 \otimes ( D_q g_1 \Delta Q_1 + D_{\lambda } g_1 \Delta \Lambda _1)) \right] \\ \Delta P&= {1_s} \otimes \Delta p_0 + h \left[ \tilde{\delta }_P + (\hat{A} \otimes I_n) D_p g \Delta P + (\underline{\hat{A}} \otimes I_n) ( D_q \tilde{g} \Delta \tilde{Q} + D_{\lambda } \tilde{g} \Delta \tilde{\Lambda }) \right. \\&\quad + \left. (\tilde{\hat{A}}_1 \otimes ( D_q g_1 \Delta Q_1 + D_{\lambda } g_1 \Delta \Lambda _1) ) \right] \\ 0&= D_q \tilde{\phi } \Delta \tilde{Q} + D_p \tilde{\phi } \Delta \tilde{L} + D_q \phi _1 \Delta Q_1 + D_p \phi _1 \Delta L_1 + \theta \\ \end{aligned}$$

Our mission is to solve for $\Delta \Lambda$, but due to the singularity of A it will not be possible to solve for the entire vector and instead we will solve only for $\Delta \tilde{\Lambda }$. We will first insert $\Delta \tilde{Q}$ and $\Delta \tilde{L}$ in the constraint equation. This eliminates the latter variables from the analysis.

$$\begin{aligned} 0&= D_q \tilde{\phi } \left\{ h (\overline{A} \otimes I_n) D_p f \Delta P + h (\tilde{A} \otimes I_n) D_q \tilde{f} \Delta \tilde{Q} + (\tilde{A}_1 \otimes D_q f_1 \Delta Q_1 ) + \cdots \right\} \\&\quad + D_p \tilde{\phi } \left\{ h (\overline{A} \otimes I_n) D_p g \Delta P + h (\tilde{A} \otimes I_n) ( D_q \tilde{g} \Delta \tilde{Q} + D_{\lambda } \tilde{g} \Delta \tilde{\Lambda })\right. \\&\quad + \left. h(\tilde{A}_1 \otimes ( D_q g_1 \Delta Q_1 + D_{\lambda } g_1 \Delta \Lambda _1)) + \cdots \right\} \end{aligned}$$

From the hypotheses we have that $D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g}$ is invertible, so we can indeed solve for $\Delta \tilde{\Lambda }$ in terms of $\Delta Q$, $\Delta P$ and $\Delta \Lambda _1$.

$$\begin{aligned} h \Delta \tilde{\Lambda }&= - \left( D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g}\right) ^{-1}\nonumber \\&\quad \times \left\{ \tilde{\theta } + h \left[ D_q \tilde{\phi } (\tilde{A} \otimes I_n) D_q \tilde{f} + D_p \tilde{\phi } (\tilde{A} \otimes I_n) D_q \tilde{g} \right] \Delta \tilde{Q} \right. \nonumber \\&\quad + h \left[ D_q \tilde{\phi } (\overline{A} \otimes I_n) D_p f + D_p \tilde{\phi } (\overline{A} \otimes I_n) D_p g \right] \Delta P\nonumber \\&\quad +\left. h \tilde{A}_1 \otimes ( D_q g_1 \Delta Q_1 + D_{\lambda } g_1 \Delta \Lambda _1) + \cdots \right\} \end{aligned}$$

(3.5)

Substituting this back into the equations we can read off the results from the theorem. $\square$

Lemma 3.1

In addition to the hypotheses of Theorem 3.1, suppose that C(q), $\hat{C}(\hat{q})$ and that $(D_q \phi \cdot f)(q_0,p_0) + (D_p \phi \cdot g)(q_0,p_0,\lambda _0) = \mathcal {O}(h^\kappa )$, with $\kappa \ge 1$. Then the solution of Eq. (3.1), $Q_i$, $P_i$ and $\Lambda _i$ satisfies:

$$\begin{aligned} \begin{aligned} Q_i&= q_0 + \displaystyle \sum _{j = 1}^{\mu } \dfrac{c_i^j h^j}{j!} DQ_{(j)}(q_0,p_0,\lambda _0) + \mathcal {O}(h^{\mu + 1})\\ P_i&= p_0 + \displaystyle \sum _{j = 1}^{\nu } \dfrac{c_i^j h^j}{j!} DP_{(j)}(q_0,p_0,\lambda _0) + \mathcal {O}(h^{\nu + 1})\\ \Lambda _i&= \lambda _0(q_0,p_0) + \displaystyle \sum _{j = 1}^{\xi } \dfrac{c_i^j h^j}{j!} D\Lambda _{(j)}(q_0,p_0,\lambda _0) + \mathcal {O}(h^{\xi + 1}) \end{aligned} \end{aligned}$$

where $\lambda _0(q_0,p_0)$ is implicitly defined by the condition $(D_q \phi \cdot f)(q_0, p_0) + (D_p \phi \cdot g)(q_0, p_0,$ $\lambda _0(q_0,p_0)) = 0$, $\mu = \min (\kappa + 1, q, \max (\hat{q} + 1, Q + 1))$, $\nu = \min (\kappa , \hat{q})$, $\xi = \min (\kappa - 1, q - 1)$, and $DQ_{(i)}$, $DP_{(i)}$ and $D\Lambda _{(i)}$ are functions composed by products of the derivatives of f, g and $\phi$ of i-th order evaluated at $(q_0, p_0, \lambda _0(q_0,p_0))$.

Proof

Following [5], Lemma 4.3, we can use the implicit function theorem to obtain $\lambda _0(q_0,p_0) - \lambda _0 = \mathcal {O}(h^\kappa )$. Assume $(q(t), p(t), \lambda (t))$ is the exact solution of Eq. (1.2) with $q(t_0) = q_0$, $p(t_0) = p_0$ and $\lambda (t_0) = \lambda _0$, and let $Q_i = q(t_0 + c_i h)$, $L_i = P_i = p(t_0 + c_i h)$ and $\Lambda _i = \lambda (t_0 + c_i h)$ in the result of Theorem 3.3. Finally, let $\hat{Q}_i$, $\hat{p}_i$, $\hat{P}_i$ and $\hat{\Lambda }_i$ be the solution of Eq. (3.2) with $\hat{q}_0 = q_0$, $\hat{p}_0 = p_0$, $\hat{\lambda }_0 = \lambda _0(q_0,p_0)$ and $\theta = 0$. As we satisfy the conditions of Theorem 3.2 we are left with:

$$\begin{aligned} \left\| \Delta Q_i \right\|&\le C \left( h^{\kappa + 2} + h \left\| \delta _Q \right\| + h^2 \left\| \delta _L \right\| + h^2 \left\| \delta _P \right\| \right) \\ \left\| \Delta P_i \right\|&\le C \left( h^{\kappa + 1} + h^2 \left\| \delta _Q \right\| + h \left\| \delta _L \right\| + h \left\| \delta _P \right\| \right) \\ \left\| \Delta \Lambda _i \right\|&\le C \left( h^{\kappa } + \left\| \delta _Q \right\| + \left\| \delta _L \right\| \right) \end{aligned}$$

where we have made use of the fact that $\left\| \Delta \lambda _0 \right\| = \mathcal {O}(h^\kappa )$. What remains is to compute $\delta _Q$, $\delta _L$, $\delta _P$ to obtain the result we are after.

Inserting the exact solution into Eq. (3.2) we obtain:

$$\begin{aligned} q(t_0 + c_i h)&= q_0 + h \sum _{j = 1}^s a_{i j} f(q(t_0 + c_j h),p(t_0 + c_j h)) + h\delta _{Q,i}\\&= q_0 + h \sum _{j = 1}^s a_{i j} \dot{q}(t_0 + c_i h) + h\delta _{Q,i}\\ p(t_0 + c_i h)&= p_0 + h \sum _{j = 1}^s \hat{a}_{i j} g(q(t_0 + c_j h),p(t_0 + c_j h),\lambda (t_0 + c_j h)) + h\delta _{P,i}\\&= p_0 + h \sum _{j = 1}^s \hat{a}_{i j} \dot{p}(t_0 + c_i h) + h\delta _{P,i} \end{aligned}$$

Now, expanding in Taylor series about $t_0$ and taking into account that for a RK satisfying C(q) we have that

$$\begin{aligned} y({t_0} + c_i h) = y({t_0}) + \sum _{j = 1}^{q-1} \frac{1}{j!} y^{(j)}(t_0) c_i^j h^j + \mathcal {O}(h^{q}), \end{aligned}$$

we get:

$$\begin{aligned} \delta _{Q,i}&= \frac{h^{q} q^{(q+1)}({t_0})}{q!} \left( \frac{c_i^{q+1}}{q+1} - \sum _{j=1}^{s} a_{i j} c_j^q\right) + \mathcal {O}(h^{q+1})\\ \delta _{P,i}&= \frac{h^{\hat{q}} p^{(\hat{q}+1)}({t_0})}{\hat{q}!} \left( \frac{c_i^{\hat{q}+1}}{\hat{q}+1} - \sum _{j=1}^{s} \hat{a}_{i j} c_j^{\hat{q}}\right) + \mathcal {O}(h^{\hat{q}+1}). \end{aligned}$$

Finally, we obtain:

$$\begin{aligned} \left\| \Delta Q_i \right\|&\le C \left( h^{\min (\kappa + 2, q+1, \max (\hat{q} + 2, Q + 2))}\right) \\ \left\| \Delta P_i \right\|&\le C \left( h^{\min (\kappa + 1, q+1, \hat{q} + 1)}\right) \\ \left\| \Delta \Lambda _i \right\|&\le C \left( h^{\min (\kappa , q)}\right) \end{aligned}$$

which proves our lemma. $\square$

Remark 3.1

For the Lobatto IIIA-B methods we have that $\hat{q} + 2 = Q = q = s$ and this result implies that:

$$\begin{aligned} \left\| \Delta Q_i \right\|&= \mathcal {O}(h^{\min (\kappa + 2, s+1)}),\\ \left\| \Delta P_i \right\|&= \mathcal {O}(h^{\min (\kappa + 1, s-1)}),\\ \left\| \Delta \Lambda _i \right\|&= \mathcal {O}(h^{\min (\kappa , s)}) \end{aligned}$$

Theorem 3.3

In addition to the hypotheses of Theorem 3.2, suppose that A and $\hat{A}$ are symplectically conjugate and, C(q), $\hat{C}(r)$, D(r), $\hat{D}(q)$, $D\hat{D}(p-r)$, $\hat{D}D(p-q)$ and H3 hold. Furthermore, suppose $(D_q \phi \cdot f)(q_0,p_0) + (D_p \phi \cdot g)(q_0,p_0,\lambda _0) = \mathcal {O}(h^\kappa )$, with $\kappa \ge 1$. Then we have:

$$\begin{aligned} \Delta q_1&= \Delta q_0 + \mathcal {O}\left( h \left\| \Delta p_0 \right\| + h^{m + 2} \left\| \Delta \lambda _0 \right\| + h \left\| \delta _Q \right\| + h^2 \left\| \delta _P \right\| + h \left\| \theta \right\| \right) \end{aligned}$$

(3.6)

$$\begin{aligned} \Delta p_1&= \Pi _{Q,0}(q_0, p_0, \lambda _0) \Delta q_0 + \Pi _{P,0}(q_0, p_0, \lambda _0) \Delta p_0\nonumber \\&\quad + \mathcal {O}\left( h^{m + 2} \left\| \Delta \lambda _0 \right\| + h^2 \left\| \delta _Q \right\| + h \left\| \delta _P \right\| + \left\| \theta \right\| \right) \end{aligned}$$

(3.7)

$$\begin{aligned} \Delta \lambda _1&= \mathcal {R}_A(\infty ) \Delta \lambda _0\nonumber \\&\quad + \mathcal {O}\left( \left\| \Delta q_0 \right\| + \left\| \Delta p_0 \right\| + h \left\| \Delta \lambda _0 \right\| + \left\| \delta _Q \right\| + \left\| \delta _P \right\| + \left\| \theta \right\| /h \right) \end{aligned}$$

(3.8)

where $m = \min (\kappa - 1, q - 1, r, p - q, p - r)$, $\mathcal {R}_A$ is the stability function of the method A, $\Pi _{Q,0} = - D_{\lambda } g (D_p \phi D_{\lambda } g)^{-1} D_q \phi$ and $\Pi _{P,0} = I_n - D_{\lambda } g (D_p \phi D_{\lambda } g)^{-1} D_p \phi$.

Proof

This proof follows closely that of [5], Theorem 4.4. The idea is to take the results from Theorem 3.2, insert them in Eqs. (3.4a) and (3.4c) and solve for $\Delta Q$ and $\Delta P$. Later, we insert the results into

$$\begin{aligned} \Delta q_1&= \Delta q_0 + h (b^T \otimes I_n) (D_q f \Delta Q + D_p f \Delta P) \end{aligned}$$

(3.9)

$$\begin{aligned} \Delta p_1&= \Delta p_0 + h (b^T \otimes I_n) (D_q g \Delta Q + D_p g \Delta P) + h (\tilde{b}^T \otimes I_n) D_{\lambda } \tilde{g} \Delta \tilde{\Lambda }\nonumber \\&\quad + h (b_1 \otimes I_n) D_{\lambda } g_1 {\Delta \Lambda _1} \end{aligned}$$

(3.10)

where $\Delta \tilde{\Lambda }$ is a function of $(Q, P, \Lambda _1, \hat{Q}, \hat{P}, \hat{\Lambda }_1)$, and perform a Taylor expansion of each term. Just as in [5], the important result here is the $h^{m+2}$ factor in front of $\left\| \Delta \lambda _0\right\|$, which means that we need to pay special attention to $\Delta \Lambda _1$.

In our case ${\Delta \lambda _1} = \Delta \Lambda _s$ coincides with $\Delta Z_s$ in [5] of the same theorem without changes. The differences appear in the rest of the components, where having two sets of RK coefficients makes the Taylor expansion of the terms and the tracking of each component much more difficult.

From here on we will forget about all terms except for the ones with $\Delta \Lambda _1$, as the rest vary little from what was found in theorem 3.2 and they can be easily obtained, thus barring the need to carry them around any longer.

Inserting Eq. (3.5) into Eq. (3.10) we can collect all terms multiplying by $\Delta P$, $\Delta \tilde{Q}$ and $\Delta \Lambda _1$ separately. Let

$$\begin{aligned} \Pi _Q&= -(\tilde{b}^T \otimes I_n) \tilde{X}_q\\ \Pi _P&= \tilde{e}_s \otimes I_n - (\tilde{b}^T \otimes I_n) \tilde{X}_p \end{aligned}$$

with

$$\begin{aligned} \tilde{X}_i&:= D_{\lambda } \tilde{g} \left( D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g} \right) ^{-1} D_i \tilde{\phi }\nonumber \\&= D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) ^{-1} \left( D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) ^{-1}\right) ^{-1} D_i \tilde{\phi } \end{aligned}$$

(3.11)

where $i = q, p$. Thus, we can write

$$\begin{aligned} \Delta p_1&= h (\Pi _Q (\tilde{A} \otimes I_n) (D_q \tilde{f} \Delta \tilde{Q} + \overline{D_{p} f} \Delta {P} + \Pi _P (\overline{A} \otimes I_n) (\underline{D_q g} \Delta \tilde{Q} + D_p g \Delta P) \nonumber \\&\quad + (b_1 \otimes I_n) D_{\lambda } g_1 \Delta \Lambda _1 - {(\tilde{b}^T \otimes I_n ) \tilde{X}_p} (\tilde{A}_1 \otimes D_3 g_1 \Delta \Lambda _1) ) + \cdots \end{aligned}$$

(3.12)

Similar groupings can be done for $\Delta P$ after inserting Eq. (3.5) into Eq. (3.4c)

$$\begin{aligned} \Xi _Q&= -(\underline{\hat{A}} \otimes I_n) \tilde{X}_P (\overline{A} \otimes I_n)\\ \Xi _P&= \hat{A} \otimes I_n - (\underline{\hat{A} }\otimes I_n) \tilde{X}_Q (\overline{A} \otimes I_n) \end{aligned}$$

so that

$$\begin{aligned} \Delta P = h [ \Xi _Q \Delta \tilde{Q} + \Xi _P \Delta P + \hat{A}_1 \otimes D_{\lambda } g_1 \Delta \Lambda _1 - (\underline{\hat{A}} \otimes I_n) \tilde{X}_p (\tilde{A}_1 \otimes D_{\lambda } g_1 \Delta \Lambda _1)] + \cdots \end{aligned}$$

(3.13)

In order to account for the implicit dependence on $\Delta \Lambda _1$ in Eq. (3.12), we need to solve the system formed by Eq. (3.13) together with

$$\begin{aligned} \Delta \tilde{Q} = h \left[ (\tilde{A} \otimes I_n) D_q \tilde{f} \Delta \tilde{Q} + (\overline{A} \otimes I_n) D_p f \Delta P \right] + \cdots \end{aligned}$$

(3.14)

Before solving that system, let us first expand the terms multiplying $\Delta \Lambda _1$. Inside $\tilde{X}_p$, we find the product $D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) ^{-1}$ composed of:

$$\begin{aligned} D_p \tilde{\phi }= & {} {\sum _{i = 0}^\chi } h^i \tilde{C}^i \otimes D_p \tilde{\phi }_{i} + \mathcal {O}(h^{{\chi } + 1})\\&\quad \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) ^{-1} = \sum _{i = 0}^\omega h^i \tilde{A} \tilde{C}^i \tilde{A}^{-1} \otimes D_{\lambda } \tilde{g}_{i} + \mathcal {O}(h^{\omega + 1}) \end{aligned}$$

where, from Lemma 3.1, $\chi = \min (\mu ,\nu )$ and $\omega = \min (\mu ,\nu ,\xi )$. This results in:

$$\begin{aligned} D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) ^{-1} = \sum _{0 \le i + j \le \omega }^\omega h^{i + j} \tilde{C}^i \tilde{A} \tilde{C}^j \tilde{A}^{-1} \otimes D_p \tilde{\phi }_i D_{\lambda } \tilde{g}_j + \mathcal {O}(h^{\omega + 1}). \end{aligned}$$

Inversion of this product can be carried out as a Taylor expansion resulting in a so-called von Neumann series $(I - T)^{-1} = \sum _{i=0}^{\infty } T^i$. To do this, first, let us rewrite the former expression as

$$\begin{aligned}&D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) ^{-1}\\&= \left( I_{s-1} \otimes I_n + \sum _{1< i + j \le \omega }^\omega h^{i + j} \tilde{C}^i \tilde{A} \tilde{C}^j \tilde{A}^{-1} \otimes D_p \tilde{\phi }_i D_{\lambda } \tilde{g}_j \left( D_p \tilde{\phi }_0 D_{\lambda } \tilde{g}_0\right) ^{-1}\right) \\&\quad \times \left( I_{s-1} \otimes D_p \tilde{\phi }_0 D_{\lambda } \tilde{g}_0\right) + \mathcal {O}(h^{\omega + 1})\\&= \left( I_{s-1} \otimes I_n - \sum _{1< i + j \le \omega }^\omega - h^{i + j} \tilde{C}^i \tilde{A} \tilde{C}^j \tilde{A}^{-1} \otimes D_p \tilde{\phi }_i D_{\lambda } \tilde{g}_j {\Psi }\right) \\&\quad \times \left( I_{s-1} \otimes {\Psi }^{-1}\right) + \mathcal {O}(h^{\omega + 1})\\&= \left( I_{s-1} \otimes I_n - \sum _{1 < \left| \alpha \right| }^\omega - h^{\left| \alpha \right| } G_{\alpha } \otimes H_{\alpha } \right) \times \left( I_{s-1} \otimes {\Psi }^{-1}\right) + \mathcal {O}(h^{\omega + 1}) \end{aligned}$$

where $\Psi = \left( D_p \tilde{\phi }_0 D_{\lambda } \tilde{g}_0\right) ^{-1}$. In the last line we have introduced the multi-index $\alpha$ of $\dim \alpha = 2$, i.e. $\alpha \in \mathbb {N}^2$. We will denote the k-th component of $\alpha$ by $\alpha _{(k)}$. If $\alpha = (i,j)$, then $\left| \alpha \right| = \sum _{k = 1}^{\dim \alpha } \alpha _{(k)} = i + j$ and

$$\begin{aligned} G_{\alpha } = \tilde{C}^i \tilde{A} \tilde{C}^j\tilde{A}^{-1}, \quad H_{\alpha } = D_p \tilde{\phi }_i D_{\lambda } \tilde{g}_j {\Psi } \end{aligned}$$

Defining

$$\begin{aligned} \widehat{G}_{\beta } = \prod _{i = 1}^n G_{\alpha _i}, \quad \widehat{H}_{\beta } = \prod _{i = 1}^n H_{\alpha _i}, \end{aligned}$$

where now $\beta$ can be interpreted as:

• a multi-index of even dimension, $\dim \beta \le 2 \vert \beta \vert$, such that for i odd $\beta _{(i)}$ and $\beta _{(i+1)}$ are never both 0, or

• a multi-index of $\alpha$-multi-indices, i.e. $\beta = (\alpha _1,\ldots , \alpha _n)$, running for $1 \le n \le \vert \beta \vert$, and $1 \le \vert \alpha _i\vert \le \vert \beta \vert$,

the inverse of this expression may be written as

$$\begin{aligned}&\left( D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) ^{-1}\right) ^{-1}\\&\quad = \left( I_{s-1} \otimes {\Psi }\right) \times \left( \sum _{\left| \beta \right| = 0}^\omega \sum _{{\mathop {\text {even}}\limits ^{\dim \beta \ge 2}}}^{2 \vert \beta \vert } (-1)^{\frac{\dim \beta }{2}} h^{\left| \beta \right| } \widehat{G}_{\beta } \otimes \widehat{H}_{\beta } \right) + \mathcal {O}(h^{\omega + 1}). \end{aligned}$$

We can sandwich the expression between $D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right)$ and $D_p \tilde{\phi }$ to obtain:

$$\begin{aligned} \tilde{X}_p&= D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) \left( D_p \tilde{\phi } \left( \tilde{A} \otimes I_{n}\right) D_{\lambda } \tilde{g} \left( \tilde{A} \otimes I_{m}\right) ^{-1}\right) ^{-1} D_p \tilde{\phi }\\&= \left( \sum _{\left| \gamma \right| = 0}^\omega \sum _{{\mathop {\text {even}}\limits ^{\dim \gamma \ge 2}}}^{2 \vert \gamma \vert } (-1)^{\frac{\dim \gamma }{2} - 1} h^{\left| \gamma \right| } R_{\gamma } \otimes S_{\gamma } \right) + \mathcal {O}(h^{\omega + 1}) \end{aligned}$$

where:

$$\begin{aligned} R_{\gamma }&= \tilde{C}^{\gamma _{(1)}} \tilde{A}^{-1} \left[ \prod _{{\mathop {\text {even}}\limits ^{i> 0}}}^{\dim \gamma - 2}\tilde{C}^{\gamma _{(i)}} \tilde{A} \tilde{C}^{\gamma _{(i+1)}} \tilde{A}^{-1} \right] \tilde{C}^{\gamma _{(\dim \gamma )}}\\ S_{\gamma }&= D_{\lambda } \tilde{g}_{\gamma _{(1)}} {\Psi } \left[ \prod _{{\mathop {\text {even}}\limits ^{i > 0}}}^{\dim \gamma - 2} D_p \tilde{\phi }_{\gamma _{(i)}} D_{\lambda } \tilde{g}_{\gamma _{(i+1)}} {\Psi }\right] D_p \tilde{\phi }_{\gamma _{(\dim \gamma )}} \end{aligned}$$

with $\gamma$ multi-index of $\dim \gamma \le 2 \omega$ even, and such that for i even, $\gamma _{(i)}$ and $\gamma _{(i+1)}$ are never both 0.

With this result, we can go back to Eq. (3.13). Note that if we expand $D_{\lambda } g_1$ as in Lemma 3.1 and apply H1, we have that $c_1 = 0$ and, therefore, the only term that survives is the 0-th order term, $D_{\lambda } g_{1,0}$. Also note that $(\tilde{A}_1 \otimes I_n ) D_{\lambda } g_{1,0} \Delta \Lambda _1 = (I_{s-1} \otimes D_{\lambda } g_{1,0}) (\tilde{A}_1 \otimes \Delta \Lambda _1) = D_{\lambda } \tilde{g}_{0} (\tilde{A}_1 \otimes \Delta \Lambda _1)$. This point is crucial:

Assume we have two valid multi-indices, $\gamma$ and $\gamma '$, with $\dim \gamma ' = \dim \gamma + 2$, such that $\gamma ' = (\gamma _{(1)},\ldots ,\gamma _{(\dim _{\gamma })},0,0)$. This implies that $\gamma _{(\dim \gamma )} \ne 0$, because otherwise $\gamma '$ would not be valid. Then $R_{\gamma } = R_{\gamma '}$. Of course $S_{\gamma } \ne S_{\gamma '}$, but $S_{\gamma '} = S_{\gamma } D_{\lambda } \tilde{g}_0 {\Psi } D_p \tilde{\phi }_0$ and thus $S_{\gamma '} D_{\lambda } \tilde{g}_0 = S_{\gamma } D_{\lambda } \tilde{g}_0 {\Psi } {\Psi }^{-1} = S_{\gamma } D_{\lambda } \tilde{g}_0$. Furthermore, their contributions have opposite signs and therefore, they vanish. Thus, the only terms of the expansion that can survive are those such that $\gamma _{(\dim \gamma -1)} \ne 0$, $\gamma _{(\dim \gamma )} = 0$ and this in turn means that all surviving RK symbol combinations $R_{\gamma }$ must end in $\tilde{A}^{-1}$ ( no free $\tilde{C}$ at the end).

Using the notation

$$\begin{aligned} A^{-} = \left[ \begin{array}{cc} 0 &{}\quad 0\\ 0 &{}\quad \tilde{A}^{-1} \end{array} \right] , \end{aligned}$$

and with our previous analysis, the expansion of the terms explicitly multiplying $\Delta \Lambda _1$ in Eq. (3.13) takes the form:

$$\begin{aligned}&(\hat{A}_1 - \hat{A} A^{-} A_1) \otimes D_{\lambda } g_0 \Delta \Lambda _1\\&\quad + \sum _{\left| \rho \right| = 0}^{\omega } h^{\left| \rho \right| + 1} \left[ \hat{A} \left( \prod _{{\mathop {\text {odd}}\limits ^{i \ge 1}}}^{\dim \rho - 1} C^{\rho _{(i)}} A^{-} C^{\rho _{(i+1)}} A\right) C A^{-} A_1 \otimes O_\rho \Delta \Lambda _1\right] + \mathcal {O}(h^{\omega + 1})\nonumber \end{aligned}$$

where $O_\rho$ is a term composed by multiplication of ${\Psi }$ and derivatives of g and $\phi$ evaluated at the initial condition.

For the remaining expansions we do not need to be as precise as with this last one as there will not be cancellations due to signs. Thus, we will only care about the different symbol combinations that arise.

Now, we need to solve the system formed by Eqs. (3.14) and (3.13). This involves inverting a matrix of the form $\left( I -h \Gamma \right)$, where

$$\begin{aligned} \Gamma = \left[ \begin{matrix} (\tilde{A} \otimes I_n) D_q \tilde{f} &{}\quad (\overline{A} \otimes I_n) D_p f \\ -(\underline{\hat{A}} \otimes I_n) \tilde{X}_P (\overline{A} \otimes I_n) &{} \quad \; \hat{A} \otimes I_n - (\underline{\hat{A} }\otimes I_n) \tilde{X}_Q (\overline{A} \otimes I_n) \end{matrix} \right] . \end{aligned}$$

If we write

$$\begin{aligned} I - h \Gamma = \left[ \begin{array}{cc} I - J &{}\quad - K\\ - M &{} \quad I - N \end{array} \right] \end{aligned}$$

where the matrices J, K, M, N are $\mathcal {O}(h)$, then its inverse is:

$$\begin{aligned} \left[ \begin{array}{cc} T &{}\quad U\\ V &{}\quad W \end{array} \right] \end{aligned}$$

with:

$$\begin{aligned} T&= (1 - J - K (1 - N)^{-1} M)^{-1},\\ U&= (1 - J)^{-1} K (1 - N - M (1 - J)^{-1} K)^{-1},\\ V&= (1 - N)^{-1} M (1 - J - K (1 - N)^{-1} M)^{-1},\\ W&= (1 - N - M (1 - J)^{-1} K)^{-1}. \end{aligned}$$

The only terms we are interested in are U and W, as those are the only ones that connect with $\Delta \Lambda _1$. The Taylor expansion of any of these terms is a daunting task given the amount of nested expansions involved, but it will suffice to see which types of symbol combinations can appear.

We can see that $U = (1 - J)^{-1} K W$. This means that once we know the behaviour of W, the behaviour of U will be easy to derive. Also from this, we can see that all the resulting symbol combinations of U must start with the coefficient matrix A, while for W they must start with the coefficient matrix $\hat{A}$ with the exception of the zero-th order term.

Given the expression of W, its expansion must contain A, C, $\hat{A}$ or $A^{-} C A$ to the right of $\hat{A}$. As for U, all the terms in W will show up multiplied by $(1 - J)^{-1} K$. The symbols this factor adds at order n are $A \times [ (n-1)\text {-element variations of} \left\{ A,C\right\} ]$, thus, no $A^{-} C A$ can appear in U until after the first $\hat{A}$ coming from W is in place.

Finally we can go back to Eq. (3.12). Expanding the terms involving $\Pi _Q$ and $\Pi _P$ is essentially the same as expanding $\tilde{X}_q$ and $\tilde{X}_p$, the latter of which we have already done and not much differs. It is important to note that as we are multiplying those terms with A on the right, we will always have one $A^{-}$ less than the number of As, which prevents $A C^k A^{-}$ terms from appearing at the very end of a symbol combination.

Performing a Taylor expansion of $\Delta q_1$ in terms of $\Delta \tilde{Q}$ and $\Delta P$ we get

$$\begin{aligned} \sum _{i = 0}^\omega h^{i} \left[ A C^{i} \otimes \bar{H}_{i} \right] + \mathcal {O}(h^{\omega + 1}) \end{aligned}$$

where $\bar{H}_{i}$ are linear combinations of derivatives of g and f evaluated at the initial condition. Doing the same for $\Delta p_1$, we get more variety,

$$\begin{aligned} \sum _{\left| \alpha \right| + \left| \beta \right| = 0}^\omega h^{\left| \alpha \right| + \left| \beta \right| } \left[ C^{\alpha } A \prod _{{\mathop {\text {odd}}\limits ^{i \ge 1}}}^{\dim \beta - 1} \left( C^{\beta _{(i)}} A^{-} C^{\beta _{(i+1)}} A\right) \otimes \bar{J}_{\alpha , \beta } \right] + \mathcal {O}(h^{\omega + 1}) \end{aligned}$$

where $\bar{J}_{\alpha , \beta }$ are terms involving ${\Psi }$ and derivatives of f, g and $\phi$ evaluated at the initial condition. The main difference here is that we can have Cs to the left of the first A, as well as the possibility of having $C \mapsto A^{-} C A$ substitutions to its right.

Putting everything together, and keeping in mind that $\omega = \min (\mu , \nu , \xi )$, the respective $\Delta \Lambda _1$-dependent terms resulting from the expansion of Eqs. (3.9) and (3.10) can be brought to the form:

$$\begin{aligned}&h^2 \sum _{i = 0}^{m-1} h^{i} \left( \sum _{\alpha } \bar{K}_{Q, \alpha _i} \otimes \bar{U}_{Q, \alpha _i}\right) \Delta \Lambda _1 + \mathcal {O}(h^{m+2} \left\| \Delta \Lambda _1\right\| )\\&h^2 \sum _{i = 0}^{m-1} h^{i} \left( \sum _{\alpha } \bar{K}_{p, \alpha _i} \otimes \bar{U}_{p, \alpha _i}\right) \Delta \Lambda _1 + \mathcal {O}(h^{m+2} \left\| \Delta \Lambda _1\right\| ) \end{aligned}$$

where each $\bar{U}_{j,\alpha _i}$ is again a combination of products of the derivatives of f, g, $\phi$ with ${\Psi }$ evaluated at the initial condition, and $\bar{K}_{j, \alpha _i}$ is a RK symbol combination of order $\vert \alpha _i\vert$ as in Lemma 3.2. The difference between $\bar{K}_{Q, \alpha _i}$ and $\bar{K}_{p, \alpha _i}$ lies in the fact that $\bar{K}_{Q, \alpha _i}$ cannot begin with $C^i$ and there cannot be $C \mapsto A^{-}CA$ substitutions between the initial A and the first $\hat{A}$, while on $\bar{K}_{p, \alpha _i}$ there can be. Applying the result of Lemma 3.2, all these terms vanish which is what we set out to prove. $\square$

Lemma 3.2

Assume an s-stage symplectic partitioned Runge–Kutta method with coefficients A satisfying hypotheses H1, H2, H3 (and consequently $\hat{A}$ satisfying H1’ and H2’), together with conditions D(r), $\hat{D}(q)$, $D\hat{D}(p - r)$ and $\hat{D}D(p - q)$. Then, we have:

$$\begin{aligned} b^T \left( \prod _{i = 1}^{k} M_i \right) (\hat{A}_1 - \hat{A} A^{-} A_1) = 0, \quad 0 \le k \le \min (r, q, p - r, p - q) - 1 \end{aligned}$$

(3.15)

and

$$\begin{aligned} b^T \left( \prod _{i = 1}^{k} N_i \right) C A^{-} A_1, \quad 0 \le k \le \min (r, q, p - r, p - q) - 1 \end{aligned}$$

(3.16)

where $M_i$ and $N_i$ can be C, A, $\hat{A}$, $A^{-} C A$, $A C A^{-}$ for any i except k where $M_k = A C A^{-}$ cannot occur.

Proof

Multiplying D(r) by $A^{-}$ we may obtain that:

$$\begin{aligned} b^T C^k A^{-}&= e_s^T - k b^T C^{k-1}, \quad 1 \le k \le r. \end{aligned}$$

(3.17)

As A satisfies H3, we also have that $e_s^T A = b^T$, and consequently $b^T A^{-} = e_s^T$.

The vanishing of the different symbol terms rests in both the vanishing of the following reduced combinations and the fact that any symbol combination that appears in the expansion can be brought to one of these.

• Combination 1:

  $$\begin{aligned} b^T C^{k-1} (\hat{A}_1 - \hat{A} A^{-} A_1) = 0, \quad 1 \le k \le \min (r,\hat{r}). \end{aligned}$$

  This is said to be of order $k-1$, as that is the number of times C appears. It vanishes because:

  $$\begin{aligned} b^T C^{k-1} \hat{A}_1&= k^{-1} b_1\\ b^T C^{k-1} \hat{A} A^{-} A_1&= k^{-1} b^T (1 - C^{k}) A^{-} A_1\\&= k^{-1} b^T A^{-} A_1 - k^{-1} b^T C^{k} A^{-} A_1\\&= k^{-1} b_1 - k^{-1} \left( b_1 - k b^T C^{k-1} A_1\right) \\&= k^{-1} b_1. \end{aligned}$$

  The application of the simplifying assumption $\hat{D}(\hat{r})$ in the second line and D(r) in the fourth line are the limiting factors for the order.

• Combination 2:

  $$\begin{aligned} b^T C^{k} A^{-} A_1 = 0, \quad 1 \le k \le r \end{aligned}$$

  This is said to be of order k, as that is the number of times C appears

  $$\begin{aligned} b^T C^{k} A^{-} A_1&= b_1 - k b^T C^{k-1} A_1\\&= b_1 - b_1\\&= 0. \end{aligned}$$

  Again, the application of the simplifying assumption D(r) in the first line is the limiting factor for the order.

Combination 1 and combination 2 can be generalized to the form (3.15) and (3.16) respectively.

After recursive application of D, $\hat{D}$, $D\hat{D}$, $\hat{D}D$ and Eq. (3.17), each of these expressions can be brought to a linear combination of one of the reduced combinations with different values of k, which proves the theorem.

Remark 3.2

This theorem admits a slight generalization. Instead of $b^T$ being the left-most term, by H3 we can substitute it by $e_s^T C^{\alpha } A$, for any $\alpha \ge 0$.

Remark 3.3

For an s-stage Lobatto III A-B method we have that $s - 2 = r = p - q = q - 2 = p - r - 2$, thus:

$$\begin{aligned}&b^T \left( \prod _{i = 1}^{k} M_i \right) (\hat{A}_1 - \hat{A} A^{-} A_1) = 0, \quad 0 \le k \le s - 3 \end{aligned}$$

(3.18)

$$\begin{aligned}&b^T \left( \prod _{i = 1}^{k} N_i \right) C A^{-} A_1, \quad 0 \le k \le s - 3 \end{aligned}$$

(3.19)

Theorem 3.4

Assume an s-stage symplectic partitioned Runge–Kutta method with coefficients A satisfying hypotheses H1, H2, H3 (and consequently $\hat{A}$ satisfying H1’ and H2’), together with conditions B(p), C(q), D(r) (and consequently $\hat{B}(p)$, $\hat{C}(r)$, $\hat{D}(q)$). Then we have:

$$\begin{aligned} \delta q_h (x)&= \mathcal {O}(h^{\min (p, q + r + 1) + 1}), \end{aligned}$$

(3.20a)

$$\begin{aligned} \delta p_h (x)&= \mathcal {O}(h^{\min (p, 2 q, q + r) + 1}), \end{aligned}$$

(3.20b)

$$\begin{aligned} \delta \lambda _h (x)&= \mathcal {O}(h^{q}). \end{aligned}$$

(3.20c)

Proof

The proof of this theorem is similar to that of [5], Theorem 5.1, which follows that of [2], Theorem 5.9, and [4], Theorem 8.10.

Fig. 1

This order 6 tree represents the term $f_{p q}\left( g_{\lambda } (-\phi _p g_{\lambda })^{-1}\phi _{q p}(f,g), f_{p q}(g,f)\right)$. Note that the order is derived from the number of round nodes minus the number of triangle nodes. The tree itself can be written as $\left[ [[\tau _Q,\tau _P]_{\lambda }]_P,[\tau _P,\tau _Q]_Q\right] _Q$ and corresponds to the RK term: $b_i \hat{a}_{i j} a^{-}_{j k} c_k^2 a_{i l} c_l^2$, where $a^{-}_{i j}$ are the components of the $A^{-}$ matrix

The arguments are essentially the same as those used in [2] for A invertible, but using a bi-colored tree extension (see Fig. 1). The inverses that appear only need to be swapped by $A^{-}$. In these results two trees are used, t and u trees, referring to y and z equations respectively. In our case we will have both $t_Q$ and $t_P$ for Q and P equations, plus u for $\lambda$ equations.

The key difference with respect to both this and [5] is that instead of only needing to set the limit such that for $[t,u]_y$ either t or u are above the maximum reduction order by C(q) ($q + 1$ and $q - 1$), which leads to 2q, we need to be careful because we have two types of trees and two simplifying assumptions C(q) and $\hat{C}(r)$. First of all, it is impossible to have $[t_Q, u]_Q$ as f does not depend on $\lambda$, and we can only have $[t_Q, t_P]_Q$, which pushes the limit to $q + r + 2$. On the other hand, $[t_P,u]_P$ also sets a limit, which as it turns out is $q + r$. For both there is also the limit $q + r + 1$ set by D(r), which is more restrictive than the limit set for Q equations but less so than the limit set for P, so this last one prevails. $\square$

Theorem 3.5

Consider the IVP posed by the partitioned differential-algebraic system of Eq. (1.2), together with consistent initial values and the Runge–Kutta method (2.6). In addition to the hypotheses of Theorem 3.4, suppose that $\left| \mathcal {R}_A(\infty )\right| \le 1$ and $q \ge 1$ if $\mathcal {R}_{A}(\infty ) = 1$. Then, for $t_n - t_0 = n h \le C$, where C is a constant, the global error satisfies:

$$\begin{aligned} q_n - q(t_n)&= \mathcal {O}(h^{\min (p, q + r + 1)}) \end{aligned}$$

(3.21a)

$$\begin{aligned} p_n - p(t_n)&= \mathcal {O}(h^{\min (p, 2 q, q + r)}) \end{aligned}$$

(3.21b)

$$\begin{aligned} \lambda _n - \lambda (t_n)&= \left\{ \begin{array}{ll} \mathcal {O}(h^{q}) &{} \quad \text {if}\quad -1 \le \mathcal {R}_A(\infty ) < 1,\\ \mathcal {O}(h^{q - 1}) &{} \quad \text {if}\quad \mathcal {R}_A(\infty ) = 1. \end{array} \right. \end{aligned}$$

(3.21c)

Proof

Following the steps of [5], Theorem 5.2, for $\left| \mathcal {R}_A(\infty ) \right| < 1$ and $\left| \mathcal {R}_A(\infty )\right| = 1$, $\lambda _n - \lambda (t_n)$ can be found to be of order $\mathcal {O}(h^{q})$ and $\mathcal {O}(h^{q - 1})$ respectively. As stated there, the result for $\mathcal {R}_A(\infty ) = -1$ can actually be improved to $\mathcal {O}(h^{q})$ by considering a perturbed asymptotic expansion.

Now, we proceed as in [4], Theorem VI.7.5, applying (3.8)(3.6)(3.7) to two neighbouring RK solutions, $\left\{ \tilde{q}_n, \tilde{p}_n, \tilde{\lambda }_n\right\}$ and $\left\{ \hat{q}_n, \hat{p}_n, \hat{\lambda }_n\right\}$, with $\delta _i = 0$, $\theta = 0$. Using the notation $\Delta x_n = \tilde{x}_n - \hat{x}_n$, we can write:

$$\begin{aligned} \Delta q_{n+1}&= \Delta q_n + \mathcal {O}\left( h \left\| \Delta p_n \right\| + h^{m + 2} \left\| \Delta \lambda _n \right\| \right) \\ \Delta p_{n+1}&= \Pi _{1,n} \Delta q_n + \Pi _{2,n} \Delta p_n + \mathcal {O}\left( h^{m + 2} \left\| \Delta \lambda _n \right\| \right) \\ \Delta \lambda _{n+1}&= \mathcal {R}_A(\infty ) \Delta \lambda _n + \mathcal {O}\left( \left\| \Delta q_n \right\| + \left\| \Delta p_n \right\| + h \left\| \Delta \lambda _n \right\| \right) \end{aligned}$$

where $\Pi _{1,n}$ and $\Pi _{2,n}$ are the projectors defined in the statement of Theorem 3.3, evaluated at $\hat{q}_n$, $\hat{p}_n$, $\hat{\lambda }_n$, and $m = \min (q - 1, r, p - q, p - r)$ for $-1 \le \mathcal {R}_A(\infty ) < 1$ or $m = \min (q - 2, r, p - q, p - r)$ for $\mathcal {R}_A(\infty ) = 1$.

We can follow the same philosophy of [2], Lemma 4.5, and try to relate $\left\{ \Delta q_{n},\Delta p_{n},\right.$ $\left. \Delta \lambda _{n}\right\}$ with $\left\{ \Delta q_{0},\Delta p_{0},\Delta \lambda _{0}\right\}$. For this, we make use of the fact that $\Pi _{i,n+1} = \Pi _{i,n} + \mathcal {O}(h)$, $\left( \Pi _{2,k}\right) ^2 = \Pi _{2,k}$ and $\Pi _{2,k} \Pi _{1,k} = 0$ (these latter facts can be readily derived from their definition).

This leads to:

$$\begin{aligned} \left\| \Pi _{1,n+1} \Delta q_{n+1} \right\|&= \left\| \Pi _{1,n} \Delta q_n \right\| + \mathcal {O}\left( h \left\| \Delta p_n \right\| + h^{m + 2} \left\| \Delta \lambda _n \right\| \right) \\ \left\| \Pi _{2,n+1} \Delta p_{n+1} \right\|&= \left\| \Pi _{2,n} \Delta p_n \right\| + \mathcal {O}\left( h\left\| \Delta q_n \right\| + h^{m + 2} \left\| \Delta \lambda _n \right\| \right) \\ \left\| \mathcal {R}_A(\infty ) \Delta \lambda _{n+1} \right\|&= \left| \mathcal {R}_A(\infty ) \right| ^2 \left\| \Delta \lambda _{n} \right\| + \mathcal {O}\left( \left\| \Delta q_n \right\| + \left\| \Delta p_n \right\| + h \left\| \Delta \lambda _n \right\| \right) \end{aligned}$$

Thus, the error estimates become:

$$\begin{aligned} \left\| \Delta q_{n} \right\|&\le C_q \left( \left\| \Delta q_0 \right\| + h \left\| \Delta p_0 \right\| + h^{m + 2} \left\| \Delta \lambda _0 \right\| \right) \\ \left\| \Delta p_{n} \right\|&\le C_p \left( \left\| \Pi _{1,0} \Delta q_0 \right\| + \left\| \Pi _{2,0} \Delta p_0 \right\| + h^{m + 2} \left\| \Delta \lambda _0 \right\| \right) \\ \left\| \Delta \lambda _{n} \right\|&\le C_{\lambda } \left( \left| \mathcal {R}_A(\infty ) \right| ^n \left\| \Delta \lambda _{0} \right\| + \left\| \Delta q_0 \right\| + \left\| \Delta p_0 \right\| + h \left\| \Delta \lambda _0 \right\| \right) . \end{aligned}$$

Proceeding as in [2] to use the Lady Windermere’s Fan construction and using the results from Theorem 3.4 for $\delta q_h(t_k), \delta p_h(t_k)$, and the results we derived for $\delta \lambda _h(t_k)$, with $m = \min (q - 1, r, p - q, p - r)$ for $-1 \le \mathcal {R}_A(\infty ) < 1$ as well as $m = \min (q - 2, r, p - q, p - r)$ for $\mathcal {R}_A(\infty ) = 1$, we find the global error by addition of local errors, which gives the result we were looking for. $\square$

Corollary 3.1

The global error for the Lobatto IIIA-B method applied to the IVP posed by the partitioned differential-algebraic system of Eq. (1.2) is:

$$\begin{aligned} q_n - q(t_n)&= \mathcal {O}(h^{\min (2 s - 2)}), \end{aligned}$$

(3.22a)

$$\begin{aligned} p_n - p(t_n)&= \mathcal {O}(h^{\min (2 s - 2)}), \end{aligned}$$

(3.22b)

$$\begin{aligned} \lambda _n - \lambda (t_n)&= \left\{ \begin{array}{ll} \mathcal {O}(h^{s}) &{}\quad \text {if}\quad s\,\hbox {even},\\ \mathcal {O}(h^{s - 1}) &{}\quad \text {if}\quad s\,\hbox {odd}. \end{array} \right. \end{aligned}$$

(3.22c)

Proof

To prove this it suffices to substitute $p = 2 s - 2$, $q = s$, $r = s - 2$ and $\mathcal {R}_A(\infty ) = (-1)^{s - 1}$ in Theorem 3.5. $\square$

Fig. 2

Relative error w.r.t. reference values obtained for $h = \texttt {1e-4}$ for integrators of various orders. The behaviour of the Lagrange multiplier $\lambda$ differs from the other variables, as predicted

4 Numerical experiment: nonholonomic particle in an harmonic potential

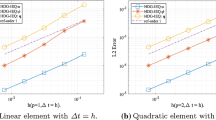
For the purposes of testing, we performed a series of simulations of a system with the Lobatto IIIA-B family with 2, 3, 4 and 5 stages and different values of the step h. Simulations with $h = \texttt {1e-4}$ were taken as ground truth and we produce log–log plots of the error w.r.t. ground truth versus step to check the order.

The system in question is known as the nonholonomic particle in a harmonic potential, a classic academic example. Its equations are of the form of Eq. (1.3). We have $N = Q \times P$, $Q = P = \mathbb {R}^3$, $(x, y, z) \in Q$ representing position, $(p_x, p_y, p_z) \in P$ representing canonical momenta, $\lambda \in \mathbb {R}$, and Hamiltonian (energy) and constraint

$$\begin{aligned} H(x, y, z, p_x, p_y, p_z)= & {} \frac{1}{2}(p_x^2 + p_y^2 + p_z^2) + \frac{1}{2}(x^2 + y^2)\\&\quad \phi (x, y, z, p_x, p_y, p_z) = p_z - y p_x \end{aligned}$$

The initial condition chosen for the experiments is $(1,0,0) \in Q$, $(0,1,0) \in P$. As it can be seen in Fig. 2, the numerical order obtained coincides with the expected one.

5 Conclusion

In this paper we have proposed a new numerical scheme for partitioned index 2 DAEs proving its order. The method opens the possibility to construct high-order methods for nonholonomic systems in a systematic way, preserving the nonholonomic constraints exactly. So far, geometric methods to numerically integrate a given nonholonomic system were constructed using discrete gradient techniques or modifications of variational integrators based on discrete versions of the Lagrange–d’Alembert’s principle. Integrators in the latter category, in which our method falls, tend to display a certain amount of arbitrariness, particularly in the way constraints are discretized or imposed. In most cases, with the exception of SPARK methods [7], the resulting methods are limited to low order unless composition is applied, and without a general framework for error analysis. However, our methods offer a clear and natural way to construct them to arbitrary order. Further considerations about our construction, particularly with respect to its interpretation will be left for [1].