Delay-dependent stability of numerical methods for delay differential systems of neutral type

Abstract

We are concerned with stability of numerical methods for delay differential systems of neutral type. In particular, delay-dependent stability of numerical methods is investigated. By means of the H-matrix norm, a necessary and sufficient condition for the asymptotic stability of analytic solution of linear neutral differential systems is derived. Then, based on the argument principle, sufficient conditions for delay-dependent stability of Runge–Kutta and linear multi-step methods are presented, respectively. Furthermore, two algorithms are provided for checking delay-dependent stability of analytical and numerical solutions, respectively. Numerical examples are given to illustrate the main results.

1 Introduction

We are concerned with linear delay differential system of neutral type with a single delay described by

$$\begin{aligned} \dot{u}(t)=Lu(t)+Mu(t-\tau )+N\dot{u}(t-\tau ) \quad \text{ for }\quad t \ge 0 \end{aligned}$$

(1.1)

with the condition

$$\begin{aligned} \rho (N)<1, \end{aligned}$$

(1.2)

where $u(t)\in \mathbb {R}^{d},$ parameter matrices $L, M, N\in \mathbb {R}^{d\times d}$ and delay $\tau >0.$ Throughout the present paper, the NDDE system refers to Eq. (1.1) with (1.2).

Stability of delay and neutral systems can be divided into two categories according to its dependence upon the size of delays. The stability which does not depend on delays is called delay-independent, otherwise it is referred to as delay-dependent (they are discussed in [1, 2, 4, 9,10,11, 19]). Each case is extended to the neutral type and the reader can refer to [2, 10] for the delay-independent and to [2, 9, 11, 19] for the delay-dependent case. Then, the stability of numerical methods is also divided into delay-independent and delay-dependent according to which system the method is applied to. The present paper is devoted to study the delay-dependent stability of numerical methods for the systems of neutral type, for we believe it gives more precise insight of the methods.

Although numerical delay-independent stability has been discussed in [1, 2, 10], only a few works have been reported for the delay-dependent case [2, 7, 13, 18]. The literature [2, 7, 18] proposed the delay-dependent stability of numerical methods for the system

$$\begin{aligned} \dot{u}(t)=Lu(t)+Mu(t-\tau ), \end{aligned}$$

(1.3)

and called it as D-stability. However, as pointed out in [2], delay-dependent stability of numerical methods for the system is a real challenge. In fact, in [18] it is proved that for any A-stable natural Runge–Kutta method for system (1.3) and for any step-size $h={\tau }/{m}$ (m is a positive integer), there exists an asymptotically stable linear system of dimension $d=4$ for which $u_{n}\rightarrow 0 \quad \text{ as }\quad n\rightarrow \infty$ does not hold. Later, the same negative result for $d=2$ is obtained in [7]. In short, no A-stable natural Runge–Kutta method for system (1.3) is D-stable.

This suggests that the definition of D-stability is too restricted. Its definition requires the resulting difference system from a Runge–Kutta method is asymptotically stable for all asymptotically stable system (1.3) and for all the step-sizes. Hence almost all the standard Runge–Kutta methods are excluded in the D-stability sense. However, practical computations shows it is not the case. Our experiences are as follows. When we numerically solve an asymptotically stable NDDE system, it is possible that by carefully choosing a small step-size $h={\tau }/{m}$ numerical solutions by a standard Runge–Kutta or linear multi-step method exhibit an asymptotically stable behaviour. Thus we are motivated to present a relaxed definition for delay-dependent stability of numerical methods. We will give a new definition of delay-dependent stability, which only requires the conditions of asymptotically stable difference system derived from a numerical method for an asymptotically stable NDDE system with a certain integer giving the step-size $h={\tau }/{m}$.

This paper is organized as follows. A necessary and sufficient condition for the asymptotic stability of analytic solution of linear neutral differential systems is derived in Sect. 2. In Sect. 3, the new delay-dependent stability of Runge–Kutta and linear multi-step methods are discussed, respectively. Numerical examples in Sect. 4 are provided to illustrate the main results. Conclusions are given in Sect. 5.

Throughout the paper, for a complex matrix F,  $\Vert F \Vert$ means any matrix norm. The Hermitian conjugate of a complex vector or matrix is denoted by $\varvec{x}^{*}$ or $F^{*}$. The $j^{\text {th}}$ eigenvalue of F is denoted by $\lambda _{j}(F)$. The symbol $\rho (F)$ represents its spectral radius. $\mathrm{Re}\,z$ and $\mathrm{Im}\,z$ stand for the real and the imaginary parts of a complex number z,  respectively. The open left half-plane $\{s: \mathrm{Re}\,s<0\}$ is denoted by $\mathbb {C}^{-}$ and the right half-plane $\{s: \mathrm{Re}\,s\ge 0\}$ by $\mathbb {C}^{+}$.

2 Preliminaries

In this section, several lemmas and definitions are reviewed which will be used in Sects. 3 and 4.

A function P(s) is said to be meromorphic in a domain D if it is analytic throughout D except poles. The following argument principle is well-known.

Lemma 2.1

(e.g. [5]) Suppose that

• (i) a function P(s) is meromorphic in the domain interior to a positively oriented simple closed contour $\gamma ;$

• (ii) P(s) is analytic and nonzero on $\gamma ;$

• (iii) counting multiplicities, Z is the number of zeros and Y is the number of poles of P(s) inside $\gamma .$

Then

$$\begin{aligned} \frac{1}{2\pi }\triangle _{\gamma }\arg P(s)=Z-Y, \end{aligned}$$

where $\triangle _{\gamma }\arg P(s)$ represents the change of the argument of P(s) along $\gamma$.

The following result is useful to check the existence of inverse matrix.

Lemma 2.2

(e.g. [17]) For a complex matrix F,  if $\rho (F)<1,$ then the matrix $(I-F)^{-1}$ exists and

$$\begin{aligned} \Vert (I-F)^{-1}\Vert \le \frac{1}{1-\Vert F\Vert }. \end{aligned}$$

Now we review the H-matrix norm based on Stein Eq. [12].

Definition 2.1

(e.g. [17]) A matrix $F\in \mathbb {C}^{d \times d}$ is said to be stable with respect to the unit circle if all its eigenvalues $\lambda _{i}(F)\ (1\le i\le d)$ lie inside the unit circle, that is, $|\lambda _{i}(F)|<1$ holds for all $1\le i\le d$.

Lemma 2.3

(e.g. [17]) Assume $F, V\in \mathbb {C}^{d \times d}$ and furthermore V be positive definite. The matrix F is stable with respect to the unit circle, if and only if there exists a positive definite matrix H satisfying Stein equation

$$\begin{aligned} H-F^{*}HF=V. \end{aligned}$$

(2.1)

Furthermore, the matrix Eq. (2.1) has a unique solution H if and only if $\lambda _i(F^{*})\cdot \lambda _j(F) \ne 1$ holds for all possible indices i and j.

Then, the Lemma guarantees the unique existence of H in our case of Lemma 2.3, for we assume a stable matrix F with respect to the unit circle. Furthermore, we note that the matrix H is computable in our case and computing algorithms have been developed (e.g. [6]). In fact, the software Matlab has the functions slstst (for stable Stein equations) and slgest (for generalized Stein equations) ([3]). Thus an introduction of H-norm by the following definition is meaningful in conjunction with the stable matrix with respect to the unit circle.

Definition 2.2

(e.g. [12]) For any vector $\varvec{x}$, any matrix F and any positive definite matrix H, the H-norm of $\varvec{x}$ and F are defined, respectively, by

$$\begin{aligned} \Vert \varvec{x} \Vert _H = \sqrt{x^{*}Hx},\quad \quad \Vert F\Vert _H=\max _{\varvec{x} \ne 0}\frac{\Vert F \varvec{x}\Vert _H}{\Vert \varvec{x} \Vert _H}. \end{aligned}$$

(2.2)

By the above definition, we have the following formula for estimating the H-norm of F.

Lemma 2.4

For any matrix $F\in \mathbb {C}^{d \times d}$ and any positive definite matrix H, we introduce the positive Cholesky decomposition of H as $H_{0}=\sqrt{H}$ and put $\tilde{F}=H_{0}F{H_{0}}^{-1}$. Then we have

$$\begin{aligned} \Vert F\Vert _H=\sqrt{\lambda _{\max }(\tilde{F}^{*}\tilde{F})}, \end{aligned}$$

(2.3)

where $\lambda _{\max }(W)$ stands for the maximal eigenvalue of a symmetric matrix W.

Proof

By Definition 2.2, we can calculate

$$\begin{aligned} \Vert F\Vert ^{2}_H= & {} \max _{\varvec{x} \ne 0}\frac{\Vert F \varvec{x} \Vert ^{2}_H}{\Vert \varvec{x} \Vert ^{2}_H} =\max _{\varvec{x} \ne 0}\frac{\varvec{x}^{*}F^{*}HF \varvec{x}}{\varvec{x}^{*}H \varvec{x}} = \max _{\varvec{x} \ne 0}\frac{\varvec{x}^{*}F^{*}H_{0}^{*} H_{0}F\varvec{x}}{(H_{0}\varvec{x})^{*}(H_{0} \varvec{x})} \\= & {} \max _{\varvec{x}\ne 0}\frac{(H_{0}\varvec{x})^{*}(H_{0}F{H_{0}}^{-1})^{*}(H_{0}F{H_{0}}^{-1})(H_{0}\varvec{x})}{(H_{0}\varvec{x})^{*}(H_{0}\varvec{x})} \\= & {} {\lambda _{\max }(\tilde{F}^{*}\tilde{F})}\, , \end{aligned}$$

which is the desired result.    $\square$

For a stable matrix, the following Lemma asserts an evaluation of its H-norm by $\rho (H)$.

Lemma 2.5

[12] If a matrix $F\in \mathbb {C}^{d \times d}$ is stable, then there exists a unique positive definite matrix H which satisfies the following Stein equation

$$\begin{aligned} H-F^{*}HF=I \end{aligned}$$

(2.4)

and the equality

$$\begin{aligned} \Vert F\Vert _H=\sqrt{1-\frac{1}{\rho (H)}} \end{aligned}$$

(2.5)

holds.

Proof

Because of the condition $\rho (F)<1$, Lemma 2.3 gives the positive definite matrix H satisfying the equation $F^{*}HF-H=-I$. Then, by virtue of Definition 2.2 we can obtain

$$\begin{aligned} \Vert F\Vert ^{2}_H= & {} \max _{\varvec{x}\ne 0} \frac{\Vert F \varvec{x} \Vert ^{2}_H}{\Vert x\Vert ^{2}_H} = \max _{\varvec{x} \ne 0}\frac{\varvec{x}^{*}F^{*}HF\varvec{x}}{\varvec{x}^{*}H\varvec{x}} \\= & {} \max _{\varvec{x}\ne 0}\frac{\varvec{x}^{*}(H-I)\varvec{x}}{\varvec{x}^{*}H\varvec{x}} = \max _{\varvec{x} \ne 0}\left( 1-\frac{\varvec{x}^{*}\varvec{x}}{\varvec{x}^{*}H\varvec{x}} \right) = 1 - \frac{1}{\rho (H)} \end{aligned}$$

which implies the assertion of (2.5).    $\square$

3 Stability criterion

In this section, by means of the H-matrix norm, a necessary and sufficient condition for asymptotic stability of the NDDE system is presented to extend the results in [11]. We will consider the stability of the system (1.1). Its characteristic equation reads

$$\begin{aligned} P(s)=\det [sI-L-M\exp (-\tau s)-sN\exp (-\tau s)]=0, \end{aligned}$$

(3.1)

whose root is called a characteristic root. The asymptotic stability of the NDDE system is determined by the location of the characteristic roots. That is, the system is asymptotically stable if and only if all the characteristic roots lie in the open left complex half-plane $\mathbb {C}^-$ [9].

If there exists unstable characteristic roots of (3.1), i.e., $P(s)=0$ for $\mathrm{Re}\,s\ge 0$, they are bounded due to the following result.

Theorem 3.1

Assume that condition $\rho (N)<1$ holds. Let s be an unstable characteristic root of Eq. (3.1) of system (1.1), i.e., $\mathrm{Re}\,s\ge 0$, then there exists a positive definite matrix H, satisfying Stein equation $H - N^{*} H N = I$, which gives the bound of s as

$$\begin{aligned} |s|\le \beta \mathop {=}\limits ^\mathrm{def}\frac{||L||_H+||M||_H}{1-||N||_H}. \end{aligned}$$

(3.2)

Remark 3.1

Taking Lemmata 2.3, 2.4 and 2.5 into consideration, we can calculate the H-norm of matrices L, M and N in the following manner. Put $H_0 = \sqrt{H}$, $\tilde{L}=H_{0}L{H_{0}}^{-1}$ and $\tilde{M}=H_{0}M{H_{0}}^{-1}$, then we have

$$\begin{aligned} \Vert L\Vert _H=\sqrt{\lambda _{\max }(\tilde{L}^{*}\tilde{L})},\quad \Vert M\Vert _H=\sqrt{\lambda _{\max }(\tilde{M}^{*}\tilde{M})}\quad \text{ and }\quad \Vert N\Vert _H=\sqrt{1-\frac{1}{\rho (H)}}. \nonumber \\ \end{aligned}$$

(3.3)

Proof of Theorem 3.1

Since N is a stable matrix, by means of Lemma 2.5, there is a positive definite matrix H giving $\Vert N\Vert _H<1$. The matrix H is determined by the Stein equation. As we are discussing an unstable root, we assume $\mathrm{Re}\,s \ge 0$ throughout the proof. Since the identity $\lambda _{j}(N\exp (-\tau s))=\exp (-\tau s)\lambda _{j}(N)$ is obvious for $j=1, \ldots , d$, we can estimate as

$$\begin{aligned} |\lambda _{j}(N\exp (-\tau s))|=|\exp (-\tau s)\lambda _{j}(N)|\le |\lambda _{j}(N)|. \end{aligned}$$

Hence we have $\rho (N\exp (-\tau s)) \le \rho (N)<1$, which assures the existence of $(I-N\exp (-\tau s))^{-1}$ by Lemma 2.2. Introduction of

$$\begin{aligned} W(s)=(I-N\exp (-\tau s))^{-1}(L+M\exp (-\tau s)) \end{aligned}$$

rewrites P(s) as

$$\begin{aligned} P(s)= & {} \det [sI-L-M\exp (-\tau s)-sN\exp (-\tau s)]\\= & {} \det \left( [I-N\exp (-\tau s)][sI-W(s)]\right) . \end{aligned}$$

Since $\rho (N\exp (-\tau s)) < 1$, the equation

$$\begin{aligned} \det [sI-W(s)]=0 \end{aligned}$$

(3.4)

must hold. This implies the s is an eigenvalue of the matrix W(s) and there exists an integer $j\ (1\le j\le d)$ such that

$$\begin{aligned} s=\lambda _{j}(W(s)), \end{aligned}$$

(3.5)

Since $\mathrm{Re}\,s\ge 0,$ we have

$$\begin{aligned} 0\le \Vert N\exp (-\tau s)\Vert _H\le \Vert N\Vert _H \end{aligned}$$

(3.6)

According to (3.5) and (3.6), we can estimate

$$\begin{aligned} |s|= & {} |\lambda _{j}(W(s))|\le \Vert W(s)\Vert _H =\Vert (I-N\exp (-\tau s))^{-1}(L+M\exp (-\tau s))\Vert _H \\\le & {} \Vert (I-N\exp (-\tau s))^{-1}\Vert _H \Vert (L+M\exp (-\tau s))\Vert _H \\\le & {} \frac{\Vert L+M\exp (-\tau s)\Vert _H}{ 1-\Vert N\exp (-\tau s)\Vert _H} \le \frac{\Vert L\Vert _H +\Vert M\Vert _H}{1-\Vert N\Vert _H}. \end{aligned}$$

Thus the proof is completed.    $\square$

The theorem means that there is a bounded region in the right-half complex plane $\mathbb {C}^+$ which includes all the unstable characteristic roots of (3.1).

Remark 3.2

Since $\rho (N)\le \Vert N\Vert$ holds generally, the condition $\rho (N)< 1$ in Theorem 3.1 is weaker than the condition $\Vert N\Vert < 1$ in [11]. Hence the theorem is an extension of the results in [11].

Definition 3.1

Assume that the conditions of Theorem 3.1 hold and the bound $\beta$ is obtained. The half-disk $D_{\beta }$ in s-plane is the closed set given by

$$\begin{aligned} D_{\beta } = \{s:\mathrm{Re}\,s\ge 0 \quad \text{ and }\quad |s|\le \beta \}. \end{aligned}$$

Moreover, the boundary of $D_{\beta }$ is denoted by $\varGamma _{\beta }$. See Fig.1, where $d_{1}=i\beta ,d_{2}=-i\beta .$

Fig. 1

Set $D_{\beta }$

By means of the argument principle, a computable criterion for system (1.1) can be derived. Now we present the main result in this section. The following theorem will exclude all the unstable characteristic root of Eq. (3.1) from the set $D_{\beta }$.

Theorem 3.2

Assume that the conditions of Theorem 3.1 hold and the bound $\beta$ is obtained. Then the system (1.1) is asymptotically stable if and only if the two conditions

$$\begin{aligned} P(s)\ne 0 \quad \text{ for }\quad s \in \varGamma _{\beta } \end{aligned}$$

(3.7)

and

$$\begin{aligned} \triangle _{\varGamma _{\beta }}\arg P(s)=0 \end{aligned}$$

(3.8)

hold, where P(s) is defined by (3.1) and $\triangle _{\varGamma _{\beta }}\arg P(s)$ has the same meaning in Lemma 2.1. See Fig. 1.

Proof

Suppose the system is asymptotically stable. All zeros of P(s) are located on the left half plane $\mathbb {C}^-$. It means that $P(s)\ne 0$ when $\mathrm{Re}\,s\ge 0$. By the argument principle, we have that (3.7) and (3.8) hold.

Conversely, assume that the conditions (3.7) and (3.8) hold. According to Theorem 3.1, it means that P(s) never vanishes for $\mathrm{Re}\,s\ge 0$. Hence (3.7) and (3.8) imply the system (1.1) is asymptotically stable. Thus the proof completes. $\square$

Now we describe an algorithm to check the stability due to Theorem 3.2.

Algorithm 1

Step 0:

Solve Stein equation

$$\begin{aligned} H - N^{*} H N = I \end{aligned}$$

and obtain the positive definite matrix H. Put $H_0 = \sqrt{H}$, $\tilde{L}=H_{0}L{H_{0}}^{-1}$ and $\tilde{M}=H_{0}M{H_{0}}^{-1}$, and calculate

$$\begin{aligned} \qquad \Vert L\Vert _H=\sqrt{\lambda _{\max }(\tilde{L}^{*}\tilde{L})},\quad \Vert M\Vert _H=\sqrt{\lambda _{\max }(\tilde{M}^{*}\tilde{M})},\quad \Vert N\Vert _H=\sqrt{1-\frac{1}{\rho (H)}}\ \end{aligned}$$

and

$$\begin{aligned} \beta \mathop {=}\limits ^\mathrm{def}\frac{||L||_H+||M||_H}{1-||N||_H}. \end{aligned}$$

Then as the boundary of $D_{\beta }$ we have the curve $\varGamma _{\beta }$, which consists of two parts, i.e., the segment $\{ s = i t;\ -\beta \le t \le \beta \}$ and the half-circle $\{ s;\ | s | = \beta \ \text{ and }\ -\pi /2 \le \mathrm{arg}\, s \le \pi /2 \}$.

Step 1:

Take a sufficiently large integer $n \in \mathbb {N}$ and distribute n node points $\{ s_{j} \}\ (j = 1, 2, \ldots , n)$ on $\varGamma _{\beta }$ as uniformly as possible. For each $s_{j}$, we evaluate $P(s_{j})$ by computing the determinant as

$$\begin{aligned} P(s_j) = \det \left[ s_{j}I - L - M\exp \left( -\tau s_{j}\right) - s_{j}N\exp \left( -\tau s_{j}\right) \right] . \end{aligned}$$

Also we decompose $P(s_j)$ into its real and imaginary parts.

Step 2:

We examine whether $P(s_{j})=0$ holds for each $s_j$ ($j =1, \ldots , n$) by checking its magnitude satisfies $| P(s_{j}) |\le \delta _{1}$ with the preassigned tolerance $\delta _{1}$. If it holds, i.e., $s_{j}\in \varGamma _{\beta }$ is a root of P(s), then the NDDE system is not asymptotically stable and stop the algorithm. Otherwise, to go to the next step.

Step 3:

We examine whether $\triangle _{\varGamma _{\beta }}\arg P(s)=0$ holds along the sequence $\{ P(s_{j}) \}$ by checking $|\triangle _{\varGamma _{\beta }}\arg P(s)| \le \delta _{2}$ with the preassigned tolerance $\delta _{2}$. If it holds, it means that the change of the argument is 0 along the sequence $\{ P(s_{j}) \},$ then the system is asymptotically stable, otherwise not stable.

Remark 3.3

Algorithm 1 avoids a computation of the coefficients of the characteristic polynomial P(s). Instead it evaluates the determinant $P(s_{\ell })$ through the elementary row (or column) operations which are relatively efficient ways [14].

4 Delay-dependent stability of numerical methods

In this section, a delay-dependent stability of both Runge–Kutta (RK) and linear multi-step (LM) methods for linear delay differential systems of neutral type is discussed. Based on the argument principle, sufficient conditions for delay-dependent stability of the numerical methods are presented.

First, we assume the numerical solution we are now discussing gives a sequence of approximate values $\{ u_0, u_1, \ldots , u_n, \ldots \}$ of $\{ u(t_0), u(t_1), \ldots , u(t_n), \ldots \}$ of (1.1) on certain equidistant step-values $\{ t_n (= n h) \}$ with the step-size h. We introduce the following new definition of delay-dependent stability of numerical methods for system (1.1).

Definition 4.1

Assume that the NDDE system is asymptotically stable for given matrices L, M, N and a delay $\tau$. A numerical method is called weakly delay-dependently stable for system (1.1) if there exists a positive integer m such that the step-size $h={\tau }/{m}$ and the numerical solution $u_{n}$ with h satisfies

$$\begin{aligned} u_{n}\rightarrow 0 \quad \text{ as }\quad n\rightarrow \infty \end{aligned}$$

for any initial function.

Remark 4.1

In [2, 7, 18], the definition of delay-dependent stability, which is called D-stability there, is too restricted since it requires for all asymptotically stable delay differential system (1.3) and for all the natural numbers m the resulting numerical solution is asymptotically stable. Therefore, almost all the standard RK methods are excluded in the D-stability sense. It is obvious that Definition 4.1 is weaker than D-stability in the literature.

4.1 Runge–Kutta case

For the initial value problem of ordinary differential equations (ODEs)

$$\begin{aligned} \dot{y}(t)=f(t, y(t)), \quad \text{ for }\quad t\ge 0 \end{aligned}$$

(4.1)

an s-stage (implicit) Runge–Kutta method for ODEs (4.1) is defined (e.g., [16]) by

$$\begin{aligned} k_{i}=f\left( t_{n}+c_{i}h,y_{n}+h\sum _{j=1}^{s}a_{ij}k_{j} \right) \quad (i = 1, 2, \ldots , s) \end{aligned}$$

(4.2)

with

$$\begin{aligned} y_{n+1}=y_{n}+h\sum _{i=1}^{s}b_{i}k_{i}. \end{aligned}$$

(4.3)

We associate the s-square matrix A and the s-dimensional vector $\varvec{b}$ as

$$\begin{aligned} A \mathop {=}\limits ^\mathrm{def}(a_{ij}) \quad \text{ and } \quad \varvec{b} \mathop {=}\limits ^\mathrm{def}(b_i). \end{aligned}$$

We analyse RK method which is extended to apply to the NDDE system. Taking advantage of the constant step-size $h = \tau /m$, we can employ the so-called natural Runge–Kutta scheme [1, 2] for (1.1) given by

$$\begin{aligned} K_{n,i}= & {} h L \left( u_{n} + \sum _{j=1}^{s}a_{ij}K_{n,j} \right) \nonumber \\&\quad +\,h M \left( u_{n-m}+\sum _{j=1}^{s}a_{ij}K_{n-m,j} \right) + N K_{n-m,i} \quad (i = 1, 2, \ldots , s) \qquad \qquad \end{aligned}$$

(4.4)

and

$$\begin{aligned} u_{n+1}=u_{n}+\sum _{i=1}^{s}b_{i}K_{n,i}, \end{aligned}$$

(4.5)

where the symbol $K_{\ell ,i}$ means the i-th stage value of the RK at the $\ell$-th step-point.

Lemma 4.1

The characteristic polynomial $P_{RK}(z)$ of the linear difference system (4.4) and (4.5) is given by

$$\begin{aligned} P_{RK}(z)= & {} \det \left\{ \left[ \begin{array}{cc} I_{sd}-h(A\bigotimes L) &{} 0 \\ -\varvec{b}^\mathrm{T}\bigotimes I_{d} &{} I_{d} \end{array}\right] z^{m+1} - \left[ \begin{array}{cc} 0 &{} h(\varvec{e}\bigotimes L) \\ 0 &{} I_{d} \end{array}\right] z^{m} \right. \nonumber \\&\left. -\left[ \begin{array}{cc} h(A\bigotimes M)+I_{s}\bigotimes N &{} 0 \\ 0 &{} 0\end{array}\right] z - \left[ \begin{array}{cc} 0 &{} h(\varvec{e} \bigotimes M) \\ 0 &{} 0 \end{array}\right] \right\} , \end{aligned}$$

(4.6)

where the s-dimensional vector $\varvec{e}$ is defined by $\varvec{e}=(1,1,\ldots ,1)^\mathrm{T}.$

Proof

The difference system (4.4) and (4.5) can be expressed with the Kronecker product as follows:

$$\begin{aligned}&\left[ \begin{array}{cc} I_{sd}-h(A\bigotimes L) &{} 0 \\ -\varvec{b}^\mathrm{T}\bigotimes I_{d} &{} I_{d} \end{array}\right] \left[ \begin{array}{c} K_{n} \\ u_{n+1} \end{array}\right] - \left[ \begin{array}{cc} 0 &{} h(\varvec{e}\bigotimes L) \\ 0 &{} I_{d} \end{array}\right] \left[ \begin{array}{c} K_{n-1} \\ u_{n} \end{array}\right] \nonumber \\&\quad - \left[ \begin{array}{cc} h(A\bigotimes M)+I_{s}\bigotimes N &{} 0 \\ 0 &{} 0\end{array}\right] \left[ \begin{array}{c} K_{n-m} \\ u_{n-m+1} \end{array}\right] - \left[ \begin{array}{cc} 0 &{} h(\varvec{e}\bigotimes M) \\ 0 &{} 0 \end{array}\right] \left[ \begin{array}{c} K_{n-m-1} \\ u_{n-m} \end{array}\right] =0, \nonumber \\ \end{aligned}$$

(4.7)

where the (ds)-dimensional vector $K_{n}$ means

$$\begin{aligned} K_{n}=[K_{n,1}^\mathrm{T},K_{n,2}^\mathrm{T}, \ldots , K_{n,s}^\mathrm{T}]^{\mathrm{T}}. \end{aligned}$$

Hence the dimension of the vector $\displaystyle { \left[ \begin{array}{c} K_{n} \\ u_{n+1} \end{array}\right] }$ becomes $(s+1)d$.

Taking z-transform to (4.7) and introducing as $\displaystyle { Z\left\{ \left[ \begin{array}{c} K_{n-m-1} \\ u_{n-m} \end{array}\right] \right\} }= V(z)$, we obtain that

$$\begin{aligned}&\left\{ \left[ \begin{array}{cc} I_{sd}-h(A\bigotimes L) &{} 0 \\ -\varvec{b}^\mathrm{T}\bigotimes I_{d} &{} I_{d} \end{array}\right] z^{m+1} - \left[ \begin{array}{cc} 0 &{} h(\varvec{e}\bigotimes L) \\ 0 &{} I_{d} \end{array}\right] z^{m} \right. \nonumber \\&\quad \left. -\left[ \begin{array}{cc} h(A\bigotimes M)+I_{s}\bigotimes N &{} 0 \\ 0 &{} 0\end{array}\right] z - \left[ \begin{array}{cc} 0 &{} h(\varvec{e}\bigotimes M) \\ 0 &{} 0 \end{array}\right] \right\} V(z) =0. \end{aligned}$$

Hence, the characteristic polynomial of difference system is given as desired. $\square$

For an explicit RK method, that is, the one with $a_{ij} = 0$ for $i \le j$, we have the following result.

Theorem 4.1

For an explicit RK method, assume that

• (i) the NDDE system is asymptotically stable for given matrices L, M, N and delay $\tau$ (therefore, Theorem 3.2 holds);

• (ii) the RK method is of s-stage and natural with the step-size $h={\tau }/{m}$;

• (iii) The characteristic polynomial $P_{RK}(z)$ never vanishes on the unit circle $\mu =\{z:|z|=1\}$ and its change of argument satisfies

  $$\begin{aligned} \frac{1}{2\pi }\triangle _{\mu }\arg P_{RK}(z) = d(s+1)(m+1). \end{aligned}$$

  (4.8)

Then the RK method for the NDDE system is weakly delay-dependently stable.

Proof

The difference system (4.7) is asymptotically stable if and only if all the characteristic root of $P_{RK}(z)=0$ lie in the inner of the unit circle. Notice that the coefficient matrix of the term $z^{m+1}$ in $P_{RK}(z)=0$ is

$$\begin{aligned} \left[ \begin{array}{cc} I_{sd}-h(A\bigotimes L) &{} 0 \\ -\varvec{b}^\mathrm{T}\bigotimes I_{d} &{} I_{d} \end{array}\right] . \end{aligned}$$

Since the Runge–Kutta method is explicit, $\lambda _{i}(A)=0$ holds for $i=1, \ldots , s.$ It means that all the eigenvalues of matrix $h(A\bigotimes L)$ vanish because of

$$\begin{aligned} \text{ eigenvalue } \text{ of }\ (hA\bigotimes L)=h\lambda _{i}(A)\lambda _{j}(L)=0 \end{aligned}$$

with $i=1, \ldots , s$ and $j=1, \ldots , d$. Thus that matrix $I_{sd}-h(A\bigotimes L)$ is nonsingular by Lemma 2.2 and the matrix

$$\begin{aligned} \left[ \begin{array}{cc} I_{sd}-h(A\bigotimes L) &{} 0 \\ -\varvec{b}^\mathrm{T}\bigotimes I_{d} &{} I_{d} \end{array}\right] \end{aligned}$$

is also nonsingular. Since the degree of $P_{RK}(z)$ is $d (s+1) (m+1)$, it has $d (s+1) (m+1)$ roots in total by counting their multiplicity. By the argument principle, the condition (iii) implies that the condition $|z| < 1$ holds for all the $d (s+1) (m+1)$ roots of $P_{RK}(z)=0$. The proof completes. $\square$

For an implicit RK method applied to the NDDE system, we derive the following result.

Theorem 4.2

For an implicit RK method, assume that

• (i) the conditions (i),(ii) and (iii) in Theorem 4.1 hold;

• (ii) the product $h \lambda _i(A) \lambda _j(L)$ never equals to unity for all $i\ (1 \le i \le s)$ and $j\ (1 \le j \le d)$.

Then the RK method for the NDDE system is weakly delay-dependently stable.

Proof

The proof can be carried out similarly to that of Theorem 4.1. Notice that the condition (ii) ensures the matrix

$$\begin{aligned} \left[ \begin{array}{cc} I_{sd}-h(A\bigotimes L) &{} 0 \\ -\varvec{b}^\mathrm{T}\bigotimes I_{d} &{} I_{d} \end{array}\right] \end{aligned}$$

is nonsingular since the matrix $I_{sd}-h(A\bigotimes L)$ is nonsingular. Thus the degree of the polynomial $P_{RK}(z)$ becomes $d (s+1) (m+1)$.    $\square$

4.2 Linear multi-step case

When applied to ODEs (4.1), a linear k-step method is given as follows (e.g., [16]):

$$\begin{aligned} \sum _{j=0}^{k}\alpha _{j}y_{n+j}=h\sum _{j=0}^{k}\beta _{j}f_{n+j}, \end{aligned}$$

(4.9)

where h stands for the step-size, $\alpha _{j},$ $\beta _{j}$ are the formula parameters satisfying $\alpha _k = 1$ and $|\alpha _0| + |\beta _0| \ne 0$. and $f_j = f(t_j, y_j)$. As in the case of RK method, in order to apply the LM method to the delay differential systems of neutral type (1.1), we employ the step-size h of an integral fraction of $\tau$, i.e., $h={\tau }/{m}$ for a certain $m \in \mathbb {N}$.

For the application to the linear system (1.1), we introduce the same reformulation given by [10]. That is, with an auxiliary variable v(t) the system (1.1) is rewritten as the simultaneous system:

$$\begin{aligned} \dot{u}(t)=v(t) \end{aligned}$$

(4.10)

and

$$\begin{aligned} v(t)=Lu(t)+Mu(t-\tau ) + N {v}(t-\tau ). \end{aligned}$$

(4.11)

Then, an application of the method (4.9) to (4.10) and (4.11) yields

$$\begin{aligned} \sum _{j=0}^{k}\alpha _{j}u_{n+j}=h\sum _{j=0}^{k}\beta _{j}v_{n+j}, \end{aligned}$$

(4.12)

and

$$\begin{aligned} v_{n+j} = L u_{n+j} + M u_{n-m+j} + N v_{n-m+j}. \end{aligned}$$

(4.13)

This reformulation can ease the derivation of its characteristic polynomial.

Lemma 4.2

The characteristic polynomial of (4.12) and (4.13) is given by

$$\begin{aligned} P_{LM}(z)=\det \left[ \sum _{j=0}^{k}\left( (\alpha _{j}I - h\beta _{j}L)z^{m} - \alpha _{j}N-h\beta _{j}M\right) z^{j}\right] . \end{aligned}$$

(4.14)

Proof

Equation (4.12) derives

$$\begin{aligned} h N \sum _{j=0}^{k}\beta _{j}v_{n-m+j}=N\sum _{j=0}^{k}\alpha _{j}u_{n-m+j}, \end{aligned}$$

which, together with (4.12) and (4.13), leads

$$\begin{aligned} \sum _{j=0}^{k}\alpha _{j}u_{n+j}= & {} h\sum _{j=0}^{k}\beta _{j}(Lu_{n+j}+Mu_{n-m+j}+N v_{n-m+j}) \nonumber \\= & {} h\sum _{j=0}^{k}\beta _{j}(Lu_{n+j}+Mu_{n-m+j})+hN\sum _{j=0}^{k}\beta _{j} v_{n-m+j} \nonumber \\= & {} h\sum _{j=0}^{k}\beta _{j}(Lu_{n+j}+Mu_{n-m+j})+N\sum _{j=0}^{k}\alpha _{j}u_{n-m+j}. \end{aligned}$$

(4.15)

The above is the difference equation to be solved after eliminating v’s. Taking its Z-transform and putting $Z\{u_{n-m}\}=U(z)$, we obtain

$$\begin{aligned} \left[ \sum _{j=0}^{k}\alpha _{j}z^{m+j}\right] U(z) = \left[ h \sum _{j=0}^{k}\beta _{j}(Lz^{m+j}+Mz^{j})+N\sum _{j=0}^{k}\alpha _{j}z^{j}\right] U(z). \end{aligned}$$

Hence, the characteristic polynomial is given as desired. $\square$

For delay-dependent stability of an LM method, we have the following result.

Theorem 4.3

Assume that

• (i) the NDDE system is asymptotically stable for given matrices L, M, N and delay $\tau$;

• (ii) for the underlying LM method with the step-size $h={\tau }/{m}$, the matrix $\alpha _{k}I-h\beta _{k}L$ is nonsingular;

• (iii) the characteristic polynomial $P_{LM}(z)$ never vanishes on the unit circle $\mu =\{z:|z|=1\}$ and its change of argument satisfies

  $$\begin{aligned} \frac{1}{2\pi }\triangle _{\mu }\arg P_{LM}(z)=d(k+m). \end{aligned}$$

  (4.16)

Then the LM method for the NDDE system is weakly delay-dependently stable.

Proof

The difference system (4.15) is asymptotically stable if and only if all the characteristic roots of $P_{LM}(z)=0$ lie in the inside of the unit circle. Because of the condition (ii) the parameter matrix $\alpha _{k}I-h\beta _{k}L$ of the term $z^{m+k}$ in (4.14) is nonsingular. Therefore, we know that the degree of $P_{LM}(z)$ is $d(k+m)$. Hence $P_{LM}(z)=0$ has $d(k+m)$ roots. By means of the argument principle, the condition (iii) means that all the $d(k+m)$ roots of $P_{LM}(z)=0$ lie inside of the unit circle $|z|=1$. $\square$

Remark 4.2

When LM methods are explicit, $\beta _{k}=0,$ we have that $\alpha _{k}I-h\beta _{k}L=I$ for $\alpha _{k}=1,$ i.e., condition (ii) of Theorem 3.3 holds automatically.

Now we can describe an algorithm to check the conditions of Theorems 4.1, 4.2 and 4.3. This is parallel to Algorithm 1.

Algorithm 2

Step 1:

Taking a sufficiently big $n \in \mathbb {N}$, we compute n nodes $\{ z_0, z_1, \ldots , z_{n-1} \}$ upon the unit circle $\mu$ of z-plane so as $\mathrm{arg}\, z_{\ell } = (2 \pi ) \ell /n$. For each $z_{\ell }\ (\ell =0,1 \ldots n-1)$, we evaluate the characteristic polynomials of the numerical scheme. That is, in RK case, we evaluate it by computing the determinant

$$\begin{aligned} P(z_{\ell })= & {} \det \left\{ \left[ \begin{array}{cc} I_{sd}-h(A\bigotimes L) &{} 0 \\ -\varvec{b}^\mathrm{T}\bigotimes I_{d} &{} I_{d} \end{array}\right] {z_{\ell }}^{m+1} - \left[ \begin{array}{cc} 0 &{} h(\varvec{e}\bigotimes L) \\ 0 &{} I_{d} \end{array}\right] {z_{\ell }}^{m} \right. \\&-\left. \left[ \begin{array}{cc} h(A\bigotimes M)+I_{s}\bigotimes N &{} 0 \\ 0 &{} 0\end{array}\right] z_{\ell } - \left[ \begin{array}{cc} 0 &{} h(\varvec{e}\bigotimes M) \\ 0 &{} 0 \end{array}\right] \right\} , \end{aligned}$$

while in LM case by computing the determinant

$$ P(z_{\ell }) = \det \left[ \sum _{j=0}^{k}\left( (\alpha _{j}I - h\beta _{j}L)z_{\ell }^{m} - \alpha _{j}N-h\beta _{j}M\right) z_{\ell }^{j}\right] . $$

Also we decompose $P(z_{\ell })$ into its real and imaginary parts.

Step 2:

We examine whether $P(z_{\ell })=0$ holds for each $z_{\ell }$ $(\ell = 0, 1, \ldots , n-1)$ by checking its magnitude satisfies $| P(z_{\ell }) |\le \delta _{1}$ with the preassigned small positive tolerance $\delta _{1}$. If it holds, i.e., $z_{\ell }\in \mu$ is a root of P(z), then the numerical scheme for the NDDE system is not asymptotically stable and stop the algorithm. Otherwise, to go to the next step.

Step 3:

We examine whether $\frac{1}{2\pi }\triangle _{\mu }\arg P(z_{\ell })=d(s+1)(m+1)$ in RK case (or $d(k+m)$ in LM case ) holds along the sequence $\{ P(z_{\ell })\}$ by checking $|\frac{1}{2\pi }\triangle _{\mu }\arg P(z_{\ell })-d(s+1)(m+1)|\le \delta _{2}$ in RK case ( or $|\frac{1}{2\pi }\triangle _{\mu }\arg P(z_{\ell })-d(k+m)|\le \delta _{2}$ in LM case ) with the preassigned tolerance $\delta _{2}.$ If it holds, it means that the change of the argument along the sequence $\{ P(z_{\ell })\}$ is $d(s+1)(m+1)$ in RK case (or $d(k+m)$ in LM case ), then the numerical scheme for the NDDE system is asymptotically stable, otherwise not stable.

Remark 4.3

From the above three theorems, in order to solve numerically an asymptotically stable delay differential system of neutral type by an RK or LM method, it is enough for us to choose a positive integer m such that the resulting difference system is asymptotically stable. When the positive integer m is determined, the step-size $h= {\tau }/{m}$ is obtained such that the RK or LM method can work. Theorems 4.1, 4.2 and 4.3 do not contradict the results reported in [7, 18] which assert for any A-stable natural RK method for system (1.3) and for any step-size $h={\tau }/{m},$ (where m is a positive integer) there exists an asymptotically stable linear system for which the resulting system is not asymptotically stable, i.e., $u_{n}\rightarrow 0 \quad \text{ as }\quad n\rightarrow \infty$ does not hold.

Remark 4.4

Both Schur–Cohn and Jury stability criteria [15] need information of all the coefficients of the characteristic polynomial $P_{RK}(z)$ (or $P_{LM}(z)$). It is a well-known ill-posed problem to compute all the coefficients of the characteristic polynomial for a high dimensional matrix [8]. Although Schur–Cohn and Jury stability criteria can be applied to the resulting difference systems from RK and LM methods in theoretical sense, they can not work well in practice when m or d are big. Algorithm 2 avoids computation of the coefficients of the characteristic polynomial $P_{RK}(z)$ (or $P_{LM}(z)$). It evaluates the determinant $P_{RK}(z_{\ell })$ or $P_{LM}(z_{\ell })$ through the elementary row (or column) operations which are relatively efficient ways [14].

5 Numerical examples

In this section, two numerical examples are given to demonstrate the main results in Sects. 2 and 3. The matrix norm $\Vert F \Vert _{2}$ is defined by

$$\begin{aligned} \Vert F \Vert _{2}=\sqrt{\lambda _{\max }(F^{*}F)}, \end{aligned}$$

which is equal to the special case of the H-norm for $H = I$, i.e., $\Vert F\Vert _{I} = \Vert F \Vert _{2}$ holds. The number of significant digits is 4,  and all the equality signs hold in this sense. The classical fourth-order RK formulas for ODEs (4.1), which is given as

$$\begin{aligned} k_{1}= & {} f(t_{n},y_{n}),\\ k_{2}= & {} f(t_{n}+\frac{h}{2},y_{n}+\frac{h}{2}k_{1}),\\ k_{3}= & {} f(t_{n}+\frac{h}{2},y_{n}+\frac{h}{2}k_{2}),\\ k_{4}= & {} f(t_{n+1},y_{n}+hk_{3}),\\ y_{n+1}= & {} y_{n}+\frac{h}{6}(k_{1}+2k_{2}+2k_{3}+k_{4}), \end{aligned}$$

is our underlying scheme of the natural RK for (1.1).

Example 1

The two-dimensional linear neutral system (1.1) with the parameter matrices

$$\begin{aligned} L=\left[ \begin{array}{cc} -2 &{} 0\\ 0&{} -0.9 \end{array} \right] , \quad M=\left[ \begin{array}{cc} -1 &{}0\\ -1 &{}-1 \end{array} \right] , \quad \quad N=\left[ \begin{array}{cccc} 0.9 &{}\quad 0.45\\ 0 &{}\quad 0.05 \end{array} \right] . \end{aligned}$$

We have that $\rho (N)=0.9<1,$ i.e, condition (1.2) holds. Since $\Vert N\Vert _{2}=1.0065>1,$ we have to solve Stein equation to obtain a matrix H such that $\Vert N\Vert _{H}<1.$ We have that

$$\begin{aligned} H=\left[ \begin{array}{cc} 5.2632 &{} 2.2320\\ 2.2320&{} 2.1717 \end{array} \right] \quad \text{ and }\quad H_{0}=\left[ \begin{array}{cc} 2.2942 &{}1.4940\\ 1.4940 &{}1.4737 \end{array} \right] . \end{aligned}$$

Furthermore,

$$\begin{aligned} \Vert L\Vert _{H}=5.8109,\quad \Vert M\Vert _{H}=4.0785\quad \text{ and } \quad \Vert N\Vert _{H}=0.9190. \end{aligned}$$

Since $\Vert N\Vert _{H}<1,$ we have that

$$\begin{aligned} \beta = \frac{||L||_{H}+||M||_{H}}{1-||N||_{H}}=122.0731. \end{aligned}$$

Let the initial vector function be

$$\begin{aligned} u(t)=\left[ \begin{array}{c} \sin {t}-2\\ t+2 \end{array} \right] \quad \text{ for } \quad t \in [-\tau , 0]. \end{aligned}$$

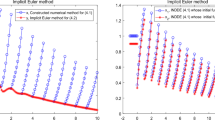
• The case of $\tau =1.1$. Algorithm 1 is employed to check stability of the system. As we have $\triangle _{\varGamma _{\beta }}\arg P(s)=0$ along the curve $\varGamma _{\beta }$, Theorem 3.2 tells that the system with the given parameter matrices is asymptotically stable. Now using Algorithm 2 with $n=3.2\times 10^{5}$ to check delay-dependent stability of the RK method for the system. When $m=100,$ we obtain that $\triangle _{\mu }\arg P_{RK}(z) = d(s+1)(m+1)=2(4+1)(100+1)=1010.$ Theorem 4.1 asserts the RK method is weakly delay-dependently stable. The numerical solution, which is converging to 0, is depicted in Fig. 2. Conversely, when $m=10,$ we obtain $\triangle _{\mu }\arg P_{RK}(z)=97 \ne d(s+1)(m+1)=2(4+1)(10+1)=110$ and the theorem does not hold. The numerical solution is divergent and its behaviour is shown in Fig. 3.

• The case of $\tau =3.0$. Again we employ Algorithm 1 to check stability of the system. As we have $\triangle _{\varGamma _{\beta }}\arg P(s)=2$ along the curve $\varGamma _{\beta }$, Theorem 3.2 tells that the system with the given parameter matrices is not asymptotically stable. Then the assumptions of Theorem 4.1 do not hold and the numerical solution is not guaranteed to be asymptotically stable. In fact, its figure given in Fig. 4 shows a divergence for $m=100$. We also carried out several numerical experiments for $m>100,$ whose numerical solutions are still divergent.

Fig. 2

Numerical solutions are asymptotically stable when $m=100$ for $\tau =1.1$ in Example 1

Fig. 3

Numerical solutions are not stable when $m=10$ for $\tau =1.1$ in Example 1

Fig. 4

Numerical solutions are not stable when $m=100$ when $\tau =3$ in Example 1

Example 2

We take the following four-dimensional linear neutral system with the parameter matrices given by

$$\begin{aligned} L=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 1 &{} -1&{} 0\\ -3.346 &{} -2.715 &{}2.075 &{}-2.007\\ -4 &{}0 &{}-2 &{}0\\ -3 &{}0 &{}0 &{}-6 \end{array} \right] , \quad M=\left[ \begin{array}{cccc} -1 &{}2 &{}2 &{}-1\\ 3 &{}3 &{}-2 &{}0\\ 1 &{}2 &{}-1 &{}1\\ 2 &{}3 &{}1 &{}-3 \end{array} \right] , \end{aligned}$$

$$\begin{aligned} \quad N=0.1\times \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0.2 &{}-0.1 &{}0.5 &{}-0.1\\ -0.3 &{}0.09 &{}-0.15 &{}-0.027\\ -3.333 &{}0.1 &{}0.2 &{}1\\ -1 &{}2 &{}0.5 &{}1 \end{array} \right] . \end{aligned}$$

We have $\rho (N)=0.08540<1,$ i.e, the condition (1.2) holds. Furthermore,

$$\begin{aligned} \Vert L\Vert _{2}=8.0597,\quad \Vert M\Vert _{2}=6.3230\quad \text{ and } \quad \Vert N\Vert _{2}=0.3848. \end{aligned}$$

Since $\Vert N\Vert _{2}<1,$ we can take $H=I$ and we have

$$\begin{aligned} \beta = \frac{||L||_{2}+||M||_{2}}{1-||N||_{2}}=23.3782. \end{aligned}$$

Let the initial vector function be

$$\begin{aligned} u(t)=\left[ \begin{array}{c} 2\sin {t}+1\\ \cos {t}-2\\ t+2\sin {t}\\ 3t+\cos {t} \end{array} \right] \quad \text{ for } \quad t\in [-\tau , 0]. \end{aligned}$$

• The case of $\tau =0.1$. The procedure goes similarly to Example 1. Since our computation gives $\triangle _{\varGamma _{\beta }}\arg P(s)=0$ along the curve $\varGamma _{\beta },$ according to Theorem 3.2, we can confirm that the system with the given parameter matrices is asymptotically stable.

  Now using Algorithm 2 with $n=3.2\times 10^{5}$ to check delay-dependent stability of the RK method for the system. In the case of $m=100$, our computation gives that $\triangle _{\mu }\arg P_{RK}(z) = d(s+1)(m+1)=4(4+1)(100+1)=2020.$ Thus, by Theorem 4.1, the RK method is weakly delay-dependently stable. In fact, the numerical solution is convergent as shown in Fig. 5. Even when $m=1,$ we can compute $\triangle _{\mu }\arg P_{RK}(z) = d(s+1)(m+1)=4(4+1)(1+1)=40.$ Hence again the RK method is weakly delay-dependently stable and the numerical solution is convergent as shown in Fig. 6.

• The case of $\tau =0.3$. Since the computation in Algorithm 1 gives $\triangle _{\varGamma _{\beta }}\arg P(s)=2$ along the curve $\varGamma _{\beta },$ according to Theorem 3.2, we can confirm that the system with the given parameter matrices is not asymptotically stable. Then, the assumptions of Theorem 4.1 do not hold and the numerical solution is divergent for $m=100$, whose computed results are shown in Fig. 7. We also carried out several other numerical experiments for $m>100$, but the numerical solutions are still divergent.

Fig. 5

Numerical solutions are asymptotically stable when $m=100$ for $\tau =0.1$ in Example 2

Fig. 6

Numerical solutions are asymptotically stable when $m=1$ for $\tau =0.1$ in Example 2

Fig. 7

Numerical solutions are not stable when $m=100$ for $\tau =0.3$ in Example 2

The two numerical examples show that our main results work well in the actual computations. Therefore, we can employ them to seek a step-size h so as to give numerically stable solution by Runge–Kutta or linear multi-step method. That is, assume that we are given an asymptotically stable system (1.1), then we can select an appropriate natural number m for the step-size $h = \tau /m$ which yields an asymptotically stable numerical solution by utilizing our criterion.

6 Conclusions

For the asymptotic stability of analytical solution of the NDDE system (1.1) with (1.2), Theorem 3.2 provides a novel necessary and sufficient condition, which extends the results in the literature. Then, we present a relaxed definition, Definition 4.1, for delay-dependent stability of numerical methods. By applying this, Theorems 4.1, 4.2 and 4.3 provide sufficient conditions for delay-dependent stability of RK and LM methods, respectively. They show that it is possible to seek a step-size $h={\tau }/{m}$ such that the resulting difference system by a standard RK or a LM method is asymptotically stable for an asymptotically stable NDDE system. Theorems can not guarantee an existence of such a step-size $h= {\tau }/{m}$ for all asymptotically stable NDDE systems. However, for many cases of the system the theorems can hold. Furthermore, two algorithms are provided for checking delay-dependent stability of analytical and numerical solutions, respectively.