Free energy: a user’s guide

Abstract

Over the last fifteen years, an ambitious explanatory framework has been proposed to unify explanations across biology and cognitive science. Active inference, whose most famous tenet is the free energy principle, has inspired excitement and confusion in equal measure. Here, we lay the ground for proper critical analysis of active inference, in three ways. First, we give simplified versions of its core mathematical models. Second, we outline the historical development of active inference and its relationship to other theoretical approaches. Third, we describe three different kinds of claim—labelled mathematical, empirical and general—routinely made by proponents of the framework, and suggest dialectical links between them. Overall, we aim to increase philosophical understanding of active inference so that it may be more readily evaluated. This paper is the Introduction to the Topical Collection “The Free Energy Principle: From Biology to Cognition”.

Overview

Over the past fifteen years, a novel explanatory framework spearheaded by Karl Friston has inspired both excitement and confusion in the philosophy of biology and cognitive science. Active inference, whose most famous tenet is the free energy principle, purports to unify explanations in biology and cognitive science under a single class of mathematical models. Unfortunately, the framework is notoriously difficult to understand, hampering efforts at critical evaluation. The Topical Collection aims to widen the field for proper assessment of active inference, and this introduction provides a jumping-off point.

There are broadly three reasons why the active inference framework is difficult to understand. First, the mathematics are unfamiliar to many philosophers, and even to biologists and cognitive scientists. Second, the framework was developed rapidly by a small but dedicated group of researchers, limiting its accessibility while expanding its scope. Third, the framework makes claims across both mathematical and empirical domains, and the dialectical relationships between these are unclear.

Here we attempt to redress the situation by targeting each source of potential confusion. First, we offer simplified versions of the models used in active inference (“Simple models of the free energy principle for inference, action, and selection” section). Second, we describe the historical trajectory of the framework and highlight its novel features (“A brief history of the free energy principle” section). Third, we distinguish three kinds of claim (labelled mathematical, empirical, and general) that proponents of active inference make (“Dialectic: the free energy principle and related claims” section). We illustrate the ways these kinds of claim are used to justify one another with reference to papers in the Topical Collection.

Our goal is neither to defend nor attack active inference, but to enable philosophers to pursue more effective critical evaluation. A wider and deeper understanding of the framework is required if it is to be given a proper hearing.

Simple models of the free energy principle for inference, action, and selection

A note on ‘models’

Let us begin with a warning. The word ‘model’ takes on two distinct senses throughout our discussion. The sense more familiar to philosophers is what we will call a scientific model: a representation of some possible or actual system, which a scientist uses to reason about, or discover features of, that system and related systems. By contrast, in the active inference literature a narrower sense is typically meant; what we will call a generative model. This is a mathematical object with applications in statistics and various sciences. Our simplified models of the free energy principle are scientific models. They in turn posit generative models, possessed by agents and employed by them to perform inference and action.

Note further that some scholars opt for a deflationary stance on generative models, using them only to describe the dynamics of agents. It is an open question whether this kind of model building precludes any form of scientific realism about the relation between the model and the target system. These issues are discussed in “Dialectic: the free energy principle and related claims” section.

In each of our scientific models, the generative model in question takes the form of a joint probability distribution like $p(w,x)$ or $p(w,x,z)$. If we use the term ‘model’ in isolation, context will be sufficient to indicate which sense is intended.

A simple model of inference

The inference problem addressed by the active inference framework concerns an agent who can observe data $x$ and must infer the value of an unobservable state $w$. The unobservable state is assumed to cause observable data (Fig. 1). The agent is capable of harbouring beliefs about the unobservable state, and knows the statistical relationship between it and the observable data, which is represented as a joint probability distribution $p(w,x)$.

Fig. 1

The basic model of inference. An agent can observe $x$ and must infer the value of $w$. The agent knows the statistical connection between them, encapsulated by the joint probability distribution $p(w,x)$

For example, imagine you have a cat that spends its time in either the kitchen or the bedroom. When it’s in the kitchen, it often meows for food; when it’s in the bedroom, it often purrs contentedly. Suppose you tally the proportion of the times your cat is in each place and making each noise. The results might look something like this:

$$\begin{aligned} \begin{array}{ccc} &{} &{} \text {Cat noise}\\ &{} &{} \begin{array}{cc} \text {meow} &{} \ \text {purr} \end{array}\\ \text {Cat location}&{} \begin{array}{c} \text {kitchen}\\ \text {bedroom}\end{array} &{} \left( \begin{array}{c|c} 40\% &{} 20\%\\ \hline 10\% &{} 30\% \end{array}\right) \end{array} \end{aligned}$$

The table describes a joint probability distribution $p(w,x)$, where $w$ ranges over possible cat locations: $w\in \{\text {kitchen, bedroom}\}$, and $x$ ranges over possible cat sounds: $x\in \{\text {meow, purr}\}.$ You can see that 40% of the time the cat is in the kitchen and meowing, and 30% of the time it is in the bedroom and purring. It does sometimes mix and match those locations and noises—sometimes it purrs in the kitchen or meows in the bedroom—but less frequently. (We are assuming that the cat cannot be anywhere but the kitchen or the bedroom, that it cannot make sounds other than meowing or purring, and that it is always making one of these sounds.)

Now suppose you are in the living room and you hear a meow. You can’t tell whether the sound came from the kitchen or bedroom, but you do know the statistics given in the table above. What is the probability of the cat being in one location or the other, given that you heard it meowing? This is an inference problem. We will say that you must give your solution in the form of a probability distribution, which we denote by $q(w)$. This can be said to capture your degrees of belief—what philosophers sometimes call ‘credences’—in the two possible locations of the cat.

Of course, there is a sense in which you already possess a distribution of this kind. The joint distribution that is your generative model, $p(w,x)$, implies a distribution $p(w)$. But these are your prior credences, the probabilities you implicitly assign before you hear the cat make a sound. We are asking what probabilities you should assign—what your credences, represented by $q(w)$, should be—after hearing a meow.

Many philosophers will be familiar with one famous method for solving this problem: Bayesian conditionalization. This method can be stated as a principle saying how an agent using a model $p(w,x)$ ought to choose their beliefs $q(w)$ upon observing data $x$:

Bayesian Principle: $q(w) \xleftarrow []{} p(w|x)$

The left-pointing arrow $\xleftarrow []{}$ means, ‘set the value of the thing on the left to the value of the thing on the right.’ So this statement says, ‘set the value of $q(w)$ equal to the value of $p(w|x)$’. We have called this rule Bayesian Principle because $p(w|x)$, which is called the posterior, is calculated via Bayes’ theorem:

$$\begin{aligned} p(w|x) = \frac{p(x|w)p(w)}{p(x)} \end{aligned}$$

(1)

Since the numerator is equal to the joint probability, and the denominator is its marginal distribution, we can rewrite (1) in terms of what the agent already knows:

$$\begin{aligned} p(w|x)&= \frac{p(x|w)p(w)}{p(x)}\\= \frac{p(w,x)}{\sum _{w}p(w,x)} \end{aligned}$$

Following Bayesian Principle, the solution to the cat example is as follows:

$$\begin{aligned} q(\text {kitchen})&= p(\text {kitchen}|\text {meowing})\\&= \frac{p(\text {kitchen},\text {meowing})}{\sum _{w}p(w,\text {meowing})}\\&=\frac{\frac{4}{10}}{\frac{4}{10}+\frac{1}{10}}\\&= \frac{4}{5}\\ q(\text {bedroom})&= p(\text {bedroom}|\text {meowing})\\&= \frac{p(\text {bedroom},\text {meowing})}{\sum _{w}p(w,\text {meowing})}\\&=\frac{\frac{1}{10}}{\frac{4}{10}+\frac{1}{10}}\\&= \frac{1}{5} \end{aligned}$$

Upon hearing a meow, according to Bayesian Principle, you should have 80% credence that the cat is in the kitchen and 20% credence that it is in the bedroom.

It is worth noting that following Bayesian Principle is much simpler than the Bayesian statistical practices performed by many scientists. Usually the scientist aims to improve the accuracy of a generative model of some real-world phenomenon, which would mean improving the accuracy of $p(w,x)$.¹ This learning task is relatively difficult. It should be distinguished from the simpler task of estimating $w$ from an observation of $x$, which is called inference. In the present example we are assuming for simplicity that the agent’s generative model is already accurate. We return to this point in “Extensions to the models: more things to learn, more ways to act” section.

The formalism at the heart of active inference begins with the observation that it is sometimes impossible to follow Bayesian Principle. In many of the situations in which statisticians would like to find $p(w|x)$, the sum $\sum _{w}p(w,x)$ is computationally intractable so $p(x)$ cannot be calculated. This usually happens when the state space is continuous rather than discrete, so the sum $\sum$ becomes an integral $\int$ over an infinite number of points.

In these cases, what is needed instead is a way to choose $q(w)$ so as to make it close to $p(w|x)$. Even if you cannot formulate the true posterior, you will end up with a distribution that is optimal given the computational resources at your disposal.

When this problem is formulated by statisticians, we usually begin with a set of possible distributions q, and search for the member of that set which lies as close to $p(w|x)$ as possible. We can do this indirectly by using a measure of inaccuracy. Active inference employs a measure of inaccuracy called variational free energy, labelled F. Because it is a measure of inaccuracy, smaller values are better than larger values. Given a set of candidate distributions q, the best is the one that produces the lowest value of F. Although the lowest possible value of F is given by the true posterior $p(w|x)$, that might not be one of the available distributions q. In that case, the optimal q is the member of the set that yields the lowest value of F from among the available members.

In short, according to active inference, the goal of inference is to adopt credences q that minimize variational free energy F. We will now build up to the definition of F by giving an intuitive overview of its component parts.

Variational free energy captures two sources of inaccuracy in belief and dictates how they ought to be traded off against one another. The two sources of inaccuracy are overfitting and failing to explain the data. We will introduce them in turn before displaying the full definition of F, then showing how it can provide the same solution to the cat problem as the simpler Bayesian Principle.

Overfitting. According to lexico.com (2021), overfitting is “The production of an analysis which corresponds too closely or exactly to a particular set of data, and may therefore fail to fit additional data or predict future observations reliably.” In the cat example, the prior $p(w)$ implied by the generative model captures general statistics about the cat’s location,² while $q(w)$ is your ‘analysis’; that is, your belief about its current location. You overfit when you choose a distribution $q(w)$ that explains the current data very well, but fails to account for the wider range of statistical possibilities encapsulated by $p(w)$. The cost of overfitting can therefore be measured by checking how far $q(w)$ diverges from $p(w)$. The first term of F is a measure of this kind:

$$\begin{aligned} \sum _{w} q(w) \log \frac{q(w)}{p(w)} \end{aligned}$$

(2)

This term, which is also called relative entropy or Kullback-Leibler divergence, measures how far a distribution $q(w)$ differs from a distribution $p(w)$.³ When q and p are identical, they coincide for every value of the sum. In this case the logarithm is always zero (because $\log {\frac{a}{a}}=0$) so the total value of the sum is zero. As q and p get more and more different, the total value of the term increases. To avoid overfitting, $q(w)$ should be close to $p(w)$.

Failing to explain the data. Mathematically, ‘explaining the data’ means assigning high probability to events $w$ that make the probability of $x$ high. The penalty for failing to explain data is captured by the second term of F:

$$\begin{aligned} \sum _{w} q(w) \log \frac{1}{p(x|w)} \end{aligned}$$

(3)

Higher values of $p(x|w)$ should be matched with high values of $q(w)$ to keep this term low.

Variational free energy F is the sum of the penalties for overfitting and failing to explain the data:

$$\begin{aligned} F(p,q,x)= \underbrace{ \sum _{w} q(w) \log \frac{q(w)}{p(w)}}_{ \begin{array}{c} \text {Penalty for overfitting} \end{array} } + \underbrace{ \sum _{w} q(w) \log \frac{1}{p(x|w)}}_{ \begin{array}{c} \text {Penalty for failing} \\ \text {to explain the data} \end{array} } \end{aligned}$$

(4)

Suppose you happen to choose beliefs $q(w)$ that are identical to $p(w)$. Then the first term is zero, but the second term may be inordinately high. You have avoided overfitting at the expense of failing to explain the data. On the other hand, suppose you happen to choose $q(w)$ such that its high values correspond to high values of $p(x|w)$. Then the second term remains low, but the first term may be high as a result. Your beliefs explain the data well at the expense of overfitting. The optimal value of F occurs when $q(w)$ lies between these two extremes.⁴ In a moment we will see how this works in the solution to the cat example. But first we should address a practical issue with Eq. (4).

We set up the inference problem by saying that the agent knows the statistics $p(w,x)$, but might not have access to the marginal distribution $p(x)$. The agent was prohibited from following Bayesian Principle for this reason. However, we did not address whether the agent has access to the prior $p(w)$ or the likelihood $p(x|w)$. Since $F$ includes both those terms, one would expect the agent needs them in order to use $F$ to guide inference. As it turns out, the agent does not need access to the prior or the likelihood, because (4) simplifies to:

$$\begin{aligned} F(p,q,x)= \sum _{w} q(w) \log \frac{q(w)}{p(w,x)} \end{aligned}$$

(5)

Given our assumptions so far, the agent has access to all three inputs to F in Eq. (5):

• p: A joint distribution over $w$ and $x$. The agent’s generative model and, in this simple example, also the true general statistical connection between $w$ and $x$.

• q: A distribution over $w$. The agent’s credences about the unobservable state, in light of observing a specific piece of data $x$.

• $x$: A value of a random variable. The specific piece of data the agent has just observed.

The inference problem is posed in the following way: given p and $x$, what should q be? Considering F as a measure of the inaccuracy of belief, a new principle suggests itself:

Free energy principle (inference): $q(w) \xleftarrow []{} \underset{q}{{\text {argmin}}}\ F$

Here $\underset{q}{{\text {argmin}}}$ means ‘choose the distribution q that makes the following term as small as possible’.

Notice that the form of Free energy principle (inference) is the same as that of Bayesian principle. In both cases you are told to perform a calculation and set $q(w)$ equal to the resulting value. The difference is that Bayesian principle counsels a direct calculation via Bayes’ theorem. In contrast, Free energy principle (inference) counsels what might be called an indirect calculation. You must assess candidate distributions q in order to find the one that produces the lowest value of F. Happily, in practice this can be done by trial-and-improvement rather than trial-and-error. Various algorithms for finding q are available depending on the details of the generative model (MacKay 2003, chapter 33). One of the developments that prefigured active inference was the implementation of such an algorithm in a neural network (Friston 2005).

In our cat example, p was given by the table of statistics of cat locations and noises, and we assumed the observer heard the cat meowing ($x=\text {meow}$). To solve the cat problem using Free energy principle (inference) we could use one of the aforementioned algorithms, or simply test lots of different values of $q(w)$ to see which one produces the lowest value of F in combination with these values of p and $x$. Fortunately, the example is so simple that we can draw a graph of F against q and look for the smallest value (Fig. 2). The minimum point is at $q(\text {kitchen})=\frac{4}{5}$, implying that $q(\text {bedroom})=\frac{1}{5}$. This solution agrees with that given by Bayesian principle. It is important to note, however, that the situations in which variational inference is most useful are those in which the graph in Fig. 2 cannot be drawn. For illustrative purposes, we have here made use of information that is usually unknown to the agent. Instead, the optimal q would be found using an algorithm of the kind described above.

Fig. 2

Variational free energy $F(p,q,x)$ as a function of the belief distribution $q(w)$ when $x=\text {meow}.$ The penalty for overfitting takes its minimum value when $q(\text {kitchen})=0.6=p(\text {kitchen}).$ That is because choosing a posterior that is identical to the prior is the extreme opposite of overfitting. The penalty for failing to explain the data takes its minimum value when probability 1 is assigned to the cat being in the kitchen. That is because the kitchen is the best explanation for the cat’s meowing. Variational free energy F takes its minimum value at 0.8 (solid black circle) between the minima of its two component costs. Free energy principle (inference) therefore counsels that $q(\text {kitchen})=0.8=\frac{4}{5}$, in agreement with the solution given by Bayesian Principle. The code to generate this graph can be found at https://github.com/stephenfmann/fep

A simple model of action

Now suppose you can perform an action, $z$, that will place the cat in one of the two rooms. By changing the hidden state $w$ you can indirectly change future values of $x$ (Fig. 3).

Fig. 3

The basic model of action. An agent can produce an act, $z$, in order to bring about states $w$ that in turn produce outcomes $x$. Active inference employs a controversial dual interpretation of $p(w)$ and $p(x)$ as probability distributions and preference distributions over hidden states and sensory states respectively

While the previous section dealt with an inference rule—how to choose $q(w)$—this section deals with a decision rule—how to choose $z$. Traditionally, decision rules stem from measures of preference, which we have not yet introduced. One of the potentially confusing aspects of active inference is that it treats the statistical model p as a measure of both probabilities and preferences at the same time. Later we will discuss possible justifications of this move; for now we assume it is interpretatively valid, in order to give as smooth an exposition as possible.

Recall that Free energy principle (inference) counsels choosing beliefs by minimising a function that measures the cost of inaccuracy. That function, $F$, is a sum of two kinds of penalty. Action selection is governed in the same way, but with a slightly different cost function called expected free energy and labelled G. The definition of G is closely related to that of F. The interpretation of the two penalty terms changes as the formalism is updated to reflect the fact we are now making measurements over expected future states. Since future states have yet to be observed, the agent must average over them to obtain expected values. The penalties are associated with failing to satisfy preferences and failing to minimize future surprise.

Failing to satisfy preferences. $q(w|z)$ is the assumed distribution over hidden states given our action. If we place the cat in the bedroom, where do we expect it to be? $p(w)$ is now a preference distribution over hidden states. The first penalty term in G is a measure of how far the expected distribution of hidden states diverges from the preference distribution:

$$\begin{aligned} \sum _{w} q(w|z) \log \frac{q(w|z)}{p(w)} \end{aligned}$$

(6)

Compare Eq. (2). Again this is relative entropy, a standard way to measure the divergence of one distribution from another. Again, its minimum value is attained when $q(w|z)=p(w)$ for every state.

Not only is it unusual to treat p as a preference distribution, it is unusual to treat the goal of decision-making to produce a distribution that matches that distribution, rather than maximising expected utility. So perhaps it is best to keep in mind that ‘preference’ in this sense might mean something different from ‘utility’ in the traditional sense.

Failing to minimize future surprise. One of the tenets of active inference is that agents should act to ensure that future data are not too surprising. The second penalty term of G therefore measures how surprising future data would be, on average, if you performed $z$:

$$\begin{aligned} \sum _{w} q(w|z) \sum _{x} p(x|w) \log \frac{1}{p(x|w)} \end{aligned}$$

(7)

Compare Eq. (3). In addition to conditionalizing on $z$, this term also changes from calculating the logarithm directly to calculating its expectation over $x$. That is because $x$ is here a future sensory state: we do not yet know what it will be, so we must employ its expected value. As a result, the inner term that begins with $\sum _{x}$ is the entropy of $X$—the expected surprise of your future observations—given that a certain hidden state $w$ occurs.⁵ You want this inner term to be low. To do this, you should aim to bring about hidden states that lead to predictable observations. That means you should perform acts that give a high value to $q(w|z)$ when $w$ produces a low value for that inner term.

Overall, expected free energy is a sum of these penalties:

$$\begin{aligned} G (p,q,z) = \underbrace{\sum _{w} q(w|z) \log \frac{q(w|z)}{p(w)}}_{ \begin{array}{c} \text {Penalty for failing to}\\ \text {satisfy your preferences} \end{array} } + \underbrace{\sum _{w} q(w|z) \sum _{x} p(x|w) \log \frac{1}{p(x|w)}}_{ \begin{array}{c} \text {Penalty for failing to minimize}\\ \text {expected surprise of future data} \end{array} } \end{aligned}$$

(8)

The third input to G is $z$ rather than $x$. As mentioned above, this is because we are calculating the expected value over possible future sensory states, rather than inferring on the basis of a sensory state that has just occurred.

As with F, the measure G suggests a principle:⁶

Free energy principle (action): $z\xleftarrow []{}\, \underset{z}{{\text {argmin}}}\ G$

In the same sense that Free energy principle (inference) approximates Bayesian inference, it has been suggested that minimizing expected free energy can be read as an approximation of optimal Bayesian design and Bayesian decision theory.⁷

It is worth restating just how unusual it is to interpret p as a measure of both probabilities and preferences. There is nothing wrong with treating a distribution as a measure of preferences: distributions don’t demand to be interpreted as probabilities, after all. But what is unorthodox, and in need of justification, is giving the very same mathematical term two different interpretations within the same equation. One thing worth noting is that in communication theory, p(x) is a probability and $\log {\frac{1}{p(x)}}$ is a measure of cost (specifically: the number of binary symbols you are required to expend in order to encode an outcome x, whose probability is p(x), under the assumption that your code is optimised for the distribution p). These are the components of entropy, $H(X)=\sum _{x}p(x)\log {\frac{1}{p(x)}}$, which can be interpreted as the uncertainty about the outcome of event X and as the optimal expected cost of encoding the outcome. We are not aware of proponents of active inference taking this interpretive line, but it appears to be a viable option.

Finally, let us present a solution to the cat example. For the problem to have a determinate solution we need a conditional distribution $q(w|z)$. Let’s suppose that if we put the cat in the kitchen it usually stays there, but if we put it in the bedroom it tends to wander:

$$\begin{aligned}&q(\text {kitchen}|\text {put cat in kitchen})&= \frac{9}{10}\\&q(\text {bedroom}|\text {put cat in kitchen})&= \frac{1}{10}\\&q(\text {bedroom}|\text {put cat in bedroom})&= \frac{5}{10}\\&q(\text {kitchen}|\text {put cat in bedroom})&= \frac{5}{10} \end{aligned}$$

We obtain two different values of G, corresponding to the two different possible acts $z$ (Fig. 4). The smallest expected free energy results from putting the cat in the bedroom, so that is what you ought to do according to Free energy principle (action).

Fig. 4

Expected free energy $G(p,q,z)$ when putting the cat in the kitchen or bedroom. The value of G is lowest when $z=\text {bedroom}$, so Free energy principle (action) dictates that that is where you should put the cat. The surprise penalty for both acts is about the same, because in either case you cannot be very certain about whether the cat will be meowing or purring at the next time step. However, the preference penalty for putting the cat in the bedroom is relatively small, because $q(w|\text {put cat in bedroom})=\left( \frac{5}{10},\frac{5}{10}\right)$ is relatively close to the distribution $p(w)=\left( \frac{6}{10},\frac{4}{10}\right)$. Intuitively: if you want the cat to spend roughly equal time in both places, you shouldn’t put it in the kitchen, because it will stay there. The code to generate this graph can be found at https://github.com/stephenfmann/fep

The duality between probability and preference can be made a little more intuitive with another example. Suppose you take your cat’s temperature three times a day for several weeks. If your cat is healthy, you will end up with a frequency distribution whose points fall between 38.1$^\circ$C and 39.2$^\circ$C. Now suppose you are asked what you would prefer your cat’s temperature to be in future. Assuming you want your cat to continue being healthy, you would prefer that its temperature fall within the range defined by this distribution.

There are at least two reasons why this interpretation should be distinguished from utilities as decision theory traditionally understands them. First, you should not simply prefer that your cat always be the temperature that happens to occur most often according to the frequency distribution. Healthy functioning entails some fluctuation of temperatures throughout the day. The goal is not to maximise the value of this distribution, but to match future event frequencies to it. Second, preferences are just one consideration that must be taken into account when choosing actions. The preference penalty must be balanced against the surprise penalty. The tension between exploiting your circumstances to achieve your goals and exploring your circumstances to gain a better understanding of how acts produce outcomes enables some of the more complex applications of active inference.

One of the ways proponents of the framework turn this unusual interpretation to their advantage is by casting action as a form of inference:

The mechanism underlying [minimizing expected free energy] is formally symmetric to perceptual inference, i.e., rather than inferring the cause of sensory data an organism must infer actions that best make sensory data accord with an internal representation of the environment.

Buckley et al. (2017: p.57), emphasis added

Hence the name ‘active inference’. The treatment of action as inference in disguise helps avoid perceived problems with purely utility-based theories of decision-making (Schwartenbeck et al. 2015). By starting with an inference problem in the form of expected free energy minimization, preferences emerge as the first term of Eq. (8). But attempting to achieve these preferences must be balanced against the second term, which explicitly counsels minimizing future surprise. Proponents take this to be both more general and more principled than traditional behavioural theories, which employ utility functions alone (DeDeo 2019).

Further aspects of the duality between action and perception are brought to the fore by Friston’s more recondite work on selection dynamics. We now turn to these deeper themes.

A simple model of selection

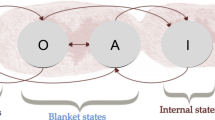
In our model $x$ and $z$ are the inputs and outputs of the agent. The set $\{x,z\}$ is called the agent’s Markov blanket. This term is derived from Judea Pearl’s work on statistical inference using Bayesian networks (Pearl 1988). Roughly, in Pearl’s sense the ‘Markov blanket’ of a focal node is the set of nodes that provide total information about the focal node. However, Markov blankets have taken on a special usage within active inference (Bruineberg et al. 2021). In the sense required here, a Markov blanket can be understood as the set of nodes that ‘screen off’ the agent from nodes considered external to it. Using the concept of a Markov blanket, Friston has developed an account of selection based on a fundamental claim about free energy. He claims that Markov blanket systems that persist over time within certain kinds of (mathematically defined) environments will come to act in a manner that can be interpreted as minimizing F via inference and minimizing G via action.

Another toy model will help illustrate. Consider an agent whose surface temperature $x$ can safely lie between -3 and 3 units. If it drops to -4 or increases to 4, it dies. The external state $w$ controls whether the temperature increases or decreases by 1 unit at the next timestep. The agent’s preference distribution over available temperatures might look something like this:

$$\begin{aligned} \begin{array}{ccc} &{} &{} x\\ &{} &{} \begin{array}{lcccccccc} -4\quad \ -3\ &{} -2\ &{} -1\quad &{} 0\quad \ &{} 1\quad \ &{} 2\quad &{} 3\quad \ &{} 4\quad \end{array}\\ w&{} \begin{array}{c} +1\\ -1 \end{array} &{} \left( \begin{array}{c|c|c|c|c|c|c|c|c} 0&{}0.025&{}0.05&{}0.075&{}0.2&{}0.075&{}0.05&{}0.025&{}0 \\ \hline 0&{}0.025&{}0.05&{}0.075&{}0.2&{}0.075&{}0.05&{}0.025&{}0 \end{array} \right) \end{array} \end{aligned}$$

(9)

Notice that the value of $w$ does not affect the agent’s preferences: all the agent directly cares about is its surface temperature, denoted by $x$. That is why the two rows are identical.

Suppose the agent can act to affect the external state. We will say it can try to set the value to either − 1 or +1, and in both cases it is successful 95% of the time:

$$\begin{aligned} w&\in \{-1,+1\}\\ z&\in \{-1,+1\}\\ z=-1 \implies p(w|z)&= (0.95,\ 0.05)\\ z=+1 \implies p(w|z)&= (0.05,\ 0.95) \end{aligned}$$

Given this set-up and the model in Fig. 3 we have an agent who will survive if and only if it keeps $x$ within a certain bound. When the temperature is high, it would be best for the agent to act with $z=-1$. When the temperature is low, it would be best for the agent to act with $z=+1$.

To make the appropriate causal link between the current surface temperature and the act, the agent needs to employ an inner state $y$. It can initiate two strategies: $p(y|x)$ for inference, and $p(z|y)$ for action. Let us allow the inner state to also take the values $\{-1,\ +1\}$. Then the question that active inference attempts to answer is, what can we say about the strategies of successful agents?

We will simulate the problem using two agents: a smart agent who tries to increase low temperatures and decrease high temperatures, and an oblivious agent who acts randomly. The smart agent sets $y=+1$ if $x<=0$, and $y=-1$ otherwise. The random agent chooses $y$ by flipping a coin. Both agents set the act to be identical to the inner state, so in this simple case there is no difference between inference and action. In order to calculate variational free energy, we would usually need to make a choice about how the inner state $y$ corresponds to a probability distribution over the external state $q(w)$. However, because $p(w,x)$ has identical rows, the value of free energy is the same no matter what q is chosen. The only thing that affects F is therefore $x$.

Results from a single run are shown in Figs. 5 and 6. The smart agent keeps values of $x$ mostly between $-\,$1 and 1, which keeps F around 2 nats. The random agent eventually spirals away from the optimal sensory states, and its F increases to values much higher than those for the smart agent. After 80 timesteps the random agent dies: its value for $x$ reached 4, and since $p(w,4)=0$ for both values of $w$, its free energy takes an infinite value.

Fig. 5

Variational free energy over time for an agent that controls its external state in a survivable manner. The agent’s control over its external state is 95% accurate; occasionally its grasp slips and free energy increases beyond the average. The code to generate this figure can be found at https://github.com/stephenfmann/fep

Fig. 6

Variational free energy over time for an agent that acts randomly. After 80 timesteps the agent dies and free energy takes an infinite value. The code to generate this figure can be found at https://github.com/stephenfmann/fep

The correspondence between high values of F and life-threatening states leads to a third form of the free energy principle:

Free energy principle (selection): any system that survives long enough will act so as to appear to be minimizing F.

This is not a normative principle—not a suggestion to agents regarding how they should perform inference—but a means of describing how agents behave. In recent work Friston gives a deflationary interpretation on which agents do not in fact minimize anything, but perform acts which can be interpreted as minimizing F. That is the reason for the emphasized phrase ‘so as to appear to be minimizing F’. Despite this deflationary approach, there is a link between this and the earlier principle. Agents subject to Free energy principle (inference) ought to minimize $F$, so if this ‘ought’ is tied to their survival, then the normative principle has the same underlying justification as the descriptive principle.

Free energy principle (selection) interprets p as a kind of fitness function in the form of a probability distribution over sensory states. When we measured the temperature of our cat, we obtained a frequency distribution that acted both as a description of what happened when the cat was previously healthy and as a prescription of what temperatures the cat should have if we want it to remain healthy. Free energy principle (selection) expands the scope of this basic idea, from cats to every biological system, and from temperature to every measurable property. Supposing our smart and oblivious agents stood at the end of a long line of evolved organisms, the probability distribution given by the table in (9) could be constructed from the frequencies with which those ancestors found themselves in the relevant states. What is important here is that only direct ancestors count for tallying the frequencies. Cousins of direct ancestors may have found themselves in the state $x=4$, but they immediately died. The event does not count towards the tally because it is not survivable. As a result, necessarily $p(w,x)=0$ when $x$ is an unsurvivable state.

The principle seems to imply that parts of the system (or the system-environment pairing) will come to correspond to the component terms of F. The way those parts change over time will correspond to F getting smaller. However, in this toy case, the inner state $y$ cannot obviously be interpreted as corresponding to a distribution q because q does not affect the value of F. What is doing the work in this example is the definition of $p(w,x)$: because states that are not survivable are assigned probability zero, their variational free energy is infinitely large. In this case, Free energy principle (selection) captures the rather banal point that systems can only ever occupy survivable states. If you are likely to be in states your successful ancestors were in, then you are likely to be successful. This trivial observation is reflected mathematically by the fact that variational free energy contains a reciprocal of $p(w,x)$: high values of $p(w,x)$ therefore produce low values of $F$. Indeed, any function that contains this reciprocal (or its logarithm) as a component will be infinite when the probability is zero.

What, then, is the rationale for choosing variational free energy as the function we should interpret organisms as minimizing?

Ultimately, organisms are said to be acting so as to minimize the surprisal of $x$, defined as $\log {\frac{1}{p(x)}}$. But there are said to be limitations on the ability to minimize surprisal ‘directly’, meaning that variational free energy must be used as a proxy. It is easy to show that variational free energy is an upper bound on surprisal.⁸ But any number of functions are upper bounds on surprisal. In the literature, different and not obviously compatible reasons are given for the move from minimizing surprisal to minimizing variational free energy. From a purely mathematical perspective, we can outline the set of systems for which surprisal is difficult to evaluate (MacKay 2003, pp. 358 ff.): they are high-dimensional. So proponents of Free energy principle (selection) seem committed to the claim that the systems it refers to are high-dimensional systems. But the justifications given in the literature do not obviously line up with this. As part of justifying the hypothesis that the visual system minimizes variational free energy, Friston (2002, p. 118) asserts that “nonlinear mixing may not be invertible [...]. For example, no amount of unmixing can discern the parts of an object that are occluded by another.” On the other hand, Hohwy gives an informal account of what a creature would have to ‘know’ in order to perform Bayesian inference:

There is no way the creature can assess directly whether some particular state is surprising or not, to do that it would have to do the impossible task of averaging over an infinite number of copies of itself (under all possible hypotheses that could be entertained by the model) to see whether that is a state it is expected to be in or not.

Hohwy (2013, p. 52)

Hohwy gives a very different rationale from Friston. This move from minimizing surprisal to minimizing free energy is made very often in the literature. In this Topical Collection alone, it is cited or endorsed by Fabry (2021, p. 10), Constant (2021, p. 9), Kiverstein and Sims (2021, pp. 5–6), and Corcoran et al. (2020, p. 5). However, two unanswered questions remain. First, there is no clear justification for treating organisms as employing continuous (rather than discrete) generative models, and without this premise the claim of computational intractability is tenuous. Second, minimizing variational free energy is not the only way to minimize surprise. Any non-negative function added to surprisal is an upper bound on surprisal. Proponents need another premise that singles out variational free energy as the function organisms should be treated as minimizing.

Moving on to another interpretive issue, in each of the three examples discussed in this section, there has been a distinct role for the distribution p, and thus a distinct interpretation of each model:

• 1. In our first model, p was a generative model employed by an agent. It was therefore interpreted as representing probabilities.

• 2. In our second model, in addition to representing probabilities, p measured the desirability of certain future states over others. It was therefore interpreted as representing preferences.

• 3. In our third model, p tallied the historical frequencies of a set of (hypothetical) ancestors. It was therefore interpreted as representing the fitness of different states.⁹

Supporters of the framework often point to the third role to explain how p can simultaneously fulfil the first two. A historical tally of successful states denotes probabilities (i.e. ancestral frequencies) and preferences (i.e. future expected fitness). However, it does not immediately follow that the sense in which successful organisms appear to minimize F is relevantly similar to the sense in which (for example) predictive processing systems actually minimize F (see “A brief history of the free energy principle” section). Organisms are said to “entail a generative model” (Ramstead et al. 2021, p. 111) as a consequence of existing, whereas predictive processing systems are said to employ a generative model that gets updated through prediction error minimization. It is not yet clear what warrants treating these two kinds of system in the same way. The organism that entails a generative model, and whose actions entail minimizing free energy with respect to that model, is like the ball bearing that entails a measure of gravitational potential energy, and whose ‘actions’—falling to the lowest point in its local region—entail minimizing gravitational potential energy. From the fact that a ball bearing can be treated as though it were attempting to minimize gravitational potential energy, it does not follow that a unified framework can be developed encompassing the ball and (for example) a species of animal that always seeks the lowest point in its local area in order to evade predators. Entities that employ representations to act successfully are distinct in important ways from entities that can be treated as if they employ representations as a consequence of the effects of physical laws.

In sum, there is a disconnect between the two major domains in which the free energy principle is usually said to apply. The disconnect must be addressed if philosophers—even those with mathematical inclinations—are to properly evaluate the active inference framework.

Extensions to the models: more things to learn, more ways to act

If you open a random journal article in the active inference tradition, its scientific models—comprising agents who employ generative models to solve problems in their environments—will likely be much more complex than ours. Over the last decade much effort has been devoted to extending and adapting these basic models in order to fit them to empirical data. Active inference models can be augmented seemingly indefinitely. Some examples follow.

We assumed that $p(w,x)$ denoted both the agent’s generative model and the true statistical connection between unobserved state and observable data. Realistically, agents do not have perfect knowledge of these statistics. There are two ways to generalize the situation in this regard. First, agents can learn to improve their estimates of $p(w)$. Second, agents can learn the causal relationship $p(x|w)$. Since $p(w,x)=p(w)p(x|w),$ this offers two distinct routes to learning a more accurate statistical model. Some of Friston’s early work is geared towards showing that these statistics can be learned by employing algorithms that minimize variational free energy through methods known as empirical Bayes (Friston 2005).

We also assumed that there was a single cause, $w$, of sensory data. Realistically, the external world is a panoply of criss-crossing causal paths. An adequate generative model would contain terms representing at least some of the interactions between unobservable states. Active inference captures these features by treating agents as employing hierarchical models of their external worlds. The first level of the hierarchy $x$ is the sensory data, the second level $w_1$ represents whatever causes sensory data, the third level $w_2$ represents whatever causes $w_1$, and so on.

The simplest models assume that the agent is correct about all these features. The more features the agent can be incorrect about, the more features it is able to learn, and the more complex the generative model and method of updating. In principle, agents could be uncertain about any aspect of their representation of the world, so every model component can be subject to updating in light of evidence. Furthermore, in principle, the hierarchy of external causes is not restricted to a certain number of levels. Scientific models of agents performing active inference can therefore be extended indefinitely. This might be considered a problem when it comes to justifying the view: if the active inference framework can be extended to fit any empirical phenomenon, then there needs to be some principled way to assess the framework, other than by fitting it to data. More broadly speaking, the worry is that we cannot empirically confirm or falsify scientific models that can, in principle, explain all possible states of affairs.

Regarding action, instead of a single act $z$ the framework enables decisions about sequences of acts. Such sequences are called policies and are usually labelled $\pi$. Expected free energy can be calculated across an entire policy in order to determine which sequence of acts is optimal. Our model used only a single act, which is equivalent to a policy that is evaluated at the next time step only.

A great deal of extra complexity can be added to the story about Markov blankets (Friston 2013). The Free energy principle (selection) is usually introduced with more complex mathematical terms like ergodic densities (Friston 2013), solenoidal flows (Aguilera et al. 2021), nonequilibrium steady-state (Ramstead et al. 2018), and so on. One issue is whether or not this complexity is really needed to justify Free energy principle (selection). We saw above that a simple toy system will obey the principle by virtue of the definition of p. If proponents are aiming at a more precise claim, then perhaps the extra complexity is necessary. Some work along those lines is already tempering enthusiasm about the generality of the principle (Aguilera et al. 2021); on the other hand, proponents are working hard to deliver pure mathematical results that can be evaluated in isolation from biological hypotheses (Da Costa, et al. 2021; Friston 2019; Friston and Ao 2012; Friston et al. 2014). Active inference is a work in progress and should be evaluated as such.

A brief history of the free energy principle

The free energy principle is a modern incarnation of ideas that have been raised sporadically over at least the last five decades. It combines traditions from physics, biology, neuroscience and machine learning.

Free energy from physics to predictive processing

Although the term ‘variational free energy’ used in active inference has a purely statistical meaning, it first appeared in physics, where it has a sense connected to the more familiar physical meaning of energy. The term is used to help determine the states of certain physical systems (MacKay 2003, Sect. 33.1), (MacKay 1995, p. 191 n. 1). In statistical mechanics, many systems have states whose probabilities are functions of their energies. For example, a state with very high energy might have a low probability of obtaining, and vice versa. However, the functions p that describe exactly how probability depends on energy can be very complex. Calculating the statistical properties of such systems is computationally intractable (MacKay 2003, p. 423). Adequate approximations can be found by defining simpler probability functions q and then minimizing variational free energy. The name arises from the fact that F is related to an existing term called “free energy” (MacKay 2003, p. 423)—which explicitly denotes the more familiar physical sense of ‘energy’.

Variational methods were first deployed in physics, most famously by Feynman (1972).¹⁰ By the 1980s it had become clear that techniques from statistical physics could be adopted in machine learning (Fahlman et al. 1983; Hopfield 1982) (Hofstadter 1985, pp. 654–9). By at least 1989 Hinton and colleagues were referring to free energy in a purely statistical sense (Dayan et al. 1995; Hinton 1989; Hinton and van Camp 1993; Neal and Hinton 1998). The term ‘variational free energy’ came to mean ‘the function that must be minimized in order to improve your approximation of a system’s statistical properties’, even though physical energy was no longer the feature that determined those statistical properties. The systems in question were no longer ‘physical’ systems: they were sets of inputs to an automated inference engine whose job was to reconstruct the causes of those inputs (MacKay 1995). Some of the methods developed in this body of work became known as ‘variational Bayesian inference’ or just ‘variational Bayes’, because of the relationship with Bayes’ rule discussed in “Simple models of the free energy principle for inference, action, and selection” section. These techniques continue to be used, and are now a standard method in statistics and machine learning (Bishop 2006, Sect. 10.1). Variational free energy is sometimes called an ‘objective function’, which is the general name for a function that must be minimized (or maximized) to solve an inference task.

Because forerunners of these methods were implemented in neural network models, the question of biological plausibility was often raised (Hinton 1989, p. 143) (Dayan et al. 1995, pp. 899–900). But the most successful neural models were perhaps those spawned by the predictive processing tradition. Predictive processing was inspired by predictive coding, a technique in communications engineering (Elias 1955). In the 1980s and 1990s neuroscientists began investigating its plausibility as a model of visual perception (Kawato et al. 1993; Rao and Ballard 1999; Srinivasan et al. 1982). In the early 2000s, Friston (2002, p. 131) claimed that a predictive processing system could be constructed that performs variational inference (see also Friston 2003, pp. 1339–1340).

Very roughly, we can understand the relationship between these aspects in terms of Marr’s hierarchy, which is usually said to have three levels: computational, algorithmic, and implementational (Marr 1982). In Friston’s scientific model of predictive processing, the computation is variational inference. The algorithm is the expectation-maximisation algorithm, a two-step process whereby two different mathematical operations are performed iteratively. Neal and Hinton (1998) had already shown that a version of that algorithm minimizes variational free energy. Friston claimed the algorithm could be implemented by the activities of (and structural relations between) individual neurons (for a simplified example see Bogacz 2017, Sect. 2–3).

As part of this work, Friston (2003, 2005) began to make strong claims about the generality of his scientific model. He also cited empirical evidence that supposedly matched model behaviour. This generality, and concordance with data, led him to develop the free energy principle.

Free energy minimization as a general principle

Most proponents of predictive processing assert relatively modest claims. Friston began similarly, claiming we have evidence to believe the visual cortex implements a hierarchical generative model with variational free energy as the objective function (Friston 2003). By 2006, however, he extrapolated from this position to the much stronger claim that minimizing free energy is almost everything the brain does (Friston et al. 2006). Not only inferential processes, but also action, were said to be geared towards minimizing free energy. He reached these conclusions seemingly by extending earlier predictive processing models and identifying empirical phenomena his models faithfully mimic.

By 2012, Friston was asserting that minimizing free energy is almost everything every biological system does (Friston 2012, 2013) (earlier examples of claims of this kind appear in Friston and Stephan (2007)). Rather than being based on extensions to existing scientific models, this generalized claim is based rather on considerations of selection (“A simple model of selection” section). It is worth emphasizing that the proposed justification for the biological version of the free energy principle is different from the justification of the original, brain-related claims. Originally, the principle was a claim about the generality of scientific models of predictive processing. Gershman (2019) has noted that the free energy principle inherits some justification from the explanatory success of those models, which have been discussed extensively in the literature on computational cognitive neuroscience (Huang et al. 2019; Rao and Ballard 1999; Wiese and Metzinger 2017), theoretical neuroscience (Abbott and Dayan 2005, Sect. 10.2) and philosophy (Cao 2020; Clark 2013). In contrast, the biological version of the claim relies on a priori justification via mathematical proofs of statements like Free energy principle (selection). There is no pre-existing scientific modelling practice whose success extends to active inference here. Proponents must find empirical support themselves.

The past decade has seen applications and elaborations of active inference for biology. Calvo and Friston (2017) apply the framework to plant activity. Tschantz et al. (2020) simulate bacterial chemotaxis, and give an active inference interpretation. Three contributions to the present Topical Collection discuss E. Coli in an active inference context: Corcoran et al. (2020); Kirchhoff and van Es (2021); and Kiverstein and Sims (2021). Baltieri and Buckley (2019) argue that a certain kind of control process called Proportional-Integral-Derivative (PID) control, which has been used to explain the behaviour of bacteria and amoebae, can be understood in terms of active inference. The question for philosophers is what theoretical or explanatory virtues result from applying active inference in this way. In “Dialectic: the free energy principle and related claims” section we discuss the dialectical structure of active inference, highlighting key questions philosophers need to ask in order to evaluate the framework.

Dialectic: the free energy principle and related claims

Mathematical, empirical, and general claims

Part of the difficulty in understanding the body of work associated with the free energy principle is a lack of transparency over the dialectic. We think a great deal of confusion can be overcome by considering three kinds of claim. First, there are mathematical claims. These are claims about the status of theorems, features of scientific models and statistical techniques. Some of the core mathematical features of active inference predate the framework itself (“A brief history of the free energy principle” section); however, Friston and colleagues have since introduced many novel mathematical elements. Importantly, claims in this category do not need to be interpreted as statements about real systems in order to be evaluated. Second, there are empirical claims about cognitive and biological mechanisms, how brains and bodies actually work. These are the remit of cognitive neuroscience and biology. Third, there are general claims that typically abstract across a wide class of empirical claims. Active inference grew out of an increasingly generalized explanatory approach to cognition, such that its central claims crossed over from the empirical to the general category.

When these categories are distinguished, it is easier to see the dialectical relationship between their constituent claims, and to delineate specific topics for investigation. For example, discoveries about neural network capabilities (mathematical) are sometimes used to justify hypotheses about neural organisation in biological brains (empirical). Such arguments are not restricted to the free energy program, but are part of a broader disciplinary movement known as computational cognitive neuroscience (Gregory Ashby and Helie 2011). Similarly, general claims are sometimes used to justify the relevance of empirical claims, by providing reason to believe that all biological systems minimize free energy. And mathematical claims support general claims when mathematical theorems and scientific models are argued to be widely applicable to real biological systems.

In the remainder of this subsection we describe each category in more detail and highlight key claims in each. In the following subsection we outline dialectical links between categories. Throughout, we use Hamilton’s rule—which will be familiar to philosophers of biology—to illustrate the different categories and their relationships. Hamilton’s rule can be construed as a mathematical claim when interpreted as a statement as part of a mathematical model. It can also be construed as a general claim when interpreted as a statement about conditions on selection for genes influencing social behaviour in real populations. And the rule can guide the verification of empirical claims about the mechanisms of social behaviour, e.g. the genetic control of parental behaviour towards offspring.

Mathematical claims

Mathematical claims are statements about mathematical models and objects. This category contains all of the formal statements deployed as part of modelling practices in biology and cognitive science, including mathematical claims relating to active inference. For example, assertions about the computational abilities of neural networks belong to this category, as long as such claims do not mention the explanatory power of neural networks with regard to brains.

To take an example better known to philosophers of biology, Hamilton’s rule states the conditions under which genes for certain kinds of socially-oriented behaviour would be favoured by selection. In essence, Hamilton’s rule is a mathematical statement constructed as part of a model of an evolving population. It can be evaluated—i.e. proven, and have its proof checked—without recourse to real systems. Because of the way the mathematical model is defined, it is not necessary that there be any real examples of selection for Hamilton’s rule to be true within its mathematical context.¹¹

For an example from active inference, the claim that a small neural network is capable of minimizing variational free energy via encoding prediction error is verifiable by actually building such a network, as Bogacz (2017, Sect. 2–3) shows. Recent models of variational message passing constitute similar claims, with message-passing being a distinct way to minimize variational free energy (Parr et al. 2019)—a different implementation and algorithm, but the same computation. Similarly, it is possible to verify the claim that variational inference approximates Bayesian inference by demonstrating that variational free energy takes its lowest value when the true posterior is used.

Friston makes a number of claims that can be evaluated mathematically. But the formal framework he employs is idiosyncratic, and based upon work that is already complex. These novel claims are difficult to assess for philosophers, even those of us with a mathematical background. The good news is that because the mathematical claims are screened off from questions about realism and model interpretation, they can be evaluated in isolation. Indeed, the mathematics of active inference are still being developed (Da Costa, et al. 2021), so it is possible that it currently lacks a coherent, comprehensive formalism. Proponents have pointed out to us that that is the state of many early sciences: often mathematical rigour comes after scientific discovery and theory-building.

The term ‘free energy principle’ is sometimes used to denote a purely mathematical statement (see for example Friston and Stephan 2007, p. 434). Andrews’s contribution to this Topical Collection endorses this usage. Their opponents are those that critique the free energy principle under the assumption that it is truth-apt. Andrews contends that the principle is not truth-apt, because as a set of mathematical tools it does not by itself entail any empirical claims. For example, Andrews claims that “when we take the existence or qualities of a model to constitute knowledge of the natural world we make a category error and reify the model” (Andrews 2021, p. 14). Interestingly, Andrews downplays the relevance of general claims—the feature of active inference usually emphasised by Friston and colleagues.

Models of active inference may bear interesting relations to other formal concepts in philosophy. Mann & Pain argue that models in which the free energy principle is formulated are importantly related to models in which the concept of proper function is defined (Mann and Pain forthcoming). Proper function, a species of selected-effects function defined by Millikan (1984, Sect. 1–2), has applications in the philosophies of biology, cognitive science, language and mind. By drawing this comparison, Mann & Pain aim to demonstrate the relevance of claims made by proponents of active inference to traditional debates in those subjects, as well as highlight the distinction between claims about models and claims about real systems.

Empirical claims

Empirical claims are statements about the structure, function and operation of real biological systems. For example, the claim that the mammalian visual system works via prediction error feedback is an empirical claim. With regard to mainstream biology this is probably the largest category. Most experimental science and fieldwork is geared towards gathering evidence to establish or refute empirical claims.

Different empirical claims can comprise specific instances of the same general claim. For example, Bourke (2014, Table 1, p. 3) presents a diverse list of socially-oriented behaviours across a variety of species, some of which can be explained with respect to Hamilton’s rule. Although Hamilton’s rule does not mention particular behaviours (nor even particular species), empirical claims can be seen as instantiations of the more abstract rule. Similarly, although the active inference framework does not mention specific systems, we can ask whether its features are instantiated in particular cases. The empirical category includes specific features of brain activity that have been argued to be better explained by appeal to minimisation of free energy. For example, Friston and Stephan (2007, p. 429) claim that the brain uses a mean-field approximation to minimize free energy. This claim is empirical because it is in principle verifiable: either the brain possesses structures corresponding to the different components of a mean-field approximation that change according to the dynamics of free energy minimization, or it does not. The importance of computational cognitive neuroscience is that it provides methods for assessing and verifying claims like these.

Both Corcoran, Pezzulo and Hohwy’s and Kiverstein and Sims’s contributions to this Topical Collection make empirical claims about the nature of allostasis—“anticipating needs and preparing to satisfy them before they arise” (Sterling 2012, p. 5)—and both are interested in demarcating behaviour that is distinctively cognitive. Corcoran et al. (2020) use the free energy principle to conclude that the term ‘cognition’ should be reserved for organisms that engage in counterfactual inference, and hence that allostasis is not properly cognitive. Kiverstein and Sims (2021) disagree. On their reading of the free energy principle, what they call “allostatic control” is a properly cognitive process. The range of organisms to which the term ‘cognition’ applies thus extends beyond those that have a nervous system. In both cases, these claims are in principle verifiable: either allostasis operates according to the dynamics of free energy minimisation, or it does not. If, for instance, it turns out that allostasis operates according to the dynamics of reinforcement learning, then free energy treatments are in error.¹²

At the same time, empirical claims are sometimes used to justify aspects of the modelling framework. The problem is that there has been no independent verification of the soundness of these connections. For example, Friston and Stephan (2007, p. 432) assert, “At the level of perception, psychophysical phenomena suggest that we use generalised coordinates, at least perceptually: for example, on stopping, after looking at scenery from a moving train, the world is perceived as moving but does not change its position.” We do not know of any computational cognitive science work that explicates the sense of ‘generalised coordinates’ and confirms whether the phenomenological evidence described by the authors in fact supports their claims.

Empirical claims include negative claims. For example, Friston (2009, p. 298) states “there is no electrophysiological or psychophysical evidence to suggest that the brain can encode multimodal approximations”. He uses this as evidence for a positive claim about the mathematical features of distributions the brain does encode, on his view. Again, this is the kind of claim on which computational cognitive scientists could weigh in.

Several other empirical claims, said to be derivable by applying active inference models to real systems, are listed by Da Costa et al. (2020, Table 1 pp. 3–4). During the last decade, the rate at which these hypotheses have been formulated has outpaced the ability of independent evaluators to determine whether they can be substantiated or not. Proponents will point to a long list of citations, but the complexity of the mathematics makes determining the relevant empirical evidence difficult. We need computational cognitive science to determine what kinds of evidence would count in favour of empirical claims made on the basis of active inference.

General claims

General claims are highly abstract or generalized empirical claims. This includes empirical claims whose scope is very wide, perhaps ranging over every organism or biological system.

When formulated as a claim about real populations, Hamilton’s rule fits this description. This is a general claim because its scope is so wide: it applies to every population of genes subject to selective forces, stating conditions under which a gene influencing behaviour that impacts the fitness of social partners would be promoted by selection.

General claims abstract from empirical claims. Empirical claims can therefore be derived by replacing abstract terms with concrete cases. For example, Hamilton’s rule could be related to specific empirical claims by replacing the abstract notion of ‘a gene for cooperative behaviour’ with a specific gene, and replacing the terms for cost, benefit and relatedness with estimated values for real populations (Bourke 2014).

Because proponents of active inference often move swiftly between the mathematical framework and real systems, some general claims have been given the label ‘the free energy principle’. For example,

The free-energy principle discussed here is not a consequence of thermodynamics but arises from population dynamics and selection. Put simply, systems with a low free-energy will be selected over systems with a higher free-energy.

Friston and Stephan (2007, p. 451)

It seems that “systems” here are real systems such as organisms. But sometimes the exposition of the principle blurs the lines between mathematical and general claims. For example, Hohwy says that “FEP [the free energy principle] moves a priori—via conceptual analysis and mathematics—from existence to notions of rationality (Bayesian inference) and epistemology (self-evidencing). [...] [T]his a priori aspect is central to how we should assess FEP” (Hohwy 2020, p. 8); later continuing: “FEP says organisms “must” minimise free energy [... this] is a ‘must’ of conceptual analysis and mathematics, for that is all that was needed to arrive at FEP. FEP is therefore rightly called a ‘principle’ rather than a law of nature” (Hohwy 2020, p. 8) (for Hohwy, a principle is something that may or may not hold of a given system). By deducing a statement about real organisms from mathematical premises, Hohwy seems to be overriding the distinction between mathematical and general categories. In contrast, Andrews distinguishes them while allowing that the free energy principle has both mathematical and general aspects:

Not unlike Charles Darwin’s theory of evolution by natural selection, the free energy principle can be interpreted alternatively as mathematical model or as meta-theoretical framework; [...] It is only as its constituent variables are mapped onto measureable, observable (or inferable, latent) processes in the world that it attains genuine explanatory power, and becomes capable of generating testable hypotheses.

Andrews (2017, p. 14)

Whether or not there is a claim deserving the title of the free energy principle, and whether or not it is really mathematical or general, is moot: what matters is that there is a mathematical claim—something akin to Free energy principle (selection), but formulated in a more complex mathematical setting—and there is a corresponding general claim. Given this, they ought to be evaluated separately.

The distinction between general and empirical claims is not sharp. An empirical claim that generalizes over a species or a class of biological systems may not be broad enough to deserve being called general, but a claim that generalizes over entire kingdoms may well be. The point of distinguishing the categories is to highlight the different kinds of justification that each type of claim requires. Empirical claims may be made plausible by scientific modelling and wide generalisations, but they can only be ultimately validated through evidence. General claims can also be made plausible by modelling, but can only be fully validated by confirmation of the empirical claims they entail.

The most pressing philosophical issues about general claims are familiar from the literature on scientific models. The models involved in these claims are typically extremely abstract, and a common refrain regarding biological systems is that models which attempt to explain everything end up explaining nothing. This line of thought is often cashed out in terms of trade-offs between generality, realism and precision. In particular, drawing on Levins’ work, it is thought that maximising the generality of a model will require sacrifices in terms of realism and/or precision (Levins 1966; Weisberg 2006). Realism, or accuracy, is typically understood in terms of the amount of causal structure that a model represents. Consequently, the more target systems a model encompasses (i.e. the more general it is) the less accurately it represents them. Precision is understood in statistical terms, as the closeness of repeated measurements of some quantity. Consequently, as a model’s parameters become more finely specified, the number of systems which lie outside those parameters increases (i.e. the less general it is). So it looks as though the free energy principle will be useful for building highly general models that will score low on realism and/or precision. Levins’ work is normally thought to deliver a pragmatic lesson: we cannot produce one model to rule them all, so which trade-off you make should be relativized to your aims. For instance, models that score highly on realism—and thus capture a lot of the causal structure of a system—will be better for predicting the effects of some intervention.

In their contribution, Colombo and Palacios take up this line of critique (Colombo and Palacios 2021). On their analysis, the free energy principle’s “...foundations in concepts and mathematical representations from physics allow free energy theorists to build models that are applicable to theoretically any (biological) system” (p. 19). However, “...achieving this generality comes at the cost of minimal biological realism, as those models fail to accurately capture any real-world factor for most biological systems” (p. 19). Carls-Diamante raises a challenge for the generality of the principle in the form of daredevils, humans who seem to seek out surprising states (Carls-Diamante forthcoming). There are solutions available to proponents of the principle that would widen the class of entities to which it applies—by encompassing these aberrant individuals—but would simultaneously jeopardise the ability to provide realistic or precise models of behaviour—because those individuals’ cognitive mechanisms may differ from the norm. In striving to attain universal applicability, active inference must deploy different models to capture widely varying behaviour while still asserting that those models belong to a single family. This is a difficult balance to strike.

If all this is right, then it suggests that the usefulness of models produced by active inference will be importantly restricted (Brown et al. 2020). These concerns speak also to the practicality and disciplinary scope of the free energy principle. If its utility lies in its ability to provide a general theory of biological processes, but what working biologists need are models high on precision and/or realism, then its application will be confined to theoretical and philosophical aspects of biology. If, however, it can deliver the latter type of models, then it will have potential implications for biology in practice. On the other hand, proponents of active inference might simply reject the terms of the trade-off outlined above. Bhat and colleagues’ contribution takes this line (Bhat et al. 2021). They seek to explain certain correlations between autoimmune disease and psychiatric disorder. They argue that a general active inference model encompassing immunology and psychology explains increased sensitivity across both systems. Unifying psychiatric disorders and immune responses using the free energy framework has, in their view, consequences for the treatment of disorders such as schizophrenia and Cushing’s syndrome.

Justificatory links between dialectic categories

How can mathematical claims justify empirical claims?

Brain structures posited by empirical claims are often related to properties of artificial neural networks. As mentioned above, computational cognitive neuroscience is the branch of cognitive science dedicated to constructing scientific neural models and evaluating their biological plausibility. Scholars have long appealed to scientific models originally produced in the context of machine learning to explain biological facts (Dayan et al. 1995).

At this point, a few remarks about the relationship between machine learning and neuroscience are in order. Machine learning intersects with neuroscience in at least two distinct ways. First, large datasets derived from experiments and measurements can be processed and analysed using machine learning techniques. In this regard, the relationship between the two fields is no different than that between machine learning and any other branch of science that generates large datasets that need to be processed efficiently. Call this the general relationship. In contrast, there is a unique connection between machine learning in the context of neural network models and neuroscience. There is a substantial body of scientific and philosophical work dedicated to the question of correspondence between scientific neural models and actual neural systems, i.e. biological brains. This relationship is familiar to philosophers of mind and cognitive science, with its roots in connectionism of the 1980s. Because these issues are unique to the relationship between machine learning and neuroscience, call it the special relationship.

The general relationship uses certain modelling techniques to discover what the brain is doing; the special relationship asserts that certain modelling techniques are what the brain is doing. With regard to the free energy principle, what we are interested in is the special relationship. Whether scientific neural models can explain brain functioning depends in large part on how well those models correspond to biological brains. This is the remit of computational cognitive neuroscience. In general, justifying empirical claims by appealing to a scientific model requires critical evaluation of how good the model is. This is the remit of both scientists and philosophers of science.

The mathematical $\xrightarrow []{}$ empirical direction invites philosophical analysis due to novel interpretations of scientific model terms. For example, in active inference it is claimed that the same term p can be interpreted as representing both probabilities and preferences. Mathematically there is nothing stopping this, but the problem comes when we seek the real entity that corresponds to that term in the real world. Is it possible for a component of a neural system to represent probabilities and preferences at the same time? It is not even clear that this is what is being claimed, because some proponents takes a deflationary or instrumentalist stance on active inference models, disclaiming the requirement that mathematical terms map neatly onto components of real systems. It remains an open question whether this instrumentalist stance is justified merely because the scientific model (or map) does reflect all variables in the target system (territory). For example, in the philosophy of science literature about model construction some (e.g. Williamson 2017) suggest that scientific model building is entirely consistent with scientific realism. This is a discussion still to be had in the active inference literature.

Typically biologists and computational cognitive neuroscientists are more modest than proponents of active inference. In mainstream science, models are often presented with caveats about their idealised nature and indications of how their realism can be improved. In contrast, it sometimes seems as though proponents of active inference take their scientific models to be definitionally accurate. Active inference doesn’t get a free pass on model validation. Its proponents almost certainly know this, but an outsider reading the literature might wonder why their dialectic slips so easily between claims about scientific models and claims about real systems. We think it is because the need for justification has not been sufficiently emphasised. This is probably a cultural accident rather than genuine overconfidence.

Consider an example from the active inference literature. In a discussion of techniques the brain might be using to minimize variational free energy, Da Costa et al. (2020, p. 10) assert that “the marginal free energy currently stands as the most biologically plausible.” It is not clear how the reasons they cite lead to that conclusion. It seems that marginal free energy minimization is the most accurate technique for which there is a known neural implementation (that is, a neural network model whose dynamics are at least consistent with what is observed in the brain). But it is not clear why we should believe the brain employs the most accurate technique. It is also not clear whether consistency provides strong evidence in favour of biological plausibility. Sometimes Friston describes a scientific model as biologically plausible just because it is a neural network model. Again, computational cognitive science can weigh in on the question of what makes a neural network model of cognition more or less plausible.

Finally, although the justificatory link in question concerns the special relationship between machine learning and brains, some of Friston’s work is squarely within the general relationship. For example, his proposals about “variational filtering” (Friston 2008) are engineering techniques for building machine-learning systems. These systems would be used to process data from neuroimaging studies. The important aspects of these proposals lie with the data-processing abilities of the engineered system, not any correspondence there may be between such systems and biological brains (see also Colombo and Palacios 2021, pp. 20–1). It might be the case that Friston’s claims pertaining to the special relationship were inspired by or otherwise related to his earlier work developing such techniques. But more premises are needed to support claims of correspondence between a brain and a scientific neural model, beyond the mere fact that one was inspired by the other. After all, connectionism was itself inspired by neuroscientific discovery of brain structure, but this did not automatically render connectionism a viable explanatory framework.

How can mathematical claims justify general claims?

When it comes to justifying the active inference framework, emphasis is usually placed on Free energy principle (selection). For example, Ramstead et al. (2018) assert:

The FEP is a mathematical formulation that explains, from first principles, the characteristics of biological systems that are able to resist decay and persist over time. It rests on the idea that all biological systems instantiate a hierarchical generative model of the world that implicitly minimises its internal entropy by minimising free energy.

Ramstead et al. (2018, p. 2)

To our knowledge, this mathematical claim has not been independently evaluated, though Aguilera et al. (2021) offer reasons to think the constraints on systems that satisfy it are more restrictive than proponents of active inference usually assume. Similarly, it is difficult to evaluate the corresponding general claim because there is not enough understanding of the mathematical theorem and how it maps onto real systems. Recently, however, Beni (2021) and Bruineberg et al. (2021) have critiqued the framework on grounds of its applicability to real systems. We are starting to see critical analysis of active inference from outside the tradition. This is a healthy development.

The analogy with Hamilton’s rule can help illuminate the situation. Hamilton’s rule as a mathematical statement is reasonably simple and relatively easy to prove within a given mathematical framework. Variations on the rule can be clearly defined mathematically because of the precision offered by formalism. Interesting questions arise when it comes to using the rule, or its variations, to explain the evolution of social behaviour. But its relative simplicity enables philosophers to understand the basic components of Hamilton’s rule and what the rule says, even though there are still interpretive questions to ask (Birch 2014).

Constant’s contribution to this Topical Collection uses a mathematical claim to make a general claim (Constant 2021). On the basis of a numerical example, he argues against the misconception that minimising free energy entails future survival. Rather, he believes the converse is true: an organism that has survived up to the present must have done so by minimizing free energy.

How can general claims justify empirical claims?

Proponents of active inference distinguish process theories (roughly, our category of empirical claims) from normative principles (roughly, general claims). For example, Hohwy (2020) argues that the generalized form of the free energy principle should be treated as a regulatory principle guiding the construction of process theories. The idea is to add assumptions about the structure of specific systems to the general claims in order to yield testable empirical claims. These would include computational, algorithmic, and implementational claims about brain activity. However, Parr and Friston (2017, p. 4) use the phrase “computational architectures implied by active inference”, which conceals the fact that extra premises are required to get from general claims at the core of active inference to empirical claims about system architectures.

In their contribution Kirchhoff & van Es are interested in whether or not active inference can overcome what they call the universal ethology challenge (Kirchhoff and van Es 2021). Active inference can only unify biology and cognition if low-level biological systems are explained in terms of inference, but—so the challenge goes—explaining such systems does not require inference. So active inference cannot unify biology and cognition. Kirchhoff and van Es disagree with this assessment. They argue that it is possible to explain chemotaxis in bacteria using inference. They tentatively conclude that this gives us reason to think that active inference might be able to address the universal ethology challenge.

While Kirchhoff and van Es use an empirical example to motivate a general claim, Fabry’s contribution uses an empirical example to restrict a general claim (Fabry 2021). She distinguishes between three types of niche construction: selective niche construction, developmental niche construction, and organism-niche coordination dynamics. She then assesses attempts by proponents of extended active inference (who marry active inference with ideas from extended cognition research) to account for these various types of niche construction. She concludes that, while extended active inference is successful in the case of organism-niche coordination dynamics, it fails to explain selective niche construction and developmental niche construction.

Concluding remarks

The active inference framework is incredibly ambitious in its explanatory scope. From humble beginnings as a theory of brain function, it is now positioned as a framework for understanding life itself. There is a critical tradition in the philosophy of biology, inspired by Levins, with regard to such ambitions. Many, then, will approach active inference with scepticism. Healthy scepticism is a good thing, but healthy scepticism is informed scepticism. Unfortunately, getting one’s head around the details of active inference is no small task.

Our goal in this introduction has been to clarify the basic mathematics, history and internal dialectics of active inference, and draw attention to some key concerns. With these details on the table, philosophers of biology are in a better position to critically evaluate the framework. We look forward with interest to seeing the results.