Introduction

The biogeochemical cycles of nitrogen (N) and phosphorus (P) in forest ecosystems are assumed to be closely synchronized, especially in ecosystems relying on tight recycling of nutrients. Thus, the inorganic nutrients circulate from soil to vegetation to soil organic matter and associated microbial communities back to the soil’s nutrient pools (Rastetter et al. 2013). The close relationship of different nutrients in ecosystems is affected by significantly higher loss or addition of one nutrient relative to the other, which induces adaption processes of organisms to maintain their required stoichiometry (Chapin et al. 1987; Rastetter et al. 1997). Changed environmental conditions, such as rising atmospheric CO2 concentrations and temperature, enforce these processes. Thus, the P limitation in European forest ecosystems appears to be linked to an enhanced P demand of trees. This situation is caused by increased N availability resulting from continuously high atmospheric N deposition and the combined effects of climate change (Gress et al. 2007; Braun et al. 2010; Vitousek et al. 2010; Jonard et al. 2015; Talkner et al. 2015; Heuck et al. 2018). A global meta-analysis on effects of anthropogenic N addition on P cycling in terrestrial ecosystems found that the contents of soil labile P and microbial P were not significantly influenced (Deng et al. 2017). Furthermore, the effects on total P in mineral soil and litter P contents were unclear, despite a clearly enhanced phosphatase activity after N addition (Olander and Vitousek 2000; Deng et al. 2017). The degree of response of the soil P cycle therefore might be dependent on the prevailing nutrition strategy and on the ability of an ecosystem to adapt to alterations in nutrient availability. In systems with satisfying supply in available mineral P (acquiring systems), where parent rock is the dominant factor controlling the nutrition strategy (Porder et al. 2007; Lang et al. 2016, 2017), N addition might have less significant impacts on the P cycle (Finzi 2009; Groffman and Fisk 2011). In strongly P-limited systems, where the ecosystem’s retention capacity for N already is declined, additional N is assumed to increase N losses with seepage water (Magill et al. 1996; Emmett 2007), whereas P will be retained by tight recycling (Lang et al. 2016, 2017). An addition of P (or both N and P) in such a recycling system is expected to alleviate effects of N surplus (Stevens et al. 1993; Blanes et al. 2012), retain the nutrient stoichiometry and therefore increase plant growth (e.g. Prietzel et al. 2008; Gradowski and Thomas 2008). The driving processes of P mobilization and transport under conditions of an altered nutrient availability in forest soils are not well understood so far and quantitative estimates for soil P fluxes are rarely available.

In general, the seepage P transport in forest soils is driven by heavy rainfall events when fast flow through preferential flow pathways (PFPs) occurs and bypasses large parts of the soil matrix (Julich et al. 2017a; Makowski et al. 2020b). These fast flow pathways are supposed to link P fluxes from soils into stream water, what might lead to considerable P losses in forest ecosystems (Benning et al. 2012; Julich et al. 2017c). However, it is not clear how an additional input of the macronutrients N and P might affect these P transport processes and, thus, the risk for P losses. We assume that P-limited systems which rely on a tight recycling of P can use the additionally applied N or both N and P more efficiently than acquiring systems (P-rich) and consequently retain P by incorporation into biomass. As a result, P concentrations in seepage water and associated P translocation fluxes through the soil profile should be very low. For an input of additional P only, it can be assumed, that P transport in these soils will increase because the systems are not adapted to high P availability and therefore cannot rapidly integrate it into the tight recycling (Hauenstein et al. 2020). Mesocosm experiments indicated that N addition affected downward translocation (first 20 cm of a soil column) stronger in a P-poor soil as compared to a P-rich soil (Holzmann et al. 2016). By contrast, systems with a high P availability may not have developed strategies to minimize P losses and transport to deeper subsoil is expected to occur. However, it is not clear how a changed availability of N and P will affect P fluxes through fast PFPs which represent the predominant transport pathways for P through forest soils. In our study, we therefore investigated and quantified P fluxes via fast flow at contrasting sites with regard to the P nutrition strategy (availability of mineral P in the soil). Furthermore, we examined if such contrasting systems produce different responses in P transport after experimental treatment with nutrients (N, P, and P+N).

Methods

Study sites

The experiments were implemented in two beech (F. sylvatic L.) forests with contrasting status of soil P available from mineral sources. The high-P site (P stock: 678 g m−2 up to 1 m soil depth, Lang et al. 2017) is located on a hillslope in the Bavarian Forest (SE-Germany) on paragneiss and the soil can be classified as hyperdistric chromic cambisol (WRB 2015) with loam texture in topsoil and sandy loam in subsoil. The contrasting low-P site (P stock: 164 g m−2 up to 1 m soil depth) is located in the NW-German lowlands. Here, a hyperdystric folic cambisol has developed on glacial sandy till with loamy sand in topsoil and sand texture in subsoil (Lang et al. 2017; Makowski et al. 2020b).

At each site, six plots (20 m × 20 m each) were established in summer 2016: control plots (ctl) in three repetitions to estimate spatial heterogeneity, and one treatment plot each for N, P, and P+N application. A summary of the experimental treatments and setup is given in Table 1. The nutrients were applied in dissolved form on the plots as NH4NO3 (N and P+N plots) and as KH2PO4 (P and P+N plots). The N and control plots were treated additionally with KCl dissolved in water to account for potassium (K) addition in the P and P+N plots (Hauenstein et al. 2020).

Table 1 Summary of experimental setup for sampling of preferential flow water (artificial rain experiments) and soil from preferential flow pathways (tracer experiments) at two contrasting sites with high (high-P) and low availability of mineral P (low-P)
Full size table

After N and P application, each plot was instrumented in 2018 with zero-tension lysimeters in three depths (d1—below topsoil, d2—in middle subsoil, d3—in deep subsoil) below undisturbed soil columns (for lysimeter and installation details see Table 1 and Figure S1 in Supplement 1). Due to small-scale heterogeneities associated with very high stone contents at the high-P site, only one working lysimeter could be installed in the N treatment plot. All plots were covered with tarpaulins and after four weeks were irrigated with an artificial rain solution to simulate a heavy rainfall event after a dry period (20 mm h−1 for 4 h). These sprinkling conditions were found to stimulate P transport through preferential flow pathways (Julich et al. 2017c; Makowski et al. 2020a, b). During the course of the experiments, water representing preferential flow was sampled in zero-tension plate lysimeters in the three soil depth d1-d3 (Table 1). The samples were not collected in defined time periods, but quantity-dependent to ensure that the required amount for laboratory analyses (500 mL per sample) was provided. The number of samples per lysimeter varied from zero (water has not reached the collection depth) to 14, with a total number of collected samples of 103.

The sampled water volume, pH value, and electric conductivity were determined immediately after collection; samples for analyses were stored at 5 °C. After the experiments, the plots were further covered for three weeks until soil sampling. We conducted dye tracer experiments to visualize PFPs (cf. Julich et al. 2017b, Table 1 and Figure S2 in Supplement 1). The dye solution containing 4 g L−1 Brilliant Blue was applied on all plots with same intensity as in the artificial rain experiments before, but with shorter duration (2 h). Soil samples were collected from three vertical profile cuts (20 cm distance) within each plot and horizon-wise for stained (PFP) and unstained (MA) material, respectively. For better comparison, the soil horizons were aggregated for each site considering their physical and chemical properties to: L—litter layer (1–2 cm thickness), O—organic layer (4–10 cm thickness), A—mineral topsoil horizon (up to 14 cm soil depth), B1—upper subsoil horizon (up to 48 cm soil depth), B2—lower subsoil horizon (up to 92 cm soil depth). Details on sampling design for preferential flow collection are described in Makowski et al. (2020b), and the methodical approach of tracer experiments in Julich et al. (2017b). In Makowski et al (2020b), we described the results for preferential flow distribution and P translocation during three sequential artificial irrigations at the three control plots of the two sites. Data presented here are derived from the last irrigation in autumn 2018 followed by the tracer experiment and excavation of all plots.

Chemical analysis

The samples from preferential flow water were analyzed for P forms by autoclave-digestion with persulfate of unfiltered (TPw—total P) and filtered (TDPw—total dissolved P) samples, and direct measurement of filtered (DIPw—dissolved inorganic P) samples. Dissolved organic P (DOPw) was calculated as difference between TDPw and DIPw. Particle-bound P (PPw) was defined as difference between TPw and TDPw, and thus per definition includes all P fractions > 0.45 µm. All solutions were measured photometrically (UV-Mini 1240, Shimadzu Deutschland GmbH, Duisburg, Germany) as molybdenum blue complex.

The mineral soil samples collected from stained PFPs and unstained soil matrix (MA) were dried at 40 °C, organic layer material at 60 °C. All samples were sieved (< 2 mm) and subsamples were ground for the determination of total P (TPs) contents in soil. The contents of total P (TPs), inorganic P (TPi,s), and organically bound P (TPo,s) were determined according to Saunders and Williams (1955). An amount of 0.5 g sieved sample was extracted with 0.5 M H2SO4 with preceding ignition at 550 °C as well as without ignition. Phosphate-P in the extracts was analyzed colorimetrically using the molybdenum-blue method. Total organic P was quantified as difference between ignited (TPs) and non-ignited values (TPi,s). The surface‐adsorbed, readily available P fraction (labPs) was determined as sum of resin-extractable P (anion exchange resin Dowex 22, 16‐50 mesh, Sigma‐Aldrich, Germany) and bicarbonate-extractable P (0.5 M NaHCO3) after a modified method of Hedley et al. (1982) and Julich et al. (2017a). Inorganic P contents of the resin and bicarbonate fractions were analyzed directly in the extracts using the molybdenum-blue method. In sum, they represent readily available (labile) inorganic P, here named as labPi,s. In the bicarbonate extracts, we determined total P concentrations by oxidation with ammonium persulfate in an autoclave. The difference of total and inorganic P in this fraction is defined as organically-bound labile P (labPo,s). All extracts mentioned above were measured colorimetrically using UV-Mini 1240 (Shimadzu GmbH, Duisburg, Germany).

Data analysis and model building

Because of the flow-dependent sampling, the time steps of sample collection and number of samples differed for the lysimeters. Therefore, the concentrations and water amounts were averaged per hour of experiment to enable plot comparison. Thus, data were aggregated into four time steps (each 1 h length with n = 0…4) during artificial rain (sprinkling) and one after-sprinkling time step (cumulated for 4 h sampling with n = 0…3) (Makowski et al. 2020b). The element loads per lysimeters were calculated by multiplying measured concentration with the amount of collected water for each sample, summarized for each time steps, and finally cumulated for over all time steps to gain the cumulative load per experiment.

For data exploration, we followed the protocol of Zuur et al. (2010). Here, the three control plots per site were treated as repetitions in preferential flow water and soil data set to assess spatial heterogeneity per site. In the first step of data exploration, the means and variances between the plots per site were computed separately for each subgroup to account for the hierarchical structure of the sampling in groups on several scales (site, plot, profile cuts, depth/horizon, flow region). Whereas, profile cuts in the soil data set can be treated as repetitions per plot, grouped observations such as in horizons may induce dependencies between data and unequal variances (heteroscedasticity). Furthermore, the grouped soil sampling in flow/non-flow regions (PFP/MA) resulted in missing values, e.g. when horizons were bypassed by water flow and could not be sampled as PFP, or when horizons were completely stained (as litter layer)—then lacking MA samples. The nested structure of our data sets is visualized in Fig. 1. To account for these complex issues in our data, we extended our approach by the protocol of Zuur and Ieno (2016) and applied a linear mixed-effect modeling (lme). Two model approaches were tested to identify: (1) the effect of initial P status (site), soil depth, and (non-)flow region on P fractions in soil (Model 1A) and in preferential flow water (Model 1B) respectively using the data of the control plots only; and (2) the effect of treatment (nutrient application) on P fractions in soil (Model 2A) and in preferential flow water (Model 2B) respectively using the whole set. For the preferential flow data set, we additionally fitted models using the element loads instead of concentrations as dependent variables to differentiate between effects on concentrations and transport loads (Models 1C and 2C).

Fig. 1
figure 1

Nested structure of the data sets “Preferential flow” and “Soil”. Sample collection was conducted at three control plots (ctl) and three plots treated with N or P or P+N (one each) at the high-P and low-P site. Observations in flow data contain three soil depths (d1–d3). Soil data were gained in three profile cuts per plot (c1–c3), for five horizons (L, O, A, B1, B2) each cut, and for flow pathways (PFP) and soil matrix (MA) each horizon

Full size image

We did not test how soil P contents or soil stocks affected concentrations or loads in preferential flow water with the lme approach because the necessary data aggregation to merge the soil and water data sets reduces the total number of observations to 11 for control plot modeling and to 22 for treatment plot modeling respectively. This was considered as not-sufficient for the statistical approach.

The model approaches were implemented using the lme function from nlme package in R (version R i386 4.0.2, R 150 Foundation for Statistical Computing 2014, Vienna, Austria). The fixed part of the model describes the response variable as function of the explanatory variables (fixed effects). The random part contains terms that allow for heterogeneity, nested data (random effects), temporal or spatial correlations (cf. Zuur et al. 2009). For the soil data set, we hypothesized that contents of P are affected by the variables site (high-P, low-P), horizon (organic layers, mineral topsoil and two subsoil horizons), and path (PFP, MA). Consequently, these variables and interactions between them were set as fixed effects in the full lme-model (for explanation of all variables see Table 2). In the preferential flow water data set, there is no path component, because the sampling strategy implies to collect water from PFPs. The depth component here represents the depth of the installed lysimeter instead of a categorical horizon to allow for more detailed information on depth transport of preferential flow water. The factor time of water collection (above defined time steps) was included in the fixed effects because we expected a variation of element concentrations during the artificial rain experiments. The influence of nutrient application (treat) on concentrations, both in soil and in water, as well as on collected loads was integrated in model approach 2 (A, B, C) as fixed effect with interaction to each other explanatory variables. This allows for different extent of effects of nutrient applications at the two sites, in each soil depth/horizon, in the specific flow path region, and with collection time. For random effects, all models included plot and for the soil data (models 1A and 2A) set the profile cut. Including a variance structure term in the random part of the model allowed the residuals to differ depending on categorical variables of the fixed term with the aim to account for heterogeneity of residual distribution.

Table 2 Overview of model building and variables in the statistical analysis using mixed-effect modeling (nlme package in R, Pinheiro et al. 2017) based on the soil samples data set (models 1A and 2A) and on the preferential flow water data set (models 1B, 1C, 2B, 2C)
Full size table

In model building, we started with full models including all test variables (see summary in Table 2) and stepwise reduced covariates and complexity. Each step was tested against the full model (likelihood ratio test using the anova function of the nlme package in R, Pinheiro et al. 2017) and the Akaike information criterion (AIC) (Zuur et al. 2009). The final models only include variables which significantly improved the models or were of fundamental importance for the scientific question. In some cases, the inclusion of a random term did not significantly improve the model. Here, a generalized least square (gls) function was used to fit an extended linear model and allow for inclusion of heterogeneity (Zuur et al. 2009). Thus, the gls function can be viewed as lme function without the argument random (Pinheiro and Bates 2000). For the final models, the residuals were plotted against fitted values and explanatory variables to validate model performance. The F and t statistics were calculated using anova(model) and summary(model) in the nlme package. It has to be mentioned that the F statistic applies sequential testing of variables. Consequently, the order of variables and variable interactions is important for the test results and meaningful for the last tested variable/interaction term only (cf. Zuur et al. 2009). Therefore, a post hoc comparison among groups (t test) was conducted using the commands emmeans(model) and constrast(model) in the R package emmeans (Lenth et al. 2021). For assessment of model quality, the marginal and conditional coefficients of determination (R2mar, R2con) were calculated (Bartoń 2020). This allows for comparison of the proportion of variance explained by the fixed factors with the proportion of variance explained by fixed and random factors (Nakagawa and Schielzeth 2013).

Results

Phosphorus in solid soil

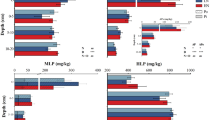
For all treatment plots, both the total P contents (TPs, total size of bars in Fig. 2) and the labile P forms (labPs, Fig. 3) were higher at the high-P site compared with the low-P site. The depth distribution showed a strong depth gradient of TPs and labile P forms (labPs, Fig. 3) at the low-P side but were more evenly distributed along the vertical profile at the high-P site. The absolute P contents and the depth distribution reflect the contrasting P status at the two sites.The predominant soil P form at the low- and high-P site was organically-bound P. For labile P forms, the inorganic labile P fractions (labPi,s) were predominant in the litter, slightly decreasing in the O-layer, and clearly decreased against labPo,s in the mineral soil horizons.

Fig. 2
figure 2

Total inorganic (TPi,s) and organically bound (TPo,s) phosphorus contents in preferential flow pathways (PFP) and soil matrix (MA) in forest soil of a low-P and high-P site. Soil horizons are visualized at the right side (organic layers: L and O, mineral horizons: A, B1, and B2). Plot treatments are indicated at the left side (ctl: no treatment, N: nitrogen addition, P: phosphorus addition, P+N: combined phosphorus and nitrogen addition). Error bars: standard deviation of plot repetition (ctl plots only); na: sample not available

Full size image
Fig. 3
figure 3

Easily available inorganic (labPi,s) and organically bound (labPo,s) phosphorus contents in preferential flow pathways (PFP) and soil matrix (MA) in forest soil of a low-P and high-P site. Soil horizons are visualized at the right side (organic layers: L and O, mineral horizons: A, B1, and B2). Plot treatments are indicated at the left side (ctl: no treatment, N: nitrogen addition, P: phosphorus addition, P+N: combined phosphorus and nitrogen addition). Error bars: standard deviation of plot repetition (ctl plots only); na: sample not available

Full size image

The occurrence of P in preferential flow pathways as compared to soil matrix (PFP vs. MA in Fig. 2 and 3) exhibited no clear pattern in total as well as labile P fractions. In most cases, differences were low and not significant in statistical tests on subgroup level (per horizon, plot, or site). However, the distribution of flow patterns clearly differed between the sites with vertical and lateral macropore flow as well as flow along stone surfaces at the high-P site. Flow conditions at the low-P site were characterized by macropore flow in the upper soil horizons and highly connected (laterally and vertically) flow in the sandy subsoil, included fingering and in parts also matrix flow.

At the low-P site, N additions in the N and P treatments (both N and P+N) caused smaller TPs contents in the organic layers as compared to the controls, but higher TPs in all treatment plots (P, N, P+N) in the mineral soil horizons. For the high-P site, we found comparable TPs contents in the control and treatment plots in the organic layers. The only exception is the value in PFP in the N plot which was lower than in all other plots. In mineral soil (A and B horizons) at the high-P site, TPs was generally lower than control in the P and P+N plots. The distribution of labPs was similar as TPs at the low-P site with lower P contents after nutrient application in the organic layers, but higher labPs in mineral soil. The results for labPs at the high-P site were highly variable. The P treatment seemed to raise labPs slightly in organic layers and mineral A horizon, especially in PFPs, but was lower than the control in the subsoil. For the N treatment, labPs was higher than control in the subsoil.

The statistical approach of mixed effects modeling confirmed the assumed site-specific differences (Table 3 and Table S3 in Supplement 1) for the soil P fractions (Model 1A and 2A). The tested soil response variables (TPs, labPs) were significantly different for the explanatory variables site (high-P and low-P) and horizon, and for the interaction term site:horizon. The residuals were allowed to differ depending on the site and horizon to account for their heterogeneity of residual distribution. This was incorporated as random slope and variance structure terms in the random part of the models and has significantly improved them. The inclusion of flow path region (PFP, MA) as fixed effect and profile cut repetition as random effect has not improved the model significantly and therefore was omitted in the final models. The coefficient R2mar as measure for the variance explained by the fixed factors was generally lower than R2con (proportion of variance explained by fixed and random factors). However, the differences were rather small, indicating that inclusion of random effects only slightly improve the model performance even if the other validation criteria AIC showed significant improvement by involving them into the model (Table S3 in Supplement 1).

Table 3 Summary statistics from linear mixed effect models for soil and preferential flow data sets
Full size table

The statistical model to test the influence of treatments on soil parameters (model 2A) indicated a general significant effect (p < 0.05) of nutrient application on soil contents of TPs and labPs. The interaction treatment:horizon was significant for all parameters with p < 0.001 indicating that the treatment effects occurred horizon-dependent. Nevertheless, we found no significant differences in soil parameters between any treatment and control in the more robust post hoc between-groups statistics (Table S4 in Supplement 1).

In sum, the models 1A and 2A show that the variables site and horizon are important to explain differences in the tested soil parameters and that they have different gradients along depth (horizon effect) at the high-P and the low-P site with heterogeneous variances (significance of the random variance term). A treatment effect as suspected in Fig. 2 and 3 could not be proved with the model approach. The main problem here was the high variability of data from control plot replicates, which must be assumed in the same extent for the treatment plots. Furthermore, data are unbalanced and therefore care is needed with the interpretation of the results (Zuur et al. 2009). Nevertheless, there seem to be a combined horizon and treatment effect, because including this interaction significantly improved the model for all soil response variables.

Phosphorus transport with preferential flow water

The concentrations of the different P forms in the seepage water samples (Fig. 4) show a different pattern at the high-P and low-P site with regard to depth distribution and occurring P forms. At the low-P site, the TPw concentrations (total size of bars) were highest in upper soil (d1) and strongly decreased with subsoil samples (d2, d3) in all treatment plots. In particular, the dissolved P forms (DIPw and DOPw), which had a predominant share in samples from upper soil, were strongly diminished in the samples from deeper lysimeters. At the low-P site, the preferential flow reached the subsoil lysimeters later (time step t5 in Fig. 4) and to a lesser extent (lower amount of collected water, data not shown) as compared to the upper lysimeters. In several plots, water has not reached the deeper lysimeters during the experiments or collected water amounts were not sufficient for chemical analyses. At the high-P site, the P concentrations collected in the upper lysimeters (d1, Fig. 4) in most cases were lower than in the low-P site, except for the P+N plot. The P concentrations (especially DIPw) in the middle lysimeters (d2) were slightly higher at the high-P site than at the low-P site and consistently measurable through the experiment. This indicates a good connection of flow pathways between infiltration zone and lysimeter depth. The strong depth gradient of observed P concentrations as found at the low-P site was not clearly detectable at the high-P site, except for the P+N plot. The occurrence of preferential flow water in lower subsoil points towards a good connection of fast flow pathways through the profile.

Fig. 4
figure 4

Concentrations of particle-bound (PPw), dissolved organic (DOPw) and dissolved inorganic P (DIPw) in fast seepage collected in forest soil of a low-P and high-P site. The time steps t1–t4 represent hourly aggregated data (mean values) during sprinkling, t5 the after-sprinkling data aggregated for 4 h. Collection depths are visualized at the right side (d1: below topsoil, d2: middle subsoil, d3: lower subsoil). Plot treatments are indicated at the left side (ctl: no treatment, N: nitrogen addition, P: phosphorus addition, P+N: combined phosphorus and nitrogen addition). Error bars: standard deviation of plot repetition (ctl plots only); na: no sampler could be installed, lines with no value indicated samplers with no or limited flow

Full size image

The statistical analysis found no treatment effects on concentrations of DIPw and PPw in preferential flow water at the two sites (Table S5 in Supplement 1). For DOPw, the concentrations at the P treatment plot significantly differed from the control but the effect differed in dependence of depth and timestep: DOPw concentrations after P addition were slightly higher than control in upper soil of the two sites in the late irrigation period (d1, time step t4 in Fig. 4). At the high-P site, this was also observed in the subsoil (d2). The P+N addition significantly influenced the concentrations of TPw (p < 0.05) for both sites but to different degree: At the low-P site, TPw concentrations after P+N addition were more than 50% lower as compared to the control throughout the sampling period. By contrast, TPw was clearly higher than control in the P+N plot at the high-P site (d1, Fig. 4). Comparable to the soil data model (2A), the flow data model (2B) revealed the factors site and depth as variables which explained most of the variance of the response variables. For all response variables except DIPw, the variable timestep (t1–t5) was also significantly important to explain the variances. The coefficients of determination demonstrate that including the random effect factor plot noticeably can improve the model performance (Table 2) for TPw and DIPw but could be dropped completely for the other response variables.

For the cumulative P loads as sum of collected P per lysimeter and experiment, a wide range of values were observed, between zero (no water reached the lysimeter) up to 4.5 mg m−2 within 8 h (4 h sprinkling + 4 h after-sprinkling sampling) in one of the control plots at the low-P site (Fig. 5). At the low-P site, the cumulative loads were dominated by dissolved P forms in upper soil but a higher proportion of particle-bound P in the subsoil samples. At the high-P site, dissolved P loads considerably contributed in upper and middle horizons. The P loads in the P treatment plot at this site were by far higher in middle subsoil as compared to the upper soil. The reason is a very high volume of collected water in the subsoil lysimeter whereas the collected water amount in the upper soil was comparably low. As it can be seen in the graph of concentrations (Fig. 4), the water also reached the subsoil earlier (in timestep t3) than in the upper lysimeter (timestep 4). This points to a highly variable connectivity of fast flow pathways from upper soil to subsoil within this plot.

Fig. 5
figure 5

Cumulative loads per experiment of particle-bound (L_PPw), dissolved organic (L_DOPw) and dissolved inorganic P (L_DIPw) in fast seepage collected in forest soil of a low-P and high-P site (collection period: 4 h sprinkling + 4 h after- sprinkling). Collection depths are visualized at the right side (d1: below topsoil, d2: middle subsoil, d3: lower subsoil). Plot treatments are indicated at the left side (ctl: no treatment, N: nitrogen addition, P: phosphorus addition, P+N: combined phosphorus and nitrogen addition). Error bars: standard deviation of plot repetition (ctl plots only); na: no sampler could be installed, lines with no value indicated samplers with no or limited flow

Full size image

In the statistical modeling, it was found that the mixed effects models (1C, 2C) often delivered no significantly better model performance than linear models without a random part for explanation of variances (gls model). Consequently, the random effects often could not improve the models and were dropped in some cases (Table 3). For Model 2C, the inclusion of all variables (site, depth, timestep, treat) improved the model performance for the response variables. This means, that these factors were important to explain the variances of element loads in the water samples. An exception is the model for DOPw loads, where only the factor timestep could be included as significant variable in the final model. In general, most of the load models had a poor model performance (low coefficients of determination). At the two sites, we found no significant differences in the post-hoc test for the P forms between the sites, depths or treatments (Table S5 in Supplement 1). Generally, the use of loads instead of concentrations seems not to be favorable to explain our observations, perhaps because of the combined and heterogeneous influence of concentrations and water amounts on load values.

Discussion

Site effect on P transport through preferential flow pathways

Our results confirm the assumption that the contrasting nutrition strategies at the two test sites exhibited different status and depth distribution of P forms in the soils. The contents of TPs and labPs in soil were far lower and exhibited a very strong decreasing gradient with soil depth at the low-P site. A similar decrease of P concentrations with depth was observed in collected seepage water representing preferential flow. In particular, the dissolved P forms were hardly detectable in water samples from subsoil lysimeters. The high values for P concentrations in preferential flow and for related cumulative P fluxes in the upper soil of all plots at the low-P site revealed that plant-available P forms (especially DIPw) are mobilized in the organic layer and translocated into upper mineral soil, whereas transport into deeper soil layers is minimal. This confirms earlier studies at the same sites where labPs contents were in a similar range in organic layers of low-P and high-P sites resulting in a clearly higher proportion of labile P forms on total P in the low-P soil (Julich et al. 2017a). Thus, our results strongly support the conceptional idea of a recycling (low-P) system which is able to gain their main nutrient supply from organic layer (cf. Lang et al. 2017; Hauenstein et al. 2018; Rinderer et al. 2021). Bünemann et al. (2016) found biological/biochemical processes to predominantly control TPi,s availability in the low-P-adsorbing sandy soil at the low-P site. If we combine the results from those previous studies with our experimental findings for the low-P site, we can derive the clear conclusion that the microbial turnover of organic P is high and causes considerable release of DIPw in the organic layer. This easily available P then is subject to re-uptake by microbes and plant roots in the upper mineral soil with a very low potential for translocation into the subsoil.

By contrast, a considerable amount of P was observed in the subsoil samples of preferential flow at the loamy high-P site, and even measurable P fluxes down to lower subsoil could be detected there. The connectivity of fast flow pathways obviously strongly influenced vertical water and P transport at the high-P site. In some cases, water passed the layers above the upper lysimeter far slower and in lower amounts than the thicker soil column above the subsoil sampler in depth d2 and d3, most likely due to better connected flow pathways. Thus, the temporal occurrence of preferential flow during the artificial rain experiments (arrival of water in the lysimeters) and the spatial distribution of flow pathways (as observed in the dye tracer experiments) was highly heterogeneous with a considerably higher degree of variability at the high-P site compared to the low-P site (Julich et al. 2017a). Consequently, the P transport through the soil profiles appears to be substantially driven by specific properties of the soil at the given site.

Further important factors controlling the P fluxes through fast flow pathways are the intensity and duration of rainfall, soil moisture, and soil physical properties that control water flow (Backnäs et al. 2012; Bol et al. 2016; Dinh et al. 2016; Julich et al. 2017c). The rainfall and moisture conditions in our study were defined by the setup of the sprinkling experiments and therefore can be assumed to be similar for all experiment plots. However, the soil physical conditions for water fluxes and in consequence also for P fluxes differed. At the high-P site, flow conditions are characterized by a combination of macropore flow and flow along stone surfaces. Additionally, the position at a hillslope favors laterally directed subsurface flow which is supposed to contribute to P (re-)distribution at this site (cf. Julich et al. 2017a). At the low-P site, macropore flow dominated in the upper soil horizons, but PFPs were highly connected in the sandy subsoil. Fast moving seepage here rarely reached the deeper mineral soil. An assumption is that the transition of flow conditions from macropore flow in topsoil to interconnected preferential and matrix flow strongly decelerated vertical flow into the sandy subsoil. The infiltrated water was distributed also horizontally, the lateral flow area increased and with this reduced the hydrostatic pressure for downward flow, especially under dry environment as simulated in our experiments (cf. Hardie et al. 2011; Guo and Lin 2018). Following, these specific flow conditions in the subsoil would have required a far higher rate of experimental rainfall to activate subsoil flow pathways and connect the water fluxes to the deeper lysimeters.

The calculated values for P fluxes in different depths were surprisingly high with amounts up to 4.5 mg P m−2 per experiment (8 h). We decided against the estimation of annual P fluxes based on our experiments, because both the water fluxes and the P concentration involve high spatial and temporal variability. Thus, an estimate based on this short-term experiment would be rather rough with very high uncertainty. Only few studies on P fluxes within forest soils are available so far. Rinderer et al. (2021) conducted sprinkling experiments on a slope in the Conventwald catchment (SW-Germany midrange mountains). They estimated total annual P losses for the hillslope soil area of 3.2 mg P m−2 a−1. This was in the same range of values as calculated groundwater P fluxes (2.5 mg P m−2 a−1) at the same site, based on biweekly water sampling (Sohrt et al. 2019). The estimates for P fluxes in different soil depths strongly differed in these studies due to different methods to estimate water fluxes: For P export from the forest floor, Rinderer et al. (2021) estimated 45 mg P m−2 a−1 (lateral + vertical) against 0.001 mg P m−2 a−1 (lateral only) reported in the study of Sohrt et al. (2019). In the mineral soil, the mentioned studies calculated a range of 6–20 mg m−2 a−1 for total P fluxes. This indicates a decrease of P fluxes with depth as also found in our study. Fluxes of DOPw from the organic layer into the mineral soil were in a range between 15 and 62 mg m−2 a−1 in leachate collected by suction cups, and from mineral subsoil between 1.7 and 38 mg m−2 a−1 (summarized in Bol et al. 2016). For DIPw, published values were in the range of 4–15 mg m−2 a−1 for organic layer and 0.5–3 mg m−2 a−1 for subsoil. In our experiments, we detected up to 0.6 mg m−2 for DOPw and up 3.9 mg m−2 for DIPw during an artificial rain event (20 mm h−1, 4 h irrigation, 8 h sample collection), each with highest loads in the upper mineral soil; and up to 0.7 mg m−2 for PP, where high values occurred in all depths. Thus, the observed P fluxes during our experiments were in a comparable range of values for annual P loads as in above mentioned studies. With regard to the different considered time intervals, even the tenfold lower value for P fluxes from organic layer which was observed in our few-hours experiment seems to be rather high in comparison to the annual estimates of Rinderer et al. (2021). This result can be suspected in the setup of the artificial rain experiments. We simulated a heavy rainfall event with in total 80 mm within 4 h at all plots and simulated a four weeks’ dry period before the sprinkling, because these conditions were assumed to activate preferential flow with high potential for P transport (cf. Benning et al. 2012; Bol et al. 2016; Julich et al. 2017c). Therefore, different estimates for P fluxes through soils often are the consequence of different monitoring strategies (e.g. inclusion/exclusion of heavy rainfall events) as well as different calculation methods for water fluxes (measured data, model-derived series, etc.) (Julich et al. 2017c). For the monitoring of P fractions in soil water, a further problem is the collection of different components of soil water by application of different samplers (e.g. zero-tension lysimeters vs. suction cups). Based on our results, we recommend to monitor P fluxes in short timesteps and essentially to include heavy rainfall events, which activate fast flow pathways. This ensures to detect short-time pulses of P through soils, which bear the potential for remarkable P translocation into deeper soil where P may no longer available for plant uptake, especially for low-P ecosystem which are adapted to nutrient acquisition from upper soil compartments (cf. Lang et al. 2017).

Nutrient application effect on P transport through preferential flow pathways

The statistical models indicate that N and P application had a horizon-dependent effect on P concentrations in the soil and in fast-moving preferential flow water. However, the effects were weak due to the high variability of observed data. This variability is results of spatial heterogeneity as well as temporally varying flow pattern (Makowski et al. 2020b). Furthermore, the period between nutrient application and sampling, especially at the P treatment plots, is an important factor affecting the occurrence and availability of P both in solid soil and soil solution (seepage). The question arises how fast a system can adapt to increased nutrient availability and, as consequence of the experimental setup, if nutrient application in several treatments over a longer period (as for N application) might have had a stronger impact on the systems than an application in only one treatment in the beginning of the period (as P addition in our case). Another study using labeling experiments with 18O detected shortly (few days) after the nutrient application distinct effects of the P addition (P, P+N) on P uptake of beech trees (Hauenstein et al. 2020). The authors investigated the same low-P site as in our study but examined another high-P site (P stock: 904 g m−2 up to 1 m soil depth, Lang et al. 2017), however, both under same experimental treatments. At the high-P site, the authors attributed the observed increase in inorganic P concentrations in tree xylem sap to P addition and accelerated biological P cycling in the soil. Those findings indicate fast incorporation of added P into biological cycles. By contrast, these processes of 18O incorporation appeared to be much slower at the low-P site. Whereas the low-P system was supposed to mostly rely on the organic layer for P and water uptake, the P uptake by trees might be decoupled at a P-rich site where water is taken up from deeper soil layers, too (Hauenstein et al. 2020).

Our experimental data for depth transport of P point towards relevant control by the same processes, still two years after P application. At the P addition plots, increased P fluxes into the subsoil occurred at the high-P site, which may be a result of an accelerated microbial turnover with increased release of P and less efficient uptake of surplus P in the organic layer and upper soil. Along PFPs with good connection between the upper and lower parts of the mineral soil, P is vertically translocated within the profile. The slightly increased contents of soil labile P at the P and P+N treatment plots of the high-P site (Fig. 3) also indicated an increased P availability in the upper soil layers here. Such an increase of easily-available P contents after P and N+P application as well was observed in a study by Fisk et al. (2014) in northern hardwood forest in New Hampshire (USA).

At the low-P site, P concentrations in the organic layer and soil water of the upper soil surprisingly were lower in all treatment plots as compared to the controls (Figs. 2, 3, 4). The strongly decreasing P contents at the transition to mineral topsoil occurred in all plots, but in the mineral horizon the soil P contents were slightly higher in the treatment plots than in controls. In the light of the results of Hauenstein et al. (2020), who assumed slower biological incorporation of P at the low-P site, this clearly indicates, that the period between nutrient application and our artificial rain experiments was sufficient for the incorporation of the added nutrients. The turnover rates for forest floor at the low-P site were observed to be very low (39 years, Lang et al. 2017). Here, the increased nutrient availability by nutrient addition might have (slowly) accelerated microbial processes resulting in release of mineralized P. The observed decrease in soil P contents in the treated plots compared to the controls in combination with very low depth translocation strongly indicates that released P is taken up by plants and thus slowly incorporated into the biological cycle.

Conclusion

Data on P fluxes in forest soils in high temporal resolution, which is required to understand rain event-driven P transport, is rarely available so far. Our study contributes to closing this gap in providing values for P fluxes via preferential flow (fast seepage) in soils. Our results reveal that rain event-driven P fluxes occur with pronounced spatial and temporal variability. The connectivity of preferential flow pathways as result of physical soil properties at the contrasting test sites strongly influenced P translocation in the soil profiles. These different flow pattern in combination with the P nutrition strategy (high-P: acquiring/low-P: recycling) led to different P distribution at the test plots: P translocation into deeper soil was higher and included all determined P forms (DIPw, DOPw, PPw) in the loamy high-P soil with well-connected flow pathways. By contrast, far smaller amounts of P (DOPw and PPw only) were translocated in deeper layers in the sandy P-poor soil. Clear effects of the N and P additions on soil P contents and P concentrations in fast seepage could not be observed with statistical significance due to the high variability of the data set. Our approach of mixed effects modelling appears to be useful to identify general effects, such as a general treatment effect on the combined dynamic character and small-scale variation of labile P in the soil. However, even if the method can handle sporadic missing values, it cannot compensate for bigger gaps in the data set or missing experimental repetitions.