Abstract
Increasing exports of Fe and DOC from soils, causing browning of freshwaters, have been reported in recent decades in many regions of the northern hemisphere. Afforestation, and in particular an increase of Norway spruce forest in certain regions, is suggested as a driver behind these trends in water chemistry. In this study, we tested the hypothesis that the gradual accumulation of organic soil layers in spruce forests, and subsequent increase in organic acid concentrations and acidity enhances mobilization of Fe. First generation Norway spruce stands of different ages (35, 61, 90 years) and adjacent arable control plots were selected to represent the effects of aging forest. Soil solutions were sampled from suction lysimeters at two depths (below organic soil layer and in mineral soil) during two years, and analyzed for Fe concentration, Fe speciation (XAS analysis), DOC, metals, major anions and cations. Solution Fe concentrations were significantly higher in shallow soils under older spruce stands (by 5- and 6-fold) than in control plots and the youngest forest. Variation in Fe concentration was best explained by variation in DOC concentration and pH. Moreover, Fe in all soil solutions was present as mononuclear Fe(III)-OM complexes, showing that this phase is dominating Fe translocation. Fe speciation in the soil was also analyzed, and found to be dominated by Fe oxides with minor differences between plots. These results confirmed that Fe mobilization, by Fe(III)-OM complexes, was higher from mature spruce stands, which supports that afforestation with spruce may contribute to rising concentrations of Fe in surface waters.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Exports of iron (Fe) from catchment soils to surface waters are increasing in many northern regions and are observed as rising Fe concentrations in surface waters (Björnerås et al. 2017; Neal et al. 2008; Sarkkola et al. 2013). The increase in Fe concentrations is generally synchronous with that of terrestrially derived dissolved organic carbon (DOC). These trends have received much attention in recent years, as they lead to an increase in water color, also known as browning or brownification (Kritzberg and Ekstrom 2012). Browning affects freshwater species distributions, the structure and production of food-webs (Creed et al. 2018; Solomon et al. 2015), biogeochemical cycles (Tranvik et al. 2009) and brings challenges for drinking water production (Matilainen et al. 2010).
In soils, wetlands and sediments, Fe mineral surfaces bind organic carbon and protect it from microbial mineralization, thereby acting as an important carbon (C) sink (Lalonde et al. 2012; Wagai and Mayer 2007). Understanding the processes behind the increasing Fe mobilization and subsequent export to surface waters is therefore important to predict the fate of C in the environment, and the potential effects on the global C cycle. Moreover, Fe influences the mobility and transport of environmentally relevant elements, such as arsenic (Bauer and Blodau 2006; Cummings et al. 1999; Mudroch and Clair 1986) and phosphorous (Johnson and Loeppert 2006; Jones et al. 1993) in both terrestrial and aquatic ecosystems.
While many have studied the drivers of increasing DOC concentrations in surface waters (de Wit et al. 2016; Erlandsson et al. 2008; Finstad et al. 2016), less is known about factors controlling the increase in Fe and whether they are the same as for DOC. An early study on increasing Fe concentrations by Neal et al. (2008), suggested that a recovery from acidification and a subsequent increase in soil pH resulted in higher DOC solubility in soils, which enhanced transport of Fe from soils and stabilized it in surface waters. This is in line with a study of 340 surface waters across Europe and North America where regional trends in declining S deposition corresponded well to trends of increasing Fe concentrations (Björnerås et al. 2017). Other studies have proposed that reducing conditions in the catchment, promoted by elevated precipitation and temperature, drive the increasing exports of Fe from soils to surface waters (Sarkkola et al. 2013; Ekstrom et al. 2016). Reducing conditions, caused by enhanced microbial activity, promote reduction of Fe(III)-(oxy)hydroxides (FeOOH) to the more soluble Fe(II), thereby making more Fe available for export to surface waters. Finally, effects of changing land-use, in particular expanding coniferous forest, have been shown to be an important factor driving browning (Kritzberg 2017; Škerlep et al. 2020). Although the latter studies did not distinguish between Fe and DOC as the cause of increasing water color, Björnerås et al. (2017) observed that the rate at which Fe concentrations were increasing was correlated to the proportion of coniferous forest in the catchments.
Although Fe is abundant in bedrock in the majority of soils, most of the Fe is bound in minerals of low solubility (Lindsay and Schwab 1982). The mobilization of Fe from soil minerals to soil solution and subsequently to surface waters is dependent on pH, redox conditions and availability of organic matter (OM) (Schwertmann 1991). At oxic conditions and circumneutral pH (≈ 7), the solubility of Fe is low, however this drastically increases at pH ~ 3 (Lindsay and Sadiq 1983). Under anoxic conditions, free ferrous ions (Fe2+) can be present in water, but oxidize and precipitate as FeOOH in the presence of oxygen, unless pH is strongly acidic (Suter et al. 1991). Certain functional groups of OM can stabilize Fe in solution by forming Fe(II)-OM or Fe(III)-OM complexes (Bhattacharyya et al. 2019; Catrouillet et al. 2014; Karlsson and Persson 2012; Theis and Singer 1974). In well-drained soils, we would therefore expect the Fe mobilized into solution to be complexed by OM, or to reside as free ions if pH is strongly acidic.
As vegetation cover and land-use exert a major control on soil OM accumulation and pH, it is expected that land-use can also affect the mobility of Fe in soils. Indeed, mineral weathering rates have been shown to be higher in coniferous than deciduous forest soils owing mostly to lower pH and higher production of organic acids in coniferous soils (Augusto et al. 2000). Iron minerals were found to be more amorphous and less crystalline in soils under coniferous forest than in agricultural soils (Li and Richter 2012), suggesting Fe in the former soils could be more easily mobilized into soil solution. Furthermore, soils under Norway spruce (Picea abies (L.) Karst.) forest were shown to contain considerably higher concentrations of extractable Fe than soils under deciduous tree species (Hagen-Thorn et al. 2004). Björnerås (2019) suggested that the gradual build-up of organic soil layers under coniferous forests, and the subsequently increased leaching of DOC and lowering of pH (Rosenqvist et al. 2010b), should promote mobilization of Fe and that this was a major factor behind the observed doubling of Fe concentrations in a lake in southern Sweden.
Many northern regions have undergone afforestation during the last century (Fuchs et al. 2013). Large parts of Sweden have drastically changed in land-use and vegetation cover, from a more heterogeneous and open landscape with mostly deciduous tree species, towards a dominance of Norway spruce forest and intensive forestry (Fredh et al. 2012). Southern Sweden in particular has seen an increase in Norway spruce forest (Lindbladh et al. 2014), and is the area where the highest increases in surface water Fe have been reported (Kritzberg and Ekstrom 2012).
The overarching aim of this study was to better understand how growing coniferous forests influence soil processes that affect speciation and mobilization of Fe in soils and soil solutions. To this effect, we performed a field study exploiting a chronosequence of first generation Norway spruce stands, that were planted 35, 61 and 90 years before the onset of the experiment. For reference, we chose an adjacent arable plot for each tree stand, which had not been forested and had only grass growing, i.e. representing 0 years of tree growth. Soils and soil solutions (sampled by suction lysimeters) were studied to determine the effects of stand age on the speciation and mobility of Fe, as well as its relationship with OM. With increasing age of spruce stands, organic soil layers are generally thicker and pH lower due to biological acidification, and we hypothesized that this would promote dissolution, complexation and solubility of Fe, resulting in higher Fe concentrations in soil solution. As adsorption and precipitation of Fe phases is likely to increase as soil solution moves vertically (since OM is mineralized and pH increasing), the effect on Fe concentrations in soil solution is expected to be less apparent in deeper soil water. For the same reason, we hypothesized that there would be more easily extractable Fe in soils under older spruce stands, reflecting deposited Fe-OM complexes and ferrihydrite.
Materials and methods
Site description and experimental setup
Tönnersjöheden Experimental Forest (56°40′ N, 13°04′ E) is located approximately 15 km east of the city Halmstad in southwestern Sweden at 60–140 m above sea level. Climate in the area is maritime temperate with an average yearly precipitation of 1099 mm (2003–2019, SMHI, station Marbäck D; www.smhi.se/data/meteorologi), and average daily air and ground temperatures at the experimental forest site were 7.5 °C and 8.3 °C, respectively. The growing season (days above 5 °C) lasted on average 222 days per year (2003–2019), generally extending from mid-April to November. During the experimental period in 2018 and 2019, the average air temperature at the site was 8.5 °C both years and there was 947 and 1276 mm annual precipitation for the respective years. Soils in the area have developed on glacio-fluvial material, which contains a large amount of stones, are well drained with deep ground-water tables, and are classified as Arenosols (Rosenqvist et al. 2010b). The old forested plots have developed an O horizon, but the soil profiles lack a developed E horizon.
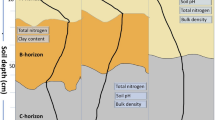
For the experiment, three plots (15 × 25 m) with first generation Norway spruce forest (Picea abies (L.) Karst.) plantations of different stand ages (35, 61 and 90 years) were selected to represent a chronosequence. In addition, in the proximity of each forested plot an arable plot with grass was selected as a control, which also represents zero year old forest (Fig. 1). The younger forest plot was established on former agricultural land, while the two older have historically been Calluna heathlands used for grazing and have not been forested since at least 1890 (prior to current plantation). The depth of the organic soil horizon (O-layer) differed between spruce plots according to the time they have been afforested. The 35-year old forested plot had the thinnest organic layer (2–3 cm) that was only partially developed and contained mineral particles. The 61- and 90-year old forested plots, had fully developed organic layers, with depths of 5–7 and 8–10 cm respectively (Fig. 1).
Schematic figure of the experimental layout and corresponding stand properties of the forested plots with accompanying control plots. Grey dots show the horizontal position for soil samples and lysimeters. White shapes in soil profile represent lysimeter depth position in each plot. Dashed white lines represent the surface of the mineral layer on each plot
On each plot five sampling positions were allocated, one in the center of the plot and 4 half way between the center and each corner of the plot (Fig. 1). At each sampling position two suction cup lysimeters (Prenart Super Quartz Standard 2.1 cm diameter; PRENART Equipment ApS, Frederiksberg, Denmark) were installed. One lysimeter was installed 10 cm below the soil surface or 3 cm beneath the organic (O) soil layer at plots with > 7 cm deep O layer. The motivation behind the selected depths of the shallow lysimeters was that a depth of 10 cm is required for the lysimeter to consistently give water in well drained soil, and that all lysimeters would be placed slightly below the organic layer for a comparable influence of adsorption in the mineral soil. Since the lysimeters extract porewater from the nearest few centimeters, the shallow lysimeters should collect water flowing from the organic rich layer of each soil plot. Another lysimeter was installed 25 cm beneath the surface of the mineral layer.
Sampling
Soil solution sampling
Quartz suction cup lysimeters (pore size 2 µm) were installed in November 2017, set under pressure and emptied twice before the start of sampling. For sampling, under-pressure was applied to the lysimeters 5–7 days before the lysimeter water was collected. Sampling of soil solution was performed on seven occasions between April 2018 and November 2019. The sampling in spring was performed at the offset of soil frost, while the first sampling in autumn was done as soon as the lysimeters provided enough water after the summer dry period. On each sampling occasion, the volume of the collected solution from each lysimeter was measured and 50 ml of the collected soil solution were transferred to a polypropylene Falcon tube. Solution samples were not further filtered, meaning that all material passing through the 2 µm pore of the lysimeter was collected and analyzed. The subsamples were stored at 4 °C in the dark until analysis. When the lysimeters yielded less than 15 ml of solution, the samples were discarded. On occasions when lysimeters produced large volumes of soil solution, the excess solution was frozen and later freeze-dried. The freeze-dried samples were used for analysis of Fe speciation with X-ray absorption spectroscopy (XAS) analysis (described in Sect. 2.4). After each sampling, the lysimeter bottles were thoroughly rinsed with deionized water.
Soil sampling
Soil samples were collected during autumn 2018 and 2019. Using a shovel, a vertical soil profile was exposed in the proximity of each lysimeter, but far enough to not disturb the lysimeter samplings. From the forested plots, soil samples were collected from the O-layer, the 10 cm of mineral soil below the O-layer (0–10 cm; upper mineral) and 10–25 cm below the O-layer (lower mineral). For the 35-year old forested plot, the O-layer was not fully developed and contained mineral fractions to a higher extent that in the two plots with older forest. In control plots where O-layers were lacking, only two samples were taken at each sampling spot; 0–10 cm (upper mineral) and 10–25 cm (lower mineral) below the soil surface (Fig. 1). In the lab, larger stones and roots were removed and the soil samples were sieved wet through a nylon mesh (2 mm), to avoid metal contamination and to not alter the soil properties by drying them. Soils were stored in zip-lock bags at 4 °C until analysis. For the purpose of XAS and X-ray diffraction (XRD) subsamples of the sieved soil were ground to powder, using a mortar.
Analytical methods
Soil analysis
Loss of ignition (LOI), the difference in weight before and after combustion at 400 °C during 8 h, was measured to estimate soil OM content. Soil pH was determined by mixing soil and deionized water (1:5) and measuring pH in solution after 1 h.
To determine Fe crystallinity and content, oxalate and dithionite, as well as total Fe extractions were used. Oxalate extractable iron (Feox) represents less crystalline Fe phases, mostly ferrihydrite, which is the mineral Fe phase easiest to mobilize. The extraction, in short, was performed with a mixture of ammonium oxalate (0.2 M; (NH4)2C2O4 × H2O) and oxalic acid (0.2 M; H2C2O4 × 2H2O) at pH 3 at room temperature in the dark for 4 h (McKeague and Day 1966). Dithionite extractable iron (Fedit) represents total reactive Fe, which includes crystalline and amorphous Fe(III) oxide phases, acid volatile sulfides and amorphous Fe-containing silicates. The extraction was performed with a mixture of sodium dithionite (Na2S2O4), trisodium citrate dihydrate (C6H5Na3O7⋅2H2O), sodium acetate (C2O3NaO2), glacial acetic acid (C2H4O2) and nitric acid (HNO3), at pH 4.8 and 60 °C, for 3.5 h (ISO 12782-2 2012 Swedish Institute for Standards). To determine the total iron (Fetot), 3 soil samples from each plot and depth were digested in a 1:1 mixture of 68% HNO3− and Milli-Q water, and autoclaved at 120 °C for 1 h. This should extract the vast majority of Fe from soil samples, with the exemption of Fe incorporated in larger Si crystals. After each extraction, Fe concentrations were determined by ICP (ICP-OES; Perkin Elmer Optima 8300) and recalculated to mg extractable Fe per g dry soil.
Soil solution analysis
Within 3 days after sampling the samples were analyzed for pH (913 pH Meter; Metrohm AG, Switzerland), conductivity (inoLab Cond 730, WTW, Germany). A subsample for total organic carbon (TOC) analysis was acidified (2 M HCl) and later analyzed by high-temperature catalytic-oxidation, using the non-purgeable organic carbon (NPOC) method (TOC V-CPN; Shimadzu, Japan). Another subsample was stored frozen for metal and ion analysis. Analysis of Fe, Mn, Si, Al, Na, K, Ca and Mg concentrations were done by ICP (ICP-OES; Perkin Elmer Optima 8300), and Cl−, NO3−-N and SO42−-S concentrations were determined by Ion-chromatography (816 Advanced Compact IC, Metrohm, Switzerland). For ICP analyses, samples were acidified (1% HNO3) 24 h prior to analysis.
XAS and XRD data collection and analysis
XAS data was collected at Stanford Synchrotron Radiation Lightsource (SSRL), beamline 4-1, California, USA. The beamline was equipped with a Si[2 2 0] double crystal monochromator, one passive implanted planar silicon (PIPS) detector for fluorescence measurement and had three consecutive ion chambers to monitor the incident beam as well as the beam passing through the sample and a Fe(0) reference foil. A manganese filter and Soller slits were used to reduce unwanted scattering contributions to the measured signal. Samples were mounted at 45° relative to the beam and in a liquid nitrogen cryostat (ca. 80 K) to prevent sample damage. For each sample 2–5 scans were recoded and recordings of the Fe(0) reference were made simultaneously for energy calibration. The edge from consecutive scans was closely monitored to make sure that samples were not damaged. Only samples with no detectable change were analyzed. Fe K-edge spectra were collected up to 14 Å−1 in fluorescence mode.
XAS data reduction was accomplished using the VIPER software (Klementiev 2001). Scans were energy calibrated to the lowest-energy inflection point of Fe foil set to 7111.08 eV. Spectral repeats were then averaged, normalized, and Extended X-ray Absorption Fine Structure (EXAFS) background was removed using a Bayesian smoothing spline function. Shell-by-sell fitting of k3-weighted EXAFS oscillations was accomplished using a non-linear least-squares refinement procedure. Theoretical phase and amplitude functions were calculated for model spectra of trisoxalatoiron(III) complex (Persson and Axe 2005) and goethite (Szytuła et al. 1968) using ab initio code FEFF7 (Zabinsky et al. 1995). The amplitude reduction factor \(({S}_{0}^{2})\) was set to 0.8 for soil samples and 1.0 for lysimeter samples. The threshold energy (ΔE0) was permitted to float but correlated to be equal for each scattering path. Debye–Waller factors (σ2) were fixed to literature values where indicated: the Fe − Fe paths were fixed to 0.0100 (Sundman et al. 2014), Fe − C paths were fixed to 0.0075 (Sundman et al. 2016) and 0.0056 (Sundman et al. 2014) for soil and lysimeter samples, respectively. The CN and σ2 of the Fe − C − O multiple scattering path was correlated to be double the CN and σ2 of the Fe − C path to model carboxylic-like structures. EXAFS oscillations were further fit by least-squares optimization using linear combinations of model compound spectra using the program DATFIT (George 2000). Model compounds comprised of Suwannee River fulvic acid (SRFA; 1S101F) complexed with Fe(III), biotite, ferrihydrite, goethite, and hematite. The software Fityk (Wojdyr 2010) was used to identify the integrated intensity and centroid energy position of the pre-edge peaks. Briefly, the pre-edge peaks were baseline subtracted using a spline function then fit with 50:50 pseudo-Voigt functions (Wilke et al. 2001).
The freeze-drying procedure used to pre-concentrate Fe in the soil solutions may potentially alter the speciation. Nonetheless, the great variation in Fe speciation from previous studies that use freeze-drying to concentrate the Fe, suggests that the procedure preserves the local structures of Fe(II)/Fe(III), mononuclear organic complexes, FeOOH and clays (Björnerås 2019; Herzog et al. 2020). An exception appear to be Fe(II) sulfides, which were not stable to freeze-drying of sediment samples, probably due to oxidation (Björnerås 2019). However, as these soils were well drained, we do not expect Fe(II)-S to be present in our samples.
X-ray diffraction (XRD) spectra were recorded for powdered mineral soil samples using a vertical STOE Stadi MP diffractometer (STOE and Cie GmbH, Germany), using a Cu Kα (λ = 0.154184 nm) radiation source. Data was collected from 2θ = 10–119°, with a step of 0.03° and an acquisition time of 9-14 s. The collected spectra were analyzed in R package `powdR´ (Butler and Hillier 2020), where spectra were fitted to reference spectra from the `rockjock_powdRlib´ mineral library.
Geochemical modelling of Fe speciation in soil solutions
The geochemical equilibrium model Visual MINTEQ ver. 3.1 (Gustafsson 2020) was used to calculate the solution speciation of Fe(III) and saturation indices of possible mineral phases. In the calculations, all major ions measured in the lysimeter solutions were used as input. The model’s default setup was used to account for complexation reactions with dissolved organic matter, i.e. 82.5% of the DOC was assumed to be fulvic acids, being the only organic ligand contributing to metal complexation (Sjöstedt et al. 2013a). The temperature was set to 8 °C in all calculations, which corresponds to the average temperature of the site. Due to missing data for anion concentration from the October 2018 sampling, this sampling occasion was excluded from geochemical modelling.
Statistical analysis
Statistics were performed using RStudio version R 3.4.3 (Kite-Eating Tree). To test the effects of depth on soil variables, a pairwise t-test was run on upper and lower soil samples from the same sampling spot. When comparing forest plots and adjacent control plots and when comparing forest plots of different age, the Welsh’s t-test was used. In cases when the assumption of normality was not fulfilled, the Mann–Whitney–Wilcoxon test was used.
To test for relationships between variables measured in the extracted solution, Partial Least Square (PLS) analysis was performed, with the package “plsdepot”. The number of significant PLS components was determined by cross-validation. The PLS analysis was run on several levels of lysimeter data; (1) all data, (2) data from forested plots, (3) data from control plots, (4) data from shallow lysimeters in forested plots and (5) data from deep lysimeters in forested plots. PLS analysis were performed for each variable measured in the lysimeter solution, for each of the five abovementioned levels (only models for Fe, DOC and pH are presented in this study). To quantify the separate contributions of each variable in explaining the variance in the predicted variable, standard regression coefficients (SRC) are reported. When data for one or more variables in a sample was missing, missing values were imputed using a PCA prediction approach based on the relationships between variables in the whole dataset (Josse and Husson 2016). This was done using packages “missMDA” and “FactoMineR”.
Results
Soil characterization
pH and soil organic matter content
pH was significantly lower in the O-layers of the forested plots than in the underlying mineral soils (p < 0.001), and the pH of the O-layers in the 61- and 90-year old forest were significantly lower than that of the 35-year old forest (p < 0.01; Table 1). When comparing the pH in mineral forest soils and control soils, only the upper (0–10 cm) 90-year old forest soil was significantly lower (p < 0.01) than its corresponding control soil.
The less developed and distinct O-horizon in the 35-year old forest was reflected in its lower soil OM content (measured as LOI), compared to the two older forest stands. Overall, LOI declined with increasing depth and was by far highest in the O-layers of forested soils (Table 1). LOI was also significantly higher in the upper (p < 0.05) and the lower (p < 0.01) mineral soil in the 90-year old forest than in the corresponding control plots. There were no significant differences between the mineral soil layers of 35-year old forest and the corresponding control plots.
Iron extractions
Oxalate extractable Fe (Feox) and dithionite extractable (Fedit) represented 6–10% and 29–82% of Fetot in mineral soils, while Feox represented 9, 4, and 2% and Fedit represented 38, 90, and 74% of Fetot in the 35-, 61- and 90-year old forest O-layers, respectively (Table 1). The high Fetot in the O-layer of the 35-year old forest reflect the incomplete development of this layer and thereby the presence of minerals. Fedit was consistently higher than Feox, but the general patterns when comparing between depths and plots were generally similar for both extractions. Significantly more Fe could be extracted from mineral soil layers than in organic layers of all forested plots (0.001 < p < 0.032; Table 1). Moreover, more Fe could be extracted from lower mineral soils than upper mineral soils in forest plots (p < 0.001), but not in control soils (p = 0.16). There was more extractable Fe in the upper mineral soils of the 35-year old forest than in the adjacent control plots (p = 0.001), while in the 90-year old forest Feox was significantly lower (p < 0.05) than in the adjacent control plot. There was no difference in extractable Fe for the top 10 cm of the 61-year old forest and corresponding control plot (p = 0.54 and p = 0.36). In the lower mineral soil layer (10–25 cm), no significant differences in Feox were observed between forest and control plots (0.051 < p < 0.650). Fedit concentrations were significantly higher in the 35- and 61-year old forest lower mineral layers than in the corresponding control layers (p = 0.019 and p = 0.042), while there was no difference in Fedit between the 90-year old forest and control plots at that depth (p = 0.64). As for the ratio between oxalate and dithionite extractable Fe, as a proxy for crystallinity, no clear differences between forest and control plots were detected.
XAS and XRD analyses of soil
Linear combination fitting of the EXAFS region showed that Fe was present in soils mainly as Fe oxides, 70–93% (ferrihydrite, goethite, hematite), irrespectively of stand age and horizon (Fig. 2, Table S1). Organically complexed Fe represented 7–23% of the Fe in the O-layer and 0–11% in the mineral soil layers. No clear pattern with Fe-OM contribution and stand age could be observed. The amorphous FeOOH, ferrihydrite, represented 24–27% of the Fe in the O-layer and 18–33% in the mineral forest soils. The proportion of non-crystalline Fe (Fe-OM and ferrihydrite) to crystalline Fe (goethite, hematite, biotite) in the O-layer was higher for the 61- and 90- than in the 35-year old forest (Fig. 2). In the upper mineral layer however, the proportion of amorphous Fe was highest in the 35-year old forest. Generally, there were no clear trends in Fe speciation as an effect of stand age or depth. The XRD analysis showed that all mineral soils were highly dominated by quartz (Fig. S1).
Soil solution
Chemistry
Chemistry of the soil solution was highly variable within plots and over time, but some patterns could be discerned (Fig. 3). pH in the soil solution was distinctly lower in the forested than in control plots, for both the shallow (pHcontrol 5.6 ± 0.05; pHforest 4.2 ± 0.04) and deep (pHcontrol 5.6 ± 0.03; pHforest 4.6 ± 0.05) lysimeters. Moreover, pH was consistently lower in the plots with 61- and 90-year old forest than in the 35-year old forest. Thus, across all plots and depths, most of the variation in pH could be attributed to forest stand age where lower pH was explained by increasing age of spruce stands when control plots were considered as 0 years old (SRCall = − 0.68). In forested plots, pH was lower at shallow depth (SRCforest = 0.20), while in the control plots pH was independent of depth (SRCcontrol = − 0.01).
DOC concentrations in shallow lysimeter solution were highest in the 90- and 61-year old forest plots (55 ± 5.4 and 38 ± 5.2 mg/L), while there was little difference between the 35-year old forest and control plots (28 ± 3.2 and 22 ± 2.1 mg/L; Fig. 3). In soil solution from the deeper lysimeters, DOC was still generally highest in the 90-year old forest (24 ± 1.1 mg/L), while concentrations from the 35- and 61-year old forest were not higher than in control plots (9 ± 1.4, 14 ± 1.8 and 15 ± 1.2 mg/L). Across all plots, 72% of the variance in DOC could be explained by the PLS model (Table S2). In forested plots, DOC concentrations increased with stand age (SRCforest = 0.17) and were negatively correlated with depth (SRCforest = − 0.25). In control plots, variation in DOC was not explained by depth (SRCcontrol = − 0.08). The control plots showed seasonal variability, with DOC concentrations being higher in early fall, while forested plots did not exhibit any clear seasonal pattern.
Similarly to DOC, Fe concentrations were highest in lysimeters in the shallow soil of the 90- and 61-year old forest (1.1 ± 0.19 and 0.8 ± 0.07 mg/L respectively), while concentrations in the 35-year old forest (0.29 ± 0.04 mg/L) were similar to those of control plots (0.20 ± 0.02 mg/L; Fig. 3). Fe concentrations in the solution from deeper lysimeters were overall considerably lower (0.12 ± 0.001), and there were no clear differences between forest and control plots. Across all plots and depths, 62% of the variance in Fe concentrations could be explained by the PLS models. DOC explained most of that variation (SRCall = 0.49), while a smaller part was explained by stand age (SRCall = 0.13) and depth (SRCall = − 0.23). Among the forested plots, 67% of the variance in Fe could be explained, with DOC being the strongest correlated (SRCforest = 0.43) along with depth (SRCforest = − 0.24), pH (SRCforest = − 0.19) and stand age (SRCforest = 0.10). In control plots, 77% of the variation in Fe could be explained and was again best correlated with DOC (SRCcontrol = 0.43), positively correlated with pH (SRCcontrol = 0.20) and negatively with depth (SRCcontrol = − 0.12). In the control plots, Fe seemed to follow a similar temporal pattern as DOC, with higher concentrations in early autumn.
Of the other metals, Al concentrations in forested plots were positively correlated with DOC (SRCforest = 0.19) and conductivity (SRCforest = 0.17), while there was a weak correlation with both pH (SRCforest = 0.09) and Fe (SRCforest = 0.10). Al and Fe were positively correlated in the shallow, but negatively in the deep forest soil solution samples (SRCshallow = 0.18; SRCdeep = − 0.23), while Al, like Fe, was positively correlated with DOC at both depths (SRCshallow = 0.20; SRCdeep = 0.39). In the control plots, Al and Fe were positively correlated (SRCcontrol = 0.23). Mn was poorly correlated to both Fe and DOC in all plots and depths (Fig. S2). In the forested plots, Mn was correlated with NO3− (SRCforest = 0.23) and conductivity (SRCforest = 0.13), while in the control plots it was correlated with Al (SRCforest = 0.23) and pH (SRCforest = -0.18). Only a small proportion of variation in Si could be explained for both forest (18%) and control (34%) plots. Si was not correlated with Fe at any of the combination of analysed plots or depths.
Iron speciation in soil water
The strong Fe–Fe scattering detected in soil samples (Table S3, Fig. S3), was absent in soil solution samples, from both control and forest plots. In soil solution samples only Fe–O, Fe–C and Fe–C–O scattering paths contributed to the total EXAFS, indicating a dominance of mononuclear Fe-OM complexes (Fig. 4, Table S4, Fig. S4). That Fe in soil solution was bound to OM as a mononuclear complex was further confirmed by linear combination fitting of the EXAFS region, which showed that Fe(III)-NOM was the only reference spectra aligning with the soil solution samples. The integrated pre-edge centroid position and intensity (Fig. S5), indicated that all the samples were dominated by six-coordinated Fe(III). Geochemical modelling suggest that almost all (95–100%) of the Fe in solution was present in the form of Fe(III) complexed with OM (Table 2), which is in line with results obtained from XAS. In all plots, soil solutions were under-saturated with respect to ferrihydrite and over-saturated with both goethite and hematite.
Discussion
Iron in soil solution
The overarching aim of this study was to understand how mobility of Fe in soils is affected by the age of spruce stands and associated soil process. In line with our hypothesis, we observed higher Fe concentrations in shallow soil solution of older spruce stands—by 5-andd 6-fold under 61- and 90-year old forest respectively—than in arable control plots. Fe concentrations under 35-year old forest did not differ from control plots, suggesting that soil processes that enhance Fe mobilization are linked to the slow and gradual buildup of organic moor layers. Elevated Fe concentrations have previously been found in soil solution under spruce trees, compared to areas without trees but the same ground vegetation in the Taiga (Lukina et al. 2018). Higher Fe concentrations in soil solution under spruce forest compared to grasslands were also reported in Wales, UK (Hughes et al. 1990). While the effect of older forest was clear in soil solutions collected from shallow lysimeters, Fe concentrations in the deeper lysimeters were drastically lower and not affected by the presence of spruce.
Analyses of soil solution chemistry revealed a tight connection between Fe and DOC. Like for Fe, the highest DOC concentrations were found in the soil solution from shallow lysimeters of the older spruce stands, i.e. twofold higher than in corresponding controls, while DOC under 35-year old forest did not deviate from the control. Higher DOC concentrations were widely found in coniferous forest soils than in broadleaved forests (Camino-Serrano et al. 2014; Strobel et al. 2001). This is the result of higher OM accumulation in coniferous and particularly spruce forests soils, especially in surface O-layers (Hagen-Thorn et al. 2004; Hansson et al. 2013). However, the current and previous studies demonstrate that the accumulation of OM in spruce forest soils is slow, meaning that it takes several decades, before they become elevated in DOC, and thereby an increased source of DOC (Cerli et al. 2006; Hagen-Thorn et al. 2004; Rosenqvist et al. 2010b). Despite the tight coupling between Fe and DOC concentrations in the current dataset, Fe concentrations under older spruce stands were much more elevated than DOC concentrations. That the response in Fe was not proportional to DOC, suggests that enhanced mobilization of Fe cannot be solely due to a quantitative change in DOC, but may also link to composition of DOC, chemical factors or biotically mediated processes.
The speciation of Fe in soil solution using XAS confirmed the strong link between Fe and DOC mobilization. Mononuclear Fe-OM complexes dominated in all soil solution samples, and no ferrihydrite or crystalline Fe minerals were detected (Fig. 4, Table S4, Fig. S4). This result was in line with geochemical modelling, predicting ≥ 95% of Fe to be complexed by organic matter and most solutions being under-saturated with respect to amorphous ferrihydrite (Table 2). FTIR data further supports that carboxyl groups, which have been found to be key to complexation of Fe (Karlsson and Persson 2012), were a dominant feature of the dissolved OM in this study (data not shown). The dominance of mononuclear Fe complexes, demonstrated that this is the prevailing structure of Fe translocation from superficial soil layers, and that OM likely controls Fe solubility since organic complexation suppresses the hydrolysis of Fe (Karlsson and Persson 2012).
Dominance of mononuclear Fe complexes and absence of FeOOH in soil solution is also in line with XAS results from a boreal catchment (Sundman et al. (2014) and ATR-FTIR and thermodynamic modelling of soil solution from a temperate spodosol (Bazilevskaya et al. 2018). In lake water however, Sjöstedt et al. (2013b), found a combination of mononuclear Fe(III)-OM complexes and ferrihydrite, as well as hydrated Fe2+. This suggests that Fe(III)-OM complexes are reduced along the aquatic continuum, likely through photochemical reduction (Collienne 1983), and that the resulting Fe(II) can re-oxidize and precipitate as ferrihydrite in lake waters (Helms et al. 2013; Neubauer et al. 2013).
Iron phases in the soil profiles
Observations of higher Fe concentrations with increasing stand age in the shallow, but not in the deeper lysimeters, suggest that upon vertical transport Fe-OM has been adsorbed or precipitated as Fe oxides. XAS analyses revealed significant contributions of both organically complexed Fe and ferrihydrite to the Fe soil pool at all depths, and is in accordance with recent mobilization of Fe followed by either complexation with OM or hydrolysis and precipitation of FeOOH. However, the major pool of secondary Fe in all soil horizons consisted of crystalline phases (goethite and hematite). This was in line with the geochemical modelling results showing that solutions collected from both depths and all plots were supersaturated with respect to goethite and hematite (Table 2). Accordingly, these phases are thermodynamically stable at the conditions prevailing in these soils. Very likely, the more soluble and reactive phases, ferrihydrite and Fe-OM, are being transformed to these crystalline phases with time. This process however, is significantly slowed down by the presence of OM, which, together with pH also determines the type of newly formed Fe minerals in soil (Colombo et al. 2015; Cornell and Schwertmann 1979; Pédrot et al. 2011). The main constituents of the soil Fe pool in this study (mononuclear Fe(III)-OM complexes, ferrihydrite, goethite, hematite and biotite) conformed with findings from previous studies that probed boreal soils with high organic content (Karlsson et al. 2008; Sundman et al. 2014).
Due to weathering of primary minerals there will be a continuous supply of Fe to the more reactive pools. The translocation of Fe in the soil profile upon plantation of spruce is indicated by the fact that extractable Fe was elevated in the lower compared to the upper mineral layers of forest plots, but not of control plots. This is also in line with other studies showing that concentrations of extractable Fe in mineral soils were higher decades after reforestation with coniferous forest, than when the land remained cultivated for agriculture (Li and Richter 2012; Li et al. 2008). In the present study, differences in Fe characteristics in the soil matrix were much less pronounced than differences in soil solution Fe concentrations, reflecting the slow turnover of much of the Fe in the soil.
What we observed in the soils below older forest stands may well be early signs of podsolization, where Fe is mobilized and translocated by organic acids downward in the soil horizon. In the lower mineral soil, microbial degradation of organic compounds results in higher Fe:OC ratios and subsequent adsorption of Fe-OM on mineral surfaces or precipitation of Fe as ferrihydrite (Lundström et al. 1995; Lundström et al. 2000a; Lundström et al. 2000b). Podzol formation is a slow process, which takes hundreds of years depending on climate, soil conditions and former land-use (reviewed in Lundström et al. (2000a)), but is accelerated in soils under spruce forest, owing to the higher accumulation of OM (Sohet et al. 1988). In this study, the oldest soils have only had 90 years to develop under spruce forest, which was likely the reason that we did not observe any clear changes in mineral soil Fe speciation as an effect of stand age.
Mobilization of Fe from soils
While we could demonstrate that organic complexation is controlling translocation, these results do not reveal the mechanism that provides soluble Fe to a larger extent in soil under older spruce forest. In theory, higher Fe concentrations may originate from the higher deposition of Fe-containing litter. A simplified mass balance calculation (Eq. 1), where input of Fe from litter deposition (Felitter; 30.8 mg m−2 year−1 for ~ 60-year old Norway spruce forest in Tönnersjöheden (Hansson et al. 2011)) was compared to Fe concentration in soil solution of the 61-year old stand from this study ([Fe]; 0.84 mg L−1) and modelled annual water recharge (i.e., water leaching flux) for 65–92 year old spruce forest at the site (Q; 468 L m−2 year−1, Rosenqvist et al. (2010a)), indicate that only 8% of the Fe leached from the upper soils layers can be sustained by Fe originating from the annual litter fall.
Although this is a simplified flux calculation, it does imply that there need to be other sources of Fe to sustain the high Fe flux in soil solution leaving the topsoil in the older spruce stands. It is therefore likely that a significant fraction of the Fe found in soil solution originates from soil minerals. The mobilization of Fe from mineral phases may be driven by weathering in the top soil, but may also take place in lower parts of the soil and be transported to more shallow soil layers by roots or mycelia.
Mobilization of Fe to soil solution depends on dissolution rates of mineral Fe phases and Fe solubility in soil solution. Dissolution of Fe is governed by three main processes; proton promoted dissolution, reduction and ligand promoted dissolution, with the rates of these processes being controlled by pH, redox potential and OM (Schwertmann 1991). For soils dominated by FeOOH, like in this study, solubility increases with lower pH in soil solution (Tyler and Olsson 2001). pH was lower in the soil solution below older forest stands, which will enhance proton-promoted dissolution and the solubility of Fe. However, the relatively weak correlation between Fe and pH indicates that pH was likely not the most important factor promoting Fe mobilization. Moreover, thermodynamic modelling suggests that the effect of lowering pH (from 5 to 4) at a similar DOC concentration would enhance solubility by less than 50%, and thus could not alone explain the observed (fivefold- and sixfold) increase in Fe concentration under older forest stands.
Another Fe mobilization pathway is through reductive dissolution of mineral Fe phases in low oxygen environments, where Fe(III) is the preferred electron acceptor for microbial respiration (Schwab and Lindsay 1983; Weber et al. 2006). Reducing conditions have been proposed as important for mobilization of Fe from catchment soils to surface waters (Ekstrom et al. 2016; Knorr 2013; Sarkkola et al. 2013). In the riparian zone of a boreal stream, Fe(II) was found in Fe-OM complexes (Sundman et al. 2014), which indicates reductive mobilization in periodically waterlogged soils. However, while reducing conditions may exist in micro-environments in the well-drained soils of this experiment, they are unlikely to be prevalent enough to be the major driver of Fe mobilization. The fact that Fe(III) was the prevailing redox state is in line with predominantly oxidizing conditions. Nevertheless, it is possible that Fe was reductively dissolved and that Fe(II) was oxidized and stabilized by OM complexation.
Organic molecules which promote dissolution of mineral forms of Fe can be a byproduct of OM decomposition, or can be actively excreted by plants and microorganisms to mobilize Fe (Jones et al. 1996; Robinson et al. 1999; Schmidt 1999) or phosphorus from mineral surfaces (Johnson and Loeppert 2006). Low molecular weight organic acids, excreted by mycorrhiza, are indicated to contribute to mineral weathering and Fe complexation in podzolized soils (Lundström et al. 2000b). While dissolutions of crystalline Fe minerals in the presence of organic acids such as oxalate, malate and citrate has been suggested to be rather slow (Reichard et al. 2007), the rate of dissolution may be underestimated due to reabsorption of organic acid-Fe complexes onto mineral surfaces (Loring et al. 2008). Mineral Fe dissolution rates drastically increase in the presence of siderophores, produced by plants or microorganism, which complex labile Fe and remove it from the mineral surface, allowing for new labile Fe formation and recycling of organic acids (Reichard et al. 2007). In addition, Fe has been found to be reduced or oxidized by microorganisms, to produce reactive oxygen radicals that can help degrade complex OM such as lignin and proteins (Goodell et al. 2006; Op De Beeck et al. 2018). Some fungi also secrete extracellular metabolites that reduce FeOOH, producing Fe2+, which then acts as a reagent in the Fenton reaction (Fe2+ + H2O2 + H+ → Fe3+ + ⋅OH + H2O), producing highly reactive hydroxyl radicals (⋅OH) that drive lignocellulose or protein decay (Krumina et al. 2017; Op De Beeck et al. 2018; Zhu et al. 2016). These reactions have been shown to be favored at low pH (3–4) and are mostly present in brown-rot fungi but are also utilized by some ectomycorrhizal fungi (Lindahl and Tunlid 2015), such as Paxillus involutus a common Norway spruce symbiont (Pignatello et al. 2006; Shah et al. 2015). It has been found that as forest stands age, less C is allocated to ectomycorrhizal fungi, at the same time as soil C:N ratios increase (Wallander et al. 2010). This leads to a succession in the fungal community, where the abundance in fungi capable of mobilizing nutrients (N, P) from complex organic matter increases (Kyaschenko et al. 2017). One could therefore expect that in older forest stands, fungi produce more reducing extracellular metabolites, in order to access nutrients in the more complex OM sources, which in turn could lead to higher Fe mobilization. Although the potential of fungi induced Fenton reactions in mobilizing soil Fe have not been studied in natural environments, Björnerås et al. (2019) suggested that they could partially explain mobilization of Fe from organic spruce forest soils in a microcosm experiment.
Afforestation influences export of Fe and DOC both by regulating biogeochemical processes in soils, as discussed above, and by altering hydrology (Bowering et al. 2020). The water fluxes to and through the soils differ with e.g. stand age, tree density and understory vegetation (Rosenqvist et al. 2010a). A recent study demonstrated that despite lower soil organic carbon stocks, the flux of DOC from a harvested forest plot was higher than that from an 80-year old spruce stand, since the water flux through the soil was so much larger (Bowering et al. 2020). Coniferous afforestation increases interception and evapotranspiration, with a subsequent reduction in soil water flux that is most pronounced for young stands (Rosenqvist et al. 2010a). For the specific area studied here, modelled water leaching flux was lower in 30–40 years old spruce stands, than in older stands (> 60 years, Rosenqvist et al. (2010a)). Thus, differences in Fe and DOC fluxes between the young and old stands of this study were probably larger than the difference in concentration. Regional budgets of Fe and DOC fluxes need to consider that both biogeochemical and hydrological processes are regulated by land cover.
Conclusions and implications
The higher soil Fe mobilization under older stands of Norway spruce, which we show here, is in line with previous suggestions that trends of increasing Fe concentrations and water color in surface waters are at least partly linked to afforestation (Björnerås 2019; Škerlep et al. 2020). It also corresponds with the finding that long-term increases of Fe concentrations are more frequently found in catchments with high coniferous vegetation cover (Björnerås et al. 2017). Since vertical flow of soil solution results in precipitation and/or adsorption of Fe, lateral flow is a more likely route for the organically complexed Fe to reach surface waters. Hydrology exerts a primary control on site specific fluxes of Fe and DOM and also on which parts of the catchment that are hydrologically connected, with forested surface soil layers being the dominant source of Fe and DOM at high flow and wetlands dominating at low flow in boreal catchments (Bjorkvald et al. 2008; Laudon et al. 2011). Previous studies show that the contribution of organically complexed Fe in boreal running waters is elevated during high flow conditions and closer to the terrestrial source, i.e. lower order streams (Herzog et al. 2019, 2020). At the terrestrial-aquatic interface of forested catchments, riparian zones with high OM content have a strong influence on stream water chemistry (Ledesma et al. 2018; McClain et al. 2003), and soil solution in riparian zones is highly enriched in Fe compared to upland soils (Lidman et al. 2017). Furthermore, topographical depressions in the landscape create hydrological focal points—discrete riparian inflow points (DRIPs)—that can have a disproportionally high influence on stream water chemistry (Ploum et al. 2020). When predicting the effects of land-use on exports of Fe to surface waters it is therefore important to consider hydrological connectivity, as well as Fe mobilization. Continued forestry intensification and aging of spruce forest may lead to further increase in surface water Fe concentrations and browning of freshwaters.
Data availability
Additional data is presented as online Supplementary information. The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Augusto L, Turpault M-P, Ranger J (2000) Impact of forest tree species on feldspar weathering rates. Geoderma 96(3):215–237
Bauer M, Blodau C (2006) Mobilization of arsenic by dissolved organic matter from iron oxides, soils and sediments. Sci Total Environ 354(2–3):179–190
Bazilevskaya E, Archibald DD, Martínez CE (2018) Mineral colloids mediate organic carbon accumulation in a temperate forest Spodosol: depth-wise changes in pore water chemistry. Biogeochemistry 141(1):75–94
Bhattacharyya A, Schmidt MP, Stavitski E, Azimzadeh B, Martínez CE (2019) Ligands representing important functional groups of natural organic matter facilitate Fe redox transformations and resulting binding environments. Geochim Cosmochim Acta 251:157–175
Bjorkvald L, Buffam I, Laudon H, Morth CM (2008) Hydrogeochemistry of Fe and Mn in small boreal streams: the role of seasonality, landscape type and scale. Geochim Cosmochim Acta 72(12):2789–2804
Björnerås C, Weyhenmeyer GA, Evans CD, Gessner MO, Grossart HP, Kangur K, Kokorite I, Kortelainen P, Laudon H, Lehtoranta J, Lottig N, Monteith DT, Nõges P, Nõges T, Oulehle F, Riise G, Rusak JA, Räike A, Sire J, Sterling S, Kritzberg ES (2017) Widespread increases in iron concentration in European and North American freshwaters. Glob Biogeochem Cycles 31(10):1488–1500
Björnerås C, Škerlep M, Floudas D, Persson P, Kritzberg ES (2019) High sulfate concentration enhances iron mobilization from organic soil to water. Biogeochemistry 144(3):245–259
Björnerås C (2019) Drivers of increasing iron concentrations in freshwaters. In. Lund University
Bowering KL, Edwards KA, Prestegaard K, Zhu X, Ziegler SE (2020) Dissolved organic carbon mobilized from organic horizons of mature and harvested black spruce plots in a mesic boreal region. Biogeosciences 17(3):581–595
Butler BM, Hillier S (2020) powdR: an R package for quantitative mineralogy using full pattern summation of X-ray powder diffraction data. Comput Geosci 147:104662
Camino-Serrano M, Gielen B, Luyssaert S, Ciais P, Vicca S, Guenet B, Vos BD, Cools N, Ahrens B, Altaf Arain M, Borken W, Clarke N, Clarkson B, Cummins T, Don A, Pannatier EG, Laudon H, Moore T, Nieminen TM, Nilsson MB, Peichl M, Schwendenmann L, Siemens J, Janssens I (2014) Linking variability in soil solution dissolved organic carbon to climate, soil type, and vegetation type. Glob Biogeochem Cycles 28(5):497–509
Catrouillet C, Davranche M, Dia A, Bouhnik-Le Coz M, Marsac R, Pourret O, Gruau G (2014) Geochemical modeling of Fe (II) binding to humic and fulvic acids. Chem Geol 372:109–118
Cerli C, Celi L, Johansson M-B, Kogel-Knabner I, Rosenqvist L, Zanini E (2006) Soil organic matter changes in a spruce chronosequence on Swedish former agricultural soil: I. Carbon and lignin dynamics. Soil Sci 171(11):837–849
Collienne R (1983) Photoreduction of iron in the epilimnion of acidic lakes. Limnol Oceanogr 28(1):83–100
Colombo C, Palumbo G, Sellitto VM, Cho HG, Amalfitano C, Adamo P (2015) Stability of coprecipitated natural humic acid and ferrous iron under oxidative conditions. J Geochem Explor 151:50–56
Cornell R, Schwertmann U (1979) Influence of organic anions on the crystallization of ferrihydrite. Clays Clay Miner 27(6):402–410
Creed IF, Bergstrom AK, Trick CG, Grimm NB, Hessen DO, Karlsson J, Kidd KA, Kritzberg E, McKnight DM, Freeman EC, Senar OE, Andersson A, Ask J, Berggren M, Cherif M, Giesler R, Hotchkiss ER, Kortelainen P, Palta MM, Vrede T, Weyhenmeyer GA (2018) Global change-driven effects on dissolved organic matter composition: Implications for food webs of northern lakes. Glob Change Biol 24(8):3692–3714
Cummings DE, Caccavo F, Fendorf S, Rosenzweig RF (1999) Arsenic mobilization by the dissimilatory Fe (III)-reducing bacterium Shewanella alga BrY. Environ Sci Technol 33(5):723–729
de Wit HA, Valinia S, Weyhenmeyer GA, Futter MN, Kortelainen P, Austnes K, Hessen DO, Räike A, Laudon H, Vuorenmaa J (2016) Current browning of surface waters will be further promoted by wetter climate. Environ Sci Technol Lett 3(12):430–435
Ekstrom SM, Regnell O, Reader HE, Nilsson PA, Lofgren S, Kritzberg ES (2016) Increasing concentrations of iron in surface waters as a consequence of reducing conditions in the catchment area. J Geophys Res-Biogeosci 121(2):479–493
Erlandsson M, Buffam I, Folster J, Laudon H, Temnerud J, Weyhenmeyer GA, Bishop K (2008) Thirty-five years of synchrony in the organic matter concentrations of Swedish rivers explained by variation in flow and sulphate. Glob Change Biol 14(5):1191–1198
Finstad AG, Andersen T, Larsen S, Tominaga K, Blumentrath S, de Wit HA, Tommervik H, Hessen DO (2016) From greening to browning: catchment vegetation development and reduced S-deposition promote organic carbon load on decadal time scales in Nordic lakes. Sci Rep 6:31944
Fredh D, Brostrom A, Zillen L, Mazier F, Rundgren M, Lageras P (2012) Floristic diversity in the transition from traditional to modern land-use in southern Sweden AD 1800–2008. Veg Hist Archaeobot 21(6):439–452
Fuchs R, Herold M, Verburg PH, Clevers JGPW (2013) A high-resolution and harmonized model approach for reconstructing and analysing historic land changes in Europe. Biogeosciences 10(3):1543–1559
George GN (2000) http://ssrl.slac.stanford.edu/exafpak.html
Goodell B, Daniel G, Jellison J, Qian Y (2006) Iron-reducing capacity of low-molecular-weight compounds produced in wood by fungi. Holzforschung 60(6):630–636
Gustafsson J (2020) Visual MINTEQ, version 3.1. KTH, Stockholm
Hagen-Thorn A, Callesen I, Armolaitis K, Nihlgård B (2004) The impact of six European tree species on the chemistry of mineral topsoil in forest plantations on former agricultural land. For Ecol Manag 195(3):373–384
Hansson K, Olsson BA, Olsson M, Johansson U, Kleja DB (2011) Differences in soil properties in adjacent stands of Scots pine, Norway spruce and silver birch in SW Sweden. For Ecol Manag 262(3):522–530
Hansson K, Froberg M, Helmisaari HS, Kleja DB, Olsson BA, Olsson M, Persson T (2013) Carbon and nitrogen pools and fluxes above and below ground in spruce, pine and birch stands in southern Sweden. For Ecol Manag 309:28–35
Helms JR, Mao J, Schmidt-Rohr K, Abdulla H, Mopper K (2013) Photochemical flocculation of terrestrial dissolved organic matter and iron. Geochim Cosmochim Acta 121:398–413
Herzog SD, Conrad S, Ingri J, Persson P, Kritzberg ES (2019) Spring flood induced shifts in Fe speciation and fate at increased salinity. Appl Geochem 109:104385
Herzog SD, Persson P, Kvashnina K, Kritzberg ES (2020) Organic iron complexes enhance iron transport capacity along estuarine salinity gradients of Baltic estuaries. Biogeosciences 17(2):331–344
Hughes S, Reynolds B, Roberts J (1990) The influence of land management on concentrations of dissolved organic carbon and its effects on the mobilization of aluminium and iron in podzol soils in Mid-Wales. Soil Use Manag 6(3):137–145
ISO 12782-2:2012 Swedish Institute for Standards (2012) Soil quality - Parameters for geohemical modelling of leaching and speciation of constituents in soils and materials - Part 2: Extraction of Crystalline iron oxides and hydroxides with dithionite (ISO 12782-2:2012). Stockholm, Sweden
Johnson SE, Loeppert RH (2006) Role of organic acids in phosphate mobilization from iron oxide. Soil Sci Soc Am J 70(1):222–234
Jones RI, Shaw PJ, De Haan H (1993) Effects of dissolved humic substances on the speciation of iron and phosphate at different pH and ionic strength. Environ Sci Technol 27(6):1052–1059
Jones DL, Darah PR, Kochian LV (1996) Critical evaluation of organic acid mediated iron dissolution in the rhizosphere and its potential role in root iron uptake. Plant Soil 180(1):57–66
Josse J, Husson F (2016) missMDA: a package for handling missing values in multivariate data analysis. J Stat Softw 70(1):1–31
Karlsson T, Persson P (2012) Complexes with aquatic organic matter suppress hydrolysis and precipitation of Fe (III). Chem Geol 322:19–27
Karlsson T, Persson P, Skyllberg U, Mörth C-M, Giesler R (2008) Characterization of iron (III) in organic soils using extended X-ray absorption fine structure spectroscopy. Environ Sci Technol 42(15):5449–5454
Klementiev K (2001) VIPER for windows. J Phys D Appl Phys 34(2):209–217
Knorr KH (2013) DOC-dynamics in a small headwater catchment as driven by redox fluctuations and hydrological flow paths: are DOC exports mediated by iron reduction/oxidation cycles? Biogeosciences 10(2):891–904
Kritzberg ES (2017) Centennial-long trends of lake browning show major effect of afforestation. Limnol Oceanogr Lett 2(4):105–112
Kritzberg ES, Ekstrom SM (2012) Increasing iron concentrations in surface waters: a factor behind brownification? Biogeosciences 9(4):1465–1478
Krumina L, Lyngsie G, Tunlid A, Persson P (2017) Oxidation of a dimethoxyhydroquinone by ferrihydrite and goethite nanoparticles: iron reduction versus surface catalysis. Environ Sci Technol 51(16):9053–9061
Kyaschenko J, Clemmensen KE, Hagenbo A, Karltun E, Lindahl BD (2017) Shift in fungal communities and associated enzyme activities along an age gradient of managed Pinus sylvestris stands. ISME J 11(4):863–874
Lalonde K, Mucci A, Ouellet A, Gelinas Y (2012) Preservation of organic matter in sediments promoted by iron. Nature 483(7388):198–200
Laudon H, Berggren M, Agren A, Buffam I, Bishop K, Grabs T, Jansson M, Kohler S (2011) Patterns and dynamics of dissolved organic carbon (DOC) in boreal streams: the role of processes, connectivity, and scaling. Ecosystems 14(6):880–893
Ledesma JL, Futter MN, Blackburn M, Lidman F, Grabs T, Sponseller RA, Laudon H, Bishop KH, Köhler SJ (2018) Towards an improved conceptualization of riparian zones in boreal forest headwaters. Ecosystems 21(2):297–315
Li J, Richter DD (2012) Effects of two-century land use changes on soil iron crystallinity and accumulation in Southeastern Piedmont region, USA. Geoderma 173–174:184–191
Li J, Richter Dd, Mendoza A, Heine P (2008) Four-decade responses of soil trace elements to an aggrading old-field forest: B, Mn, Zn, Cu, and Fe. Ecology 89(10):2911–2923
Lidman F, Boily Å, Laudon H, Köhler SJ (2017) From soil water to surface water: how the riparian zone controls element transport from a boreal forest to a stream. Biogeosciences 14(12):3001–3014
Lindahl BD, Tunlid A (2015) Ectomycorrhizal fungi–potential organic matter decomposers, yet not saprotrophs. New Phytol 205(4):1443–1447
Lindbladh M, Axelsson A-L, Hultberg T, Brunet J, Felton A (2014) From broadleaves to spruce: the borealization of southern Sweden. Scand J for Res 29(7):686–696
Lindsay W, Sadiq M (1983) Use of pe+ pH to predict and interpret metal solubility relationships in soils. Sci Total Environ 28(1–3):169–178
Lindsay W, Schwab A (1982) The chemistry of iron in soils and its availability to plants. J Plant Nutr 5(4–7):821–840
Loring JS, Simanova AA, Persson P (2008) Highly mobile iron pool from a dissolution: readsorption process. Langmuir 24(14):7054–7057
Lukina N, Ershov V, Gorbacheva T, Orlova M, Isaeva L, Teben’kova D (2018) Assessment of soil water composition in the northern taiga coniferous forests of background territories in the industrially developed region. Eurasian Soil Sci 51(3):277–289
Lundström U, Van Breemen N, Jongmans A (1995) Evidence for microbial decomposition of organic acids during podzolization. Eur J Soil Sci 46(4):489–496
Lundström US, van Breemen N, Bain D (2000) The podzolization process: a review. Geoderma 94(2–4):91–107
Matilainen A, Vepsalainen M, Sillanpaa M (2010) Natural organic matter removal by coagulation during drinking water treatment: a review. Adv Colloid Interface 159(2):189–197
McClain ME, Boyer EW, Dent CL, Gergel SE, Grimm NB, Groffman PM, Hart SC, Harvey JW, Johnston CA, Mayorga E (2003) Biogeochemical hot spots and hot moments at the interface of terrestrial and aquatic ecosystems. Ecosystems 6:301–312
McKeague J, Day J (1966) Dithionite-and oxalate-extractable Fe and Al as aids in differentiating various classes of soils. Can J Soil Sci 46(1):13–22
Mudroch A, Clair T (1986) Transport of arsenic and mercury from gold mining activities through an aquatic system. Sci Total Environ 57:205–216
Neal C, Lofts S, Evans C, Reynolds B, Tipping E, Neal M (2008) Increasing iron concentrations in UK upland waters. Aquat Geochem 14(3):263–288
Neubauer E, Köhler SJ, von der Kammer F, Laudon H, Hofmann T (2013) Effect of pH and stream order on iron and arsenic speciation in boreal catchments. Environ Sci Technol 47(13):7120–7128
Op De Beeck M, Troein C, Peterson C, Persson P, Tunlid A (2018) Fenton reaction facilitates organic nitrogen acquisition by an ectomycorrhizal fungus. New Phytol 218(1):335–343
Pédrot M, Le Boudec A, Davranche M, Dia A, Henin O (2011) How does organic matter constrain the nature, size and availability of Fe nanoparticles for biological reduction? J Colloid Interface Sci 359(1):75–85
Persson P, Axe K (2005) Adsorption of oxalate and malonate at the water-goethite interface: molecular surface speciation from IR spectroscopy. Geochim Cosmochim Acta 69(3):541–552
Pignatello JJ, Oliveros E, MacKay A (2006) Advanced oxidation processes for organic contaminant destruction based on the Fenton reaction and related chemistry. Crit Rev Environ Sci Technol 36(1):1–84
Ploum S, Laudon H, Tapia AP, Kuglerová L (2020) Are dissolved organic carbon concentrations in riparian groundwater linked to hydrological pathways in the boreal forest? Hydrol Earth Syst Sci 24:1709
Reichard P, Kretzschmar R, Kraemer SM (2007) Dissolution mechanisms of goethite in the presence of siderophores and organic acids. Geochim Cosmochim Acta 71(23):5635–5650
Robinson NJ, Procter CM, Connolly EL, Guerinot ML (1999) A ferric-chelate reductase for iron uptake from soils. Nature 397(6721):694–697
Rosenqvist L, Hansen K, Vesterdal L, van der Salm C (2010a) Water balance in afforestation chronosequences of common oak and Norway spruce on former arable land in Denmark and southern Sweden. Agric for Meteorol 150(2):196–207
Rosenqvist L, Kleja DB, Johansson M-B (2010b) Concentrations and fluxes of dissolved organic carbon and nitrogen in a Picea abies chronosequence on former arable land in Sweden. For Ecol Manag 259(3):275–285
Sarkkola S, Nieminen M, Koivusalo H, Lauren A, Kortelainen P, Mattsson T, Palviainen M, Piirainen S, Starr M, Finer L (2013) Iron concentrations are increasing in surface waters from forested headwater catchments in eastern Finland. Sci Total Environ 463–464:683–689
Schmidt W (1999) Mechanisms and regulation of reduction-based iron uptake in plants. New Phytol 141(1):1–26
Schwab A, Lindsay W (1983) Effect of redox on the solubility and availability of iron. Soil Sci Soc Am J 47(2):201–205
Schwertmann U (1991) Solubility and dissolution of iron oxides. Plant Soil 130(1–2):1–25
Shah F, Schwenk D, Nicolás C, Persson P, Hoffmeister D, Tunlid A (2015) Involutin is an Fe3+ reductant secreted by the ectomycorrhizal fungus Paxillus involutus during Fenton-based decomposition of organic matter. Appl Environ Microb 81(24):8427–8433
Sjöstedt C, Andrén C, Fölster J, Gustafsson JP (2013a) Modelling of pH and inorganic aluminium after termination of liming in 3000 Swedish lakes. Appl Geochem 35:221–229
Sjöstedt C, Persson I, Hesterberg D, Kleja DB, Borg H, Gustafsson JP (2013b) Iron speciation in soft-water lakes and soils as determined by EXAFS spectroscopy and geochemical modelling. Geochim Cosmochim Acta 105:172–186
Škerlep M, Steiner E, Axelsson AL, Kritzberg ES (2020) Afforestation driving long-term surface water browning. Glob Change Biol 26(3):1390–1399
Sohet K, Herbauts J, Gruber W (1988) Changes caused by Norway spruce in an ochreous brown earth, assessed by the isoquartz method. J Soil Sci 39(4):549–561
Solomon CT, Jones SE, Weidel BC, Buffam I, Fork ML, Karlsson J, Larsen S, Lennon JT, Read JS, Sadro S, Saros JE (2015) Ecosystem consequences of changing inputs of terrestrial dissolved organic matter to lakes: current knowledge and future challenges. Ecosystems 18(3):376–389
Strobel BW, Hansen HCB, Borggaard OK, Andersen MK, Raulund-Rasmussen K (2001) Composition and reactivity of DOC in forest floor soil solutions in relation to tree species and soil type. Biogeochemistry 56(1):1–26
Sundman A, Karlsson T, Laudon H, Persson P (2014) XAS study of iron speciation in soils and waters from a boreal catchment. Chem Geol 364:93–102
Sundman A, Karlsson T, Sjöberg S, Persson P (2016) Impact of iron–organic matter complexes on aqueous phosphate concentrations. Chem Geol 426:109–117
Suter D, Banwart S, Stumm W (1991) Dissolution of hydrous iron (III) oxides by reductive mechanisms. Langmuir 7(4):809–813
Szytuła A, Burewicz A, Dimitrijević Ž, Kraśnicki S, Rżany H, Todorović J, Wanic A, Wolski W (1968) Neutron diffraction studies of α-FeOOH. Physica Status Solidi (b) 26(2):429–434
Theis TL, Singer PC (1974) Complexation of iron (II) by organic matter and its effect on iron (II) oxygenation. Environ Sci Technol 8(6):569–573
Tranvik LJ, Downing JA, Cotner JB, Loiselle SA, Striegl RG, Ballatore TJ, Dillon P, Finlay K, Fortino K, Knoll LB, Kortelainen PL, Kutser T, Larsen S, Laurion I, Leech DM, McCallister SL, McKnight DM, Melack JM, Overholt E, Porter JA, Prairie Y, Renwick WH, Roland F, Sherman BS, Schindler DW, Sobek S, Tremblay A, Vanni MJ, Verschoor AM, von Wachenfeldt E, Weyhenmeyer GA (2009) Lakes and reservoirs as regulators of carbon cycling and climate. Limnol Oceanogr 54(6):2298–2314
Tyler G, Olsson T (2001) Concentrations of 60 elements in the soil solution as related to the soil acidity. Eur J Soil Sci 52(1):151–165
Uv L, Van Breemen N, Bain D, Van Hees P, Giesler R, Gustafsson JP, Ilvesniemi H, Karltun E, Melkerud P-A, Olsson M (2000) Advances in understanding the podzolization process resulting from a multidisciplinary study of three coniferous forest soils in the Nordic Countries. Geoderma 94(2–4):335–353
Wagai R, Mayer LM (2007) Sorptive stabilization of organic matter in soils by hydrous iron oxides. Geochim Cosmochim Acta 71(1):25–35
Wallander H, Johansson U, Sterkenburg E, Brandström Durling M, Lindahl BD (2010) Production of ectomycorrhizal mycelium peaks during canopy closure in Norway spruce forests. New Phytol 187(4):1124–1134
Weber KA, Achenbach LA, Coates JD (2006) Microorganisms pumping iron: anaerobic microbial iron oxidation and reduction. Nat Rev Microbiol 4(10):752–764
Wilke M, Farges F, Petit P-E, Brown GE Jr, Martin F (2001) Oxidation state and coordination of Fe in minerals: an Fe K-XANES spectroscopic study. Am Miner 86(5–6):714–730
Wojdyr M (2010) Fityk: a general-purpose peak fitting program. J Appl Crystallogr 43(5–1):1126–1128
Zabinsky S, Rehr J, Ankudinov A, Albers R, Eller M (1995) FEFF code for ab initio calculations of XAFS. Phys Rev B 52(4):2995–3009
Zhu Y, Zhuang L, Goodell B, Cao J, Mahaney J (2016) Iron sequestration in brown-rot fungi by oxalate and the production of reactive oxygen species (ROS). Int Biodeter Biodegrad 109:185–190
Acknowledgements
We would like to thank Dimitrios Floudas, for critical inputs on the manuscript. We would also like to acknowledge The Swedish Research Council Formas, The Royal Physiographic Society, Kungl. Skogs- och Lantbruksakademien for providing funds for the project. Synchrotron work was conducted at beamline line 4‐1 at the Stanford Synchrotron Radiation Lightsource (SSRL), California, USA. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract DE‐AC02‐76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research and by the National Institutes of Health, National Institute of General Medical Sciences (including P41GM103393). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIGMS or NIH. Author contributions
All authors contributed to the study conception and design. All authors at different parts of the research process performed material preparation, data collection and/or analysis. MŠ and ESK wrote the first draft of the manuscript and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Funding
Open access funding provided by Lund University. The Swedish Research Council; Grant Number: 2015‐01407; 2019-00889. Royal Physiographic Society; Grant Number: 38794. Kungl. Skogs- och Lantbruksakademien; Grant Number: GFS2017-0077.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of competing interests to report.
Additional information
Responsible Editor: Susan Ziegler.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Škerlep, M., Nehzati, S., Johansson, U. et al. Spruce forest afforestation leading to increased Fe mobilization from soils. Biogeochemistry 157, 273–290 (2022). https://doi.org/10.1007/s10533-021-00874-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10533-021-00874-9