Abstract
We constructed nitrogen (N) budgets for the lawns of three simulated residences built to test the environmental impacts of three different residential landscape designs in southern California. The three designs included: a “Typical” lawn planted with cool season tall fescue (Schedonorus phoenix), fertilized at the recommended rate for this species (192 kg−1 ha−1 year−1) and irrigated with an automatic timer; a design intended to lower N and water requirements (“Low Input”) with the warm season seashore paspalum (Paspalum vaginatum) fertilized at 123 kg−1 ha−1 year−1 and irrigated with a soil moisture-based system; and a design incorporating local best practices (“Low Impact” lawn) that included the native sedge species Carex, fertilized at 48 kg−1 ha−1 year−1 and irrigated by a weather station-based system. Plant N uptake accounted for 33.2 ± 0.5 (tall fescue), 53.7 ± 0.7 (seashore paspalum), and 12.2 ± 1.3 % (Carex) of annual N inputs, while estimated N retention in soil was relatively large and similar in the three lawns (41–46 %). At lower N and water inputs than Typical, Low Input showed the highest annual clipping yield and N uptake, although it also had higher denitrification rates. Leaching inorganic N losses remained low even from the Typical lawn (2 %), while gaseous N losses were highly variable. The Low Input lawn was most efficient in retaining N with relatively low water and N costs, although its fertilization rates could be further reduced to lower gaseous N losses. Our results suggest that the choice of a warm-season, C4 turf species with reduced rates of irrigation and fertilization is effective in this semi-arid region to maintain high productivity and N retention in plants and soils at low N and water inputs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
N biogeochemistry of urban ecosystems has likely been greatly altered by intensive inputs of reactive N from fossil fuel burning and N fertilizer application (Galloway et al. 2003). However, urban ecosystems are less studied and relatively poorly understood compared to natural ecosystems. Urban lawns, which are usually heavily fertilized (Law et al. 2004), are an important component of urban landscapes and are estimated to occupy 1.9 % of the total area of the U.S and 40–60 % of the area estimated to be under urban development (Milesi et al. 2005). Management practices can strongly affect plant and soil N dynamics in urban lawns. As urban areas continue to expand, there is a great need for datasets that can be used to develop and test theories about N biogeochemistry of managed lawns within urban ecosystems.
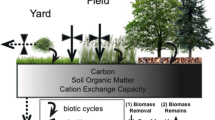
Relieved from limitations of N and water and not as regularly tilled as croplands, urban lawns can accumulate soil organic carbon (SOC) and N at similar or even greater rates than natural grasslands and forests (Huh et al. 2008; Qian and Follett 2002; Pataki et al. 2006; Pouyat et al. 2003, 2006; Raciti et al. 2011a). Therefore, it is important to study the N biogeochemistry of fertilized urban lawns within the context of global change. 15N-tracer studies have shown that mineral soil and plant biomass are usually the primary sinks for fertilizer N in lawns (Engelsjord et al. 2004; Frank et al. 2006; Horgan et al. 2002a, b; Raciti et al. 2008). Raciti et al. (2008) and Frank et al. (2006) similarly reported a peak recovery of 15N-labeled fertilizer in plant biomass within a short period (days), while soils dominated the long-term 15N recovery (≥1 year) in urban lawns. However, a large portion of 15N could remain in clipping biomass, if such clippings were removed from the lawns instead of being left on site (Engelsjord et al. 2004; Horgan et al. 2002a, b).
Fertilizer N that exceeds plant needs and soil capacity may leave lawns in various ways, while the potential of high N losses in response to over-fertilization may increase with lawn age (Frank et al. 2006). Excessive N inputs to lawns may enter groundwater as ammonium (NH4 +) and nitrate (NO3 −, Jiao et al. 2004; Petrovic 1990) through leaching, causing threats to public health (Scanlon et al. 2007), or enter the atmosphere through ammonia (NH3) volatilization (Torello et al. 1983) and emissions of nitrous oxide (N2O) and nitrogen monoxide (NO) in nitrification and denitrification (Bouwman et al. 2002; Clayton et al. 1997; Eichner 1990; Firestone and Davison 1989; Townsend-Small et al. 2011). Kaye et al. (2004) showed that urban lawns occupied 6.4 % of their study region of urban soils (including urban impervious, urban lawns, agricultural land, and native grassland) but contributed 30 % of the regional emissions of N2O, which is a powerful greenhouse gas (IPCC 2001).
Lawn irrigation is another concern with regard to both landscape water use and soil N losses. Lawns are the largest irrigated crop in the U.S. (Milesi et al. 2005), and receive approximately 70 % of the water used in landscape irrigation in California (Gleick et al. 2003). Increases in soil moisture may significantly accelerate soil N cycling in arid/semi-arid ecosystems (Wang and Pataki 2012), while a combination of high soil N availability and high soil moisture levels in managed lawns could lead to considerable drainage and N leaching (Morton et al. 1988) as well as high N2O emissions, especially at warm temperatures (Bijoor 2008). “Smart” irrigation controllers can reduce water use by automatically adjusting water application based on soil moisture or weather conditions (Davis et al. 2009; Devitt et al. 2008a; McCready et al. 2009). However, relatively few studies have examined lawn plant and soil N dynamics other than leaching losses in response to irrigation (Morton et al. 1988; Pathan et al. 2007; Synder et al. 1984).
Finally, the choice of turfgrass species could modify the seasonality and magnitudes of plant N uptake and soil N losses. In general, plant urease activities and root uptake of N and water can affect the magnitudes of NH3 volatilization (Frankenberger and Tabatabai 1982), N leaching (Bowman et al. 2002; Crush et al. 2005), and denitrification (Virginia et al. 1982). C4, warm-season turf species are known for low water requirements (Huang et al. 1997; Youngner et al. 1981). In semi-arid urban ecosystems, these species may be associated with reduced water and N inputs and smaller ecosystem N losses relative to C3, cool-season species because of higher productivity and high efficiencies in N and water use under warm temperatures (Long 1999). However, there have been few studies comparing the performance of C3 and C4 turf species with regard to their efficiency in N retention under their recommended management regimes.
In this study, we measured N dynamics and constructed N budgets of the lawn portions of three simulated residences designed to test the environmental performance of common versus recommended residential landscape designs in southern California. The residences differed in the design and management regimes of the lawn portions of the yards: one was designed to represent typical landscape design and management practices in southern California (“Typical”), including the use of a C3 fescue species and automated irrigation timers; the second utilized recommendations for retrofitting landscapes to reduce N and water inputs (“Low Input”) with a C4 turf species and a soil moisture-based irrigation system; and the third was a “state-of-the-art” design intended to maximize water and N conservation (“Low Impact”) with a native sedge lawn and a weather station-controlled irrigation system. Each lawn was fertilized according to the recommendations of the University of California Cooperative Extension.
We conducted a suite of measurements to construct relatively complete N budgets for each of these lawns, including: major N inputs (fertilizer application, atmospheric N deposition, and irrigation water); gaseous (NH3, N2, N2O, and NO) and leaching losses of inorganic N (NH4 + and NO3 −); N outputs in removed plant clippings; the residual N fluxes, and potential changes in N stocks in soil. We constructed N budgets at two time scales: a 30-day scale following fertilizer application and the annual scale. Our specific hypotheses were: (1) plant clippings and 0–10 cm mineral soil would be the primary N sinks in all three lawns, as suggested by previous 15N studies; (2) the productivity and N uptake of the C4 turf species would be higher than the C3 species in warmer seasons even at much lower rates of fertilization and irrigation; (3) gaseous and aqueous N losses would be important fluxes in the Typical lawn, which received the highest rates of fertilization and irrigation, but relatively minor fluxes in Low Input and Low Impact. By testing the performance of these three landscape designs and their management practices, we sought to improve our understanding of urban lawn biogeochemistry and the best management practices for reducing N losses from fertilized ecosystems.
Materials and methods
Study site and climatic data
This study was conducted at a research facility at the South Coast Research and Extension Center in Irvine, Orange County, California (33°41′20.16″N, 117°43′24.26″W, 123 m above mean sea level, Mediterranean climate). The simulated residences consisted of model houses complete with driveways, curb and gutter, and both front and backyards designed and managed to simulate typical versus recommended practices for southern California (Photo 1). The experiment was designed and operated by the University of California Cooperative Extension of Orange County, and reflects their local expertise in assessing both common and best management practices for local landscapes (http://ceorange.ucdavis.edu/). The goals of the study were to facilitate complete instrumentation of water and N budgets and surface runoff from both pervious and impervious surfaces of Orange County residential parcels, using methods that are usually too intrusive for studies of actual residences.
This study focused on the lawn portions of the landscapes, though each contained other vegetation types and either pervious or impervious surfaces surrounding the lawns, as the study incorporated complete, parcel-scale landscape designs. Hence, the sizes of the lawns varied by landscape. The lawns in the Typical landscape (129 m2) and the Low Input landscape (43 m2) were both established in September 2006 by placing pallets of sods on a layer (5–7.5 cm) of biosolids (compost, the Biosolid Program of Orange County Sanitation District, or OCSD) on top of local soil. The typical lawn consisted of tall fescue (Schedonorus phoenix, a cool-season, C3 species formerly known as Festuca arundinacea) and was established from Marathon II sod (Southland Sod Farms, Oxnard, CA, USA) with a 6.3–7.5 cm root/soil base (sod soil N%: 0.06 ± 0.002 %),. The Low Input lawn consisted of seashore Paspalum (Paspalum vaginatum, a C4 species) established from Sea Spray sod (West Coast Turf, Winchester, CA, USA) with a 5 cm root/soil base (sod soil N%:0.11 ± 0.01 %). The Low Impact lawn (54 m2) was established in January 2007 with plugs of the cool-season, C3, California native sedge Carex (Euro American Propagators, Bonsall, CA, USA) grown in a layer of 1.3–2.5 cm OCSD biosolids on local soil. The total N% of OSCD biosolids was 1.4 % (Soil Control lab, 2007), while the local soil originally had an organic matter content of 0.42 ± 0.17 %, and a texture of 79.2 ± 2.9 % sand, 9.4 ± 1.3 % silt, and 11.4 ± 1.7 % clay (UC Davis Analytical Laboratory, 2005).
The lawn in the Typical landscape was irrigated on a regular schedule (3 days per week, 12 min per time) with an automated timer (Rain Bird 4 Station ESP Modular Series Controller, Rain Bird, Azusa, CA, USA, Hartin and Harivandi 2001) and fertilized at 192 kg N ha−1 year−1 in four equal applications, as is recommended for this lawn type (Henry et al. 2002). The fertilizer was Scotts ® Turf Builder® 29-2-4 (Scotts Miracle-Gro, Marysville, OH, USA) in 2010 and Schultz® super 21-0-0 (United Industries Cooperation, St. Louis, MO, USA) in 2011, both of which are mainly urea/coated urea. During our study, there were 6 fertilization events on March 29, May 24, August 16, and September 21 in 2010 and March 8 and May 16 in 2011. The Low Input lawn was irrigated by an automated system utilizing soil moisture sensors (Watermark Electronic Module, Irrometer, Riverside, CA, USA) which triggers at low soil moisture levels (~25 kPa at 25 cm depth) and fertilized with the same fertilizer and schedule as Typical, but at only half the rate, consistent with recommendations (25 kg N ha−1 application−1, Henry et al. 2002). However, there was a one-time application of doubled rate at 48 kg N ha−1 on August 16, 2010 to maintain visual quality, resulting in a total rate of 123 kg N ha−1 year−1 in 2010, and the first fertilization in 2011 was on March 29 instead of March 8. The lawn in the Low Impact landscape was irrigated by a weather-based Hunter ET System connected to a Hunter ICC irrigation controller (Hunter, San Marcos, CA, USA) that adjusts water application according to crop evapotranspiration (ET) rates calculated with onsite weather observations in a modified version of the Penman equation (Pruitt and Doorenbos 1977; Snyder and Pruitt 1985) and crop-specific coefficients by the California Irrigation Management Information System (CIMIS, www.cimis.water.ca.gov). The Low Impact Lawn was not fertilized before 2010, but was fertilized on March 29, 2010 and March 8, 2011 at 48 kg N ha−1 year−1 with Vigoro® Ornamental 8-4-8 Plus Minors (Vigoro Corp., Chicago, MI, USA). Following each fertilizer application, the fertilized lawns were irrigated for about 2 min. The Typical lawn and Low Input lawn were mowed regularly during the growing season once a week or every other week to a height of 7.6 and 2.5 cm, respectively, while the Low Impact lawn was only mowed once a year to the height of 2.5 cm. The clippings from all lawns were directly captured by mower and removed from the lawns.
Three time-domain reflectometers (CS616, Campbell Scientific, Inc., Logan, UT, USA) were installed in each lawn in 2008 to measure soil moisture. The installation depth was 15 cm for Typical, 20 cm for Low Input, and 25 cm for Low Impact, to correspond to rooting depth. The sensors were logged (CR10X, Campbell Scientific, Inc., Logan, UT, USA) every 30 s and averaged every 30 min. Climatic data, such as air temperature, soil temperature, and precipitation, were obtained from a CIMIS network station which was located at the site (Irvine station, #75, http://www.cimis.water.ca.gov).
N inputs from atmospheric deposition and irrigation water
The total N inputs (Ntotal ± SEt) were calculated as
where Nfert, Natm, and Nirr are N inputs from fertilizer application, atmospheric N deposition, and irrigation water, respectively. Natm and Nirr were estimated as
where Ndry and Nwet are atmospheric dry and wet deposition, and INirr and Virr are the average IN concentrations of irrigation water and irrigation volume, respectively.
Nwet during the rainy winter seasons was measured with ion exchange resin (IER) collectors based on the design by Fenn and Poth (2004), which can last 3–12 months as needed. Five IER collectors were installed in the open area around the study site on December 12, 2010 and collected on July 21, 2011. Briefly, an IER column was attached to the bottom of a dark-colored funnel with 20-cm diameter and 10-cm vertical side walls, and was mounted at 2 m above the ground. The IER was Amberlite IRN 150 Mixed Bed IER (Amberlite™ IRN 77 + Amberlite™ IRN78), with polyester fibers in both ends to prevent particles from entering. After removal, the IER columns were sent to the Forest Fire Laboratory, US Forest Service Pacific Southwest Station (Riverside, CA. USA), where the IER was extracted with 2 M potassium chloride (KCl) and analyzed for inorganic N (NH4 +–N and NO3 −–N) concentrations colorimetrically with an TRAACS 800 Autoanalyzer (Tarrytown, NY, USA, Fenn et al. 2006). Although we used a coarse mesh screen to prevent material from entering the funnel, litter contamination was still severe, leaving only one usable sample for NH4 +–N; the NO3 −–N data were not affected. Ndry, which is usually the largest component of N deposition in California and could be 10 times higher than Nwet (Bytnerowicz and Fenn 1996; Fenn et al. 2003), was not directly measured in our study. According to Fenn et al. (2010), the atmospheric dry deposition in central Orange County ranged from 9 to 15 kg N ha−1 year−1, so we applied a value of 12 kg N ha−1 year−1 for our N budgets. Our method may tend to slightly over-estimate the atmospheric N deposition as the IER results might overlap with part of the dry deposition.
Virr was monitored on a weekly basis using five randomly placed cups, with 5 ml mineral oil added to each to prevent evaporation from June 23 2010 to May 29 2011. Irrigation water was sampled directly from the irrigation valve onsite in January, March, June, October, and December 2010 and stored at 4 °C until analyzed colorimetrically for NH4 +–N and NO3 −–N concentrations using the phenol-hypochlorite method by Weatherburn (1967) and the vanadium method by Doane and Horwath (2003). INirr was calculated as the average of the IN concentrations of the five samples.
N output in plant clippings
The biomass N in plant clippings at 30-day (Nclip_30 ± SE i ) or annual (Nclip_365 ± SEp) scales was calculated as
where n is the number of mowing events in 2010 for each lawn. Equations are only shown for errors (SE) that were propagated from other errors, i.e., SEp, but not for those directly calculated from samples, i.e., SE i .
There were 36 and 32 mowing events for Typical and Low Input, respectively, while Low Impact was only mowed once a year. All plant clippings were collected, oven dried at 70 °C for 1 week (extended drying time due to the large quantities of clippings), and weighed. Clippings were sub-sampled at intervals throughout for analysis of N% from Typical (n = 17) and Low Input (n = 13). Three random portions of plant clippings were weighed (~10 g) from each subsample, homogenized, and ground to fine power for analysis on an elemental analyzer (EA, Fisons NA1500 NC, San Carlos, CA, USA) coupled to an Isotope Ratio Mass Spectrometer (Delta Plus IRMS, Thermofinnigan, San Jose, CA, USA). N output in plant clippings within 30 days following each fertilization event in the Typical and Low Input lawns was calculated as the product of the clipping biomass and N% during that time period. At the annual scale, clipping biomass N for each of the three lawns was estimated as the sum of biomass N from all mowing events. We did not measure the aboveground biomass that remained after mowing (verdure), since it was always left at similar height and not likely to vary very much in N stocks (Engelsjord et al. 2004; Frank et al. 2006).
N outputs in gaseous and aqueous forms
Gaseous N fluxes at 30 day (Ngas_30 ± SE g30) and annual (Ngas_365 ± SE g365) scales were estimated as
where a i ± SE i represents the average daily fluxes of gaseous N following fertilization and b ± SE b is the background flux estimated based on pre-fertilization sampling; k, m, and n represent the number of sampling days following fertilization, the number of months with fertilization, and the number of months without fertilization (m = 4, n = 8 for Typical and Low Input, m = 1, n = 11 for Low Impact), respectively.
We measured NH3 volatilization following fertilization with four open containers, each with 40 ml 2 % (v:v) sulfuric acid (H2SO4), randomly placed on each lawn and tightly covered with PVC chambers (diameter = 25 cm) for 24 h, after which the solution was collected and stored at 4 °C for IN analysis. Daily NH3 volatilization from the lawn was calculated as the increase in NH4 +–N in the solution per unit chamber area per day (Schlesinger and Peterjohn 1991). This procedure was repeated in each lawn following every fertilization event for up to 7 days, except that Low Impact was only measured following its single fertilization event in 2011. Pre-fertilization sampling was conducted 1 day before each of the 6 fertilization events in every lawn. Background NH3 fluxes from each lawn were estimated as the average of all 6 pre-fertilization sampling events.
N2O fluxes were measured using static PVC chambers (n = 4, diameter = 25 cm, Townsend-Small and Czimczik 2010; Townsend-Small et al. 2011) randomly placed on each lawn the day before fertilization and on a daily basis following each of the 6 fertilization events (early morning) for 5-7 days. Air samples were removed from the chamber using 30 ml nylon syringes at 0, 7, 14, 21, and 28 min, injected into air-tight, pre-evacuated headspace vials, and analyzed within 24 h on a gas chromatograph (GC) fitted with an electron capture detector (GC-2014 Nitrous Oxide Analyzer, Shimadzu Scientific Instruments). N2O fluxes were calculated from the slope of the fitted regression line of N2O concentrations versus time in each chamber. Fluxes were considered undetectable, i.e., zero, if R2 < 0.9. Volumetric soil water content (0–5 cm) was measured beneath each chamber immediately following sampling using a portable soil moisture meter (TH2O, Dynamax, Inc, Houston, TX, USA). NO fluxes were not directly measured; however, we estimated a range based on the two extremes of the reported NO/N2O ratios from field measurements or model simulation of lawns or fields fertilized with urea (0.005–14.7, Gu et al. 2009; Hall et al. 2008; Parton et al. 2001; Stehfest and Bouwman 2006; Williams et al. 1998). As a comparison, NO fluxes were also estimated as 1–3 % of nitrification (Baumgartner and Conrad 1992; Hutchinson and Davidson 1993) based on the net nitrification rates of each lawn.
To measure denitrification rates, four soil cores (0–10 cm), one from under each of the four PVC chambers, were extracted following the removal of chambers after each N2O sampling event and transferred to the lab immediately for denitrification analysis using the acetylene-blocking technique (Drury et al. 2008). An additional soil core was taken from the lawns in March and May 2011 in order to increase the sample size (n = 5 in total). To minimize damage to the lawns, cores were only 1.5 cm in diameter. Acetylene gas was used to block denitrification pathways and convert all denitrification products to N2O. Chambers were constructed from 8 oz mason jars with two syringe stopcocks installed in the lid. Each soil core was placed in a chamber and flushed with N2 for 5 min. At time 0, 15, 30, 45, and 60 min, air samples were removed with a 30 ml nylon syringe, and acetylene gas was injected. N2O concentrations in the air samples were analyzed and calculated in the same way as in situ air samples from the lawns. After the acetylene-blocking test, the soil cores were sieved at 2 mm, oven dried at 110 °C for 48 h, and weighed. The denitrification rates of the soil cores were estimated from the N2O fluxes over time per unit of dry soil. Measurements were conducted on a daily basis up to 7 days. Pre-fertilization sampling was conducted 1 day before each of the 6 fertilization events in every lawn. Background denitrification rates in each lawn were estimated as the average of all 6 pre-fertilization sampling events.
To assess the leaching IN concentrations, three lysimeters with ceramic tips (Irrometer® Soil Solution Access Tubes, Riverside, CA, USA) were installed in summer 2010 at 40 cm, below the rooting zone (0–10 cm). Soil solution samples were extracted every day following fertilization for up to 5 days in March 2011 from Low Impact and following fertilization in the other two lawns in August 2010, September 2010, March 2011, and May 2011. Pre-fertilization sampling was conducted in every lawn before each fertilization event. Each lysimeter was evacuated with an air pump for 60 s and left overnight in the soil to allow soil solution to flow into the tube through the ceramic tip; soil solution samples were extracted with a 60 ml nylon syringe on the second day. All samples were filtered with 0.2 μm microfilters, stored at 4 °C until analyzed colorimetrically for NH4 +–N and NO3 −–N using the phenol-hypochlorite method by Weatherburn (1967) and the vanadium method by Doane and Horwath (2003). Due to varying soil moisture conditions, we were not always able to collect all three samples. Drainage was estimated with the simplified equation:
where D, I, P, and R represents drainage, irrigation, precipitation, and runoff, respectively. Daily precipitation and ET0 rates were obtained from the CIMIS network station nearby (Irvine station, #75, http://www.cimis.water.ca.gov). Runoff was measured by collecting all surface runoff in 0.3 × 0.3 m concrete vaults downslope of each landscape. Electronic water sensing sump pumps (Water Ace, Ashland, OH, USA) transported runoff through an oscillating piston type water meter pulse flow meter (C700, Elster AMCO Water, Langley, Canada) which was logged daily (CR1000, Campbell Scientific, Inc., Logan, UT, USA).
The leaching inorganic N fluxes at 30 day (Nleach_30 ± SE l30) and annual (Nleach_365 ± SE l365) scales were estimated as
where INfert ± SEfert/Dfert ± SEdf and INbkgd ± SEbkgd/Dbkgd ± SEdb represent the mean ± SE of inorganic N (IN) concentrations/drainage in soil leaching solution following fertilization and at background levels, and SElb represents the error (SE) of the total leaching IN in the months without fertilization in 2010; m represent the number of months with fertilization (m = 4 for Typical and Low Input, m = 1 for Low Impact).
Residual N fluxes and potential changes in N stocks (soil and roots)
Residual N fluxes (NR ± SEr), or the difference between N outputs and inputs, were calculated for each lawn at both 30-day and annual scales as
where (N clip ± SEp) represents the N output in plant clippings calculated from Eqs. (4a)–(4c) \( \left( {N_{{{\text{NH}}_{3} }} \pm {\text{SE}}_{{{\text{NH}}_{3} }} } \right) \) and \( \left( {N_{{{\text{N}}_{2} + {\text{N}}_{2} {\text{O}}}} \pm {\text{SE}}_{{{\text{N}}_{2} + {\text{N}}_{2} {\text{O}}}} } \right) \) represent the fluxes of NH3 and N2 + N2O, calculated from Eqs. (5a)–(5d), and (N leach ± SEl) represent N leaching losses, calculated from Eqs. (7a)–(7e). We did not include estimated NO fluxes in the residual calculation, as these were not directly measured; in addition, our estimates indicated that NO fluxes likely represent a very small portion of the N inputs.
Soil N immobilization/mineralization potentials (0–10 cm) at the 30 day scale (Nsoil_30 ± SE) were estimated by 30 day lab incubation (Wang and Zhu 2012; Zhu and Carreiro 1999; Zhu and Wang 2011) of soil samples with (NFS) or without (NNFS) N addition. Briefly, to determine the net N mineralization and net nitrification potentials of the lawn soils, a set of pre-fertilization soil cores were taken from the Typical and Low Input lawns in March 2010 and from the Low Impact lawn in March 2011 at five random locations each, 3 cores per location. The 3 cores from the same location were combined into one sample, sieved, and homogenized. Soil net N potentials were determined by incubating subsets (~10 g each, n = 5) of sieved soils at room temperature and field moisture levels for 30 days. The incubated soils, as well as a subset of soils before incubation, were extracted with 1.5 M KCl and measured for IN concentrations (NH4 +–N and NO3 −–N). The net potentials of soil N mineralization (or immobilization) and nitrification (μg N g−1 dry soil day−1) were calculated as:
where INinitial and INfinal were the soil IN concentrations before and after incubation, NO3 −Ninitial and NO3 −Nfinal were the NO3 −N concentrations before and after incubation, and Tincu was the incubation time. Two sets of soils were incubated, one as “Control”, and the other as “Plus-N”, to which high-concentration ammonium chloride (NH4Cl) solution was added at a rate equivalent to the fertilization rates they receive in the field. The annual change in soil N stocks (Nsoil_365 ± SE s ) due to soil N immobilization was estimated as
where m and n are the number of months with or without fertilizer application in 2010 (m = 4, n = 8 for Typical and Low Input, m = 1, n = 11 for Low Impact).
We also assessed soil N retention with other methods for comparison. We made direct measurements of soil N% and root biomass N in 2010 and 2011: five soil cores each were collected from each lawn before fertilization in March, 2010 and 2011 to assess the annual differences. Soils were sieved to 2 mm, homogenized, oven dried for 48 h at 110 °C, weighed, ground to fine powder, and analyzed for total C% and N% on the elemental analyzer. We assumed no significant variation in soil bulk density during our study period, and averaged the bulk density of soil cores in each lawn, which were 1.2 ± 0.03, 0.81 ± 0.04, and 1.2 ± 0.1 Mg m−1 for Typical, Low Input, and Low Impact, respectively. In order to assess the variation in root N content between 2010 and 2011, roots (≥2 mm) were separated from the soil cores described above, oven dried for 48 h at 70 °C, weighed, ground to fine powder, and analyzed for total C% and N%. The total N mass in soil or roots was calculated as the product of density and N%. To account for possible variation in root N at the 30 day scale, another 5 soil cores were sampled from each lawn 30 days after fertilization in March 2011 and the roots were separated and analyzed for total C% and N%.
Data analysis and residual calculation
N budgets were constructed for Typical and Low Input at a 30-day scale following each of the 6 fertilization events from January 2010 to June 2011 and for all lawns at an annual scale for 2010. Repeated measures ANOVA was used to test the effects of lawn type, time (day), and their interactions (lawn type*day) on the daily averages of soil volumetric water content, while an F test was used to compare the variances of the daily averages. Nested Analysis of Variance (ANOVA) was used to compare IN concentrations of lysimeter samples below the rooting zones (40 cm) and denitrification rates, with time (day) as the nominal factor nested in lawn types. Multivariate regression analyses were used to evaluate the relationship between denitrification rates and potential driving variables (soil water content and NO3 −–N concentrations), and the relationship between plant productivity and environmental factors (air temperature, soil water content, and plant N%, as an indicator of N availability). We used ANOVA tests to compare the soil total C%, N%, and net N potentials among the three lawns, and Student’s t tests (α = 0.05) to compare these variables in 2010 and 2011, as well as root densities and root N% of roots at the 30-day and annual scales. All analyses were performed with SAS software v9.1.3 (SAS, Cary, NC, USA).
Results
Climatic data
During our study period, air and soil temperatures ranged from 6.2 to 28.9 °C and 8.3 to 25.3 °C, respectively. The total annual rainfall at our study site in 2010 was 995.2 mm, with monthly rainfall highest in December (269.5 mm) and almost none from June to September. Irrigation rates varied greatly among the three lawns as well as among seasons (Fig. 1). During summer 2010, the irrigation rates were as high as 350–400 mm month−1 for Typical and 100–150 mm month−1 for the other two lawns, while in winter 2010, all irrigation rates were about 50 mm month−1 or lower. Daily average soil volumetric water content ranged from 13.4 ± 0.5 to 19.3 ± 0.7 % in Typical, from 11.6 ± 0.9 to 19.6 ± 0.4 % in Low Input, and from 18.45 ± 2.48 to 22.92 ± 4.79 in Low Impact. Over the entire study period, the Low Impact site had the highest daily average soil moisture (20.2 % ± 0.04) followed by the Typical (16.8 % ± 0.03) and the Low Input (15.5 % ± 0.03, P < 0.0001, repeated measures ANOVA).
N inputs from fertilization, atmospheric deposition and irrigation water
Fertilization, atmospheric deposition, and irrigation water contributed 76–90, 7–23, and 1 %, respectively, of the total N inputs to the lawns (Table 1a). The bulk atmospheric N deposition during the collection period was 0.69 kg N ha−1 (or 1.1 kg ha−1 year−1) for NH4 +–N (n = 1) and 0.68 ± 0.08 kg N ha−1 (or 1.1 ± 0.1 kg N ha−1 year−1) for NO3 −–N (n = 5). The total irrigation volumes from June 2010 to May 2011 were 2,399 ± 298 mm for Typical, 698 ± 112 mm for Low Input, and 1,008 ± 226 mm for Low Impact. The average NH4 +–N and NO3 −–N concentrations in irrigation water in 2010 were 0.07 ± 0.01 and 0.02 ± 0.01 ppm (n = 5).
N outputs in plant clippings
The overall clipping biomass removed from the Typical, Low Input, and Low Impact lawns in 2010 was 2,674, 3,866, and 772 kg ha−1 year−1 (Fig. 2a), while the mean N% in plant clippings was 2.6 ± 0.1, 2.1 ± 0.1, and 1.0 ± 0.1 %, respectively (Fig. 2b); the clipping biomass N was 69.2 ± 0.5, 74.1 ± 0.5, and 7.7 ± 0.4 kg N ha−1 year−1 (Fig. 2c), which accounted for about 33, 54, and 12 % of the total annual N inputs in 2010 (Table 1b). In the 30-day periods after fertilization, the average growth rates of the Typical and Low Input lawns were 1.2 ± 0.2 and 1.7 ± 0.7 g biomass m−2 day−1, compared to their annual growth rates of 0.73 and 1.1 g biomass m−2 day−1; the average 30-day clipping biomass and biomass N were 351 ± 36 kg ha−1 and 9.3 ± 0.01 kg N ha−1 for Typical and 507 ± 116 kg ha−1 and 12.1 ± 0.1 kg N ha−1 for Low Input, while the individual 30-day clipping biomass N of six fertilization periods accounted for 12–33 and 9–87 % of their respective fertilization rates (Table 1b; Fig. 3).
Time series of a aboveground productivity (top panel), b clipping N% (middle panel), and c clipping biomass N (bottom panel) of tall fescue (Schedonorus phoenix) in Typical (filled triangles) and seashore paspalum (Paspalum vaginatum) in Low Input (open triangles) from Jan 2010 to June 2011. The vertical lines show the fertilization dates (March 29, May 24, August 16, and September 21, 2010; March 08/Mar 29 for Typical/Low Input, May 16, 2011). Data are shown as mean ± SE
Inputs and outputs of reactive N to soil in the a Typical, b Low Input, and c Low Impact lawns during the 30-day periods following fertilization events in 2010 and 2011 (Mar 10, May 10, Aug 10, Sep 10, Mar 11, and May 11) and the non-fertilized period in 2010 (NF 10, 245 days). The error bars show propagated uncertainties (SE) of all inputs or outputs. (Color figure online)
Interestingly, multivariate regression analysis showed that the aboveground productivity of seashore paspalum in Low Input was positively affected by both plant N% (P = 0.0146, partial R2 = 0.2930), an indicator of available N for plant uptake, and average air temperature (P = 0.0012, partial R2 = 0.4714), while that of tall fescue in Typical only increased with plant N% (P = 0.0316, adj. R2 = 0.2553). At half the fertilization rate as tall fescue, seashore paspalum had higher clipping biomass N in the 30-day periods after fertilization than tall fescue in May, while the opposite was true in September and March (all P < 0.0001). In August 2010, the only period when the two lawns were fertilized at the same rate, seashore paspalum obtained twice as much biomass N as tall fescue.
Soil net N potentials and leaching N losses
In the 30-day lab incubation, soils from Typical and Low Input lawns showed net N mineralization in the Control treatment of 1.6 ± 0.7 and 1.2 ± 1.1 kg N ha−1 month−1 and net N immobilization in the Plus-N treatment as equivalent to 25.2 ± 2.7 and 16.4 ± 3.4 kg N ha−1 month−1. Soils from Low Impact showed net N immobilization in both Control and Plus N treatments, as 1.2 ± 0.4 and 16.3 ± 5.2 kg N ha−1 month−1. Soil net nitrification potentials significantly increased with N addition in all three types of soils (P < 0.05), from 0.54 ± 0.25 to 32.2 ± 2.5, from undetectable to 6.7 ± 3.4, and from 0.6 ± 0.6 to 37.2 ± 9.2 kg N ha−1 month−1 in Typical, Low Input, and Low Impact, respectively. In the Plus-N treatment, Typical and Low Impact had significantly higher net nitrification rates than Low Input (P < 0.0001), while the soil net N immobilization potentials were not significantly different among the three lawns.
The pre-fertilization IN concentrations in the soil solutions at 40 cm were generally low or undetectable. NH4 +–N concentrations peaked sharply in 1–3 days following fertilization; such post-fertilization NH4 +–N peaks varied among seasons in both Typical (P = 0.0011) and Low Input (P = 0.0095), with both maximums seen in March 2011. NO3 −–N concentrations were generally low to undetectable with no apparent seasonal variations. The precipitation/ET0 rates from the CIMIS network were 0/149, 53/83, 63/99, 9/129 mm in 30 days following the last 4 fertilization events and 397/542 mm for the rest of year (245 days). The corresponding drainage volumes were 181, 288, 88, 113, and 1278 mm for Typical but zero for the other two lawns. Therefore, the leaching IN was about 2 % of the annual N inputs to Typical and none in the other two lawns (Table 1b).
Gaseous and leaching N losses
NH3 fluxes peaked and declined quickly following fertilization (Fig. 4). The average NH3 volatilization in 30 days was 0.06 ± 0.01 and 0.13 ± 0.02 kg N ha−1 month−1 from Typical and Low Input following the 6 fertilization events, and 0.35 ± 0.02 kg N ha−1 month−1 for Low Impact following the fertilization on March 8, 2011. The background NH3 fluxes were similar in the three lawns, about 0.001 ± 0.001 kg N ha−1 day−1. The annual NH3 loss in 2010 was no more than 1 % of N inputs from each lawn (Table 1b).
NH3 volatilization in Typical (filled squares), Low Input (gray squares), and Low Impact (dark gray squares) following fertilization. In March 2011, Typical and Low Impact were fertilized on the 8th while Low Input was fertilized on the 29th. Data are shown as mean ± SE. The fertilization dates (Day 1) are shown in each panel
The total denitrification potentials were 10–100 times higher than NH3 volatilization at both time scales. The denitrification rates in 30 days following fertilization were 1.3 ± 0.2, 4.0 ± 0.3, and 1.5 ± 0.3 kg N ha−1 month−1 in Typical, Low Input (both n = 6), and Low Impact (n = 1, Fig. 5). The background denitrification rates were 0.04 ± 0.04, 0.07 ± 0.09, and 0.03 ± 0.06 kg N ha−1 day−1, respectively. Denitrification accounted for up to 3.5 ± 2.9, 17.5 ± 8.4, and 3.1 ± 1.3 % of N inputs from a single application of the lawns, and 7.9 ± 6.3, 20.2 ± 15.2, and 20.2 ± 30.0 % of their annual N inputs. Although Low Input received only half the fertilization rate as Typical, it showed significantly higher soil denitrification potentials following 4 out of 6 fertilization events (P < 0.05). There was no significant relationship between denitrification and soil NO3 −–N or soil relative water content. However, the maximum peak of denitrification during each fertilization period was correlated with soil relative water content (Fig. 6).
Denitrification fluxes in Typical (filled squares), Low Input (empty squares), and Low Impact (gray squares) following each of the 6 fertilization events in 2010 and 2011. P values are from an ANOVA with time (day) as the nominal factor nested in lawn types. Error bars represent the standard error. The fertilization dates (Day 1) were given in each panel
N2O fluxes after fertilization were relatively low or even undetectable in many cases. Peak N2O fluxes ranged from 3.4 ± 3.4 to 19.5 ± 11.3 μg N m−2 h−1 for Typical and from 9.1 ± 5.9 to 54.6 ± 10.4 μg N m−2 h−1 for Low Input. There was a single peak of 1.99 ± 1.99 μg N m−2 h−1 in Low Impact following fertilization on March 8, 2011, but no detectable N2O flux otherwise. NO emissions estimated based on N2O fluxes were lower than 0.1 % of the annual N inputs, while values estimated based on net nitrification rates accounted for less than 2 %.
Residual N fluxes and change in soil N stocks
The residual N fluxes ranged from 28.9 ± 2.9 to 42.6 ± 0.2 and from 3.1 ± 2.2 to 21.1 ± 0.8 kg N ha−1 month−1in the Typical and Low Input lawns in the 30 days following fertilization. The annual residual N fluxes were 117.8 ± 18.4, 35.0 ± 25.7, and 42.0 ± 21.3 kg N ha−1 year−1 in Typical, Low Input, and Low Impact (Table 1b). Soil net N immobilization accounted for 52.5 ± 5.2, 68.3 ± 14.2, and 33.9 ± 10.8 % of N inputs from a single fertilization to these lawns on average, and about 41.9 ± 6.0, 41.0 ± 10.7, and 45.8 ± 14.8 % annually (Table 1b). However, we were unable to detect any significant 30-day or annual variation in root density (live and dead), root N%, root N mass, or annual variation of soil N% in any lawn. The total C% of 0–10 cm soil was 2.3 ± 0.6, 5.8 ± 1.2, and 1.78 ± 0.4 % for Typical, Low Input, and Low Impact (n = 6 each), while the corresponding total N% was 0.15 ± 0.04, 0.38 ± 0.08, and 0.10 ± 0.03 %. The average C:N ratios were 14.4 ± 0.6, 15.6 ± 0.2, and 17.7 ± 0.5, respectively. The soil C% and N% were highest in Low Input and lowest in Low Impact (P < 0.0001), while the C:N ratios were highest in Low Impact and lowest in Typical (P < 0.0001).
Discussion
In this study, clipping biomass and mineral soil were primary N sinks at both 30-day and annual scales (Fig. 3). At half the fertilization rates as Typical, the seashore paspalum clippings from Low Input accounted for an average of 33 % of N inputs in 30 days and 54 % at the annual scale, compared to 19 and 33 % in tall fescue of Typical and 12 % (annual) in the Carex of Low Impact. However, Low Input also had higher post-fertilization denitrification rates most of the time. Due to relatively low IN concentrations in leaching solution, the leaching IN loss was low (2 %) from Typical and estimated as zero (undetectable) in Low Input and Low Impact. The gaseous N losses were of similar magnitudes in all three lawns, dominated by denitrification. However, due to relatively large uncertainties, denitrification rates have a large possible range (Table 1b).
N output in plant clippings
The 30-day clipping biomass N after fertilization of tall fescue and seashore paspalum was 19.4 ± 3.8 and 30.4 ± 11.1 % of N input from single application, compared to the annual N output in clipping biomass of 33 and 54 % of the annual N input. Therefore, in our study where clippings were removed from the lawns, clipping biomass represented an important N output in the short term as well as the long term (Fig. 3; Table 1b). While many studies similarly found plant biomass and mineral soils as the primary N sinks in lawns, their magnitudes varied over time and differed depending on whether grass clippings were removed or returned to lawns. Engelsjord et al. (2004) showed that when all clippings in experimental turf plots were regularly collected, 15N-labeled fertilizer N accumulated in clipping biomass over a year (from about 21–25 to 40–46 %), while 15N recovery in 0–40 cm soil gradually decreased (from about 20–27 to 9–14 %). However, when clippings were left in place, labeled fertilizer N retained in mineral soil increased over time and became the dominant long-term pool (from 20 to 33 %), while plant biomass only dominated the short-term recovery of 15N label but not the long term (from 30 to less than 10 %, Raciti et al. 2008). Frank et al. (2006) also reported high retention of 15N-labeled fertilizer N in soil (43–67 %) and much smaller 15N in clipping biomass (7–9.7 %) in 2 years’ time. We did not measure the thatch N in our studies because there was no visible thatch layer or verdure left after mowing at our sites, such that this was likely a very small portion of the annual N output, if any (Engelsjord et al. 2004; Frank et al. 2006).
Even at half the rate of fertilization as tall fescue and about one-third of the irrigation, seashore paspalum had a higher annual growth rate than tall fescue (1.06 vs. 0.73 g biomass m−2 day−1) in 2010 and a similar annual N output in turf clippings (74.1 ± 0.5 vs. 69.2 ± 0.5 kg−1 ha−1 year−1) at a lower mean plant N% (Table 1b). Considering their fertilization rates, seashore paspalum was nearly twice as efficient in plant N uptake (54 % of annual N inputs) as the tall fescue in Typical (33 %). The Carex in Low Impact required the lowest N fertilization rates of all, but also had the lowest N uptake efficiency, only 12 % of the annual N inputs. In addition, the ET0-based irrigation system did not result in a lower water input than the soil moisture-based system (1,008 ± 226 vs. 698 ± 112 mm), though both were lower than the Typical lawn (2,399 ± 298 mm). Denitrification rates and N2O fluxes were still high in Low Input compared to Typical, while inorganic N concentrations in leaching solutions were not significantly different from Typical, suggesting that the fertilization rates might still have been greater than plant requirements and could be further reduced.
C4 species are known for their high efficiency in water and N usage and consequentially high productivity at lower plant N% than C3 species, especially under warm temperatures (Long 1999). Throughout the study period, the growth rate of seashore paspalum was positively affected by both air temperature and plant N% (as an indicator of N availability), while that of tall fescue was only affected by plant N%. Biomass N in tall fescue clippings peaked in cool seasons while biomass N of seashore paspalum peaked in warmer seasons (Fig. 2c); the former was higher than the latter in March 2010, September 2010, and March 2011, while the opposite was true for May 2010 and August 2010. Wherley et al. (2009) also reported a similar seasonal pattern associated with temperature in a C4 turf species (bermudagrass), which assimilated as much as 49 % of 15N-labeled fertilizer N in 16 days in August, about 25 % in May and October, but none in January. High productivity of seashore paspalum might have promoted accumulation of organic C in the soil of Low Input, and in turn, N immobilization and retention in soil. Low Input was higher than Typical in soil C% (5.8 ± 1.2 vs. 2.3 ± 0.6 %) and N% (0.38 ± 0.08 vs. 0.15 ± 0.04 %). Under simulated N fertilization, soil net immobilization rates in both lawns were similar (0.94 ± 0.11 vs. 0.71 ± 0.12 μg N g−1 dry soil day−1), despite the lower fertilization rate in Low Input. We were not able to directly compare the soil C and N accumulation rates in the two lawns due to the lack of soil data at lawn establishment. Since plant clippings were removed after mowing, the accumulation of C and N largely depended on belowground productivity, which we did not measure directly, but was likely related to aboveground productivity.
N losses through gaseous and aqueous forms
Denitrification dominated gaseous N losses and was of similarly high magnitudes and temporal patterns in all three lawns, despite the differences in the fertilization and irrigation regimes. The daily average denitrification fluxes were higher in Low Input than Typical following 4 out of 6 fertilization events, which might be explained by the higher soil C% and N% in Low Input that could promote higher denitrification. However, there was a high degree of spatial variability in these fluxes and consequentially large uncertainties of N losses through this pathway. At the annual scale, gaseous N losses through denitrification were 16.4 ± 13.2, 27.9 ± 20.9, and 12.8 ± 19.0 kg−1 ha−1 year−1 for Typical, Low Input, and Low Impact, compared to the mean denitrification rates of 13 kg−1 ha−1 year−1for fertilized agricultural soils estimated by Barton et al. (1999) and 14 ± 3.6 kg−1 ha−1 year−1 for fertilized suburban lawns (Raciti et al. 2011b). Denitrification accounted for 7.9 ± 6.3, 20.2 ± 15.2, and 20.2 ± 30.4 % of total annual N inputs in Typical, Low Input, and Low Impact. With relatively large uncertainties due to spatial variation, the estimated fluxes at the annual scale might have a large possible range, from 0 to 50 %, of total N inputs (Table 1b). Relatively large gaseous N losses through denitrification are expected if N fertilization rates exceed plant needs (Barton et al. 1999; Raciti et al. 2011b), while long-term fertilization could substantially increase the denitrification potential of soil (Drury et al. 1997; Horgan et al. 2002b; Šimek et al. 2000). Although denitrification may help reduce NO3 −–N leaching from fertilized lawns by converting NO3 −–N to N2, high denitrification rates may also increase soil emissions of NO, an air pollutant, and N2O, a greenhouse gas.
Increased soil moisture may positively affect soil net nitrification in semi-arid ecosystems (Wang and Pataki 2012) as well as soil denitrification due to anaerobic conditions (Davidson 1991), increasing the potential for gaseous N losses through nitrification and denitrification. We did not find a significant relationship between denitrification and soil NO3 −–N or soil relative water content in this study; however, there was a positive correlation between the maximum peak of denitrification during each fertilization period and the corresponding relative soil water content (Fig. 6). Denitrification is usually concentrated in “hot spots” and “hot moments” due to the high spatial and temporal heterogeneities of its required conditions: organic C, NO3 −–N, and anaerobic environments (Groffman et al. 2009a). Therefore, the maximum peak of denitrification in each sampling period might represent the “hot spots” of most concentrated substrates and preferable conditions combined. In other words, anaerobic conditions caused by high relative soil water content became a dominant factor affecting denitrification only in the presence of sufficient substrates. We may have underestimated or overestimated the field denitrification rates because of limited sample size and because soil moisture (field moisture) and temperature were kept constant within each set of the acetylene-blocking incubation soils. The acetylene-blocking method might also lead to underestimation of base denitrification, as 10 % acetylene gas in the incubation jar could inhibit nitrification, reducing NO3 −–N for denitrification process.
N2O emissions from all three lawns were mostly low or undetectable following fertilization. Peak fluxes from Typical (3.4 ± 3.4 to 19.5 ± 11.3 μg N m−2 h−1) were similar in magnitude to the natural desert sites measured by Hall et al. (2008), while peak fluxes from Low Input were 2-threefold higher (9.1 ± 5.9 to 54.6 ± 10.4 μg N m−2 h−1) and closer to those reported by Hall et al. (2008) from urban lawns in Arizona (18 to 80 μg N m−2 h−1). Usually, N2O emissions are much higher in fertilized urban soils than in natural ecosystems (Hall et al. 2008; Kaye et al. 2004); however, fertilization rates and N2O fluxes are not always correlated (Jungkunst et al. 2006; Townsend-Small et al. 2011). We did not directly measure NO fluxes from nitrification, but our estimated ranges of NO emissions based on either NO/N2O ratios (<0.1 %) or net nitrification rates (<2 %) suggest that this is not a large possible pathway of N loss. The difference between the two estimates comes from a combination of low N2O emissions from actual measurements and relatively high nitrification potentials measured in lab incubations. Given that the nitrification potentials from lab incubations could differ from actual field nitrification because of the variation of temperature and moisture as well as differences in leaching conditions, the estimates based on lab nitrification potentials might deviate more from the actual NO emissions. Consequently, direct measurements of NO fluxes would be useful to verify this conclusion. NH3 losses through fertilizer volatilization were also minimal compared to denitrification as the values were less than 1 % in our study (Table 1b) in all three lawns, probably because slow-release coated-urea was used. NH3 volatilization of urea-based fertilizer varies greatly among studies with fertilizer types and rates, but coated urea tends to have significantly lower volatilization rates than uncoated urea. Torello et al. (1983) reported NH3 volatilization of 0.2–10.3 % of applied urea-N in various forms (prilled urea, coated urea, or dissolved urea, at 49–293 kg N ha−1) to Kentucky bluegrass. Vaio et al. (2007) reported 12–46 % volatilization of urea-N (urea polymer, urea-NH4NO3, or granular urea, at 50 kg N ha−1) applied to tall fescue plots. Huckaby Knight et al. (2012) reported significantly lower volatilization of coated urea-N than uncoated urea from warm-season turfgrass (e.g., 3.6–4.4 vs. 11.7–17.9 %) fertilized at 146 kg N ha−1.
Surprisingly, leaching IN losses only constituted 2 % of annual N inputs in Typical. N leaching could be as high as 41 % of applied N from agriculture fields (Mosier et al. 2002) and up to 30 % from turfgrass (Barton and Colmer 2006). Previous studies have shown low leaching inorganic N losses from relatively young turf lawns even under high fertilization rates (Barton and Colmer 2006), e.g., 1.1 % from a 1-year-old couch grass lawn (C4) fertilized at 195 kg N ha−1 year−1 (Pathan et al. 2007) and 1.5 % from a 3-year-old mixed cool-season turf fertilized at 147 kg N ha−1 year−1 (Guillard and Kopp 2004). Much higher leaching IN loss was reported from over-fertilized mature turfgrass. Frank et al. (2006) conducted a two-year study in a 10-year-old Kentucky bluegrass turf and found 10 times higher leaching of 15N-labeled fertilizer N from the high-N treatment (245 kg N ha−1 year−1, ~10 % loss) than the low-N treatment (98 kg N ha−1 year−1, ~1 % loss). The lawns in our study are relatively young (4–5 years old); the inorganic N concentrations in soil solution at 40 cm were constantly low except for a short peak following fertilization, suggesting effective controls on soil inorganic N by plant uptake and microbial immobilization. There is uncertainty in our estimated volume of drainage; however, at such low inorganic N concentrations, even if we assume that all irrigation water was lost in drainage (i.e., zero runoff and ET), the leaching inorganic N estimates would be no more than 4 % of the N inputs in Typical and 1 or 2 % of N inputs in Low Input and Low Impact.
The largest uncertainty in our leaching N loss estimate is the absence of dissolved organic nitrogen (DON) measurements, which have been reported to constitute up to 10–70 % (average at 40 %) of total leaching N losses within 55 days (Pare et al. 2008) and up to 50 % in 2 years (Barton et al. 2009) from lawns fertilized at various rates. Pare et al. (2008) showed in a 15N-tracer experiment that most DON in leachate was from soil instead of labeled fertilizer, while Barton et al. (2009) reported that the majority of DON leaching occurred during the first year of lawn establishment from sod instead of fertilizer. Therefore, at relatively low N fertilization rates, it is possible for young lawns established from sod, or lawns with high soil organic matter (SOM) in general, to have relatively high DON leaching losses. Many current studies of leaching N from lawns focused on inorganic N, especially NO3 −–N, since NO3 −–N is highly leachable and may be a threat to public health in groundwater (e.g., Amador et al. 2007; Bowman et al. 2006; Devitt et al. 2008b; Frank et al. 2006; Groffman et al. 2009b; Guillard and Kopp 2004; Wu et al. 2007). Future studies may verify the magnitudes of DON leaching from lawns under different management regimes.
Due to the distinct seasonal pattern of plant N uptake, the timing of fertilization is also an important factor that affects soil N losses. The highest denitrification rates occurred in the cool season of March for Low Input (C4) but in summer for Typical (C3), during which the lawns were relatively inactive and therefore presumably in less competition for N with soil microbes. Similarly, Horgan et al. (2002a) reported denitrification fluxes from a C3 lawn as about 17–26 % in summer versus 4–6 % in spring of 15N-labeled fertilizer N. These results show how N losses and emissions of pollutants such as N2O, and NO3 −–N from lawn soils are enhanced when fertilizer is applied during the seasons when plant growth is less active.
N retention in soil and implications for N saturation
Based on the SOC accumulation rate in 0–20 cm depth soil of ornamental lawns in parks in Irvine, California (0.14 kg OC m−2 year−1, Townsend-Small and Czimczik 2010) and the range of lawn soil C:N ratios in our study (15.2–18.0), the soil organic N accumulation rates in our lawns could be as high as 80–90 kg N ha−1 year−1. Raciti et al. (2011a) investigated 32 residential lawns in Baltimore, Maryland and found potential soil C and N accumulation rates as 0.082 kg C m−2 year−1 and 83 kg N ha−1 year−1. Selhorst and Lal (2013) reported soil C sequestration rates from 0.09 to 0.54 kg C m−2 year−1 from home lawns in 16 sites across the U.S.
Soil N immobilization (biotic and abiotic) may be an important mechanism for N retention in soil, especially at the 30 day scale following fertilization. In the 30 day soil incubation with simulated fertilizer application, we found similar, high net N immobilization rates of 25.2 ± 5.4, 16.4 ± 6.8, and 16.3 ± 10.3 kg N ha−1 month−1 for Typical, Low Input, and Low Impact, respectively, accounting for approximately 30–65 % of N inputs. This suggests “luxury uptake” and storage of N by the microbial community when N was supplied in large amount (Fog 1988), or rapid abiotic immobilization of N into mineral soil, which has been reported to occur within minutes to a few hours in many 15N tracer studies (e.g., Aber et al. 1998; Dail et al. 2001; Davidson et al. 2003; Zhu and Wang 2011). An uncertainty in our estimate is the lack of seasonality: the soils were only sampled in spring and incubated at constant temperature and soil moisture. We applied this single value over the study period (Fig. 3). However, soil net N immobilization potential may have shown seasonal variations associated with climate, microbial activities, and plant uptake (Horgan et al. 2002a; Wherley et al. 2009; Yao et al. 2011). This may explain why the total N outputs plus estimated immobilization in soil exceeded the total N inputs in Low Input in May 2010 (Fig. 3). At the annual scale, the estimates of N retention in soil through biotic and abiotic immobilization were relatively high: 87, 57, and 29 kg N ha−1 year−1 in Typical, Low Input, and Low Impact, respectively, which is fairly proportional to their fertilization rates (Table 1b). The three lawns might have similarly retained as much as 40 % of the fertilizer N in soil through immobilization annually, even without clipping return, which is similar to the findings of previous 15N studies that showed that mineral soil is the long-term sink for fertilizer N in lawns (Frank et al. 2008; Raciti et al. 2008, 2011b).
Other mechanisms might also have played a role in soil N retention of urban lawns in general, such as the accumulation of plant litter, the variation in root biomass N, and N assimilated into thatch. However, these factors likely played less important roles in our study. For example, the accumulation of plant litter mainly depends on the rates of litter production and microbial decomposition, both of which may be affected by lawn species and management regimes. Kopp and Guillard (2004) showed rapid C and N losses from clipping decomposition of about 90 % within 16 weeks; however, at our sites, clippings were removed. The Low Input lawn may have relatively high accumulation rates of plant litter and associated organic N in soil due to the high biomass productivity. We did not directly measure the litter decomposition rates, but the Low Input lawn had the highest foliar C:N ratio, root C:N ratio (Typical: 37.0 ± 2.3, Low Input: 52.0 ± 3.2, Low Impact: 40.3 ± 5.9, P < 0.001), and the lowest irrigation rates, all of which may negatively impact litter decomposition. Also, we did not see any significant monthly or annual variation in root biomass N, and there was no visible thatch layer, probably due to consistent removal of clippings.
Qian and Follett (2012) hypothesized that high rates of soil N accumulation are driven by rapid C sequestration in young turf ecosystems; however, once soil C accumulation reaches a steady state, continuous N fertilization may lead to increasing gaseous and aqueous N losses as initial signs of N saturation. Such N losses may increase in magnitude over time and eventually approach or even exceed N inputs as the final stage of N saturation (Aber et al. 1989; Agren and Bosatta 1988). The rate and duration of N accumulation in lawn soils are tightly coupled to those of soil C accumulation and are also affected by the temporal variation in soil C:N ratio, which represents the net balance between soil immobilization and mineralization over time. With simulations of lawn dynamics generated from the CENTURY model, Qian and Follett (2002) and Bandaranayake et al. (2003) similarly showed that SOC accumulation in urban lawns could continue for up to 30–45 years, with a rapid linear increase in the first 25–30 years at an approximate rate of 0.9–1.2 Mg C ha−1 year−1 (or 0.09–0.12 kg C m−2 year−1). Field observations supported this hypothesis. Townsend-Small and Czimczik (2010) investigated 0–20 cm soils of ornamental lawns (2, 8, 27, and 33 year) in parks in Irvine, California, and showed that SOC increased linearly within 35 years at an approximate rate of 0.14 kg OC m−2 year−1. Shi et al. (2006) reported linear increases in both soil C and N densities in a chronosequence of a turf system (1, 6, 23, and 95 year golf courses) in North Carolina, which suggests that SOC accumulation may even continue after 45 years and maintain a strong soil sink for N.
This study was intended to measure the consequences of “typical”, i.e., high water and N input landscape designs, as well as designs intended to reduce the environmental impacts of lawns. Our results generally support the effectiveness of the alternative designs at reducing water use and N outputs. However, urban landscape design and management vary greatly among parcels, neighborhoods, and municipalities, and N budgets should be constructed in additional landscapes to develop a more general framework for N processes in urban residences. In addition, there are potentially useful management practices that were not explicitly tested here. Currently, clippings are commonly disposed of as waste. However,to facilitate accumulation of organic matter in lawn soils and reduce the need for fertilization, leaving clippings on site during the growing season (i.e., clipping return, or “grasscycling”), is usually recommended (Harivandi and Gibeault 1999; Hartin and Harivandi 2001; Milesi et al. 2005). Qian et al. (2003) showed with a CENTURY model simulation that clipping return may increase soil sequestration of C and N by 11–59 and 12–78 %, with greater improvements under lower rather than higher fertilization rates (75 vs. 150 kg N ha−1 year−1); meanwhile, this practice may reduce the N requirement of lawns from 25–60 % depending on lawn age. Other studies also showed that clipping return, along with appropriate mowing frequencies, may reduce the need for fertilization (Heckman et al. 2008; Kopp and Guillard 2002), preserve soil moisture (Harivandi and Gibeault 1999; Hartin and Harivandi 2001), and improve plant N uptake (Kopp and Guillard 2002); however, it might also potentially increase leaching loss of NO3 −, especially when fertilization was not reduced or irrigation was excessive (Kopp and Guillard 2005). These practices should be further tested in an ecosystem N budget framework.
Conclusions
In constructing N budgets described here, we accounted for virtually all of the measured N inputs and outputs, albeit with a high degree of uncertainty in some estimated pathways of N loss. We attempted to sample a range of landscape designs, from a design that utilizes intensive N and water inputs to two alternative designs intended to maintain lawns with lower to minimal inputs. Overall, our results showed that the Low Input lawn was relatively efficient in assimilating N inputs in plant biomass and soil stocks with low water and N costs, which may make this design a good choice for semi-arid urban ecosystems like those in the Los Angeles Basin, where both water use and N pollution is a concern. Additional adjustments to the management practices in this design such as reducing fertilization rates during the dormant seasons (March for seashore paspalum) or according to temperature may further increase the efficiency of N fertilization and reduce denitrification losses.
Our study also showed that all three lawns, despite receiving different rates of N and water inputs, appear to be accumulating C and N rapidly in the soil, especially during the fertilization periods, with surprisingly small N losses. Management of lawn species adapted to the local climate type (e.g., a warm-season C4 species for a semi-arid ecosystem) may maximize the recreational and aesthetic benefits of lawns and minimize the potential environmental impacts. Clipping return, reduced fertilization rates, and targeting fertilization during the active growing season are all recommended management strategies, especially as lawns age, not only to increase soil C accumulation but also to reduce consumption of water and fertilizer as well as potential detrimental environmental impacts of soil N saturation.
References
Aber JD, Nadelhoffer K, Steudler P, Melillo J (1989) Nitrogen saturation in northern forest ecosystems. Bioscience 39:378–386
Aber JD, Ollinger S, Driscoll C (1998) Modeling nitrogen saturation in forest ecosystems in response to land use and atmospheric deposition. Ecol Model 101:61–78
Agren GI, Bosatta E (1988) Nitrogen saturation of terrestrial ecosystems. Environ Pollut 54:185–197
Amador JA, Hull RJ, Patenaude EL, Bushoven JT, Gorres JH (2007) Potential nitrate leaching under common landscaping plants. Water Air Soil Pollut 185:323–333
Bandaranayake W, Qian YL, Parton WJ, Ojima DS, Follett RF (2003) Estimation of soil organic carbon changes in turfgrass systems using the CENTURY model. Agron J 95:558–563
Barton L, Colmer TD (2006) Irrigation and fertiliser strategies for minimizing nitrogen leaching from turfgrass. Agric Water Manag 80:160–175
Barton L, McLay CDA, Schipper LA, Smith CT (1999) Annual denitrification rates in agricultural and forest soils: a review. Aust J Soil Res 37:1073–1093
Barton L, Wan GGY, Buck RP, Colmer TD (2009) Does N fertiliser regime influence N leaching and quality of different-aged turfgrass (Pennisetum clandestinum) stands? Plant Soil 316:81–96
Baumgartner M, Conrad R (1992) Effects of soil variables and season on the production and consumption of nitric oxide in oxic soils. Biol Fertil Soils 14:166–174
Bijoor NS (2008) Effects of temperature and fertilization on nitrogen cycling and community composition of an urban lawn. Glob Change Biol 14:2119–2131
Bouwman AF, Boumans LJM, Batjes NH (2002) Emissions of N2O and NO from fertilized fields: summary of available measurement data. Glob Biogeochem Cycles. doi:10.1029/2001GB001811
Bowman DC, Cherney CT, Rufty TW Jr (2002) Fate and transport of nitrogen applied to six warm-season turfgrasses. Crop Sci 42:833–841
Bowman DC, Devitt DA, Miller WW (2006) The effect of moderate salinity on nitrate leaching from Bermudagrass turf: a lysimeter study. Water Air Soil Pollut 175:49–60
Bytnerowicz A, Fenn ME (1996) Nitrogen deposition in California forests: a review. Environ Pollut 92:127–146
Clayton H, McTaggart IP, Parker J, Swan L, Smith KA (1997) Nitrous oxide emissions from fertilised grassland: a 2-year study of the effects of N fertiliser form and environmental conditions. Biol Fertil Soils 25:252–260
Crush JR, Waller JE, Care DA (2005) Root distribution and nitrate interception in eleven temperate forage grasses. Grass Forage Sci 60:385–392
Dail DB, Davidson EA, Chorover J (2001) Rapid abiotic transformation of nitrate in an acid forest soil. Biogeochemistry 54:131–146
Davidson EA (1991) Fluxes of nitrous oxide and nitric oxide from terrestrial ecosystems. In: Rogers JW, Whitman WB (eds) Microbial production and consumption of greenhouse Gases: Methane, nitrogen oxides and halomethane. American Society of Microbiology, Washington, D.C., pp 219–235
Davidson EA, Chorover J, Dail DB (2003) A mechanism of abiotic immobilization of nitrate in forest ecosystems: the ferrous wheel hypothesis. Glob Change Biol 9:228–236
Davis SL, Dukes MD, Miller GL (2009) Landscape irrigation by evapotranspiration-based irrigation controllers under dry conditions in Southwest Florida. Agric Water Manag 96:1828–1836
Devitt DA, Carstensen K, Morris RL (2008a) Residential water savings associated with satellite-based ET irrigation controllers. J Irrigation Drainage Eng 134:74–82
Devitt DA, Wright L, Bowman DC, Morris RL, Lockett M (2008b) Nitrate-N concentrations in the soil solution below reuse irrigated golf course fairways. HortScience 43:2196–2202
Doane TA, Horwath WR (2003) Spectrophotometric determination of nitrate with a single reagent. Anal Lett 36:2713–2722
Drury CF, Oloya TO, Tan CS, vanLuyk CL, McKenney DJ, Gregorich EG (1997) Long-term effects of fertilization and rotation on denitrification and soil carbon. Soil Sci Soc Am J 62:1572–1579
Drury CF, Myrold DD, Beauchamp EG, Reynolds WD (2008) Denitrification techniques for soils. In: Carter MF, Gregorich EG (eds) Soil sampling and methods of analysis, 2nd edn. CRC Press, Bota Raton, pp 471–494
Eichner MJ (1990) Nitrous oxide emissions from fertilized soils: summary of available data. J Environ Qual 19:272–280
Engelsjord ME, Branham BE, Horgan BP (2004) The fate of nitrogen-15 ammonium sulfate applied to Kentucky bluegrass and perennial ryegrass turfs. Crop Sci 44:1341–1347
Fenn ME, Poth MA (2004) Monitoring nitrogen deposition in throughfall using ion exchange resin columns: a field test in the San Bernardino Mountains. J Environ Qual 33:2007–2014
Fenn ME, Haeuber R, Tonnesen GS, Baron JS, Grossman-Clarke S, Hope D, Jaffe DA, Geiser L, Rueth HM, Sickman JO (2003) Nitrogen emissions, deposition, and monitoring in the Western United States. Bioscience 53:391–403
Fenn ME, Geiser L, Bachman R, Blubaugh TJ, Bytnerowicz A (2006) Atmospheric deposition inputs and effects on lichen chemistry and indicator species in the Columbia River Gorge, USA. Environ Pollut 146:77–91
Fenn ME, Allen EB, Weiss SB, Jovan S, Geiser L, Tonnesen GS, Johnson RF, Rao LE, Gimeno BS, Yuan F, Meixner T, Bytnerowicz A (2010) Nitrogen critical loads and management alternatives for N-impacted ecosystems in California. J Environ Manag 91:2404–2423
Firestone MK, Davison EA (1989) Microbiological basis of NO and N2O production and consumption in soil. In: Andreae MO, Schimel DS (eds) Exchange of trace gases between terrestrial ecosystems and the atmosphere. Wiley, New York, pp 7–21
Fog K (1988) The effect of added nitrogen on the rate of decomposition of organic matter. Biol Rev 63:433–462
Frank KW, O’Reilly KM, Crum JR, Calhoun RN (2006) The fate of nitrogen applied to a mature Kentucky Bluegrass turf. Crop Sci 46:209–215
Frankenberger WT, Tabatabai MA (1982) Amidase and urease activities in plants. Plant Soil 64:53–166
Galloway JN, Aber JD, Erisman JW, Seitzinger SP, Howarth RW, Cowling EB, Cosby BJ (2003) The nitrogen cascade. Bioscience 53:341–356
Gleick PH, Haasz D, Henges-Jeck C, Srinivasan V, Wolff G, Kao Cushing K, Mann A (2003) Waste not, want not: the potential for urban water conservation in California. Pacific Institute, Oakland
Groffman PM, Butterbach-Bahl K, Fulweiler RW, Gold AJ, Morse JL, Stander EK, Tague C, Tonitto C, Vidon P (2009a) Challenges to incorporating spatially and temporally explicit phenomena (hotspots and hot moments) in denitrifcation models. Biogeochemistry 93:49–77
Groffman PM, Williams CO, Pouyat RV, Band LE, Yesilonis ID (2009b) Nitrate leaching and nitrous oxide flux in urban forests and grasslands. J Environ Qual 38:1848–1860
Gu C, Maggi F, Riley WJ, Hornberger GM, Xu T, Oldenburg CM, Spycher N, Miller NL, Venterea RT, Steefel G (2009) Aqueous and gaseous nitrogen losses induced by fertilizer application. J Geophys Res. doi:10.1029/2008JG000788
Guillard K, Kopp KL (2004) Nitrogen fertilizer form and associated nitrate leaching from cool-season lawn turf. J Environ Qual 33:1822–1827
Hall SJ, Huber D, Grimm NB (2008) Soil N2O and NO emissions from an arid, urban ecosystem. J Geophys Res. doi:10.1029/2007JG000523
Harivandi A, Gibeault VA (1999) Mowing your lawn and “Grasscycling”. University of California, Oakland
Hartin JS, Harivandi A (2001) Reusing turfgrass clippings to improve turfgrass health and performance in central and northern California. California Integrated Waste Management Board, Publ. 443-01-021
Heckman J, Liu H, Hill W, DeMila M, Anastasia W (2008) Kentucky bluegrass responses to mowing practice and nitrogen fertility management. J Sustain Agric 15:25–33
Henry JM, Gibeault VS, Lazaneo VF (2002) Practical lawn fertilization. University of California, Oakland
Horgan BP, Branham BE, Mulvaney RL (2002a) Mass balance of 15N applied to Kentucky Bluegrass including direct measurement of denitrification. Crop Sci 42:1595–1601
Horgan BP, Branham BE, Mulvaney RL (2002b) Direct measurement of denitrification using 15N-labeled fertilizer applied to turfgrass. Crop Sci 42:1602–1610
Huang B, Duncan RR, Carrow RN (1997) Drought-resistance mechanisms of seven warm-season turfgrasses under surface soil drying: II. Root aspects. Crop Sci 37:1863–1869
Huckaby Knight EC, Wooda CW, Guertal EA (2012) Nitrogen source effects on ammonia volatilization from warm-season sod. Crop Sci 52:1379–1384. doi:10.2135/cropsci2011.04.0198
Huh KY, Deurer M, Sivakumaran S, McAuliffe K, Bolan NS (2008) Carbon sequestration in urban landscapes: the example of a turfgrass system in New Zealand. Aust J Soil Res 46:610–616
Hutchinson GL, Davidson EA (1993) Processes for production and consumption of gaseous nitrogen oxides in soil. In: Harper LA, Mosier AR, Duxbury M, Rolston DE (eds) Agricultural ecosystem effects on trace gases and global climate change. American Society of Agronomy, Madison, pp 79–93
Intergovernmental Panel on Climate Change (2001) Third assessment report. Working group I. Cambridge University Press, New York
Jiao Y, Hendershot YH, Whalen JK (2004) Agricultural practices influence dissolved nutrients leaching through intact soil cores. Soil Sci Soc Am J 68:2058–2068
Jungkunst HF, Freibauer A, Neufeldt H, Bareth G (2006) Nitrous oxide emissions from agricultural land use in Germany—a synthesis of available annual field data. J Plant Nutr Soil Sci 169:341–351
Kaye JP, Burke IC, Mosier AR, Guerschman JP (2004) Methane and nitrous oxide fluxes from urban soils to the atmosphere. Ecol Appl 14:975–981
Kopp K, Guillard K (2002) Clipping management and nitrogen fertilization of turfgrass: growth, nitrogen utilization, and quality. Crop Sci 42:1225–1231
Kopp K, Guillard K (2004) Decomposition and nitrogen release rates of turfgrass clippings. In: Proceedings of the 4th international crop science congress. 26 September–1 October, 2004. Brisbane, QLD, Australia
Kopp K, Guillard K (2005) Clipping contributions to nitrate leaching from creeping bentgrass under varying irrigation and N rates. Int Turfgrass Soc Res J 10:80–85
Law NL, Band LE, Grove JM (2004) Nitrogen input from residential lawn care practices in suburban watersheds in Baltimore County, MD. J Environ Plan Manag 47:737–755
Long SP (1999) Environmental responses. In: Sage RF, Monson RK (eds) C4 plant biology. Academic Press, San Diego, pp 215–250
McCready MS, Dukes MD, Miller GL (2009) Water conservation potential of smart irrigation controllers on St. Augustine grass. Agric Water Manag 96:1623–1632
Milesi C, Running SW, Elvidge CD, Dietz JB (2005) Mapping and modeling the biogeochemical cycling of turf grasses in the United States. Environ Manag 36:426–438
Morton TG, Gold AJ, Sullivan WM (1988) Influence of overwatering and fertilization on nitrogen losses from home lawns. J Environ Qual 17:124–140
Mosier AR, Doran JW, Freney JR (2002) Managing soil denitrification. J Soil Water Conserv 57:505–512
Pare K, Chantigny MH, Carey K, Dionne J (2008) Leaching of mineral and organic nitrogen from putting green profiles supporting various turfgrasses. Crop Sci 48:2010–2016
Parton WJ, Jolland EA, Del Grosso SJ, Hartman MD, Martin RE, Mosier AR, Ojima DS, Schimel DS (2001) Generalized model for NOx and N2O emissions from soils. J Geophys Res 106:17403–17419
Pataki DE, Alig RJ, Fung AS, Golubiewski NE, Kennedy CA, McPherson EG, Nowak DJ, Pouyat RV, Romero Lankao P (2006) Urban ecosystems and the North American carbon cycle. Glob Change Biol 12:2092–2101
Pathan SM, Barton L, Colmer TD (2007) Evaluation of a soil moisture sensor to reduce water and nutrient leaching in turfgrass (Cynodon dactylon cv. Wintergreen). Aust J Exp Agric 47:215–222
Petrovic AM (1990) The fate of nitrogenous fertilizers applied to turfgrass. J Environ Qual 19:1–14
Pouyat RV, Russell-Anelli J, Yesilonis ID, Groffman PM (2003) Soil carbon in urban forest ecosystems. In: Heath LS, Birdsey RA, Lal R, Kimble JM (eds) The potential of U.S. forest soils to sequester carbon and mitigate the greenhouse effect. CRC, Boca Raton
Pouyat RV, Yesilonis ID, Nowak DJ (2006) Carbon storage by urban soils in the USA. J Environ Qual 35:1566–1575
Pruitt WO, Doorenbos J (1977) Empirical calibration, a requisite for evapotranspiration formulae based on daily or longer mean climatic data. In: International round table conference on evapotranspiration, International Committee on Irrigation and Drainage, Budapest, Hungary
Qian YL, Follett RF (2002) Assessing soil carbon sequestration in turfgrass systems using long-term soil testing data. Agron J 94:930–935
Qian YL, Follett RF (2012) Carbon dynamics and sequestration in urban turfgrass ecosystems. In: Lai R, Augustin B (eds) Carbon sequestration in urban ecosystems. Springer, Amsterdam, pp 161–172
Qian Y, Bandaranayake W, Parton W, Mecham B, Harivandi M, Mosier A (2003) Long-term effects of clipping and nitrogen management in turfgrass on soil organic carbon and nitrogen dynamics: the CENTURY model simulation. J Environ Qual 32:1695–1700
Raciti SM, Groffman PM, Fahey TJ (2008) Nitrogen retention in urban lawns and forests. Ecol App 18:1615–1626
Raciti SM, Burgin AJ, Groffman PM, Lewis DN, Fahey TJ (2011a) Denitrification in suburban lawn soils. J Environ Qual 40:1932–1940
Raciti SM, Groffman PM, Jenkins JC, Pouyat RV, Fahey TJ, Pickett STA, Cadenasso ML (2011b) Accumulation of carbon and nitrogen in residential soils with different land-use histories. Ecosystems 14:287–297
Scanlon BR, Jolly I, Sophocleous M, Zhang L (2007) Global impacts of conversions from natural to agricultural ecosystems on water resources: quantity versus quality. Water Resour Res. doi:10.1029/2006WR005486
Schlesinger WH, Peterjohn WT (1991) Processes controlling ammonia volatilization from Chihuahuan Desert soils. Soil Biol Biochem 23:637–642
Selhorst A, Lal R (2013) Net carbon sequestration potential and emissions in home lawn turfgrasses of the United States. Environ Manag 51:198–208
Shi W, Yao H, Bowman D (2006) Soil microbial biomass, activity and nitrogen transformations in a turfgrass chronosequence. Soil Biol Biochem 38:311–319
Šimek M, Cooper JE, Picek T, Šantrůčková H (2000) Denitrification in arable soils in relation to their physico-chemical properties and fertilization practice. Soil Biol Biochem 32:101–110
Snyder R, Pruitt W (1985) Estimating reference evapotranspiration with hourly data, chapter VII, vol 1. In: California irrigation management information system final report, land, air and water resources paper #10013-A, University of California, Davis, CA, USA
Stehfest E, Bouwman L (2006) N2O and NO emission from agricultural fields and soils under natural vegetation: summarizing available measurement data and modeling of global annual emissions. Nutr Cycl Agroecosyst 74:207–228
Synder GH, Augustin BJ, Davidson JM (1984) Moisture sensor-controlled irrigation for reducing N leaching in bermudagrass turf. Agron J 76:964–969
Torello WA, Wehner DJ, Turgeon AJ (1983) Ammonia volatilization from fertilized turfgrass stands. Agron J 75:454–456
Townsend-Small A, Czimczik CI (2010) Carbon sequestration and greenhouse gas emissions in urban turf. Geophys Res Lett. doi:10.1029/2009GL041675
Townsend-Small A, Pataki DE, Czimczik C, Tyler S (2011) Nitrous oxide emissions and isotopic composition in urban and agricultural systems in southern California. J Geophys Res 116:G01013. doi:10.1029/2010JG001494
Vaio N, Cabrera ML, Kissel DE, Rema JA, Newsome JF, Calvert VH II (2007) Ammonia volatilization from urea-based fertilizers applied to tall fescue pastures in Georgia, USA. Soil Sci Soc Am J 72:1665–1671
Virginia RA, Jarrell WM, Franco-Vizcaino E (1982) Direct measurement of denitrification in a Prosopis (Mesquite) dominated Sonoran Desert ecosystem. Oecologia 53:120–122
Wang W, Pataki DE (2012) Drivers of spatial variability in urban plant and soil isotopic composition in the Los Angeles basin. Plant Soil 350:323–338
Wang W, Zhu WX (2012) Soil retention of 15N in a simulated N deposition study: effects of live plant and soil organic matter content. Plant Soil 351:61–72
Weatherburn MW (1967) Phenol-hypochlorite reaction for determination of ammonia. Anal Chem 39:971–974
Wherley BG, Shi W, Bowman DC, Rufty TW (2009) Fate of 15N-nitrate applied to a bermudagrass system: assimilation profiles in different seasons. Crop Sci 49:2291–2301
Williams PH, Jarvis SC, Dixon E (1998) Emission of nitric oxide and nitrous oxide from soil under field and laboratory conditions. Soil Biol Biochem 30:1885–1893
Wu L, Green R, Yates MV, Pacheco P, Klein G (2007) Nitrate leaching in overseeded Bermudagrass fairways. Crop Sci 47:2521–2528
Yao H, Bowman D, Shi W (2011) Seasonal variations of soil microbial biomass and activity in warm- and cool-season turfgrass systems. Soil Biol Biochem 43:1536–1543
Youngner VB, Marsh AW, Strohman RA, Gibeault VA, Spaulding S (1981) Water use and turf quality of warm-season and cool-season turfgrasses. In: Sheard R (ed) Proceedings of the 4th international turfgrass research conference, Guelph, ON, Canada, International Turfgrass Society and University of Guelph, ON, Canada, pp 257–259, 19–23 Jul 1981
Zhu WX, Carreiro MM (1999) Chemoautotrophic nitrification in acidic forest soils along an urban-to-rural transect. Soil Biol Biochem 31:1091–1100
Zhu WX, Wang W (2011) Does soil organic matter variation affect the retention of 15NH4 + and 15NO3 − in forest ecosystems? Forest Ecol Manag 261:675–682
Acknowledgments
We thank Tammy Majcherek, Neeta Bijoor, Amy Townsend-Small, and Claudia Czimczik for site information and field assistance. We thank Dachun Zhang for laboratory instructions and assistance. For the measurements of atmospheric N deposition, we thank Mark Fenn and Andrzej Bytnerowicz for instructions and access to their lab facilities and Christopher Ross for his kind help in instrument installation and sample analysis. This study was funded by U.S. Department of Agriculture grant 2006-04686, UCI Urban Water Research Center, and National Science Foundation grant DEB 0919381.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Sujay Kaushal.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Wang, W., Haver, D. & Pataki, D.E. Nitrogen budgets of urban lawns under three different management regimes in southern California. Biogeochemistry 121, 127–148 (2014). https://doi.org/10.1007/s10533-013-9942-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10533-013-9942-1