Amplitude and duration hazard-consistent ground-motion selection for seismic risk assessment in Mexico City

Abstract

The emphasis of seismic design regulations on applying nonlinear dynamic analyses (NDAs) promotes using accelerograms that characterize site-specific ground motions. Commonly, amplitude levels of such accelerograms are defined by a target spectrum that could be based on a uniform hazard spectrum (UHS), which is determined by a probabilistic seismic hazard analysis (PSHA) and represents a response spectrum with ordinates having an equal probability of being exceeded within a given return period, ${T}_{r}$. Conversely, the definition of ground-motion duration levels is not yet properly defined in current regulations to select accelerograms. Thus, adhering to data handling as that for amplitude ground-motion parameters, this study motivates executing PSHAs to define hazard-consistent levels for the ground-motion duration. That is, accelerograms can be selected to match both amplitude and duration ground-motion levels associated with ${T}_{r}$. Further, fragility functions conditional on ${T}_{r}$ that cover typical performance objectives can be developed using sets of hazard-consistent accelerograms to implement, e.g., multiple stripe analyses (MSAs). To demonstrate the importance of choosing fully hazard-consistent accelerograms to perform NDAs, this study includes the displacement- and energy-based seismic-response evaluation of a steel frame building located at different soil-profile sites in Mexico City. Sets of fully hazard-consistent accelerograms and solely amplitude-based hazard-consistent accelerograms were artificially generated per site for values of ${T}_{r}$ up to 5000 years. Results indicate that the probability of failure can be underestimated if the ground-motion duration is unvaried in MSAs, e.g., structural damage caused by 50-year return-period or higher events can be more noticeable when fully hazard-consistent accelerograms take place.

1 Introduction

A seismic risk analysis (SRA) aims to estimate the probability of structural failure at least once during an exposure time, $T$. For instance, being the ground shaking the most widespread and damaging earthquake hazard, one can estimate the annual probability of damage, ${P}_{F}$, as follows (McGuire 2004):

$${P}_{F}=\int P\left(EDP>DS|Y=y\right){f}_{Y}\left(y\right)\text{d}y$$

(1)

where $P\left(EDP>DS|Y=y\right)$ is the probability that an engineering demand parameter, $EDP$, exceeds a discrete damage state, $DS$, given that a ground-motion parameter, $Y$, takes a value equal to $y$, and ${f}_{Y}$ denotes the probability density function of $Y$. The conditional exceedance probability of $DS$ is typically evaluated using a fragility function, whereas ${f}_{Y}$ can be obtained from a PSHA.

On the one hand, a PSHA allows estimating the exceedance probability of $y$ considering the broad set of earthquakes that might affect a site of interest (McGuire 2008). As an instance, using the law of total probability one can estimate the probability that $Y$ takes a value greater than $y$ as follows (Kramer 1996):

$$P\left(Y>y\right)=\int P\left(Y>y|{x}_{1},\dots ,{x}_{p}\right){f}_{{X}_{1},\dots ,{X}_{p}}\left({x}_{1},\dots ,{x}_{p}\right)\text{d}{x}_{1}\cdots \text{d}{x}_{p}$$

(2)

where $P\left(Y>y|{x}_{1},\dots ,{x}_{p}\right)$ denotes the complementary distribution function of $Y$ conditional on a set of explanatory variables ${X}_{1}, \dots , {X}_{p}$ that are defined by the joint density function ${f}_{{X}_{1},\dots ,{X}_{p}}$. The conditional probability of exceeding $y$ can be evaluated using a ground motion prediction equation (GMPE), which is a mathematical expression that allows estimating the ground motion expected at a site of interest from specific earthquake scenarios. Various GMPEs for the ground-motion duration have been developed in the last two decades, but to a lesser extent in comparison to GMPEs for amplitude-based ground-motion parameters (Douglas 2022). For instance, one can find in the literature GMPEs developed by Kempton and Stewart (2006), Bommer et al. (2009), Yaghmaei et al. (2014), Lee and Green (2014), Afshari and Stewart (2016), and Du and Wang (2017). These authors used data provided by the Pacific Earthquake Engineering Research Center (PEER) to develop the GMPEs. Also, Meimandi-Parizi et al. (2020) and Yaghmaei et al. (2022) have recently developed GMPEs for the ground-motion duration using Iranian and Turkish strong-motion datasets, respectively, whereas Jaimes and Garcia-Soto (2021) and López-Castañeda and Reinoso (2021, 2022) developed GMPEs using information from Mexican strong-motion databases. The citied researchers studied the relative significant duration, ${D}_{Sr}$, which is defined as the interval between the times at which different specified values of the normalized Arias intensity, ${I}_{A}$, are reached (Bommer and Martínez-Pereira 1999). The scarcity of GMPEs for the ground-motion duration prevents its inclusion in PSHAs (Raghunandan and Liel 2013). Incidentally, only Otárola et al. (2023) and López-Castañeda (2022) report hazard curves for the duration of ground-motions. The main results of the latter will be included in this article.

A fragility function, which defines the first term of the integral in Eq. (1), can be developed from the results of a MSA. First, an NDA is a step-by-step analysis of the nonlinear dynamic response of a structural system to a specified loading that varies with time, $t$, which is generally an accelerogram, i.e., a record of the ground acceleration, ${\ddot{u}}_{g}$, as a function of $t$. Then, an MSA involves performing several NDAs for different ground-motion levels $y$ (Jalayer and Cornell 2009). A different set of accelerograms is commonly used to carry out the NDAs at each $y$. Hence, with the MSA results at each stripe, i.e., at each $y$, the probability of exceeding predefined damage states $DS$ can be evaluated by means of statistical inference. Likewise, many researchers have preferred to perform an IDA to develop fragility functions. An IDA consists on scaling a single set of accelerograms to the predefined ground-motion levels $y$ to accomplish the NDAs (Vamvatsikos and Cornell 2002; Jalayer and Cornell 2009). By standard, the sets of accelerograms are scaled to meet values for a single amplitude ground-motion parameter, e.g., the peak ground acceleration, ${PGA}$, while keeping the ground-motion frequency content and the duration unvaried.

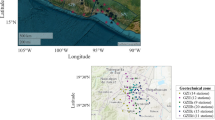
Thus, several studies have evaluated the effects of the ground-motion duration on the structural response using conventional IDAs. In some of studies, the sets of accelerograms have been classified as short- or long-lasting depending on, e.g., predefined thresholds (Iervolino et al. 2006; De Luca et al. 2013; Chandramohan et al. 2016a; Barbosa et al. 2017; Belejo et al. 2017; Bravo-Haro and Elghazouli 2018; Molazadeh and Saffari 2018; Liapopoulou et al. 2019; Vega and Montejo 2019; Bravo-Haro et al. 2020). For instance, following the work of Chandramohan et al. (2016a), various researchers have labeled as “short-duration records” those accelerograms having ${D}_{Sr}\hspace{0.17em}$< 25 s (measuring ${D}_{Sr}$ from the points at which 5% and 75% of the normalized ${I}_{A}$ is reached). Looking closely at the databases used in the referred studies, the authors noticed that accelerograms related to ground-motions caused by shallow-crustal earthquakes are commonly classified as short-lasting, whereas those related to subduction interplate or intraslab earthquakes as long-lasting. Nonetheless, such a classification loses sense because even ground-motions originated by the same tectonic environment could be treated as short- or long-lasting (López-Castañeda et al. 2022). For example, Fig. 1 shows a set of accelerograms recorded at four different sites in Mexico City during the March 20, 2012, earthquake with epicenter in Oaxaca, Mexico. The sites are located within an 8-km radius and exhibit values of the dominant period of the soil, ${T}_{s}$, equal to 0.5 s, 1.3 s, 2.5 s, and 4.0 s (SOS-CDMX 2020). Likewise, ground-motions caused by two distinct tectonic environments tend to be similarly classified as short- or long-lasting. For example, it is regrettable to mention the havoc due to the long-lasting ground motions originated by the 1985 and 2017 Mexico earthquakes on September 19, as well as the 2023 Turkey–Syria earthquake on February 6. While the 1985 and 2017 Mexico earthquakes are associated with reverse and normal focal mechanisms, respectively, the 2023 Turkey–Syria earthquake is associated with a strike-slip focal mechanism (GEER-EERI 2023). Thus, the frequency content, amplitude, and duration of the ground motions generated by such events are entirety different. Then, classifying ground motions as long-lasting could be arbitrary. Beyond the mentioned categorical classification, the influence of the ground-motion duration on the nonlinear structural response (mostly observed when using energy-based $EDPs$) has been demonstrated by the cited researchers. Thus, the importance of addressing such a relevant topic is major.

Fig. 1

Left: map showing the territorial delimitation of Mexico City and the geographical location of four ground-motion recording stations, namely, CUP5, UC44, BO39, and AU11. Right: collection of accelerograms recorded during the 2012 Oaxaca earthquake on March 20. The accelerograms are bounded by ${a}_{0}\hspace{0.17em}$= 2 cm/s². The shaded areas stand for the strong-motion lapse of each accelerogram

One can find in the literature some studies that address the effects of the ground-motion duration on seismic risk results (Raghunandan 2015; Chandramohan et al. 2016b; Hwang et al. 2020; López-Castañeda et al. 2022). For example, Chandramohan et al. (2016b) used the generalized conditional intensity measure (GCIM) method to select ground motions that account for the correlation among the spectral acceleration ordinate, ${S}_{a}$, at the fundamental elastic period, ${T}_{1}$, of the structure under study, and a ${D}_{Sr}$ for the seismic collapse assessment of a reinforced concrete building. In brief, the GCIM approach is based on the conditional mean spectrum (CMS) approach, and therefore accounts for (Bradley 2010): (a) vectors of total residuals for the ground-motion parameters of interest defined from GMPEs, and (b) the linear correlation between such vectors of residuals but considering disaggregation weights corresponding to contributing earthquake scenarios.

The utilization of UHSs for the selection of ground motions has been regarded with some drawbacks because it is argued that it leads to conservative results for structural analysis. Notwithstanding, although the use of the CMS approach to select ground-motions has been recommended in various United States (US) seismic design standards, e.g., NIST GCR 11-917-15 (NEHRP-NIST 2011), the UHS has not been ruled out as reported in the ASCE 7-22 standard (ASCE 2022). Even other worldwide regulations based their design ground motions on target UHSs, e.g., the construction regulations for Mexico City (NTC-2023) consider UHSs for values of ${T}_{r}$ equal to 250 years and 475 years (SOS-CDMX 2023). Whichever is the criteria used to define the design spectra for the selection of accelerograms, current design regulations define the ground-motion duration based on the hazard disaggregation of an amplitude-based ground-motion parameter (e.g., $PGA$ as in the NTC-2023) or just establish predefined values for the ground-motion duration, e.g., the EN 1998-1:2010 (CEN 2010) states that the duration of the stationary part of the seismic motion should be equal to 10 s when site-specific data are not available.

In view of the foregoing, the main objective of this research article is to propose an alternative and accessible criterion for the selection of hazard-consistent accelerograms that account not only for the amplitude and frequency content characterizing the expected ground motion at a particular site, but also its duration. Such an approach requires no hazard disaggregation as it directly considers the results of hazard curves to select ground-motion levels. A detailed performance-based evaluation of a steel frame building hypothetically located at various sites in Mexico City is presented in this article as an application example. The case study includes: (a) the determination of hazard curves for both amplitude- and duration-based ground motion parameters, (b) the simulation of multiple sets of mutually independent hazard-consistent accelerograms, (c) the definition and evaluation of the inelastic behavior of the building via NDAs, (d) the development of fragility functions and SRA conditional on ${T}_{r}$. Moreover, a comparison between performing the NDAs using both fully hazard-consistent accelerograms and amplitude-based hazard-consistent accelerograms is performed. At the end, a brief conclusion is given underling how the proposed approach for ground-motion selection was achieved under the stablished scope and some recommendations are given for future work on topics related to ground-motion duration.

2 Methodology

This study proposes defining sets of accelerograms that would intervene in NDAs using amplitude and duration ground-motion levels associated with predefined values of ${T}_{r}$. This way, the probability of damage suffered by a structural system, i.e., the first term of the integral given in Eq. (1), can be rewritten as $P\left(EDP>DS|{T}_{r}=z\right)$, which means the probability that the structural response exceeds a damage state given that ${T}_{r}$ takes a predefined value $z$. The following steps can be used to achieve the goal:

• 1. Select values of ${T}_{r}$ that cover typical performance objectives. Preferably, those for the design or economical life of the analyzed structure should be included.

• 2. Obtain amplitude and duration ground-motion levels associated with each of the predefined values of ${T}_{r}$. This step involves performing PSHAs for a set of ground-motion parameters selected to characterize the amplitude and duration of the ground-motions at the site where the structure is located. Following the convention, $PGA$ and ${S}_{a}\left({T}_{e}\right)$ should be considered as the amplitude-based ground motion parameters. Either the total ground-motion duration or the strong-motion duration can be used to describe the length of the accelerograms.

• 3. Generate a set of $n$ hazard-consistent accelerograms having both amplitude and duration ground-motion levels per value of ${T}_{r}$.

• 4. Quantify the response of the structure of interest performing multiple NDAs, i.e., via an MSA, considering the sets of hazard-consistent accelerograms defined in Step 3. The authors suggest presenting the MSA results as plots of the structural response versus ${T}_{r}$, which already associate both amplitude and duration ground-motion levels.

• 5. Use the hazard-consistent MSA results to develop fragility functions. A continuous fragility function is generally determined using the form of a lognormal distribution, with parameters $\mu$ and $\sigma$, as follows:

  $$P\left(EDP>DS|{T}_{r}=z\right)=\Phi \left[\frac{\text{ln}\left(z\right)-\mu }{\sigma }\right]$$

  (3)

where $\Phi$ is the distribution function of the standard normal distribution. Estimates of $\mu$ and $\sigma$ can be determined from linear regression, knowing that ${\Phi }^{-1}\left[P\left(EDP>DS|{T}_{r}=z\right)\right]=\frac{1}{\sigma }\text{ln}\left(z\right)-\frac{\mu }{\sigma }$ resembles a linear model.

• 6. Perform SRAs. By convention, and based on Eq. (1), ${P}_{F}$ is computed as follows:

  $$P_{F} = \int \lambda_{y} \left| {\frac{{{\text{d }}P\left( {EDP > DS|Y = y} \right)}}{{{\text{d}}y}}} \right|{\text{ d}}y$$

  (4)

  where ${\lambda }_{y}$ is the mean annual rate of exceedance of $y$. But based on the hazard-consistent fragility functions, ${P}_{F}$ can be directly computed as:

  $$P_{F} = \int \frac{1}{{T_{r} = z}}\left| {\frac{{{\text{d }}P\left( {EDP > DS|T_{r} = z} \right)}}{{{\text{d}}z}}} \right|{\text{ d}}z$$

  (5)

Notice that step 3 recommends generating artificial hazard-consistent accelerograms. The latter is encouraged because it is almost unattainable to have enough hazard-consistent accelerograms to perform a stripe analysis at every intensity level. Even so, real accelerograms with alike values of amplitude and duration ground-motion levels associated to predefined values of ${T}_{r}$ can be selected to perform a number of hazard-consistent NDAs.

It is worth mentioning that the methodology proposed in this article for the selection of hazard-consistent accelerograms can be adapted for the selection of either displacement- or velocity-based ground-motion signals. Also, hazard-consistent ground-motions that account for the association among amplitude- and duration-based ground-motion parameters can be defined. In such a case, it would remain to analyze the joint seismic hazard of the selected set of ground-motion parameters to define the correlated ground-motion levels for desired levels of ${T}_{r}$.

3 Seismic hazard analysis for Mexico City

This section presents the probabilistic evaluation of the seismic hazard for three sites located in Mexico City where stations UC44, BO39, and AU11 are installed (see Fig. 1). The sites are characterized by values of ${T}_{s}$ equal to 1.3 s, 2.5 s, and 4.0 s, respectively. For each site, the PSHA will be carried out considering the contribution of all interplate earthquake sources affecting Mexico City and taking as explanatory variables the earthquake magnitude, $M$, and the hypocentral distance, $R$. Following Eq. (2), and assuming that $M$ and $R$ are independent variables with marginal density functions ${f}_{M}$ and ${f}_{R}$, respectively, one can estimate ${\lambda }_{y}$ as (Kramer 1996):

$${\lambda }_{y}=\sum_{i=1}^{{N}_{S}}{{\lambda }_{{m}_{{0}_{i}}}}\iint P\left(Y>y|M=m,R=r\right){f}_{{M}_{i}}\left(m\right){f}_{{R}_{i}}(r)\text{d}m\text{d}r$$

(6)

where, for each $i=1,\dots ,{N}_{S}$ earthquake source, ${\lambda }_{{m}_{{0}_{i}}}$ is the mean annual rate at which an earthquake with a magnitude equal to ${m}_{0}$ will be exceeded and $P\left(Y>y|M=m,R=r\right)$ is the probability of exceeding $y$ given that $M$ and $R$ take specific values $m$ and $r$, respectively.

The characterization of the intraplate earthquake sources is described first in Sect. 3.1. Then, PSHAs for duration and amplitude ground-motion parameters are performed in Sects. 3.2 and 3.3, respectively. Section 3.4 presents artificial accelerograms that can be used to develop hazard-consistent fragility functions for any structure located at the sites under study. The earthquake catalog used to perform the PHSAs is given in Appendix B of the doctoral dissertation of López-Castañeda (2022).

3.1 Identification and characterization of interplate earthquake sources

Identifying earthquakes of similar nature requires extensive knowledge of the tectonic and geologic structures that characterize the region of interest. For this purpose, many ad hoc research works were consulted, including those of Ramírez-Herrera and Urrutia-Fucugauchi (1999), Ordaz and Reyes (1999), and Zúñiga et al. (2017). Four source zones for interplate earthquakes were identified. They are areas in which earthquakes occur at many different locations along the Middle American Trench (MAT). A map depicting the four source zones is given in Fig. 2.

Fig. 2

Map depicting source zones for interplate earthquakes occurring along the MAT. The abbreviation RP means Rivera Plate. The earthquake epicenters used to estimate the seismicity of each source zone are marked with circles. The blue triangle stands for an observational site located in Mexico City

The quantitative description of the time, size, and spatial distribution of earthquake occurrences is defined next under the assumption that each source zone describes a domain within which earthquakes (a) are equally likely in space, (b) conform to a single magnitude distribution, (c) have the same maximum magnitude, and (d) are independent of each other (McGuire and Arabasz 1990).

3.1.1 Earthquake occurrence model and magnitude distribution

The “shifted and truncated” form of the Gutenberg and Richter law was used to define the earthquake occurrence within each source zone. It can be expressed as follows (Kramer 1996):

$${\lambda }_{m}={\lambda }_{{m}_{0}}\frac{\text{exp}\left[-\beta \left(m-{m}_{0}\right)\right]-\text{exp}\left[-\beta \left({m}_{u}-{m}_{0}\right)\right]}{1-\text{exp}\left[-\beta \left({m}_{u}-{m}_{0}\right)\right]}$$

(7)

where $\beta$ describes the ratio between the number of small and large earthquakes, and ${m}_{0}$ and ${m}_{u}$ are lower and upper magnitude limits, respectively. Then, based on Eq. (7), ${f}_{M}$ can be written as:

$${f}_{M}\left(m\right)=\frac{\beta \text{exp}\left[-\beta \left(m-{m}_{0}\right)\right]}{1-\text{exp}\left[-\beta \left({m}_{u}-{m}_{0}\right)\right]}$$

(8)

The approach proposed by Kijko and Smit (2012) was used in this study to estimate $\beta$ and ${\lambda }_{{m}_{0}}$. That is, consider that an incomplete earthquake catalog, with ${N}_{T}$ earthquakes, is divided into $j=1,\dots ,{N}_{C}$ sub-catalogs, each with ${N}_{{E}_{j}}$ earthquakes. Each sub-catalog $j$ is complete for time periods ${T}_{j}$ and earthquakes with $m\ge {m}_{{0}_{j}}$. Then, $\beta$ was computed as follows (Kijko and Smit 2012):

$$\beta =\frac{{N}_{T}}{{\sum }_{j=1}^{{N}_{C}}{S}_{j}}$$

(9)

where ${S}_{j}$ is defined as:

$${S}_{j}=\sum_{k=1}^{{N}_{{E}_{j}}}\left({m}_{k,j}-{m}_{{0}_{j}}\right)$$

(10)

If $\beta$ is known, ${\lambda }_{{m}_{{0}_{1}}}$ can be obtained as follows:

$${\lambda }_{{m}_{{0}_{1}}}=\frac{{N}_{T}}{{\sum }_{j=1}^{{N}_{C}}{T}_{j}\text{exp}\left(\beta {\Delta }_{j}\right)}$$

(11)

where ${\Delta }_{j}$ is equal to ${m}_{{0}_{j}}-{m}_{{0}_{1}}$.

Table 1 summarizes some statistics used in the estimation process of $\beta$ and ${\lambda }_{{m}_{0}}$, and Table 2 reports the results. Figure 3 shows the recurrence curves for each source zone. Note that in Fig. 3 the lower-bound ${m}_{0}$ was set equal to 6.0 for all source zones; therefore, ${\lambda }_{{m}_{0}}$ equals ${\lambda }_{{m}_{{0}_{1}}}$. The magnitude thresholds ${m}_{u}$, which are reported in Table 2, were specified as ${m}_{max}+0.2$, with ${m}_{max}$ being the magnitude of the maximum probable earthquake known from each source zone as reported by López-Castañeda (2022).

Table 1 Statistics used to estimate the $\beta$-values and seismicity rates ${\lambda }_{{m}_{0}}$

Table 2 Estimates of the $\beta$-values, seismicity rates ${\lambda }_{{m}_{0}}$, and magnitude thresholds ${m}_{u}$

Fig. 3

Annual exceedance rates of magnitude ${\lambda }_{m}$ for the interplate source zones depicted in Fig. 1. Points indicate the empirical fitting of the data: first sub-catalog in green, second sub-catalog in blue, and third sub-catalog in yellow

3.1.2 Source-to-site distance distribution

Statistical inference was used to define the probability distribution of $R$. This decision was made to reduce uncertainties related to modeling complex fault planes that are (at least for the authors) imperfectly understood. The distances from an observation site located in Mexico City to the earthquake hypocenters were computed for each source zone. The observational site was set at the geographic coordinates 19.35°N, 99.15°W (see Fig. 2), and has an altitude, ${H}_{s}$, equal to 2240 m. Table 3 summarizes the minimum and maximum values of $R$, ${r}_{min}$ and ${r}_{max}$, respectively, computed for each source zone. Various probability distributions were evaluated to determine which describes $R$ the best. The GEV distribution fitted the data fine. Therefore, ${f}_{R}$, can be defined as follows:

$$f_{R} \left( s \right) = \left\{ {\begin{array}{*{20}l} {\exp \left( { - s} \right)\exp \left[ { - \exp \left( { - s} \right)} \right]} \hfill & {\kappa = 0} \hfill \\ {\left( {1 + \kappa s} \right)^{{ - \left( {1 + 1/\kappa } \right)}} \exp \left[ { - \left( {1 + \kappa s} \right)^{{ - \frac{1}{\kappa }}} } \right]} \hfill & {\kappa \ne 0{\text{ and }}\kappa s > - 1} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$

(12)

where $s=\left(r-{\mu }_{r}\right)/{\sigma }_{r}$ is a standardized variable, with ${\mu }_{r}$ and ${\sigma }_{r}$ being the GEV distribution parameters. The parameter estimates of the GEV distribution are presented in Table 4.

Table 3 Lower and upper point-source distance limits ${r}_{min}$ and ${r}_{max}$ observed in each source zone

Table 4 Estimates of the GEV distribution parameters ${\mu }_{r}$, ${\sigma }_{r}$, and $\kappa$, and distance thresholds ${r}_{1}$ and ${r}_{2}$ corresponding to the levels at which ${F}_{R}$ equals 0.05 and 0.95, respectively

3.2 Strong-motion duration hazard curves

A parameter termed strong-motion duration has been adopted to account for the portion of an accelerogram to be considered for earthquake-engineering purposes (Salmon et al. 1992). Various definitions for the strong-motion duration can be found in the literature of which the most used is ${D}_{Sr}$, whose definition is based on the accumulation of energy in an accelerogram (Bommer and Martínez-Pereira 1999). If the energy is represented as a function of ${\ddot{u}}_{g}$, ${D}_{Sr}$ can be computed as:

$${D}_{Sr}=\int \left\{H\left[h\left(t\right)-{a}_{1}\right]-H\left[h\left(t\right)-{a}_{2}\right]\right\}\text{d}t$$

(13)

where $H$ is the Heaviside step function, ${a}_{1}$ and ${a}_{2}$ are fractions that equal 0.05 and 0.95, respectively, and $h$ stands for the normalized ${I}_{A}$ as function of $t$ and can be defined as follows:

$$h\left(t\right)=\frac{{I}_{A}\left(t\right)}{{{I}_{A}}_{max}}$$

(14)

where ${I}_{A}$ can be computed as follows (Arias 1970):

$${I}_{A}\left(t\right)=\frac{\pi }{2g}{\int }_{{t}_{1}}^{{t}_{2}}{\ddot{u}}_{g}{\left(t\right)}^{2}\text{d}t$$

(15)

with $g$ being the gravitational acceleration near Earth’s surface, and ${I}_{{A}_{max}}$ is the maximum value of ${I}_{A}$ defined by Eq. (15). Using the criterion established by López-Castañeda and Reinoso (2022), ${t}_{1}$ and ${t}_{2}$ are the time instants associated with the first and last excursion, respectively, of a specified acceleration threshold, ${a}_{0}$, equal to 2 cm/s². That is, the accelerograms had to be bounded by ${a}_{0}$ to compute ${D}_{Sr}$ (see Fig. 1). Following the stated criterion to measure ${D}_{Sr}$, the mean annual rate of exceedance a strong-motion duration level $d$, ${\lambda }_{d}$, was estimated evaluating numerically Eq. (6) as follows:

$${\lambda }_{d}=\sum_{i=1}^{{N}_{S}}\sum_{j=1}^{{N}_{M}}\sum_{k=1}^{{N}_{R}}{\lambda }_{{m}_{{0}_{i}}}P\left({D}_{Sr}>d|M={m}_{j},R={r}_{k}\right)P\left(M={m}_{j}\right)P\left(R={r}_{k}\right)$$

(16)

where ${\lambda }_{d}$ is the exceedance rate of $d$, ${N}_{M}$ is the total number of elements in a finite set of earthquake magnitudes bounded by the thresholds ${m}_{0}$ and ${m}_{u}$, and ${N}_{R}$ is the total number of elements in a finite set of source-to-site distances bounded by the thresholds ${r}_{1}$ and ${r}_{2}$, defined as the levels at which the distribution function of $R$, ${F}_{R}$, equals 0.05 and 0.95, respectively. For each source zone, the values of ${r}_{1}$ and ${r}_{2}$ are reported in Table 4. The conditional probability that ${D}_{Sr}$ exceeds $d$ as presented in Eq. (16) can be expressed as follows:

$$P\left({D}_{Sr}>d|M={m}_{j},R={r}_{k}\right)=1-{F}_{{D}_{Sr}}\left(d\right)$$

(17)

where ${F}_{{D}_{Sr}}$ is the distribution function of ${D}_{Sr}$. For the case study, ${F}_{{D}_{Sr}}$ in Eq. (17) was defined from a recent GMPE for the natural logarithm of ${D}_{Sr}$, $\text{ln}\left({D}_{Sr}\right)$, proposed by López-Castañeda and Reinoso (2022). Such a GMPE was developed using a linear mixed-effects model and has the following form:

$$\text{ln}\left({D}_{Sr}\right)=5.5590+0.5241\text{ln}\left({T}_{s}\right)+\left(-0.7859+0.0735M\right)\text{ln}\left(R\right)+\eta$$

(18)

where $\text{ln}\left({T}_{s}\right)$ and $\text{ln}\left(R\right)$ are the natural logarithms of ${T}_{s}$ and $R$, respectively, and $\eta ={b}_{0}+e$ is the composite model error whose terms have prior distributions ${b}_{0}\sim \mathcal{N}\left(0,{\sigma }_{b}^{2}\right)$ and $e\sim \mathcal{N}\left(0,{\sigma }_{w}^{2}\right)$, respectively. The estimates of ${\sigma }_{b}^{2}$ and ${\sigma }_{w}^{2}$ are 0.0120 and 0.0345, respectively. Under the assumption that ${b}_{0}$ and $e$ are normally distributed, it can be said that $\text{ln}\left({D}_{Sr}\right)$ is normally distributed with mean, ${\mu }_{\text{ln}\left({D}_{Sr}\right)}$, equal to the estimated function $\mathcal{g}\left({T}_{s},M,R\right)$ defining Eq. (18) and variance, ${\sigma }_{\text{ln}\left({D}_{Sr}\right)}^{2}$, equal to the sum of ${\sigma }_{b}^{2}$ and ${\sigma }_{w}^{2}$. Then, ${D}_{Sr}$ can be characterized by a lognormal distribution; therefore, its mean, ${\mu }_{{D}_{Sr}}$, and standard deviation, ${\sigma }_{{D}_{Sr}}$, can be computed as follows:

$${\mu }_{{D}_{Sr}}=\text{exp}\left({\mu }_{\text{ln}\left({D}_{Sr}\right)}+\frac{{\sigma }_{\text{ln}\left({D}_{Sr}\right)}^{2}}{2}\right)$$

(19)

and

$${\sigma }_{{D}_{Sr}}^{2}=\left\{\text{exp}\left[{\sigma }_{\text{ln}\left({D}_{Sr}\right)}^{2}\right]-1\right\}\text{exp}\left[2{\mu }_{\text{ln}\left({D}_{Sr}\right)}+{\sigma }_{\text{ln}\left({D}_{Sr}\right)}^{2}\right]$$

(20)

Note that in Sect. 3.1.2$R$ was characterized by a point-source distance measure that is indeed the hypocentral distance. Therefore, $R$ in Eq. (18) also stands for such a seismological variable.

Figure 4 shows the strong-motion duration hazard curves for the UC44, BO39, and AU11 sites. The expected values of ${D}_{Sr}$ for nine values of ${T}_{r}$ are summarized in Table 5. Recall that ${T}_{r}\hspace{0.17em}$= $1/{\lambda }_{d}$.

Fig. 4

Hazard curves of ${D}_{Sr}$ that consider the contribution of all seismic sources of interplate earthquakes that occur at the MAT for the sites where stations UC44, BO39, and AU11 are located

Table 5 Expected values of ${D}_{Sr}$ associated to values of ${T}_{r}$ varying from 10 to 5000 years

3.3 Uniform hazard spectra

As mentioned in Sect. 1, UHSs can be constructed from hazard curves for $PGA$ and ${S}_{a}\left({T}_{e}\right)$. Unfortunately, the lack of reported GMPEs for the mentioned amplitude ground-motion parameters for sites located in Mexico City other than the main campus of the National Autonomous University of Mexico (UNAM, for its acronym in Spanish) prevents up to a point the performance of PSHAs for the sites of interest (López-Castañeda 2022). Although it is possible to develop some GMPEs for the sites of interest to achieve such an aim, these are out of the scope of this study. Nonetheless, the path taken to construct UHSs at stations UC44, BO39, and AU11 considers the use of spectral ratios because there is substantial information from a station named CUP5 (at the main UNAM campus). The next steps were followed:

• 1. Collect recordings at stations CUP5, UC44, BO39, and AU11 that include accelerograms in two orthogonal horizontal components of the ground motion.

• 2. Obtain values of $PGA$ and ${S}_{a}\left({T}_{e}\right)$ associated with each accelerogram. The response-spectral ordinates were defined by the absolute acceleration (Anderson 2003) for values of ${T}_{e}$ up to 5 s.

• 3. For each ground-motion recording, compute the geometric mean of each pair of values of $PGA$ and ${S}_{a}\left({T}_{e}\right)$ obtained from the accelerograms.

• 4. Compute event-compatible spectral ratios between geometric mean spectra obtained from ground motions recorded at stations UC44, BO39, and AU11 and those from station CUP5.

• 5. For each site, calculate the average of the event-compatible spectral ratios.

• 6. Develop UHS for the CUP5 site associated with the values of ${T}_{r}$ given in Table 5. The mean annual rate of exceedance of a given level $a$ of either $PGA$ or ${S}_{a}\left({T}_{e}\right)$, ${\lambda }_{a}$, was estimated by evaluating numerically Eq. (2) and using an ad hoc GMPE proposed by López-Castañeda (2022).

• 7. Obtain UHSs for the UC44, BO39, and AU11 sites by multiplying each UHS for the CUP5 site and the spectral ratios computed in step 5.

The earthquakes that generated the ground-motion recordings that were used to obtain the spectral ratios (step 1) occurred on: September 14, 1995, January 22, 2003, January 1, 2004, June 30, 2010, March 20 and April 11, 2012, August 21, 2013, April 18, May 8, and May 10, 2014, and February 16, 2018. Station UC44 disregard the first and fifth earthquakes, whereas station AU11 disregard the fourth earthquake. Stations CUP5 and BO39 recorded all the mentioned events. An illustrative guide of steps 2 to 5 defined above is provided in Figs. 5 and 6. First, Fig. 5 shows pairs of acceleration response spectra and their geometric mean obtained from ground-motions recorded at stations CUP5, UC44, BO39, and AU11 during three earthquakes (steps 2 and 3). Then, Fig. 6 shows the event-compatible spectral ratios and their average (steps 4 and 5), as well as the developed UHSs for each site (step 7).

Fig. 5

Response spectra of horizontal components of ground motion recorded at stations CUP5, UC44, BO39, and AU11 during the earthquakes of January 22, 2003, March 20, 2012, and April 18, 2014

Fig. 6

Left: event-compatible spectral ratios and their average. Right: UHSs associated with values of ${T}_{r}$ varying from 10 to 5000 years (see Table 5)

3.4 Hazard-consistent accelerograms

Nine sets of forty statistically-independent artificial accelerograms were generated per site by employing stochastic simulation from random vibration theory (Gasparini and Vanmarcke 1976). Each set of accelerograms has specific values of $PGA$ and ${D}_{Sr}$, as well as response spectra, associated with one value of ${T}_{r}$ given in Table 5. As an instance, Fig. 7 shows three accelerograms (one per site) for ${T}_{r}\hspace{0.17em}$= 250 years. Notice from Fig. 7 that only time windows in which the accelerograms may be considering as strong (according to the definition of ${D}_{Sr}$) were simulated.

Fig. 7

Left: response spectra from the synthetic accelerograms generated for the UC44, BO39, and AU11 sites for ${T}_{r}\hspace{0.17em}$= 250 years. Right: three artificial accelerograms (one per site) for such a value of ${T}_{r}$

4 Building case study

The building case study consists of a four-story one-bay steel frame building that was conceived using plastic design criteria (Goel and Chao 2008). It was defined from a structure simple enough for its capacity to be reliably studied and replicated in the analyses performed herein, as well as a structure whose characteristics could be considered representative of the buildings that could be affected in Mexico City. The gravity loads acting on the building, structural profiles, and dimensions are presented in Fig. 8. A classical modal analysis of the building was used to find the periods at which the building naturally resonates. A triangular-shaped first mode controls the response of the system. A natural period, ${T}_{1}$, equal to 1.2 s and mass participation of 0.82 are associated with such a vibration mode. The seismic capacity of the building was determined using an incremental nonlinear static analysis (NSA). For this purpose, a monotonically increasing lateral force with a linearly variant height-wise distribution pattern concordant with the first mode of the building was used. Figure 8 shows a pushover curve determined from the incremental NSA results. Specifically, the pushover curve plots the horizontal shear force at the base of the building, ${V}_{b}$, versus the roof displacement, ${u}_{e}$, which is result of the lateral forces acting along the heigh of the building.

Fig. 8

Schematic of the building case study (left). Nonlinear static pushover curve of the building considering a first mode lateral load pattern and capacity curve of its equivalent SDOF system (right)

An equivalent SDOF system of the building case study was defined to perform a massive number of NDAs at an affordable computational cost. A scheme for such an equivalent model is given in Fig. 9. The lateral stiffness, ${k}_{e}$,of the equivalent SDOF system was determined from the linear interval in the pushover curve for the building (see Fig. 8) and its mass, ${m}_{e}$, was computed so that the period of the equivalent SDOF system matched ${T}_{1}$. The fraction of critical damping, ${\zeta }_{e}$, was assumed as 5%. In Fig. 9${c}_{e}$ is the viscous damping coefficient, ${u}_{t}$ is the total displacement of the equivalent SDOF system, and ${\alpha }_{e}$ is a fraction of ${k}_{e}$ determined from the maximum strength of the building, ${F}_{u}$, and, the ultimate displacement limit, ${u}_{u}$ (see Fig. 8). The constitutive model for the equivalent SDOF system, depicted in Fig. 9, considers an elastic–plastic behavior with hardening. The bilinear loop shown in Fig. 9 represents the forces on the spring of the equivalent SDOF system, ${F}_{k}$, versus deformations ${u}_{e}$ in the equivalent SDOF system caused by inelastic behavior. In Fig. 9${F}_{y}$ and ${u}_{y}$ stand for the yield strength and yield deformation at the roof, respectively, of the building case study. The capacity curve of the equivalent SDOF system is shown in Fig. 8. As noticed from Fig. 8, the area under the capacity curve of the equivalent SDOF is smaller than the area under the pushover curve for the steel frame building. Expressly, there is a difference of less than 5%. This difference is not expected to cause biases in the NDAs results. As demonstrated by De Luca et al. (2013), maintaining the values of ${k}_{e}$ and ${u}_{u}$ when employing an equivalent bilinear SDOF system with hardening ensures negligible errors in the structural response despite small differences in the area beneath the curves. Regarding the analyzed structural model, consider that the application example aims to address general scenarios rather than delve into specific structures or study behavior details. Consequently, the chosen constitutive model does not incorporate stiffness degradation or pinching behavior. In structures with such characteristics, it is very likely that there could be a notorious influence of the strong-motion duration in the inelastic response. However, the verification of such an assumption remains a subject for future studies.

Fig. 9

Schematics of the SDOF system (left) and constitutive model (right) used to create an equivalent model of the building case study. A schematic for the determination of ${E}_{s}\left({u}_{u}\right)$ and ${E}_{h}\left({u}_{u}\right)$ is also shown on the right

5 Hazard-consistent fragility functions

For each site, an MSA of the equivalent SDOF system was carried out using the hazard-consistent accelerograms defined in Sect. 3.4. The peak displacement, ${u}_{max}$, and maximum hysteretic energy, ${E}_{{h}_{max}}$, were selected as $EDP$ s. The former is defined as the maximum absolute displacement exhorted in the equivalent SDOF system when subjected to an accelerogram. The second is the energy dissipated in the inelastic behavior of the equivalent SDOF system. The MSA results for ${u}_{max}$ and ${E}_{{h}_{max}}$ are presented in Fig. 10 in the form of boxplots (Evans and Rosenthal 2010). Results indicate that estimates of either displacement- or energy-based damage measures increase as ${T}_{r}$ increases. Also, the whiskers length of the boxplots shown in Fig. 10 demonstrate the increase in structural response uncertainty as ${T}_{r}$ increases. The latter is attributed to the amplitude distribution during the accelerograms (López-Castañeda et al. 2022).

Fig. 10

Hazard-consistent MSA results for ${u}_{max}$ (top) and ${E}_{{h}_{max}}$ (bottom)

Figures 11 and 12 depict a closer view of the influence of strong-motion amplitude and duration on inelastic displacement and hysteresis. Specifically, Fig. 11 shows the seismic response of the equivalent SDOF system when subjected to a sample of accelerograms representative of values of ${T}_{r}$ equal to 25 years, 250 years, and 2500 years for the UC44 site. Likewise, Fig. 12 shows the seismic response of the equivalent SDOF system for the AU11 site. As those accelerograms shown in Fig. 7, accelerograms in Figs. 11 and 12 stand for the intense part of the ground-motion and are part of the artificial sample simulated to perform the MSAs. Figures 11 and 12 show that the hysteretic energy dissipated by the equivalent SDOF system when subjected to the 2500-year return-period accelerograms is much greater than that dissipated when the structure is subjected to accelerograms for ${T}_{r}$ equal to 25 years or 250 years. Site effects, e.g., resonance, are noticeable as estimates of both ${u}_{max}$ and ${E}_{{h}_{max}}$ are larger for the UC44 site (${T}_{s}\hspace{0.17em}$= 1.3 s) in comparison with those estimates for the AU11 site (${T}_{s}$ = 4.0 s).

Fig. 11

Influence of strong-motion amplitude and duration on hysteresis (UC44 site, ${T}_{s}\hspace{0.17em}$= 1.3 s)

Fig. 12

Influence of strong-motion amplitude and duration on hysteresis (AU11 site, ${T}_{s}\hspace{0.17em}$= 4.0 s)

Figure 13 shows the trend among the displacement and energy results obtained per each site; notice that, for better appreciation, ${u}_{max}$ is normalized by ${u}_{y}$ and ${E}_{{h}_{max}}$ is normalized by ${u}_{p}{F}_{y}$, where ${u}_{p}$ equals ${u}_{u}-{u}_{y}$. Figure 13 illustrates that regardless of the site, the association between the displacement-and energy-based structural responses is maintained. Moreover, the largest hysteretic energy and displacement results are found from the UC44 and BO39 sites. This is owed mainly to the large spectral acceleration amplitudes near ${T}_{1}$ at each site, and the strong-motion duration as well. i.e., although the largest values of ${D}_{Sr}$ are found in the AU11 site, the combination of amplitude and duration at the BO39 and UC44 sites produce the largest displacements and hysteretic energy dissipation, since the system is more likely to exceed the elastic range for a longer time at these sites.

Fig. 13

Scatter plots of the displacement and energy structural response obtained per each site

Then, fragility functions were developed using Eq. (3) and the hazard-consistent MSA results. The following damage states were defined to represent a full range of structural performance levels of the building case study (SEAOC Seismology Committee 1999): (a) Occupational, the building continues in operation with negligible damage. (b) Operational, the building continues in operation with minor to moderate damage and minor disruption in nonessential services. (c) Life safety, damage is moderate to major, extensive structural repairs are expected to be required. (d) Near collapse, life safety is at risk, damage is severe, structural collapse is prevented. (e) Collapse, the building has collapsed.

Section 5.1 gives the hazard-consistent fragility functions derived from the displacement capacity of the equivalent SDOF system, whereas Sect. 5.2 gives those formulated from its energy capacity.

5.1 Fragility functions based on displacement capacity

The threshold values for the displacement-based damage states are given in Table 6. They were defined from the capacity curve of the equivalent SDOF system (see Fig. 8) as recommended in the “Blue Book” by the Seismology Committee of the Structural Engineers Association of California (SEAOC) (1999). As per Table 6, the first damage state (DS1) is linked to ${u}_{y}$, whereas the fifth damage state (DS5) is related to ${u}_{u}$. The remaining damage states, namely, DS2, DS3, and DS4, are defined as ${u}_{y}$ plus a fraction of ${u}_{p}$. The areas associated with such damage states are filled in Fig. 10 for the displacement-based MSR results.

Table 6 Displacement-based damage states and corresponding performance levels

Table 7 summarizes the estimates of $\mu$ and $\sigma$ that describe the probabilities of exceeding the displacement-based damage states given in Table 6. The corresponding hazard-consistent fragility curves are presented in Fig. 14. As per Fig. 14, the equivalent SDOF system displays a higher probability of exceeding DS1 and DS2 for the UC44 site, whereas the probability of exceeding DS3 and DS4 grows steeper for the BO39 site. The lower values of fragility for all damage states are found in the AU11 site, where only two damage states show probability of being exceeded. Such results are concordant with the acceleration response spectra of each site (see Fig. 6), where the largest spectral amplitudes near the elastic period of the equivalent SDOF system, i.e., ${T}_{1}\hspace{0.17em}$= 1.2 s, are the ones for the UC44 site. Regarding the inelastic response, ${u}_{max}$ will be larger the longer the equivalent SDOF system continues to be excited once it has sustained damage. Thus, the inelastic response is nearly as high for the BO39 site than for the UC44 site. In the case of the AU11 site, accelerograms are longer than that of the other two sites. Still, the spectral amplitudes near ${T}_{1}$ are much lower at the AU11 site, thus the equivalent SDOF system sustains less damage even with longer accelerograms.

Table 7 Estimates of $\mu$ and $\sigma$ for the fragility functions

Fig. 14

Hazard-consistent fragility curves for the displacement-based structural response

5.2 Fragility functions based on energy capacity

For the energy-based fragility functions, the response of the equivalent SDOF system was defined in terms of a damage index proposed by Díaz et al. (2017). Such a damage index, hereafter denoted $D{I}_{EC}$, was determined using a linear relation between ${E}_{{h}_{max}}$ and the maximum strain energy, ${E}_{{s}_{max}}$, each normalized with respect to their correspondent energy capacity of the equivalent SDOF system associated to the damage states defined in Table 6. Thus, $D{I}_{EC}$ can be computed as (Díaz et al. 2017):

$$D{I}_{EC}={\eta }_{E}{E}_{{s}_{max}}^{N}+\left(1-{\eta }_{E}\right){E}_{{h}_{max}}^{N}$$

(21)

where ${E}_{{s}_{max}}^{N}$ and ${E}_{{h}_{max}}^{N}$ are the normalized maximum strain and hysteretic energy, respectively. The normalized maximum strain energy ${E}_{{s}_{max}}^{N}$ can be estimated as follows (Díaz et al. 2017):

$$E_{{s_{max} }}^{N} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {0 \le u_{e} \le u_{y} } \hfill \\ {\frac{{E_{{s_{max} }} }}{{E_{s} \left( {u_{u} } \right)}}} \hfill & {u_{y} < u_{e} \le u_{u} } \hfill \\ \end{array} } \right.$$

(22)

and $E_{{h_{max} }}^{N}$ as follows:

$$E_{{h_{max} }}^{N} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {0 \le u_{e} \le u_{y} } \hfill \\ {\frac{{E_{{h_{max} }} }}{{E_{h} \left( {u_{u} } \right)}}} \hfill & {u_{y} < u_{e} \le u_{u} } \hfill \\ \end{array} } \right.$$

(23)

where ${E}_{s}\left({u}_{u}\right)$ and ${E}_{h}\left({u}_{u}\right)$ are the strain and hysteretic energy, respectively, associated with ${u}_{u}$. They can be obtained from the capacity curve of the equivalent SDOF system (see Fig. 9). Here, ${\eta }_{E}=$ 0.68.

The selected threshold values for the energy-based damage states were also computed using Eq. (21) but considering values of ${E}_{s}\left({u}_{d}\right)$ and ${E}_{h}\left({u}_{d}\right)$ instead of ${E}_{{s}_{max}}$ and ${E}_{{h}_{max}}$ in Eqs. (22) and (23), respectively. The estimates of $\mu$ and $\sigma$ that describe the energy-based fragility functions are given in Table 7. The corresponding fragility curves are presented in Fig. 15. The tendencies displayed in Fig. 15 are concordant to the ones for displacement-based fragility. The UC44 site is the one displaying the higher probabilities of damage, followed by the results at the BO39 site. As in the evaluation of structural displacement, the hysteretic energy dissipated by the equivalent SDOF system at long values of ${T}_{r}$ is nearly as high at the BO39 site than at the UC44 site.

Fig. 15

Hazard-consistent fragility curves for energy-based structural response measure

6 Seismic risk analysis

The fragility functions presented in Sect. 5 allow performing SRAs conditional on ${T}_{r}$ using Eq. (5). Table 8 summarizes the estimates of ${P}_{F}$ for both displacement- and energy-based damage states for the building case study. For comparison, Table 8 also gives the estimates of ${P}_{F}$ but applying Eq. (4) and considering ${D}_{Sr}$ as the ground-motion parameter of interest. As noticed, such estimates are practically the same as those obtained using Eq. (5) either for displacement- or energy-based damage states. Similar results are expected if an amplitude-based ground-motion parameter, e.g., $PGA$ or ${S}_{a}\left({T}_{e}\right)$, is chosen for the evaluation of Eq. (4).

Table 8 Annual probabilities of exceeding displacement- and energy-based damage states

7 Discussion

Although the main remarks on the outcomes were made throughout the text, some comments on the ground-motion simulation and seismic hazard analysis are made in Sects. 7.1 and 7.2, respectively. Section 7.3 gives some comments on how the strong-motion duration is treated in current earthquake engineering regulations; the attention is focused on the NTC-2023 (SOS-CDMX 2023) which define the criteria for structures located in Mexico City.

7.1 Ground-motion simulation

This study presented a procedure to select hazard-consistent accelerograms to perform NDAs and beyond, MSAs. The criteria consist of establishing levels of both amplitude and duration ground-motion parameters associated with predefined values of ${T}_{r}$. Since it is unlikely to find real accelerograms that match such hazard-consistent levels, simulation of artificial accelerograms is encouraged. In this study, the pioneer SIMQKE program is used to simulate the accelerograms—particularly, the time windows that define the strong-phase of the ground-motions measured by ${D}_{Sr}$ (see Fig. 7)—. Such a software estimates a power spectral density function from a target response spectrum and, by iteration, generates statistically-independent artificial accelerograms that match the specified response spectrum (Gasparini and Vanmarcke 1976). To simulate the strong-phase time-windows of the artificial accelerograms it was necessary to establish amplitude-duration envelopes consistent with the intense phase of accelerograms recorded at each site during major interplate earthquakes (e.g., those presented in Fig. 1). It is worth mentioning that preliminary sets of artificial accelerograms, whose response spectra matched those of real accelerograms, were used to evaluate the goodness of the signals to carry out NDAs. The results displayed a good agreement on the inelastic structural response. Other simulation methods, e.g., based on distinct stochastic simulation techniques, an empirical Green’s function technique, or composite source modelling techniques, can be used to obtain more refined artificial motions (Arora et al. 2020).

7.2 Seismic hazard analysis

Although the theoretical basis for both the deterministic and probabilistic characterization of the seismic hazard has been stated for many years, there are regions in the world that lack such studies, either due to lack of strong-motion data or information reported in literature. For instance, this study presents for the very first time a PSHA for ${D}_{Sr}$ related to interplate earthquakes occurred in the MAT. The seismic-source parameters reported in Sect. 3 can be used to perform PSHAs for other ground-motion parameters of earthquake engineering interest, e.g., for displacement response-spectral ordinates, ${S}_{d}$, or for another duration-based ground-motion parameter.

The urgency of developing PSHAs for the duration of ground-motions is justified by the evidence that it can accelerate failure when structures exceed their elastic limit. Constraining the duration of accelerograms to perform IDAs or MSAs could bias the seismic response. For example, Fig. 16 shows a comparison among MSA results for the UC44 site considering sets of fully hazard-consistent accelerograms (the same described in Sect. 3.4, see Fig. 10) and solely amplitude-based hazard-consistent accelerograms. For the latter, nine sets of forty artificial accelerograms per each value of ${T}_{r}$ were generated. Each set of accelerograms is characterized by a UHS associated with a value of ${T}_{r}$ varying from 50 to 5000 years. However, all consider the time window that defines the strong phase of the ground motion and have a duration equal to 119 s, which is the expected value of ${D}_{Sr}$ for ${T}_{r}\hspace{0.17em}$= 100 years at the site where station UC44 is located. The areas that delimit the associated structural performance levels are filled in the MSA results for ${u}_{max}$. Figure 16 shows the scatter plots of the displacement and energy structural response results for the UC44 site considering the sets of fully hazard-consistent accelerograms and solely amplitude-based hazard-consistent accelerograms. Although the duration influences the size of the nonlinear structural response, apparently it does not modify the observed trend between the displacement- and energy-based EDPs (see Fig. 13).

Fig. 16

Comparison among MSA results for the UC44 site considering sets of fully hazard-consistent accelerograms and solely amplitude-based hazard-consistent accelerograms

7.3 Strong-motion duration and current seismic deign regulations

The insufficiency of specific regional studies on the effects of ground-motion duration on structural response prevents its proper inclusion as a main design parameter in earthquake engineering regulations. For instance, the NTC-2023 (SOS-CDMX 2023) for Mexico City state that the ground-motion duration associated to interplate earthquakes had to be equal to 80 + 20 (${T}_{s}\hspace{0.17em}$ − 0.5), with ${T}_{s}\hspace{0.17em}$ = 0.5 s for sites characterized by rock or firm soil. According with the NTC-2020 (SOS-CDMX 2020), the 80 s in that mathematical expression were determined considering a scenario earthquake with ${M}$ = 7.8 occurred at ${R}$ = 265 km that was defined from the disaggregation of the earthquake hazard associated with ${T}_{r}\hspace{0.17em}$= 250 years. Considering the mentioned earthquake scenario and applying the GMPE proposed by López-Castañeda et al. (2021), one will find that ${D}_{Sr}\hspace{0.17em}$ = 85 s. At a first glance, it is comparable to the 80 s given in the NTC-2023 (SOS-CDMX 2023) for sites in GZI. However, this standard does not define the strong-motion duration, but the total duration of the ground motion. Therefore, a value of 80 s greatly underestimates the expected strong-motion duration at sites located in GZI. Similar observations are made for sites located in GZII or GZIII.

Quite different to other standards, the US earthquake engineering regulations propose to select ground-motions based on the CMS as an alternative (NEHRP-NIST 2011). Recall that such a spectrum conditions the spectrum estimates on a single spectral acceleration ordinate, which is commonly ${S}_{a}\left({T}_{1}\right)$. Due to this condition, the CMS amplitude is usually smaller than that of a the UHS, but almost the same at the conditioning spectral ordinate. The above can result in a disadvantage, since as the structural damage increases, an increase in ${T}_{1}$ occurs. Therefore, the inelastic structural response could be underestimated. Also, to compute a CMS it is necessary to have information on the hazard disaggregation, e.g., for ${S}_{a}\left({T}_{1}\right)$, as well as the vectors of total residuals defined from GMPEs. Such information is not as easy to obtain for many practitioner earthquake engineers as it is for earthquake engineers in the research area (who have access to strong-motion data and have the tools to develop seismic hazard analyses). In this regard, we recognize the effort of the US Geological Survey (USGS), which provides a tool to directly download CMSs for sites located in the US. Similar comments are made to the related conditional spectra approach (Jayaram et al. 2011), in which the variability in response spectra at other periods ${T}_{e}$ than the conditioning period, say ${T}_{1}$, is taken into account. As mentioned in Sect. 1, the selection of ground motions based on UHSs is also an alternative in US standards such as the ASCE 7-22 (ASCE 2022). Such an approach is also used in the NTC-2023 (SOS-CDMX 2023) and, in the opinion of the authors, appears to be a more conservative and practical one than the CMS-based approach.

Thus, the advantage of the proposed methodology for ground-motion record selection is that it avoids the selection of ground-motion duration levels based on the seismic hazard disaggregation of a given amplitude ground-motion parameter, e.g., $PGA$ as in the NTC-2020 (SOS-CDMX 2020). Also, the authors agree with the following statement by Jayaram et al. (2011): “PSHA already accounts for variability in spectral accelerations at each period being considered, and construction of the UHS is a conservative method of combining these spectral values. No further variance needs to be applied to the UHS, as varying the spectral values is equivalent to varying the associated exceedance rate of the spectral accelerations from period to period (an operation which is unlikely to produce meaningful results).” A parallel commentary can be made for the hazard-consistent levels of ground-motion duration.

Furthermore, with the criterion adopted herein, it is possible to express the fragility as a function of ${T}_{r}$ (see Sect. 5). This is advantageous, since it allows a complete evaluation of the structural performance accounting for different ground-motion parameters all related to the same seismic hazard. The challenges ahead stand for evaluating the effects of amplitude- and duration-based hazard-consistent accelerograms on the seismic response of structures with different mechanical properties than the one (case study) analyzed in this article. Explicitly, when accumulated structural damage comes into play. This will allow members of regulatory committees to define more suitable seismic loadings for nonlinear structural design in the upgrades of earthquake engineering regulations.

8 Conclusions

This article explores an approach for the selection of ground motions considering hazard-consistent values of both amplitude- and duration-based ground-motion parameters to perform SRAs. In general, the selection consists of defining values of ${T}_{r}$ that cover typical performance objectives and obtain amplitude and duration ground-motion levels associated with each of the predefined values of ${T}_{r}$ using PSHAs. One of the advantages of the proposed approach is that it does not rely on any disaggregation information to obtain the ground-motion duration levels. With this information, sets of hazard-consistent ground motions can be selected to perform MSA. Subsequently, fragility functions and SRAs conditional on ${T}_{r}$ can be developed.

A performance-based evaluation of a steel frame building defined as an equivalent SDOF system hypothetically located at various sites in Mexico City was presented in this article as an application example. The case study included: (a) Performing PHSAs for both amplitude- and duration-based ground motion parameters. (b) Simulating multiple sets of hazard-consistent accelerograms for values of ${T}_{r}$ between 10 and 5000 years. (c) Evaluating the inelastic behavior of a steel frame building defined as an equivalent SDOF system via MSA. (d) Defining hazard-consistent fragility functions and SRA that are function of ${T}_{r}$. Results indicate that properly designed and built steel frame buildings must not suffer extensive damage (or even collapse) with earthquake-induced forces associated with ${T}_{r}\le$ 1000 years. There might be minor structural damage (without disruption of operations) or moderate structural damage (where life is in danger and major repairs are necessary) for earthquake-induced forces associated with ${T}_{r}>$ 50 years. The results led the authors to deliberate that those structural systems with stiffness degradation, e.g., masonry, reinforced concrete, or composite structures, will be even more sensitive to the ground-motion duration effects when they stop behaving elastically, and therefore higher values of both displacement- and energy-based estimates of ${P}_{F}$ will be expected.