Seismic hazard study for the duration of ground-motions triggered by intraslab earthquakes

Abstract

This paper presents a probabilistic seismic hazard analysis for the duration of ground motions in Mexico City caused by intraslab earthquakes. The study implies establishing criteria to measure the duration of ground motions and developing predictive equations (GMPEs) for its estimation. Focus is placed on the relative significant duration, $D_{Sr}$, which is based on the accumulation of energy of ground motions. The study extends to the development of hazard curves that allow estimating the annual probability of exceedance of said parameter. The scope is limited to ground motions caused by intraslab earthquakes occurring in Mexico and that engineeringly affect its capital, Mexico City, which is in a geographical region where the effects of soil-dynamic amplification are manifested considerably. A strong-motion database that includes 1517 horizontal accelerograms, with peak ground acceleration, $PGA$, greater than or equal to 3 cm/s², recorded during 21 earthquakes from 1994 to 2023 were used to develop the GMPEs. The quantitative description of the time, size, and spatial distribution of the seismic-activity occurrence was defined using a catalog of 46 earthquakes that occurred from 1900 to 2023. The earthquakes have moment magnitude, $M_{w}$, greater than or equal to 6. With the tools developed, amplitude- and duration-based hazard-consistent accelerograms can be simulated and used in nonlinear dynamic analyses (NDAs) of structures. This study includes an application example where three sites in Mexico City are selected to compute inelastic response spectra. Hysteretic-energy demands up to 5 times higher are found after a comparison between the inelastic-response spectra from hazard-consistent accelerograms and those provided by current Mexican regulations.

1 Introduction

The duration of ground motions is of the utmost importance for the evaluation of the nonlinear response of civil engineering structures. Several studies have demonstrated that, while the effects of such a ground-motion parameter are not apparent in the course of the linear behavior of structures, its influence is noticeable when structures surpass their yielding point, and becomes more and more remarkable as they get closer to collapse; the effects are observable when evaluating either displacement and energy damage measures (Hancock and Bommer 2006; López-Castañeda et al. 2022). Hence, together with amplitude- and frequency-based ground-motion parameters, the ground-motion duration should be properly defined to specify the seismic actions that would act on under-design or already-constructed structures.

When performing NDAs, seismic actions are commonly characterized as series of either the ground-motion displacement, $u_{g}$, or the ground-motion acceleration, $\ddot{u}_{g}$, in time, $t$; the second kind of ground-motion records are called accelerograms. The choice of ground-motion records for the evaluation of critical infrastructure is usually determined according to the criteria given in current structural design standards, which establish that ground-motion records must have response-spectra comparable to a target response spectrum associated to a scenario earthquake. If the scenario earthquake is related to a given return period, $T_{r}$, the target-response spectrum is defined by a uniform hazard spectrum (UHS). Such structural design recommendations restrict the number of suitable real ground-motion records (recorded at or near the site of interest) to be used in NDAs. Thus, selecting ground-motion records translates into scaling ground-motion records or a simulation process for the generation of artificial motions.

Among the preferred scaling methods are the geometric-mean scaling of pairs of ground motions, the spectrum matching of ground motions, and the first-mode period scaling to a target response-spectral parameter (Huang et al. 2011). As an instance, the third scaling method is widely used when going forward and performing an incremental dynamic analysis (IDA). This type of scaling is justified in isolating the effect of different ground-motion parameters, keeping only that of the selected target-spectral ordinate, in structural response. Notwithstanding, not adjusting the level of duration, as well as other amplitude- and frequency-based parameters, leads to the erroneous representation of the ground-motion phenomenon. On the other hand, diverse methodologies, such as those based on the random vibration theory, allow simulating ground-motion records keeping the most important characteristics of the ground shaking, including its duration.

Hence, obtaining accurate estimates of both amplitude- and duration-based parameters to select ground-motion records requires data from seismic hazard analyses. In this regard, few studies have developed ground-motion prediction equations (GMPEs) for the duration of ground motions (Douglas 2022; López-Castañeda 2022). Notice that a GMPE relates a ground-motion parameter of interest with seismological parameters that quantitatively characterize the earthquake source, the wave propagation path between the source and the site, and the soil and geological profile beneath the site. Regarding the duration of ground motions, the strong-motion duration has been preferred by earthquake engineers instead of the total duration of ground-motions for the design and analysis of structures. As an instance, one can find in the literature various GMPEs for $D_{Sr}$ (Afshari and Stewart 2016; Bommer et al. 2009; Jaimes et al. 2024; Jaimes and García-Soto 2021; Kempton and Stewart 2006; López-Castañeda and Reinoso 2021, 2022; Meimandi-Parizi et al. 2020; Yaghmaei-Sabegh et al. 2014).

Up to this point, GMPEs permit to calculate the expected ground motion at a site given a controlling earthquake, say, with a given magnitude and source-to-site distance. Nevertheless, it provides no information on the likelihood of occurrence of the scenario earthquake or the level of ground motion that might be expected during a finite period of time. In this circumstance, it is convenient to resort to a probabilistic seismic hazard analysis (PSHA), which provides estimates of the mean annual rate of exceedance of ground-motion levels. In turn, such estimates can be directly related to return periods $T_{r}$ as those required in current seismic design standards for the selection of ground motions. In this context, only the study conducted by López-Castañeda et al. (2024) can be found in the literature that probabilistically advances the seismic hazard associated with the duration of ground motions. Their study comprises the evaluation of ground motions in Mexico City caused by interplate earthquakes. Moreover, López-Castañeda et al. (2024) gave an easy-to-follow methodology to develop fragility functions and, further, perform a seismic risk analysis (SRA) based on a multiple stripe analysis (MSA) that accounts for sets of ground-motion records having hazard-consistent levels in both amplitude and duration. As an application example, they evaluate the performance of a steel frame building, and conveyed that its median global response (measured by the maximum roof displacement and hysteretic energy) can be highly underestimated if the duration is constrained (e.g., when performing a conventional IDA).

Given the results reported by López-Castañeda et al. (2024), the authors resolve that for a complete SRA for critical infrastructure in Mexico City it is necessary to carry on studies on the effects of the duration caused not only by interplate earthquakes, but also intraslab ones. The importance of performing PSHAs for Mexico City, as well as for nearby suburbs of other states, relies on the fact that it houses the sixth-largest metropolitan area in the world, with nearly 22 million inhabitants, in a geographical region that is highly affected by a range of distinct tectonic-environment earthquakes. Two relevant seismic events can be mentioned as an instance: the 1985 and 2017 earthquakes both occurred on September 19. The first is classified as an interplate earthquake with epicenter in the state of Michoacan and that exhibit $M_{w}$ = 8.0. The second is classified as an intraslab earthquake that occurred at the state boundaries of Puebla and Morelos and had $M_{w}$ = 7.1. During the 2017 Puebla-Morelos earthquake 44 buildings collapsed, one pedestrian overpass, and one pedestrian bridge between two buildings; such statistic data exceed the number of collapsed structures due to the 1985 Michoacan earthquake (Galvis et al. 2017). Ninety one percent of the collapsed buildings in 2017 were built before 1985 (Galvis et al. 2020). Then, the 2020 census by the Mexican National Institute of Statistics, Geography, and Informatics reported that only in Mexico City there were almost 2.8 million of dwell private houses and about 1100 collective-housing facilities, which include apartment buildings (INEGI 2020). The question remaining is how many of these structures will continue to stand during an earthquake to happen, since many of them have been already diagnosed with poor structural health. Given that the influence of the duration of ground motions is significant when structures present cumulative damage, having precise estimates of the duration of ground motions from both interplate and intraslab earthquakes would increase a reliable evaluation of their response.

2 Ground-motions in Mexico City caused by intraslab earthquakes

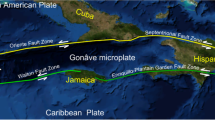
As introduced in Sect. 1, one of the largest metropolises in the world is in Mexico City, the capital of Mexico. Mexico City is subject to ground motions caused by very frequent interplate earthquakes occurring at the Middle American Trench (MAT) due to the contact between the subducting Cocos and Rivera plates within the North American Plate, as well as due to intraslab earthquakes occurring within the subducted Cocos and Rivera plates. Also, infrequent shallow-crustal earthquakes occurring in the Trans-Mexican Volcanic Belt (TMVB) can originate ground motions in Mexico City, but there are generally not harmful because of its low amplitudes and short duration (Reinoso 2007; Singh et al. 2015). Of the mentioned tectonic environments, this study focuses on intraslab earthquakes. They are characterized by a normal focal mechanism and occur down-dip at some distance from the strongly coupled interplate interface (Gardi et al. 2000; Kostoglodov and Pacheco 1999). The dipping planar (flat) zone where intraslab earthquakes occur is known as the Wadati-Benioff zone (Uyeda 2003). Also, Gardi et al. (2000) reported that many intraslab earthquakes occur just below or near the down dip edge of the coupled interface between the Rivera and Cocos plates and the North American Plate. The work of Kostoglodov and Pacheco (1999) present detailed schematics of typical modes of subduction in Mexico.

The selection of intraslab earthquakes that occurred in the Mexican territory was possible due to the online catalogs provided by the Global Centroid Moment Tensor (CMT) Project (Dziewonski et al. 1981; Ekström et al. 2012), the International Seismological Centre (International Seismological Centre 2023), and the National Earthquake Information Center from the United States Geological Survey (NEIC-USGS 2023). The works of Singh et al. (1984) and Zúñiga et al. (2017) were also consulted. The search was focused on moderate and large intraslab earthquakes. The moment magnitude $M_{w}$ was chosen among other conventional magnitude scales to evaluate the size of the earthquakes because it does not saturate for large earthquakes. That is, magnitude saturation occurs when the fault dimension greatly exceeds the wavelength of the seismic waves to which a particular scale is keyed (Heaton et al. 1986). The compiled intraslab earthquake catalog is presented in Appendix A. The catalog includes 46 earthquakes that occurred from 1900 to 2023 and had $M_{w}$ ≥ 6. Such a level of $M_{w}$ was chosen to consider all earthquakes that can cause structural damage in Mexico City, however small the damage may be. Figure 1 shows a map of southern Mexico that depicts the earthquake epicenters.

Fig. 1

At the top: epicenters and source zones of intraslab earthquakes. Ground-motions records from earthquakes marked in red were used to develop GMPEs for duration-based parameters. At the bottom: location of free-field ground-motion recording stations

Ground motions in Mexico City undergo considerable amplification due to highly heterogeneous local site conditions encompassed in an area of 1,485 km²; it is the smallest state as it occupies only 0.1% of the Mexican territory (INEGI 2005). Traditionally, Mexico City has been divided into three zones, each one encompassing sites with similar geotechnical characteristics, namely, the hill zone, transition zone, and lake zone (Jaime-Paredes 1987; Marsal and Mazari 1969). On the west side of Mexico City, the hill zone is characterized by deposits of granular soil and volcanic tuffs, with interspersed sandy deposits in the loose or relatively soft cohesive state. On the other hand, the lake zone is characterized by highly compressible clay deposits separated by sandy layers containing silt, clay, and volcano ash, and covered by alluvial soils, dried materials, and debris. The total thickness of these deposits can exceed 50 m in depth. The transition zone separates the hill zone from the lake zone. It is characterized by intercalated sandy layers on clay deposits, but with a thickness that varies from centimeters to a few meters. Hereafter, the hill, the transition, and the lake zones are referred to as GZI, GZII, and GZIII, respectively. By standard, the GZIII has been divided into four subzones, namely, a, b, c, and d.

Not many ground motions caused by historical intraslab earthquakes were recorded in Mexico City. Some of the recording devices used in the early years had very high trigger acceleration thresholds and almost null pre- and post-event memory availabilities (varying from approximately 0 s to 8 s), which led to a significant loss in the recording of the first and last movements of the ground. Then, although such ground-motion records are valuable to estimate amplitude-based parameters of the ground motion, like $PGA$, they are inadequate to accurately measure the duration. For this reason, all incomplete ground-motion records had to be discarded. Besides incompleteness, many ground-motion records had to be discarded for retaining bad quality, e.g., low resolution.

Hence, the final strong-motion database consisted of 791 ground-motion records from 21 intraslab earthquakes that occurred in the Mexican territory from 1994 to 2023. The ground-motions were recorded at 81 free-field stations. Appendix B organizes the selected stations per geotechnical zone and Fig. 1 shows their geographical location. It should be noted that recordings supplied in the CIRES and II-UNAM catalogs contain accelerograms in three orthogonal components of the ground motion. Specifically, each ground-motion record includes two orthogonal horizontal accelerograms and one vertical accelerogram. This study considers only horizontal accelerograms having $PGA$ ≥ 3 cm/s². Table 1 recaps the number of ground-motion records per earthquake and per geotechnical zone used in this study. All ground-motion records have two horizontal accelerograms except 12, 4, 8, 21, 11, and 7 ground-motion records at GZI, GZII, GZIIIa, GZIIIb, GZIIIc, and GZIIId, respectively, which have only one accelerogram. Notice that Table 1 considers the date provided by the USGS earthquake catalog, which is based on the Coordinated Universal Time (UCT).

Table 1 List of intraslab earthquakes and number of ground-motion records considered for the development of the GMPEs for the ground-motion duration

The selected ground-motion records were filtered following the recommendations given by Carreño et al. (1999) and Boore and Bommer (2005). In particular, the following steps were attained for each accelerogram in a ground-motion recording: (1) a baseline correction was carried out and (2) a 4th order Butterworth bandpass filter was applied. The high-pass cutoff frequency, $f_{c}$, was set based on a visual examination of where the long-period portion of the Fourier amplitude spectrum (FAS) of the accelerogram deviates from the tendency of decay in the proportion of the frequency squared, considering 0.15 Hz as the maximum possible value for $f_{c}$. The low-pass cutoff frequency was set at 30 Hz. Before the application of the bandpass filter, a pad of zeros equal to 1.5 $n_{b}$/$f_{c}$, where $n_{b}$ is the order of the Butterworth filter, was added to the signal. Half of this path was added at the beginning and the other half at the end of the accelerogram. One of the advantages of processing the accelerograms is that the unphysical velocities and displacements obtained from direct integration are compensated. For instance, Fig. 2 shows the velocity and displacement ground-motion signals, $\dot{u}_{g} \left( t \right)$ and $u_{g} \left( t \right)$, respectively, obtained from direct integration of an unprocessed and then processed accelerogram recorded at station AU46 during the September 8, 2017, earthquake.

Fig. 2

Acceleration, velocity, and displacement signals from the September 8, 2017, earthquake at station AU46. In black (left) are shown the velocity and displacement ground-motion signals derived from the unprocessed accelerogram and in blue (right) are those derived from the filtered accelerogram

A careful exploration of each ground-motion recording was necessary to fully understand the behavior of the duration of ground motions. For standardization of the strong-motion database, the part of the accelerograms encompassing the first and last excursion of an acceleration threshold, $a_{0}$, equal to 2 cm/s² were evaluated (López-Castañeda 2022). Such a threshold ensures to measure reliable quantities of the strong-motion duration in terms of the relative significant duration, $D_{Sr}$, which can be computed as follows:

$$ D_{Sr} = \smallint \left\{ {H\left[ {h\left( t \right) - a_{1} } \right] - H\left[ {h\left( t \right) - a_{2} } \right]} \right\}{\text{d}}t $$

(1)

where $H$ is the Heaviside step function, $a_{1}$ and $a_{2}$ are fractions that equal 0.05 and 0.95, respectively, and $h$ stands for the normalized Arias intensity, $I_{A}$, as function of time, $t$, and can be defined as follows:

$$ h\left( t \right) = \frac{{I_{A} \left( t \right)}}{{I_{{A_{max} }} }} $$

(2)

where $I_{{A_{max} }}$ is the maximum value of $I_{A}$, which can be computed as follows (Arias 1970):

$$ I_{A} \left( t \right) = \frac{\pi }{2g}\int_{{t_{1} }}^{{t_{2} }} {\ddot{u}_{g} } \left( t \right)^{2} {\text{d}}t $$

(3)

with $g$ being the gravitational acceleration near Earth’s surface.

Employing $D_{Sr}$ to define the strong-motion duration would not be an issue if “ideal” accelerograms were recorded at the sites of interest, i.e., that they truly represent the arrival of the first seismic wave and the departure of the last one without capturing noise. However, the accelerograms provided by II-UNAM and CIRES accelerograph networks were recorded using devices with different acceleration trigger thresholds and with different pre- and post-event memory availabilities. This inconsistency led to problems when computing the significant duration. For instance, consider two devices located closely: “device A” has a trigger threshold of 8 cm/s² and “device B” has a trigger threshold of 4 cm/s². Whereas the PGA recorded by both devices will be the same during a ground motion, the measured “total” duration and, consequently, $D_{Sr}$, will be different. Thus, the question to be answered by the authors was: what is the minimum trigger threshold to be set to standardize the accelerograms that permits to obtain consistent values of $D_{Sr}$ giving almost the same result as that for an ideal record? Such a threshold was set equal to 2 cm/s². A lower value will be impossible as many of the accelerograms related to historical earthquakes were recorded precisely with devices having such trigger threshold and discarding them implies the neglection of important historical data.

The difference between the computed values of $D_{Sr}$ from as-recorded accelerograms having values of $PGA$ greater than 15 cm/s² and from the time windows delimited by $a_{0}$ = 2 cm/s² is trivial for engineering purposes (López-Castañeda and Reinoso 2021). Moreover, setting $a_{0}$ = 2 cm/s² meets serviceability criteria for human perception of vibrations, e.g., those given in the AIJES-V001–2004 (AIJ 2014). Furthermore, $a_{0}$ = 2 cm/s² is half the minimum limit defined for human perception criteria, as recommended in the ISO 10137:2007 (ISO 2007). Therefore, the information loss using this threshold is expected to be negligible for structural engineering purposes.

Figure 3 shows a set of six accelerograms bounded by $a_{0}$ = 2 cm/s² that were recorded during the 2017 Puebla-Morelos earthquake at six different stations, namely, CUP5, DX37, UC44, SP51, BA49, and AE02 located in GZI, GZII, GZIIIa, GZIIIb, GZIIIc, and GZIIId, respectively. The stations are located within a 5-km radius. As observed from Fig. 3, there is a wide variation in the duration of ground motions. For instance, the value of $D_{Sr}$ for the accelerogram recorded at station AE02 is almost 2.5 times that from the accelerogram recorded at station CUP5. Regarding the duration of ground motions bounded by $a_{0}$ = 2 cm/s², which is hereafter denoted has $D_{{a_{0} }}$, there is an increase of about 150% comparing data from station CUP5 and AE02. These observations mean that the duration of ground motions increases with the dominant period of the soil, $T_{s}$. In fact, such a seismological parameter is used in this study to characterize the local site conditions. For sites located in GZI $T_{s}$ was set equal to 0.5 s, and for sites located in GZII or GZIII it was measured as the inverse of the frequency $f_{H/V}$ as follows:

$$ f_{H/V} = \sqrt {\frac{{\left[ {\max \left( {\frac{{F_{1} \left( \omega \right)}}{{F_{V} \left( \omega \right)}}} \right)} \right]^{2} + \left[ {\max \left( {\frac{{F_{2} \left( \omega \right)}}{{F_{V} \left( \omega \right)}}} \right)} \right]^{2} }}{2}} $$

(4)

where $\max \left( {F_{1} \left( \omega \right)/F_{V} \left( \omega \right)} \right)$ and $\max \left( {F_{2} \left( \omega \right)/F_{V} \left( \omega \right)} \right)$ are the ordinary frequencies, $f$, associated with the maximum spectral ratios $F_{1} \left( \omega \right)/F_{V} \left( \omega \right)$ and $F_{2} \left( \omega \right)/F_{V} \left( \omega \right)$, respectively, with $F_{1} \left( \omega \right)$ and $F_{2} \left( \omega \right)$ being the FAS of the horizontal orthogonal components of a ground-motion recording at the site and, likewise, $F_{V} \left( \omega \right)$, being the FAS of the vertical component of the ground-motion recording. Here, $\omega$ = $2\pi f$ is the angular frequency. The values of $T_{s}$ were computed from the unfiltered records. Particularly, only spectral smoothing was applied prior to the calculation of the spectral ratios. Thus, the sites where stations CUP5, DX37, UC44, SP51, BA49, and AE02 are located exhibit values of $T_{s}$ equal to 0.5 s, 0.9 s, 1.3 s, 1.9 s, 2.5 s, and 4.5 s, respectively.

Fig. 3

Accelerograms recorded in Mexico City during the 2017 Puebla-Morelos earthquake at stations CUP5, DX37, UC44, SP51, BA49, and AE02. The accelerograms are bounded by $a_{0}$ = 2 cm/s². The red shaded areas correspond to the intense phase of the ground motions defined by $D_{Sr}$

Figure 4 shows scatter plots of $D_{Sr}$ and $D_{{a_{0} }}$ for sites in GZI; the data is grouped by earthquake event. Results given in Fig. 4 imply a positive dependence between $D_{Sr}$ and $D_{{a_{0} }}$. Indeed, a Pearson correlation coefficient, $\rho$, greater than 0.85 was estimated for Events 1, 2, 4, 7, 10, 14, 15, and 17. Values of $\rho$ varying from 0.27 to 0.79 were computed for the remaining earthquake events. Likewise, a positive dependence between $D_{Sr}$ and $D_{{a_{0} }}$ was found considering observations from sites located in GZII or GZIII.

Fig. 4

Scatter plots of $D_{Sr}$ versus $D_{{a_{0} }}$, grouped by earthquake event, for sites located in GZI

The observed trends between the duration of ground motions and $M_{w}$, $T_{s}$, and the hypocentral distance, $R_{hyp}$, are briefly discussed next. The first seismological parameter, $M_{w}$, represents the size of an earthquake and it is strongly dependent on the dimensions of the seismic source zone or the length of the fault. The longer the fault plane the longer the time is needed to break the whole fault (Pezeshk 2024.). Thus, the duration of ground motions is expected to increase as $M_{w}$ increases. The second seismological parameter, $T_{s}$, characterizes the soil and geological profile beneath a site. Due to high amplification caused by the strong local site effects in Mexico City, the duration of ground motions is expected to increase as $T_{s}$ increases. In this regard, the seismic waves reach Mexico City extremely attenuated, but they undergo considerable amplification due to local site condition effects. In fact, through ground-motion records is observed that, at values of $f$ between 0.2 and 0.7 Hz, amplifications could be up to ~ 500 times greater in Mexico City than those observed in near-source sites. At GZI ground-motion amplifications can be up to 10 times greater than the expected amplitudes for sites outside Mexico City at similar source-to-site distances, whereas ground motions at GZII and GZIII are amplified by a factor ranging from 10 to 50 with respect to GZI (Lermo and Chávez-García 1994; Singh et al. 1995). The last seismological parameter, $R_{hyp}$, characterizes the effects of attenuation, which is the decrease in seismic wave amplitude with propagation, caused by intrinsic absorption and/or scattering (Lay 2002). Therefore, the duration of ground motions decreases as $R_{hyp}$ increases because such a ground motion parameter is measured from the recorded accelerations. For instance, the time elapsed between the first and last excursions of a specified value $a_{0}$ will be shortened as $R_{hyp}$ increases (even if $a_{0}$ is almost zero, as for ideal accelerograms). It is important to mention that the duration of ground motions measured at a given site should by no means be confused with the time it takes for seismic waves to arrive from a given earthquake source to the site. Clearly, the farther the site, the longer it will take for the waves to arrive. Figure 5 includes the distribution of $D_{Sr}$ in $M_{w}$, $T_{s}$, and $R_{hyp}$ considering data from sites located in GZII or GZIII grouped by earthquake event.

Fig. 5

Distribution of $D_{Sr}$ in $M_{w}$, $T_{s}$, and $R_{hyp}$ using data from sites in GZII or GZIII grouped by earthquake event

Although in Fig. 5 the data is grouped by earthquake event, the direction of the correlation between $D_{Sr}$ and $R_{hyp}$ is not so easy to identify when all the observations are considered a as a single set including data from sites with different values of $T_{s}$. As mentioned above, the peculiar local site conditions of Mexico City cause the seismic waves to be greatly amplified even though they arrive very attenuated. Thus, the negative correlation between $D_{Sr}$ and $R_{hyp}$ can be perceived by grouping the data by both earthquake event and geotechnical zone. For instance, Fig. 6 shows the distribution of $D_{Sr}$ and $R_{hyp}$ considering data from GZII and GZIII and the earthquakes occurred on December 10, 1994, January 16, 2002, and November 15, 2012.

Fig. 6

Distribution of $D_{Sr}$ in $R_{hyp}$, considering data from GZII and GZIII and the earthquakes that occurred on December 10, 1994 (Event 2), January 16, 2002 (Event 9), and November 15, 2012 (Event 15)

3 Ground-motion prediction equations

In this study, the GMPEs for the duration of ground motions are developed using linear mixed-effects models, which are a class of statistical models containing both fixed and random effects. The former are parameters associated with an entire population or with certain repeatable levels of experimental factors and the latter are parameters associated with individual experimental units drawn at random from a population (Pinheiro and Bates 2000). In the linear mixed-effects models both fixed and random effects occur linearly in the model function.

In principle, a linear mixed-effects model allows for describing the relationship between a response variable and some covariates in data that are grouped according to one or more classification factors. For a single level of grouping, the linear mixed-effects model can be expressed in matrix notation as follows (Laird and Ward 1982):

$$ \begin{array}{*{20}c} {{\varvec{y}}_{i} = {\varvec{X}}_{i} {\varvec{\alpha}} + {\varvec{Z}}_{i} {\varvec{b}}_{i} + {\varvec{e}}_{i} } & {i = 1, \ldots ,N_{C} } \\ \end{array} $$

(5)

where ${\varvec{y}}_{i}$ is an $n_{i} \times 1$ vector of responses of the $i$th cluster, ${\varvec{\alpha}}$ is a $p \times 1$ vector of fixed effects, ${\varvec{b}}_{i}$ is a $q \times 1$ vector of random effects, ${\varvec{X}}_{i}$ is an $n_{i} \times p$ design matrix of fixed effects, ${\varvec{Z}}_{i}$ is an $n_{i} \times q$ design matrix of random effects, and ${\varvec{e}}_{i}$ is an $n_{i} \times 1$ error vector with independent components, each of them having zero mean and variance $\sigma^{2}$.

It is assumed that ${\varvec{b}}_{i}$ and ${\varvec{e}}_{i}$ are normally distributed with a mean of $0$ and variance–covariance and variance matrices ${\varvec{\sigma}}_{{\varvec{b}}}^{2} = \sigma^{2} {{\varvec{\Upsilon}}}$ and ${\varvec{\sigma}}_{{\varvec{w}}}^{2} = \sigma^{2} {\varvec{I}}$, respectively, where ${{\varvec{\Upsilon}}}$ is a symmetric and positive semi-definite matrix parameterized by a variance component vector $\vartheta$ and ${\varvec{I}}$ is an identity matrix. Also, the random effects vectors ${\varvec{b}}_{i}$ are assumed to be independent of each other and of the error vectors ${\varvec{e}}_{i}$ (Demidenko 2004; Pinheiro and Bates 2000). As ${\varvec{b}}_{i}$ is defined to have a mean of $0$, any nonzero mean for a term in the random effects must be expressed as part of the fixed-effects terms. Thus, the columns of ${\varvec{Z}}_{i}$ are usually a subset of the columns of ${\varvec{X}}_{i}$.

Hence, two GMPEs for $D_{Sr}$ were developed based on the linear mixed-effects model given in Eq. (5). Specifically, one GMPE for sites located in GZI and another for sites located either in GZII or GZIII. The seismological parameters used to define ${\varvec{X}}$ and ${\varvec{Z}}$ are $M_{w}$, $R_{hyp}$, and $T_{s}$. Although the vertical component of ground motions caused by intraslab earthquakes can be of interest for earthquake engineering purposes, the scope of this article only considers data from the horizonal accelerograms of the ground-motion records (see Table 9).

The functional form for sites located in GZI and in GZII or GZIII are, respectively (López-Castañeda 2023):

$$ \ln \left( {D_{Sr} } \right)_{ik} = \alpha_{0} + \left( {\alpha_{1} + \alpha_{2} M_{{w_{i} }} } \right)\ln \left( {R_{hyp} } \right)_{ik} + b_{{0_{i} }} + e_{ik} $$

(6)

and

$$ \ln \left( {D_{Sr} } \right)_{ik} = \alpha_{0} + \alpha_{1} \ln \left( {T_{s} } \right)_{ik} + \left( {\alpha_{2} + \alpha_{3} M_{{w_{i} }} } \right)\ln \left( R \right)_{ik} + b_{{0_{i} }} + e_{ik} $$

(7)

where $\ln \left( {D_{Sr} } \right)_{ik}$, $\ln \left( R \right)_{ik}$, and $\ln \left( {T_{s} } \right)_{ik}$ are the natural logarithms of $D_{Sr}$, $R_{hyp}$, and $T_{s}$, respectively, of the $k$th accelerogram recorded during the $i$th earthquake, and $M_{wi}$ is the moment magnitude of the $i$th earthquake event. In this study, the maximum likelihood estimation (MLE) method was used to estimate both fixed-effects coefficients ${\varvec{\alpha}}$ and variance components $\sigma^{2}$ and $\vartheta$.

Tables 2 and 3 summarize the estimates of the components of ${\varvec{\alpha}}$, together with their standard error (SE), and p-value for a t-test, obtained from the regression analysis for Eqs. (6) and (7), respectively. Note that the t-test is any statistical hypothesis in which the test statistic follows a Student’s t distribution under the null hypothesis. Such a distribution is commonly applied to the testing of one-sided hypotheses related to normally distributed data. In this study, the probability of rejecting the null hypothesis, given that it was assumed to be true, i.e., the significance level, was set at 0.05. Recall that the p-value is the probability of obtaining test results as extreme, or more extreme than, the results observed, under the assumption that the null hypothesis is true.

Table 2 Estimates of the elements of ${\varvec{\alpha}}$ for the GMPEs for $\ln \left( {D_{{a_{0} }} } \right)$ and $\ln \left( {D_{Sr} } \right)$ for sites in GZI

Table 3 Estimates of the elements of ${\varvec{\alpha}}$ for the GMPEs for $D_{{a_{0} }}$ and $D_{Sr}$ for sites in GZII or GZIII

Notice from Eqs. (6) and (7) that regression analyses were carried out considering only the intercepts, $\alpha_{0}$, as random and the design matrices of random effects ${\varvec{Z}}_{i}$ as a vector of ones. Then, the terms $b_{{0_{i} }}$ and $e_{ik}$ have the prior distributions $b_{{0_{i} }} \sim {\mathcal{N}}\left( {0,\sigma_{b}^{2} } \right)$ and $e_{ik} \sim {\mathcal{N}}\left( {0,\sigma_{w}^{2} } \right)$, respectively. The estimates of $\sigma_{b}^{2}$ and $\sigma_{w}^{2}$ and their 95% confidence intervals for Eqs. (6) and (7) are given in Table 4, respectively. The variance, $\sigma_{T}^{2}$, for the developed GMPEs can be calculated as follows (Hedeker and Gibbons 2006):

$$ \sigma_{T}^{2} = \sigma_{b}^{2} + \sigma_{w}^{2} $$

(8)

Table 4 Estimates of $\sigma_{b}$ and $\sigma_{w}$, and their 95% confidence intervals, and values of $\varrho$ and $\sigma_{T}^{2}$ for the developed GMPEs

Table 4 summarizes the computed values of $\sigma_{T}^{2}$. In addition, the intraclass correlation, $\varrho$, which represents the degree of association of the strong-motion data within earthquake events can be calculated as (Demidenko 2004):

$$ \varrho = \frac{{\sigma_{b}^{2} }}{{\sigma_{b}^{2} + \sigma_{w}^{2} }} $$

(9)

The computed values of $\varrho$ are also summarized in Table 4.

The variances $\sigma_{b}^{2}$ and $\sigma_{w}^{2}$ are commonly referred to as the between-events variability and within-event variability, respectively. From the results given in Table 4, the major source of variation for GMPEs for GZI can be attributed to the between-events variability. By contrast, the within-event and between-events variability contribute more evenly to the uncertainty of the GMPEs for the duration of ground motions in GZII and GZIII.

The authors consider important to develop GMPEs for $\ln \left( {D_{{a_{0} }} } \right)$. The same functional forms given in Eqs. (6) and (7) were used for sites located in GZI and GZII or GZIII, respectively; the estimates of the components of ${\varvec{\alpha}}$ are given in Tables 2 and 3, and the computed values of $\sigma_{b}^{2}$, $\sigma_{w}^{2}$, $\varrho$, and $\sigma_{T}^{2}$ are given in Table 4. As per Tables 2 and 3, the sign of the component estimates of ${\varvec{\alpha}}$ for the GMPEs of $\ln \left( {D_{{a_{0} }} } \right)$ are the same as those for the GMPEs of $\ln \left( {D_{Sr} } \right)$. The above confirms that the observed trends between the seismological parameters $M_{w}$, $R_{hyp}$, and $T_{s}$ and any definition of the duration of ground motions are maintained (see Figs. 5 and 6). Also, the estimates of $\alpha_{1}$ obtained for the GMPEs for $\ln \left( {D_{{a_{0} }} } \right)$ are approximately one and a half times larger than those for the GMPEs for $\ln \left( {D_{Sr} } \right)$. The latter is consistent with the sample observations, where higher values of $D_{{a_{0} }}$ than for $D_{Sr}$ are measured given that all the explanatory variables held constant (see Fig. 3).

It must be noted that the selection of the optimal GMPEs for the duration of ground motions was determined by: (i) likelihood ratio tests, such as the Akaike information criterion (Sakamoto et al. 1986) and Bayesian information criterion (Schwarz 1978), which are penalized likelihood criteria that allow determining the quality of a model among a finite set of models, (ii) ensuring that all fixed-effects coefficients and variance components were statistically significant, and (iii) guaranteeing that the behavior observed in the empirical data was well-represented by the fitted GMPEs. Thus, the GMPEs proposed in this study reached the best statistics. Also, residual analyses were conducted to assess compliance with the considerations that frame the use of linear mixed-effects models and to identify the presence of outliers as part of the GMPEs fitting process. For example, the GMPEs for $\ln \left( {D_{Sr} } \right)$ were initially fitted considering the entire datasets of 174 observations from GZI and 1343 observations from GZII and GZIII; however, it was observed that 6 and 50 datapoints appeared to be outliers, respectively. Such observations were discarded to perform the final regression analyses. Figure 7 shows box plots of the residuals displaying the outliers identified when considering the entire datasets to fit the GMPEs for $\ln \left( {D_{Sr} } \right)$. For comparison, Fig. 7 also shows box plots of the residuals disregarding the outliers. Thus, the results presented from Tables 2, 3, and 4 are those excluding the detected outliers.

Fig. 7

Box plot of the residuals, grouped by earthquake event: (top) considering all observations and (bottom) disregarding outliers to fit the GMPEs for $D_{Sr}$

Notice that, under the assumption that $b_{{0_{i} }}$ and $e_{ik}$ are random variables, $\ln \left( {D_{Sr} } \right)\sim {\text{Normal}}\left( {\mu_{{\ln \left( {D_{Sr} } \right)}} ,\sigma_{T}^{2} } \right)$, i.e., $\ln \left( {D_{Sr} } \right)$ has a normal distribution with mean $\mu_{{\ln \left( {D_{Sr} } \right)}}$ and variance $\sigma_{T}^{2}$. The parameter $\mu_{{\ln \left( {D_{Sr} } \right)}}$ can be computed from the ${\varvec{X}}{\varvec{\alpha}}$ used to develop the GMPEs. Then, the expected value of $D_{Sr}$, $\mu_{{D_{Sr} }}$, can be computed as follows:

$$ \mu_{{D_{Sr} }} = \exp \left[ {\mu_{{\ln \left( {D_{Sr} } \right)}} + \frac{{\sigma_{T}^{2} }}{2}} \right] $$

(10)

and its variance as:

$$ \sigma_{{D_{sr} }}^{2} = \left[ {\exp \left( {\sigma_{T}^{2} } \right) - 1} \right]\exp \left( {2\mu_{{\ln \left( {D_{Sr} } \right)}} + \sigma_{T}^{2} } \right) $$

(11)

Considering the GMPE for $\ln \left( {D_{Sr} } \right)$ at sites located in GZI, i.e., using Eq. (6), Fig. 8 shows the distribution of $\mu_{{\ln \left( {D_{Sr} } \right)}}$ and $\mu_{{\ln \left( {D_{Sr} } \right)}} \pm 2.5\sigma_{T}$ in $R_{hyp}$ for the values of $M_{w}$ given in Table 1. Also, the strong-motion data considered in the regression analysis are superimposed in Fig. 8. As noticed from Fig. 8, the behavior perceived in the empirical data is satisfactorily reflected. Note that observations associated with the closest distances (about 140 km) correspond to the 2017 Puebla-Morelos earthquake (Event 19) and those associated with the uttermost distances (about 750 km) are those associated with the September 8 earthquake that occurred on the same year (Event 18).

Fig. 8

Distribution of $\mu_{{\ln \left( {D_{Sr} } \right)}}$ and $\mu_{{\ln \left( {D_{Sr} } \right)}} \pm 2.5\sigma_{T}$ with respect to $R_{hyp}$ and $M_{w}$ considering Eq. (6)

Contemplating the GMPE for $\ln \left( {D_{Sr} } \right)$ at sites located in GZII or GZIII, i.e., using Eq. (7), Fig. 9 shows the distribution of $\mu_{{\ln \left( {D_{Sr} } \right)}}$ and $\mu_{{\ln \left( {D_{Sr} } \right)}} \pm 2.5\sigma_{T}$ in $R_{hyp}$ for values of $M_{w}$ equal to 6.9, 7.1, 7.4, and 8.2. In addition, the strong-motion data considered in the regression analysis that match such values of $M_{w}$ are superimposed in Fig. 9. The proposed GMPE adequately adjusted to the observations.

Fig. 9

Distribution of $\mu_{{\ln \left( {D_{Sr} } \right)}}$ and $\mu_{{\ln \left( {D_{Sr} } \right)}} \pm 2.5\sigma_{T}$ with respect to $R_{hyp}$ and $T_{s}$ for values of $M_{w}$ equal to 6.9, 7.1, 7.4, and 8.2 and using Eq. (7)

3.1 Comparison with other predictive models

Some comments are made on the similarities and differences between the GMPEs developed in this study and those reported by other authors that also consider data from the horizontal components of ground-motions recorded in Mexico City; namely, the pioneer works of Guerrero (1997) and Reinoso and Ordaz (2001), as well as recent works of López-Castañeda and Reinoso (2021, 2022) and Jaimes et al. (2024) are discussed.

We will focus first on the works of Guerrero (1997) and Reinoso and Ordaz (2001). They developed GMPEs for ${D}_{Sr}$ using the method of least squares (which finds the estimates of $\boldsymbol{\alpha }$ that minimize the sum of squared terms of ${\varvec{e}}$) and a database of ground-motions caused by interplate and intraslab earthquakes occurred until 1995 and recorded at various states of Mexico, including Mexico City. Similar to the criteria adopted in this study, they trimmed the accelerograms at a fixed acceleration threshold (say ${a}_{0}$) prior the estimation of ${D}_{Sr}$. Guerrero (1997) set ${a}_{0}$ equal to 1 cm/s², 2 cm/s², and 4 cm/s² for accelerograms recorded at GZI, GZII, and GZIII, respectively. Likewise, Reinoso and Ordaz (2001) set ${a}_{0}$ = 4 cm/s² for those accelerograms recorded at GZII or GZIII and left those from GZI untrimmed. Thus, the employed regression, the limited strong-motion database, and the treatment of the ground-motion records somehow overshadow some effects among seismological parameters and the duration of ground motions. For instance:

• The intrinsic characteristics of the method of least squares disregard the variability resulting from strong-motion data from the same earthquake event, as well as the variability resulting from differences in data from different earthquake events. Thus, although Guerrero (1997) and Reinoso and Ordaz (2001) recognized the effects of the local site conditions, tectonic environment, or focal mechanism in the estimates of the strong-motion duration, some trends were not adequately reflected in the GMPEs proposed by them.

• Establishing different values for ${a}_{0}$ to trim the accelerograms leads to the fact that values of ${D}_{Sr}$ cannot be comparable at different geotechnical zones. In the case at hand, the measured values of ${D}_{Sr}$ at GZII and GZIII by of Guerrero (1997) and Reinoso and Ordaz (2001) were underestimated because higher acceleration boundary thresholds were considered at such geotechnical zones in comparison to the bounds set for GZI.

Note that the estimates of the components of ${\varvec{\alpha}}$ defined in this study will be practically the same as those obtained using a fixed-effects model (which assumes that observations are independent and identically distributed) if and only if the between-events variability is close to zero (which was not the case of the results obtained in this study). Thus, it is very important to consider correlations between strong-motion data from the same earthquake event. Neglecting this relation can lead to biased results—which can be considered the case of the GMPEs proposed by Guerrero (1997) and Reinoso and Ordaz (2001).

On the other hand, the GMPEs developed by López-Castaneda and Reinoso (2021, 2022) and Jaimes et al. (2024) were developed with a robust strong-motion database and using mixed-effects models, which constitute a class of regression models for data that is collected and summarized in groups (e.g., see the explanation of linear mixed-effects models given in page 13). López-Castañeda and Reinoso (2021, 2022) developed GMPEs for the duration of ground-motions in Mexico City caused by interplate earthquakes. Indeed, the criteria used in this study to standardize the accelerograms by $a_{0}$ = 2 cm/s² to obtain comparable values of $D_{Sr}$ was proposed by them. As in this article, they found a positive dependence between $D_{Sr}$ and $M_{w}$ or $T_{s}$ and a negative dependence between $D_{Sr}$ and $R_{hyp}$. The almost-simultaneous publication of the GMPEs by Jaimes et al. (2024) allows us to make some observations. They also developed GMPEs for interplate and intraslab earthquakes, respectively. They reported a positive dependence between $D_{Sr}$ and $M_{w}$, $T_{s}$, and $R_{hyp}$. Based on the reported residual analyses, all GMPEs by either López-Castaneda and Reinoso (2021, 2022) or Jaimes et al. (2024) adequately fit the considered data. Thus, the difference in the observed trend between $D_{Sr}$ and $R_{hyp}$ reported in this article and that reported by Jaimes et al. (2024) is attributed to the treatment of the data.

Jaimes et al. (2024) carried out a fine processing of the accelerograms, which included a baseline correction and filtering of the signals. Yet, they computed $D_{Sr}$ from unstandardized accelerograms (that is, not bounded by $a_{0}$). For instance, the effects of using unstandardized accelerograms to estimate $D_{Sr}$ can be appreciated in Figs. 10 and 11, which show accelerograms recorded at stations CUP5 ($T_{s}$ = 0.5 s) and UC44 ($T_{s}$ = 1.3 s) during the September 8 and 19, 2017 earthquakes, respectively. The stations are located about 5 km from each other. Considering the as-recorded accelerograms shown in Fig. 10, it will be understood that both the total duration of the ground motion and $D_{sr}$ would be higher in a place with a lower value of $T_{s}$. On the other side, if the accelerograms are bounded by $a_{0}$ = 2 cm/s² would lead to rational values of duration. As noticed by López-Castañeda and Reinoso, a portion of the P-waves will be discarded when bounding accelerograms with small $PGA$ (less than 15 cm/s²); however, this has no repercussions for structural engineering purposes. It is important to standardize all accelerograms to obtain comparable values of the duration of ground motions from different earthquakes and at different sites. For instance, considering the accelerograms unstandardized it would be said that the ground motion recorded at station CUP5 lasted longer during the September 8, 2017, earthquake than during the 2017 Puebla-Morelos earthquake. The latter is demonstrated in Fig. 11. Another interesting point to appreciate from Figs. 10 and 11 is that the effect of wave attenuation was not so severe during the 2017 Puebla-Morelos earthquake (which occurred at $R_{hyp}$ of about 140 km from the recording stations) in comparison with the notorious attenuation of the seismic wave as it propagates away from the seismic source of the September 8, 2017, earthquake (which occurred at $R_{hyp}$ of about 750 km from the recording stations). In addition, the ground motion occurred more suddenly during the 2017 Puebla-Morelos earthquake and, hence, caused $D_{Sr}$ to be much shorter compared to that during the September 8, 2017, earthquake. The latter can be corroborated from the Husid plots shown in Fig. 12. Notice that the graphical representation of $h\left( t \right)$ in Eq. (2) is known as a Husid plot (Husid 1969). Figure 12 shows that, either at station CUP5 or UC44, 95% of the energy had already been released within 50 s of the ground shaking (considering the accelerograms bounded by $a_{0}$ = 2 cm²). On the other hand, the 95% of energy accumulated up to about 85 s and 120 s at the CUP5 and UC44 sites, respectively, during the September 8, 2017, earthquake.

Fig. 10

Estimation of $D_{Sr}$ from two accelerograms recorded during the September 8, 2017, earthquake. At the left are shown the accelerograms as-recorded, whereas at the right the accelerograms are bounded by $a_{0}$ = 2 cm/s²

Fig. 11

Estimation of $D_{Sr}$ from two accelerograms recorded during the 2017 Puebla-Morelos earthquake. At the left are shown the accelerograms as-recorded, whereas at the right the accelerograms are bounded by $a_{0}$ = 2 cm/s²

Fig. 12

Husid plots from accelerograms (bounded by $a_{0}$= 2 cm/s²) recorded at stations CUP5 and UC44 during the September 8 and 19, 2017, earthquakes

The authors want to comment that, although this article focuses on the horizontal components of ground motions, examinations of the vertical component were also carried out. The effect of this component on the structural response becomes important if near source-to-site earthquakes occur (Jaimes and Ruiz-García 2019; Nayak 2021). Following the proposed criteria to measure $D_{Sr}$ from a standardized database of accelerograms bounded by $a_{0}$ = 2 cm/s², it was found that $D_{Sr}$ increases as $M_{w}$ and $T_{s}$ increase and decreases as $R_{hyp}$ increases. The observed trend among $D_{Sr}$ and $R_{hyp}$ contrasts with the results presented by Jaimes et al. (2024), which recently published GMPEs for $D_{Sr}$ from the vertical component of ground Motions in Mexico City. Again, the difference is believed to arise from the fact that accelerograms are not standardized by the same “trigger” threshold. Notwithstanding, the development of GMPEs for the vertical component demands a more detailed treatment of the databases and it is left outside the scope of this study.

4 Probabilistic seismic hazard analysis

A PSHA is a recognized technique, formerly developed by Professors Luis Esteva Maraboto and Carl Allin Cornell, capable of addressing the effects of any uncertainties involved in the modeling of the timing, location, size, and resulting level of future ground motions because it considers the broad set of earthquakes that can occur on each fault or source zone that might affect a site of interest to calculate not merely the expected levels of ground motion at the site, but their exceedance probabilities (McGuire 2008; McGuire and Arabasz 1990). At its core, a PSHA uses the law of total probability to estimate the probability that a ground-motion parameter exceeds a certain value. For instance, the probability that $D_{Sr}$ takes a value greater than $d$ can be computed as follows:

$$ P\left( {D_{Sr} > d} \right) = \int {\int P } \left( {D_{Sr} > d|M_{w} = m,R_{hyp} = r} \right)f_{{M_{w} }} \left( m \right)f_{{R_{hyp} }} \left( r \right)dm\,dr $$

(12)

where $P\left( {D_{Sr} > d|M_{w} = m,R_{hyp} = r} \right)$ is the complementary distribution function of $D_{Sr}$ conditional on $M_{w}$ and $R_{hyp}$, which are defined by the marginal distribution functions $f_{{M_{w} }}$ and $f_{{R_{hyp} }}$, respectively. Considering the contribution of $N_{S}$ earthquake sources affecting a site of interest, the mean annual rate of exceedance of $d$, $\lambda_{d}$, can be computed as:

$$ \lambda_{d} = \mathop \sum \limits_{i = 1}^{Ns} \lambda_{{m_{0i} }} \smallint \smallint P\left( {D_{Sr} > d|M_{w} = m,R_{hyp} = r} \right)f_{{M_{wi} }} \left( m \right)f_{{R_{hyp} }} {}_{i}\left( r \right)dm\,dr $$

(13)

where $\lambda_{{m_{0} }}$ is the rate of occurrence of earthquakes which magnitude is greater than $m_{0}$.

The GMPEs presented in Sect. 3 can be used to estimate the first term of the integrals in Eqs. (12) and (13). Thus, what remains to solve such equations is the probabilistic characterization of all intraslab earthquake sources capable of inducing ground motions of engineering significance in Mexico City. For this purpose, this study relies in the work of Zúñiga et al. (2017) for the identification of the earthquake sources. They defined three areal source zones for intraslab earthquakes in the Mexican territory (see Fig. 1). The quantitative description of the time, size, and spatial distribution of earthquake occurrences was defined under the assumption that each intraslab source zone describes a domain within which earthquakes (i) are equally likely in space, (ii) conform to a single magnitude distribution, (iii) have the same maximum magnitude, $m_{u}$, and (iv) are independent of each other. The considerations to define $f_{{R_{hyp} }}$, $f_{{M_{w} }}$, and $\lambda_{{m_{0} }}$ are described next.

The distribution in space was modeled using statistical inference. The values of $R_{hyp}$ were computed considering an observational site located at the geographic coordinates 19.35°N, 99.15°W, and an altitude equal to 2240 m. Table 5 summarizes the minimum and maximum values of $R_{hyp}$, $r_{min}$ and $r_{max}$, respectively, computed for each intraslab source zone. The closest source-to-stie distance given in Table 5, i.e., $r_{min}$ = 138 km at SZA, corresponds to the 2017 Puebla-Morelos earthquake, whereas the farthest source-to-site distance, i.e., $r_{max}$= 896 km at SZC, corresponds to the earthquake occurred on February 1, 2019.

Table 5 Values of $r_{min}$ and $r_{max}$, estimates of the GEV distribution parameters $\mu_{r}$, $\sigma_{r}$, and $\kappa$, and distance thresholds $r_{1}$ and $r_{2}$ corresponding to the levels at which $F_{{R_{hyp} }}$ equals 0.05 and 0.95, respectively

Diverse graphical goodness-of-fit tests were carried out to determine which probability distribution best described the set of point-source distance observations corresponding to each intraslab source zone. The one-sample Kolmogorov–Smirnov (KS) test was also used to evaluate how well each probability distribution fits each set of point-source distances. Concretely, the one-sample KS test is a nonparametric test of the null hypothesis that the data comes from a population with a specific distribution function (Massey 1951). In this study, the significance level was set at 0.05.

Table 6 gives the computed $p$-values for each seismic source obtained from the one-sample KS test for the generalized extreme value (GEV), lognormal, and normal distributions. All $p$-values in Table 6 are above the predetermined 5% significance level. Then, results indicate that the one-sample KS test fails to reject the null hypothesis for any case. The empirical, GEV, lognormal, and normal cumulative distribution functions (CDF) of $R_{hyp}$ for each intraslab source zone are given in Fig. 13. Such a figure shows that all the considered probability distributions fit the data well for SZA and through SZC. In Fig. 13$F_{{R_{hyp} }}$ means the distribution function of $R_{hyp}$.

Table 6 Probability of observing a test statistic at least as extreme as the observed value under the null hypothesis that the point-source distances came from a population with a specific distribution function

Fig. 13

Empirical, GEV, lognormal, and normal cumulative distribution functions of $R_{hyp}$

Based on the GEV distribution, $f_{{R_{hyp} }}$ can be defined as:

$$ f_{{R_{hyp} }} \left( s \right) = \left\{ {\begin{array}{*{20}c} {\exp \left( { - s} \right)\exp \left[ { - \exp \left( { - s} \right)} \right]} & {\kappa = 0} \\ {\left( {1 + \kappa s} \right)^{{ - \left( {1 + 1/\kappa } \right)}} \exp \left[ { - \left( {1 + \kappa s} \right)^{{ - \frac{1}{\kappa }}} } \right]} & {\kappa \ne 0 {\text{and}} \kappa s > - 1} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right. $$

(14)

where $s = \left( {r - \mu_{r} } \right)/\sigma_{r}$ is a standardized variable, and $\mu_{r}$, $\sigma_{r}$, and $\kappa$ are the location, scale, and shape distribution parameters, respectively. Equation (14) is valid for $s > - 1/\kappa$ in the case $\kappa$ > 0, and for $s < - 1/\kappa$ in the case of $\kappa$ < 0. The parameters $\mu_{r}$ and $\kappa$ can be any real number, whereas $\sigma_{r}$ > 0. The estimates of the GEV distribution parameters obtained for the intraslab seismic zones are presented in Table 5. Regarding the estimated parameters for the GEV distribution given in Table 5, the distance data displayed a tendency towards the Type I GEV distribution, i.e., the well-known Weibull distribution. This can be inferred by looking at the estimated values for the shape parameter.

Considering the lognormal and normal distribution to characterize $R_{hyp}$, $f_{{R_{hyp} }}$ ca be defined, respectively, as:

$$ f_{{R_{hy} }} \left( r \right) = \frac{1}{{r\sigma_{r} \sqrt {2\pi } }}\exp \left[ { - \frac{{\left( {\ln \left( r \right) - \mu_{r} } \right)^{2} }}{{2\sigma_{r}^{2} }}} \right] $$

(15)

and

$$ f_{{R_{hyp} }} \left( r \right) = \frac{1}{{\sigma_{r} \sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}\left( {\frac{{r - \mu_{r} }}{{\sigma_{r} }}} \right)^{2} } \right] $$

(16)

where $\mu_{r}$ and $\sigma_{r}$ are the parameters defining the normal and lognormal distributions; in the case of the normal distribution, they correspond to its mean and standard deviation. Note that the parameters for the different distributions evaluated for $R_{hyp}$ are repeated to avoid excessive use of symbols. Table 7 presents the estimates of the lognormal and normal distribution parameters for each intraslab seismic zone.

Table 7 Estimates of the lognormal and normal distribution parameters $\mu_{r}$ and $\sigma_{r}$, and distance thresholds $r_{1}$ and $r_{2}$ corresponding to the levels at which $F_{{R_{hyp} }}$ equals 0.05 and 0.95, respectively

The effects of the probability distribution characterizing $R_{hyp}$ will be seen latter with the PSHA results.

The size distribution of earthquakes $f_{{M_{w} }}$ was computed as follows:

$$ f_{{M_{w} }} \left( m \right) = \lambda_{{m_{0} }} \frac{{\exp \left[ { - \beta \left( {m - m_{0} } \right)} \right] - \exp \left[ { - \beta \left( {m_{u} - m_{0} } \right)} \right]}}{{1 - \exp \left[ { - \beta \left( {m_{u} - m_{0} } \right)} \right]}} $$

(17)

Equation (17) is based on the “shifted and truncated” Gutenberg and Richter law (Youngs and Coppersmith 1985). The “shifted and truncated form of the Gutenberg and Richter law was considered as it sets both an upper and lower limit of magnitude, $m_{0}$ and $m_{u}$, in the earthquake occurrence model. That is, it disregards those earthquakes that are unlikely to cause significant damage at the site of interest. Also, it disregards an infinite range of values of $M_{w}$ that would impossibly be generated in a source zone of interest.

Various mathematical approaches are available in the literature for estimating $\beta$ and $\lambda_{{m_{0} }}$ from historical data (López-Castañeda 2017). For instance, the well-known Aki-Utsu estimator of $\beta$ is typically preferred (Aki 1965; Utsu 1965). However, a complete earthquake catalog, starting from the specified level of completeness $m_{0}$, is needed to apply it. The latter can be quite challenging because observation periods $T$ for large earthquakes are usually longer than those for small or even moderate earthquakes. For example, the catalog compiled for this study is complete for $M_{w}$ ≥ 7.0 since 1900, for $M_{w}$ ≥ 6.5 since 1950, and for $M_{w}$ ≥ 6.0 since 1976. Thus, the approach proposed by Kijko and Smit (2012), which contemplates unequal-observation time periods $T$, was used to estimate $\beta$ and $\lambda_{{m_{0} }}$.

Let’s consider that an incomplete earthquake catalog, with $N_{T}$ earthquakes, is divided into $j = 1, \ldots ,N_{C}$ sub-catalogs, each with $N_{{E_{j} }}$ earthquakes. Each sub-catalog $j$ is complete for time periods $T_{j}$ and earthquakes with $m \ge m_{0j}$. Then, $\beta$ can be computed as follows (Kijko and Smit 2012):

$$ \beta = \frac{{N_{T} }}{{\mathop \sum \nolimits_{j = 1}^{{N_{C} }} S_{j} }} $$

(18)

where ${S}_{j}$ is defined as:

$$ S_{j} = \sum\limits_{k = 1}^{{N_{{E_{j} }} }} {\left( {m_{k,j} - m_{{0_{j} }} } \right)} $$

(19)

If $\beta$ is known, $\lambda_{{m_{{0_{1} }} }}$ can be obtained as follows:

$$ \lambda_{{m_{{0_{1} }} }} = \frac{{N_{T} }}{{\mathop \sum \nolimits_{j = 1}^{{N_{C} }} T_{j} \exp \left( {\beta \Delta_{j} } \right)}} $$

(20)

where ${\Delta }_{j}$ is equal to $m_{{0_{j} }} - m_{{0_{1} }}$. Thus, the estimates of $\beta$ and $\lambda_{{m_{0} }}$ were obtained using Eqs. (18) and (20), respectively. Table 8 summarizes the results.

Table 8 Estimates of the $\beta$-values, seismicity rates $\lambda_{{m_{0} }}$, and magnitude thresholds $m_{u}$

Given the probabilistic characterization of the intraslab seismic sources, Eq. (13) was solved numerically to obtain hazard curves, which plot the estimated ${\lambda }_{d}$ for a finite set of strong-motion levels $d$. Explicitly, it was evaluated numerically by converting the integrals into discrete summations as follows (Kramer 1996):

$$ \lambda_{d} = \sum\limits_{i = 1}^{{N_{S} }} {\sum\limits_{j = 1}^{{N_{M} }} {\sum\limits_{k = 1}^{{N_{R} }} {\lambda_{{m_{{0_{i} }} }} } } } P\left( {D_{Sr} > d|M_{w} = m_{j} ,R_{hyp} = r_{k} } \right)P\left( {M_{w} = m_{j} } \right)P\left( {R_{hyp} = r_{k} } \right) $$

(21)

where $N_{M}$ is the total number of elements in a finite set of earthquake magnitudes $M_{w}$ bounded by the thresholds $m_{0}$ and $m_{u}$, and $N_{R}$ is the total number of elements in a finite set of source-to-site distances $R_{hyp}$ bounded by the thresholds $r_{1}$ and $r_{2}$. A lower-bound $m_{0}$ was set equal to 6.0 for all intraslab source zones. The upper-bound $m_{u}$ was specified as $m_{max} + 0.2$, where $m_{max}$ is the magnitude of the maximum probable earthquake known from each intraslab source zone. Such a magnitude upper bound was defined judiciously, trying to account for the possibility of occurrence of larger earthquakes than the ones included in the catalogues for the studied zones. Although this criterion appears subjective, it stands on the conservative side for the analysis of structures. Table 8 summarizes the values of $m_{u}$ for each intraslab source zone. The thresholds $r_{1}$ and $r_{2}$ were defined as the levels at which $F_{{R_{hyp} }}$ equals 0.05 and 0.95, respectively. Table 5 summarizes their values considering that $R_{hyp}$ is characterized by the GEV distribution and Table 7 those if the lognormal or normal distributions are employed.

Figure 14 shows the hazard curve for $D_{Sr}$ using the GMPEs for sites in GZI given in Eq. (6). The hazard contribution of each seismic source is also depicted in Fig. 14; as noted, SZC produces the greatest contribution to the estimates of $D_{Sr}$. Similarly, using the GMPEs for sites located in GZII or GZIII given in Eq. (7), Fig. 14 shows the hazard curve for $D_{Sr}$ considering the contribution of all intraslab seismic sources and values of $T_{s}$ that vary from 1 to 4 s, in steps of 1 s. Notice that, to explore the effects of the probability distribution of $R_{hyp}$ on the PSHA results, hazard curves for $D_{Sr}$ were developed considering either the GEV, lognormal, and normal distributions to probabilistically characterize $R_{hyp}$. Figure 15 shows the results: negligible differences are seen on the estimated value of $D_{Sr}$ for values of $\lambda_{d}$ up to 0.00001. Thus, as per the Occam’s razor principle, a simple model can be satisfactory used to define $f_{{R_{hyp} }}$.

Fig. 14

Hazard curves of $D_{Sr}$ for sites located in GZI (left) and in GZII and GZIII (right)

Fig. 15

Hazard curves of $D_{Sr}$ for sites located in GZI (left) and in GZII and GZIII (right) considering distinct probability distributions to characterize $R_{hyp}$

It should be discussed that some researchers have argued that in a PSHA the concept of design earthquake is lost. This may be true because a single influential earthquake cannot be simply linked with the results of a PSHA (Baker 2013; Sen 2009). Nevertheless, it is possible to identify the dominant contributor to the earthquake hazard through a process called disaggregation and this can serve as a convenient design earthquake. The disaggregation of the earthquake hazard allows identifying the combination of values of $M_{w}$ and $R_{hyp}$ that contributes the most to the probability of exceeding a hazard-consistent ground-motion level. For the case in hand, the probability distribution of $M_{w}$ and $R_{hyp}$ conditional that $D_{Sr}$ exceeds $d$ at a site of interest can be computed as follows:

$$ P\left( {M_{w} = m_{j} ,R_{hyp} = r_{k} \left| {D_{Sr} } \right\rangle d} \right) = \frac{{P\left( {M_{w} = m_{j} } \right)P\left( {R_{hyp} = r_{k} } \right)\mathop \sum \nolimits_{i = 1}^{{N_{S} }} \lambda_{{m_{{0_{i} }} }} P\left( {D_{Sr} > d|m_{j} ,r_{k} } \right)}}{{\lambda_{d} }} $$

(22)

Based on Eq. (22), Fig. 16 shows the joint mass function of $M_{w}$ and $R_{hyp}$ conditional on exceeding $D_{Sr}$ = 125 s, which is associated with a value of $T_{r}$ = 250 years at a site located in GZI (see Fig. 14). From the results given in Fig. 16, it is likely that an earthquake with $M_{w}$ = 7.45 occurred at $R_{hyp}$ = 205 km and an earthquake with $M_{w}$ = 8.35 occurred at $R_{hyp}$ = 740 km to contribute more to the hazard. In addition, Fig. 16 shows the joint mass function of $M_{w}$ and $R_{hyp}$ conditional on exceeding $D_{Sr}$ = 125 s, which is also associated with a 250-year return period but related to interplate earthquakes (López-Castañeda et al. 2024). In this case, an earthquake with $M_{w}$ = 8.15 occurred at $R_{hyp}$ = 280 km is the most likely to cause the exceedance of the specified strong-motion duration.

Fig. 16

Joint mass distribution of $M_{w}$ and $R_{hyp}$ conditional on exceeding 250-year return period values of $D_{Sr}$ (at GZI) considering intraslab- (left) and interplate- (right) earthquake data

5 Ground-motion duration and structural response

As mentioned in Sect. 1, current seismic design standards encourage the selection of ground-motion records on the application of NDAs to determine the response of critical structures. Most standards provide refined values of hazard-consistent amplitude-based parameters to be met when selecting ground-motion records. However, they do not provide a proper specification for their duration. For instance, in the case of the Mexico City’s newest standard, named NTC-2023 (SOS-CDMX 2023), there is stated that the “free-field input ground-motion duration” had to be equal to $40{ } + { }20\left( {T_{s} { } - { }0.5} \right)$ for ground-motion records related to intraslab earthquakes. Hence, the cited equation was developed considering that the duration of ground motions at sites located in GZI equals 40 s. In accordance with the previous version of the NTC-2023, i.e., the NTC-2020 (SOS-CDMX 2020), such a value of duration was determined (using an unspecified GMPE and) considering a scenario earthquake with $M_{w}$ = 7.5 occurred at $R_{hyp}$ = 110 km. The scenario earthquake was defined from the disaggregation of the earthquake hazard (the authors assume that for $PGA$) associated with $T_{r}$ = 250 years.

Based on the GMPEs given in Sect. 3, it can be said that the values of the ground-motion duration recommended in the NTC-2023 to select ground-motion records are considerably underestimated. Among others, the following key-point observations stand out:

• 1. Using Eq. (6) and considering the same scenario earthquake as in the NTC-2023 for intraslab earthquakes, the expected value of ${D}_{Sr}$ for a site located in GZI equals 92 s. Then, the value of 40 s given in the NTC-2023 is underestimated by almost 130% assuming that it represents the strong-motion duration for sites in GZI. Note that this standard does not define a measure for the strong-motion duration. It defines the “input ground-motion duration”, which the authors interpret as the total duration of the ground motion. Therefore, a value of 40 s not only underestimates the expected strong-motion duration (e.g., measured by $D_{Sr}$) at sites in GZI but also the total duration of ground-motions itself.

• 2. As per Fig. 9, the increment of the strong-motion duration as ${T}_{s}$ increases is not linear. Thus, the equation given in the NTC-2023 could be causing bias in the estimates of the duration of ground motions for sites located in GZII or GZIII.

It should me mentioned that, despite the differences on the estimates of $D_{Sr}$ reported by Jaimes et al. (2024), they also reported that the accelerograms given in the NTC-2023 are miscalculated.

Many times, there is an insufficient number of real site-specific accelerograms to perform the required NDAs or, further, to perform an IDA or MSA. Therefore, the simulation of ground-motion records is resorted to. In a recent work, López-Castañeda et al. (2024) propose to simulate ground-motions for seismic design purposes having hazard-consistent values of both amplitude- and duration-based parameters. For instance, in the application example described ahead, such a criterion was adopted.

For purposes of comparison among the capacity of site-specific strong-motion duration caused by interplate and intraslab earthquakes to have an effect on the inelastic structural response, several single degree of freedom (SDOF) systems with different fundamental frequencies were analyzed following the approach for ground-motion selection proposed by López-Castañeda et al. (2024). Such a comparison is very important because the ground response in Mexico City, and consequently of structures, can differ significantly depending on the tectonic setting that originates the ground motions (García et al. 2005; Jaimes and Reinoso 2006; Montalvo-Arrieta et al. 2003; Singh et al. 2015). For instance, intraslab earthquakes tend to affect low-rise structures because they have shown to have larger energy content at higher frequencies. On the contrary, interplate earthquakes commonly affect long-period structures as they have lower-frequency contents. Regarding the structural systems analyzed, the structural behavior of the SDOF systems was assumed to be represented by a bi-linear constitutive model, which can be described defining its ductility, $\mu_{e} ,$ and its secondary stiffness, $\beta_{e}$. The former is defined as the deformation capacity of the system in terms of its yielding strength, whereas the latter is defined as a fraction of the elastic stiffness. In this study, while $\mu_{e}$ was set equal to 1 (elastic response), 2, 3, and 4, $\beta_{e}$ was set equal to 0.25. Notice that, after some preliminary analyses of the influence of both parameters describing the selected constitutive model, it was found that variation in $\beta_{e}$ in ranges from 0 to 0.25 had little influence in the maximum inelastic displacements, thus, only a value of 0.25 was used. Moreover, bear in mind that the application example is meant to cover general cases, rather than dive into specific details of structural behavior. Therefore, the selected hysteretic model accounts for no stiffness degradation or pinching behavior.

The considered SDOF systems were subjected to ground motions concordant to different sites in Mexico City. The sites were stations CUP5 ($T_{s}$ = 0.5 s), UC44 ($T_{s}$ = 1.3 s), and BO39 ($T_{s}$ = 2.5 s) were selected as hypothetical locations (see Appendix B for coordinates). Eight accelerograms were simulated per site; specifically, only the time windows representing the strong-motion phase defined by $D_{Sr}$ were used for the simulations. Therefore, it was necessary to establish amplitude envelopes using the intervals over which accelerograms recorded at each site may be considered as strong. The site-specific accelerograms were simulated to have response spectra as those provided in the NTC-2023 and durations concordant to $T_{r}$ = 250 years. For 250-year return period, Fig. 14 shows that the expected value of $D_{Sr}$ approximates 132 s, 183 s, and 311 s for the CUP5, UC44, and BO39 sites, respectively. On the other hand, for the accelerograms related to interplate earthquakes values of $D_{Sr}$ are defined equal to 125 s, 131 s, and 185 s (López-Castañeda et al. 2024). Figure 17 presents the elastic acceleration response spectra from the eight simulated accelerograms per site compared with the target response spectra specified in NTC-2023 (UHS for $T_{r}$ = 250 years); note that the acceleration response-spectral ordinates are denoted as $S_{a}$. As noted from Fig. 17, a fair approximation from the simulated accelerograms to the target spectra is evident.

Fig. 17

Acceleration response spectra from the NTC-20223 (black line) and of the simulated ground-motion records

The NDAs were carried out considering the eight synthetic accelerograms per site and per tectonic mechanism to build inelastic response spectra for the specified values of $\mu_{e}$. The displacement, $\delta$, and the hysteretic energy per unit of mass, $E_{h}$, were selected to evaluate the response of the SDOF systems. To summarize the results, Figs. 18 and 19 present the median from the $\delta$ and $E_{h}$ spectra for the intraslab- and interplate-related accelerograms, respectively, obtained for each site. As noted from such figures, a greater amplitude is notorious from the interplate earthquakes.

Fig. 18

Medians from the $\delta$ and $E_{h}$ spectra considering the intraslab-related hazard-consistent accelerograms

Fig. 19

Medians from the $\delta$ and $E_{h}$ spectra considering interplate-related hazard-consistent accelerograms

Another relevant comparison comes from the inelastic response spectra between the accelerograms from intraslab earthquakes that provide the NTC-2023 and those for intraslab earthquakes given in Fig. 18. As with the amplitude-and duration-based hazard-consistent accelerograms described in the previous paragraph, a set of eight accelerograms provided by the NTC-2023 were considered for each site. For a fair comparison, only the strong-motion phase of the ground motions provided by the NTC-2023 was used to compute the NDAs; so, values of $D_{sr}$ were computed from the bounded signals by $a_{0}$ = 2 cm/s². Figure 20 presents the results of the computed $\delta$ and $E_{h}$ spectra.

Fig. 20

Medians from the $\delta$ and the $E_{h}$ spectra using the intraslab-related accelerograms provided by the NTC-2023

As per Fig. 20, both the displacement and energy spectra correspondent to the hazard-consistent accelerograms display greater spectral amplitudes. This fact is more notorious for the $E_{h}$ spectra, where the spectral amplitudes from the amplitude-and-duration hazard consistent accelerograms are up to three times those of the results from the NTC-2023 for structural periods from 1 to 2 s. The differences are justified in the fact that, since the hazard-consistent ground-motion duration values are greater than the those provided by the NTC-2023, and the system behavior is inelastic, the more the structure displaces, the more energy it must dissipate through damage. A clearer depiction of the differences between the inelastic response spectra from the accelerograms specified currently in NTC-2023 and the ones simulated as described in this section is presented in the ratios shown in Fig. 21 (hazard-consistent amplitude divided by the NTC-amplitude). As per Fig. 21, differences of nearly two times can be seen for the displacement spectra, whereas the differences go nearly to six in the $E_{h}$ spectra.

Fig. 21

Ratios between the median spectral amplitudes from the amplitude- and duration-consistent accelerograms obtained in this study and the only-amplitude hazard consistent accelerograms provided by the NTC-2023

The differences between the $\delta$ spectra summarized by Fig. 21 are less than the those for $E_{h}$ spectra. Notwithstanding, whereas the differences in $E_{h}$ are owed almost completely to the different values of strong-motion duration used for each set of accelerograms, the differences in $\delta$ are owed to other factors as well. It must be noted that, if the synthetic accelerograms were simulated using a similar method, the lines in Fig. 21 would be very likely almost horizontal at a value of 1, at least for the elastic responses. However, as observed in the black lines from Fig. 20, there are ranges of structural periods where the $\delta$ spectra seem to diverge. This might imply an underestimation of structural displacement from the NTC-2023 at certain periods owing to the simulation methods used by such standard. Such an underestimation is more notorious at sites with longer periods. Figure 22 presents a summary of the elastic displacement spectra from the synthetic accelerograms provided by the NTC-2023 and the one correspondent to the UHS provided by the same standard.

Fig. 22

Elastic acceleration and displacement response spectra of the accelerograms provided by the NTC-2023

The inelastic response of the analyzed SDOF systems can also be expressed in terms of the strength reduction factor, $R_{\mu }$. Such a parameter represents the reduction in the strength demand due to inelastic behavior. A reduction factor greater than 1 implies that the system does not have the strength to resist the earthquake with linear behavior, since it is defined as the ratio between the lateral yielding strength needed for the system to remain elastic, and the yielding strength required to meet the ductility demand —see Chopra (2011) for a more detailed definition—. Figure 23 presents the medians of $R_{\mu }$ for the simulated accelerograms and the analyzed values of $\mu$. The structural periods $T_{e}$ are normalized with respect to $T_{g}$, which is defined as the structural period where the maximum elastic spectral-velocity ordinate occurs (Miranda and Ruiz-García 2002). Although a direct comparison between the results displayed in Fig. 23 and those from other works is not straightforward, the tendencies displayed from Fig. 23 are in concordance with, e.g., the work of Miranda and Ruiz-García (2002), where the proportion of $R_{\mu } \left( {\mu_{e} = 3} \right)$ with respect to $R_{\mu } \left( {\mu_{e} = 2} \right)$ at $T_{e} /T_{g} = 1$ is near the double, and the ordinates from $R_{\mu } \left( {\mu_{e} = 4} \right)$ are around three times those of $R_{\mu } \left( {\mu_{e} = 2} \right)$ at the same period ratio.

Fig. 23

Strength-reduction factors $R_{\mu }$ from the medians of the $\delta$ spectra computed from the intraslab-related hazard-consistent accelerograms (see Fig. 18)

6 Conclusions

This article presented a detailed investigation of the duration of ground motions caused by intraslab earthquakes. Mexico City was the geographical area of interest. The study extends to the development of GMPEs and hazard curves. The motivation of the investigation relies on evaluating the proper definition of such a ground-motion parameter for seismic design in earthquake engineering. To fulfill the amendment of this article it was necessary to: (1) compile a robust strong-motion database, (2) define the strong-motion duration, (3) develop GMPEs that allow its estimation, (4) generate site-specific hazard curves of said ground-motion parameter, and (5) evaluate its effects on structural performance. The highlights of these points will be made below.

• The selected recordings came from free-field stations and include two orthogonal horizontal accelerograms with peak ground acceleration (denoted as $PGA$) greater than or equal to 3 cm/s².

• The relative significant duration (denoted as $D_{Sr}$) was selected to measure the strong-motion duration. It is the time required to accumulate between 5 and 95% of the total energy of an accelerogram. To standardize the strong-motion database and obtain comparable values of $D_{Sr}$, the accelerograms were bounded to an acceleration threshold (denoted as $a_{0}$) equal to 2 cm/s². The time that encompasses such a time-window was denoted as $D_{{a_{0} }}$.

• Linear mixed-effects models were used to describe relationships between either $D_{Sr}$ or $D_{{a_{0} }}$ and the moment magnitude (denoted as $M_{w}$), the hypocentral distance (denoted as $R_{hyp}$), and the dominant period of the soil (denoted as $T_{s} )$ in strong-motion data grouped per earthquake event. The proposed GMPEs satisfactorily fit the empirical observations. Yet, the authors encourage their refinement over the years. If that were the case, it is advisable to follow the established criteria to define $D_{Sr}$. The latter includes bounding the accelerograms by $a_{0}$ = 2 cm/s².

• An intraslab earthquake catalog from 1900 to 2023 was compiled to perform PSHAs. The characterization of the interplate source zones was defined under the assumption that each one described a domain within which earthquakes: (i) were equally likely in space, (ii) conformed to a single magnitude distribution, (iii) had the same maximum magnitude (denoted as $m_{u}$), and (iv) were independent of each other. The “shifted and truncated” form of the exponential Gutenberg-Richter law was used to define the probability distribution of $M_{w}$. The probability distribution of $R_{hyp}$ was determined using statistical inference.

• Examinations were carried out in this article to evaluate the effects of the strong-motion duration (related to both interplate and intraslab earthquakes) on the response of single degree of freedom (abbreviated as SDOF) systems via nonlinear dynamic analysis (abbreviated NDAs). The analyzed SDOF systems were represented by an elasto-plastic constitutive model with hardening, considering values of ductility (denoted as $\mu_{e}$) up to 4. The generation of displacement and hysteretic energy spectra demonstrates the influence of the duration on the response of structures when they engage in inelastic behavior. Thus, the importance of adequately characterizing the hazard for such a ground-motion parameter.

• When comparing the structural response from SDOF systems under the hazard-consistent accelerograms and those provided by the NTC-2023, lower hysteretic-energy demands up to five times were found from the synthetic accelerograms provided by the NTC-2023, whereas the inelastic-displacement demands from such signals were found to be nearly two times less at some structural periods. Thus, the synthetic accelerograms provided by Mexico City’s current regulations might be underestimating the inelastic demand on structures, according to the results from the application examples presented herein.

• The results from interplate earthquake data displayed (in general) higher energy content at lower frequencies than the intraslab ones. Such results agree with the findings from other research works. It can also be said from this study, that although interplate events produce larger spectral amplitudes, the intraplate earthquakes produce longer ground motions for a given seismic hazard level.

Appendices

Appendix

Appendix A

A list of intraslab earthquakes that occurred along the Mexican territory from 1900 to 2023 is given in Table 9. The catalog is complete for $M_{w}$ ≥ 7.0 since 1900, $M_{w}$ ≥ 6.5 since 1950, and $M_{w}$ ≥ 6.0 since 1976. The earthquakes are grouped in accordance with the source zonation given in Sect. 4. The hypocenters for earthquakes that occurred up to 2022 were taken from the catalog provided by the ISC (International Seismological Centre 2023), whereas the hypocenters of earthquakes that occurred on 2023 were taken from the Global CMT Project catalog (Dziewonski et al. 1981; Ekström et al. 2012). The works of Singh et al. (1984) and Zúñiga et al. (2017) were also consulted. Recall that most of the consulted catalogs provide values of the surface wave magnitude, $M_{s}$, instead of $M_{w}$ for earthquakes that occurred before 1976. However, values of $M_{s}$ were taken as values of $M_{s}$ for such earthquakes as estimates of $M_{w}$ and $M_{s}$ do not depart significantly from each other for moderate to large earthquakes.

Table 9 List of intraslab earthquakes

Appendix B

Table 10 lists the geographical coordinates of the free-field ground-motion recording stations located in Mexico City that were considered to develop the GMPEs for the duration of ground motion.

Table 10 List of free-field ground-motion recording stations