Closed-form expressions for partial safety factors used in the seismic assessment of existing RC buildings

Abstract

A new set of partial safety factors is proposed for the seismic safety assessment of existing reinforced concrete buildings. These safety factors are derived using a framework that focuses on the determination of the uncertainty in the limit state capacities. Existing seismic safety assessment standards, such as EN1998-3 or ASCE 41-17, follow a component-based approach that consider limit-state acceptance criteria based on capacity-related parameters to verify the safety of ductile and brittle failure modes. Despite their similar limit-state philosophy, these standards consider different conceptual formats for introducing the effects of uncertainties: the current version of EN1998-3 adopts confidence factors (CF) that factorize the mean values of material strength, while ASCE 41-17 uses a knowledge factor (k) to reduce the capacity of the component. The CF-based approach of EN1998-3 has been seen to lead to unclear levels of safety that may not reflect the impact of all the uncertainties about the different parameters or the sensitivity of different capacity models to these parameters. To address these issues, the proposed framework establishes a set of partial safety factors derived using an approach similar to that of ASCE 41-17, and involves recent capacity models, their uncertainties and a clear uncertainty management strategy. Furthermore, these new partial safety factors can also be seen to be compatible with the safety format proposed by the upcoming second-generation EN1998-3.

1 Introduction

Eurocode 8-Part 3 (EC8/3) (CEN 2005a) was the first European standard for the seismic safety assessment of existing structures, providing component-level procedures for the evaluation of the seismic performance of existing buildings, as well as for designing seismic retrofitting measures. Given the novel character of this standard in the European context, and the narrow level of knowledge on this subject at the time, the extent of EC8/3 was limited and a large portion of its volume was considered informative (included in the annexes) (Bisch 2018; Kappos 2018). It is thus not surprising that the publication of EC8/3 was followed by several studies and applications, highlighting issues and shortcomings related with this global framework and its contents. In the context of reinforced concrete (RC) buildings, a comparative application of the EC8/3 procedures was performed by Romão et al. (2010a), highlighting the difficulties in meeting the criterion that allows the use of linear elastic analysis, and showing the applicability of this type of analysis might be restricted to the limit state of damage limitation. In the same context, similar conclusions were drawn by Pinto and Franchin (2008), Mpampatsikos et al. (2008), Caprili et al. (2012), Araújo and Castro (2016) and Manfredi and Masi (2017), further highlighting the strengths and limitations of linear elastic analysis methods. Mpampatsikos et al. (2008) also compared assessment results obtained with different assumptions regarding the ductile and the brittle capacity of structural elements in RC buildings. The authors underlined the impact of different definitions for the initial stiffness of structural elements and for the length of the shear span in the verification of the referred failure modes. Romão et al. (2010b) and Araújo and Castro (2017) complemented these observations by showing the influence of exact and approximated methods to quantify the seismic demand of beam-column elements in RC and in steel moment resisting frames, respectively.

Significant attention and criticism have also targeted the definition of the EC8/3 knowledge levels (KLs) and confidence factors (CFs). Romão et al. (2010a) showed that selecting different KLs for the structural properties may lead to significant differences on the seismic demand and capacity results. The correlation between the CFs and the KLs for different limit states was also analysed by Jalayer et al. (2011) and Franchin et al. (2010). The study by Jalayer et al. (2011) focussed on assessing if the CFs applied solely to the mean material properties would be able to reflect the effect of other uncertainties, while, following a similar principle, Franchin et al. (2010) performed a conceptual analysis of the CF role in the overall safety assessment EC8/3 framework. After a consistent and extensive study, the authors identified the main issues associated with the current safety assessment format of the standard that include the inability to differentiate CF values as a function of different analysis methods and structural typologies (e.g. in terms of load-resisting systems, size of the building, construction materials), the non-conservative character of using average material properties in the analysis model, and the lack of rationale behind the assumption of a state of complete knowledge when only a sample of structural elements is surveyed. This last issue was also noted by Monti and Alessandri (2009) and Romão et al. (2012) who revised the formulation of the CF values based on statistical models and on the uncertainty about the mean material properties.

Previous research from the authors of this study (Pereira and Romão, 2016a, b) focused on improving the in situ quantification of concrete and reinforcing steel properties by proposing a strategy based on finite population statistics to assess the uncertainty about the mean value of these variables. Next, a coefficient (CF_mat) was proposed to correlate the uncertainty about the mean, the number of in situ tests and the inherent variability and obtain a conservative value for the mean. A set of simplified models were then also developed (Pereira and Romão 2018) to define an estimate of the concrete strength variability based solely on non-destructive tests. This approach was in line with the procedure of ASCE 41-17 (ASCE 2017) that recommends using a lower quantile of the sampling distribution of the concrete strength when the corresponding coefficient of variation (CoV) exceeds a given value. Aside from this connection between a representative value of the concrete strength and the CoV of its distribution, ASCE 41-17 also considers a knowledge factor κ which is used to factor the deformation or strength capacity limits of components. These limits are associated with qualitative inspection and testing plans but are not connected to the results of the survey. Similar to the principles of ASCE 41-17, Franchin and Pagnoni (2018) proposed a partial safety factor γ_Rd that is used to factor the nominal value of the capacity obtained by a given model. The factor γ_Rd is established by developing the total logarithmic standard deviation of the predicted capacity, which allows controlling the variability and the sensitivity of each parameter of the capacity model. Franchin and Pagnoni (2018) went further and developed a set of variability factors using simulations to account for the sampling uncertainty of each parameter, leading to a γ_Rd that can be directly connected to inspection and testing plans.

In this context, the present study combines the key features of ASCE 41-17 and EC8/3 to establish a complete and integrated safety assessment framework for RC buildings. The proposed framework is based on the proposal by Franchin and Pagnoni (2018), but provides component-level partial safety factors for the nominal capacity, termed herein by $\mathrm{}S{F}_{R}$, that correlate more explicitly the results of a survey and the corresponding epistemic uncertainty. In particular, these factors explicitly address issues associated with the possible member-to-member variability of structural detailing, the potentially large concrete strength uncertainty, the case where design documents are not available, and the difference between structural elements whose properties are surveyed and those where they are inferred. By proposing partial safety factors accounting for the individual specificities of those components (or members), the framework establishes a flexible alternative to existing code-based procedures that provides the engineer with more control of the safety assessment and with the ability to have a more sustainable approach to the design of retrofitting/strengthening measures.

2 Brief comparison between ASCE 41-17 and EC8/3 procedures

The present section revisits the seismic assessment procedures provided in the current version of EC8/3 and in ASCE 41-17 that are relevant for the proposed framework, namely aspects related with how the two standards address the different uncertainty sources. More particularly, a comparison of the provisions by the two standards is performed, highlighting their main differences. This comparison provides the background for understanding the safety format of the proposed framework that is presented in the subsequent sections.

2.1 Performance levels, rehabilitation objectives and importance classes

EC8/3 and ASCE 41-17 are seismic safety assessment standards that are part of the last generation of performance-based earthquake engineering codes and guidelines. Therefore, both codes consider a performance-based assessment approach, incorporating a set of performance and rehabilitation objectives, along with several aspects related with uncertainty characterisation and propagation. EC8/3 provides a set of performance objectives involving the pairing of specific levels of damage for structural and non-structural components and selected seismic hazard levels. Three different levels are defined in EC8/3: Near Collapse (NC), Significant Damage (SD) and Damage Limitation (DL). In the case of ASCE 41-17, similar principles are followed but performance objectives are defined as Operational (OP), Immediate Occupancy (IO), Life Safety (LS) and Collapse Prevention (CP). Nonetheless, while EC8/3 defines a set of performance objectives associated to specific seismicity levels, ASCE 41-17 sets different pairs of hazard and performance levels that can be considered, depending on the rehabilitation objectives. Figure 1 shows a direct comparison of the different rehabilitation objectives (i.e. combination of hazard levels and performance requirements) defined according to ASCE 41-17 and EC8/3 for ordinary buildings. As seen in Fig. 1, while ASCE 41-17 establishes multiple combinations of performance levels and seismicity levels to define the rehabilitation objectives, EC8/3 only defines a single combination. In EC8/3, the rehabilitation objectives only change with the importance class of the building, but these modifications are introduced by increasing the return period at which the performance level is verified.

Fig. 1

Comparison of the ASCE 41-17 and the EC8/3 combinations of performance levels and the corresponding hazard levels of the ground motion intensity associated to different rehabilitation objectives (adapted from Araújo et al. (2012)). a to p are combinations of performance levels and seismic hazard scenarios to be assessed in order to comply with a given set of performance objectives according to ASCE 41-17. The x markers refer to the combinations recommended in the general document of EC8/3, which can be changed by National Annexes

2.2 Data collection, level of in situ testing and partial safety factors

Existing RC buildings differ from new ones namely because knowledge about the design assumptions is often unavailable and the quality control employed during the construction stage is also usually unknown. As a result, in situ properties often exhibit significant deviations from current best practices or from the design documentation, particularly in older buildings. Therefore, there is a significant uncertainty when characterizing these properties, depending on factors such as the intrinsic variability of the material characteristics or the conformity level between documentation and in situ properties. In general, the in situ properties of RC structures can be disaggregated among 3 classes: 1) parameters related to the global and sectional geometry of the structural components (class X_G); 2) parameters related to the reinforcement detailing such as the number of longitudinal bars or the stirrup diameter and spacing (class X_D); 3) parameters related to the material properties of the structural component, typically the concrete compressive strength and the reinforcing steel yield strength (class X_M). Class X_M can therefore be further decomposed into the subclasses ${X}_{{f}_{c}}$ (concrete compressive strength) and ${X}_{{f}_{y}}$ (reinforcing steel yield strength). Given these classes, the overall uncertainty of as-built data can also be disaggregated into uncertainties associated to these classes of parameters that reflect the existing knowledge about these properties.

2.2.1 Accounting for uncertainty in ASCE 41-17

ASCE 41-17 accounts for the uncertainty in the referred classes by establishing specific KLs for which particular uncertainty factors are provided. The KLs are defined based on the amount of information available from the building records (design drawings, construction documents, material reports), on the type of condition assessment that was adopted (visual or comprehensive) and on the selected level of in situ testing (None, Usual or Comprehensive). Depending on the amount of information gathered during the inventory and survey campaigns, the corresponding KL will: 1) specify the knowledge factor (κ) that can be adopted, i.e., a factor used to reduce the capacity of each individual component due to the lack of knowledge about its properties; 2) constrain the method of analysis that can be used; 3) limit the performance levels that can be assessed. Table 1 presents the levels of information and testing associated to different KLs and their corresponding knowledge factors (κ), the admissible methods of analysis and the maximum performance levels that can be analysed.

Table 1 ASCE 41-17 correlation between the KL, the performance levels and κ

As seen in Table 1, if a Performance Level greater than LS is to be considered, the Comprehensive KL must be guaranteed, which considers that construction documents or equivalent are available, that a visual (CA1) or a comprehensive (CA2) condition assessment is performed (covering geometric variables (X_G) and variables related to construction details (X_D)), and that documents regarding the material properties (X_M) and tests are available or a comprehensive in situ test campaign is performed.

Table 2 shows the inspection levels defined in ASCE 41-17 and the corresponding number of structural components that must be surveyed. The condition assessment (inspection level) CA1 implies that a direct visual inspection of accessible and representative primary components and connections has to be performed. For CA2 (comprehensive), the condition assessment implies the need to locally remove the cover concrete to inspect reinforcement details. Specific sampling plans are proposed in ASCE 41-17 for the material properties (X_M) that define two levels of testing (Usual and Comprehensive). Table 3 summarizes the number of structural elements where concrete samples and reinforcing steel coupons must be collected from and tested. Furthermore, ASCE 41-17 indicates that a κ value of 0.75 must be considered when: 1) components are found to be damaged or their condition is damaged during the assessment; 2) the coefficient of variation (CoV) of the mechanical properties exceeds 20%; or 3) components contain archaic or proprietary material and the condition is uncertain.

Table 2 ASCE 41-17 inspection levels (IL) and minimum number of components that must be surveyed in RC structures

Table 3 ASCE 41-17 testing levels (TL) and minimum number of tests that must be conducted in RC structures

2.2.2 Accounting for uncertainty in EC8/3

EC8/3 considers the epistemic uncertainty about the building properties by defining specific testing and inspection levels which are then associated to a CF. The CF reflects the level of confidence that exists about the values adopted for each parameter of classes X_G, X_D and X_M. EC8/3 proposes 3 values for the CF that are connected to 3 KLs: limited (KL1), extended (KL2) and comprehensive (KL3). The correlation between the CF and the KLs established in EC8/3 is shown in Table 4.

Table 4 EC8/3 correlation between the KL, the performance levels and CF

With respect to the X_G variables, EC8/3 specifies that a visual survey of the overall geometry of the structure and sectional dimensions can be carried out to check the conformity with construction documents. If discrepancies are observed, a full survey must be carried out to produce a new set of structural drawings, identifying the components and their dimensions. 

For the construction details (X_D), three different inspection levels are considered: Limited, Extended and Comprehensive. The amount of structural elements that needs to be surveyed for each inspection level is shown in Table 5.

Table 5 EC8/3 inspection levels (IL) and minimum number of components that must be surveyed

As opposed to the inspection levels, which incorporate relative quantities (i.e., surveying n out of N components), the testing levels specify absolute values for the number of elements where concrete cores and reinforcing steel coupons have to be extracted and tested. Table 6 shows the number of tests associated to the EC8/3 testing levels.

Table 6 EC8/3 testing levels and minimum number of tests that must be conducted in RC structures

2.2.3 Acceptance criteria and format of the safety assessment methodology

ASCE 41-17 proposes a safety assessment methodology that is divided into three tiers: Tier 1 and 2 refer to a simplified screening and to a deficiency-based evaluation procedure, respectively, while Tier 3 involves a comprehensive analytical procedure. On the contrary, EC8/3 only has one tier that is similar to Tier 3 in ASCE 41-17. In these two cases, the safety verifications associated to the limit state conditions and the corresponding performance objectives are based on the analysis of acceptance criteria for individual structural elements. Although the same principle is considered by both standards, the format of the safety inequality that must be verified is not the same, as shown in Fig. 2 for the case where nonlinear analysis is considered in the assessment.

Fig. 2

Comparison of the limit state conditions defined in ASCE 41-17 and EC8/3. Parameter ${{\zeta}}$ is a partial safety factor that depends on the type of mechanism, ${{{\gamma}}}_{{{e}}{{l}}}$ is a factor that varies with the performance level under analysis and $\widehat{{\overline{{X}}}}_{{{M}}}$ represents the estimates obtained for the expected values of the material properties

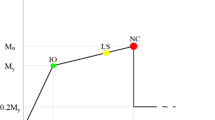
According to both standards, a demand value S must be quantified using either linear or nonlinear methods of analysis. In ASCE 41-17, when nonlinear analysis is considered, the demand values must be obtained using the mean material properties or a reduced value (e.g., for the case of concrete strength, when it exhibits a high variability). The same expected mean value of the material properties is adopted to quantify the capacity R. No particular information is provided regarding which values should be adopted for parameters of class ${X}_{G}$ and class ${X}_{D}$. The uncertainty is accounted for by multiplying the capacity R, either in terms of plastic rotations (defined by specific values) or shear strength (computed using an analytical model), by the knowledge factor κ. As a result, the uncertainty is included directly in this factor and the approach establishes a lower bound of the capacity R of each component. Furthermore, for the plastic rotation capacity, ASCE 41-17 correlates the acceptance criteria of each structural component directly with the corresponding behaviour modelling approach, which corresponds to the generalized backbone model represented in Fig. 3 for the case of RC components.

Fig. 3

Generalized moment-rotation relation defined in ASCE 41-17 for RC frame elements

By providing values for each model parameter (a, b and c in Fig. 3, where M_y is the yield moment), ASCE 41-17 ensures a complete compatibility between the modelling approach and the acceptance criteria by defining them as a function of a and b. For example, for a RC column whose behaviour is not controlled by inadequate development or splicing of reinforcement (ASCE 2017), the limit state criterion for IO is defined by a plastic rotation equal to 15% of a, while for LS and CP, the acceptance criteria are set as 50% of b and 70% of b, respectively.

As opposed to the ASCE 41-17 approach, the CF defined by EC8/3 is not applied globally to R. Instead, the CF is used to factor the concrete compressive strength and the reinforcing steel yielding strength in the analytical expressions that define $R$. As shown in Fig. 2, when nonlinear analysis is adopted, the capacity $R$ of the element is computed using mean material properties that have to be divided by CF and by a partial safety factor $\zeta$. The partial safety factor $\zeta$ is equal to 1.0 when ductile mechanisms are analysed, and is equal to ${\gamma }_{c}$ and ${\gamma }_{s}$ for the peak concrete compressive strength and the reinforcing steel yield strength, respectively, when $R$ refers to the capacity associated to brittle mechanisms. For both mechanisms, the value of $R$ is also divided by an additional factor ${\gamma }_{el}$ which is independent of the KL. The factor ${\gamma }_{el}$ depends on the performance level (as κ indirectly does in ASCE 41-17) and varies according to the type of mechanism. Therefore, the EC8/3 acceptance criteria include a factor ${\gamma }_{el}$ that reduces the capacity $R$ independently of the adopted KL. The KL is embedded in the concept of CF, which is expected to represent the epistemic uncertainty about the mean value adopted for the material properties (since the CF only affects class ${X}_{M}$) and, therefore, only reflects the KL about the materials. Furthermore, parameter $\zeta$ factors the mean material properties to define a lower quantile of the expected distribution while the role of ${\gamma }_{el}$ can be associated with the empirical nature of the $R$ models defined by EC8/3. As mentioned by Franchin and Pagnoni (2018), $R$ can be defined by:

$$R = \hat{R}\left( {X_{G} ,X_{D} ,X_{{f_{c} }} ,X_{{f_{y} }} } \right) \cdot \varepsilon_{R}$$

(1)

where $\widehat{R}$ is an analytical function that defines the median value of the capacity based on the input vectors X_G, X_D, ${X}_{{f}_{c}}$ and ${X}_{{f}_{y}}$, and ${\varepsilon }_{R}$ is a lognormal random variable representing the epistemic error of the model of $\widehat{R}$ with median ${\widehat{\varepsilon }}_{R}$ and logarithmic standard deviation ${\sigma }_{\mathit{ln}R}$. Based on this assumption, when the real values of X_G, X_D, ${{X}}_{{{f}}_{{c}}}$ and ${{X}}_{{{f}}_{{y}}}$ are known, there is a certain quantile of ${\varepsilon}_{R}$ that, when multiplied by the value obtained by the model $\widehat{R}$ defined by the standard, leads to the equality:

$$\frac{1}{{\gamma }_{el}}\cdot \widehat{R}\left({X}_{G},{X}_{D},{X}_{{f}_{c}},{X}_{{f}_{y}}\right)=\widehat{R}\left({X}_{G},{X}_{D},{X}_{{f}_{c}},{X}_{{f}_{y}}\right)\cdot {\left({\varepsilon }_{R}\right)}_{q}\iff \frac{1}{{\gamma }_{el}}={\left({\varepsilon }_{R}\right)}_{q}$$

(2)

Due to the format of the EC8/3 limit state assessment framework, the CF is assumed to implicitly account also for the lack of knowledge or the uncertainties about the geometric variables (${X}_{G}$) and the construction details (${X}_{D}$). However, neither EC8/3 nor ASCE 41-17 indicate how to account for differences found between expected data (e.g. from design documents) and surveyed data. Furthermore, unlike in the limit state assessment of ASCE 41-17, the role of the CF, ${\gamma }_{el}$ and $\zeta$ in EC8/3 is more difficult to interpret and to correlate with the existing uncertainties. Furthermore, the previous discussion suggests that ${\gamma }_{el}$ could be interpreted as a partial safety factor ($S{F}_{R}$), similar to κ in ASCE 41-17, while CF can be seen to be a measure of the reliability of the estimate of the mean properties of the materials. Nonetheless, the latter should be redefined individually for parameters ${X}_{G}$, ${X}_{D}$_, ${X}_{{f}_{c}}$ and ${X}_{{f}_{y}}$, since EC8/3 currently proposes a single CF for all parameters. Therefore, a consistent safety assessment framework must be defined and should include a consistent derivation of $S{F}_{R}$ factors, as well as a new set of variables that can be used to adequately estimate the mean properties.

3 Proposed component-based limit-state assessment framework

3.1 Principles and key features

The framework proposed herein combines the strengths of the ASCE 41-17 and EC8/3 methodologies and introduces key elements that support the definition of more consistent probability-based limit state acceptance criteria. These key elements address certain limitations identified in current standards, while also providing a general strategy that covers all the necessary steps to evaluate an existing RC building:

• (1) Knowledge: The framework provides a new strategy to define the uncertainty and the expected values of structural properties for the case where design documents are available and the case where those documents are missing. Furthermore, it recognizes differences in the variables involved in the survey, namely in terms of the different treatment that can be considered for continuous variables (e.g. material properties) and discrete variables (e.g. geometry and structural details).

• (2) Survey: The framework considers the concepts of finite structure and testing/inspection regions, which define the domain over which the variability and the expected value of the properties are determined. By using these concepts, the survey can be conducted using an n-out-of-N approach, which allows defining a multitude of possible sampling plans that can be carried out across the structure.

• (3) Parameter uncertainty: The framework provides a new strategy and uncertainty factors that are used to evaluate the properties of each structural element within a given region. The strategy is tailored to the type of variable under analysis (connecting it to the Knowledge) and is connected to the survey plans considered in an explicit and closed-form way (connecting it to the Survey). In this context, it provides estimates for the expected value of the material properties and the structural details, which are central for the nonlinear modelling of the structure. Furthermore, it also provides a new approach that distinguishes between the uncertainty about the structural elements whose properties are surveyed and those whose properties are not surveyed.

• (4) Partial safety factors: The framework follows the principles outlined in Franchin and Pagnoni (2018), connecting the survey plan, the survey results, their uncertainties and the SF_R factors. Furthermore, it proposes new closed-form expressions for the SF_R factors which are connected to the variability factors also developed within the framework, thus making it applicable to cases with varying levels of member-to-member variability and multiple survey plans. As an alternative to existing code-based procedures, the framework proposes member-by-member SF_R factors that account for the individual specificities of those components (or members) and provide the engineer with more control of the safety assessment.

3.2 Existing knowledge, groups of variables and their properties

The capacity of a RC structural component is defined by a set of variables belonging to the four classes of parameters: X_G, X_D, $\it {\text{X}}_{{\text{f}}_{\text{c}}}$ and $\it {\text{X}}_{{\text{f}}_{\text{y}}}$. As seen in Sect. 2, existing codes for the safety assessment of existing RC buildings establish different strategies for each one of these groups of variables and set different approaches for the cases when design documents are either available or unavailable. The major impact of the existence of design documentation is seen in the estimates made for X_G and X_D. Usually, X_G and X_D represent variables that are discrete, and, in some cases, that are completely unknown. While variables belonging to X_G are usually easy to characterize, this is often not the case for those belonging to class X_D. When design documents are available, their characteristics can be extracted from that information and used for numerical modelling and safety assessment. Otherwise, the information of class X_D must be fully determined by in-situ inspection, which may induce significant damage to structural and non-structural components. Alternatively, as pointed out in current codes, simulated design can provide reference design data about detailing parameters such as the expected to number of rebars, sizing and spacing, etc. Nevertheless, in this case, a complete knowledge about X_G is of the upmost importance. Thus, in this framework, it is assumed that having complete knowledge about X_G is a necessary condition to be able to carry out a safety assessment. Otherwise, simplified methods of analysis (such as those of Tier 1 in ASCE 41-17) should be adopted due to insufficient knowledge about the structural properties since the reliability of the results that are obtained may be questionable.

In any case, a reference set of parameters X_D,ref can be established for an existing RC building, obtained either from design drawings or by simulated design. Based on these reference values, the uncertainty can be estimated by adopting a tailored inspection to verify the adequacy of X_D,ref. The uncertainty about X_D,ref can be divided into that associated to the transverse reinforcement, X_D,w, and that associated to the longitudinal reinforcement, X_D,l. These two variables can then be used to define conformity indexes k_D,w and k_D,l whose distributions across the structure can be assumed to be continuous and defined by the ratios between X_D,w, and X_D,l, and their corresponding reference values X_D,w,ref, and X_D,l,ref, respectively, for all the structural components. The conformity indexes k_D,w and k_D,l of a given structural component j are defined as:

$${k}_{D,w,j}=\frac{{x}_{D,w,j}}{{x}_{D,w,ref,j}},\hspace{0.33em}{k}_{D,l,j}=\frac{{x}_{D,l,j}}{{x}_{D,l,ref,j}}$$

(3)

where x_D,w,j, x_D,l,j, x_D,w,ref,j and x_D,l,ref,j are the values of X_D,w, X_D,l, X_D,w,ref, and X_D,l,ref, respectively, for the jth component. By using the conformity indexes and the reference values, it is possible to evaluate the level of conformity between the designed and the constructed building. This aspect is important for defining appropriate partial safety factors for the capacity of each structural component (or member), but it assumes an even more critical significance when performing the numerical modelling of the building to compute the demand.

As opposed to the case of the X_G and X_D, material properties are usually continuous over a given domain where some level of homogeneity is expected to exist. Therefore, parameters ${\text{X}}_{{\text{f}}_{\text{c}}}$ and ${\text{X}}_{{\text{f}}_{\text{y}}}$ can be assumed to be continuous properties following probability distributions defined by mean values ${\mu }_{{\text{f}}_{\text{c}}}$ and ${\mu }_{{\text{f}}_{\text{y}}}$, respectively, and by standard deviations ${\sigma }_{{\text{f}}_{\text{c}}}$ and ${\sigma }_{{\text{f}}_{\text{y}}}$, respectively. Thus, it is important to clearly define this survey domain to minimize the damage induced to the building.

3.3 The survey domain and the type of inspection/testing plans

The key features that are proposed to establish the survey domain for each group of variables identified in the previous section account for the properties of each variable when defining the domain and the inspection/testing plans, and adopt the concept of finite structure which assumes that each structural component can be represented by a single array of properties y_j:

$${y}_{j}=\left\{{x}_{D,w,ref,j},{x}_{D,l,ref,j},{x}_{G,j},{k}_{D,w,j},{k}_{D,l,j},{x}_{{f}_{c},j},{x}_{{f}_{y},j}\right\}=\left\{{\left({Z}_{i}\right)}_{j}\right\},i=1:\mathit{dim}\left(Y\right)$$

(4)

Accordingly, the structure or any of its sub-regions (storey, floor, etc.) can be assumed to have N components and a matrix Y containing the N values of each variable Z_i, allowing for the definition of survey plans using an n-out- of-N approach. The definition of these regions (composed by N components) can vary according to the group of variables (X_D, $\it {\text{X}}_{{\text{f}}_{\text{c}}}$ or $\it {\text{X}}_{{\text{f}}_{\text{y}}}$) that is considered. For the case of structural details (X_D), N can be established considering all the elements of the structure with a similar function, (e.g. N columns and N beams). Pereira and Romão (2016a, b) have previously discussed the concept of region for the case of $\it {\text{X}}_{{\text{f}}_{\text{c}}}$ and $\it {\text{X}}_{{\text{f}}_{\text{y}}}$, and proposed the disaggregation of columns by storey and of beams by floor. Moreover, they also proposed different strategies to account for the uncertainty of $\it {\text{X}}_{{\text{f}}_{\text{c}}}$ and $\it {\text{X}}_{{\text{f}}_{\text{y}}}$, which affect the adopted testing plans. Since the variability of $\it {\text{X}}_{{\text{f}}_{\text{y}}}$ is usually limited, testing plans involving the survey of a reduced number of structural elements can usually be considered in this case. However, the opposite can be expected for $\it {\text{X}}_{{\text{f}}_{\text{c}}}$, particularly in older structures. The authors proposed an inspection campaign involving at least 30% of the N structural elements using non-destructive tests (NDTs) (e.g. rebound hammer or ultrasonic pulse velocity) to obtain an approximation for the variability, following the general expressions proposed in Pereira and Romão (2018).

In light of this, the proposed framework assumes that regions can be disaggregated by type of structural element (columns, beams, walls) and by storey/floor. Within each one of these regions, adequate inspection levels should be implemented to cover n/N structural elements (with a minimum of 30%) that include performing NDTs and characterizing k_D,w and k_D,l for the relevant structural details. With these results and based on the expected variability for $\it {\text{X}}_{{\text{f}}_{\text{c}}}$, adequate inspection levels must be adopted to obtain adequate estimates of the concrete strength. Finally, $\it {\text{X}}_{{\text{f}}_{\text{y}}}$ must be characterized using a limited testing campaign, reflecting the expected value of the variability of  this property. As a result, multiple n/N samples will be available for X_D, $\it {\text{X}}_{{\text{f}}_{\text{c}}}$ and $\it {\text{X}}_{{\text{f}}_{\text{y}}}$, which require the adoption of factors that reflect their corresponding uncertainties.

3.4 Uncertainty factors for different groups of variables

The proposed rationale for defining survey plans implies that different n/N samples can be adopted for X_D, $\it {\text{X}}_{{\text{f}}_{\text{c}}}$ and $\it {\text{X}}_{{\text{f}}_{\text{y}}}$ within a given region of the structure. As a result, matrix Y is incomplete since only n structural components of each region have parameters ${Z}_{i}\in Y$ while the remaining ones have missing data. Since matrix Y needs to be fully defined to perform the safety assessment of the structure (namely to compute the demand and the capacity of each structural component), estimates for the missing values must be obtained. The strategy proposed herein to deal with these missing data involves using the information collected from the $n$ surveyed components to infer the properties of the remaining $N-n$ non-surveyed components. To achieve this, the proposed method uses the information about the $n$ out of $N$ components where observations of ${Z}_{i}$ are available to quantify their sampling mean ${m}_{{Z}_{i}}$ and standard deviation ${s}_{{Z}_{i}}$. Based on ${m}_{{Z}_{i}}$ and ${s}_{{Z}_{i}}$, the real mean ${\mu }_{{Z}_{i}}$ and the real standard deviation ${\sigma }_{{Z}_{i}}$ of each variable ${Z}_{i}$ can be defined. The relation between any ${\sigma }_{{Z}_{i}}$ and ${s}_{{Z}_{i}}$ can be defined as:

$${\sigma }_{{Z}_{i}}=V{F}_{{Z}_{i}}\cdot {s}_{{Z}_{i}}$$

(5)

where $V{F}_{{Z}_{i}}$ is a variability factor accounting for the uncertainty about ${s}_{{Z}_{i}}$ due to the number of non-surveyed components. Similarly, ${\mu }_{{Z}_{i}}$ can be defined based on ${m}_{{Z}_{i}}$ by:

$${\mu }_{{Z}_{i}}=M{F}_{{Z}_{i}}\cdot {m}_{{Z}_{i}}$$

(6)

where ${MF}_{{Z}_{i}}$ is a mean factor used to define the probabilistic range that ${\mu }_{{Z}_{i}}$ may assume given the estimate ${m}_{{Z}_{i}}$. ${MF}_{{Z}_{i}}$ and ${VF}_{{Z}_{i}}$ introduce the effect of uncertainty on the estimates and can be established differently according to the type of component. For the n components that were surveyed, the information directly obtained from the surveys can be used to estimate the properties, meaning that $M{F}_{{Z}_{i}}$ =1 and $V{F}_{{Z}_{i}}$ =1 can be assumed for each variable Z_i. For the remaining $N-n$ non-surveyed components, ${MF}_{{Z}_{i}}$ and ${VF}_{{Z}_{i}}$ can be established using a confidence interval (CI) that is defined based on the data from the n surveyed components. In this case, the expression to compute ${MF}_{{Z}_{i}}$ can be obtained following the principles outlined in Pereira and Romão (2016a) and in Pereira and Romão (2016b), while O’Neill (2014) can be used to establish $V{F}_{{Z}_{i}}$. Hence, for variables belonging to the group X_D, where it may be difficult to have a prior value for the variability of the conformity indexes, $M{F}_{{Z}_{i}}$ can be estimated by:

$$M{F}_{{Z}_{i}}=1\pm {t}_{n-\mathrm{1,1}-\alpha /2}\frac{1}{\sqrt{n}}\cdot \sqrt{\frac{N-n}{N-1}} \, \cdot\, Co{V}_{{Z}_{i}}$$

(7)

which depends on the coefficient of variation $Co{V}_{{Z}_{i}}$ estimated based on the n out of N structural components where the property was surveyed, and where ${t}_{n-\mathrm{1,1}-\alpha /2}$ is the $1-\alpha /2$ quantile of the t distribution with $n-1$ degrees of freedom. Conversely, for $\it {\text{X}}_{{\text{f}}_{\text{c}}}$ and $\it {\text{X}}_{{\text{f}}_{\text{y}}}$, it might be assumed there is enough information to consider that ${\sigma }_{{Z}_{i}}$ is known, which leads to:

$$M{F}_{{Z}_{i}}=1\pm {z}_{1-\alpha /2}\frac{1}{\sqrt{n}}\cdot \sqrt{\frac{N-n}{N-1}}\,\cdot\, Co{V}_{{Z}_{i}}$$

(8)

where ${z}_{1-\alpha /2}$ is the $1-\alpha /2$ quantile of the standard normal distribution. For the case of $V{F}_{{Z}_{i}}$, it can be computed for all the variables using:

$$V{F}_{{Z}_{i}}=\sqrt{\left(\frac{n-1}{N-1}\right)+\left(\frac{N-n}{N-1}\right)\cdot \frac{1}{{F}_{\alpha }\left(n-1,N-n\right)}}$$

(9)

where ${F}_{\alpha }$ is the $\alpha$ quantile of the F distribution with ($n-1$) and ($N-n$) degrees of freedom.

Using the proposed approach, the $N - n$ structural components that are left without specific information from the survey must be treated differently from the n components that were surveyed. As a result, the partial safety factors defined for surveyed and non-surveyed elements can also be different.

3.5 Closed-form partial safety factors

3.5.1 General principles

The safety of the jth component is ensured by complying with the following inequality

$$\widehat{D}\left({y}_{j}\right)\le {R}_{q}\left({y}_{j}\right)$$

(10)

where $\widehat{D}\left({y}_{j}\right)$ is a representative value of demand (e.g. a mean or a median value) obtained with the expected values of ${y}_{j}$ and ${R}_{q}\left({y}_{j}\right)$ is the qth percentile of the distribution of capacity $R\left({y}_{j}\right)$. In code-based procedures, ${R}_{q}\left({y}_{j}\right)$ corresponds to a lower percentile and can be established based on a representative value of capacity $\widehat{R}\left({y}_{j}\right)$ that is based on the expected values of the necessary parameters and $S{F}_{R}$ by:

$${R}_{q}\left({y}_{j}\right)=\frac{\widehat{R}\left({y}_{j}\right)}{{\left(S{F}_{R}\right)}_{j}}$$

(11)

Franchin and Pagnoni (2018) proposed a new $S{F}_{R}$ factor for the seismic safety assessment of existing buildings with the following format:

$${\left(S{F}_{R}\right)}_{j}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\sigma }_{\mathit{ln}R\left({y}_{j}\right)}^{2}}\right)$$

(12)

where $\Phi \left(q\right)$ is the number of standard deviations away from the logarithmic mean of the qth percentile of the distribution of $\mathit{ln}R\left({y}_{j}\right)$ for each structural component, and ${\sigma }_{\mathit{ln}R\left({y}_{j}\right)}$ is the corresponding standard deviation. The framework proposed herein assumes that $\Phi \left(q\right)$ can be associated with the rehabilitation objectives (in ASCE 41-17) or the building importance (in EC8/3) adopted by current standards. By doing so, a direct correlation can be defined between the mandatory level of safety (at the component level) and the adopted performance levels (i.e., the admissible damage state). Tentative values of $\Phi \left(q\right)$ are proposed in Table 7, where these factors are defined as a function of the building classes (based on Eurocode 8—Part 1 (EC8/1) (CEN 2005b)).

Table 7 Variation of the factor ${\Phi }\left({{q}}\right)$ with the accepted level of safety for different importance classes of EC8/1

Since the aim of the proposed framework is to provide a closed-form format for $S{F}_{R}$, the format provided by Franchin and Pagnoni (2018) was adopted (Eq. (12)), and analytical approximations for ${\sigma }_{\mathit{ln}R\left({y}_{j}\right)}^{2}$ were developed considering multiple capacity models available in the literature. The process that was followed is based on the approximation for the expected value and the variability of $\mathit{ln}R\left({y}_{j}\right)$ using a Taylor series expansion about the mean value of ${y}_{j}$, ${\mu }_{{y}_{j}}$, truncated after the first order terms. According to Ang and Tang (2006; p. 186), ${\mu }_{\mathit{ln}R\left({y}_{j}\right)}$ and ${\sigma }_{\mathit{ln}R\left({y}_{j}\right)}^{2}$ can be defined by:

$$\mu_{{\ln R\left( {y_{j} } \right)}} = \ln \left( {R\left( {\mu_{{y_{j} }} } \right)} \right) + \overline{\varepsilon }_{\ln R}$$

(13)

$${\sigma }_{\mathit{ln}R\left({y}_{j}\right)}^{2}\cong \sum \limits_{i=1}^{t}{\left({\sigma }_{{Z}_{i}}^{2}\right)}_{j}\cdot {\left(\frac{\partial \mathit{ln}R\left({\mu }_{{y}_{j}}\right)}{\partial {Z}_{i}}\right)}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{R}}^{2}$$

(14)

where $\partial /{\partial }_{{Z}_{i}}$ is the partial derivative of $\mathit{ln}R$ with respect to the generic variable ${Z}_{i}\in Y$ evaluated at the vector of mean values ${\mu }_{{y}_{j}}$, and $t=\mathit{dim}\left({y}_{j}\right)$ is the number of elements of Y. Thus, the generic format of ${\left(S{F}_{R}\right)}_{j}$ can be established by:

$$\left( {SF_{R} } \right)_{j} = \exp \left( { - \Phi \left( q \right) \cdot \sqrt {\sum _{{i = 1}}^{t} \left( {\sigma _{{Z_{i} }}^{2} } \right)_{j} \cdot \left( {\frac{{\partial \ln R\left( {\mu _{{y_{j} }} } \right)}}{{\partial Z_{i} }}} \right)^{2} + \sigma _{{\ln \varepsilon _{R} }}^{2} } } \right)$$

(15)

Equation (15) provides the framework for determining ${\left(S{F}_{R}\right)}_{j}$ given any testing or survey level of the component, including the cases where the component was surveyed and was not surveyed. In the former, all the ${Z}_{i}$ characteristics of the structural component j are assessed, which means that ${\left({\sigma }_{{f}_{c}}\right)}_{j}\cong 0$, ${\left({\sigma }_{{f}_{y}}\right)}_{j}\cong 0$, ${\left({\sigma }_{{k}_{D,w}}\right)}_{j}\cong 0$ and ${\left({\sigma }_{k,l}\right)}_{j}\cong 0$. In this particular case, ${y}_{j}$ is fully known and Eq. (15) simplifies to:

$${\left(S{F}_{R}\right)}_{j}=\mathit{exp}\left(-\Phi \left(q\right)\cdot {\sigma }_{\mathit{ln}{\varepsilon }_{R}}\right)$$

(16)

Capacity models for RC columns and beams that define both the expected value and the variability of the capacity have been previously defined for the purpose of numerical modelling and safety assessment. Among the models available in literature, four different sets were considered in the present framework to define closed-form partial safety factors: 1) RC columns with deformation-controlled mechanisms with smooth bars based on the proposal made by Verderame and Ricci (2018); 2) RC columns with deformation-controlled mechanisms with ribbed bars using the proposal of Haselton et al. (2016); 3) RC columns with force-controlled mechanisms following the model provided in ASCE 41-17; and 4) deformation and force-controlled mechanisms in beams following the models also adopted for columns with additional simplifications or corrections such as the modification proposed by Fardis and Biskinis (2003). Details about the above-mentioned models, along with the corresponding values for ${\sigma }_{\mathit{ln}{\varepsilon }_{R}}^{2}$ can be found in the respective references and are summarized in the next section. Based on these models, the corresponding expressions for the ${\left(S{F}_{R}\right)}_{j}$ partial safety factors of each component j are presented in the following sections. These expressions represent the expansion of Eq. (15) for the selected capacity models and for the case where the jth component is not surveyed. These expressions revert to the simplified form of Eq. (16) by setting the necessary variability terms to zero when the jth component is surveyed. To enhance readability, the subscript j referring to the jth component is dropped from the following expressions.

3.5.2 Capacity models for RC frame components in ASCE 41-17 and EC8/3

The application of the proposed framework implies there must be a direct correlation between the modelling techniques used to quantify the median demand of component j, $\widehat{D}\left({y}_{j}\right)$, and the corresponding capacity. In current standards, the seismic performance assessment of RC frame buildings is analysed for a set of deformation-controlled mechanisms, usually defined by chord rotation limits, and additional force-controlled mechanisms, defined in terms of shear and axial force limits. ASCE 41-17 defines an explicit hinge model for beam-column components, providing modelling parameters and limit state acceptance criteria for different performance levels. The modelling parameters are the effective flexural stiffness, $E{I}_{eff}$, the pre-capping plastic rotation capacity (a), and the total plastic rotation (b) until a given residual moment ratio (c times the yielding moment ${M}_{y}$) is reached. The limit state criteria corresponding to the performance levels of Immediate Occupancy (IO), Life Safety (LS) and Collapse Prevention (CP) are defined as function of a and b. Tables of values are provided in the standard for these limits for beams, column and beam-column joints, but continuous analytical models are not explicitly defined.

Conversely, EC8/3 provides limit state values for chord rotations of beams and columns associated to different performance levels. The first limit state defines the yielding chord rotation (${\theta }_{DL}$), and corresponds to the Damage Limitation (DL) performance level. The Near Collapse limit state is characterised by the rotation (${\theta }_{NC}$) corresponding to a decay of 20% from the maximum moment ${M}_{c}$, whereas the significant damage limit state criterion (${\theta }_{SD}$) is defined by a chord rotation with a value equal to 75% of ${\theta }_{NC}$. None of the codes includes an ultimate collapse limit state (C), which can be considered as the rotation corresponding to a zero bending capacity.

Modelling parameters and performance level acceptance criteria defined in ASCE 41-17 are constant values associated with specific conditions regarding stirrup spacing, axial load level, amount of transverse reinforcing steel and correlation with the shear failure capacity. Among the effects that critically govern the response of RC frame elements, the most relevant are the use of smooth reinforcing steel bars and the likely occurrence of brittle failure modes induced by pure shear or flexure-shear mechanisms. Pure shear refers to the type of failure mechanism included in the force-controlled limit state defined in both EC8/3 and ASCE 41-17. Therefore, these standards can be seen to define only one force-controlled limit state that is associated to a maximum value of shear force and one performance level (NC in EC8/3, by default), unlike the deformation-controlled mechanisms which are established for several performance levels.

3.5.3 Capacity models for RC columns with different characteristics

The models adopted in the proposed framework were selected in order to allow for the definition of both the numerical model used to compute the demands and the limit state criteria, as done in ASCE 41-17 and shown in Fig. 4a.

Fig. 4

Generalized moment-rotation model and identification of the component limit states defined by ASCE 41-17 (ASCE 2017) (a), limit state values proposed by EC8/3 (CEN 2005a) (b) and representation of the modelling/limit state criteria adopted in this study for beam-column elements with smooth (c) and ribbed (d) steel bars

A similar rationale can be used to construct a moment-rotation backbone model based on the limit states presented in EC8/3, as shown in Fig. 4b. Recent studies (Verderame et al. 2010; Verderame and Ricci 2018) have highlighted the differences between the seismic response of RC components with ribbed and smooth steel bars. Therefore, since the proposed seismic assessment framework must be able to address all the possible existing RC frame buildings, a distinction is introduced herein between old RC components (with smooth bars) and modern components (with ribbed bars). The corresponding generalized moment-rotation models assumed in this study are, therefore, those shown in Fig. 4c, d.

The rotation capacity of RC frame elements with smooth bars was studied by Verderame and Ricci (2018) due to the importance that old RC building typologies may have in the existing building stock—these correspond to most of the buildings constructed prior to the 1960s in Europe. The modelling parameters suggested in Verderame and Ricci (2018) include a quadrilinear cyclic backbone model (Fig. 4c) defined by the flexural stiffness $E{I}_{eff,old}$, the capping rotation ${\theta }_{cap,old}$, the near collapse post-capping rotation ${\theta }_{pc,old}$ and the collapse post-capping rotation ${\theta }_{c,old}$. The empirical relations developed by Verderame and Ricci (2018) for the abovementioned parameters are:

$$E{I}_{eff,old}=0.074\cdot 8.{1}^{\nu }\cdot \left(1+0.3\cdot \frac{{L}_{s}}{d}\right)\cdot E{I}_{g}\cdot {\varepsilon }_{E{I}_{eff,old}}\to {K}_{eff,old}=\frac{3\cdot E{I}_{eff,old}}{{L}_{s}}$$

(17)

$${\theta }_{cap,old}=0.0097\cdot 0.2{7}^{\nu }\cdot \left(1+0.28\cdot \frac{{L}_{s}}{d}\right)\cdot \left(0.58+0.42\cdot \frac{\mathit{min}\left(\frac{{l}_{0}}{{d}_{b}};50\right)}{50}\right)\cdot {\varepsilon }_{{\theta }_{cap,old}}$$

(18)

$${\theta }_{pc,old}=0.037\cdot 0.04{2}^{\nu }\cdot {\omega }_{w}^{0.19}\cdot \left(1+0.5\cdot \frac{{L}_{s}}{d}\right)\cdot \left(0.84+0.16\cdot \frac{\mathit{min}\left(\frac{{l}_{0}}{{d}_{b}};50\right)}{50}\right)\cdot {\varepsilon }_{{\theta }_{pc,old}}$$

(19)

$${\theta }_{c,old}=0.086\cdot 0.02{4}^{\nu }\cdot 4{4}^{100\cdot {\rho }_{w}}\cdot {\varepsilon }_{{\theta }_{c,old}}$$

(20)

where $E{I}_{g}$ is the flexural stiffness of the gross cross section, $\nu$ represents the axial load ratio, ${L}_{s}$ is the shear span length (${L}_{s}=M/V$), d is the effective cross-section depth, ${l}_{0}$ is the longitudinal reinforcement splice length, ${d}_{b}$ is the longitudinal bar diameter, ${\rho }_{w}$ is the geometrical transverse reinforcement ratio, ${\omega }_{w}$ is the mechanical transverse reinforcement ratio and ${\varepsilon }_{E{I}_{eff,old}}$, ${\varepsilon }_{{\theta }_{cap,old}}$, ${\varepsilon }_{{\theta }_{pc,old}}$ and ${\varepsilon }_{{\theta }_{c,old}}$ are random error terms. The parameters defining the lognormal distribution of the error terms for these models are shown in Table 8.

Table 8 Median and logarithmic standard deviation of the models defined by Eqs. (17)–(20)

Given this modelling approach for a component, the limit state associated to the DL performance level can be defined by the condition involving the secant stiffness ($M/\theta$) exceeding the value of ${K}_{eff,old}$ defined in Eq. (17) for the double-bending case. The limit state compatible with the performance level SD can be defined by the occurrence of the chord rotation ${\theta }_{cap,old}$ (Eq. (18)), while for the NC and C (collapse) performance levels, the occurrence of the chord rotations ${\theta }_{pc,old}$ (Eq. (19)) and ${\theta }_{c,old}$ (Eq. (20)) can be used as limit state conditions, respectively.

In European buildings constructed after the 1960s, the occurrence of smooth bars is limited. As discussed by Verderame and Ricci (2018), although the model developed by Haselton et al. (2016) may be inadequate to model RC frame columns with smooth bars, it is an adequate modelling approach for columns of more recent buildings. The model defined by Haselton et al. (2016) for this type of components was calibrated based on experimental cyclic results in beam-column elements and is defined by a trilinear backbone curve (Fig. 4d). This backbone curve is defined by the yielding moment ${M}_{y}$ and the initial stiffness based on $E{I}_{eff}$, the plastic rotation corresponding to the capping point ${\theta }_{cap,pl}$, which corresponds to the difference between ${\theta }_{cap}$ and the yield rotation, the post-capping plastic rotation ${\theta }_{pc,pl}$ which corresponds to the difference between the collapse rotation ${\theta }_{c}$ and ${\theta }_{cap}$ (see Fig. 4d). The main parameters of the model are defined based on Eqs. (21)–(24),

$$E{I}_{eff}=0.30\cdot {\left(1+\nu \right)}^{0.80}\cdot {\left(\frac{{L}_{s}}{H}\right)}^{0.72}\cdot {E}_{c}\cdot {I}_{g}\cdot {\varepsilon }_{E{I}_{eff}}\to {K}_{eff}=\frac{3\cdot E{I}_{eff}}{{L}_{s}}$$

(21)

$${\theta }_{cap}=0.14\cdot \left(1+0.4\cdot {a}_{sl}\right)\cdot {\left(0.19\right)}^{\nu }\cdot {\left(0.02+40\cdot {\rho }_{w}\right)}^{0.54}\cdot {\left(0.62\right)}^{\frac{{f}_{c}}{100}}\cdot {\varepsilon }_{{\theta }_{cap}}$$

(22)

$${\theta }_{pc}=4/3\cdot {\theta }_{cap}$$

(23)

$${\theta }_{c}={\theta }_{cap}+{\theta }_{pc,pl}={\theta }_{cap}+0.76\cdot {\left(0.031\right)}^{\nu }\cdot {\left(0.02+40{\rho }_{w}\right)}^{1.02}\cdot {\varepsilon }_{{\theta }_{pc,pl}}$$

(24)

where ${f}_{c}$ is the concrete compressive strength (in MPa), ${a}_{sl}$ is a binary factor equal to 1.0 in case fixed-end rotations due to bar pull out are expected and 0.0 otherwise, and ${\varepsilon }_{E{I}_{eff}}$, ${\varepsilon }_{{\theta }_{cap}}$, ${\varepsilon }_{{\theta }_{pc,pl}}$ are random error terms. The medians and logarithmic standard deviations of ${\varepsilon }_{E{I}_{eff}}$, ${\varepsilon }_{{\theta }_{cap}}$, ${\varepsilon }_{{\theta }_{pc,pl}}$ are shown in Table 9.

Table 9 Median and logarithmic standard deviation of the models shown in Eqs. (21)–(24)

The value of ${\theta }_{pc}$ can be associated to a decay of 20% in the maximum bending moment in order to be consistent with the EC8/3 NC performance level. The backbone proposed by Haselton et al. (2016) is a monotonic envelope to which a cyclic degradation parameter is added to introduce this cyclic effect. Due to the effect of cyclic degradation, Haselton et al. (2016) proposed replacing ${\theta }_{pc,pl}$ by ${\theta }_{pc,pl,cyclic}$ defined as 50% of ${\theta }_{pc,pl}$ and ${\theta }_{cap,pl}$ by ${\theta }_{cap,pl,cyclic}$ defined as 70% of ${\theta }_{cap,pl}$. In light of this, the limit state acceptance criterion for the DL performance level can be defined based on the effective stiffness of the moment-rotation model, as done above using ${K}_{eff,old}$, while for the SD performance level the maximum rotation can be limited to ${\theta }_{SD}=0.80\cdot {\theta }_{cap}$. For the NC and C performance levels, the acceptance criteria can be defined by the rotation limits ${\theta }_{NC}=4/3\cdot {\theta }_{SD}$ and ${\theta }_{C}={\theta }_{SD}+0.50\cdot {\theta }_{pc,pl}$, respectively.

Apart from the deformation-controlled mechanisms, force-controlled mechanisms also need to be analysed to account for the effect of brittle failure modes. In RC beam-column elements, this usually involves analysing a limit state that controls the maximum shear force. Based on ASCE 41-17, the shear force capacity of RC beam-column elements can be defined by:

$${V}_{NC}=k\cdot \left[\frac{{A}_{sw}\cdot {f}_{y}\cdot 0.8\cdot H}{{s}_{w}}+\left(\frac{0.5\sqrt{{f}_{c}}}{{L}_{s}/\left(0.8\cdot H\right)}\cdot \sqrt{1+\frac{N}{0.5\cdot \sqrt{{f}_{c}}\cdot B\cdot H}}\right)\cdot 0.8\cdot B\cdot H\right]$$

(25)

where k is equal to $1.0-0.075\cdot \left({\mu }_{\Delta }^{pl}-2\right)\ge 0.70$ (in which ${\mu }_{\Delta }^{pl}$ is the displacement ductility). Considering that, for the purpose of deriving the proposed $S{F}_{R}$, the most conservative situation (i.e., the situation that maximizes $S{F}_{R}$) corresponds to the case where k is considered equal to 1.0 (its maximum value according to ASCE 41-17), Eq. (25) can be rewritten as:

$${V}_{NC}=\frac{{A}_{sw}}{{s}_{w}}\cdot {f}_{y}\cdot 0.8\cdot H+\left(\frac{0.5\sqrt{{f}_{c}}}{{L}_{s}/\left(0.8\cdot H\right)}\cdot \sqrt{1+\frac{N}{0.5\cdot \sqrt{{f}_{c}}\cdot B\cdot H}}\right)\cdot 0.8\cdot B\cdot H\cdot {\varepsilon }_{{V}_{n}}$$

(26)

To account for the random error of the model, the term ${\varepsilon }_{{V}_{n}}$ was added to Eq. (26) whose median and logarithmic standard deviation are 1.05 and 0.15, respectively (Gokkaya et al. 2016). For the case of elements with smooth bars, the same expression can be considered.

3.5.4 Derivation of SF _R for deformation-controlled mechanisms with smooth bars

The computation of $\partial /{\partial }_{{Z}_{i}}$ for the deformation-controlled limit states based on Eqs. (17) to (20) was performed by computing the partial derivatives with respect to the relevant variables. For all limit states, the limit state values of a given component depend on several geometrical variables such as ${L}_{s}$, ${\sigma }_{N}=N/\left(B\cdot H\right)$ and the corresponding parameters N, B, and H, considered herein as being known so the seismic analysis of the building can be performed. Furthermore, they also depend on the value of the concrete compressive strength ${f}_{c}$, the reinforcing steel yield strength ${f}_{y}$, the area of transverse reinforcement per meter ${A}_{sw}/{s}_{w}$ and ${l}_{0}/{d}_{b}$. Parameter ${A}_{sw}/{s}_{w}$ has a reference value of ${\left({A}_{sw}/{s}_{w}\right)}_{ref}$ and its corresponding conformity index is ${k}_{D,w}={\left({A}_{sw}/{s}_{w}\right)}_{obs}/{\left({A}_{sw}/{s}_{w}\right)}_{ref}$. On the other hand, parameter ${l}_{0}/{d}_{b}$ has an expected value of ${\left({l}_{0}/{d}_{b}\right)}_{ref}$ that must be corrected by the observed ${k}_{D,l}$ value given by ${\left({l}_{0}/{d}_{b}\right)}_{obs}/{\left({l}_{0}/{d}_{b}\right)}_{ref}$. Based on these conditions, the value of $S{F}_{DL,old}$ that is used to assess the DL performance level based on ${K}_{eff,old}$ and the values of $S{F}_{SD,old}$, $S{F}_{NC,old}$ and $S{F}_{C,old}$ that are used to assess the SD, NC and C performance levels, respectively, can be defined as:

$$S{F}_{DL,old}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left(\frac{0.50\cdot \left(m{f}_{c}-4.18\cdot {\sigma }_{N}\right)}{{\left(m{f}_{c}\right)}^{2}}\right)}^{2}\cdot {\left({v}_{{f}_{c}}\right)}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{E{I}_{eff,old}}}^{2}}\right)$$

(27)

$$S{F}_{SD,old}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left(\frac{1.31\cdot {\sigma }_{N}}{{\left(m{f}_{c}\right)}^{2}}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\left(\frac{0.0084\cdot {\left(\frac{{l}_{0}}{{d}_{b}}\right)}_{ref}}{0.58+0.0084\cdot {\left(\frac{{l}_{0}}{{d}_{b}}\right)}_{ref}\cdot m{k}_{D,l}}\right)}^{2}\cdot {v}_{{k}_{{D}_{l}}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{cap,old}}^{2}}\right)$$

(28)

$$S{F}_{NC,old}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{\begin{array}{c}{\left(\frac{3.17\cdot {\sigma }_{N}-0.19\cdot m{f}_{c}}{m{{f}_{c}}^{2}}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\left(\frac{0.19}{m{f}_{y}}\right)}^{2}\cdot {v}_{{f}_{y}}^{2}+{\left(\frac{0.19}{m{k}_{D,w}}\right)}^{2}\cdot {v}_{{k}_{Dw}}^{2}+\\ +{\left(\frac{0.0032\cdot {\left(\frac{{l}_{0}}{{d}_{b}}\right)}_{ref}}{0.84+0.0032\cdot {\left(\frac{{l}_{0}}{{d}_{b}}\right)}_{ref}\cdot m{k}_{D,l}}\right)}^{2}\cdot {v}_{{k}_{{D}_{l}}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{pc.old}}^{2}\end{array}}\right)$$

(29)

$$S{F}_{C,old}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left(\frac{3.73\cdot {\sigma }_{N}}{m{{f}_{c}}^{2}}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\left(3.78\cdot \frac{1}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\right)}^{2}\cdot {v}_{{k}_{D,w}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{C,old}}^{2}}\right)$$

(30)

where $m{f}_{c}$ represents the range of the concrete strength sampling mean $\left( {MF_{{f_{c} }} \cdot \overline{f}_{c} } \right)$, $mf_{y}$ is the range of the reinforcing steel yield strength sampling mean $\left( {MF_{{f_{y} }} \cdot \overline{f}_{y} } \right)$, $m{k}_{D,w}$ is the range of the mean of the conformity index $k_{D,w}$ $\left( {MF_{{k_{D,w} }} \cdot \overline{k}_{D,w} } \right)$, and $mk_{D,l}$ is the range of the mean of $k_{D,l}$ $\left( {MF_{{k_{D,l} }} \cdot \overline{k}_{D,l} } \right)$. The ranges of the variability terms $V{F}_{{f}_{c}}\cdot {s}_{{f}_{c}}$, $V{F}_{{f}_{y}}\cdot {s}_{{f}_{y}}$, $V{F}_{{k}_{D,w}}\cdot {s}_{{k}_{D,w}}$ and $V{F}_{{k}_{D,l}}\cdot {s}_{{k}_{D,l}}$ are represented in Eqs. (27)–(30) by the terms ${v}_{{f}_{c}}$, ${v}_{{f}_{y}}$, ${v}_{{k}_{D,l}}$ and ${v}_{{k}_{D,w}}$, respectively.

3.5.5 Derivation of SF _R for deformation-controlled mechanisms with ribbed bars

For the case of components with ribbed bars, the derivation of $S{F}_{DL}$ used to assess the DL performance level based on ${K}_{eff}$ and of $S{F}_{SD}$, $S{F}_{NC}$ and $S{F}_{C}$ used to assess the SD, NC and C performance levels, respectively, followed principles similar to those outlined for the case of components with smooth bars. The relevant parameters for this case are also${L}_{s}$, ${\sigma }_{N}$ (involving N, B, and H),${f}_{c}$, ${f}_{y}$ and${A}_{sw}/{s}_{w}$. Using the capacity models presented in Eqs. (21)–(24) and applying Eq. (15), the following partial safety factors were obtained:

$$S{F}_{DL}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left(\frac{0.5\cdot m{f}_{c}-0.30\cdot {\sigma }_{N}}{m{f}_{c}\cdot \left({\sigma }_{N}+m{f}_{c}\right)}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{E{I}_{eff}}}^{2}}\right)$$

(31)

$$S{F}_{SD}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left(\frac{1.66\cdot {\sigma }_{N}}{m{{f}_{c}}^{2}}-0.0048\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\left(\frac{\frac{21.6}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}}{0.02+\frac{40}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\cdot m{k}_{D,w}}\right)}^{2}\cdot {v}_{{k}_{D,w}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{cap}}^{2}}\right)$$

(32)

$$S{F}_{NC}=S{F}_{SD}$$

(33)

$$S{F}_{C}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{\begin{array}{c}{\left(\frac{\left(0.076+0.030\cdot {a}_{sl}\right)\cdot \frac{40}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}+{u}_{1}\cdot {u}_{2}^{0.48}\cdot \frac{31.2}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}}{\left(0.14+0.056\cdot {a}_{sl}\right)\cdot {u}_{2}+0.76\cdot {u}_{1}\cdot {u}_{2}^{1.48}}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{C}}^{2}\\ +{\left(\frac{\left(0.14+0.056\cdot {a}_{sl}\right)\cdot \left(1.66\cdot {\sigma }_{N}-0.0048\right)\cdot {u}_{2}^{0.54}+3.47\cdot {u}_{1}\cdot {\sigma }_{N}\cdot m{k}_{D,w}\cdot {u}_{2}^{1.02}}{m{{f}_{c}}^{2}\cdot \left(\left(0.076+0.030\cdot {a}_{sl}\right)\cdot {u}_{2}^{0.54}+0.76\cdot {u}_{1}\cdot {u}_{2}^{1.02}\right)}\right)}^{2}\cdot {v}_{{k}_{D,w}}^{2}\end{array}}\right)$$

(34)

where ${u}_{1}$, ${u}_{2}$ and ${\sigma }_{\mathit{ln}{\varepsilon }_{C}}^{2}$ (excluding the correlation between ${\varepsilon }_{{\theta }_{cap}}$ and ${\varepsilon }_{{\theta }_{pc,pl}}$) are given by:

$$\begin{gathered} u_{1} = 0.14 \cdot \left( {1 + 0.4 \cdot a_{sl} } \right) \cdot 0.62^{{mf_{c} }} \cdot u_{2}^{0.54} \hfill \\ u_{2} = 0.02 + \frac{40}{B} \cdot \left( {\frac{{A_{sw} }}{{s_{w} }}} \right)_{ref} \cdot mk_{D,w} \hfill \\ \sigma_{{\ln \varepsilon_{C} }}^{2} = \sigma_{{\ln \varepsilon_{cap} }}^{2} + \sigma_{{\ln \varepsilon_{pc,pl} }}^{2} \hfill \\ \end{gathered}$$

(35)

3.5.6 Derivation of SF _R for force-controlled mechanisms

The partial safety factors defined for force-controlled mechanisms are associated to the NC performance level irrespective of the remaining performance levels that are considered in a given seismic assessment procedure. Based on the capacity model defined in Eq. (26), the corresponding factor $S{F}_{NC,V}$ can be defined as:

$$S{F}_{NC,V}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left({a}_{1}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\left({a}_{2}\right)}^{2}\cdot {v}_{{f}_{y}}^{2}+{\left(\frac{m{f}_{y}}{m{k}_{D,w}}\cdot {a}_{2}\right)}^{2}\cdot {v}_{{k}_{Dw}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{NC,V}}^{2}}\right)$$

(36)

where

$${a}_{1}=\frac{0.64\cdot B\cdot {H}^{2}\cdot \left({\sigma }_{N}+\sqrt{m{f}_{c}}\right)}{{L}_{s}\cdot m{f}_{c}\cdot \left(3.2\cdot H\cdot \frac{{A}_{sw}}{{s}_{w}}\cdot m{f}_{y}\cdot m{k}_{D,w}\cdot \sqrt{1+\frac{2\cdot {\sigma }_{N}}{\sqrt{m{f}_{c}}}}+2.56\cdot \frac{B\cdot {H}^{2}}{{L}_{s}}\cdot \left({\sigma }_{N}+\sqrt{m{f}_{c}}\right)\right)}$$

(37)

$${a}_{2}=\frac{1}{m{f}_{y}+0.40\cdot \frac{B\cdot H}{m{k}_{D,w}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\cdot {L}_{s}}\cdot \sqrt{m{f}_{c}}\cdot \sqrt{1+\frac{2\cdot {\sigma }_{N}}{\sqrt{m{f}_{c}}}}}$$

(38)

3.5.7 Derivation of SF _R factors for different limit states of RC beams

The case of RC beams can be considered as a particular case of the previously analysed models for columns, the main differences being the inexistence of axial load and the existence of asymmetric longitudinal reinforcement layouts. The former is covered by the cases where very low or zero axial load are considered. Based on Haselton et al. (2016), the latter can be accounted for by considering the correction term CT proposed by Fardis and Biskinis (2003) when quantifying ${\theta }_{SD,old}$, ${\theta }_{NC,old}$, ${\theta }_{C,old}$, ${\theta }_{SD}$, ${\theta }_{NC}$ and ${\theta }_{C}$ that is given by:

$$CT = \left( {\frac{{max\left( {0.01;{\mkern 1mu} \;\omega _{l}^{\prime } } \right)}}{{max\left( {0.01;{\mkern 1mu} \;\omega _{l}^{{tot}} - \omega _{l}^{\prime } } \right)}}} \right)^{{0.225}} \approx \left( {\frac{{A_{{sl}}^{\prime } }}{{A_{{sl}} }}} \right)^{{0.225}}$$

(39)

where ${A}_{sl}^{\hspace{0.33em}{\prime}}/{A}_{sl}$ is the ratio between the area of longitudinal reinforcing steel in compression ${A}_{sl}^{\hspace{0.33em}{\prime}}$ and in tension${A}_{sl}$. The correction term CT is therefore affected by the conformity index ${k}_{D,\rho }$, associated with the longitudinal reinforcement. By introducing these two aspects into Eqs. (17)–(20), revised versions of the $S{F}_{R}$ factors presented in Eqs. (27)–(30) for components with smooth rebars were obtained, assuming that the variability parameters ${\sigma }_{\mathit{ln}\varepsilon }^{2}$ are approximately the same as those in Eqs. (17)–(20):

$$S{F}_{DL,old}=\mathit{ex}p\left(-\Phi \left(q\right)\cdot \sqrt{{\left(\frac{1}{2\cdot m{f}_{c}}\right)}^{2}\cdot {\left({v}_{{f}_{c}}\right)}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{E{I}_{eff,old}}}^{2}}\right)$$

(40)

$$SF_{SD,old} = \exp \left( { - \Phi \left( q \right) \cdot \sqrt {\left( {\frac{{0.0084 \cdot \left( {\frac{{l_{0} }}{{d_{b} }}} \right)_{ref} }}{{0.58 + 0.0084 \cdot \left( {\frac{{l_{0} }}{{d_{b} }}} \right)_{ref} \cdot mk_{D,l} }}} \right)^{2} \cdot v_{{k_{D,l} }}^{2} + \left( {\frac{0.225}{{mk_{D,\rho } }}} \right)^{2} \cdot v_{{k_{D,\rho } }}^{2} + \sigma_{{\ln \varepsilon_{cap,old} }}^{2} } } \right)$$

(41)

$$S{F}_{NC,old}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{\begin{array}{c}-{\left(\frac{0.19}{m{f}_{c}}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\left(\frac{0.19}{m{f}_{y}}\right)}^{2}\cdot {v}_{{f}_{y}}^{2}+{\left(\frac{0.225}{m{k}_{D,\rho }}\right)}^{2}\cdot {v}_{{k}_{D,\rho }}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{pc.old}}^{2}\\ +{\left(\frac{0.0032\cdot {\left(\frac{{l}_{0}}{{d}_{b}}\right)}_{ref}}{0.84+0.0032\cdot {\left(\frac{{l}_{0}}{{d}_{b}}\right)}_{ref}\cdot m{k}_{D,l}}\right)}^{2}\cdot {v}_{{k}_{{D}_{l}}}^{2}\end{array}}\right)$$

(42)

$$S{F}_{C,old}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{+{\left(3.78\cdot \frac{1}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\right)}^{2}\cdot {v}_{{k}_{D,w}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{C,old}}^{2}}\right)$$

(43)

Considering the models for the case of columns with ribbed bars, revised versions of the $S{F}_{R}$ factors can also be obtained for beams following the same principles outlined before regarding the axial load, the asymmetric reinforcement and the ${\sigma }_{\mathit{ln}\varepsilon }^{2}$ terms. Based on Eqs. (31)–(34), $S{F}_{DL}$, $S{F}_{SD}$, $S{F}_{NC}$ and $S{F}_{C}$ can be rewritten as:

$$S{F}_{DL}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left(\frac{1}{2\cdot m{f}_{c}}\right)}^{2}\cdot {\left({v}_{{f}_{c}}\right)}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{E{I}_{eff}}}^{2}}\right)$$

(44)

$$S{F}_{SD}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left(-0.0048\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\left(\frac{\frac{21.6}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}}{0.02+\frac{40}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\cdot m{k}_{D,w}}\right)}^{2}\cdot {v}_{{k}_{D,w}}^{2}+ \left( {\frac{1}{{mk_{D,\rho } }}} \right)^{2} \cdot v_{{k_{D,\rho } }}^{2} +{\sigma }_{\mathit{ln}{\varepsilon }_{cap}}^{2}}\right)$$

(45)

$$S{F}_{NC}=S{F}_{SD}$$

(46)

$$S{F}_{C}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{\begin{array}{c}{\left(\frac{-0.067\cdot 0.6{2}^{m{f}_{c}}\cdot \left(1+0.4\cdot {a}_{sl}\right)\cdot {u}_{1}^{0.54}}{-0.14\cdot 0.6{2}^{m{f}_{c}}\cdot \left(1+0.4\cdot {a}_{sl}\right)\,\cdot {u}_{1}^{0.54}+100\cdot {\left(\frac{{A}_{sl}^{\hspace{0.33em}\mathrm{^{\prime}}}}{{A}_{sl}}\right)}_{ref}\cdot {u}_{1}^{1.02}}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+\frac{1}{m{k}_{D,\rho }}\\ +{\left(\frac{0.54\cdot {u}_{2}+1.02\cdot \frac{40}{B}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\cdot {u}_{1}^{0.48}}{{u}_{2}\cdot {u}_{1}+{\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\cdot {u}_{1}^{1.48}}\right)}^{2}\cdot {v}_{{k}_{D,w}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{C}}^{2}\end{array}}\right)$$

(47)

where ${u}_{1}$, ${u}_{2}$ and ${\sigma }_{\mathit{ln}{\varepsilon }_{C}}^{2}$ are given by:

$$\begin{gathered} u_{1} = 0.14 \cdot \left( {1 + 0.4 \cdot a_{sl} } \right) \cdot 0.62^{{mf_{c} }} \cdot u_{2}^{0.54} \hfill \\ u_{2} = 0.02 + \frac{40}{B} \cdot \left( {\frac{{A_{sw} }}{{s_{w} }}} \right)_{ref} \cdot mk_{D,w} \hfill \\ \sigma_{{\ln \varepsilon_{C} }}^{2} = \sigma_{{\ln \varepsilon_{cap} }}^{2} + \sigma_{{\ln \varepsilon_{pc,pl} }}^{2} \hfill \\ \end{gathered}$$

(48)

Finally, for the case of the shear force limit state, the previously presented expression of $S{F}_{NC,V}$ can be simplified to obtain:

$$S{F}_{NC,V}=\mathit{exp}\left(-\Phi \left(q\right)\cdot \sqrt{{\left({a}_{1}\right)}^{2}\cdot {v}_{{f}_{c}}^{2}+{\left({a}_{2}\right)}^{2}\cdot {v}_{{f}_{y}}^{2}+{\left(\frac{m{f}_{y}}{m{k}_{D,w}}\cdot {a}_{2}\right)}^{2}\cdot {v}_{{k}_{Dw}}^{2}+{\sigma }_{\mathit{ln}{\varepsilon }_{NC,V}}^{2}}\right)$$

(49)

where

$${a}_{1}=\frac{0.32\cdot B\cdot {H}^{2}}{{L}_{s}\cdot m{f}_{c}\cdot \left(1.6\cdot H\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\cdot m{f}_{y}\cdot m{k}_{D,w}\cdot \sqrt{m{f}_{c}}+\frac{0.32\cdot {H}^{2}\cdot m{f}_{c}}{{L}_{s}}\right)}$$

(50)

$${a}_{2}={\left(1+\frac{0.40\cdot H\cdot \sqrt{m{f}_{c}}}{{L}_{s}\cdot {\left(\frac{{A}_{sw}}{{s}_{w}}\right)}_{ref}\cdot m{k}_{D,w}}\right)}^{-1}$$

(51)

4 Simplified standard-based inspection and testing levels

Although the presented formulation can be adopted for integrating multiple combinations of sources of uncertainty, testing and inspection plans can be used to formulate simplified approaches that are more compatible with standard-based methods. By considering the testing plans proposed in Pereira and Romão (2018), limit values for $M{F}_{{Z}_{i}}$ and $V{F}_{{Z}_{i}}$ can be defined by separating the ${Z}_{i}$ variables according to the type of survey operations that are needed to determine them. Accordingly, the elements of ${X}_{{f}_{c}}$ and ${X}_{{f}_{y}}$ require destructive testing and must, therefore, be connected to a certain testing plan that includes the number of structural components where concrete cores and reinforcing steel coupons need to be extracted for testing. Conversely, elements of ${k}_{{D}_{w}}$ and ${k}_{{D}_{l}}$ only require a non-destructive survey (i.e. only finishing materials need to be removed) and they also need to be associated to an inspection plan that includes the number of structural elements that should be surveyed with rebar detectors.

By considering the analysis made in Pereira and Romão (2016b), three inspection (IL) and testing levels (TL) can be proposed. The TLs suggested herein follow what is proposed in Pereira and Romão (2016b), including the increase in the confidence level as more tests are performed (α = 0.05, α = 0.10 and α = 0.25 for TL1, TL2 and TL3, respectively), to quantify the mean value of the material properties. Furthermore, it is considered that an indirect estimate of $Co{V}_{{f}_{c}}$ can be obtained based on non-destructive tests (NDTs) (see Pereira and Romão (2018)), which typically may be up to 0.30. For $Co{V}_{{f}_{y}}$, an upper-bound estimate of 0.10 can be assumed instead. Table 10 shows the testing levels that are obtained using this approach and the corresponding uncertainty factors obtained using Eq. (8) that are based on the previously referred considerations. The interval $[M{F}_{{f}_{c}}^{low};\hspace{0.33em}M{F}_{{f}_{c}}^{up}]$ involves several approximations and considers a $Co{V}_{{f}_{c}}$ of 0.30 as a limit case, as shown in Fig. 5. Conversely to ${f}_{c}$, and since $Co{V}_{{f}_{y}}$ is typically limited to a value not larger than 0.10, constant values are adopted for $[M{F}_{{f}_{y}}^{low};M{F}_{{f}_{y}}^{up}]$ based on the analysis shown in Fig. 6.

Table 10 Testing levels and corresponding uncertainty factors

Fig. 5

Approximations for the correlation between the number of components N and ${{M}}{{{F}}}_{{{{f}}}_{{{c}}}}^{{{u}}{{p}}}$ for TL1 (a), TL2 (b) and TL3 (c) and between N and ${{M}}{{{F}}}_{{{{f}}}_{{{c}}}}^{{{l}}{{o}}{{w}}}$ for TL1 (d), TL2 (e) and TL3 (f)

Fig. 6

Relations between the number of components N and ${{M}}{{{F}}}_{{{{f}}}_{{{y}}}}^{{{u}}{{p}}}$ for TL1 (a), TL2 (b) and TL3 (c) and between N and ${{M}}{{{F}}}_{{{{f}}}_{{{y}}}}^{{{l}}{{o}}{{w}}}$ for TL1 (d), TL2 (e) and TL3 (f)

With respect to the ILs, a similar simplification can be introduced but, in this case, a larger percentage of surveyed components decreases the impact of n/N on the mean, when compared to what happens with the proposed TLs. Hence, even though $Co{V}_{{k}_{D,l}}$ and $Co{V}_{{k}_{D,w}}$ are unknown, the larger variability is connected to the quantification of ${\sigma }_{{k}_{D,l}}$ and ${\sigma }_{{k}_{D,w}}$. Therefore, by assuming a ${\alpha }_{F}$ of 0.16 (and $1-{\alpha }_{F}=0.84$) to quantify $[V{F}_{k}^{low};\,V{F}_{k}^{up}]$ (let k represent either ${k}_{D,l}$ or ${k}_{D,w}$) using Eq. (9) and considering the previous rationale for estimating $[M{F}_{k}^{low};\,M{F}_{k}^{up}]$, i.e. assuming an upper value of 0.30 for $Co{V}_{k}$ and a variable confidence level, Table 11 was obtained for the different proposed ILs. The approximate models developed for $[M{F}_{k}^{low};\,M{F}_{k}^{up}]$ and for $[V{F}_{k}^{low};\,V{F}_{k}^{up}]$ are shown in Figs. 7 and 8, respectively.

Table 11 Inspection levels and corresponding uncertainty factors

Fig. 7

Approximations for the correlation between the number of components N and ${{M}}{{{F}}}_{{{k}}}^{{{u}}{{p}}}$ for IL1 (a), IL2 (b) and IL3 (c) and between N and ${{M}}{{{F}}}_{{{k}}}^{{{l}}{{o}}{{w}}}$ for IL1 (d), IL2 (e) and IL3 (f)

Fig. 8

Approximations for the correlation between the number of components N and ${{V}}{{{F}}}_{{{k}}}^{{{u}}{{p}}}$ for IL1 (a), IL2 (b) and IL3 (c) and between N and ${{V}}{{{F}}}_{{{k}}}^{{{l}}{{o}}{{w}}}$ for IL1 (d), IL2 (e) and IL3 (f)

5 Application example

A simulated five storey RC frame building was adopted herein to demonstrate the calculation of the different $S{F}_{R}$ factors that were proposed in the previous sections, and to demonstrate the impact that different types of variables and uncertainties associated to the survey may have on their values. Generally, determining the $S{F}_{R}$ factors involves the following steps:

• Select the inspection and testing levels that define the number n of surveyed components for which the surveyed parameters will be obtained (e.g. the material properties and the construction details);

• Select the n surveyed components and perform the corresponding inspection and the tests to obtain the surveyed parameters and the relevant conformity indexes;

• Establish the statistics of the data obtained for the surveyed parameters (i.e. mean values and standard deviations);

• Determine the uncertainty factors $M{F}_{{Z}_{i}}$ and $V{F}_{{Z}_{i}}$ (see Tables 10 and 11 for the case of predefined survey plans or Sect. 3.4 for the general case) that will be used to establish the $S{F}_{R}$ factors of the non-surveyed components;

• Compute the $S{F}_{R}$ factors using the relevant expressions established in Sects. 3.5.4, 3.5.5, 3.5.6 and 3.5.7 according to the type of component and mechanism under analysis. For the case of surveyed components, any term ${v}_{x}^{2}$ corresponding to a surveyed parameter x is zero, and $S{F}_{R}$ only depends on the error of the capacity model.

In this example, the columns of the ground storey of the building are taken as the region under evaluation. As discussed by Pereira and Romão (2016a), a separation of regions in the building by storey and by floor may favour the ability to capture potential zones with homogenous properties that reflect the systematization of construction practice (namely workmanship and construction quality). The plan layout of the storey analysed herein is shown in Fig. 9.

Fig. 9

Layout of the structural system considered in the example application involving 20 columns and 31 beams and that represent one storey of a residential building

The selected building is assumed to be a residential building designed for gravity loads only. The reference values of the properties of the columns (assumed herein as the true values) are shown in Table 12, which include the geometry of the sections, the reinforcement details, and the material properties of each column of the storey. In the table, RN refers to the rebound hammer number, while Nψ₂ is the quasi-permanent value of the axial load (kN). The presented values of RN and f_c are results of tests performed in a real building (Monteiro and Gonçalves 2009), while the dataset f_y refers to steel yield strength values obtained for 16 mm diameter bars collected from an existing building in Portugal. The longitudinal and transversal bar diameters were randomly generated by adding to the nominal values (16 mm and 6 mm, respectively) a uniform error ranging between − 1.2 and 1.2 mm. The spacing of the transversal reinforcement was randomly generated by adding to the nominal value (0.15 m) a uniform error ranging between − 4 and 4 cm. The variable l₀/d_b was also obtained by simulation using a lognormal distribution where the underlying gaussian distribution has a zero mean and a standard deviation of 0.20 to establish an error factor which was then multiplied by the expected design value (i.e. 35). Since the selected building is a residential building, the value of $-\Phi \left(q\right)$ is equal to 1.00 (see Table 7). The reference values of the rotation capacity of the columns for the SD, NC and C performance levels are shown in Fig. 10, while the corresponding $S{F}_{R}$ values obtained for the case where only the uncertainty of the limit state model is considered (${\varepsilon }_{\mathit{ln}R}$) are shown in Fig. 11.

Table 12 Reference values of the properties of the 1st storey of a residential building with five storeys designed for gravity loading only

Fig. 10

Median values of the capacity of the columns for the SD, NC and C performance levels

Fig. 11

${{S}}{{{F}}}_{{{R}}}$ values obtained for the case where only the uncertainty of the limit state models is considered (${{{\varepsilon}}}_{{{ln}}{{R}}}$)

For the purpose of this application example, none of the material properties were assumed to be known prior to the survey, while the geometry of the building is assumed to be fully known. It is also assumed that design documents are available, indicating that all columns are supposed to have 4 smooth longitudinal steel bars with a 16 mm diameter (d_b) and that the corresponding embedment length (${l}_{0}$) is designed to be at least 35 times the longitudinal bar diameter (i.e. ${\left({l}_{0}/{d}_{b}\right)}_{ref}=35$). Information about the transverse reinforcement of the columns is also assumed to be available from the design documents, which indicate that it should be made of stirrups with 6 mm diameter steel bars and a spacing of 15 cm at the bottom and top regions of each column, i.e. ${\left({A}_{sw}/{s}_{w}\right)}_{ref}=0.000377$. Furthermore, a region that includes all the 20 columns of the storey was considered for the survey (N = 20).

To simulate more realistic conditions, it is assumed that, given the available data, an engineer could decide to perform a limited survey of the storey to reduce the amount of damage to the structure. This implies selecting inspection and testing levels compatible with IT1 and IL1, respectively. As a result, the uncertainty factors presented in Table 13 are obtained from Tables 10 and 11. Furthermore, based on IL1 and IT1, 6 out the 20 columns must be surveyed for details and using concrete NDTs, while 2 concrete cores and 1 reinforcing steel coupon must be extracted and tested. In a real-world scenario, at this stage, the engineer would typically select specific structural elements for inspection and sample extraction. However, various factors such as serviceability conditions, accessibility, or other constraints may limit the elements available for selection. As a result, different combinations of structural elements may be selected, which will ultimately affect the estimates of uncertainty factors, material strengths, and conformity indexes. These estimates, in turn, will influence the values of the SF_R and the actual deformation and strength capacity values of each structural element used in the safety assessment. To assess the impact of selecting different structural elements when surveying the same building (or region of the building), a simulation study was conducted. The simulation considered all the selection options available, i.e. all the combinations of 6 columns to survey the longitudinal and transverse reinforcement layouts. For each simulation, 3 out of the 6 selected columns where randomly selected for sample extraction and testing (2 concrete cores + 1 reinforcing steel coupon). Furthermore, when randomly selecting 6 out of 20 columns, the corresponding RN results were also obtained and their subsequent coefficient of variation $Co{V}_{RN}$ was estimated. An estimate of $Co{V}_{{f}_{c}}$ was then obtained using the proposal by Pereira and Romão (2018), i.e. $Co{V}_{{f}_{c}}\approx 1.95\cdot Co{V}_{RN}$. The uncertainty of f_y was assumed to be compatible with a $Co{V}_{{f}_{y}}$= 0.05 as discussed in the previous section. In light of these estimates, it was assumed that the only remaining uncertainty was that of the mean of f_c and f_y. Therefore, the factors $m{f}_{c}$ and $m{f}_{y}$ for all the columns from which material samples were not extracted are obtained by multiplying the estimates for the mean value of the material property ($\overline{f}_{c}$ and $\overline{f}_{y}$) by the corresponding uncertainty factors ($M{F}_{{f}_{c}}$ and $M{F}_{{f}_{y}}$). Furthermore, this assumption simplifies the determination of factors ${v}_{{f}_{c}}$ and ${v}_{{f}_{y}}$ for these columns. In this case, the factors ${v}_{{f}_{c}}$ and ${v}_{{f}_{y}}$ are obtained by multiplying the estimates for the mean value of the material property ($\overline{f}_{c}$ and $\overline{f}_{y}$), by the corresponding estimates of the coefficient of variation ($Co{V}_{{f}_{c}}$ and $Co{V}_{{f}_{y}}$) and the uncertainty factors of the mean value ($M{F}_{{f}_{c}}$ and $M{F}_{{f}_{y}}$).

Table 13 Uncertainty factors for the properties of the 1st storey of the residential building

To determine the conformity indexes ${k}_{D,w}$ and ${k}_{D,l}$ (see Sect. 3.2) for the 6 surveyed columns of each simulation, the values of ${\left({A}_{sw}/{s}_{w}\right)}_{obs}$ and ${\left({l}_{0}/{d}_{b}\right)}_{obs}$ are obtained from Table 12. for the corresponding columns. Based on the 6 values of ${k}_{D,w}$ and ${k}_{D,l}$, the corresponding estimates of the mean values $\overline{k}_{D,w}$ and $\overline{k}_{D,l}$, and of the standard deviations ${s}_{{k}_{D,w}}$ and ${s}_{{k}_{D,l}}$ are determined. These estimates are then combined with the corresponding uncertainty factors to determine the value of $m{k}_{D,w}$, $m{k}_{D,l}$, ${v}_{{k}_{Dw}}$ and ${v}_{{k}_{Dl}}$ for the 14 unsurveyed columns. It is reminded that, for columns where the values of f_c, f_y, ${k}_{D,w}$ and ${k}_{D,l}$ are known (from the material samples or the survey), the values of ${\sigma }_{{f}_{c}},$ ${\sigma }_{{f}_{y}},$ ${\sigma }_{{k}_{D,w}}$ and ${\sigma }_{k,l}$, respectively, are zero. Therefore, their $S{F}_{R}$ values are those obtained when only the uncertainty of the limit state model is considered.

To establish more conservative values of the factors $S{F}_{R}$, the values of $m{f}_{c}$, $m{f}_{y}$, $m{k}_{D,w}$, $m{k}_{D,l}$, ${v}_{{f}_{c}}$, ${v}_{{f}_{y}}$, ${v}_{{k}_{Dw}}$ and ${v}_{{k}_{Dl}}$ need to be determined for both bounds of the range of their corresponding uncertainty factor (see Table 13) and should be considered in the expressions $S{F}_{R}$ using the following criteria:

• In the terms of the $S{F}_{R}$ expressions where higher values of the factors $m{f}_{c}$, $m{f}_{y}$, $m{k}_{D,w}$, $m{k}_{D,l}$, ${v}_{{f}_{c}}$, ${v}_{{f}_{y}}$, ${v}_{{k}_{Dw}}$ or ${v}_{{k}_{Dl}}$ lead to an increase of $S{F}_{R}$, the larger values of these factors should be considered.

• In the terms of the $S{F}_{R}$ expressions where lower values of the factors $m{f}_{c}$, $m{f}_{y}$, $m{k}_{D,w}$, $m{k}_{D,l}$, ${v}_{{f}_{c}}$, ${v}_{{f}_{y}}$, ${v}_{{k}_{Dw}}$ or ${v}_{{k}_{Dl}}$ lead to an increase of $S{F}_{R}$, the lower values of these factors should be considered.

Since all possible combinations of 6 out of 20 columns were considered in this example, multiple estimates of ${\theta }_{SD}$, ${\theta }_{NC}$, ${\theta }_{C}$, ${V}_{NC}$ and of the corresponding factors $S{F}_{SD,old}$, $S{F}_{NC,old}$, $S{F}_{C,old}$ and $S{F}_{NC,V}$ were also obtained. Figure 12 shows the violin plots of all the $S{F}_{SD,old}$, $S{F}_{NC,old}$, $S{F}_{NC,V}$ and $S{F}_{NC,V}$ values that were obtained for the different survey plans compatible with IL1 and TL1. In this representation, the domain of the kernel density fits was truncated to fit the domain of the $S{F}_{SD,old}$, $S{F}_{NC,old}$, $S{F}_{NC,V}$ and $S{F}_{NC,V}$ values that were obtained. These results highlight the potential variability of the different $S{F}_{R}$ factors given the different options for selecting the structural elements that are going to be surveyed. Based on these results, it was found that the median of all the partial safety factors (i.e. considering all the columns and all the possible combinations) are 1.35, 1.32, 1.51 and 1.71 for ${\theta }_{SD}$, ${\theta }_{NC}$, ${\theta }_{C}$ and ${V}_{NC}$, respectively, while their minimum values are those plotted in Fig. 11. Furthermore, it can be seen that the data obtained for all the $S{F}_{R}$ factors are mostly bimodal. The first mode is related to the minimum values of the $S{F}_{R}$ factors that refer to cases governed solely by the epistemic error of the capacity model, ${\varepsilon }_{\mathit{ln}R}$, (which corresponds to structural elements whose properties are surveyed). On the other hand, the second mode reflects $S{F}_{R}$ values that are influenced both by the epistemic error of the capacity model and the uncertainty of the survey plan.

Fig. 12

Violin plots representing distribution of ${{S}}{{{F}}}_{{{S}}{{D}},{{o}}{{l}}{{d}}}$, ${{S}}{{{F}}}_{{{N}}{{C}},{{o}}{{l}}{{d}}}$, ${{S}}{{{F}}}_{{{C}},{{o}}{{l}}{{d}}}$ and ${{S}}{{{F}}}_{{{N}}{{C}},{{V}}}$ values obtained for each column considering all the possible survey and testing plans compatible with TL1 and IL1

As seen from these plots, $S{F}_{SD,old}$ has a smaller variation and leads to values that are closer to the value obtained when considering only ${\varepsilon }_{\mathit{ln}R}$ (see Figs. 11 and 12a). Conversely, the larger values of $S{F}_{R}$ are obtained for the shear strength, which is also the case where the difference between the uncertainty of the epistemic error of the capacity model and that of the survey plan is larger (the former is smaller for shear strength than for the other capacities, while the latter is larger). The remaining cases show that a variation of the axial load level (i.e. of factor ${\sigma }_{N}$) leads to different weights being assigned to the uncertainty of the concrete properties and, therefore, leads to larger and more disperse values for $S{F}_{NC,old}$ and for $S{F}_{C,old}$. To further validate the values obtained for the proposed $S{F}_{R}$ factors, Fig. 13a–c shows the boxplots of the ratios between the rotations ${\theta }_{SD}$, ${\theta }_{NC}$ and ${\theta }_{C}$ determined from a realistic assessment divided by the corresponding $S{F}_{R}$ and the rotations ${\theta }_{SD,real}$, ${\theta }_{NC,real}$ and ${\theta }_{C,real}$ which correspond to the values plotted in Fig. 10 divided by the corresponding $S{F}_{R}$ factor that only considers the uncertainty of the limit state model (i.e. the values plotted in Fig. 11). Similar ratios $V/{V}_{real}$ are also shown in Fig. 13d for the shear strength. It is noted that, for a given combination of 6 out of 20 columns, for columns where the values of f_c, f_y, ${k}_{D,w}$ and ${k}_{D,l}$ are known (from the material samples or the survey), the values of ${\theta }_{SD}$, ${\theta }_{NC}$, ${\theta }_{C}$ and ${V}_{NC}$ are equal to those of ${\theta }_{SD,real}$, ${\theta }_{NC,real}$, ${\theta }_{C,real}$, and ${V}_{real}$, respectively. For the remaining columns, the values of ${\theta }_{SD}$, ${\theta }_{NC}$, ${\theta }_{C}$ and ${V}_{NC}$ are determined using the mean estimates of f_c, f_y, ${k}_{D,w}$ and ${k}_{D,l}$, and will be, therefore, different from the ${\theta }_{SD,real}$, ${\theta }_{NC,real}$, ${\theta }_{C,real}$, and ${V}_{real}$ values.

Fig. 13

Boxplots of the ratios ${{{\theta}}}_{{{S}}{{D}}}/{{{\theta}}}_{{{S}}{{D}},{{r}}{{e}}{{a}}{{l}}}$, ${{{\theta}}}_{{{N}}{{C}}}/{{{\theta}}}_{{{N}}{{C}},{{r}}{{e}}{{a}}{{l}}}$, ${{{\theta}}}_{{{C}}}/{{{\theta}}}_{{{C}},{{r}}{{e}}{{a}}{{l}}}$ and ${{V}}/{{{V}}}_{{{r}}{{e}}{{a}}{{l}}}$

Based on the results of Fig. 13, it was found that the median of all the ratios (i.e. considering all the columns and all the possible combinations) is 0.88, 0.61, 0.57 and 0.56 for ${\theta }_{SD}/{\theta }_{SD,real}$, ${\theta }_{NC}/{\theta }_{NC,real}$, ${\theta }_{C}/{\theta }_{C,real}$ and $V/{V}_{real}$, respectively. These results also show that the bulk of the data is concentrated around these values, as can be seen from the 25% quartile values of ${\theta }_{SD}/{\theta }_{SD,real}$, ${\theta }_{NC}/{\theta }_{NC,real}$, ${\theta }_{C}/{\theta }_{C,real}$ and $V/{V}_{real}$ that are 0.81, 0.56, 0.50 and 0.45, respectively, and from the corresponding 75% quartile values that are 0.97, 0.67, 0.65 and 0.75, respectively. Therefore, it can be seen that the adopted IL and TL are able to control the probability of underestimating the limit state capacity, even for the current example that adopts the lower levels of testing and inspection that were proposed (TL1 and IL1). In terms of cases where the capacity is overestimated when considering the proposed $S{F}_{R}$ factors, the results show that the maximum value of the ratios is 1.24, 1.03 1.07 and 1.35, for ${\theta }_{SD}/{\theta }_{SD,real}$, ${\theta }_{NC}/{\theta }_{NC,real}$, ${\theta }_{C}/{\theta }_{C,real}$ and $V/{V}_{real}$, respectively. Furthermore, the results show that combinations where ${\theta }_{SD}/{\theta }_{SD,real}$ and $V/{V}_{real}$ are greater than 1.10 correspond to less than 3% and 2%, respectively, of the total number of combinations. For ${\theta }_{NC}/{\theta }_{NC,real}$, and ${\theta }_{C}/{\theta }_{C,real}$, the probability of getting values above 1.0 is close to zero. Therefore, despite the lower level of testing and inspection adopted in the current example, which leads to higher uncertainty, most of the estimates for the limit state capacities that would be used in a safety assessment are still on the safe side.

6 Conclusions

This study proposes a new framework for the safety format that can be used for the seismic safety assessment of existing RC buildings. This proposal is an alternative to the current EC8/3 framework and focusses on providing a more adequate characterization of the uncertainty in the limit state capacities. Based on the limitations identified by Jalayer et al. (2011) and other studies, a new formulation is proposed for the limit state verification that shifts from the use of CF values to a format that involves partial safety factors ($S{F}_{R}$) that divide the capacity of RC frame building components. The proposed partial safety factors were developed for RC beams and columns with smooth and ribbed bars considering different levels of uncertainty of the parameter classes involved in the assessment (i.e. the concrete strength, the reinforcing steel yield strength, the geometric properties and the reinforcement details). The calibration that was performed provides a direct link between the testing and inspection plans that can be adopted and the admissible range of values for the mean properties of the parameters. To address the difficulties associated with the assessment of reinforcement details and their uncertainty, a new methodology was proposed that involves defining a reference structure which characteristics based on the available design documents or on simulated design. The uncertainty of the reinforcement details is then analysed by estimating the average conformity between the reference structure and what is observed in the real building.

The proposed methodology provides the basis for defining flexible survey plans of a building, while controlling the uncertainty of the relevant parameters and focusing the outputs on the endpoint of the assessment, i.e. an adequate definition of the component capacities that will be used in the safety assessment verifications. Furthermore, the framework is inspired by and merges the main strengths of the ASCE 41-17 safety assessment approach regarding the definition of partial safety factors, the connection between the admissible analysis methods and the available knowledge, and between numerical models and acceptance criteria. Last but not least, the proposed framework is compatible with the procedure proposed by Franchin and Pagnoni (2018) that is connected with the one expected to be part of the second-generation EC8/3, and provides a more explicit correlation between the building survey results and the epistemic uncertainty of the capacity models that are used to assess seismic safety.

Finally, by developing component-by-component partial safety factors that account for the individual characteristics of those components, the proposed framework is seen as a more flexible alternative to existing code-based procedures that provides the engineer with more control over the safety assessment. Furthermore, such an approach to the safety assessment of existing buildings also provides the engineer with the ability to optimize the design of the necessary retrofitting/strengthening measures, ultimately leading to a more sustainable attitude to the management of existing buildings and their seismic safety.