Customary light-gauge steel framing construction with flat strap bracing: seismicity limits for low to mid-rise buildings in Europe

Abstract

Ordinary (customary) light gauge steel framing is a convenient construction technology; however, given the studs low axial capacity, it has been considered mainly for low-rise buildings in low seismicity regions. This paper investigates the boundaries of application of this type of steel framing (in moderate and high seismicity areas) by designing the structures of three representative 5, 7 and 10-storey buildings in order to examine their feasibility. The necessity of using built-up columns consisting of two or more sections is investigated. The axial capacity of studs is estimated by code-type analyses. The critical buckling stress is determined with well-known closed-form expressions; as they do not contemplate the flexibility of the screwed connections (in built-up sections), the obtained results are complemented with those of the finite strip method and generalized beam theory formulations.

1 Introduction

According to the United Nations (2022), the population of cities is growing faster than that of the whole world, as towns and rural areas are experiencing a slowdown; future projections show that the world urban population will increase from almost 6 billion in 2020 to nearly 7.5 billion by 2070. Therefore, cities will tend to grow more vertically than horizontally; this trend highlights the need to develop construction technologies that are suitable for multi-storey buildings. In this context, light-gauge steel framing is a convenient construction solution; it consists basically of vertical wall-like panels with supporting cold-formed studs, and composite slabs (concrete-steel or timber-steel). The main advantages of steel framing compared to traditional steel and concrete-based solutions are its fast erection, high construction quality, rather moderate cost, and lightness; the latter provides relevant benefits in poor foundations soils and in seismic areas, as the seismic forces are proportional to mass. However, given the rather low axial capacity of cold-formed steel studs, steel framing has been considered mainly for low-rise buildings only; even code limitations on the number of storeys apply (ASCE/SEI 7-22 2022). On the other hand, horizontal actions generate additional axial forces on the extreme studs (chord studs) of each wall panel; therefore, wind and earthquakes also prevent increasing the building height. To overcome this limitation, built-up or tube sections have been proposed for such end studs.

In the context described in the previous paragraph, the objective of this paper is to investigate the boundaries of application of light-gauge steel framing construction for low to mid-rise buildings located in seismic areas. In order to maintain the main aforementioned advantages of this construction technology, customary (habitual) and inexpensive features are not modified; this refers basically to ordinary steel, thin plates, and also thin wall panels. To perform this study, steel framing structures of three representative five, seven and ten-storey housing buildings located in moderate and high seismicity areas (PGA = 0.2 g, 0.3 g, 0.4 g peak ground acceleration) are preliminary designed to analyse their feasibility. The demanding internal axial forces on the supporting members (steel studs) of these prototype buildings are approximately obtained by simplified (although reliable and reasonably accurate) hand calculations. Several options are considered for the abovementioned extreme (chord) studs by combining Cee profiles: single, back-to-back, toe-to-toe (face-to-face), nested, and a stud pack (4C component section Phan et al. 2021, 2022). The axial capacity of such members is estimated by code-type analyses following the forthcoming European regulations; all the feasible buckling modes are considered: member (flexural and flexural–torsional), local and distortional. The slenderness is obtained as the square root of the ratio between the yield and buckling stresses or loads. The critical stress is determined with well-known closed-form expressions; as these formulations do not contemplate the flexibility of the screwed connections (in built-up sections), the obtained results are complemented with those of FSM (finite strip method) (Li et al. 2014) and GBT (generalized beam theory) (Schardt 1994; Silvestre and Camotim 2002).

2 State-of-the-art of steel framing for mid to high-rise buildings

Cold-formed steel (CFS) framing is commonly used as load-bearing structures for 1 to 2-storey buildings, particularly in North America, where this technology has benefited from the timber framing tradition; in Europe, the development of steel framing apparently stems from traditional and composite constructions. Report LGSF (2022) discusses the worldwide prospects of this technology.

As horizontal actions are a major limitation for tall buildings, the first CFS framing load-bearing structures in mid to high-rise buildings are gravity load-carrying systems supplemented with additional elements to resist horizontal actions (wind and seismic); usually, these elements are RC stair (and elevator) cases (shafts). An example is the SFIA Matsen Tower (Ford 2016); it is a hypothetical 40-storey residence building designed for a non-seismic area. The next steps have focused on structures made entirely of CFS framing; however, recent examples are also located in non-seismic regions: two 7-storey Hotels in Chicago, and an 8-storey (seven storeys of cold-formed steel framing over a pre-cast concrete podium) apartment building in Green Bay (WI).

Horizontal actions on steel framing require the wall panels are strengthened to resist the ensuing shear forces. An overview of the proposed strategies can be found in Sharafi et al. (2018), Taranu et al. (2023) and Yilmaz et al. (2023); those that do not alter the CFS nature of the steel frames are: timber sheathing boards, X-bracing steel straps, additional bolting, and concrete or mortar filling, among others. Among these options, strap bracing (Fig. 4) is the most convenient and versatile, given its superior strength and stiffness; however, the subsequent tensile forces in the bracing straps generate over-compression in the chord (end) studs. This effect is highly limiting, and may require using built-up sections, made by joining two or more profiles. The influence of the joining technique and design in their performance can be analysed using (AISI S100-16 2016) prescriptions (reduced overall slenderness) or, more deeply, using the aforementioned FSM or GBT approaches.

An early attempt to explore the boundaries of application of CFS constructions under earthquake excitation can be found in Madsen et al. (2011); Nakata et al. (2012), where a two-storey building is preliminarily analysed. In Torabian et al. (2016), archetype mid-rise pure CFS buildings (4–20 storeys) located in a high seismic area are used to assess the height limits of steel frames, and to aid in the development of new CFS technologies; the main conclusion is that hold-downs and high-capacity studs are needed. A more recent study is the seismic analysis of a 10-storey building (Zhang et al. 2022) to be built and tested (full scale); this research is aimed to investigate the seismic performance of buildings exceeding the height limitation of 19.8 m (65 ft) set by ASCE/SEI 7-22 (2022).

The above studies belong to the US context; this paper presents a rather similar study for the European situation.

3 Seismic performance of steel framing buildings

As discussed in Sects. 1 and 2, wind and earthquakes are major limitations for the use of steel framing for mid and high-rise buildings.

Earthquakes are one of the most damaging environmental effects on civil construction. Unless other actions (gravity, wind, thermal, etc.), strength is neither the only, nor the main requirement; in brief, an adequate seismic design of buildings pursues, among others, the following major qualities: (i) lightweight to mitigate the mass inertial effects, (ii) bilateral stiffness to prevent excessive inter-storey drift and collisions with adjoining buildings, (iii) bilateral strength to resist the equivalent seismic forces, (iv) plan symmetry (this is a mechanical issue, not a geometrical one), and torsional resistance and stiffness (to avoid highly damaging twisting motion), (v) uniformity along height to put off damage concentration in soft storeys, (vi) rigid diaphragms to guarantee solidarity between the lateral resisting systems, and providing a regular, simple and predictable seismic behaviour, (vii) adequate foundation to foil uplift, (viii) structural simplicity mainly to facilitate detecting hidden failure modes, (ix) structural redundancy to maintain a reserve of strength, and (x) ductility to allow for rather light design (as long as some damage is accepted). Steel framing structures are particularly well suited for issues i, v, vi (if a topping RC layer is provided), viii and ix; the remaining issues are discussed next.

• Lateral stiffness and strength The rigidity and resistance in both horizontal directions can be reached with the measures described in Sect. 2, particularly cross-bracing with steel straps. As discussed in that section and in Sect. 6.6, this requires the over-strengthening of the end (chord) studs; if only CFS profiles are accepted, built-up sections need to be used. Obviously, this poses relevant limitations in the use of this construction solution in high seismicity areas.

• Mechanical plan symmetry This type of symmetry is not related to any geometrical regularity, but to small eccentricity between the centres of gravity (G) and rotation (R). As an important number of braced wall panels can be placed in any horizontal direction, symmetric or near-symmetric arrangements can be achieved in all situations.

• Uplift prevention In rather slender buildings located in high seismicity areas, uplift is a serious risk for any building. Noticeably, lightweight is not a relevant advantage, as both gravity and seismic forces are proportional to the building weight; however, the uplift forces can be rather easily compensated with heavy foundations. Hold-down ties need only a moderate section (area), and can be easily embedded in the steel framing structure.

• Ductility Steel framing buildings should be rather ductile, as the only employed material is steel, which is a highly ductile material. Although x-braced wall panels are not as ductile as moment-resisting frames, a minimum ductility is largely ensured. This is particularly relevant, given that several buckling instabilities (flexural, torsional-flexural, local and distortional) are possible, mainly in the chord studs. The dissipative structural elements are the brace straps; as the chord studs are over-compressed due to the axial tension in such bracing members, the design of these studs shall be based on conservative capacity equilibrium conditions. This strategy protects against the abovementioned fragile buckling instabilities.

Other particular seismic design recommendations, such as “no long cantilevers”, “no interrupted columns”, “no short columns”, “tying of footings and pile caps”, “strong column-weak beam”, “separation to adjoining buildings”, “compact plan layout” and “protection of non-structural components” (among others) are not related to steel framing technology, and do not require particular discussion.

The paper Torabian et al. (2016) contains a rather similar discussion.

The main remark of these considerations is that pure steel framing buildings are rather well suited for seismic resistance; the most critical issue is the high axial compressive demands on the chord studs.

4 5, 7 and 10-storey prototype buildings

4.1 Buildings description

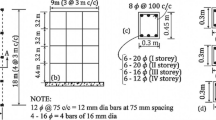
Three 5, 7 and 10-storey residential buildings are used as case studies representative of common low to mid-height buildings. They are regular, the storey height is 3 m, and the plan layout is square 18 m × 18 m. These buildings have 3 apartments (flats) per floor and a central hall, containing stairs and elevators; the wall panel distribution is the same on each floor. The building structure consists of prefabricated wall panels and floor and roof slab panels. In the walls, only CFS profiles (studs, tracks and diagonal straps) contribute to the load-bearing capacity (“all steel” approach AISI S240-15 2015). The wall panels are completed with insulation, EPS (Expanded polystyrene) lightweight mortar, mortar rendering and gypsum lining. Furthermore, a concrete layer 60 mm thick is poured on site above the metal structure of floor and roof panels, where the sliding between the metal frame and the concrete layer is prevented by shear connectors; this layer is reinforced (with a welded wire mesh) to provide some in-plane strength and prevent shrinkage cracks. Figure 1 displays an elevation of the 10-storey building, and a plan view of a generic storey. The global reference axes (x, y, z) used in Fig. 1 are maintained along this paper.

Fig. 1

Prototype buildings

Figure 1b describes the aforementioned three apartments; the internal partitions (not represented) are made with dry walls. Figure 1a depicts the openings of a façade of the building with 10 levels; Fig. 1b shows the correspondence with the architectural distribution. In fact, the architectural layouts of these buildings and their impact on the wall panels distribution have been carefully considered in order to have realistic and representative examples.

4.2 Steel framing system

As described in Sect. 2 and Sect. 4.1, the wall panels are composed of vertical supporting studs framed by top and bottom tracking profiles; the slab panels have a similar composition, although they are topped with a 60 mm RC layer. Figure 2 displays views of wall (Fig. 2a) and slab (Fig. 2b) panels.

Fig. 2

Steel framing structure

The structural capacity of the wall panels represented in Fig. 2a but without the braces is sufficient for gravity loads, but their lateral strength and stiffness are not enough to resist relevant wind and seismic effects. For that reason, some wall panels (all of them apart from those with openings) are braced with steel straps located at both wall sides (front and rear, Fig. 2a). Figure 3 presents several bracing arrangements.

Fig. 3

Strap-braced wall panels

Figure 3a shows a basic X (diagonal) bracing, and Fig. 3b, c describe similar arrangements with one and two horizontal bridging members, respectively. The purpose of these members is to provide buckling restraint in the wall plane. It is assumed that this bridging system is capable of sufficiently blocking the intermediate in-plane displacements of the studs, or that it is adequately reinforced with complementary elements (additional straps or blocking elements) to fulfil this function.

As the horizontal structural elements (floor and roof slabs, Fig. 2b) do not significantly contribute to the building lateral seismic capacity, only the vertical members (wall panels, Fig. 2a) are described herein. All of them are either 100 or 150 mm thick, and the tracks are made of channel 105 × 40 × 1.5 or 155 × 40 × 1.5 profiles, respectively. The internal (middle) studs are Cee single or built-up sections (pairs) spaced between 400 and 600 mm, the external (chord) studs are Cee built-up sections (pairs or foursomes) (Fig. 6), and the diagonal braces are straps (Figs. 2a, 4).

Fig. 4

Braced (red) and unbraced (white) wall panels in both directions

Figure 4 displays, similarly to Fig. 1b, a building plan view detailing the location and length of the braced wall panels. Figure 4 is aimed to deliver deeper information about the vertical elements that provide lateral stiffness and strength.

Figure 4 shows that there are several adjacent wall panels; however, their chord studs are considered to work independently (that is, they are not connected along their length). In other words, the building is designed as a series of uncoupled shear panels in each direction; such panels are connected to floor slabs that behave as rigid diaphragms. Thus, the horizontal shear forces on each floor are distributed between the panels proportionally to their stiffness. Figure 4 also shows that the braced wall panels in x and y directions are similar (in number and length). The panels in y direction are symmetrically distributed; conversely, the distribution of panels in x direction is rather asymmetric. This choice is intentional, and aims to reveal circumstances that can occur in real life (because of architectural requirements), even in externally symmetrical buildings. As mentioned in Sect. 3, this might impair their seismic performance; this effect is expected to be moderate.

5 Simplified formulation for the global structural analysis of the prototype buildings

5.1 General considerations

This section presents a simplified formulation for the global structural analysis of the prototype buildings described in Sect. 4. This analysis consists in obtaining approximately the internal forces in the building structural elements; Sect. 7 contains a local structural analysis providing the strength of the most critical structural elements, thus allowing to verify whether they exceed or not the demanding forces determined in this section. In fact, this process is only performed for the most critical members, mostly the chord studs of the first-storey façade braced wall panels.

Given the particular characteristics of the seismic action, its effects are discussed in an individual section (Sect. 6).

5.2 Load combinations

The prototype buildings are designed for the major actions, namely: gravity, wind and seismic. The actions and their combinations are determined according to European regulations (EN 1990 2005). Gravity loads are divided in permanent (dead) and variable (live), being commonly represented as G and Q, respectively; wind forces are variable, named as W_X and W_Y (W stands for wind). Finally, seismic actions are accidental, being ordinarily denoted as E_X and E_Y (E stands for earthquake). The combinations involve safety and combination factors; for this simplified analysis, the following six major combinations are considered:

$$\begin{array}{*{20}l} {({\text{I}})\quad {1}.{35}G + {1}.{5}Q + 0.{9}W_{\text{X}} } \hfill & {({\text{II}})\quad {1}.{35}G + {1}.{5}Q + 0.{9}W_{\text{Y}} } \hfill \\ {({\text{III}})\quad {1}.{35}G + {1}.0{5}Q + {1}.{5}W_{\text{X}} } \hfill & {({\text{IV}})\quad {1}.{35}G + {1}.0{5}Q + {1}.{5}W_{\text{Y}} } \hfill \\ {({\text{V}})\quad G + 0.{3}Q + E_{\text{X}} + 0.{3}E_{\text{Y}} } \hfill & {({\text{VI}})\quad G + 0.{3}Q + E_{\text{Y}} + 0.{3}E_{\text{X}} } \hfill \\ \end{array}$$

(1)

5.3 Global analysis for gravity loads

The vertical actions are determined according to the current European regulations (EN 1991-1-1 2002). The permanent loads are distributed between the levels (slabs); the estimated values are 2430 kN for the storeys and 2592 kN for the roof. The variable loads arise from an average distributed force of 2 kN/m²; the total force for each level is 648 kN. The internal forces in the studs are determined by assuming that the load on each slab is distributed isostatically (i.e. as if all the joists supports were hinged) between all the supporting studs; this criterion is common, and leads to small inaccuracies only.

5.4 Global analysis for wind forces

The static wind forces (pressure and suction) in each direction are determined according to the current European regulations (EN 1991-1-4 2005) by assuming a roughness length for terrain category IV. Then, the storey shear forces are obtained by equilibrium conditions; inside each storey, such forces are distributed between all the wall panels in the corresponding direction (Fig. 4) according to their lateral stiffness. The axial compressive force in the corresponding chord stud of each panel is determined as the vertical projection of the tensile force in the steel strap brace. In turn, this force is obtained through a simplified structural analysis of the panel, neglecting the contribution of the internal studs to its lateral stiffness (Sect. 6.1). Noticeably, both gravity and wind axial compressive forces on the studs are assumed to be applied on the chord stud central axis (passing through the section centroids); in other words, these elements undergo a centred compression only.

6 Seismic analysis of the prototype buildings

6.1 Analysis approach

The seismic design of the prototype buildings is performed, in a simplified way, according to the upcoming version of the European seismic design code (EN 1998-1 2023); whenever required, that regulation is supplemented with the American document (AISI S400-20 2020). The vertical seismic action is not considered.

EN 1998-1 (2023) proposes two 2-D static design strategies: Lateral Force and Response Spectrum Methods; they consist basically in considering the contribution of one and several modes, respectively. Several conditions must be met (in each direction) to allow the use of the most simplified approach (Lateral Force Method): (i) buildings not taller than 30 m, and (ii) fundamental period in the considered direction (T₁) not exceeding neither 1.5 s nor four times the corner period T_C (Sect. 6.4, Table 2). Obviously, the first condition is fulfilled (Fig. 1); regarding the limitations for the building fundamental period, the obtained results (Table 11) also fulfil the required conditions. Hence, the Lateral Force Method is adopted in this research; in this formulation, the base shear force in the considered direction is given by:

$$F_{\text{b} } = \lambda m S_{\text{r}} \left( {T_1 } \right)$$

(2)

In Eq. (2), m is the mass corresponding to the building seismic weight (Sect. 6.5), and λ is a dimensionless coefficient being equal to 1 if the building has more than two storeys and T₁ is greater than two times the corner period T_C, and 0.85 otherwise. S_r(T₁) is the design spectral ordinate (Sect. 6.4) corresponding to period T₁ (Sect. 6.5). Table 3 displays the adopted values of λ in each direction.

In Eq. (2), F_b represents the equivalent static effect of the design accelerograms in every horizontal direction; it shall be distributed between all the storeys proportionally to their masses and height (with respect to the building base). Then, the demanding seismic internal forces in the chord studs are determined similarly than in the wind analysis (Sect. 5.4); the main difference is that the seismic shear storey forces are assumed to be applied in the centre of gravity of each storey (G), and this point exhibits actual and accidental eccentricity with respect to the corresponding centre of rotation (or rigidity, R). This issue is discussed more deeply next.

Table 1 displays the actual eccentricity in the y direction (Fig. 4) between the centres of mass (G) and rigidity (R) of the first storey of the prototype buildings.

Table 1 Eccentricity e_y (m) between the centres of mass (G) and rigidity (R)

In Table 1, S_α,475 refers to the site seismicity (Sect. 6.2); the indicated values correspond to the final situation, once the structure has been finally designed (Sect. 8).

The real eccentricity in Table 1 shall be complemented with the accidental eccentricity; EN 1998-1 (2023) states that ± 5% must be taken in any direction. By adding the actual and accidental eccentricities, the forces at each braced wall panel are determined proportionally to their stiffnesses; noticeably, both translational and rotational geometric compatibility conditions need to be imposed (rigid diaphragm effect).

On the other hand, although regularity in the plan is not specifically required, this is equally considered, as it prevents twisting (torsional) behaviour, having proven to be extremely damaging. Three types of conditions are basically entailed for each level and direction: geometrical symmetry (including compact configuration), rigid diaphragm, and torsional stiffness. The first two conditions are largely fulfilled, while the third one involves the contentment of two inequalities: e_y ≤ 0.3 r_y and r_y ≤ l_s; the subindexes correspond to verification for the x direction. In these expressions, r_y is the square root of the ratio between torsional and lateral stiffness (“torsional radius”), and l_s is the radius of gyration of the floor mass in plan (square root of the ratio between the polar mass moment of inertia -with respect to point G- and the floor mass). Noticeably, condition e_y ≤ 0.3 r_y refers to a small eccentricity between points G and R, and r_y ≤ l_s is equivalent to the first 3-D mode of the building being translational. These inequalities are satisfactorily fulfilled in all the analysed situations.

6.2 Site seismicity

As discussed in Sect. 1, the building is located in a seismic area; three levels of PGA (peak ground acceleration) are considered: 0.2 g (moderate seismicity), 0.3 g and 0.4 g (high seismicity). This parameter broadly represents the maximum expected acceleration at the engineering bedrock (soil type A) for 475 years return period; conversely, in EN 1998-1 (2023), the site seismicity is mainly characterized by the maximum response spectral acceleration (5% damping) S_α,475, corresponding to the constant acceleration range (plateau) of the horizontal elastic response spectrum. Assuming that, approximately, the ratio between PGA and S_α,475 is equal to 2.5, the considered site seismicity levels in terms of S_α,475 are 0.5 g, 0.75 g and 1 g.

The soil type (site category in EN 1998-1 2023) is an inherent component of the site seismicity; in this study it is soil B. In EN 1998-1 (2023) this site category refers to stiff soil, and corresponds to v_s,H ranging between 400 and 800 m/s and H₈₀₀ deeper than 5 m. Parameters H₈₀₀ and v_s,H are the engineering bedrock depth (characterized by a shear wave velocity of 800 m/s), and the weighted harmonic average of the shear wave velocity in soil depth H; H is equal to the lowest of H₈₀₀ and 30 m. Noticeably, this soil would be rated as C in the American documents.

EN 1998-1 (2023) classifies the seismicity in four levels in terms of S_α,475: very low (S_α,475 < 1.0 m/s²), low (1.0 m/s² ≤ S_α,475 < 2.5 m/s²), moderate (2.5 m/s² ≤ S_α,475 < 5.0 m/s²) and high (5.0 m/s² ≤ S_α,475). These results confirm that S_α,475 = 0.5 g corresponds to moderate seismicity, while S_α,475 = 0.75 g and S_α,475 = 1 g are referred to as high seismicity.

6.3 Building behaviour factor

The behaviour factor (q) in the European regulations corresponds to the response modification factor (R) in the American documents. With regard to European regulations, in recent years there has been an urgent need to address the dissipative design of steel framing structures, since it was not properly covered in previous versions of Eurocode 8 (Landolfo et al. 2022; Fiorino et al. 2017; Hatami et al. 2010). Estimating q from cyclic and incremental tests on individual panels (Kasaeian et al. 2020; Hatami et al. 2010) results in considerably high values (up to 5). Conversely, proper numerical pushover and IDA analyses for an illustrative set of prototype buildings undergoing a sufficiently representative collection of ground motions provide smaller values (Fiorino et al. 2017); this work results in a moderate value of q = 2.5, which is taken by the new version of the Eurocode (“Structural type g” in EN 1998-1 2023) for ductility class DC3. As a matter of fact, for S_α,475 = 0.75 g and S_α,475 = 1 g, such ductility class is strictly required (Table 11.3 of EN 1998-1 2023). The conditions for obtaining such a level of ductility are fulfilled, and therefore, q = 2.5 is assumed in this study for all the prototype buildings. Noticeably, in the American documents this ductility class (DC3) corresponds broadly to “special buildings”.

6.4 Design spectra

The design spectra are based on the forthcoming version of the European seismic design code (EN 1998-1 2023).

The design spectrum according to EN 1998-1 (2023) considers an elastic response spectrum referred to as S_e(T); it has five branches:

• 1. Short horizontal branch (extremely short periods, T ≤ T_A) S_e(T) = S_α/F_A.

• 2. Linear growing branch (very short periods, T_A ≤ T ≤ T_B) S_e(T) = [S_α/(T_B − T_A)] [η (T − T_A) + (T_B − T)/F_A].

• 3. Constant branch (plateau, short periods, T_B ≤ T ≤ T_C) S_e(T) = η S_α.

• 4. Hyperbolically decreasing branch (mid periods, T_C ≤ T ≤ T_D) S_e(T) = η S_β T_β/T.

• 5. Faster decreasing branch (long periods, T_D ≤ T) S_e(T) = η T_D S_β T_β/T².

In these expressions, F_A = 2.5, T_β = 1 s, S_α = F_T F_α S_α,475 and S_β = F_T F_β S_β,475; F_T is the topography amplification factor, and F_α = 1.3 (1 − 0.1 S_α,475) and F_β = 1.6 (1 − 0.2 S_β,475) are the short and intermediate period site amplification factors, respectively. It is assumed that F_T = 1 (there is no topography amplification). S_α,475 can be taken as a_g 2.5 in EN 1998-1 (2023), and S_β,475 = f_h S_α,475, where f_h is equal to 0.3 and 0.4 for moderate and high seismicity levels, respectively. The corner periods T_A, T_B, T_C and T_D are given by T_A = 0.02 s, T_C = S_β T_β/S_α, T_B = T_C/4, and T_D = 1 + S_β,475. Finally, the damping correction factor η is taken as 1, as the building damping ratio is assumed to be 5%.

Then, the reduced spectrum S_r includes the influence of the behaviour factor q, through R_q(T): S_r(T) = S_e(T)/R_q(T). In the first branch R_q(T) = 1.5, in the second branch R_q(T) = 1.5 + (q − 1.5) (T − T_A)/(T_B − T_A), and in the other branches R_q(T) = q. Finally, the minimum value of S_r(T) is β S_α,475, where β = 0.08.

Table 2 and Fig. 5 display the parameters and plots of the three design spectra, respectively.

Table 2 Main parameters of the reduced spectra

Fig. 5

Reduced spectra (S_r) according to EN 1998-1 (2023). Behaviour factor q = 2.5 and soil type B

6.5 Natural periods of the buildings

Prior to any structural calculation, the building fundamental periods in the direction under consideration (T_1,est) can be estimated according to the simplified empirical expression for framed wall buildings in EN 1998-1 (2023): T_1,est = 0.05 $H_{\text{b}}^{{\text{3/4}}}$ (s), where H_b is the building height (m). The obtained results for the 5, 7 and 10-storey prototype buildings are:

$$T_{1{\text{,est~}}} = ~0.05H_{\text{b}}^{{\text{3/4}}} = 0.05 \times 15^{{\text{3/4}}} = 0.38\,{\text{s}}\quad T_{1{\text{,est~}}} = 0.05H_{\text{b}}^{{\text{3/4}}} = 0.05 \times 21^{{\text{3/4}}} = 0.49\,{\text{s}}\quad T_{1{\text{,est~}}} = 0.05H_{\text{b}}^{{\text{3/4}}} = 0.05 \times 30^{{\text{3/4}}} = 0.64\,{\text{s}}$$

(3)

There is a big uncertainty involved in the determination of these values; therefore, it would not be surprising that further calculations (once the structural parameters are known) provide significantly different results. In this context, the building modal parameters (natural periods and mode shapes) are determined by solving the classical eigenvalue problem (K − ω² M) ϕ = 0, where K is the stiffness matrix (in each horizontal direction), M is the mass matrix, and ω and ϕ represent the eigenvalues (natural frequencies) and eigenvectors (modal shapes), respectively. Matrix M is diagonal, containing the masses of each storey; matrix K is generated as tri-diagonal, by assuming that the steel framing structure behaves as a shear building. Storey masses (Sect. 5.3) are determined according to the permanent load combined with 15% of the variable one: 2.576 × 10⁵ kg; for the roof, the combination involves 30% of the variable load: 2.840 × 10⁵ kg. These values correspond to the seismic weight. Storey stiffnesses in x and y directions are determined according to AISI S400-20 (2020); the contribution of the non-structural components to the building stiffness is neglected. This last consideration might introduce important inaccuracies, as the non-structural elements contribution can be significant; it has been adopted as, for moderate and strong seismic inputs, usually such elements are damaged, thus leaving the structure alone. On the other hand, the influence of the non-structural components in the building fundamental period would be highly difficult to assess, given the large number of cladding and partitioning elements. The periods determined from the modal analyses are discussed in Sect. 6.7.

6.6 Seismic design of the chord studs

The chord studs are non-dissipative elements that support the strap braces, being dissipative elements as the only source of ductility; therefore, they should be designed with protective capacity conditions intended to prevent their brittle (buckling) failure. These conditions consist in replacing the actual value of the axial force in the chord studs due to seismic effects by an amplified value of the maximum force that can be transmitted by the strap braces; in other words, designing the chord studs to withstand this axial force (adding the contribution of gravity forces) guarantees that the plastic capacity of the strap braces can be fully developed. The demanding internal axial force in the chord studs is equal to EN 1998-1-1 (2023) and Landolfo et al. (2022):

$$E_{\text{Ed }} = E_{\text{Ed,G}} + {\upomega }_{\text{rm }} {\upomega }_{\text{sh }} {\Omega }_{\text{d}} E_{\text{Nfy}} = E_{\text{Ed,G}} + 1.595 E_{\text{Nfy}}$$

(4)

In Eq. (4), E_Ed is the demand internal force due to combinations V or VI (Eq. (1)), E_Ed,G is the contribution of non-seismic actions, and E_Nfy is the internal force corresponding to the axial yielding capacity of the brace straps. Again in this equation, ω_rm is the material overstrength factor, ω_sh is the factor accounting for hardening of the dissipative zone, and Ω_d is the minimum design overstrength. For the steels considered in this study ω_rm = 1.45 can be assumed; ω_sh is taken equal to 1.1, and Ω_d is taken equal to 1 (EN 1998-1-1 2023).

6.7 Seismic global analysis

The global seismic analysis must be performed iteratively, as prior to the first design of the structural members, it is not possible to calculate the building fundamental period. Given this circumstance, the seismic design codes (in this case, EN 1998-1 2023) provide empirical expressions for such a period that depend only on the structural configuration and the building height; these expressions have been utilized to obtain the first estimates (Eq. (3)). The values of the fundamental period provide the spectral ordinates (Sect. 6.4); in turn, such ordinates allow obtaining the base shear forces and the demanding axial forces in the chord studs (Sect. 6.1) and all the structural members. These forces are to be combined with those from other actions (Eq. (1)), thus allowing a proper structural dimensioning (Sect. 6.6). Then, a new value of the fundamental period can be determined (Sect. 6.5), and the iterative process continues. Iterations are stopped when the periods do not change significantly, when their change has no effect on the spectral ordinates (as they lie in the plateau range), or when the demanding axial forces in the chord studs exceed their capacities.

The most important results of this iterative process (for the 5, 7 and 10-storey buildings) are described in Table 3. The convergence criterion is based on the base shear (F_bx and F_by) and the demanding axial forces in the chord studs (${N}_{\mathrm{Edx}}^{\mathrm{max}}$ and ${N}_{\mathrm{Edx}}^{\mathrm{max}}$, Table 11): when the differences between two consecutive iterations are less than 5%, the iterations are stopped. It is shown in Table 3 that iterations do not start from the initially estimated periods (Eq. (3)), but from longer ones (typically, 1 s); this is because the periods in Eq. (3) are too short, thus providing excessively high spectral ordinates that generate axial forces in the chord studs that cannot be withstood by them.

Table 3 Main results of the global seismic analyses for the prototype buildings

In Table 3, ${m}_{1}^{*}/m$ represents the 1^st mode mass participation factor; obviously, subindexes x and y denote the horizontal directions (Fig. 4).

6.8 Drift verification

The drift displacements of the building storeys are obtained from the lateral stiffness of the wall panels; such stiffness is taken from simplified expressions in the American document (AISI S400-20 2020). EN 1998-1 (2023) prescribes that drift should be limited for two reasons: to prevent damage to non-structural components (mainly brittle cladding and partitioning elements connected to two consecutive floors), and to investigate the need for performing second-order analyses. Noticeably, recent studies indicate that geometric non-linear effects can be significant in cold-formed steel braced panels (Papargyriou et al. 2021). The first limitation is established as d_r,SD ≤ 0.01 h_s, where h_s is the storey height, and d_r,SD is the drift for the significant damage (SD) limit state; this drift is calculated from the average lateral displacements d_s obtained by multiplying the reduced displacements d_r by q (for the range of periods of interest in this study). The second limitation is set as θ ≤ 0.1, where θ (inter-storey drift sensitivity coefficient) is basically the ratio between the first and second-order moments, and is precisely defined as ${{\uptheta }} = \frac{{P_{{\text{tot}}} d_{r,{\text{SD}}} }}{{1.5 V_{{\text{tot}}} h_s }}$; in this expression, P_tot and V_tot are the vertical gravity and horizontal seismic forces on the storey under consideration, respectively. Table 4 displays the obtained values of the first storey drift (d_r,SD, mm) and the corresponding inter-storey drift sensitivity coefficient (θ).

Table 4 First storey reduced drifts d_r,SD (mm) and inter-storey drift sensitivity coefficients (θ) in the prototype buildings

Table 4 shows that d_r,SD does not exceed the bound (30 mm) in any case. Regarding θ, all its values are clearly below the bound (0.1). These trends show that drift is not excessive.

7 Member buckling analysis

7.1 Global observations

The objective of this section is to determine the characteristics of the cold-formed structure members that have to withstand the forces defined in Sect. 6. The study focuses on the panel studs, especially the chord ones, which are the most critical members.

The structural capacity of the stud configurations that are typically used in low-rise steel framed buildings is insufficient for mid-rise buildings undergoing seismic action; such buildings would require innovative configurations of built-up sections. Therefore, this section briefly introduces the behaviour and design of these types of sections. Different design approaches are considered, as well as several factors that govern their behaviour, namely cross-section configuration, fastener spacing, the effect of End Fastener Groups, wall thickness, sheet thickness, material properties and intermediate restraints.

7.2 Built-up members

The intermediate studs of the panels are designed with individual profiles, while the chord studs with built-up sections. Initially, only combinations of two profiles had been investigated (back-to-back, toe-to-toe and nested), but given the high demand on some chord studs (Sect. 8), stud packs composed of 4 profiles had to be added.

Figure 6 displays the stud cross-sections considered in the study. They are composed of channel 100 × 50 × 20 mm and 150 × 50 × 20 mm profiles (Fig. 6a). Figure 6b–d exhibit different combinations of two Cee profiles; Fig. 6e describes a combination of such four profiles.

Fig. 6

Studs cross-sections (dimensions in mm)

All built-up sections are considered to be fastened by means of screws, except for the toe-to-toe (face-to-face) section (Fig. 6d), which is welded (screwing is not possible). The location of fasteners is also shown in Fig. 6. Two longitudinal spacings between screws are studied: L/3 and L/6 (L is the member length). The screws stiffness is defined from values used in similar studies of the literature: 10 kN/mm for axial direction (Fratamico et al. 2018), and the same value for shear (Rasmussen et al. 2020; Pham and Moen 2015; Phan et al. 2022); these directions refer to the screw axis.

The study involves various sheet thicknesses: 1.0, 1.5, 2.0, 2.5 and 3.0 mm; as well steel grades: S250GD, S280GD, S320GD and S350GD (EN 1993-1-3 2006,2023).

7.3 Member design procedure

The resistance of the studs is determined following (EN 1993-1-3 2006,2023) accounting for all relevant buckling phenomena: local, distortional and member. The effects of the sectional buckling are considered through the effective area of the cross-section, which is calculated as follows:

• Local buckling The effective width approach is applied, according to clauses 7.6.1. and 7.6.2 of EN 1993-1-3 (2023). Noticeably, the effective width is determined independently for each element of the cross-section based on its plate buckling stress and associated slenderness. The calculation procedure is similar to that proposed by other codes, such as AISI S100-16 (2016).

• Distortional buckling A reduced thickness of the edge and web stiffeners undergoing distortional buckling is determined following clauses 7.6.1 and 7.6.3 of EN 1993-1-3 (2023). The Code proposes a stiffener buckling approach, where distortional buckling stress is determined by hand (in principle, see next section). The calculation utilizes a model of the stiffened element (with its stiffener) where it is assumed that it behaves as a compressed member with continuous partial restraint. The spring stiffness of the restraint depends on the boundary conditions and the flexural stiffness of the adjacent plane elements. The reduced thickness is computed from the distortional buckling stress, and the corresponding slenderness, using a specific buckling curve.

Studs are considered to be subjected to pure compression. Since we are dealing with a preliminary dimensioning of the structure, additional bending moment caused by the shift between the centroidal axes of the effective cross-section and the gross cross-section, if it exists, is not considered. Actually, the effect of the shift would only be relevant for the intermediate studs, which consist of individual mono-symmetric profiles. All the investigated built-up cross-sections are doubly symmetric and, consequently, there is not any centroid shift.

Member buckling verification for the case of pure compression involves two checks: (i) flexural buckling; and (ii) torsional or torsional-flexural buckling. The studs composed of a single profile, i.e. mainly the intermediate studs, have to be verified against flexural and torsional-flexural buckling; whereas the governing buckling failure of built-up studs is flexural buckling (torsional buckling is rarely relevant). All the verifications are carried out according to clauses 8.2.2 and 8.2.3 of EN 1993-1-3 (2023), which use the following equations of EN 1993-1-1 (2023):

$$N_{\text{b,Rd}} = \frac{{\chi A f_{\text{yb} }}}{{\gamma_{{\text{M1}}} }}\quad N_{\text{b,Rd}} = \frac{{\chi A_{{\text{eff}}} f_{{\text{yb} }}}}{{\gamma_{{\text{M1}}} }}$$

(5)

Left and right equations correspond to Class 1, 2 and 3 cross-sections (fully effective), and Class 4 cross-sections (slender), respectively. In Eq. (5), A is the gross cross-section area, A_eff is the effective area of the cross-section, f_yb is the basic yield strength of the material, γ_M1 is the partial safety factor for resistance of members to instability (the adopted value herein is 1.00), and χ is the reduction factor for flexural buckling (clauses 8.2.2 of EN 1993-1-3 2023 and 8.3.1.3 of EN 1993-1-1 2023) or torsional-flexural buckling (clauses 8.2.3 of EN 1993-1-3 2023 and 8.3.1.4 of EN 1993-1-1 2023). There are two factors that should be specified concerning the calculation of χ: (1) buckling curve b is applied in all calculations, except for the flexural buckling about the y of the back-to-back section, for which curve a should be used (Table 8.7 of EN 1993-1-3 2023), and (2) the buckling lengths considered in the determination of member buckling load and associated member slenderness are displayed in Table 5.

Table 5 Buckling length. L is the physical length of the stud: 2780 mm

The torsion buckling lengths are based on assuming that in the end sections torsional rotation is restrained and warping is free.

7.4 Buckling stresses and loads. Model of the composite action

The design procedures introduced in Sect. 7.3 require the calculation of a buckling stress or buckling load to determine the instability reduction factor from a slenderness and a buckling curve. Three approaches are considered for the calculation of such buckling stresses and buckling loads in the present study: closed form-hand calculations, the finite strip method (FSM) and the generalized beam theory (GBT). The composite action is modelled differently in each method, with the hand calculation being the most basic approach and the GBT the most sophisticated.

7.4.1 Hand calculation approach

The initial aim was to assess the performance of many different built-up configurations from a simple estimation of their ultimate resistance. Consequently, the hand calculation approach is applied first because it can easily be implemented in a spreadsheet, allowing parametrization and quick assessment. Local and distortional buckling stresses are determined according to the Eurocode 3 formulations and simplified analysis introduced in Sect. 7.3. The effective cross-section properties of the built-up member are calculated by multiplying those of the individual effective cross-sections by the number of profiles. Non-composite action is considered. For typical built-up members with common fastener arrangements, this approach can be considered acceptable for local buckling and slightly conservative for distortional buckling (Abbasi et al. 2018; Fratamico et al. 2018; Phan et al. 2021). On the other hand, member global buckling loads are determined twice, with non-composite and fully composite action. The calculations are carried out using the classical formulations for flexural buckling from the corresponding individual or fully compound cross-section properties of the profiles. It is noted that considering fully composite action may lead to an overestimation of the member buckling load. The accuracy of hand calculations for global buckling of built-up columns can be improved by using the formulation recently developed in Rasmussen et al. (2020) and Phan et al. (2021, 2022). However, in the present study it is preferred to move to numerical methodologies, i.e., FSM and GBT (see Sects. 7.4.2 and 7.4.3).

As an example, Table 6 shows the buckling stresses and loads of the 2.5 mm thick channel section. In this table, the rows called 2 × Single and 4 × Single, correspond to the situation of non-composite action; and the other rows below correspond to the situation where composite action is considered. At this point, only preliminary conclusions can be drawn for this section given the approximate nature of the calculation: (1) flexural–torsional buckling governs when the stud consists of a single section; in built-up sections (2) flexural buckling about the z axis governs, if L_bz = L; (3) when the intermediate restraint is considered (L_bz = L/2), flexural buckling about the y axis becomes the governing mode; and (4) the second intermediate restraint (L_bz = L/3) does not seem necessary. Similar conclusions can be derived for the other analysed single and built-up cross-sections.

Table 6 Hand calculation buckling stress and loads for single and built-up 100 × 50 × 20 channel sections with 2.5 mm sheet thickness

The hand calculation approach is applied to the cross-sections in Fig. 6, considering sheet thicknesses from 1 to 2.5 mm. This preliminary study concluded that the thickness needed for the buildings under study should be 2 or 2.5 mm, or even 3 mm. Consequently, only these three values are used in the subsequent calculations and analyses.

7.4.2 FSM approach

In the second phase of the study of the member, the FSM is applied considering the partial composite action of the built-up sections by smearing the stiffness of the fasteners along the column length (Fratamico and Schafer 2014; Abbasi et al. 2018). The CUFSM software is used to model the compound cross-sections. The effect of fasteners is introduced by means of springs between the individual cross-sections, whose axial and shear stiffness is defined from the fasteners stiffness and the distance between them presented in Sect. 7.2: 10 N/mm/mm and 20 N/mm/mm for screw longitudinal spacing of L/3 and L/6, respectively. In the toe-to-toe cross-sections, welding is represented by means of additional FSM elements of the same thickness as the profile’s walls (construction thickness approach Fratamico and Schafer 2014).

When local and distortional buckling stresses derived from an LBA (Linear buckling analysis) of the member are used, the Eurocode 3 procedure for the calculation of the effective area is slightly different from the standard effective width procedure described in Sect. 7.3; paragraph 7.6.1(7) of EN 1993-1-3 (2023) provides guidance in this calculation. In the present study, (1) the minimum local buckling stress of the signature curve derived with CUFSM is used to define the effective width of all cross-section elements; and (2) the minimum distortional buckling stress is used to determine the reduced thickness of the edge stiffeners and the adjacent effective parts of the flanges, which are the elements undergoing distortional buckling.

Member global buckling loads are determined considering simple end supports. Consequently, they are also derived from the CUFSM signature curve. These loads are directly used to determine the member slenderness in a similar way as it is done in the hand calculation approach. It is worth noting that the constrained FSM option is not activated in CUFSM; consequently, the member buckling loads do not correspond to pure member buckling modes. This can result in slightly conservative predictions of the buckling resistance, but they are considered acceptable in the preliminary design framework of the present study (see also comments in Sect. 7.5).

Table 7 displays the buckling stresses and loads resulting from FSM for the 2.5 mm thick 100 × 50 × 20 channel cross-sections with fastener spacing L/3 and L/6.

Table 7 CUFSM buckling stress and loads for single and built-up 100 × 50 × 20 channel sections with 2.5 mm sheet thickness and L/3 and L/6 fastener distance

These results prompt the following remarks concerning the analysis procedures and column behaviour:

• Local and distortional buckling As expected, the local and distortional buckling stresses are different from those obtained by hand calculation (see first columns of Tables 6, 7). Nevertheless, the differences can be considered reasonable given the approximate nature and the limitations of the methods proposed by EN 1993-1-1 (2023) and EN 1993-1-3 (2023). Furthermore, as observed in the literature (Fratamico et al. 2018), it is verified that the effect of fasteners on the local buckling loads is null (see third column of Table 7). The effect on distortional buckling is relatively relevant, but only in those built-up sections where fasteners constrain flange rotations, i.e. nested and 4-pack sections. The increase in buckling loads ranges between 3 and 17% (see fourth column of Table 7). This can be clearly observed in Fig. 7, that shows the ratio of the distortional buckling loads corresponding to the partial and fully composite action with respect to those of non-composite action. In Fig. 7, NC refers to non-composite action, PC L/3 and PC L/6 refer to partial composite actions for fastener distance L/3 and L/6, respectively (except for the welded toe-to-toe section), and FC stands for fully composite action. On the other hand, welding significantly improves the toe-to-toe section’s performance with respect to distortional buckling, but not with respect to local buckling (see Table 7).

• Built-up members consisting of two profiles The flexural buckling loads about the y axis are similar to those obtained by hand when fully composite action is considered. Since the fasteners are not active, it is reasonable to have such similar results. They have just a small influence on the buckling loads due to the constraining effects on the distortional buckling, which is interacting with the member y buckling. Contrarily, their impact on buckling about the z axis of back-to-back cross-sections is relevant, especially when there are no intermediate constraints (L_bz = L). The buckling load increases 17% with respect to the non-composite situation (the 2 × Single case of Table 7). This beneficial effect of the fasteners is offset by the detrimental effect of the interacting distortional buckling when intermediate constraints are used (L_bz = L/2 and L_bz = L/3). It can be seen in Fig. 8a that the interaction of member z buckling, and symmetric distortion can be significant in the studied built-up sections. Concerning the nested section, the effect of fasteners is small on member z buckling loads. Its geometric configuration, with the webs close to the centroidal z axis, does not involve any advantage in this sense. There is only small improvement for L_bz = L/3 due to the effect of fasteners in restraining the distortional mode component interacting with the member z buckling mode. Finally, it is noted that the best option in terms of section efficiency is the toe-to-toe welded solution. All these comments are summarized in Fig. 9, where the ratio of the member z buckling loads corresponding to the partial and fully composite action with respect to those of non-composite action is shown.

• 4-pack built-up section For the buckling about the y axis, CUFSM shows that fasteners cannot fully constrain the buckling modes of the individual Cee profiles. For example, in Fig. 8b it can be observed how the flexural buckling of the whole section is combined with the flexural–torsional and distortional buckling of the individual profiles. This results in low buckling loads, that are not significantly higher than those of the 4 × Single case. As for buckling about the z axis, the use of fasteners involves a significant increase in the buckling loads, from 20 to 60%, but they are still far from those of fully composite action (see Fig. 9).

• Fasteners spacing It is also observed that decreasing the spacing between fasteners from L/3 to L/6 produces a moderate increase of z axis buckling loads in the case of back-to-back built-up sections (maximum 10%); and a relatively significant increase in the case of 4-pack sections (between 13 and 17%).

Fig. 7

Ratios between the distortional buckling loads corresponding to the partial and fully composite actions, and those of non-composite action (100 × 50 × 20 profiles with 2.5 mm sheet thickness)

Fig. 8

Interaction between buckling modes

Fig. 9

Ratios between the CUFSM member z buckling loads corresponding to the partial and fully composite actions, and those of non-composite action (100 × 50 × 20 profiles with 2.5 mm sheet thickness)

7.4.3 GBT approach

The approach presented in Sect. 7.4.2 can be improved by introducing the actual distribution of discrete fasteners in the LBA instead of using smeared properties. The FEM (Finite Element Method) is probably the most powerful tool for accurately dealing with discrete fasteners. However, it is considered to be unpractical for the daily design of this type of structures. Alternatively, various practical methodologies for determining the buckling loads have been recently developed, such as the compound finite strip method (Abbasi et al. 2018; Mahar et al. 2021) or the effective rigidity approach (Rasmussen et al. 2020; Phan et al. 2021, 2022). In the present study, GBT is applied because it allows the numerical model to be created as quickly as with the FSM and, at the same time, explicitly account for discrete fasteners as in FEM. Furthermore, GBT is also used herein to assess the effectiveness of EFGs (End Fastener Groups), which consist of two columns of 8 screws at each end section. The study of this effect cannot be tackled with standard FSM (Fratamico and Schafer 2014; Rasmussen et al. 2020).

The GBT linear buckling analyses have been carried out by means of the formulation described in Bonada et al. (2021). All deformation modes (conventional, natural shear, transverse extension and local shear modes) have been included. Each fastener is directly modelled through three 1-Dimensional linear springs (x, y and z global directions), which connect the nodal displacement (in global coordinates) of the two sectional nodes where the screw is located. Therefore, the axial and shear screw stiffness can be reproduced. The stiffness values are those presented in Sect. 7.2.

The GBT buckling loads are used to determine the corresponding slenderness, buckling reduction factors and final resistances in the same way as in the FSM approach (Sect. 7.4.2). Table 8 displays the GBT buckling stresses and loads for single and built-up 100 × 50 × 20 channel sections with 2.5 mm sheet thickness, and Table 9 exhibits the ratio between such values and those of FSM.

Table 8 GBT buckling stresses and loads for single and built-up 100 × 50 × 20 channel sections with 2.5 mm sheet thickness

Table 9 Ratios between GBT vs FSM buckling stresses and loads for single and built-up 100 × 50 × 20 channel sections with 2.5 mm sheet thickness

Figure 10 contain similar results than Fig. 9, but from GBT.

Fig. 10

Ratios between the GBT member z buckling loads corresponding to the partial and fully composite actions, and those of non-composite action (100 × 50 × 20 profiles with 2.5 mm sheet thickness)

The observation of Tables 8, 9, and Fig. 10 leads to the following remarks:

• The study on the FSM buckling loads in Sect. 7.4.2 shows that the performance of the built-up nested section is rather lower than in the other options; consequently, they are not analysed with GBT and their results are not included in Table 8.

• The GBT member z buckling loads with two intermediate constraints (N_cr,Z with L_b,Z = L/3) are not included in Table 8 because the interaction of member and distortional buckling is strong. This makes identifying the modes and the corresponding buckling loads very difficult. Furthermore, as observed in Sects. 7.4.1 and 7.4.2, the member z buckling mode does not govern the design.

• Table 9 shows a reasonable agreement between the FSM and GBT buckling loads: the mean GBT/FSM ratio is 0.96, and the standard deviation is 0.06. It is observed that in built-up sections, the GBT results are slightly lower than those of FSM. This is attributed to the fact that modelling discrete fasteners decreases the degree of restraint of sectional buckling modes. In this sense, it is noted that the agreement between GBT and FSM is better when fasteners are closer (L/6) and such sectional phenomena are more constrained in GBT.

• The agreement between FSM and GBT supports the comments regarding the behaviour of the built-up sections based on the FSM results presented in Sect. 7.4.2.

• Table 8 and Fig. 10 show that EFGs have a relevant positive effect on the behaviour of built-up sections (Fratamico et al. 2018; Rasmussen et al. 2020). The increase in buckling loads can be up to 25% and 50% for the back-to-back and 4-pack configurations, respectively.

7.5 Stud resistance

The buckling resistance of the investigated built-up sections is determined from the buckling stresses and loads obtained by hand calculation, the FSM and the GBT. However, the study of the feasibility of the cold-formed chord studs is finally based on the FSM buckling values. The hand calculation procedure applied does not allow partial composite action to be considered and can only estimate the studs’ resistance. Furthermore, the GBT results are sufficiently similar to those of the FSM to focus only on the latter and avoid repetitions. Only the built-up sections with EFGs are calculated from GBT buckling results.

For the sake of completeness, hand-calculated and FSM resistances are compared in Table 10 as an example. The table corresponds to 100 × 50 × 20 channel built-up sections with 2.0 mm sheet thickness, made of S350GD steel, without intermediate restraints and L/6 fastener spacing. The results of 2.5 mm channel profiles are not shown because their section is fully effective, which does not allow for assessing the effect of the different buckling stresses on the final effective area. In this sense, it is observed that the effective area determined from the FSM local and distortional buckling stresses is slightly lower than that obtained from the buckling stresses calculated with the formulations of EN 1993-1-3 (2023). On the other hand, the member resistances determined from FSM buckling loads lie between those corresponding to the hand-calculated non-composite and fully composite action, as expected. In the case of toe-to-toe, the FSM resistance is almost the same as the FC hand-calculated value, because welding involves fully-composite action. Contrarily, in the 4-pack option the FSM result is more similar to the NC hand-calculated value. This is due to the factors discussed in Sect. 7.4.2.

Table 10 Effective areas and buckling resistances determined from hand-calculated and FSM buckling stresses and loads

The final buckling resistance of the built-up studs is shown in Figs. 11 and 12. Results are presented for 2.0, 2.5 and 3.0 mm thickness and L/6 fastener spacing. It is noted that the use of L/3 is finally dismissed due to its low efficiency. Before going into the discussion of the feasibility of the chord studs, some preliminary comments on the performance of the built-up sections are included first:

• Increasing the thickness and grade of the steel has a significant positive effect on the ultimate buckling resistance of the studs.

• In general, the strength of 150 × 50 × 20 studs is significantly higher than of 100 × 50 × 20 ones: from 15 to 50% for 4-pack sections, and from 5 to 35% for toe-to-toe sections. However, for back-to-back sections, the strength increase ranges between 0% (or even slightly lower) and 5%; this is due to its higher tendency to suffer from sectional instabilities (see, for instance, the distortional buckling stresses of Table 7).

• The use of an intermediate restraint (L_bz = L/2) is relevant and a key factor in the performance of back-to-back and toe-to-toe built-up cross-sections because it constraints member z buckling, which is the weak buckling axis and the one under the effects of the fasteners’ partial composite action. This restraint is unnecessary in 4-pack cross-sections where member z buckling is not governing.

• The effect of EFGs in back-to-back sections is significant when there are no intermediate restraints and the member z buckling effects are relevant. For instance, the increase in resistance in unrestrained channel built-up studs ranges from 11 to 21%, which is an improvement similar to that observed in experiments (Fratamico et al. 2018).

• It was expected that the EFGs would improve the behaviour of 4-pack sections with respect to member y buckling. Intermediate restraints cannot be used to constraint buckling about the y axis and, as a consequence, the only way to get better resistances is by adding fasteners. In the end, however, the effect of EFGs is limited, with improvements ranging from 6 to 9% in 100 × 50 × 20 channel 4-pack; and from 1 to 3% in 150 × 50 × 20 channel 4-pack. In Table 9 it can be seen that EFGs have a significant effect on member z buckling, but it is lower in the case of member y buckling.

• The stud resistances have been determined from member buckling loads of modes showing high interaction between sectional and member instabilities, especially in the case of 150 × 50 × 20 studs with intermediate restraints (L_bz = L/2). Consequently, the resistance of the built-up member is doubly penalized: through the reduction in the effective area, and the “member” buckling load corresponding to buckling modes involving several coupled instabilities. This effect is more significant when the studs with EFG are calculated, because the interaction between modes is higher in GBT buckling analyses, as discussed in Sect. 7.4.3. Consequently, there are some strength values of EFG studs that resulted in being similar or lower than those of the same studs without EFG, which have been determined from FSM member buckling loads. These cases are not considered in the discussion of the two previous comments. This aspect is to be improved in future research.

• Finally, the most important remark is that the maximum axial capacity of the chord studs analysed (Fig. 6f) is 747 kN.

Fig. 11

Buckling resistance (kN) of the 100 × 50 × 20 built-up channel sections

Fig. 12

Buckling resistance (kN) of the 150 × 50 × 20 built-up channel sections

8 Main results of the global structural analyses of the prototype buildings

This section presents the main results of the iterative global structural analyses of the prototype buildings (Sects. 5 and 6), and compares them with the axial capacity of the most demanded structural elements, namely the chord studs (Sect. 7.5). Table 11 displays the main results of the global structural analyses of the 5, 7 and 10-storey prototype buildings, respectively.

Table 11 Main results of the global structural analyses for the prototype buildings

In Table 11, ${N}_{\mathrm{Ed}}^{\mathrm{max}}$ is the maximum design value of the demanding axial force in the chord studs, and “Comb.” refers to the load combination to which it corresponds (Eq. (1)); obviously, subindexes x and y denote the horizontal directions (Fig. 4). The values of ${N}_{\mathrm{Ed}}^{\mathrm{max}}$ and ${N}_{\mathrm{Ed}}^{\mathrm{max}}$ that exceed the axial capacity of the chord studs (Sect. 7.5) are highlighted, as they show an insufficient capacity.

Table 11 shows that the 5, 7 and 10-storey buildings withstand moderate ground motions (S_α,475 = 0.5 g), and 5, and 7-storey buildings also resist high ones (S_α,475 = 0.75 g); finally, none of the buildings can resist earthquakes with S_α,475 = 1 g. Two-component built-up chord studs (Fig. 6c, e) suffice in the 5-storey building under moderate seismicity; conversely, packs of four (Fig. 6f) are needed in the other cases.

In Table 11, most of the axial force ${N}_{\mathrm{Ed}}^{\mathrm{max}}$ is contributed by the seismic action (Eq. (1)) in virtually all the cases; this indicates that there is a certain risk of uplift, and hold-down anchors might be necessary.

Comparison between the demanding forces in Table 11 and the capacities in Figs. 11 and 12 provides the demand-to-capacity ratios. In this sense, Table 12 displays the required sections for the most demanded (first storey) chord studs.

Table 12 Required section for the most demanded chord studs (Fig. 6)

This paragraph describes the characteristics of the main structural members other than the chord studs. Intermediate studs are made of single profiles in the upper storeys, and nested, back-to-back, or toe-to-toe sections in the bottom ones. Strap braces are made of steel grade S 250 GD; for the 5-storey building the required area in the first storey is 950 mm² for S_α,475 = 0.5 g, and 2400 mm² for S_α,475 = 0.75 g. For the 7-storey building the area is 1000 mm² for S_α,475 = 0.5 g and 2550 mm² for S_α,475 = 0.75 g. For the 10-storey building such value is 1500 mm² (S_α,475 = 0.5 g).

9 Conclusions

This paper studies the seismic boundaries of application of structures made of customary light-gauge steel framing panels with flat strap braces (dissipative elements) and several types of built-up cold-formed steel chord studs; in this context, “customary” refers to ordinary steel (yield point not exceeding 350 MPa), thin plates (not more than 3 mm), and rather thin walls (slightly above 100 or 150 mm thickness). Three prototype buildings representative of the low to mid-rise ranges (5, 7 and 10 storeys) are designed according to the forthcoming European seismic design code, by accounting for Ultimate and Serviceability Limit States. Three seismicity levels have been considered, from moderate (peak ground acceleration 0.2 g) to high (0.3 and 0.4 g); in all the cases, soil type is B. The chord studs are designed according to European regulations by considering three approaches to determine the buckling loads: closed-formed expressions based on classical buckling theory, the finite strip method, and the generalized beam theory.

The major conclusions of this research are:

• The most critical structural elements are the chord studs of the lowest levels. Such members are connected to the dissipative elements (strap braces); therefore, they must be protected against brittle buckling failure by capacity conditions. Being limited to pure cold-formed steel sections, this proves to be a strong limitation for the seismic design of low to mid-rise buildings.

• The 5, 7 and 10-storey buildings withstand moderate ground motions (0.2 g), 5 and 7-storey buildings also high ones (0.3 g), and none of the buildings resist the highest earthquake (0.4 g).

• The performed research corroborates that, except for low seismicity, high capacity bracing panels are required: thick walls (150 mm), four component built-up chord studs, rather thick-walled profiles (3 mm), moderate to short fastening spacing (minimum L/6), and one intermediate in-plane restraint.

• The fundamental periods of the buildings analysed are determined by neglecting the stiffening effect of the non-structural components (cladding and partitioning walls); they are significantly longer than those arising from the empirical expressions in the code. This circumstance makes the code limitation of the period to two times the aforementioned empirical one overconservative; this limitation has been ignored in this study.

• Built-up sections undergo interaction between sectional and member instabilities (more than in single sections). This issue, together with the fasteners partial action, causes a lower performance than sections with full composite action.

• This research shows that the generalized beam theory is helpful for calculating buckling loads, allowing efficient modelling, addressing all relevant buckling phenomena, and accurately considering the fasteners partial composite action (in complex situations, such as the 4-pack sections with End Fastener Groups). It overcomes the limitations of the manual calculation procedures and the finite strip method. Furthermore, it may also be an excellent tool to deal with the modes interaction, due to its capacity to isolate modes (or groups of).

Further research includes eliminating the customary condition; this implies higher grade steel, thicker plates, and larger profiles. As well, solutions to improve the performance of 4-pack section will be investigated. Finally, more detailed building designs will be performed.